Modeling Carbonation Depth in Hardened Alkali-Activated Slag Under Accelerated Curing: A Multi-Physics Finite Element Approach

Abstract

This study develops a numerical model based on a multi-physics coupled finite element method to predict the carbonation depth of hardened alkali-activated slag under accelerated carbonation curing conditions. Drawing on existing literature data, the chemical composition and porosity of alkali-activated slag at different ages were determined under non-carbonation conditions, supported by thermodynamic and kinetic analyses of alkali activation reactions. A differential equation governing CO₂ diffusion—incorporating diffusion rate, diffusion coefficient, carbonation reaction rate, and related parameters—was established using Fick’s second law. The influence of humidity and carbonation degree on the reaction rate was quantified, and a correlation between carbonation degree and porosity was derived through thermodynamic analysis. These equations were solved numerically in a two-dimensional domain to predict carbonation depth over time. The results demonstrate that the proposed model, using only raw material composition and curing conditions, achieves reasonable accuracy in predicting carbonation depth.

1. Introduction

The carbonation of cement-based materials is a critical research area due to its dual implications for durability and sustainability. In reinforced concrete structures, carbonation reduces the alkalinity of the concrete cover, degrading the passive film on steel reinforcements and accelerating corrosion, thereby compromising structural longevity [1]. While conventional concrete absorbs carbon dioxide (CO₂) from the atmosphere at a negligible rate under natural conditions, recent advancements in carbonation curing and CO₂ utilization technologies have enabled cementitious materials to play a more active role in carbon reduction [2,3]. For instance, accelerated carbonation curing and the incorporation of CO₂ during material processing can significantly enhance CO₂ sequestration, offering a promising pathway to mitigate greenhouse gas emissions [4]. Unlike ordinary Portland cement (OPC), which relies solely on gaseous CO₂ absorption for carbonation, alkali-activated materials (AAMs) exhibit two distinct carbon sequestration mechanisms: (1) absorption of gaseous CO₂ and (2) the use of carbonates as alkali activators. However, carbonate-based activators can impede early-age strength development [5]. Given the prominence of alkali-activated slag (AAS) as a high-performance AAM [6,7], this study focuses on gaseous CO₂ absorption as the primary carbonation pathway for AAS.

Extensive research has been conducted on carbonation in OPC systems, encompassing theoretical, experimental, and numerical approaches. For instance, Reddy [8] employed thermodynamic modeling to analyze phase transformations during carbonation, while Greve-Dierfeld [9] reviewed the influence of environmental factors (e.g., humidity, temperature) on carbonation kinetics in blended cements. Shi [10] numerically simulated carbonation in loaded concrete, correlating stress levels with carbonation depth. In contrast, the carbonation behavior of AAMs remains less systematized, owing to the variability in precursor compositions and activators. Divergent findings persist in the literature: some studies report that carbonation enhances AAM compressive strength [11], while others observe the opposite. Similarly, Zhao [12] attributed reduced carbonation resistance to higher calcium content, whereas Rashad [13] suggested the contrary. Discrepancies also exist regarding porosity evolution—Xie [14] found increased porosity after carbonation, while Azar [15] reported densification. These contradictions stem from the complex, coupled processes governing AAM carbonation, including alkali activation, CO₂ diffusion, reaction kinetics, and moisture transport, all influenced by material composition and curing conditions.

For AAS, carbonation involves a multi-stage process. Early-age non-carbonated curing ensures sufficient alkalinity for reaction product formation, while subsequent accelerated carbonation curing introduces CO₂-driven physicochemical changes. The latter includes CO₂ diffusion, dissolution in pore solution, reaction with hydroxyl ions to form carbonates/bicarbonates, and their subsequent interaction with alkali-activated products (e.g., calcium-alumino-silicate-hydrate, i.e., C-A-S-H). Key factors influencing CO₂ transport include slag particle size distribution, pore tortuosity, and saturation degree. Volume changes during solid-phase reactions and water consumption/generation further alter porosity and saturation, complicating the system.

To evaluate carbonation resistance, phenolphthalein indicator tests are widely adopted [16,17,18,19]. After accelerated carbonation, the specimen’s cross-section is sprayed with phenolphthalein; regions with pH < 9.5 remain colorless (carbonated), while uncarbonated zones turn purple-red. The depth of the colorless region serves as a proxy for carbonation resistance.

This study proposes a novel multi-physics finite element model to predict carbonation depth in hardened AAS under accelerated curing, addressing critical gaps in existing research. Unlike previous studies that rely on empirical or simplified approaches, our framework integrates thermodynamic analysis and kinetic modeling to systematically capture the coupled physicochemical processes governing carbonation. Specifically, the model uniquely combines thermodynamic analysis, kinetic modeling, and validation against experimental data.

This approach eliminates the need for extensive experimental trials, reducing time and resource consumption while enabling tailored assessments of AAS formulations. By providing a predictive tool for carbonation depth, the study advances the understanding of carbonation mechanisms in AAS and offers practical insights for optimizing material design, enhancing durability, and maximizing the potential of carbonation curing and CO₂ utilization technologies for carbon reduction.

2. Methodology

To accurately predict the carbonation depth of alkali-activated slag (AAS), mathematical models were employed to describe the physical and chemical changes of AAS at different stages of non-carbonation curing and carbonation curing. During the non-carbonization curing stage, numerical simulation methods were used to predict the phase composition and porosity of alkali-activated slag material products based on the chemical composition of raw materials, slag particle size distribution, curing temperature, and curing age. The diffusion process of CO₂ in AAS during the carbonation curing stage is described by Fick’s second law equation with a source term. Based on this, the AAS carbonation reaction kinetics equation was employed to describe the relationship between carbonation rate, carbonation degree, and carbon dioxide concentration, and combined thermodynamic modeling to determine the relationship between carbonation reaction degree and porosity.

2.1. Reaction Degree Model

According to Zuo’s [20] research, in the AAS reaction, when NaOH solution is used as an activator, the product grows continuously with slag as the nucleation site, and when Na₂SiO₃ solution is used as an activator, the product uses slag and soluble silicon in the solution as nucleation sites. Therefore, a partial differential equation can be derived to describe the reaction rate of alkali-activated slag materials with respect to pH value, water content, and other parameters, as shown in Equation (1).

$${\displaystyle \frac{d\delta }{dt}}=k_0\times F_T\times F_w\times {[{({\displaystyle \raisebox{1ex}{${\delta }_{tr}$}\!\left/ \!\raisebox{-1ex}{${\delta }_{shell}$}\right.})}^{{\beta }_1}]}^{\lambda }\times F_{pH,slag}$$

(1)

where dδ denotes the penetration depth of slag particles over the time interval dt, while k₀ is the alkali-activation rate constant. F_T represents the influence of temperature on the reaction rate, with its expression in Equation (2). F_w denotes the effect of water content on the reaction rate. When the initial water content w₀ exceeds the water requirement w_n for complete slag reaction, F_w = 1. When the initial water content w₀ is less than required, F_w is the ratio of remaining water w_r to required water w_n, i.e., F_w = w_r/w_n. The term [(δ_tr/δ_shell)^β₁]^λ represents the effect of the reaction product shell on reaction rate. For sodium hydroxide-activated slag, it is assumed that the reaction products uniformly coat the surface of slag particles. Based on the volume ratio of the reaction products to the slag, the thickness of the product shell can be derived. When the shell thickness is less than the critical thickness δ_shell, the product shell does not affect slag dissolution, and λ = 0. When δ_shell exceeds δ_tr, the product shell hinders slag dissolution, and λ = 1. β₁ is a calibration parameter. F_{pH, slag} represents the effect of pH and slag composition on the dissolution rate of slag, with its expression in Equation (3).

$$F_T=\exp \{{\displaystyle \frac{{\mathrm{E}}_a}{R\times 298}}-{\displaystyle \frac{{\mathrm{E}}_a}{R\times \left(273+T\right)}}\}$$

(2)

where E_a is the chemical reaction activation energy, T is the temperature, and R is the ideal gas constant.

$$F_{p\mathrm{H},\mathrm{slag}}=V_{Si}\times {10}^{pH(0.0155{\displaystyle \frac{NBO}{T}}+0.0727)+0.6199{\displaystyle \frac{NBO}{T}}-9.0309}$$

(3)

where V_Si is the volume of slag containing 1 mole of silicon (in cubic centimeters), while NBO/T is the ratio of the non-bridging oxygen atoms to oxygen atoms in tetragonal coordination. The formula for calculating NBO/T is shown in Equation (4),

$$NBO/T={\displaystyle \frac{2[CaO+MgO+K_{2}O+N{a}_{2}O+3f_{Fe}\ast F{e}_2{O}_3+3f_{Al}\ast A{l}_2{O}_3-(1-f_{Fe})\ast F{e}_2{O}_3-(1-f_{Al})\ast A{l}_2{O}_3]}{Si{O}_2+Ti{O}_2+2(1-f_{Fe})\ast F{e}_2{O}_3+2(1-f_{Al})\ast A{l}_2{O}_3}}$$

(4)

When a mixed solution of sodium hydroxide and sodium silicate is used to activate slag, reaction products form with either slag particles or soluble silicon as nucleation sites. The proportion of products nucleated from soluble silicon is positively correlated with the concentration of sodium silicate solution, as shown in Equation (5),

$$\mathrm{y}=1-\exp (-ax)$$

(5)

where y is the proportion of products nucleated from soluble silicon, while x is the concentration of sodium silicate solution, and a is the calibration parameter.

The overall reaction degree can then be calculated using Equation (6).

$$\alpha \left(t\right)={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^k\left[\frac{4}{3}\pi r_i^3-\frac{4}{3}\pi {\left(r_i-{\delta }_{in,r_i}\right)}^3\right]\ast n_i}{{{\displaystyle \sum }}_{i=1}^k\frac{4}{3}\pi r_i^3\ast n_i}}=1-{\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^k{\left(r_i-{\delta }_{in,r_i}\right)}^3\ast n_i}{{{\displaystyle \sum }}_{i=1}^k{r}_i^3\ast n_i}}$$

(6)

where k is the type of slag particles, n_i denotes the number of particles with a radius of r_i, and δ_in,ri represents the penetration depth.

2.2. Carbonation Depth Model

2.2.1. Carbon Dioxide Diffusion

Based on Yu [21] and Mi’s [22] research, Fick’s second law with a source term was employed to model the CO₂ diffusion within AAS, as presented in Equation (7).

$${\displaystyle \frac{\mathit{\partial }C}{\mathit{\partial }t}}=\nabla (D\nabla C)-R_C$$

(7)

where C represents the CO₂ molar concentration per unit volume, D is the diffusion coefficient, and R_C indicates the rate of CO₂ consumption per unit volume and per unit time. It should be noted that the product volume includes the volume of the solid, liquid, and gas phases.

Through regression analysis of extensive empirical data [23], the CO₂ diffusion coefficient can be obtained. Thiery [24] derived an empirical formula to relate the CO₂ diffusion coefficient in unsaturated porous media to saturation and porosity, as shown in Equation (8).

$$D_0=1.6\times {10}^{-5}\times n^{4/3}\times {(1-S)}^{10/3}$$

(8)

where n represents porosity, and S represents saturation. Based on the relationship outlined in Equation (9) [25], which links the CO₂ diffusion coefficient at different temperatures to its value at ambient temperature, the relationship between the CO₂ diffusion coefficient, porosity, and saturation across various temperatures can be established.

$$\ln ({\displaystyle \frac{D_T}{D_0}})=-2.35\times {10}^3({\displaystyle \frac{1}{T}}-{\displaystyle \frac{1}{25}})-3\times {10}^{-4}$$

(9)

The GEMS3 software was utilized in combination with the Cemdata18 and MINES thermodynamic databases to model the carbonation reactions in AAS; the relationship between the consumption of alkali-activated reaction products and porosity and pore saturation is therefore derived.

2.2.2. Carbonation Reaction

In modeling the carbonation reaction, it is assumed that the dissolution of CO₂ in water, its reaction with water to form carbonic acid, and the dissociation of carbonic acid into carbonate and bicarbonate ions occur simultaneously. Equation (10) presents the relationship between the CO₂ concentration within the specimen and its concentrations in the gas phase and aqueous solution.

$$c=c_g(n-nS)+c_{w}nS$$

(10)

Based on Henry’s law, the CO₂ molar concentration relationship between the gas and liquid phases at standard temperature and pressure is given in Equation (11) [26]. By combining Equations (10) and (11), the relationship between CO₂ concentration within the specimen and that in the gas phase can be derived, as shown in Equation (12).

$$C_w=0.8317C_g$$

(11)

$$C_w=0.8317C{\displaystyle \frac{1}{n(1-0.1683S)}}$$

(12)

Following the carbonation reaction kinetics model proposed by Saetta [27] for Portland cement, a carbonation reaction kinetics equation for AAS was established in this study, as presented in Equation (13).

$${\displaystyle \frac{\mathit{\partial }{R}_p}{\mathit{\partial }t}}=k_C\times f_1(S)\times f_2(C_w)\times f_3(R_p)\times f_4(T)$$

(13)

where R_p denotes the ratio between the volume of alkali-activated reaction products participating in the carbonation reaction and their volume at the onset of carbonation, while k_c is the carbonation coefficient. f₁(S) represents the influence of saturation on the carbonation reaction rate, with f₁(S) assumed to be equal to the saturation level S. f₂(C_w) indicates the effect of CO₂ concentration in the pore solution on the carbonation rate, with f₂(C_w) assumed to equal C_w. f₃(R_p) captures the effect of carbonation reaction extent on the reaction rate, and the specific form of f₃(R_p) is provided in Equation (14).

$$f_3(R_p)=1-R_p$$

(14)

Due to the limited research on the activation energy of carbonation reactions in AAS, the activation energy of the carbonation reaction in AAS is assumed to be comparable to that of the carbonation reaction in cement. The expression for f₄(T) is thus proposed as shown in Equation (15) [21].

$$f_4(T)=\exp ({\displaystyle \frac{48096}{296R}}-{\displaystyle \frac{48096}{RT}})$$

(15)

The carbonation coefficient k_c represents various factors that are not directly modeled, and its accurate determination is essential for the numerical modeling of carbonation in cementitious materials [28]. Given the known initial chemical composition, porosity, and carbonation curing conditions of AAS, the carbonation coefficient k_c is the sole undetermined parameter for modeling carbonation progression. In this study, it is assumed that the carbonation depth—defined as the distance from the specimen’s surface to the fully carbonated front (100% carbonation)—matches the colorless region depth seen when phenolphthalein is applied to the cross-section of the AAS. Based on Nguyen’s [29] experimental findings, a trial-and-error approach was applied to estimate the carbonation coefficient. By iteratively comparing predicted carbonation depths to measured values, an optimal carbonation coefficient value was determined. This process ultimately yielded an estimated coefficient value of k_c = 2 × 10⁻⁷.

2.3. Experimental Data

This study references the parameter values from Gao’s [30] research and determines the calibration coefficient a through iterative calculations based on experimental data from Ben Haha’s [31] research. Values of the parameters used in this study are shown in Table 1 and Table 2.

Table 1. The proportion of slag consumption and hydroxide ion consumption.

Symbol	Meaning	Value
k0	Alkali-activation rate constant	0.00009
β1	Calibration parameter	1
Ea	Reaction activation energy	58 kJ/mol
fFe	Fraction of Fe2O3 acting as a network breaker	0.91
fAl	Fraction of Al2O3 acting as a network breaker	0.91
δtr	Critical thickness	0.188 μm
a	Calibration parameter	0.6

Table 2. Accelerated carbonation conditions.

Symbol	Meaning	Value
C	CO2 concentration	1%
T	temperature	Above 31 °C
RH	humidity	60% RH
t	Exposure time	28 day

3. Results and Discussion

3.1. Verification of the Carbonation Reaction Degree

To validate the accuracy of the predicted reaction degree, experimental data from Haha’s study [32] were utilized. Since Haha’s study provided only the specific surface area of the slag without detailing the particle size distribution, this study assumed a Rosin–Rammler distribution for slag particle sizes, employing a typical slag particle size distribution in the prediction model. The predicted reaction extent was calculated using the chemical composition of the alkali-activated slag (AAS), slag particle size distribution, and curing temperature as inputs. As shown in Figure 1, the comparison between the predicted and experimental values for slag reaction degree yielded a coefficient of determination (R²) of 0.73, indicating reasonable agreement.

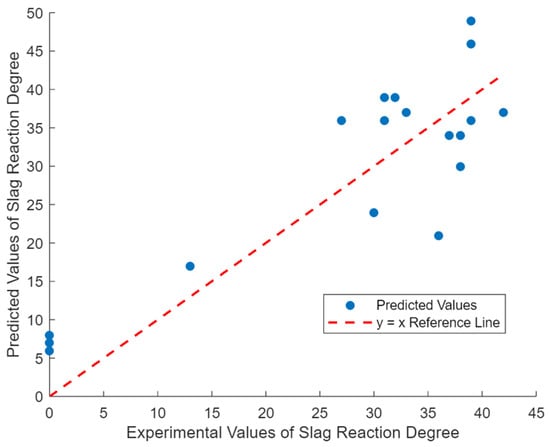
Figure 1. Experimental and predicted values of AAS reaction degree.

Additionally, thermodynamic modeling was used to calculate the volume of solution within the specimen, assuming that the solution volume equals the pore volume. This allowed for the estimation of the pore volume. Figure 2 compares the predicted porosity with experimentally measured values, achieving an R² of 0.82, further validating the model’s accuracy in predicting porosity.

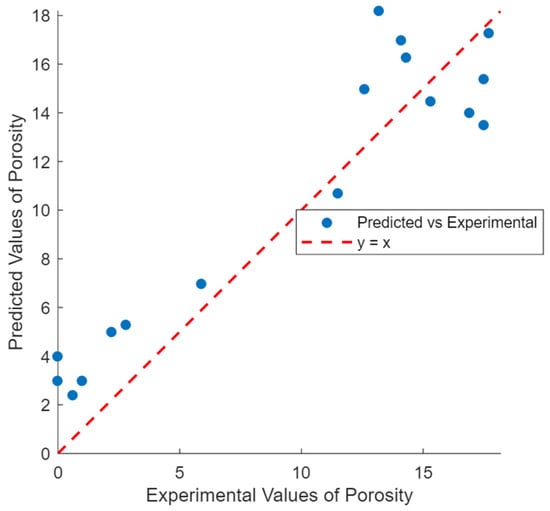
Figure 2. Experimental and predicted values of porosity.

3.2. Verification of the Carbonation Depth Predication

The carbonation depth prediction model was validated using experimental data from Nguyen’s study [33]. The initial chemical composition of AAS and the slag particle size distribution were provided as inputs to the model. The model predicted the proportions of reaction products, porosity, and pore saturation in the AAS specimens at 28 days. Using these predictions, the carbonation depths of the specimens at various ages were calculated. Figure 3 demonstrates the comparison between the predicted and experimental carbonation depths, with the model achieving an R² of 0.97, indicating high predictive accuracy.

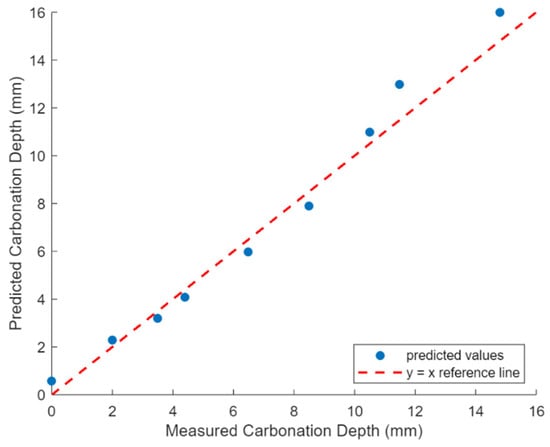
Figure 3. Comparison of experimental and predicted carbonation depth.

3.3. Model Validation and Limitations

The model’s predictions were validated against experimental data from independent studies, demonstrating strong agreement for reaction degree, porosity, and carbonation depth. However, certain limitations should be noted: (1) The model assumes a Rosin–Rammler distribution for slag particle sizes, which may not capture the full variability in particle size distributions across different slags. (2) The assumption that solution volume equals pore volume may oversimplify the complex relationship between pore structure and solution distribution in AAS. (3) The model relies on input parameters such as chemical composition and curing conditions, which may vary in practice and affect accuracy. (4) The validation was limited to specific datasets, and the model’s performance under broader conditions (e.g., different curing environments or slag sources) remains to be tested.

4. Conclusions

This study consolidates previous findings on the reaction kinetics of alkali activation and carbonation in alkali-activated slag (AAS) to develop a numerical model for predicting carbonation depth. The model incorporates input parameters such as the chemical composition of raw materials, particle size distribution of slag, curing conditions, and time, achieving satisfactory accuracy in its predictions. While the model is specifically applied to AAS, its framework is adaptable to other types of alkali-activated binders, offering a valuable tool for evaluating the carbonation resistance of alkali-activated materials (AAMs) without extensive experimental testing. This capability facilitates the broader application of AAMs in practical engineering contexts.

However, discrepancies in predicted carbonation depth were observed and are largely attributable to the following factors:

(1)

Moisture Evaporation: The effect of moisture evaporation on the reaction process during both non-carbonation and carbonation curing stages was not accounted for.

(2)

Crack Formation: The impact of cracks within the AAS specimens on the diffusion coefficient of carbon dioxide was omitted.

(3)

Pore Tortuosity: The influence of pore tortuosity, which affects the diffusion path and the effective diffusion coefficient of carbon dioxide, was not considered.

(4)

Pore Structure: The ratio of closed to open pore volumes, which affects gas permeability, was disregarded.

(5)

Drying Shrinkage: The influence of drying shrinkage on the porosity of the specimen was not included in the analysis.

To improve the accuracy and applicability of the model, some areas such as incorporating moisture evaporation, crack formation and propagation, pore tortuosity and structure, drying shrinkage effects are recommended for further investigation. By addressing these limitations and incorporating the suggested improvements, the model can be refined to provide more accurate and reliable predictions, ultimately enhancing the understanding and practical application of AAMs in carbonation-prone environments.