An Improved Van Genuchten Soil Water Characteristic Model Under Multi-Factor Coupling and Machine Learning-Based Parameter Prediction

Abstract

Accurately constructing a soil–water characteristic curve (SWCC) model that accounts for the combined effects of multiple factors is of great significance for in-depth understanding of the physical and mechanical behaviors of soils in complex environments. Based on the van Genuchten (vG) model, this study systematically analyzed the effect of the coupling mechanism of void ratio, temperature, and salinity on SWCC. An SWCC model capable of characterizing multi-factor coupling effects was established by incorporating multi-factor influence terms. Fitting verification with experimental data demonstrates that the proposed model can effectively depict soil water retention characteristics under the combined action of multiple factors. Furthermore, parameter sensitivity analysis clarifies the influence laws of each model parameter on the air entry value and the slope of the transition segment of SWCC. To address the challenge of cumbersome determination of model parameters, a parameter prediction method based on the Bayesian regularized neural network (BRNN) was proposed. By training a large volume of SWCC experimental data under multi-factor conditions, effective prediction of model parameters was achieved, with the input being the basic physical properties of soil and environmental variables and the output being the target model parameters. Considering that the influence of salinity introduces additional parameters, the training set was divided into two scenarios (saline and non-saline conditions) for separate modeling to enhance the pertinence and accuracy of parameter prediction. Prediction results indicate that the proposed method exhibits reliable parameter prediction capability, and its prediction accuracy is mainly influenced by the quantity and quality of training data.

1. Introduction

The soil water characteristic curve (SWCC) is a curve that describes the relationship between suction and saturation or water content in unsaturated soil, and it is also a key function used to describe the microscopic connections between different phases of unsaturated soil [1]. It can be used to quantitatively analyze the characteristics of interaction between water and air in unsaturated soil and then study the strength, hydraulic conductivity, and deformation of unsaturated soil [2,3]. In general, suction increases with decreasing saturation, and the shape of the SWCC varies for different types of soil. The SWCC is generally represented in semi-logarithmic coordinates and can be roughly divided into three regions—the boundary effect zone, transition zone, and unsaturated residual zone [4,5] as shown in Figure 1. Taking the drying process as an example, the matric suction in the capillary zone starts from 0 and reaches the air entry value, indicating the beginning of the drying process. The air entry value can be taken as the intersection of the horizontal line at saturation and the slope of the curve. As the drying process progresses, the suction is already at a high value near the residual moisture content. Further drainage is then impossible.

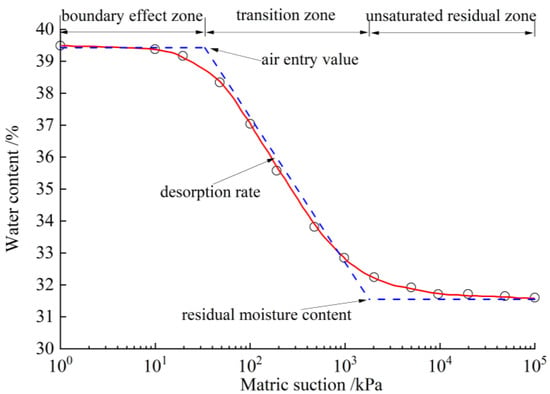
Figure 1. Schematic diagram of the SWCC.

SWCC equations are used, given the physical difficulties of obtaining the SWCC completely experimentally. In addition, these equations make it easier and more practical to use the experimental data collected in numerical models. By fitting experimental data, the mathematical form of SWCC can be derived, such as the widely used FX model [6] and the vG model [7]. In geotechnical engineering in complex environments, such as the stability assessment of buffer layers in deep geological disposal of high-level radioactive waste [8], ecological restoration in saline soil areas [9], and the safety of urban solid waste isolation [10], soils are generally subject to the coupled effects of multiple physical fields, including dynamic evolution of pore structure, fluctuations in temperature gradients, and variations of pore water chemical fields. Consequently, the morphology and parameters of SWCC undergo significant restructuring.

In such cases, traditional SWCC models that only consider a single suction factor can no longer meet the demand for accurate prediction of unsaturated soil properties in engineering design. There is an urgent need to establish a theoretical framework of SWCC integrating multi-field effects and efficient methods for parameter acquisition [11,12,13]. Therefore, some scholars have also explored the morphology and variation patterns of SWCC in unsaturated soil under the influence of this multi-factor coupling effect to solve environmental engineering problems [14,15]. For example, the deformation of the soil skeleton can affect the SWCC of unsaturated soil [16], because the deformation affects the pore structure of the soil, which in turn affects the position and shape of the SWCC. There are currently two main methods for establishing SWCC that consider deformation effects [17,18]. One is to express the air entry value in the SWCC as a function of porosity or volume variation, thereby reflecting the influence of deformation on soil water characteristics. Another approach is to establish an SWCC model considering deformation characteristics based on experimental results and theoretical analysis.

In the study of the multi-field coupling characteristics of unsaturated soil under the influence of temperature, it is essential to study the influence of temperature on the SWCC. Elkehsky (2011) [19] analyzed the influence of temperature, plasticity index, and other parameters on the SWCC based on experimental data, and they found that there is an inverse relationship between temperature and suction, with the influence of temperature being more pronounced at lower saturation levels (<20%). Wang et al. (2014) [20] divided pore water into free water, weakly bound water, and strongly bound water based on the internal structure of soil. When heated, weakly bound water converts to free water, resulting in changes in the SWCC. Generally, based on commonly used SWCC models (such as in a classical version of the van Genuchten model, where the temperature is not considered), the influence of temperature on suction is considered, or a temperature effect factor is added to reflect the influence of temperature on the SWCC [21,22]. Meanwhile, the presence of salt in pore solutions can change the interaction between soil and water, thereby altering the microstructure and water retention properties of the soil [23]. Therefore, some scholars have studied the water retention characteristics of soil at different salinity levels. The influence of salinity on the soil water characteristic curve is closely related to the mineral composition of the soil, with soil containing more montmorillonite mineral components being more affected. However, only a few scholars have made preliminary attempts at an SWCC model considering the influence of salinity [13,24].

Based on the current literature, there is a wealth of research on the SWCC taking into account factors such as void ratio, temperature, and salinity. However, most of these discussions are conducted from a single-factor perspective, and there are relatively few research reports on the coupling effect of void ratio, temperature, and salinity on the SWCC; there is a particular lack of research on the primary and secondary positions of different influencing factors. Moreover, although corresponding fitting equations have been established for describing SWCC, obtaining SWCC through experiments and curve fitting creates both time-consuming and uneconomical issues. Therefore, some scholars have attempted to use data mining methods to construct SWCC prediction models based on machine learning methods, thereby transforming the determination of SWCC into a simple problem of obtaining soil parameters and environmental factors [25,26,27]. Several models have been developed for predicting the SWCC. Artificial neural networks (ANNs), which are machine learning systems based on biological neural networks, are among the techniques used for SWCC prediction [28,29]. Da Silva et al. (2023) [30] analyzed the main machine learning algorithms used to build a pedotransfer function and found that ANNs had a large advantage over other methods. Pereira et al. (2025) [31] have even provided a detailed account of the challenges faced by ANNs in SWCC prediction, thereby offering a reference for future research. However, little work has been carried out on SWCC prediction under the influence of factor coupling. On the one hand, this may be due to the limited amount of involved experimental data; on the other hand, there are no suitable models that reflect soil–water characteristics under the influence of multiple factors.

In view of this, this paper establishes an SWCC mathematical model that can reflect the effects of void ratio, temperature, and salinity by introducing relevant influencing factors based on existing SWCC models. Meanwhile, through statistical analysis of experimental data from the literature, machine learning methods are used to conduct sensitivity analysis between various influencing factors and model parameters. Thus, a physics–data fusion-driven SWCC prediction model is developed. Furthermore, a fully data-driven SWCC prediction model considering multiple factors is also developed based on machine learning methods for training a large amount of SWCC experimental data under different conditions. The prediction ability of the two models is verified by comparison with the experimental data.

2. SWCC Model Under Multi-Factor Coupling

2.1. Establishment of the SWCC Mathematical Model

The expression of the commonly used vG model is as follows:

$$s_r={\left[1+{\left({\displaystyle \frac{s}{a}}\right)}^n\right]}^{-m}$$

(1)

where S_r is the effective degree of saturation, s is matric suction, a is generally believed to be related to the air entry value, n is related to the slope of the soil water characteristic curve, and m is related to the asymmetry of the curve; they are all fitting parameters. For the drying and wetting curves, the values of a, n, and m are also different.

Experimental studies have found that both deformation and temperature have an impact on SWCC. Some scholars [32,33,34] have proposed SWCC models that consider the effects of deformation or temperature based on the vG model. For example, Gallipoli et al. (2003) [32] proposed an SWCC model considering deformation effects based on the vG model by fitting experimental data. The expression is as follows:

$$s_r={\left[1+{\left(as\right)}^n\right]}^{-m}$$

(2)

where $a=\varphi {\left(v-1\right)}^{\phi }$, v is the specific volume, and n, m, $\varphi$, and $\phi$ can be obtained through fitting.

Tarantino (2009) [34] found through experimental research that there is a power function relationship between pore water content e_w and suction s, i.e., $e_w=a_1{s}^{b_1}$, especially in the high suction range, where a₁ and b₁ are related to the intercept and slope of the relationship curve, respectively. Similarly, based on the vG model, the expression for SWCC considering density effects is given as

$$s_r={\left\{1+{\left[{\left({\displaystyle \frac{e}{a_1}}\right)}^{1/b_1}s\right]}^n\right\}}^{-b_1/n}$$

(3)

where a₁ and b₁, are two parameters associated with the intercept and slope of the straight line interpolating experimental data in plane ln(s) − ln(e_w); e is the void ratio; n is the fitting parameter; and m = b₁/n, which is the same as m in the vG model.

Actually, Equation (3) is a modification based on the vG model, which takes into account the influence of void ratio on the SWCC. Moreover, it can be seen that the void ratio has a significant influence on soil–water characteristics. With the increase in void ratio, the water-holding capacity of the soil will show a certain degree of decrease, which is also the result presented by another experiment [34].

Grant and Salehzadeh (1996) [33] proposed a model with which to describe the relationship between matric suction and temperature. Zhou et al. (2014) [11] introduced it into the vG model and presented the expression of SWCC considering the influence of temperature, as follows:

$$s_r={\left[1+{\left({\displaystyle \frac{b_2+T_0}{b_2+T}}{\displaystyle \frac{s}{a}}\right)}^n\right]}^{-m}$$

(4)

where $b_2=a^{\prime }/b^{\prime }$, and n and m are the same as those in the vG model. The relationship between the surface tension of the water vapor contact surface and temperature can be approximated as ${\sigma }_T=a^{\prime }+b^{\prime }T$ [35], where ${\sigma }_T$ is the surface tension, and $a^{\prime }$, $b^{\prime }$ are fitting parameters. Grant and Salehzadeh (1996) [33] obtained through parameter calibration that for the contact surface between pure water and air, $a^{\prime }=0.1177 \mathrm{N}\cdot {\mathrm{m}}^{-1}$, $b^{\prime }=-0.0001535 \mathrm{N}\cdot {\mathrm{m}}^{-1}\cdot {\mathrm{K}}^{-1}$. The pores of unsaturated soils are also mainly filled with water and air; therefore, the values of a′ and b′ calibrated by Grant and Salehzadeh (1996) [33] are also adopted here as approximate values.

Some scholars have fitted and analyzed the experimental results of soil water characteristic curves under different NaCl solution concentrations using different SWCC models, and they have found that the vG model has the best fitting results [36,37]. Based on the basic theory of interface chemistry, the surface tension of inorganic salt solutions roughly changes linearly with the increase in solution concentration. Then, according to the relationship between surface tension and matric suction, it can be deduced that the matric suction considering the influence of salinity can be expressed as $s=s_0{e}^{bClnC-NC}$, where C is the concentration of solute in the pore solution, and b and N are model parameters. The influence of salinity on SWCC is mainly reflected in its impact on pore volume [13,15]; therefore, based on the vG model, the SWCC model considering the influence of salinity can be expressed as

$$s_r={\left[1+{\left({\displaystyle \frac{s}{a{e}^{bClnC-NC}}}\right)}^n\right]}^{-m}$$

(5)

It is not difficult to find that Equations (3)–(5) are all derived from the vG model by introducing relevant influencing factors. Equation (3) introduces density influencing factors ${\left({\displaystyle \frac{e}{a_1}}\right)}^{1/b_1}$, Equation (4) introduces temperature influencing factors ${\displaystyle \frac{b_2+T_0}{b_2+T}}$, and Equation (5) introduces salinity influencing factors ${\displaystyle \frac{1}{e^{bClnC-NC}}}$. By combining Equations (3)–(5) and introducing the influence factors of density, temperature, and salinity on the vG model, the soil water characteristic curve can be represented as

$$s_r={\left\{1+{\left[{\displaystyle \frac{b_2+T_0}{b_2+T}}{\left({\displaystyle \frac{e}{a_1}}\right)}^{1/b_1}{\displaystyle \frac{s}{e^{bClnC-NC}}}\right]}^n\right\}}^{-b_1/n}$$

(6)

Equation (6) is the SWCC model that considers the effects of deformation, temperature, and salinity simultaneously, including six model parameters. The proposed model is indeed an empirical engineering framework designed for practical SWCC prediction under multi-factor influences, rather than a fully derived thermodynamic constitutive model. Its primary contribution lies in the integration of well-established single-factor mechanisms into a unified, usable vG model framework. The selection of each term is grounded in recognized physical mechanisms.

2.2. Analysis of Model Parameters

The SWCC model in Equation (6) is proposed based on the vG model considering the effects of density, temperature, and salinity, and it includes six model parameters a₁, b₁, b₂, n, b, and N. Among them, b₂ can be considered a constant, a₁, b₁ the control air entry value, n the fitting parameter, and b and N parameters related to salinity. Under different conditions, the values of each parameter also vary accordingly. Thus, accurate prediction of various parameters is a matter of great concern.

In order to explore the influence of model parameters on the shape of the SWCC, a sensitivity analysis was carried out with different parameter variation ranges. Under specific initial conditions (initial void ratio e = 0.7, salinity C = 0.5 mol/L, temperature T = 25 °C), a set of model parameters were fitted using Equation (6) based on the test results, where a₁, b₁, b₂, n, b, and N are 40, 25, 0.5, −23, and −14, respectively. It is worth noting that here, only the analysis of the influence of model parameters in terms of numerical values is conducted by means of the control variable method.

(1)

Sensitivity analysis of a₁

Under the condition that other parameter values remain unchanged, a₁ takes seven values of different orders of magnitude from the range of 0.04–40,000, and the change in the SWCC can be observed, as shown in Figure 2. It can be seen that with the increase in a₁, the air entry value gradually increases, and in the saturation (s_r)-suction (s) coordinate plane, the SWCC as a whole shifts to the right. However, although the value of a₁ changes significantly, the impact on SWCC is relatively small.

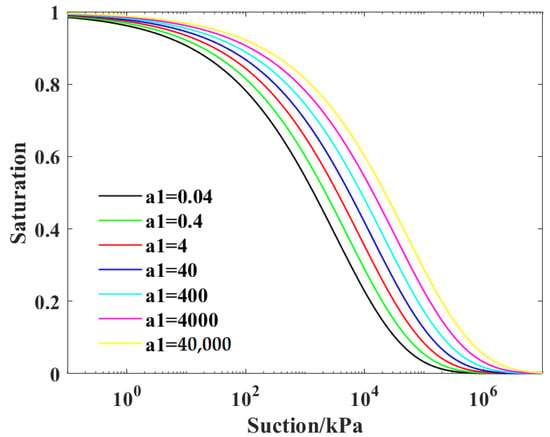
Figure 2. Effect of parameter a₁ on SWCC.

(2)

Sensitivity analysis of b₁

Under the condition that other parameter values remain unchanged, b₁ takes seven different values in the range of 5–65, and the SWCC changes can be observed, as shown in Figure 3. It can be seen that with the increase in the b₁ value, the air entry value gradually decreases, the slope of the curve in the transition section increases slightly, and the curve as a whole shifts to the left. Moreover, the plot is more sensitive to changes in b₁ when these values are small.

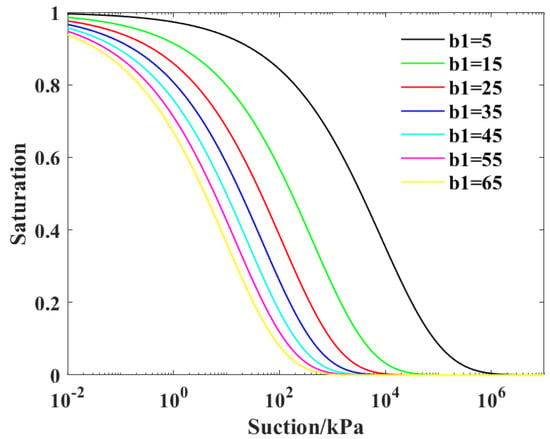
Figure 3. Effect of parameter b₁ on SWCC.

(3)

Sensitivity analysis of n

Similarly, n takes seven different values in the range of 0.08–1.4, and the SWCC changes can be observed, as shown in Figure 4. With the increase in the n value, the air entry value increases gradually, the slope of SWCC transition section decreases slightly, and the curve moves to the right as a whole. A small change in the n value has a significant impact on SWCC.

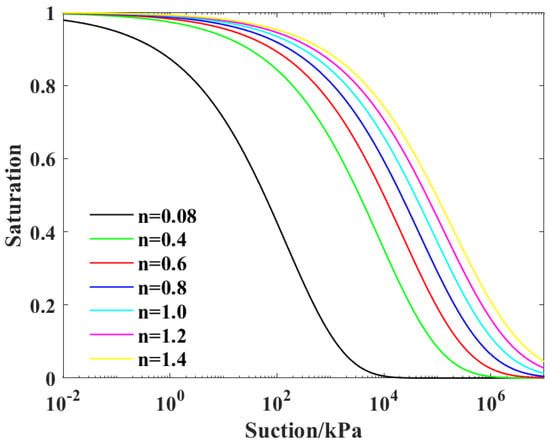
Figure 4. Effect of parameter n on SWCC.

(4)

Sensitivity analysis of b and N

b and N are parameters related to salinity. The variation of SWCC with the two values is shown in Figure 5. It can be seen from the figure that small parameter changes will have a greater impact on SWCC. The values of parameters b and N are mainly negative, and with the increase in b and N, the air entry value gradually decreases, and SWCC moves to the left.

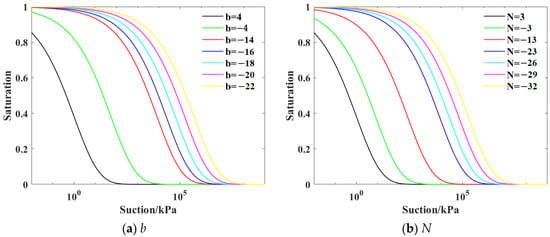
Figure 5. Effect of parameters b and N on SWCC.

Through the sensitivity analysis of model parameters, we can clearly understand the impact of various parameters on SWCC so as to provide some reference for the prediction of model parameters. The key to the validity of the model lies in the determination of parameters. The parameters of the model can be predicted by means of machine learning, so that the proposed SWCC mathematical model can achieve strong prediction ability.

2.3. Validity Verification of the SWCC Model

In order to verify the effectiveness of the proposed SWCC model (Equation (6)) considering the influence of multiple factors, four representative experimental datasets were used to validate the fitting ability of the model. The first test dataset only considers the influence of void ratio (e = 0.622, T = 22 °C, C = 0; Jacinto et al. 2009 [38]); then, Equation (6) can be simplified to the form of Equation (3). The second test dataset considers the effects of temperature and void ratio (e = 0.564, T = 40 °C, C = 0; Jacinto et al. 2009 [38]), and Equation (6) can be simplified as

$$s_r={\left\{1+{\left[{\displaystyle \frac{b_2+T_0}{b_2+T}}{\left({\displaystyle \frac{e}{a_1}}\right)}^{1/b_1}s\right]}^n\right\}}^{-b_1/n}$$

(7)

The third test dataset considers the effects of salinity and void ratio (e = 0.7, T = 22 °C, C = 0.5 mol/L; Liu et al. 2021 [39]), and Equation (6) can be simplified as

$$s_r={\left\{1+{\left[{\left({\displaystyle \frac{e}{a_1}}\right)}^{1/b_1}{\displaystyle \frac{s}{e^{bClnC-NC}}}\right]}^n\right\}}^{-b_1/n}$$

(8)

The fourth test dataset takes into account the effects of temperature, salinity, and void ratio (e = 0.6875, T = 6 °C, C = 1.0 mol/L; Ji et al. 2023 [40]) and can be fitted using Equation (6).

The fitting results of the model parameters of the four groups of test data [38,39,40] are listed in Table 1 as an example, and the fitting effect is shown in Figure 6. It can be seen that the SWCC model proposed in this paper can accurately simulate the complete soil water characteristic curve under the influence of multiple factors. Although the cross influences among various factors (such as temperature and salinity) have not been fully considered in the model derivation, the soil–water characteristic curve under the coupling effect of multiple factors can be reflected by adjusting the parameter combination values.

Table 1. The fitting values of formula parameters under different conditions.

Test Data	a1	b1	n	b	N
Test data 1 [38]	3.653636	0.393699	0.731296	/	/
Test data 2 [38]	12.96582	0.685902	0.601168	/	/
Test data 3 [39]	2.18159	0.3205	4.62404	−0.817475	0.73667
Test data 4 [40]	60.35245	1.9717287	0.4015235	/	6.9401843

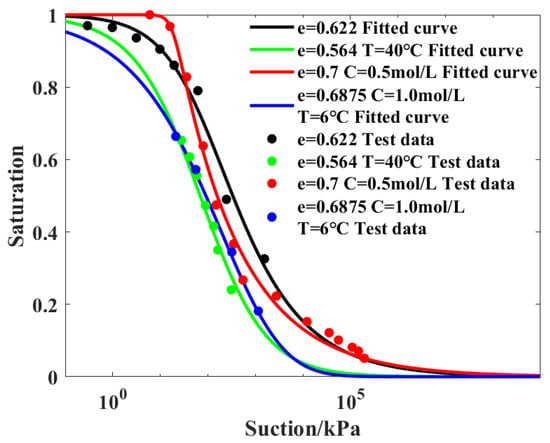
Figure 6. Fitting effect of SWCC model [38,39,40].

3. Machine Learning-Based SWCC Model Parameter Prediction

Although the proposed SWCC model can well reflect the influence of multiple factors, the determination of model parameters still needs an SWCC test for calibration. With the continuous maturity and popularity of machine learning algorithms, some scholars have tried to use machine learning methods to predict SWCC model parameters [19,41,42,43]. Compared with the traditional test data fitting method, the machine learning method can learn the existing test dataset as samples and can directly predict the corresponding model parameters, which saves a significant amount of time and labor costs. Therefore, this paper attempts to use a machine learning method to predict the parameters of the proposed SWCC model considering the influence of multiple factors.

(5)

Data collection and processing

The training data used in this paper are from the SWCC test data in the literature [32,42,43,44,45,46,47] and the SWCC test data of soil No. 10749-11433 in the SoilVision database (shared dataset), with a total of 1600 sets of valid data. The 1600 sets of valid data collected include the basic physical property parameters of soil, environmental parameters, and the corresponding SWCC data. Formula fitting was performed on each set of SWCC data using the proposed model, yielding the corresponding model parameters. A dataset containing soil physical parameters, environmental parameters, and the corresponding model parameters was thus obtained. This dataset was then used as the training dataset for machine learning, in which soil physical property parameters and environmental parameters served as the input and model parameters served as the output. Therefore, when the neural network machine learning method was used to predict the parameters of the SWCC model, the following were selected as input parameters: the indexes representing the basic physical properties of soil (e, specific gravity G_s) and the parameters related to particle size distribution (d₁₀, d₃₀, d₆₀, uniformity coefficient c_u, and curvature coefficient c_c), where d₁₀, d₃₀, d₆₀ are types of particle size. The mass of soil particles smaller than these sizes accounted for 10%, 30% and 60% of the total mass, respectively, and environmental parameters were also used as input (T, C). The output parameters were the SWCC model parameters (a₁, b₁, n, b, N).

ANNs are computational models inspired by the structure of biological neural networks, exhibiting sophisticated architectures that consist of multiple layers, each one comprising several neurons. These neurons perform calculations through linear combinations of inputs from the previous layer, utilizing specific weights associated with each connection. The ANN approach has been demonstrated to be capable and superior when compared to traditional pedotransfer function models that do not utilize machine learning [48]. Thus, this paper focuses on an ANN because of its complex structure and recurrent use in the literature over the past few decades [27,28,29,49,50,51]. Moreover, this study adopts a special form of ANN—a Bayesian regularization neural network (BRNN). Its core advantage lies in suppressing overfitting by incorporating a weight decay term (regularization term) into the loss function [29]. During the training process, we further reduced the risk of overfitting through “adjusting the number of neurons in the hidden layer” and “the early stopping method”.

Using 80% of the 1600 groups of valid data as the training set and 20% of the data as the test set, the model prediction method is shown in Figure 7. For feature preprocessing, we selected complete and valid experimental data, removed outliers, and performed standardization on input features. By continuously adjusting the number of hidden-layer nodes in the model, the number of hidden-layer neurons was determined to be 25, and the model was optimized until the best predictive model was obtained. The learning rate was 1 × 10⁻³, balancing training efficiency and convergence stability; the regularization parameter was 1 × 10⁻⁴, which suppressed overfitting while maintaining the physical meaning of parameters; and the number of iterations was determined to be 1000 through the early stopping method, ensuring the MSE of the validation set remained stable. According to the proposed model, considering the influence of salinity will produce two additional parameters, and there are fewer test data considering changes in salinity, temperature, and void ratio at the same time. Therefore, in the process of machine learning, the training dataset was divided into two parts; one part did not consider the influence of salinity (three predicted parameters, and 1000 sets of valid data), and the other part considered the influence of salinity (five predicted parameters, and 600 sets of valid data). It is worth noting that the experimental data used to verify the model’s performance were not included in the training dataset at all so as to demonstrate the model’s generalization ability.

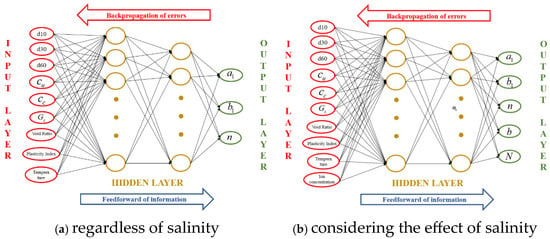
Figure 7. Logic diagram of the machine learning prediction model.

(6)

Prediction of model parameters without considering the effect of salinity

Without considering the effect of salinity, the SWCC model only contains three parameters a₁, b₁ and n, and the number of output nodes of machine learning prediction is 3. The accuracy and reliability of the prediction model were tested by calculating the correlation coefficient (R²), mean square error (MSE), mean absolute error (MAE), and root mean square error (RMSE). The smaller the MSE value and the closer the R² value is to 1, the stronger the prediction ability of the model is. The training results are shown in Figure 8, which show good prediction accuracy.

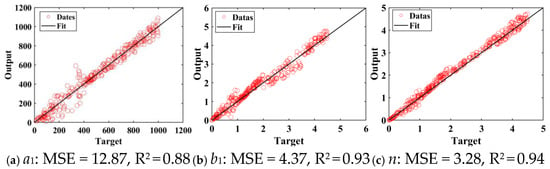
Figure 8. Model training results.

To further evaluate the robustness and generalization capability of the proposed BRNN model, a 10-fold cross-validation was conducted [52]. The entire dataset was randomly partitioned into 10 equal-sized subsets. For each fold, nine subsets were used for training, and the remaining subset was used for validation. This process was repeated 10 times, and the mean ± standard deviation (SD) of each performance metric was calculated, which reflected the robustness of the model across different data subsets. The results are shown in Table 2.

Table 2. Ten-fold cross-validation results for model parameter prediction without salinity.

Target Parameter	R2	MSE	MAE	RMSE
a1	0.88 ± 0.03	12.87 ± 1.45	2.96 ± 0.32	3.59 ± 0.21
b1	0.93 ± 0.02	4.37 ± 0.51	1.78 ± 0.15	2.09 ± 0.12
n	0.94 ± 0.02	3.28 ± 0.43	1.51 ± 0.11	1.81 ± 0.10

The performance metrics (R², MSE, MAE, RMSE) were calculated for each fold and then averaged to obtain the overall cross-validation performance. This approach provided a more reliable estimate of model performance by reducing the variance associated with a single training–testing split.

We selected soil No. 11265 in the SoilVision database, and its input parameters are shown in Table 3. The results obtained by formula fitting and machine learning prediction are shown in Figure 9. This set of data only considers the influence of void ratio and does not take into account the effects of temperature (room temperature) and salinity. It can be seen that the machine learning prediction results (R² = 0.94) are consistent with the test data and fitting results (R² = 0.92).

Table 3. Input parameters of soil No.11265.

Soil Number	d10	d30	d60	cu	cc	e	Gs	T
11,265	0.00074	0.01767	0.03406	46.208	12.437	0.89	2.66	25

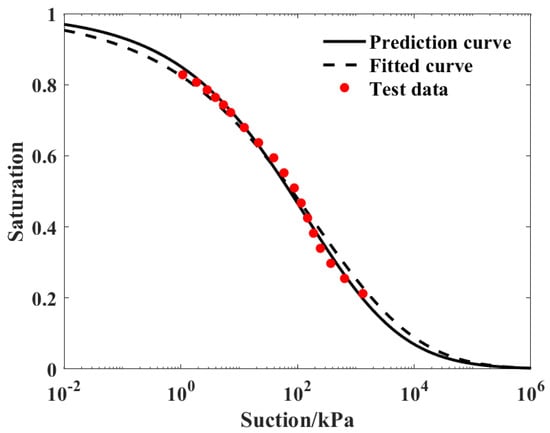
Figure 9. Prediction of SWCC model parameters considering void ratio.

The trained model was used to predict the change in SWCC under different void ratios, as shown in Figure 10, and it accurately predicted the characteristics of the variation of SWCC with void ratio.

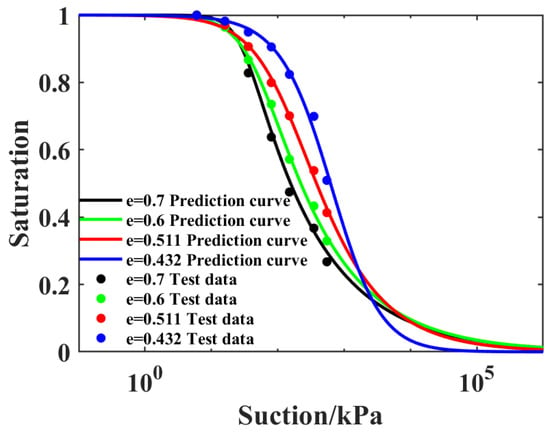
Figure 10. Prediction of SWCC model parameters with different void ratios [39].

For different temperature conditions, the parameters to be solved in the model are still a₁, b₁, and n. We selected a group of test data at a temperature of 40 °C, compared the fitting results based on the test data with the prediction results of machine learning, and verified the prediction ability of the model under various temperature conditions, as shown in Figure 11.

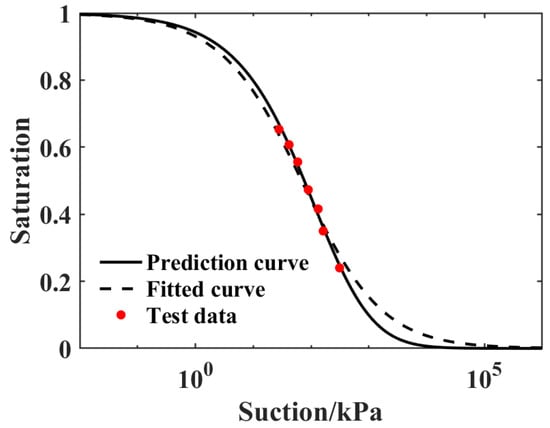
Figure 11. Prediction of SWCC model parameters considering temperature [53].

Based on the prediction model, the SWCC model parameters of two soils with initial void ratios of 0.72 and 0.564 under different temperature conditions were predicted, and the prediction results are shown in Figure 12. It can be seen that the prediction results are in good agreement with the test data, indicating that the proposed model parameter prediction method has a good prediction effect for the SWCC, considering the effects of temperature and void ratio.

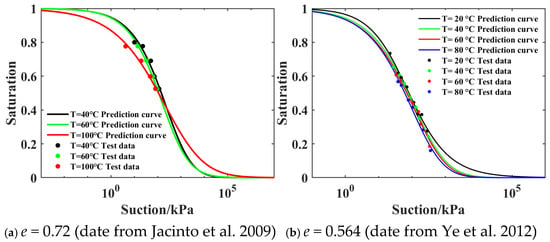
Figure 12. Prediction of SWCC model parameters with different void ratios and temperatures [38,53].

(7)

Prediction of model parameters considering the effect of salinity

When considering the effect of salinity, the model has five parameters to be calibrated, which are a₁, b₁, n, b, and N. Under this condition, the number of output nodes of machine learning is also 5. The SWCC test data related to salinity were trained by machine learning, and the training results are shown in Figure 13. Similarly, analogous to the scenario without salinity, 10-fold cross-validation was also performed for the prediction of five parameters for the scenario with salinity, and the corresponding validation results are presented in Table 4.

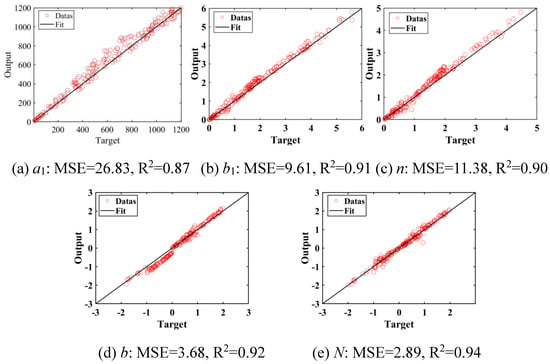
Figure 13. Model training results.

Table 4. Ten-fold cross-validation results for model parameter prediction with salinity.

Target Parameter	R2	MSE	MAE	RMSE
a1	0.87 ± 0.03	26.83 ± 3.22	4.82 ± 0.53	5.18 ± 0.31
b1	0.91 ± 0.03	9.61 ± 1.15	2.75 ± 0.30	3.10 ± 0.019
n	0.90 ± 0.03	11.38 ± 1.37	3.02 ± 0.33	3.37 ± 0.20
b	0.92 ± 0.03	3.68 ± 0.44	1.52 ± 0.17	1.92 ± 0.12
N	0.94 ± 0.02	2.89 ± 0.35	1.35 ± 0.15	1.70 ± 0.10

SWCC test data considering the effect of salinity were selected to verify the prediction model, as shown in Figure 14. The prediction results are basically consistent with the fitting effect of the model, being even better than the fitting curve; this means they are well matched with the test data.

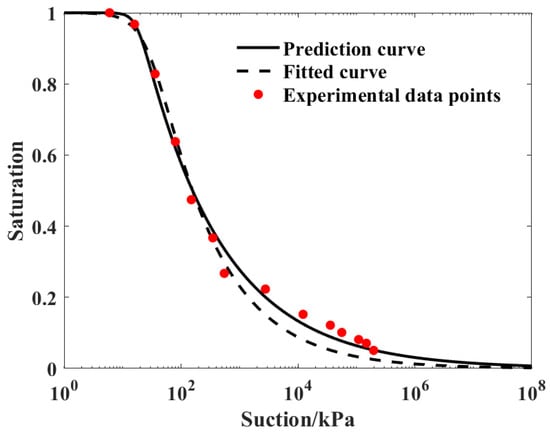
Figure 14. Prediction of SWCC model parameters considering salinity [39].

In addition, the change characteristics of SWCC with different salinity and void ratio were predicted, and the results are shown in Figure 15. It can be seen that the prediction results are consistent with the test data, which also verifies the prediction ability of the prediction model for SWCC model parameters considering the effect of salinity.

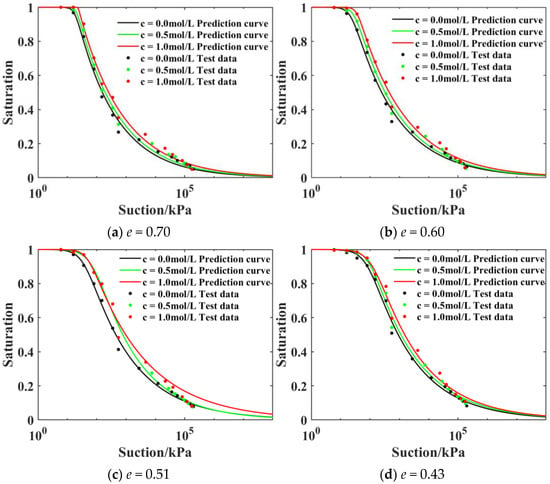
Figure 15. Prediction of SWCC model parameters with different void ratios and salinity levels [39].

SWCC test data under the joint influence of temperature and salinity are scarce, and most of the existing studies concern the analysis of frost heave characteristics of saline soil. The model is used to predict SWCC characteristics under the influence of low temperature and salinity, and the results are shown in Figure 16. Although there were few data regarding the joint effect of temperature and salinity used in model training, the model can still accurately predict the SWCC’s characteristics under this condition.

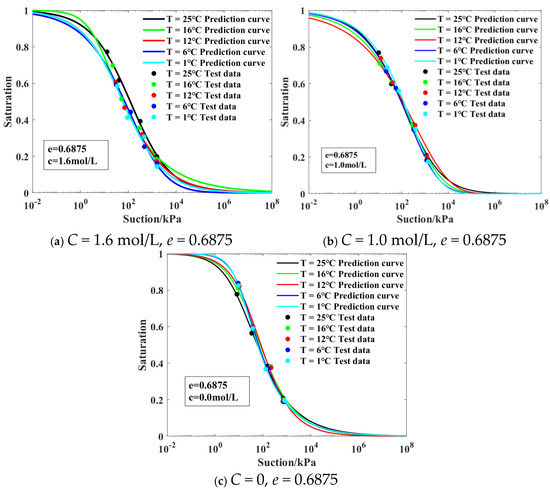
Figure 16. Prediction of SWCC model parameters under different temperatures and salinity levels [40].

4. Discussion

(1)

Given that the vG model is inherently an empirical mathematical fitting formula, although many scholars have introduced influence factors based on this model to characterize their effects on SWCC, such studies are mostly exploratory attempts, and their theoretical mechanisms have not been fully clarified. Accordingly, this paper also builds on the vG model; integrates multi-factor coupling into the model framework by analyzing the mechanism of action of each influencing factor on soil–water characteristics; constructs an SWCC empirical model that can consider the influence of multiple factors; and verifies its applicability through experimental data. It should be noted that this model still has limitations in explaining physical mechanisms, such as the cross-effects between salinity and temperature. The model’s primary contribution lies in integrating multiple factors into a unified framework and demonstrating the feasibility of ML for parameter prediction. Future research will further deepen the exploration of its intrinsic physical mechanism.

(2)

In terms of model parameter analysis, this paper adopts the control variable method, only conducts analysis on the parameter value level, and focuses on the law of influence of parameter value changes on SWCC. It should be pointed out that some parameter values may exceed the theoretical reasonable range, but they have no substantial impact on the analysis of the core conclusions of this paper.

(3)

Restricted by the scarcity of SWCC experimental data under multi-factor coupling, using existing experimental data, it is difficult to simultaneously cover the coupling effects of deformation, temperature, and salinity; such data are mostly limited to specific suction ranges. Therefore, model verification is mostly based on working conditions with fixed specific parameters, which to a certain extent restrict the verification of the model’s universality. Using the experimental data selected in this paper, we tried to cover the influence of multiple factors as much as possible, and the proposed model also shows a good fitting effect. In the future, with the accumulation and improvement of experimental data, the universality of the model can be further verified.

(4)

When using machine learning methods for model parameter prediction, their accuracy has high requirements in terms of the quantity and quality of training data. The training data used in this paper are mostly concentrated in low suction ranges, which may lead to deviations in the prediction accuracy of high suction intervals; at the same time, the sample data are mainly from clay, which may affect the effectiveness of predictions for special soils or sandy soils. This paper focused on expounding the prediction method of SWCC model parameters, and this method achieved good prediction accuracy. In the future, with the expansion of data volume and the improvement of data quality, prediction accuracy is expected to be further improved.

(5)

Through rational dataset division, independent verification, parameter sensitivity analysis, and the statistical basis of the model optimization process, the verification strength of the model’s reliability and accuracy has been ensured as much as possible. However, there is still room for deepening existing statistical analyses; the lack of quantitative analysis of parameter uncertainty may be improved upon.

5. Conclusions

Based on the vG model, this paper analyzed the mechanisms of action of void ratio, temperature, and salinity on the SWCC, integrated multi-factor influence coefficients, and developed an SWCC model under multi-factor coupling effects. Furthermore, accurate prediction of the model parameters was achieved using machine learning methods. The main conclusions are as follows:

(1)

Within the framework of the vG model, an SWCC model capable of characterizing multi-factor coupling effects was established by integrating the influence coefficients of void ratio, temperature, and salinity. Fitting verification was conducted on SWCC test data under multi-factor conditions, and the results showed that this model can effectively describe soil–water characteristics under multi-factor coupling effects. It should be noted that the model still has certain limitations in terms of physical mechanism interpretation and universality, which require further in-depth research.

(2)

The analysis of the laws of influence of changes in model parameter values on SWCC characteristics (i.e., the air entry value and slope of the transition segment) revealed the following. The value range of parameter n is relatively small; as n increases, the air entry value increases, and the slope of the transition segment curve decreases slightly. Parameter a1 has low sensitivity to SWCC changes; as a₁ increases, the air entry value shows an increasing trend. The value range of parameter b₁ is also relatively small; as b₁ increases, the air entry value decreases, and the slope of the transition segment increases slightly. Parameters b and N, which are related to salinity, have a significant impact on the air entry value; as b and N increase, the air entry value decreases. It should be pointed out that although some parameter values may exceed the theoretically reasonable range, they did not substantially interfere with the analysis of the influence laws of parameters.

(3)

To address the parameter prediction issue of the proposed SWCC model, effective prediction of the model parameters was realized using the Bayesian regularized neural network-based machine learning method through training a large amount of SWCC test data under the influence of different factors, with its prediction accuracy depending on the quantity and quality of training data. The input parameters of the model include indicators characterizing the basic physical properties of soil and environmental variables, while the output parameters are the model parameter values. Considering the difference in the number of model parameters involved with and without the influence of salinity, the training set was divided into two parts, one considering salinity’s influence and the other not. Through prediction verification of SWCC characteristics under the influence of different factors, the overall prediction strength under the influence of multiple factors was above 0.9, indicating relatively good prediction performance.