Steel Strand Corrosion and Corrosion-Induced Cracking in Prestressed Concrete Under Stray Current
Abstract
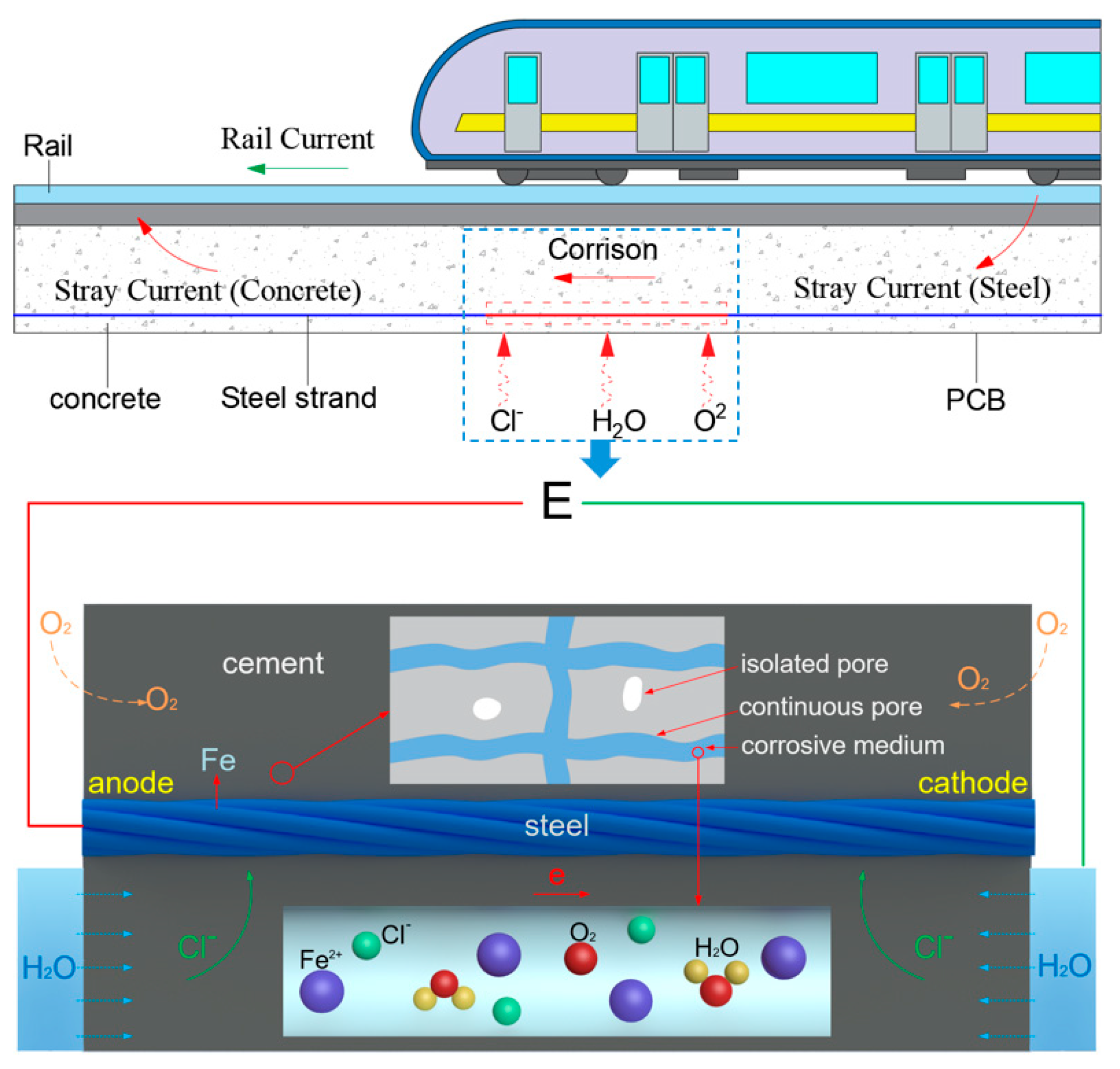
1. Introduction
2. Materials and Methods
2.1. Materials and Specimens
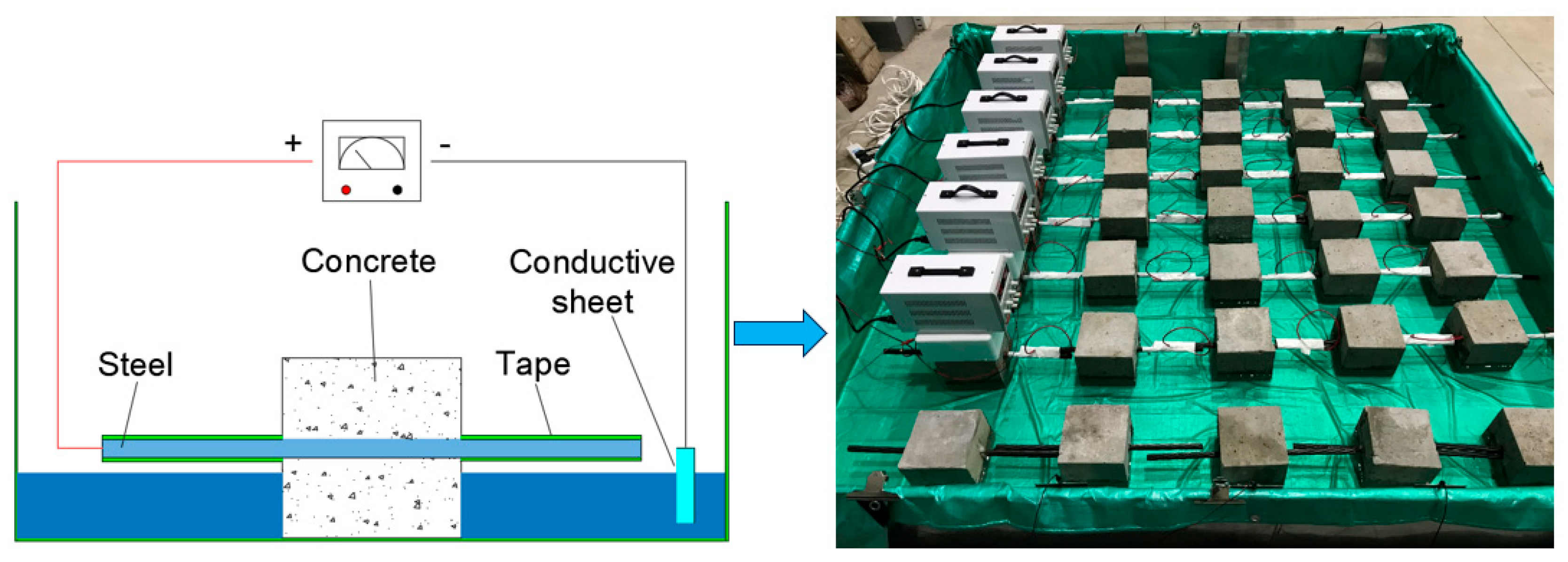
2.2. Experimental Setup
2.3. Measurement of Steel Strand Corrosion Rate
2.4. Measurement of Cracks in Concrete Protective Layer
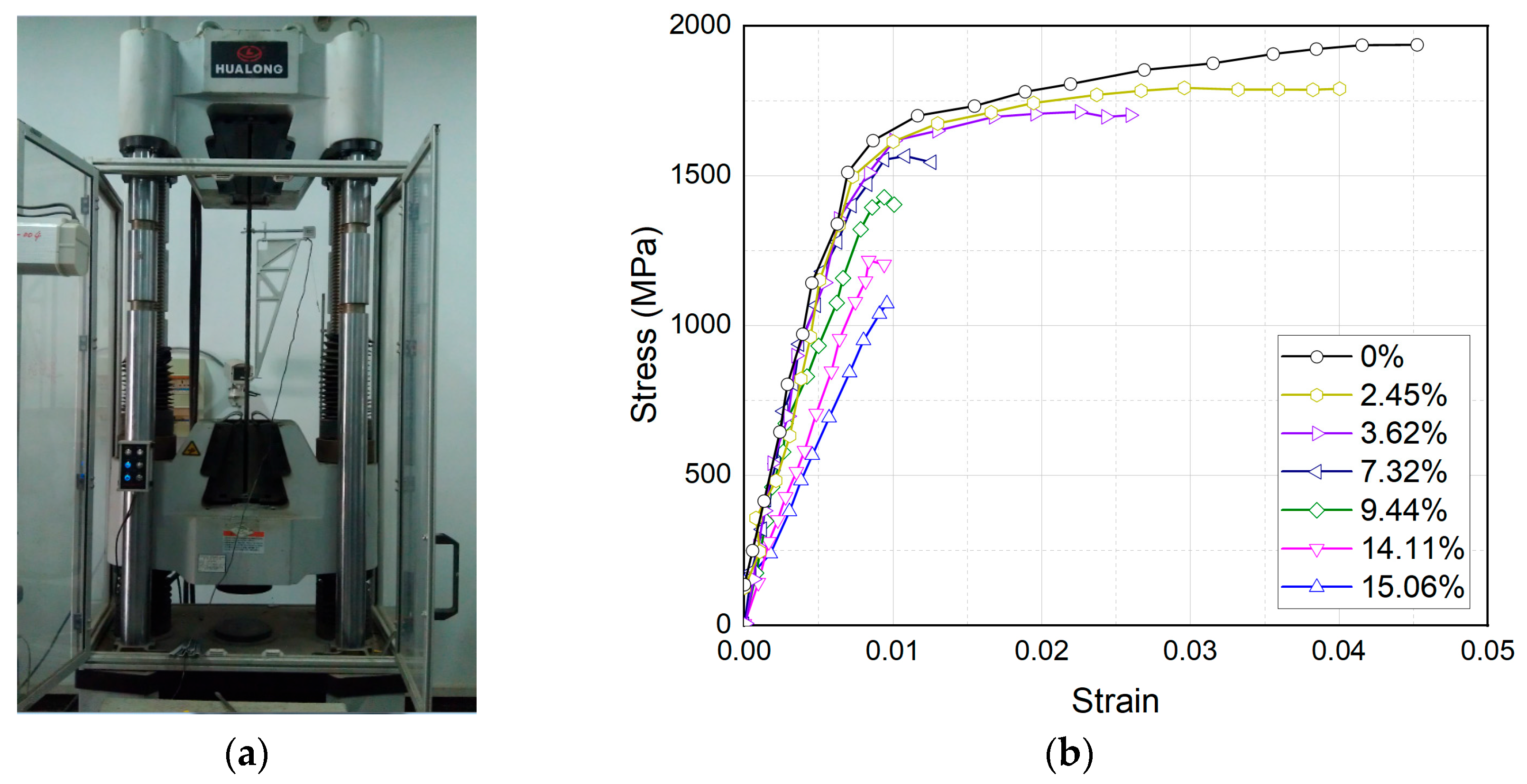
2.5. Mechanical Performance Tests of Corroded Steel Strands
3. Results and Discussion
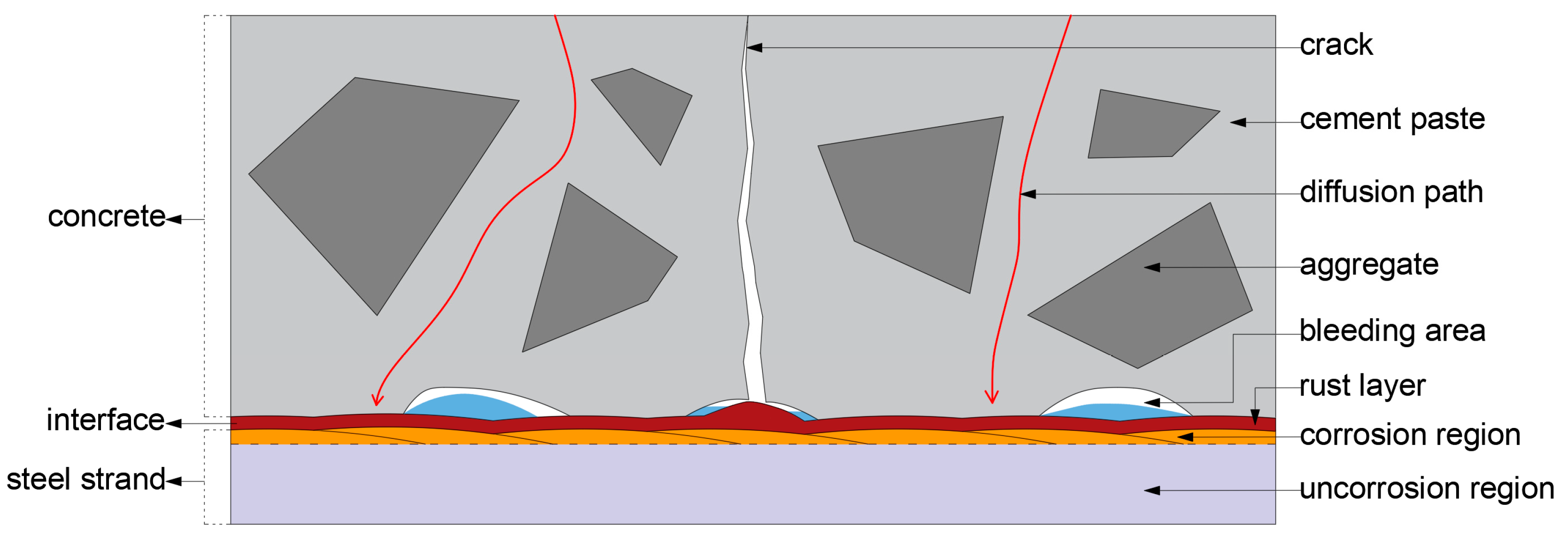
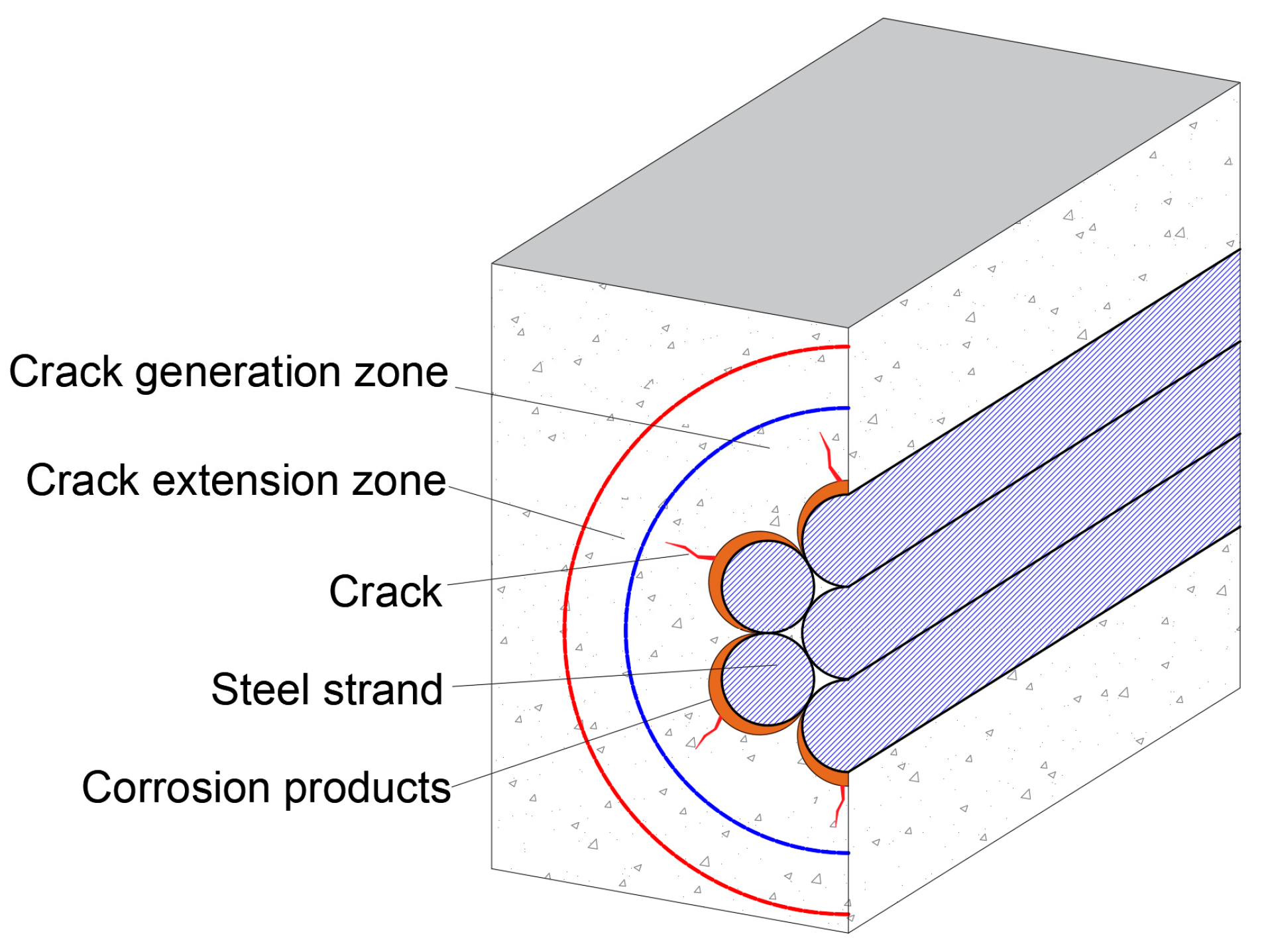
3.1. Concrete Cracking from Steel Strand Corrosion
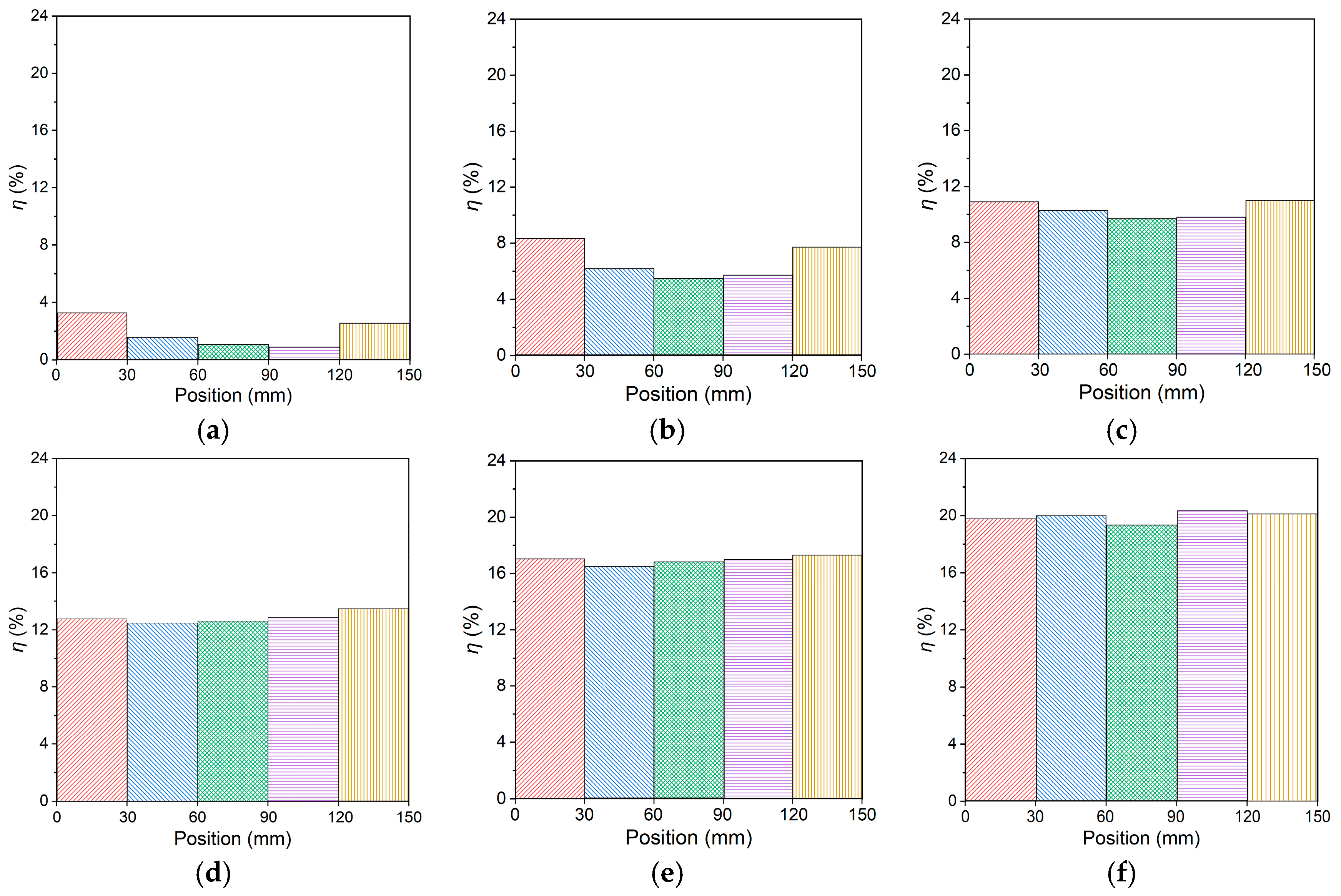
3.2. Corrosion Characteristics of Steel Strands
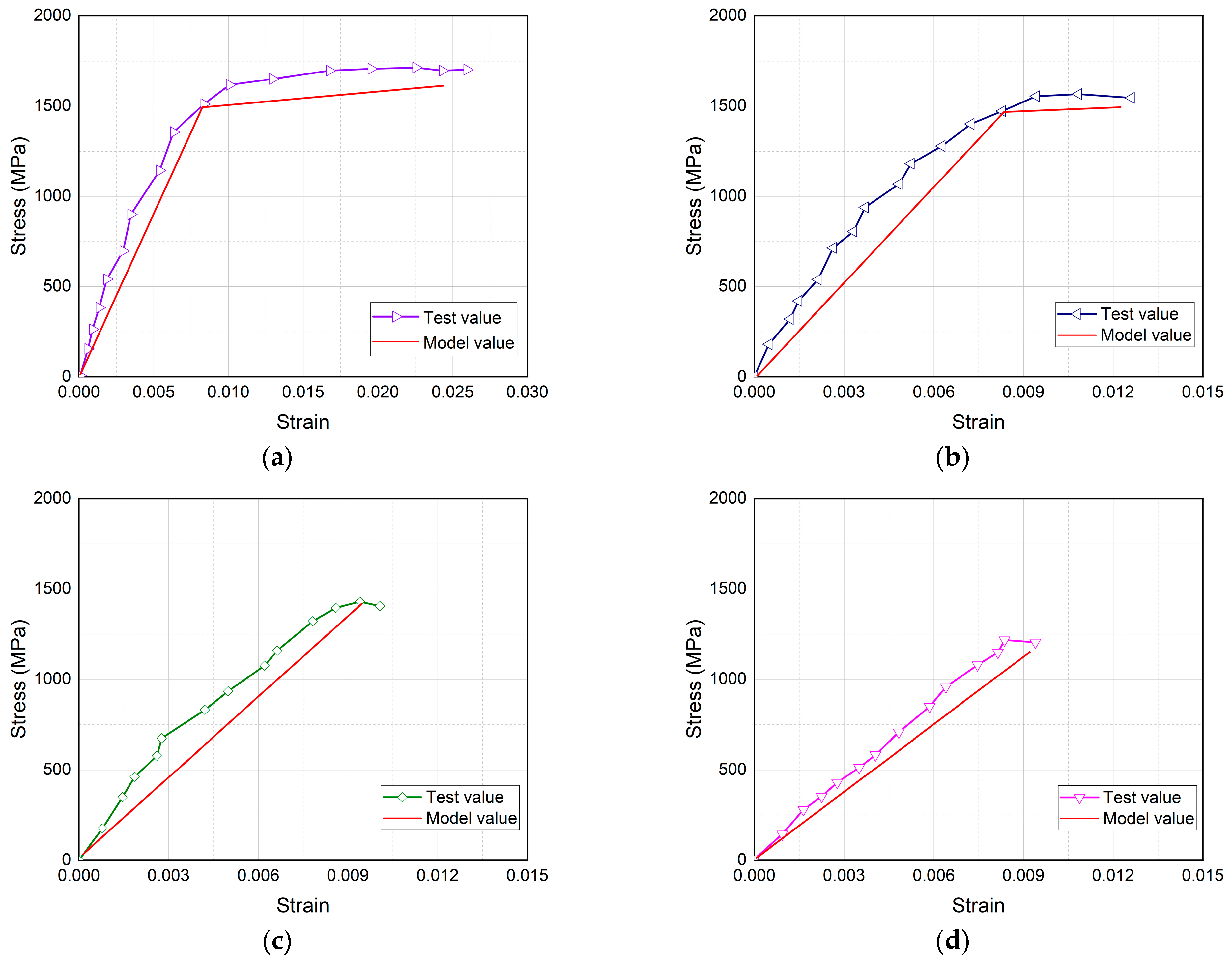
3.3. Mechanical Properties of Corroded Steel Strands
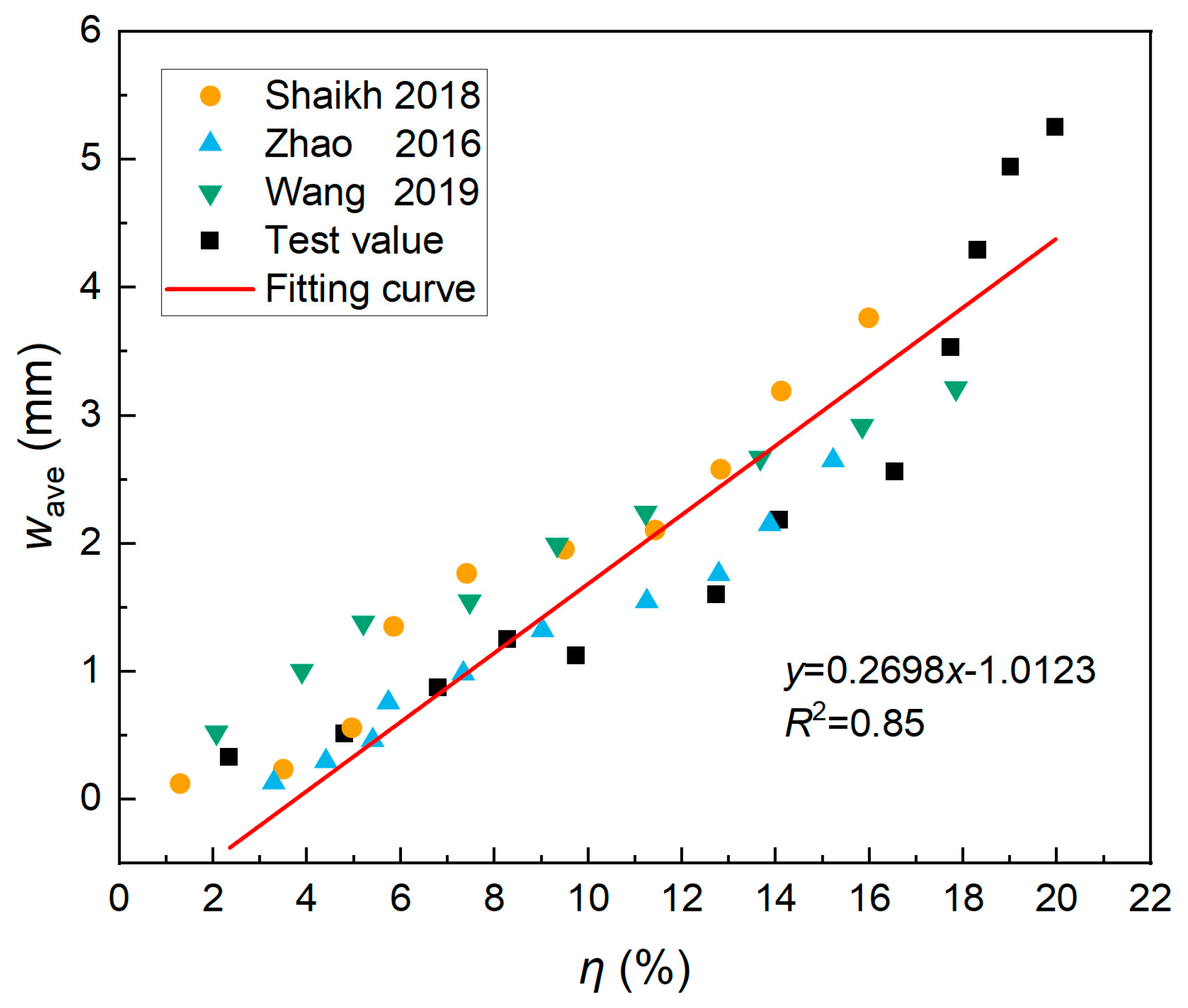
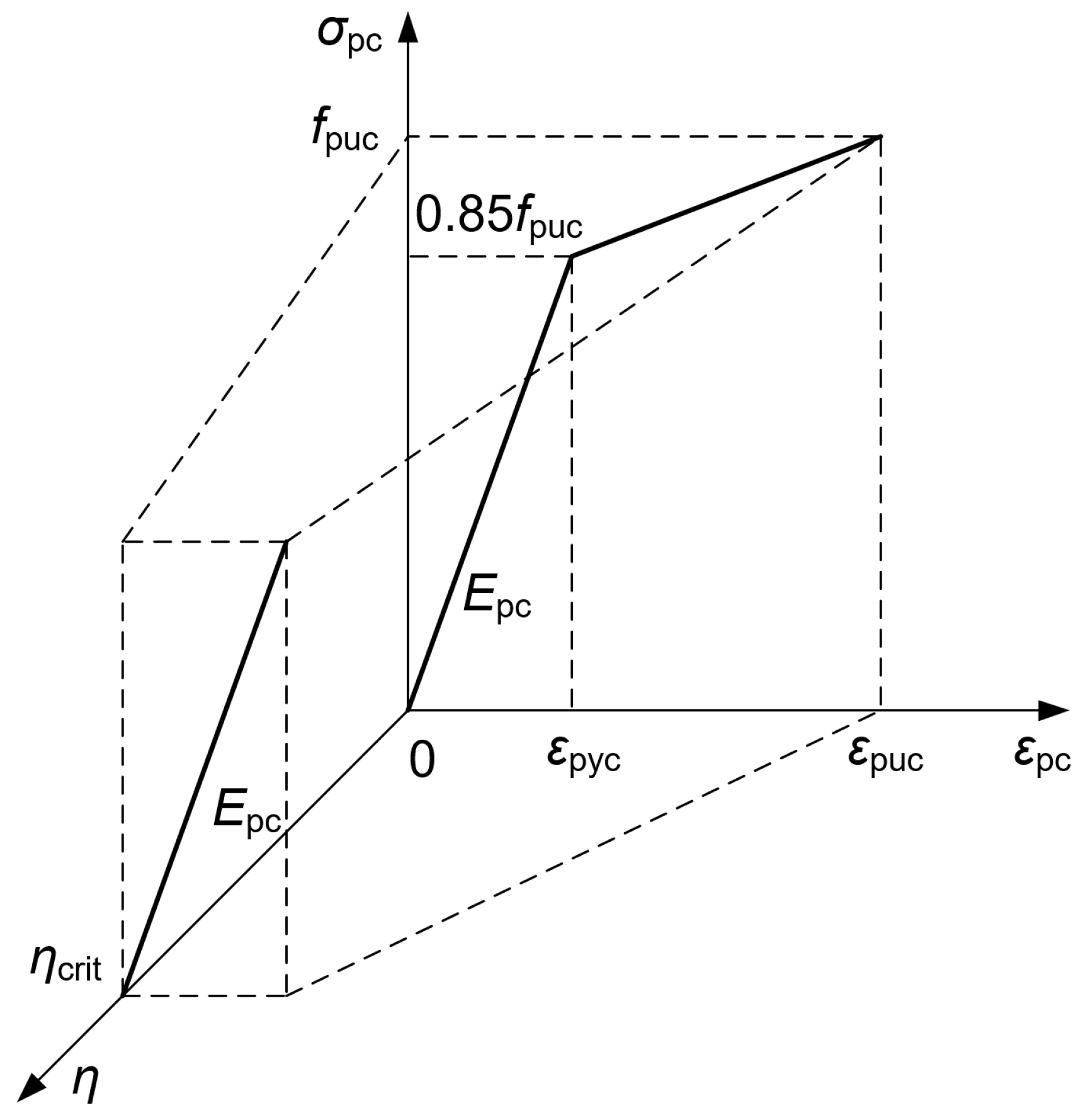
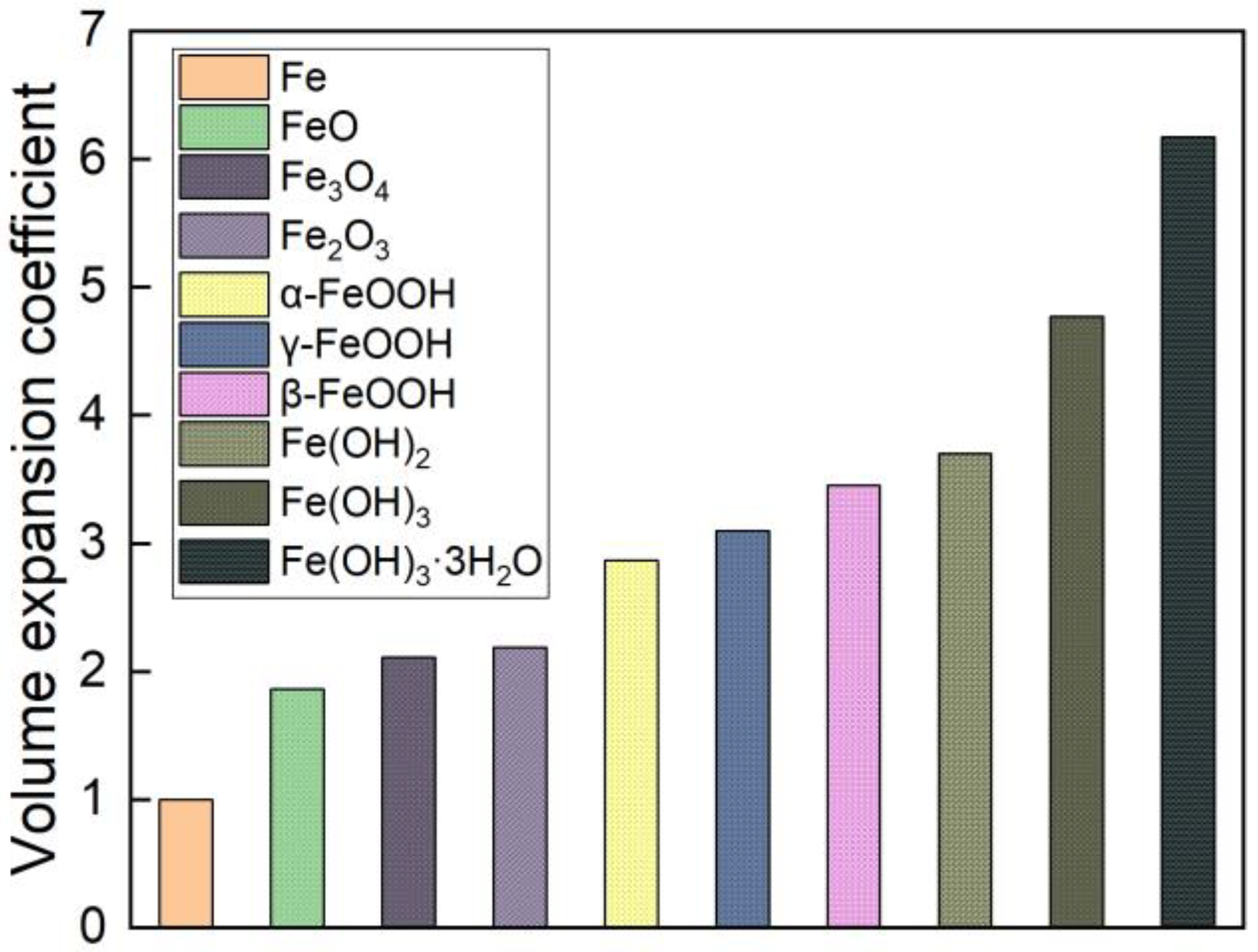
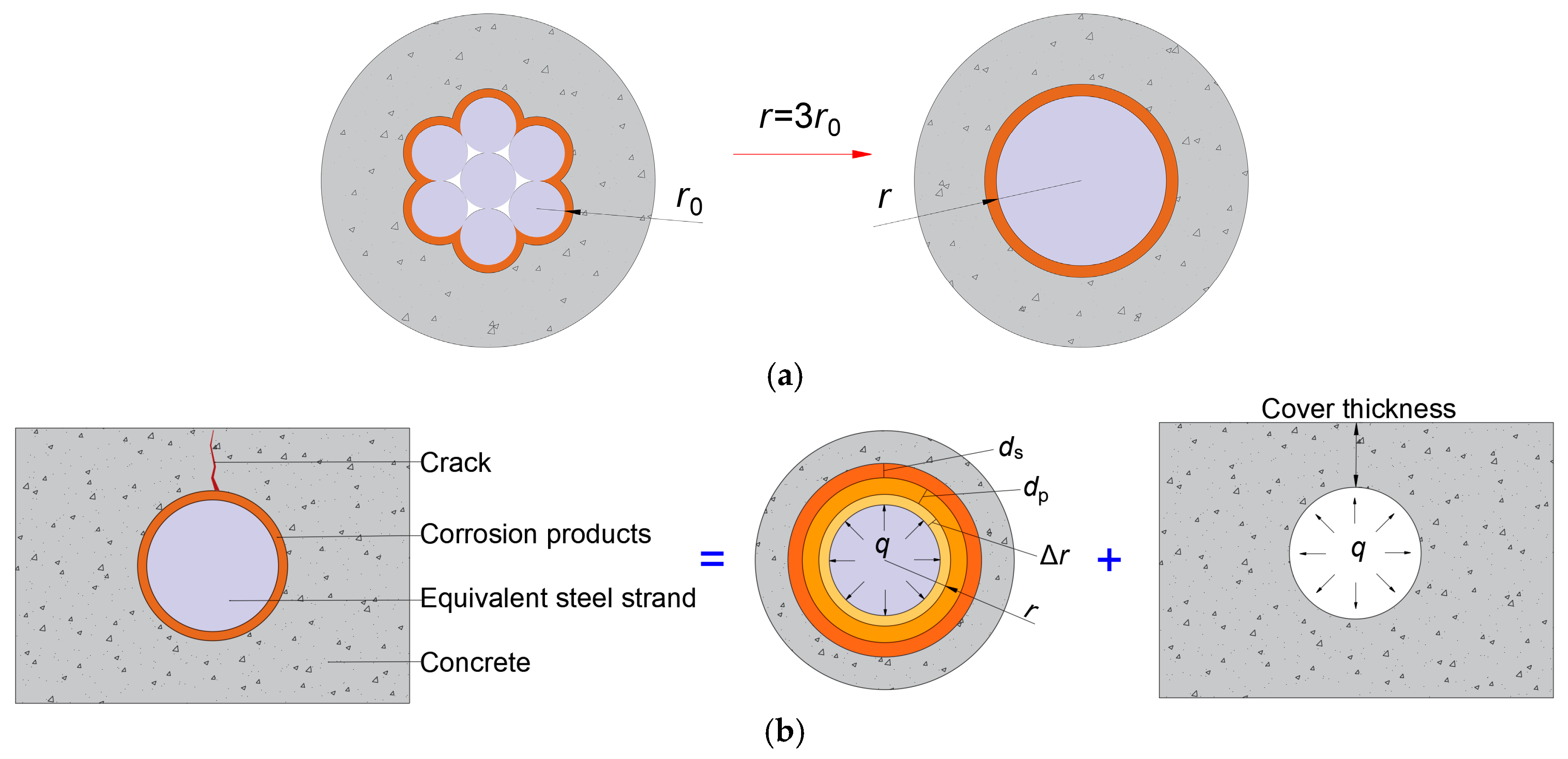
3.4. Corrosion-Induced Cracking Analysis of Prestressed Concrete Under Stray Current
- (1)
- Free expansion stage. As the corrosion spreads on the surface of the steel, the porous area will gradually be filled with corrosion products. When the total amount of corrosion products mt is less than the amount of corrosion products mp required to fill the porous area around the steel–concrete interface, the formation of corrosion products does not exert corrosion expansion stress on the surrounding concrete.
- (2)
- Stress development stage. As the corrosion process accumulates and intensifies, when the total amount mt of corrosion products exceeds the amount mp of corrosion products required to fill the porous area around the steel–concrete interface, the formation of corrosion products begins to exert expansion pressure on the surrounding concrete, and this pressure increases with corrosion products.
- (3)
- Cracking stage. When the total amount mt of corrosion products reaches the critical amount mcrit of corrosion products, the corrosion expansion force exceeds the tensile strength of the concrete, causing the concrete to crack. mcrit mainly depends on the performance of the concrete and the thickness of the protective layer.
4. Conclusions
- (1)
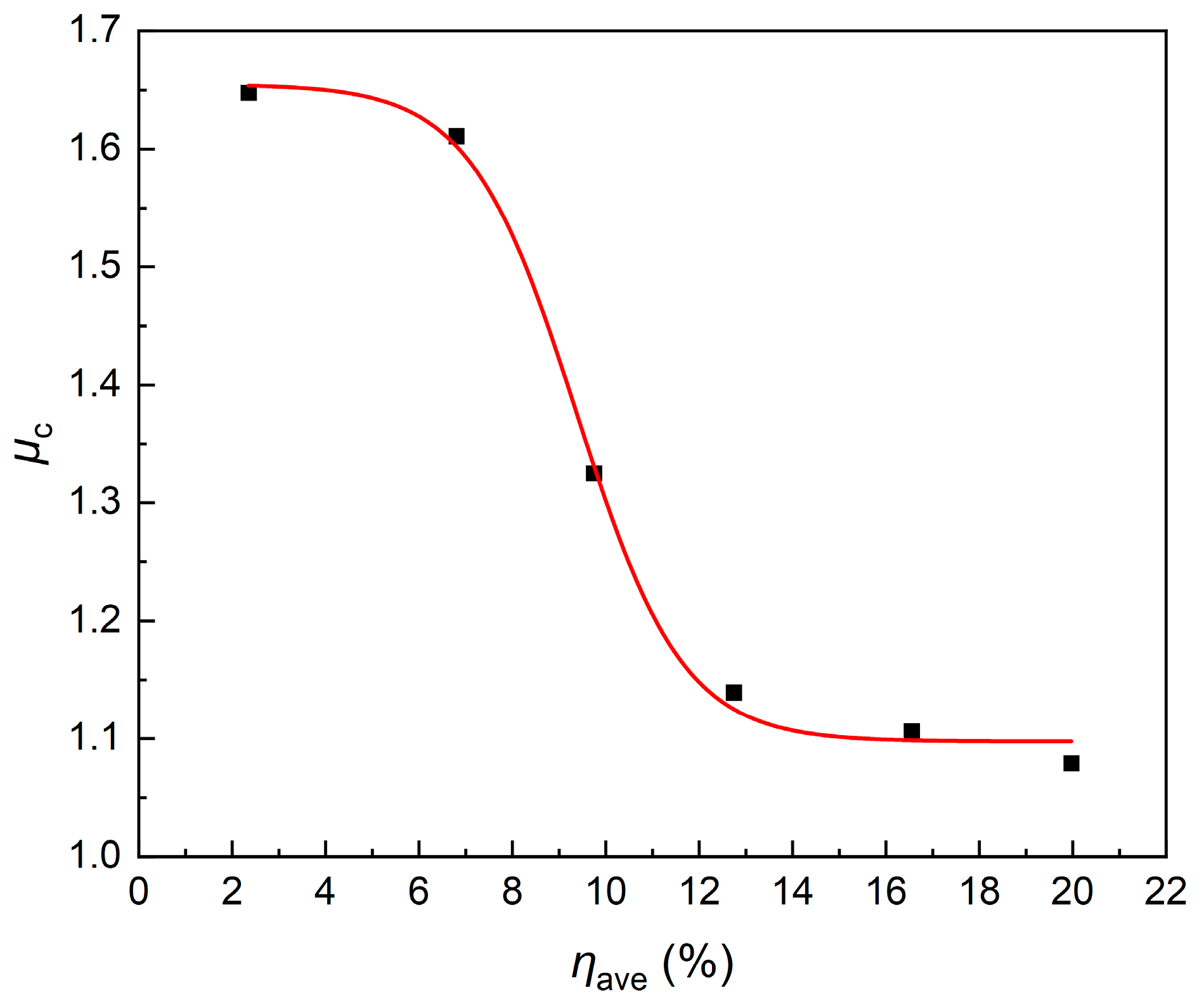
- Electrochemical corrosion tests were conducted on specimens to simulate the characteristics of the metro environment. The results indicate that the stray current had a significant impact on the corrosion cracking of the specimens. The width of the rust-swelling crack was roughly linearly related to the corrosion rate under stray current. Due to the influence of stray current, the corrosion degree of the steel strand was relatively low in the middle, and the difference decreased as the corrosion rate increased. When the average corrosion degree ηave of the steel strand was less than 7%, the corrosion difference coefficient μc at different positions was greater than 1.6. When the average corrosion degree ηave was greater than 12%, the corrosion rates at different positions were basically the same, and the corrosion difference coefficient μc was less than 1.1.
- (2)
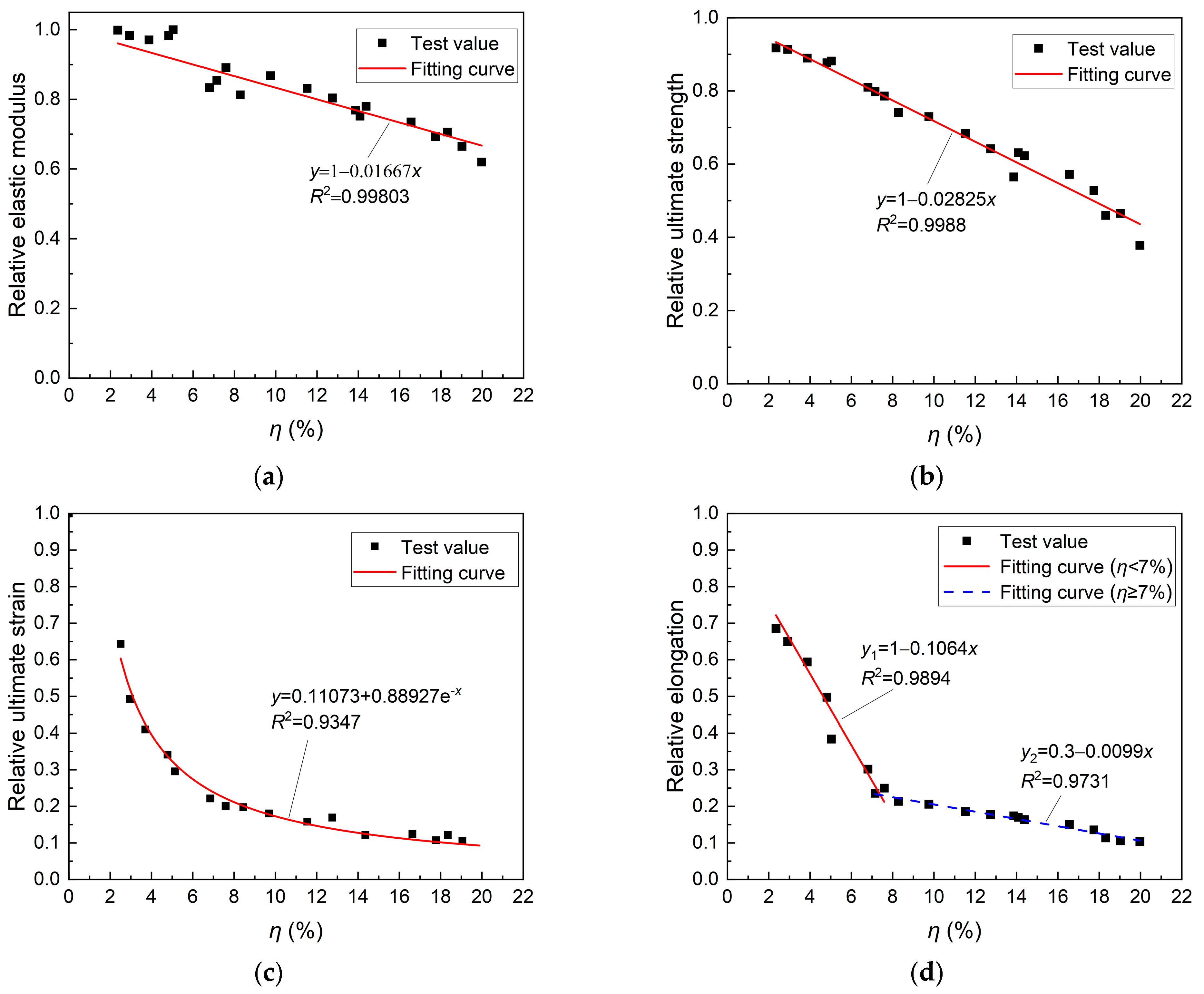
- Mechanical property tests were conducted on the steel strands after electrification corrosion. The results indicate that when the corrosion rate was low (η < 7%), the failure mode of the corrosion specimens was mainly toughness failure with a small change in elastic modulus, which could maintain common mechanical properties, and the ultimate strength and elongation changed significantly. When the corrosion rate was high (η > 7%), the failure mode of the steel strand gradually changed from toughness mode to brittle mode, with a significant cross-sectional loss of individual steel wire and a significant decrease in elastic modulus. The steel strands broke suddenly during stretching, resulting in a relatively discrete ultimate strength value at a high corrosion rate. Based on the test results, a model for the degradation of mechanical properties of corroded steel strands was presented.
- (3)
- Considering the cracking of prestressed concrete caused by the stray current corrosion of steel strands, the corrosion cracking process was simplified and analyzed based on the test results. The corroded steel strand was treated equivalently, and a prediction model for prestressed concrete corrosion cracking considering the influence of stray current was established. The main influencing factors of the model are stray current intensity, concrete tensile strength, and the protective layer thickness of the prestressed concrete.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tu, B.; Dong, Y.; Fang, Z. Time-Dependent Reliability and Redundancy of Corroded Prestressed Concrete Bridges at Material, Component, and System Levels. J. Bridge Eng. 2019, 24, 04019085. [Google Scholar] [CrossRef]
- Vereecken, E.; Botte, W.; Lombaert, G.; Caspeele, R. Assessment of Corroded Prestressed and Posttensioned Concrete Structures: A Review. Struct. Concr. 2021, 22, 2556–2580. [Google Scholar] [CrossRef]
- Bui, H.T.; Maekawa, K.; Tan, K.H. Microcell and Macrocell Corrosion of Steel Bars in Reinforced Concrete Slabs under Different Corrosive Environments and Cathode/Anode Configurations. Cem. Concr. Compos. 2023, 138, 104989. [Google Scholar] [CrossRef]
- Peng, L.; Zeng, W.; Zhao, Y.; Li, L.; Poon, C.; Zheng, H. Steel Corrosion and Corrosion-Induced Cracking in Reinforced Concrete with Carbonated Recycled Aggregate. Cem. Concr. Compos. 2022, 133, 104694. [Google Scholar] [CrossRef]
- Tian, Y.; Jiang, H.; Fan, X.; Zhang, G.; Jin, N.; Zeng, Q.; Jin, X.; Yan, D.; Peng, Y.; Wang, J. Corrosion Damages of Reinforced Concrete Characterized by X-Ray CT and DVC Techniques. Constr. Build. Mater. 2023, 409, 134218. [Google Scholar] [CrossRef]
- Chen, F.; Li, C.-Q.; Baji, H.; Ma, B. Quantification of Non-Uniform Distribution and Growth of Corrosion Products at Steel-Concrete Interface. Constr. Build. Mater. 2020, 237, 117610. [Google Scholar] [CrossRef]
- Hu, J.; Deng, P.; Li, X.; Zhang, J.; Wang, G. The Vertical Non-Uniform Corrosion of Reinforced Concrete Exposed to the Marine Environments. Constr. Build. Mater. 2018, 183, 180–188. [Google Scholar] [CrossRef]
- Xi, X.; Yang, S.; Li, C.-Q. A Non-Uniform Corrosion Model and Meso-Scale Fracture Modelling of Concrete. Cem. Concr. Res. 2018, 108, 87–102. [Google Scholar] [CrossRef]
- Zhou, Y.; Gencturk, B.; Willam, K.; Attar, A. Carbonation-Induced and Chloride-Induced Corrosion in Reinforced Concrete Structures. J. Mater. Civ. Eng. 2015, 27, 04014245. [Google Scholar] [CrossRef]
- Campione, G.; Zizzo, M. Influence of Strands Corrosion on the Flexural Behavior of Prestressed Concrete Beams. Structures 2022, 45, 1366–1375. [Google Scholar] [CrossRef]
- Li, R.; Miao, C.; Zhang, Y.; Wang, Y.; Chen, X. Corrosion Characteristics and Damage Constitutive Model of Galvanized Steel Wires for Bridge Cables. Structures 2021, 34, 3414–3426. [Google Scholar] [CrossRef]
- Jikal, A.; Majid, F.; Chaffou, H.; Ghorba, M.E. Influence of Corrosion on the Mechanical Behavior of Strand of a Non-Rotating Wire Rope: Experimental Study. Procedia Struct. Integr. 2019, 18, 731–741. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.-J.; Shim, C.-S. Probabilistic Prediction of Mechanical Characteristics of Corroded Strands. Eng. Struct. 2020, 203, 109882. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Wang, X.; Tang, H. Effects of the Position and Chloride-Induced Corrosion of Strand on Bonding Behavior between the Steel Strand and Concrete. Structures 2023, 58, 105500. [Google Scholar] [CrossRef]
- Xia, R.; Zhou, J.; Zhang, H.; Zhou, D.; Zhang, Z. Experimental Study on Corrosion of Unstressed Steel Strand Based on Metal Magnetic Memory. KSCE J. Civ. Eng. 2019, 23, 1320–1329. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, Y.; Fang, K.; Zhang, Y.; Wang, C. Developing Fully Recycled Alkali-Activated Mortar Made with Waste Concrete Fines as a Substitute for Both Binder and Sand: Multi-Properties Evaluation. Constr. Build. Mater. 2025, 477, 141323. [Google Scholar] [CrossRef]
- Wang, C.; Lu, Y.; Dai, Y.; Wu, H.; Ma, Z. In-Situ 4D CT Analysis of Microcrack Evolution in Carbonated Fiber-Reinforced Recycled Aggregate Concrete. Cem. Concr. Compos. 2025, 163, 106161. [Google Scholar] [CrossRef]
- Shaikh, F.U.A. Effect of Cracking on Corrosion of Steel in Concrete. Int. J. Concr. Struct. Mater. 2018, 12, 3. [Google Scholar] [CrossRef]
- Cheng, X.; Su, Q.; Ma, F.; Liu, X.; Liang, X. Investigation on Crack Propagation of Concrete Cover Induced by Non-Uniform Corrosion of Multiple Rebars. Eng. Fract. Mech. 2018, 201, 366–384. [Google Scholar] [CrossRef]
- Guzmán, S.; Gálvez, J.C. Modelling of Concrete Cover Cracking Due to Non-Uniform Corrosion of Reinforcing Steel. Constr. Build. Mater. 2017, 155, 1063–1071. [Google Scholar] [CrossRef]
- Zhu, W.; Yu, K.; Xu, Y.; Zhang, K.; Cai, X. A Prediction Model of the Concrete Cracking Induced by the Non-Uniform Corrosion of the Steel Reinforcement. Materials 2020, 13, 830. [Google Scholar] [CrossRef]
- Otieno, M.; Beushausen, H.; Alexander, M. Chloride-Induced Corrosion of Steel in Cracked Concrete–Part II: Corrosion Rate Prediction Models. Cem. Concr. Res. 2016, 79, 386–394. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, J.; Wu, Y.; Jin, W. Corrosion-Induced Concrete Cracking Model Considering Corrosion Product-Filled Paste at the Concrete/Steel Interface. Constr. Build. Mater. 2016, 116, 273–280. [Google Scholar] [CrossRef]
- Michel, A.; Otieno, M.; Stang, H.; Geiker, M.R. Propagation of Steel Corrosion in Concrete: Experimental and Numerical Investigations. Cem. Concr. Compos. 2016, 70, 171–182. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Jin, W. Influence of Environment on the Development of Corrosion Product-Filled Paste and a Corrosion Layer at the Steel/Concrete Interface. Corros. Sci. 2017, 124, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Dai, L.; Bian, H.; Ma, Y.; Zhang, J. Concrete Cracking Prediction under Combined Prestress and Strand Corrosion. Struct. Infrastruct. Eng. 2019, 15, 285–295. [Google Scholar] [CrossRef]
- Charalambous, C.A.; Aylott, P.; Buxton, D. Stray Current Calculation and Monitoring in DC Mass-Transit Systems: Interpreting Calculations for Real-Life Conditions and Determining Appropriate Safety Margins. IEEE Veh. Technol. Mag. 2016, 11, 24–31. [Google Scholar] [CrossRef]
- GB/T 50082-2024; Standard for Test Methods of Long-Term Performance and Durability of Concrete. Ministry of Housing and Urban-Rural Development: Beijing, China, 2024.
- GB/T 5224-2023; Steel Strand for Prestressed Concrete. State Administration for Market Regulation and Standardization Administration of China: Beijing, China, 2023.
- Raman, A.; Kuban, B.; Razvan, A. The Application of Infrared Spectroscopy to the Study of Atmospheric Rust Systems-I. Standard Spectra and Illustrative Applications to Identify Rust Phases in Natural Atmospheric Corrosion Products. Corros. Sci. 1991, 32, 1295–1306. [Google Scholar] [CrossRef]
- Dillmann, P.; Mazaudier, F.; Hœrlé, S. Advances in Understanding Atmospheric Corrosion of Iron. I. Rust Characterization of Ancient Ferrous Artefacts Exposed to Indoor Atmospheric Corrosion. Corros. Sci. 2004, 46, 1401–1429. [Google Scholar] [CrossRef]
- Andrade, C.; Alonso, C.; Molina, F.J. Cover Cracking as a Function of Bar Corrosion: Part I-Experimental Test. Mater. Struct. 1993, 26, 453–464. [Google Scholar] [CrossRef]
- Zhang, R.; Castel, A.; François, R. Concrete Cover Cracking with Reinforcement Corrosion of RC Beam during Chloride-Induced Corrosion Process. Cem. Concr. Res. 2010, 40, 415–425. [Google Scholar] [CrossRef]
- Vidal, T.; Castel, A.; François, R. Analyzing Crack Width to Predict Corrosion in Reinforced Concrete. Cem. Concr. Res. 2004, 34, 165–174. [Google Scholar] [CrossRef]
- Liu, T.; Weyers, R.W. Modeling the Dynamic Corrosion Process in Chloride Contaminated Concrete Structures. Cem. Concr. Res. 1998, 28, 365–379. [Google Scholar] [CrossRef]
- Alonso, C.; Andrade, C.; Rodriguez, J.; Diez, J.M. Factors Controlling Cracking of Concrete Affected by Reinforcement Corrosion. Mat. Struct. 1998, 31, 435–441. [Google Scholar] [CrossRef]





| Material | CaO | SiO2 | Al2O3 | Fe2O3 | MgO | SO3 | K2O |
|---|---|---|---|---|---|---|---|
| Cement | 64.64 | 18.62 | 4.66 | 4.18 | 2.35 | 3.27 | 0.92 |
| W/C Ratio (%) | Cement (kg/m3) | Water (kg/m3) | Fine Aggregate (kg/m3) | Coarse Aggregate (kg/m3) |
|---|---|---|---|---|
| 0.45 | 422.5 | 190 | 537 | 1361 |
| Group | I (mA) | t (d) | Group | I (mA) | t (d) |
|---|---|---|---|---|---|
| S1-0 | 10 | / | PS1-1 | 20 | 42 |
| S1-1 | 20 | 42 | PS1-2 | 49 | |
| S1-2 | 49 | PS1-3 | 56 | ||
| S1-3 | 56 | PS1-4 | 63 | ||
| S1-4 | 63 | PS1-5 | 70 | ||
| S2-0 | 30 | / | PS2-1 | 40 | 42 |
| S2-1 | 40 | 42 | PS2-2 | 49 | |
| S2-2 | 49 | PS2-3 | 56 | ||
| S2-3 | 56 | PS2-4 | 63 | ||
| S2-4 | 63 | PS2-5 | 70 | ||
| S3-0 | 50 | / | PS3-1 | 60 | 42 |
| S3-1 | 60 | 42 | PS3-2 | 49 | |
| S3-2 | 49 | PS3-3 | 56 | ||
| S3-3 | 56 | PS3-4 | 63 | ||
| S3-4 | 63 | PS3-5 | 70 |
| Group | η (%) | I (mA) | t (d) | wave (mm) | wmax (mm) | lc (mm) | Sc (mm2) |
|---|---|---|---|---|---|---|---|
| S1-1 | 2.35 | 20 | 42 | 0.33 | 0.38 | 168.24 | 63.93 |
| S1-2 | 2.92 | 20 | 49 | 0.61 | 0.67 | 177.35 | 118.82 |
| S1-3 | 3.86 | 20 | 56 | 0.87 | 1.02 | 182.10 | 185.74 |
| S1-4 | 4.81 | 20 | 63 | 1.25 | 1.27 | 185.42 | 235.48 |
| S2-1 | 6.80 | 40 | 42 | 1.12 | 1.18 | 179.68 | 212.02 |
| S2-2 | 7.59 | 40 | 49 | 1.60 | 1.63 | 180.93 | 294.92 |
| S2-3 | 8.28 | 40 | 56 | 2.18 | 2.21 | 188.71 | 417.05 |
| S2-4 | 9.75 | 40 | 63 | 2.56 | 2.58 | 180.57 | 465.87 |
| S3-1 | 11.52 | 60 | 42 | 3.53 | 3.59 | 177.25 | 636.33 |
| S3-2 | 12.74 | 60 | 49 | 4.29 | 4.31 | 183.96 | 792.87 |
| S3-3 | 14.37 | 60 | 56 | 4.94 | 4.96 | 178.19 | 883.82 |
| S3-4 | 15.08 | 60 | 63 | 5.25 | 5.34 | 176.64 | 943.26 |
| Group | η (%) | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (GPa) | Elongation (%) | |||
|---|---|---|---|---|---|---|---|---|
| Test | Relative | Test | Relative | Test | Relative | |||
| PS1-1 | 2.45 | 1623 | 0.972 | 1783 | 0.918 | 201.7 | 0.999 | 3.43 |
| PS1-2 | 2.87 | 1615 | 0.967 | 1774 | 0.914 | 198.5 | 0.983 | 3.25 |
| PS1-3 | 3.62 | 1608 | 0.963 | 1726 | 0.890 | 196.2 | 0.971 | 2.97 |
| PS1-4 | 4.91 | 1596 | 0.956 | 1702 | 0.877 | 198.5 | 0.983 | 2.49 |
| PS1-5 | 5.23 | 1604 | 0.960 | 1711 | 0.882 | 201.9 | 1.000 | 1.92 |
| PS2-1 | 6.67 | / | / | 1572 | 0.810 | 198.4 | 0.834 | 1.51 |
| PS2-2 | 7.32 | / | / | 1524 | 0.786 | 192.9 | 0.891 | 1.25 |
| PS2-3 | 8.03 | / | / | 1549 | 0.798 | 192.7 | 0.855 | 1.18 |
| PS2-4 | 9.44 | / | / | 1437 | 0.741 | 191.3 | 0.813 | 1.07 |
| PS2-5 | 10.01 | / | / | 1416 | 0.730 | 190.3 | 0.868 | 1.03 |
| PS3-1 | 11.71 | / | / | 1327 | 0.684 | 188.1 | 0.832 | 0.93 |
| PS3-2 | 12.12 | / | / | 1245 | 0.642 | 182.5 | 0.804 | 0.89 |
| PS3-3 | 14.11 | / | / | 1208 | 0.623 | 177.5 | 0.780 | 0.82 |
| PS3-4 | 14.88 | / | / | 1224 | 0.631 | 177.0 | 0.752 | 0.85 |
| PS3-5 | 15.06 | / | / | 1109 | 0.572 | 174.3 | 0.769 | 0.87 |
| Parameter | Epc | fpuc | εpuc |
|---|---|---|---|
| Expression | (1 − 0.01667η) Ep | (1 − 0.02825η) fpu | (0.11073 + 0.88927e−η) εpu |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, Y.; Zhu, E.; Chen, L. Steel Strand Corrosion and Corrosion-Induced Cracking in Prestressed Concrete Under Stray Current. Buildings 2025, 15, 3681. https://doi.org/10.3390/buildings15203681
Ni Y, Zhu E, Chen L. Steel Strand Corrosion and Corrosion-Induced Cracking in Prestressed Concrete Under Stray Current. Buildings. 2025; 15(20):3681. https://doi.org/10.3390/buildings15203681
Chicago/Turabian StyleNi, Yuancheng, Eryu Zhu, and Liangjiang Chen. 2025. "Steel Strand Corrosion and Corrosion-Induced Cracking in Prestressed Concrete Under Stray Current" Buildings 15, no. 20: 3681. https://doi.org/10.3390/buildings15203681
APA StyleNi, Y., Zhu, E., & Chen, L. (2025). Steel Strand Corrosion and Corrosion-Induced Cracking in Prestressed Concrete Under Stray Current. Buildings, 15(20), 3681. https://doi.org/10.3390/buildings15203681