1. Introduction
Pile foundations are widely used in construction projects in karst regions because of their high load-bearing capacity, ability to penetrate karst cavities, and effectiveness in transferring loads to more competent rock layers [
1,
2,
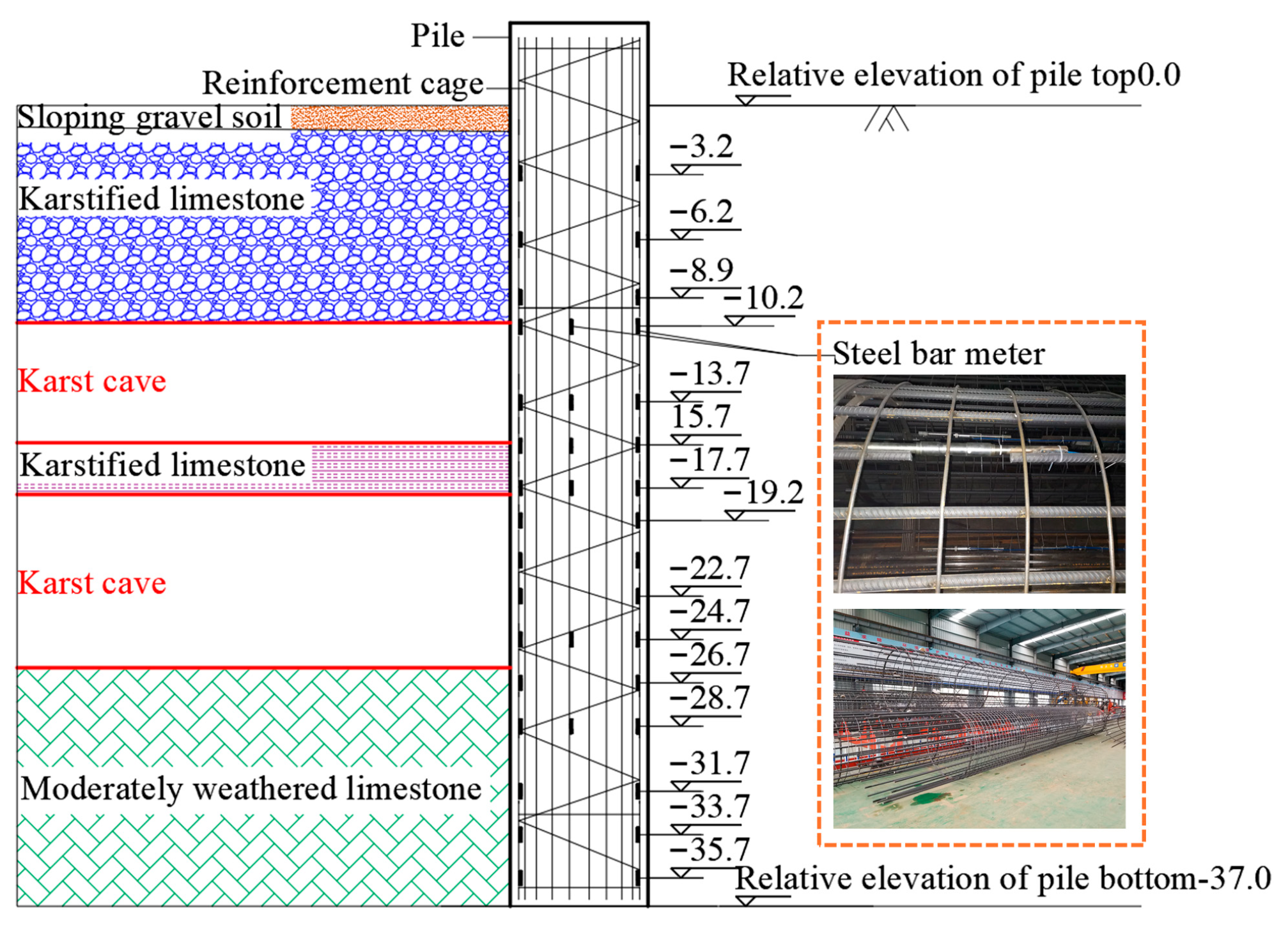
3]. When piles pass through karst cavities, backfilling with rubble and clay is commonly employed as a treatment method, typically at a ratio of 4:6. However, the consolidation settlement of the backfill can induce negative skin friction along the sides of the pile foundations. Neglecting the effects of negative skin friction may lead to safety risks in engineering construction. Therefore, investigating the distribution and calculation methods of negative skin friction in pile foundations within karst regions is of great practical significance.
Currently, many scholars are investigating the vertical bearing characteristics and the calculation methods of negative skin friction for pile foundations in karst regions. Chen investigated the load-bearing characteristics of piles under 11 different karst cavity conditions through centrifuge model tests and established a formula for calculating pile bearing capacity [
4]. Feng conducted a load test on a pile passing through a 25.5 m giant cavity and determined the influence range of the pile when the backfilling method was applied [
5]. Jiang established a formula for calculating the backfill–settlement curve in the super-large karst cave in the karst area based on the load transfer exponential function and verified the calculated results with engineering examples [
6]. Zhao proposed a calculation method for the safe roof thickness of the karst cave, considering the side resistance of the rock-socking section of the pile foundation in the karst area using a theoretical method [
7]. Kiyosumi analyzed the model tests of shallow foundations above karst cavities and proposed three failure modes for the cavity–foundation system [
8]. Dong conducted the static load tests on bridge pile foundations in karst areas and found that the hyperbolic model provided conservative and highly accurate predictions of the pile’s ultimate bearing capacity [
9]. Yin studied the influence of the underlying cave on the bearing characteristics of a single pile. This research showed that the influence of the cave height on the ultimate bearing capacity of a single pile was not obvious. The influence of the roof thickness, span and rock strength on the bearing capacity of pile was greater [
10]. Huang used the numerical simulation software to analyze the failure modes of the karst cavities under load, concluding that the ratio of top slab thickness to cavity span significantly affected the failure mechanism [
11]. Xie conducted orthogonal numerical simulations on karst pile foundations under various influencing factors and found that cavity height had little impact on the vertical bearing characteristics of the piles, while the ultimate vertical bearing capacity decreased with increasing cavity span and increased with the strengthening of the top slab rock [
12]. Wang and Hei combined field tests and theoretical methods to provide design and calculation methods for pile foundations in karst areas under different influencing factors [
13,
14]. Johanssen proposed using the limit equilibrium method to calculate negative skin friction by determining the average vertical effective stress in the surrounding soil, then applying a negative skin friction coefficient to obtain the final value [
15].
At present, the main method for calculating negative skin friction is to use a negative skin friction coefficient. This coefficient is primarily an empirical value, and therefore the accuracy of the calculation is relatively low. Although this method is simple to apply, it is generally adopted in design specifications [
16,
17,
18,
19]. Huang regarded the pile response as a weighted average of complete and adjusted states and analyzed the load transfer function of the pile foundation, proposing parameter selection strategies and investigating the influence of different factors [
20]. Zhou proposed a novel method for calculating negative skin friction that comprehensively accounts for the whole process of stress state alterations occurring during soil deformation and described the relationship between soil deformation and stress using a hyperbolic mechanical model [
21]. Chen conducted field tests on bridge pile foundations treated by backfilling and provided guidelines for determining the range of negative skin friction at different cavity heights [
22]. Qiu derived the variation patterns of the end resistance and side friction under different pile diameters based on the Mindlin, representing side friction distributions as stress coefficients multiplied by unit resistance and proposing a novel formula for stress coefficients under spatial conditions [
23]. Mao and Zhao studied the calculation model of pile side friction resistance in elastic and plastic sections of the pile’s foundation. They proposed a calculation method for determining the neutral point position of piles and the magnitude and distribution law of the negative skin friction resistance of the pile foundation. This was based on load transfer and the effective stress method [
24,
25]. Few previous studies have investigated the negative skin friction of piles induced by the settlement of backfilling materials after karst cave treatment.
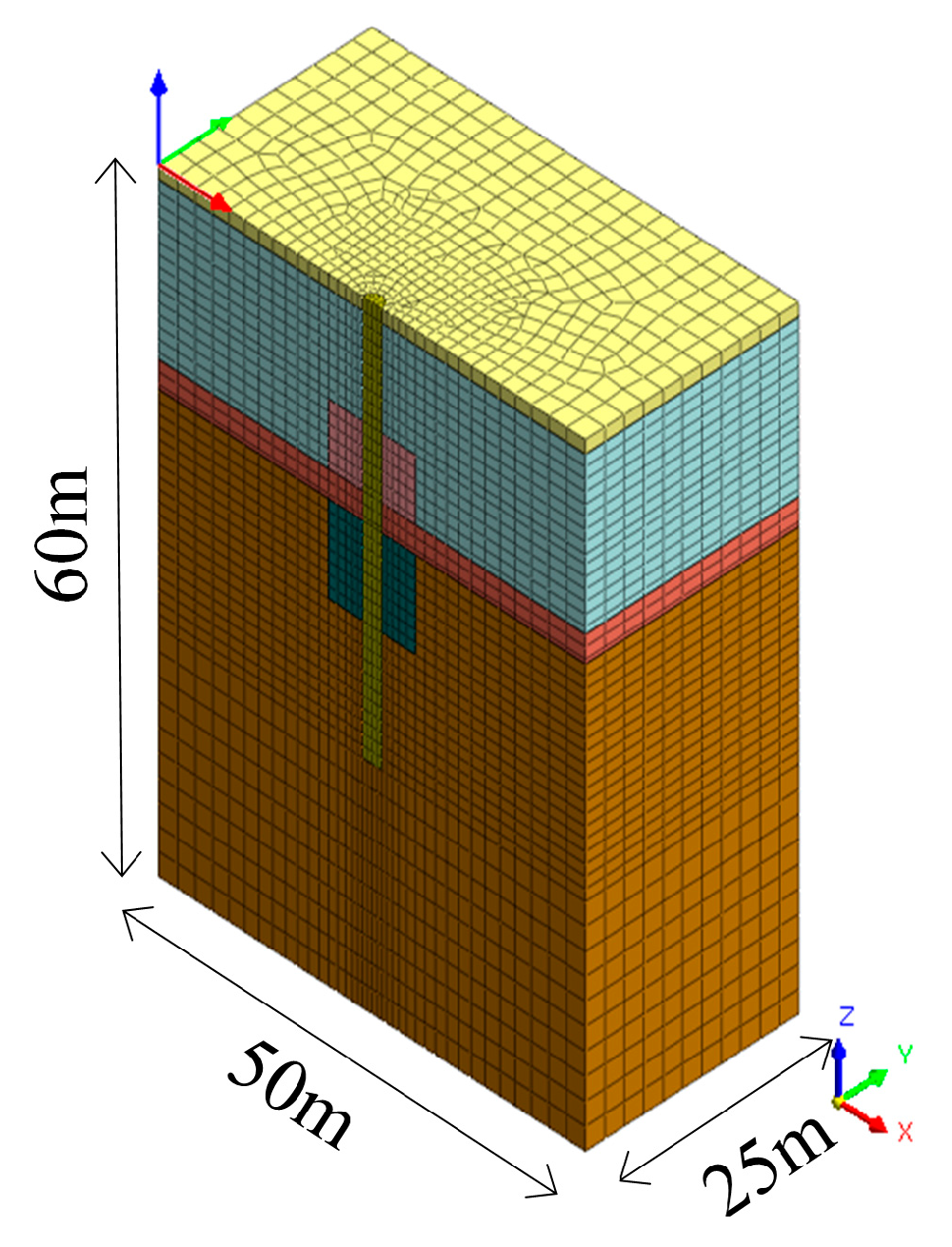
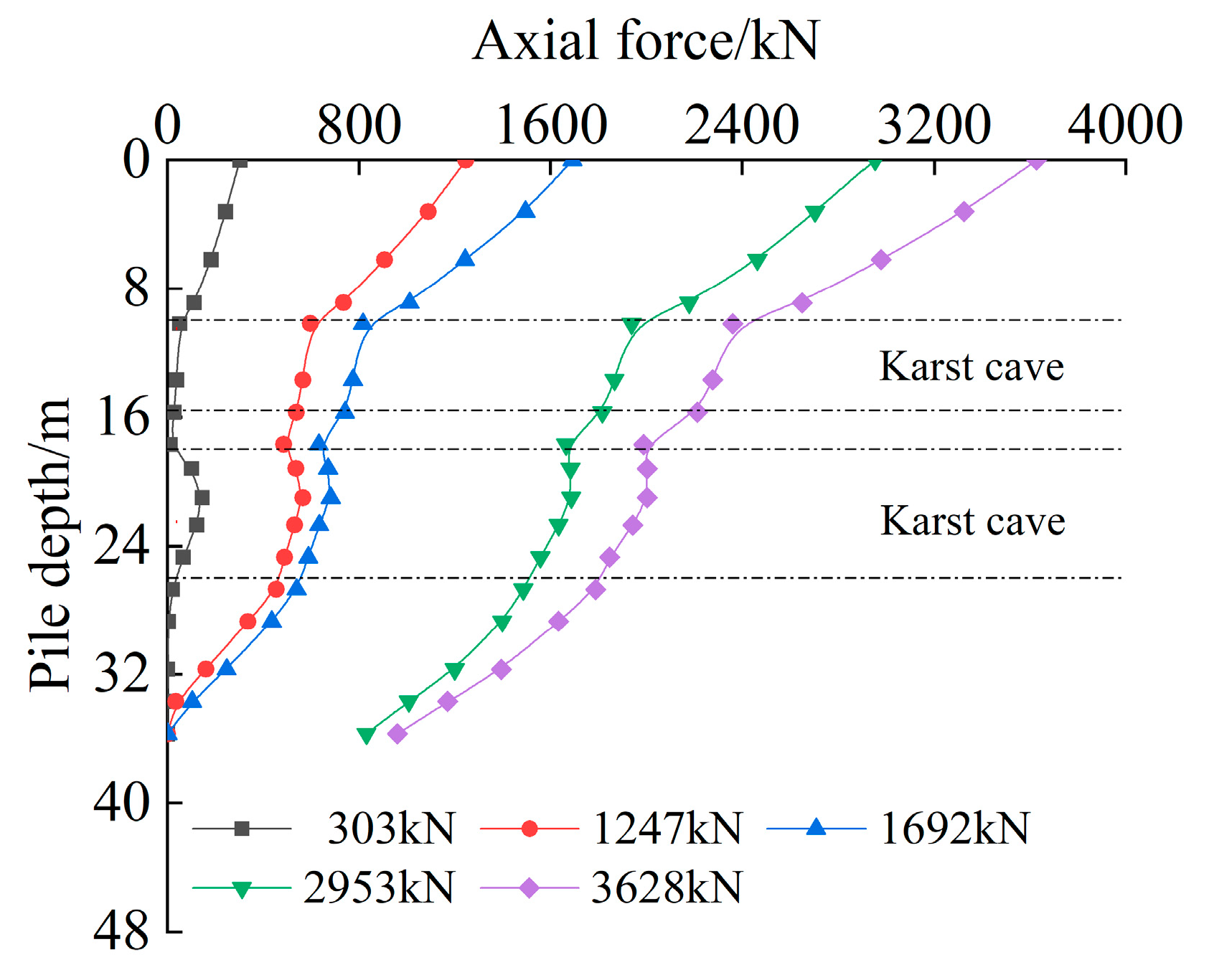
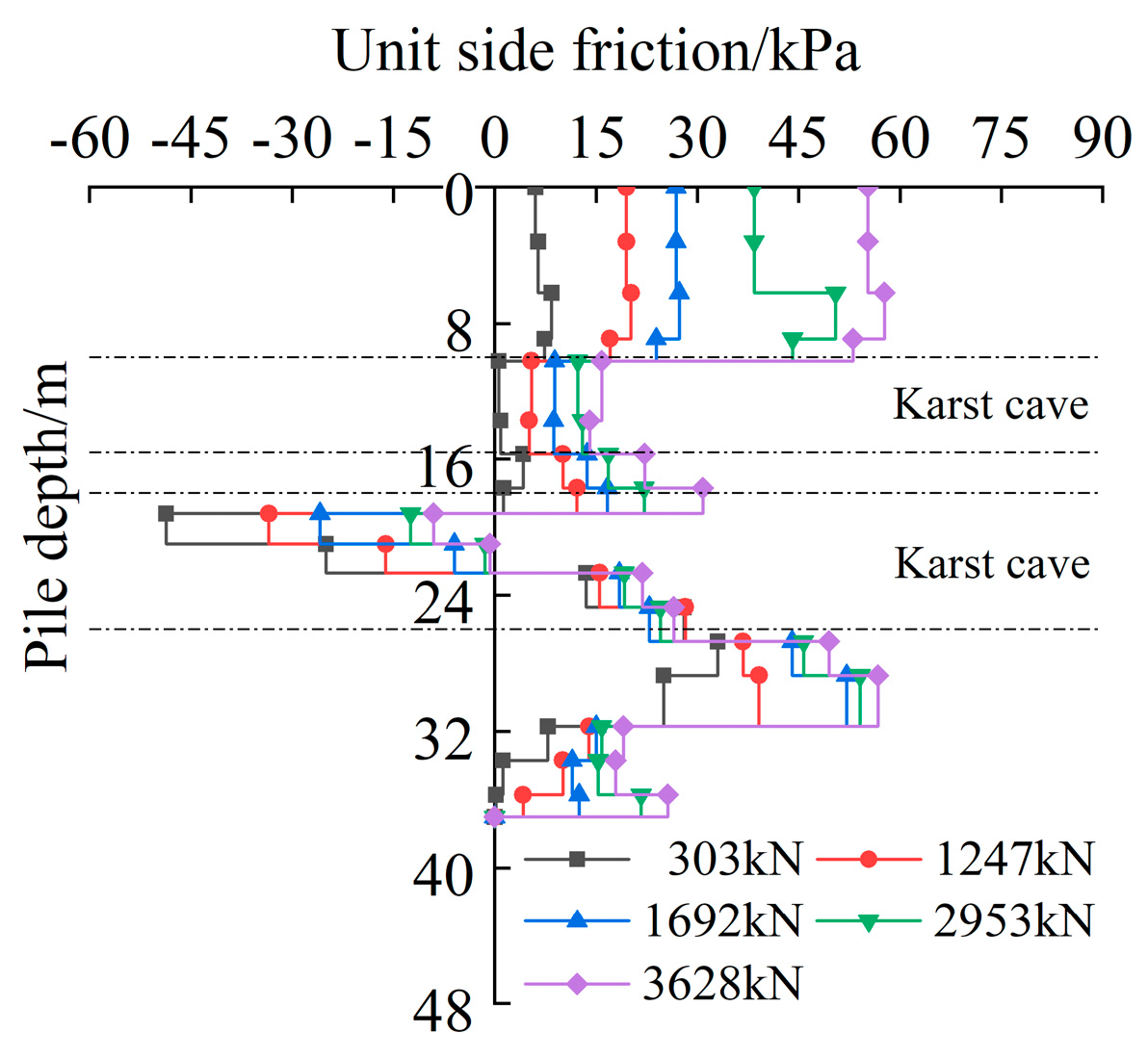
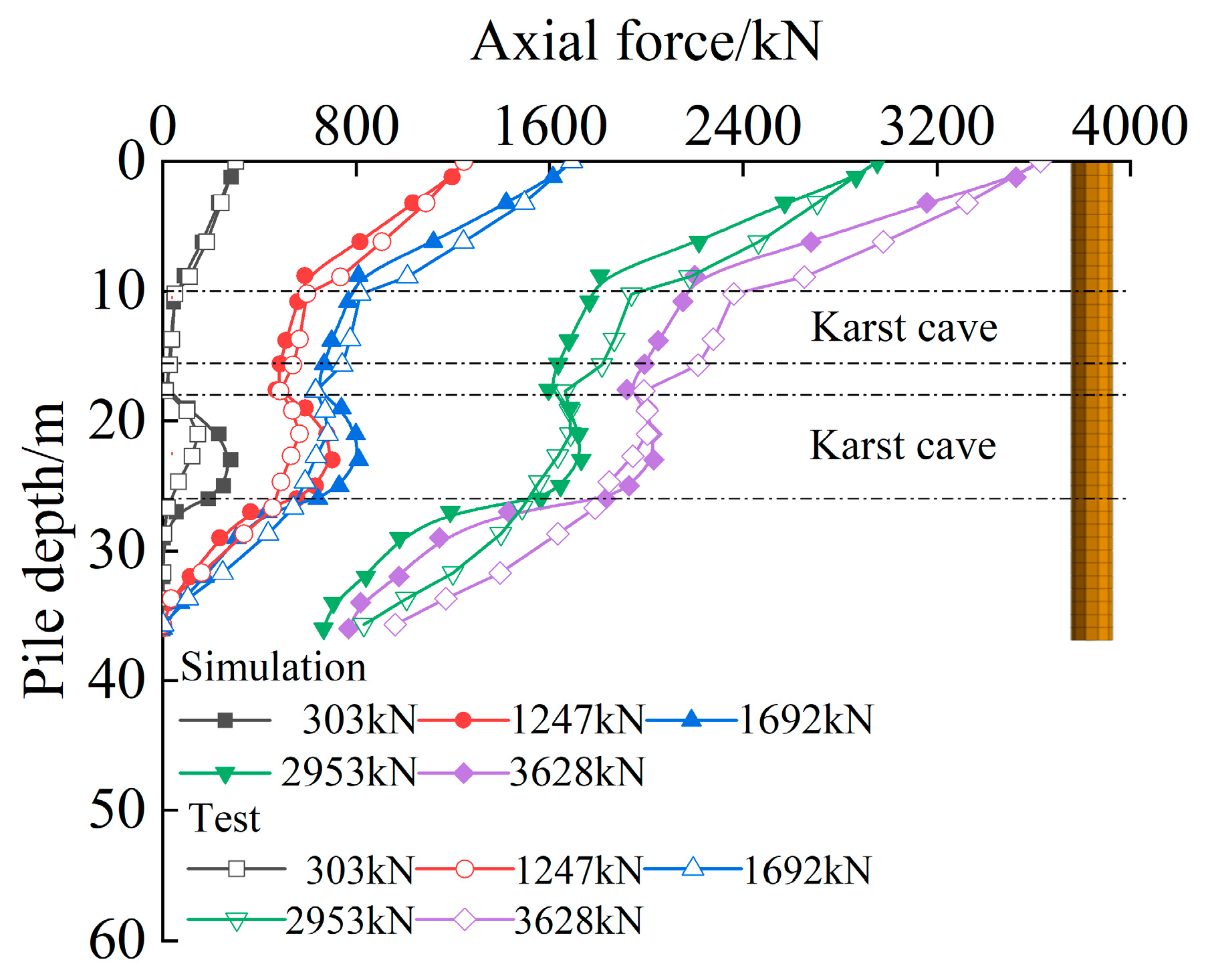
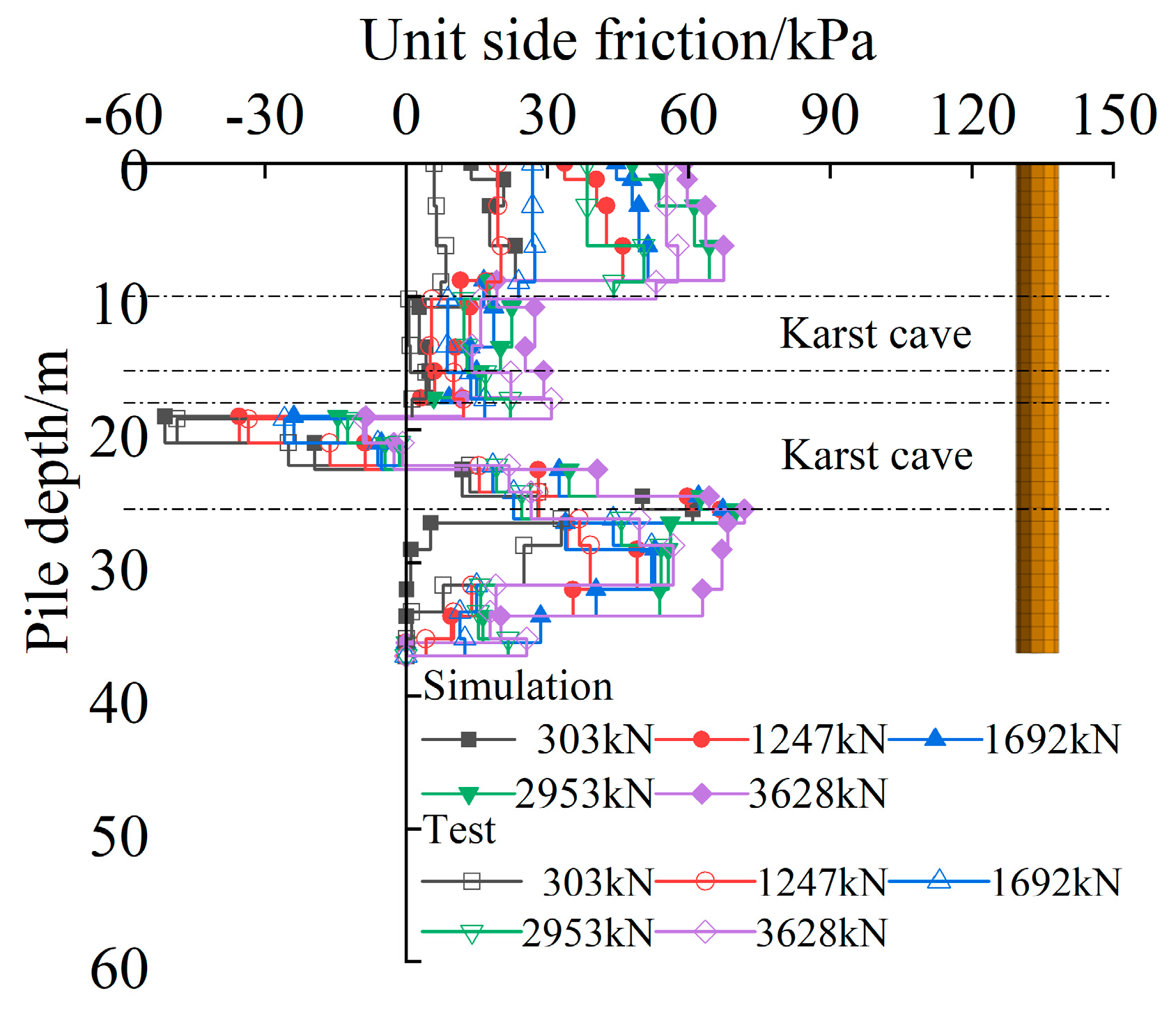
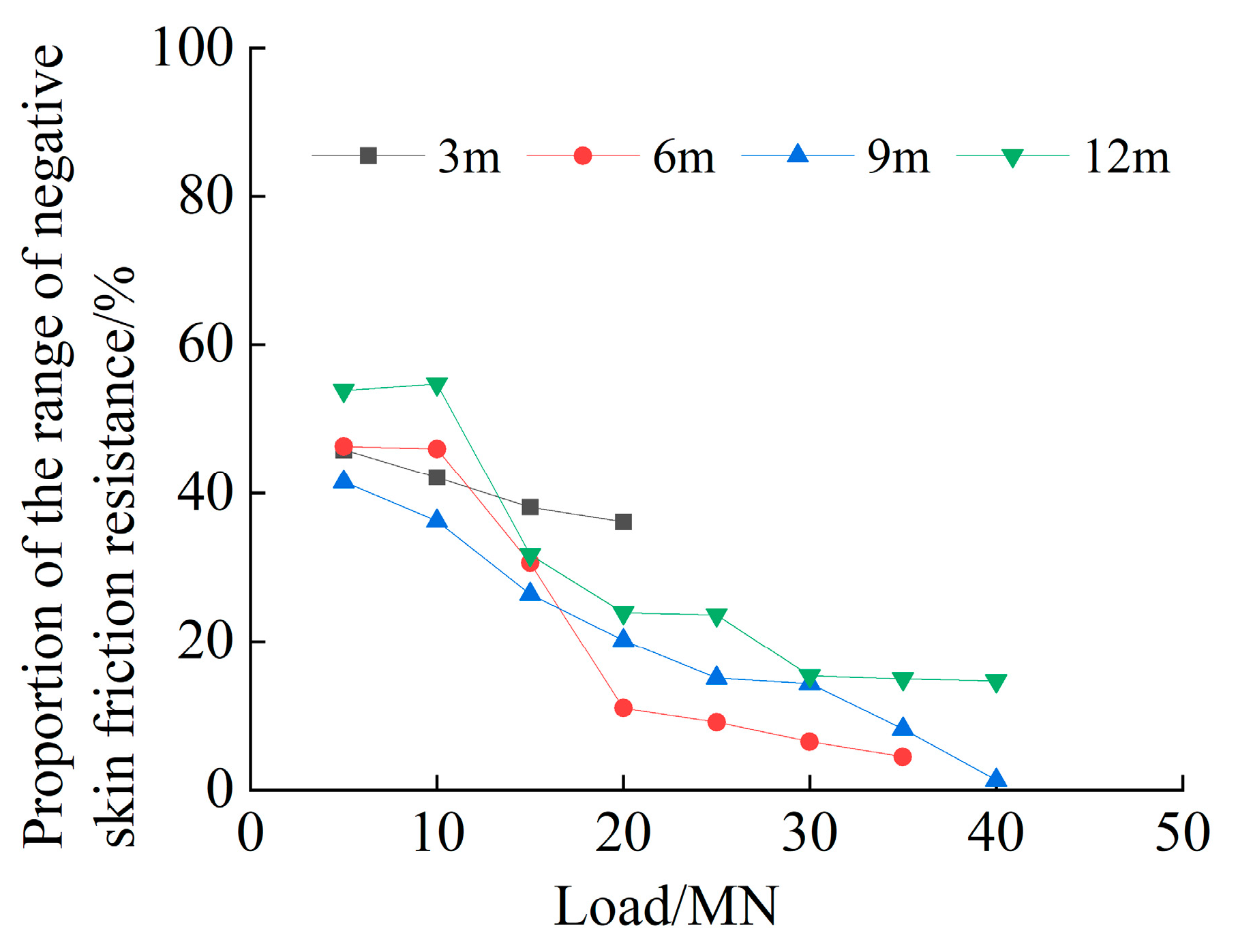
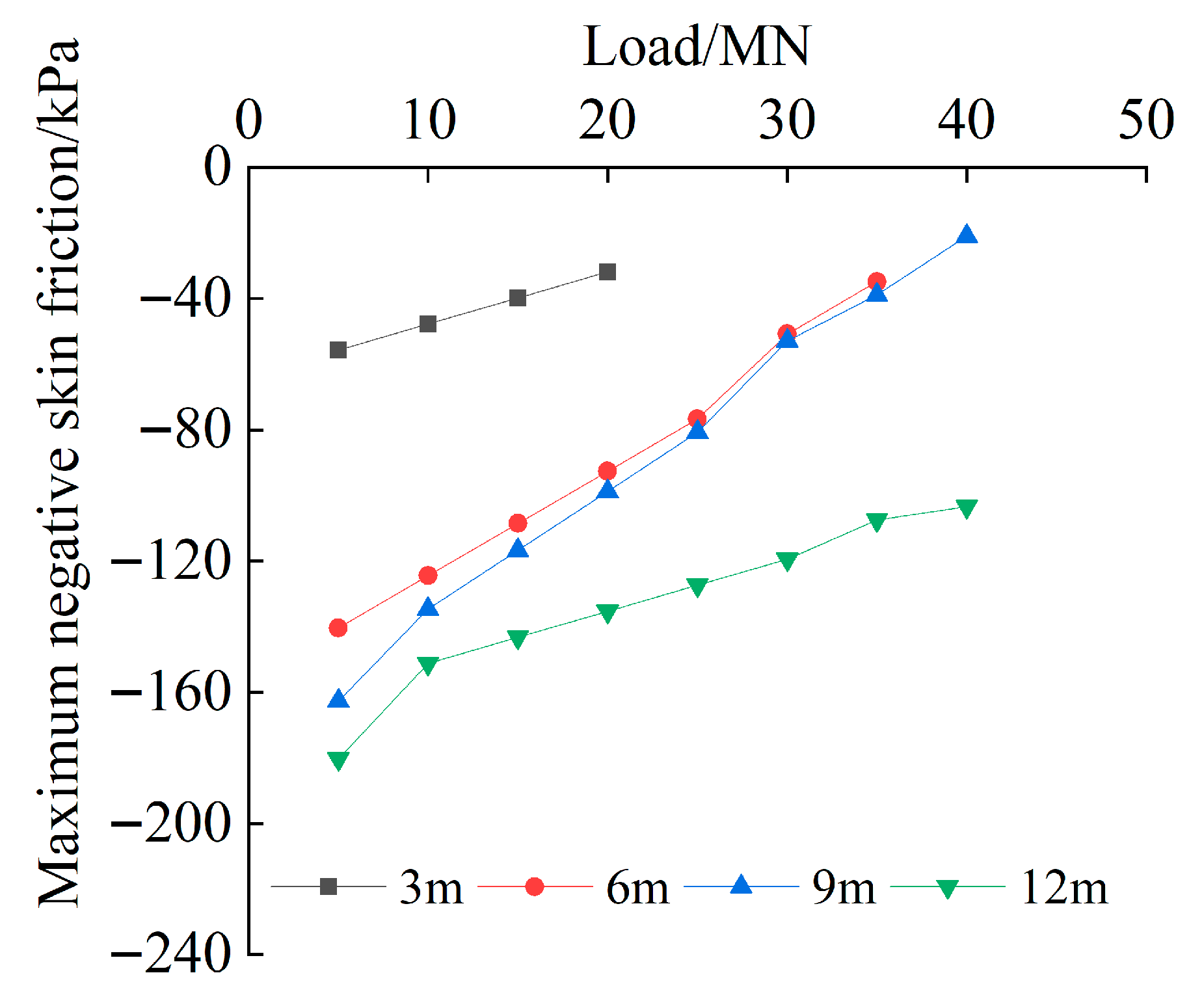
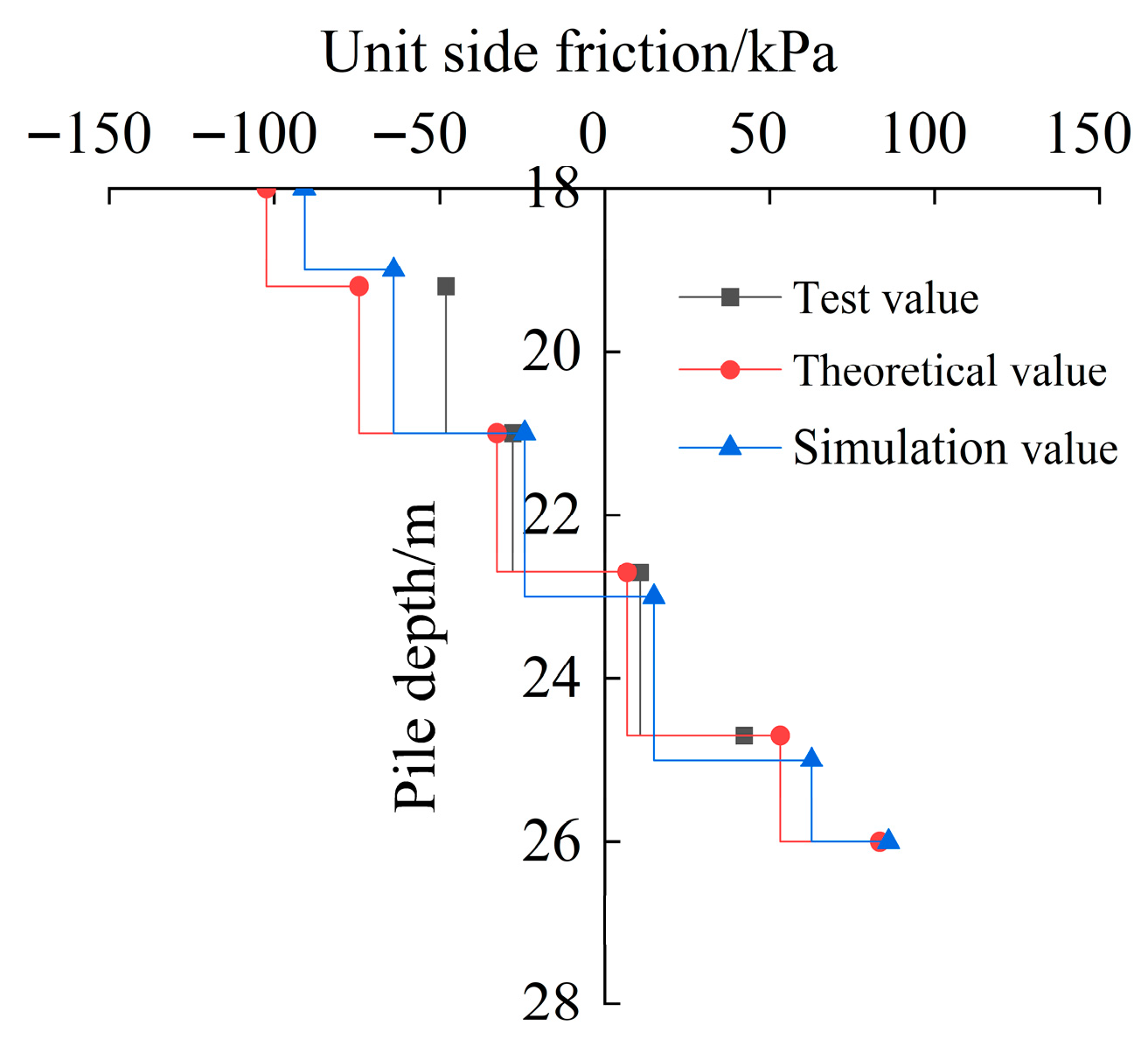
This study addresses this gap by combining orthogonal testing with field validation to establish a calculation method for negative skin friction under such conditions. The load transfer mechanism of the pile foundation of the bridge passing through the karst cave was studied using a field test. The influence of different fillings on the load transfer mechanism of the pile foundation was investigated. The negative skin friction range at different cave heights was analyzed using numerical simulation. A calculation method was adopted for negative skin friction in pile foundations treated with the backfilling method in karst areas. In addition, the sensitivity of negative skin friction in pile foundations to the above factors was evaluated.
4. Discussion
The calculation method for negative skin friction proposed in this paper demonstrates variation patterns that are consistent with the field results. The calculated values and ranges of negative skin friction are slightly higher, thereby providing a safer design basis for bridge pile foundations in karst areas. This method offers a useful reference for the design of pile foundations under the backfilling treatment of karst cavities.
In this study, single representative values of interface cohesion (16 kPa) and friction angle (15°) were adopted. In practice, these parameters should vary with soil type and depth. This simplification is acknowledged as a limitation, and future work will incorporate depth-dependent and soil-specific interface parameters to refine the model. Inevitably, the numerical model also involved other simplified assumptions. These may not fully capture the complexity of karst conditions. Nevertheless, these assumptions were necessary to ensure computational feasibility and to emphasize the key factors influencing negative skin friction. The close agreement between model predictions and field test results supports the reliability of the proposed approach within the defined scope.