Shear Capacity of Masonry Walls Externally Strengthened via Reinforced Khorasan Jacketing
Abstract
1. Introduction
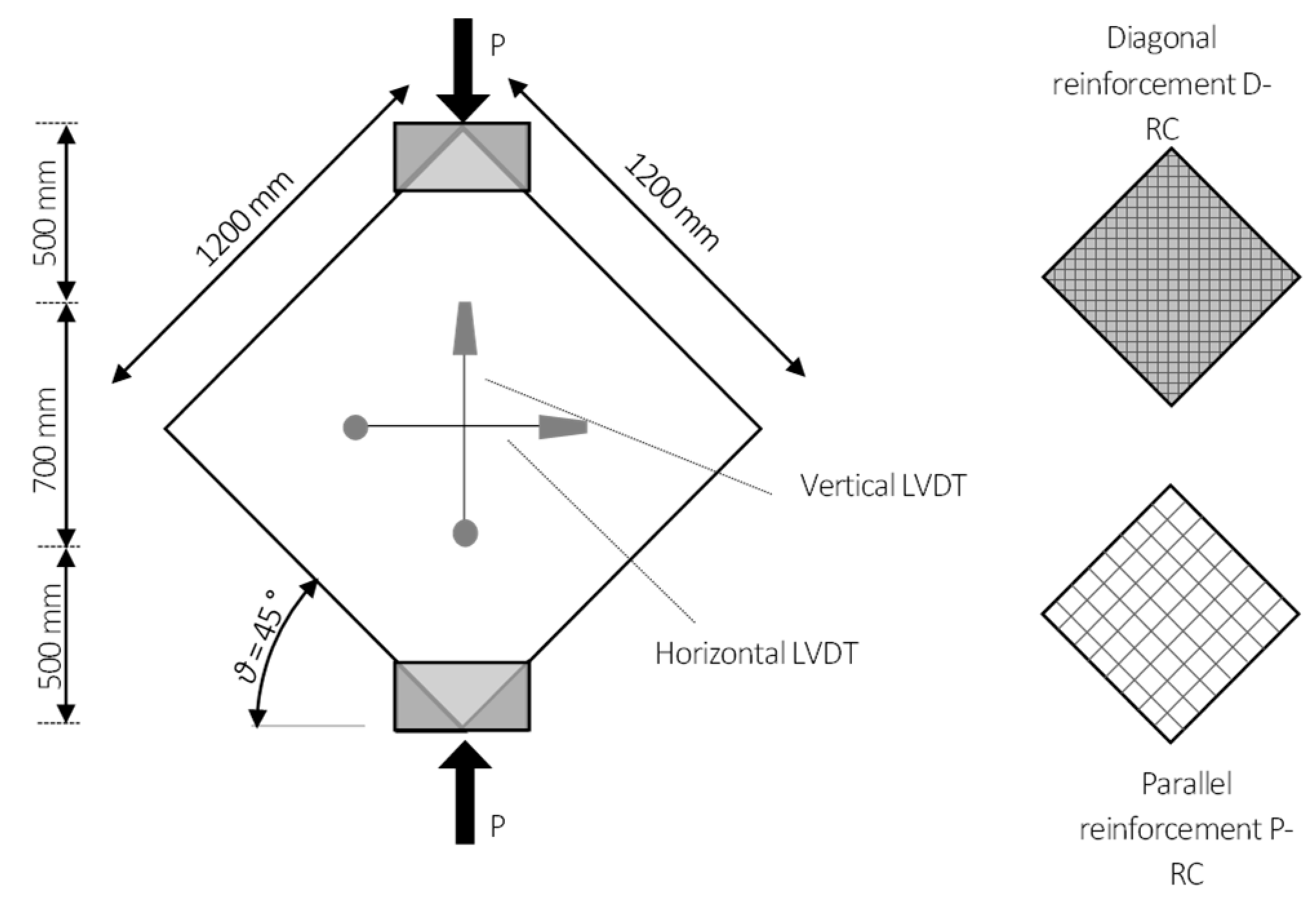
2. Materials and Methods
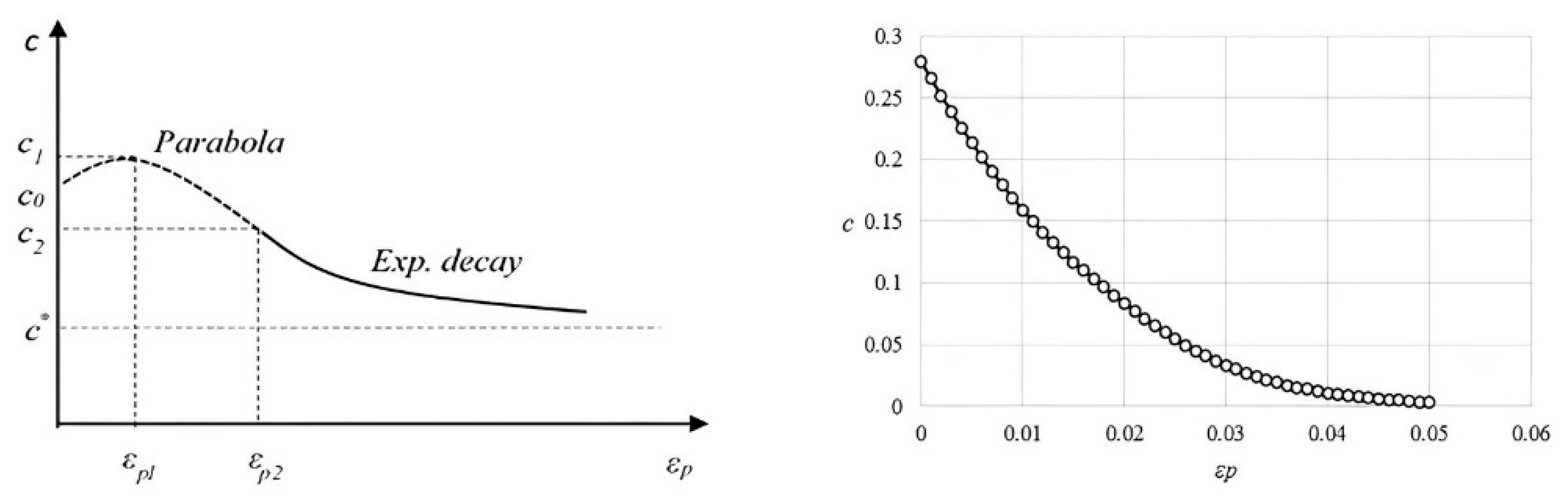
3. Numerical Modeling
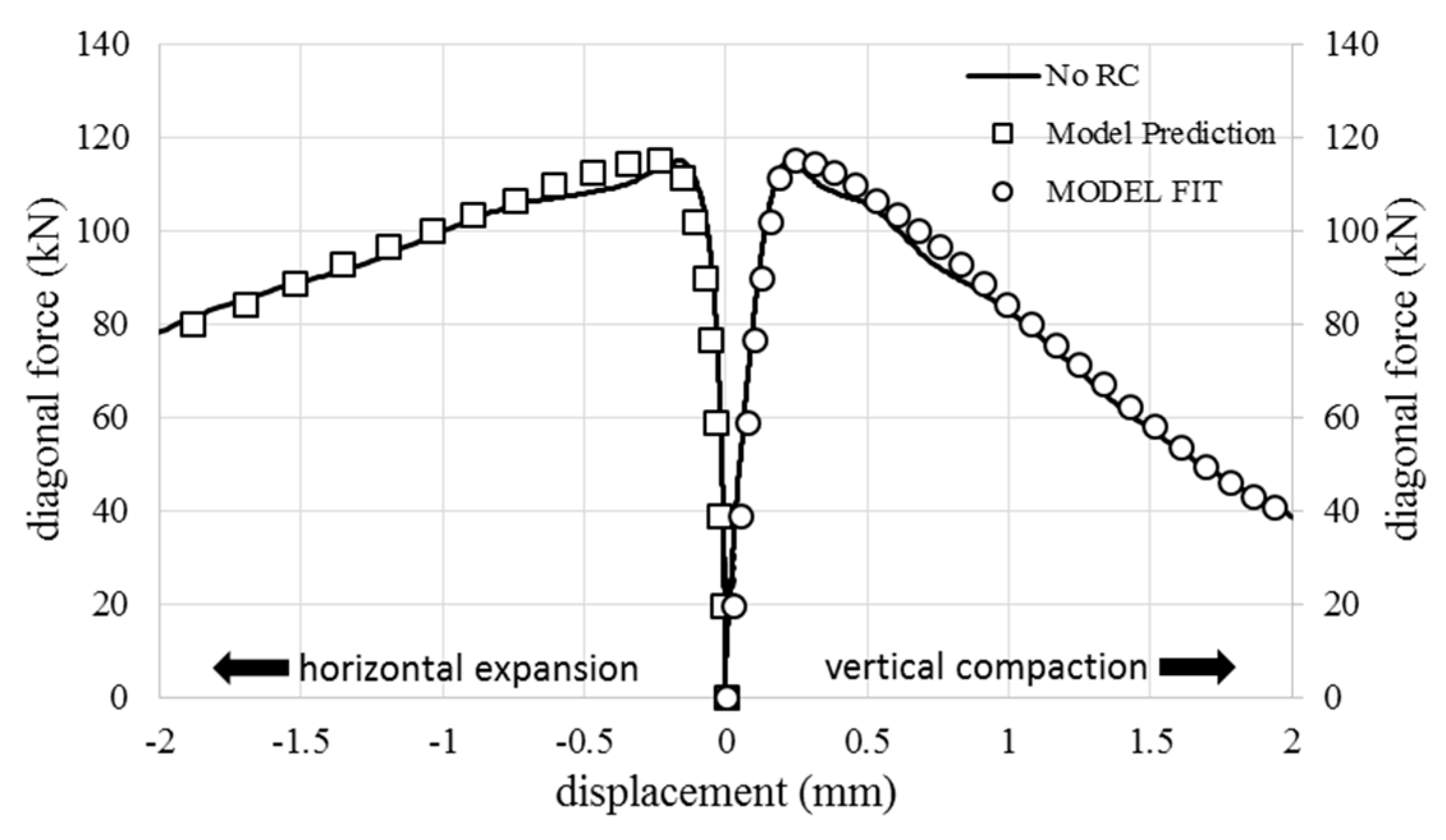
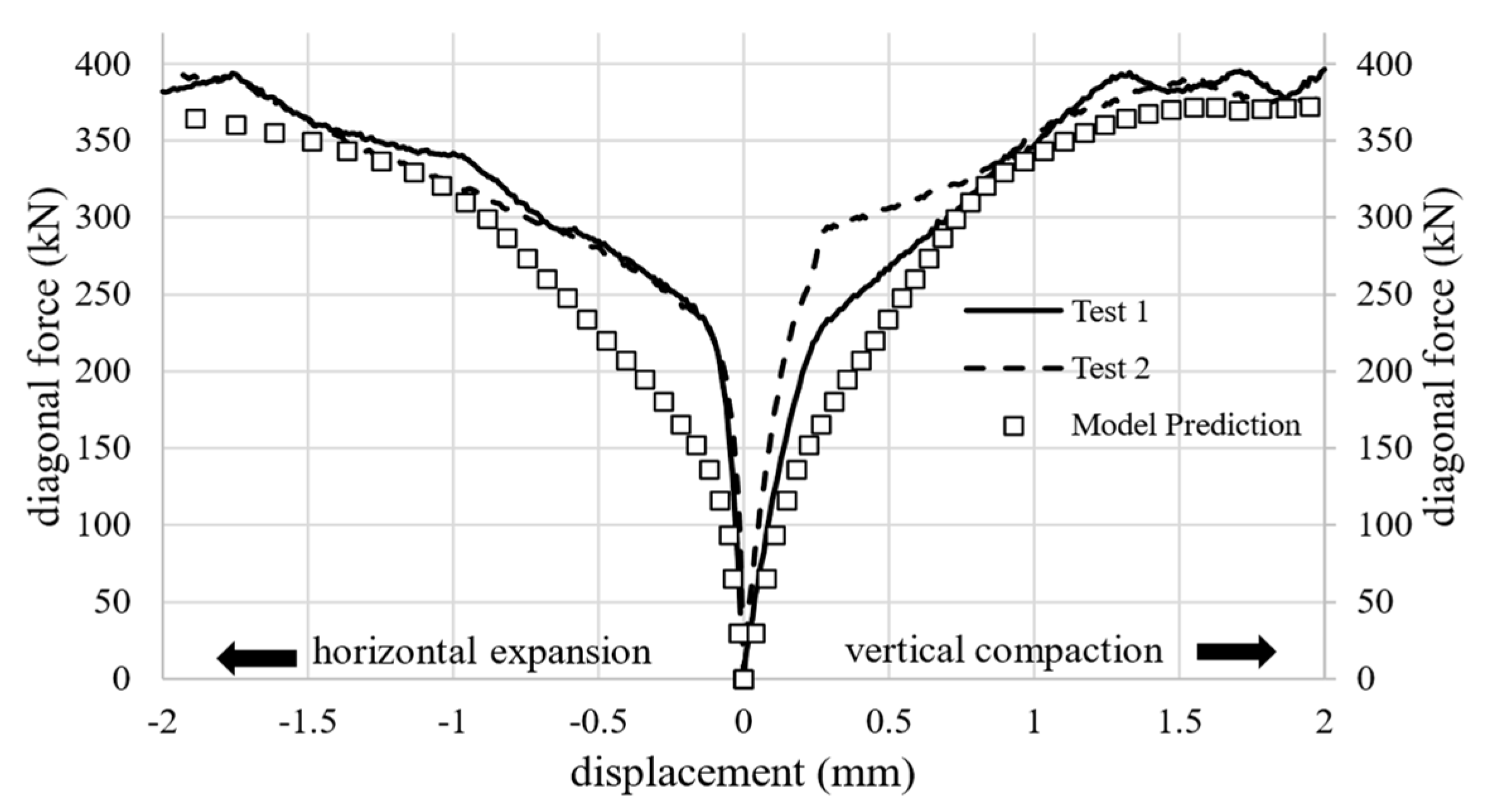
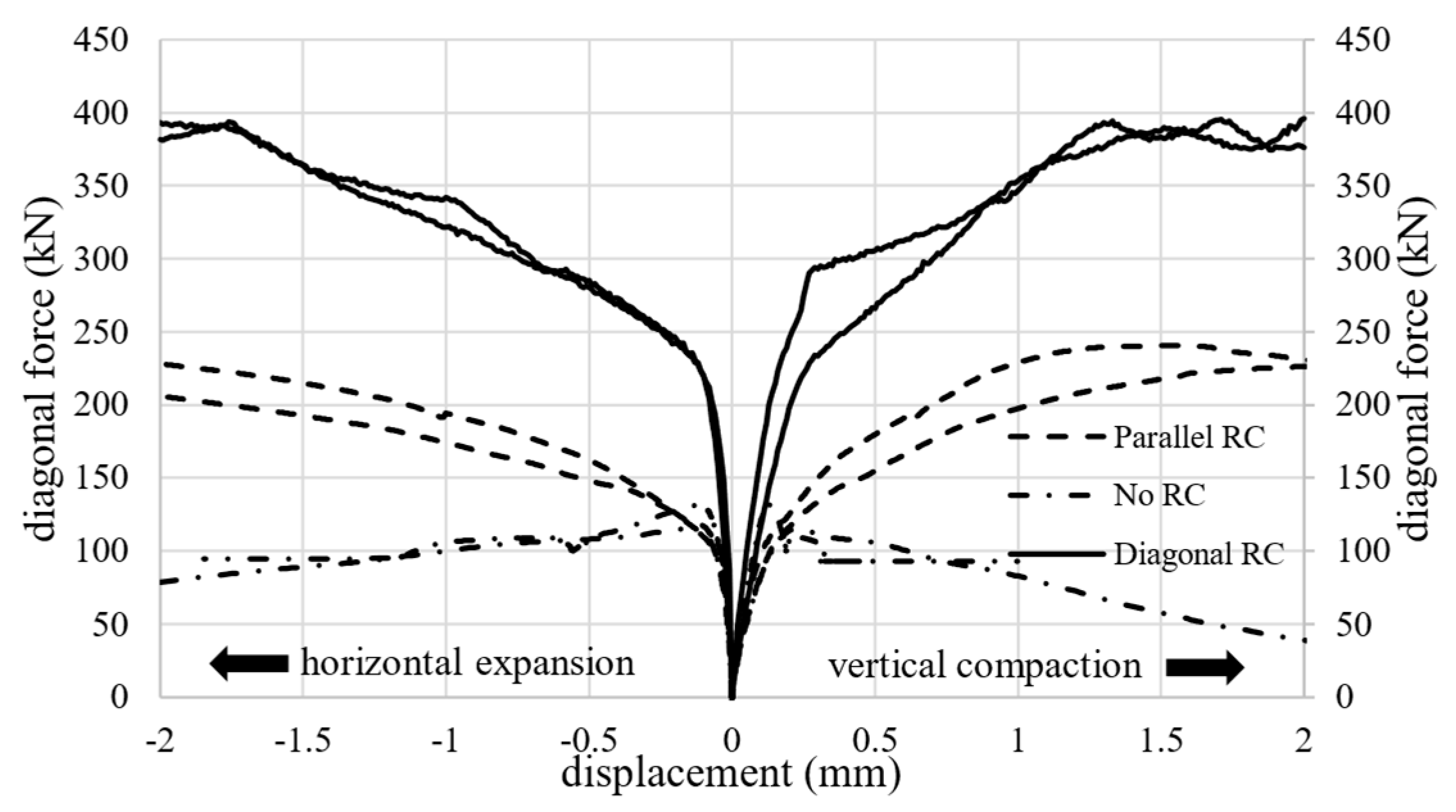
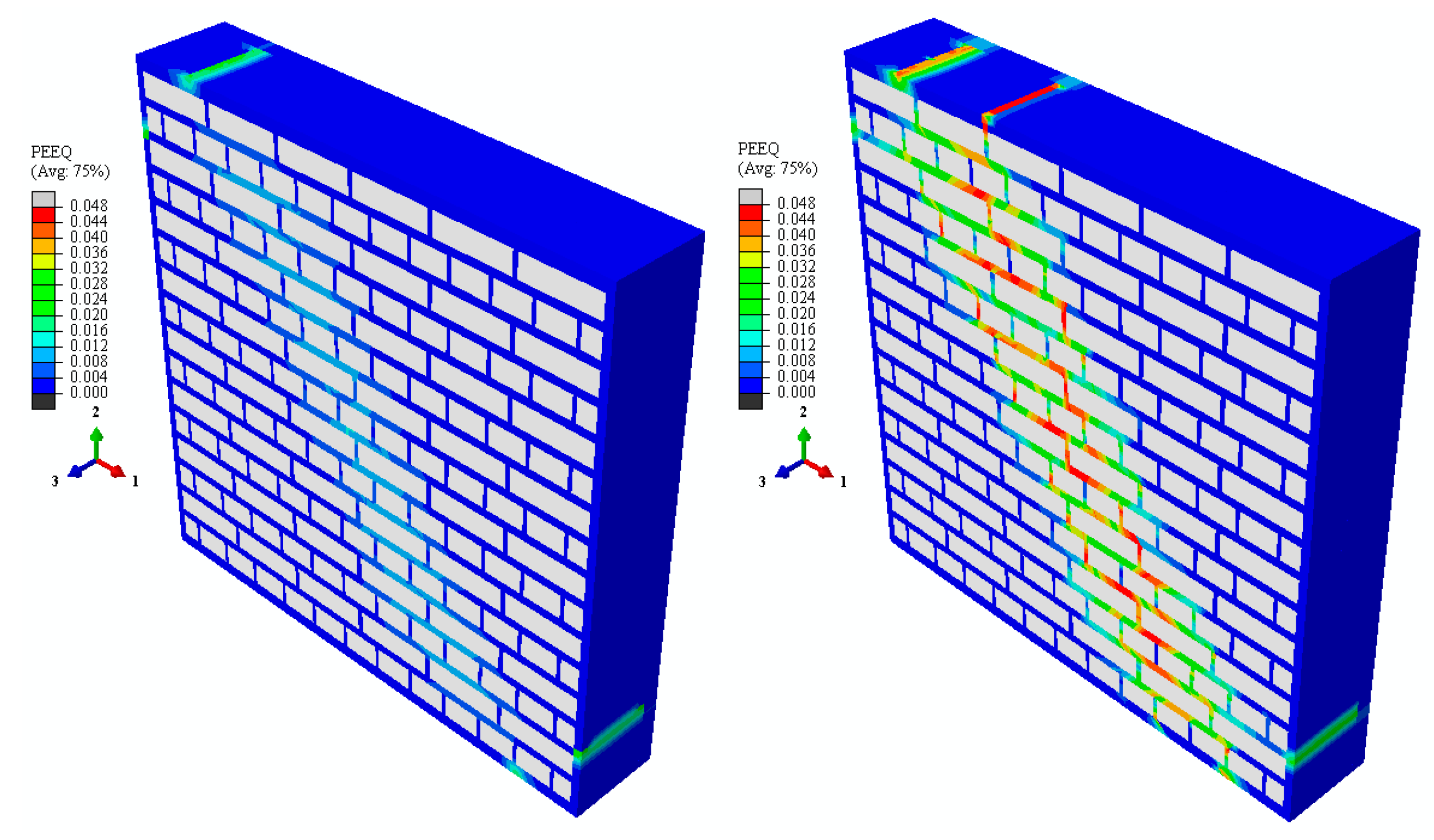
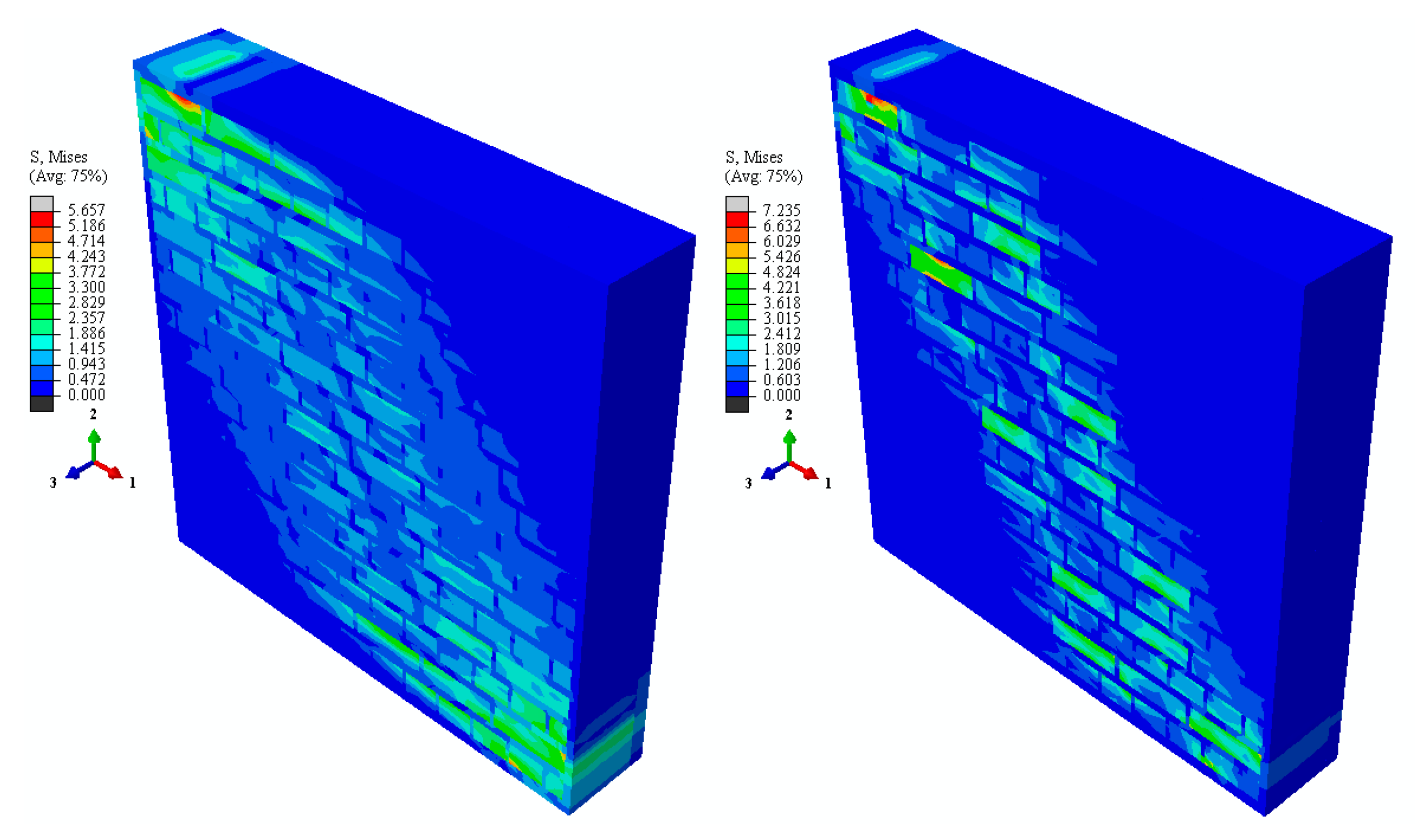
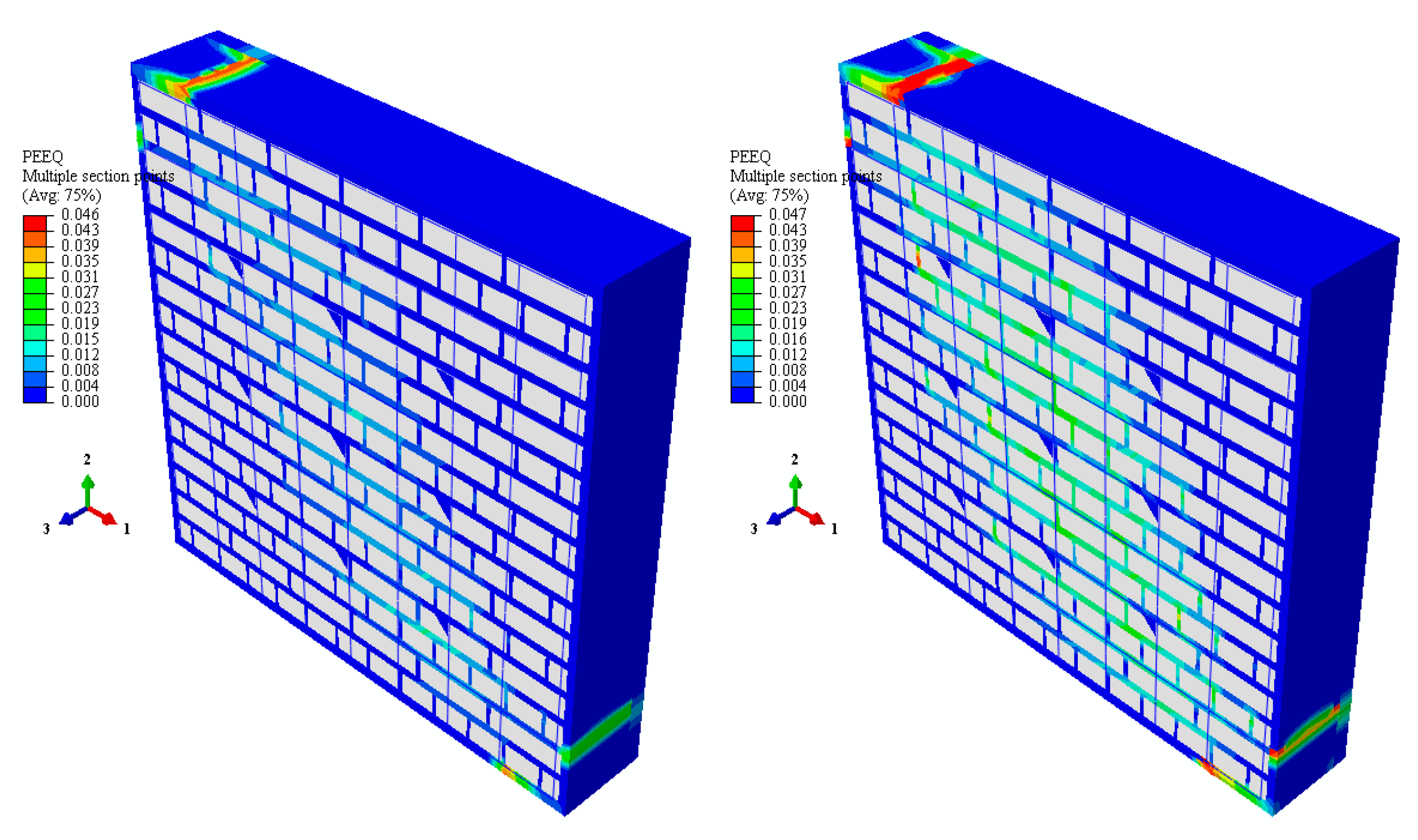
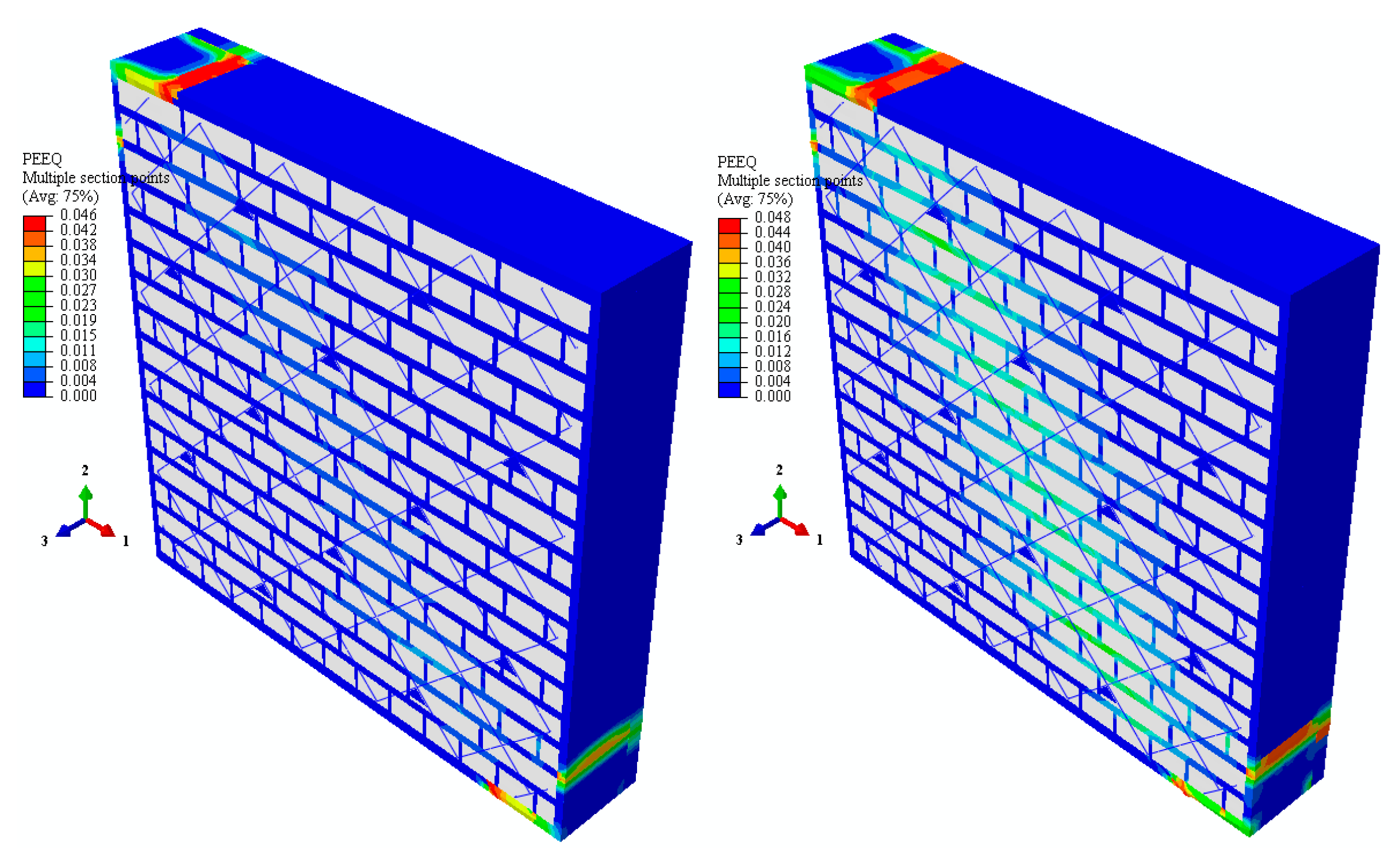
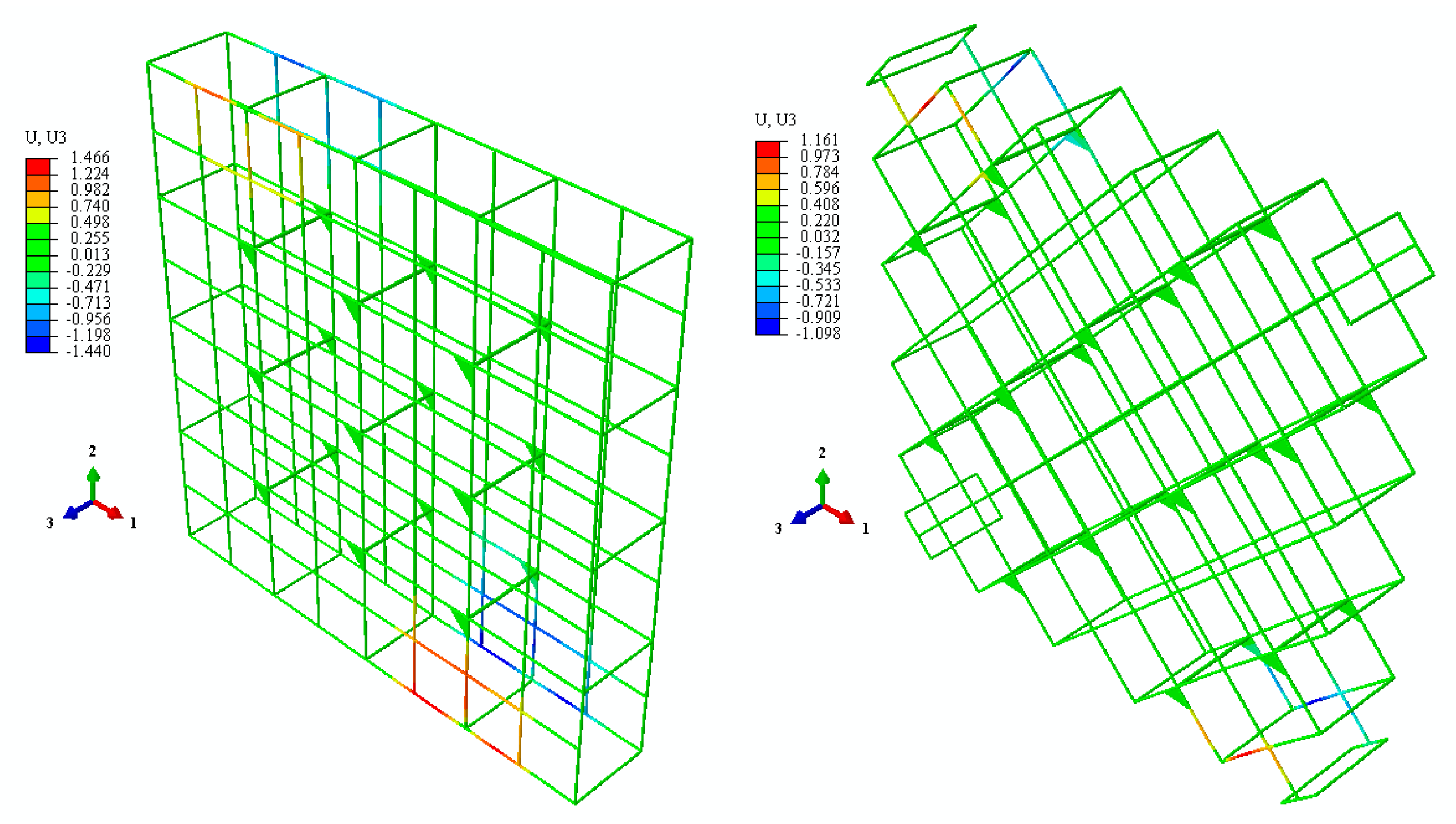
4. Results and Discussion
5. Conclusions
- Both reinforcement schemes led to significant improvements in shear strength and ductility.
- Diagonal reinforcement (D-RC) exhibited superior shear performance compared to edge-parallel reinforcement (P-RC).
- Reinforced specimens maintained structural integrity up to the onset of RC bar buckling, indicating a transition from brittle to ductile failure modes.
- The use of Khorasan mortar, characterized by lower stiffness than Portland cement, facilitated compatibility with historical masonry and enabled effective reinforcement integration without inducing damage to brick units.
- Brick units exhibited highly rigid behavior relative to the surrounding mortar.
- The Mohr-Coulomb material model, incorporating hardening and softening behavior, effectively captured the nonlinear response, particularly under vertical compression.
- The Nelder-Mead algorithm successfully optimized the model parameters, yielding a satisfactory match with experimental load-displacement curves and ultimate load levels, despite the inherent inhomogeneity of masonry.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ehsani, M.; Saadatmanesh, H.; Velazquez-Dimas, J. Behavior of retrofitted URM walls under simulated earthquake loading. J. Compos. Constr. 1999, 3, 134–142. [Google Scholar] [CrossRef]
- Velazquez-Dimas, J.; Ehsani, M. Modeling out-of-plane behavior of URM walls retrofitted with fiber composites. J. Compos. Constr. 2000, 4, 172–181. [Google Scholar] [CrossRef]
- ElGawady, M.A.; Lestuzzi, P.; Badoux, M. Shear strength of URM walls retrofitted using FRP. Eng. Struct. 2006, 28, 1658–1670. [Google Scholar] [CrossRef]
- Öztaş, V.; Torunbalcı, N. An Experimental Study of Strength Increase in Masonry Wall Reinforced by One-sided Khorasan Mortar with Steel Mesh. Civ. Eng. J. 2023, 9, 3233–3253. [Google Scholar] [CrossRef]
- Yardim, Y.; Lalaj, O. Shear strengthening of unreinforced masonry wall with different fiber reinforced mortar jacketing. Constr. Build. Mater. 2016, 102, 149–154. [Google Scholar] [CrossRef]
- Faella, C.; Martinelli, E.; Nigro, E.; Paciello, S. Shear capacity of masonry walls externally strengthened by a cement-based composite material: An experimental campaign. Constr. Build. Mater. 2010, 24, 84–93. [Google Scholar] [CrossRef]
- Bui, T.L.; Larbi, A.S.; Reboul, N.; Ferrier, E. Shear behaviour of masonry walls strengthened by external bonded FRP and TRC. Compos. Struct. 2015, 132, 923–932. [Google Scholar] [CrossRef]
- Wang, B.; Yin, S.; Qu, F.; Wang, F. Cyclic shear test and finite element analysis of TRC-reinforced damaged confined masonry walls. Constr. Build. Mater. 2024, 421, 135766. [Google Scholar] [CrossRef]
- Jafarian, S.; Esmaelian, M.; Shekarchi, M.; Ghassemieh, M. Performance of low-carbon textile-reinforced mortar: Out-of-plane response of strengthened masonry walls. Constr. Build. Mater. 2024, 415, 134904. [Google Scholar] [CrossRef]
- Khan, I.U.; Gul, A.; Shahzada, K.; Khan, K.; Khan, S.W.; Ullah, A.; Khan, F.A. Restoring seismic capacity of damaged dry stacked Self-Interlocking masonry structure through ferrocement overlay. Eng. Struct. 2023, 293, 116687. [Google Scholar] [CrossRef]
- Ma, P.; Xin, R.; Yao, J. Assessment of failure mode and seismic performance of damaged masonry structures retrofitted with grout-injected ferrocement overlay reinforcement (GFOR). Constr. Build. Mater. 2021, 305, 124778. [Google Scholar] [CrossRef]
- Gan, B.L.; Zhang, D.M.; Huang, Z.K.; Zheng, F.Y.; Zhu, R.; Zhang, W. Ontology-driven knowledge graph for decision-making in resilience enhancement of underground structures: Framework and application. Tunn. Undergr. Space Technol. 2025, 163, 106739. [Google Scholar] [CrossRef]
- Saingam, P.; Hlaing, H.H.; Suwannatrai, R.; Ejaz, A.; Hussain, Q.; Khan, K.; Joyklad, P. Enhancing the flexural behavior of brick masonry walls with ferrocement overlays and low-cost anchors. Case Stud. Constr. Mater. 2023, 19, e02558. [Google Scholar] [CrossRef]
- El-Diasity, M.; Okail, H.; Kamal, O.; Said, M. Structural performance of confined masonry walls retrofitted using ferrocement and GFRP under in-plane cyclic loading. Eng. Struct. 2015, 94, 54–69. [Google Scholar] [CrossRef]
- Marshall, O.S.; Sweeney, S.C.; Trovillion, J.C. Seismic rehabilitation of unreinforced masonry walls. In Proceedings of the Fourth International Symposium on Fiber Reinforced Polymer Reinforcement for Reinforced Concrete Structures, Baltimore, MD, USA, 31 October–5 November 1999; Volume 188, pp. 287–296. [Google Scholar] [CrossRef]
- Prawel, S.P.; Reinhorn, A.M.; Qazi, S. Upgrading the seismic resistance of unreinforced brick masonry using ferrocement coatings. In Proceedings of the 8th International Brick and Block Masonry Conference (8th IBMAC), Dublin, Ireland, 19–21 September 1988; Volume 2, pp. 785–791. [Google Scholar]
- Ashraf, M.; Khan, A.N.; Naseer, A.; Ali, Q.; Alam, B. Seismic behavior of unreinforced and confined brick masonry walls before and after ferrocement overlay retrofitting. Int. J. Arch. Herit. 2012, 6, 665–688. [Google Scholar] [CrossRef]
- Churilov, S.; Dumova-Jovanoska, E. In-plane shear behaviour of unreinforced and jacketed brick masonry walls. Soil Dyn. Earthq. Eng. 2013, 50, 85–105. [Google Scholar] [CrossRef]
- Kolsch, H. Carbon fiber cement matrix (CFCM) overlay system for masonry strengthening. J. Compos. Constr. 1998, 2, 105–109. [Google Scholar] [CrossRef]
- Luciano, R.; Sacco, E. Damage of masonry panels reinforced by FRP sheets. Int. J. Solids Struct. 1998, 35, 1723–1741. [Google Scholar] [CrossRef]
- Kalali, A.; Kabir, M.Z. Experimental response of double-wythe masonry panels strengthened with glass fiber reinforced polymers subjected to diagonal compression tests. Eng. Struct. 2012, 39, 24–37. [Google Scholar] [CrossRef]
- Hasnat, A.; Ahsan, R.; Yashin, S.M. Quasi-static in-plane behavior of full-scale unreinforced masonry walls retrofitted using ferrocement overlay. Asian J. Civ. Eng. 2022, 23, 649–664. [Google Scholar] [CrossRef]
- Pérez-Pinedo, L.; Sandoval, C.; Alvarado, R.; Vargas, L.; Calderón, S.; Bernat, E. Seismic strengthening of partially grouted masonry walls with openings: Evaluation of ferrocement and BTRM solutions. J. Build. Eng. 2024, 88, 109235. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kaushik, H.B. Strengthening of unreinforced masonry buildings with ferrocement composite overlay: Material characterization and numerical study. Case Stud. Constr. Mater. 2025, 22, e04177. [Google Scholar] [CrossRef]
- Ehsani, M.R.; Saadatmanesh, H.; Al-Saidy, A. Shear behavior of URM retrofitted with FRP overlays. J. Compos. Constr. 1997, 1, 17–25. [Google Scholar] [CrossRef]
- Saadatmanesh, H. Extending service life of concrete and masonry structures with fiber composites. Constr. Build. Mater. 1997, 11, 327–335. [Google Scholar] [CrossRef]
- Albert, M.L.; Elwi, A.E.; Cheng, J.R. Strengthening of unreinforced masonry walls using FRPs. J. Compos. Constr. 2001, 5, 76–84. [Google Scholar] [CrossRef]
- ElGawady, M.A.; Lestuzzi, P.; Badoux, M. Dynamic versus static cyclic tests of masonry walls before and after retrofitting with GFRP. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, 1–6 August 2004; p. 2913. [Google Scholar]
- Capozucca, R. Double-leaf masonry walls under in-plane loading strengthened with GFRP/SRG strips. Eng. Struct. 2016, 128, 453–473. [Google Scholar] [CrossRef]
- Bouyahyaoui, A.; Elmalyh, S.; Cherradi, T. Behaviour of masonry walls reinforced by fiber reinforced polymers. Mater. Today Proc. 2023; in press (corrected proof). [Google Scholar] [CrossRef]
- Christensen, J.B.; Gilstrap, J.; Dolan, C.W. Composite materials reinforcement of existing masonry walls. J. Arch. Eng. 1996, 2, 63–70. [Google Scholar] [CrossRef]
- Hamilton III, H.R.; Dolan, C.W. Flexural capacity of glass FRP strengthened concrete masonry walls. J. Compos. Constr. 2001, 5, 170–178. [Google Scholar] [CrossRef]
- Luccioni, B.; Rougier, V.C. Shear behaviour of brick–mortar interface in CFRP retrofitted or repaired masonry. Int. J. Mech. Sci. 2010, 52, 602–611. [Google Scholar] [CrossRef]
- Wang, H.; Yu, J.; Dong, F.; Jiang, F.; Yu, K. Seismic shear behavior of masonry walls strengthened with engineered cementitious composites (ECC). J. Build. Eng. 2025, 104, 112230. [Google Scholar] [CrossRef]
- Xu, C.; Nehdi, M.L.; Wang, K.; Marani, A.; Zhang, L. Seismic behavior of autoclaved aerated concrete masonry walls reinforced with glass-fiber geogrid. Structures 2023, 58, 105367. [Google Scholar] [CrossRef]
- Capozucca, R. Experimental analysis of historic masonry walls reinforced by CFRP under in-plane cyclic loading. Compos. Struct. 2011, 94, 277–289. [Google Scholar] [CrossRef]
- Stratford, T.; Pascale, G.; Manfroni, O.; Bonfiglioli, B. Shear strengthening masonry panels with sheet glass-fiber reinforced polymer. J. Compos. Constr. 2004, 8, 434–443. [Google Scholar] [CrossRef]
- Briccoli Bati, S.; Rovero, L.; Tonietti, U. Strengthening masonry arches with composite materials. J. Compos. Constr. 2007, 11, 33–41. [Google Scholar] [CrossRef]
- Işıkdağ, B.; Topçu, İ.B. The effect of ground granulated blast-furnace slag on properties of Horasan mortar. Constr. Build. Mater. 2013, 40, 448–454. [Google Scholar] [CrossRef]
- Dinç-Şengönül, B.; Yüzer, N.; Şengönül, C.; Ulukaya, S.; Oktay, D.; Ündül, Ö. Behavior of grout injected solid stone masonry walls under in-plane loading. Structures 2023, 58, 105411. [Google Scholar] [CrossRef]
- Triantafillou, T.C. Strengthening of masonry structures using epoxy-bonded FRP laminates. J. Compos. Constr. 1998, 2, 96–104. [Google Scholar] [CrossRef]
- Corradi, M.; Castori, G.; Sisti, R.; Borri, A.; Pesce, G.L. Repair of block masonry panels with CFRP sheets. Materials 2019, 12, 2363. [Google Scholar] [CrossRef]
- Corbi, I. FRP reinforcement of masonry panels by means of C-fiber strips. Compos. Part B Eng. 2013, 47, 348–356. [Google Scholar] [CrossRef]
- Magenes, G.; Calvi, G.M. In-plane seismic response of brick masonry walls. Earthq. Eng. Struct. Dyn. 1997, 26, 1091–1112. [Google Scholar] [CrossRef]
- Wang, X.; Lam, C.C.; Iu, V.P.; Kou, K.P. Numerical study of NSM FRP Strengthened Masonry walls. In Structural Analysis of Historical Constructions; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1670–1678. [Google Scholar] [CrossRef]
- Al-Jaberi, Z.; Myers, J.J.; El Gawady, M.A. Pseudo-static cyclic loading comparison of reinforced masonry walls strengthened with FRCM or NSM FRP. Constr. Build. Mater. 2018, 167, 482–495. [Google Scholar] [CrossRef]
- Konthesingha, K.M.C.; Masia, M.J.; Petersen, R.B.; Mojsilovic, N.; Simundic, G.; Page, A.W. Static cyclic in-plane shear response of damaged masonry walls retrofitted with NSM FRP strips–An experimental evaluation. Eng. Struct. 2013, 50, 126–136. [Google Scholar] [CrossRef]
- Abdulla, K.F.; Cunningham, L.S.; Gillie, M. Out-of-plane strengthening of adobe masonry using hemp fibre ropes: An experimental investigation. Eng. Struct. 2021, 245, 112931. [Google Scholar] [CrossRef]
- Lin, Y.W.; Wotherspoon, L.; Scott, A.; Ingham, J.M. In-plane strengthening of clay brick unreinforced masonry wallettes using ECC shotcrete. Eng. Struct. 2014, 66, 57–65. [Google Scholar] [CrossRef]
- Lin, Y.; Lawley, D.; Wotherspoon, L.; Ingham, J.M. Out-of-plane testing of unreinforced masonry walls strengthened using ECC shotcrete. Structures 2016, 7, 33–42. [Google Scholar] [CrossRef]
- Dassault Systèmes. Abaqus 2024 Documentation; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2024. [Google Scholar]






| Technique | Description | Advantages | Disadvantages |
|---|---|---|---|
| FRP Strengthening [7,29,41,42,43] | Externally bonded fiber-reinforced polymer laminates on masonry | High strength-to-weight ratio; non-corrosive; fast to apply | High cost; poor fire resistance; requires surface prep |
| Ferrocement Overlay [10,11,12,13,17,25] | Cementitious mortar reinforced with mesh applied as a thin overlay | Cost-effective; improves ductility and stiffness | Labor-intensive; adds dead load |
| NSM FRP Bars or Ropes [44,45,46,47,48] | Near-surface mounted FRP bars inserted into slits in masonry surface | Better bond than EB-FRP; minimal esthetic impact | Skilled labor needed; long-term durability under debate |
| Cementitious Grouting [49,50] | Injecting grout into cracked or voided masonry to restore integrity | Restores strength and stiffness; compatible with masonry | May not work if voids are inaccessible or too small |
| Material | Compressive Strength (MPa) | Modulus of Elasticity (MPa) |
|---|---|---|
| Brick | 16.2 | 9856 |
| Mortar * | 1.6 | 973 |
| φ (deg.) | ψ (deg.) | c0 (MPa) | c1 (MPa) | c2 (MPa) | εp1 | εp2 | κ |
|---|---|---|---|---|---|---|---|
| 26.4 | 26.3 | 0.282 | 0.185 | 0.113 | 0.0075 | 0.016 | 0.0045 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mollamahmutoglu, C.; Ozturk, M.; Yilmaz, M.O. Shear Capacity of Masonry Walls Externally Strengthened via Reinforced Khorasan Jacketing. Buildings 2025, 15, 2177. https://doi.org/10.3390/buildings15132177
Mollamahmutoglu C, Ozturk M, Yilmaz MO. Shear Capacity of Masonry Walls Externally Strengthened via Reinforced Khorasan Jacketing. Buildings. 2025; 15(13):2177. https://doi.org/10.3390/buildings15132177
Chicago/Turabian StyleMollamahmutoglu, Cagri, Mehdi Ozturk, and Mehmet Ozan Yilmaz. 2025. "Shear Capacity of Masonry Walls Externally Strengthened via Reinforced Khorasan Jacketing" Buildings 15, no. 13: 2177. https://doi.org/10.3390/buildings15132177
APA StyleMollamahmutoglu, C., Ozturk, M., & Yilmaz, M. O. (2025). Shear Capacity of Masonry Walls Externally Strengthened via Reinforced Khorasan Jacketing. Buildings, 15(13), 2177. https://doi.org/10.3390/buildings15132177






