Abstract
The pre-inserted method for precast shear walls involves casting concealed beams at floor slabs between upper and lower structures, with precast concrete supports spaced at intervals. Vertical rebars at the base of upper walls are pre-inserted and anchored in the beams before slab casting. It offers advantages such as convenient construction without the need for grouting, demonstrating broad application prospects and significant promotional value. To evaluate seismic performance, quasi-static cyclic loading tests were conducted on five specimens: three full-scale pre-inserted precast walls and two cast-in-place counterparts. Under increasing lateral displacement, low axial-load specimens failed via tensile fracture of the outermost rebars, while high axial-load specimens failed by concrete crushing in compression. The test results showed that under identical axial-load ratios, the precast walls exhibited comparable bearing capacity, stiffness degradation, and energy dissipation to cast-in-place walls, but superior deformation ductility. The ultimate drift ratios of pre-inserted walls exceeded those of cast-in-place walls by 16.7% (axial-load ratio 0.2) and 22.2% (axial-load ratio 0.4), demonstrating robust seismic performance.
1. Introduction
Precast reinforced concrete shear walls are widely used in large-scale prefabricated residential construction due to their reliable mechanical performance, efficient construction methods, and low-carbon environmental benefits. The precast solid shear wall structural system is currently the most extensively applied type of prefabricated concrete shear wall system. However, compared to cast-in-place shear walls, the connections between adjacent precast components often become a critical factor affecting the overall seismic performance of the structure [1].
Current research primarily focuses on improving vertical connections. Qian et al. [2,3,4] tested precast walls with grouted sleeve connections, demonstrating reliability and failure modes matching cast-in-place walls. Jiang et al. [5] and Guo et al. [6] proposed grouted duct lap splices to reduce construction precision demands, though challenges like high grout costs and inspection difficulties persist. To address the limitations of grouted connection precast shear walls, Xue Weichen et al. [7,8] proposed replacing conventional wet connections with dry connections, conducting a series of seismic performance studies on full-scale precast reinforced concrete shear walls with bolted connections. The results indicated favorable seismic performance, but revealed challenges such as excessively stringent bolt installation tolerances and insufficient corrosion resistance.
Wu Honglei et al. [9] proposed a novel prefabricated shear wall connection method that uses ultra-high-performance concrete (UHPC) to replace longitudinal connecting reinforcement bars with large-diameter screws for anchorage. They conducted a study on its seismic performance, and the results showed that compared to cast-in-place shear walls, this method improves crack resistance and offers excellent anchorage performance while eliminating the need for grouting sleeve operations. However, this approach imposes higher requirements on the performance of the concrete. Zhi et al. [10] proposed integrated grouting via a single port, enhancing interface strength and seismic performance. The study revealed that prefabricated specimens utilizing this integrated grouting technique with enhanced wall–foundation interface strength demonstrated better seismic performance than other precast specimens. Jiao et al. [11,12,13] introduced cast-in-place segments with U-bar interlocking, achieving cast-in-place-equivalent performance but retaining construction complexity. Zhang et al. [14,15] innovated shear–key connections, improving joint shear resistance at the cost of node complexity.
Jun Zhao et al. [16] developed a precast shear wall system utilizing steel fiber-reinforced sulfoaluminate cement concrete with non-contact lapped connections. This innovative connection method optimizes the assembly construction process while effectively enhancing concrete compactness. Qihao Hao et al. [17,18] proposed a novel hybrid-connected precast concrete shear wall system. This system adopts high-strength bolted “strong connections” in the horizontal direction and steel keyway “weak connections” in the vertical direction. Experimental and finite element studies were conducted on this structural system, with the research results providing valid technical references for a high-rise residential construction case.
To effectively improve construction accuracy, simplify construction methods, and enhance connection quality in precast shear walls, this study developed a pre-inserted precast shear wall system. As illustrated in Figure 1, the system features the following:
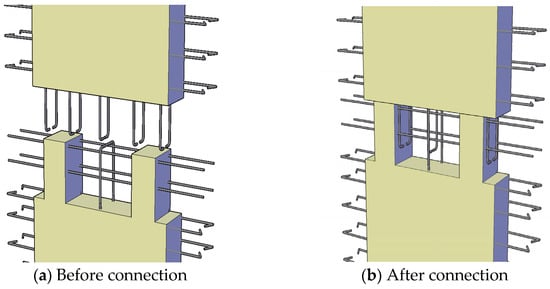
Figure 1.
Schematic diagram of pre-inserted prefabricated shear wall.
Cast-in-place concealed beams integrated into floor slabs at upper/lower levels.
Precast concrete support legs spaced at regular intervals within the beams.
The vertical rebars from the upper wall are anchored into the concealed beams prior to casting the current floor slab—hence termed pre-inserted prefabricated shear wall (PPSW).
To evaluate its seismic performance, three full-scale PPSW specimens and two cast-in-place counterparts were designed per the following:
Code for Design of Concrete Structures (GB 50010-2010) [19].
Code for Seismic Design of Buildings (GB 50011-2010) [20].
Quasi-static cyclic loading tests were conducted to compare their seismic behaviors under varying axial compression ratios.
2. Experimental Overview
2.1. Specimen Design
Five full-scale specimens were tested: three PPSW and two cast-in-place walls. Cross-sections measured 200 × 1700 mm with 1.15% edge-constrained column reinforcement. Legs extended 130 mm into loading beams (height: 2870 mm). Details are shown in Figure 2 and Table 1.

Figure 2.
Dimensions and steel reinforcement layout of specimens.

Table 1.
Specimen specification.
2.2. Material Mechanical Properties
The shear wall specimens were designed with C30-grade concrete. During the three successive casting batches of the shear wall specimens, three concrete cube specimens (totaling 9) with an edge length of 150 mm were prepared per batch and cured under identical conditions as the main specimens. The calculated mechanical property parameters of the concrete were as follows: the cubic compressive strengths (fcu) of the three batches were 45.6 MPa, 44.7 MPa, and 45.2 MPa, respectively; the elastic modulus (Ec) was 32.5 GPa; and the axial tensile strength (ft) was 2.4 MPa.
The steel bars used in the tensile tests were from the same batch of HRB400 reinforcement as those employed in the specimens, including three diameters: 14 mm, 10 mm, and 8 mm. For each diameter, three individual bars were selected. Table 2 presents the averaged mechanical property parameters of the steel reinforcement, including the elastic modulus (Es), yield strength (fy), ultimate tensile strength (fu), and elongation at maximum force (Agt).

Table 2.
Parameters of mechanical properties of reinforcement.
2.3. Loading Apparatus and Loading Protocol
2.3.1. Loading Apparatus
The loading system (Figure 3) includes a reaction frame, reaction beam, horizontal and vertical actuators, a steel baseplate, and an L-shaped beam. A 300-ton vertical actuator at the top and a 200-ton horizontal actuator on the east side apply loads. The vertical actuator features an articulated joint and a horizontal sliding mechanism to maintain axial compression at the specimen’s center.
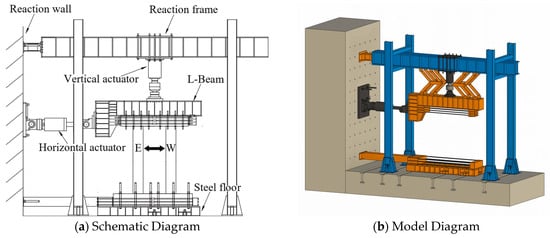
Figure 3.
Loading device.
The L-shaped beam, positioned above the specimen, uniformly distributes vertical and horizontal loads to the loading beam, avoiding stress concentration. High-strength vertical bolts connect the shear wall specimen to the loading system, while lateral restraints at both ends of the ground and loading beams prevent slippage.
During loading, the four-bar linkage remains detached from the L-shaped beam, allowing unrestricted flexural deformation. Out-of-plane bracing beams on both sides of the L-shaped beam ensure strictly in-plane loading.
2.3.2. Loading Protocol
The axial compression capacity of the shear wall’s normal section was calculated per Ref. [21], following the provisions for reinforced concrete eccentrically compressed members (rectangular, T-shaped, or I-shaped) with distributed longitudinal reinforcement. The flexural capacity was then determined.
Additionally, the inclined section shear capacity of the eccentrically compressed shear wall was calculated following the relevant provisions of the Technical Specification for Concrete Structures of Tall Buildings (JGJ 3-2010) [22]. The smaller of the two values (normal section flexural capacity and inclined section shear capacity) was adopted to determine the force-controlled loading stage. In accordance with the Specification for Seismic Testing of Buildings (JGJ/T 101-2015) [23], a low-cycle reversed loading test was conducted. The force control phase ensures the specimen gradually approaches the yield point, avoiding overload caused by inaccurate stiffness estimation under displacement control. When nearing yield (e.g., when the load–displacement curve exhibits significant nonlinearity), switching to displacement control allows more accurate capture of the yield point and better management of subsequent plastic deformation. The loading protocol defined east-to-west loading as positive and west-to-east loading as negative. The corresponding loading protocol is specified as follows:
- Preloading: A preload not exceeding 10% of the specimen’s yield load was applied to verify the proper functioning of all instrumentation. Following preloading, the instruments were calibrated, and initial readings were recorded.
- Formal loading: The vertical load was first applied according to the design axial compression ratio and maintained constant. Subsequently, horizontal low-cycle reversed loading was implemented. The loading protocol employed a force–displacement hybrid control method as illustrated in Figure 4, where the force-controlled phase consisted of five incremental loading steps up to the estimated yield load Py with one cycle per step, while the estimated yield displacement Δy and displacement increment Δ0 for the displacement-controlled phase were determined based on experimental observations. During the displacement-controlled phase, the displacement amplitude was incrementally increased by Δ0 at each loading step, with three complete loading cycles performed per displacement level.
 Figure 4. Loading history diagram of specimens.
Figure 4. Loading history diagram of specimens. - The specimen is considered to have failed, and loading is stopped, when its bearing capacity drops to 80% of the peak load or when it can no longer sustain the applied load.
2.3.3. Different Damage States
This experiment will analyze the test phenomena according to the following methodology:
- Initial cracking state: First visible cracks (crack width typically ≤0.1 mm).
- Reinforcement yielding state: Steel bars yield (strain of outermost reinforcement εy ≈ 0.002).
- Peak load state: Maximum load-bearing capacity (ultimate strength reached).
- Post-peak degradation state: Strength deterioration (load drops below 85% of peak load).
- Ultimate failure state: Concrete crushing (spalling of confined edge concrete or buckling of longitudinal reinforcement).
3. Results and Phenomenological Section
3.1. Test Phenomena and Failure Modes
3.1.1. CSW-0.2
The test results showed that when the horizontal load reached +250.0 kN (corresponding displacement: +1.67 mm), initial cracks appeared at the east concealed column 350 mm above the ground beam surface. Upon loading to the estimated yield load level of +500 kN (displacement: +8.97 mm), the strain of the outermost tensile reinforcement reached 2363 × 10−6. The east tension zone developed seven cracks with a maximum height of 1300 mm and maximum width of 0.36 mm. The loading continued to +10 mm displacement (+510 kN horizontal load). At the 60 mm displacement level, the negative-direction load-bearing capacity dropped to 58% of peak capacity. Final failure was declared when all outer-layer reinforcement bars fractured and the capacity fell below 80% of peak value. Figure 5 illustrates the wall crack pattern and failure mode.

Figure 5.
Distribution of wall cracks and damage.
3.1.2. CSW-0.4
The test results showed that when the horizontal load reached +462.2 kN (corresponding displacement: +2.07 mm), initial cracks appeared at the east concealed column 180 mm above the ground beam surface.
Upon loading to the estimated yield load level of +600 kN (displacement: +4.93 mm), the strain of the outermost tensile reinforcement reached 1776 × 10−6. The east tension zone developed three cracks with a maximum height of 750 mm and a maximum width of 0.26 mm.
The loading continued until the 45 mm displacement level, at which point the concealed column concrete spalled extensively, and the compressive reinforcement buckled. Due to sustained high axial compression, the shear wall base experienced concrete crushing failure, leading to a loss of load-bearing capacity and test termination. Figure 6 illustrates the wall crack distribution and final failure mode.

Figure 6.
Distribution of wall cracks and damage.
3.1.3. PPW-0.2
The test results showed that when the horizontal load reached +275.0 kN (corresponding displacement: +2.46 mm), initial cracks appeared at the east concealed column 330 mm above the ground beam surface.
Upon loading to the estimated yield load level of +500 kN (displacement: +9.48 mm), the strain of the outermost tensile reinforcement reached 2344 × 10−6. The east tension zone developed eight cracks with a maximum height of 1200 mm and a maximum width of 0.22 mm. Additionally, vertical cracks appeared at the interface between the concealed column and precast wall body, with a maximum width of 0.2 mm.
At the 60 mm displacement level, all outer-layer reinforcement bars in the concealed column fractured, causing the load-bearing capacity to drop below 80% of the peak value. The specimen was then declared failed, and the test was terminated. Figure 7 illustrates the wall crack distribution and final failure mode.

Figure 7.
Distribution of wall cracks and damage.
3.1.4. PPW-0.4
The test results showed that when the horizontal load reached +235.0 kN (corresponding displacement: +1.62 mm), initial cracks appeared at the east concealed column 430 mm above the ground beam surface.
When loaded to the estimated yield load level of +600 kN (displacement: +4.85 mm), the strain of the outermost tensile reinforcement reached 1868 × 10−6, with five cracks developing in the east tension zone showing a maximum height of 900 mm and maximum width of 0.16 mm, while vertical cracks with a width of 0.1 mm appeared at the interface between the concealed column and precast wall. At the 45 mm displacement level, concrete spalling occurred on both concealed columns accompanied by extensive reinforcement yielding, and a fully developed plastic hinge formed at the wall base resulting in no significant crack propagation.
During the third cycle of positive loading at +44.74 mm displacement, concrete crushing occurred in the west concealed column causing rapid strength degradation, and the test was terminated due to a loss of load-bearing capacity. The specimen was declared failed, with Figure 8 documenting the final crack pattern and failure mode of the wall.

Figure 8.
Distribution of wall cracks and damage.
3.1.5. PPW-0.5
The test results indicated that when the horizontal load reached +505.0 kN (corresponding displacement: +3.64 mm), initial cracks developed in the east concealed column at 210 mm above the ground beam surface.
Upon reaching the estimated yield load level of +675 kN (displacement: +5.35 mm), the outermost tensile reinforcement exhibited a strain of 1898 × 10−6, with four cracks forming in the east tension zone measuring up to 600 mm in height and 0.26 mm in maximum width, while vertical cracks with a 0.16 mm width appeared at the concealed column-precast wall interface. At the 45 mm displacement level, concrete spalling occurred on both concealed columns accompanied by extensive reinforcement yielding, and a fully developed plastic hinge at the wall base prevented significant further crack propagation.
During the third cycle of positive loading at +34.44 mm displacement, concrete crushing in the east concealed column led to rapid load-bearing capacity deterioration, prompting test termination. The specimen was declared failed, with Figure 9 documenting the final crack distribution and failure pattern.

Figure 9.
Distribution of wall cracks and damage.
3.2. Hysteretic Behavior
During the loading process, the shear wall was subjected not only to horizontal loads but also to axial compression provided by vertical actuators. As displacement increased, the P-Δ effect became progressively more pronounced, leading to a corresponding increase in additional bending moments caused by axial forces. In practical engineering design, inter-story drift ratios are typically used to control lateral structural deformation. To account for the additional bending moments induced by vertical loads and P-Δ effects, the load–displacement hysteresis curves were converted into moment–drift ratio hysteresis curves. The transformed moment–drift ratio hysteresis curves are presented in Figure 10.

Figure 10.
Hysteresis curve characteristics.
Analysis of the figures reveals that all five specimens exhibited “bow-shaped” hysteresis loops with distinct pinching phenomena. Under identical axial compression ratios, the prefabricated and cast-in-place specimens demonstrated similar hysteresis loop shapes, with axial compression ratio variations producing comparable effects on the hysteresis curve trends.
During the initial loading stages, the hysteresis curves of all specimens appeared nearly linear, indicating elastic behavior. As loading progressed into the elastoplastic phase, the curves gradually developed pinching characteristics. Specimens with lower axial compression ratios displayed fuller curves with less pronounced pinching. Post-peak load, specimens under lower axial compression ratios demonstrated superior stability, exhibiting gradual load reduction with increasing displacement.
At the 0.2 axial compression ratio, both the CSW-0.2 and PPW-0.2 specimens failed due to the fracture of the outer tensile reinforcement, though retained residual load-bearing capacity after failure. In contrast, the PPW-0.4 and PPW-0.5 specimens at 0.4 and 0.5 axial compression ratios failed through crushing of the compression zone’s concealed column concrete, with their moment–drift angle hysteresis curves showing abrupt drops and complete loss of load-bearing capacity at failure.
3.3. Bearing Capacity and Ductility Analysis
As shown in Figure 11, the skeleton curves of all specimens exhibit an ‘S’-shaped pattern, indicating that the specimens underwent four distinct phases during loading: elastic stage, elastoplastic stage, plastic development stage, and failure stage.

Figure 11.
Comparison of moment–drift angle skeleton curves.
During the elastic stage, the moment–drift angle curves of the five shear wall specimens exhibited nearly linear growth until reaching the cracking point. Upon crack initiation, the specimens entered the elastoplastic stage, characterized by the progressive extension and widening of the concrete cracks. The moment–drift angle curves began to show slight nonlinearity, with their slopes gradually decreasing as the drift angle increased.
Following the yielding of longitudinal reinforcement and the development of plastic hinges at the wall base, the specimens transitioned into the plastic development stage, displaying pronounced nonlinearity in the moment–drift angle curves. The load-bearing capacity peaked upon reaching full plastic development. Post-peak, the skeleton curves exhibited a descending trend due to the gradual degradation of the concrete compression zone and increased plastic deformation of the reinforcing bars.
As evidenced by Table 3, both the precast and cast-in-situ shear wall specimens demonstrated increased load-bearing capacity with higher axial compression ratios, while their ductility coefficients and ultimate drift angles exhibited a gradual decrease. All specimens achieved ductility coefficients exceeding 5.0, indicating superior deformation capacity. Notably, the precast specimens showed larger ductility coefficients and ultimate drift angles than their cast-in-situ counterparts under identical axial compression ratios, attributable to progressive crack propagation at the interface between new and existing concrete during loading.

Table 3.
Moments and drift angles at characteristic points of specimens.
3.4. Stiffness Degradation Analysis
To clarify the stiffness degradation behavior of the specimens, the secant stiffness K at peak load points of each loading cycle under reciprocating load is defined as the equivalent secant stiffness. Equation (1) presents the calculation method for this equivalent secant stiffness. For a more intuitive comparison of the stiffness degradation rates among specimens, normalized stiffness is adopted by converting to the equivalent stiffness ratio, where Ke represents the initial stiffness of the specimen.
where
- Ki = secant stiffness at the i-th level of cyclic loading (kN/mm).
- Pi = peak load value of the i-th loading cycle (kN).
- Δi = displacement corresponding to the peak load point of the i-th cycle (mm).
As observed from the stiffness degradation curves of each specimen shown in Figure 12, the stiffness of all specimens gradually decreases with the increasing drift ratio. Figure 12a,b indicates that under the same axial compression ratio, the precast shear wall specimens exhibit a slightly slower stiffness degradation rate compared to the cast-in-place shear wall specimens, though the difference is marginal. Figure 12 reveals that the stiffness degradation rate of PPW-0.2 (with an axial compression ratio of 0.2) is significantly lower than that of PPW-0.4 and PPW-0.5 (with axial compression ratios of 0.4 and 0.5, respectively), while the difference in degradation rates between specimens with axial compression ratios of 0.4 and 0.5 is negligible.

Figure 12.
Stiffness degradation of specimens.
3.5. Energy Dissipation Capacity
The energy dissipation capacity of structures or structural members serves as a critical indicator for evaluating their seismic performance. In this study, two metrics are employed to assess the energy dissipation capacity of the shear walls: the energy dissipation coefficient (E) and the equivalent viscous damping coefficient (ξeq).
From Figure 13, it can be observed that in the early loading stage, the equivalent viscous damping coefficient (ξeq) of all specimens decreased. However, with increasing displacement, the plastic deformation of the specimens gradually intensified, accompanied by repeated crack opening/closing and concrete friction, leading to enhanced energy dissipation. Consequently, the ξeq values exhibited a progressive increase.
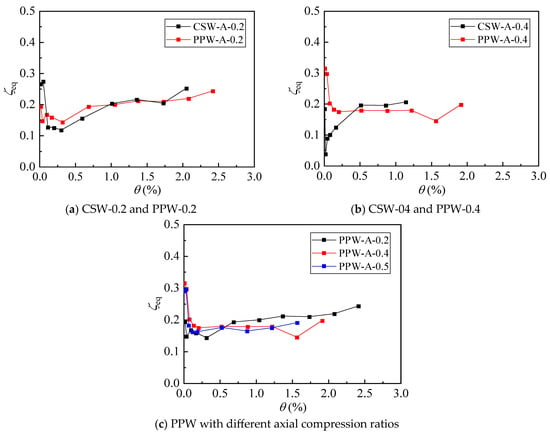
Figure 13.
Equivalent viscous damping coefficient comparison.
Overall, the ξeq of all specimens followed an upward trend, with the final values for the five shear wall specimens converging around 20%, demonstrating excellent energy dissipation capacity. Furthermore, it was found that variations in the axial compression ratio had no significant influence on the ξeq of the specimens.
4. Finite Element Analysis
4.1. Finite Element Model
To validate the rationality of the experimental results, a nonlinear finite element analysis was conducted using DIANA 10.5 software. Five computational models (CSW-0.2, CSW-0.4, PPW-0.2, PPW-0.4, and PPW-0.5) were established with identical parameters to the experimental setup. Figure 14 illustrates the meshing of the finite element models for the two specimens.
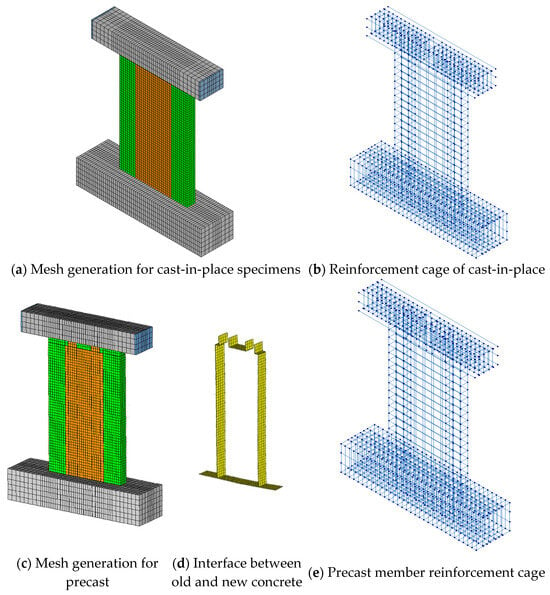
Figure 14.
Finite element mesh generation.
In the finite element models of the shear walls, to account for the influence of lateral confinement on the compressive behavior of concrete, the concrete within the boundary element stirrups was simulated using the confined concrete constitutive model proposed by Mander [24]. For other regions, the unconfined concrete constitutive model (Maekawa model) was adopted. The tensile stress–strain relationship of concrete was modeled using Hordijk’s [25] tensile softening curve, while the steel reinforcement was characterized by the Menegotto–Pinto model [26].
To prevent stress concentration during loading, rigid bearing plates were installed at the loading points of the loading beam. The concrete components (loading beam, foundation beam, and shear wall) and bearing plates were modeled using DIANA’s 8-node 3D solid element (HX24L). The reinforcement was simulated using embedded truss elements. The wall body was discretized into 50 mm cubic elements, and a 10 mm thick interface layer was introduced at the junction between the precast and cast-in-place portions. The interface layer had a mesh size of 50 mm in the longitudinal and transverse directions and 5 mm in the thickness direction. Coarser meshing was applied to the loading beam and foundation beam.
The boundary conditions included fully fixing the foundation beam at its base (restraining Z-direction displacement) and both ends (restraining X-direction displacement), as well as the front and rear surfaces (restraining Y-direction displacement), creating a fully fixed support. The loading beam was constrained against out-of-plane displacement to prevent lateral buckling during loading. The numerical simulation followed the same loading protocol as the experiment. The nonlinear equations were solved using the BFGS quasi-Newton method, with force and displacement increment-based convergence criteria. The convergence tolerance was set to 0.01, with a maximum of 50 iterations.
4.2. Comparison Between Experimental and Finite Element Simulation Results
The hysteretic curves and skeleton curves of the five shear walls obtained from numerical simulation are compared with the experimental results in Figure 15.
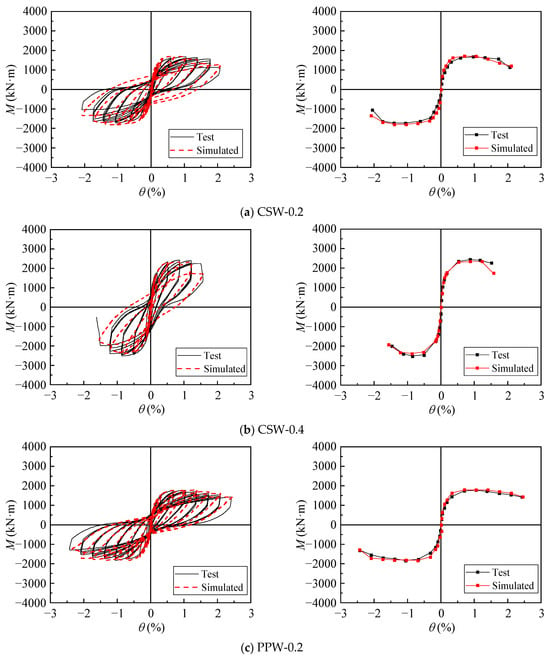
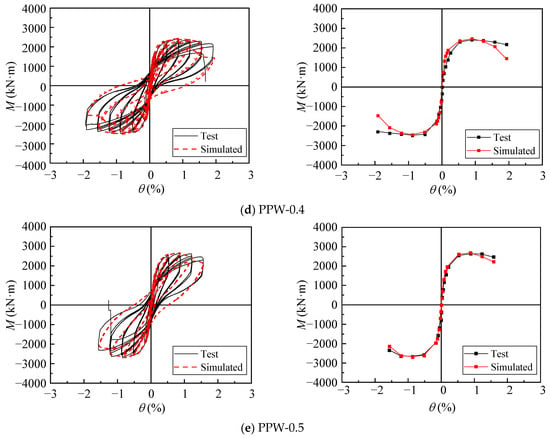
Figure 15.
Comparison between experimental and simulation.
The numerical simulation results show good agreement with the experimental results. Before the component failure, the shapes and areas of the hysteresis loops are similar, both exhibiting a “bow” shape, while the skeleton curve follows an “S” shape. This indicates that both the simulated and experimental components underwent the same four stages: elastic, elastoplastic, plastic development, and failure. However, the hysteresis curves from the finite element simulation are fuller, and the initial stiffness of the skeleton curve is slightly higher. This discrepancy arises because, in the experiment, factors such as the loading rate and material properties exhibit a certain variability, internal force redistribution occurs during loading, and systematic and human errors exist in data collection.
As shown in Table 4, the differences between the experimental yield capacity (Mty) and the simulated yield capacity (Msy), as well as between the experimental peak capacity (Mtmax) and the simulated peak capacity (Msmax), are all within 10%. This indicates that the finite element model meets the accuracy requirements and can reliably reflect the seismic performance of the shear wall components.

Table 4.
Load–displacement angle characteristic parameter comparison.
The crack strain diagrams provided by DIANA can effectively simulate crack propagation. As shown in Figure 16, the crack distribution of the shear wall in the test is well-matched with the simulation results. The legend on the right side of the computer simulation plot, ranging from 2.00e-02 to 4.00e-04, means 2.00 × 10−2 to 4.00 × 10−4.
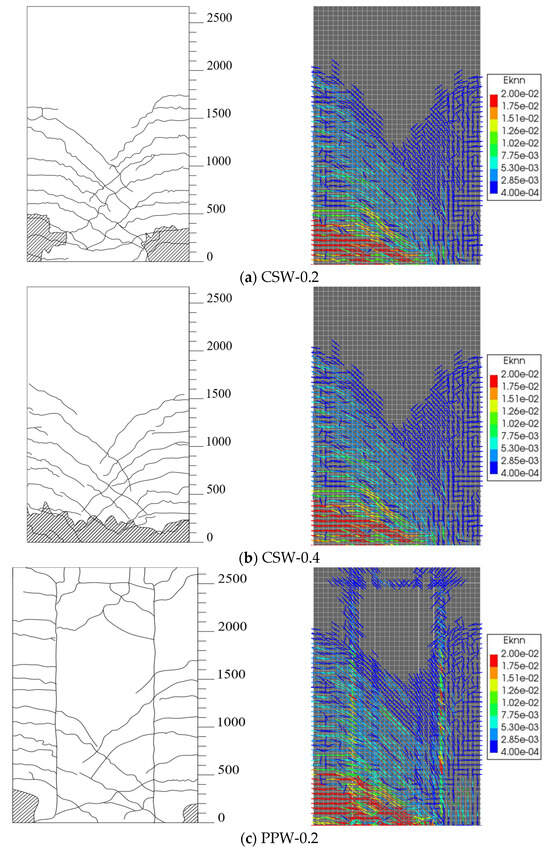
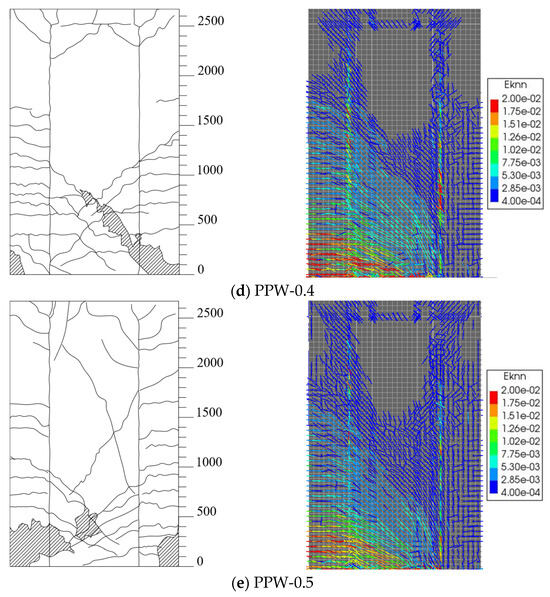
Figure 16.
Comparison of Fracture Distribution.
A comparison between experimental and simulation results indicates that the finite element model accurately captures the cracking characteristics of the shear wall: The crack strains are primarily induced by tensile and shear stresses, developing diagonally at 45° from the tension-side edge, consistent with the flexural-shear crack distribution observed in the tested specimen. The maximum crack strain concentrates at the base of the tension-side boundary element and decreases along the wall height, matching the severe damage observed in the same region during testing. While cracks in the cast-in-situ shear wall are mainly distributed below 1600 mm, those in the precast wall’s boundary element extend beyond 2000 mm, with higher crack strains at the precast–cast interface (10 mm thin layer), aligning with experimental observations. Both testing and simulation demonstrate that under identical axial compression ratios, precast shear walls with smaller shear–span ratios exhibit more pronounced diagonal shear cracks, and the simulation confirms that reducing the shear–span ratio increases diagonal crack strains.
5. Conclusions
Through seismic performance research on pre-installed rebar precast shear walls, the following conclusions were drawn:
- Under low-cycle reversed loading, cracks in the shear wall specimens initially developed from the tensile edge and propagated diagonally at approximately 45° as loading progressed. Precast shear wall specimens exhibited more extensive crack distribution compared to cast-in-place shear walls, with additional cracking occurring at the interface between new and existing concrete.Failure modes varied with axial compression ratios:
- At the 0.2 axial compression ratio, both precast and cast-in-place shear walls failed due to the fracture of tensile reinforcement;
- At higher axial compression ratios (0.4, 0.5), failure transitioned to the compressive crushing of concrete.
- All shear wall specimens exhibited “bow-shaped” hysteresis loops with significant pinching effects. Under identical axial compression ratios, the precast shear walls using the pre-inserted method and cast-in-place walls demonstrated comparable hysteresis loop areas. However, with increasing axial compression ratios, both precast and cast-in-place specimens showed more pronounced pinching in their hysteresis loops.
- The skeleton curves of all five shear wall specimens exhibited an “S-shape,” indicating that the specimens underwent four distinct stages during loading: elastic, elastoplastic, and plastic development, and failure. Under the same axial compression ratio, the prefabricated shear wall specimens with the pre-inserted method demonstrated comparable stiffness and peak load-bearing capacity to the cast-in-place shear walls. As the axial compression ratio increased, all specimens showed a significant improvement in peak load-bearing capacity.
- Cracking at the interface between new and old concrete during loading led to prefabricated shear wall specimens (pre-inserted method) exhibiting greater deformation capacity and a slightly slower stiffness degradation rate compared to cast-in-place specimens. As the axial compression ratio increased, both wall types showed reduced displacement ductility coefficients and accelerated stiffness degradation. The shear deformation proportion was similar for both wall types and remained nearly unaffected by axial compression ratio changes.
- The pre-inserted prefabricated shear walls and cast-in-place shear walls exhibited similar trends in relative energy dissipation capacity. After entering the elastoplastic stage, the equivalent viscous damping coefficient gradually increased with displacement, and variations in the axial compression ratio had no significant effect on the relative energy dissipation capacity. Before failure, the equivalent viscous damping coefficients of all specimens were concentrated around 20%, indicating that each specimen possessed favorable relative energy dissipation performance.
- The hysteretic curves obtained from numerical analysis closely match those from experimental tests in terms of shape and enclosed area, with less than 10% difference in both yield capacity and peak load-bearing capacity, demonstrating that the numerical results can accurately reflect the seismic performance of the precast shear wall with the pre-inserted method. The concrete crack strains derived from the simulation effectively characterize the cracking behavior of the shear wall, and the crack distribution patterns align well with the experimental observations.
- This shear wall can be widely applied in residential buildings and high-rise structures with stringent lateral resistance requirements, effectively improving its prefabrication level. Currently, only quasi-static tests have been conducted on this shear wall. Future research could include pseudo-dynamic tests, more extensive numerical simulation parameter analyses, as well as refined theoretical studies and pilot projects for practical application.
Author Contributions
Q.X. contributed to conceptualization, funding acquisition, and supervision. S.Y. performed investigation, formal analysis, and visualization, as well as writing the original draft and reviewing and editing the manuscript. B.L. participated in conceptualization, resource provision, and supervision. M.X. conducted formal analysis and visualization and assisted in writing the original draft. M.Z. contributed to conceptualization, funding acquisition, and resource management. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data of this study are sourced from a master’s thesis of Zhejiang University (DOI: [10.27461/d.cnki.gzjdx.2023.001020]), and the complete data can be accessed in the CNKI Dissertation Database.
Conflicts of Interest
Authors Quanbiao Xu, Benyue Li and Mingshan Zhang were employed by the company Zhejiang University Architectural Design & Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Xue, W.; Hu, X. State of the art of studies on precast concrete shear wall structures. J. Build. Struct. 2019, 40, 44–55. [Google Scholar]
- Qian, J.; Peng, Y.; Zhang, J.; Qin, H.; Li, J.; Liu, G.; Zhao, F.; Li, L. Tests on seismic behavior of pre-cast shear walls with vertical reinforcements spliced by grout sleeves. Build. Struct. 2011, 41, 1–6. [Google Scholar]
- Qian, J.; Yang, X.; Qin, H.; Peng, Y.; Zhang, J.; Li, J. Tests on seismic behavior of pre-cast shear walls with various methods of vertical reinforcement splicing. J. Build. Struct. 2011, 32, 51–59. [Google Scholar]
- Qian, J.; Han, W.; Zhao, Z.; Qin, H.; Zhang, Y.; Yu, J.; Ma, T.; Tian, D. Pseudo-dynamic substructure test on a 3-story full-scale model of prefabricated concrete shear wall structure with rebars splicing by grout sleeves. J. Build. Struct. 2017, 32, 26–38. [Google Scholar]
- Jiang, H.; Chen, Z.; Zhang, J.; Wu, B.; Tian, Y.; Liu, W. Quasi-static test of precast reinforced concrete shear wall structure. J. Build. Struct. 2011, 32, 34–40. [Google Scholar]
- Chen, Y.G.; Liu, J.B.; Guo, Z.X.; Zhang, J.X. Test on seismic performance of precast shear wall with reinforcements grouted in holes and spliced indirectly in horizontal connections. J. Harbin Inst. Technol. 2013, 45, 83–89. [Google Scholar]
- Xue, W.; Gu, X.; Hu, X.; Li, X. Experimental study of assembled monolithic concrete shear wall with bolted connection under low reversed cyclic loading. China Civ. Eng. J. 2014, 47, 221–226. [Google Scholar]
- Xue, W.; Hu, X.; Chu, M. Experimental Study of Precast Concrete Shear Wall with Bolted Connection Under Low Reversed Cyclic Loading; Tongji University College of Civil Engineering: Shanghai, China, 2018; pp. 33–94. [Google Scholar]
- Wu, H.; Liu, B.; Jiang, H.; Wang, S.; Yi, X.; Liu, H. Experimental study on seismic performance of precast shear walls connected by large-diameter screws and UHPC. J. Build. Struct. 2022, 43, 61–68. [Google Scholar]
- Zhi, Q.; Yuan, Z.; Zheng, Y.; Jia, L.; Guo, Z. Experimental Research on Seismic Performance of Precast Concrete Shear Walls with a Novel Grouted Sleeve Used in the Connection. J. Earthq. Eng. 2023, 28, 1379–1403. [Google Scholar] [CrossRef]
- Jiao, A.L.; Zhang, P.; Li, Y.H.; Zhi, X.D. Tests on seismic behavior of pre-cast shear walls with annular closed reinforcements. J. Build. Struct. 2015, 36, 103–109. [Google Scholar]
- Gao, Y.F.; Jiao, A.L.; Zhang, Z.S.; Liu, J.; Zhi, X.D. Tests on out-of-plane bending of precast shear walls with annular closed reinforcements. Build. Struct. 2016, 46, 439–442. [Google Scholar]
- Jiao, A.; Zhang, P.; Gao, Y.; Zhang, Z. Research on anchoring performance mechanism of vertical connection of prefabricated shear walls with annular closed reinforcements. Ind. Constr. 2019, 49, 69–76+129. [Google Scholar]
- Xizhi, Z.; Jian, M.; Peng, H. Shear behavior on prefabricated shear wall alveolar type connection. J. Build. Struct. 2017, 38, 93–100+121. [Google Scholar]
- Zhang, X.Z.; Li, X.Q.; Zhang, S.H.; Li, Q.; Xu, S. Experimental study on seismic behavior of prefabricated shear wall with composite alveolar connection and U-type reinforcements overlap. J. Build. Struct. 2020, 41, 79–88. [Google Scholar]
- Zhao, J.; Yin, L.; Li, X.; Li, B.; Zhao, T. Study on seismic performance of prefabricated shear walls using non-contact lapping with steel fiber reinforced sulphoaluminate concrete connection. J. Build. Eng. 2023, 78, 107681. [Google Scholar] [CrossRef]
- Han, Q.; Wang, D.; Xu, S.; Zheng, Z.; Mao, J. Numerical investigation of a new precast concrete shear wall system with horizontal connections. Structures 2024, 70, 107616. [Google Scholar] [CrossRef]
- Han, Q.; Yasir, N.; Wang, D.; He, J. Aseismic performance of prefabricated concrete shear walls with strong horizontal and weak vertical hybrid connections. J. Vib. Shock. 2024, 43, 306–318. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.
- Zhang, X.; Li, F.; Li, Y.; Li, X.; Zhang, S.; Yu, Z. Experimental Study on Shear Behavior of Precast Shear Wall with Composite Alveolar Connections. J. Tianjin Univ. (Sci. Technol.) 2022, 55, 57–65. [Google Scholar]
- JGJ3-2010; Technical Specification for Concrete Structure of Tall Building. China Architecture & Building Press: Beijing, China, 2010.
- JGJ/T 101-2015; Specifications for Seismic Test of Buildings Code; Beijing. China Architecture & Building Press: Beijing, China, 2015.
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Hordijk, D.A. Local Approach to Fatigue of Concrete. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1991. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending. In Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structural Acted on by Well-Defined Repeated Loads, Lisbon, Portugal, 13–14 September 1973; pp. 15–22. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).