Experimental Study of Hardening Small Strain Model Parameters for Strata Typical of Zhengzhou and Their Application in Foundation Pit Engineering

Abstract

The hardening small strain (HSS) model, which considers the non-linear characteristics of the shear modulus of soil in the small strain range, is commonly utilized in the numerical analysis of excavations in sensitive environments. In order to ascertain the parameters of an HSS model for strata typical of Zhengzhou, an extensive series of laboratory tests was executed. Subsequently, a statistical analysis was utilized to establish the relationships between the principal parameters. A three-dimensional finite element model was established based on the excavation of representative strata in Zhengzhou. The accuracy and applicability of the model parameters were verified using the field measurement data. In addition, an analysis of the sensitivity of the main HSS model parameters to the foundation pit deformation was also carried out. The results show that the HSS model can analyze excavation deformation with greater precision than the hardening soil (HS) model or the Mohr–Coulomb (MC) model. The small strain parameters $G_0^{\mathrm{ref}}$ and ${\gamma }_{0.7}$ have a great influence on the horizontal displacement of the support and the vertical displacement of soil behind the wall, respectively. The research results serve as a reliable foundation for both the analysis of excavation deformation and the determination of HSS model parameters for strata typical of Zhengzhou.

1. Introduction

Excavation engineering is vital for the development of underground spaces in urban areas. As these excavations become increasingly deeper, larger, and more complex, it is crucial to prioritize safety, not only for the excavation itself but also for neighboring structures and infrastructure. Thus, the main focus of foundation pit support design is to control deformation and maintain stability. The continuous media finite element method has emerged as the most effective approach to assess the impact of excavations on the surrounding environment. In this context, the proper selection of a soil constitutive model and the accurate determination of model parameters are critical [1,2]. A substantial amount of field measurements and numerical simulation analyses have corroborated that the strain of soil in engineering projects is typically within the small strain range of 0.01% H to 0.3% H (H represents the depth of excavation) [3], as is depicted in Figure 1. Atkinson and Sallfors [4] categorized strain levels into three groups: very small strain levels with a constant stiffness modulus within the elastic range; small strain levels with a nonlinear variation in stiffness modulus with strain; and large strain levels where the soil approaches failure, resulting in relatively small soil shear stiffness.

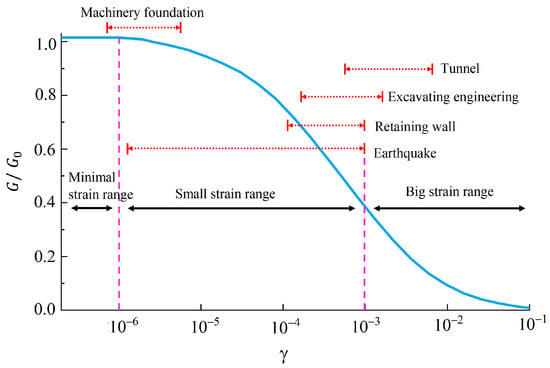
Figure 1. Soil shear stiffness curve and strain division range.

While common constitutive models such as the Mohr–Coulomb (MC) model, the Modified Cam-clay (MCC) model [5], and the hardening soil (HS) model [6,7,8] can be utilized for numerical analyses, they are deemed unsuitable for computations involving small strain problems. Controlling the impact of excavation construction on the surrounding environment within a small strain range is of the utmost importance in complex and sensitive urban environments. However, the ability of common constitutive models to accurately predict relationship behavior within the small strain range is often limited. For instance, the MC model assumes a linear relationship between the force and the deformation, neglecting the time dependency and nonlinearity of soil behavior. The MCC model is an improved version of the MC model which takes into account stress–strain behavior to obtain more accurate deformation predictions. However, strain-softening characteristics cannot be effectively simulated, especially in clay. The HS model, which is a nonlinear constitutive model, incorporates the dilatancy and hardening characteristics of soil deformations. However, it cannot reflect the small strain behavior of soil. In response to these limitations, the hardening small strain (HSS) model [9,10] has emerged as an alternative. Derived from the HS model, it incorporates the modified Hardin–Drnevich shear modulus relationship and takes into account the effect of the stress path and the multi-axial expansion of the yielding surface to establish a more essential representation of soil behavior. In the HSS model, the Matsuoka–Nakai yield surface criterion and the non-associated Drucker–Prager potential are used [11]. Notably, the HSS model comprehensively considers the basic characteristics of soil, such as strain hardening and dilatancy, and can distinguish the loading and unloading stiffness, enabling it to effectively depict the deformation characteristics in the small strain range.

In studies on excavation engineering, to obtain reliable displacement predictions, it is essential to appropriately consider the non-linear dependence between the small strain stiffness and the magnitude of strain amplitudes. Likitlersuang et al. [1] introduced a method for measuring the small strain stiffness of soils before failure and proposed an empirical prediction model. Benz et al. [10] used the HSS model to conduct a three-dimensional finite element analysis of the Sülfeld foundation pit. It was demonstrated that, under zero strain at the initial loading stage, the calculated results of the HSS model were more closely aligned with the measured values compared to those of the HS model. Kung et al. [12] investigated the application of the small strain characteristics of soils in deep excavations, suggesting that the settlement profiles calculated using the HSS model ware more realistic. Schweiger et al. [13] performed a comparative analysis, utilizing a simple finite element excavation case, to investigate the discrepancies in the results calculated using the HS model, the HSS model, and the MC model. The results showed that the HSS model had a high ability to predict soil deformations caused by excavations under small strain conditions. Furthermore, Huynh et al. [14] utilized the HSS model for a back-analysis of displacement in underground diaphragm walls across three excavation cases, demonstrating its superiority over the HS model in accurately predicting the displacement of such retaining structures. For foundation pit engineering in sensitive environments, it is necessary to evaluate the impact of foundation pit excavation on the surrounding environment in the design stage, and then take reasonable engineering measures to ensure the safety of the surrounding environment. Li et al. [15] employed both the HSS and MC models to analyze the deformation in a foundation pit at varying excavation depths. They revealed that the MC model, which neglects soil stiffness under small strain conditions, produced significant overestimations of displacement as the excavation depth increased. Consequently, for excavation depths exceeding 15 m, the HSS model is advocated for numerical analysis. Gu et al. [16] ascertained small strain shear modulus $G_0$ through indoor resonance column and field tests and examined its impact on the deformation analysis of deep foundation pit excavations, revealing that sampling disturbances result in significantly lower values in indoor tests compared to field tests. Hence, values derived from field tests are recommended for deformation analyses.

Zhengzhou is characterized by a wide distribution of silt and silty clay strata. Owing to these unique engineering properties [17,18,19], the HSS model parameter values significantly deviate from those used in other regions, with relevant research still in its infancy. This paper establishes the HSS model parameters for strata typical of Zhengzhou through extensive laboratory tests and statistically analyzes the relationships among the primary moduli parameters. A three-dimensional finite element model was established based on a foundation pit excavation project in Zhengzhou constructed using a pile-anchor composite support system which is unlike the internal support systems used in soft soil areas. The accuracy and applicability of the HSS model parameters were verified by analyzing the entire process of the foundation pit excavation deformation. Additionally, a sensitivity analysis of key HSS model parameters was conducted. The research results can provide a reference for the determination and application of numerical analysis parameters for foundation pit engineering in the Zhengzhou area.

2. Materials and Methods

2.1. Introduction of HSS Model Parameters

The HSS model consists of 13 parameters, and these can be categorized into three groups: strength-related parameters, stiffness-related parameters, and small strain parameters. The strength-related parameters encompass the effective cohesion $c^{\prime }$, the effective internal friction angle ${\phi }^{\prime }$, the dilation angle $\psi$, and the failure ratio $R_{\mathrm{f}}$. The stiffness-related parameters consist of the reference secant modulus value $E_{50}^{\mathrm{ref}}$, the loading–unloading modulus value $E_{\mathrm{ur}}^{\mathrm{ref}}$, the reference tangent modulus value $E_{\mathrm{oed}}^{\mathrm{ref}}$, the reference stress $p^{\mathrm{ref}}$, the loading–unloading Poisson’s ratio $v_{\mathrm{ur}}$, the power exponent of stiffness–stress level correlation m, and the initial static lateral pressure coefficient $K_0$. The small strain parameters include the initial dynamic shear modulus value $G_0^{\mathrm{ref}}$ and the shear strain corresponding to the initial dynamic shear modulus at 70% strain ${\gamma }_{0.7}$. In the HSS model, the values of parameters such as $\psi$, m, $v_{\mathrm{ur}}$, and $p^{\mathrm{ref}}$ can be determined by referencing the existing research outcomes [20]. The determination methods for each parameter are detailed in Table 1.

Table 1. Determination methods for HSS model parameters.

Model Parameter	Determination Method
Reference tangent modulus value $E_{\mathrm{oed}}^{\mathrm{ref}}$	Standard consolidation test
Effective cohesion $c^{\prime }$, effective internal friction angle ${\phi }^{\prime }$, failure ratio $R_{\mathrm{f}}$ and reference secant modulus value $E_{50}^{\mathrm{ref}}$	Triaxial consolidated drained (CD) test
Initial static lateral pressure coefficient $K_0$	K0 consolidation test
Loading–unloading modulus value $E_{\mathrm{ur}}^{\mathrm{ref}}$	Triaxial loading–unloading test
Initial dynamic shear modulus value $G_0^{\mathrm{ref}}$ and shear strain corresponding to the initial dynamic shear modulus at 70% strain ${\gamma }_{0.7}$	Resonant column test
Dilation angle $\psi$	For sand, when ${\phi }^{\prime }$ > 30°, take (${\phi }^{\prime }$ − 30) and when ${\phi }^{\prime }$ < 30°, take 0°; for clay and silt, generally take 0°
Power exponent of stiffness–stress level correlation m	For silt and sand, m = 0.5; for clay, m = 0.5–1.0
Loading–unloading Poisson’s ratio $v_{\mathrm{ur}}$	0.2
Reference stress $p^{\mathrm{ref}}$	100 kPa

2.2. Experimental Materials

The soil specimens used in the experimental study were obtained from a foundation pit project located in Zhengzhou. The sampling process employed a thick-walled sampler for drilling at depths of 3.6–3.8 m, 8.6–8.8 m, 12.4–12.6 m, and 15.4–15.6 m. These depths correspond to the characteristic geological layers of silty clay ①, silt ②, silty clay ③, and sand ④. In accordance with ASTM D854-14 [21], D4318-10 [22], D422-63 [23], and D698-12 [24], the basic physical properties of the soil specimens are presented in Table 2. Soil specimens of appropriate dimensions were prepared from undisturbed soil samples and used to conduct standard consolidation tests, triaxial consolidated drained (CD) tests, K₀ consolidation tests, triaxial loading–unloading tests, and resonant column tests.

Table 2. Basic physical indexes of soil samples.

Stratum	Water Content w/%	Density ρ/g·cm−3	Plasticity Index IP
Silty clay ①	10.35	1.80	12.04
Silt ②	11.27	2.02	6.64
Silty clay ③	14.49	1.85	14.10
Sand ④	15.20	2.00	ND

2.3. Experimental Methods

2.3.1. Standard Consolidation Test

The standard consolidation test was conducted using a one-dimensional consolidation apparatus with a cylindrical soil specimen measuring 61.8 mm in diameter and 20 mm in height. The loading sequence applied was 12.5, 25, 50, 100, 200, 300, 400, 800, and 1600 kPa, with each load level being maintained for a duration of 24 h.

2.3.2. Triaxial Consolidated Drained (CD) Test

The triaxial consolidated drained (CD) test was performed using a GDS stress path triaxial apparatus. The cylindrical specimen, measuring 76 mm in height and 38 mm in diameter, was firstly saturated by applying vacuum and then back pressure. The saturation level was determined using the B-value method. Subsequently, the specimen was consolidated and then sheared under a drained condition at the effective confining pressures of 100 kPa, 200 kPa, and 300 kPa. The shearing process was conducted at a steady rate of 0.011%/min.

2.3.3. K₀ Consolidation Test

In the K₀ consolidation test, the specimen preparation and saturation process was the same as in the triaxial consolidated drained (CD) test. During the consolidation stage, the K₀ consolidation module was selected. The lateral pressure was calculated using the depth of the undisturbed soil sample, and the pressure loading rate was set at 0.1 kPa/min for the duration of the test, which lasted 16 h.

2.3.4. Triaxial Loading–Unloading Test

The apparatus and specimen consolidation procedures used in the triaxial loading–unloading test were identical to those employed in the triaxial consolidated drained (CD) test. During the loading phase, the specimen underwent axial loading, unloading, and reloading sequences using an advanced module. A confining pressure of 100 kPa was established as a reference value. With reference to the results obtained from the CD test on the same soil stratum, the anticipated failure deviator stress $q_{\mathrm{f}}$ of the specimen was estimated. Initially, loading was applied until 40% of the estimated failure deviator stress $q_{\mathrm{f}}$ was reached. Upon reaching this level, axial unloading was performed, followed by reloading to 60% of the estimated failure deviator stress $q_{\mathrm{f}}$.

2.3.5. Resonant Column Test

The resonant column test was conducted using a GDS resonant column testing system. Cylindrical specimens with diameters of 50 mm and heights of 100 mm were utilized. The consolidation procedures conducted prior to the test were consistent with those used in the triaxial consolidated drained (CD) test. Subsequently, a vibrational force was applied to the consolidated specimens at different voltages (0.001 V, 0.002 V, 0.004 V, 0.008 V, 0.016 V, 0.032 V, 0.064 V, 0.128 V, and 0.256 V). The specimens were subjected to torsional vibration in ascending order of voltage, and the resulting dynamic shear strain and resonant frequency values were recorded based on the peak frequency observed during the test.

3. HSS Model Parameter Test Results

3.1. Standard Consolidation Test

Through the standard consolidation tests conducted on the soil samples from different strata, an understanding of the relationship between consolidation pressure and axial strain was obtained. After fitting the data points, the slope of the curve at a consolidation pressure of 100 kPa was taken as the reference tangent modulus value $E_{\mathrm{oed}}^{\mathrm{ref}}$ of the soil. The R² values for the fitted curves were all 0.99, as is shown in Figure 2. The axial strain of each specimen increased with the increase in consolidation pressure. Among the different strata typical of Zhengzhou, the reference tangent modulus value $E_{\mathrm{oed}}^{\mathrm{ref}}$ for sand ④ was the highest (14.6 MPa), while the values for silty clay ①, silty clay ③, and silt ② were 7.02 MPa, 5.58 MPa, and 4.12 MPa, respectively.

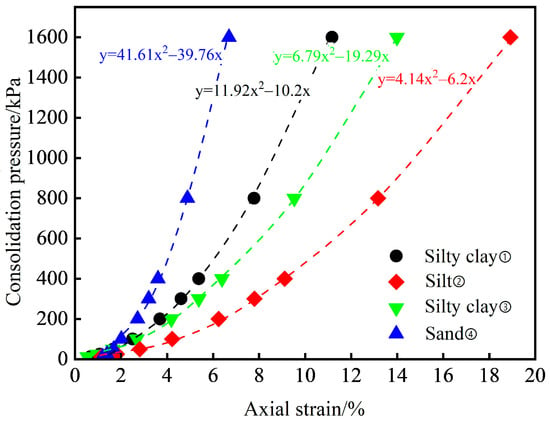
Figure 2. Relationship curves between consolidation pressure and axial strain.

3.2. Triaxial Consolidated Drained (CD) Test

Triaxial consolidated drained (CD) shearing tests were conducted to determine the effective cohesion $c^{\prime }$, the effective internal friction angle ${\phi }^{\prime }$, the failure ratio $R_{\mathrm{f}}$, and the reference secant modulus $E_{50}^{\mathrm{ref}}$ for the various representative soil strata. Figure 3 shows the stress Mohr circles of the representative Zhengzhou soil strata ① to ②; it reveals that the variations in effective cohesion $c^{\prime }$ and effective internal friction angle ${\phi }^{\prime }$ are influenced by distinct confining pressures.

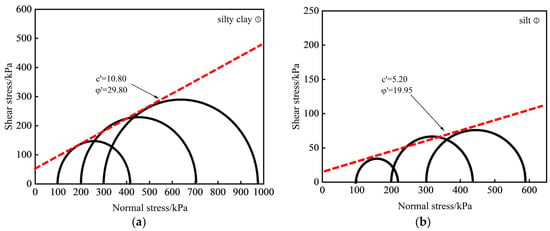
Figure 3. Stress Mohr circles of representative Zhengzhou soil strata under different confining pressures: (a) silty clay ①; (b) silt ②.

The stress–strain relationship curves of the representative strata under a confining pressure of 100 kPa are shown in Figure 4. By analyzing the stress–strain relationship curves of each representative stratum, the reference secant modulus value $E_{50}^{\mathrm{ref}}$ and the failure ratio $R_{\mathrm{f}}$ can be obtained. The peak deviator stress achieved during soil sample failure is taken as the failure deviator stress $q_{\mathrm{f}}$. The slope of the straight line connecting the origin and point $1/2q_{\mathrm{f}}$ in the diagram represents the reference secant modulus value $E_{50}^{\mathrm{ref}}$.

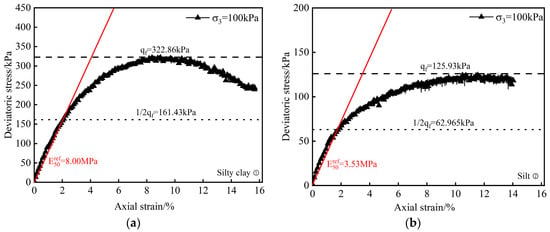
Figure 4. Stress–strain curves of representative Zhengzhou soil strata under a confining pressure of 100 kPa: (a) silty clay ①; (b) silt ②.

In the HS model [8], deviator stress $q$ and axial strain ${\epsilon }_1$ can be expressed by Equation (1):

$${\epsilon }_1=\frac{1}{2E_{50}}\cdot \frac{q}{q-q/q_{\mathrm{a}}}(q<q_{\mathrm{f}})$$

(1)

Equation (1) can be transformed to obtain Equation (2):

$$\frac{{\epsilon }_1}{q}=\frac{{\epsilon }_1}{q_{\mathrm{a}}}+\frac{1}{2E_{50}}(q<q_{\mathrm{f}})$$

(2)

In order to reduce the influence of human factors, Liang et al. [25] proposed that the relationship curve of ${\epsilon }_1/q$ and ${\epsilon }_1$ can be obtained through the linear fitting of the points with 70% and 95% of $q/q_{\mathrm{f}}$, as shown in Figure 5. The reciprocals of the slopes of the fitted lines are the $q_{\mathrm{a}}$ values of the representative strata (①–④), which were 476.19 kPa, 153.84 kPa, 400 kPa, and 476.19 kPa, respectively. The failure ratio $R_{\mathrm{f}}$ is the ratio of the failure deviator stress $q_{\mathrm{f}}$ to $q_{\mathrm{a}}$.

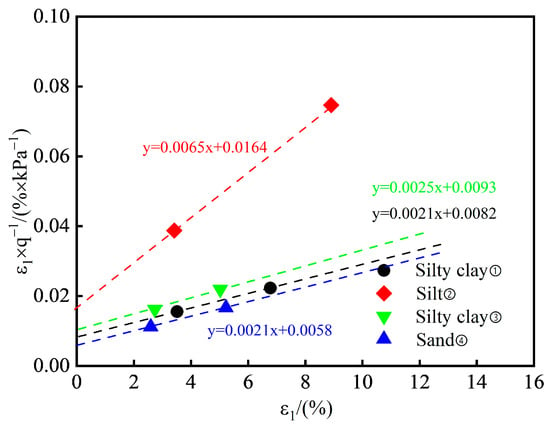
Figure 5. The relation curves between ${\epsilon }_1$ and ${\epsilon }_1/q$ for the representative Zhengzhou soil strata.

3.3. K₀ Consolidation Test

The initial static lateral pressure coefficient $K_0$ can be determined through K₀ consolidation tests. The initial value $K_0$ is 1, and it gradually stabilizes and reaches its final value during the consolidation process. As the loading process progresses, the deviatoric stress continues to increase until the test is completed. The test results for the representative strata are shown in Figure 6. The $K_0$ values of the silt and silty clay were relatively close, ranging from 0.51 to 0.53. The $K_0$ value of the sand was larger (0.58).

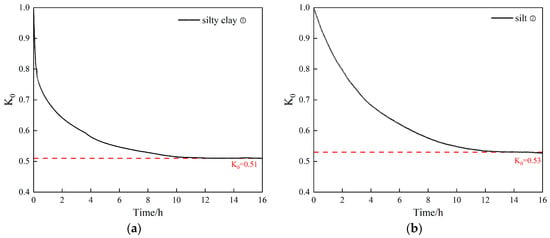
Figure 6. K₀ consolidation test results of typical strata in Zhengzhou: (a) Silty clay ①. (b) Silt ②.

3.4. Triaxial Loading–Unloading Test

The reference loading–unloading modulus value $E_{\mathrm{ur}}^{\mathrm{ref}}$ can be obtained through triaxial loading–unloading tests, as illustrated in Figure 7. The end of the unloading point and the intersection of the unloading and reloading curves are connected by a straight line. The slope of the straight line is the reference loading–unloading modulus value $E_{\mathrm{ur}}^{\mathrm{ref}}$ of the stiffness parameter. The reference loading–unloading modulus values $E_{\mathrm{ur}}^{\mathrm{ref}}$ of the representative strata (①–④) were 31.06 MPa, 25.3 MPa, 34.76 MPa, and 46.08 MPa, respectively.

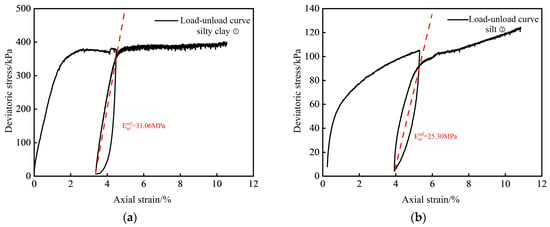
Figure 7. Triaxial loading–unloading test results for representative Zhengzhou soil strata: (a) silty clay ①; (b) silt ②.

3.5. Resonant Column Test

The small strain parameters $G_0^{\mathrm{ref}}$ and ${\gamma }_{0.7}$ can be obtained using the resonant column test [26,27,28]. The relationship between the dynamic shear stress $\tau$ and the shear strain $\gamma$ obtained via the resonant column test can be expressed as Equation (3):

$$\tau =\frac{\gamma }{\mathrm{a}+\mathrm{b}\gamma }$$

(3)

where $\tau$ is the dynamic shear stress, a and b are constants, and $\gamma$ is the shear strain.

The dynamic shear modulus value G of the soil can be expressed as Equation (4):

$$G=\frac{\tau }{\gamma }$$

(4)

According to Equations (3) and (4):

$$1/G=\mathrm{a}+\mathrm{b}\gamma$$

(5)

Figure 8 shows the dynamic shear modulus attenuation curves of the representative strata under a reference confining pressure 100 kPa. The small strain parameters $G_0^{\mathrm{ref}}$ and ${\gamma }_{0.7}$ can be obtained from the shear modulus attenuation curves of the different representative strata. When the shear strain $\gamma$ is 0, the maximum dynamic shear modulus is the initial dynamic shear modulus value $G_0^{}$, and the initial dynamic shear modulus value $G_0^{}$ under the reference confining pressure of 100 kPa is the small strain parameter $G_0^{\mathrm{ref}}$. The small strain parameter ${\gamma }_{0.7}$ is the shear strain corresponding to 70% of $G_0^{}$.

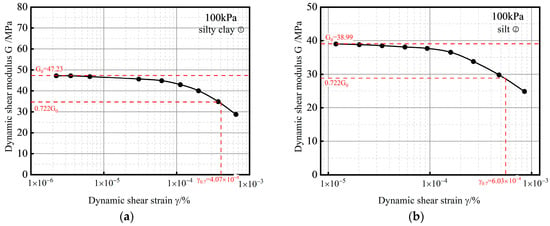
Figure 8. The resonance column test results for the representative Zhengzhou soil strata: (a) silty clay ①; (b) silt ②.

3.6. Statistical Analysis of HSS Model Parameters

Through the above tests and methods, 13 HSS model parameters were obtained for each representative stratum, and these are shown in Table 3. By summarizing and analyzing the above parameters, the proportion relationships of the main parameters were obtained, and these are shown in Table 4. The compression modulus value $E_{\mathrm{s}1-2}$ can be obtained from geological survey reports.

Table 3. Summary of HSS model parameter values.

Parameter	Silty Clay ①	Silt ②	Silty Clay ③	Sand ④
$E_{50}^{\mathrm{ref}}$/MPa	8.00	3.53	6.75	10.66
$E_{\mathrm{oed}}^{\mathrm{ref}}$/MPa	7.02	4.12	5.58	14.60
$E_{\mathrm{ur}}^{\mathrm{ref}}$/MPa	31.60	25.30	34.76	46.08
m	0.60	0.60	0.60	0.60
$c^{\prime }$/kPa	10.80	5.20	9.66	0.45
${\phi }^{\prime }$/°	29.80	19.95	28.50	37.70
$\psi$/°	0.00	0.00	0.00	0.00
$R_{\mathrm{f}}$	0.67	0.82	0.60	0.68
$K_0$	0.51	0.53	0.51	0.58
$v_{\mathrm{ur}}$	0.20	0.20	0.20	0.20
$p^{\mathrm{ref}}$/kPa	100	100	100	100
$G_0^{\mathrm{ref}}$/MPa	47.23	38.99	48.23	55.72
${\gamma }_{0.7}$	$4.54\times {10}^{-4}$	$6.67\times {10}^{-4}$	$3.87\times {10}^{-4}$	$5.53\times {10}^{-4}$

Table 4. Summary of proportional relationships of main HSS model parameters.

Stratum	${\mathit{E}}_{\mathbf{s}1-2}$/MPa	${\mathit{E}}_{\mathbf{oed}}^{\mathbf{ref}}$$/{\mathit{E}}_{\mathbf{s}1-2}$	${\mathit{E}}_{50}^{\mathbf{ref}}$$/{\mathit{E}}_{\mathbf{oed}}^{\mathbf{ref}}$	${\mathit{E}}_{\mathbf{ur}}^{\mathbf{ref}}$$/{\mathit{E}}_{50}^{\mathbf{ref}}$	${\mathit{G}}_0^{\mathbf{ref}}$$/{\mathit{E}}_{\mathbf{ur}}^{\mathbf{ref}}$
Silty clay ①	8.35	0.84	1.14	4.13	1.52
Silt ②	4.47	0.92	0.86	7.73	1.54
Silty clay ③	5.61	0.99	1.21	5.00	1.39
Sand ④	21.16	0.69	0.73	4.32	1.21

A comparative analysis was performed to compare the values of the HSS model parameters for Zhengzhou and those of other regions [29,30,31,32,33,34]. The statistical analysis results for clay are presented in Figure 9. The proportion relationships among various parameters for clay in Zhengzhou were within the range of the proportion relationships observed in other regions. The fitting results obtained using a linear regression method that involves passing through the origin align closely with the statistical analysis results. In the absence of measured model parameters, empirical values can be used as references based on their fitting relationships: $E_{\mathrm{oed}}^{\mathrm{ref}}$ = 0.89 $E_{\mathrm{s}1-2}$, $E_{50}^{\mathrm{ref}}$ = 1.13 $E_{\mathrm{oed}}^{\mathrm{ref}}$, $E_{\mathrm{ur}}^{\mathrm{ref}}$ = 3.89 $E_{50}^{\mathrm{ref}}$, and $G_0^{\mathrm{ref}}$ = 2.0 $E_{\mathrm{ur}}^{\mathrm{ref}}$. Due to the limited availability of experimental research on HSS model parameters for silt and sand, reliable statistical data are lacking. Therefore, empirical values were adopted based on the experimental results obtained in this study, and these are presented in Table 4.

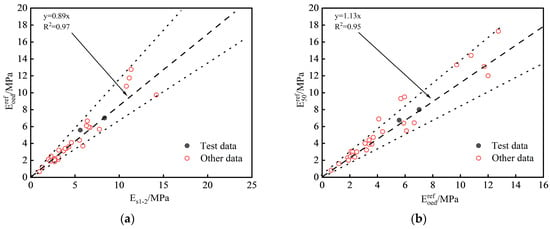
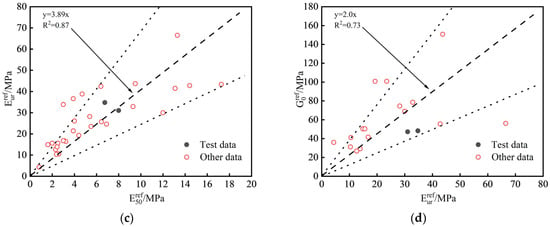
Figure 9. Statistical analysis of the proportional relationships between the parameters of the HSS model for silty clay: (a) $E_{\mathrm{oed}}^{\mathrm{ref}}$ and $E_{\mathrm{s}1-2}$; (b) $E_{50}^{\mathrm{ref}}$ and $E_{\mathrm{oed}}^{\mathrm{ref}}$; (c) $E_{\mathrm{ur}}^{\mathrm{ref}}$ and $E_{50}^{\mathrm{ref}}$; (d) $G_0^{\mathrm{ref}}$ and $E_{\mathrm{ur}}^{\mathrm{ref}}$.

4. Numerical Simulation of Foundation Pit

4.1. Establishment of Finite Element Model

The entire process of excavating a foundation pit in Zhengzhou was simulated and analyzed using Plaxis 3D V20. In order to eliminate the size effect of the model, the depth of the model should be greater than two times the depth of the supporting structure, and the distance between the foundation pit supporting structure and the edge of the model should be three to five times the excavation depth. Therefore, the dimensions of the finite element model were 200 m in length, 20 m in width, and 50 m in height. The bottom of the model was set as a fixed impermeable boundary, the horizontal displacement around the model was limited, and the surrounding and surface were set as permeable boundaries.

The soil element utilized in the model was a 10-node wedge shape. The model was divided into 67,499 units and 10,897 nodes. The finite element model is shown in Figure 10. The foundation pit support system used a pile-anchor composite support structure, which mainly consists of soil nails, fully bonded anchor rods, soil nail walls, sheet piles, crown beams, and waist beams. The finite element model support form is shown in Figure 11. The sheet pile and soil nail wall were simulated by a six-node triangular plate element, the waist beam and crown beam were simulated by a beam element, and the soil nail and fully bonded anchor rod were simulated by an embedded pile element. The specific parameters are shown in Table 5. It should be noted that in this case, the sheet pile support was made up of mixed piles and concrete cast-in-place piles. In order to accurately simulate the mechanical properties of sheet piles, a plate element of an equivalent thickness was used in the simulation. Finally, the whole process of the excavation of the foundation pit was simulated, including the layered excavation of the soil and the construction of the soil nails, anchor rods, and sheet piles. The excavation depth of each layer was 1.5 m, the initial groundwater level was set to -10.6 m, and the precipitation was synchronized during the excavation. Due to the level of the simulated site, the initial stress field was generated by the K₀ process. The construction steps were as shown in Table 6.

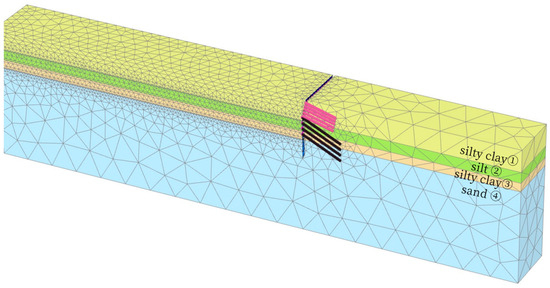
Figure 10. Three-dimensional finite element model of foundation pit.

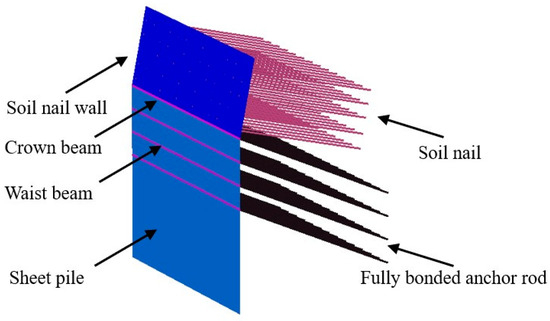
Figure 11. Three-dimensional finite element model of supporting structure system.

Table 5. Supporting structure parameters of finite element model.

Supporting Structure	Simulation Unit Type	Elastic Modulus E/Pa	Thickness, Diameter, or Size/m
Soil nail wall	Plate element	$25.5\times {10}^6$	0.08
Sheet pile	Plate element	$30.0\times {10}^6$	0.7
Soil nail	Embedded pile element	$5.36\times {10}^6$	0.12
Fully bonded anchor rod	Embedded pile element	$5.36\times {10}^6$	0.18
Crown beam	Beam element	$30.0\times {10}^6$	0.7 × 0.5
Waist beam	Beam element	$200\times {10}^6$	0.18 × 0.02

Table 6. Three-dimensional finite element foundation pit excavation construction steps.

Construction Step	Working Condition
Phase 0	Calculation of initial stress field
Phase 1	The first layer of earthwork excavation, the first layer of soil nail construction
Phase 2	The second layer of earthwork excavation, the second layer of soil nail construction
Phase 3	The third layer of earthwork excavation, the third layer of soil nail construction
Phase 4	The fourth layer of earthwork excavation, the fourth layer of soil nail construction
Phase 5	The fifth layer of earthwork excavation, shotcrete surface construction
Phase 6	The sixth layer of earthwork excavation, sheet pile and crown beam construction, the first layer of fully bonded anchor rod construction
Phase 7	The seventh layer of earthwork excavation, the second layer of fully bonded anchor rod construction, foundation pit dewatering
Phase 8	The eighth layer of earthwork excavation, the third layer of fully bonded anchor rod construction, foundation pit dewatering
Phase 9	The ninth layer of earthwork excavation, the fourth layer of fully bonded anchor rod construction, foundation pit dewatering
Phase 10	The final earthwork excavation, foundation pit dewatering

4.2. Verification of HSS Model Parameters

Figure 12 is a total deformation cloud map of the foundation pit and the surrounding soil after the excavation is completed, based on the HSS model parameters. Positive values appear along the positive direction of the coordinate axis, and negative values appear in the opposite direction of the coordinate axis. The maximum deformation value in the finite element model was that of the uplift deformation in the middle of the foundation pit, and a representative section in the center of the model was selected to further analyze the deformation characteristics.

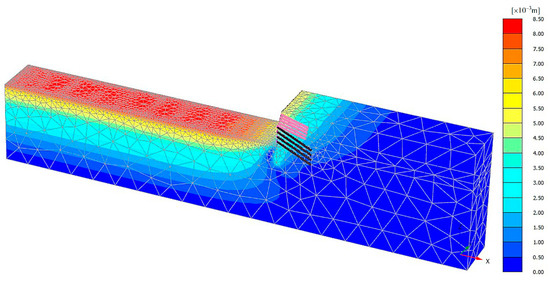
Figure 12. Total deformation cloud map of foundation pit at the final excavation stage.

In order to verify the reliability and accuracy of the HSS model parameters obtained in Section 3.6, the values of the deep horizontal displacement of the supporting structure were calculated using different constitutive models and compared with the measured data, as is shown in Figure 13. When compared, the deformation patterns between the calculated values and the values measured using the HSS model were highly consistent. When the excavation reached phase 6, the horizontal displacement of the upper deep layer was large, and the displacement value decreased rapidly with the increase in the depth of the foundation pit. The finite element calculation showed that the maximum horizontal displacement of the pile top was 4.03 mm from excavation to phase 10, and the maximum horizontal displacement of the measured pile top was 3.93 mm. In contrast, the results calculated using the MC model showed significant deviations from the measured values. The results computed using the HS model lay between those of the MC and HSS models. Overall, for deformations in the small strain range of excavations, the HSS model, which considers the small strain characteristics of the soil, provides more accurate calculations. The suitability of the HSS model for analyzing deformations in excavations under small strain conditions was demonstrated by the relatively precise results that were obtained. This indicates that a finite element analysis based on the HSS model can provide a practical reference for the design and investigation of a typical stratified excavation in the Zhengzhou region.

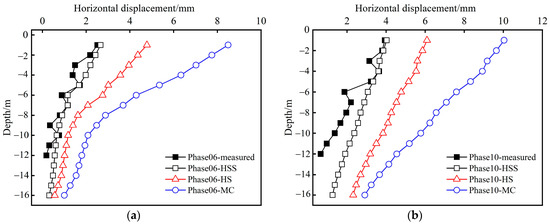
Figure 13. Comparison of the measured horizontal displacement data and the results calculated using different constitutive models: (a) phase 6; (b) phase 10.

4.3. Analysis of Three-Dimensional Finite Element Calculation Results

4.3.1. Horizontal Displacement

Based on the results calculated using the HSS model, the deformation characteristics of the foundation pit excavation were analyzed. Figure 14 shows a horizontal displacement cloud map of the different construction steps in a typical section. Positive values denote outward displacement from the foundation pit, while negative values indicate inward displacement. When the foundation pit is excavated to phase 4 (as shown in Figure 14a), the maximum horizontal displacement of the foundation pit is 2.8 mm. When the excavation reaches phase 6 (as shown in Figure 14b), the construction of the first layer of fully bonded anchor rods begins, and the maximum horizontal displacement of the foundation pit is 3.75 mm, which is 34% higher than that of phase 4. When the excavation reaches the final stage (as shown in Figure 14c), the maximum horizontal displacement of the foundation pit is 4.13 mm, which is 10% higher than that of phase 6, indicating that the fully bonded anchor rods play an important role in controlling the horizontal displacement of the foundation pit. The final deformation of the foundation pit diffuses into the soil outside the pit in the form of concentric circles which resemble the form of the slip surface of the foundation pit. As the depth increases, the horizontal deformation of the supporting structure gradually decreases. In addition, the soil at the junction of the pile and the bottom of the excavated foundation pit moves to the outside of the foundation pit, and this may be caused by the uplift deformation inside the foundation pit and the extrusion of the soil at the junction of the supporting structure and the bottom of the foundation pit. The horizontal displacement of the soil outside the pit also increases as the excavation of the foundation pit progresses, and the influence range continues to expand.

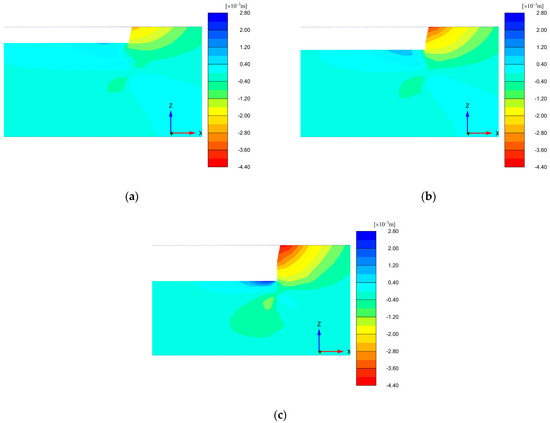
Figure 14. Nephograms showing horizontal displacement of soil in typical sections of a foundation pit during different construction steps: (a) phase 4; (b) phase 6; (c) phase 10.

4.3.2. Vertical Displacement

Figure 15 presents nephograms showing the vertical displacement of soil in typical sections of a foundation pit during different construction steps. Positive values represent uplift of the foundation pit, and negative values represent downward settlement. As the excavation of the foundation pit progresses, the uplift of the foundation pit and the settlement of the surrounding soil increase. In comparison, the uplift in the middle of the foundation pit is less than the maximum settlement of the foundation pit at Phase 4 (as is shown in Figure 15a). When the foundation pit is excavated to Phase 6 (as shown in Figure 15b), the maximum settlement value of the foundation pit is not much different from the uplift value in the middle of the foundation pit. As the excavation depth increases, the uplift value of the foundation pit increases continuously and exceeds the maximum settlement value (as is shown in Figure 15c). This is due to the continuous excavation of the soil and the release of stress. The uplift of the foundation pit presents the characteristics of elastic uplift, and the uplift deformation of the foundation pit is larger toward the middle of the foundation pit. In addition, as the excavation of the foundation pit progresses, the influence range of the surrounding soil settlement expands.

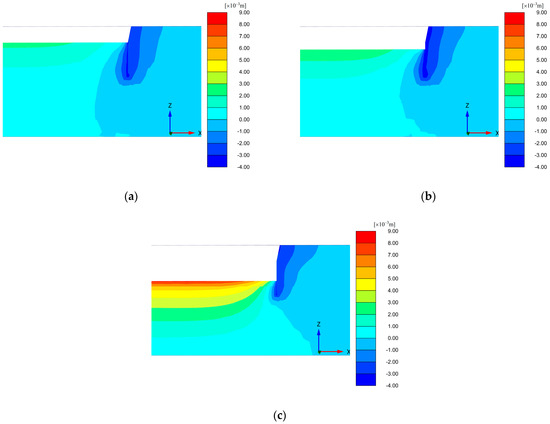
Figure 15. Nephograms showing vertical displacement of soil in typical sections of a foundation pit during different construction steps: (a) phase 4; (b) phase 6; (c) phase 10.

4.3.3. Deep-Level Horizontal Displacement of Supporting Structure

The deep-level horizontal displacement of the excavation support structure is shown in Figure 16. Significant variations in horizontal displacement are observed in the upper part of the support structure, while the lower part exhibits smaller changes. The horizontal displacement values decrease as the depth increases with the progress of the excavation construction. Before Phase 6, there was almost no significant deep-level horizontal displacement in the lower support structure. However, after the completion of Phase 6, the maximum deep-level horizontal displacement value occurred at the top of the pile, measuring 2.65 mm. This indicates that the row pile construction had a significant impact on the deep-level horizontal displacement. By Phase 9, the maximum deep-level horizontal displacement value increased to 2.94 mm, representing a growth of only 10.94% and indicating that a bolt can effectively control the deep horizontal displacement of the pile. Finally, after the excavation was completed (Phase 10), the maximum deep-level horizontal displacement value was 4.03 mm.

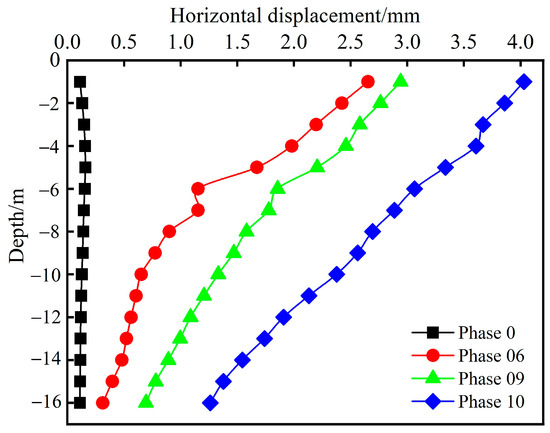
Figure 16. Deep-level horizontal displacement of the excavation support structures during different construction steps.

4.3.4. Vertical Displacement of Soil behind the Wall

Figure 17 shows the vertical displacement curves for the soil behind the wall during different construction steps. The vertical displacement curves of the soil behind the wall are parabolic, and the closer to the supporting structure, the greater the displacement value. Upon reaching construction phases 2 and 4, the maximum vertical displacement values of 1.76 mm and 2.20 mm, respectively, were recorded for the soil behind the wall. This shows that in the construction stage of the upper soil nailing wall, the vertical displacement value of the soil behind the wall develops rapidly. This is due to the influence of the upper earthwork excavation on the shallow soil disturbance and the active earth pressure at the edge of the foundation pit. Upon completion of the soil nailing wall, maximum vertical displacement values of 2.59 mm and 2.94 mm were recorded for the soil behind the wall at the end of phases 6 and 9, respectively. This shows that the excavation of the lower soil has a relatively small influence on the vertical displacement of the soil behind the wall. In the final excavation stage (phase 10), the vertical displacement behind the wall increased slightly, indicating that as the excavation depth increases, the constraint of the supporting structure on the vertical displacement of the soil behind the wall begins to weaken.

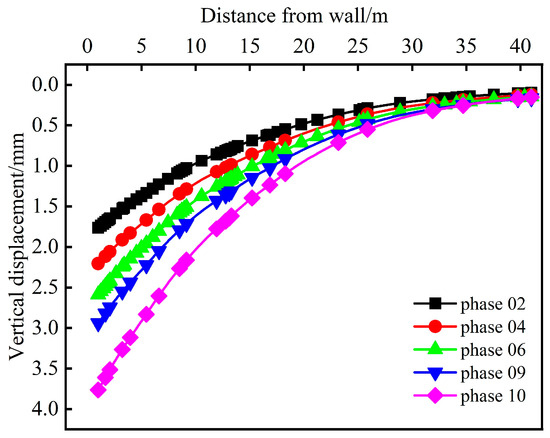
Figure 17. Vertical displacement of soil behind the wall under during different construction steps.

4.4. Sensitivity Analysis of HSS Model Parameters

4.4.1. Sensitivity Analysis Method

To analyze the influence of different HSS model parameters on the deformation of the foundation pit, a finite element model was established for a silty homogeneous stratum (shown in Figure 18). As the value ranges of some of the parameters ($K_0$, $\psi$, $p^{\mathrm{ref}}$, $v_{\mathrm{ur}}$, $E_{50}^{\mathrm{ref}}$, $E_{\mathrm{oed}}^{\mathrm{ref}}$, and $E_{\mathrm{ur}}^{\mathrm{ref}}$) in the HSS model are limited and the value method is fixed, a parameter sensitivity analysis was carried out using the parameter change method for the small strain parameters ($G_0^{\mathrm{ref}}$, ${\gamma }_{0.7}$) and the stiffness–stress level correlation m with flexible values for the large strain parameters. This method involves changing one parameter while keeping the others unchanged and not considering their correlations. By comparing the varying ranges of deep-level horizontal displacement and vertical displacement of the soil behind the wall under different parameter values, the sensitivity of each parameter to the deformation of the foundation pit was analyzed.

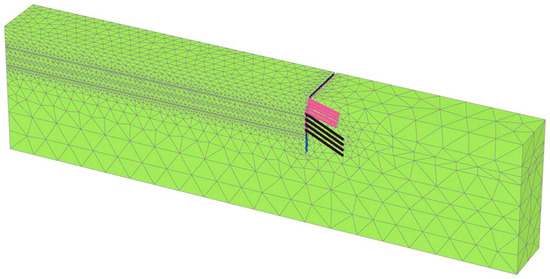
Figure 18. Parametric influence analysis of finite element model.

4.4.2. Sensitivity Analysis of Different Parameters

Figure 19 shows that the maximum deep-level horizontal displacement and the maximum vertical displacement behind the wall are positively correlated with the initial dynamic shear modulus value $G_0^{\mathrm{ref}}$. When $G_0^{\mathrm{ref}}$ increases by 10%, the maximum deep-level horizontal displacement increases by 8.5% and the maximum vertical displacement of the soil behind the wall increases by 5.7%. When $G_0^{\mathrm{ref}}$ decreases by 10%, the maximum deep-level horizontal displacement decreases by 8.9% and the maximum vertical displacement of the soil behind the wall decreases by 6.3%.

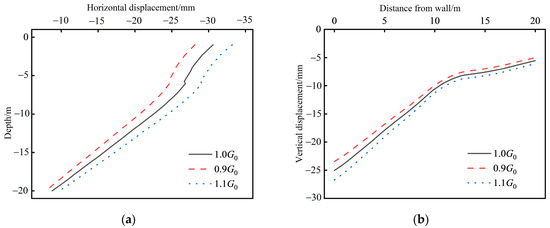
Figure 19. Results of sensitivity analysis of parameter $G_0^{\mathrm{ref}}$: (a) horizontal displacement; (b) vertical displacement.

The maximum deep-level horizontal displacement decreases as the shear strain γ_0.7 increases, and the change is obvious. When γ_0.7 increases by 20%, the maximum deep-level horizontal displacement decreases by 12.8% and the maximum vertical displacement of the soil behind the wall decreases by 14%. When γ_0.7 decreases by 20%, the maximum deep-level horizontal displacement increases by 14.2% and the maximum vertical displacement of the soil behind the wall increases by 14.5% (as is shown in Figure 20).

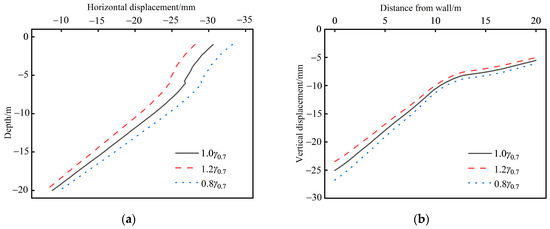
Figure 20. Results of sensitivity analysis of parameter ${\gamma }_{0.7}$: (a) horizontal displacement; (b) vertical displacement.

When the power exponent of the stiffness–stress level correlation m increases by 50% and decreases by 50%, it can be seen from Figure 21 that the maximum deep-level horizontal displacement and the maximum vertical displacement of the soil behind the wall decrease as the power exponent increases, and the change is even more obvious. When the power exponent m increases by 50%, the maximum deep-level horizontal displacement of the wall decreases by 16.8% and the maximum vertical displacement of the soil behind the wall decreases by 18.3%. When the power exponent m decreases by 50%, the maximum deep-level horizontal displacement increases by 14.4% and the maximum vertical displacement of the soil behind the wall increases by 18%.

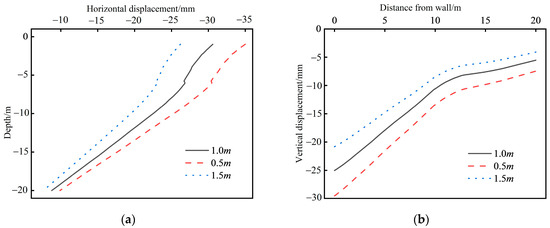
Figure 21. Results of sensitivity analysis of parameter m: (a) horizontal displacement; (b) vertical displacement.

4.4.3. Sensitivity Analysis Results

In order to analyze the influence of parameter changes on the maximum deep-level horizontal displacement and the maximum vertical displacement of the soil behind the wall, the percentage changes in the maximum deep-level horizontal displacement and the maximum vertical displacement of the soil behind the wall were divided by the percentage change in each parameter (taking the absolute value), and the corresponding change values of the maximum deep-level horizontal displacement and the maximum vertical displacement of the soil behind the wall were obtained when the parameters changed by 1%.

Figure 22 shows that the small strain parameters $G_0^{\mathrm{ref}}$ and ${\gamma }_{0.7}$ had a great influence on the deformation of the foundation pit. Every 1% change in the small strain parameters caused the deformation of the foundation pit to change more than 0.6%. While the influence of $G_0^{\mathrm{ref}}$ on the deep-level horizontal displacement of the foundation pit was the most obvious, and the influence of ${\gamma }_{0.7}$ on the vertical displacement of the soil behind the foundation pit wall was also obvious, and they were more sensitive to decreases in the parameter values than increases. The influence of the parameter m in the large strain range on the deformation of the foundation pit is obviously smaller than that of the small strain parameters. When the large strain parameter m changed by 1%, the deformation of the foundation pit was about 0.3%.

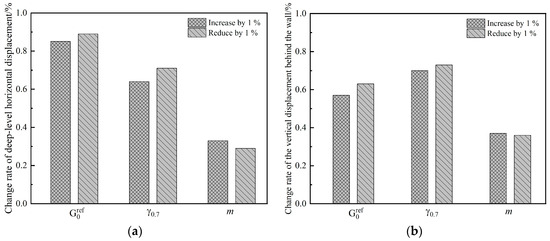
Figure 22. Analysis of sensitivity of HSS model parameters to foundation pit deformation: (a) deep-level horizontal displacement; (b) vertical displacement of soil behind the wall.

5. Discussion

The small strain parameter $G_0^{}$ in the HSS model is primarily influenced by the void ratio e and the mean stress p, whereas ${\gamma }_{0.7}$ is mainly influenced by the mean stress p and the plasticity index Ip. Benz et al. [9,10] verified the HSS model through a drained triaxial test of dense Hostun sand, which showed that the small strain stiffness had little effect on the overall stress–strain curve and that the difference in the secant modulus of the stress–strain curve was only reflected in the small strain stage. Xie et al. [34] conducted a sensitivity analysis of the small strain parameters and found that the slope of the initial compression curve increased as $G_0^{\mathrm{ref}}$ increased. At the same time, as ${\gamma }_{0.7}$ increased, the range of soil needed to maintain the stiffness of $G_0^{}$ also increased.

In a study by Shi et al. [35] on geological layers typical of Xiamen, a finite element simulation of a foundation pit project was performed using the HSS model, and it was demonstrated that the parameter $G_0^{\mathrm{ref}}$ has a significant impact on surface settlement and retaining wall movements, and that the parameter ${\gamma }_{0.7}$ has an increasing influence on surface settlement as the excavation depth increases. This aligns with the substantial impact of the small strain parameters on the deformation of the foundation pit observed in this study.

In addition, all the parameters of the HSS model used in this study were derived from laboratory tests on undisturbed soil. It is important to note that the properties of undisturbed soil can alter during transport and preservation, leading to discrepancies between laboratory-derived parameters and those derived from field tests. The study of the relationship between small strain parameters derived from field tests on undisturbed soil and those derived from laboratory tests is a promising area for further exploration.

6. Conclusions

This paper derived the HSS model parameters of strata typical of Zhengzhou through extensive laboratory tests and established the empirical relationship between the main moduli parameters. Using the excavation of a typical stratum foundation pit in Zhengzhou as an example, a three-dimensional finite element model was constructed. After verifying that the values of the HSS model parameters were reasonable and accurate, the deformation characteristics and the impact of small strain parameters on foundation pit deformation were further investigated. The conclusions are as follows:

(1)

The values of the HSS model parameters of strata typical of the Zhengzhou area were obtained through standard consolidation tests, triaxial consolidation drainage (CD) tests, K₀ consolidation tests, triaxial loading–unloading tests, and resonance column tests. The parameter value method was verified in the actual project, and a general HSS model parameter value method suitable for the soil formations typical of this area was obtained.

(2)

A proportional relationship between different moduli was established by statistically analyzing the main HSS parameter values across various regions, ensuring parameter value rationality and significantly reducing testing time.

(3)

The simulation results were compared with the measured data and the calculation results of the HS model and the MC model. The calculation results of the MC model were quite different from the measured values, and the HS model was between the MC model and the HSS model. The HSS model was more accurate when considering the small strain characteristics of the soil than the HS model or the MC model.

(4)

The small strain parameters $G_0^{\mathrm{ref}}$ and ${\gamma }_{0.7}$ significantly influenced the deformation of the foundation pit. $G_0^{\mathrm{ref}}$ was particularly sensitive to the deep-level horizontal displacement of the supporting structure, while ${\gamma }_{0.7}$ was more responsive to the vertical displacement of the soil behind the wall. Furthermore, a decrease in parameter values had a higher sensitivity than an increase.