Mechanical Behavior of Special-Shaped Reinforced Concrete Composite Columns Encased with GFRP Core Columns

Abstract

In order to investigate the mechanical behavior of special-shaped reinforced concrete composite columns encased with GFRP core columns (EGCSSCs) subjected to axial load, twenty-seven full-scale EGCSSCs were designed with varying parameters: axial compressive strength of core concrete (f_cc), axial compressive strength of peripheral concrete (f_co), thickness of GFRP tube (t_gfrp), ratio of longitudinal reinforcement (ρ_v), stirrup ratio (ρ_s) and GFRP ratio in the cross-section (α). The three-dimensional finite element refined models of EGCSSCs were established by ABAQUS finite element software, and the response of EGCSSCs under axial load was studied based on the verification of finite element modeling. The influence of different parameters on the ultimate axial compressive strength (N_us), initial stiffness (K), and ductility index (µ) of EGCSSCs was obtained, and the typical failure mode of EGCSSCs was clearly described. The results showed that the main failure mode of the EGCSSCs subjected to axial load was bulging outward at the middle of the EGCSSCs, showed yielding of the longitudinal steel bars, and was crushing both ends of the peripheral concrete. When the column was damaged, the peripheral concrete reached peak stress earlier than the core concrete. All specimens exhibited excellent load-carrying capacity and good ductility. Moreover, with the existence of GFRP core columns, the N_us and µ of the columns were increased by 11.61% and 140.86%. In addition, K increased with the increase in f_cc, f_co, t_gfrp and α, and the largest increments were 23.99%, 50.54%, 21.77%, and 34.19%, respectively. µ decreased with the increase in f_cc and f_co, which decreased by 14.05% and 40.28%, respectively. By using statistical regression and introducing the constraint effect coefficients and the reduction coefficient, the calculation formula for the axial compression-bearing capacity of EGCSSCs was derived, which could lay a foundation for the popularization and application of this kind of composite column in practical engineering.

1. Introduction

Special-shaped reinforced concrete (RC) columns can not only increase indoor space but can also avoid frame columns protruding outward because the column limbs are hidden in the wall [1]; therefore, special-shaped RC columns are widely used in construction projects. With the development of building structures to super high-rise, heavy load, and large spans, conventional special-shaped RC columns cannot meet the strength and stiffness requirements of the structure well; thus, it is extremely urgent to propose a novel kind of special-shaped reinforced concrete composite column. Fiber-reinforced polymers (FRP) have been widely used to strengthen different concrete components, such as beams, plates and columns [2,3,4,5], which can significantly improve the bending, tensile and interlaminar shear strength of the reinforced objects [6]. Moreover, composite materials have been widely used in the construction of subway support brackets, and the lifetime of the support brackets can be significantly improved by the application of composite materials [7,8]. Glass fiber-reinforced polymer (GFRP) tubes are composed of composite materials and have the advantages of excellent tensile performance in the circumferential direction, good corrosion resistance ability, eminent constraint effect on encased concrete and light self-weight; thus, the organic combination of concrete-filled GFRP tubes and the special-shaped columns can effectively improve the bearing capacity and stiffness of the composite columns [9]. Based on this, a novel kind of special-shaped reinforced concrete composite column encased with GFRP core columns (EGCSSCs) is proposed. The transversal deformation of the core concrete can be significantly reduced by the constraint of GFRP, and the failure of the external reinforced concrete can also be delayed [10,11,12,13]. The new kind of composite columns will be widely applied to the special-shaped frame structures [14].

The research on the mechanical properties of special-shaped columns and GFRP-confined concrete columns has become a popular topic for scholars. From 2018 to 2020, a series of experimental studies on triangular, 1/4 circular, semi-circular, fan-shaped, D-shaped, L-shaped, and T-shaped concrete-filled steel tubular (CFST) columns were carried out by Han et al. [15,16] and Liu et al. [17,18]. The results showed that the failure modes of special-shaped columns with triangular, fan-shaped, D-shaped, 1/4 circular and semi-circular under axial load were similar to those of circular, square and rectangular hollow CFST columns, and the corresponding calculation formulas of the compressive- and flexural-bearing capacity of the special-shaped CFST columns were established. The experiments on the seismic behavior of twelve steel-reinforced concrete L-shaped columns under compression–bending–shear–torsion combined action were conducted by Chen et al. [19], and the influences of variables on the failure modes, hysteretic curves, ductility, stiffness degradation and energy dissipation of the composite columns were compared and analyzed. In 2021, Hassam et al. [20] conducted experimental and numerical analyses of cross-shaped stub CFST under axial compression, and the rationality of the finite element modeling (FEM) method was verified by existing experiments, the influence regularity of different parameters on the axial compression behavior of the composite columns was obtained, and finally, the calculation equation for axial compression-bearing capacity was derived relying on the constitutive theoretical model of the constrained concrete. Tests and simulations on seven L-shaped steel–concrete composite columns under axial load were conducted by Wang et al. [21], and a theoretical model was proposed to calculate the axial strength; then, the simplified formula for determining the axial strength was derived based on the FEM and the theoretical model. From 2018 to 2022, a series of numerical analyses on the mechanical properties of H-shaped honeycombed steel web composite members with rectangular CFST flanges were carried out by Ji et al. [22,23,24,25], and the nonlinear buckling load, eccentric compression-bearing capacity formula and the restoring force models of this kind of column were established. An experimental study on the axial compression performance of cross-shaped and L-shaped multi-cavity CFST special-shaped column (CFSTSSC) was carried out by Li et al. [26], and according to the limit equilibrium theory, equations for calculating the ultimate bearing capacity of the composite columns were proposed.

A large number of experimental studies on FRP-confined concrete composite columns were successively conducted by many scholars [27]. In 2017, an experimental study on the dynamic behavior of 24 concrete columns confined by both GFRP tube and steel spiral reinforcement (GFRP-SR) under impact loadings was carried out by Huang et al. [28], and the results showed that the failure pattern of this hybrid structure was highly dependent on the level of impact energy, and increasing the tube thickness and steel spiral reinforcement volumetric ratio could enhance the impact-resistant capabilities of the structure remarkably. In 2019, experiments and numerical simulation analysis on the hysteretic behavior of 11 buckling-restrained brace specimens (BRBs) with concrete-filled GFRP tubes and 3 BRBs with CFST were conducted by Sun et al. [29], and the results showed that all BRBs exhibited good seismic behavior, and the GFRP tube could be used as an alternative to the traditional outer restraining tube. Experiments on the uniaxial compression behavior of 41 FRP tube-concrete-encased steel (FTCES) columns were carried out by Ren et al. [30], and an analysis-based path-dependent load-strain model was proposed and confirmed. Quasi-static experiments of 13 GFRP-tube-confined recycled concrete columns and GFRP-tube-confined high-strength ordinary concrete columns under cyclic axial compression were studied by Hui et al. [31], and the failure trend of GFRP tubes confined by recycled concrete columns was similar to that of GFRP-tube-confined high-strength ordinary concrete columns, and the axial compression-bearing capacity of the composite columns could be effectively improved by GFRP tubes; finally, the axial load-bearing capacity of GFRP tube concrete columns was derived based on the mechanical equilibrium conditions.

In recent years, composite structures encased with GFRP tubes have also been widely used in civil engineering. An experimental study on axial compressive behavior of concrete-filled circular hollow section stub columns with inner FRP was carried out by Long et al. [32], and the ultimate load-bearing capacity of the composite columns was slightly overpredicted by a simple superposition theory; finally, by introducing a reduction coefficient, a reasonable formula for calculating the ultimate axial compression-bearing capacity was proposed. In 2019, experimental research and numerical analysis of FRP-confined concrete core-encased rebar for RC columns under seismic load were conducted by Wang et al. [33], and by considering the compressive behavior enhancement effect, the minimum FRP tube diameter required for the composite columns was calculated. In 2022, a series of studies on the mechanical properties of rectangular hollow section concrete-filled GFRP tubes (HS-CFGT) were performed by Chen et al. [34] and Yuan et al. [35], and the ultimate bending capacities, load–displacement curves, moment–strain curves and failure modes could be obtained, and the results showed that the flexural behavior highly depended on the material properties of the GFRP tubes.

Thus far, although there have been many kinds of research on the mechanical properties of GFRP-confined concrete columns and special-shaped columns, there are few studies on the mechanical properties of special-shaped composite columns with GFRP core columns. In order to obtain the axial compression performance of this new type of composite column, this paper carried out a numerical analysis for the axial compression performance of 27 special-shaped composite columns with GFRP core columns by ABAQUS finite element software, and the influenced regularity of different parameters on the axial compression performance of this kind of composite column was obtained, and then, the stress mechanism of the special-shaped composite columns was clarified. Finally, by introducing the restraint effect coefficients of GFRP tubes (λ_f) and the stirrups (λ_s), and the reduction coefficient (η), the formula for calculating the axial-bearing capacity of this new type of composite column was proposed by statistical regression, which could lay a foundation for the popularization and application of this kind of column in practical projects.

2. Specimen Design

In order to investigate the mechanical behavior of EGCSSCs subjected to axial load, 27 full-scale EGCSSCs were designed, and the main parameters were the axial compressive strength of core concrete (f_cc), axial compressive strength of peripheral concrete (f_co), thickness of GFRP tube (t_gfrp), ratio of longitudinal reinforcement (ρ_v), stirrup ratio (ρ_s) and GFRP ratio in the cross-section (α). The specimens were designed and parameters were selected according to the technical specification for concrete structures with specially shaped columns (JGJ149-2017) and reference [13]. The schematic diagram of the EGCSSC is shown in Figure 1. The specific parameters of the EGCSSCs are shown in Table 1. Hot rolled ribbed bar with yield strength of 335 MPa (HRB335) [36] was adopted as longitudinal steel bars with a diameter of 14, 16 and 18 mm, and HRB335 was adopted as stirrups with a diameter of 8 mm, and the protective layer thickness (α_s) was set to 20 mm.

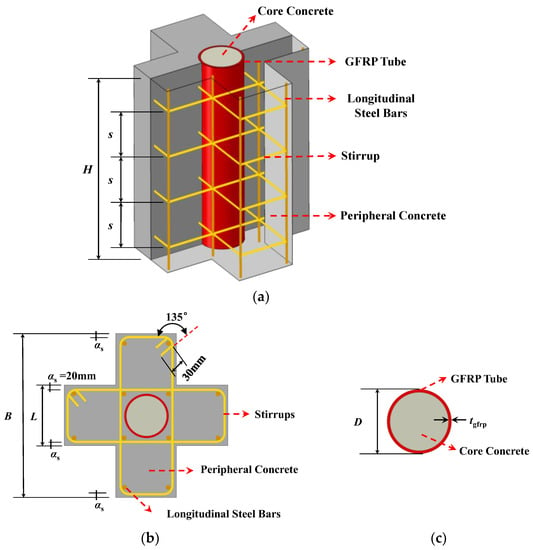
Figure 1. The schematic diagrams of the EGCSSC: (a) the composition of EGCSSC; (b) the cross-section of EGCSSC; (c) the cross-section of the GFRP core column.

Table 1. Specific parameters of 27 EGCSSCs.

Specimen	B/mm	H/mm	L/mm	D/mm	tgfrp/mm	fcc/MPa	fco/MPa	ρv/%	ρs/%	α/-
SSC-1	800	2400	260	156	3	44.5	26.8	0.9	0.5	0.6
SSC-2	800	2400	260	156	3	44.5	20.1	0.9	0.5	0.6
SSC-3	800	2400	260	156	3	44.5	32.4	0.9	0.5	0.6
SSC-4	800	2400	260	156	3	38.5	26.8	0.9	0.5	0.6
SSC-5	800	2400	260	156	3	50.2	26.8	0.9	0.5	0.6
SSC-6	800	2400	260	104	3	44.5	26.8	0.9	0.5	0.4
SSC-7	800	2400	260	208	3	44.5	26.8	0.9	0.5	0.8
SSC-8	800	2400	260	156	1	44.5	26.8	0.9	0.5	0.6
SSC-9	800	2400	260	156	5	44.5	26.8	0.9	0.5	0.6
SSC-10	800	2400	260	156	3	44.5	26.8	0.5	0.5	0.6
SSC-11	800	2400	260	156	3	44.5	26.8	1.5	0.5	0.6
SSC-12	800	2400	260	156	3	44.5	26.8	0.9	1	0.6
SSC-13	800	2400	260	156	3	44.5	26.8	0.9	1.5	0.6
SSC-14	1000	3000	340	204	3	44.5	20.1	0.9	0.5	0.6
SSC-15	1000	3000	340	204	3	44.5	32.4	0.9	0.5	0.6
SSC-16	1000	3000	340	204	3	44.5	26.8	0.9	0.5	0.6
SSC-17	1000	3000	340	204	3	38.5	26.8	0.9	0.5	0.6
SSC-18	1000	3000	340	204	3	50.2	26.8	0.9	0.5	0.6
SSC-19	1000	3000	340	136	3	44.5	26.8	0.9	0.5	0.4
SSC-20	1000	3000	340	272	3	44.5	26.8	0.9	0.5	0.8
SSC-21	1000	3000	340	204	1	44.5	26.8	0.9	0.5	0.6
SSC-22	1000	3000	340	204	5	44.5	26.8	0.9	0.5	0.6
SSC-23	1000	3000	340	204	3	44.5	26.8	0.5	0.5	0.6
SSC-24	1000	3000	340	204	3	44.5	26.8	1.5	0.5	0.6
SSC-25	1000	3000	340	204	3	44.5	26.8	0.9	1	0.6
SSC-26	1000	3000	340	204	3	44.5	26.8	0.9	1.5	0.6
SSC-27	800	2400	260	0	0	44.5	26.8	0.9	0.5	0

Note: B is the cross-section height of EGCSSCs. H is the height of the EGCSSCs. L is the cross-section width of EGCSSCs. D is the diameter of the GFRP tube. ρ_v = A_ss/A_co; ρ_s = A_sv∙l/(A_co∙s). α = D/L. s = 150 mm. A_co is the section area of the EGCSSCs. A_ss is the section area of longitudinal steel bars. A_sv is the section area of the stirrup. l is the length of the stirrup. s is the spacing of the stirrups.

3. Finite Element Model of EGCSSCs

3.1. Materials Constitutive Model

3.1.1. Steel Bars and Stirrups

Considering the yield strengthening of steel bars, the ideal bilinear model was adopted as the elastic–plastic constitutive model (CM) of the steel bars and stirrups as shown in Figure 2a and Equation (1), where ε_sy and f_sy are the yield strain and yield strength of steel, respectively, and E₀ is equal to 0.01 E_s.

$${\sigma }_i=\{\begin{array}{c}{E}_s\times \epsilon \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \left(\epsilon \le {\epsilon }_{\mathrm{y}}\right)\hfill \\ f_{\mathrm{sy}}+E_0\times \left(\epsilon -{\epsilon }_{\mathrm{sy}}\right)\hspace{1em}\left({\epsilon }_{\mathrm{y}}<\epsilon \right)\hfill \end{array}$$

(1)

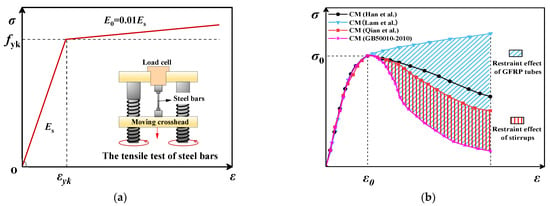
Figure 2. Constitutive models for materials: (a) steel bars and stirrups; (b) concrete [15,27,37,38].

3.1.2. Concrete

By comparing the CMs of concrete proposed by Qian et al. [37], Lam et al. [27], Han et al. [15], and the Code for Design of Concrete Structure (GB50010-2010) [38], the CMs of confined concrete proposed by Qian and Lam were selected as the CMs for periphery concrete and core concrete, respectively. The comparisons of CMs for concrete are shown in Figure 2b. The proposed stress–strain models for peripheral and core concrete under axial compression are shown in Equations (2)–(4).

The stress–strain relationship of peripheral concrete under axial compression:

$$y=\{\begin{array}{c}ax+\left(3-2a\right)x^2+\left(a-2\right)x^3\hspace{1em} \left(0\le x\le 1\right)\hfill \\ \frac{x}{\left(1-0.87{\lambda }_{\mathrm{v}}^{0.2}\right){\rm T}{\left[x-1\right]}^2+x}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \left(1<x\right)\hfill \end{array}$$

(2)

where x = ε/ε₀. y = σ/σ₀. σ₀ = (1 + 1.79 λ_v) f_co1. ε₀ = (1 + 3.50 λ_v) ε_co1. a = 2.1 − 0.001 f_cu. Τ = 0.132 f_cu 0.785 − 0.905. σ₀ is axial compression strength of concrete. ε₀ is peak strain corresponding to σ₀. λ_v is stirrup characteristic value. f_co1 is axial compressive strength of plain concrete. ε_co1 is peak strain corresponding to f_co1. f_cu is the concrete cube compressive strength. Τ is the descending parameter.

The stress–strain relationship of core concrete under axial compression:

$${\sigma }_{\mathrm{c}}^{\prime }=\{\begin{array}{c}{E}_{\mathrm{c}}{\epsilon }_{\mathrm{c}}-\frac{{\left(E_{\mathrm{c}}-E_2^{\prime }\right)}^2}{4f_{\mathrm{co}}^{\prime }}{\epsilon }_{\mathrm{c}}^2\hspace{1em} \left(0\le {\epsilon }_{\mathrm{c}}\le {\epsilon }_{\mathrm{t}}\right)\hfill \\ f_{\mathrm{co}}^{\prime }+E_2^{\prime }{\epsilon }_{\mathrm{c}}\hspace{1em}\hspace{1em}\hspace{1em} \left({\epsilon }_{\mathrm{t}}<{\epsilon }_{\mathrm{c}}<{\epsilon }_{\mathrm{cc}}^{\prime }\right)\hfill \end{array}$$

(3)

where ε_t = 2 f′_co/(E_c − E′₂). E′₂ = (f′_cc − f′_co)/ε′_cc.

E_c is the elastic modulus of concrete. E′₂ is the initial elastic modulus of concrete. ε_t is the strain corresponding to the intersection of the curves. f′_cc and f′_co are the compressive strengths of the confined and the unconfined concrete, respectively. ε′_cc is the ultimate strain.

The stress–strain relationship of concrete under axial tension:

$$y=\{\begin{array}{c}1.2x-0.2x^6\hspace{1em} \left(0<x\le 1\right)\hfill \\ \frac{x}{0.31{\sigma }_{\mathrm{P}}^2{\left[x-1\right]}^{1.7}+x}\hspace{1em}\hspace{1em} \left(1<x\right)\hfill \end{array}$$

(4)

where x = ε_c/ε_p, y = σ_c/σ_p, σ_p = 0.26 (1.25 f_c) 2/3, ε_p = 43.1σ_p, σ_c is tensile stress, ε_c is concrete strain, σ_p is the peak tensile stress, and ε_p is the peak tensile strain.

3.1.3. GFRP Tube

GFRP tube is a kind of fiber-reinforced composite material with anisotropic mechanical properties. Therefore the single-layer plate model and the Hashin failure criterion in ABAQUS were adopted as the CM of the GFRP tube. The mechanical behavior of the GFRP material is shown in Table 2.

Table 2. Mechanical behavior of the GFRP material.

E1 /MPa	E2 /MPa	v12 /-	G12 /MPa	XT /MPa	Xc /MPa	YT /MPa	Yc /MPa	θ /°	tr /mm
52,000	8000	0.32	3000	584	203	43	187	±80	0.5

Note: E₁ and E₂ represent the elastic modulus of GFRP in the tangential and normal directions, respectively. v₁₂ is the Poisson’s ratio. G₁₂ represents the shear modulus. X_T and X_c are the longitudinal tensile strength and compressive strength, respectively. Y_T and Y_c are the transverse tensile strength and compressive strength. θ is the relative laying angle adjacent layers of GFRP. t_r is the relative thickness of adjacent layers of GFRP.

3.1.4. Concrete Plastic Damage Model

In this paper, the concrete plastic damage model was adopted to simulate the concrete element in the column. The definition of concrete plastic damage is shown in Table 3.

Table 3. The parameters of concrete plastic damage model.

Dilation Angle/°	Eccentric Ratio/-	fbo/fco/-	K′/-	Viscosity Parameter/-
30	0.1	1.16	0.667	0.0005

Note: K′ is the second stress invariant ratio. f_bo/f_co is the Bi-axial to uni-axial strength ratio.

3.2. Establishment of Refined Finite Element Model

3.2.1. Element Type and Meshing

The finite element models of EGCSSCs were established by ABAQUS in this paper. Steel bars and stirrups were established by T3D2, core and peripheral concrete were established by C3D8R, and GFRP tube was established by S4R. To simplify the model and improve the calculation accuracy, 20 mm was set as the global mesh size of the finite element model [39,40].

3.2.2. Interaction and Boundary Conditions

During the process of finite element modeling, it was assumed that there was no bond slip between GFRP tube and core and peripheral concrete, which are connected by binding. The hard contact was adopted between the GFRP tube and core and peripheral concrete in the normal direction. Considering the relative slip, the friction contact was adopted between the GFRP tube and core and peripheral concrete in the tangential direction, and the friction coefficient was set to 0.5 [39]. Two reference points RP₁ and RP₂ were set at a distance of 10 mm away from the center between two ends of EGCSSCs. RP₁ was limited by displacement and rotation (U₁ = U₂ = 0, UR₁ = UR₂ = 0 rad/s), and RP₂ was completely fixed, restricting the displacement in X, Y, and Z directions (U₁ = U₂ = U₃ = 0) and the rotation in three directions (UR₁ = UR₂ = UR₃ = 0 rad/s). The finite element model of EGCSSCs is shown in Figure 3.

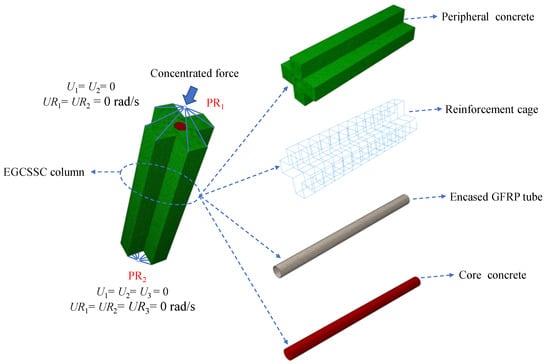
Figure 3. The finite element model of EGCSSCs.

4. Experimental Validation of Finite Element Models

Eight rectangular reinforced concrete columns under axial compression designed by Che et al. [41] and Radnic et al. [42] and eight middle-long columns of high-strength concrete-filled square steel tube with inner CFRP circular tube under axial compression designed by Li et al. [43,44] were selected to verify the rationality of the above modeling method. The specific data of sixteen specimens are shown in Table 4.

Table 4. The comparison of the bearing capacity under axial compression between the simulation and experiment for sixteen specimens.

Specimens		H × bcor× ds× s (×s2) or B1 × Dc × H × tc ×ts/(mm)	fy/MPa	fc/MPa	Ns/kN	Nt/kN	$\frac{\left|{\mathit{N}}_{\mathbf{s}}-{\mathit{N}}_{\mathbf{t}}\right|}{{\mathit{N}}_{\mathbf{s}}}/\%$
Che et al. [41]	A-1	354 × 95 × 3.5 × 27 × 13.5	383	42.31	387.89	384.90	0.77
	B-1	630 × 176 × 6 × 50 × 25	532	42.31	1030.00	978.20	5.03
	C-1	780 × 218 × 8 × 62.5 × 31.3	644	44.43	1985.27	1997.10	0.60
	D-1	1140 × 326 × 12 × 92.5 × 43.6	382	49.73	4408.98	4298.20	2.51
Radnic et al. [42]	RC-1	600 × 90 × 8 × 50	560	24.9	386.61	387.36	0.19
	RC-2	600 × 90 × 8 × 50	560	35.2	519.33	532.6	2.56
	RC-3	600 × 90 × 8 × 50	560	45.1	634.89	657.11	3.50
	RC-4	600 × 90 × 4 × 75	500	45.1	554.75	538.59	2.91
Li et al. [43]	CFSSC-3	200 × 150 × 800 × 0.334 × 5	320	90	4421.49	4560.00	3.13
	CFSSC-6	200 × 150 × 1200 × 0.334 × 5	320	90	4535.05	4374.00	3.55
	CFSSC-8	200 × 150 × 1600 × 0.334 × 5	320	90	4267.99	4280.00	0.28
	CFSSC-10	200 × 150 × 2000 × 0.334 × 5	320	90	4445.83	4209.00	5.33
Li et al. [44]	CFSSC-2-1	200 × 150 × 2600 × 0.334 × 5	320	92	3926.6	3986	1.51
	CFSSC-2-2	200 × 150 × 2800 × 0.334 × 5	320	92	4068.13	3910	3.89
	CFSSC-2-3	200 × 150 × 3000 × 0.334 × 5	320	92	3879.7	3760	3.09
	CFSSC-2-4	200 × 150 × 3200 × 0.334 × 5	320	92	3331.13	3490	4.77

Note: B₁ is the width of the section. D_c is the diameter of the CFRP tube. t_c is the thickness of the CFRP tube. t_s is the thickness of the steel tube. b_cor is the length of the core concrete. d_s is the diameter of the stirrup. S₁ is the stirrup spacing in the densification zone. f_y is the yield strength of the rectangular steel tube or the steel bar. f_c is the compressive strength of the concrete.

By finite element simulation, the load–strain (N-ε) curves of the above composite columns could be obtained, which are shown in Figure 4. It can be seen that the N-ε curves were in good agreement. The comparative results of the ultimate bearing capacity obtained by simulations (N_s) and experiments (N_t) are shown in Table 4 and Figure 5, and the maximum error (Error_MAX) between N_s and N_t was 5.33%; therefore, the rationality of the FEM was verified, and the ultimate bearing capacity of the specimen could be predicted accurately by the finite element model.

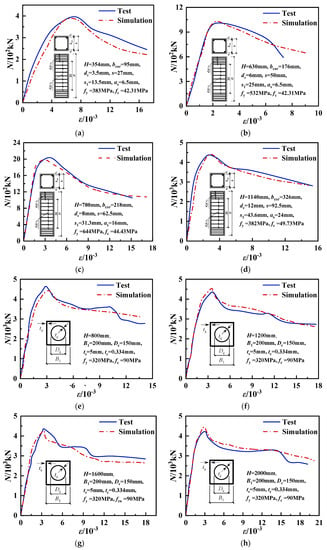
Figure 4. Comparison of N-ε curves between simulation and test: (a) A-1. (b)B-1. (c) C-1. (d) D-1. (e) CFSSC-3. (f) CFSSC-6. (g) CFSSC-8. (h) CFSSC-10.

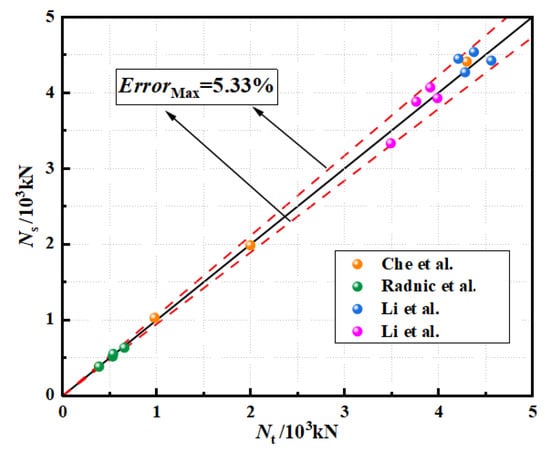
Figure 5. Comparison of N_s and N_t for sixteen specimens [41,42,43,44].

5. Parameter Analysis of EGCSSCs

The initial stiffness (K) and ductility index (μ) of EGCSSCs were calculated by the equivalent elastoplastic energy method [45,46]. The calculation formula of μ is shown in Equation (5) and Figure 6. The results of K and μ of 27 specimens are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 and Table 5. The N-ε curves of the 27 EGCSSCs under axial load are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19. The main parameters are: (1) Axial compressive strength of core concrete (f_cc) (from 38.5 to 50.2 MPa). (2) Axial compressive strength of peripheral concrete (f_co) (from 20.1 to 32.4 MPa). (3) Thickness of GFRP tube (t_gfrp) (from 1 to 5 mm). (4) Ratio of longitudinal reinforcement(ρ_v) (from 0.5% to 1.5%). (5) Stirrup ratio (ρ_s) (from 0.5% to 1.5%). (6) GFRP ratio of section (α) (from 0 to 0.8).

$$\mu =\frac{{\Delta }_u}{{\Delta }_y}$$

(5)

where ∆_u is the ultimate displacement of EGCSSCs. ∆_y is the yielding displacement of EGCSSCs.

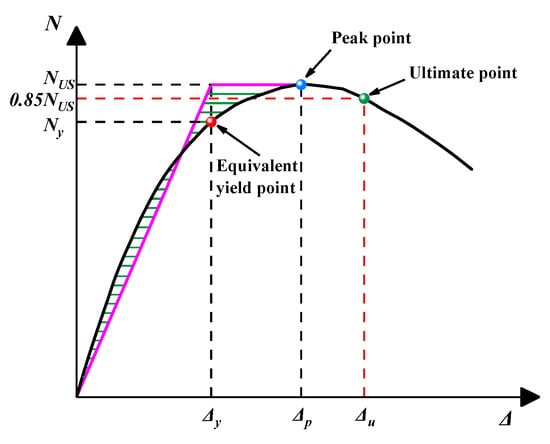
Figure 6. The equivalent elastoplastic energy method.

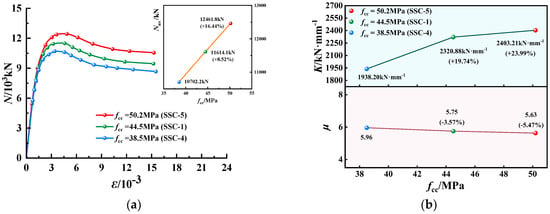
Figure 7. N-ε curves, K and µ of EGCSSCs with different f_cc: (a) N-ε curves of specimens with cross-section height of 800 mm. (b) K and µ of specimens with cross-section height of 800 mm.

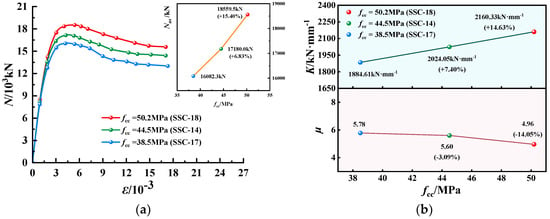
Figure 8. N-ε curves, K and µ of EGCSSCs with different f_cc: (a) N-ε curves of specimens with cross-section height of 1000 mm. (b) K and µ of specimens with cross-section height of 1000 mm.

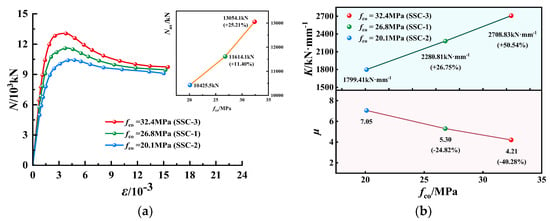
Figure 9. N-ε curves, K and µ of EGCSSCs with different f_co: (a) N-ε curves of specimens with cross-section height of 800 mm. (b) K and µ of specimens with cross-section height of 800 mm.

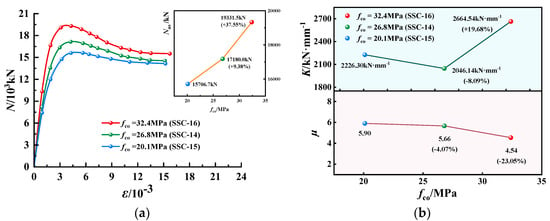
Figure 10. N-ε curves, K and µ of EGCSSCs with different f_co: (a) N-ε curves of specimens with cross-section height of 1000 mm. (b) K and µ of specimens with cross-section height of 1000 mm.

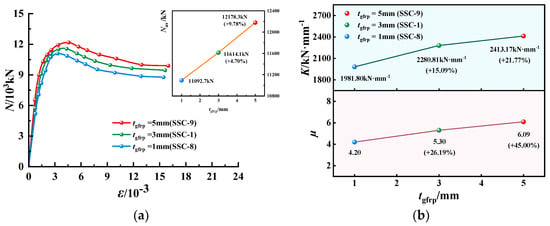
Figure 11. N-ε curves, K and µ of EGCSSCs with different t_gfrp: (a) N-ε curves of specimens with cross-section height of 800 mm. (b) K and µ of specimens with cross-section height of 800 mm.

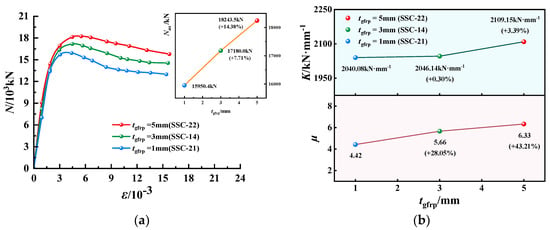
Figure 12. N-ε curves, K and µ of EGCSSCs with different t_gfrp: (a) N-ε curves of specimens with cross-section height of 1000 mm. (b) K and µ of specimens with cross-section height of 1000 mm.

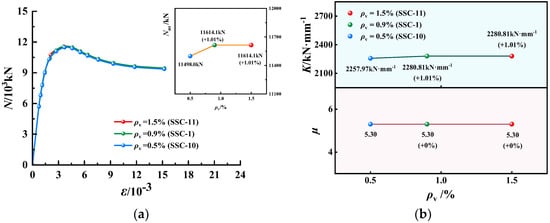
Figure 13. N-ε curves, K and µ of EGCSSCs with different ρ_v: (a) N-ε curves of specimens with cross-section height of 800 mm. (b) K and µ of specimens with cross-section height of 800 mm.

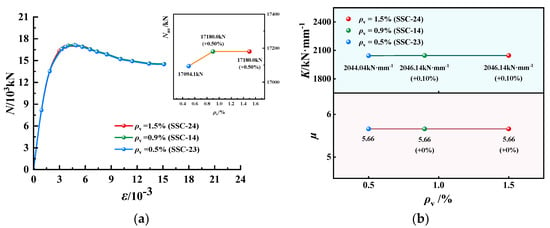
Figure 14. N-ε curves, K and µ of EGCSSCs with different ρ_v: (a) N-ε curves of specimens with cross-section height of 1000 mm. (b) K and µ of specimens with cross-section height of 1000 mm.

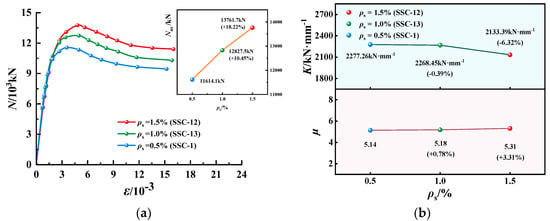
Figure 15. N-ε curves, K and µ of EGCSSCs with different ρ_s: (a) N-ε curves of specimens with cross-section height of 800 mm. (b) K and µ of specimens with cross-section height of 800 mm.

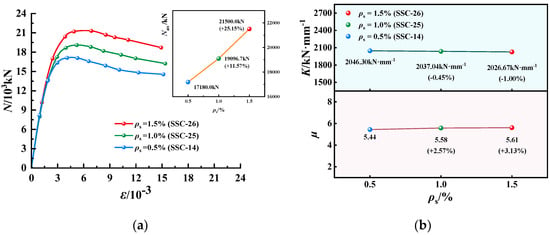
Figure 16. N-ε curves, K and µ of EGCSSCs with different ρ_s: (a) N-ε curves of specimens with cross-section height of 1000 mm. (b) K and µ of specimens with cross-section height of 1000 mm.

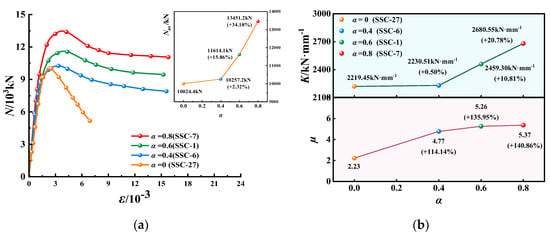
Figure 17. N-ε curves, K and µ of EGCSSCs with different α: (a) N-ε curves of specimens with cross-section height of 800 mm. (b) K and µ of specimens with cross-section height of 800 mm.

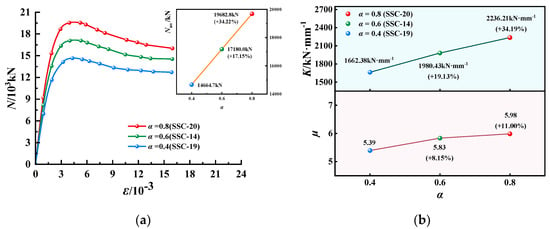
Figure 18. N-ε curves, K and µ of EGCSSCs with different α: (a) N-ε curves of specimens with cross-section height of 1000 mm. (b) K and µ of specimens with cross-section height of 1000 mm.

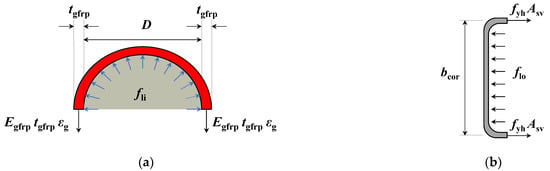
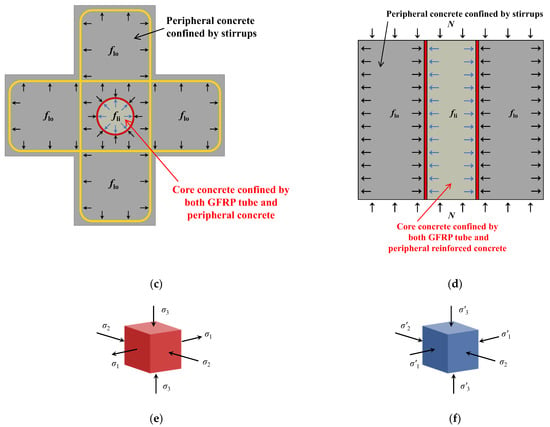
Figure 19. The stress states of different parts: (a) Concrete constrained by GFRP tube. (b) Concrete constrained by stirrup. (c) The cross-section of EGCSSCs. (d) The profile of EGCSSCs. (e) The element of GFRP tube. (f) The element of core and peripheral concrete.

Table 5. K and µ of EGCSSCs with different parameters.

Specimens			B/mm	K/kN·mm−1	∆y/mm	∆u/mm	µ/-
SSC-4	fcc/MPa	38.5	800	1938.20	5.08	30.28	5.96
SSC-1		44.5	800	2320.88	4.36	25.06	5.75
SSC-5		50.2	800	2403.21	4.16	23.44	5.63
SSC-17		38.5	1000	1884.61	7.96	45.97	5.78
SSC-14		44.5	1000	2024.05	7.41	41.47	5.60
SSC-18		50.2	1000	2160.33	6.89	34.2	4.96
SSC-2	fco/MPa	20.1	800	1799.41	5.11	36.05	7.05
SSC-1		26.8	800	2280.81	4.54	24.07	5.30
SSC-3		32.4	800	2708.83	4.30	18.11	4.21
SSC-15		20.1	1000	226.30	6.19	36.53	5.90
SSC-14		26.8	1000	2046.14	7.33	41.47	5.66
SSC-16		32.4	1000	2664.54	6.43	29.20	4.54
SSC-8		1	800	1981.80	4.87	20.45	4.20
SSC-1		3	800	2280.81	4.54	24.07	5.30
SSC-9	tgfrp/mm	5	800	2413.17	4.41	26.85	6.09
SSC-21		1	1000	2040.08	7.02	41.47	4.42
SSC-14		3	1000	2046.14	7.33	47.28	5.66
SSC-22		5	1000	2109.15	7.47	41.34	6.33
SSC-10	ρv/%	0.5	800	2257.97	4.54	24.07	5.30
SSC-1		0.9	800	2280.81	4.54	24.07	5.30
SSC-11		1.5	800	2280.81	4.54	24.07	5.30
SSC-23		0.5	1000	2044.04	7.30	41.47	5.66
SSC-14		0.9	1000	2046.14	7.33	41.47	5.66
SSC-24		1.5	1000	2046.14	7.33	41.47	5.66
SSC-1	ρs/%	0.5	800	2277.26	4.68	24.07	5.14
SSC-13		1.0	800	2268.45	4.87	25.26	5.18
SSC-12		1.5	800	2133.39	5.40	28.68	5.31
SSC-14		0.5	1000	2046.30	7.62	41.47	5.44
SSC-25		1.0	1000	2037.04	8.25	46.08	5.58
SSC-26		1.5	1000	2026.67	8.55	48.00	5.61
SSC-27	α/-	0.0	800	2219.45	4.22	9.40	2.23
SSC-6		0.4	800	2230.51	4.65	22.18	4.77
SSC-1		0.6	800	2459.30	4.38	23.02	5.26
SSC-7		0.8	800	2680.55	4.41	23.66	5.37
SSC-19		0.4	1000	1662.38	7.86	42.38	5.39
SSC-14		0.6	1000	1980.43	7.35	42.86	5.83
SSC-20		0.8	1000	2236.21	7.23	43.27	5.98

5.1. Axial Compressive Strength of Core Concrete (f_cc)

N-ε curves, K and µ of EGCSSCs with different f_cc are shown in Figure 7 and Figure 8. As seen in Figure 7, when the values of f_cc are given from 38.5 to 44.5 and 50.2 MPa, the ultimate axial-bearing capacity (N_us) of specimens with the cross-section height of 800 mm could be increased from 10702.2 to 11614.1 and 12461.8 kN, respectively, which increased by 8.52% and 16.44%. K could be increased from 1938.20 to 2320.88 and 2403.21 kN·mm⁻¹, respectively, which increased by 19.74% and 23.99%. However, µ could be decreased from 5.96 to 5.75 and 5.63, respectively, which decreased by 3.57% and 5.47%. As can be seen in Figure 8, when the values of f_cc are given from 38.5 to 44.5 and 50.2 MPa, N_us of specimens with the cross-section height of 1000 mm could be increased from 16082.3 to 171180.0 and 18,559.5 kN, respectively, which increased by 6.83% and 15.40%. K could be increased from 1884.6 to 2024.05 and 2160.33 kN·mm⁻¹, respectively, which increased by 7.40% and 14.63%. However, µ could be decreased from 5.78 to 5.60 and 4.96, respectively, which decreased by 3.09% and 14.05%. It was summarized that with the increase in f_cc, the N_us and K gradually increased, while µ gradually decreased. Therefore, f_cc was the important parameter to the ultimate axial compression-bearing capacity of EGCSSCs.

5.2. Axial Compressive Strength of Peripheral Concrete (f_co)

N-ε curves, K and µ of EGCSSCs with different f_co are shown in Figure 9 and Figure 10. As seen in Figure 9, when the values of f_co are given from 20.1 to 26.8 and 32.4 MPa, N_us of specimens with the cross-section height of 800 mm could be increased from 10,425.5 to 11,614.1 and 13,054.1 kN, respectively, which increased by 11.40% and 25.21%. K could be increased from 1799.41 to 2280.81 and 2780.83 kN·mm⁻¹, respectively, which increased by 26.75% and 50.54%. However, µ could be decreased from 7.05 to 5.30 and 4.21, respectively, which decreased by 24.82% and 40.28%. It can be seen in Figure 10, when the values of f_co are given from 20.1 to 26.8 and 32.4 MPa, N_us of specimens with the cross-section height of 1000 mm could be increased from 15,706.7 to 17,180.0 and 19,331.5 kN, respectively, which increased by 9.38% and 37.55%. K could be decreased from 2226.30 to 2046.14 kN·mm⁻¹ firstly, and then increased to 2664.54 kN·mm⁻¹. µ could be decreased from 5.90 to 5.66 and 4.54, respectively, which decreased by 4.07% and 23.05%. It was summarized that with the increase in f_co, the N_us and K gradually increased, while the ductility of the EGCSSCs decreased, and the parameter f_co had a great influence on the N_us, K and µ.

5.3. The Thickness of GFRP Tube (t_gfrp)

N-ε curves, K and µ of EGCSSCs with different t_gfrp are shown in Figure 11 and Figure 12. As seen in Figure 11, when the values of t_gfrp are given from 1 to 3 and 5 mm, N_us of specimens with the cross-section height of 800 mm could be increased from 11,092.7 to 11,614.1 and 12,178.3 kN, respectively, which increased by 4.70% and 9.78%. K could be increased from 1981.80 to 2280.81 and 2413.14 kN·mm⁻¹, respectively, which increased by 15.09% and 21.77%. µ could be increased from 4.20 to 5.30 and 6.09, respectively, which increased by 26.19% and 45.00%. It can be seen in Figure 12, when the values of t_gfrp are given from 1 to 3 and 5 mm, N_us of specimens with the cross-section height of 1000 mm could be increased from 15,950.4 to 17,180.0 and 18,243.5 kN, respectively, which increased by 7.71% and 14.38%. K could be increased from 2040.08 to 2046.14 and 2109.15 kN·mm⁻¹, respectively, which increased by 0.30% and 3.39%. µ could be increased from 4.42 to 5.56 and 6.33, respectively, which increased by 28.05% and 43.21%. It was summarized that the N_us, K and µ of the specimens gradually increased with the increase in t_gfrp, and the specimens all showed good load-holding capacity and excellent deformation ability.

5.4. The Ratio of Longitudinal Reinforcement (ρ_v)

N-ε curves, K and µ of EGCSSCs with different ρ_v are shown in Figure 13 and Figure 14. As seen in Figure 13, when the values of ρ_v are given from 0.5% to 0.9% and 1.5%, N_us of specimens with the cross-section height of 800 mm could be increased from 114,985.0 to 11,614.1 kN firstly, and then N_us kept unchanged. K could be increased from 2257.97 to 2280.81 kN·mm⁻¹ firstly, and then K kept unchanged. µ was 5.30 and kept unchanged. It can be seen in Figure 14, when the values of ρ_v are given from 0.5% to 0.9% and 1.5%, N_us of specimens with the cross-section height of 1000 mm could be increased from 1709.4 to 17,180.0 kN firstly, and then kept unchanged. K could be increased from 2044.04 to 2046.14 kN·mm⁻¹ firstly, and then K kept unchanged. µ was 5.66 and kept unchanged. It was summarized that the change in ρ_v had little effect on the axial compression performance of the EGCSSCs.

5.5. The Stirrup Ratio (ρ_s)

N-ε curves, K and µ of EGCSSCs with different ρ_s are shown in Figure 15 and Figure 16. As seen in Figure 15, when the values of ρ_s are given from 0.5% to 1% and 1.5%, N_us of specimens with the cross-section height of 800 mm could be increased from 11,614.1 to 12,827.5 and 13,761.7 KN, respectively, which increased by 10.45% and 18.22%. K could be decreased from 2277.26 to 2268.45 and 2133.39 kN·mm⁻¹, respectively, which decreased by 0.39% and 6.32%. µ could be increased from 5.14 to 5.18 and 5.31, respectively, which increased by 0.78% and 3.31%. It can be seen in Figure 16, when the values of ρ_s are given from 0.5% to 1% and 1.5%, N_us of specimens with the cross-section height of 1000 mm could be increased from 17,180.0 to 19,096.7 and 21,500.0 kN, respectively, which increased by 11.57% and 25.15%. K could be decreased from 2046.30 to 2037.04 and 2026.67 kN·mm⁻¹, respectively, which decreased by 0.45% and 1.00%. µ could be increased from 5.44 to 5.58 and 5.61, respectively, which increased by 2.57% and 3.13%. It was summarized that the N_us and µ of the specimens gradually increased with the increase in ρ_s. However, K decreased slowly with the increase in ρ_s.

5.6. The GFRP Ratio in the Cross-Section (α)

N-ε curves, K and µ of EGCSSCs with different α are shown in Figure 17 and Figure 18. As seen in Figure 17, when the values of α are given from 0 to 0.4, 0.6 and 0.8, N_us of specimens with the cross-section height of 800 mm could be increased from 10,024.4 to 110,257.2, 1161.4 and 13,451.2 kN, respectively, which increased by 2.32%, 15.86% and 34.18%. K could be increased from 2219.45 to 2230.51, 2459.30 and 2680.55 kN·mm⁻¹, respectively, which increased by 0.50%, 10.81% and 20.78%. µ could be increased from 2.23 to 4.77, 5.26 and 5.37, respectively, which increased by 114.14%, 135.95% and 140.86%. It can be seen in Figure 18, when the values of α are given from 0.4 to 0.6 and 0.8, N_us of specimens with the cross-section height of 1000 mm could be increased from 14,664.7 to 17,180.0 and 19,682.8 kN, respectively, which increased by 17.15% and 34.22%. K could be increased from 1662.38 to 1980.43 and 2236.21 kN·mm⁻¹, respectively, which increased by 19.13% and 34.19%. µ could be increased from 5.39 to 5.83 and 5.98, respectively, which increased by 8.15% and 11.00%. It was summarized that the N_us, K and µ of the specimens gradually increased with the increase in α. The specimens all showed good load-holding capacity and excellent deformation ability. Therefore, the axial compression behavior of the specimens could be improved significantly by the GFRP tube.

In summary, the N_us increased with the increase in f_cc, f_co, t_gfrp, ρ_s and α, and µ decreased with the increase in f_cc and f_co. The reasons for the above changes in the N_us and µ are as follows. With the increase in f_cc and f_co, the load-carrying capacity of the specimens increased while the ultimate compressive strain and transverse deformation capacity of the concrete decreased, which made the restraint effects of the GFRP tube and stirrups decrease [13,37], resulting in the increase in the N_us and the decrease in the µ. The core and peripheral concrete were constrained by the GFRP tube and stirrups, respectively, and with the increase in t_gfrp, ρ_s and ρ_s, the lateral deformation of the core concrete and the development of internal cracks became smaller, and the compressive strength of the core and peripheral concrete increased, thereby the N_us and µ were improved [9,37,43,44]. Moreover, the change in ρ_v had little effect on the N_us and µ; this was due to the small change in the cross-sectional area of the steel bars.

6. Force Mechanism of EGCSSCs

The relationship between the longitudinal compressive strain (ε₁) and the circumferential strains of EGCSSCs is shown in Equation (6) [39,47], and ε₁ increases with the increase in the axial compression (N).

$$\{\begin{array}{c}{\epsilon }_{\mathrm{f}}={\mu }_{\mathrm{f}}{\epsilon }_1\hfill \\ {\epsilon }_{\mathrm{c}}^{\prime }={\mu }_{\mathrm{c}}{\epsilon }_1\hfill \\ {\epsilon }_{\mathrm{s}}={\mu }_{\mathrm{s}}{\epsilon }_1\hfill \end{array}$$

(6)

where ε′_c is the circumferential strain of the core and peripheral concrete, ε_f is the circumferential strain of GFRP, ε_s is the circumferential strain of the stirrups, μ_c is Poisson’s ratio of the core and peripheral concrete, μ_f is Poisson’s ratio of the GFRP, and μ_s is Poisson’s ratio of the stirrups.

At the initial stage, μ_c < μ_s < μ_f, so ε′_c < ε_s < ε_f, which means that GFRP tube and stirrups have no restraint effect on core and peripheral concrete. When the longitudinal stress is approximately equal to the proportional limit of the steel bars (σ₃ ≈ f_p), the circumferential strain of steel and core and peripheral concrete is approximately equal. As the N continues to increase, f_p < σ₃ < σ_f (the longitudinal stress of GFRP tube when ε_f equals ε_c), so ε_s < ε′_c < ε_f, which means that the circumferential deformation of the peripheral concrete is constrained by the stirrups. As the N further increases, σ_f < σ₃; thus, ε_s < ε_f < ε′_c, which means that the circumferential deformation of the core concrete is constrained by both the GFRP tube and peripheral concrete. The stress states of concrete constrained by GFRP tube and stirrups are shown in Figure 19a,b, where f_yh is the yield strength of the stirrup, A_sv is the cross-sectional area of the stirrup, f_lo is the circumferential stress of the stirrup, E_gfrp is the elastic modulus of GFRP tube, ε_g is the circumferential stress of GFRP tube, and f_li is the circumferential stress of GFRP tube. The stress state of EGCSSCs is shown in Figure 19c,d. The GFRP tube, core concrete, and peripheral concrete are in a three-dimensional stress state. The GFRP tube under circumferential compressive stress (σ₁), circumferential tensile stress (σ₂), and longitudinal compressive stress (σ₃) is shown in Figure 19e. The core and peripheral concrete under circumferential compressive stress (σ′₁), circumferential compressive stress (σ′₂), and longitudinal compressive stress (σ′₃) is shown in Figure 19f.

With the increase in N, the constraint effect becomes more obvious, and the middle of the specimen bulges. Both ends of the peripheral concrete are crushed locally, and the bulge at the middle of the concrete is visible. The core concrete has almost no expansion deformation due to the constraining effect of the GFRP tube and the peripheral concrete. There is not obvious expansion deformation on the GFRP tube, the longitudinal steel bars in the steel reinforcement cage are obviously yielding, and the length of stirrups at the middle of the reinforcement cage increase. Finally, the specimen exhibits outward bulge failure mode.

In order to study the stress of core concrete and peripheral concrete elements in the column section, elements A, B, C, D, E and F were successively selected in the direction far from the section center to explore the stress variation law of concrete elements in the column section from inside to outside. Figure 20a shows the distribution of six concrete elements in the middle of the SSC-1. Elements A, B and C are from core concrete, and elements D, E and F are from peripheral concrete. It can be seen from Figure 20b that from element A to element F, the peak stress gradually decreases, and the peak stress is 55.5, 51.8, 43.6, 34.7, 31.5 and 29.4 MPa, respectively, which decreases by 7.7%, 21.4%, 37.5%, 43.2% and 47.0%, and the peak strains of the elements of core concrete are much larger than those of the peripheral concrete elements. It shows that when the specimen SSC-1 reaches the ultimate axial compressive stress, the peripheral concrete reaches the peak stress earlier than the core concrete. Moreover, the confinement effect of the core concrete is greater than that of the peripheral concrete, because the core concrete is restrained by both the GFRP tube and the peripheral concrete. In this paper, the confinement effects of the core and peripheral concrete are simplified as the restraint effect coefficients of core concrete (λ) and peripheral concrete (λ_s), and λ > λ_s, which is consistent with the change law of the constraint effect.

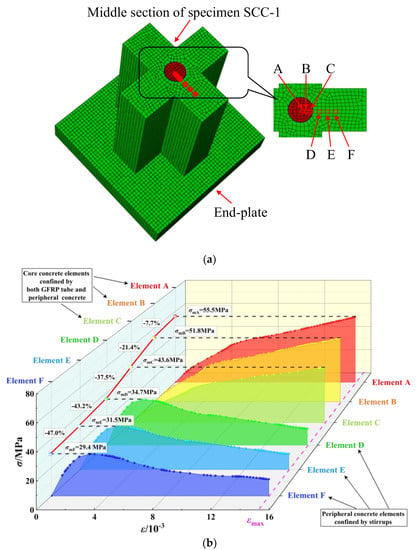
Figure 20. Stress–strain curves of concrete elements at the middle section of specimen SSC-1: (a) distribution of concrete elements; (b) stress–strain curves of elements A, B, C, D, E and F.

7. The Axial Compression-Bearing Capacity Formula of EGCSSCs

According to the analysis of the stress mechanism of the EGCSSCs, it can be concluded that the core concrete is subject to the double restraint effect of both the GFRP tube and peripheral reinforced concrete. Ghanem et al. [48] also provide a reasonable argument for this hypothesis, and it is proven that FRP has the greatest influence on the compressive stress and strain of composite columns, and stirrup is very important to the compressive strain.

From the literature [37], the bearing capacity formula of the concrete columns confined by stirrups under axial compression (N_co) is proposed:

$$N_{\mathrm{co}}=A_{\mathrm{co}}^{\prime }{f}_{\mathrm{co}}(1+1.79{\lambda }_{\mathrm{s}})+A_{\mathrm{s}}{}_{\mathrm{s}}{f}_{\mathrm{y}}$$

(7)

$${\lambda }_{\mathrm{s}}=\rho \frac{f_{\mathrm{yh}}}{f_{\mathrm{c}1}}$$

(8)

where f_yh is the yield strength of the stirrup. f_c1 is the characteristic value of concrete compressive strength. A′_co is the cross-sectional area between the stirrup and the GFRP tube.

From the literature [27,49], the bearing capacity formula of concrete columns confined by FRP tubes under axial compression (N_cc) is proposed:

$$N_{\mathrm{cc}}=A_{\mathrm{cc}}{f}_{\mathrm{cc}}\left(1+\sqrt{\lambda }+1.1\lambda \right)$$

(9)

$${\lambda }_{\mathrm{f}}={\mu }_{\mathrm{f}}\frac{f_{\mathrm{u}}}{f_{\mathrm{c}}}=\frac{2t_{\mathrm{gfrp}}}{D}\frac{f_{\mathrm{l}}}{f_{\mathrm{c}1}}$$

(10)

where λ = λ_s + λ_f. f_l =E_gfrp × ε_rup. f_l is the tensile strength of the GFRP tube in the circumferential direction. ε_rup is the fracture strain of the GFRP tube in the circumferential direction.

The axial compression-bearing capacity formula of EGCSSCs (N′_u) is obtained by using the simple superposition principle, as follows:

$$N_{\mathrm{u}}^{\prime }=N_{\mathrm{co}}+N_{\mathrm{cc}}$$

(11)

N′_u calculated by Equation (11) is shown in Table 6, and the comparison between N′_u and N_us is shown in Figure 21a. It can be seen from the figure that the Error_Max is 17.54%, and the calculation error is large, which is not suitable for calculating the axial compression ultimate bearing capacity of EGCSSCs.

Table 6. Comparison between N′_u, N_u and N_us.

Specimen	μ	λf	λs	N′u/kN	Nu/kN	Nus/kN	|N′u − Nus|/N′u/%	|Nu – Nus|/Nu/%
SSC-1	0.905	0.69	0.05	12,858.5	11,571.4	11,614.1	9.68	0.37
SSC-2	0.905	0.69	0.07	10,688.1	9607.2	10,425.5	2.46	8.52
SSC-3	0.905	0.69	0.05	14,680.7	13,220.5	13,054.1	11.08	1.26
SSC-4	0.905	0.8	0.05	12,682.2	11,411.9	10,702.2	15.61	6.22
SSC-5	0.905	0.61	0.05	13,023.1	11,720.4	12,461.8	4.31	6.33
SSC-6	0.905	1.04	0.05	12,132.5	10,914.4	10,257.2	15.46	6.02
SSC-7	0.905	0.52	0.06	13,734.5	12,364.2	13,451.2	2.06	8.79
SSC-8	0.905	0.09	0.05	12,176.2	10,954	11,092.7	8.90	1.27
SSC-9	0.905	1.73	0.05	13,459.1	12,115	12,178.3	9.52	0.52
SSC-12	0.905	0.69	0.05	14,241.2	12,822.8	13,761.7	3.37	7.32
SSC-13	0.905	0.69	0.05	14,824.0	13,350.2	12,827.5	13.47	3.92
SSC-14	0.905	0.69	0.04	19,276.4	17,379.6	17,180	10.88	1.15
SSC-15	0.905	0.53	0.06	16,548.6	14,911	15,706.7	5.09	5.34
SSC-16	0.905	0.53	0.04	23,009.7	20,758.3	19,331.5	15.99	6.87
SSC-17	0.905	0.61	0.04	19,174.7	17,287.6	16,082.3	16.13	6.97
SSC-18	0.905	0.47	0.04	20,330.7	18,333.8	18,559.5	8.71	1.23
SSC-19	0.905	0.79	0.04	17,784.4	16,029.4	14,664.7	17.54	8.51
SSC-20	0.905	0.4	0.05	21,375.8	19,279.6	19,682.8	7.92	2.09
SSC-21	0.905	0.07	0.04	19,117.3	17,235.7	15,950.4	16.57	7.46
SSC-22	0.905	1.1	0.04	20,885.1	18,835.5	18,243.5	12.65	3.14
SSC-25	0.905	0.53	0.04	21,650.2	19,527.9	19,096.7	11.79	2.21
SSC-26	0.905	0.53	0.04	22,225.5	20,048.6	21,500	3.26	7.24

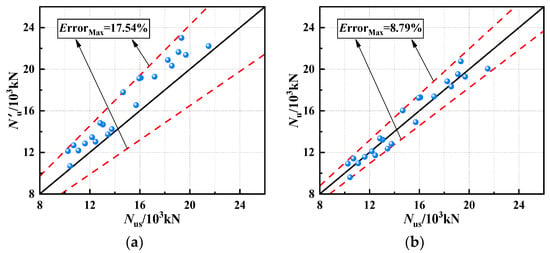
Figure 21. Comparison between N′_u, N_u and N_us. (a) Comparison between N_u and N_us. (b) Comparison between N_u and N_us.

According to the force mechanism of EGCSSCs, it can be seen that the core concrete and peripheral concrete cannot reach peak stress at the same time, because ρ_v has little effect on the axial compression-bearing capacity. Therefore, the bearing capacity provided by the steel bar is ignored, and the calculation formula for the ultimate bearing capacity of EGCSSCs under axial compression (N_u) is established by introducing the reduction coefficient (η), which could be expressed as follows:

$$N_{\mathrm{u}}=\eta \left[N_{\mathrm{co}}+A_{\mathrm{co}}^{\prime }{f}_{\mathrm{co}}(1+1.79{\lambda }_{\mathrm{s}})\right]$$

(12)

The global optimization algorithm (Leveberg–Marquardt) of 1st Opt software is used to determine the value of η. The formula reaches the convergence criterion, and η is determined to be 0.905 after 17 iterations of operation, R = 0.95, and R² = 0.91. Finally, the axial compression-bearing capacity formula of EGCSSCs is obtained by substituting the value of η into Equation (12), which is shown in Equation (12).

$$N_{\mathrm{u}}=0.905\left[A_{\mathrm{co}}{f}_{\mathrm{co}}(1+1.79{\lambda }_{\mathrm{s}})+A_{\mathrm{cc}}{f}_{\mathrm{cc}}(1+\sqrt{\left({\lambda }_{\mathrm{f}}+{\lambda }_{\mathrm{s}}\right)}+1.1\left({\lambda }_{\mathrm{f}}+{\lambda }_{\mathrm{s}}\right)\right]$$

(13)

Table 6 lists the N_u calculated by Equation (13) and N_us of EGCSSCs. Figure 21b compares N_u and N_us. The Error_Max between the N_u and N_s was 8.79%, which could meet the requirements of practical engineering.

8. Conclusions

In order to investigate the mechanical behavior of EGCSSCs under axial load, 27 full-scale EGCSSCs were designed with varying parameters: axial compressive strength of core concrete (f_cc), axial compressive strength of peripheral concrete (f_co), thickness of GFRP tube (t_gfrp), ratio of longitudinal reinforcement (ρ_v), stirrup ratio (ρ_s) and GFRP ratio in the cross-section (α). Then, 27 EGCSSCs finite element models were established by ABAQUS finite element software. Based on the range of parameters in this paper, the conclusions could be drawn as follows:

(1)

Based on the simplified bilinear constitutive model of steel bars and stirrups, and the nonlinear constitutive models of core and peripheral concrete considering restraint, and the reasonable FEM method, 27 finite element models of composite columns were numerically simulated by ABAQUS finite element software.

(2)

All specimens showed excellent load-carrying capacity and good ductility. The axial compression behavior of EGCSSCs increased significantly with the increase in f_cc, f_co, t_frp, ρ_s and α. However, the change in ρ_v had little effect on its axial compression behavior. Moreover, with the existence of GFRP core columns, the N_us and µ of the columns were increased by 11.61% and 140.86%. In addition, K increased with the increase in f_cc, f_co, t_frp and α, and the largest increments were 23.99%, 50.54%, 21.77% and 34.19%, respectively. µ decreased with the increase in f_cc and f_co, which decreased by 14.05% and 40.82%, respectively.

(3)

The restraint effects on the element of EGCSSCs distributed along the circumferential direction were different, and the maximum stress of concrete elements gradually decreased from the center of EGCSSCs to the edges, indicating that the restraint effect on the core concrete was larger than that on the peripheral concrete. Moreover, the peripheral concrete reached peak stress earlier than the core concrete, and the peak stress of the peripheral concrete elements was close to that of ordinary concrete. In this paper, the confinement effects of core and peripheral concrete were simplified as the restraint effect coefficients of core concrete (λ) and peripheral concrete (λ_s), and λ > λ_s, which was consistent with the change law of the constraint effect. Because the core and peripheral concrete could not reach the peak stress at the same time, the bearing capacity of the column had a certain loss.

(4)

The axial compression-bearing capacity formula of EGCSSCs was proposed by introducing the reduction coefficient (η). The global optimization algorithm (Leveberg–Marquardt) of 1st Opt software was used to determine the value of η. The Error_Max between the calculation results and simulation results was 8.79%, which could meet the engineering accuracy requirements.

In this paper, the influence of parameters on the mechanical behavior of EGCSSCs under axial compression was carried out. However, the axial compressive mechanical behavior was also affected by the interaction between parameters. Therefore, in the future, statistical analysis methods can be used to study the main effects and interaction effects. Future research in this area can include the effect of eccentric loading on axial-bearing capacity. Moreover, in addition to composite columns, this type of composite beam can also be included in the study, using the finite element analysis to predict compressive strength and flexural strength.

The authors believe that the axial-bearing capacity formula based on the finite element model simulation analysis is simple to calculate and meets the error requirements of engineering, which can provide a design basis for engineers’ practice to a large extent.