Field Measurement on Translational and Torsional Wind-Induced Response of a High-Rise Building during Typhoon Khanun

Abstract

Full measurements for the wind field atop a 32-storey building (supported by four huge columns) and for the dynamic responses of different floors were conducted on 15 October 2017 to obtain the translational and torsional responses of the high-rise building during the Typhoon Khanun. The time histories of the torsional angular acceleration responses on the 24th and 32nd floors of the high-rise building were obtained using RA013 rotational accelerometer, and those of the translational acceleration responses on the 6th, 12th, 18th, 24th, 30th and 32nd floors along axial direction were recorded by the translational accelerometer. The variation rules of the translational and torsional acceleration responses with floor height and mean wind speed were disclosed, and the response ratios between the torsional and translational acceleration were analyzed when basic time intervals were 10 min. Based on the target probability method, the value range of the acceleration peak factor with different target reliability under Typhoon Khanun was proposed. The results show that the translational and torsional acceleration peak values and root mean squares are the power functions of mean wind speed. The values of acceleration peak factors are recommended to be 3.0 and 5.0 if target reliabilities are determined as 99.38% and 100%, respectively. Research on torsional response measurements can accumulate valuable scientific data and lay solid foundations for the subsequent studies on the torsional wind-resistant design of high-rise buildings.

1. Introduction

A large number of super-tall buildings have emerged in recent years with the development of new materials, construction technology and analytical technology. The Burj Khalifa Tower in Dubai, known as the tallest building in the world with a height of 828 m, was completed in 2010. The tallest building in China—the Shanghai Tower was completed in 2016 and ranked third in the world with a height of 632 m. Gradually, the existing tallest buildings both in China and the world will be replaced by the taller buildings due to the rapid development of technology. Consequently, the dynamic response will be amplified at an increased floor height under the excitation of strong winds, especially typhoons or hurricanes.

Real-time monitoring has been widely used to obtain dynamic responses of high-rise buildings in the past three decades with the development of data acquisition and analysis technology. Many scholars (Fujii et al., 2002 [1]; Kijewski-Correa and Kochly, 2007 [2]; Brownjohn et al., 2008 [3]; Siringoringo and Fujino, 2017 [4]) have conducted massive full-scale measurements on the wind-induced responses of high-rise buildings. Jeary (1992) [5] obtained modal parameters of a 350 m building. Miyashita et al. (1998) [6] conducted field measurements on the 212 m Hamamatsu ACT tower in Japan and analyzed the structural dynamic response under typhoon conditions. Campbell et al. (2005) [7] studied the dynamic responses of two high-rise buildings with the heights of 218 m and 206 m in Hongkong under the influence of typhoons Imbudo and Dujuan. Kilpatrick et al. (2003) [8] conducted field measurements on three Chicago high-rise buildings under the action of strong wind and compared the results of dynamic responses with those obtained from wind tunnel testing and finite element analysis. Similarly, Chinese scholars conducted massive field measurements in the southeast coastal areas of China. Li et al. (2017 [9]; 2014 [10]; 2011 [11]) conducted a series of full-scale measurements of dynamic responses of super-tall buildings during typhoons. Li et al.(2012 [12]; 2018 [13]) conducted field measurements of wind-induced responses on five high-rise buildings during typhoons from 2008–2017. All of these studies can provide precious scientific data to identify dynamic parameters, such as mode shapes, natural frequencies and damping ratios, but the field measurements on the wind-induced responses of high-rise buildings under typhoons in the southeast coastal areas of China are still insufficient due to the restraints from testing funds and testing conditions.

The dynamic response of high-rise buildings is usually tested using a three-way accelerometer. The measured acceleration is often considered as the translational response in the east-west, north-south and vertical directions (Xu and Zhan, 2001 [14]; Brownjohn et al., 2000 [15]; Satake et al., 2003 [16]; Şahin et al., 2011 [17]; Wu et al., 2007 [18]). In fact, the complete motion characteristics of a rigid body at a certain point also include rotations, which include six parts, namely three translational and three rotational degrees of freedom to describe the vibration response.

Most of the field measurements on the wind-induced responses of high-rise buildings during typhoons emphasized translational responses(He et al., 2022 [19]; Zhi et al., 2021 [20]; Zhang et al., 2020 [21]), and only few of them were concerned with torsional responses due to the lack of the torsional accelerometer sensors; thus, the research on torsional vibration responses of high-rise buildings under the influence of typhoons has great practical significance and scientific research value(Liang et al., 2004 [22]; Hui et al., 2017 [23]; Yu et al., 2016 [24]). Based on the field measurement on a high-rise building in Haikou city, the translational acceleration responses of the 6th, 12th, 18th, 24th, 30th and 32nd floors were obtained, and the torsional acceleration responses of the 24th and 32nd floors were also monitored using model RA013 rotational accelerometer, and afterwards the translational and torsional responses were compared systematically. Moreover, the target probability method was adopted to study the value range of acceleration peak factors of measured high-rise building during Typhoon Khanun under different guarantee rates. The full-scale study of the torsional vibration response under typhoons is expected to provide reliable case data on the subsequent studies on the torsional wind-resistant design of high-rise buildings.

2. Description of Field Measurements

2.1. Typhoon Khanun

As reported by Wenzhou Typhoon Network of China (http://www.wztf121.com/ (accessed on 12 May 2022)), the Typhoon Khanun formed in waters near the east of the Philippines on 11 October 2017. It further intensified into a typhoon, reaching its peak intensity with the estimated maximum wind of level 10 near its center and the lowest central pressure of 988 hPa. Then, it landed in the coastal area in the east of Xuwen county, with the estimated maximum sustained winds of 28 m/s. Figure 1 presents the path of Typhoon Khanun.

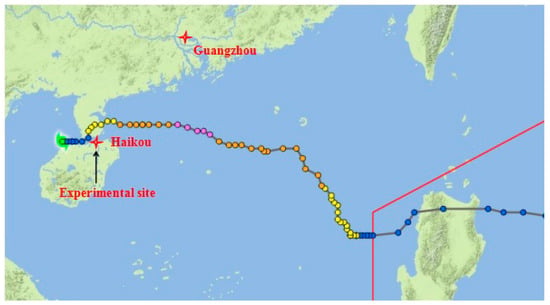
Figure 1. Path of Typhoon Khanun.

2.2. The Object Building

The high-rise building is located in the urban area of Haikou city, Hainan province. It is a huge, 32-story tower supported by four giant columns. It was completed in the 1990s. The measured building has a height of 108 m with the length–width ratio of 1.47 and the aspect ratio of 6.71, as shown in Figure 2.

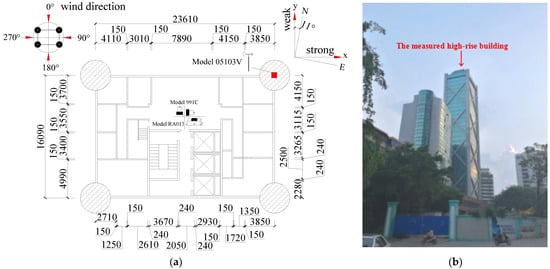
Figure 2. External elevation and plan views of the measured building. (a) Building plan; (b) External elevation of building.

2.3. Field Instrumentation and Measurement Scheme

The wind speed, wind direction and acceleration of the high-rise building were all collected by the dynamic data acquisition system produced by Wuhan uTekL Electronic Technology Co., Ltd. A mechanical anemometer (Model 05103V) was adopted to obtain wind field at a height of 115 m (7 m higher than the top of the building) and was installed in the north east of the measured building. More details are shown in Figure 2. The translational acceleration responses of the 6th, 12th, 18th, 24th, 30th and 32nd floors were monitored using model 991C ultra-low frequency vibration gauge, and the translational accelerometers were placed along both x and y axes. The torsional angular acceleration responses of the 24th and 32nd floors were monitored using model RA013 rotational accelerometer (Yang et al., 2015 [25])installed along the horizontal direction of the measured building. The sampling frequency of the dynamic data acquisition was 128 Hz, and the installations of the translational and torsional accelerometers are shown in Figure 3.

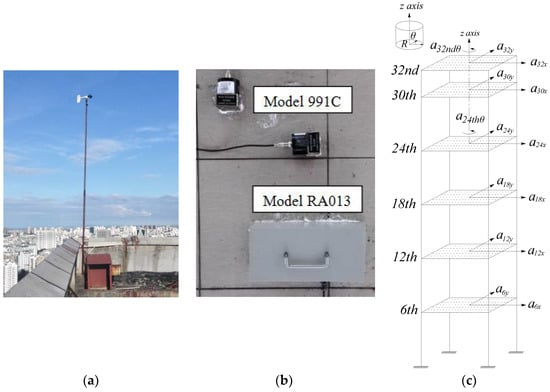
Figure 3. Layout of sensors. (a) Installation position of anemometer; (b) Physical drawing of sensor layout; (c) Sensor layout schemes of model 991C and model RA013.

The RA013 accelerometer, a type of sensor widely used to measure the rotational acceleration of structure, shows excellent performance in linearity, ultra-low frequency and large scale dynamic measurement. The specifications of RA013 accelerometer are as follows: the pass band is 0.01~20 Hz, the resolution is less than or equal to 2 × 10⁻⁴ rad/s², the size is 330 mm × 130 mm × 105 mm and the weight is about 6 kg. Figure 4 demonstrates the rotating sensitive axis of the rotating accelerometer. The z axis perpendicular to the base plate of the rotational accelerometer is the rotating sensitive axis of the rotational accelerometer. The installation method showned in Figure 4 measures the rotation acceleration around the z axis. When measuring the rotation acceleration around the x axis, the rotational accelerometer is turned inward by 90° (i.e., with the output plug upward). When measuring the rotational acceleration around the y axis(Yang et al., 2015 [25]).

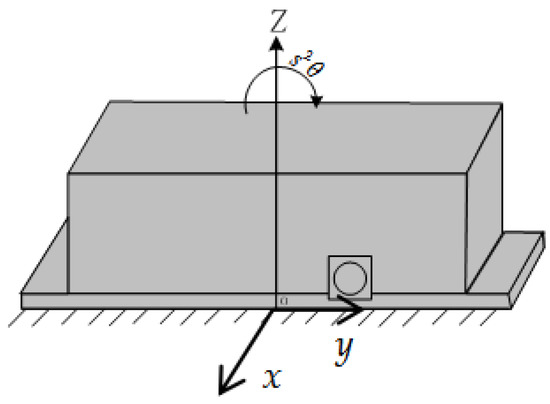
Figure 4. Rotating sensitive axis of the rotational accelerometer.

3. Wind Characteristics and Wind-Induced Responses

3.1. Wind Field Atop the Building

Wind field data collected for more than 30 h from 17:17 on October 15, 2017 were analyzed. The 0° direction of the anemometer, representing 11° north by west, was parallel to the y axis, and the negative direction of x axis was 90°, and the clockwise direction was positive (Figure 2a). The measured maximum instantaneous wind speed was 22.2 m/s. Figure 5 showed that the maximum 10-min mean wind speed was about 15.0m/s and the mean wind direction was from 300° to 350° during Typhoon Khanun.

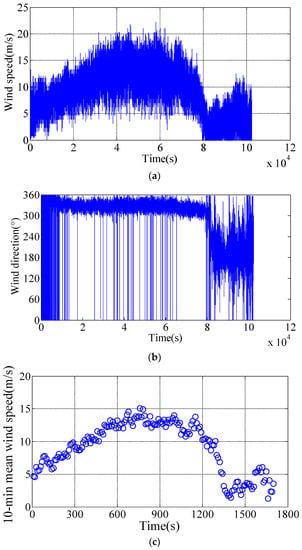
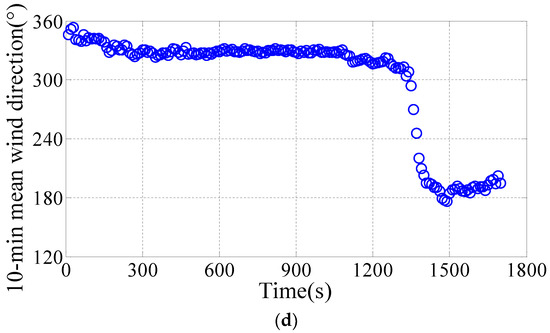
Figure 5. Wind field characteristics atop the building. (a) Wind speed; (b) Wind direction; (c) 10-min mean wind speed; (d) 10-min mean wind direction.

3.2. The Translational Acceleration

Time histories of the translational acceleration on the 6th, 12th, 18th, 24th, 30th and 32nd floors were measured, and Figure 6 illustrates the time histories of partially translational responses on the 24th and 32nd floors along the x and y axes at high wind speeds. The acceleration time history showed that the acceleration amplitude increased with the increasing wind speed and floor height. When the recorded wind speed reached its maximum value, namely, when the 10-min mean wind speed was about 15.0 m/s, the peaks of the maximum acceleration were 9.9 mm/s² and 11.5 mm/s² along x and y axes, respectively. In the process of typhoon landing, the peak acceleration in y direction is greater than the peak acceleration in x direction at the same measuring point. The main reason is that the y direction is a weak axis and the x direction is a strong axis, indicating that the acceleration response under the action of typhoon is closely related to the axial stiffness.

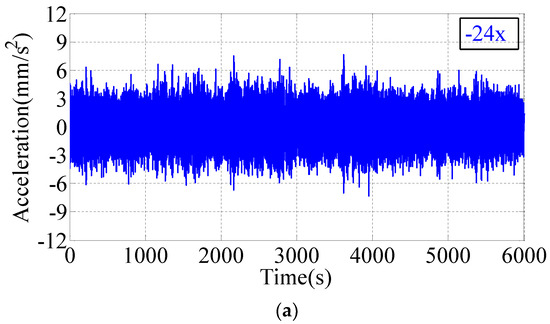
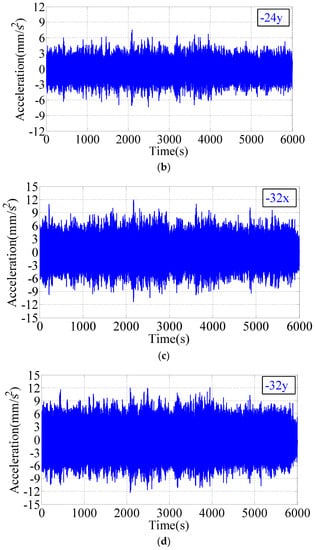
Figure 6. Time histories of translational acceleration response. (a) Acceleration of the 24th floor along the x axis; (b) Acceleration of the 24th floor along the y axis; (c) Acceleration of the 32nd floor along the x axis; (d) Acceleration of the 32nd floor along the y axis.

In order to show the measured acceleration power spectral density function (APSDF) of different floors better, the logarithmic spectrum (10 × log10(P_i)) is adopted for all data in vertical axis; P_i is the self-power spectral value (P) of the acceleration at the ith floor, the identification method is shown in detail in the literature (Li et al., 2018 [13]), and the specific identification of APSDF is shown in Figure 7. The wind energy during Typhoon Khanun is basically concentrated in the range of 0 Hz~1.0 Hz, and the first-order modal frequency of the x axis of measured high-rise building is 0.69 Hz. Because the wind energy is concentrated in the low frequency region, the measured first-order modal frequency is greatly affected. The measurement results show that the peak values of the first three resonant bandwidth frequencies increase significantly with the increasing wind speed.

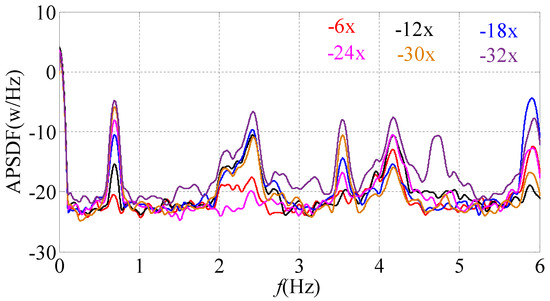
Figure 7. APSDF of different floors during Typhoon Khanun.

3.3. The Torsional Angular Acceleration

Time histories of the torsional angular acceleration on the 24th and 32nd floors were monitored, and Figure 8 presented the time histories of partially torsional angular acceleration on the 24th and 32nd floors along z axis at high wind speeds. The acceleration time history illustrated that the acceleration amplitude increased with the increasing wind speed and story height. When the 10-min mean wind speed reached its maximum value, the peaks of the maximum acceleration on the 24th and 32nd floors were 0.0041 rad/s² and 0.0049 rad/s² along the z axis, respectively.

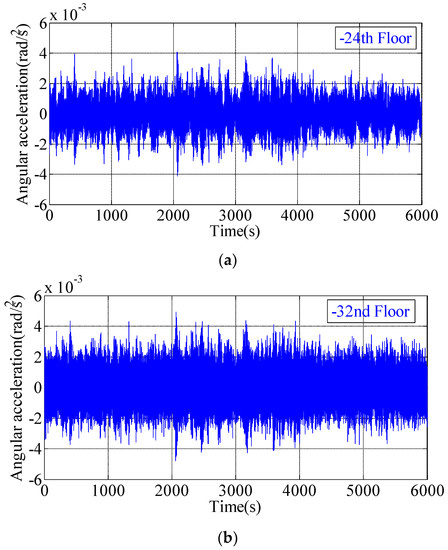
Figure 8. Time histories of angular acceleration response. (a) Angular acceleration of the 24th floor; (b) Angular acceleration of the 32nd floor.

4. Comparisons of Wind-Induced Responses under Different Wind Speeds

4.1. Comparisons of the Translational Acceleration

Figure 9 demonstrated the 10-min translational variations of the root-mean-square of acceleration (RMS of Acc) and peak acceleration on the 6th, 12th, 18th, 24th, 30th and 32nd floors at different wind speeds under Typhoon Khanun. Equation (1) was obtained by fitting the relationship between the RMS and peak of 10-min translational acceleration according to the power function curve, noting that the unit of acceleration is mm/s²:

$${\sigma }_a=c_1{U}^{c2}$$

(1)

where ${\sigma }_a$ is the RMS of Acc or peak acceleration; U is the 10-min mean wind speed; and c₁ and c₂ are the fitting parameters of Equation (1), and the fitting results of parameters are shown in Table 1. Figure 9a–d shows the relationships between RMS of Acc and peak accelerations with respect to the 10-min mean wind speed, which illustrated that both the 10-min RMS of Acc and peak acceleration increase in accordance with the power function as the wind speed increased along both the x and y axes.

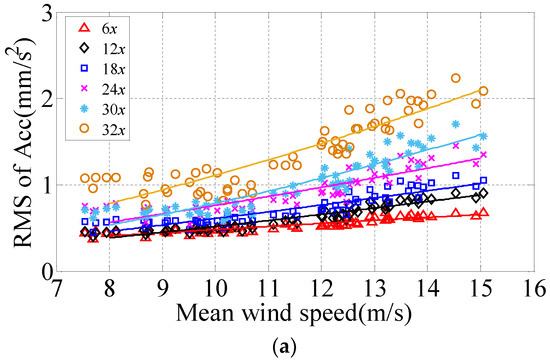
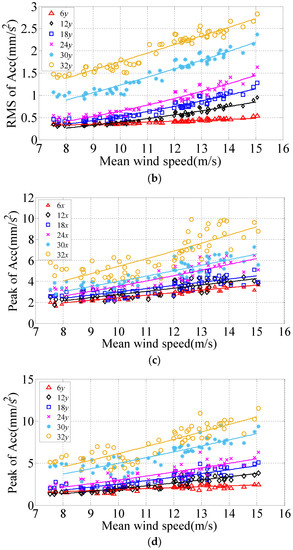
Figure 9. Translational acceleration responses under different wind speeds. (a) RMS of Acc along the x axis. (b) RMS of Acc along the y axis. (c) Peak acceleration along the x axis. (d) Peak acceleration along the y axis.

Table 1. Fitting parameters between translational acceleration responses and mean wind speeds.

Acceleration	Direction	Parameters	6th Floor	12th Floor	18th Floor	24th Floor	30th Floor	32nd Floor
RMS	x	c1	0.084	0.025	0.034	0.036	0.015	0.030
		c2	0.758	1.321	1.256	1.331	1.725	1.567
	y	c1	0.091	0.005	0.007	0.007	0.046	0.147
		c2	0.614	1.867	1.904	1.992	1.431	1.079
Peak	x	c1	0.244	0.222	0.288	0.147	0.231	0.268
		c2	0.998	1.091	1.017	1.380	1.239	1.306
	y	c1	0.425	0.048	0.076	0.094	0.238	0.288
		c2	0.642	1.611	1.524	1.505	1.322	1.329

4.2. Comparisons of the Torsional Angular Acceleration

Figure 10 presented the 10-min torsional angular variations of the RMS of Acc and peak acceleration on the 24th and 32nd floors at different wind speeds under Typhoon Khanun. Table 2 illustrates the fitting parameters between torsional angular acceleration responses and mean wind speeds, noting that the unit of torsional angular acceleration is 10⁻³ rad/s².

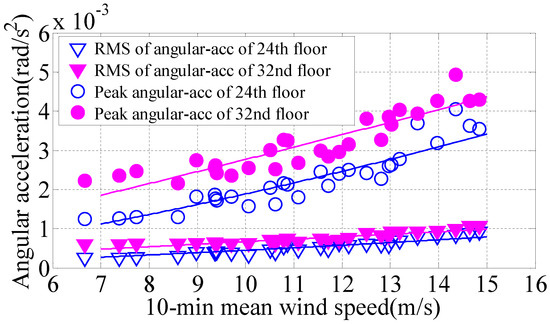
Figure 10. Angular acceleration RMS and peak values under different 10min mean wind speeds.

Table 2. Fitting parameters between angular acceleration responses and mean wind speeds.

Angular Acceleration	Parameters	24th Floor	32nd Floor
RMS	c1	1.83 × 10−5	7.47 × 10−5
	c2	1.39	0.95
Peak	c1	6.48 × 10−5	2.04 × 10−4
	c2	1.46	1.13

4.3. The Ratio between Torsional and Translational Responses

Figure 11 shows the ratios between torsional and translational accelerations on different floor. The results show that acceleration response grew with the increasing wind speed, while the ratio between the torsional and translational response p (the unit of p is rad/m) tended to be stable with the increasing wind speed. The ratio between torsional and translational responses p on the top floor was the lowest compared with those on other floors, and the ratios between torsional and translational responses p of the top floor approximated 0.50 and 0.40 along x and y axes.

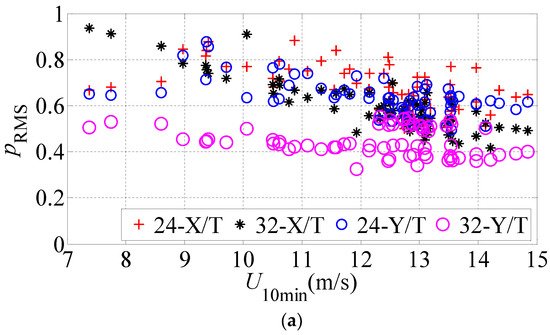
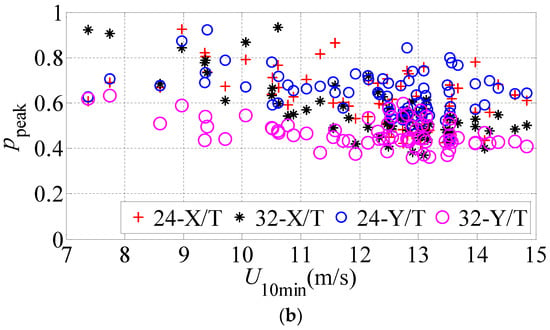
Figure 11. Response ratios between torsional and translational accelerations on different floors. (a) The ratio between the torsional and translational RMS of Acc(p_RMS); (b) The ratio between the torsional and translational peak acceleration(p_peak).

5. Peak Factors of Acceleration under Typhoon

The peak wind-induced response of high-rise buildings within a duration T can be expressed by a function with respect to the mean value $\overline{x}$, the peak factor ($g_{\mathbf{f}}$) and the standard deviation (${\sigma }_x$), as shown in Equation (2).

$$\widehat{x}=\overline{x}+g_{\mathbf{f}}{\sigma }_x$$

(2)

The peak factor is determined as 2.5 to calculate wind-induced vibration coefficient in the Load Code for the Design of Building Structures (GB 50009-2012, 2012) [26]. The American code determines the average peak factor according to the wind-induced vibration displacement, and the Canadian code designates average peak factor by the fluctuating wind pressure, thus the peak factors in both American and Canadian codes are within 3~5, which are bigger than that determined in the Chinese code (Zhang et al., 2007) [27]. Based on the response time histories on different floors, the peak factors of acceleration were analyzed under Typhoon Khanun.

5.1. Probability Density Function of Total Samples

Based on the measured translational and torsional parameters on the 32nd floor of the object building, the overall sample probability distribution of acceleration time histories under Typhoon Khanun was obtained. The sample length was 10 h and the sampling frequency was 128 Hz. The acceleration probability density curves on the 32nd floor along both x and y axes are also presented in Figure 12. The skewness coefficient S and kurtosis coefficient K can be used to judge whether the measured time history data conforms to the Gaussian distribution, as they conform to the Gaussian distribution in the context of S = 0 and K = 3.

$$S=\frac{1}{n}{{\displaystyle \sum _{j=1}^n\left[\frac{C_{ai}\left(t_j\right)-C_{ai,mean}}{C_{ai,std}}\right]}}^3$$

(3)

$$K=\frac{1}{n}{{\displaystyle \sum _{j=1}^n\left[\frac{C_{ai}\left(t_j\right)-C_{ai,mean}}{C_{ai,std}}\right]}}^4$$

(4)

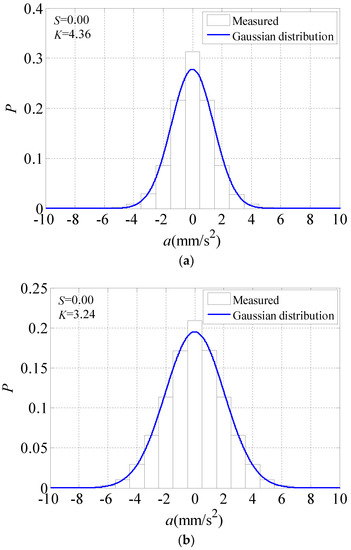
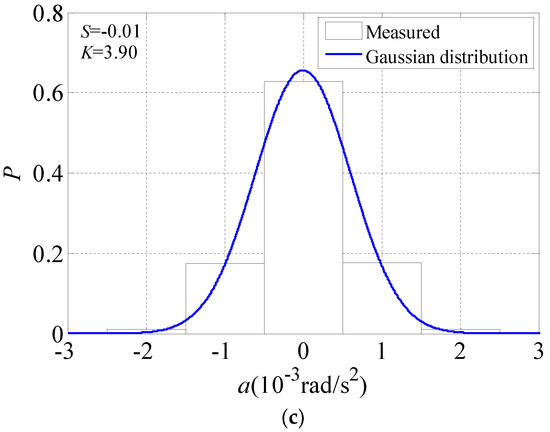
Figure 12. Acceleration probability density of the 32nd floor. (a) Along the x axis; (b) Along the y axis; (c) Along the torsional direction.

In Equations (3) and (4), n is the sample size, $C_{ai,mean}$ is the sample mean value and $C_{ai,std}$ is the sample standard deviation. Figure 12 presents the measured acceleration probability density curve on the 32nd floor as symmetrical and that the skewness and kurtosis coefficients along x axis were 0.00 and 4.36, respectively, while they were 0.00 and 3.24, respectively, along the y axis. The skewness and kurtosis coefficients along the torsion direction were 0.01 and 3.90, respectively. Although the measured acceleration data are very close to the Gaussian distribution characteristics, especially along the Y axis, they still show non-Gaussian characteristics.

5.2. The Skewness and Kurtosis Coefficients

The overall sample probability distribution diagram illustrates that the probability distribution density at the top floor of the measured high-rise building was symmetrical and approximated to the Gaussian distribution. Provided that the point of the kurtosis and skewness coefficients deviate from (0, 3), then the sample probability distribution follows non-Gaussian characteristics. According to the Gaussian distribution, the peak factor is determined as 2.5 in the Load Code for the Design of Building Structures (GB 50009-2012, 2012), which has a target guarantee rate of 99.38%. Time histories of the 32nd floor were adopted to analyze the kurtosis and skewness coefficients of the acceleration probability density on condition that 10 min was selected as the basic time interval of the wind-induced response characteristics during typhoons, as shown in Figure 13.

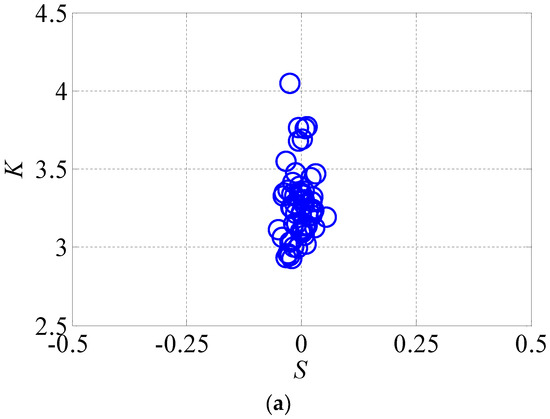
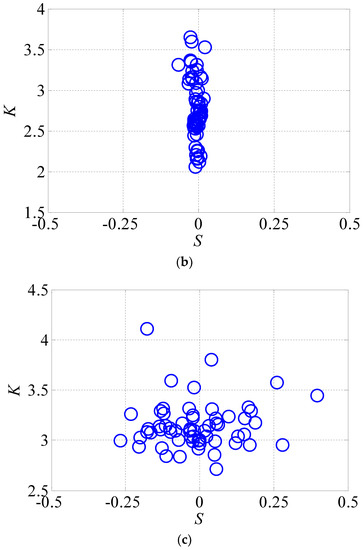
Figure 13. Skewness and kurtosis coefficients of acceleration probability density of the 32nd floor. (a) Along the x axis; (b) Along the y axis; (c) Along the torsional direction.

Figure 13 illustrates that the variation of the kurtosis coefficient of the 10-min translational and torsional acceleration time histories was not significantly associated with that of the skewness coefficient, because the measured skewness coefficient was within(−0.5, 0.5), while the measured kurtosis coefficient was within (2.0, 4.5), which explained that the acceleration probability density approximated to the Gaussian distribution.

5.3. The Peak Factor of Acceleration Based on the Target Probability Method

The target probability method was proposed (Davenport, 1967 [28]) to estimate the measured peak factor of wind pressure. Assuming a certain guarantee rate as the target, the target probability method gradually approaches to the guarantee rate and finally reaches the target guarantee rate. Because this method is independent to Gaussian distribution, it is widely used to calculate peak factor. Therefore, the peak factor of acceleration can be calculated by Equation (5) is based on the target probability method.

$$P\left\{\left|\frac{C_{ai}(t_j)-C_{ai,mean}}{C_{ai,std}}\right|\le g_{abj}+k\delta \right\}=P_{abj}$$

(5)

where $g_{abj}$ is the peak factor of the measured acceleration when it accords with the target guarantee rate of $P_{abj}$. A relatively small initial value $g_{abo}$ is first designed and the initial guarantee rate $P_{abo}$ is then obtained. In order to approach to the target $P_{abj}$, k times of increment $\delta$ is applied successively. When K = M, the absolute value of the difference between $P_{abj}$ and P_abM can be expressed by:

$$\left|P_{abj}-P_{abM}\right|\le \epsilon$$

(6)

where the accuracy standard $\epsilon$ is designated as 10⁻⁶. When $\epsilon$ reaches accuracy requirement, then $P_{abj}\approx P_{abM}$. According to the Gaussian distribution characteristic, the peak factor is determined as 2.5 in Chinese code (GB50009-2012), which has a target guarantee rate of 99.38%. The target guarantee rates with respect to the peak factors of the measured accelerations were defined as 99.38%, 99.50%, 99.60%, 99.70%, 99.80%, 99.90% and 100.00%, respectively, to compare with the Chinese code, through which the 10-min peak factors of acceleration time histories along the translational and torsional directions were obtained. Because the measured acceleration response amplitude of the top floor was the largest, the 10-min peak factors of the translational and torsional acceleration under the set target guarantee rate were obtained by selecting the time history data of the 32nd floor as samples. More details are given in Figure 14.

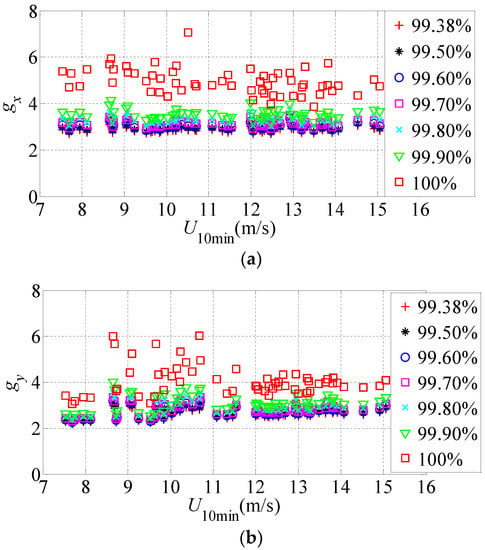
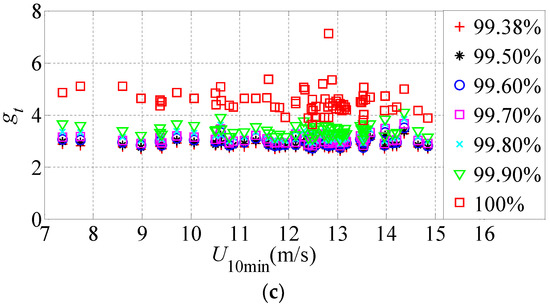
Figure 14. Translational and torsional peak factors. (a) g_x; (b) g_y; (c) g_t.

Figure 14a–c illustrates the acceleration peak factors along the x and y axes and torsional direction, which shows that peak factors were closely dependent to the set target guarantee rates. The increase of target guarantee rate resulted in the larger peak factor and discrete degree of the measured acceleration, and the peak factor of the building response was rarely relevant to the wind speed during the typhoon.

Figure 14 shows that the average values of acceleration peak factors g_x, g_y and g_t were 2.86, 2.60 and 2.81, respectively, under a target guarantee rate of 99.38%, which exceeds the 2.5 determined in the Chinese code (GB50009-2012). The acceleration peak factor increased with the growth of target guarantee rate, and the peak factors g_x, g_y and g_t were 4.95, 4.07 and 4.52, respectively, if the target guarantee rate was designated as 100%, which was also much greater than the 2.5 determined in the Chinese code, thus the measured acceleration peak factor under typhoon was greater than that designated in the Chinese code. Therefore, the acceleration peak factor was suggested to be 3.0 if the target guarantee rate was 99.38%, while it was suggested to be 5.0 when the target guarantee rate was 100.00%. Table 3 lists the average, maximum and minimum values of the acceleration peak factor under different target guarantee rates.

Table 3. Statistical results of acceleration peak factors under different target reliability.

Target Guarantee Rate	Measured Vibration Direction	Minimum Value	Maximum Value	Average Value
99.38%	Along x axis	2.70	3.19	2.86
	Along y axis	2.18	3.00	2.60
	Along torsional axis	2.60	3.27	2.81
99.50%	Along x axis	2.76	3.30	2.94
	Along y axis	2.23	3.10	2.66
	Along torsional axis	2.66	3.37	2.89
99.60%	Along x axis	2.83	3.39	3.03
	Along y axis	2.26	3.21	2.73
	Along torsional axis	2.73	3.51	2.97
99.70%	Along x axis	2.92	3.52	3.14
	Along y axis	2.31	3.36	2.81
	Along torsional axis	2.81	3.65	3.06
99.80%	Along x axis	3.04	3.70	3.29
	Along y axis	2.38	3.54	2.92
	Along torsional axis	2.91	3.83	3.19
99.90%	Along x axis	3.19	4.14	3.55
	Along y axis	2.49	4.03	3.12
	Along torsional axis	3.05	4.10	3.40
100.00%	Along x axis	3.86	7.06	4.95
	Along y axis	3.06	6.04	4.07
	Along torsional axis	3.63	7.12	4.52

6. Conclusions

The RA013 rotating accelerometer was adopted for the first time to measure the torsional vibration response of high-rise buildings under the influence of a typhoon, and the translational and torsional acceleration responses on different floors of the high-rise building under typhoon are obtained, which enriches the pure torsional vibration response measurement of high-rise buildings. Taking 10 min as the basic time interval, the wind-induced responses on different floors and the ratio between translational and torsional responses on the same floor are systematically compared, and the translational and torsional acceleration peak factor under different target guarantee rates are discussed based on the target probability method. The main conclusions are as follows:

(1)

The measured torsional and translational response ratio of acceleration tends to be stable with the sharply increasing wind speeds. Moreover, the torsional and translational response ratios of acceleration along the x and y axes approximate to 0.50 and 0.40, respectively.

(2)

The measured acceleration probability density approximates to the Gaussian distribution. The variation of the kurtosis coefficient of the 10-min translational and torsional acceleration time histories was not significantly associated with that of the skewness coefficien.

(3)

Peak factors are closely related to the designated target guarantee rates. The larger target guarantee rate has a larger peak factor and a discrete degree of the measured acceleration. The average values of acceleration peak factors g_x, g_y and g_t are 2.86, 2.60 and 2.81, respectively, under a target guarantee rate of 99.38%, and they are 4.95, 4.07 and 4.52, respectively, if the target guarantee rate is designated as 100%, which are greater than the 2.5 determined in the Load Code for the Design of Building Structures (GB 50009-2012, 2012).

(4)

Considering that the measured acceleration peak factor is greater than the 2.5 determined in the Chinese code, the acceleration peak factor is suggested to be 3.0 if the target guarantee rate is 99.38%, while it is suggested to be 5.0 when the target guarantee rate is 100.00%.