Abstract
While continuous reinforced concrete deep beams with fixed and hinged support conditions are every so often found in structures, little research has focused on their performance. This, in part, can be attributed to the demanding nature of ensuring fixed supports in experimentally testing such members. Nonetheless, conducting numerical analysis in comparison with experimental study has been a typical technique for producing a reliable numerical model as an alternative to destructive tests. This paper is aimed at numerically investigating the impact of different support conditions in the performance of two-span continuous reinforced concrete deep beams. A numerical model of three experimentally tested beams with two exterior rollers and interior hinge support conditions was generated. Good comparison, with an acceptable variation between numerical and experimental results, was achieved by tuning a few parameters in the numerical model, including element type, mesh size, and material constitutive relations. The refined numerical model was used as an alternative to destructive tests to conduct a parametric study to further investigate the impact of different sets of support conditions in the performance of two-span continuous reinforced concrete deep beams. This study highlights the potentially serious consequences of the support conditions in the performance of such deep beams.
1. Introduction
Deep reinforced concrete (RC) beams are of interest to researchers and engineers because their use has become more prevalent in structures and their strength is difficult to evaluate. Studies on simple deep beams can be found in the literature; however, little research has focused on the comportment of continuous deep beams. Mihaylov et al. [1] presented a theory that uses a three-degree-of-freedom kinematic model to assess the performance of continuous deep beams subjected to differential settlements. The study concluded that the beam load carrying capacity can be significantly decreased due to the redistribution of forces prompted by the beam support differential settlements. Liu and Mihaylov [2] proposed a model formulated as a macroelement to predict the complete shear response of simply supported and continuous deep girders. The derivation of the macroelement was based on a three-parameter kinematic theory, and the results were compared with test results. The macroelement improved the predictions of the shear strength of deep beams and estimated the crack widths and deflections of the beams. Liu et al. [3] proposed a model of one-dimensional beam elements and an original one-dimensional macroelement for members with disturbed regions. The proposed model was employed using available software, VecTor5, to simulate the behavior of 18 test members and a reinforced concrete frame of 20 stories. Using macroelement displayed an improvement in the predictions after the peak load was reached in a building exposed to severe loading. A kinematic model with two degrees of freedom and suitable material properties was presented by Mihaylov et al. [4] to calculate fiber-reinforced concrete (FRC) deep member shear strengths. The presented model centered on the effects of material properties and change in position of critical shear cracks on the FRC deep member shear strengths. Rogowsky et al. [5] fabricated and tested twenty-three reinforced concrete deep beams. The beams included seventeen two span continuous beams—each span was 2 m long—and six simple span beams. It was observed that for the simple span deep beams the cracks started with flexural cracks initiating at the bottom reinforcement. As for the continuous deep beams, this was followed by the formation of hogging flexural crack at the interior support location. Ashour [6] tested eight RC continuous deep beams with different span-to-depth ratios, web reinforcement ratios, and longitudinal reinforcement ratios. It was reported that failure was triggered by a major diagonal crack in the middle shear span between the load and interior support, and that the comparison between test results and code provisions, specifically the ACI Building Code (318-89) and CIRIA Guide 2, showed slight agreement. Zinkaah et al. [7] and Zinkaah and Ashour [8] tested one steel-reinforced and nine (Glass Fiber Reinforced Polymer) GFRP-reinforced continuous shear-critical members. The experimental member load-carrying capacities were compared with capacities predicted by a strut-and-tie model (STM) following the American (ACI 318-2014) and Canadian (S806-2012) code guidelines. The comparison revealed that the American code predicted higher load capacities, while the Canadian code was more conservative. Yang et al. [9] experimentally tested 12 two-span RC deep beam specimens to evaluate the effect of beam depth on shear strength capacity. Sagging and hogging longitudinal reinforcement ratios were the same in all specimens, and no web reinforcement was provided. The failure of all beams tested was due to a major diagonal crack linking the ends of the loading plate and interior support plate. Twelve simply supported deep beam specimens were tested experimentally by Tuchscherer and Kettelkamp [10] to link their serviceability behavior metrics to the internal strain energy predicted by STM. The study findings showed that the beams with the smallest strain energy predicted by the STM demonstrated lower crack widths and exhibited the best performance. Rezaei et al. [11] carried out numerical and experimental research on the impact of the strut angle, development length, shape, and overhang length on the conduct of statically determinate concrete members with disturbed regions. Thirty-five simple deep beam specimens were tested and numerically modeled. It was found that tensile stresses at the support nodes were affected by the development length, and that a rectangular beam geometry resulted in diagonal tensile stresses in the struts. Beams with rectangular geometry demonstrated higher strength with greater strut angles. In addition, the inadequate development length in the studied deep beams was credited to the beams having lower strength. Chen et al. [12] studied the validity of the current strut-and-tie model in predicting the shear strength of simple and continuous RC deep beams. Their study showed that for a simple deep beam, the crack pattern contrasted with that of a continuous deep beam. Moreover, the diagonal strut in a simple deep beam had a lower degree of deterioration than that of a continuous deep beam, and therefore had a higher effective compressive strength. A simple STM was recommended by Arabzadeh and Hizaji [13] to estimate the strength of one-span deep beams with fixed supports. The recommended STM had key struts and sub struts to mimic the spreading of the loads within the simple deep beams. The results of the recommended STM were verified and compared with 31 tests in the literature. As a result, the recommended STM was used to simulate the performance of five tested simple reinforced concrete deep beams with fixed supports. The model output showed that the recommended STM predicted the strength of the simple fixed-fixed deep beams fairly well.
Test studies were executed to observe the shear comportment of simple deep beams, beams with disturbed regions, and corbel members with carbon/glass fiber reinforced polymer (GFRP/FRP) reinforcement [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The experimentally tested specimens had different concrete grades, different span-to-depth ratios, different FRP/GFRP reinforcement ratios, and were with or without web reinforcements; while other tests concerned the strengthening of disturbed regions using FRP schemes. The experimental outcomes of these investigations were compared with the analytical results obtained from code-related STM analysis. In addition to the STM comparison, some of these test results were also compared with numerical results derived from numerically modeling the tested specimens.
Experimental and numerical examinations of the behavior of statically determinate deep beams have been available previously, but few studies have considered continuous deep beams. However, almost no research could be found in the literature related to the effects of different support types on the behavior of continuous deep beams. The current design code provisions, which developed from statically determinate deep beams investigations, are not directly appropriate for continuous deep beams nor are they fitting for simple or continuous deep beams with different support types like fixed and hinged support conditions. This research aims at introducing the first numerical investigations on the strengths of continuous RC deep beams with different sets of support conditions, as relevant experimental studies are not yet available. The existing research does not consider continuous deep beams with different support types. Therefore, the importance of this research is that it presents a numerical model as an alternative to destructive tests, of predicting the strength of RC deep beams with varying support types.
2. Generation of the 3D Numerical Model
2.1. Test Results
To numerically explore the impact of different sets of support conditions on the response of two-span continuous RC deep beams, and due to the scarcity of experimental studies on such members with different support types, a reliable numerical model needs to be produced as an alternative to destructive tests. To fulfil this objective, this study was divided into two tasks. The first task verified a three-dimensional (3D) finite element numerical model generated using ATENA 3D software [31] to simulate the behavior of three two-span continuous RC deep beams tested by Yang et al. [9]. Each one of these tested two-span continuous deep beams had a set of two exterior Roller and an interior Hinge (RHR) supports, as in Figure 1a. Numerical and test results were compared. Good comparison, with an acceptable variation between the numerical and experimental results, was achieved after tuning and refining a few parameters in the generated numerical model. It is worth noting that the authors have used ATENA software [31] in previous studies [32,33,34] on simple and continuous RC beams and verified the validity of the FE model outcomes with experimental results. However, since this paper concerns continuous RC deep beams the authors used the published paper by Yang et al. [9] as an extra evaluation and verification of the proposed FE model generated using ATENA software [31]. Another reason for referring to this published paper is that it not only provides the needed specimen dimensions, material properties, and experimentally generated crack types and patterns, but also provides details on the test beam support types, which are highly critical in this study. The obtained model was reliable enough to be used as an alternative to destructive tests of beams similar to the tested ones. The second task of this study used the model generated in the first task to conduct a parametric examination to further probe the effects of different support condition sets in the performance of the tested two-span continuous RC deep beams.
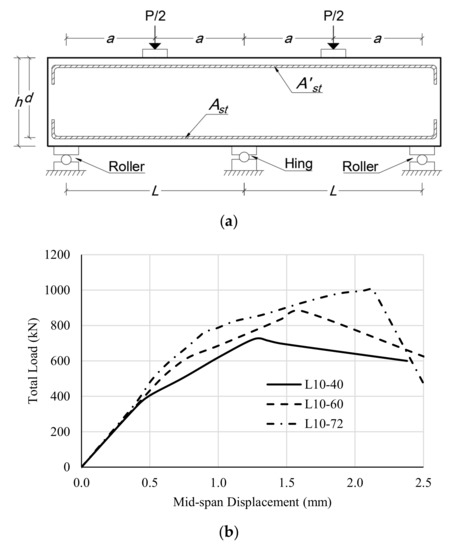
Figure 1.
(a) Details of beam geometry and support conditions; (b) experimental total load-midspan displacement relations [9].
In this study, the member dimensions, material types, and mechanical properties employed in the generated numerical models correspond to those of the experimentally tested deep beams, as shown in Table 1. The experimental results reported by Yang et al. [9] are shown in Figure 1b.

Table 1.
Test specimen specifics (Yang et al. [9]).
2.2. Mesh Generation of Test Beams
ATENA 3D v5.6 (Advanced Tool for Engineering Nonlinear Analysis 3D) software [31] was used in the study to develop the numerical models of the beams tested by Yang et al. [9]. The software has a graphical user interface through which input data can be entered in an easy fashion. ATENA 3D [31] employs the Updated Lagrange formulation in its structural analysis computations, and it is intended for three-dimensional nonlinear analysis for solids, particularly for reinforced concrete structures. Using Lagrange formulation, the governing equilibrium equations could be derived based on the model undeformed shape or based on the most recent deformed shape of the model at any time (updated Lagrange formulation). With the updated Lagrange deformation, the model configuration is updated after each time step, whereas in one step, the configuration from the beginning of the step is used. Stresses and strains at the end of the step are, therefore, evaluated with respect to the configuration at the step commencement. The updated Lagrange deformation is capable of simulating the actual performance of the structure including capturing concrete cracking, concrete crushing, and reinforcement yielding. Multiple input parameters were changed in this study to reach a set of inputs that yielded a model with numerical results and predictions comparable to the experimental findings. The software is equipped with various built-in material constitutive models. The user is required to choose the desired material constitutive models and define the required mechanical properties of the materials. In addition, the software offers an option for the user to manually define or adjust material constitutive models. The ATENA predefined fracture-plastic model for concrete, “CC3DNonLinCementitious2User” solid brick element [31], was adopted in this investigation. The concrete fracture-plastic model is based on a strain discretizing scheme. The concrete cube compressive strength (fcu) was the only required input, which was 37.8 MPa. This corresponded to cylinder compressive strength (f′c) of 32.1 MPa, which was identical to the concrete strength reported by Yang et al. [9]; Table 1. The tensile strength (ft) was taken as half of ft generated by the software (1.35 MPa) [35]. The concrete compressive and tensile stress-strain relation began with a linear relationship, with a slope equal to the concrete modulus of elasticity (Ec), until reaching a strain value equal to the localized strain (εloc). The value of εloc was generated automatically by the software as a function of the concrete cube strength. After reaching εloc, the strain is localized to the finite element by the software. The value of εloc was equal to zero and 0.00097 under tension and compression, respectively. The post-peak localized strain is affected by the L/Lch ratio, where L = crushing band size for the compression behavior or crack band size for the tension behavior, and Lch = characteristic length, having a default value of 0.1 generated by the software for the compression behavior. The value of Lch under tension was set to be equal to the mesh size, as recommended by the software manual [31]. The compressive and tensile behavior after strain localization as generated by the software for the given set of inputs is shown in Figure 2 [31].
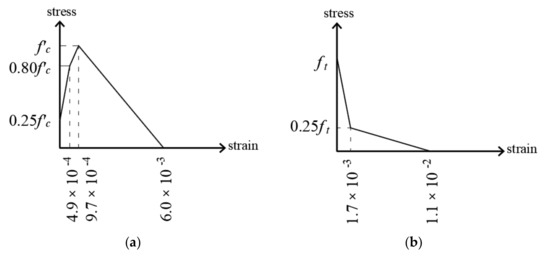
Figure 2.
Concrete material model: (a) Compressive behavior; (b) tensile softening.
The concrete material model used in this study facilitates strength reduction for cracked concrete. The functions of reduction factors for compressive strength (rc) and shear strength (fsh) are presented in Figure 3. The reduction factor for compressive strength is affected by the fracturing strain (εf) determined from the strain tensor at the finite element integration points. The reduction factor for shear strength is affected by fracturing strain after localization () determined by Equation (1) [31].
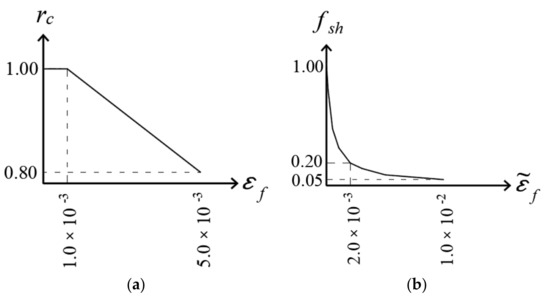
Figure 3.
Functions of concrete strength reduction factors: (a) Compressive strength; (b) shear strength.
Table 2 shows a summary of the parameters of concrete martial constitutive model that were adopted in this research. A displacement-controlled applied load was assigned in the FE analysis to detect the beam behavior after the total ultimate load is reached.

Table 2.
Parameters of the concrete material model.
Tension and compression reinforcement were modeled as one-dimensional bar elements, and the steel material constitutive law was chosen as the elastic-perfectly plastic model with a perfect bond between concrete and steel bars. The steel stress-strain behavior is presented in Figure 4. The yielding strength of compression and tension steel (fy) is 420 MPa. The modulus of elasticity (E) for steel is 200 GPa and the strain at yielding (εy) is 0.0021. The chosen concrete and steel material models were used to simulate the performance of the continuous deep beams tested by Yang et al. [9] using ATENA software [31]. A mesh sensitivity study was carried out to warrant solution convergence during the numerical analysis of the tested beam while minimizing the computational time. To find the best model mesh, different element sizes were tried prior to choosing the mesh layout exhibited in Figure 5.
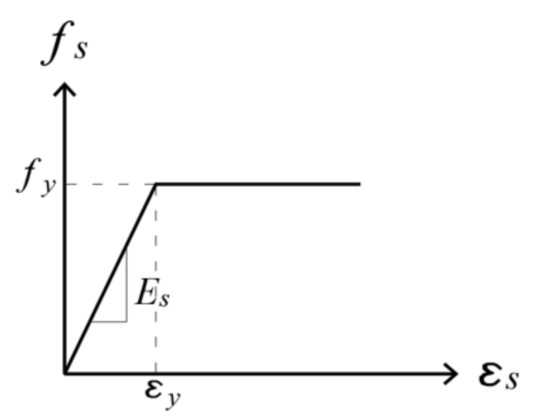
Figure 4.
Steel material model.
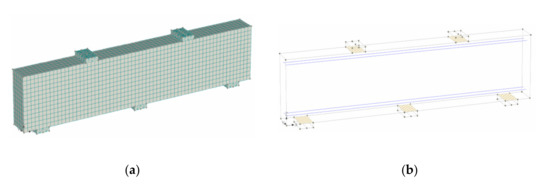
Figure 5.
Generated 3D finite element modeling of beams: (a) Mesh configuration; (b) geometry and reinforcement bars.
2.3. Verification of the Generated 3D Numerical Model
The generated 3D numerical model was assessed by comparing its outcomes with the test results obtained by Yang et al. [9]. Figure 6 shows the experimental and numerical load-deflection relations and crack patterns in specimen L10-40. Figure 6a indicates that the numerical stiffness of the specimen was almost double the test stiffness in the pre-cracking stage. This discrepancy in the performance may be credited to the heterogeneous nature of concrete, resulting in different material properties between the tested specimens and those specified numerically. Other possible factors might be the initial micro cracks generated in concrete due to the temperature and shrinkage effects that were not possible to define numerically. These possible factors are in agreement with conclusions reported by Ibrahim and Mahmood [36] and Obaidat et al. [37]. Following cracking, the numerical stiffness of the specimen decreased and became almost the same as the test stiffness, and both numerical and test deflections increased at nearly the same rate, until both behaviors reached a load of 724 kN, which was a failure total load for the test specimen. The numerical behavior, however, showed that the specimen exhibited a plastic performance as the load increased where the deflection continued to increase rapidly associated with a small increase in the load until a total failure load of 781 kN was reached. As for the test behavior, the development of diagonal cracks caused the beam stiffness to decrease leading the beam to deflect at a higher rate. Nonetheless, the numerical and experimental total failure loads were both reached at deflections of 1.4 mm and 1.3 mm, respectively. Figure 6b,c show that the two spans displayed practically the same numerical and test crack patterns. More shear and flexural cracks were generated and spread as the load increased, and a main oblique shear crack in the left span of the test beam abruptly occurred at the failure load linking the ends of the loading plate and interior support plate. This is in agreement with the numerically predicted crack pattern manifested in the wide diagonal crack width band. Figure 6b,c also show that the loads in the two spans are transmitted to the supports through the diagonal paths of compressive struts. The stress distribution, shown in Figure 6d, indicated that the stresses in the interior struts were higher than those of the exterior struts. As a result, the interior shear span failed first, which was in accordance with the experimentally observed failure; Figure 6b.
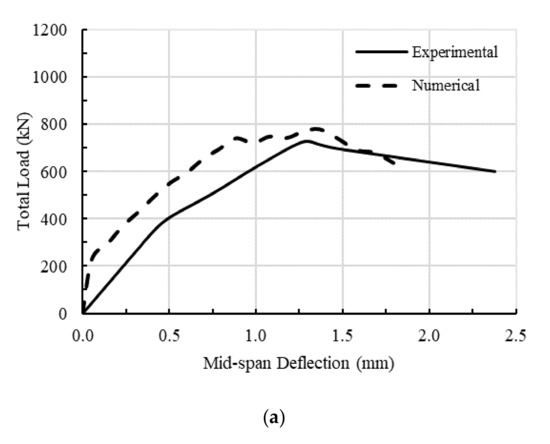

Figure 6.
Experimental and numerical responses of specimen L10-40 (RHR supports): (a) Experimental [9] and numerical load-deflection curves for specimen L10-40; (b) experimental crack pattern [9]; (c) numerical crack pattern; (d) stress distribution (MPa).
It is worth stating that at any load level, the numerical and test deflections only vary by a fraction of a millimeter, which makes the numerical simulation almost identical to the test results. Therefore, it can be concluded that for specimen L10-40, both the simulation and test results are almost the same with respect to strength (ultimate load) and crack pattern.
Figure 7 shows the experimental and numerical load-deflection relations and crack patterns of specimen L10-60. Similar to specimen L10-40, Figure 6a reveals that the numerical stiffness of specimen L10-60 was almost twice the test stiffness in the pre-cracking stage. After cracking, there were several occurrences of load dwindling in the numerical behavior of the post-cracking stage of the specimen due to progressive expansion of diagonal cracks within the shear span. This was less evident in numerical behavior of specimens L10-40. As for the test behavior, the development of diagonal cracks caused the beam stiffness to decrease leading the beam to deflect at a higher rate.
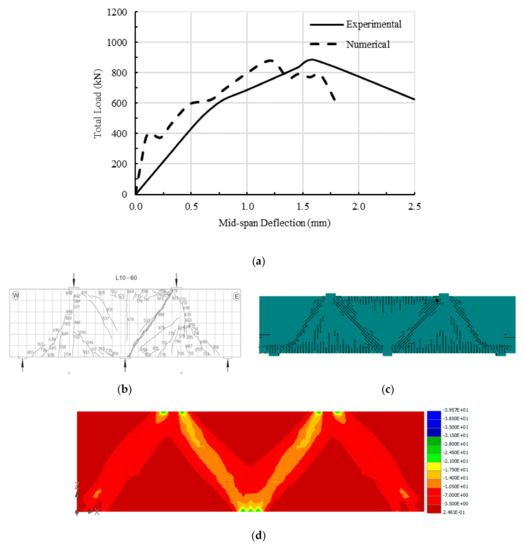
Figure 7.
Experimental and numerical responses of specimen L10-60 (RHR supports): (a) Experimental [9] and numerical load-deflection curves for specimen L10-60; (b) experimental crack pattern [9]; (c) numerical crack pattern; (d) stress distribution (MPa).
However, the failure load predicted by the numerical model was 871 kN and the test failure load was 883 kN. Both numerical and test total loads were almost the same. On the other hand, as the deflection increased, the numerical behavior got closer to the test behavior. The numerical and experimental total failure loads were both reached at deflections of 1.3 mm and 1.6 mm, respectively. The same as for specimen L10-40, Figure 7b,c show that the two spans displayed just about the same numerical and test crack patterns. More shear and flexural cracks were generated and spread as the load increased, although less than the cracks developed in specimen L10-40, and a main shear crack in the right span of the test beam was developed at the failure load, linking the ends of the loading plate and interior support plate. Similar to Figure 6, Figure 7b,c also demonstrate that the loads in the two spans are transmitted to the supports through the diagonal paths of compressive struts. Similar to Figure 6d, the stress distribution, shown in Figure 7d, indicates that the stresses in the interior struts were higher than those of the exterior struts. As a result, the interior shear span failed first, which was in accordance with the experimentally observed failure; Figure 7b.
It is worth stating that at any load level, the numerical and test deflections only vary by a fraction of a millimeter, making the numerical simulation almost identical to the test results. Therefore, it is concluded that for specimen L10-60, both the simulation and test results are really the same with respect to both total load carrying capacity and crack pattern.
Figure 8 shows the experimental and numerical load-deflection relations and crack patterns of specimen L10-72. Similar to Figure 6a and Figure 7a, Figure 8a indicates that the numerical stiffness of the specimen was almost double the test stiffness prior to cracking. Subsequent to cracking, the numerical stiffness of the specimen decreased, and the behavior almost matched the test behavior. Both numerical and experimental outcomes showed that the specimen exhibited similar ductility and failed at total numerical and test loads of 994 kN and 1008 kN, respectively, corresponding to numerical and test deflections of 1.8 mm and 2.1 mm, respectively. As for the crack pattern, Figure 8b,c show that specimen L10-72 exhibited just about the same numerical and test crack patterns in the two spans. It is worth noting that this specimen had fewer flexural and diagonal cracks than the other two specimens. Nonetheless, Figure 8b,c also show that this specimen had more apparent parallel diagonal cracks, especially in the right span, where a main shear crack developed at the failure load, linking the ends of the loading plate and interior support plate. Figure 8b,c similarly show that the loads in the two spans are conveyed to the supports by the diagonal paths of compressive struts. Like the other two specimens, the stress distribution, shown in Figure 8d, indicates that the stresses in the interior struts were higher than those of the exterior struts. As a result, the interior shear span failed first, which was in accordance with the experimentally observed failure, Figure 8b.
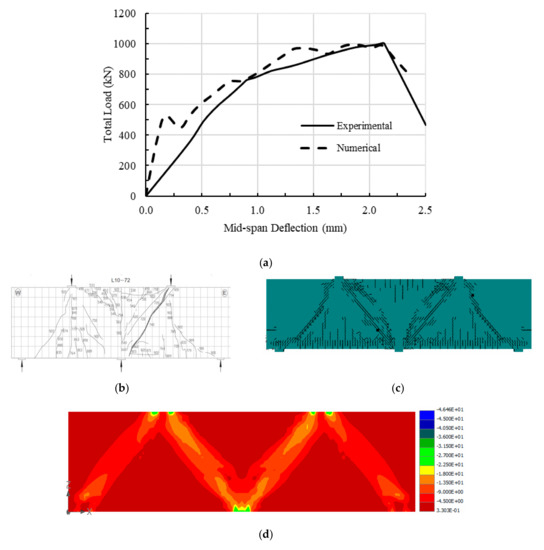
Figure 8.
Experimental and numerical responses of specimen L10-72 (RHR supports): (a) Experimental [9] and numerical load-deflection curves for specimen L10-72; (b) experimental crack pattern [9]; (c) numerical crack pattern; (d) stress distribution (MPa).
It is worth stating that at any load level, the numerical and test deflections only vary by a fraction of a millimeter, making the numerical simulation almost identical to the experimental outcomes. Therefore, it can be concluded that for specimen L10-72, the numerical simulation predicted values for strength (ultimate load) and crack pattern that were very close to those of the test specimen.
Figure 6, Figure 7 and Figure 8 demonstrate that the numerical simulations and test results reported by Yang et al. [9] are nearly identical with spect to strength, ductility, crack patterns, and location of failure. Therefore, the developed numerical model adequately predicted the strengths and ductility of the three two-span continuous deep beams that had a set of two Roller and a Hinge support conditions (RHR).
As a result of satisfactorily verifying the developed numerical model with test results, the developed model was considered reliable enough to serve as an alternative to destructive tests, and its application can be applied to the tested beams with different sets of support conditions.
Consequently, the second task of this study used the verified developed numerical model to further investigate the performance of the continuous two-span reinforced concrete deep beams tested by Yang et al. [9], but with sets of support conditions other than the hinge and two roller supports that these beams had when tested; Figure 1a.
3. Parametric Study
3.1. Sets of Support Conditions Considered in This Study
The parametric study deployed the numerical model developed and verified in the first task to further investigate the performance of two-span deep beams with different sets of support conditions. The test beams by Yang et al. [9], with two exterior Roller and interior Hinged supports (RHR), were considered to further simulate and examine the effects of the following three different sets of support conditions on their structural behaviors:
- Hinged-Roller-Hinged support set—HRH (two exterior hinged supports; interior roller support)
- Hinged-Hinged-Hinged support set—HHH (all three supports are hinged)
- Fixed-Hinged-Fixed support set—FHF (two exterior fixed supports; interior hinged support)
3.2. Changing Specimen L10-40 Support Conditions
The effect of the support types on the behavior of specimen L10-40 was numerically examined by changing its test RHR support types to the numerical HRH support set, HHH support set, and FHF support set. The numerically simulated performances of specimen L10-40, in addition to the experimental performance, are presented in Figure 9.
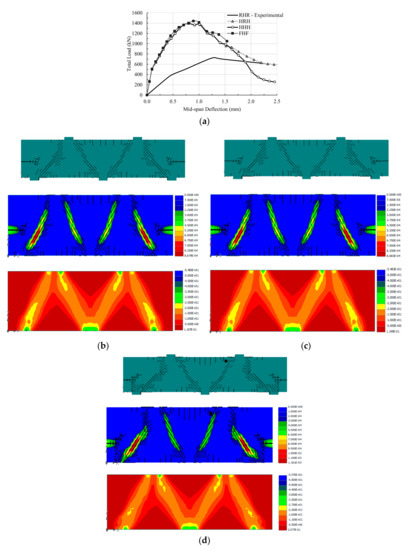
Figure 9.
Responses of specimen L10-40 with three different sets of support conditions: (a) Experimental (RHR, [9]) and numerical Load-deflection curves for specimen L10-40; (b) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—HRH support conditions; (c) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—HHH support conditions; (d) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—FHF support conditions.
Figure 9a shows that specimen L10-40 with numerical HRH, HHH, or FHF support sets reached a much higher total load capacity and possessed greater stiffness than it did experimentally with the RHR support conditions. The figure also shows that the numerical behaviors of the specimen with any of the three numerical support sets were virtually identical. As summarized in Table 3, for the cases of HRH and HHH support sets the specimen L10-40 reached an equal total load of 1394 kN associated with equal numerical deflection of 0.8 mm. This is a 93% increase in numerical total load in comparison with the experimental total load of 724 kN, and 38% decrease in numerical deflection in comparison with the experimental deflection of 1.3 mm. For the case of FHF support set, the specimen reached a total load of 1441 kN accompanied by a numerical deflection of 0.9 mm. This a 99% increase in numerical total load in comparison with the test total load of 724 kN, and a 31% decrease in numerical deflection in comparison with the test deflection of 1.3 mm.

Table 3.
Parametric study result summary.
It can be concluded that when the specimen was restrained using any set of the numerical HRH, HHH, or FHF support types, the beam became stiffer, more robust, and exhibited fairly identical numerical behavior in terms of strength, stiffness, and ductility.
Figure 9b–d show the crack patterns, crack widths, and stress distributions for the cases of the three numerical support sets. The crack patterns in the three sets show dominant diagonal shear cracks with narrow bandwidth and remarkably less and minor sagging and hogging flexural cracks. This was not the case for the specimen L10-40 with test RHR support conditions, as shown in Figure 6c. It is worth noting that for the cases of the HRH and HHH support sets, the crack patterns are identical as demonstrated in Figure 9b,c; however, when the FHF support set was used, the sagging flexural cracks became less and the hogging flexural cracks increased, while the cracks at exterior fixed supports amplified, as shown in Figure 9d. Figure 9b–d also show that at failure, the crack widths in the diagonal struts of exterior shear spans were larger than those of the interior shear span diagonal struts. Similarly, the stress distributions presented in these figures demonstrated that the stresses in the diagonal struts of exterior shear spans were higher than those of interior shear span diagonal struts. As a result, the exterior shear span of the beam specimens failed first.
Unlike the test beams, the numerical analysis revealed that using hinged or fixed supports at the ends of the continuous beam specimens, L10-40, caused the load path to actively engage the exterior diagonal struts in the specimen resistance due to restraining the displacements of these supports, and to instigate faster development of exterior struts as opposed to the interior ones. Consequently, the beam shear strength increased, and the beam deflection decreased. As the load increased the development of diagonal struts of the exterior shear spans advanced, causing widespread cracks, wider cracks, and higher stresses than those of the interior diagonal struts. Eventually, the specimen ultimate loads were controlled by the failure of the exterior shear spans.
3.3. Changing Specimen L10-60 Support Conditions
The effect of the support types on the behavior of specimen L10-60 was numerically examined by changing its test RHR support set to numerical HRH, HHH, and FHF support sets. The numerically simulated performances of specimen L10-60, in addition to the experimental performance, are presented in Figure 10.
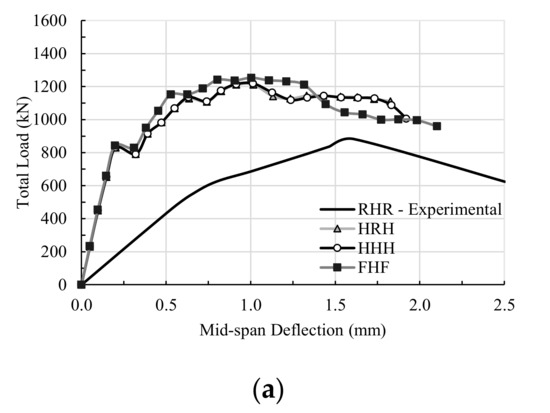
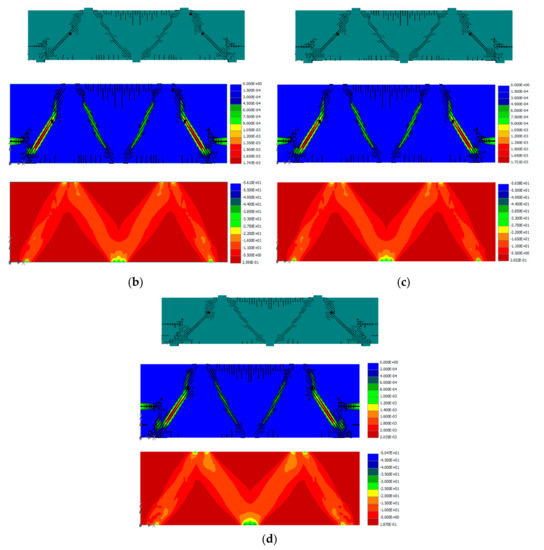
Figure 10.
Responses of specimen L10-60 with three different sets of support conditions: (a) Experimental (RHR, [9]) and numerical Load-deflection curves for specimen L10-60; (b) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—HRH support conditions; (c) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—HHH support conditions; (d) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—FHF support conditions.
Figure 10a shows that the specimen L10-60 reached much higher total load capacity and possessed greater stiffness than it did experimentally, with a set of RHR support conditions. The figure also shows that the numerical behaviors of the specimen for the three numerical support sets were nearly identical. As summarized in Table 3, for the cases of HRH and HHH support sets, the specimen L10-60 reached total loads of 1212 kN and 1219 kN, respectively, associated with equal numerical deflection of 1.0 mm. These are 37% and 38% increases, respectively, in numerical total load in comparison to the experimental total load of 883 kN, and a 37% decrease in numerical deflection in comparison with the experimental deflection of 1.6 mm. For the case of the FHF support set, the specimen reached a total load of 1254 kN accompanied by a deflection of 1.0 mm. This a 42% increase in numerical total load in comparison with the test total load of 883 kN, and a 37% decrease in numerical deflection in comparison with the test deflection of 1.6 mm.
It can also be concluded that when the specimen was restrained using any set of the numerical HRH, HHH, or FHF support types, the beam became stiffer, more robust, and exhibited nearly identical numerical behavior in terms of strength, stiffness, and ductility.
Figure 10b–d show the crack patterns, crack widths, and stress distributions for the three numerical support sets. The crack patterns in the three sets show dominant diagonal shear cracks with narrow bandwidth and remarkably fewer sagging flexural cracks than hogging flexural cracks. This was not the case for specimen L10-60 with test RHR support conditions, as shown in Figure 7c. It is worth noting that for the cases of HRH and HHH support sets, the crack patterns are identical, as demonstrated in Figure 10b,c; however, when the FHF support set was used, the sagging flexural cracks almost disappeared, with the exception of a couple of very minor cracks, and the hogging flexural crack increased, while the cracks at the exterior fixed supports amplified; Figure 10d. Figure 10b–d also show that at failure, the crack widths in the diagonal struts of exterior shear spans were larger than those of interior shear span diagonal struts. Similarly, the stress distributions presented in these figures demonstrated that the stresses in the diagonal struts of exterior shear spans were higher than those of interior shear span diagonal struts. As a result, the exterior shear span of the beam specimens failed first.
Similar to specimens L10-40, the numerical analysis revealed that using hinged or fixed supports at the ends of the continuous beam specimens, L10-60, caused the load path to robustly involve the exterior diagonal struts in the specimen resistance due to restraining the displacements of these supports, and to set off faster development of exterior struts in comparison to interior ones. Consequently, the beam shear strength improved, and the beam deflection decreased. As the load increased, the growth of diagonal struts of the exterior shear spans advanced causing widespread cracks, wider cracks, and higher stresses than those of the interior diagonal struts. Eventually, the specimen ultimate loads were controlled by the failure of the exterior shear spans.
3.4. Changing Specimen L10-72 Support Conditions
The effect of the support conditions on the behavior of specimen L10-72 was numerically examined by changing the test beam specimen RHR support types to numerical HRH, HHH, and FHF support sets. The numerically simulated performances of specimen L10-72, in addition to the experimental performance, are presented in Figure 11.
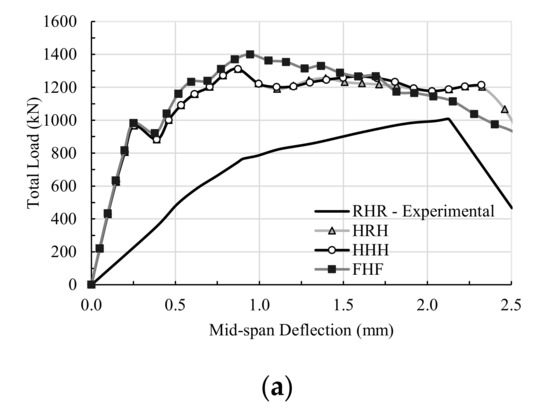
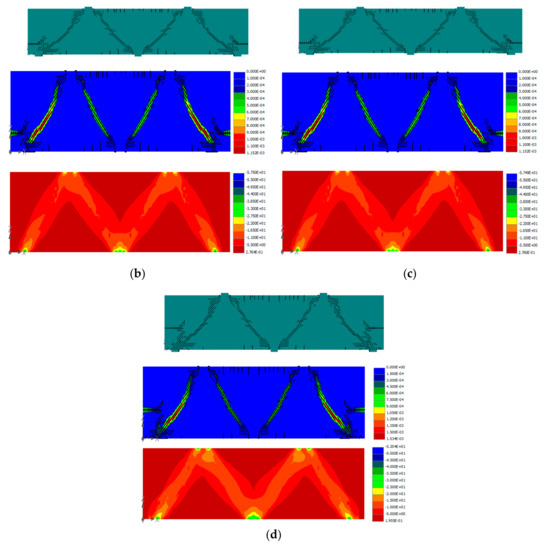
Figure 11.
Responses of specimen L10-72 with three different sets of support conditions: (a) Experimental (RHR, [9]) and numerical Load-deflection curves for specimen L10-72; (b) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—HRH support conditions; (c) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—HHH support conditions; (d) crack pattern (top), crack width (middle), and stress distribution (MPa) (bottom)—FHF support conditions.
Figure 11a shows that the specimen L10-72 reached much higher total load capacity and possessed greater stiffness than it did experimentally with a set of RHR support conditions. The figure also shows that the numerical behaviors of the specimen for the three numerical support sets were nearly identical. As summarized in Table 3, for the cases of numerical HRH and HHH support sets, the specimen L10-72 reached an equal total load of 1311 kN associated with an equal numerical deflection of 0.9 mm. This is a 30% increase in numerical total load in comparison with the experimental total load of 1008 kN, and a 57% decrease in numerical deflection in comparison with the experimental deflection of 2.1 mm. For the case of the FHF support set, the specimen reached a total load of 1400 kN accompanied by a deflection of 1.0 mm. This a 39% increase in numerical total load in comparison with the test total load of 1008 kN, and a 52% decrease in numerical deflection in comparison with the test deflection of 2.1 mm.
It can be concluded that when the specimen was restrained using any set of the numerical HRH, HHH, or FHF support types, the beam became stiffer, more robust, and exhibited fairly identical numerical behavior in terms of strength, stiffness, and ductility.
Figure 11b–d show the crack patterns, crack widths, and stress distributions for the three numerical support sets. The crack patterns in the three sets show dominant diagonal shear cracks with narrow bandwidth and, remarkably, very little and very minor sagging and hogging flexural cracks. This was not the case for the specimen L10-72 with test RHR support conditions, as shown in Figure 8c. It is worth noting that for the cases of HRH and HHH support sets, the crack patterns are identical to those demonstrated in Figure 11b,c; however, when the FHF support set was used, the sagging flexural cracks almost disappeared with exception of couple of minor cracks and the hogging flexural crack did not change much, while the cracks at the exterior fixed supports were amplified; Figure 11d. Furthermore, Figure 11b–d demonstrate that at failure, the crack widths in the diagonal struts of exterior shear spans were larger than those of interior shear span diagonal struts. Similarly, the stress distributions presented in these figures demonstrate that the stresses in the diagonal struts of exterior shear spans were higher than those of the interior shear span diagonal struts. Hence, the beam exterior shear span failed first.
Like specimens L10-40 and L10-6, the numerical analysis revealed that using hinged or fixed supports at the ends of the continuous beam specimens, L10-72, caused the load path to actively engage the exterior diagonal struts in the specimen resistance due to restraining the displacements of these supports, and to initiate faster development of exterior struts as opposed to the interior ones. Consequently, the beam shear strength improved, and the beam deflection deteriorated. As the load increased, the development of diagonal struts of the exterior shear spans advanced, causing widespread cracks, wider cracks, and higher stresses than those of the interior diagonal struts. In the end, the specimen ultimate loads were controlled by the failure of the exterior shear spans.
In addition, the numerical analysis confirmed that the importance of the crack pattern is that it shows where the failure first started in the beam. It showed which shear span (internal or external) failed first. This would be an important information to consider when designing continuous deep beams with varying supports.
Figure 9, Figure 10 and Figure 11 demonstrate that all of the major cracks in all specimens for the three different numerical support sets (HRH, HHH, and FHF) were diagonal cracks connecting the edges of the loading plates to the edges of the supporting plates, with remarkably few and very minor sagging and hogging flexural cracks. Therefore, the failure mode of all the beams was shear failure. It is worth mentioning that as the beam depth increased, the diagonal shear crack bandwidth narrowed and the shear cracks became more localized diagonally, as can be clearly observed in the figures. Moreover, the flexural cracks degenerated and converted into minor cracks.
Figure 9, Figure 10 and Figure 11 also show that each one of the specimens exhibited nearly identical behavior, indicating that using different restraining support sets (HRH, HHH, and FHF) did not significantly affect the beam behavior. However, the specimens revealed much higher total load capacity and gained better stiffness than they did experimentally with a set of RHR support conditions.
The numerical total loads and their corresponding mid-span deflections as well as the test total loads and their corresponding mid-span deflections are summarized in Table 3 for comparison.
4. Conclusions
A Three-Dimensional (3D) numerical FE model was developed and verified, as the first task of the study, for the simulation of the performance of three two span continuous reinforced deep beam specimens with two rollers and a hinged support. The model numerically predicted total load strengths and deflections that were nearly identical to the values of the test outcomes.
The second task of this study was to extend the numerical simulation to further explore the effect of different sets of support conditions on the performance of the test specimens using the numerical 3D FE model developed in the first task. Three different sets of support conditions were considered in each of the three test specimens above: Hinged-Roller-Hinged (HRH), Hinged-Hinged-Hinged (HHH), and Fixed-Hinged-Fixed (FHF) support condition sets.
The numerical results revealed that, when restrained using any of the HRH, HHH, or FHF support sets, each of the beam specimens became stiffer and more robust, and the exterior shear span of the beams failed first. The specimens exhibited fairly identical numerical behavior in terms of strength, stiffness, and ductility. Specimen L10-40 exhibited 93%, 93%, and 99% increases in the numerical total load in comparison with the test total load when HRH, HHH, or FHF support sets were used, respectively. Similarly, specimen L10-60 presented 37%, 38%, and 42% increases in the FE total load in comparison with the test total load when HRH, HHH, or FHF support sets were used, respectively. Likewise, specimen L10-60 displayed 37%, 38%, and 42% increases in the numerical total load in comparison with the test total load when HRH, HHH, or FHF support sets were applied, respectively. Remarkably, on the other hand, all specimens reached their numerical total loads at almost the same numerical deflection, 0.9 ± 0.1 mm. It can be concluded that none of the HRH, HHH, and FHF support sets had any substantial influence on the beam ductility.
The numerical simulations showed that the major cracks in any of the specimens with any of the HRH, HHH, or FHF support types were parallel, with diagonal cracks connecting the edges of loading plates to the edges of supporting plates. It is worth noting that as the beam depth increased, the diagonal shear crack bandwidth narrowed and the shear cracks became more localized diagonally, while the sagging flexural cracks degenerated, and the hogging flexural cracks were converted into insignificant cracks.
It is recommended to investigate the effects of other factors such as concrete compressive strength, shear span-to-depth ratio, and reinforcement ratio on the behavior of two-span RC deep beams in a future study.
Author Contributions
Conceptualization, B.E.-A. and M.M.; methodology, B.E.-A. and M.M.; software, M.M. and T.E.-M.; validation, B.E.-A., M.M. and T.E.-M.; formal analysis, B.E.-A.; investigation, M.M. and B.E.-A.; resources, T.E.-M.; data curation, M.M.; writing—Original draft preparation, B.E.-A. and M.M.; writing—Review and editing, B.E.-A. and M.M.; visualization, M.M.; supervision, B.E.-A.; project administration, B.E.-A.; funding acquisition, B.E.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the United Arab Emirates University, grant number 31N324 and grant number 31N371.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mihaylov, B.I.; Hunt, B.; Bentz, E.C.; Collins, M.P. Three-Parameter Kinematic Theory for Shear Behavior of Continuous Deep Beams. ACI Struct. J. 2015, 112, 47–58. [Google Scholar] [CrossRef]
- Liu, J.; Mihaylov, B.I. Macroelement for Complete Shear Behavior of Continuous Deep Girders. ACI Struct. J. Farmington Hills 2018, 115, 1089–1099. [Google Scholar] [CrossRef]
- Liu, J.; Guner, S.; Mihaylov, B.I. Mixed-Type Modeling of Structures with Slender and Deep Beam Elements. ACI Struct. J. 2019, 116, 253–264. [Google Scholar] [CrossRef]
- Mihaylov, B.; Liu, J.; Tvrznikova, K. Two-parameter kinematic approach for complete shear behavior of deep FRC beams. Struct. Concr. 2020, 21, 362–375. [Google Scholar] [CrossRef]
- Rogowsky, D.M.; MacGregor, J.G.; Ong, S.Y. Tests of Reinforced Concrete Deep Beams; Structural Engineering Report, No. 109; Department of Civil Engineering, The University of Alberta: Edmonton, AB, Canada, 1983. [Google Scholar]
- Ashour, A.F. Tests of Reinforced Concrete Continuous Deep Beams. Struct. J. 1997, 94, 3–12. [Google Scholar] [CrossRef]
- Zinkaah, O.H.; Ashour, A.; Sheehan, T. Experimental tests of two-span continuous concrete deep beams reinforced with GFRP bars and strut-and-tie method evaluation. Compos. Struct. 2019, 216, 112–126. [Google Scholar] [CrossRef]
- Zinkaah, O.H.; Ashour, A. Load capacity predictions of continuous concrete deep beams reinforced with GFRP bars. Structures 2019, 19, 449–462. [Google Scholar] [CrossRef]
- Yang, K.-H.; Chung, H.-S.; Ashour, A.F. Influence of section depth on the structural behaviour of reinforced concrete continuous deep beams. Mag. Concr. Res. 2007, 59, 575–586. [Google Scholar] [CrossRef]
- Tuchscherer, R.; Kettelkamp, J. Estimating the Service-Level Cracking Behavior of Deep Beams. ACI Struct. J. 2018, 115, 875–883. [Google Scholar] [CrossRef]
- Rezaei, N.; Klein, G.; Garber, D.B. Effect of Development and Geometry on Behavior of Concrete Deep Beams. ACI Struct. J. 2019, 116, 171–181. [Google Scholar] [CrossRef]
- Chen, H.; Yi, W.-J.; Ma, Z.J.; Hwang, H.-J. Shear Strength of Reinforced Concrete Simple and Continuous Deep Beams. ACI Struct. J. 2019, 116, 31–40. [Google Scholar] [CrossRef]
- Arabzadeh, A.; Hizaji, R. A Simple Approach to Predict the Shear Capacity and Failure Mode of Fix-ended Reinforced Concrete Deep Beams based on Experimental Study. Int. J. Eng. 2019, 32, 474–483. [Google Scholar] [CrossRef]
- Nehdi, M.; Omeman, Z.; El-Chabib, H. Optimal efficiency factor in strut-and-tie model for FRP-reinforced concrete short beams with (1.5 < a/d < 2.5). Mater. Struct. 2008, 41, 1713–1727. [Google Scholar] [CrossRef]
- El Maaddawy, T.; Sherif, S. FRP composites for shear strengthening of reinforced concrete deep beams with openings. Compos. Struct. 2009, 89, 60–69. [Google Scholar] [CrossRef]
- Andermatt, M. Concrete Deep Beams Reinforced with Internal FRP. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2010. [Google Scholar]
- Kara, I.F. Prediction of shear strength of FRP-reinforced concrete beams without stirrups based on genetic programming. Adv. Eng. Softw. 2011, 42, 295–304. [Google Scholar] [CrossRef]
- Cho, J.-S.; Kim, M.-S.; Lee, Y.-H.; Kim, H.-C. Experimental Study on Shear Strength of Concrete Deep Beam Reinforced FRP Bars. J. Comput. Struct. Eng. Inst. Korea 2011, 24, 23–31. [Google Scholar]
- El-Sayed, A.K.; El-Salakawy, E.F.; Benmokrane, B. Shear strength of fibre-reinforced polymer reinforced concrete deep beams without web reinforcement. Can. J. Civ. Eng. 2012, 39, 546–555. [Google Scholar] [CrossRef]
- Andermatt, M.F.; Lubell, A.S. Behavior of Concrete Deep Beams Reinforced with Internal Fiber-Reinforced Polymer—Experimental Study. ACI Struct. J. 2013, 110, 585–594. [Google Scholar] [CrossRef]
- Farghaly, A.S.; Benmokrane, B. Shear Behavior of FRP-Reinforced Concrete Deep Beams without Web Reinforcement. J. Compos. Constr. 2013, 17, 04013015. [Google Scholar] [CrossRef]
- Kim, D.-J.; Lee, J.; Lee, Y.H. Effectiveness factor of strut-and-tie model for concrete deep beams reinforced with FRP rebars. Compos. Part B Eng. 2014, 56, 117–125. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, H.; Park, H.; Ahn, N.; Lee, Y.H. Evaluation of shear behavior of deep beams with shear reinforced with GFRP plate. Sci. Iran. Trans. B Mech. Eng. 2015, 22, 2142. [Google Scholar]
- Thomas, J.; Ramadassa, S. Design for shear strength of concrete beams longitudinally reinforced with GFRP bars. Struct. Eng. Mech. 2015, 53, 41–55. [Google Scholar] [CrossRef]
- Mohamed, K.; Farghaly, A.S.; Benmokrane, B. Strut Efficiency-Based Design for Concrete Deep Beams Reinforced with Fiber-Reinforced Polymer Bars. ACI Struct. J. 2016, 113, 791–800. [Google Scholar] [CrossRef]
- Mohamed, K.; Farghaly, A.S.; Benmokrane, B. Effect of Vertical and Horizontal Web Reinforcement on the Strength and Deformation of Concrete Deep Beams Reinforced with GFRP Bars. J. Struct. Eng. 2017, 143, 04017079. [Google Scholar] [CrossRef]
- Nie, J.-G.; Pan, W.-H.; Tao, M.-X.; Zhu, Y.-Z. Experimental and Numerical Investigations of Composite Frames with Innovative Composite Transfer Beams. J. Struct. Eng. 2017, 143, 04017041. [Google Scholar] [CrossRef]
- Abu-Obaida, A.; El-Ariss, B.; El-Maaddawy, T. Behavior of Short-Span Concrete Members Internally Reinforced with Glass Fiber–Reinforced Polymer Bars. J. Compos. Constr. 2018, 22, 04018038. [Google Scholar] [CrossRef]
- Albidah, A.; Abadel, A.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Experimental and analytical study of strengthening schemes for shear deficient RC deep beams. Constr. Build. Mater. 2019, 216, 673–686. [Google Scholar] [CrossRef]
- Gergely, V.; Pop, M.; Campian, C.; Chira, N. Finite element modelling of different strengthening strategies for reinforced concrete deep beams. IOP Conf. Ser. Mater. Sci. Eng. 2019, 586, 012023. [Google Scholar] [CrossRef]
- ATENA; Version 5.6; Červenka Consulting s.r.o.: Prague, Czech Republic, 2020.
- El-Maaddawy, T.A.; Sherif, E.-S.I. Response of Concrete Corbels Reinforced with Internal Steel Rebars and External Composite Sheets: Experimental Testing and Finite Element Modeling. J. Compos. Constr. 2014, 18, 04013020. [Google Scholar] [CrossRef]
- Awani, O.; El-Maaddawy, T.; El Refai, A. Numerical Simulation and Experimental Testing of Concrete Beams Strengthened in Shear with Fabric-Reinforced Cementitious Matrix. J. Compos. Constr. 2016, 20, 04016056. [Google Scholar] [CrossRef]
- Alkhalil, J.; El-Maaddawy, T. Finite element modelling and testing of two-span concrete slab strips strengthened by externally-bonded composites and mechanical anchors. Eng. Struct. 2017, 147, 45–61. [Google Scholar] [CrossRef]
- Nilson, A.H.; Darwin, D.; Dolan, C.W. Design of Concrete Structures, 14th ed.; McGraw Hill: New York, NY, USA, 2010; ISBN 0073293490/9780073293493. [Google Scholar]
- Ibrahim, A.M.; Mahmood, M.S. Finite element modeling of reinforced concrete beams strengthened with FRP laminates. Eur. J. Sci. Res. 2009, 30, 526–541. [Google Scholar]
- Obaidat, Y.T.; Heyden, S.; Dahlblom, O. The effect of CFRP and CFRP/concrete interface models when modelling retrofitted RC beams with FEM. Compos. Struct. 2010, 92, 1391–1398. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).