The ESTPHAD Concept: An Optimised Set of Simplified Equations to Estimate the Equilibrium Liquidus and Solidus Temperatures, Partition Ratios, and Liquidus Slopes for Quick Access to Equilibrium Data in Solidification Software Part II: Ternary Isomorphous Equilibrium Phase Diagram

Abstract

In a previous article, an estimation procedure for calculating the liquidus and solidus lines of binary equilibrium phase diagrams was presented. In this article, keeping the thermodynamic basics, the estimation method for the approximate calculation of the liquidus and solidus surfaces of ternary phase diagrams was further developed. It is shown that the procedure has a hierarchical structure, and the ternary functions contain the binary functions. The applicability of the method is checked by calculating the liquidus and solidus surfaces of the Ag-Au-Pd isomorphous ternary equilibrium phase diagram. The application of each level of the developed four-level procedure depends on the data available and the aim. It is shown that in the case of a concentration range close to the base alloy pure element, the liquidus and solidus surfaces of the ternary equilibrium phase diagram can be calculated from the liquidus and solidus functions of the binary equilibrium phase diagrams with a few K errors, which is 0.2 at% at 10 K/at% slope. The equilibrium phase diagrams were available in graphical form, so the data obtained via digitalisation of the diagrams for the calculations was used. The functions describe the slope of the surfaces, and the approximate method developed for the calculation of the partition ratios is also shown.

1. Introduction

In foundry practice (mould casting, continuous steel, aluminium, and copper casting), simulation software working with finite element processes plays an increasingly important role in the design of technologies (like MAGMA, Inspire Cast, ProCast, and so on). Even in simple cases, dividing the cast into thousands of finite elements, the solid phase fraction, the temperature, and, in many cases, the flow of the melt are calculated as a function of time. The number of time steps is also very large. To perform the calculations, it is necessary to know the equilibrium concentrations of the phases. The most accurate procedure is to use CALPHAD-type software as a subroutine to calculate the concentrations [1,2]. This procedure can be used if the data for the calculation of the given equilibrium phase diagram are contained in the database (someone have already calculated them). Thus, the authors of some of the most recent works have used the CALPHAD calculation of thermodynamic data [3,4,5,6,7,8,9,10]. Several authors have found that this method is not very efficient because, especially in the case of three- or multi-component alloys, the time required for CALPHAD-type calculations is very long, and the concentrations of each finite element must be calculated several times in one time step [4,11,12,13].

In addition, there may be several studies for which the required equilibrium phase diagrams are only available in graphical form.

The solution to this problem is to create a temperature–concentration map with CALPHAD-type software, if the necessary database is available, or by digitising the graphical diagram. If anybody wants to use the maps directly, they need to create a large map (containing a lot of data, e.g., with a resolution of 0.00001% for each alloying element) for sufficient calculation accuracy, the size of which may exceed the size of the computer’s memory. There are two ways to reduce the resolution and then the size of the map:

(i)

Producing the necessary maps with reduced resolution (liquidus and solidus temperatures vs. concentration) and finding the correct temperature with iteration [11,12] (mapping method);

(ii)

Using the data of the maps to create a temperature vs. concentration regression function [13,14,15,16].

In [14], the authors compared the results of three different procedures (direct coupling, mapping method, and regression function) in the simulation of the solidification of a two-dimensional blade-like casting. The total mesh number for half of the casting domain was 1680. The alloy was Al-10.5 wt% Cu-7.5 wt% Si. They showed that the calculated solidification path was practically the same. They found that the calculation results of the three different methods were almost identical, but the computational efficiency was rather different. The computation time of the direct coupling method, the mapping method, and the regression functions was 13,163 s, 226 s, and 147 s, respectively. Thus, the simulation method of direct coupling was much more inefficient than the other two methods, and the calculation time of the regression method was ~65% of the mapping method.

The regression functions for calculating the liquidus temperature and the partition coefficients are a simple polynomial without any thermodynamic background in the case of aluminium alloys [14,17,18,19], steels [20,21,22], ceramics [23], and salts [24].

In an earlier paper [25], we presented a new thermodynamic-based method to calculate the liquidus and solidus temperatures, partition ratio, and slope of the liquidus as a function of the concentration of the alloying element using polynomial (regression) functions. The aim of that work was to develop a simple and fast method usable during the simulation of solidification processes and to shorten the CPU time of the simulation. The method’s usability was demonstrated in the cases of isomorphous-type Ge-Si and eutectic-type Al-Mg and Al-Si binary alloys. The constants of the polynomials were determined through the digitalisation of Ge-Si and by using the ThermoCalc database of Al-Mg and Al-Si equilibrium phase diagrams.

The alloys used in practice usually contain more than two components. (i.e., steels and Al and Cu alloys). The developed method can be extended easily to multicomponent alloys. This paper shows its extension in the ternary alloy system. The method’s usability is demonstrated in the cases of isomorphous-type Ag-Au-Pd ternary alloy systems.

2. The Thermodynamic Basis of the ESTPHAD Formalism in the Case of Ternary Alloys

Similarly to the binary system [25], the free energy of an ideal ternary liquid or solid solution is as follows:

$$G=G_A{X}_A+G_B{X}_B+G_C{X}_C+RT(X_A\mathit{ln}{X}_A+X_B\mathit{ln}{X}_B+X_C\mathit{ln}{X}_C)$$

(1)

The partial molar free enthalpies are as follows:

$${\mu }_A=G_A+R{T}_L\mathit{ln}{X}_A, {\mu }_B=G_B+R{T}_L\mathit{ln}{X}_B,{\mu }_C=G_C+R{T}_L\mathit{ln}{X}_C$$

(2)

In equilibrium

$${\mu }_A^l={\mu }_A^s, {\mu }_B^l={\mu }_B^s, {\mu }_C^l={\mu }_C^s$$

(3)

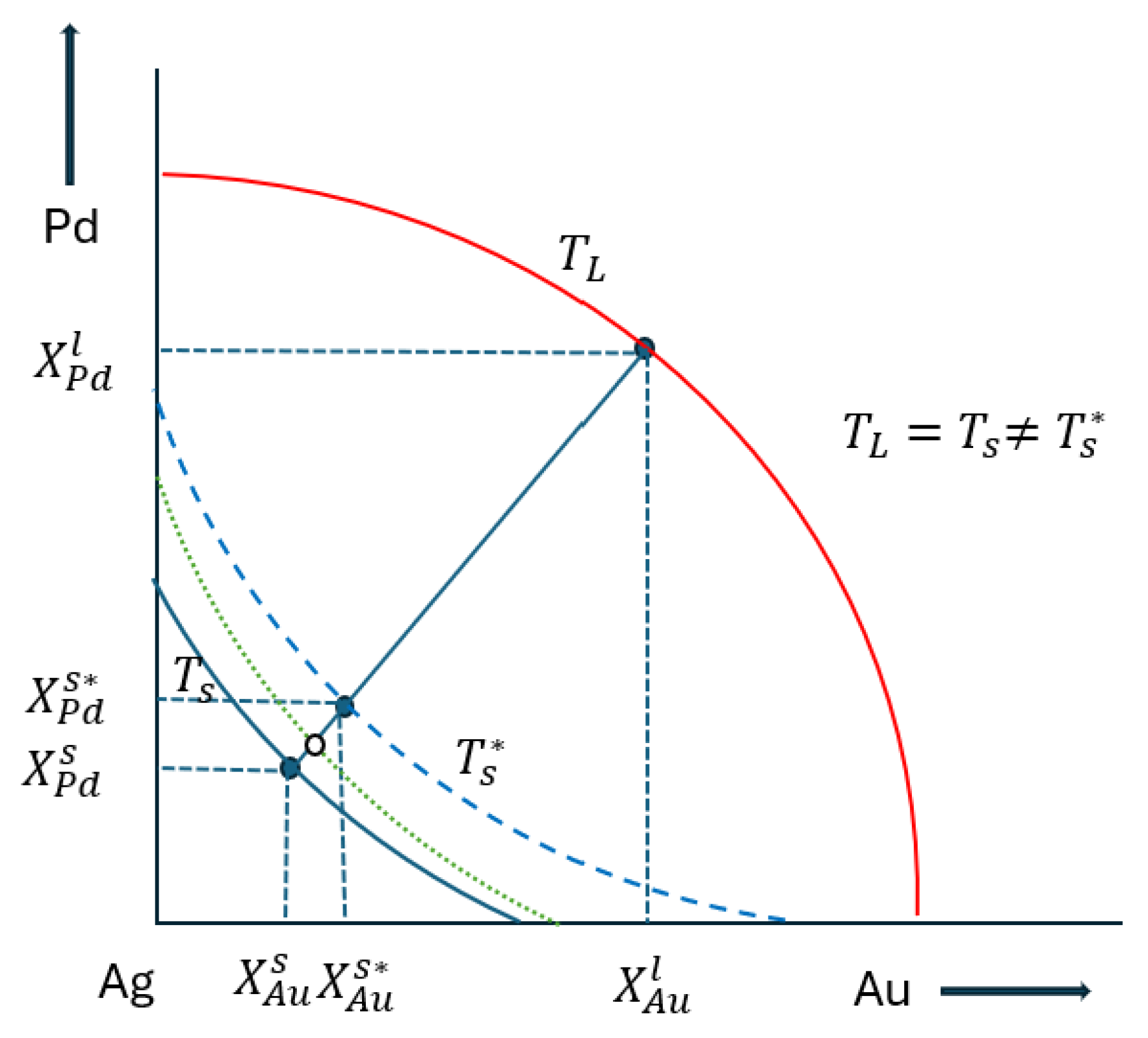
3. Determination of the Liquidus (T_L) and Solidus (T_s) Temperature

3.1. Liquidus Temperature

Based on Equation (3), it can be written as follows:

$$G_A^s+R{T}_L{(X}_B^l,X_C^l)ln{X}_A^s=G_A^l+R{T}_L{(X}_B^l,X_C^l)ln{X}_A^l$$

(4)

$$G_A^s-G_A^l=\mathrm{\Delta }{G}_A^{l\to s}=R{T}_L{(X}_B^l,X_C^l)ln{(X}_A^l/X_A^s)$$

(5)

It follows that

$$\mathrm{\Delta }{G}_A^{l\to s}={\mathrm{\Delta }H}_A^{l\to s}(T_A-T_L{(X}_B^l,X_C^l))/T_A$$

(6)

Using Equations (5) and (6), it can be written as follows:

$${\displaystyle \frac{{\mathrm{\Delta }H}_A^{l\to s}\left(T_A-T_L\right)}{T_A}}=R{T}_L{(X}_B^l,X_C^l)\mathit{ln}\left(X_A^l/X_A^s\right)$$

(7)

$$T_L{(X}_B^l,X_C^l)=T_A/[{\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}\ln \left(X_A^l/X_A^s\right)+1]$$

(8)

We consider that:

$$X_A^l=1-X_B^l-X_C^l , { X}_A^s=1-X_B^s-X_C^s\mathrm{and} X_B^s=k_B{X}_B^l,{X_C^s=k}_C{X}_C^l$$

(9)

$$T_L(X_B^l,X_C^l)=T_A/([{\displaystyle \frac{R{T}_A}{{\mathrm{\Delta }H}_A^{l\to s}}}\left[ln\left(1-X_B^l-X_C^l\right)-ln\left(1-{k_{B}X}_B^l-{k_{C}X}_C^l\right)+1\right])$$

(10)

Used the Taylor series instead of the ln function:

$$T_L\left(X_B^l{,X}_C^l\right)=T_A/[{\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}\{{\sum }_{i=1}^m{\displaystyle \frac{1}{i}}{\left(X_B^l\right)}^i{\left(k_B-1\right)}^i+{\sum }_{i=1}^m{\displaystyle \frac{1}{i}}{\left(X_c^l\right)}^i{\left(k_c-1\right)}^i+{\sum }_{i=1}^{m-1}{\sum }_{j=1}^{m-1}{\left(X_B^l\right)}^i{\left(X_c^l\right)}^j{\displaystyle \frac{1}{i}}({k_B-1)}^i{\displaystyle \frac{1}{j}}({k_C-1)}^j\}+1]$$

(11)

where:

$${\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}\left\{{\sum }_{i=1}^m{\displaystyle \frac{1}{i}}{\left(X_B^l\right)}^i({k_B-1)}^i\right\}={\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}{f}_{AB}^l\left(X_B^l\right)=F_{AB}^l\left(X_B^l\right)$$

(12)

$${\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}\left\{{\sum }_{i=1}^m{\displaystyle \frac{1}{i}}{\left(X_c^l\right)}^i{{(k}_c-1)}^i\right\}={\displaystyle \frac{T_{A}R}{\mathrm{\Delta }{H}_A^{l\to s}}}{f}_{AC}^l\left(X_C^l\right){=F}_{AC}^l\left(X_C^l\right)$$

(13)

came from the A-B and A-C binary equilibrium phase diagram (BEPD).

And:

$${\displaystyle \frac{T_{A}R}{H_A^{l\to s}}}\{{\sum }_{i=1}^{m-1}\sum _{j=1}^{m-1}{\left(X_B^l\right)}^i{\left(X_c^l\right)}^j{\displaystyle \frac{1}{i}}({k_B-1)}^i{\displaystyle \frac{1}{j}}({k_C-1)}^j\}={\displaystyle \frac{T_{A}R}{\mathrm{\Delta }{H}_A^{l\to s}}}{f}_{ABC}^l\left(X_B^l,X_C^l\right)=\mathrm{\Delta }{F}_{ABC}^l\left(X_B^l,X_C^l\right)$$

(14)

came from the A-B-C ternary equilibrium phase diagram (TEPD).

Finally:

$$T_L\left(X_B^l{,X}_C^l\right)=T_A/\left[F_{AB}^l\left(X_B^l\right)+F_{AC}^l\left(X_C^l\right)+\mathrm{\Delta }{F}_{ABC}^l\left(X_B^l,X_C^l\right)+1\right]$$

(15)

where:

$$F_{AB}^l\left(X_B^l\right)=A_{AB}^l(\mathrm{1,0})X_B^l+{A_{AB}^l(\mathrm{2,0})\left(X_B^l\right)}^2+{A_{AB}^l(\mathrm{3,0})\left(X_B^l\right)}^3+$$

(16)

$$F_{AC}^l\left(X_C^l\right)=A_{AC}^l(\mathrm{0,1})X_C^l+{A_{AC}^l(\mathrm{0,2})\left(X_C^l\right)}^2+{A_{AC}^l(\mathrm{0,3})\left(X_C^l\right)}^3+$$

(17)

$${\mathrm{\Delta }F}_{ABC}^l\left(X_B^l,X_C^l\right)=A_{ABC}^l\left(\mathrm{1,1}\right)X_B^l{X}_C^l+A_{ABC}^l\left(\mathrm{1,2}\right)X_B^l{(X_C^l)}^2+A_{ABC}^l\left(\mathrm{2,1}\right){(X_B^l)}^2 X_C^l +$$

(18)

3.2. Solidus Temperature

$$T_s\left({\displaystyle X_B^s}{,X}_C^s\right)=T_A/[{\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}\{{\sum }_{i=1}^m{\displaystyle \frac{1}{i}}{\left(X_B^s\right)}^i{{({\displaystyle \frac{1}{k}}}_B-1)}^i+{\sum }_{i=1}^m{\displaystyle \frac{1}{i}}{\left(X_c^l\right)}^i{{({\displaystyle \frac{1}{k}}}_c-1)}^i+{\sum }_{i=1}^{m-1}{\sum }_{j=1}^{m-1}{X}_B^i{X}_C^j{\displaystyle \frac{1}{i}}(1/{k_B-1)}^i{\displaystyle \frac{1}{j}}(1/{k_C-1)}^i\}]$$

(19)

where:

$${\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}\left\{{\sum }_{i=1}^m{\displaystyle \frac{1}{i}}{\left(X_B^s\right)}^i(1/{k_B-1)}^i\right\}={\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}{f}_{AB}^s\left(X_B^l\right)=F_{AB}^s\left(X_B^s\right)$$

(20)

$${\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}\left\{{\sum }_{i=1}^m{\displaystyle \frac{1}{i}}{\left(X_c^s\right)}^i(1/{k_C-1)}^i\right\}={\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}{f}_{AC}^s\left(X_C^s\right){=F}_{AC}^s\left(X_C^s\right)$$

(21)

came from the BEPD A-B and A-C

And:

$${\displaystyle \frac{T_{A}R}{{\mathrm{\Delta }H}_A^{l\to s}}}\{{\sum }_{i=1}^{m-1}{\sum }_{j=1}^{m-1}{X}_B^i{X}_C^j{\displaystyle \frac{1}{i}}({{{\displaystyle \frac{1}{k}}}_B-1)}^i {\displaystyle \frac{1}{j}}(1/{k_C-1)}^i={\displaystyle \frac{T_{A}R}{\mathrm{\Delta }{H}_A^{l\to s}}}{f}_{ABC}^s\left(X_B^s,X_C^s\right)=\mathrm{\Delta }{F}_{ABC}^s\left(X_B^s,X_C^s\right)$$

(22)

came from the TEPD A-B-C.

Finally:

$$T_s\left(X_B^s{,X}_C^s\right)=T_A/\left[F_{AB}^s\left(X_B^s\right)+F_{AC}^s\left(X_C^s\right)+{\mathrm{\Delta }F}_{ABC}^s\left(X_B^s,X_C^s\right)+1\right]$$

(23)

where:

$$F_{AB}^s\left(X_B^s\right)=A_{AB}^s(\mathrm{1,0})X_B^s+{A_{AB}^s(\mathrm{2,0})\left(X_B^s\right)}^2+{A_{AB}^s(\mathrm{3,0})\left(X_B^s\right)}^3+\dots$$

(24)

$$F_{AC}^s\left(X_C^s\right)=A_{AC}^s(\mathrm{0,1})X_C^s+{A_{AC}^s(\mathrm{0,2})\left(X_C^s\right)}^2+{A_{AC}^s(\mathrm{0,3})\left(X_C^s\right)}^3+\dots$$

(25)

$${\mathrm{\Delta }F}_{ABC}^s\left(X_B^s,X_C^s\right)=A_{ABC}^s\left(\mathrm{1,1}\right)X_B^s{X}_C^s+A_{ABC}^s\left(\mathrm{1,2}\right)X_B^s{{(X}_C^s)}^2+A_{ABC}^s\left(\mathrm{2,1}\right){(X_B^s)}^2 X_C^s +\dots$$

(26)

The constants of Equations (16)–(18) and (24)–(26) are calculable if the alloy is ideal, and the partition ratios k_B and k_C are known as a function of the T_L and T_s temperatures, or they are constant. In the other cases, the k_B and k_C obtained from the BEPD can be used as the initial data for the iteration.

In the practical case, the constants can be determined from the $T_L\left(X_B^l,X_C^l\right)$ and $T_s\left(X_B^s,X_C^s\right)$ dataset given by a Calphad-type calculation or digitalisation of the liquidus and solidus surfaces.

4. Determination of the Partition Ratios

4.1. $k_B^{ABC}$ as a Function of Liquidus Concentrations $(X_B^l,X_C^l)$

$$G_B^s-G_B^l=\mathrm{\Delta }{G}_B^{l\to s}=R{T}_L(X_B^l{,X}_C^l)ln{(X}_B^l/X_B^s)=R{T}_L(X_B^l{,X}_C^l)ln{\displaystyle \frac{1}{k_B^{ABC}}}(X_B^l{,X}_C^l)$$

(27)

$$\mathrm{\Delta }{G}_B^{l\to s}={\mathrm{\Delta }H}_B^{l\to s}(T_B-T_L\left(X_B^l{,X}_C^l\right))/T_B=R{T}_L(X_A^l{,X}_C^l)ln{\displaystyle \frac{1}{k_B^{ABC}}}(X_B^l{,X}_C^l)$$

(28)

$${ln{\displaystyle \frac{1}{k_B^{ABC}}}(X_B^l{,X}_C^l)=\mathrm{\Delta }H}_B^{l\to s}(T_B-T_L{(X}_B^l{,X}_C^l))/{RT}_B{T}_L(X_B^l{,X}_C^l)$$

(29)

Using Equation (15) and considering that:

$$ln{\displaystyle \frac{1}{k_B^{ABC}}}=-ln{k}_B^{ABC}$$

$${{lnk}_B^{ABC}(X_B^l,X_C^l)=(\mathrm{\Delta }H}_B^{l\to s}/{R)[{1/T}_B-(1+F_{AB}^l(X_A^l)+F_{AC}^l(X_C^l)+{\mathrm{\Delta }F}_{ABC}^l\left(X_A^l,X_C^l\right))/T}_A]$$

(30)

where:

$${{lnk}_B^{AB}(X_B^l)=(\mathrm{\Delta }H}_B^{l\to s}/{R)[1/T_B-1/T_A+F_{AB}^l(X_B^l)/T}_A]$$

(31)

If X_B = X_C = 0

$${{lnk}_{B,0}^{ABC}(X_B^l,X_C^l)=(\mathrm{\Delta }H}_B^{l\to s}/R)[1/T_B-1/T_A]$$

(32)

$${{lnk}_B^{ABC}(X_B^l,X_C^l)=(\mathrm{\Delta }H}_B^{l\to s}/{R)[F_{AC}^l(X_C^l)+{\mathrm{\Delta }F}_{ABC}^l\left(X_A^l,X_C^l\right))/T}_A]$$

(33)

Finally:

$${lnk}_B^{ABC}\left(X_A^l,X_C^l\right)=ln{k}_B^{AB}\left(X_B^l\right)+\mathrm{\Delta }ln{k}_B^{ABC}(X_B^l,X_C^l)$$

(34)

where:

$$ln{k}_B^{AB}(X_A^l)=B_{AB}^l\left(\mathrm{0,0}\right)+B_{AB}^l\left(\mathrm{1,0}\right){{(X}_B^l)}^1+B_{AB}^l\left(\mathrm{2,0}\right){{(X}_A^l)}^2+B_{AB}^l\left(\mathrm{3,0}\right){{(X}_B^l)}^3+\dots$$

$$\begin{gathered} \mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^l,X_C^l\right)=B_{ABC}^l(\mathrm{0,1}){\left(X_B^l\right)}^0{X}_C^l+B_{ABC}^l(\mathrm{0,2}){\left(X_B^l\right)}^0{\left(X_C^l\right)}^2+B_{ABC}^l(\mathrm{0,3}){\left(X_B^l\right)}^0{\left(X_C^l\right)}^3+...+B_{ABC}^l(\mathrm{1,1})X_A^l{X}_C^l+B_{ABC}^l(\mathrm{2,1}){\left(X_B^l\right)}^2{X}_C^l \\ +B_{BCB}^l(\mathrm{1,2})X_B^l{\left(X_C^l\right)}^2+... \end{gathered}$$

(35)

And

$$k_B^{ABC}(X_B^l,X_C^l)=\mathrm{e}\mathrm{x}\mathrm{p}(ln{k}_B^{AB}(X_B^l)+\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^l,X_C^l\right))$$

(36)

4.2. $k_B^{ABC}$ as a Function of Solidus Concentrations $(X_B^s,X_C^s)$

$${lnk}_B^{ABC}(X_B^s,X_C^s)=ln{k}_B^{AB}(X_B^s)+\mathrm{\Delta }ln{k}_B^{ABC}(X_B^s,X_C^s)$$

(37)

where:

$$ln{k}_B^{ABC}(X_B^s{,X}_C^s)=B_{AB}^s\left(\mathrm{0,0}\right)+B_{AB}^s\left(\mathrm{1,0}\right){{(X}_B^s)}^1+B_{AB}^s\left(\mathrm{2,0}\right){{(X}_B^s)}^2+B_{AB}^s\left(\mathrm{3,0}\right){{(X}_B^s)}^3\dots$$

(38)

$$\begin{gathered} \mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^s,X_C^s\right)=B_{ABC}^s(\mathrm{0,1}){\left(X_B^s\right)}^0{X}_C^s+B_{ABC}^s(\mathrm{0,2}){\left(X_B^s\right)}^0{\left(X_C^s\right)}^2+B_{ABC}^s(\mathrm{0,3}){\left(X_B^s\right)}^0{\left(X_C^s\right)}^3+...+B_{ABC}^s(\mathrm{1,1})X_B^s{X}_C^s \\ +B_{ABC}^s(\mathrm{2,1}){\left(X_B^s\right)}^2{X}_C^s+B_{ABC}^s(\mathrm{1,2})X_B^s{\left(X_C^s\right)}^2+... \end{gathered}$$

(39)

And

$$k_B^{ABC}(X_B^s,X_C^s)=\mathrm{e}\mathrm{x}\mathrm{p}(ln{k}_B^{AB}(X_B^s)+\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^s,X_C^s\right))$$

(40)

The structure of the constants is the same as for the $ln{k}_B^{ABC}(X_B^l,X_C^l)$.

4.3. $k_C^{ABC}$ as a Function of Liquidus Concentration $(X_B^l,X_C^l)$

$${lnk}_C^{ABC}(X_B^l,X_C^l)=ln{k}_C^{AC}(X_C^l)+\mathrm{\Delta }ln{k}_C^{ABC}{(X}_B^l,X_C^l)$$

(41)

where:

$$ln{k}_C^{AC}(X_B^l{,X}_C^l)=C_{AC}^l\left(\mathrm{0,0}\right)+C_{AC}^l\left(\mathrm{1,0}\right){{(X}_C^l)}^1+C_{AC}^l\left(\mathrm{2,0}\right){{(X}_C^l)}^2+C_{AC}^l\left(\mathrm{3,0}\right){{(X}_C^l)}^3+\dots$$

(42)

$$\begin{gathered} ln{k}_C^{ABC}\left(X_B^l,X_C^l\right)=C_{ABC}^l\left(\mathrm{0,1}\right)X_B^l{{(X}_C^l)}^0+{{C_{ABC}^l(\mathrm{0,2})(X}_B^l)}^2{{(X}_C^l)}^0+ \\ +C_{ABC}^l\left(\mathrm{0,3}\right){{(X}_B^l)}^3{{(X}_C^l)}^0+..C_{ABC}^l{\left(\mathrm{1,1}\right)X}_B^l{X}_C^l{+C}_{ABC}^l{{(\mathrm{1,2})(X}_B^l)}^2{X}_C^l{+C}_{ABC}^l(\mathrm{2,1}){{(X}_C^l)}^2{X}_B^l+\dots \end{gathered}$$

(43)

$$k_C^{ABC}(X_B^l,X_C^l)=\mathrm{e}\mathrm{x}\mathrm{p}(ln{k}_C^{AC}(X_C^l)+\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^l,X_C^l\right))$$

(44)

4.4. $k_C^{ABC}$ as a Function of Solidus Concentration $(X_B^s,X_C^s)$

$${lnk}_C^{ABC}(X_B^s,X_C^s)=ln{k}_C^{AC}(X_C^s)+\mathrm{\Delta }ln{k}_C^{ABC}(X_B^s,X_C^s)$$

(45)

where:

$$ln{k}_C^{AC}(X_B^s{,X}_C^s)=C_{AC}^s\left(\mathrm{0,0}\right)+C_{AC}^s\left(\mathrm{0,1}\right){{(X}_C^s)}^1+C_{AC}^l\left(\mathrm{0,2}\right){{(X}_C^s)}^2+C_{AC}^s\left(\mathrm{0,3}\right){{(X}_C^s)}^3\dots$$

(46)

$$\begin{gathered} \mathrm{\Delta }ln{k}_C^{ABC}\left(X_B^s,X_C^s\right)=C_{ABC}^s\left(\mathrm{1,0}\right)X_B^S{{(X}_C^s)}^0+{{C_{ABC}^S(\mathrm{2,0})(X}_B^s)}^2{{(X}_C^s)}^0+ \\ +C_{ABC}^s\left(\mathrm{3,0}\right){{(X}_B^s)}^3{{(X}_C^s)}^0+...+C_{ABC}^s{\left(\mathrm{1,1}\right)X}_B^s{X}_C^s{+C}_{ABC}^s{{(\mathrm{2,1})(X}_B^s)}^2{X}_C^s{+C}_{ABC}^s(\mathrm{1,2}){{X_B^s(X}_C^s)}^2+\dots \end{gathered}$$

(47)

$$k_C^{ABC}(X_B^s,X_C^s)=\mathrm{e}\mathrm{x}\mathrm{p}(ln{k}_C^{AC}(X_C^s)+\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^s,X_C^s\right))$$

(48)

Similarly to the liquidus and solidus temperature, in the case of ideal alloy, the lnk functions are calculable if the F_AB, F_AC, and ΔF_ABC functions are known. In the practical case, the constants can be determined from the $T_L\left(X_B^l,X_C^l\right)$ and $T_s\left(X_B^s,X_C^s\right)$ dataset given by a Calphad-type calculation or digitalisation of the liquidus and solidus surfaces.

5. Determination of the Constants of Liquidus Slopes

In this case, two independent slopes exist:

$$M_{ABC}^B\left(X_B^l,X_C^l=const\right)={\displaystyle \frac{\partial T_L}{\partial X_B^l}}=={\displaystyle \frac{T_A\frac{\partial (1+F_{AB}^l\left(X_B^l\right)+{\mathrm{\Delta }F}_{ABC}^l\left(X_{B,C}^l\right))}{\partial X_B^l}}{{(1+F_{ABC}^l\left(X_B^l,X_C^l\right))}^2}}={\displaystyle \frac{T_A{S}_{ABC}^B\left(X_B^l,X_C^l=const\right)}{{(1+F_{ABC}^l\left(X_B^l,X_C^l\right))}^2}}$$

(49)

In the case of BEPD:

$$M_{AB}^B\left(X_B^l\right)={\displaystyle \frac{\partial T_L}{\partial X_B^l}}={\displaystyle \frac{T_A\frac{\partial (1+F_{AB}^l\left(X_B^l\right))}{\partial X_B^l}}{{(1+F_{AB}^l\left(X_B^l\right))}^2}}={\displaystyle \frac{T_A{S}_{AB}^B\left(X_B^l\right)}{{(1+F_{AB}^l\left(X_B^l\right))}^2}}$$

(50)

$$M_{ABC}^C\left(X_B^l=const,X_C^l\right)={\displaystyle \frac{\partial T_L}{\partial X_C^l}}={\displaystyle \frac{T_A\frac{\partial (1+F_{AC}^l\left(X_B^l\right)+{\mathrm{\Delta }F}_{ABC}^l\left(X_{B,C}^l\right))}{\partial X_C^l}}{{(1+F_{ABC}^l\left(X_B^l,X_C^l\right))}^2}}={\displaystyle \frac{T_A{S}_{ABC}^C\left(X_B^l=const,X_C^l\right)}{{(1+F_{ABC}^l\left(X_B^l,X_C^l\right))}^2}}$$

(51)

6. Calculation Methods of the Constants

6.1. Calculation of the Constants of Liquidus and Solidus Functions

To calculate the constants, a database from a CALPHAD-type calculation or the digitisation of the lines of BEPD and TEPD can be used.

6.1.1. First Estimation (Only the A-B and A-C BEPD Are Known)

Calculation of the $F_{AB}^l\left(X_B^l\right),F_{AC}^l\left(X_C^l\right)$ and $F_{AB}^s\left(X_B^s\right),F_{AC}^s\left(X_C^s\right)$ maps:

$$F_{AB}^l\left(X_B^l\right)={\displaystyle \frac{T_A}{T_{AB}^l(X_B^l)}}-1 \mathrm{and} F_{AB}^s\left(X_B^s\right)={\displaystyle \frac{T_A}{T_{AB}^s(X_B^s)}}-1$$

(52)

and

$$F_{AC}^s\left(X_C^s\right)={\displaystyle \frac{T_A}{T_{AC}^s(X_C^s)}}-1 \mathrm{and} F_{AC}^s\left(X_B^s\right)={\displaystyle \frac{T_A}{T_{AC}^s(X_C^s)}}-1$$

(53)

Using these two maps, the constant of the ${\mathit{F}}_{\mathit{A}\mathit{B}}^{\mathit{l}}\left(X_B^l\right), {\mathit{F}}_{\mathit{A}\mathit{C}}^{\mathit{l}}\left(X_C^l\right)$ and ${\mathit{F}}_{\mathit{A}\mathit{B}}^{\mathit{s}}\left(X_B^s\right),{\mathit{F}}_{\mathit{A}\mathit{C}}^{\mathit{s}}\left(X_C^s\right)$ functions are calculable by regression. Knowing the liquidus and solidus functions of BEPDs, the liquidus and solidus temperatures of the ABC TEPD can be calculated, assuming that the effect of the two alloys in the liquid and solid phases are negligible, i.e., $∆{\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{l}}\left(X_B^l,X_C^l\right)=0 \mathrm{a}\mathrm{n}\mathrm{d} ∆{\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{s}}\left(X_B^s,X_C^s\right)=0.$

Then:

$${\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{l}}\left(X_B^l{,X}_C^l\right)={\mathit{F}}_{\mathit{A}\mathit{B}}^{\mathit{l}}\left(X_B^l\right)+{\mathit{F}}_{\mathit{A}\mathit{C}}^{\mathit{l}}\left(X_C^l\right) \mathrm{and} {\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{s}}\left(X_B^s{,X}_C^s\right)={\mathit{F}}_{\mathit{A}\mathit{B}}^{\mathit{s}}\left(X_B^s\right)+{\mathit{F}}_{\mathit{A}\mathit{C}}^{\mathit{s}}\left(X_C^s\right)$$

(54)

6.1.2. Second Estimation (The A-B, A-C and B-C BEPD Are Known)

If the third B-C BEPD, which does not contain the base element, is known, then its data can be used to calculate the constants of the function $∆{\mathit{F}}_{ABC}^s\left(X_B^s,X_C^s\right)$.

6.1.3. Third Estimation (The A-B and A-C BEPD and the Data of the Liquidus and Solidus Surfaces of the TEPD Are Known, the B-C BEPD Is Unknown)

If that the effect of the two alloys in the liquid and solid phases is not negligible, considering the temperature for all known concentrations in the TEPD, except for the B-C BEPD data:

$$F_{ABC}^l\left(X_B^l,X_C^l\right)={\displaystyle \frac{T_A}{T_{ABC}^l}}-1\mathrm{and} F_{ABC}^s\left(X_B^s\right)={\displaystyle \frac{T_A}{T_{ABC}^s}}-1$$

(55)

Since the liquidus and solidus temperature of the TEPD are also affected by BEPDs (see the first estimation), the effect resulting from the interaction between the two alloys is the difference in the two effects:

$$∆F_{ABC}^l\left(X_B^l,X_C^l\right)=F_{ABC}^l\left(X_B^l{,X}_C^l\right)-F_{AB}^l\left(X_B^l\right)-F_{AC}^l\left(X_C^l\right)$$

(56)

$$∆F_{ABC}^s\left(X_B^s,X_C^s\right)=F_{ABC}^l\left(X_B^s{,X}_C^s\right)-F_{AB}^s\left(X_B^s\right)-F_{AC}^s\left(X_C^s\right)$$

(57)

From these two maps, the constants of the $∆{\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{l}}\left(X_B^l,X_C^l\right)$ and $∆{\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{s}}\left(X_B^s,X_C^s\right)$ functions can be determine by regression.

Finally:

$${\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{l}}\left(X_B^l,X_C^l\right)={\mathit{F}}_{\mathit{A}\mathit{B}}^{\mathit{l}}\left(X_B^l\right)+{\mathit{F}}_{\mathit{A}\mathit{C}}^{\mathit{l}}\left(X_C^l\right)+{∆\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{l}}\left(X_B^l{,X}_C^l\right)$$

(58)

$${\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{s}}\left(X_B^s,X_C^s\right)={\mathit{F}}_{\mathit{A}\mathit{B}}^{\mathit{s}}\left(X_B^s\right)+{\mathit{F}}_{\mathit{A}\mathit{C}}^{\mathit{s}}\left(X_C^s\right)+{∆\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{s}}\left(X_B^s{,X}_C^s\right)$$

(59)

6.1.4. Fourth Estimation (The A-B, A-C, B-C BEPD and the Data of the Liquidus and Solidus Surface of the TEPD Are Known)

Upon the calculation of the constants of ${\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{l}}\left(X_B^l,X_C^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{s}}\left(X_B^s,X_C^s\right)$ functions, we also take into account the data of the BC BEPD in order to calculate the liquidus and solidus temperatures of the BC BEPD as accurately as possible from the ${\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{l}}\left(X_B^l,X_C^l\right) {\mathrm{a}\mathrm{n}\mathrm{d} \mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{s}}\left(X_B^s,X_C^s\right)$ functions.

6.1.5. Determination of the Liquidus and Solidus Isotherms Using an Iteration Method

Keeping the concentration of one element constant (e.g., X_B), the concentration of the other element (e.g., X_C) was increased by 0.001 at% step until the temperature calculated with the two concentrations reached the temperature of the selected isotherm.

6.2. Calculation of the Constants of the Partition Ratio

There are two different possibilities: the tie lines are known or unknown in the TEPD.

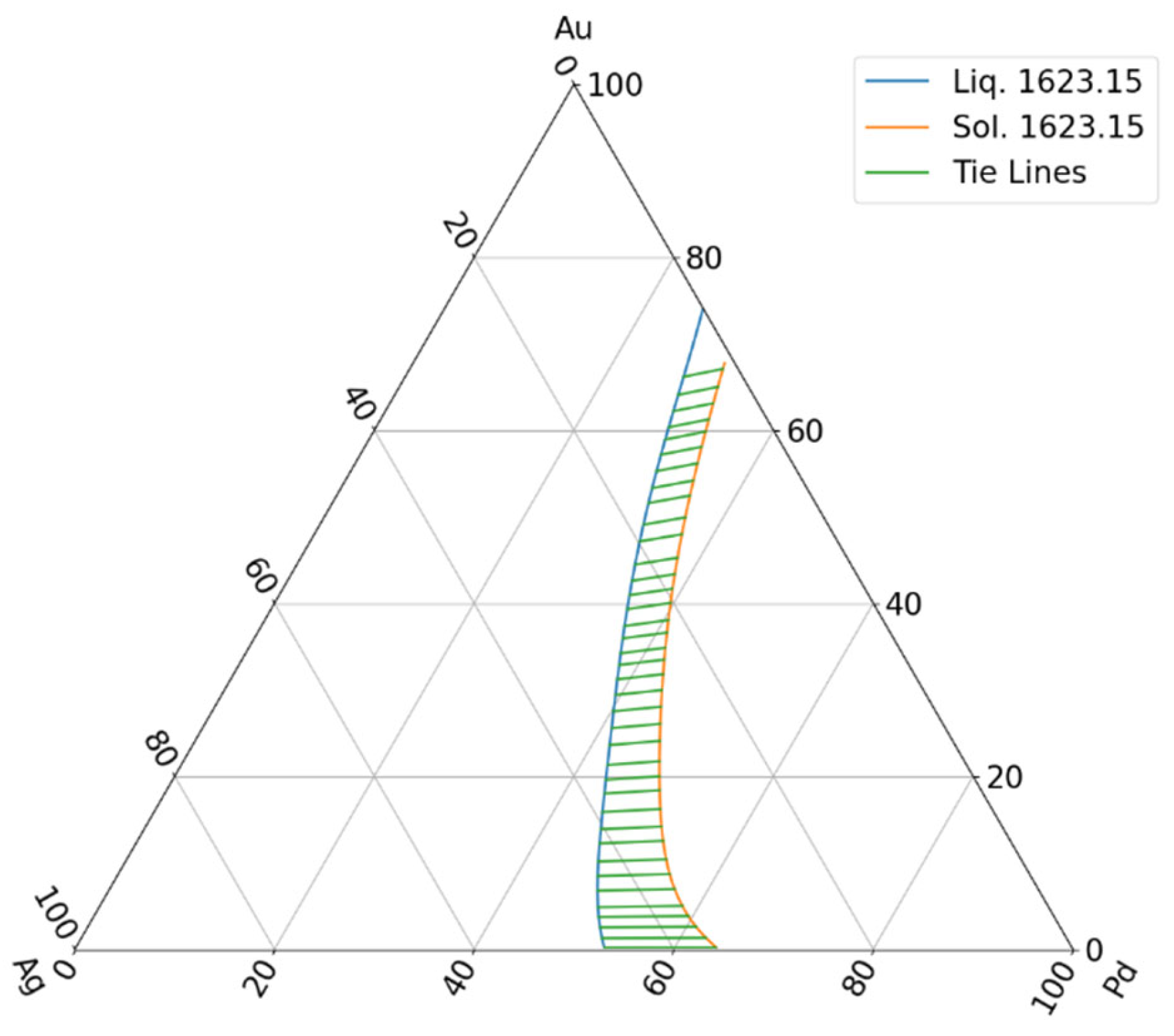
6.2.1. The Tie Lines (The Liquidus and Solidus Concentration Pairs) in TEPD Are Known from the CALPHAD-Type Calculation

First step

Calculation of the $ln{k}_B^{AB}\left(X_B^l\right),$ $ln{k}_B^{AB}(X_B^s)$ and $ln{k}_C^{AC}\left(X_C^l\right),$ $ln{k}_C^{AC}(X_C^s)$ maps from the calculated ${k_B^{AB}=X}_B^s/X_B^l$ and ${k_C^{AC}=X}_C^s,X_C^l$ maps using CALPHAD-type software or digitalised binary equilibrium phase diagrams. From these maps, the constants of the $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}\left(X_B^l\right),$ $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}(X_B^s)$ and $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{C}}\left(X_C^l\right),$ $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{C}}(X_C^s)$ functions can be determined by regression (see [18]).

Second step

Calculation of $ln{k}_B^{ABC}\left(X_B^l,X_C^l\right),$ $ln{k}_B^{ABC}\left(X_B^s,X_C^s\right),$ and $ln{k}_C^{ABC}\left(X_B^l,X_C^l\right),$ $ln{k}_C^{ABC}(X_B^s,X_C^s)$ maps from ${k_B^{ABC}=X}_B^s/X_B^l$ and ${k_C^{ABC}=X}_C^s/X_C^l$ maps.

Third step

Calculation of $\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^l,X_C^l\right),$ $\mathrm{\Delta }ln{k}_B^{ABC}(X_B^s,X_C^s)$ and $\mathrm{\Delta }ln{k}_C^{ABC}(X_B^l,X_C^l)$, $\mathrm{\Delta }ln{k}_C^{ABC}\left(X_B^s,X_C^s\right)$ maps from the ternary part of the liquidus and solidus concentration.

$$\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^l,X_C^l\right)=ln{k}_B^{ABC}\left(X_B^l,X_C^l\right)-ln{k}_B^{AB}\left(X_B^l\right)$$

(60)

$$\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^s,X_C^s\right)=ln{k}_B^{ABC}\left(X_B^s,X_C^s\right)-ln{k}_B^{AB}(X_B^s)$$

(61)

$$\mathrm{\Delta }ln{k}_C^{ABC}\left(X_B^l,X_C^l\right)=ln{k}_C^{ABC}(X_B^l,X_C^l)-ln{k}_C^{AC}\left(X_C^l\right)$$

(62)

$$\mathrm{\Delta }ln{k}_C^{ABC}\left(X_B^s,X_C^s\right)=ln{k}_C^{ABC}\left(X_B^s,X_C^s\right)-ln{k}_C^{AC}(X_C^s)$$

(63)

Fourth step

Calculation from these four maps of the constants of the $\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right),$ $\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}(X_B^s,X_B^s)$ and $\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right),$ $\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}(X_B^s,X_C^s)$ functions by regression.

Finally:

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)=\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)+\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}\left(X_B^l\right)$$

(64)

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)=\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)+\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}(X_B^s)$$

(65)

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)=\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)+\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{C}}\left(X_C^l\right)$$

(66)

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)=\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)+\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{C}}(X_C^s)$$

(67)

6.2.2. If the Tie Lines (Liquidus and Solidus Concentration Pairs) Are Unknown, the T_L and T_s Temperatures Are Determined at Many Concentrations Through Digitalisation of the Liquidus and Solidus Isotherms, and Another Method Must Be Followed

First step

Calculation of the $ln{k}_B^{AB}\left(X_B^l\right),$ $ln{k}_B^{AB}(X_B^s)$ and $ln{k}_C^{AC}\left(X_C^l\right),$ $ln{k}_C^{AC}(X_C^s)$ maps from the calculated ${k_B^{AB}=X}_B^s/X_B^l$ and ${k_C^{AC}=X}_C^s/X_C^l$ maps calculated through digitalised BEPDs. From these maps, the constants of the $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}\left(X_B^l\right),$ $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}(X_B^s)$ and $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{C}}\left(X_C^l\right),$ $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{C}}(X_C^s)$ functions can be determined by regression (see [18]).

Second step:

Using these functions, calculate the solid-phase concentrations ($X_B^s, X_C^s$) from the liquid-phase concentrations $(X_B^l,X_C^l)$ along the calculated liquidus isotherms (first estimation)

Third step

Usually, the ($X_B^s, X_C^s$) concentrations are not on the same calculated solidus isotherm, with an iteration method being used to search for the valid solid-phase concentration ($X_B^{s*}, X_C^{s*}$) on the solidus isotherm.

Using the map of the valid solid-phase concentrations ($X_B^{s*}, X_C^{s*}$), calculate the $ln{k}_B^{ABC}\left(X_B^l,X_C^l\right),$ $ln{k}_B^{ABC}\left(X_B^s,X_C^s\right),$ and $ln{k}_C^{ABC}\left(X_B^l,X_C^l\right),$ $ln{k}_C^{ABC}(X_B^s,X_C^s)$ maps from ${k_B^{ABC}=X}_B^{s*}/X_B^l$ and ${k_C^{ABC}=X}_C^{s*}/X_C^l$ maps.

Fourth step

Calculation of the $\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^l,X_C^l\right)$, $\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^s,X_C^s\right)$ and $\mathrm{\Delta }ln{k}_C^{ABC}\left(X_B^l,X_C^l\right)$, $\mathrm{\Delta }ln{k}_C^{ABC}\left(X_B^s,X_C^s\right)$ maps

$$\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^l,X_C^l\right)=ln{k}_B^{ABC}\left(X_B^l,X_C^l\right)-ln{k}_B^{AB}\left(X_B^l\right)$$

(68)

$$\mathrm{\Delta }ln{k}_B^{ABC}\left(X_B^s,X_C^s\right)=ln{k}_B^{ABC}\left(X_B^s,X_C^s\right)-ln{k}_B^{AB}\left(X_B^s\right)$$

(69)

and

$$\mathrm{\Delta }ln{k}_C^{ABC}\left(X_B^l,X_C^l\right)=ln{k}_C^{ABC}\left(X_B^l,X_C^l\right)-ln{k}_C^{AC}\left(X_C^l\right)$$

(70)

$$\mathrm{\Delta }ln{k}_C^{ABC}\left(X_B^s,X_C^s\right)=ln{k}_C^{ABC}\left(X_B^s,X_C^s\right)-ln{k}_C^{AC}\left(X_C^s\right)$$

(71)

Fifth step

From the above four maps, calculate the constants of the $\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)$, $\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)$ and $\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)$, $\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)$ functions.

Finally:

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)=\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)+\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}\left(X_B^l\right)$$

(72)

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)=\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)+\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}\left(X_B^s\right)$$

(73)

and

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)=\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^l,X_C^l\right)+\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{C}}\left(X_C^l\right)$$

(74)

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)=\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{B}\mathit{C}}\left(X_B^s,X_C^s\right)+\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{C}}^{\mathit{A}\mathit{C}}\left(X_C^s\right)$$

(75)

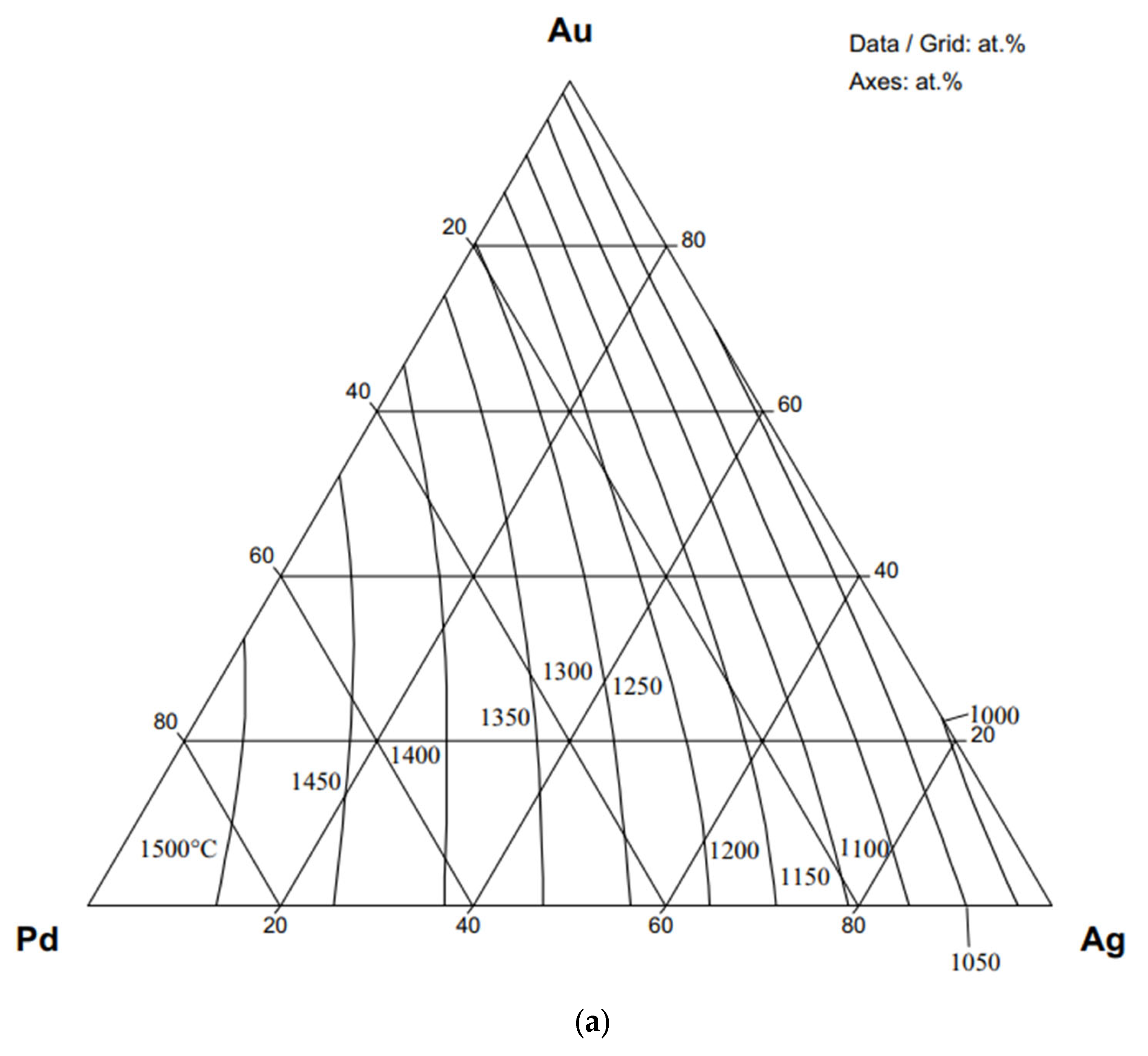
7. An Example for Calculating the Liquidus and Solidus Surfaces, Partition Coefficients, and Slope of the Liquidus Surface of an Isomorphous Ternary Equilibrium Phase Diagram (TEPD)

There are several A-B-C TEPDs, in which case, the BEPDs A-B, B-C, and A-C are isomorphous and then the A-B-C TEPDs are also isomorphous. α(A-B-C) is a solid solution phase of a ternary solid solution in which A, B, and C are completely soluble in each other in both the molten and the solid state. In particular, there are many such TEPDs among alloys of so-called noble metals (including Cu and Ni) (e.g., Au-Ag-Pd, Au-Cu-Pd, Au-Ni-Pd, Au-Pd-Pt, Pd-Pt-Cu, Ni-Pd-Cu, and Ni-Pt-Cu) and many others like Cr-Ti-V, Ti-Mo-Cr, Mo-Cr-V, Ti-Mo-V, and so on. The AuAgPd TEPD was chosen to demonstrate the possibility of using the calculation method.

Ag-Au-Pd alloys have many important applications, like jewellery, as a catalyst in the chemical industry, and as a dental alloy, because of their high corrosion resistance and biocompatibility [26,27,28].

7.1. Data for Calculation

As shown in the theoretical part (Equations (15) and (23)), the ESTPHAD method has a hierarchical structure, using the functions of two-component equilibrium phase diagrams to calculate the liquidus and solidus surfaces of three-component equilibrium phase diagrams. To perform the calculations, the phase diagrams of both BEPDs (Figure 1) [29] and the TEPDs (Figure 2) [30] were only available graphically, so the data were determined through digitalisation. In the case of BEPDs, the concentration of the liquidus and solidus was determined at every 1 at% between the melting points of the two elements. The Ag and Au concentration data of the liquidus and solidus isotherms of the TEPDs were determined step by step, changing the Pd concentration by ~1 at%. The isotherms were included in the diagrams in 50 K steps.

7.2. Calculation of the Liquidus and Solidus Temperatures, Liquidus Slopes, and Partition Ratios of BEPDs

7.2.1. Calculation of the Functions of the Liquidus and Solidus Temperatures of the BEPDs

In the case of the TEPDs, Ag, Au, and Pd can all be the “A” elements (see Equations (15) and (23)). Therefore, for the BEPDs of Ag-Au, Au-Ag, Ag-Pd, Pd-Ag, Pd-Au, and Au-Pd, it is necessary to know the ${\mathit{F}}_{\mathit{A}\mathit{B}}^{\mathit{l}}\left(X_B^l\right) ,{\mathit{F}}_{\mathit{A}\mathit{B}}^{\mathit{s}}\left(X_B^s\right)$ and ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{B}}^{\mathit{l}}\left(X_B^l\right), {\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{B}}^{\mathit{s}}\left(X_{AB}^s\right)$ functions. Using the data from the digitalised BEPDs, the constants of the functions were determined through regression analysis (

Table 1. Constants of the liquidus of the BEPDs (R² > 0.98).

BEPD	${({\mathit{X}}^{\mathit{l}})}^1$	${({\mathit{X}}^{\mathit{l}})}^2$	${({\mathit{X}}^{\mathit{l}})}^3$	${({\mathit{X}}^{\mathit{l}})}^4$	${({\mathit{X}}^{\mathit{l}})}^5$	${({\mathit{X}}^{\mathit{l}})}^6$	${({\mathit{X}}^{\mathit{l}})}^7$
${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}}\right)$	−0.001525122	9.83954E-06	−2.21084E-08
${\mathit{F}}_{\mathit{A}\mathit{u}\mathit{A}\mathit{g}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{A}\mathit{g}}^{\mathit{l}}\right)$	0.000275973	2.66952E-06	2.89592E-08
${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}}\right)$	−0.009145785	0.000216506	−5.02079E-06	7.36011E-08	−5.53729E-10	1.62381E-12
${\mathit{F}}_{\mathit{P}\mathit{d}\mathit{A}\mathit{g}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{A}\mathit{g}}^{\mathit{l}}\right)$	0.002466234	1.93529E-05	−1.71905E-06	5.15282E-08	−5.63012E-10	2.23671E-12
${\mathit{F}}_{\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}}\right)$	−0.015142951	0.0006576	−2.04085E-05	3.81869E-07	−4.01939E-09	2.1859E-11	−4.77362E-14
${\mathit{F}}_{\mathit{P}\mathit{d}\mathit{A}\mathit{u}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}}\right)$	0.000887203	3.54004E-05	−1.3818E-06	−6.83248E-09	9.61336E-10	−1.34325E-11	5.80735E-14

,

Table 2. Constants of the solidus of the BEPDs (R² > 0.98).

BEPD	${({\mathit{X}}^{\mathit{s}})}^1$	${({\mathit{X}}^{\mathit{s}})}^2$	${({\mathit{X}}^{\mathit{s}})}^3$	${({\mathit{X}}^{\mathit{s}})}^4$	${({\mathit{X}}^{\mathit{s}})}^5$	${({\mathit{X}}^{\mathit{s}})}^6$	${({\mathit{X}}^{\mathit{s}})}^7$	${({\mathit{X}}^{\mathit{s}})}^8$
${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{s}}\left({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}}\right)$	−0.001470912	9.08706E-06	−2.02095E-08
${\mathit{F}}_{\mathit{A}\mathit{u}\mathit{A}\mathit{g}}^{\mathit{s}}\left({\mathit{X}}_{\mathit{A}\mathit{g}}^{\mathit{s}}\right)$	0.000296244	3.02225E-06	2.30809E-08
${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{s}}\left({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}}\right)$	−0.005863031	5.10683E-05	−1.02889E-06	2.45832E-08	−2.57412E-10	8.95933E-13
${\mathit{F}}_{\mathit{P}\mathit{d}\mathit{A}\mathit{g}}^{\mathit{s}}\left({\mathit{X}}_{\mathit{A}\mathit{g}}^{\mathit{s}}\right)$	0.00464592	−1.95305E-05	−1.43628E-06	4.45352E-08	−4.12665E-10	1.32031E-12
${\mathit{F}}_{\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}}\right)$	−0.008092053	0.000174313	−1.0007E-05	4.35027E-07	−9.88E-09	1.20349E-10	−7.52722E-13	1.899E-15
${\mathit{F}}_{\mathit{P}\mathit{d}\mathit{A}\mathit{u}}^{\mathit{s}}\left({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}}\right)$	0.002002473	−8.36957E-05	2.89768E-06	−5.01666E-08	4.88935E-10	1.76718E-12

,

Table 3. The constants of the slopes.

BEPD	${({\mathit{X}}^{\mathit{s}})}^0$	${({\mathit{X}}^{\mathit{s}})}^1$	${({\mathit{X}}^{\mathit{s}})}^2$	${({\mathit{X}}^{\mathit{s}})}^3$	${({\mathit{X}}^{\mathit{s}})}^4$	${({\mathit{X}}^{\mathit{s}})}^5$
${\mathit{S}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}}\right)$	−0.001525122	2 × 9.83954E-06	3 × −2.21084E-08
${\mathit{S}}_{\mathit{A}\mathit{u}\mathit{A}\mathit{g}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{A}\mathit{g}}^{\mathit{l}}\right)$	0.000275973	2 × 2.66952E-06	3 × 2.89592E-08
${\mathit{S}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}}\right)$	−0.009145785	2 × 0.000216506	3 × −5.02079E-06	4 × 7.36011E-08	5 × −5.53729E-10	6 × 1.62381E-12
${\mathit{S}}_{\mathit{P}\mathit{d}\mathit{A}\mathit{g}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{A}\mathit{g}}^{\mathit{l}}\right)$	0.002466234	2 × 1.93529E-05	3 × −1.71905E-06	4 × 5.15282E-08	5 × −5.63012E-10	6 × 2.23671E-12
${\mathit{S}}_{\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}}\right)$	−0.015142951	2 × 0.0006576	3 × −2.04085E-05	4 × 3.81869E-07	5 × −4.01939E-09	6 × 2.1859E-11
${\mathit{S}}_{\mathit{P}\mathit{d}\mathit{A}\mathit{u}}^{\mathit{l}}\left({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}}\right)$	0.000887203	2 × 3.54004E-05	3 × −1.3818E-06	4 × −6.83248E-09	5 × 9.61336E-10	6 × −1.34325E-11

and

Table 4. The constants of the ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}\left({\mathit{X}}_{\mathit{B}}^{\mathit{l}}\right)$ functions.

BEPD	${({\mathit{X}}^{\mathit{l}})}^0$	${({\mathit{X}}^{\mathit{l}})}^1$	${({\mathit{X}}^{\mathit{l}})}^2$	${({\mathit{X}}^{\mathit{l}})}^3$	${({\mathit{X}}^{\mathit{l}})}^4$	${({\mathit{X}}^{\mathit{l}})}^5$	${({\mathit{X}}^{\mathit{l}})}^6$
${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}\left({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}}\right)$	0.040036927	−0.000181716	1.72324E-06	−3.9346E-08
${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{g}}^{\mathit{A}\mathit{u}\mathit{A}\mathit{g}}\left({\mathit{X}}_{\mathit{A}\mathit{g}}^{\mathit{l}}\right)$	−0.102745508	0.001980561	−1.26162E-05	3.06916E-08
${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}\left({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}}\right)$	0.366998634	0.011788084	−0.002026059	8.1556E-05	−1.43378E-06	1.16237E-08	−3.57194E-11
${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{g}}^{\mathit{l}\mathit{d}\mathit{A}\mathit{g}}\left({\mathit{X}}_{\mathit{A}\mathit{g}}^{\mathit{l}}\right)$	−0.613550521	−0.006202123	0.00058256	−7.83937E-06	3.24067E-08
${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}}\right)$	0.761637693	−0.04593014	0.001357858	−2.06201E-05	1.51338E-07	−4.25186E-10
${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{P}\mathit{d}\mathit{A}\mathit{u}}\left({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}}\right)$	−0.469194667	0.051179503	−0.002457681	5.18983E-05	−4.95942E-07	1.76313E-09

). The detailed calculation method is shown in Section 6.1. (Equations (52) and (53)).

The calculated and digitalised liquidus and solidus temperatures of the BEPDs are compared in Figure 3(a1,b1), Figure 4(a1,b1) and Figure 5(a1,b1). In Figure 3(a2,b2), Figure 4(a2,b2) and Figure 5(a2,b2), the difference between the digitalised and calculated liquidus and solidus temperatures as a function of the concentration of alloying elements is shown. The absolute average temperature differences are less than 1 K at all six BEPDs (

Table 5. Absolute and average differences of the digitalised and calculated temperatures.

	Pd-Ag	Pd-Au	Ag-Au	Au-Ag	Ag-Pd	Au-Pd
Abs. aver. ∆T, liq., K	0.467	0.694	0.103	0.157	0.391	0.703
Abs. aver. ∆T, sol., K	0.283	0.905	0.094	0.12	0.283	0.792

). Based on the above, it can be stated that the accuracy of the calculation is acceptable. Do not forget that the accuracy of the thermocouples is not better than 0.1%, which is ~±1.5 K at 1500 K.

Figure 3(a3,b3), Figure 4(a3,b3) and Figure 5(a3,b3) show the calculated slope of the liquidus and solidus temperatures of the BEPDs.

7.2.2. Calculation of the Functions of the Slope of the Liquidus and Solidus Temperatures of BEPDs

The slopes were calculated using Equations (49) and (51). Constants of the $S_{AB}^l$ part of the $M_{AB}^B\left(X_B^l\right)$ function are shown in Table 4.

7.2.3. Calculation of the Partition Ratios of the BEPDs

It follows from the hierarchical structure of the ESTPHAD system that the functions of the partition coefficients (k) of the TEPDs contain the functions of the partition coefficient of the BEPDs. The partition coefficients were calculated as quotients of solid- and liquid-phase concentrations determined through digitisation at a given temperature and were determined using the $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}({\mathit{X}}_{\mathit{B}}^{\mathit{l}})$, $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}({\mathit{X}}_{\mathit{B}}^{\mathit{s}})$ functions for all six BEPDs (Figure 3(a4,b4), Figure 4(a4,b4) and Figure 5(a4,b4)). The constants of the functions are shown in Table 4.

To check the accuracy of the ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}\left(X_B^l\right) \mathrm{f}\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}$, the solidus concentrations were calculated from the liquidus concentrations (X^s = k X^l). The differences between the calculated and digitalised concentrations are shown in Figure 3(a5,b5), Figure 4(a5,b5), Figure 5(a5,b5) and

Table 6. The absolute maximum and average concentration differences between the recalculated and the digitalised solidus concentration.

	Pd-Ag	Pd-Au	Ag-Au	Au-Ag	Ag-Pd	Au-Pd
Abs. max ∆c, liq., at%	0.98	1.914	0.012	0.004	1.173	1.148
Abs. aver. ∆c, liq., at%	0.175	0.543	0.002	0.002	0.22	0.241
Abs. max ∆c, sol., at%	0.7873	0.9	0.012	0.013	1.029	0.762
Abs. aver. ∆c, sol., at%	0.286	0.28	0.002	0.005	0.213	0.221

. The difference is, in most cases, a few 0.1 at%, which is sufficient accuracy for simulations.

7.3. Calculation of the Liquidus and Solidus Temperatures, Slope of the Liquidus Surface, and Partition Ratios of Au and Pd in AgAuPd TEPDs

The calculation of the liquidus and solidus temperature and partition ratios can be performed using the “A” elements, which would be all three Ag, Au, and Pd elements. The details of the calculations and the possibilities of the methods will be shown using Ag as the “A” element.

7.3.1. Calculation of the Liquidus and Solidus Temperatures

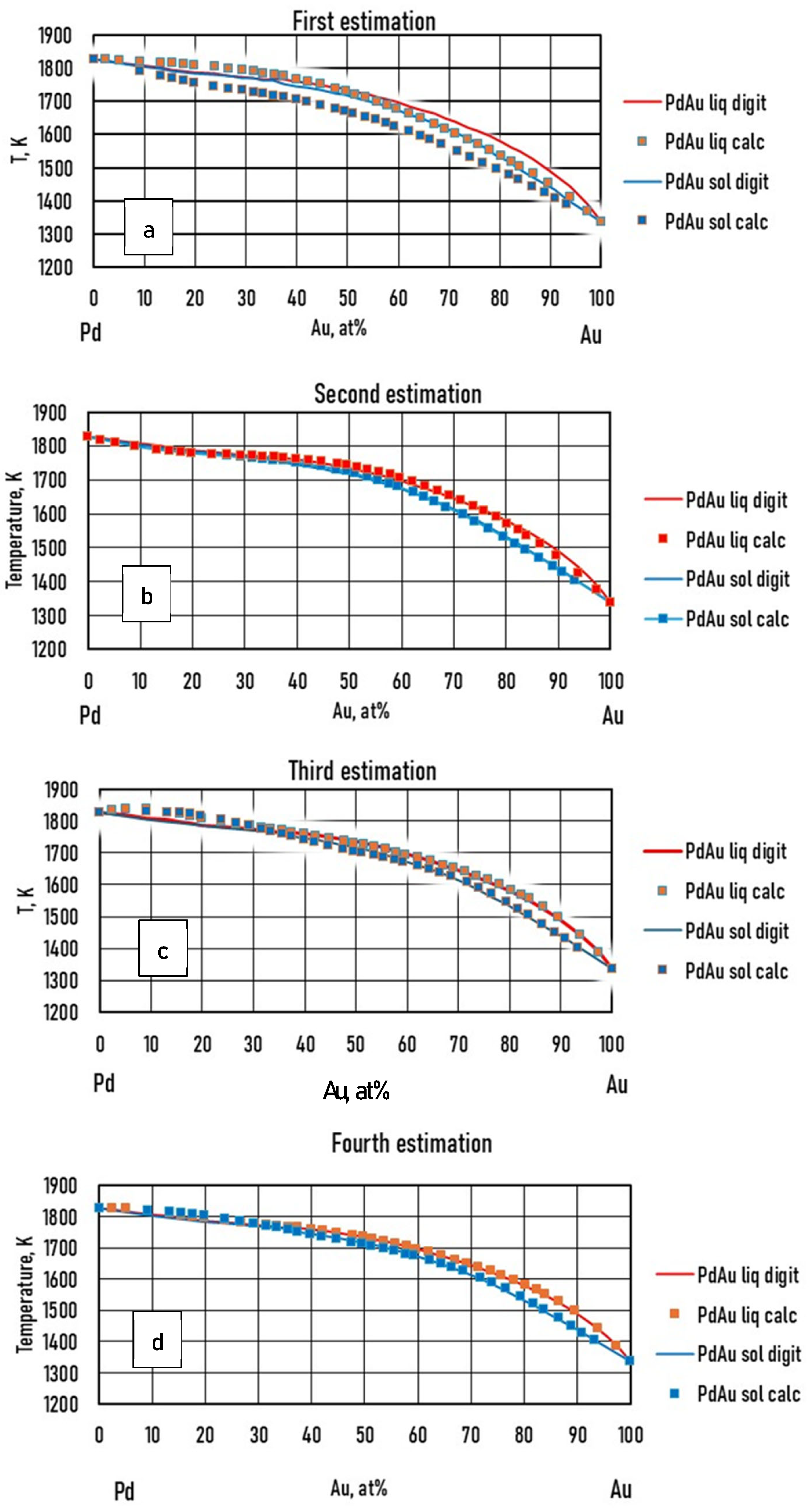
First Estimation

If the two BEPDs are known (Ag-Au and Ag-Pd), the third is not (Au-Pd), and it is also known that the TEPD is completely isomorphous, but the liquidus and the solidus isotherms are not known, the isotherm can be estimated as follows:

It is assumed that

$$∆{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au}^l,X_{Pd}^l\right)=0 \mathrm{a}\mathrm{n}\mathrm{d} ∆{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Au}^s,X_{Pd}^s\right)=0$$

(76)

$${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au}^l{,X}_{Pd}^l\right)={\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{l}}\left(X_{Au}^l\right)+{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Pd}^l\right)$$

(77)

and

$${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Au}^s{,X}_{Pd}^s\right)={\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{s}}\left(X_{Au}^s\right)+{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Pd}^s\right)$$

(78)

The calculated liquidus and solidus isotherms are compared with the known isotherms in Figure 6a,b. The constants of the ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{l}}\left(X_{Au}^l\right) , {\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{s}}\left(X_{Au}^s\right)$ and ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Pd}^l\right) , {\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Pd}^s\right)$ functions are shown in Table 1,

Table 7. The differences between the digitalised liquidus and solidus temperature and the calculated one at the four estimations of Pd-Au BEPD.

	Aver. Delta T Liq. K	Aver. Delta T Sol. K
First est.	20.72	37.7
Second est.	4.03	4.56
Third est.	10.14	7.37
Forth est.	2.98	5.64

and

Table 8. T_A = T_Ag, Liquidus, third estimation.

${\mathit{T}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^0$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^1$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^2$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^3$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^4$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^5$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^6$
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{0}}$	0	−0.009145785	0.000216506	−5.02079E-06	7.36011E-08	−5.53729E-10	1.62381E-12	Biner Ag-Pd
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{1}}$	−0.001525122	2.73627E-05	−2.53908E-06	5.42026E-08	−3.34127E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{2}}$	9.83954E-06	5.40067E-07	2.44466E-08	−2.97294E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{3}}$	−2.21084E-08	−4.45188E-08	4.13816E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{4}}$		6.57177E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{5}}$		−3.43842E-12
	Biner Ag-Au

(liquidus) and Table 2,

Table 9. T_A = T_Ag, Liquidus, fourth estimation.

${\mathit{T}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{3}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{4}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{5}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^6$
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{0}}$	0	−0.009145785	0.000216506	−5.02079E-06	7.36011E-08	−5.53729E-10	1.62381E-12	Biner Ag-Pd
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{1}}$	−0.001525122	2.10522E-05	−1.98144E-06	3.98273E-08	−2.26295E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{2}}$	9.83954E-06	6.31182E-07	1.96487E-08	−2.39973E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{3}}$	−2.21084E-08	−4.41986E-08	5.97316E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{4}}$		6.24807E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{5}}$		−3.15779E-12
	Biner Ag-Au

and

Table 10. T_A = T_Ag, Solidus, third estimation.

${\mathit{T}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{3}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{4}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{5}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^6$
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{0}}$	0	−0.005863031	5.10683E-05	−1.02889E-06	2.45832E-08	−2.57412E-10	8.95933E-13	Binary Ag-Pd
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{1}}$	−0.001470912	0.000192355	−9.44422E-06	1.3398E-07	−6.03495E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{2}}$	9.08706E-06	−7.95952E-06	2.91598E-07	−2.26559E-09
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{3}}$	−2.02095E-08	1.5897E-07	−5.22316E-09	3.06509E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{4}}$		−1.14374E-09	2.61784E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{5}}$		1.54871E-12
	Binary Ag-Au

(solidus).

Second Estimation

If it is known that the TEPD is isomorphous and the third BEPD is also known (in this case, the Au-Pd BEPD), the data of the liquidus and solidus temperature of this BEPD can be used for the calculation of the $F_{AgAuPd}^l\left(X_{Au}^l{,X}_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d}{F}_{AgAuPd}^s\left(X_{Au}^s{,X}_{Pd}^s\right)$ maps and, from those, the functions ${∆\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au}^l{,X}_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d}{∆\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Au}^s{,X}_{Pd}^s\right)$.

$${∆\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au}^l{,X}_{Pd}^l\right)={1.34318\mathrm{E}}^{-5}{\mathrm{X}}_{Au}^{*l}{X}_{Pd}^l{{-{3.10933\mathrm{E}}^{-7}(\mathrm{X}}_{Au}^l)}^2{X}_{Pd}^l$$

(79)

$${∆\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Au}^s{,X}_{Pd}^s\right)=-{3.46291\mathrm{E}}^{-6}{\mathrm{X}}_{Au}^s{X}_{Pd}^s{{{-1.15366\mathrm{E}}^{-7}(\mathrm{X}}_{Au}^s)}^2{X}_{Pd}^s$$

(80)

The digitalised and calculated liquidus and solidus isotherms can be seen in Figure 7.

Third Estimation

Considering the liquidus and solidus temperatures at all known concentrations (at the isotherms) in the TEPD (except for the Au-Pd BEPD data if they are not known,) from these data, one can calculate the $F_{AgAuPd}^l\left(X_{Au}^l,X_{Pd}^l\right)$ and $F_{AgAuPd}^s\left(X_{Au}^s,X_{Pd}^s\right)$ maps (Equation (55)), then the ${\mathrm{\Delta }F}_{AgAuPd}^l\left(X_{Au}^l,X_{Pd}^l\right)$ and ${\mathrm{\Delta }F}_{AgAuPd}^s\left(X_{Au}^s,X_{Pd}^s\right)$ maps (Equations (56) and (57)), and then the ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au}^l,X_{Pd}^l\right)$ and ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Au}^s,X_{Pd}^s\right)$ functions (Equations (58) and (59)). The constants of the ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{l}}\left(X_{Au}^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Pd}^l\right)$ functions are shown in the Table 9 (liquidus) and

Table 11. T_A = T_Ag, Solidus, fourth estimation.

${\mathit{T}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{3}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{4}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{5}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^6$
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{0}}$	0	−0.005863031	5.10683E-05	−1.02889E-06	2.45832E-08	−2.57412E-10	8.95933E-13	Binary Ag-Pd
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{1}}$	−0.001470912	0.000199224	−9.23283E-06	1.21293E-07	−4.97208E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{2}}$	9.08706E-06	−9.2756E-06	3.21833E-07	−2.36136E-09
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{3}}$	−2.02095E-08	2.01945E-07	−6.03414E-09	3.2798E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{4}}$		−1.66965E-09	3.17608E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{5}}$		3.73822E-12
	Binary Ag-Au

(solidus). The digitalised and calculated liquidus and solidus isotherms can be seen in Figure 8.

Fourth Estimation

In this case, upon calculation of the constants of ${\mathbf{\Delta }\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{l}}\left(X_B^l,X_C^l\right)$ and ${\mathbf{\Delta }\mathit{F}}_{\mathit{A}\mathit{B}\mathit{C}}^{\mathit{s}}\left(X_B^s,X_C^s\right)$ functions, the data of the Au-Pd BEPD were taken into account in order to calculate the liquidus and solidus temperatures of the Ag-Au-Pd TEPD as accurately as possible (Figure 9).

The constants of the ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au,}^l{X}_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left({X_{Au,}^{s}X}_{Pd}^s\right)$.

The differences between the digitalised and the calculated liquidus and solidus temperatures are shown in Figure 10 and Figure 11, respectively.

If the third (in this case, the Au-Pd BEPD) is known, the accuracy of the calculation can be characterised by the difference between the calculated and known (digitalised) temperature data of the third BEPD’s liquidus and solidus temperature. In Figure 12, the comparison of the digitalised and calculated liquidus and solidus temperature of the Au-Pd BEPD, and the average temperature differences in Table 7 can be seen.

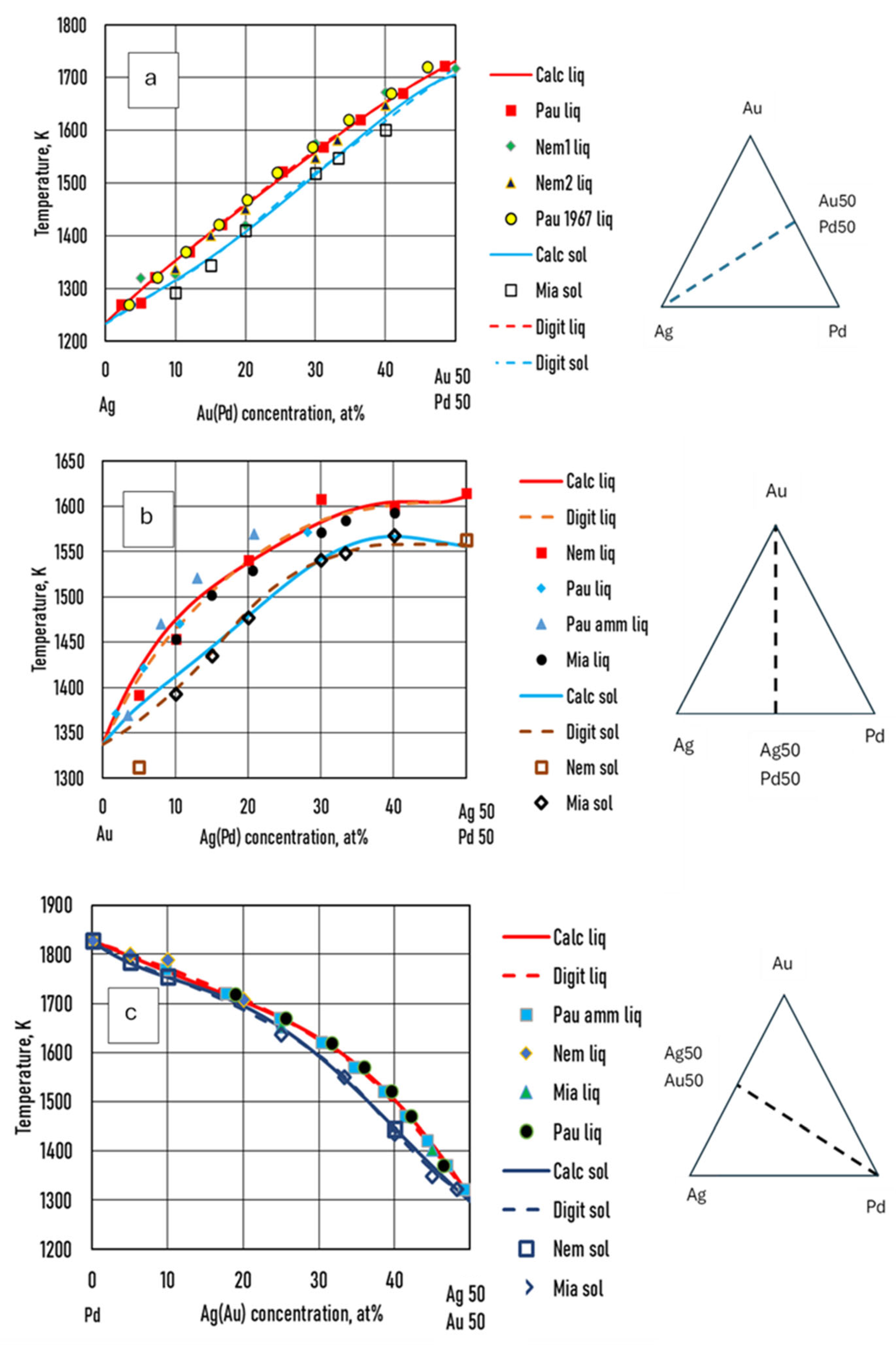
Validation by Experiments

Venudhar et al. [31], Nemilov et al. [32], Pauley [33], and Miane et al. [34] measured the liquidus and solidus temperatures at three sections of AgAuPd TEPDs. Prince et al. [30] analysed the measured data and calculated the liquidus and solidus temperatures of these sections (Digit in Figure 13). The measured, digitalized, and calculated liquidus and solidus temperatures using the fourth estimated functions are compared in Figure 13.

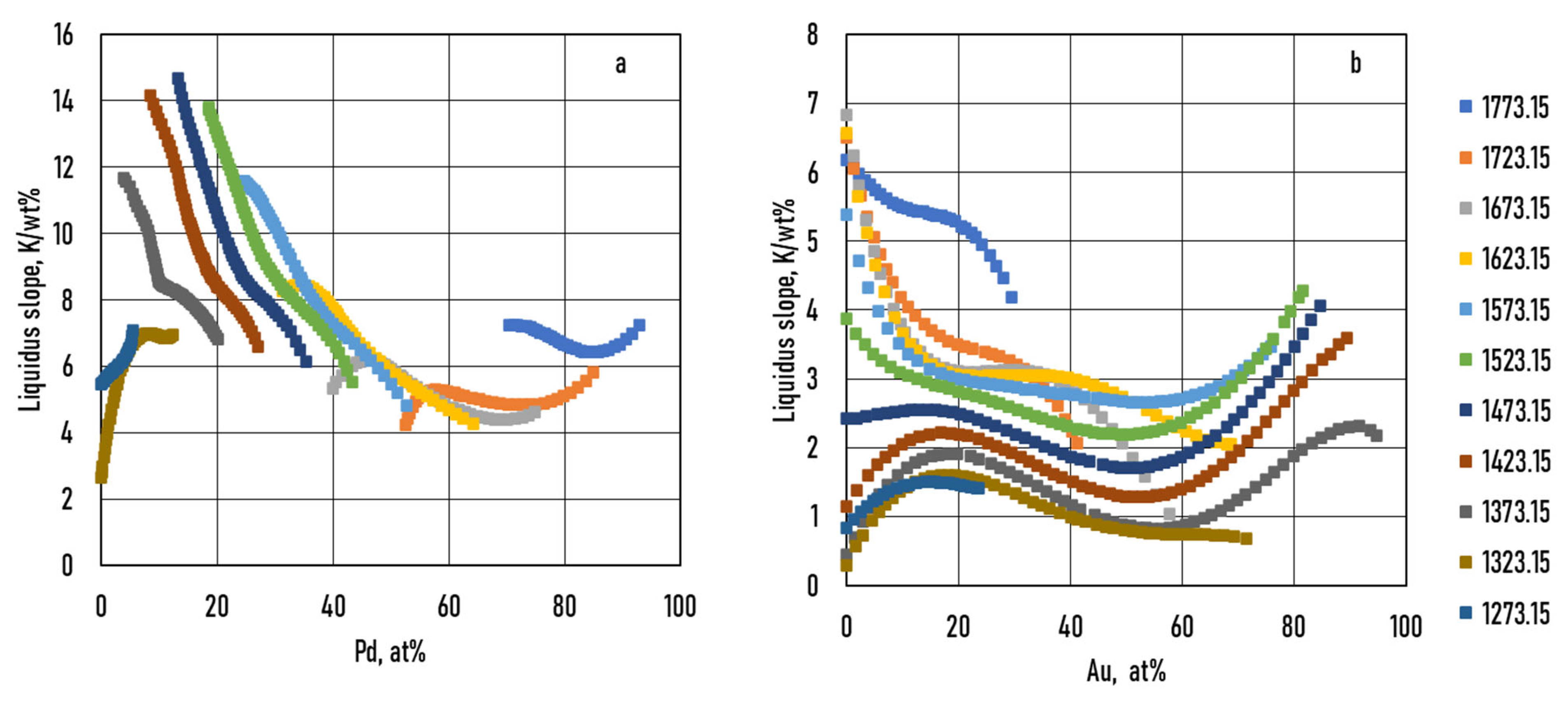
7.3.2. Calculation of the Liquidus and Solidus Slopes

As shown earlier, the slopes of the liquidus and solidus surfaces can be calculated easily using the partial derivative of the $T^l{(X}_{AgAuPd}^l$) and $T^s{(X}_{AgAuPd}^s$) functions (Equations (49) and (51)). The constants of the numerator of the derivative functions (S^l) and (S^s) are shown in

Table 12. T_A = T_Ag, Liquidus slope, $\partial T_L/X_{Au}.$

${{\mathit{S}}^{\mathit{l}}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{3}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{4}}$
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{0}}$	−0.001525122	2 × 9.83954E-06	3 × −2.21084E-08			Binary Ag-Au
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{1}}$	2.10522E-05	2 × 6.31182E-07	3 × −4.41986E-08	4 × 6.24807E-10	5 × −3.15779E-12
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{2}}$	−1.98144E-06	2 × 1.96487E-08	3 × 5.97316E-11
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{3}}$	3.98273E-08	2 × −2.39973E-10
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{4}}$	−2.26295E-10

and

Table 13. T_A = T_Ag, Liquidus slope, $\partial T_L/X_{Pd}.$

${{\mathit{S}}^{\mathit{l}}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{3}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{4}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{5}}$
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{0}}$	−0.009145785	2 × 0.000216506	3 × −5.02079E-06	4 × 7.36011E-08	5 × −5.53729E-10	6 × 1.62381E-12	Binary Ag-Pd
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{1}}$	2.10522E-05	2 × 6.31182E-07	3 × −4.41986E-08	4 × 6.2480E-10	5 × −3.15779E-12
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{2}}$	−1.98144E-06	2 × 1.96487E-08	3 × 5.97316E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{3}}$	3.98273E-08	2 × −2.3997E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{4}}$	−2.26295E-10

(liquidus) and in

Table 14. T_A = T_Ag, Solidus slope, $\partial T_L/X_{Au}.$

${\mathit{S}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{3}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{4}}$
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{0}}$	−0.001470912	2 × 9.08706E-06	3 × −2.02095E-08			Binary Ag-Au
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{1}}$	0.000199224	2 × −9.2756E-06	3 × 2.01945E-07	4 × −1.66965E-09	5 x 3.73822E-12
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{2}}$	−9.23283E-06	2 × 3.21833E-07	3 × −6.03414E-09	4 × 3.17608E-11
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{3}}$	1.21293E-07	2 × −2.36136E-09	3 × 3.2798E-11
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{4}}$	−4.97208E-10
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{5}}$

and

Table 15. T_A = T_Ag, Solidus slope, $\partial T_L/X_{Pd}.$

${\mathit{S}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{3}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{4}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{s}})}^{\mathbf{5}}$
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{0}}$	−0.005863031	2 × 5.10683E-05	3 × −1.02889E-06	4 × 2.45832E-08	5 × −2.57412E-10	6 × 8.95933E-13	Binary Ag-Pd
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{1}}$	0.000199224	2 × −9.23283E-06	3 × 1.21293E-07	4 × −4.97208E-10
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{2}}$	−9.2756E-06	2 × 3.21833E-07	3 × −2.36136E-09
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{3}}$	2.01945E-07	2 × −6.03414E-09	3 × 3.2798E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{4}}$	−1.66965E-09	2 × 3.17608E-11
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{s}})}^{\mathbf{5}}$	3.73822E-12

(solidus). The slopes calculated along the isotherms are illustrated in Figure 14 and Figure 15.

7.3.3. Calculation of the Partition Ratios of the AgAuPd TEPD

The drawn TEPD does not contain the tie lines because experimentally determining the equilibrium concentrations of the liquidus and solidus phases is very complicated. First, many concentrations were determined for the database through digitalisation of the liquidus and solidus isotherms, which were not on the same tie line. Consequently, only estimated partition ratios can be calculated. The calculation method is shown in Section 6.2.2.

First Step

The calculation of the partition ratios of Au and Pd in the Ag-Au and Ag-Pd BEPDs is shown in Section 7.2.3. The constants of the ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}\left(X_{Au}^l\right)$ and ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}\left(X_{Pd}^l\right)$ functions are shown in Table 4.

Second Step (First Estimation)

Using the ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}\left(X_{Au}^l\right)$ and ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}\left(X_{Pd}^l\right)$ partition ratios functions, solidus concentrations maps were calculated from the fourth estimated liquidus concentrations of the isotherms. As we could not consider the effect of the Au and Pd interaction, the calculated solidus concentrations were not exactly on the same isotherms of the solidus.

With a special method, the solidus concentration was determined on the solidus isotherm. One example is shown in Figure 16. Choosing the ${(X}_{Au,}^l{X}_{Pd}^l)$ point on the $T_L$ isotherm (red line), using the ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}\left(X_{Au}^l\right)$ and ${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}\left(X_{Pd}^l\right)$ functions, ${X_{Au}^{s\mathrm{*}}=k}_{Au}^{AgAu}\left(X_{Au}^l\right)X_{Au}^l$ and ${X_{Pd}^{s\mathrm{*}}=k}_{Pd}^{AgPd}\left(X_{Pd}^l\right)X_{APd}^l$ were calculated. The ${(X}_{Au,}^{s\mathrm{*}}{X}_{Pd}^s)$ point is on the $T_s^{\mathrm{*}}$ isotherm (dotted line), ${T_s^{\mathrm{*}}\ne T}_L$. The tie line is between the two black points.

Third Step (Second Estimation)

We assumed that the slope of the tie line was equal to the slope of the tie line in the TEPD, with the elongated tie line, the ${T_s=T}_L$ isoterm (blue line) was cut, and we obtained the ${(X}_{Au}^s,X_{Pd}^s)$ concentrations. We repeated this calculation at all liquidus isotherms at many liquidus concentrations and divided the obtained solidus concentrations by the liquidus concentrations, and the ${lnk}_{Au}^{AgAu}\left(X_{Au}^l,X_{Pd}^l\right)$ and ${lnk}_{Pd}^{AgPd}\left(X_{Au}^l,X_{Pd}^l\right)$ partition ratio maps were calculated. Using these maps, the $\mathrm{\Delta }ln{k}_{Au}^{AgAuPd}\left(X_{Au}^l,X_{Pd}^l\right)$ and $\mathrm{\Delta }ln{k}_{Pd}^{AgAuPd}\left(X_{Au}^l,X_{Pd}^l\right)$ maps were recalculated:

$$\mathrm{\Delta }ln{k}_{Au}^{AgAuPd}\left(X_{Au}^l,X_{Pd}^l\right)=ln{k}_{Au}^{AgAuPd}\left(X_{Au}^l,X_{Pd}^l\right)-ln{k}_{Au}^{AgAu}\left(X_{Au}^l\right)$$

(81)

and

$$\mathrm{\Delta }ln{k}_{Pd}^{AgAuPd}\left(X_{Au}^l,X_{Pd}^l\right)=ln{k}_{Pd}^{AgAuPd}\left(X_{Au}^l,X_{Pd}^l\right)-ln{k}_{Pd}^{AgPd}\left(X_{Pd}^l\right)$$

(82)

From the $\mathrm{\Delta }ln{k}_{Au}^{AgAuPd}\left(X_{Au}^l,X_{Pd}^l\right)$ and $\mathrm{\Delta }ln{k}_{Pd}^{AgAuPd}\left(X_{Au}^l,X_{Pd}^l\right)$ maps, the constants of the $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left(X_{Au}^l,X_{Pd}^l\right)$ and $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left(X_{Au}^l,X_{Pd}^l\right)$ functions was calculated by regression.

Finally:

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left(X_{Au}^l,X_{Pd}^l\right)=\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}\left(X_{Au}^l\right)+\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left(X_{Au}^l,X_{Pd}^l\right)$$

(83)

$$\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left(X_{Au}^l,X_{Pd}^l\right)=\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}\left(X_{Pd}^l\right)+\mathbf{\Delta }\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left(X_{Au}^l,X_{Pd}^l\right)$$

(84)

The constants of these functions are shown in

Table 16. Partition ratio of Au, second estimation.

${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{l}}({\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}},{\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}}$)	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{3}}$
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{0}}$	0.040036927	−0.000181716	1.72324E-06	−3.9346E-08	Binary Ag-Au
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{1}}$	0.001297726	−9.97448E-06	7.81204E-08
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{2}}$	−5.05785E-05	−5.85049E-08
${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{3}}$	4.19929E-07

and

Table 17. Partition ratio Pd, second estimation.

${\mathit{l}\mathit{n}\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{l}}({\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}},{\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{0}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{1}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{2}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{3}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{4}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^{\mathbf{5}}$	${{(\mathit{X}}_{\mathit{P}\mathit{d}}^{\mathit{l}})}^6$
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{0}}$	0.3669986	0.0117880	−0.002026	8.1556E-05	−1.43378E-06	1.16237E-08	−3.57194E-11	Binary Ag-Pd
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{1}}$	0.021171612	−0.0008127	1.45168E-05	−1.079E-07
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{2}}$	−0.0009139	1.17625E-06	4.18625E-08
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{3}}$	2.50716E-05
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{4}}$	−2.94122E-07
${{(\mathit{X}}_{\mathit{A}\mathit{u}}^{\mathit{l}})}^{\mathbf{5}}$	1.17629E-09

.

Using these functions, the solidus concentration (open circle in Figure 16) maps was recalculated and from these, the solidus temperatures were recalculated again with the ${\mathit{T}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}$ function (dotted green line in Figure 16). One example of the calculated tie lines is shown in Figure 17. The original and recalculated solidus isotherm can be seen in Figure 18.

The differences between the original isotherms and the recalculated solidus temperature are shown in Figure 19.

We note that the $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{A}\mathit{u}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left(X_{Au}^s,X_{Pd}^s\right)$ and $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{P}\mathit{d}}^{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}\left(X_{Au}^s,X_{Pd}^s\right)$ functions were not determined because most of the simulations of the solidification were not required. If they are needed for the simulation with the same method, they can be determined.

8. Liquidus and Solidus Temperatures, Liquidus Slopes, and the Partition Ratios

The liquidus and solidus temperatures, liquidus slopes, and the partition ratios of the Ag-Au, Ag-Pd, and Au-Pd BEPDs and the Ag-Au-Pd TEPD were calculated with a new thermodynamic-based method. In the case of the Ag-Au-Pd TEPD, four different methods were used in the calculation of the liquidus and solidus temperatures. In the first method (first estimation), only the functions of Ag–Au and Ag-Pd BEPDs were used in the calculation, while in the second method (second estimation), the Au-Pd BEPD was also used. In the third method, in addition to the two Ag–Au and Ag-Pd BEPDs, the digitalised liquidus and solidus temperature data of the isotherms of the Ag-Au-Pd TEPD were also taken into account (third estimation), while in the fourth method, the liquidus and solidus data of the Au–Pd BEPD were also used in the calculation. In all four methods, the liquidus and solidus isotherms were calculated. The digitalised and calculated isotherms are shown in Figure 6, Figure 7, Figure 8 and Figure 9. The digitalised and calculated liquidus and solidus temperatures were compared in two ways: firstly, the average differences were compared at five concentrations ranging from 100 at% Ag to nx20 at% Ag, and secondly at some concentration ranges between two neighbouring 20% Ag (i.e., from 40 to 20 at% Ag), which can be seen in Figure 10 and Figure 11. The slopes and partition ratios were calculated only using the data of the liquidus and solidus temperatures calculated using the fourth method.

Based on these figures, it can be stated as follows that:

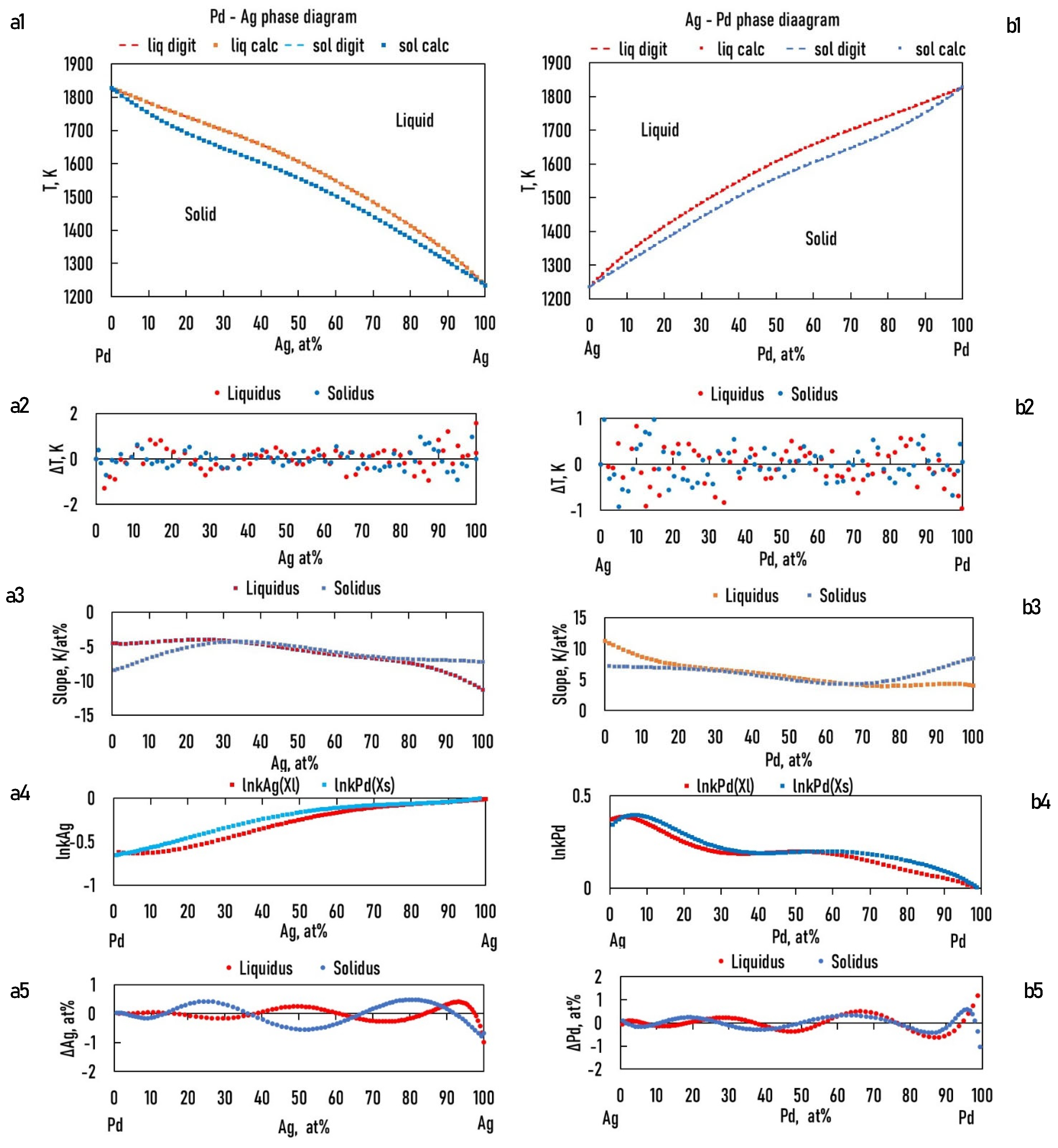
• The absolute maximum and average errors of the calculation of the liquidus and solidus temperatures of the BEPDs are less than 2 K and 0.5 K, respectively (R² < 0.98). These are less than the error of the temperature measurement by the thermocouple in the temperature range of the investigated alloys. Therefore, the calculation method is suitable for estimating the liquidus and solidus temperatures in the case of binary alloys. Using the derivative of the ${\mathit{T}}_{\mathit{L}}(X_B^l)$ function, the liquidus slope can be calculated easily. As in this case, the partition ratio can be determined from the phase diagram, and the constants of the $\mathit{l}\mathit{n}{\mathit{k}}_{\mathit{B}}^{\mathit{A}\mathit{B}}\left(X_B^l\right)$ function are also calculable.
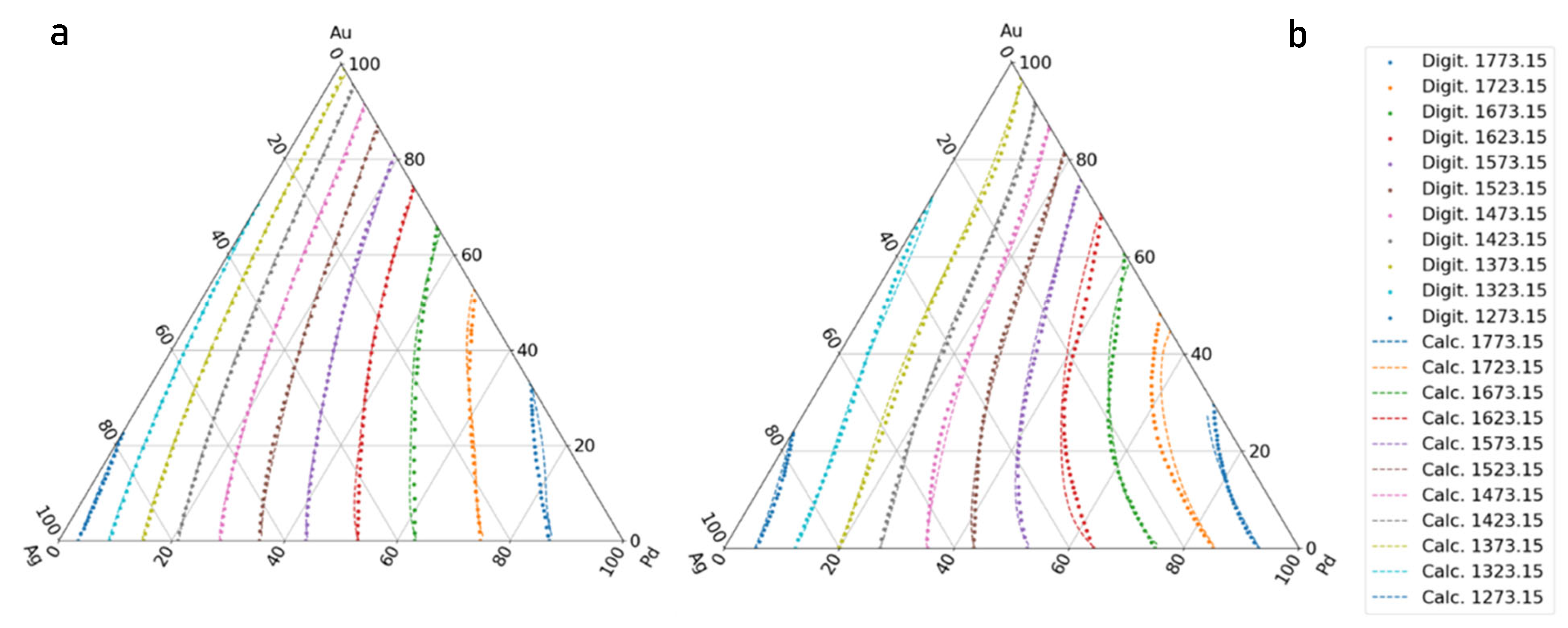
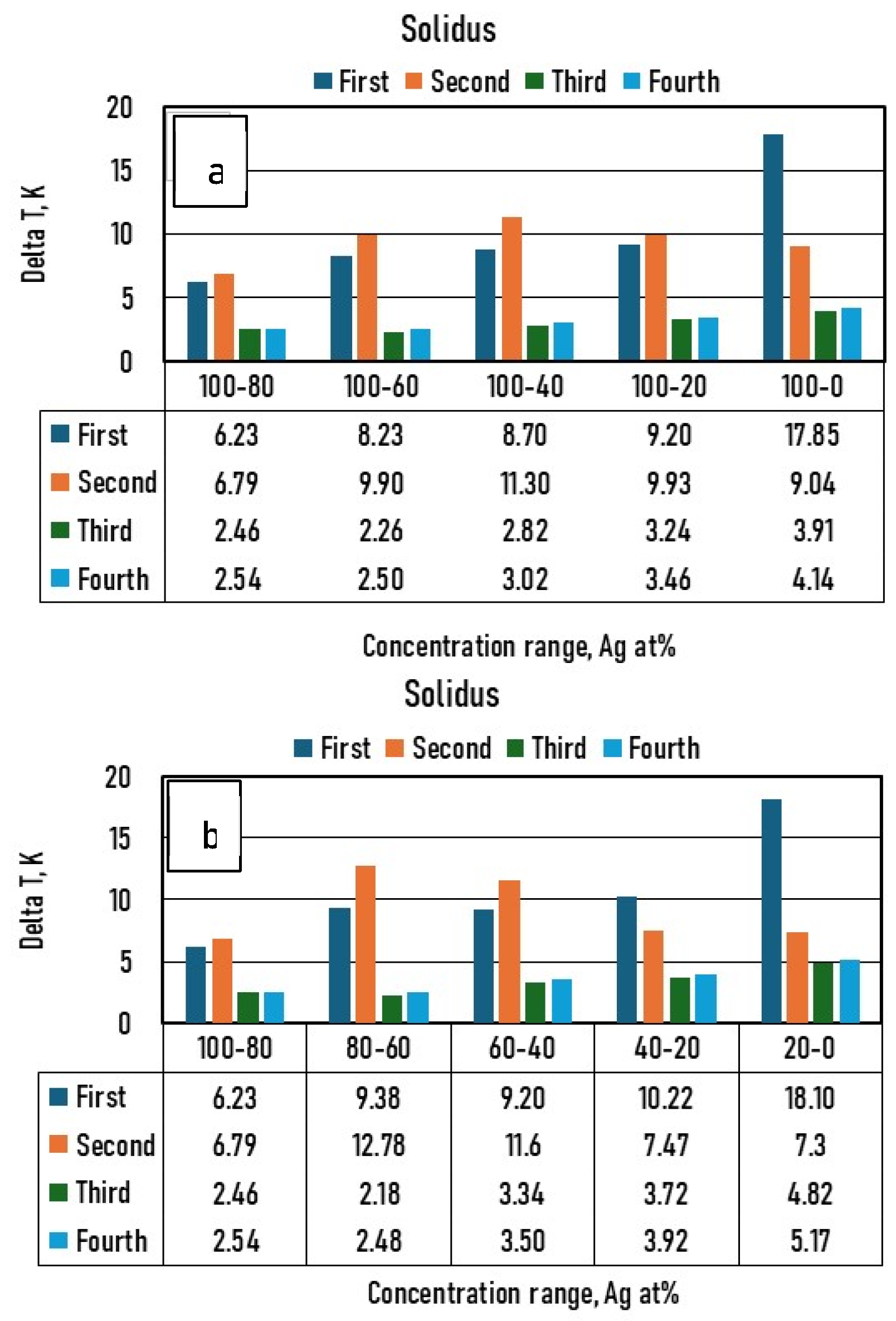
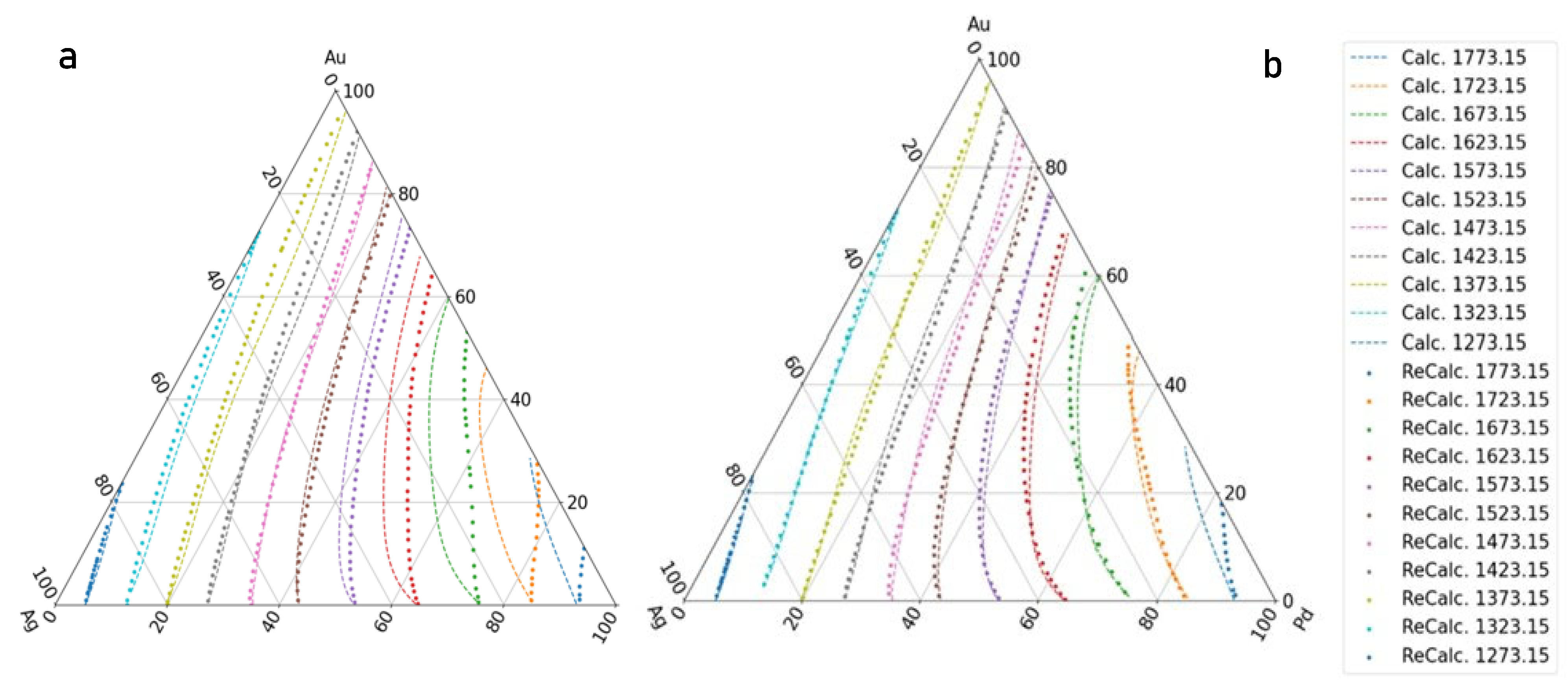
• If the liquidus and solidus isotherms of the TEPD and third BEPD (in this case, the Au-Pd) are unknown, but it is known or presumable that the TEPD is completely isomorphous, using only the ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{l}}\left(X_{Au}^l\right),{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{s}}\left(X_{Au}^s\right),{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Pd}^s\right)$ functions of the Ag–Au and Ag–Pd BEPDs for the calculation (first estimation), the liquidus (liquidus isotherms) and solidus (solidus isotherms) temperatures can be estimated. In the 100–60 at% Ag range, the average error is less than 2 K for the liquidus (Figure 10a) and 10 K for the solidus (Figure 11a). Far from the Ag corner, the error increased, in the 20–0 at% Ag ranges, 10 K for the liquidus (Figure 10b) and 18,1 K for the solidus (Figure 11b). In the entire range (100–0 at% Ag), it is 9.37 K and 17,85 K in the case of liquidus and solidus, respectively. Consequently, the liquidus temperatures can be calculated with acceptable error near the Ag corner (100–40 at% Ag) because the error of the temperature measurement by the thermocouple is not better than 0.1% (at 1500 K, it is 1.5 K), while in the case of solidus temperatures, the calculation can only give estimated data. With the first estimation, the liquidus and solidus temperatures of the Pd-Au phase diagram can be estimated with relatively high average error, 20.72 K and 37.7 K in the case of liquidus and solidus, respectively (Figure 12a, Table 11). If the third BEPD is unknown, it would be advisable to estimate this BEPD with ~2% relative error. But this is better than nothing.
• If the third BEPD is known (in this case, the Au-Pd) using the ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{l}}\left(X_{Au}^l\right),{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{s}}\left(X_{Au}^s\right),{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Pd}^s\right)$ functions of the Ag–Au and Ag–Pd BEPDs and the liquidus and solidus temperatures of the third BEPD, the ${∆\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au}^l{,X}_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {∆\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Au}^s{,X}_{Pd}^s\right)$ functions are calculable. As a result of this, the error is similar to the error of the first estimation in the 100–80 at% Ag range in both cases. In the entire range (100–0 at% Ag), it decreased in both cases, because in the 20–0 at% range, the error decreased due to the effect of the data of the Au-Pd BEPD. The error of the liquidus and the solidus tempeature at Au-Pd BEPD drastically decreased (4.03 K and 4.56 K (Table 11). With this method, the estimation of the known third BEPD is significantly improved.
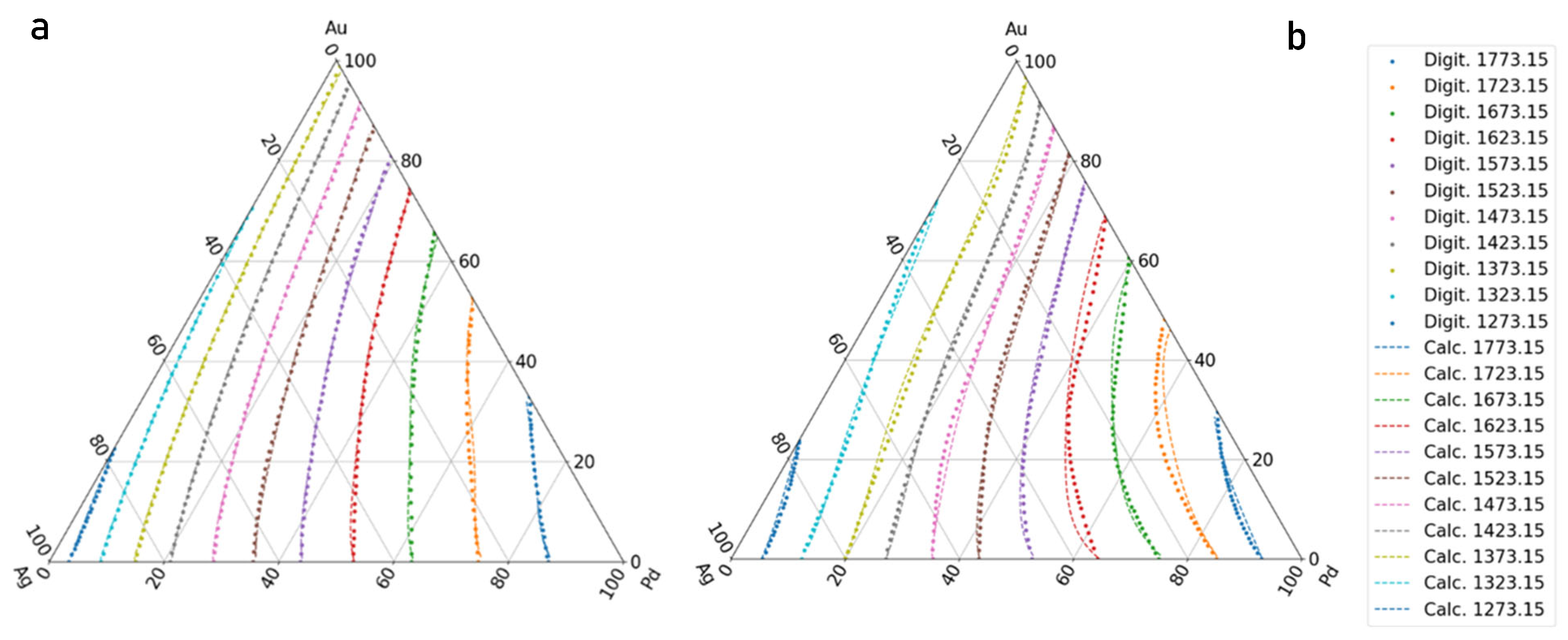
• In the third method using the ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{l}}\left(X_{Au}^l\right),{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}}^{\mathit{s}}\left(X_{Au}^s\right),{\mathit{F}}_{\mathit{A}\mathit{g}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Pd}^s\right)$ functions of the Ag–Au and Ag–Pd BEPDS and the temperature data given from the liquidus and solidus isotherms of the Ag–Au–Pd TEPD (exept the data of the Au-Pd BEPD) to calculate the ${∆\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au}^l{,X}_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {∆\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Au}^s{,X}_{Pd}^s\right)$ functions, the average error of the liquidus temperature is less than 2 K in the entire Ag concentration range. The average error is 1.34 K in the entire range of the liquidus (100–0 at% Ag). The average error of the solidus temperatures is less than 3 K in the 100–40 at% Ag range (Figure 10a), which is less than 0.2% of 1500 K. The average error of the solidus temperature in the entire range of the solidus (100–0 at% Ag, Figure 11a) is 3.91 K, and only near the Au–Pd BEPD (in the 20–0 at% Ag range, Figure 11b) does it increase to 4.82 K. Consequently, the error of the liquidus temperatures is better than the measurable one in the case of the liquidus in the entire concentration range, and then it is usable for the simulation, while the error of the solidus temperatures is slightly inorrect, and only in the 100–40 at% Ag range is precisely suitable.
  The error of the liquidus and solidus Au-Pd BEPD is greater than the error of the second estimations because the data of this BEPD were not considered (Table 11).
• Using the ${\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{l}}\left(X_{Au}^l{,X}_{Pd}^l\right) \mathrm{a}\mathrm{n}\mathrm{d} {\mathit{F}}_{\mathit{A}\mathit{g}\mathit{A}\mathit{u}\mathit{P}\mathit{d}}^{\mathit{s}}\left(X_{Au}^s{,X}_{Pd}^s\right)$ functions and the temperature data given from the liquidus and solidus isotherms of Ag–Au–Pd TEPD and the data of the Au-Pd BEPD (fourth estimation), the error of the calculated liquidus and solidus temperatures is very similar to the error of the third estimation (Figure 10 and Figure 11). The aim of this version is to improve the calculation of the liquidus and solidus temperature of the Au–Pd BEP, so the error is acceptable when calculating the liquidus and solidus isotherm using the fourth estimation (2.98 K and 5.64 K, Table 11).
• Some authors [22,23,24] have measured the liquidus and solidus temperature at three sections of the Ag-Au-Pd TEPD: Ag–50at%Au50at%Pd, Au–50at%Ag50at%Pd, and Pd–50at%Ag50at%Au (Figure 12). From these measured data, liquidus and solidus curves were constructed by the authors for these sections. These curves were digitalised (dotted curves) and compared to the ESTPHAD calculations (fourth estimation, continuous curves). The difference between the digitalised and calculated curves is negligible, and the estimation of the measured data using these curves is acceptable, considering that between 1300 and 1800 K, it is difficult to measure the temperature.
• During the solidification simulations, the liquidus slopes are used many times. In Figure 14 and Figure 15, the liquidus and solidus slopes are shown, followed by the isotherms (Equations (49) and (51)). These two figures demonstrate the capability of the ESTPHAD method.
• Since the temperature data are not derived from CALPHAD-type calculations, but from the digitalisation of the isotherms of the liquidus and solidus surfaces, there are no congruent liquidus and solidus concentrations, and tie lines are not known. Starting from the partition ratios from the BEPDs, we developed an estimation method in the TEPD to determine the partition ratios. In the first step, we used the BEPD partition ratios to calculate the concentrations of the solid phase (first estimation) in equilibrium with the concentrations of the liquid phase. In the range of 100–40 Ag at%, the error of the calculated temperature is less than 6 K, which, if nothing else, is acceptable as an estimate, but in the range of 40–0 Ag at% the error increases very significantly and cannot be used as an estimate. With the method developed by us (second estimation), the error is around 2 K in the range of 100–60 Ag at%, which causes an error of 0.2 at% at a slope of 10 K/at%, and 0.4 at% at a slope of 5 K/at%, which is acceptable even in simulations. It should be noted, however, that since the procedure contains an approximation, namely that the slope of the tie lines in the TEPD is equal to the slope of the tie lines determined from the BEPD partition ratios. If this approximation is very different from reality (which is not very likely), then the error could have been much more significant.

9. Summary

On a thermodynamic basis, it has been proven that the method developed for the calculation of the liquidus and solidus lines of BEPDs can be extended to TEPDs. The functions have a hierarchical system; the functions developed for TEPDs contain the functions of the BEPDs that make up the TEPD. The calculation of the liquidus and solidus surfaces of the isomorphic TEPD Ag-Au-Pd demonstrates the usability of the ESTPHAD. Since this TEPD is only graphically known (CALPHAD-type calculation data are not available), the temperature-concentration data were determined through digitalisation of liquidus and solidus isotherms. The liquidus surface’s slopes were calculated with the derivatives of the liquidus functions. The functions of the partition ratios were determined using an approximate procedure.

The calculations could prove the following:

(1)

The liquidus and solidus surfaces of the TEPD can be calculated even in a relatively significant alloying range using the liquidus and solidus functions of the two BEPDs, which contain the base element, when the isotherms of the TEPD are not known (first estimation);

(2)

If the third BEPD is known, which does not contain the base element, it can be used to make the calculation more accurate, as in the first estimation, (second estimation);

(3)

Knowing the data of the liquid and solidus surfaces (isotherms) of the v, the functions can calculate the liquidus and solidus temperatures in the entire concentration range with the accuracy required for the simulations (third estimation);

(4)

Using the third BEPD, if it is known (similarly to the second estimation), the calculation can be further refined (fourth estimation);

(5)

The slopes of the liquidus surface can be calculated by deriving the function of the liquid surface;

(6)

In the case of graphically known TEPDs, the partition ratios are not known, but by using the partition ratios of the BEPDs and an approximation method developed in this work, a good result can be obtained that can be used in a relatively large concentration range during the solidification simulation;

(7)

The functions used for the calculation of liquidus, solidus temperature, liquidus slopes and partition ratios have a hierarchical structure, while in the case of TEPD, the functions used in the calculations contain the functions used in BEPD, completed by delta functions calculated from the TEPD data. As we will show later, this principle can be extended to the calculation of EPDs containing four, five, etc., alloying elements.

10. Conclusions

In the case of graphically known ternary equilibrium phase diagrams (TEPDs) with the ESTPHAD method, all of the functions (liquidus, solidus, slope, and partition ratios) that are necessary for the simulation of solidification can be determined. Functions are very easy to develop if the diagrams are known. The use of functions can significantly reduce the time required for simulations (by orders of magnitude).