A Revisiting to Re-Effects on Dislocation Slip Mediated Creeps of the γ′-Ni₃Al Phase at High Temperature via a Hybrid Model

Abstract

The anomalous flow behavior of the γ′-Ni₃Al phase at high temperature is closely related to a cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. The acceleration of cross-slips induced by the addition of rhenium (Re) is known as Re-effects. In this work, by means of a series of lattice transitions, a hybrid model including a preexisting anti-phase boundary $\mathrm{APB}\left(111\right)$ was constructed to assess the difficulty of cross-slips of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations from $\left\{111\right\}$ planes to $\left\{001\right\}$ planes in the γ′-Ni₃Al phases, and the impact of the addition of Re on these dislocation mediated creep resistances was reinvestigated by first-principles calculations. The results showed that the addition of Re at preferential Al sublattice sites was indeed beneficial for the cross-slip of the first leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations, and the existence of $\mathrm{APB}\left(111\right)$ could promote cross-slip of second leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. A detailed calculation of stacking fault energies demonstrated that an obvious Suzuki segregation of Re existed at $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$, and Re preferentially occupied Ni sublattice sites. It is found Re-segregations at $\mathrm{APB}\left(111\right)$ were disadvantageous for the cross-slip of new $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations, but the formation of more Kear-Wilsdorf dislocation locks could benefit from Re-segregations at $\mathrm{APB}\left(001\right)$.

1. Introduction

Ni-based single crystal (SC) superalloys, consisting of a large number of γ′ precipitates with L1₂ structures embedded coherently in fcc γ matrix, are widely used in turbine blades for modern aero-engines and industrial gas turbines due to their exceptional mechanical properties and high-temperature creep resistance [1,2,3]. Their excellent performance is primarily attributed to their anomalous flow behavior at high temperature [4] and the presence of significant amounts of refractory strengthening elements, such as Re, W, Mo, Ta, Ti, Cr, and Ru [5,6,7]. Previous investigations have shown that refractory elements play an important role in the movement of dislocations in the γ’ phase, among which the reinforcement of creep resistance caused by the addition of Re is known as Re-effect [8,9]. Re not only can reduce intrinsic stacking fault energies ${\gamma }_{\mathrm{isf}}$ in the γ matrix and raise anti-phase boundary (APB) energies ${\gamma }_{\mathrm{APB}}^{111}$ in the γ′ phase but also can slow down the coarsening kinetics of γ′ precipitates and dislocation climb rates in the γ matrix due to its slow diffusion coefficient [10], and even facilitates modifications of the misfit between the γ matrix and γ′ precipitates and further lead to the interfacial dislocation networks to be enriched [11]. However, an excessive addition of Re easily leads to the precipitation of a topologically close-packed (TCP) phase, which can in turn accelerate alloy failure [12]. Previous investigations [13,14] have confirmed that when a part of Re is replaced by W, the mechanical properties of Ni-based SC superalloys remain virtually unchanged, which indicates that the addition of W has similar strengthening effects to that of Re.

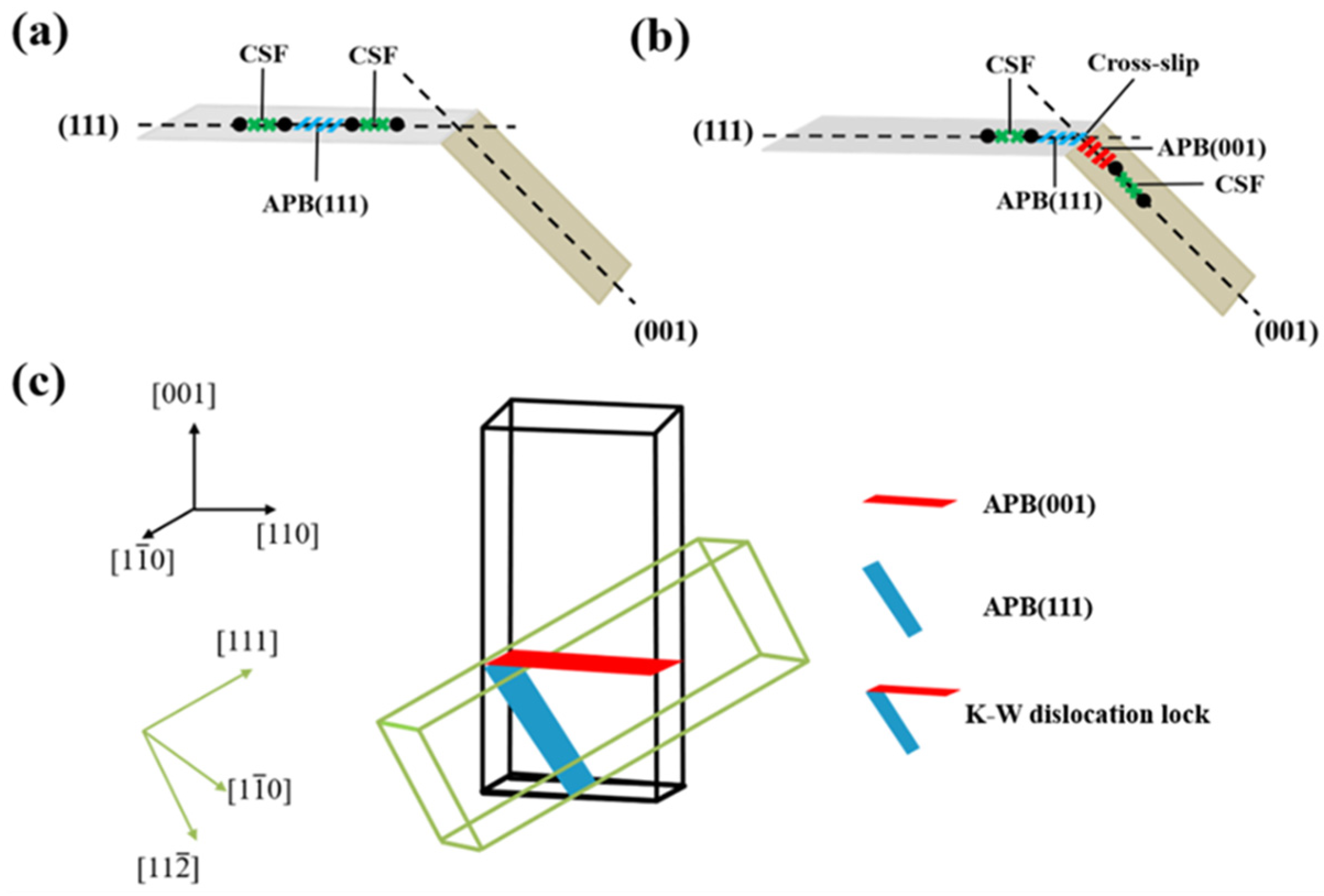
The anomalous flow behavior of the γ′ phase at high temperature, i.e., an increase in yield strengths with increasing temperature [15], can be attributed to the obstacle of Kear-Wilsdorf (K-W) dislocation lock [4] of the movement of subsequent dislocations. At the early stages of creep, a $1/2⟨110⟩\left\{111\right\}$ dislocation is first activated in the γ channels. With the increase in dislocation densities in the γ phase, a dislocation network is formed at the γ/γ′ interface, and some $1/2⟨110⟩\left\{111\right\}$ pairs can combine to form $⟨110⟩\left\{111\right\}$ super dislocations. Once inside the γ′ phase, these super locations will be separated to $1/2⟨110⟩\left\{111\right\}$ super-partial dislocation pairs connected by an anti-phase boundary (APB), i.e., $⟨110⟩\left\{111\right\}\to 1/2⟨110⟩\left\{111\right\}+\mathrm{APB}+1/2⟨110⟩\left\{111\right\}$ [16]. Then, the two $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations will further separate into $1/6⟨112⟩\left\{111\right\}$ Shockley partial dislocations separated by a complex stacking fault (CSF), i.e., $1/2⟨110⟩\left\{111\right\}\to 1/6⟨112⟩\left\{111\right\}+\mathrm{CSF}+1/6⟨112⟩\left\{111\right\}$, referred to Figure 1. That is to say, the decomposed $⟨110⟩\left(111\right)$ super dislocation consists of four Shockley dislocations separated by two CSFs and one APB. Since $1/6⟨112⟩\left\{111\right\}$ Shockley partials connected by the CSF cannot undergo a cross slip from the $\left\{111\right\}$ planes to the $\left\{001\right\}$ planes, a temporary recombination of $1/6⟨112⟩\left\{111\right\}$ Shockley partials to form a $1/2⟨110⟩\left\{111\right\}$ dislocation is required. As is well known, a high CSF energy means a narrow CSF region, and thus, a high level of CSF energy will be beneficial for the recombination of $1/6⟨112⟩\left\{111\right\}$ Shockley partials into $1/2⟨110⟩\left\{111\right\}$ dislocations. After two $1/2⟨110⟩\left\{111\right\}$ dislocations have formed by recombination, their elastic interactions can provide the driving force for a cross-slip of the leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocation from the {111} plane to the {001} plane. And a high anti-phase boundary energy ${\gamma }_{\mathrm{APB}}^{111}$ in the {111} plane relative to ${\gamma }_{\mathrm{APB}}^{001}$ in the {001} planes is more favorable for the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations [17]. In this case, a K-W dislocation lock can be formed after the cross slips of the leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocation. As a result, the subsequent movement of the trailing $1/6⟨112⟩\left\{111\right\}$ Shockley partials dislocation pair will be restricted, leading to an improvement in the creep resistance of the γ′ phase. Therefore, it is widely accepted that this cross-slip of screw dislocations should be responsible for the anomalous flow behavior of the γ′ phase at high temperature.

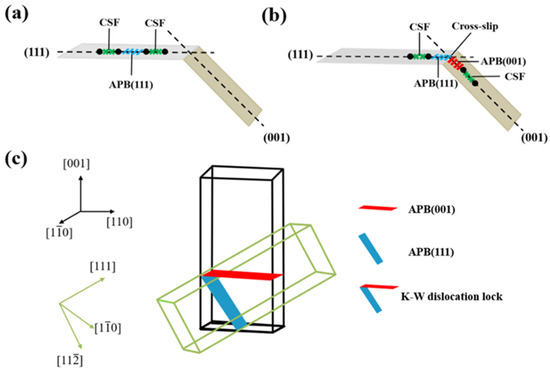
Figure 1. Schematic diagram of stacking faults (a) before cross-slip and (b) after cross-slip of $1/2[\overline{1}10](111)$ super-partial dislocations and (c) K-W dislocation lock.

Since the anomalous flow behavior of the γ′ phase was first reported in 1957 [18], and Kear et al. [19] pointed out that this anomalous flow behavior can be attributed to the cross-slips of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations, K-W dislocation locks have been widely discovered in nickel-based superalloys [20,21,22,23]. To evaluate the tendency of cross-slips of the abovementioned dislocations in L1₂ ordered alloys, a Paidar-Pope-Vitek (PPV) model was proposed in 1984 [24,25], in which the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations could take place only if an APB anisotropy ratio $\lambda$ = ${\gamma }_{\mathrm{APB}}^{111}/{\gamma }_{\mathrm{APB}}^{001}$ > $\sqrt{3}$. By the PPV model, Yu et al. [26] found that the addition of Re can promote the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations in the γ′ phase, and extra addition of Re seems to be more favorable [13]. It was revealed that the accelerated cross-slips mainly originated from an enlarged lattice misfit and an upraised APB energy ${\gamma }_{\mathrm{APB}}^{111}$ [27,28]. Moreover, Zhao et al. [29] found that a large number of Re and W atoms can even stabilize K-W dislocation locks in the γ′ phase and further impede the movement of subsequent dislocations. Obviously, Re and W play an important role in the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations in the γ′ phase. However, previous calculations [13,24,25,26] for APB anisotropy ratio $\lambda$ = ${\gamma }_{\mathrm{APB}}^{111}/{\gamma }_{\mathrm{APB}}^{001}$ were merely done using two separate models, in which the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations was separated into two irrelevant stages. In fact, the cross-slip of dislocations from $\left\{111\right\}$ to $\left\{001\right\}$ planes is a sequential and interrelated process. In the second stage of across-slips, there are some influences of the $\mathrm{APB}\left(111\right)$ generated in the first stage on the subsequent movement of dislocations in the $\left\{001\right\}$ planes. In this case, for the reconstruction of $\left(001\right)$ surface slab models, the impact of preexisting $\mathrm{APB}\left(111\right)$ on the anti-phase boundary energy ${\gamma }_{\mathrm{APB}}^{001}$ of $\mathrm{APB}\left(001\right)$ must be taken into account.

In this work, several hybrid $\left(001\right)$ slab models including $\mathrm{APB}\left(111\right)$ of L1₂-Ni₃Al(X) crystals with X = Re and W were first constructed to revisit the Re-effect in the dislocation slip mediated creep of the γ′-Ni₃Al phase. And then, a Suzuki segregation tendency of Re and W in $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$ and their preferential sites in Suzuki segregations were examined by ${\gamma }_{\mathrm{APB}}^{111}$ and ${\gamma }_{\mathrm{APB}}^{001}$. Finally, the effect of Re-segregation on the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations was investigated.

2. Calculation Method

2.1. Reconstruction of Cross-Slip Models

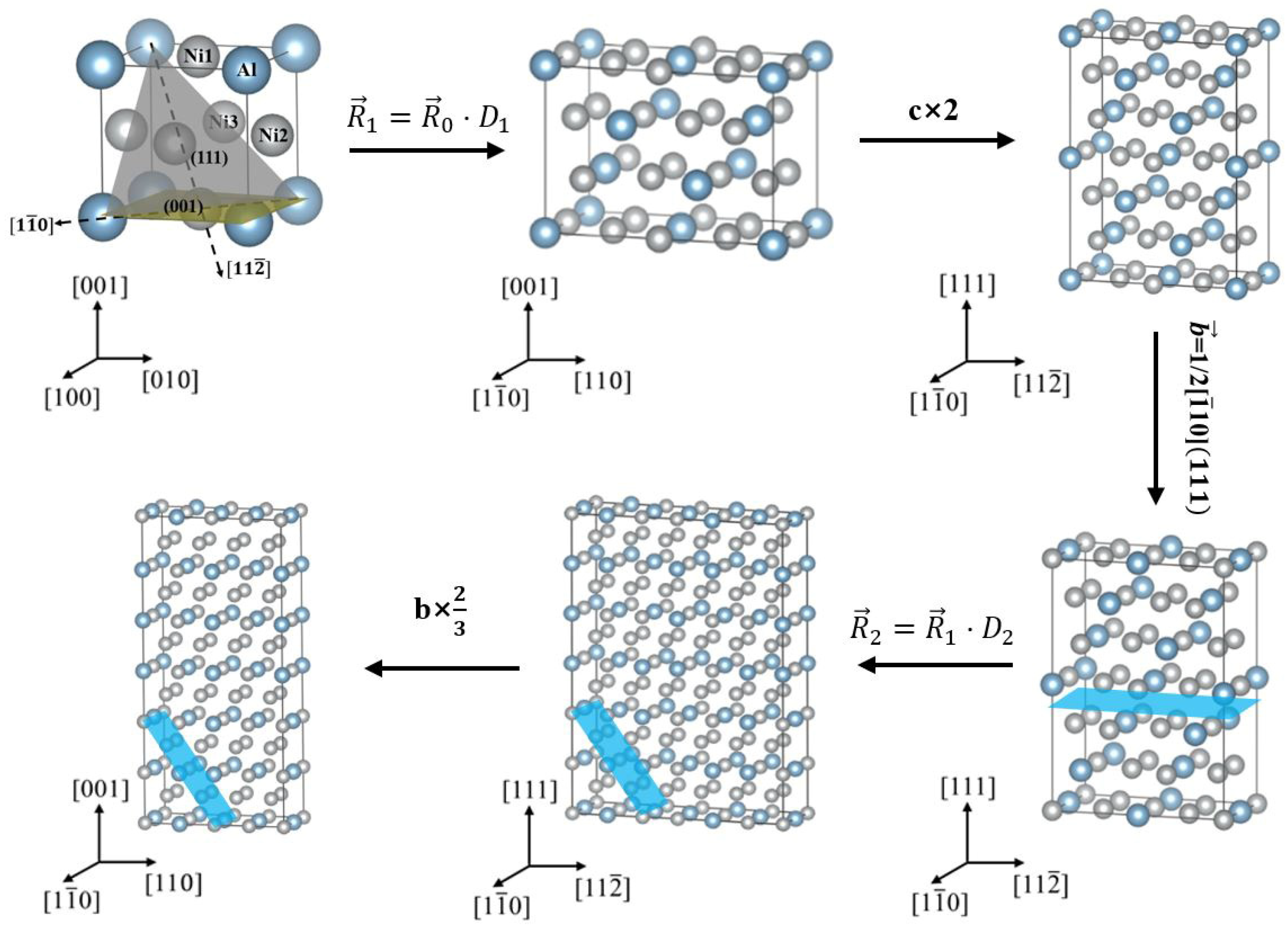
A $\left(111\right)$ slab model was first built using a redefined lattice method with rotation matrix $D_1$. Here, the shear direction $[\overline{1}10]$ and the slip plane $\left(111\right)$ were rotated to be parallel to lattice vector $\overrightarrow{a}$ and normal to lattice vector $\overrightarrow{c}$, as proposed by Roundy et al. and Ogata et al. [30,31]. In our calculation of the generalized stacking fault energies (Γ-surfaces), the atoms over the designated $\left(111\right)$ slip planes moved along the $[\overline{1}10]$ direction. As a result of shearing $\mathrm{b}={\mathrm{a}}_0/2$ in the $[\overline{1}10](111)$ direction, an anti-phase boundary could be generated in the $\left(111\right)$ slab model, named $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right)$ slab model (refer to Figure 2).

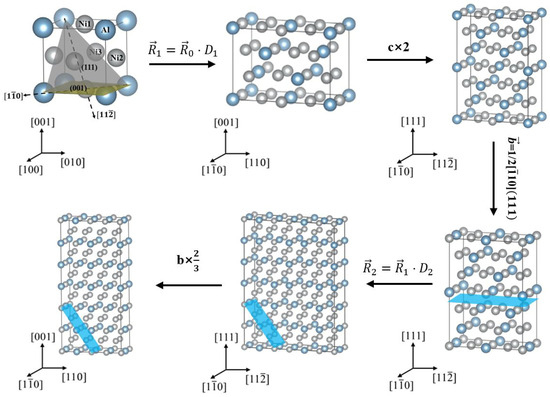
Figure 2. Schematic diagram of supercells reconstructed by matrix transformation. The gray, brown and blue shadows denote $\left(111\right)$ slipping planes, $\left(001\right)$ slipping planes, and $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right)$, respectively.

In view of the preexistence of an $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right)$ on $\left\{111\right\}$ plane before the leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocation cross-slips from the $\left\{111\right\}$ plane to the $\left\{001\right\}$ plane, a hybrid $\left(001\right)$ slab model with $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right)$ was reconstructed. In this case, an $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right)$ slab model of 48 atoms composed of 6 $\left(111\right)$ atomic layers was taken as the first cell, and then a hybrid $\left(001\right)$ slab model of 144 atoms and 12 $\left(001\right)$ atomic layers was created by a redefined lattice method with rotation matrix $D_2$. Herein, redefined lattice vectors ${\overrightarrow{R}}_1$ and ${\overrightarrow{R}}_2$ related to the $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right)$ slab model and hybrid $\left(001\right)$ slab model could be obtained by ${\overrightarrow{R}}_1={\overrightarrow{R}}_0·D_1$ and ${\overrightarrow{R}}_2={\overrightarrow{R}}_1·D_2$, respectively, where ${\overrightarrow{R}}_0$ represents the unit cell lattice vector. Their expressions are:

$${\overrightarrow{R}}_0=[{\overrightarrow{a}}_0,{\overrightarrow{b}}_0,{\overrightarrow{c}}_0]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

(1)

$${\overrightarrow{R}}_1=[{\overrightarrow{a}}_1,{\overrightarrow{b}}_1,{\overrightarrow{c}}_1]=\left[\begin{array}{ccc}1& 1& 2\\ \overline{1}& 1& 2\\ 0& \overline{2}& 2\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d} {\overrightarrow{R}}_2=[{\overrightarrow{a}}_2,{\overrightarrow{b}}_2,{\overrightarrow{c}}_2]=\left[\begin{array}{ccc}1& 3& 0\\ \overline{1}& 3& 0\\ 0& 0& 6\end{array}\right]$$

(2)

and the corresponding matrixes $D_1$ and $D_2$ are:

$$D_1=\left[\begin{array}{ccc}1& 1& 2\\ \overline{1}& 1& 2\\ 0& \overline{2}& 2\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d} D_2=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& \overline{2}\\ 0& 1& 1\end{array}\right]$$

(3)

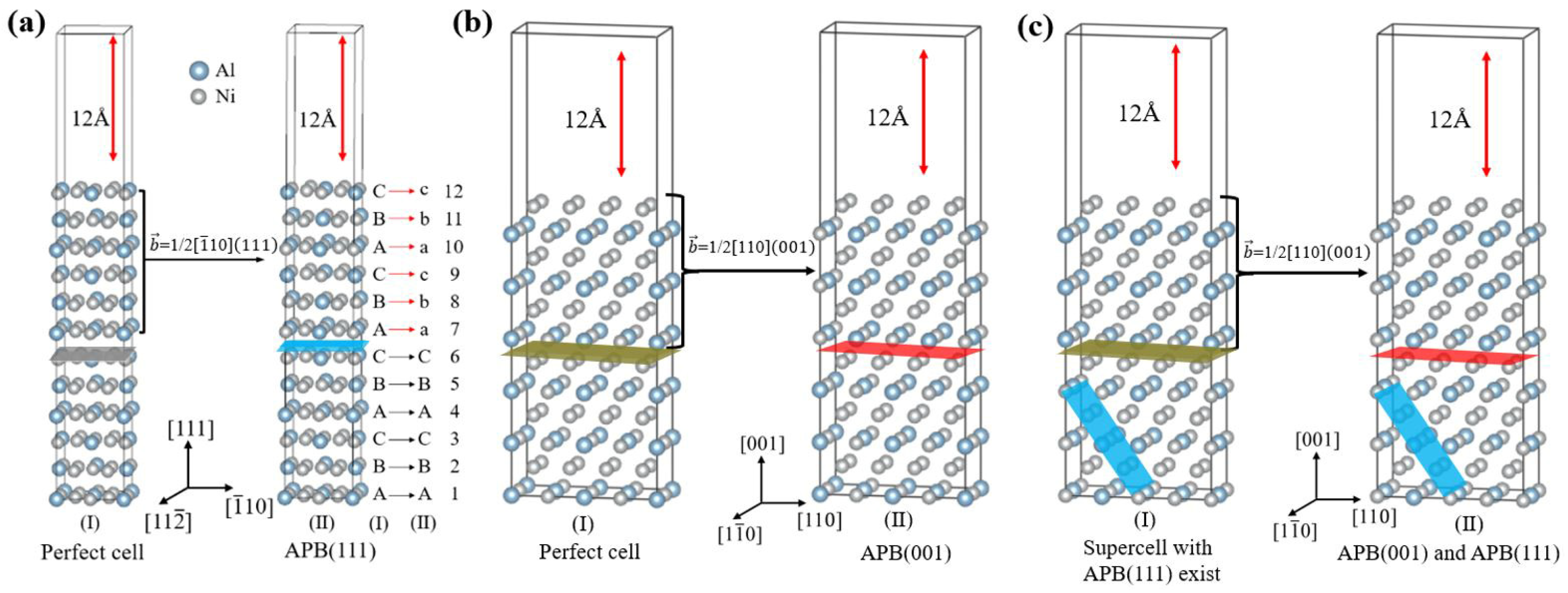
To compare the Γ-surfaces in the $\left(001\right)$ and $\left(111\right)$ surface models, this hybrid $\left(001\right)$ slab model of 144 atoms was stripped into the same 96 atoms as in the $\left(111\right)$ surface slab models along the $\left(110\right)$ plane, and a 12 Å vacuum region was added in the direction perpendicular to the slip plane to avoid interactions among faults in the two neighbor slabs. As atoms over the $\left(001\right)$ slip plane having been moved ($b=a_0/2$) in the $\left[110\right]\left(001\right)$ direction, a new anti-phase boundary, i.e., $\mathrm{A}\mathrm{P}\mathrm{B}\left(001\right)$, could be generated. Thus, a hybrid slab model of $\mathrm{A}\mathrm{P}\mathrm{B}\left(001\right)$ and $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right),$ associated with K-W dislocation lock, could be constructed, referred to Figure 3.

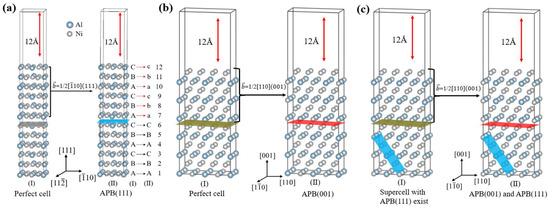
Figure 3. Schematic diagrams of (a) $\mathrm{APB}\left(111\right)$ in a simple model, (b) $\mathrm{APB}\left(001\right)$ in a simple model, and (c) $\mathrm{APB}\left(001\right)$ in a hybrid model for the calculation of Γ-surfaces. The gray and blue spares are Ni and Al atoms, respectively. The gray and brown shadows denote the $\left(111\right)$ and $\left(001\right)$ slipping planes, respectively. The blue and red shadows represent $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$, respectively.

2.2. Calculation Detail

First-principles calculations were performed using the Vienna ab initio simulation package (VASP) [32] based on density functional theory (DFT), in which a plane-wave basis set with a projector augmented wave (PAW) [33] is employed to describe the ion-electron interaction. For self-consistent field (SCF) calculation, the cutoff energy of plane wave functions was set at 400 eV, and the sampling of irreducible wedges of Brillouin zones was carried out with 7 × 5 × 1 regular Monkhorst–Pack grids of special k-points, corresponding to the 96-atom supercells. A conjugate gradient method [34] was utilized to optimize the geometry, and all atomic positions in the supercell were relaxed until the force on each atom was less than 0.009 eV/Å. The calculation of total energies and electronic structures was followed by cell optimization with an SCF tolerance of 1 × 10⁻⁵ eV under GGA-PBE potential [35].

Based on the different atomic environments around Al and Ni on the (001) and (111) surface models in the γ′-Ni₃Al phase, the site doped with Re or W was marked as $X_{\mathrm{A}\mathrm{l}}$, $X_{\mathrm{N}\mathrm{i}1}$, $X_{\mathrm{N}\mathrm{i}2}$ and $X_{\mathrm{N}\mathrm{i}3}$ (X = Re or W), corresponding to four non-equivalent sites, i.e., Al, Ni1, Ni2 and Ni3, in the Ni₃Al unit cell, as shown in Figure 2. As for the segregation of Re or W at Al, Ni1, Ni2 and Ni3 sublattice sites in $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$, the same surface slab models of 96 atoms as that in the calculation of Γ-surfaces of perfect L1₂-Ni₃Al crystals were named $X_{\mathrm{A}\mathrm{l}}$, $X_{\mathrm{N}\mathrm{i}1}$, $X_{\mathrm{N}\mathrm{i}2}$ and $X_{\mathrm{N}\mathrm{i}3}$ models, respectively.

3. Results and Discussion

3.1. A Comparison of Simple and Hybrid Models

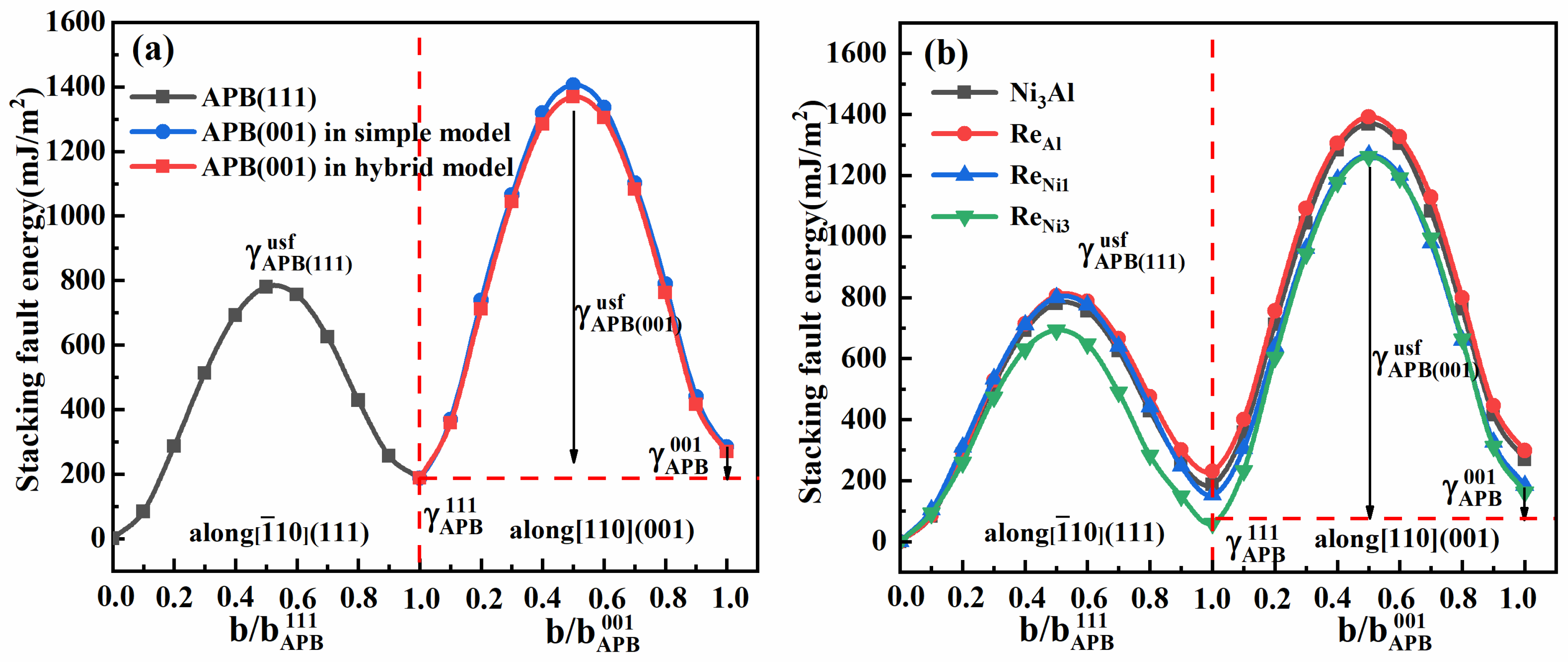
Generalized planar fault energy curves (i.e., Γ-surfaces) along the lowest energy path can provide a great deal of information on the nucleation and movement of dislocations. Since the anomalous flow behavior of the γ′-Ni₃Al phase in Ni-based SC superalloys at high temperature is closely related to the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations, the Γ-surfaces associated with the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations from $\left\{111\right\}$ to $\left\{001\right\}$ slipping planes were first calculated using two simple models, as shown in Figure 3a,b. The results are illustrated in Figure 4a and further listed in Table 1. One can see that APB energy ${\gamma }_{\mathrm{APB}}^{\left(111\right)}$ in the (111) planes and ${\gamma }_{\mathrm{APB}}^{001}$ in (001) planes was $187$ mJ/m² and $98$ mJ/m², respectively. Obviously, ${\gamma }_{\mathrm{APB}}^{111}$ is far higher than ${\gamma }_{\mathrm{APB}}^{001}$, which means that the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations was energetically favorable. However, it was observed that unstable stacking fault energies ${\gamma }_{\mathrm{APB}\left(111\right)}^{\mathrm{usf}}$ in the $[1\overline{1}0](111)$ direction and ${\gamma }_{\mathrm{APB}\left(001\right)}^{\mathrm{usf}}$ in the $\left[110\right]\left(001\right)$ direction were $780$ mJ/m² and $1219$ mJ/m², respectively. As a measure of the energy release rate for dislocation nucleation relevant to the ductile response of a material, the unstable stacking fault energy represents an intrinsic energy barrier for activated stacking faults [36]. A high ${\gamma }_{\mathrm{APB}\left(001\right)}^{\mathrm{usf}}$ means that $1/2\left[110\right]\left(001\right)$ dislocations in $\left(001\right)$ plane are difficult to nucleate compared with $1/2\left[110\right]\left(111\right)$ super partials in $\left(111\right)$ planes. As is well known [17], ${\gamma }_{\mathrm{APB}}^{111}$ strongly affects the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. As ${\gamma }_{\mathrm{APB}}^{111}$ being high, the tangential force component generated by the interaction of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations may significantly accelerate the cross-slip rate. In the PPV model [24,25], cross-slip can take place only if $\lambda ={\gamma }_{\mathrm{APB}}^{111}/{\gamma }_{\mathrm{APB}}^{001}>\sqrt{3}$, and a large ${\gamma }_{\mathrm{APB}}^{111}/{\gamma }_{\mathrm{APB}}^{001}$ means that $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations have a higher driving force from the $\left\{111\right\}$ to the $\left\{001\right\}$ planes. The present calculated $\lambda$ was $1.91>\sqrt{3}$, which demonstrated that the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations from $\left\{111\right\}$ to $\left\{001\right\}$ planes can occur in γ′ phase, as reported in previous literature [3,13,37,38,39,40].

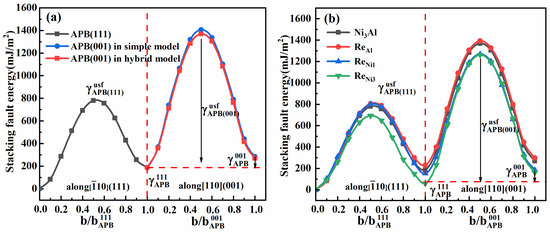
Figure 4. The Γ-surfaces of cross-slips of $1/2[\overline{1}10](111)$ super-partial dislocations from $\left(111\right)$ to $\left(001\right)$ planes in (a) Re-free and (b) Re-addition models.

Table 1. APB energies ${\gamma }_{\mathrm{APB}}$, unstable stacking fault energies ${\gamma }_{\mathrm{usf}}$ and APB anisotropy ratios $\lambda$ = ${\gamma }_{\mathrm{APB}}^{111}/{\gamma }_{\mathrm{APB}}^{001}$ in Re-free models.

Type of Stacking Fault	${\mathit{\gamma }}_{\mathbf{APB}}$ (mJ/m2)		${\mathit{\gamma }}_{\mathbf{usf}}$ (mJ/m2)	$\mathit{\lambda }$
	This Work	Reference	This Work	This Work	Reference
$\mathrm{APB}\left(111\right)$	187	215 [37], 195 [38], 178 [39]	780
$\mathrm{APB}\left(001\right)$ in simple model	98	74~102 [3], 110 [13], 104 [40]	1219	1.91	1.84 [13], 1.95 [37]
$\mathrm{APB}\left(001\right)$ in hybrid model	82		1182	2.28

Further, the Γ-surface of the leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations in the $\left\{001\right\}$ slipping planes were also calculated using the hybrid model including $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right),$ as shown in Figure 3c. The results are also illustrated in Figure 4 and listed in Table 1. From Figure 4a and Table 1, one can see that the ${\gamma }_{\mathrm{APB}}^{001}$ and ${\gamma }_{\mathrm{APB}\left(001\right)}^{\mathrm{usf}}$ in the hybrid model decreased by $16$ mJ/m² and $37$ mJ/m², respectively, relative to the corresponding simple model, indicating that the existence of $\mathrm{A}\mathrm{P}\mathrm{B}\left(111\right)$ is conducive to the formation of $\mathrm{A}\mathrm{P}\mathrm{B}\left(001\right)$ and can accelerate the K-W dislocation lock to be formed. Also, this tendency can be deduced by increase in $\lambda$ from 1.91 to 2.28. Since the anomalous flow stress of the γ′-Ni₃Al phase at high temperature mainly arises from the restriction of K-W dislocation locks to the movement of the trailing $1/2⟨110⟩\left\{111\right\}$ super-partial dislocation, the present hybrid model, which accurately describes the cross-slip of leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations, is undoubtedly more reasonable than the previous simple model. In the simple separated model, the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations is likely to be underestimated owing to a lack of interplay between $\mathrm{APB}\left(111\right)$ and dislocations.

3.2. Suzuki Segregation of Re at APB(111) and APB(001)

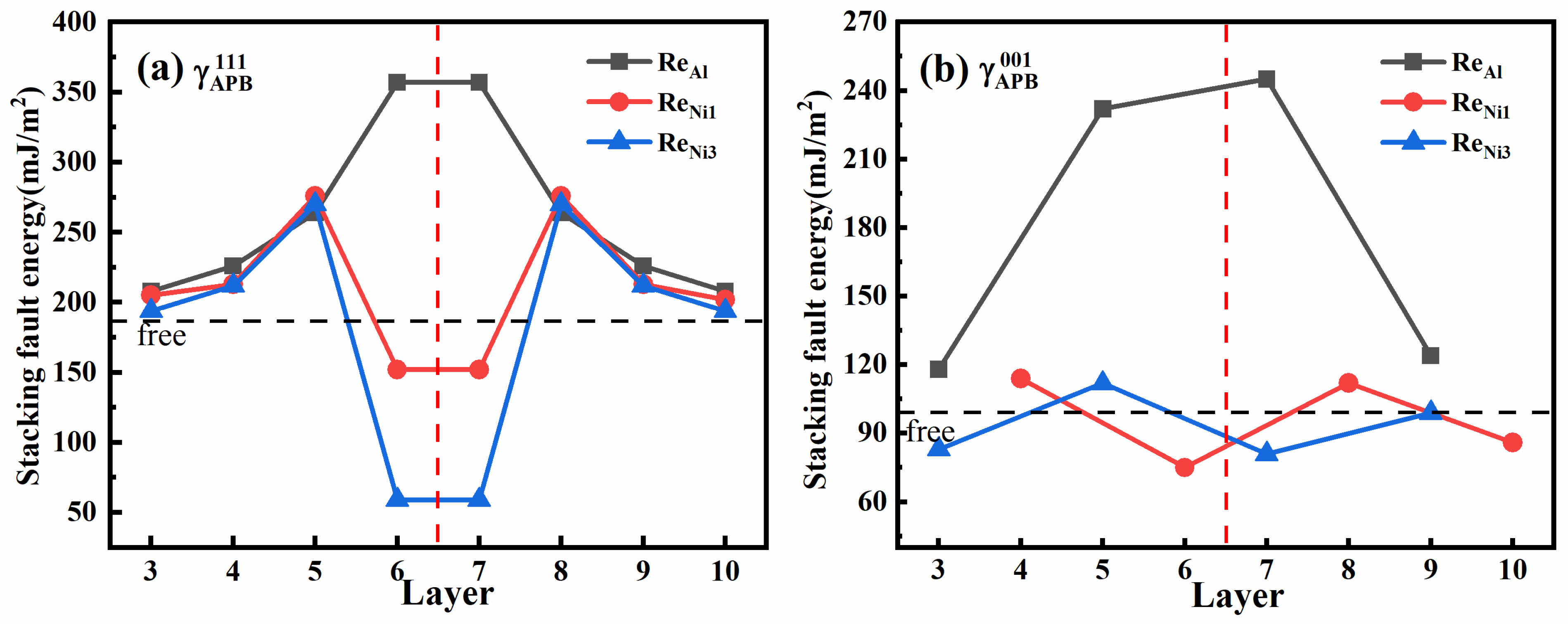
As an important strengthening element, Re mainly partitions in the γ phase, but some of them are able to enter the γ′ phase and preferentially occupy Al sublattice sites [41,42,43]. However, the question of whether Suzuki segregation occurs at stacking faults remains open. Smith et al. [44] first observed the enrichment of Re and W at superlattice extrinsic stacking fault (SESF) sites, with a depletion of Ni and Al in Ni-based SC superalloys. Later, a similar segregation of Re along superlattice intrinsic stacking fault (SISF) was discovered in CMSX-4 specimens [45,46]. But it is still unclear which sublattice site is substituted by Re at stacking faults. In order to explore the favorable site of Re in $\mathrm{APB}\left(111\right)$, the stacking fault energies of $\mathrm{APB}\left(111\right)$ were calculated by a series of substitutions of Re for Ni or Al at various sublattice sites in different atomic layers. The results are illustrated in Figure 5a. Relative to the Re-free model, a low APB energy ${\gamma }_{\mathrm{APB}}^{111}$ at the adjacent atom layer of $\mathrm{APB}\left(111\right)$ in Re-addition models indicated that Suzuki segregation of Re at $\mathrm{APB}\left(111\right)$ is energetically favorable. But, different from the preferential occupation of Re at Al sublattice sites in perfect Ni₃Al crystals [47], only Ni sublattice sites were energetically permissive. The order of ${\gamma }_{\mathrm{APB}}^{111}$ is ${\mathrm{Re}}_{\mathrm{Ni}3}$ < ${\mathrm{Re}}_{\mathrm{Ni}1}$ < Re-free < ${\mathrm{Re}}_{\mathrm{Al}}$, and the influence of the addition of Re on ${\gamma }_{\mathrm{APB}}^{111}$ is gradually weakened when the atomic layer is distant from the $\mathrm{APB}\left(111\right)$. These results clearly indicate that Re tends to segregate to $\mathrm{APB}\left(111\right)$ and preferentially occupies Ni sublattice sites, especially at Ni3 sublattice sites.

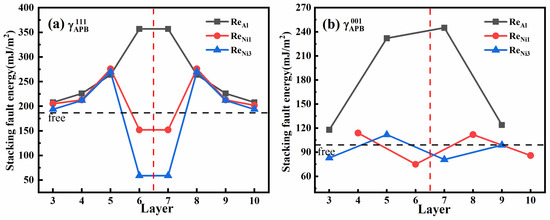
Figure 5. The variation of anti-phase boundary energies (a) ${\gamma }_{\mathrm{APB}}^{111}$ and (b) ${\gamma }_{\mathrm{APB}}^{001}$ with sublattice sites substituted by Re in different atomic layers. The red dotted line represents the fault plane of $\mathrm{APB}\left(111\right)$ or $\mathrm{APB}\left(001\right)$.

Further, the segregation tendency and preferential sites of Re in $\mathrm{APB}\left(001\right)$ were also investigated. The stacking fault energies ${\gamma }_{\mathrm{APB}}^{001}$ of $\mathrm{APB}\left(001\right)$, which are dependent on the substitution of Re for Ni or Al in different atomic layers, are shown in Figure 5b. Similar to the segregation of Re in $\mathrm{APB}\left(111\right)$, Figure 5b shows that the ${\gamma }_{\mathrm{APB}}^{001}$ in the adjacent atomic layer of $\mathrm{APB}\left(001\right)$ in the Re-addition model was lower than that in the Re-free model, indicating that Suzuki segregation of Re existed also in $\mathrm{APB}\left(001\right)$, and that only the substitution of Re for Ni was energetically permissive. The optimal segregation sites were merely Ni1 sublattice sites, rather than Ni3 sublattice sites.

In view of the fact that the partial replacement of Re by W scarcely influence the mechanical properties of nickel-based SC superalloys [14,48], the segregation tendency and preferential sites of W at $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$ were also investigated. A similar Suzuki segregation of W to Re occurred in $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$. For $\mathrm{APB}\left(111\right)$, the preferential site of W-segregation was as same as that of Re-segregation, but its optimal site changed to Ni3 sublattice sites in $\mathrm{APB}\left(001\right)$.

3.3. Re-Effects at Preferential Al Sublattice Sites

Previous investigations [13,26] have demonstrated that the addition of Re at preferential Al sublattice sites promotes the cross-slip of leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. As a revisiting, the effects of the addition of Re at preferential Al sublattice sites on the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations were studied firstly by previous simple models. The results are illustrated in Figure 4b and further tabulated in Table 2. In Figure 4b and Table 2, one can see that APB energy ${\gamma }_{\mathrm{APB}}^{111}$ and ${\gamma }_{\mathrm{APB}}^{001}$ and their ratio $\lambda ={\gamma }_{\mathrm{APB}}^{111}/{\gamma }_{\mathrm{APB}}^{001}$ in the ${\mathrm{Re}}_{\mathrm{Al}}$ model increased by $43$ mJ/m², $18$ mJ/m² and 0.07 relative to those values for a perfect Ni₃Al crystal, respectively. This upraised ${\gamma }_{\mathrm{APB}}^{111}$ indicates the leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations cross-slips from $\left\{111\right\}$ to $\left\{001\right\}$ planes to be accelerated [17], although their nucleation may have been restricted owing to an increase of $26$ mJ/m² in ${\gamma }_{\mathrm{APB}\left(111\right)}^{\mathrm{usf}}$. In this case, the K-W lock is easier to be formed. Consequently, the addition of Re at preferential Al sublattice sites are profitable for the improvement of creep strength of the L1₂-γ′ phase [13].

Table 2. APB energies ${\gamma }_{\mathrm{APB}}$, unstable stacking fault energies ${\gamma }_{\mathrm{usf}}$ and APB anisotropy ratios $\lambda$ = ${\gamma }_{\mathrm{APB}}^{111}/{\gamma }_{\mathrm{APB}}^{001}$ in Re-addition and W-addition models.

Calculation Model	Simple Model (Hybrid Model)
	$[\overline{1}10](111)$		$\left[110\right]\left(001\right)$
	${\mathit{\gamma }}_{\mathbf{usf}}$/ (mJ/m2)	${\mathit{\gamma }}_{\mathbf{APB}}$/ (mJ/m2)	${\mathit{\gamma }}_{\mathbf{usf}}$/ (mJ/m2)	${\mathit{\gamma }}_{\mathbf{APB}}$/ (mJ/m2)	$\mathit{\lambda }$
Perfect Ni3Al crystal	780	187	1219 (1182)	98 (82)	1.91 (2.28)
preferential sites of Re at Al sublattices	806	230	1231 (1162)	116 (68)	1.98 (3.38)
Re-segregation at Ni1 sublattice sites in $\mathrm{APB}\left(111\right)$	800	152	1231 (1115)	116 (32)	1.31 (4.75)
Re-segregation at Ni1 sublattice sites in $\mathrm{APB}\left(001\right)$	806	230	1132 (1101)	75 (30)	3.06 (4.67)
Re-segregation at Ni3 sublattice sites in $\mathrm{APB}\left(111\right)$	692	60	1231 (1202)	116 (102)	0.52 (0.59)
Re-segregation at Ni3 sublattice sites in $\mathrm{APB}\left(001\right)$	806	230	1183 (1174)	82 (86)	2.80 (2.67)
Preferential site of W at Al sublattice sites	806	220	1224 (1169)	112 (73)	1.96 (3.01)
W-segregation at Ni1 sublattice sites in $\mathrm{APB}\left(111\right)$	845	179	1224 (1053)	112 (32)	1.59 (4.71)
W-segregation at Ni1 sublattice sites in $\mathrm{APB}\left(001\right)$	806	220	1147 (1053)	91 (32)	2.42 (6.88)
W-segregation at Ni3 sublattice sites in $\mathrm{APB}\left(111\right)$	667	44	1224 (1194)	112 (89)	0.39 (0.49)
W-segregation at Ni3 sublattice sites in $\mathrm{APB}\left(001\right)$	806	220	1206 (1168)	72 (73)	3.06 (3.01)

Further, the above-mentioned Re-effect at preferential Al sublattice sites was also investigated using a hybrid model, as shown in Figure 3c. The result is illustrated in Figure 4b and further listed in Table 2. From Table 2, one can see that the ${\gamma }_{\mathrm{APB}\left(001\right)}^{\mathrm{usf}}$ and ${\gamma }_{\mathrm{APB}}^{\left(001\right)}$ in the ${\mathrm{Re}}_{\mathrm{Al}}$ model dropped by $20$ mJ/m² and $14$ mJ/m², respectively, relative to those values for the perfect Ni₃Al crystal, and the $\lambda$ increased by 1.1, indicating that the addition of Re at preferential Al sublattice sites is indeed beneficial for the cross-slip of leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. Compared with the values obtained using simple models, the ${\gamma }_{\mathrm{APB}\left(001\right)}^{\mathrm{usf}}$ and ${\gamma }_{\mathrm{APB}}^{001}$ decreased by $69$ mJ/m² and $48$ mJ/m², respectively, and the $\lambda$ value increased to 3.38 from 1.98, which indicates that the existence of $\mathrm{APB}\left(111\right)$ can facilitate the formation of K-W locks. Since an interplay between anti-phase boundary $\mathrm{APB}\left(111\right)$ and point defect ${\mathrm{Re}}_{\mathrm{Al}}$ was taken into account in the hybrid model, it is speculated the present results should be more accurate and reasonable for the assessment of cross-slips of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations in the γ′ phase at high temperature.

3.4. Effect of Re-Segregation on the Cross-Slip of Dislocations

As confirmed in Section 3.2, a Suzuki segregation of Re at $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$ took place along with the cross-slip of leading $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. In order to investigate the influence of Re-segregation on the cross-slips of another $1/2⟨110⟩\left\{111\right\}$ super-partial dislocation on the adjacent plane of previous slipping planes, several extra generalized planar fault energy curves were investigated on the basis of the optimal substitution of Re for Ni at $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$. In the simple models, Figure 4b and Table 2 show that for Re-segregation at Ni sublattice sites from its preferential Al sublattice sites the ${\gamma }_{\mathrm{APB}}^{111}$ dropped by $170$ mJ/m² and $78$ mJ/m² in the ${\mathrm{Re}}_{\mathrm{Ni}3}$ and ${\mathrm{Re}}_{\mathrm{Ni}1}$ models, respectively, leading to a reduction in $\lambda ={\gamma }_{\mathrm{APB}}^{111}/{\gamma }_{\mathrm{APB}}^{001}$ to 0.73 and 1.53 from 1.98, respectively. Since Re preferentially segregates to Ni3 sublattice sites in $\mathrm{APB}\left(111\right)$, a much smaller $\lambda$ than $\sqrt{3}$ in the ${\mathrm{Re}}_{\mathrm{Ni}3}$ model revealed that the Re-segregation in $\mathrm{APB}\left(111\right)$ was undoubtedly harmful for the cross-slip of new $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. However, it was noticed that relative to the preferential substitution of Re for Al, Re-segregation in $\mathrm{APB}\left(001\right)$ caused ${\gamma }_{\mathrm{APB}}^{001}$ to be lowered, resulting in an increase in the $\lambda$ in ${\mathrm{Re}}_{\mathrm{Ni}1}$ and ${\mathrm{Re}}_{\mathrm{Ni}3}$ models by 1.08 and 0.82, respectively. In this case, an upraised $\lambda$ seemed to imply that Re-segregation in $\mathrm{APB}\left(001\right)$ was favorable for the thickening of $\mathrm{APB}\left(001\right)$ and the formation of more K-W locks.

Further, the effects of Re-segregation in $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$ on the cross-slip of new $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations were also investigated using a reconstructed hybrid model. Compared with the simple models, Table 2 shows the decreases in ${\gamma }_{\mathrm{APB}}^{001}$ by $14$ mJ/m² and $45$ mJ/m², respectively, corresponding to Re-segregation at Ni3 sublattice sites in $\mathrm{APB}\left(111\right)$ and at Ni1 sublattice sites in $\mathrm{APB}\left(001\right)$. As a result, a slight increase in $\lambda$ from 0.52 to 0.59 in the ${\mathrm{Re}}_{\mathrm{Ni}3}$ model and an obvious elevation from 3.06 to 4.67 in the ${\mathrm{Re}}_{\mathrm{Ni}1}$ model was observed. These results clearly indicate that an interplay between point defect ${\mathrm{Re}}_{\mathrm{Ni}}$ and anti-phase boundary $\mathrm{APB}\left(111\right)$ may change the cross-slip rate of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. In the case of the former, a new K-W lock could not be formed, whereas more K-W locks would be generated in the latter. As for the W-segregation, a similar impact of Re-segregation on the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations was observed. That is, different from the deleterious effect of Re-segregation on $\mathrm{APB}\left(111\right)$, W-segregation at $\mathrm{APB}\left(001\right)$ was shown to promote the formation of K-W locks on new adjacent planes.

4. Conclusions

By means of lattice transition, a hybrid $\left(001\right)$ surface slab model including $\mathrm{APB}\left(111\right)$ was reconstructed to assess the cross-slip of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations in the γ′-Ni₃Al phase, and the impact of the addition of Re on the dislocation slipping mediated creep of the γ′-Ni₃Al phase at high temperature was revisited. We demonstrated that the preferential substitution of Re at Al sublattice sites is indeed favorable for cross-slips of $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations. In the hybrid model, it was revealed that the cross-slip rate could be accelerated by preexisting $\mathrm{APB}\left(111\right)$. A detailed calculation of stacking fault energies demonstrated that an obvious Suzuki segregation of Re existed in $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right),$ and Re preferentially occupied Ni sublattice sites. In this case, Re-segregation in $\mathrm{APB}\left(111\right)$ was found to be harmful for the cross-slip of new $1/2⟨110⟩\left\{111\right\}$ super-partial dislocations, whereas Re-segregation at $\mathrm{APB}\left(001\right)$ promoted the formation of more K-W dislocation locks, leading to the creep resistance of the γ′ phase to be improved. Moreover, a similar impact on the creep resistance of the γ′-Ni₃Al phase at high temperature following Re-segregation was observed in the case of W-segregation in $\mathrm{APB}\left(111\right)$ and $\mathrm{APB}\left(001\right)$.