Direct Experimental Calibration of Hosford–Coulomb and Modified Mohr–Coulomb Damage Criteria in AHSS Using Digital Image Correlation

Abstract

This study presents a Digital Image Correlation (DIC)-based experimental framework for the calibration of the Hosford-Coulomb (HC) and Modified-Mohr Coulomb (MMC) damage initiation criteria in an Advanced High Strength Steel (AHSS) DP1000. Three characteristic loading conditions in sheet metal forming—pure shear, uniaxial tension, and plane strain tension—were reproduced using flat specimens in a universal tensile testing machine, thus eliminating the need for costly and time-consuming tooling systems. An additional notch tension specimen was employed to validate the stress-state sensitivity of the proposed calibration approach. By integrating full-field strain data from DIC with tensile test results, stress–strain relationships were directly obtained without finite element modeling. The results confirm the effectiveness of dogbone, mini shear, and plane strain tension specimens in achieving proportional loading path histories up to fracture initiation, with constant stress state evolution during deformation. Comparison of the HC and MMC damage criteria reveals similar fracture loci, with the HC model exhibiting slightly higher resistance between shear and uniaxial tension conditions. This study discusses the suitability of a fully experimental DIC-based methodology for the calibration of stress-state-dependent damage initiation criteria. The results highlight the ability of the proposed methodology as a simplified and lower time-consuming alternative to traditional numerical assisted frameworks.

1. Introduction

The manufacturing of Body-in-White components in the automotive industry involves several sheet metal forming processes, such as stamping and deep drawing. However, the formability of Advanced High-Strength Steels (AHSSs) presents significant challenges due to their complex multiphase microstructure, high yield strength, and reduced sheet thicknesses [1,2,3]. These characteristics make AHSSs more susceptible to failure mechanisms not commonly observed in mild steels, particularly shear-dominated and edge fractures. Traditional Forming Limit Diagrams (FLDs) often fail to predict these fractures accurately, as they are based on necking-driven failure modes. Moreover, unlike uniaxial tension failure, shear-dominated failure mechanisms do not follow the classical void nucleation, growth, and coalescence mechanism [4].

To overcome these limitations, damage initiation criteria were introduced in the computer-aided engineering stage as a complementary tool for formability evaluation of AHSS components [5]. These criteria describe the fracture strain as a function of stress state(s), typically characterized by the stress triaxiality and the normalized Lode angle parameter. Stress triaxiality, defined as the ratio of hydrostatic stress ${\sigma }_H$, to the Von Mises equivalent stress ${\sigma }_{VM}$, influences the size and growth of voids, while the Lode angle parameters governs the void shape evolution, particularly important at low triaxialities [6]. Among various damage initiation models, the Modified-Mohr Coulomb model (MMC) criterion, developed by Bai and Wierzbicki [7], and the Hosford-Coulomb (HC) model, introduced by Mohr and Marcadet [8], account for the influence of the two stress states and have been used for fracture prediction, particularly in shear-dominated loading conditions of AHSSs.

Accurate determination of these damage initiation criteria coefficients requires experimental data covering a wide range of stress states, including shear, uniaxial tension, and plane strain tension. Experiments are performed up to fracture, and the corresponding displacement at fracture is recorded. Subsequently, numerical simulations are conducted, and the maximum equivalent strain obtained at the experimentally measured fracture displacement is taken as the fracture strain [9,10,11]. To ensure the reliability of the resulting fracture loci, the stress-state evolution at the fracture site must remain as linear and constant as possible during deformation. However, preserving proportional loading at the exact material point where fracture initiates is challenging [1]. Specimen geometry, test configuration, and boundary conditions often cause deviations from proportional loading, which can reduce the accuracy of calibrated model parameters.

Considerable research has focused on designing specimen geometries and test setups that maintain a consistent triaxiality evolution and homogeneous strain distribution at the fracture initiation site, aiming to prevent the tendency of edge cracking during tests. Various experimental techniques and specimen designs have been proposed to address these challenges [12,13,14,15,16]. For shear-dominated states, in-plane torsion tests and modified shear specimens were investigated. Yin et al. [17] successfully achieved fracture propagation under constant zero triaxiality and effectively mitigated edge cracking. Similarly, Grolleau et al. [18] modified the clamping device to make the procedure suitable for cyclic loading conditions. However, in-plane torsion tests are often costly due to the development and construction of specialized tools. Roth and Mohr [19] introduced a smiley-shear specimen that can be tested on universal tensile machines, eliminating the need for expensive tooling. Their results demonstrated the effectiveness of the specimen in achieving zero constant stress triaxiality. Khameneh et al. [20] conducted a comparative study of various shear specimen geometries, finding that a mini-shear specimen tested on DP1180 maintained zero constant triaxiality throughout the experiment.

In the context of uniaxial tension, both conventional dogbone specimens and central hole specimens have been used. However, central hole specimens produced contradictory results. While some studies suggested that central hole specimens provide a more consistent linear strain path until fracture near the hole boundary [21], others reported non-linear strain path histories [22]. It is critical to carefully select the central hole diameter and the manufacturing process to ensure reliable results [19].

Fracture during plane strain tension has often been attributed to the material’s load-carrying capacity in the out-of-plane shear direction. As with pure shear, maintaining constant triaxiality evolution under plane strain tension is challenging. Several specimen geometries and test configurations have been proposed [1,7,23,24]. Flat notch specimens offer simplified testing tooling approaches which are commonly used to induce plane strain tension conditions [22,25,26]. To avoid fracture initiation at the specimen edge width reduced region, and induce higher strain concentration at the specimen center, Wang et al. [27] designed a parallel groove. Complex tooling systems were tested by Roth and Mohr [19], reporting promising results with a V-bending testing configuration, which effectively produced linear strain path evolution under plane strain tension.

Butterfly tests, developed by Mohr and Henn [28], use a specially shaped specimen to study fracture behavior under low to intermediate stress triaxialities (0.0 to 0.6). The key advantage of this method was the ability to achieve various stress states by adjusting the specimen’s orientation, without changing its geometry [1]. The setup involved a biaxial testing machine, where the angle between the specimen and the loading axis controlled the stress triaxiality. Recent developments focused on improving stress and strain homogeneity at the fracture initiation point. Peshekhodov [29] enhanced the design to ensure strain localization regardless of load direction, while adaptive setups like those by Stockburger et al. [30] enable real-time adjustment of loading angles to maintain constant stress states, improving fracture model calibration.

In this paper, we employed a fully experimental Digital Image Correlation (DIC)-based methodology to calibrate two damage initiation criteria—the Hosford Coulomb (HC) and the Modified-Mohr Coulomb (MMC) for a AHSS DP1000 steel, which removed dependency on numerical modeling for calibration. The work also provides experimental evidence of proportional stress–strain evolution across different areas, offering a simplified and reproducible framework for AHSS fracture characterization. Four distinct stress states at the assumed fracture initiation point were achieved, namely shear, uniaxial tension, notch tension, and plane strain tension, using flat specimens tested exclusively on a universal tensile testing machine, thus eliminating the need for custom tooling. The strain field data were converted into stress-state variables to analyze the evolution of stress triaxiality and normalized Lode angle parameters. The aim was to assess the validity of the DIC-based approach to accurately determine the fracture initiation instant and onset of damage location as well as the ability of the chosen flat specimen designs to provide proportional loading path histories at the assumed fracture initiation point. Afterwards, the fracture locus of the HC and MMC models was constructed, exclusively relying on the simplified experimental methodology.

2. Materials and Methods

2.1. Material and Experimental Setup

The material investigated was a dual-phase AHSS DP1000 sheet with a nominal thickness of 1.05 mm, supplied by SSAB (Stockholm, Sweden). The material chemical composition, presented in Table 1, was obtained in a ‘Philips X’Unique II’ XRF Spectrometer (Eindhoven, The Netherlands). The mechanical tests were conducted on a Mecmesin Omni-Test electric tensile testing machine under ambient temperature. The experimental setup is shown schematically in Figure 1.

Table 1. Chemical composition of AHSS DP1000 (wt%).

$\mathit{F}\mathit{e}$	$\mathit{C}$	$\mathit{M}\mathit{n}$	$\mathit{S}\mathit{i}$	$\mathit{C}\mathit{r}$	$\mathit{N}\mathit{i}$	$\mathit{C}\mathit{o}$
95.790	0.080	2.900	0.620	0.350	0.160	0.100

Figure 1. Experimental setup.

To examine a wide range of stress states, four specimen geometries were utilized, as shown in Figure 2. Shear fracture was investigated using a mini-shear specimen, denominated ‘minishear0’, proposed by Peirs [31] and further adopted by Khameneh et al. [20] with fracture expected at the geometric center. Dogbone specimens with a gauge length of 20 mm and a width of 10 mm were used for pure uniaxial tension. Plane strain tension condition was assessed using flat specimens featuring a localized reduced-width region to promote fracture under the desired stress state. Notch tension specimens, incorporating a 20 mm notch radius as proposed by Roth and Mohr [19], represent an intermediate triaxiality between uniaxial and plane strain tension.

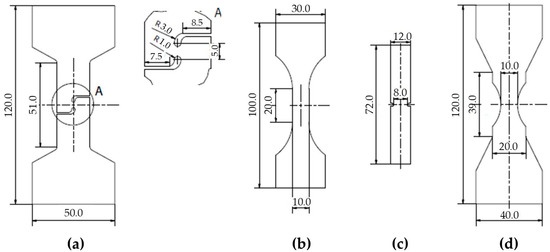
Figure 2. Stress state and corresponding specimens used in this study: (a) shear—minishear0; (b) uniaxial tension—dogbone; (c) plane strain tension—plane strain tension; (d) notch tension—notch tension.

All specimens were extracted along the rolling direction. Laser cutting was used as the manufacturing process. The inner region of the shear specimen was fabricated via electro-discharge machining to ensure dimensional accuracy and avoid heat-affected zones near the fracture region. Each test was repeated three times in accordance with ASTM E8 standards [32], at a constant crosshead speed of 0.5 mm/min. Force–displacement data were directly acquired from the test machine.

2.2. Digital Image Correlation

Two-dimensional DIC technology was employed to capture the full-field strain evolution during deformation. The specimen surface was first coated with a thin black matte paint layer, followed by a random white spray painting. The speckle pattern and size were controlled to achieve an average of 3–4 pixels per speckle, ensuring a good correlation performance.

Image acquisition was performed using a Basler 25-megapixel resolution camera equipped with a 50 mm Fujinon lens (Basler, Ahrensburg, Germany), positioned 120 mm from the specimen surface. Images were captured at 0.5 s intervals. The DIC acquisition was synchronized with force–displacement data through timestamp alignment. Displacement and strain fields were analyzed using VIC-2D Version 6.0 software provided by Correlated Solutions Inc. (Columbia, SC, USA). Key pre-processing parameters are summarized in Table 2.

Table 2. Preprocessing details of Digital Image Correlation.

Stress State	VSG [mm]	Subset [Pixel]	Step [Pixel]	Filter Size [−]	Image Scale [mm/Pixel]
Shear	2.05 ± 0.01	22.00 ± 3.00	6.50 ± 0.50	6.00 ± 1.00	0.04 ± 0
Uniaxial Tension	2.02 ± 0.03	21.67 ± 1.89	5.67 ± 0.47	5.00 ± 0	0.05 ± 0
Plane Strain Tension	2.04 ± 0.02	25.00 ± 0	8.00 ± 0	5.00 ± 0	0.04 ± 0
Notch Tension	2.04 ± 0.01	23.00 ± 0	6.00 ± 0	5.00 ± 0	0.04 ± 0

Following Jones and Iadicola [33], the Virtual Strain Gauge (VSG) defines the effective region of the image over which local strains are computed. It combines subset, step, and filter size according to the following:

$$VSG\left[\mathrm{m}\mathrm{m}\right]=\left[\left(\left(Filter Size-1\right)\times Step Size\right)+Subset Size\right]\times Image Scale$$

(1)

To ensure consistency across different stress states and minimize spatial averaging, a target VSG of 2 mm was selected for every stress state. Although smaller VSG values increase noise measurement, this value provided the best compromise between resolution and noise quality, particularly near fracture where strain gradients are higher. The subset size was chosen large enough to contain at least three distinct speckles while maintaining minimal spatial smoothing. The step size, which controls the points spacing analyzed during correlation, was chosen to be between one-fourth to one-third of the subset to ensure overlapping subsets and improved correlation stability. A small filter size was desired to allow for very localized strains as required in fracture characterization.

The Hencky strain tensor was adopted, as it provides an objective measure of true incremental strain even at large deformations.

Figure 3 presents the strain rate evolution for each specimen at the assumed fracture initiation point. Instantaneous strain rate was calculated according to Equation (2).

$$\dot{\epsilon }(t_i)={\displaystyle \frac{{\epsilon }_{i+1}-{\epsilon }_{i-1}}{2\Delta t}}$$

(2)

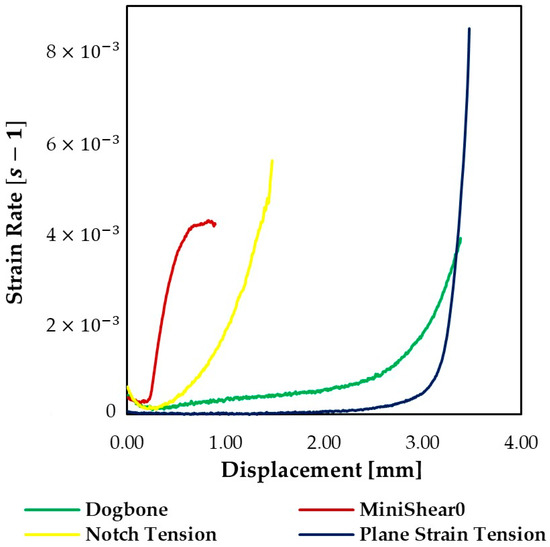
Figure 3. Strain rate evolution as a function of displacement at the assumed fracture initiation point.

A steep increase in the instantaneous strain rate is observed prior to fracture initiation. For the shear, uniaxial tension, notch tension, and plane strain tension stress states, the average strain rate was $3.15\times {10}^{-3}\pm 2.82\times {10}^{-4}$, $7.81\times {10}^{-4}\pm 1.71\times {10}^{-4}$, $1.67\times {10}^{-3}\pm 1.88\times {10}^{-4}$ and $5.43\times {10}^{-4}\pm 1.29\times {10}^{-4}$, respectively.

2.3. Transformation of Strain State to Stress State

The loading path to fracture refers to the evolution of mechanical fields and state variables at the location where ductile fracture initiates. In this study the evolution of equivalent plastic strain, ${\overline{\epsilon }}_p$, stress triaxiality, $\eta$, and the Lode angle parameter, $\overline{\theta }$, were analyzed. The fracture initiation instant was identified at the moment where the first measurable discontinuity in the displacement field was observed, and the onset of damage (i.e., fracture initiation point) corresponds to the element with the highest equivalent plastic strain. For the special case of the plane strain tension specimen, since the first discontinuity was only observed in the last recorded data point, where full material separation occurs, an equal weighted average of ten points along the width reduction region was used to represent the strain/stress path evolution.

Equivalent plastic strain was calculated according to the Von Mises criterion. Rather than relying on finite element simulations to derive stress states parameters, an analytical approach based on DIC data was used following Rickhey and Hong [34] to determine a representative $\beta$.

The stress triaxiality is expressed as

$$\eta ={\displaystyle \frac{1+\alpha }{3\sqrt{1-\alpha +{\alpha }^2}}}$$

(3)

where the principal stress ratio, $\alpha$, is given by

$$\alpha ={\displaystyle \frac{\beta +\frac{r_0}{1+r_0}}{\frac{r_0}{1+r_0}(\beta +1+\frac{1}{r_{90}})}}$$

(4)

The strain ratio $\beta$ corresponds to the ratio of the minor to major strain increments, $\beta =e_2$/$e_1$. The Lankford coefficients ($r_0$, $r_{45}$, $r_{90}$) were determined as the ratio of width to thickness strain increments, given by $r_{\theta }={d\epsilon }_W/{d\epsilon }_T$. Assuming volume conservation during plastic deformation, as in Equation (5), thickness strain was computed.

$${\epsilon }_x+{\epsilon }_y+{\epsilon }_z=0$$

(5)

Uniaxial tensile experimental testing using the dogbone specimen at the rolling, transversal, and diagonal directions were used to determine anisotropic coefficients. The average r-values, $\left(r_0,r_{45},r_{90}\right)=(0.682, 1.008, 0.906)$, indicate mild anisotropy.

The normalized Lode angle parameter, $\overline{\theta }$, was calculated as

$$\overline{\theta }=1-{\displaystyle \frac{2}{\pi }}·arcos[-{\displaystyle \frac{27}{2}}·\eta ·({\eta }^2-{\displaystyle \frac{1}{3}})]$$

(6)

The representative $\beta$ was calculated as the average slope of the $e_2-e_1$ curve at the assumed fracture initiation point, from which representative $\eta$ and $\overline{\theta }$ of each stress state were derived based on Equations (3) and (6), respectively.

2.4. Damage Initiation Criteria

2.4.1. Hosford–Coulomb (HC)

The fracture strain of the stress-state-dependent HC model is defined by Equation (7).

$${\overline{\epsilon }}_{\eta ,\overline{\theta }}^f={b(1+c)}^{1/n}{\left({\left\{{\displaystyle \frac{1}{2}}\left({\left(f_1-f_2\right)}^a+{\left(f_2-f_3\right)}^a\right)+{\left(f_1-f_3\right)}^a\right\}}^{1/a}+c\left(2\eta +f_1+f_3\right)\right)}^{-1/n}$$

(7)

The material transformation constant $n$ was assigned a value equal to the strain hardening exponent of DP1000 (n = 0.08). The HC model parameters $\left\{a,b,c\right\}$ were identified following the procedure proposed by Roth and Mohr [19]. To determine $b$ and $c$, three loading conditions—uniaxial tension, pure shear, and plane strain tension—were employed by solving Equations (8) and (9), whereas $a$ was obtained by implicitly solving Equation (10).

$$b={\overline{\epsilon }}_{UT}^f$$

(8)

$$c={\displaystyle \frac{1-{\left(\frac{{\overline{\epsilon }}_{PST}^f}{{\overline{\epsilon }}_{SH}^f}\right)}^n}{\frac{2}{\sqrt{3}}{\left(\frac{{\overline{\epsilon }}_{PST}^f}{b}\right)}^n+{\left(\frac{{\overline{\epsilon }}_{PST}^f}{{\overline{\epsilon }}_{SH}^f}\right)}^n-1}}$$

(9)

$${\left(1+2^{a-1}\right)}^{1/a}=\sqrt{3}\left(1+c\right){\left({\displaystyle \frac{b}{{\overline{\epsilon }}_{SH}^f}}\right)}^n$$

(10)

2.4.2. Modified-Mohr–Coulomb (MMC)

The relationship describing the MMC fracture strain is presented in Equation (11).

$${\overline{\epsilon }}_{\eta ,\overline{\theta }}^f={\left\{{\displaystyle \frac{A}{c_2}}\left[c_3+{\displaystyle \frac{\sqrt{3}}{2-\sqrt{3}}}\left(1-c_3\right)\left(sec\left({\displaystyle \frac{\overline{\theta }\pi }{6}}\right)-1\right)\right]\left[\sqrt{{\displaystyle \frac{1+c_1^2}{3}}}cos\left({\displaystyle \frac{\overline{\theta }\pi }{6}}\right)+c_1\left(\eta +{\displaystyle \frac{1}{3}}sin\left({\displaystyle \frac{\overline{\theta }\pi }{6}}\right)\right)\right]\right\}}^{-1/n}$$

(11)

The power hardening law parameter was set equal to $A=1418.16$. The MMC model parameters $\left\{c_1,c_2,c_3\right\}$ were identified from the best fit of ${\overline{\epsilon }}_{\eta ,\overline{\theta }}^f$ for all three investigated stress states by solving Equation (12).

$$\min {\displaystyle \frac{1}{N}}\sum _{j=1}^N\left|{\displaystyle \frac{{\overline{\epsilon }}_{MMC}^f-{\overline{\epsilon }}_{Obs}^f}{{\overline{\epsilon }}_{Obs}^f}}\right|$$

(12)

where $N$ represents the total number of experiments, ${\overline{\epsilon }}_{MMC}^f$ denotes the predicted fracture strain, and ${\overline{\epsilon }}_{Obs}^f$ is the experimentally observed fracture strain.

3. Results and Discussion

3.1. Fracture Initiation Assessment

Figure 4 illustrates the force–displacement curves obtained from the tensile testing machine, alongside the corresponding strain evolution at the assumed fracture initiation point, as captured through Digital Image Correlation (DIC). Fracture initiation sites vary according to the imposed stress state. In the uniaxial tension and notch tension specimens (Figure 4b,d), fracture initiated near the geometric center, where the strain was concentrated in an inner region of the specimens. In the shear specimen (Figure 4a), the strain field was homogeneously distributed along a narrow shear band which formed a well-defined fracture line, whereas in the plane strain tension specimen, fracture occurred within the reduced width region as expected.

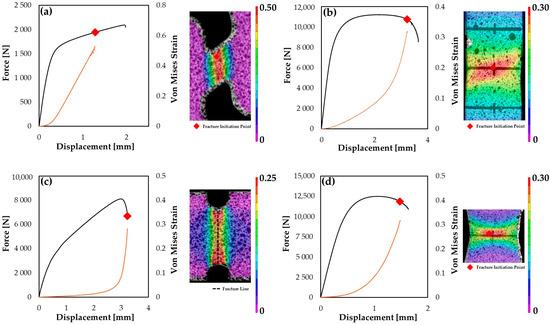
Figure 4. Load vs. displacement curves for different stress states with the corresponding Von Mises strain evolution on the secondary ordinate axis: (a) shear; (b) uniaxial tension; (c) plane strain tension; (d) notch tension.

It is generally accepted that fracture occurs when there is sudden drop in the externally applied load with respect to displacement. The ductility of damage initiation criteria and the resulting fracture locus are highly dependent on the assumed fracture initiation instant and the corresponding onset of damage in the material characterization specimens. The loading path history is extracted at the onset of damage up to the fracture initiation instant, which is then used to calibrate the fracture locus.

Based on our DIC methodology, fracture initiation in all specimens occurred after the maximum force was reached, except for the shear specimen, where the first discontinuity was observed prior to the peak load. The gradual force reduction observed in the dogbone and notch tension specimens reflects void growth and coalescence, which are typical of stress triaxialities close to pure uniaxial tension. The DIC-based fracture initiation instant and onset of damage assessment are validated since fracture initiation is defined to occur when the material was experiencing loss of global load-bearing capacity, as expected in this range of stress states, and within the central gauge area region of highest strain localization.

For the plane strain tension specimen, a sudden load drop was observed after the maximum force was reached. The plastic deformation concentrates at the reduced-width region. Damage propagation was rapid, and fracture initiation instant was defined as the point of complete material separation. Given the relatively low image acquisition interval of 0.5 s, fracture initiation identified using the DIC approach coincides with final fracture, which is considered acceptable for this stress state.

Special care should be taken for the shear specimen since the first discontinuity was observed well before maximum force was reached. Deformation concentrated along a narrow shear band before fracture with the onset of damage localized in this region. The early observable discontinuity could be explained by the well-known microcrack formation under shear-dominated stress states. However, the material’s global load-bearing capacity (Figure 4a) is not yet affected, as strain hardening continues until an abrupt post-peak load drop occurs.

Overall, the DIC-based determination of the fracture initiation instant is particularly sensitive to the density and quality of the speckle pattern. For the dogbone, notched tension, and plane strain tension specimens, the speckle pattern quality was adequate, as fracture initiation occurred in the expected deformation region (i.e., after the maximum force was reached). In the mini shear specimen, however, due to the small region where fracture occurs, image correlation was more sensitive to speckle pattern density and paint deterioration, which may explain the premature definition of fracture initiation. Therefore, the fracture strain measured in the shear stress state can only be considered as representing a lower bound for fracture strain.

3.2. Strain States

The objective of the material characterization was to analyze the stress–strain evolution at the assumed fracture initiation point across a wide range of stress states, which were later used to determine the coefficients of damage initiation criteria. The predictive accuracy of these criteria depends on maintaining proportional loading conditions at the fracture site. Deviations from proportional loading introduce variations in strain path evolution, affecting the material’s formability and reducing the reliability of the damage initiation models.

The strain path evolution at the fracture initiation point was evaluated through the relationship between major and minor strains (ε1-ε2) and the strain ratio β as a function of equivalent strain, as depicted in Figure 5. From Figure 5a, the slope of each strain path represents the strain ratio $\beta ={\epsilon }_2/{\epsilon }_1$. The nearly linear evolution and close agreement with the theoretical ideal paths indicate minimal rotation of principal strain directions and stable loading conditions. In Figure 5b, the constant β with increasing equivalent strain confirmed the suitability of the minishear0, dogbone, and plane strain tension specimens for accurately reproducing their target stress states. Such proportional evolution minimizes the uncertainty introduced by non-linear strain paths and enhances the robustness of damage model parameter identification.

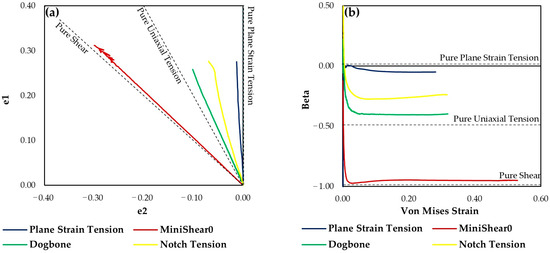
Figure 5. Strain field data evolution extracted from DIC at the assumed fracture initiation point: (a) major strain (ε1) vs. minor strain (ε2); (b) Beta vs. Von Mises strain.

The representative $\beta$ values, summarized in Table 3, deviate slightly to moderately from theoretical values: 4% for pure shear, 24% for uniaxial tension, and 1% for plane strain tension. The notch tension specimen followed a strain path which starts near the uniaxial tension condition but deviates slightly, indicating a stress state between uniaxial tension and plane strain tension. The strain path remained relatively linear, suggesting controlled deformation, though a late stage deviation from the ongoing linearity was noticed, which did not affect the overall linearity since trend line R² = 0.99.

Table 3. Representative $\beta$ and corresponding stress state values for each test condition.

Specimen	Fracture Strain ${\overline{\mathit{\epsilon }}}_{\mathit{f}}$	Representative β	Triaxiality η	Normalized Lode Angle $\overline{\mathit{\theta }}$
Shear	0.42 ± 0.11	−0.96 ± 0.01	−0.04 ± 0.00	−0.12 ± 0.01
Uniaxial Tension	0.35 ± 0.02	−0.38 ± 0.02	0.34 ± 0.01	0.96 ± 0.02
Notch Tension	0.31 ± 0.03	−0.24 ± 0.01	0.44 ± 0.00	0.63 ± 0.01
Plane Strain Tension	0.27 ± 0.05	0.01 ± 0.06	0.57 ± 0.03	0.06 ± 0.05

3.3. Stress States

Figure 6 presents the evolution of stress triaxiality and normalized Lode angle parameter for each investigated loading condition. These parameters govern the stress state dependency of ductile fracture and are therefore critical for calibrating the HC and MMC damage initiation criteria.

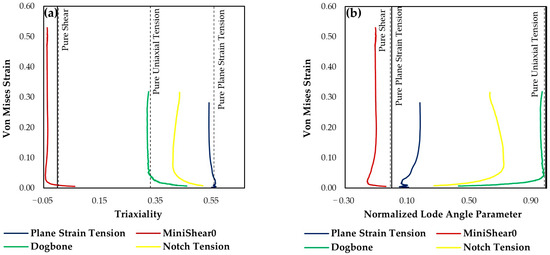
Figure 6. Equivalent strain evolution at the assumed fracture point as a function of (a) stress triaxiality; (b) normalized Lode angle parameter.

During plastic deformation, the stress state evolution was relatively stable across all specimens. As shown in Figure 6a, the stress triaxiality remained nearly constant throughout plastic deformation for all tests, confirming the proportional loading conditions indicated by the strain path analysis. The uniaxial tension specimen exhibited a triaxiality close to the theoretical value of 0.33, while the plane strain tension specimen almost reached 0.57, consistent with ideal conditions. The minishear0 specimen displayed a slightly negative triaxiality (≈−0.04), indicating a shear-dominated stress state. Even at higher equivalent strain, the triaxiality evolution remained constant. The notch tension specimen exhibited an intermediate and progressively increasing triaxiality, reflecting the transition from uniaxial tension toward plane strain tension as deformation localizes near the reduced width region.

With respect to the equivalent strain evolution as a function of the normalized Lode angle parameter (Figure 6b), the dogbone specimen reproduced the ideal value near 1.0, characteristic of uniaxial tension. The minishear0 specimen showed a small negative deviation from zero, while the plane strain specimen exhibited a slightly positive deviation: during plastic deformation, the normalized Lode angle parameter was observed to evolve progressively toward the uniaxial tension stress state, consistent with the trend noted in the stress triaxiality evolution. Comparable behavior was identified for the notch tension specimen, which likewise approached a uniaxial tension stress state as deformation progress. These deviations indicate minor variations in the local stress state but do not significantly affect the overall proportionality of loading.

The observed stress state evolution aligns with the findings of Khameneh et al. [20], who reported a stable shear triaxiality close to zero for DP1180 using a similar mini shear geometry. In the present study, the ideal condition was achieved with a 0 mm offset, while Khameneh et al. required −1 mm offset to achieve the closest condition to pure shear, highlighting that small geometric and strength differences within the same AHSS family can influence the stress state evolution at the fracture initiation point. Similarly, the plane strain results are consistent with Caro et al. [35], who observed comparable triaxiality levels for Alloy 718 under analogous deformation modes.

3.4. Damage Initiation Criteria

The proportional loading conditions achieved for the specimens under their representative stress states ensured consistent and reliable determination of the HC and MMC damage initiation criteria. Both models describe the material fracture locus in terms of fracture strain as a function of stress triaxiality and normalized Lode angle parameter, as shown in Figure 7.

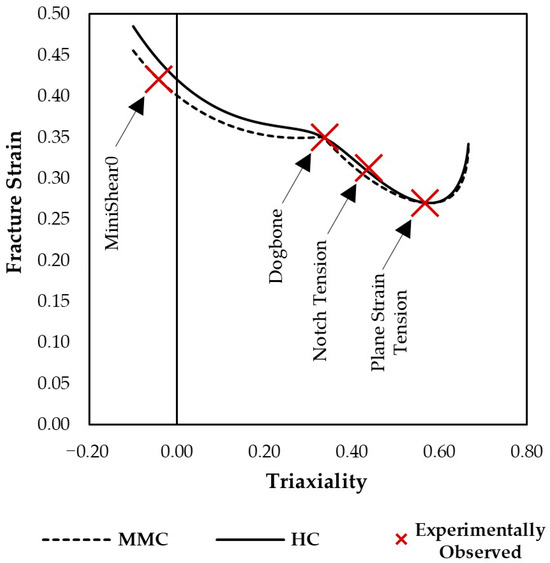
Figure 7. Fracture locus of the HC and MMC damage initiation models.

The fracture envelope of both models revealed that the material exhibited its highest ductility under shear-dominated conditions, with fracture strain progressively decreasing as the stress triaxiality increases. This behavior is consistent with the ductility–triaxiality relationship reported for AHSSs such as DP and TRIP grades [8,20,36,37,38,39,40]. At high stress triaxialities, the increased hydrostatic stress component promotes void nucleation and growth, whereas under low triaxialities ranges, the stress state promotes shear-dominated localization, allowing greater plastic deformation before fracture, rather than the conventional void growth and coalescence.

The MMC model provides slightly more conservative predictions under shear-dominated stress states. This difference aligns with the motivation for developing the HC criterion, that is to improve predictive accuracy under low triaxiality and shear-dominated loading [8]. The comparison between experimental and predicted fracture strains (Table 4) confirmed that both models accurately described the material behavior for uniaxial tension and plane strain tension, whereas the HC model better reproduced the experimental response for intermediate stress states between uniaxial tension and plane strain tension such as the notch tension condition.

Table 4. Fracture strain prediction of the HC and MMC model, the experimentally observed values, and the respective absolute error for each stress state.

Stress State	HC $(\mathit{a}=1.73;\mathit{b}=0.35;\mathit{c}=0.03)$			MMC $({\mathit{c}}_1=0.03,{\mathit{c}}_2=672.42,{\mathit{c}}_3=0.88)$
	Predicted	Observed	Abs. Error	Predicted	Observed	Abs. Error
Shear	0.44	0.42	5.47%	0.42	0.42	1.30%
Uniaxial Tension	0.35	0.35	0.35%	0.34	0.35	0%
Plane Strain Tension	0.27	0.27	0.12%	0.27	0.27	0%
Notch Tension	0.31	0.31	1.79%	0.30	0.31	4.32%

The 3D representations of the HC and MMC fracture loci, along with the loading path history of the three representative stress states are presented in Figure 8.

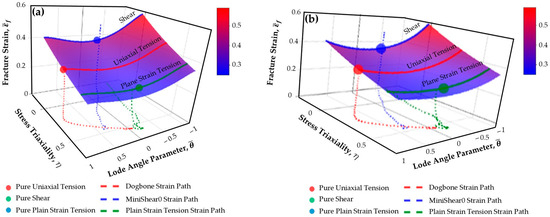
Figure 8. Three-dimensional fracture locus of the damage initiation criteria: (a) HC; (b) MMC.

The lower the stress triaxiality, the higher the influence of the Lode angle parameter in the fracture strain. This is because at higher triaxialities, fracture is primarily governed by hydrostatic tension, and the influence of the Lode angle parameter becomes less prominent. On the other hand, at low stress triaxialities, the damage evolution is dominated by microcrack evolution rather than void growth and coalescence. This physical phenomenon of damage evolution leads to a dependence on the Lode angle parameter, which is able to capture such damage evolution. This influence is better captured for the investigated AHSS DP1000 steel rather than in the high-strength AHSS grade DP1180 studied in the work of Khameneh [20], where a less pronounced influence of the Lode angle parameter between 0 and 1, for low stress triaxialities, close to 0, is noticed.

4. Conclusions

This study evaluated the suitability of a DIC-based experimental methodology for calibrating the HC and MMC damage initiation criteria for the AHSS DP1000 by investigating the ability of the employed specimen designs to deliver proportional loading conditions at the DIC-predicted onset of damage. The results can be summarized as follows:

• The proposed simplified methodology enabled the characterization of the HC and MMC fracture loci, providing a time-efficient and direct experimental approach. By allowing the extraction of loading path histories at the assumed onset of damage, the DIC-based method offers an alternative, reducing reliance on finite element (FE) modeling.
• The DIC-predicted onset of damage and fracture initiation instant are in accordance with the expected location in the load drop segment of the global force vs. displacement curve for the plane strain tension, uniaxial tension, and notch tension specimen.
• Similarly to FE modeling, where mesh quality influences strain estimations, DIC-based strain measurements are sensitive to the VSG size. The chosen approach of targeting a relatively small VSG of 2 mm across all stress states and specimen geometries allowed direct comparison of strain measurements, while mitigating displacement noise.
• The main limitation of the DIC-based methodology lies in its sensitivity to the definition of the onset of damage and fracture initiation instant, which depends on speckle pattern quality. A proper refinement of image scale is recommended for fracture modeling purposes, particularly in small and foreseeable fracture initiation regions. Moreover, as 2D DIC captures only surface strains, cracks developing under in-plane deformation conditions are neglected.
• The employed flat specimen geometries successfully produced the targeted stress states—shear, uniaxial tension, and plane strain tension—for the AHSS DP1000. The assumption of proportional loading was found to be satisfied at the onset of damage across all deformation modes, demonstrating the suitability of the proposed method.
• Both the HC and MMC criteria accurately captured the experimentally observed decrease in fracture strain with increasing stress triaxiality. The MMC model provided slightly more conservative predictions under low triaxiality conditions, while the influence of the Lode angle parameter was found to be significant primarily at low triaxialities.