Computational Model Verification and Validation of Elastoplastic Buckling Due to Combined Loads of Thin Plates

Abstract

Thin plates are widely used in various engineering applications. In some cases, these structural components may buckle due to compressive loads, which can be aggravated by lateral loads. Several authors have studied the elastoplastic buckling behavior of thin plates considering parameters such as material and geometric properties, support conditions, and initial out-of-plane imperfections. Some studies have also investigated the effects of notches and holes on the ultimate buckling stress of thin plates. The main goal of the present work is to verify and validate a computational model developed using the Finite Element Method via ANSYS^® software, to simulate the mechanical behavior of metallic plates under uniaxial or biaxial compression combined with lateral load. The proposed numerical model was verified and validated by comparing its results with analytical, numerical, and experimental solutions found in the literature, reaching maximum differences and errors of around 5%. In sequence, the verified and validated computational model was used in a simple case study: a simply supported plate with a centered rectangular perforation and subjected to an in-plane compressive biaxial load combined with a lateral load, considering five different metallic materials: AISI 4130 steel, AH-36 steel, spheroidal graphite iron (SGI), compact graphite iron (CGI) and Al 7075-T651 aluminum alloy. The results obtained are consistent and, as expected, prove the applicability of the proposed computational model. From this, the biaxial elastoplastic buckling behavior was evaluated, indicating that among the studied cases the higher ultimate stress and the smallest maximum deflection were achieved, respectively, by the plates made of AISI 4130 steel and AH-36 steel.

1. Introduction

Thin plates are commonly used in aircraft structures, ship hulls, or automobiles, and are frequently exposed to biaxial compressive loads in their plane. In several industrial or engineering applications, they are required to withstand different load types, which may be in-plane (compression, tension, shear, etc.) and/or out-of-plane (bending, torsion, etc.) [1]. In addition, due to uniaxial or biaxial compressive loads, the thin plates can suffer an unwanted phenomenon known as buckling, which can be aggravated if the compressive loads are combined with lateral loads, causing a significant reduction in the buckling resistance of the structure [2,3].

Buckling is a problem of great concern in the structural engineering field, being one of the most common instability phenomena. Some of the main parameters that are generally considered in the project of thin metallic plates include material properties, geometric properties (width/thickness ratio and aspect ratio), support conditions, and initial out-of-plane imperfections [4,5,6].

Plate buckling can occur in two forms: the first is elastic buckling, which occurs when the plate is slender and instability occurs in the elastic regime of the material; the second form is elastoplastic buckling, which is characterized when the plate reaches the plastic state of the material before the occurrence of elastic buckling because as the load increases, the stresses in all points of the plate will increase in the same proportion, and collapse may occur due to loss of strength [2,7].

In this sense, the elastoplastic buckling behavior of plates has been numerically investigated by several authors. Rasmussen et al. [8] carried out experimental and numerical analysis of the elastoplastic buckling of simply supported thin plates subjected to uniaxial compressive loading. The material used was UNS31803 stainless steel, the plate’s thickness was 3 mm, with nominal widths of 125 mm and 250 mm, while the nominal length of the two plates was 750 mm. The authors demonstrated that excellent agreement with the tests can be achieved using the stress–strain curve for longitudinal compression, assuming isotropic hardening and modeling the measured geometric imperfection. The maximum load obtained with this model was 3.6% lower and 1.2% higher than the loads experimentally determined. Furthermore, the authors indicated that the anisotropy of the material may not be important for numerical analyzes involving monotonic loading.

Mateus and Witz [4] developed the numerical analysis of thin plates subjected to uniaxial elastoplastic buckling for Grade B and API X52 steels. The authors present and discuss the results of a parametric investigation on the structural collapse of non-stiffened steel plates when subjected to variations in aspect ratio, boundary conditions, initial out-of-plane imperfection, and work hardening of the material. Through the obtained results, the authors concluded that the aspect ratio has a significant influence on the ultimate resistance of the plate. Plates with aspect ratios up to 1.5 have their ultimate strengths governed by edge length. For aspect ratios above 1.5, they were dependent on the aspect ratio, the type of initial imperfection, and the boundary condition. Therefore, the effect of work hardening of the material on the strength of the plate is negligible for the maximum resistance to collapse for plates with a slenderness ratio below 2.5.

Bezkorovainy et al. [9] investigated the effect of material properties on the compressive strength of simply supported square metal plates, with a width of 100 mm and slenderness ratios varying between 0.5 and 3. The materials studied were stainless steel and aluminum. From the results, the authors obtained a generalized formulation that allows the plate strength equation to be determined for a given alloy, requiring only the Ramberg-Osgood parameters.

Paik et al. [10] numerically studied the effects of the shape, size (depth and diameter), and location of the notches on the compressive capacity of simply supported steel plates. The geometrical measurements of the plates analyzed were as follows: width of 800 mm, aspect ratios of 1, 2, 3, 4, and 5, and thickness of 10 mm, 15 mm, and 20 mm. Through the results, the authors observed that the final compressive strength of the plate is not greatly affected by notch damage, as long as the notch diameter is small, regardless of its depth. However, as the tooth diameter increases, the ultimate compressive strength of the plate decreases significantly. In this case, the depth of the tooth also helps to accelerate the trend of strength reduction. In addition, changing the location of the notch located in the longitudinal direction of the board affects the maximum strength. As its location approaches the edges of the unloaded plate, the maximum resistance decreases by 20% compared to that of the notch in the center of the plate.

El-Sawy et al. [2] analyzed the effect of the size and location of a circular hole in the uniaxial buckling of square and rectangular plates, with different aspect ratios. The results indicated that for square plates with concentric circular holes subjected to uniaxial compression, the buckling failure remains elastic for small perforations, provided that the slenderness ratio of the plate is less than 65 (for A36 steel), greater than 55 (for Grade 50 A572 sheets of steel) and greater than 50 (for Grade 60 A572 sheets of steel). Furthermore, for the plates with concentric circular holes, the critical stress will always decrease as slenderness increases. However, this decline becomes more pronounced for large slenderness values, especially for small hole sizes, where the failure changes from elastoplastic to purely elastic.

Ndubuaku et al. [1] investigated the effect of parametric variation of the stress-strain properties of materials on the ultimate strength and on the deformation capacity of simply supported plates subjected to uniform axial compression. Through this study, the authors developed a new analytical expression to generate stress–strain curves used for parametric evaluation. This equation proved to be versatile in approximating the shape of the stress–strain curve over the entire range of strains. Therefore, they provided a reasonable approximation of the shape of the stress–strain curve using only two constitutive parameters of the model, facilitating the parameterizing process of the material stress–strain properties for a wide variety of metallic materials.

Moreover, some studies on buckling in mechanical designs can be seen in the literature. For instance, Pavlovic et al. [11] carried out the theoretical and numerical study of the structure of a telescopic boom made of AISI 4130 steel. The structure has a working height of 17 m, a platform height of 15 m, a load capacity of 200 kg (in all positions), and a working range of 9 m. The objective of this study was to obtain a better understanding of the structural strength and instability of the structure, allowing us to analyze the behavior of the system in relation to the effect of the buckling modes. The authors observed that the telescopic boom is able to withstand loads three times greater than those applied under normal operating conditions. In this way, it was possible to state that the equipment is free from the occurrence of buckling in the structure. In turn, Fragassa et al. [12] carried out the experimental analysis of a telescopic boom made of AISI 4130 steel. The objective was to validate the functionality and the level of security offered by the equipment. In this study, external loads were applied and strains were measured in order to investigate the general behavior of the bar under static and dynamic conditions, together with the presence of buckling phenomena. In the analysis of the results, the authors observed that up to the maximum load, the structure does not buckle because even before the occurrence of this instability, problems arise in the plasticization of the material.

In Pinto et al. [13], different arrangements of steel plates with rectangular or trapezoidal stiffeners were analyzed respect to their effects on deflections and stresses. In Troina et al. [14] an advanced computational model was developed and applied with the scope to perform a geometric optimization of thin steel plates with stiffeners when subjected to uniform transverse loads. In Amaral et al. [15] the same discussion was focused on the presence of symmetry boundaries and their effect on the stiffness of this plates.

In this context, the main goal of the present work is to verify and validate a computational model for the application of the Finite Element Method (FEM), using the ANSYS Workbench®, Ver. 2023R1, by ANSYS Inc., Canonsburg, PA, €US, with the purpose of evaluating the behavior of metallic plates subjected to elastoplastic buckling caused by uniaxial or biaxial compression combined with lateral pressure (or not combined with lateral pressure). The applied lateral load can have a constant or null value. Additionally, the verified and validated computational model was used to perform a simple case study of a simply supported rectangular plate with a centered rectangular hole, subjected to combined loads (in-plane biaxial compression and lateral pressure). The purpose was to evaluate the variation of the ultimate buckling stress of the plate as a function of the increase in lateral load. To do so, five different metallic alloys were considered: AISI 4130 steel, AH-36 steel, spheroidal graphite iron (SGI), compact graphite iron (CGI) and Al 7075-T651 aluminum alloy. This allowed us to investigate the plate behavior and its material mechanical properties. It is important to highlight that numerical simulation of the elastoplastic behavior of plates (which may or may not be perforated and with stiffeners) subjected to uniaxial or biaxial in-plane compressive loads associated or not with lateral loading is not a trivial task. Therefore, the development of a computational model by means of the ANSYS Mechanical APDL® [16], by ANSYS Inc., to solve this complex problem can be quite useful for scientific and practical engineering applications. In addition, the case study brings an association of geometric configuration for the plate with a type of combined load that is not easily found in the literature.

2. Computational Model

The computational model was developed in the commercial software ANSYS Mechanical APDL^®, using the finite element SHELL281. It was chosen because it is a suitable element for thin to moderate-thickness plates, having eight nodes with six degrees of freedom at each node: translations in the x, y, and z axes and rotations in the x, y, and z axes. Its formulation is based on the first-order shear-strain theory (Reissner–Mindlin Theory) [16].

According to Wang et al. [17], it is required to initially perform the analysis of elastic buckling for the plate. This is necessary because the configuration of the first elastic buckling mode is used to define the initial deformed configuration for the elastoplastic analysis. The numerical solution through the ANSYS^® software for the elastic buckling problem of plates was performed by means of an eigenvalue and eigenvector approach. For this type of analysis, according to Madenci and Guven [18], the finite element equilibrium equations are analyzed by solving the homogeneous algebraic equations. The lowest eigenvalue corresponds to the critical buckling load, and the associated eigenvector represents the first buckling mode. Thus, the global system of equations for a finite element mesh can be written as follows:

$$\left[K\right]\left\{U\right\}=\left\{F\right\}$$

(1)

where $\left[K\right]$ is the stiffness matrix of the system, $\left\{U\right\}$ is the unknown vector, and $\left\{F\right\}$ is the force vector. According to the problem, the matrix $\left[K\right]$ may be dependent on $\left\{U\right\}$, that is, $\left[K\right]=\left[K\left(U\right)\right]$ and $\left\{F\right\}$ may be time-dependent, remaining $\left\{F\right\}=\left\{F\left(t\right)\right\}$. Due to the lateral pressure applied to the external surface of each element, which is normal for the surfaces, the force vector can be described as follows [19]:

$$\left\{F\right\}=\left\{F_N\right\}+\left\{F_{PR}\right\}$$

(2)

where $\left\{F_N\right\}$ is the nodal force applied to each element and $\left\{F_{PR}\right\}$ is the pressure vector on each element.

The formulation used includes both linear and nonlinear terms, with the total stiffness matrix $\left[K\right]$ obtained by adding the conventional stiffness matrix for small deformations $\left[K_E\right]$ with the geometric stiffness matrix $\left[K_G\right]$. The latter, $\left[K_G\right]$, does not depend only on the geometry, since the internal load, $\left\{{\overline{N}}_0\right\}$, existing at the beginning of the loading must be considered. Thus, the total plate stiffness matrix for a load level $\left\{{\overline{N}}_0\right\}$, is given by

$$\left[K\right]=\left[K_E\right]+\left[K_G\right]$$

(3)

In case the load reaches a level of $\left\{\overline{N}\right\}=\lambda \left\{{\overline{N}}_0\right\}$, the stiffness matrix is written as

$$\left[K\right]=\left[K_E\right]+\lambda \left[K_G\right]$$

(4)

where $\lambda$ is a scalar.

Then, the governing equilibrium equations for the plate can be written as

$$\left[\left[K_E\right]+\lambda \left[K_G\right]\right]\left\{U\right\}=\lambda \left\{{\overline{N}}_0\right\}$$

(5)

where $\left\{U\right\}$ is the total displacement vector, which can be determined by

$$\left\{U\right\}={\left[\left[K_E\right]+\lambda \left[K_G\right]\right]}^{-1}\lambda \left\{{\overline{N}}_0\right\}$$

(6)

According to Przemieniecki [20], in the plate’s elastic buckling, the structural component under analysis presents a large growth in displacements without an increase in load. Therefore, by mathematical definition, the inverse matrix is determined as the adjoint matrix divided by the determinant of the coefficients, so the displacements tend to infinity when

$$\det \left[\left[K_E\right]+\lambda \left[K_G\right]\right]=0$$

(7)

The eigenvalue problem defined by Equation (7) is solved using the Lanczos numerical method [16]. It is the smallest eigenvalue $\left({\lambda }_1\right)$ corresponding to the critical buckling load given by

$$\left\{{\overline{N}}_{cr}\right\}={\lambda }_1\left\{{\overline{N}}_0\right\}$$

(8)

which is the limit load where the phenomenon of elastic buckling begins. In addition, the associated displacement vector $\left\{U\right\}$ defines the shape of the elastic buckling mode.

Since plate buckling is not limited to the elastic regime of the material, due to its non-linearity, it is necessary to adopt a small initial value of imperfections to perform its elastoplastic numerical simulation. In the proposed computational model, the initial imperfection was defined from the first elastic buckling mode. This consideration is necessary due to the function of the post-buckling problem not allowing an exact analysis directly, having problems of response discontinuities at the neutral equilibrium point [2]. According to El-Sawy et al. [2], the most accurate results for the ultimate stress of elastoplastic buckling were obtained when

$$w_0=\frac{b}{2000}$$

(9)

where $w_0$ is the value of the initial imperfection and $b$ is the plate width.

According to Helbig et al. [21], the ultimate load acting on the plate is given by

$$P_Y={\sigma }_{Y}t$$

(10)

where ${\sigma }_Y$ is the yield stress of the material and t is the plate thickness. The Newton-Raphson method is applied to determine the displacements that correspond to the plate equilibrium configuration for each load increment.

According to Lima et al. [22], during the beginning of the loading stage $i+1$, there is a vector of unbalanced loads $\left\{\psi \right\}$, equal to the load increment $\left\{\Delta \overline{N}\right\}$, between the vector of external loads ${\left\{\overline{N}\right\}}_{i+1}$ and the vector of nonlinear internal forces $\left\{F_{NL}\right\}$, which is equal to the vector of previous external loads ${\left\{\overline{N}\right\}}_i$. Then, the Newton-Raphson method is applied iteratively to reduce the unbalanced load vector $\left\{\psi \right\}$ to a value below the prescribed tolerance by means of the following equations:

$$\left\{\psi \right\}=\left\{\Delta \overline{N}\right\}={\left\{\overline{N}\right\}}_{i+1}-{\left\{F_{NL}\right\}}_r={\left\{\overline{N}\right\}}_{i+1}-{\left\{\overline{N}\right\}}_i$$

(11)

$${\left\{\psi \right\}}_{r+1}={\left\{\overline{N}\right\}}_{i+1}-{\left\{F_{NL}\right\}}_r$$

(12)

$${\left\{\psi \right\}}_{r+1}={\left[{\mathrm{K}}_{\mathrm{t}}\right]}_{\mathrm{r}}{\left\{\Delta U\right\}}_{r+1}$$

(13)

$${\left\{U\right\}}_{r+1}={\left\{U\right\}}_r+{\left\{\Delta U\right\}}_{r+1}$$

(14)

where ${\left\{\psi \right\}}_{r+1}$ is the updated unbalanced load vector, ${\left\{F_{NL}\right\}}_r$ is the nonlinear force vector in the iteration $r$, ${\left[K_t\right]}_r$ is the tangent stiffness matrix calculated from the displacement vector ${\left\{U\right\}}_r$, ${\left\{\Delta U\right\}}_{r+1}$ is the updated displacement increment vector, and ${\left\{U\right\}}_{r+1}$ is the updated displacement vector.

According to Madenci and Guven [18], Helbig et al. [21], and Lima et al. [22], if in a given load step it is not possible to reach convergence in the iterative process, this characterizes the obtaining of the ultimate load of the elastoplastic buckling of the plate.

3. Results and Discussions

First, the verification and validation of the proposed computational model were performed. Then, through the verified and validated computational model, the case study was carried out. Figure 1 shows the main dimensions of a thin plate: a is its length, b is its width, and t is its thickness.

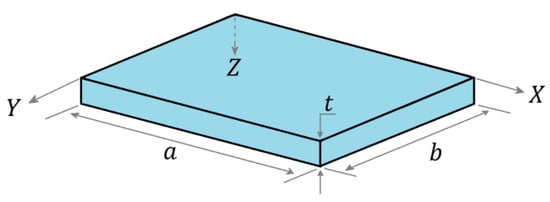
Figure 1. Main dimensions of a thin plate.

To perform the numerical simulation of the elastoplastic buckling of plates, it is necessary to define the values to be used for the load increments, as well as the value of the limit load. The value of the limit load used in each analysis is defined by Equation (10), while the load increments were defined with an initial 100 load steps (it is possible to reach a minimum of 50 steps and a maximum of 200 steps). The quantity of steps defines how many times the limit load will be divided and defines the value of the increment for each load step.

3.1. Computational Model Verification

The computational model verification process was developed by comparing the results generated in the present study with those obtained through analytical solutions or numerical solutions presented in the literature. For the first verification, according to Piscopo [23], it was performed an analysis of the elastic buckling of a thin square plate, under biaxial compressive load without lateral pressure. To do so, a holeless simply supported plate was considered. It had the following dimensions: $a=b=$1000 mm and $t=$10 mm (see Figure 1 and Figure 2). The steel mechanical properties of the plate are a modulus of elasticity $E=$ 206 GPa and Poisson’s ratio $\nu =$ 0.3.

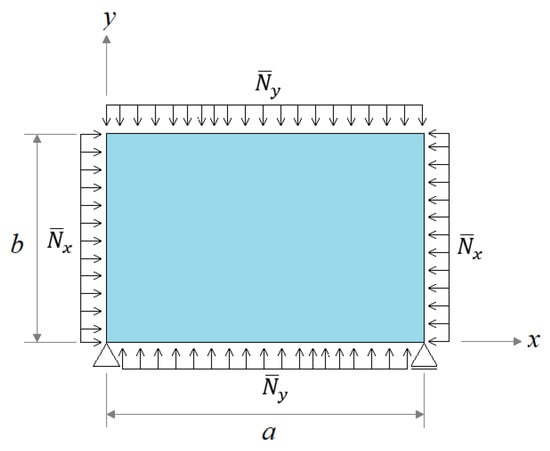
Figure 2. Simply supported square plate without holes.

Piscopo [23] obtained the critical buckling load analytically and numerically via FEM, reaching ${\overline{N}}_{cr}=$ 372 kN/m and ${\overline{N}}_{cr}=$ 373 kN/m, respectively. In turn, the proposed computational model defined a critical buckling load of ${\overline{N}}_{cr}=$ 368.89 kN/m. Therefore, we achieved differences of 0.84% and 1.10%, respectively, in relation to the analytical and numerical results of Piscopo [23], verifying the proposed elastic buckling computational model. The results of the present study, including the mesh convergence test, can be seen in Table 1. Figure 3 shows the deformed configuration for the first buckling mode.

Table 1. Mesh convergence test for the verification of the computational model by Piscopo [23].

Element Size (mm)	Number of Elements	${\overline{\mathit{N}}}_{\mathit{c}\mathit{r}}(\mathbf{kN}/\mathbf{m})$
100	100	368.75
75	196	368.89
50	400	368.89
40	625	368.89
30	1156	368.89
25	1600	368.89

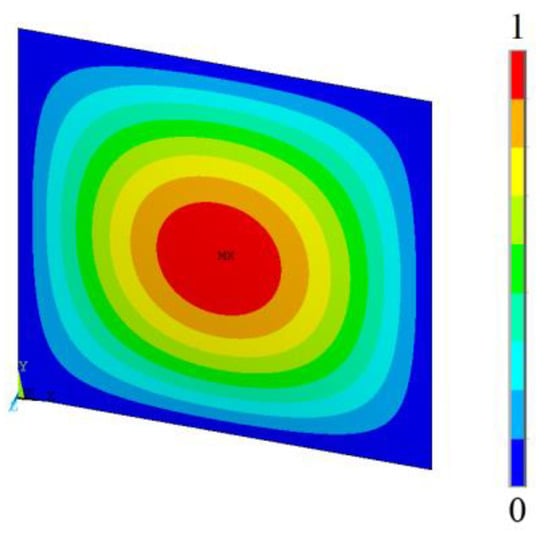
Figure 3. Out-of-plane displacement due to the biaxial elastic buckling.

Through the analysis of Figure 3, it is possible to visualize a configuration of the formed half-wave buckling, in which the blue color indicates regions with no displacement and the red color represents the maximum deflection that occurred on the plate. Thus, as expected, one can see that during the elastic buckling, the greatest displacement occurs at the center of the plate.

After that, another computational model verification was developed regarding the elastic biaxial buckling of a perforated plate, as earlier studied by Jayashankarbabu and Karisiddappa [24]. The simply supported square plate with a centered square hole in Figure 4 is subjected to a compressive in-plane load with no lateral pressure. The mechanical properties of the steel and the dimensions of the plate are $E=$ 210.924 GPa, $\nu =$ 0.3, $a=b=$ 1000 mm, and $t=$ 10 mm. In addition, two values were considered for the square perforation: $a_0=b_0=$ 250 mm and $a_0=b_0=$ 500 mm.

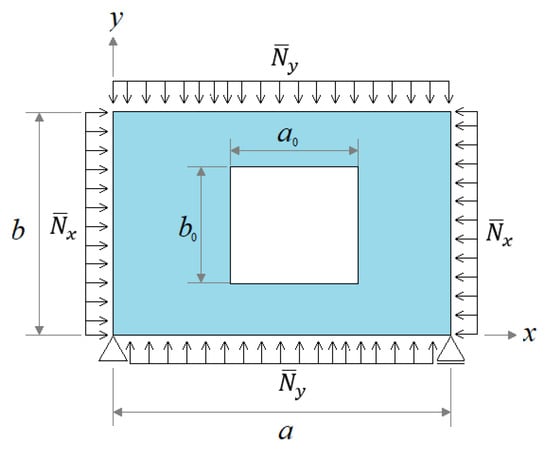
Figure 4. Simply supported square plate with centered square hole.

Jayashankarbabu and Karisiddappa [24] obtained a critical load of 314.55 kN/m for the plate with the 250 mm hole and 295.48 kN/m for the plate with the 500 mm hole. In turn, the developed computational model achieved critical loads of ${\overline{N}}_{cr}=$ 314.34 kN/m and ${\overline{N}}_{cr}=$ 297.49 kN/m, respectively, for the plate with the smallest and largest square hole. Therefore, the differences between the proposed model and the work by Jayashankarbabu and Karisiddappa [24] were 0.07% and 0.68% for the plate with a square hole of 250 mm and 500 mm side, respectively, verifying the developed numerical model. In addition, the mesh convergence test and the deformed configuration for the first biaxial elastic buckling mode are presented in Table 2 and Figure 5, respectively.

Table 2. Mesh convergence test for the verification of the computational model by Jayashankarbabu and Karisiddappa [24].

Square Hole Dimensions	${\mathit{a}}_0={\mathit{b}}_0=250\mathbf{mm}$		${\mathit{a}}_0={\mathit{b}}_0=500\mathbf{mm}$
Element Size (mm)	Number of Elements	${\overline{\mathit{N}}}_{\mathit{c}\mathit{r}}(\mathbf{kN}/\mathbf{m})$	Number of Elements	${\overline{\mathit{N}}}_{\mathit{c}\mathit{r}}(\mathbf{kN}/\mathbf{m})$
100	101	315.46	92	299.93
75	180	314.52	162	297.89
50	411	314.40	300	297.49
40	633	314.34	524	297.49
30	1116	314.34	920	297.49
25	1500	314.34	1200	297.49

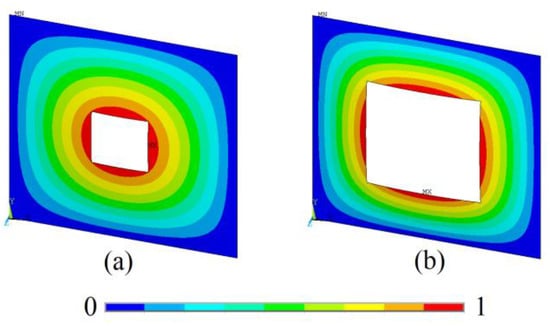
Figure 5. Out-of-plane displacement due to the biaxial elastic buckling for the plate with square hole of (a) 250 mm and (b) 500 mm side.

In Figure 5, as in Figure 4, a half-wave was formed due to the elastic buckling, ranging from no displacement in the plate edges (in blue color) and the maximum deflection in the hole edges (in red color). In addition, it can be seen that by increasing the size of the square hole, the regions with greater deflections are concentrated in the center of the edges of the holes.

In sequence, the computational model verification for the elastoplastic buckling of a holeless simply supported plate subjected to an in-plane biaxial compressive load (with no lateral load) was carried out, based on the analytical study presented by Shanmugam and Narayanan [25]. The mechanical properties of the steel used are modulus of elasticity $E=$ 205 GPa, Poisson’s ratio $\nu =$ 0.3, and yield stress ${\sigma }_Y=$ 245 MPa; the plate dimensions are $a=$ 720 mm, $b=$ 240 mm, and $t=$ 4 mm (see Figure 1). The value found by Shanmugam and Narayanan (1998) for the ultimate buckling stress was ${\sigma }_u=$ 56.35 MPa. On the other hand, the proposed numerical model obtained the ultimate buckling stress of ${\sigma }_u=$ 55.13 MPa, presenting a difference of 2.17% in comparison with Shanmugam and Narayanan [25]. The results obtained can be seen in Table 3 and Figure 6.

Table 3. Mesh convergence test for the verification of the computational model by Shanmugam and Narayanan [25].

Element Size (mm)	Number of Elements	${\mathit{\sigma }}_{\mathit{u}}\left(\mathbf{MPa}\right)$
100	24	55.13
75	40	55.13
50	75	55.13
40	108	55.13
30	192	55.13
25	290	55.13

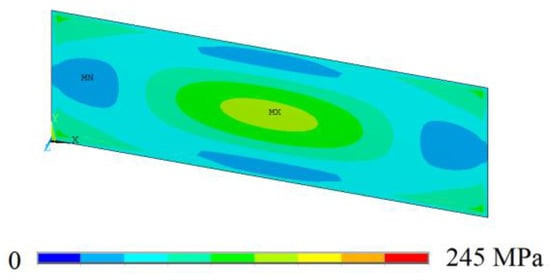
Figure 6. The von Mises stress distribution for the rectangular plate with no hole.

For the verification of the model according to Shanmugam and Narayanan [25], one can note in Figure 6 that the greatest stress points are located in the center of the plate.

Another verification for the biaxial elastoplastic buckling computational model was carried out considering a simply supported square plate with a centralized circular hole and subjected to a biaxial compressive load (without lateral load), according to Shanmugam et al. [26]. Figure 7 illustrates the thin steel plate with the following dimensions: $a=b=$ 125 mm, $t=$ 6.25 mm, and $a_0=b_0=$ 25 mm. Moreover, the mechanical properties of the plate material are modulus of elasticity $E=$ 205 GPa, Poisson’s ratio $\nu =$ 0.3, and yield stress ${\sigma }_Y=$ 323.3 MPa.

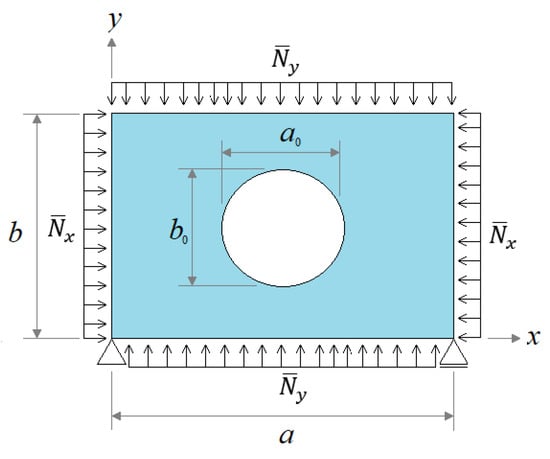
Figure 7. Simply supported square plate with centered circular hole.

Shanmugam et al. [26] used an analytical approach to achieve the ultimate stress of ${\sigma }_u=$ 257.13 MPa, while the proposed computational model obtained ${\sigma }_u=$ 263.49 MPa. The difference between the results is 2.47%, verifying the developed numerical model. One can view the results generated by the present study in Table 4 and Figure 8.

Table 4. Mesh convergence test for the verification of the computational model by Shanmugam et al. [26].

Element Size (mm)	Number of Elements	${\mathit{\sigma }}_{\mathit{u}}\left(\mathbf{MPa}\right)$
50	8	278.06
20	54	269.95
10	158	266.72
5	600	265.10
4	1010	263.49
3	1732	263.49
2.5	2400	263.49

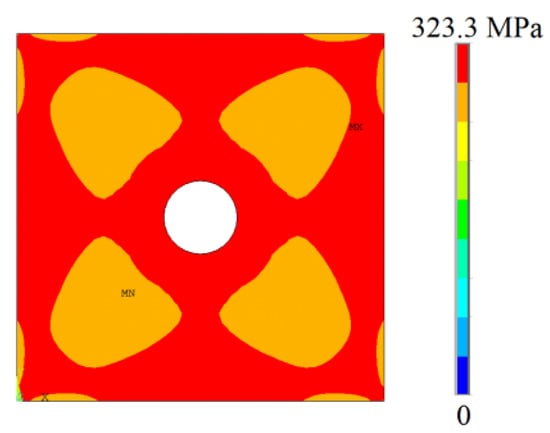
Figure 8. The von Mises stress distribution for the square plate with centered circular hole.

According to Figure 8, it can be seen that for the biaxial elastoplastic buckling of a square plate with a circular hole, there is a predominance of the highest von Mises stresses on the entire surface of the plate, indicated by the colors red and orange.

After that, the computational model was verified considering an elastoplastic buckling caused by a uniaxial compressive load combined with a lateral load, as in the numerical study presented by Kumar et al. [27]. A simply supported stiffened plate with a semi-circular cut out was considered (Figure 9) and had the following dimensions: $a$ = 1500 mm, t = 6 mm, with three different values for b (170 mm, 340 mm, and 510 mm), and d = b/2. The L-shaped stiffener in the center of the plate has $r=$ 45 mm, $s=$ 70 mm, and $t=$ 6 mm. The mechanical properties of the metallic material used in the plate and stiffener are E = 200 GPa, $\nu =$ 0.3, and ${\sigma }_Y=$ 250 MPa.

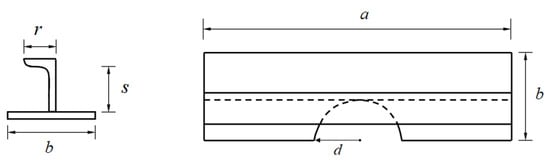
Figure 9. Simply supported stiffened plate with semi-circular opening (Adapted from [27]).

To numerically simulate the plate of Figure 9 a mesh convergence test was performed (Table 5) taking into account the width of 170 mm, defining a finite element size of 20 mm. From this, both for the width of 170 mm and for the widths of 340 mm and 510 mm, this same spatial discretization was adopted. It is important to highlight that the last column of Table 5 presents the ratio between the ultimate buckling load when the lateral load is applied (${\overline{N}}_{\mathrm{uQ}}$) and the ultimate buckling load when the lateral load is null (${\overline{N}}_{u0}$), as in Kumar et al. [27].

Table 5. Mesh convergence test for the stiffened plate with semi-circular opening and width of 170 mm.

Element Size (mm)	Number of Elements	${\overline{\mathit{N}}}_{\mathit{u}\mathit{Q}}$$/{\overline{\mathit{N}}}_{\mathit{u}0}$
50.0	390	0.896
40.0	646	0.851
30.0	1050	0.806
20.0	2280	0.776
17.5	2924	0.776
15.0	3800	0.776

Table 6 shows the numerical results of Kumar et al. [27] and those obtained in the present study, as well as their differences. One can note that these differences range between 3.66% and 4.83%, indicating that the proposed computational model was verified.

Table 6. Computational model verification by Kumar et al. [27].

Plate Width (mm)	${\overline{\mathit{N}}}_{\mathit{u}\mathit{Q}}$$/{\overline{\mathit{N}}}_{\mathit{u}0}$ (Kumar et al. [24])	${\overline{\mathit{N}}}_{\mathit{u}\mathit{Q}}$$/{\overline{\mathit{N}}}_{\mathit{u}0}$ (Present Study)	Difference (%)
170	0.750	0.776	3.66
340	0.766	0.803	4.83
510	0.766	0.796	3.92

In addition, Figure 10 depicted the von Mises stress distribution for the stiffened plate with semi-circular cut out, for the three considered plate widths.

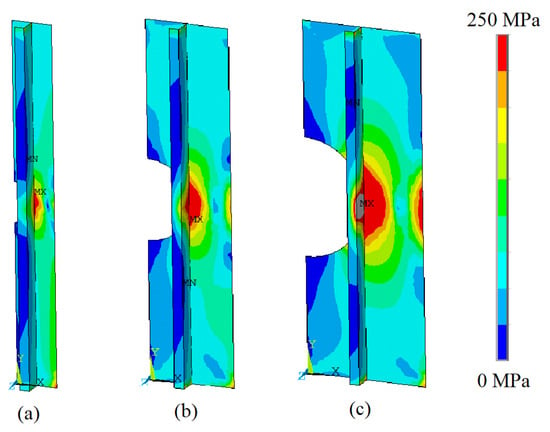
Figure 10. The von Mises stress distribution for the stiffened plate with semi-circular opening and width of (a) 170 mm, (b) 340 mm, and (c) 510 mm.

Through the analysis of Figure 10, one can note that always the highest stresses are located close to the region of contact between the stiffener and the edge of the semi-circular opening. It was also observed that as the width of the plate increases, there is an increase in the area on the edge of the plate opposite to the cutout, which is subjected to high von Mises stresses.

To finish the computational model verification step, the numerical study carried out by Yu et al. [28] was reproduced here. To do so, the elastoplastic buckling of a simply supported rectangular stiffened plate with a square centered hole was analyzed, being the structure under uniaxial compression combined with uniform lateral loading. Figure 11 illustrates the stiffened perforated plate, which has the following dimensions: $a=$ 1160 mm, b$=$ 960 mm, t = 5 mm and 12 mm (defining a plate slenderness ratio, respectively, of 2.45 and 1.02), and $a_0=b_0=$ 300 mm for the centered square perforation. Moreover, the L-shaped stiffeners have dimensions of $r=$ 30 mm, $s=$ 50 mm, and $t=$ 5 mm (see Figure 9 for the stiffener geometry). The metallic material used for the plate and stiffeners has the following mechanical properties: E = 198 GPa, $\nu =$ 0.3, and ${\sigma }_Y=$ 331 MPa.

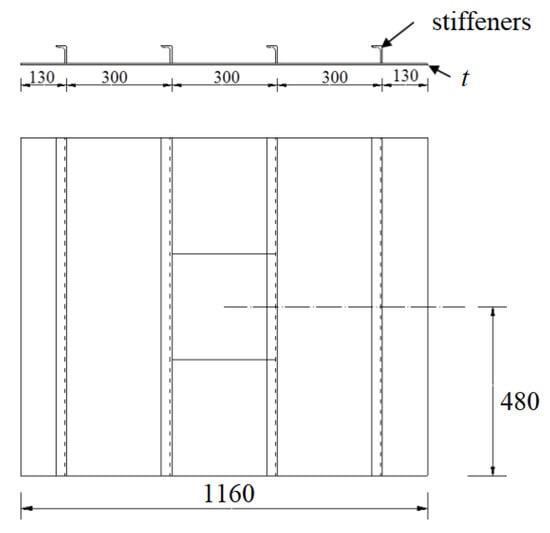
Figure 11. Simply supported stiffened plate with centered square hole (Adapted from [28]), in mm.

It is worth mentioning that the magnitudes of the lateral load considered in this case were $Q=2q_u/3$ and 5$q_u/$6, where $q_u$ is the ultimate lateral load of the specimen (which is 341.3 MPa), as presented in Yu et al. [28]. In addition, the ultimate normalized stress (defined as ${\sigma }_n={\sigma }_u/{\sigma }_Y$) was adopted for the evaluation of the results.

To define adequate spatial discretization, a mesh convergence test was promoted considering the stiffened plate with a thickness of 5 mm and under a lateral load of $2q_u/3$, being the results described in Table 7.

Table 7. Mesh convergence test for the stiffened perforated plate with t = 5 mm and $Q=2q_u/3$.

Element Size (mm)	Number of Elements	${\mathit{\sigma }}_{\mathit{n}}$
100	222	0.390
80	320	0.370
60	468	0.365
50	604	0.360
40	1080	0.335
30	1564	0.335
25	2416	0.335

One can observe in Table 7 a stabilization for the ultimate normalized stress value from an element size of 40 mm. Therefore, this element size was adopted for the spatial discretization of all simulated configurations. The results obtained in the present study and those found by Yu et al. [28] are shown in Table 8.

Table 8. Model verification according to [28].

t (mm)	$\mathit{Q}$	${\mathit{\sigma }}_{\mathit{n}}$ (Yu et al. [28])	${\mathit{\sigma }}_{\mathit{n}}$ (Present Study)	Difference (%)
5	$2q_u/3$	0.323	0.335	3.72
	5$q_u/$6	0.244	0.255	4.51
12	$2q_u/3$	0.591	0.575	2.71
	5$q_u/$6	0.546	0.565	3.48

The results of Table 8 presented relative differences ranging from 2.71% to 4.51%, ensuring that the proposed computational model can be considered verified. To illustrate, Figure 12 shows the von Mises stress distribution for the four cases of Table 8, being possible to infer that for the thickness of 5 mm, the greatest von Mises stresses are concentrated in the region around the square hole; while for the thickness of 12 mm, a wider distribution of high-stress regions occurred.

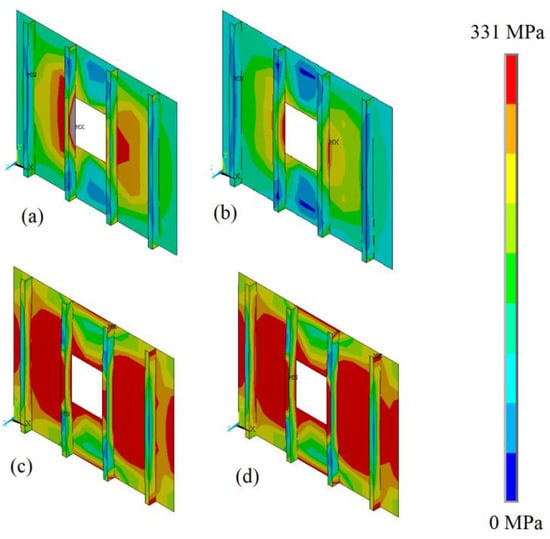
Figure 12. The von Mises stress distribution for the stiffened plate with centered square hole, with (a) t = 5 mm and $Q=2q_u/3$, (b) t = 5 mm and $Q=5q_u/6$, (c) t = 12 mm and $Q=2q_u/3$, and (d) t = 12 mm and $Q=5q_u/6$.

3.2. Computational Model Validation

The computational model validation process was performed by confronting the results of the current study with those obtained in the experimental tests found in the literature. For the first validation, the elastoplastic biaxial buckling analysis of a simply supported square plate (see Figure 1 and Figure 2) under biaxial compressive loads and no lateral loading was carried out, according to Shanmugam and Narayanan [25]. The dimensions of the metallic plate are $a=b=$ 56 mm and $t=$ 2.032 mm, while its mechanical properties are $E=$ 205 GPa, $\nu =$ 0.3, and ${\sigma }_Y=$ 334.7 MPa. The mesh convergence test performed and the ultimate biaxial buckling stress obtained can be viewed in Table 9.

Table 9. Mesh convergence test for the validation of the computational model by Shanmugam and Narayanan [25].

Element Size (mm)	Number of Elements	${\mathit{\sigma }}_{\mathit{u}}\left(\mathbf{MPa}\right)$
20.0	9	185.76
10.0	36	192.45
7.5	64	192.45
5.0	144	192.45
4.0	196	192.45
3.0	361	192.45
2.5	529	192.45

Since Shanmugam and Narayanan [25] experimentally obtained an ultimate biaxial buckling stress of 203.43 MPa, one can infer from Table 9 that the proposed computational model generated a result with an error of 5.40%, validating the developed numerical model. The von Mises stress distribution numerically generated in the present study can be viewed in Figure 13, in which the regions with the highest stress (in red color) are concentrated at the corners of the square plate.

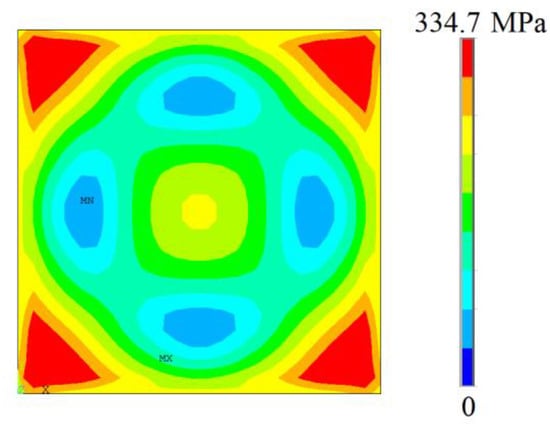
Figure 13. The von Mises stress distribution for the non-hole square plate.

After that, it was considered a simply supported square plate with a centered circular hole that was previously experimentally investigated by Narayanan and Chow [26]. The perforated plate was subjected to a biaxial compressive load with no lateral load. Its dimensions are $a=b=$ 125 mm, $t=$ 1.625 mm, and $a_0=b_0=$ 25 mm (see Figure 3). The mechanical properties of the metallic material of the plate are $E=$ 205 GPa, $\nu =$ 0.3, and ${\sigma }_Y=$ 323.3 MPa. Narayanan and Chow [29] experimentally defined an ultimate biaxial buckling stress of ${\sigma }_u=$ 73.80 MPa, while the proposed computational model obtained ${\sigma }_u=$ 77.59 MPa (as indicated in Table 10, by a mesh convergence test). Therefore, an error of 5.14% was found between the proposed numerical model and the experimental result, ensuring its validation.

Table 10. Mesh convergence test for the validation of the computational model by Narayanan and Chow [29].

Element Size (mm)	Number of Elements	${\mathit{\sigma }}_{\mathit{u}}\left(\mathbf{MPa}\right)$
20.0	54	63.34
10.0	158	77.59
7.5	301	77.59
5.0	600	77.59
4.0	1010	77.59
3.0	1732	77.59
2.5	2400	77.59

To illustrate the mechanical behavior of the perforated plate under biaxial elatoplastic buckling, Figure 14 depicted its von Mises stress distribution. It was possible to observe that, in addition to the regions of greatest stress located in the corners of the plate already observed in Figure 13, high values of von Mises stress were also identified in the region around the centered circular hole.

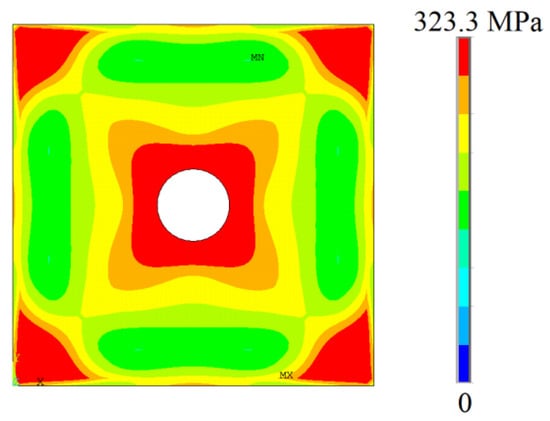
Figure 14. The von Mises stress distribution for the square plate with centered hole.

3.3. Case Study

The verified and validated computational model was employed here for the analysis of the elastoplastic buckling behavior of a metallic perforated plate subjected to an in-plane biaxial compressive load combined with a uniformly distributed lateral pressure (p_z) of 0.0507 MPa. The plate is simply supported, having a centered rectangular hole. Considering Figure 4, the plate dimensions are $a=$ 2000 mm, $b=$ 1000 mm, $t=$ 12 mm, $a_0=$ 450 mm, and $b_0=$ 667 mm. It should be noted that plates with this geometric configuration subjected to this type of combined loading are not easily found in the literature. In addition, five different metallic materials were taken into account for the perforated plate: AISI 4130 steel [30], AH-36 steel [31], spheroidal graphite iron [32,33,34], compact graphite iron [32,33,34] and Al 7075-T651 aluminum alloy [35]. Its mechanical properties are described in Table 11.

Table 11. Mechanical properties of the metallic materials considered in the case study [30,31,32,33,34,35].

Material	E (GPa)	$\mathit{\nu }$	${\mathit{\sigma }}_{\mathit{Y}}\left(\mathbf{MPa}\right)$
AISI 4130	210.0	0.30	460
AH-36	210.0	0.30	355
SGI	170	0.24	340
CGI	150	0.22	270
Al 7075-T651	71.7	0.33	502

To define the spatial discretization, a mesh convergence test was performed for the plate made of AH-36 steel, defining a regular independent mesh with an element size of 30 mm. Therefore, the numerical simulations for the case study were carried out with this finite element size. The results obtained for the ultimate biaxial buckling stress (${\sigma }_u$) and maximum out-of-plane displacement ($u_Z$) for each case are presented in Table 12. Moreover, the von Misses stress distribution for the perforated plate made of AISI 4130 steel, AH-36 steel, spheroidal graphite iron (SGI), compact graphite iron (CGI) and Al 7075-T651 aluminum alloy are illustrated in Figure 15, Figure 16 and Figure 17.

Table 12. Ultimate biaxial buckling stress and maximum deflection of the case study.

Material	${\mathit{\sigma }}_{\mathit{u}}\left(\mathbf{MPa}\right)$	${\mathit{u}}_{\mathit{Z}}\left(\mathbf{mm}\right)$
AISI 4130	31.74	63.51
AH-36	28.76	47.39
SGI	24.48	59.47
CGI	20.66	55.15
Al 7075-T651	18.32	144.02

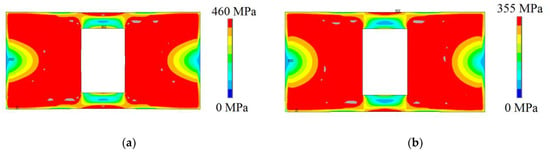
Figure 15. The von Mises stress distribution for the plate with rectangular hole made of steels: (a) AISI 4130 steel and (b) AH-36 steel.

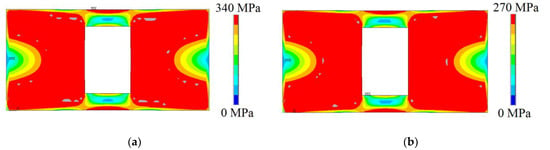
Figure 16. The von Mises stress distribution for the plate with rectangular hole made of cast irons: (a) spheroidal graphite iron (SGI) and (b) compact graphite iron (CGI).

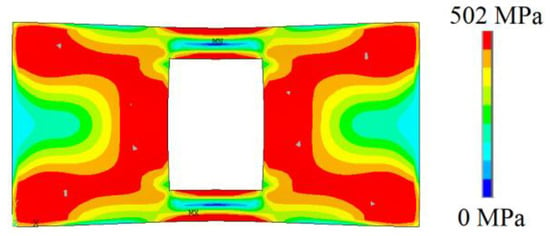
Figure 17. The von Mises stress distribution for the plate with rectangular hole made of Al 7075-T651.

The highest ultimate stress was reached by AISI 4130 steel (31.74 MPa), being:

• 9.39% higher than AH-36 steel (28.76 MPa)
• 42.28% higher than Al 7075-T651 (18.32 MPa)
• 22.87% higher than SGI (24.48 MPa)
• 34.91% higher than CGI (20.66 MPa).

The smallest deflection was achieved by AH-36 steel (47.39 mm), being:

• 34.02% less than AISI 4130 steel (63.51 mm)
• 203.90% less than Al 7075-T651 (144.02 mm)
• 25.49% less than SGI (59.47 mm)
• 16.37% less than CGI (55.15 mm).

Analyzing the von Mises stress distributions, one can infer that for the steel plates (see Figure 15), as expected, similar mechanical behavior can be observed, despite the small differences existing in the upper and lower perforation edges as well as in the plate edges. This is what also happens in the case of cast iron plates (see Figure 16), whose behavior does not differ much from what was found for steel. However, when comparing the von Mises stress distributions of the steel (Figure 15) and cast iron (Figure 16) plates with that of the Al 7075-T651 aluminum alloy plate(Figure 17), it is possible to realize that the regions submitted to the maximum stresses are much smaller for the plate made of Al 7075-T651.

Through the analysis of the data obtained in the case study, as expected, when changing the plate material, the ultimate buckling stress, the maximum out-of-plane displacement, and the von Mises stress distributions change from one case to another. This coherent behavior for the studied metallic plates also proves the effectiveness and accuracy of the proposed model.

4. Conclusions

The present work proposed a computational model for the elastoplastic biaxial buckling of plates due to combined loads, developed using the FEM in the ANSYS^® software. Numerical simulations considering uniaxial or biaxial compressive in-plane loads combined or not with lateral loading for plates with or not stiffeners and having or not perforations can be performed.

As the main objective, the verification and validation of the computational model taking into account different load type combinations, mechanical properties, and geometric configurations for metallic plates were carried out. To do so, the numerical results obtained were compared with analytical, numerical, and experimental solutions presented in the literature. Maximum relative differences of 2.47% and 4.83% were achieved when comparing the numerical results of the present study with analytical and numerical previous results, respectively. In addition, a maximum relative error of 5.40% was reached when confronting the results generated by the developed computational model with those experimentally found in the literature. Therefore, one can conclude that the developed numerical model was adequately verified and validated.

Thereafter, the computational model was employed to simulate a case study of a rectangular metal plate with a centered square perforation submitted to a biaxial compressive in-plane load combined with a lateral load. Although it is a simple case, no studies were found in the literature regarding the elastoplastic buckling of plates considering this geometric configuration associated with this type of combined loading and considering different metallic materials (AISI 4130 steel, AH-36 steel, spheroidal graphite iron (SGI), compact graphite iron (CGI) and Al 7075-T651 aluminum alloy). To do so, the ultimate stress, maximum deflection, and von Mises stress distribution were evaluated. The obtained results indicated that the AISI 4130 steel plate achieved an ultimate buckling stress of 31.74 MPa, which is 9.39%, 42.28%, 22.87% and 34.91% superior to the limit stress reached by the AH-36 steel plates, Al 7075-T651 aluminum alloy, SGI and CGI, respectively. In turn, the out-of-plane displacement of the AH-36 steel plate presented a maximum deflection of 47.39 mm, which is 34.02%, 203.90%, 25.49% and 16.37% less than the deflection achieved by the plates made of AISI 4130 steel, Al 7075-T651 aluminum alloy, SGI and CGI, respectively. With regard to the von Mises stress distributions, as expected, the plates made of AISI 4130 steel and AH-36 steel presented a similar behavior, being different from those that occurred for the Al 7075-T651 plate.

The results of the case study are coherent and corroborate with the verification and validation performed, proving that the proposed computational model is capable of numerically simulating the elastoplastic buckling of plates subjected to uniaxial or biaxial compressive loads combined with lateral loading.

Finally, it is important to mention that the results obtained by the present work are useful to the quasi-static deformation analysis. However, as per Maruschak et al. [36], when considering repeated loadings (fatigue), some approaches allow taking into account the material damages accumulated during operation and formulating criteria to evaluate deformation processes at different scale levels.