Abstract
The paper presents a simple and efficient method for identifying two-parametric isotropic pressure-independent yield criteria. The experimental procedure includes the upsetting of three types of specimens. The upsetting of cylinders and rings is used to evaluate the effect of friction. Together with the plane strain compression in a die, these tests provide two points of the yield locus on the π-plane. The experimental procedure is used in conjunction with the plasticity theory based on Hosford’s yield criterion. The plastic work is used to describe the hardening of the material. This hardening law can be reformulated in terms of the equivalent strain after the yield criterion is determined. The experimental/theoretical procedure above applies to steel C15E.
1. Introduction
A large class of metal-forming processes is described by rigid- or elastic-plastic models based on an isotropic pressure-independent yield criterion and its associated flow rule. In most cases, the von Mises yield criterion is assumed (in a broad sense that the tensile yield stress may depend on the equivalent strain rate, the equivalent strain, and other internal variables). A few recent publications include [1,2,3,4]. It is often reasonable to assume that the yield stress depends on the equivalent strain only for cold metal forming processes. In this case, a single test, usually the standard tensile test, completely determines the material model. On the other hand, experiments devoted to determining material properties show a systematic deviation of the actual yield criterion from the von Mises yield criterion. In particular, an overview of such experimental data has been presented in [5]. Polycrystal models also predict yield criteria different from the von Mises yield criterion. For example, the plane stress yield criterion for FCC metals has been computed in [6] using the Taylor polycrystal model [7]. For practical applications to metal forming simulation, it is desirable to have a simple and quick method for determining a yield criterion that is more accurate for a given material than the von Mises yield criterion.
Several isotropic generalized yield criteria have been proposed in the literature [8,9]. The criterion [8] involves two constitutive parameters. A simple and efficient method for determining these parameters is developed in the present paper. It is supposed that hardening is isotropic. Kinematic hardening is not considered. Therefore, the yield surface expands with no translation in the stress space. The method includes compression tests (cylinder, ring, and plane strain compression). Each of these tests separately is widely used for determining various material properties. A technique for minimizing friction in the cylinder compression test has been described in [10]. This technique can be extended to other specimens’ geometries (for example, [11]). Under these conditions, the cylinder compression test provides the corresponding yield stress. This yield stress equals the tensile yield stress for many metallic materials. The plane strain compression test has several applications [12,13,14,15,16,17,18,19,20,21,22,23,24]. Paper [12] has adopted this test for studying the deformation of multilayer sheets. The focus has been on the conditions that lead to the simultaneous flow of the different layers. Paper [13] has used the plane strain compression test for determining the flow stress considering the effect of friction. The microstructure development in Sanicro 28 high-alloy austenitic stainless steel has been investigated in [14]. In [15], the plane strain compression test has been combined with subsequent recrystallization annealing to study the behavior of a NiTiFe shape memory alloy. This test has been employed in [16] to determine the flow curve to increase the accuracy of the simulation results. An analytical method for interpreting the results of the plane strain compression with no die has been developed in [17]. The plane strain compression test has been combined with multi-directional forging in [18] to study the texture evolution and mechanical properties of martensitic steel. Paper [19] has extended the results reported in [15]. The hot plane strain compression test has been used in [20] to investigate the microstructure and texture development in a Mg–Dy alloy. Paper [21] has applied multiple plane strain compression to study the texture evolution in commercially pure copper. The effect of hydrogen on the flow behavior of a TiAl-based alloy has been reported in [22]. In this paper, the plane strain compression test has been carried out at elevated temperatures. The influence of temperature on material properties in plane strain compression has been studied in [23]. Uniaxial and plane strain compression tests have been employed in [24] to reveal the influence of sample geometries on determining material behavior. Note that papers [13,16,17,22,23,24] have conducted the plane strain compression test without a special die. A thin strip of metal has been compressed between two flat dies. It has been supposed that the geometric dimensions of the dies can produce plane strain deformation.
Compression tests have been widely used to determine the flow behavior of materials for metal forming applications [13,25,26]. These papers are devoted to methods to account for frictional effects. Paper [13] has treated experimental data from the cylinder and plane strain compression tests using an inverse method, assuming that the friction coefficient and the flow stress are unknown. However, it has been assumed that the material (aluminum alloy AA6082) obeys the von Mises yield criterion. Paper [25] has also utilized an inverse procedure in conjunction with a finite element modeling of a uniaxial compression test. The von Mises yield criterion with the flow stress that depends on the equivalent strain, the equivalent strain rate, and the temperature has been assumed. The material tested is 50CD4 steel. Paper [26] has proposed a method for determining the stress–strain curve using two compression tests. One of these tests is the same as that described in [10]. The other is the cylinder compression with teflon sheets or Molykote DX as lubricants. The slab method has been used to account for friction. The von Mises yield criterion has been assumed for Aluminum AL2S. Another group of tests for determining materials’ flow behavior includes combined tension and torsion tests [27,28]. Paper [27] determines the strain hardening law assuming the von Mises yield criterion. In contrast to the papers above, an experimental program for determining yield surfaces has been proposed and carried out in [28]. However, thin-wall tubular specimens have been used in this paper, which restricts the applications of this study to sheet metal forming. Moreover, even though the yield criterion has been investigated, the von Mises strain has been accepted as the effective strain. The effective strain is generally defined using the yield criterion [8].
The present paper aims to develop a simple and efficient method for identifying the yield criteria proposed in [8] and any other yield criterion that involves two constitutive parameters. As noted above, the effective strain cannot be defined without specifying the yield criterion. Therefore, the theoretical part of this paper describes the yield stresses as functions of the plastic work. Once the yield criterion has been identified, the hardening laws can be generally rewritten in terms of the effective strain. The method applies to determine the yield criterion of low carbon steel C15E.
2. Methodology and Theory
2.1. Methodology
The experimental program includes three compression tests (cylinder, ring, and plane strain). Under the ideal conditions of vanishing friction, the cylinder and ring compression tests should lead to identical results. The present approach suggests that real experimental results are used for revealing the effect of friction. Therefore, the first step of the experimental program is to show that all curves from the cylinder and ring compression tests lie within a narrow band. If this condition is satisfied, the second step is to compare these curves and curves from the plane strain compression test. This comparison should allow for a two-parametric yield criterion to be identified.
Let , , and be the principal stresses. The yield criterion proposed in [8] reads
where is the yield stress in tension and . Since , , and in pure shear, it follows from this equation that the shear yield stress is
where
The yield criterion (1) reduces to the von Mises yield criterion for n = 2 and n = 4. In this case, . Tresca yield criterion follows from (1) as . In this case, . The yield locus corresponding to (1) covers the entire region between the von Mises and Tresca loci as n varies in the range . Generally, different yield loci are obtained in the range [8].
Using experimental data from the compression tests above, one can find k from (2) and n from (3).
2.2. Theory
Hardening laws usually represent the flow stress as a function of the equivalent plastic strain or the plastic work. However, the definition of the equivalent strain depends on the yield criterion, the determination of which is the main objective of the present paper. Therefore, the hardening law below is written in terms of the plastic work. In the case of isotropic materials, the von Mises and Tresca yield criteria are most often used in metal forming applications. The Tresca criterion forms one of the two extreme bounds for all physically reasonable pressure-independent yield criteria. The other bound is usually called the Schmidt–Ishlinskii yield criterion [29]. One test completely determines each of the criteria above. The generalized isotropic yield criteria proposed in [8] require at least two tests. A theoretical description of these tests is required to interpret the experimental results.
A schematic diagram of specimens is presented in Figure 1 to introduce some notation. In particular, H0 is the initial height of all specimens, R0 is the initial radius of cylindrical specimens and the initial outer radius of ring specimens, r0 is the initial inner radius of ring specimens, L0 is the initial length of strips, and B is the width of strips. The value of B does not change in the course of deformation under plane strain conditions. The current height of all specimens is denoted as H. The dimensionless height is defined as
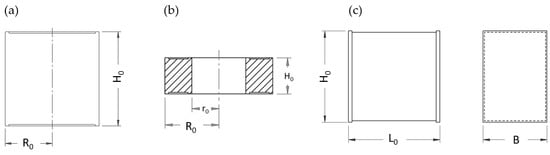
Figure 1.
Schematic diagram of specimens: cylinder (a), ring (b), and prismatic specimens (c).
Moreover, the uniaxial and shear yield stresses are denoted as and , respectively. These stresses are functions of the plastic work w. The force required to deform specimens is denoted as F.
Let , , and be the principal strain rates. The plastic work is determined from the following equation:
where t is the time and is the convected derivative. All specimens are compressed between two flat dies. One die is motionless, and the other moves with a velocity V. Therefore, and Equation (5) becomes after employing (4)
The initial condition to this equation is
for .
Friction is ignored in the solutions below.
2.2.1. Cylinder Compression
It is natural to use a cylindrical coordinate system whose z-axis coincides with the axis of the cylinder and the plane with the contact surface between the specimen and the motionless die. The radial and axial velocities are represented as
It is straightforward to verify that this velocity field is solenoidal. The only non-zero stress component is the axial stress, . The corresponding strain rate component follows from (7) as . Then, Equation (6) becomes
Since the material is incompressible, the current radius of the cylinder is . Using this equation and (4), one can find the force F as
Eliminating in (9) using (10), one can obtain
It is supposed that the experiment provides F as a function of h. Then, using (7), one can integrate Equation (11) to obtain
Here, is a dummy variable of integration. Equation (10) can be rewritten as
The experimental dependence supplies the right-hand side of (13) as a function of h. Then, Equations (12) and (13) provide the dependence in parametric form, with h being the parameter.
2.2.2. Ring Compression
Equations (8) and (9) are valid. Since the material is incompressible, the current cross-sectional area of the ring is . Using this equation, one can find the force F as
Eliminating in Equation (9) using Equation (14), one can obtain
Integrating and using (7)
Equation (14) can be rewritten as
The experimental dependence supplies the right-hand side of (17) as a function of h. Then, Equations (16) and (17) provide the dependence in parametric form, with h being the parameter.
2.2.3. Plane Strain Compression
Any plane–strain pressure-independent yield criterion can be represented as
Here, and are the principal stresses in the planes of flow. In the case under consideration,
It is natural to use a Cartesian coordinate system . The flow is everywhere parallel to the plane. The plane z = 0 coincides with the contact surface between the specimen and the motionless die. The velocity field is
It is straightforward to verify that this velocity field is solenoidal. Using (4), one can find the non-zero strain rate components from (20) as
Substituting (19) and (21) into Equation (6) leads to
Since the material is incompressible, the current length of the strip is . Using this equation, (4) and (19), one can find the force F as
Eliminating in (22) using (23), one can obtain
Integrating and using (7)
Equation (23) can be rewritten as
The experimental dependence supplies the right-hand side of (26) as a function of h. Then, Equations (25) and (26) provide the dependence in parametric form, with h being the parameter.
3. Experimental Design
In the present paper, the compression of three different groups of specimens made of low-carbon steel C15E is performed. The chemical composition of this material (Table 1) was acquired by an optical emission spectrometer ARL 2460 (method OES OES SRPS C. A1.011 (2004), Thermo Fisher Scientific, Waltham, MA, USA). The specimens were machined from a Ø 30 mm annealed rod. The annealing temperature was 720 °C and the cooling was performed in a furnace for eight hours, resulting in the hardness of annealed material of 142 HB. The compression was carried out at room temperature by different dies on a Sack&Kiesselbach 6.3 MN hydraulic press with ram speed of 0.05 mm/s. Before the compression, the specimens were lubricated with stearin. The compression force and stroke were registered by a Spider 8 Hottinger Baldwin Messtechnik electronic measuring system. A total of nine specimens were compressed: three specimens for each group.

Table 1.
Chemical composition of C15E low carbon steel.
The first group of specimens is circular cylinder Rastegaev specimens [10]. The nominal initial radius and height of the specimens are R0 = 10 mm and H0 = 20 mm, respectively. These specimens have small recesses on their end faces which retain the stearin during the compression. A pair of flat plates are used as a die. A schematic diagram of the specimens, a specimen image, and a schematic diagram of the process are presented in Figure 2.
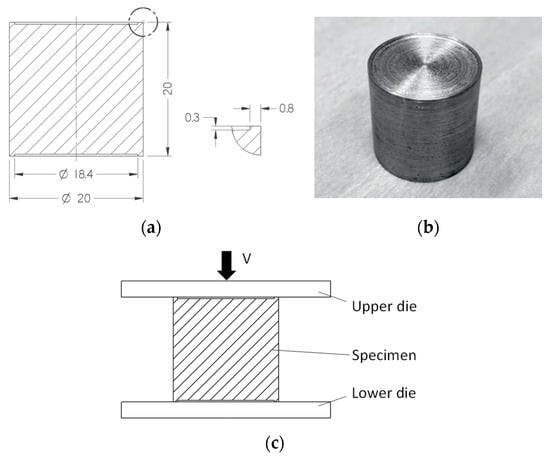
Figure 2.
Schematic diagram of the specimens (a), a specimen image (b), and a schematic diagram of the process (c).
The second group of specimens is rings conventionally used for experimental determination of friction in cold metal processes [30]. The nominal initial outer radius, inner radius, and height of the specimens are R0 = 12 mm, r0 = 6 mm and H0 = 8 mm, respectively. This nominal geometry is slightly modified to include recesses for retaining the stearin, similar to the Rastegaev specimens. A schematic diagram of the specimens, a specimen image, and a schematic diagram of the process are presented in Figure 3.
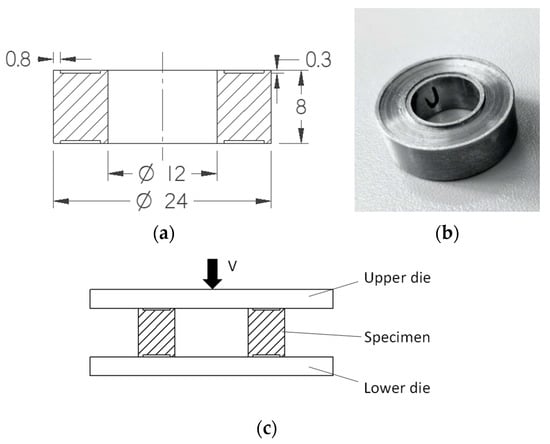
Figure 3.
Schematic diagram of the specimens (a), a specimen image (b), and a schematic diagram of the process (c).
The third group is prismatic specimens for plane strain compression. The nominal initial length, height, and width are L0 = 20 mm, H0 = 20 mm, and B = 14 mm, respectively. The compression is performed using a plane strain die [31]. The width of the die channel is 14 mm (Figure 4). Similarly to the previous groups of specimens, the nominal geometry is slightly modified to retain the stearin during the compression. A drawing and photos of the billet are presented in Figure 5.
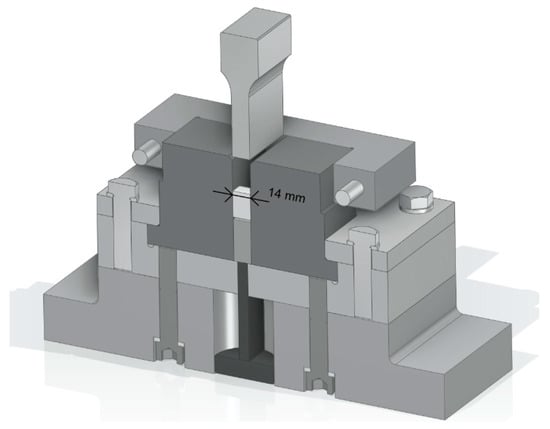
Figure 4.
Die for plane strain compression [31].
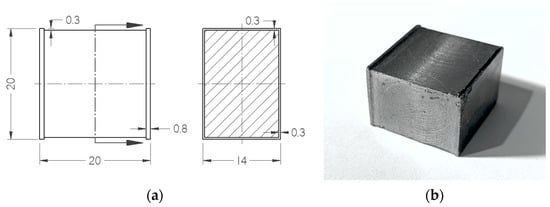
Figure 5.
Schematic diagram of the specimens (a) and a specimen image (b).
For the calculations that are described in the next section, the elastic deformation for each specimen group is removed using experimental data for the stiffness of the whole compression system, including hydraulic press, dies, and specimens.
4. Experimental Results
Figure 6 presents the images of an upset specimen from each specimen group. The average stroke for the cylindrical specimens is about 13 mm, while the maximum force is about 700 kN. The average stroke for the ring specimens is about 5.61 mm, while the maximum force is about 882 kN. Finally, the average stroke for prismatic specimens is about 12 mm, while the maximum force is about 560 kN.

Figure 6.
Upset specimens: cylinder (a), ring (b), and prismatic specimen (c).
The load curves for all the specimens are represented by monotonically increasing functions of the stroke, which is also typical for other warm and cold upsetting and forging processes (Figure 7). It is evident that the compression force is the highest in ring upsetting. The compression forces for the cylindrical and prismatic specimens are of a comparable magnitude.
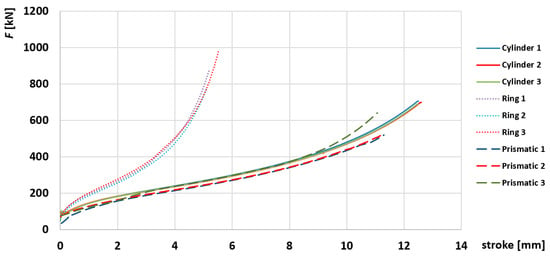
Figure 7.
Compression force for all three specimen groups.
The main factors that influence the compression force are the area of the contact surface, yield stress, friction coefficient, and die contact surface geometry. The yield stress is immaterial in this respect because all the specimens are made of the same material. Lubrication is carried out by filling the recesses (Figure 2, Figure 3 and Figure 5) with stearin, which results in low friction. Certain differences in the curves within the same specimen group (Figure 7) can be explained by unstable contact friction resulting from non-precise stearin deposition, and the inability to maintain a constant layer of stearin during the entire process. It is most evident in the case of plane strain compression. The ring and cylinder upsetting tests exhibit high repeatability, as seen from overlapping load curves.
The uniaxial and shear yield stresses are calculated according to the theoretical derivation provided in Section 2.2 using the experimental data for the compression force (Figure 7). The result of this calculation is depicted in Figure 8. All the curves in Figure 8a are within a rather narrow band, which confirms the first step of the methodology described in Section 2.1 (please see Appendix A).
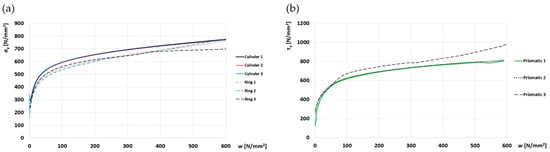
Figure 8.
Variation of σy and τy with the plastic work for cylinder and ring (a), and prismatic specimens (b).
Figure 9 presents the dependence of k on w calculated using the experimental data (Figure 8) and Equation (2).
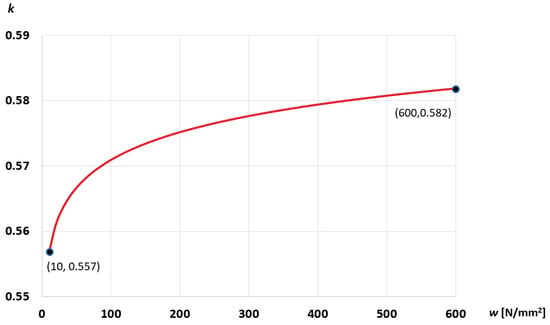
Figure 9.
Dependence of k-value on the plastic work.
The value of k varies from 0.557 to 0.582 (approximately). The value of n can be determined from Equation (3). In particular, at the beginning of the process. This result characterizes the initial yield criterion and agrees with the value calculated for randomly oriented BCC metals [8]. However, the value of n decreases from its initial value as the deformation proceeds (Figure 10). In particular, it reaches the value of 3.475 at the end of the process. Therefore, an accurate description of the material behavior of the steel investigated requires that n involved in (1) is a function of the plastic work.
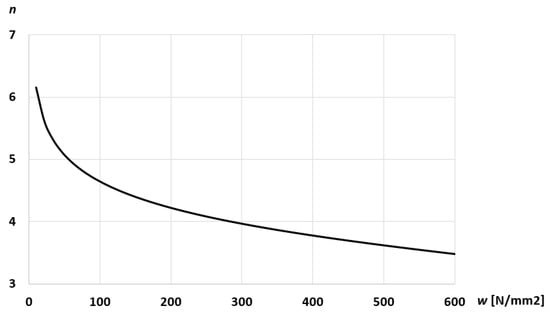
Figure 10.
Dependence of n-value on the plastic work.
It is generally possible to rewrite the constitutive equations above in terms of the equivalent strain. However, the corresponding strain rate cannot be expressed as an explicit function of the strain rate components for the n-values found. Therefore, it is more convenient to use the constitutive equations in terms of the plastic work.
5. Conclusions
A simple method for identifying isotropic pressure-independent two-parametric yield criteria has been developed. The method has been explicitly used with the yield criterion proposed in [8]. However, any other criterion of the class noted can be treated similarly. The method includes three compression tests. The compression of cylinders and rings reveals the effect of friction and determines the uniaxial yield stress. The plane strain compression determines the shear yield stress.
The method has been applied to low carbon steel C15E. The final result is presented in Figure 9. The constitutive parameter n involved in the yield criterion (1) can be determined using this curve and Equation (3). It has been found that the initial yield criterion practically coincides with the yield criterion calculated for randomly oriented BCC metals [8]. However, an accurate description of the material behavior of the steel investigated requires that n involved in (1) is a function of the plastic work.
The equivalent strain is adopted much more often as a hardening measure in metal forming applications compared to the plastic work. Although it is possible to rewrite the constitutive equations derived in terms of the equivalent strain, it requires a numerical procedure. Therefore, it is preferable to use the plastic work.
Author Contributions
Conceptualization, S.A.; Writing—original draft, S.A., M.V. and N.D.; Writing—review & editing, S.A. and Y.L.; Methodology, S.A. and M.V.; Resources, M.V. and N.D.; Supervision, Y.L.; Investigation, M.V. and N.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data is unavailable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| h | dimensionless height |
| k | ratio of the shear yield stress to the tensile yield stress |
| n | constitutive parameter |
| r | initial inner radius of ring specimens |
| s | current cross-sectional area of the ring specimens |
| t | time |
| ur, uz | radial and axial velocities |
| ux, uz | Cartesian velocity components |
| w | plastic work |
| B | width of strips |
| F | force required to deform specimens |
| H | current height of all specimens |
| H0 | initial height of all specimens |
| L | current length of strips |
| L0 | initial length of strips |
| R | current radius of cylindrical specimens |
| R0 | initial radius of cylindrical specimens and initial outer radius of ring specimens |
| V | velocity |
| dummy variable of integration | |
| , , | principal strain rates |
| , | strain rate components in x and z directions |
| , , | principal stresses |
| yield stress in tension | |
| axial stress | |
| shear yield stress |
Appendix A
In the case of compression of solid cylinders between two parallel plates without friction, the normal stress components in the cylindrical coordinate system introduced in Section 2.2.1 are
The shear stresses vanish. By definition, is the yield stress in uniaxial compression. The velocity field associated with (A1) is given in (8). The corresponding strain rate field is
The shear strain rates vanish. It is seen from (A2) that the equivalent strain rate and the equivalent strain are independent of spatial coordinates. Therefore, is independent of spatial coordinates, and the equilibrium equations are automatically satisfied. The solution above is independent of the cylinder’s radius.
In the case of compression of rings, the difference from the previous case is that there is an inner radius, which is traction free. However, it is evident that the stress distribution in (A1) satisfies this additional boundary condition. Moreover, the velocity field in (8) shows that the outer and inner surfaces of the ring remain circular cylinders after any amount of deformation. Therefore, the cylinder’s solution is also the ring’s solution. In particular, over the contact surface. Consequently, the curves in Figure 8a should coincide under the ideal conditions.
References
- Nassiraei, H.; Rezadoost, P. Static Capacity of Tubular X-Joints Reinforced with Fiber Reinforced Polymer Subjected to Compressive Load. Eng. Struct. 2021, 236, 112041. [Google Scholar] [CrossRef]
- Jantarasricha, T.; Chongbunwatana, K.; Panich, S. Comparative Study of Fracture Criteria through Bona Fide Experimental–Numerical Examinations on AA2024-T3. Int. J. Adv. Manuf. Technol. 2022, 119, 7685–7710. [Google Scholar] [CrossRef]
- Zhong, B.; Qiang, X.; Yu, Z.; Hu, S.; Yang, H. Analysis and Prediction of Maximum Contact Stress and Depth by Ultrasonic Surface Rolling with Elastic–Plastic Theory. Int. J. Adv. Manuf. Technol. 2023, 124, 3225–3239. [Google Scholar] [CrossRef]
- Dong, W.; Zhao, A.; Tong, H.; Lin, Q.; Wang, Z. A Study on Variable Friction Model in Cold Forging Process with Zinc Phosphate Coating. Int. J. Adv. Manuf. Technol. 2023, 124, 3439–3451. [Google Scholar] [CrossRef]
- Zhu, X.-K.; Leis, B.N. Average Shear Stress Yield Criterion and Its Application to Plastic Collapse Analysis of Pipelines. Int. J. Press. Vessels Pip. 2006, 83, 663–671. [Google Scholar] [CrossRef]
- Barlat, F.; Richmond, O. Prediction of Tricomponent Plane Stress Yield Surfaces and Associated Flow and Failure Behavior of Strongly Textured f.c.c. Polycrystalline Sheets. Mater. Sci. Eng. 1987, 95, 15–29. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic Strain in Metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Hosford, W.F. A Generalized Isotropic Yield Criterion. J. Appl. Mech. 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Billington, E.W. Generalized Isotropic Yield Criterion for Incompressible Materials. Acta Mech. 1988, 72, 1–20. [Google Scholar] [CrossRef]
- Reiss, W.; Pöhlandt, K. The Rastegaev Upset Test-A Method To Compress Large Material Volumes Homogeneously. Exp. Tech. 1986, 10, 20–24. [Google Scholar] [CrossRef]
- Alexandrov, S.; Vilotic, D.; Konjovic, Z.; Vilotic, M. An Improved Experimental Method for Determining the Workability Diagram. Exp. Mech. 2013, 53, 699–711. [Google Scholar] [CrossRef]
- Sliwa, R. A Test Determining the Ability of Different Materials to Undergo Simultaneous Plastic Deformation to Produce Metal Composites. Mat. Sci. Eng. A-Struct. 1991, 135, 259–265. [Google Scholar] [CrossRef]
- Han, H. The Validity of Mathematical Models Evaluated by Two-Specimen Method under the Unknown Coefficient of Friction and Flow Stress. J. Mater. Process. Technol. 2002, 122, 386–396. [Google Scholar] [CrossRef]
- Srinivasan, N.; Kain, V.; Samajdar, I.; Krishna, K.V.M.; Sivaprasad, P.V. Plane Strain Compression Testing of Sanicro 28 by Channel-Die Compression Test: A Direct Microstructural Observation. Mater. Today Proc. 2017, 4, 9888–9892. [Google Scholar] [CrossRef]
- Liang, Y.; Jiang, S.; Zhang, Y.; Zhao, C. Effect of Plane Strain Compression and Subsequent Recrystallization Annealing on Microstructures and Phase Transformation of NiTiFe Shape Memory Alloy. J. Mater. Eng. Perform. 2018, 27, 4514–4524. [Google Scholar] [CrossRef]
- Sae-Eaw, N.; Aue-U-Lan, Y. Mechanical Property Determination for Combined Sheet and Bulk Metal Forming Process by Plane Strain Compression Test. Mater. Today Proc. 2018, 5, 9376–9383. [Google Scholar] [CrossRef]
- Chermette, C.; Unruh, K.; Peshekhodov, I.; Chottin, J.; Balan, T. A New Analytical Method for Determination of the Flow Curve for High-Strength Sheet Steels Using the Plane Strain Compression Test. Int. J. Mater. Form. 2020, 13, 269–292. [Google Scholar] [CrossRef]
- Saalari, M. Comparison of Texture Evolution in Low Carbon Steel Fabricated by Plane Strain and Multi-Directional Forging of the Martensite Starting Structure. Int. J. Microstruct. Mater. Prop. 2019, 14, 524. [Google Scholar] [CrossRef]
- Jiang, S.; Yu, J.; Zhang, Y.; Xing, X. Mechanically-Induced Martensite Transformation of NiTiFe Shape Memory Alloy Subjected to Plane Strain Compression. Trans. Nonferrous Met. Soc. China 2020, 30, 1325–1334. [Google Scholar] [CrossRef]
- Guerza-Soualah, F.; Azzeddine, H.; Baudin, T.; Helbert, A.-L.; Brisset, F.; Bradai, D. Microstructural and Textural Investigation of an Mg–Dy Alloy after Hot Plane Strain Compression. J. Magnes. Alloys 2020, 8, 1198–1207. [Google Scholar] [CrossRef]
- Lagzian, Y.; Rezaee-Bazzaz, A. Texture Evolution of Commercially Pure Copper Processed by Multiple Compressions in a Channel Die. Eng. Res. Express 2020, 2, 015002. [Google Scholar] [CrossRef]
- Wen, D.; Kong, B.; Wang, S.; Zong, Y. Effect of Hydrogen on the Flow Behavior of a TiAl Based Alloy during Plane Strain Compression at Elevated Temperature. Int. J. Hydrogen Energy 2020, 45, 4897–4909. [Google Scholar] [CrossRef]
- Ghosh, A.; Roy, A.; Ghosh, A.; Ghosh, M. Influence of Temperature on Microstructure, Crystallographic Texture and Mechanical Properties of EN AW 6016 Alloy during Plane Strain Compression. Mater. Today Commun. 2021, 26, 101808. [Google Scholar] [CrossRef]
- Tamanna, N.; Slater, C.; Davis, C. Effect of Sample Geometry on Strain Uniformity and Double Hit Compression Tests for Softening Kinetics Determination. Steel Res. Int. 2022, 93, 2200157. [Google Scholar] [CrossRef]
- Diot, S.; Guines, D.; Gavrus, A.; Ragneau, E. Minimization of Friction Influence on the Evaluation of Rheological Parameters From Compression Test: Application to a Forging Steel Behavior Identification. J. Eng. Mater. Technol. 2009, 131, 011001. [Google Scholar] [CrossRef]
- Christiansen, P.; Martins, P.A.F.; Bay, N. Friction Compensation in the Upsetting of Cylindrical Test Specimens. Exp. Mech. 2016, 56, 1271–1279. [Google Scholar] [CrossRef]
- Chen, J.; Guan, Z.; Ma, P.; Li, Z.; Gao, D. Experimental Extrapolation of Hardening Curve for Cylindrical Specimens via Pre-Torsion Tension Tests. J. Strain Anal. Eng. Des. 2020, 55, 20–30. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, K.; Huang, S.; Ju, J.-W.W. Yield Surfaces and Plastic Flow of 45 Steel under Tension-Torsion Loading Paths. Acta Mech. 2012, 25, 348–360. [Google Scholar] [CrossRef]
- Semka, E.V.; Artemov, M.A.; Babkina, Y.N.; Baranovskii, E.S.; Shashkin, A.I. Mathematical Modeling of Rotating Disk States. J. Phys. Conf. Ser. 2020, 1479, 012122. [Google Scholar] [CrossRef]
- Male, A.T.; Cockcroft, M.G. A Method for the Determination of the Coefficient of Friction of Metals under Conditions of Bulk Plastic Deformation. J. Inst. Met. 1964, 93, 38–45. [Google Scholar] [CrossRef]
- Vilotic, M.; Dacevic, N.; Milutinovic, M.; Movrin, D.; Sidjanin, L. New Severe Plastic Deformation Method for 316L Medical Grade Steel Processing. Acta Tech. Corviniensis Bull. Eng. 2020, 13, 13–16. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).