Estimation of Activity and Molar Excess Gibbs Energy of Binary Liquid Alloys Al-Cu, Al-Ni, and Al-Fe from the Partial Radial Distribution Function Simulated by Ab Initio Molecular Dynamics

Abstract

To accurately and conveniently obtain the thermodynamic data of binary liquid alloys, a new method is proposed in this study. It combines ab initio molecular dynamics (AIMD) simulation with a thermodynamic model to estimate the activity and molar excess Gibbs energy of binary liquid alloys. Additionally, two methods of grouping the partial radial distribution function (PRDF) of 5000 steps obtained by simulation are proposed for the first time. The PRDF of Al50Cu50, Al50Ni50, and Al50Fe50 is obtained by AIMD simulation. These PRDF are combined with four thermodynamic models to estimate the activity and molar excess Gibbs energy. Furthermore, the estimation results of the four models are compared with those of the Miedema model. The results show that when the first peak of the PRDF is obtained by the symmetric method, the average relative deviation (ARD) of the activity and molar excess Gibbs energy of the four models are, respectively: 28% and 32% for Molecular Interaction Volume Model (MIVM); 162% and 38% for Regular Solution Model (RSM); 508% and 65% for Wilson model; 562% and 67% for Non-Random Two-Liquid (NRTL). When the first peak of PRDF is obtained by non-symmetric method, the average ARD of the activity and molar excess Gibbs energy of the four models are, respectively: 64% and 20% for MIVM; 115% and 26% for RSM; 661% and 70% for Wilson; 727% and 72% for NRTL. In addition, the average ARD of the activity and molar excess Gibbs energy of the Miedema model are 113% and 33%. These data indicate that the estimation performance of the MIVM model is superior to the other four models, and the symmetric method performs better than the non-symmetric method. The grouping treatment of PRDF data effectively improves estimation performance.

1. Introduction

Thermodynamic data are important parameters for studying structural changes, morphological transformations, and the feasibility of reactions in substances. However, in practice, especially in the field of metallurgy, the determination of thermodynamic data is often very time-consuming, expensive, and difficult to operate. Therefore, accurately and conveniently obtaining thermodynamic data has always been a critical research direction in basic thermodynamics [1]. Owing to the ability of thermodynamic models to derive preliminary approximations and reference values of thermodynamic data in complex liquid mixtures, thermodynamic models have become one of the most cost-effective prediction methods for obtaining thermodynamic data. Meanwhile, it has attracted the attention and favor of researchers by virtue of its obvious convenience, economic feasibility, and satisfactory accuracy. Not only does it provide valuable insights for industrial production, but it also saves a lot of manpower and material resources [2].

Binary aluminum-based alloys are widely used in life production; this paper mainly studies three binary liquid alloys, Al-Cu, Al-Ni, and Al-Fe. Al-Cu alloys can be prepared by Al-Cu alloy flexible nuclear shells and are used in new energy storage materials, which have the advantages of a small footprint, large capacity, and good stability, and are more suitable for high-temperature heat storage [3]. Al-Ni alloy is a typical energy-containing structural material, which has very broad application prospects in both military and civil fields, such as making energy-containing breakers and energy-containing drug masks, etc. [4]. Al-Fe alloy is mainly used for metal welding, which has the advantages of lightweight structure and good overall performance and has a wide range of prospects for application in the aerospace, nuclear energy, automotive, and electrical and electronic industries [5].

In practical experiments, metal smelting needs to meet certain conditions such as high temperature and high pressure, which can easily bring some difficulties and potential safety hazards, while computer simulation can avoid the above problems [6]. In 1985, the AIMD simulation method was proposed by Car R and Parrinello M [7], who used AIMD simulation to compute particle force conditions and trajectory motion. Since then, the successful application of AIMD simulations based on first principles has increased the acceptance of computer simulations as a research method, and AIMD simulations have been widely used to study the structure of melts [8,9]. In 2020, the structural and electronic properties of AlnVn (n = 2–12) clusters were investigated by Han et al. [10] using AIMD, and the poor intermiscibility between the components of Al-V alloys was experimentally explained. In 2023, the molecular dynamics trajectories of PbS and Sb₂S₃ at various temperatures were obtained by Xie et al. [11] using AIMD and the experimental calculations of PbS and Sb₂S₃ diffusion coefficients of gas-phase clusters at each temperature. Therefore, it is reasonable to use AIMD to obtain the PRDF of binary liquid alloys in this study.

In order to accurately and conveniently obtain thermodynamic data, such as activity and molar excess Gibbs energy of binary liquid alloys, this study proposes a new method that combines AIMD simulation with thermodynamic models to estimate the activity and molar excess Gibbs energy. Additionally, a method for processing the obtained PRDF data in two different groups, with a total of 5000 steps, is introduced for the first time in this paper. The activity and molar excess Gibbs energy of the alloy are also estimated using the Miedema model. Furthermore, a comparison between the results obtained from five different models and experimental values is conducted, calculating the standard deviation (SD) and average relative deviation (ARD), and comparing the results with those reported in similar literature. Through analysis, the feasibility of this approach is verified, and reference recommendations for selecting models and methods for calculating thermodynamic data of binary liquid alloys are provided.

2. Methods and Models

2.1. Obtaining the PRDF through AIMD Simulations

In this work, the initial configurations of the alloy cells were first established in the Materials Studio simulation software (https://software.umich.edu/titles/materials-studio) using the Packing method, which is mainly used to generate initial models of crystalline or amorphous structures, so that the atoms are randomly arranged in simple cubic cells. Three liquid alloys, Al50Cu50-1400 K, Al50Ni50-1923 K, and Al50Fe50-1823 K with densities of 4.69 g·cm⁻³ [12], 4.63 g·cm⁻³ [13], and 4.61 g·cm⁻³ [13] were set up to form the cell with 122, 128, and 116 atoms, respectively. Next, ab initio molecular dynamics (AIMD) simulation based on density functional theory (DFT) were conducted using the Vienna ab initio simulation package (VASP) software [14], specifically version VASP-5.4.1. VASP simulation encompassed two stages, namely structure optimization and dynamics. The exchange-correlation functional employed the Perdew–Burke–Ernzerhof (PBE) functional [15,16], which is based on the generalized gradient approximation (GGA). The GGA is a widely used approximation in DFT that incorporates electron density and electron density gradients to evaluate the exchange-correlation energy. The PBE functional, as a GGA functional, accurately describes the electronic structure of molecules in terms of both exchange and correlation energies. In this investigation, the ultrasoft pseudopotential (USPP) [17] was employed to characterize the electron–ion interaction within the pseudopotential file. The K-point is set to the Gamma point, and the cutoff energy is chosen to be 1.3 times higher than the maximum cutoff energy provided in the pseudopotential files [14], following the computational guidelines [18]. During the structure optimization stage, the convergence criterion for the electronic step is an energy change smaller than 10⁻⁴ eV/Å, while for the ionic step, it is an energy change smaller than 10⁻³ eV/Å. In the dynamics stage, the simulation temperature is set above the melting point of the alloys, namely 1400 K, 1923 K, and 1823 K, respectively. The simulation uses a canonical ensemble (NVT) that ensures that the number, volume, and temperature of atoms remain constant [19]. To maintain a constant system temperature, the Nose–Hoover thermostat method is employed [20,21]. For the dynamics simulation, a time step of 3 fs is utilized, and the simulation is performed for a total of 5000 steps (15 ps).

In order to comprehensively consider the variations of the partial radial distribution function (g(r)) throughout the entire simulation process and evaluate the differences in the estimation of activity and molar excess Gibbs energy at different step stages, as well as to improve the accuracy of the estimation, two data processing methods were performed on the obtained g(r) data from a total of 5000 steps (taking i-i as an example). The first method involved accumulating the g(r) data every 1000 steps, resulting in a total of five sets of g_ii(r) data: 0–1000 steps, 0–2000 steps, 0–3000 steps, 0–4000 steps, and 0–5000 steps. The second method involved segmenting the data every 1000 steps, also resulting in five sets of g_ii(r) data: 0–1000 steps, 1000–2000 steps, 2000–3000 steps, 3000–4000 steps, and 4000–5000 steps. Therefore, each alloy system obtained 5 × 2 × 3 sets of g(r) data.

2.2. Symmetric and Non-Symmetric Methods

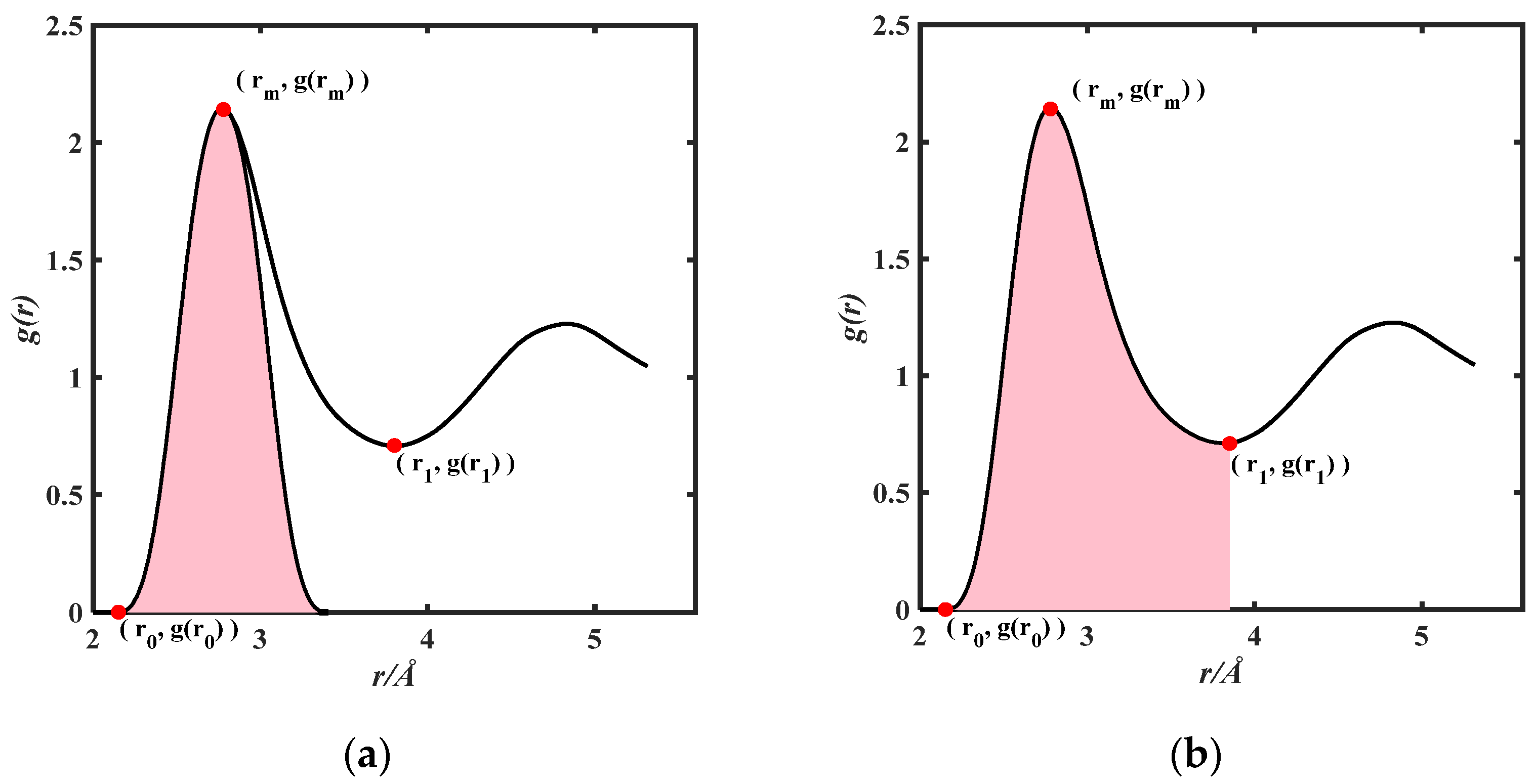
In the subsequent work, the relevant parameters of the thermodynamic model are expressed by equations containing g(r). It is widely acknowledged that the first peak contributes the most to g(r), so various methods have been commonly employed in academia to extract the first peak of g(r). In this study, symmetric and non-symmetric methods were mainly adopted by us. There are three key points for determining the first peak of g(r): r₀ represents the abscissa of the starting point of non-zero values, r_m represents the abscissa of the first peak’s maximum, and r₁ represents the abscissa of the first peak’s minimum.

Regarding the symmetric method [22], the curve on the left side of g(r) is symmetric with the line r = r_m as the symmetry axis to get the curve on the right side, and the entire image is the first peak of the PRDF obtained by using the symmetric method. As shown in Figure 1a, the curve in the r₀~r_m region of g(r) image is symmetric with the line r = r_m as the symmetry axis to obtain the curve on the right side, and the pink region represents the first peak of the PRDF obtained by using the symmetric method. As for the non-symmetric method [23], the g(r) curve within the interval from r₀~r_m represents the first peak obtained using the non-symmetric method. As shown in Figure 1b, the pink region represents the first peak of the PRDF obtained by the non-symmetric method.

Figure 1. (a) The first peak of partial radial distribution function is obtained by symmetric method; (b) the first peak of partial radial distribution function is obtained by non-symmetric method.

2.3. Thermodynamic Models

2.3.1. Molecular Interaction Volume Model (MIVM)

The Molecular Interaction Volume Model (MIVM) [24] was proposed by Tao in 2000. The MIVM possesses characteristics such as inclusivity, diffusion stability, and thermodynamic consistency. Tao used statistical thermodynamics in the derivation process to obtain configurational partition functions that include both volume and energy terms, which gives the model a clearer physical meaning and better overall prediction results.

For the binary system i-j, the molar excess Gibbs energy of the MIVM model can be expressed as:

$$\frac{G_m^E}{RT}=x_i\ln \left(\frac{V_{mi}}{x_i{V}_{mi}+x_j{V}_{mj}{B}_{ji}}\right)+x_j\ln \left(\frac{V_{mj}}{x_j{V}_{mj}+x_i{V}_{mi}{B}_{ij}}\right)-\frac{x_i{x}_j}{2}\left[\frac{Z_i{B}_{ji}\ln B_{ji}}{x_i+x_j{B}_{ji}}+\frac{Z_j{B}_{ij}\ln B_{ij}}{x_j+x_i{B}_{ij}}\right]$$

(1)

The expression for the activity coefficient of component i is:

$$\begin{array}{ll}\ln {\gamma }_i=& \ln \left(\frac{V_{mi}}{x_i{V}_{mi}+x_j{V}_{mj}{B}_{ji}}\right)+x_j\left(\frac{V_{mj}{B}_{ji}}{x_i{V}_{mi}+x_j{V}_{mj}{B}_{ji}}-\frac{V_{mi}{B}_{ij}}{x_j{V}_{mj}+x_i{V}_{mi}{B}_{ij}}\right)\\ & -\frac{x_{{}^j}^2}{2}\left(\frac{Z_i{B}_{ij}^2\ln B_{ji}}{{(x_i+x_j{B}_{ji})}^2}-\frac{Z_j{B}_{ij}^{}\ln B_{ij}}{{(x_j+x_i{B}_{ij})}^2}\right)\end{array}$$

(2)

R is the gas constant (8.314 J/(K.mol)), T is the temperature, x_i and x_j represent the mole fractions of components i and j in the mixture, V_mi and V_mj represent the molar volumes of pure substances i and j, and Z_i and Z_j represent the first coordination numbers of pure substances i and j. B_ij and B_ji are the pair-potential energy interaction parameters, which are defined as:

$$B_{ij}=\exp \left(-\frac{{\epsilon }_{ij}-{\epsilon }_{ii}}{kT}\right)\hspace{1em}{B}_{ji}=\exp \left(-\frac{{\epsilon }_{ji}-{\epsilon }_{jj}}{kT}\right)$$

(3)

Here, k is the Boltzmann constant (1.38 × 10⁻²³ J/K). ε_ii, ε_jj, and ε_ij are the molecular mean pair potentials of the molecule for i-i, j-j, and i-j, respectively.

Wang et al. [25] hypothesized that the equation ${\epsilon }_{ii}(r)=-kT\ln g_{ii}(r)$ [26], which relates the molecular pair potential of very dilute gases to the radial distribution function, can be approximately applied to binary liquid alloys. Thus, according to the probability density distribution function and the expectation principle, the expressions for the molecular mean pair potentials, ε_ii, ε_jj, and ε_ij of the binary liquid alloy can be obtained as:

$$\frac{{\epsilon }_{ii}}{kT}=-\frac{{\displaystyle {\int }_{r_0}^{r_1}\ln g_{ii}(r)g_{ii}(r)r^{2}dr}}{{\displaystyle {\int }_{r_0}^{r_1}{g}_{ii}(r)r^{2}dr}}$$

(4)

$$\frac{{\epsilon }_{ij}}{kT}=-\frac{{\displaystyle {\int }_{r_0}^{r_1}\ln g_{ij}(r)g_{ij}(r)r^{2}dr}}{{\displaystyle {\int }_{r_0}^{r_1}{g}_{ij}(r)r^{2}dr}}$$

(5)

$$\frac{{\epsilon }_{jj}}{kT}=-\frac{{\displaystyle {\int }_{r_0}^{r_1}\ln g_{jj}(r)g_{jj}(r)r^{2}dr}}{{\displaystyle {\int }_{r_0}^{r_1}{g}_{jj}(r)r^{2}dr}}$$

(6)

2.3.2. Regular Solution Model (RSM)

The Regular Solution Model (RSM) [27,28] was proposed by Hildebrand in 1929. This model assumes that the mixture enthalpy of the solution is non-zero, while the mixture entropy is equal to that of an ideal solution. In other words, this model considers the interactions between solvent molecules, but neglects the influence of volume.

For the binary system i-j, the molar excess Gibbs energy of the RSM model can be expressed as:

$$\frac{G_m^E}{RT}=\frac{w}{kT}{x}_i{x}_j$$

(7)

The expression for the activity coefficient of component i is:

$$\ln {\gamma }_i=\frac{w}{kT}{x}_j^2$$

(8)

where w is the interaction parameter, and the expression is:

$$\frac{w}{kT}=Z\left[\frac{{\epsilon }_{ij}}{kT}-\frac{1}{2}\left(\frac{{\epsilon }_{ii}}{kT}+\frac{{\epsilon }_{jj}}{kT}\right)\right]$$

(9)

where Z represents the average coordination number, assuming that it can be expressed using local coordination numbers Z_ii, Z_ij, Z_ji, and Z_jj.

$$Z=x_i(Z_{ii}+Z_{ij})+x_j(Z_{ji}+Z_{jj})$$

(10)

These local coordination numbers can be expressed using the expressions provided by Hill [26]:

$$\begin{array}{l}{Z}_{ii}=x_i{\rho }_{0}4\pi {\displaystyle {\int }_0^{\infty }{r}^2{g}_{ij}(r)dr}\hspace{1em}{Z}_{ij}=x_j{\rho }_{0}4\pi {\displaystyle {\int }_0^{\infty }{r}^2{g}_{ij}(r)dr}\\ Z_{jj}=x_j{\rho }_{0}4\pi {\displaystyle {\int }_0^{\infty }{r}^2{g}_{jj}(r)dr}\hspace{1em}{Z}_{ji}=x_i{\rho }_{0}4\pi {\displaystyle {\int }_0^{\infty }{r}^2{g}_{ji}(r)dr}\end{array}$$

(11)

where ρ₀ represents the average density of the alloy.

2.3.3. Wilson Model

The Wilson model [29] was proposed by Wilson in 1964. Wilson used the ratio of the Boltzmann distribution to define the “local concentration”, which the local volume fraction was defined and directly substituted into the Flory–Huggins equation [30].

For the binary system i-j, the molar excess Gibbs energy of the Wilson model can be expressed as:

$$\frac{G_m^E}{RT}=-x_i\ln \left(x_i+A_{ji}{x}_j\right)-x_j\ln \left(x_j+A_{ij}{x}_i\right)$$

(12)

The expression for the activity coefficient of component i is:

$$\ln {\gamma }_i=-\ln \left(x_i+A_{ji}{x}_j\right)+x_j\left[\frac{A_{ji}}{x_i+A_{ji}{x}_j}-\frac{A_{ij}}{x_j+A_{ij}{x}_i}\right]$$

(13)

where the parameters A_ij and A_ji are defined as:

$$A_{ij}=\frac{V_i}{V_j}\exp \left(-\frac{{\epsilon }_{ij}-{\epsilon }_{jj}}{kT}\right)\hspace{1em}{A}_{ji}=\frac{V_j}{V_i}\exp \left(-\frac{{\epsilon }_{ij}-{\epsilon }_{ii}}{kT}\right)$$

(14)

2.3.4. Non-Random Two-Liquid Model (NRTL)

The Non-Random Two-Liquid (NRTL) model [31] was proposed by Renon and Prausnitz in 1968. This model was derived by combining a local composition equation, based on the non-random assumption, with a potential energy expression for liquid mixtures from the two-liquid theory. The NRTL model is highly regarded in the field of organic chemistry for its balanced combination of simplicity, accuracy, and rationality.

For the binary system i-j, the molar excess Gibbs energy of the NRTL model can be expressed as:

$$\frac{G_m^E}{RT}=x_i{x}_j\left(\frac{{\tau }_{ji}\exp \left(-\alpha {\tau }_{ji}\right)}{x_i+x_j\exp \left(-\alpha {\tau }_{ji}\right)}+\frac{{\tau }_{ij}\exp \left(-\alpha {\tau }_{ij}\right)}{x_j+x_i\exp \left(-\alpha {\tau }_{ij}\right)}\right)$$

(15)

The expression for the activity coefficient of component i is:

$$\ln {\gamma }_i=x_j^2\left(\frac{{\tau }_{ji}\exp \left(-2{\alpha }_{ij}{\tau }_{ji}\right)}{\left[x_i+x_j\exp (-{\alpha }_{ij}{\tau }_{ji})\right]}+\frac{{\tau }_{ij}\exp \left(-2{\alpha }_{ij}{\tau }_{ij}\right)}{\left[x_j+x_i\exp (-{\alpha }_{ij}{\tau }_{ij})\right]}\right)$$

(16)

where the parameters τ_ij and τ_ji are defined as:

$${\tau }_{ij}=\frac{{\epsilon }_{ij}-{\epsilon }_{jj}}{kT}\hspace{1em}{\tau }_{ji}=\frac{{\epsilon }_{ji}-{\epsilon }_{ii}}{kT}$$

(17)

where α is a non-random factor, its introduction aims to take into account the volume size of the molecule through correction, with a value range of 0.2~0.47, where α_ij = α_ji = 0.3.

2.3.5. Miedema Model

The Miedema model [32,33] is a semi-empirical thermodynamic model that was proposed by Miedema et al. in 1973. Considering that the concept of cell is still applicable in alloys, the Wigner–Seitz cell model, which is often used to describe pure metals, is extended to binary alloys.

For the binary system i-j, the mixing enthalpy expression of Miedema model is:

$$\Delta H_{ij}=f_{ij}\frac{x_i\left[1+u_i{x}_j\left({\varphi }_i-{\varphi }_j\right)\right]x_j\left[1+u_j{x}_i\left({\varphi }_j-{\varphi }_i\right)\right]}{x_i{V}_i^{2/3}\left[1+u_i{x}_j\left({\varphi }_i-{\varphi }_j\right)\right]+x_j{V}_j^{2/3}\left[1+u_j{x}_i\left({\varphi }_j-{\varphi }_i\right)\right]}$$

(18)

$$f_{ij}=\frac{2p{V}_i^{2/3}{V}_j^{2/3}\left[q/p{\left(n_{wsi}^{1/3}-n_{wsj}^{1/3}\right)}^2-{\left({\varphi }_i-{\varphi }_j\right)}^2-a\left(r/p\right)\right]}{{\left(n_{wsi}^{1/3}\right)}^{-1}+{\left(n_{wsj}^{1/3}\right)}^{-1}}$$

(19)

Additionally, considering the relationship proposed by Tanaka [34]:

$$H_m^{mix}=\frac{14S_m^E{T}_{mi}{T}_{mj}}{T_{mi}+T_{mj}}$$

(20)

The molar excess Gibbs energy of the Miedema model can be expressed as:

$$G_{ij}^E=\Delta H_{ij}\left(1-T\frac{14T_{mi}{T}_{mj}}{T_{mj}+T_{mi}}\right)$$

(21)

The expression for the activity coefficient of component i is:

$$\ln {\gamma }_i=\frac{1}{RT}{\alpha }_{ij}\Delta H_{ij}\left\{1+x_j\left[\begin{array}{l}\frac{1}{x_i}-\frac{1}{x_j}-\frac{u_i\left({\varphi }_i-{\varphi }_j\right)}{\left[1+u_i{x}_j\left({\varphi }_i-{\varphi }_j\right)\right]}+\frac{u_j\left({\varphi }_j-{\varphi }_i\right)}{\left[1+u_j{x}_i\left({\varphi }_j-{\varphi }_i\right)\right]}\\ -\frac{V_i^{2/3}\left[1+u_i\left(1-2x_i\right)\left({\varphi }_i-{\varphi }_j\right)\right]+V_j^{2/3}\left[-1+u_j\left(1-2x_i\right)\left({\varphi }_j-{\varphi }_i\right)\right]}{x_i{V}_i^{2/3}\left[1+u_i{x}_j\left({\varphi }_i-{\varphi }_j\right)\right]+x_j{V}_j^{2/3}\left[1+u_j{x}_i\left({\varphi }_j-{\varphi }_i\right)\right]}\end{array}\right]\right\}$$

(22)

$${\alpha }_{ij}=1-\frac{T}{14}\left(\frac{1}{T_{m_i}}+\frac{1}{T_{m_j}}\right)$$

(23)

where V_i and V_j are the molar volumes of elements i and j, respectively, Φ_i and Φ_j are the electronegativity of elements i and j, respectively, n_wsi and n_wsj are the electron densities of elements i and j, respectively, and T_mi and T_mj are the melting points of elements i and j, respectively. u, q/p, a, p, r/p are empirical constants of the model, and specific values can be obtained from the literature [32].

2.4. Calculation Process

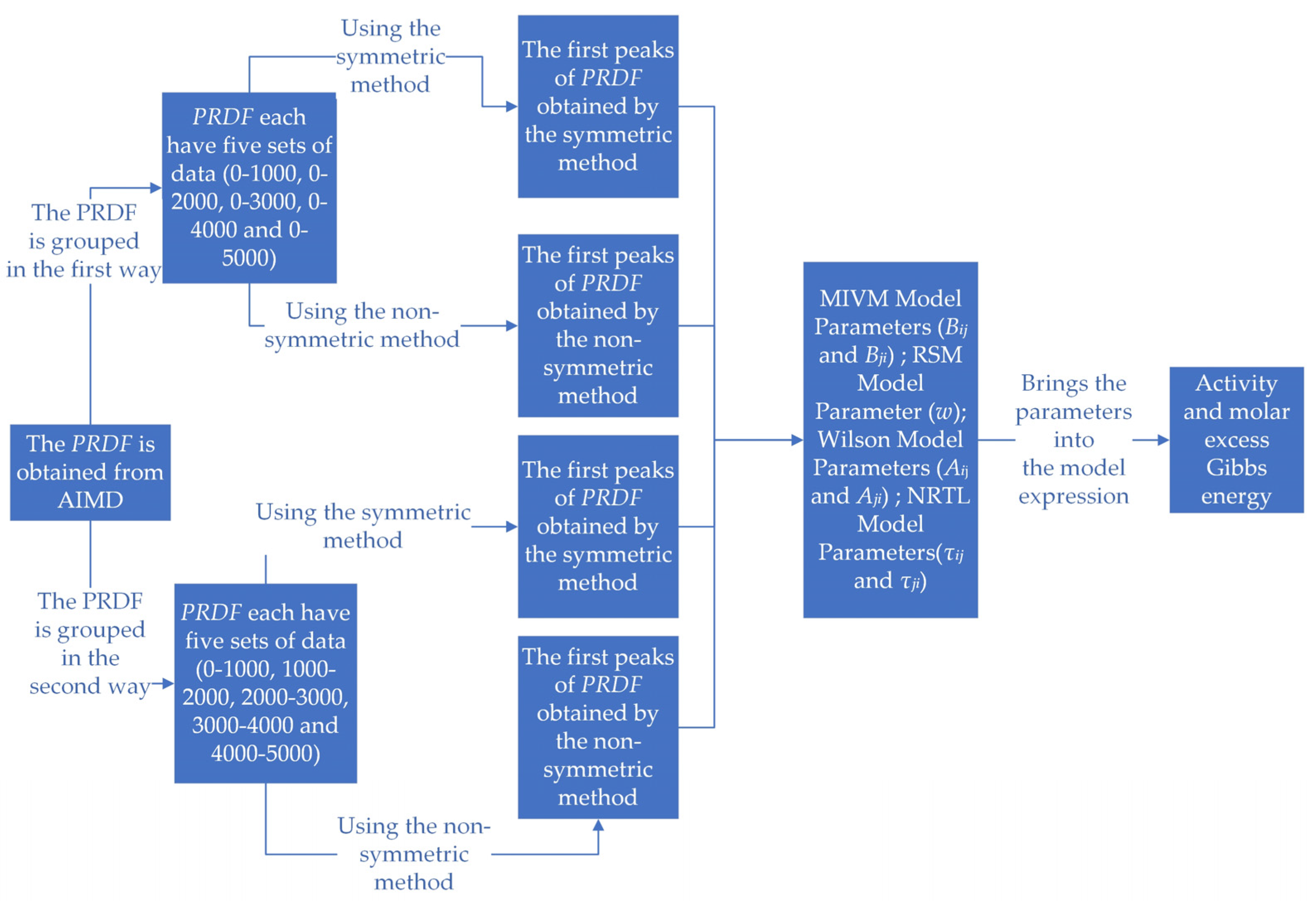
As shown in Figure 2, there are five main steps in the whole calculation process. The PRDF was obtained by AIMD. A total of 5000 steps of PRDF were processed in two groups, and a total of 5 × 2 × 3 groups of PRDF data were obtained for each alloy system. The first peak of PRDF was extracted by symmetric method and non-symmetric method, respectively. The parameters of the four models were calculated with expressions containing PRDF. The activity and molar excess Gibbs energy of the binary liquid alloy system are estimated by taking the obtained parameter values into the expressions of the model activity and molar excess Gibbs energy.

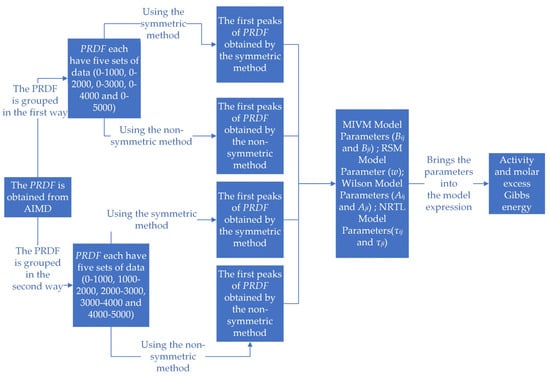
Figure 2. Calculation process chart.

Meanwhile, the parameter values of the Miedema model can be obtained from the literature [32], which can be used to estimate the activity and molar excess Gibbs energy of binary liquid alloy systems by substituting these values into the formula of the Miedema model. By comparing the results of the Miedema model with those of the other four models, the reliability of the conclusion can be comprehensively evaluated and the accuracy of the conclusion can be verified.

3. Results and Discussion

3.1. The g(r) Simulated by AIMD

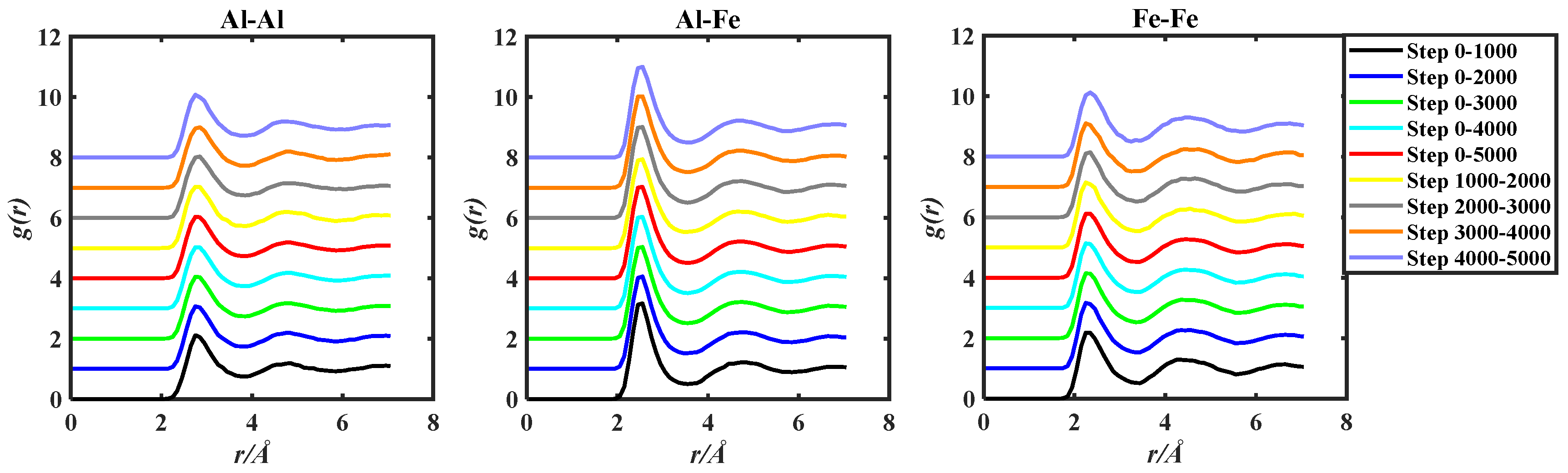
The g(r) of the three alloy systems were obtained by ab initio molecular dynamics simulation. The obtained g(r) data were processed by the two methods in the above Section 2.1, and the obtained images were shown in Figure 3, Figure 4 and Figure 5.

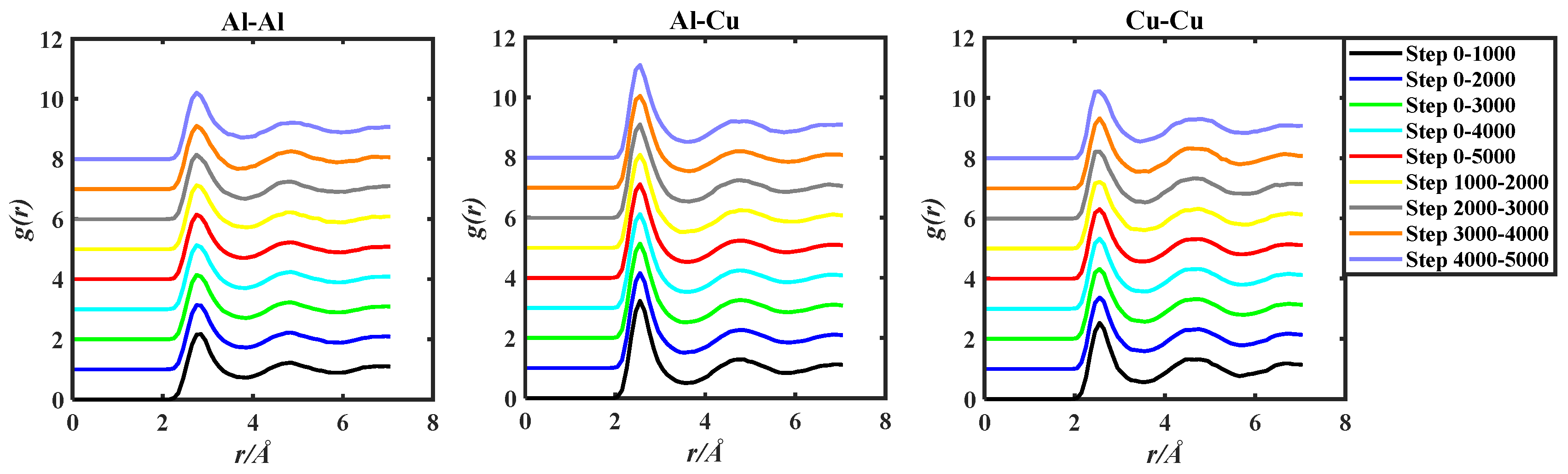
Figure 3. g_Al-Al(r), g_Al-Cu(r), and g_Cu-Cu(r) of the Al50Cu50-1400 K system, grouped by two methods based on 5000 steps PRDF data.

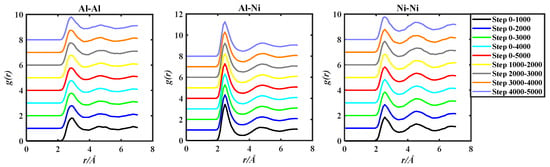
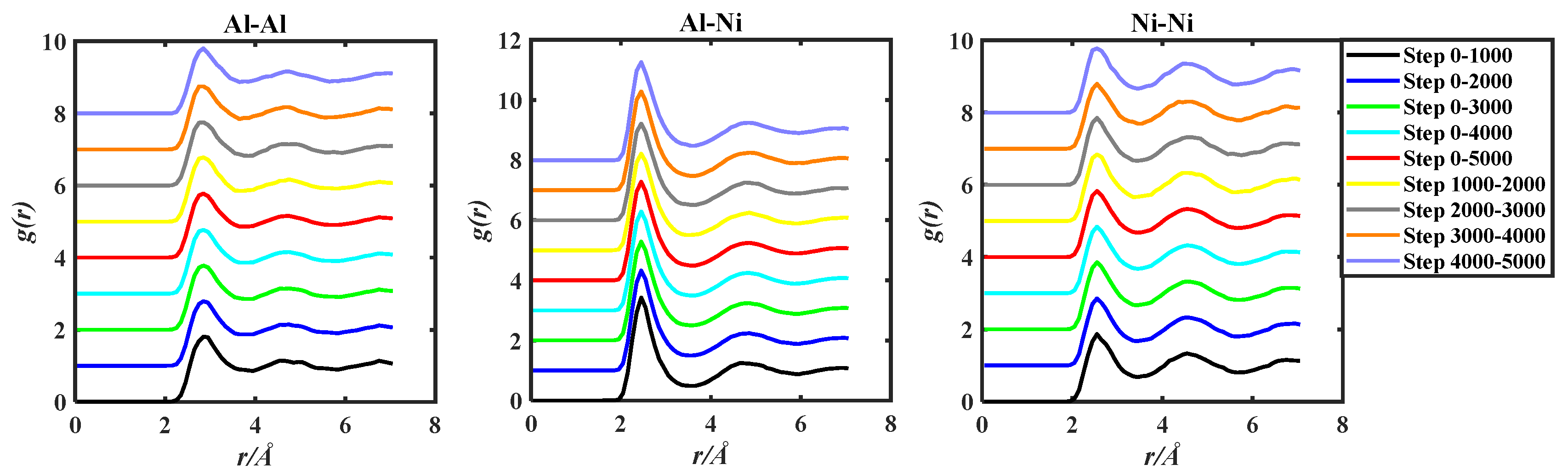
Figure 4. g_Al-Al(r), g_Al-Ni(r), and g_Ni-Ni(r) of the Al50Ni50-1923 K system, grouped by two methods based on 5000 steps PRDF data.

Figure 5. g_Al-Al(r), g_Al-Fe(r), and g_Fe-Fe(r) of the Al50Fe50-1823 K system, grouped by two methods based on 5000 steps PRDF data.

Observing Figure 3, Figure 4 and Figure 5, in order to facilitate the observation of each g_ii(r), g_ij(r), and g_jj(r) graph, the ordinate of g_ii(r), g_ij(r), and g_jj(r) is incremented by 1, so that all the graphs do not overlap. By observation, it can be found that the PRDF graphs obtained by AIMD are continuous, smooth, and without sudden large inflection points. This indicates that using the aforementioned parameters for AIMD simulation can obtain relatively accurate PRDF graphs. For the PRDF graphs at different steps, it can be observed that the changes are not very significant, with the main variations occurring at the peak and first peak-valley positions.

There were three key points about the first peak of g(r) presented in Section 2.2 above. The coordinates of the key points for the three systems Al-Cu, Al-Ni, and Al-Fe were presented in Table 1, Table 2 and Table 3, respectively.

Table 1. The three key coordinate points of the first peak of g_Al-Al(r), g_Al-Cu(r), and g_Cu-Cu(r) in the Al50Cu50-1400 K system.

Parameters		Step of Al50Cu50 (1400 K)
		0–1000	0–2000	0–3000	0–4000	0–5000	1000–2000	2000–3000	3000–4000	4000–5000
r0/Å	i-i	2.153	2.148	2.159	2.153	2.153	2.164	2.153	2.153	2.153
	i-j	1.949	1.949	1.960	1.954	1.954	1.954	1.949	1.965	1.954
	j-j	1.954	1.954	1.954	1.954	1.954	1.954	1.949	1.954	1.965
rm/Å	i-i	2.809	2.796	2.786	2.782	2.778	2.781	2.766	2.772	2.763
	i-j	2.551	2.547	2.542	2.541	2.538	2.543	2.532	2.534	2.529
	j-j	2.557	2.551	2.544	2.545	2.542	2.540	2.525	2.548	2.526
g(rm)	i-i	2.189	2.156	2.143	2.129	2.141	2.128	2.127	2.089	2.191
	i-j	3.174	3.124	3.102	3.090	3.083	3.075	3.062	3.057	3.059
	j-j	2.495	2.369	2.327	2.320	2.305	2.246	2.251	2.298	2.253
r1/Å	i-i	3.828	3.844	3.827	3.806	3.805	3.862	3.811	3.699	3.803
	i-j	3.569	3.535	3.552	3.577	3.588	3.506	3.607	3.633	3.618
	j-j	3.543	3.536	3.543	3.539	3.506	3.531	3.554	3.416	3.452
g(r1)	i-i	0.722	0.725	0.710	0.705	0.707	0.728	0.679	0.678	0.716
	i-j	0.498	0.512	0.524	0.533	0.532	0.523	0.544	0.552	0.525
	j-j	0.564	0.591	0.574	0.571	0.571	0.617	0.539	0.556	0.559

Table 2. The three key coordinate points of the first peak of g_Al-Al(r), g_Al-Ni(r), and g_Ni-Ni(r) in the Al50Ni50-1923 K system.

Parameters		Step of Al50Ni50 (1923 K)
		0–1000	0–2000	0–3000	0–4000	0–5000	1000–2000	2000–3000	3000–4000	4000–5000
r0/Å	i-i	2.153	2.153	2.159	2.159	2.153	2.159	2.153	2.159	2.153
	i-j	1.858	1.858	1.858	1.863	1.858	1.858	1.858	1.868	1.954
	j-j	1.954	1.954	1.949	1.954	1.954	1.954	1.954	1.954	1.954
rm/Å	i-i	2.877	2.858	2.846	2.838	2.837	2.833	2.817	2.816	2.836
	i-j	2.459	2.456	2.454	2.452	2.451	2.452	2.449	2.447	2.444
	j-j	2.557	2.557	2.553	2.552	2.551	2.557	2.546	2.548	2.545
g(rm)	i-i	1.811	1.795	1.783	1.779	1.780	1.785	1.766	1.771	1.784
	i-j	3.351	3.268	3.238	3.241	3.234	3.186	3.180	3.250	3.207
	j-j	1.825	1.835	1.832	1.815	1.809	1.844	1.828	1.764	1.788
r1/Å	i-i	3.916	3.823	3.841	3.785	3.777	3.666	3.847	3.684	3.703
	i-j	3.565	3.534	3.563	3.575	3.587	3.515	3.595	3.598	3.611
	j-j	3.454	3.433	3.436	3.459	3.456	3.405	3.442	3.500	3.449
g(r1)	i-i	0.863	0.868	0.852	0.856	0.861	0.849	0.821	0.853	0.879
	i-j	0.483	0.496	0.500	0.494	0.491	0.507	0.508	0.474	0.479
	j-j	0.679	0.672	0.670	0.677	0.675	0.663	0.666	0.691	0.667

Table 3. The three key coordinate points of the first peak of g_Al-Al(r), g_Al-Fe(r), and g_Fe-Fe(r) in the Al50Fe50-1823 K system.

Parameters		Step of Al50Fe50 (1823 K)
		0–1000	0–2000	0–3000	0–4000	0–5000	1000–2000	2000–3000	3000–4000	4000–5000
r0/Å	i-i	2.062	2.148	2.153	2.153	2.159	2.153	2.153	2.159	2.148
	i-j	1.954	1.954	1.960	1.954	1.954	1.949	1.954	1.954	1.954
	j-j	1.734	1.750	1.750	1.755	1.750	1.750	1.761	1.745	1.755
rm/Å	i-i	2.793	2.792	2.798	2.802	2.798	2.791	2.811	2.820	2.782
	i-j	2.512	2.512	2.511	2.510	2.511	2.511	2.508	2.509	2.513
	j-j	2.310	2.304	2.308	2.304	2.311	2.296	2.316	2.293	2.342
g(rm)	i-i	2.101	2.072	2.058	2.043	2.047	2.044	2.031	2.003	2.064
	i-j	3.180	3.070	3.058	3.057	3.050	2.959	3.035	3.054	3.019
	j-j	2.208	2.179	2.169	2.151	2.143	2.152	2.150	2.099	2.125
r1/Å	i-i	3.825	3.823	3.827	3.827	3.825	3.820	3.833	3.826	3.820
	i-j	3.561	3.532	3.539	3.542	3.544	3.508	3.546	3.547	3.555
	j-j	3.385	3.377	3.380	3.374	3.367	3.370	3.384	3.308	3.251
g(r1)	i-i	0.745	0.737	0.739	0.737	0.734	0.729	0.743	0.730	0.721
	i-j	0.497	0.517	0.512	0.512	0.508	0.535	0.501	0.512	0.495
	j-j	0.515	0.528	0.524	0.522	0.523	0.541	0.517	0.510	0.510

Analysis of Table 1, Table 2 and Table 3 reveals that with the increase in simulation steps, the coordinates of the three key points of the first peak of g_ii(r), g_ij(r), and g_jj(r) for the Al50Cu50-1400 K, Al50Ni50-1923 K, and Al50Fe50-1823 K systems exhibit minimal change. The fluctuation of peak–trough values does not consistently increase or decrease with the number of steps. However, careful analysis indicates that the value of the g(r_m) gradually decreases with the number of steps, implying that as the number of steps increases, the peak position gradually shifts downwards.

3.2. Calculating Key Parameters of the Five Models

Expressions (4)–(6) containing g(r) were substituted into model parameter expressions (3) for MIVM, (9) for RSM, (14) for Wilson, and (17) for NRTL. Then, the values of the model parameters were calculated by using the graphical integration method. Obviously, this method is different from the L-PPDF mathematical of Gaussian function fitting adopted by Wang et al. [25], which depends on the fitting parameters u and v. Therefore, no fitting parameter was introduced in the calculation process of model parameters in this study.

The specific calculation of graphical integration utilizes the trapezoidal integration method [35]. This method divides the integration region into multiple small trapezoids and sums their areas to obtain the integral value. The parameter values of each model are calculated by using the symmetric method and the non-symmetric method, as shown in Table 4. Table 5 lists the parameters of Miedema model for the three alloy systems.

Table 4. Parameters of four models calculated for Al-Cu, Al-Ni, and Al-Fe systems by symmetric and non-symmetric methods.

System	Step	MIVM				RSM		Wilson				NRTL
		Sym		Non-Sym		Sym	Non-Sym	Sym		Non-Sym		Sym		Non-Sym
		Bij	Bji	Bij	Bji	w/kT	w/kT	Aij	Aji	Aij	Aji	τij	τji	τij	τji
Al-Cu (1400 K)	0–1000	1.43	1.27	1.27	1.22	−2.00	−2.67	1.92	0.94	1.86	0.84	−0.24	−0.36	−0.20	−0.24
	0–2000	1.44	1.31	1.30	1.27	−2.05	−2.99	1.99	0.95	1.92	0.85	−0.27	−0.36	−0.24	−0.26
	0–3000	1.43	1.33	1.28	1.27	−2.04	−2.96	2.01	0.95	1.93	0.85	−0.28	−0.36	−0.24	−0.25
	0–4000	1.44	1.33	1.27	1.27	−2.05	−2.85	2.02	0.95	1.92	0.83	−0.28	−0.36	−0.24	−0.24
	0–5000	1.43	1.33	1.25	1.24	−2.01	−2.65	2.02	0.94	1.87	0.83	−0.29	−0.36	−0.21	−0.23
	1000–2000	1.44	1.35	1.32	1.31	−2.09	−3.29	2.05	0.95	1.98	0.87	−0.30	−0.36	−0.27	−0.28
	2000–3000	1.43	1.37	1.25	1.28	−2.02	−2.85	2.08	0.94	1.94	0.82	−0.31	−0.36	−0.24	−0.22
	3000–4000	1.46	1.34	1.21	1.19	−2.08	−2.16	2.03	0.96	1.80	0.80	−0.29	−0.38	−0.17	−0.19
	4000–5000	1.38	1.34	1.22	1.18	−1.84	−2.17	2.03	0.91	1.78	0.80	−0.29	−0.32	−0.16	−0.20
Al-Ni (1923 K)	0–1000	1.74	1.81	1.37	1.39	−3.81	−4.08	3.06	1.03	2.37	0.81	−0.59	−0.56	−0.33	−0.31
	0–2000	1.74	1.75	1.36	1.41	−3.62	−3.98	2.98	1.02	2.39	0.80	−0.56	−0.55	−0.34	−0.31
	0–3000	1.74	1.74	1.35	1.39	−3.54	−3.91	2.96	1.03	2.36	0.79	−0.56	−0.55	−0.33	−0.30
	0–4000	1.71	1.77	1.33	1.41	−3.58	−3.85	3.00	1.01	2.39	0.78	−0.57	−0.54	−0.34	−0.28
	0–5000	1.76	1.76	1.32	1.40	−3.56	−3.78	2.99	1.04	2.37	0.78	−0.57	−0.57	−0.34	−0.28
	1000–2000	1.58	1.70	1.31	1.40	−3.47	−3.62	2.89	0.93	2.38	0.78	−0.53	−0.46	−0.34	−0.27
	2000–3000	1.76	1.72	1.33	1.38	−3.39	−3.84	2.93	1.03	2.35	0.79	−0.55	−0.56	−0.32	−0.29
	3000–4000	1.81	1.83	1.29	1.44	−3.68	−3.79	3.10	1.07	2.44	0.76	−0.60	−0.59	−0.37	−0.26
	4000–5000	1.78	1.77	1.29	1.38	−3.53	−3.52	3.00	1.05	2.34	0.76	−0.57	−0.58	−0.32	−0.25
Al-Fe (1823 K)	0–1000	1.52	1.40	1.27	1.30	−2.42	−3.14	2.25	0.95	2.09	0.79	−0.34	−0.42	−0.26	−0.24
	0–2000	1.47	1.38	1.27	1.31	−2.23	−3.15	2.21	0.91	2.10	0.79	−0.32	−0.39	−0.27	−0.24
	0–3000	1.47	1.38	1.26	1.31	−2.25	−3.18	2.22	0.91	2.12	0.78	−0.32	−0.38	−0.27	−0.23
	0–4000	1.47	1.39	1.26	1.32	−2.27	−3.21	2.24	0.91	2.12	0.78	−0.33	−0.38	−0.28	−0.23
	0–5000	1.47	1.39	1.26	1.32	−2.27	−3.19	2.24	0.91	2.12	0.78	−0.33	−0.38	−0.27	−0.23
	1000–2000	1.42	1.35	1.27	1.31	−2.05	−3.13	2.18	0.88	2.10	0.79	−0.30	−0.35	−0.27	−0.24
	2000–3000	1.46	1.39	1.26	1.34	−2.28	−3.29	2.24	0.91	2.16	0.78	−0.33	−0.38	−0.29	−0.23
	3000–4000	1.46	1.43	1.26	1.31	−2.34	−3.14	2.30	0.91	2.11	0.79	−0.35	−0.38	−0.27	−0.23
	4000–5000	1.46	1.38	1.26	1.24	−2.24	−2.81	2.23	0.91	2.00	0.79	−0.33	−0.38	−0.22	−0.23

Table 5. Parameters for Miedema model calculation of Al-Cu, Al-Ni, and Al-Fe systems.

System	nswi1/3	nswj1/3	Φi	Φj	Vi2/3	Vj2/3	ui	uj	p	r/p
Al-Cu (1400 K)	1.39	1.47	4.2	4.55	4.6	3.7	0.07	0.04	12.3	0.57
Al-Ni (1923 K)	1.39	1.75	4.2	5.2	4.6	3.5	0.07	0.04	12.3	1.9
Al-Fe (1823 K)	1.39	1.77	4.2	4.93	4.6	3.7	0.07	0.04	12.3	1.9

Through analyzing the parameters of the four thermodynamic models calculated using both symmetric and non-symmetric methods for the Al-Cu, Al-Ni, and Al-Fe systems in Table 4, can conclude that: as the number of simulation steps increases, the changes in parameter values for the four thermodynamic models obtained from both symmetric and non-symmetric calculations are extremely small. Furthermore, there is no discernible pattern or trend in these changes, which contradicts the expected continuous increase or decrease. It is important to note that although the changes in parameter values are very minute, they still hold significance as these subtle variations can potentially impact the accuracy of the results.

3.3. Estimating the Activity and Molar Excess Gibbs Energy

For the three systems of Al-Cu, Al-Ni, and Al-Fe, the SD and ARD estimates for the activity and molar excess Gibbs energy of the five models calculated by using the symmetric method are listed in Table 6 and Table 7, respectively.

Table 6. The SD and ARD of activity estimated by symmetric method.

System	Step	MIVM		RSM		Wilson		NRTL		Miedema
		SD	ARD/%	SD	ARD/%	SD	ARD/%	SD	ARD/%	SD	ARD/%
Al-Cu (1400 K)	0–1000	0.051	21	0.096	208	0.163	520	0.170	568	0.077	143
	0–2000	0.053	19	0.094	200	0.160	502	0.167	553
	0–3000	0.055	19	0.094	201	0.159	496	0.166	547
	0–4000	0.054	19	0.094	200	0.158	493	0.166	545
	0–5000	0.055	20	0.095	206	0.159	496	0.166	548
	Average	0.054	20	0.095	203	0.160	501	0.167	552
	0–1000	0.051	21	0.096	208	0.163	520	0.170	568
	1000–2000	0.056	20	0.092	194	0.157	485	0.165	538
	2000–3000	0.058	21	0.095	204	0.156	480	0.164	534
	3000–4000	0.054	20	0.093	196	0.157	485	0.164	536
	4000–5000	0.059	24	0.103	235	0.161	506	0.169	562
	Average	0.056	21	0.096	208	0.159	495	0.166	548
Al-Ni (1923 K)	0–1000	0.076	30	0.065	222	0.157	884	0.169	984	0.053	167
	0–2000	0.071	28	0.071	248	0.160	907	0.171	1005
	0–3000	0.070	27	0.073	260	0.160	911	0.171	1008
	0–4000	0.069	27	0.072	254	0.160	911	0.172	1012
	0–5000	0.074	29	0.072	257	0.159	896	0.170	993
	Average	0.072	28	0.071	248	0.159	902	0.170	1001
	0–1000	0.076	30	0.065	222	0.157	884	0.169	984
	1000–2000	0.052	13	0.075	271	0.167	981	0.179	1091
	2000–3000	0.070	27	0.078	285	0.161	914	0.171	1010
	3000–4000	0.083	34	0.069	239	0.154	856	0.166	952
	4000–5000	0.076	30	0.074	263	0.158	889	0.169	984
	Average	0.071	27	0.072	256	0.160	905	0.171	1004
Al-Fe (1823 K)	0–1000	0.077	40	0.028	24	0.105	117	0.113	130	0.033	29
	0–2000	0.066	36	0.036	31	0.109	123	0.117	136
	0–3000	0.067	36	0.035	30	0.108	123	0.117	136
	0–4000	0.068	36	0.034	30	0.108	122	0.116	135
	0–5000	0.068	36	0.035	30	0.108	122	0.116	135
	Average	0.069	37	0.034	29	0.108	121	0.116	135
	0–1000	0.077	40	0.028	24	0.105	117	0.113	130
	1000–2000	0.055	31	0.044	40	0.113	129	0.121	143
	2000–3000	0.068	36	0.034	29	0.108	122	0.117	136
	3000–4000	0.072	38	0.032	27	0.106	119	0.115	133
	4000–5000	0.066	36	0.036	31	0.109	123	0.117	137
	Average	0.067	36	0.035	30	0.108	122	0.117	136

Table 7. The SD and ARD of molar excess Gibbs energy estimated by symmetric method.

System	Step	MIVM		RSM		Wilson		NRTL		Miedema
		SD/J	ARD/%	SD/J	ARD/%	SD/J	ARD/%	SD/J	ARD/%	SD/J	ARD/%
Al-Cu (1400 K)	0–1000	1077	11	5816	47	8360	69	8541	71	4933	39
	0–2000	1158	12	5704	46	8269	69	8468	70
	0–3000	1262	13	5727	46	8233	68	8441	70
	0–4000	1312	13	5709	46	8220	68	8427	70
	0–5000	1262	13	5789	46	8233	68	8443	70
	Average	1214	12	5749	46	8263	69	8464	70
	0–1000	1077	11	5816	47	8360	69	8541	71
	1000–2000	1486	15	5635	45	8176	68	8395	69
	2000–3000	1599	16	5765	46	8150	68	8376	69
	3000–4000	1525	15	5660	45	8173	68	8382	69
	4000–5000	1221	13	6133	49	8294	69	8516	71
	Average	1382	14	5802	46	8231	68	8442	70
Al-Ni (1923 K)	0–1000	6729	29	10,611	40	17,138	65	17,745	68	9361	35
	0–2000	5836	26	11,134	42	17,271	66	17,849	69
	0–3000	5719	25	11,356	43	17,292	66	17,863	69
	0–4000	5543	25	11,246	42	17,287	66	17,880	69
	0–5000	6365	28	11,301	43	17,212	66	17,790	68
	Average	6038	27	11,130	42	17,240	66	17,825	68
	0–1000	6729	29	10,611	40	17,138	65	17,745	68
	1000–2000	2359	11	11,550	44	17,659	68	18,248	70
	2000–3000	5673	25	11,793	45	17,315	66	17,871	69
	3000–4000	8190	35	10,965	41	16,978	65	17,584	67
	4000–5000	6778	30	11,404	43	17,169	66	17,744	68
	Average	5946	26	11,265	43	17,252	66	17,839	68
Al-Fe (1823 K)	0–1000	7016	67	2324	22	6241	59	6576	62	2647	25
	0–2000	5775	55	2805	26	6397	60	6732	63
	0–3000	5825	56	2759	26	6386	60	6726	63
	0–4000	5973	57	2712	25	6360	60	6707	63
	0–5000	5958	57	2717	25	6362	60	6709	63
	Average	6110	58	2664	25	6349	60	6690	63
	0–1000	7016	67	2324	22	6241	59	6576	62
	1000–2000	4535	43	3298	31	6553	62	6890	65
	2000–3000	5911	56	2674	25	6367	60	6715	63
	3000–4000	6439	61	2538	24	6279	59	6648	63
	4000–5000	5736	55	2777	26	6392	60	6737	63
	Average	5927	57	2722	25	6366	60	6713	63

Analysis of the results in Table 6 and Table 7 shows that: for the Al-Cu system, the average SD and average ARD of the activity estimates for the five models using the symmetric method are, respectively: 0.055 and 20% for the MIVM model; 0.095 and 205% for the RSM model; 0.159 and 498% for the Wilson model; 0.167 and 550% for the NRTL model; 0.077 and 143% for the Miedema model. The average SD and average ARD of the molar excess Gibbs energy estimates for the five models are, respectively: 1298 J and 13% for the MIVM model; 5775 J and 46% for the RSM model; 8247 J and 69% for the Wilson model; 8453 J and 70% for the NRTL model; 4933 J and 39% for the Miedema model. For the Al-Ni system, the average SD and average ARD of the activity estimates for the five models using the symmetric method are, respectively: 0.072 and 28% for the MIVM model; 0.071 and 252% for the RSM model; 0.159 and 903% for the Wilson model; 0.171 and 1002% for the NRTL model; 0.053 and 167% for the Miedema model. The average SD and average ARD of the molar excess Gibbs energy estimates for the five models are, respectively: 5992 J and 26% for the MIVM model; 11,197 J and 42% for the RSM model; 17,246 J and 66% for the Wilson model; 17,832 J and 68% for the NRTL model; 9361 J and 35% for the Miedema model.

Comparative analysis of the above data shows that when the symmetric method is used, for Al-Cu and Al-Ni systems, the MIVM model has the smallest values of average SD and average ARD for activity estimates and molar excess Gibbs energy estimates, which indicates that the MIVM model has a better estimation effect than the other four models. The average SD and average ARD values for the RSM and Miedema models are in the middle of the range for activity estimates and molar excess Gibbs energy estimates, which indicates that the RSM and Miedema models have ordinary estimation effects.

For the Al-Fe system, the average SD and average ARD of the activity estimates for the five models when using the symmetric method are, respectively: 0.068 and 36% for the MIVM model; 0.034 and 29% for the RSM model; 0.108 and 122% for the Wilson model; 0.116 and 135% for the NRTL model; 0.033 and 29% for the Miedema model. The average SD and average ARD of the molar excess Gibbs energy estimates for the five models are, respectively: 6018 J and 57% for the MIVM model; 2693 J and 25% for the RSM model; 6358 J and 60% for the Wilson model; 6702 J and 63% for the NRTL model; 2647 J and 25% for the Miedema model. Comparative analysis of the above data shows that when the symmetric method is used: for the Al-Fe system, the average ARD of the estimated activity values of the MIVM model, RSM model, and Miedema model were all less than 40%, indicating that the MIVM model, RSM model, and Miedema model all have good estimation effect, of which Miedema model had the better estimation effect.

$$\mathrm{SD}=\sqrt{\frac{{\displaystyle \sum {\left(a_{est}-a_{\exp }\right)}^2}}{N}}, \mathrm{ARD}=\frac{1}{N}{\displaystyle \sum \left|\frac{a_{est}-a_{\exp }}{a_{\exp }}\right|}\times 100\%$$

a_est is the estimated value of activity and a_exp [36] is the experimental value of activity.

$$\mathrm{SD}=\sqrt{\frac{{\displaystyle \sum {\left(G_m^E\left(est\right)-G_m^E\left(\exp \right)\right)}^2}}{N}}, \mathrm{ARD}=\frac{1}{N}{\displaystyle \sum \left|\frac{G_m^E\left(est\right)-G_m^E\left(\exp \right)}{G_m^E\left(\exp \right)}\right|}\times 100\%$$

$G_m^E\left(est\right)$ is the estimated value of the molar excess Gibbs energy and $G_m^E\left(\exp \right)$ [36] is the experimental value of the molar excess Gibbs energy.

For the three systems of Al-Cu, Al-Ni, and Al-Fe, the SD and ARD estimates for the activity and molar excess Gibbs energy of the five models calculated by using non-symmetric methods are listed in Table 8 and Table 9, respectively.

Table 8. The SD and ARD of activity estimated by non-symmetric method.

System	Step	MIVM		RSM		Wilson		NRTL		Miedema
		SD	ARD/%	SD	ARD/%	SD	ARD/%	SD	ARD/%	SD	ARD/%
Al-Cu (1400 K)	0–1000	0.062	69	0.076	125	0.174	587	0.182	641	0.077	143
	0–2000	0.061	46	0.071	96	0.170	559	0.177	614
	0–3000	0.062	48	0.071	98	0.170	559	0.178	616
	0–4000	0.063	56	0.073	108	0.171	568	0.179	625
	0–5000	0.063	70	0.076	127	0.174	585	0.182	641
	Average	0.062	58	0.073	111	0.172	572	0.180	628
	0–1000	0.062	69	0.076	125	0.174	587	0.182	641
	1000–2000	0.061	34	0.069	75	0.166	533	0.174	590
	2000–3000	0.065	59	0.073	108	0.171	567	0.180	627
	3000–4000	0.071	115	0.090	184	0.180	624	0.188	679
	4000–5000	0.071	118	0.090	183	0.181	629	0.188	682
	Average	0.066	79	0.079	135	0.175	588	0.182	644
Al-Ni (1923 K)	0–1000	0.032	97	0.057	188	0.193	1246	0.204	1365	0.053	167
	0–2000	0.032	95	0.060	201	0.193	1242	0.204	1362
	0–3000	0.035	106	0.062	209	0.194	1256	0.205	1378
	0–4000	0.036	110	0.064	217	0.194	1257	0.205	1383
	0–5000	0.038	117	0.066	226	0.195	1266	0.206	1393
	Average	0.034	105	0.062	208	0.194	1253	0.205	1376
	0–1000	0.032	97	0.057	188	0.193	1246	0.204	1365
	1000–2000	0.037	116	0.071	249	0.194	1263	0.206	1391
	2000–3000	0.038	116	0.064	218	0.195	1270	0.206	1392
	3000–4000	0.036	111	0.066	224	0.193	1249	0.205	1383
	4000–5000	0.045	144	0.074	263	0.197	1294	0.209	1425
	Average	0.038	117	0.066	228	0.195	1264	0.206	1391
Al-Fe (1823 K)	0–1000	0.020	13	0.010	4	0.123	146	0.133	163	0.033	29
	0–2000	0.022	14	0.010	4	0.123	146	0.133	162
	0–3000	0.023	15	0.010	3	0.123	145	0.132	162
	0–4000	0.024	15	0.010	4	0.122	144	0.132	161
	0–5000	0.023	15	0.010	3	0.122	145	0.132	162
	Average	0.022	14	0.010	4	0.123	145	0.133	162
	0–1000	0.020	13	0.010	4	0.123	146	0.133	163
	1000–2000	0.022	14	0.010	4	0.123	145	0.133	162
	2000–3000	0.027	17	0.010	4	0.121	142	0.131	160
	3000–4000	0.022	14	0.010	4	0.123	145	0.133	162
	4000–5000	0.008	5	0.014	10	0.128	154	0.137	169
	Average	0.020	13	0.011	5	0.124	147	0.133	163

Table 9. The SD and ARD of molar excess Gibbs energy estimated by non-symmetric method.

System	Step	MIVM		RSM		Wilson		NRTL		Miedema
		SD/J	ARD/%	SD/J	ARD/%	SD/J	ARD/%	SD/J	ARD/%	SD/J	ARD/%
Al-Cu (1400 K)	0–1000	3172	23	4510	35	8686	72	8881	74	4933	39
	0–2000	2368	16	3892	29	8556	71	8763	73
	0–3000	2451	17	3940	29	8559	71	8773	73
	0–4000	2741	19	4161	32	8601	72	8815	73
	0–5000	3215	23	4546	35	8681	72	8885	74
	Average	2789	20	4210	32	8616	72	8823	73
	0–1000	3172	23	4510	35	8686	72	8881	74
	1000–2000	1704	13	3326	24	8433	70	8653	72
	2000–3000	2821	19	4162	32	8600	72	8823	73
	3000–4000	4340	34	5496	44	8849	74	9042	75
	4000–5000	4420	34	5483	44	8869	74	9055	75
	Average	3292	25	4595	35	8687	72	8891	74
Al-Ni (1923 K)	0–1000	6859	25	9853	37	18,861	72	19,332	74	9361	35
	0–2000	6807	25	10,154	38	18,843	72	19,324	74
	0–3000	7239	26	10,344	39	18,902	73	19,379	75
	0–4000	7398	27	10,518	40	18,901	73	19,396	75
	0–5000	7672	28	10,699	40	18,938	73	19,431	75
	Average	7195	26	10,314	39	18,889	73	19,372	75
	0–1000	6859	25	9853	37	18,861	72	19,332	74
	1000–2000	7629	28	11,148	42	18,926	73	19,425	75
	2000–3000	7643	28	10,534	40	18,953	73	19,429	75
	3000–4000	7435	27	10,659	40	18,866	72	19,399	75
	4000–5000	8566	32	11,415	43	19,047	73	19,543	75
	Average	7626	28	10,722	40	18,930	73	19,425	75
Al-Fe (1823 K)	0–1000	1209	12	463	4	6968	66	7328	69	2647	25
	0–2000	1324	13	436	4	6951	65	7312	69
	0–3000	1409	14	370	3	6933	65	7302	69
	0–4000	1485	14	326	3	6920	65	7292	69
	0–5000	1424	14	363	3	6931	65	7300	69
	Average	1370	13	392	3	6940	65	7307	69
	0–1000	1209	12	463	4	6968	66	7328	69
	1000–2000	1330	13	479	4	6949	65	7312	69
	2000–3000	1746	17	236	3	6873	65	7258	68
	3000–4000	1315	13	456	4	6950	65	7314	69
	4000–5000	233	2	1305	12	7135	67	7459	70
	Average	1166	11	588	5	6975	66	7334	69

Analysis of the results in Table 8 and Table 9 shows that: it can be observed that when the non-symmetric method is employed, for the Al-Cu and Al-Ni systems, the MIVM model exhibits the smallest values for average SD and average ARD in terms of activity estimation and molar excess Gibbs energy estimation. This suggests that the MIVM model provides better estimation performance compared to the other four models. The RSM model and Miedema model show moderate values for average SD and average ARD in terms of activity estimation and molar excess Gibbs energy estimation, indicating ordinary estimation performance for the RSM and Miedema models. The specific data information is as follows. For the Al-Cu system, the average SD and average ARD of the activity estimates for the five models when using the non-symmetric method are, respectively: 0.064 and 68% for the MIVM model; 0.076 and 123% for the RSM model; 0.173 and 580% for the Wilson model; 0.181 and 636% for the NRTL model; 0.077 and 143% for the Miedema model. The average SD and average ARD of the molar excess Gibbs energy estimates for the five models are, respectively: 3041 J and 22% for the MIVM model; 4403 J and 34% for the RSM model; 8652 J and 72% for the Wilson model; 8857 J and 74% for the NRTL model; 4933 J and 39% for the Miedema model. For the Al-Ni system, the average SD and average ARD of the activity estimates for the five models when using the non-symmetric method are, respectively: 0.036 and 111% for the MIVM model; 0.064 and 218% for the RSM model; 0.194 and 1259% for the Wilson model; 0.205 and 1384% for the NRTL model; 0.053 and 167% for the Miedema model. The average SD and average ARD of the molar excess Gibbs energy estimates for the five models are, respectively: 7411 J and 27% for the MIVM model; 10,518 J and 40% for the RSM model; 18,910 J and 73% for the Wilson model; 19,399 J and 75% for the NRTL model; 9361 J and 35% for the Miedema model.

For the Al-Fe system, the average SD and average ARD of the activity estimates for the five models when using the non-symmetric method are, respectively: 0.021 and 13% for the MIVM model; 0.011 and 4% for the RSM model; 0.123 and 146% for the Wilson model; 0.133 and 163% for the NRTL model; 0.033 and 29% for the Miedema model. The average SD and average ARD of the molar excess Gibbs energy estimates for the five models are, respectively: 1268 J and 12% for the MIVM model; 490 J and 4% for the RSM model; 6958 J and 65% for the Wilson model; 7320 J and 69% for the NRTL model; 2647 J and 25% for the Miedema model. Compared with the above data analysis, it can be seen that the average ARD of the estimated activity values of the MIVM model, RSM model, and Miedema model for Al-Fe system is less than 30% when the non-symmetric method is used, indicating that the MIVM model, RSM model, and Miedema model all have good estimation effect, among which the RSM model has better estimation effect.

In conclusion, the average ARD of activity estimation values of the MIVM model, RSM model, Wilson model, NRTL model, and Miedema model are 28%, 162%, 508%, 562%, and 113%, respectively, when the symmetric method was adopted. The average ARD of the molar excess Gibbs energy estimates for the five models are 32%, 38%, 65%, 67%, and 33%, respectively. When the non-symmetric method was used, the average ARD of activity estimation values of the MIVM model, RSM model, Wilson model, NRTL model, and Miedema model are 64%, 115%, 661%, 727%, and 113%, respectively. The average ARD of the molar excess Gibbs energy estimates for the five models are 20%, 26%, 70%, 72%, and 33%, respectively. The results show that the MIVM model performs better than the other four models, the RSM model and Miedema model are second, and the Wilson model and NRTL model are not ideal. At the same time, the first peak of the partial radial distribution function obtained by the symmetric method is better than that by the non-symmetric method.

Comparing with similar studies on estimating the activity and molar excess Gibbs energy of binary liquid alloys, Wang et al. [25] utilized PRDF obtained from the literature and combined it with thermodynamic models to estimate the activity and molar excess Gibbs energy of 19 binary liquid alloys. The MIVM model achieved an ARD of less than 20% for the activity estimation of 15 alloys, while the RSM model achieved an ARD of less than 20% for 10 alloys. Therefore, Wang et al. concluded that the MIVM model performs better than other models, which is consistent with the findings of this study, thus validating the feasibility of our approach and enhancing the credibility of the conclusions.

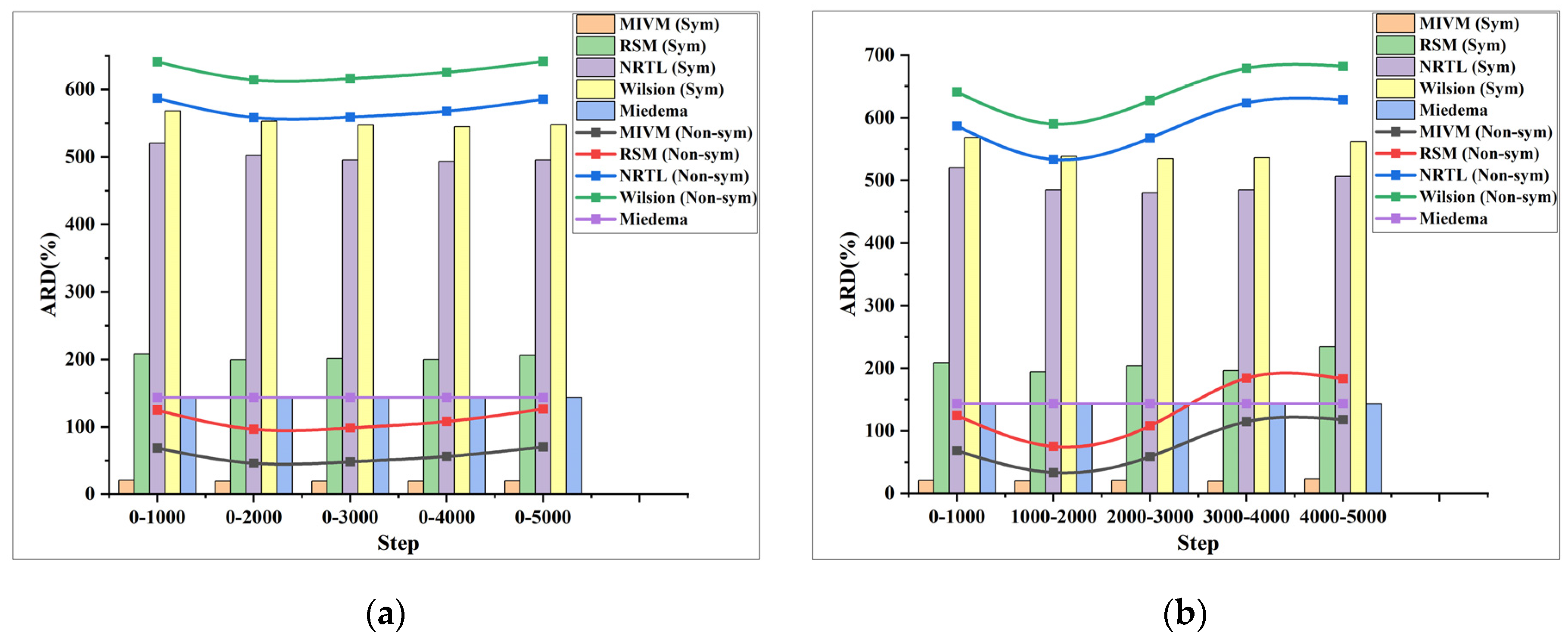
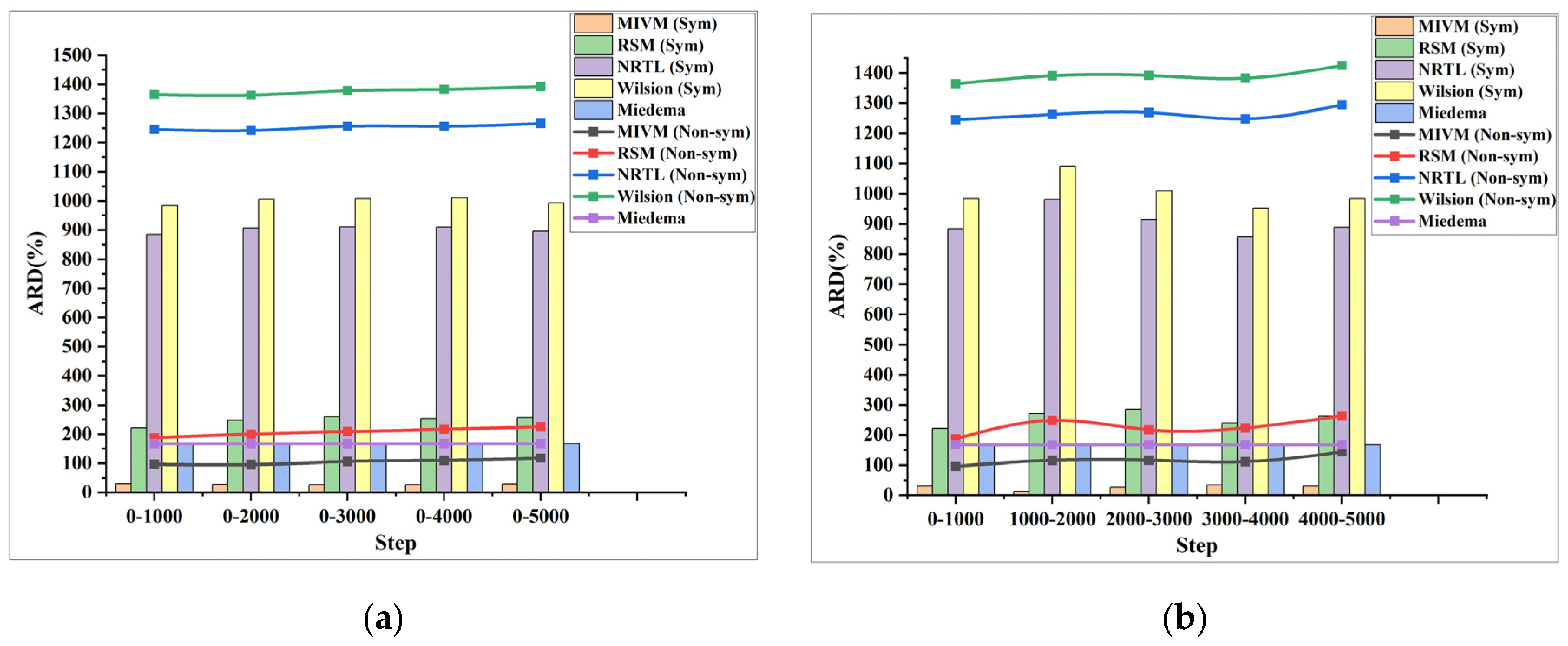
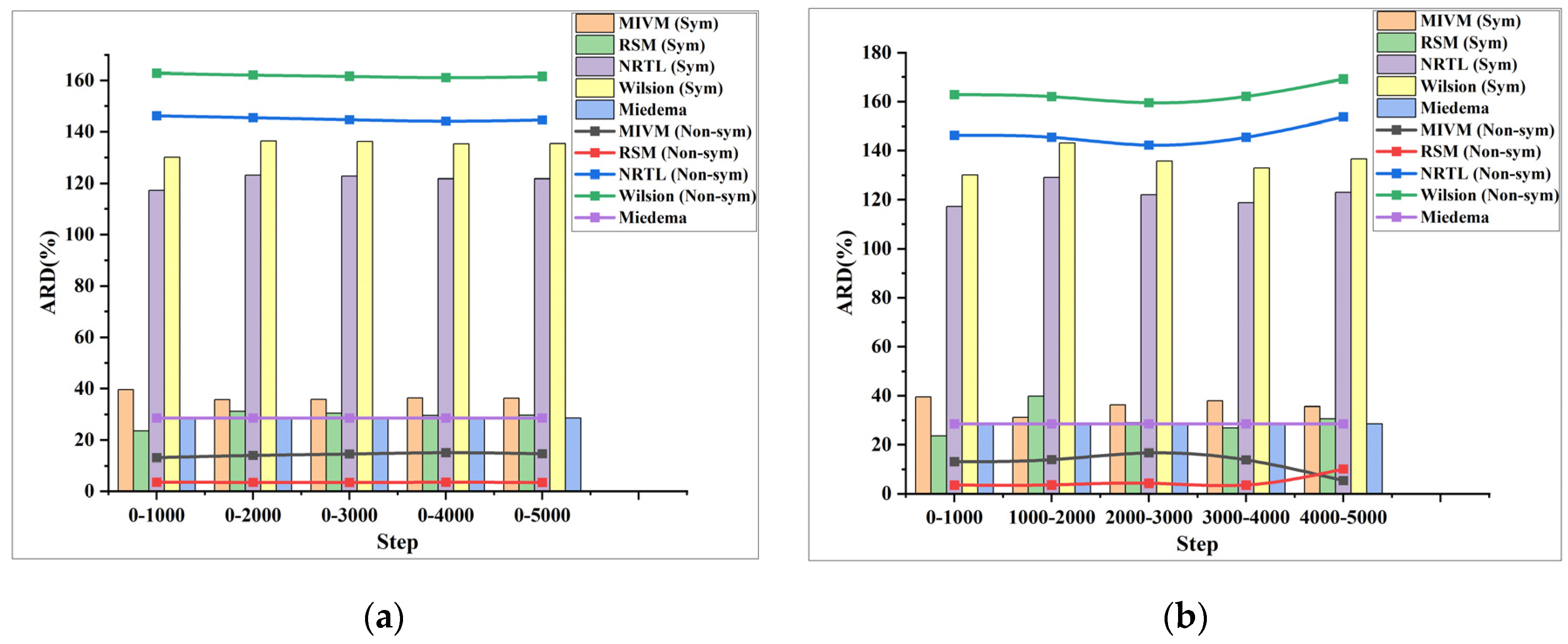
Figure 6, Figure 7 and Figure 8 depict the ARD plots for estimating the activity in the Al-Cu, Al-Ni, and Al-Fe systems. The bar charts display the ARD values obtained using the symmetric method, while the line charts illustrate the ARD values obtained using the non-symmetric method. Specifically, all of the Figures (a) and (b) in Figure 6, Figure 7 and Figure 8 show the ARD of the estimated activity of the three systems using two methods of grouping PRDF data, respectively.

Figure 6. (a) ARD for the activity of the Al-Cu system estimated by the first PRDF grouping method; (b) ARD for the activity of the Al-Cu system estimated by the second PRDF grouping method.

Figure 7. (a) ARD for the activity of the Al-Ni system estimated by the first PRDF grouping method; (b) ARD for the activity of the Al-Ni system estimated by the second PRDF grouping method.

Figure 8. (a) ARD for the activity of the Al-Fe system estimated by the first PRDF grouping method, (b) ARD for the activity of the Al-Fe system estimated by the second PRDF grouping method.

Observing Figure 5, Figure 6 and Figure 7, it can be noted that for the three systems, the ARD and SD of activity estimated using the two proposed methods of stepwise processing of PRDF fluctuate, rather than consistently increasing or decreasing. Specifically, the average ARD of activity and molar excess Gibbs energy estimated by symmetric method are 315% and 47%, respectively. The average ARD of activity and molar excess Gibbs energy estimated by non-symmetric method are 392% and 51%, respectively. Based on the combined analysis of the ARD value and Figure 6, Figure 7 and Figure 8, it is evident that the symmetric method provides a better estimation effect.

4. Conclusions

In this study, PRDF of binary liquid alloys Al-Cu, Al-Ni, and Al-Fe were obtained by AIMD simulation, and five thermodynamic models (MIVM model, RSM model, Wilson model, NRTL model, and Miedema model) were used to estimate the activity and molar excess Gibbs energy of the alloys. The average ARD of the estimated activity of MIVM model is less than 45%, and the average ARD of the estimated activity of the other four models is greater than 110%. In general, the estimated effect of MIVM model is better than the other four models. In addition, the symmetric method is better than the non-symmetric method. The two methods proposed in this paper for PRDF grouping are feasible, and the average ARD and average SD of the activity and molar excess Gibbs energy estimated by using the grouped PRDF data are lower, indicating that grouping the PRDF data before estimation can effectively improve the estimation effect. The experimental results validate the feasibility and applicability of the proposed scheme. It is hoped that it can provide reference for selecting suitable models and methods to estimate thermodynamic data such as activity and molar excess Gibbs energy of binary liquid alloys.