Abstract
Punching is the main manufacturing process with high efficiency and machining accuracy used to produce the iron cores of motors. However, it usually introduces residual stress at the cutting edge and affects the magnetic properties of the iron core. Further studies show that the tensile residual stress (TRS) has a negligible effect on the magnetic properties, compared with the compressive stress. The blunt punch tools cause local TRS and the formation of local large plastic deformation (PD) at the cutting edge as the cost. The PD has a more serious effect on the magnetic properties of materials than TRS. Therefore, this study mainly focused on local deformation distribution and the associated microstructure evolution using EBSD (Electron Backscatter Diffraction) and finite element analysis; and the formation mechanism of tensile residual stress during the punching process at the cutting edge of a non-oriented silicon steel after punching with blunt tools, by using nanoindentation and a numerical simulation. The experimental results showed the existence of a specific bending area, a highly deformed area and a large burr at the cutting edge. These direct observations were confirmed with those obtained by the simulation model. Furthermore, the tensile residual stress on the surface was verified through nanoindentation tests and by a numerical simulation. The results indicate also that the formation of a tensile residual stress zone depends especially on the bending area formed during punching with blunt tools.
1. Introduction
Non-oriented silicon steel is widely used for the production of iron cores for various motors, generators and transformers, because of its excellent magnetic permeability and low core loss (iron loss). Considering the efficiency required in industrial production, machining processes such as laser cutting, shear cutting and punching are the methods chosen from for the manufacturing of an iron core sheet. Since the punching process always gives rise to a smaller damaged area than laser cutting and shear cutting, it the most used method. It has high efficiency and machining accuracy for the production of motors [1]. Nevertheless, residual stress is inevitable at the cutting edge of the silicon steel sheet after the punching process, which impacts its magnetic properties (iron loss and magnetic susceptibility) and affects the performance of the motors [2].
There have been many studies about the residual stress distribution after the punching process. Through detailed residual stress analysis carried out by a nanoindentation experiment, Cao et al. [3] pointed out that the compressive residual stress mainly existed on the surface of the cutting edge (made using sharp punch tools), and the affected zone was about 500 µm from the cutting edge of non-oriented silicon steel. Meanwhile, Mori et al. [4] studied the effects of punching parameters on the residual stress distribution in detail. For the punching with a small clearance (0.8%), the stress introduced to the surface of the cutting edge was compressive, and its absolute value increased with the wear degree of the punch. In contrast, a large clearance (10%) introduced mainly tensile stress, which increased with the wear degree of the punch. Moreover, with the help of a qualitative FE simulation, Weiss et al. found that blunt punch tools and large clearance could form a tensile stress area on the surface of cutting edge.
Naumoski et al. [5] revealed that compressive stress could introduce significant iron loss in silicon steel, though the influence of tensile stress on iron loss was negligible. During the industrial production of iron core lamination, the mold is generally somewhat worn. This should contribute to the generation of tensile stress on the surface of the cutting edge, and reduce the influence of residual stress on iron core loss. However, it is known that a worn tool could cause a large burr at the cutting edge, with much plastic deformation, and Andy et al. indicated that the influence of plastic deformation is more serious than that of residual stress [6,7]. Therefore, this study focused on the determination of a local plastic deformation distribution and the associated mechanisms, and the analysis of a tensile stress zone at the cutting edge after punching with blunt tools, because those two phenomena are still unresolved. During this study, electron backscatter diffraction (EBSD) and nanoindentation tests were applied for the analysis of local plastic deformation and residual stress distribution at the cutting edge, respectively. In addition, an elastoplastic FE simulation with Johnson–Cook (JC) plasticity and a damage criterion was used for studying the local plastic deformation zone and the formation mechanism of the tensile residual stress zone on the surface of cutting edge. The parameters of JC plasticity and damage criterion were obtained explicitly by several series of tensile tests on steel samples with different morphologies.
2. Materials and Methods
2.1. Material Preparation
The non-oriented silicon steel with a thickness of 0.5 mm studied in this paper was produced by China Baowu Iron and Steel Group Co., Ltd. (Wuhan, China), and is commonly used in motor cores, under the brand name 50WW1300. Table 1 shows its nominal chemical composition and mechanical properties obtained with tensile tests on standard samples prepared in rolling direction (RD) and transversal direction (TD) of a silicon sheet. For this type of silicon steel, the mechanical properties are almost identical in RD and TD. The average grain orientation spread (GOS) of the initial material is 0.45°, which is less than 1° and indicates this material is completely recrystallized (Figure 1a). The average grain size of this material is about 25.7 µm, and it is textured with a complete γ {111} fiber as the main component (Figure 1a,b).

Table 1.
Nominal chemical composition and mechanical properties (obtained by tensile tests) of 50WW1300.
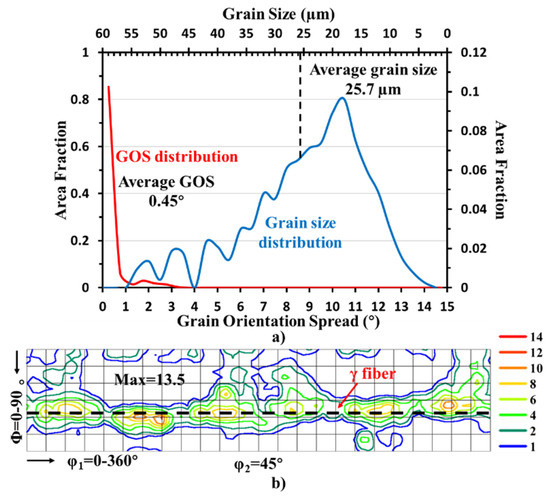
Figure 1.
(a) GOS and grain size distributions of initial material. (b) Orientation distribution function (ODF) section plot (φ2 = 45°) for initial material, and the dotted black line shows the ideal position of γ fiber.
These non-oriented silicon steel sheets were punched into discs with a diameter of 30 mm through high-precision floating molds in a four-pillar design, as proposed by Singh et al. [8]. The molds were operated with a press machine, which can provide a punching force of 5 tons. During punching process, the punch was fixed and the die moved at 13 mm/s (Figure 2). In current industrial iron core lamination, the punch clearance is generally between 2% and 10% [9], and the punch–die clearance used was 4% for this study. Moreover, a worn mold was used. There are a chamfer and a fillet at the edges of the punch and die, respectively. More detailed dimensions for the punching experiment are shown in Table 2.
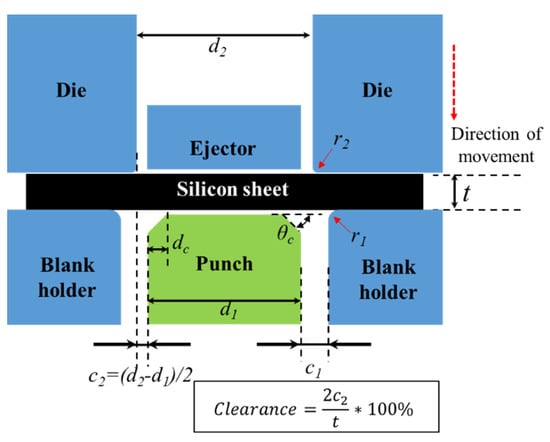
Figure 2.
Geometric illustration of the punching experiment. ( is the radius of the punch; is the inner diameter of the die; is the chamfer distance of the punch; is the chamfer angle of the punch; is the fillet radius of the blank holder; is the fillet radius of the die; is the difference value in radius between the punch and blank holder; is the difference value in radius between the punch and die; is the thickness of the silicon sheet).

Table 2.
Dimensions corresponding to the geometric illustration in Figure 2.
2.2. Microstructure Analysis
The microstructure of the cutting edge was studied by EBSD using a field emission gun-scanning electron microscope (FEG-SEM, Zeiss Sigma 300 VP, Zeiss, Oberkochen, German) fitted with an Oxford Symmetry EBSD system, and the step size of EBSD analysis was 0.5 µm. Then the EBSD data were analyzed with the help of EDAX OIM Analysis 7.0 software.
To study the distribution of deformation at the cutting edge of the punched sample, the kernel average misorientation (KAM), which calculates the average misorientation between the chosen pixel and its neighbors [10], was applied to analyze the local grain misorientation for studying the distribution of geometrically necessary dislocations (GNDs). During the KAM analysis of this study, the first neighbor was chosen to define the kernel size of calculation, and the maximum misorientation (or exclusion angle) was selected as 5° to ensure the intra-substructure analysis instead of inter-substructure analysis.
2.3. Residual Stress Determination
The residual stress and nanohardness distributions at the cutting edge of the punched sample were studied with the help of a nanoindentor (Ti980 TriboIndenter; Hysitron Corporation, Eden Prairie, MN, USA). The nanoindentation tests were performed on the ejector side of samples. During the tests, a Berkovich standard triangular pyramid indenter and a quasi-static loading method with fixed indentation depth were applied. As shown in Figure 3a, the fixed and maximum indentation depth was 300 nm. The loading and unloading processes took 5 s each. In order to reduce the influence of creep on the unloading displacement, the pressure was maintained for 2 s when the indenter arrived the fixed depth.
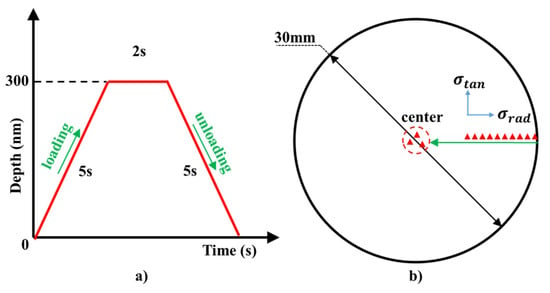
Figure 3.
(a) Diagram of loading, pressure maintaining and unloading for the nanoindentation test; (b) illustration of the locations of the test points in the surface of a punched circular sample.
To study the residual stress distribution on the surface of the cutting edge, series of nanoindentation tests were performed. For each series, several points were tested from the cutting edge (as close as possible) towards the center, with 50 µm as the interval distance (Figure 3b).
The residual stress of each test point at the cutting edge could be calculated with the following formula (Equation (1)), which was improved by Tiwari et al. from the Suresh theoretical model [11]:
where is the indenter angle (24.7° for our case). and are the hardness and indentation contact area of the stress-free zone, respectively. The center of punched sample was considered as the stress-free zone, and some positions in this zone were tested for obtaining the average values of and . is the indentation contact area of each test point in the stress affected zone.
The Suresh theoretical model is mainly used to quantify surface residual stress, and is based on the assumption that equibiaxial residual stresses exist on the surface layer of the sample [12]. In this study, we assumed that the residual stresses in the radial direction and the tangential direction ( and in Figure 3b) of the studied sample were equivalent for each test point, and these two stress components were considered equal in value as analyzed by nanoindentation test. In addition, the average nominal error of residual stress analysis was less than 25 MPa for most of the test points.
2.4. Finite Element Simulation
The FE simulation was performed with the help of the ABAQUS/Explicit module, and the Lagrangian method was applied to simulate the punching process in the current investigation. The Lagrangian method is suitable for the simulation of highly dynamic problems with nonlinear behavior, which describes the fracture process during punching. Moreover, with the help of the Lagrangian method, Laakso et al. [7] successfully simulated the microhardness distributions of electrical steels after punching, and their FE simulations showed good agreement with the experimental results.
To reduce the complexity, a simulation of the punching process was performed with an axisymmetric 2D model [13]. The geometry and related dimensional data of the FE model corresponded to the experimental data shown in Figure 2 and Table 2. During the simulation, the load was applied on the punch instead of the die (experiment case), with 13 mm/s as the displacement velocity.
The punching process causes always large deformation at the cutting edge, which will lead to a large mesh distortion during the FE simulation. Therefore, the four node bilinear axisymmetric quadrilateral elements with reduced integration (CAX4R) were used for the mesh generation. From the cutting edge to the center of sample, three grades of element size were selected (Figure 4). Considering the high strain gradients in the cutting region, and the small distance between punch and die, the element size was chosen as 5 µm for the area A, which was very close to the cutting edge. Moreover, the punch, die and holder were represented as 2D analytical rigid bodies.
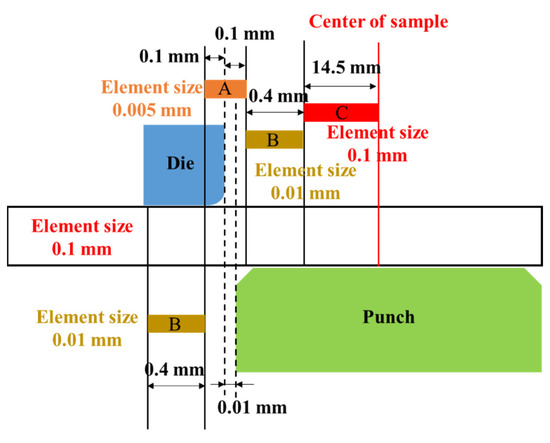
Figure 4.
Distribution of element size selection during the FE simulation.
Meanwhile, the hard contact and penalty function were used to describe normal and tangential contact behaviors during the punching process. The coulomb friction coefficient was set as 0.1, which was also used for other punching simulation [14,15].
The mechanical properties of this material in RD and TD are almost the same, and the initial texture corresponds to a complete γ fiber, which corresponds to a distribution of grain orientations around the <111> axis paralleled to the normal direction (ND) of the steel sheet (Figure 1). Therefore, the mechanical properties could be considered isotropic on the rolling surface (RD-TD). Moreover, as the sheets are very thin—negligible compared with the dimensions of a punched sample—the whole sheet was considered as an isotropic material during the simulation.
The elastic–plastic model was adopted for the mechanical properties of the material. For the elastic deformation behavior, the Young’s modulus and Poisson’s ration were set as 184 GPa and 0.3, respectively. Then the plastic deformation behavior and hardening rule were described with the JC plasticity model without considering the influence of deformation temperature (Equation (2)).
where is the yield stress considering the effects of static and kinematic strengthening; is the effective plastic strain; is the plastic strain rate; is the normalized equivalent plastic strain rate; and , , and are the model parameters [16].
To obtain the parameters of the JC plasticity model, two samples, as shown in Figure 5 and Table 3, were tested by tensile experiments with different displacement velocities (2 and 3 mm/min). The pure plastic deformation behavior of each tensile test was extracted with a calculation (Equation (3)) from true strain–stress curve. Then, the model parameters were calculated through data fitting, as shown in Table 4.
where is the true plastic strain of the material, is the total amount of strain and is the elastic strain.
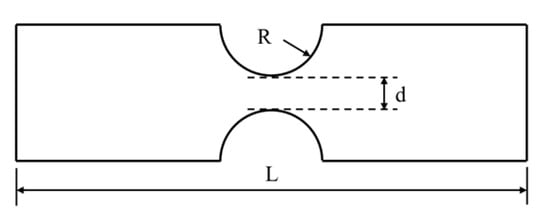
Figure 5.
Geometry of tensile samples used to obtain the parameters of JC plasticity and damage models.

Table 3.
Dimensions and stress triaxiality of tensile samples (shown in Figure 5) used to obtain the parameters of JC plasticity and damage models.

Table 4.
Parameters used in the JC plasticity model (obtained with tensile tests).
For the fracture simulation, the fracture initiation was determined by JC damage criterion, which has been successfully applied in simulations of the punching process [17,18]. The JC criterion describes the effects of stress triaxiality , plastic strain rate and nondimensional temperature on the effective plastic strain at the onset of fracture (Equation (4)).
where are failure parameters and corresponds to the normalized equivalent plastic strain rate. In our case, the punching temperature was lower than the transition temperature, so was chosen to be 0, and the JC damage equation was simplified to Equation (5). The failure parameters were determined through a series of tensile tests on samples with different morphologies (Figure 5 and Table 3) [19], as shown in Table 5.

Table 5.
Failure parameters used in the JC damage criterion (obtained with tensile tests).
Once the fracture started, the damage process continued and was monitored by the effective plastic displacement (Equation (6)). When this value reached the limit of effective plastic displacement , the fracture was complete, resulting in deletion of mesh.
where 𝐿 is the characteristic length of the element.
The whole FE simulation analysis included three analysis steps. First one corresponded to the movement of the holder with slight pressure to establish a stable contact between the sheet and the die. The second one was the punching process loaded by displacement. The last one was applied to the remove the die and let the punched sheet recover freely.
3. Results and Discussions
3.1. Deformation during Punching
A bent cutting edge could be observed after punching with blunt punch tools according to the simulation (Figure 6a). From the cutting edge to the inner part, the zone about 500 µm wide was divided into three areas.
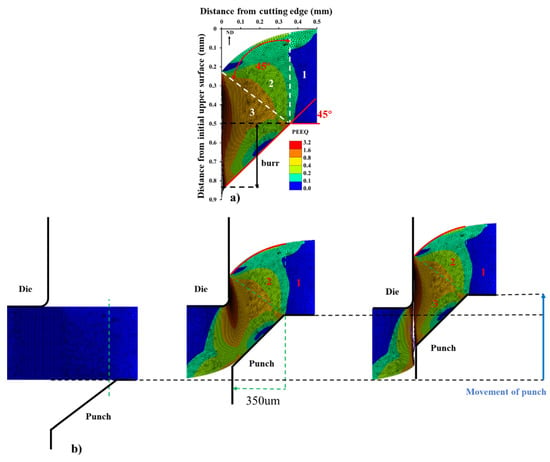
Figure 6.
(a) Equivalent plastic strain (PEEQ) distribution at the cutting edge after punching, obtained by FE simulation with blunt tools. (b) Simulation of punching process and formation of three areas at cutting edge.
Area 1, about 350 µm away from the cutting edge, was a region with a negligible deformation. Area 2 was a bent region with medium deformation. The bent angle was about 45°, and the maximum width of the surface was about 0.35 mm. This indicates the formation of a bent area depends on the wear degree of the punch tools. The plastic deformation of area 2 was mainly concentrated in the middle—near area 3—and on the upper surface. According to the simulation, area 2 was formed before fracture initiation with the bending effect between punch and die (Figure 6b). When punching continued, the distance between punch and die became small, the shear effect became more important and the fracture started. Area 3 was formed after the complete fracture (Figure 6b). The entirety of area 3 was rotated by 45° relative to the original orientation rather than being continuously curved like area 2, and the rotation angle corresponded to the chamfer angle.
We could also divide the cutting edge into three areas (Figure 7a) after the punching experiment. Area 2 was a continuous bending region with 45–50° as the total bending angle and 0.35 mm as the maximum width. At the same time, the whole of area 3 was bent by 45° instead of continuous angle change. This architecture from the experimental results is consistent with that of the above-mentioned simulation.
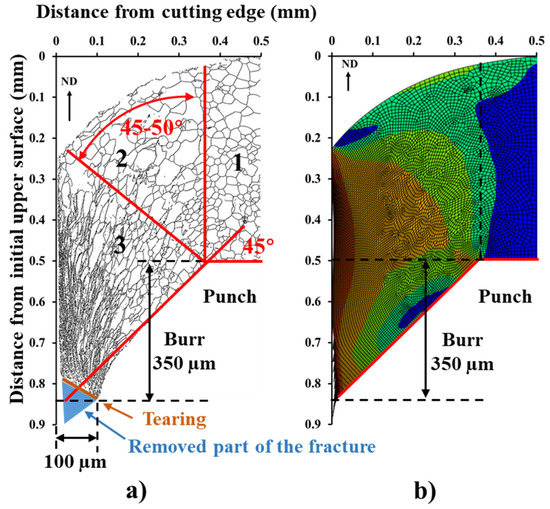
Figure 7.
(a) Blank map obtained from EBSD analysis at the cutting edge of the punched sample. (b) Diagram of burr, obtained by FE simulation with blunt tools. Black lines shown in (a) are the grain boundaries with a misorientation greater than 15°. The brown line and blue area at the end of the burr correspond to the direction of tearing failure and the removed part of burr after tearing failure, respectively.
The heights of burr obtained by both experiment and simulation were close to 350 µm. However, the width of the experimental burr was about 100 µm, and the simulated one’s width was negligible. This difference was likely mainly due to the accuracy of the punch tools, which resulted in larger local clearance, and probably due to the presence of tearing failure formed by local tensile stress [20].
Microscopically, we found that the grains near the cutting edge in area 3 were elongated and became ribbon-shaped under shear stress; the grains in area 2 were slightly elongated towards the bending direction; and the grains in area 1 were still equiaxed. From area 2 to area 3, the change in elongation direction of the grains was continuous.
The distribution of plastic deformation at cutting edge was also studied by KAM distribution analysis after EBSD testing. As mentioned above, KAM analysis is based on the misorientation between pixels. For bent areas 2 and 3 of the cutting edge, there existed a change in coordinate axis directions of the sample system relative to the detector system, which must have led to the error in orientation for each pixel in these zones. Therefore, EBSD data in our case were corrected before KAM analysis. The orientation of each pixel in area 2 was corrected one by one with pixel rotation method (PRM) [21]. However, since area 3 was an integrally bent region, EBSD data obtained in this region were corrected by overall reverse rotation of the orientations of all pixels.
The KAM distribution and IPF maps (Figure 8a,b) demonstrated that the deformation of area 1 was negligible. In area 2, the deformation was moderate and mainly near area 3. In addition, the GNDs of grains were mainly distributed near the grain boundary (Figure 8c). In area 3, the GNDs were everywhere (Figure 8d), and the grains had a high color gradient inside (Figure 8e). Moreover, the formation of a shear band, which occurs often in moderately and heavily deformed materials [22], could also be observed in some grains of this area. All these things indicated the presence of high plastic deformation in area 3.

Figure 8.
(a) KAM distribution map and (b) inverse pole figure (IPF) map obtained from EBSD analysis at the cutting edge of a punched sample; (c) KAM distribution map of red frame shown in area 2 of (a); (d) KAM distribution map; and (e) IPF map of black dotted frame shown in area 3 of (a). Black lines shown in (a,c,d) are the grain boundaries with misorientation greater than 15°.The black dotted circular frame and red lines in (e) show the presence of a shear band formed during punching.
3.2. Residual Stress Distribution after Punching
The experimental and simulated distributions of residual stress are shown in Figure 9. The experimental results correspond to residual stress analysis by nanoindentation tests on the surface of punched sheet, and show good repeatability for the tensile stress distribution. Since the simulation was mainly focused on the longitudinal section of cutting edge, only the simulated residual stress in S11 direction on the surface of the cutting edge could be compared with the experimental results. The residual stress distributions of simulated and experimental results (Figure 9a) indicate the presence of tensile residual stress on the surface of the cutting edge after punching. The tensile residual stress was relatively weak with a maximum value about 100 MPa, which is consistent with the results of Mori et al. [4].
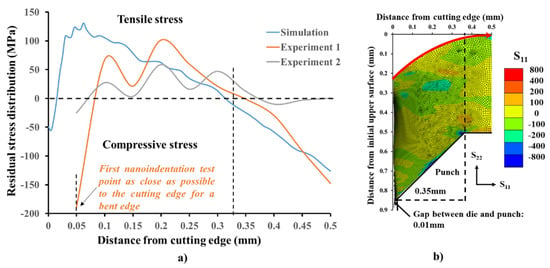
Figure 9.
(a) Residual stress distribution on the surface after punching. Blue and red lines show, respectively, the simulated residual stress in S11 direction and the residual stress tested by nanoindentation. (b) Residual stress distribution in the longitudinal section of the cutting edge. The red arrow indicates the extraction path of the simulation results in (a).
The tensile residual stress was distributed from the cutting edge to the inner part with a width about 0.33 mm, which was almost the same as the width of the bent area. This indicates the punching-induced distribution of tensile residual stress depends on the width of the bending area or the wear degree of the punch tools. However, at the cutting edge and in the zone 500 µm away from the cutting edge, the residual stress distributions obtained by simulation and experiment were different. This was likely mainly caused by the different residual stress analysis scales for the simulation (micro-scale) and experiment (nano-scale).
3.3. Formation Mechanism of Tensile Stress on the Surface
To understand the presence of tensile stress after punching, the stress distribution before and after fracture was investigated as follows. At the beginning of punching, bent area 2 was formed (Figure 10a). When without space constraints, the bent area could be divided into two regions which were subjected to tension and compression, respectively, with a neutral axis as the dividing line (Figure 10b). The gradient of change from tension to compression was continuous. However, during the punch process, the space at the cutting edge was limited by the punch, die and blank holder. Tension and compression should exist together to ensure the balance of deformation. Therefore, the tensile region in free bending theory (Figure 10b) was replaced by the coexistent regions of tension (A in Figure 10a) and compression (C in Figure 10a). Moreover, during the punching, the die would apply a compressive stress decomposed from principal force [23,24], causing relatively large compressive stress near the contact points (B in Figure 10a). When the punching process continued, it bent more seriously and region A became larger and deeper (Figure 10c). Once fracturing completed, the stresses were partially released (Figure 10d). As tensile region A—formed during the punching process—was wide and deep, it retained under tension after complete fracturing and removal from the mold (Figure 10e). We deduced that the formation of tensile residual stress on the surface depended on the bending degree of the cutting edge or the wear degree of the punch tools.
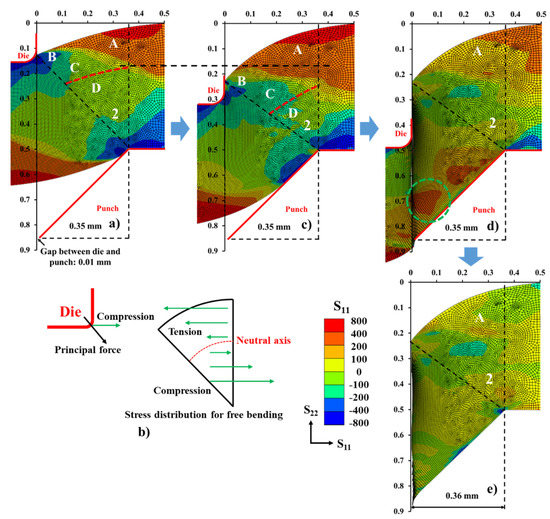
Figure 10.
(a) Simulated distribution of residual stress in S11 direction at the beginning of punching. (b) Diagram of stress distribution for free bent area and the position near the contact between die and material. Simulated distribution of residual stress in S11 direction (c) during punching, (d) after fracture initiation and (e) after complete fracture and removal of mold. Number 2 indicates bent area 2. The letters A, B, C and D were used to distinguish the regions in area 2 with different states of residual stress. The dotted lines in (a,b) are used to distinguish the depth region A with tensile stress; the green dotted circle in (d) corresponds to the area with high tensile stress.
In addition, high local tensile stress next to the end of burr could be observed (green dotted circle area in Figure 10d), and this supported the possibility of a tearing failure, considering the sudden changes in local conditions during the experiment.
4. Conclusions
The conclusions of this study are summarized as follows:
- (a)
- After the punching process using blunt tools, a large burr was formed and the cutting edge could be divided to three distinct areas: a highly deformed area, a bent area with moderate deformation and a non-deformed area. The closer to the cutting edge, the greater the plastic deformation.
- (b)
- The ribbon grains were formed in the highly deformed area, very close to the cutting edge. Dislocation slip and shear band formation were the deformation mechanisms. The mechanism of deformation in the bent area corresponds to only dislocation slip.
- (c)
- Tensile residual stress on the surface of punched sheet was observed, and the distribution width of tensile residual stress was about 0.33 mm.
- (d)
- The formation of tensile residual stress on the surface of a punched sample depends on the formation of a bent area with the blunt tools. Punch tools with high wear will form a large bending area at the cutting edge with a large and deep tensile stress region on the surface, which will be retained after punching.
Author Contributions
Conceptualization, W.W.; methodology, X.F. investigation, W.W. and X.W.; writing—original draft preparation, W.W. and X.F.; writing—review and editing, W.W., M.A. and V.J.; supervision, V.J.; project administration, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant number 51801141) and the Fundamental Research Funds for the Central Universities (WUT: 2019IVB015). The authors would also acknowledge the support from 111 Project (B17034) and Innovative Research Team Development Program of Ministry of Education of China (IRT_17R83).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saleem, A.; Alatawneh, N.; Chromik, R.R.; Lowther, D.A. Effect of Shear Cutting on Microstructure and Magnetic Properties of Non-Oriented Electrical Steel. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Peksoz, A.; Erdem, S.; Derebasi, N. Mathematical model for cutting effect on magnetic flux distribution near the cut edge of non-oriented electrical steels. Comput. Mater. Sci. 2008, 43, 1066–1068. [Google Scholar] [CrossRef]
- Cao, H.; Hao, L.; Yi, J.; Zhang, X.; Luo, Z.; Chen, S.; Li, R. The influence of punching process on residual stress and magnetic domain structure of non-oriented silicon steel. J. Magn. Magn. Mater. 2016, 406, 42–47. [Google Scholar] [CrossRef]
- Mori, K.; Abe, Y.; Kidoma, Y.; Kadarno, P. Slight clearance punching of ultra-high strength steel sheets using punch having small round edge. Int. J. Mach. Tools Manuf. 2013, 65, 41–46. [Google Scholar] [CrossRef]
- Naumoski, H.; Maucher, A.; Herr, U. Investigation of the influence of global stresses and strains on the magnetic properties of electrical steels with varying alloying content and grain size. In Proceedings of the 2015 5th International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 15–16 September 2015; pp. 1–8. [Google Scholar]
- Aydin, U.; Rasilo, P.; Martin, F.; Belahcen, A.; Daniel, L. Effect of simultaneous plastic and elastic deformation on magnetic properties of electrical steel sheets. In Proceedings of the 64th Annual Conference on Magnetism and Magnetic Materials (MMM 2019), Las Vegas, NV, USA, 4–8 November 2019. [Google Scholar]
- Laakso, S.V.A.; Aydin, U.; Krajnik, P. Verification of electric steel punching simulation results using microhardness. Int. J. Adv. Manuf. Technol. 2021, 112, 2027–2036. [Google Scholar] [CrossRef]
- Singh, U.P.; Streppel, A.H.; Kals, H.J.J. Design study of the geometry of a punching/blanking tool. J. Mater. Process. Technol. 1992, 33, 331–345. [Google Scholar] [CrossRef][Green Version]
- Saleem, A.; Goldbaum, D.; Brodusch, N.; Gauvin, R.; Chromik, R.R. Microstructure and mechanical property connections for a punched non-oriented electrical steel lamination. Mater. Sci. Eng. A 2018, 725, 456–465. [Google Scholar] [CrossRef]
- Chen, Y.-W.; Tsai, Y.-T.; Tung, P.-Y.; Tsai, S.-P.; Chen, C.-Y.; Wang, S.-H.; Yang, J.-R. Phase quantification in low carbon Nb-Mo bearing steel by electron backscatter diffraction technique coupled with kernel average misorientation. Mater. Charact. 2018, 139, 49–58. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Kumar, A.; Kumar, N.; Prakash, C. Investigation on micro-residual stress distribution near hole using nanoindentation: Effect of drilling speed. Meas. Control 2019, 52, 1252–1263. [Google Scholar] [CrossRef]
- Suresh, S.; Giannakopoulos, A.E. A new method for estimating residual stresses by instrumented sharp indentation. Acta Mater. 1998, 46, 5755–5767. [Google Scholar] [CrossRef]
- Pathak, R.K.; Ravi Kumar, A.; Ananthasuresh, G.K. Simulations and experiments in punching spring-steel devices with sub-millimeter features. J. Manuf. Process. 2013, 15, 108–114. [Google Scholar] [CrossRef]
- He, J.; Li, S.; Dong, L. Experiments and FE simulation of edge cracking considering prehardening after blanking process. Int. J. Mater. Form. 2019, 13, 547–560. [Google Scholar] [CrossRef]
- Subramonian, S.; Altan, T.; Ciocirlan, B.; Campbell, C. Optimum selection of variable punch-die clearance to improve tool life in blanking non-symmetric shapes. Int. J. Mach. Tools Manuf. 2013, 75, 63–71. [Google Scholar] [CrossRef]
- Wang, X.; Shi, J. Validation of Johnson-Cook plasticity and damage model using impact experiment. Int. J. Impact Eng. IJIE 2013, 60, 67–75. [Google Scholar] [CrossRef]
- Dabboussi, W.; Nemes, J. Modeling of ductile fracture using the dynamic punch test. Int. J. Mech. Sci. 2005, 47, 1282–1299. [Google Scholar] [CrossRef]
- Poizat, C.; Campagne, L.; Daridon, L.; Ahzi, S.; Husson, C.; Merle, L. Modeling and simulation of thin sheet blanking using damage and rupture criteria. Int. J. Form. Process. 2005, 8, 29–47. [Google Scholar] [CrossRef]
- Børvik, T.; Hopperstad, O.; Berstad, T. On the influence of stress triaxiality and strain rate on the behaviour of a structural steel. Part II. Numerical study. Eur. J. Mech. A-Solids 2003, 22, 15–32. [Google Scholar] [CrossRef]
- Chen, Z.H.; Tang, C.Y.; Lee, T.C. An investigation of tearing failure in fine-blanking process using coupled thermo-mechanical method. Int. J. Mach. Tools Manuf. 2004, 44, 155–165. [Google Scholar] [CrossRef]
- Jin, X.; Fu, B.-Q.; Zhang, C.-L.; Liu, W. Evolution of the texture and mechanical properties of 2060 alloy during bending. Int. J. Miner. Metall. Mater. 2015, 22, 966–971. [Google Scholar] [CrossRef]
- Raabe, D. Recovery and recrystallization: Phenomena, physics, models, simulation. Phys. Metall. 2014, 23, 2291–2397. [Google Scholar] [CrossRef]
- Chan, L.C.; Leung, Y.; Lee, T.; Fan, J.; Tang, C.Y. Numerical simulation for fine-blanking—A new approach. Mater. Sci. Eng. A 2004, 364, 207–215. [Google Scholar] [CrossRef]
- Romanowski, W.P. Spravochnik po Holodnoj Shtampovke, 6. Leningrad Mashinostroenie, Leningradskoe Otdelenie. 1979, pp. 15–16. Available online: https://spbarchives.ru/infres/-/archive/cgantd/R-53 (accessed on 17 April 2019).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).