Research on the Impact of Labyrinth Seal Ring Tooth Profile on the Pressure Pulsation of Leakage Chambers in High-Speed Centrifugal Pumps
Abstract
1. Introduction
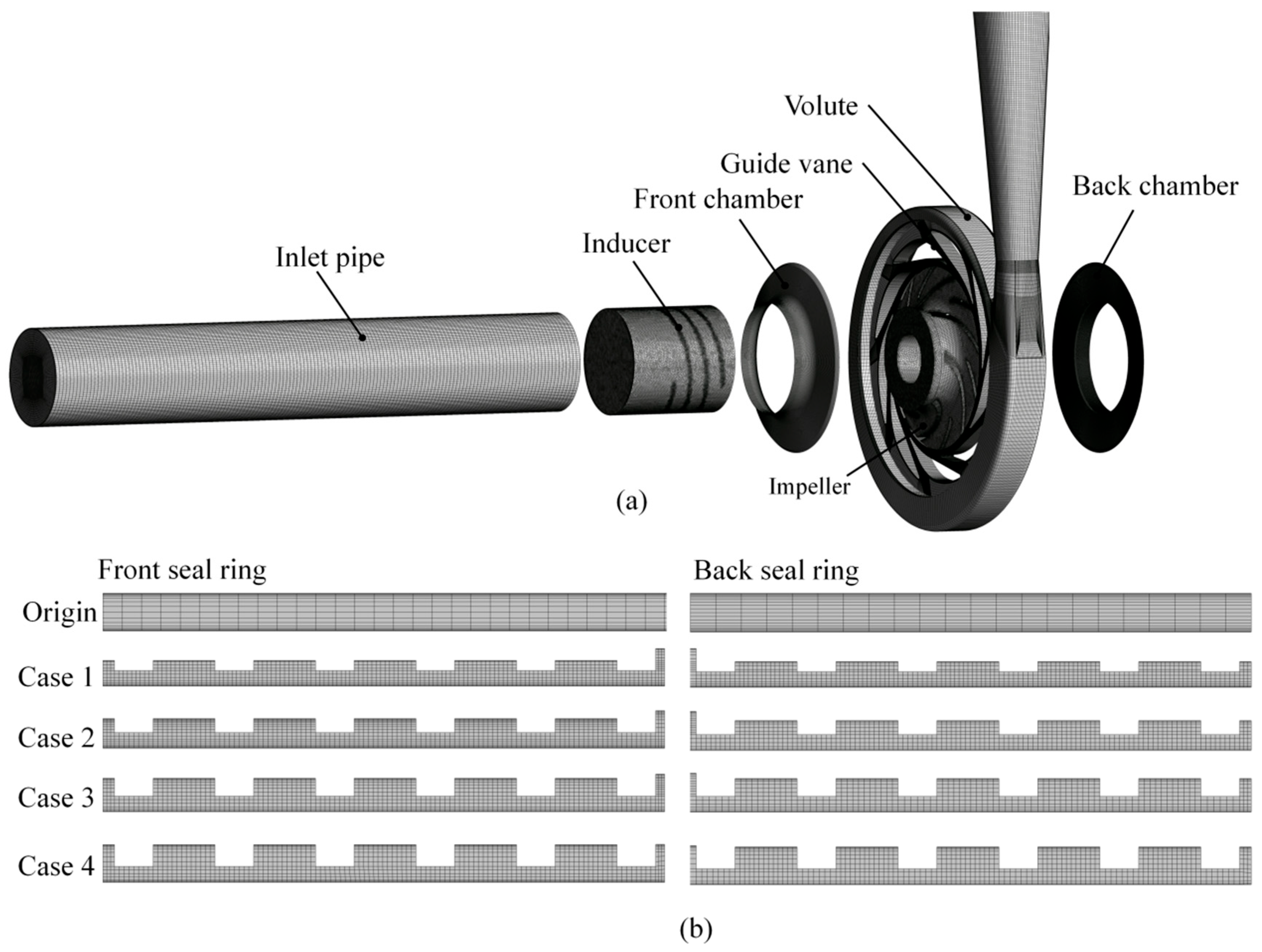
2. Physical Model
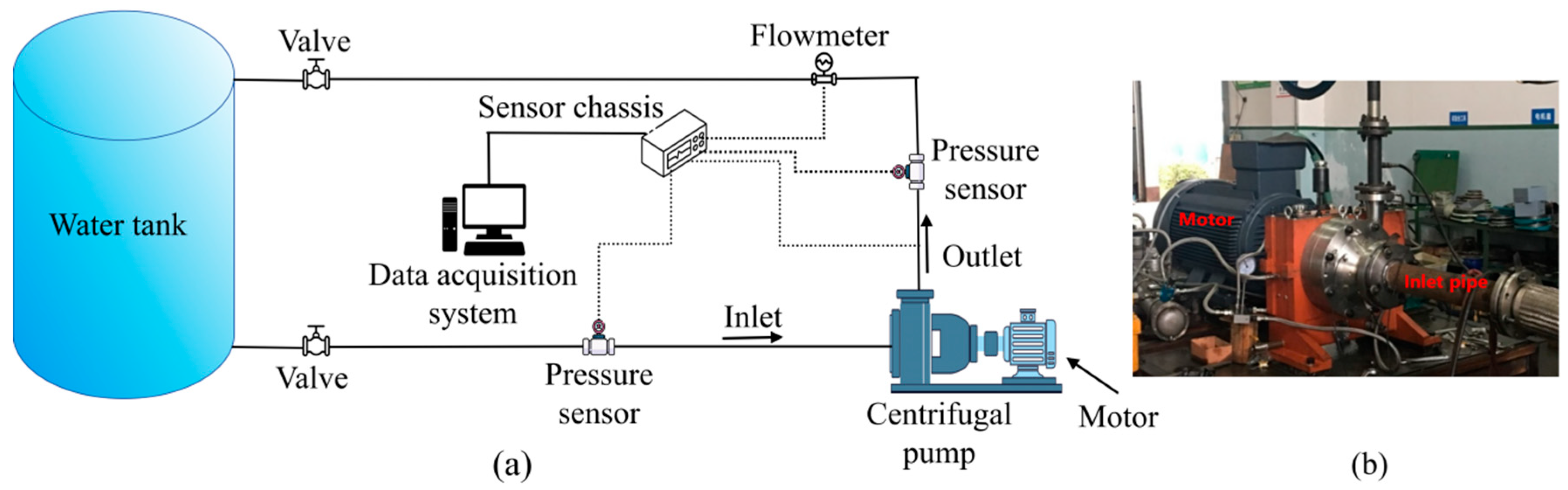
3. Experimental Setup
4. Numerical Simulation
4.1. Governing Equations
4.2. Computational Setup
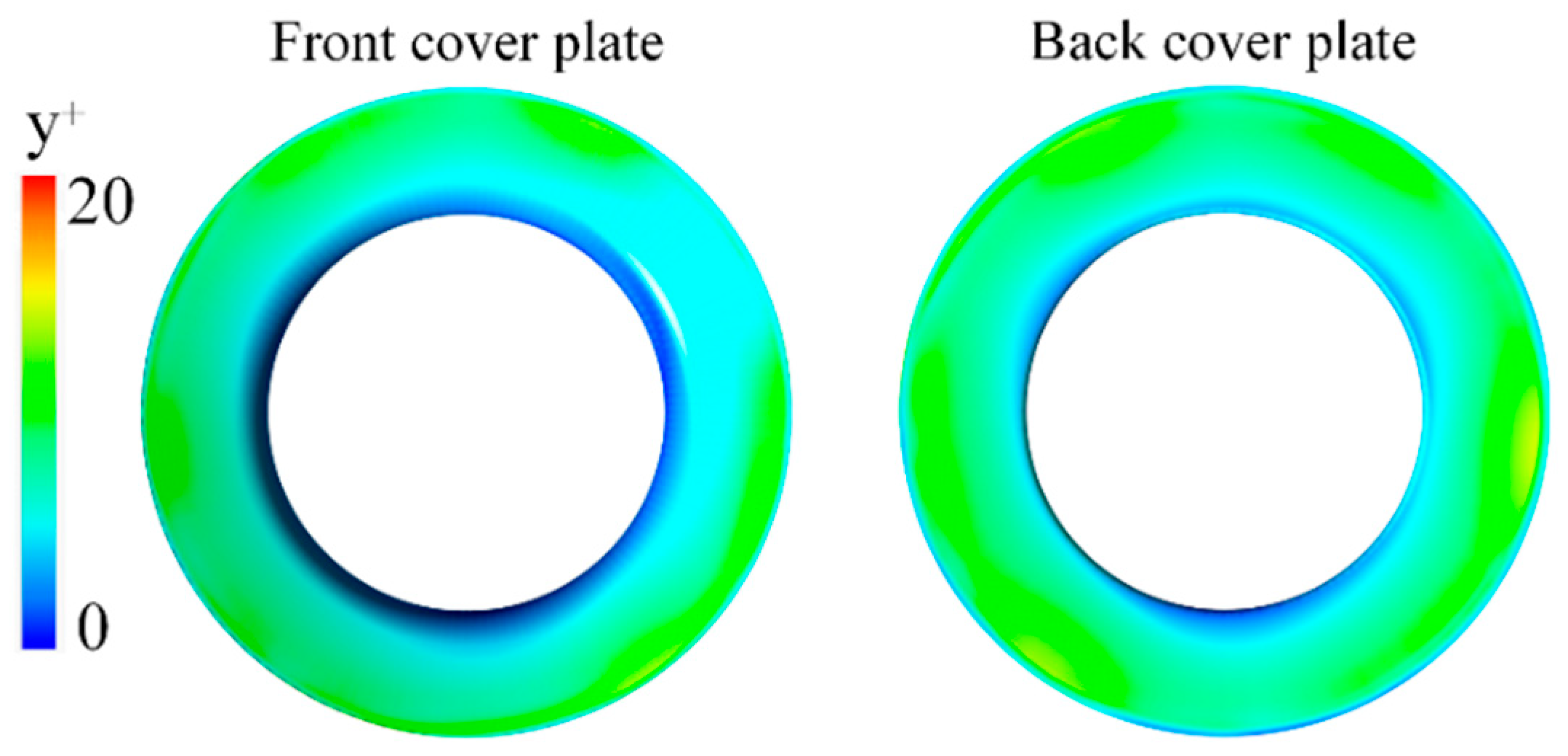
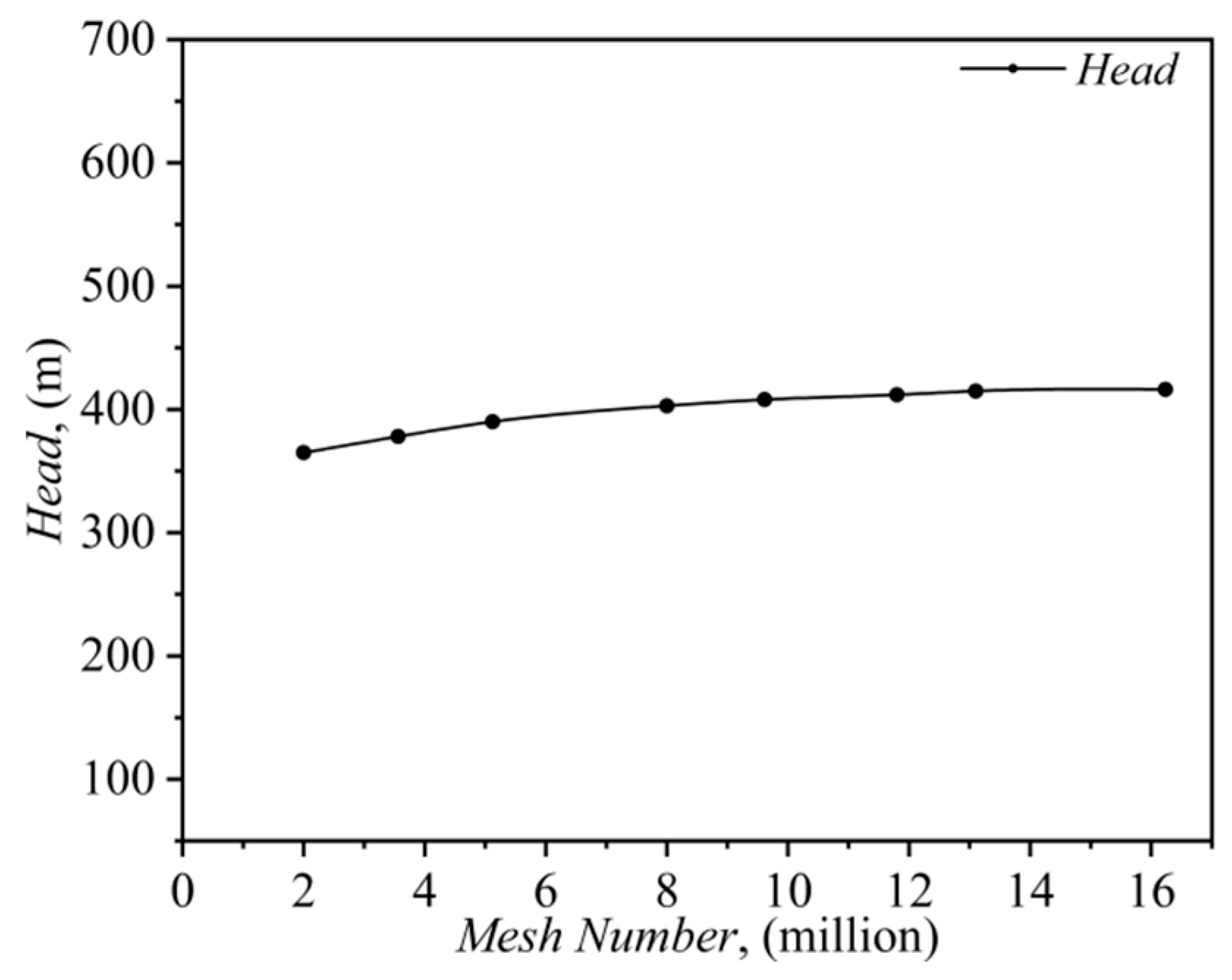
4.3. Mesh Independence Verification
5. Results and Discussion
5.1. Experimental Validation
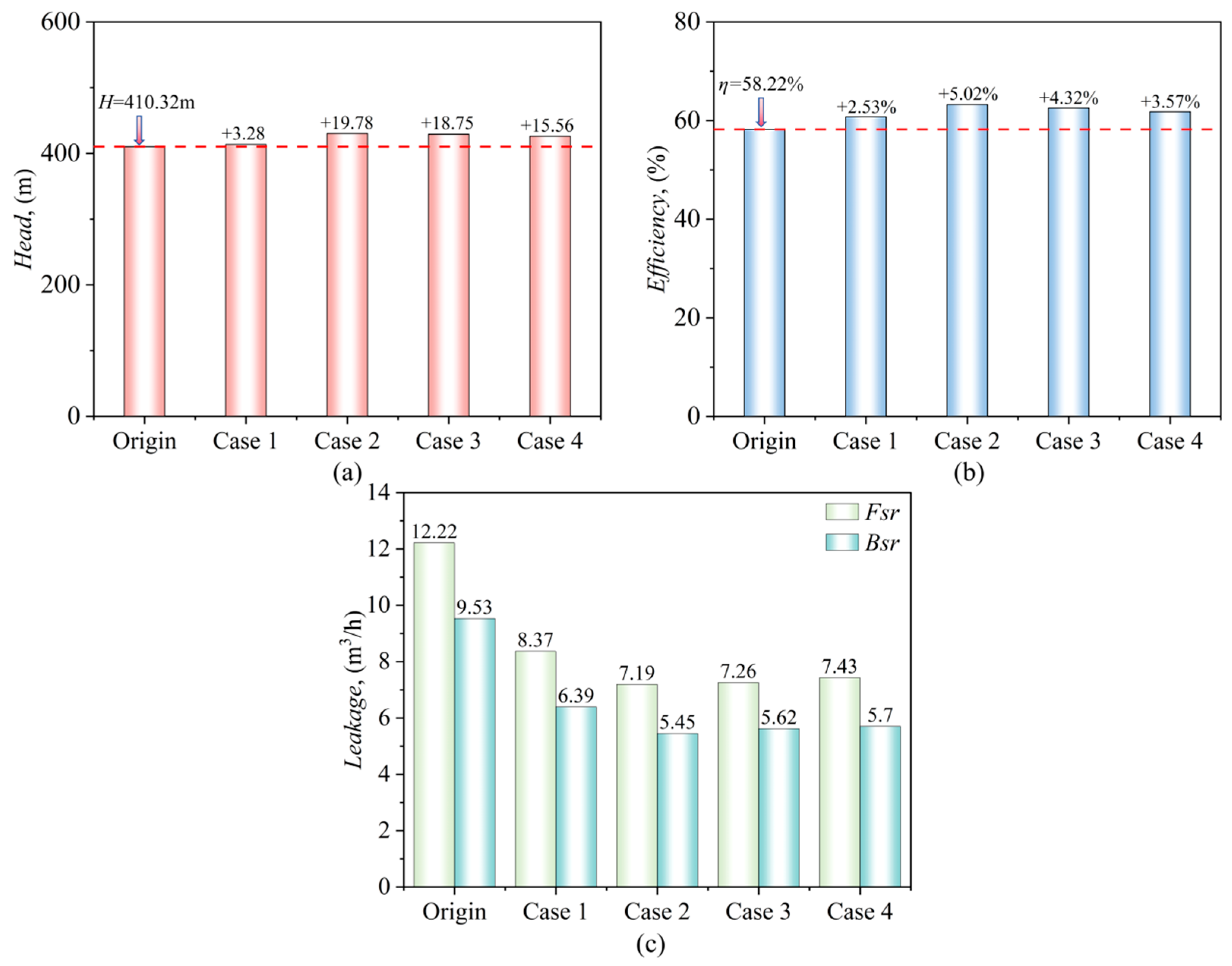
5.2. Analysis of Pump Performance and Leakage Rate
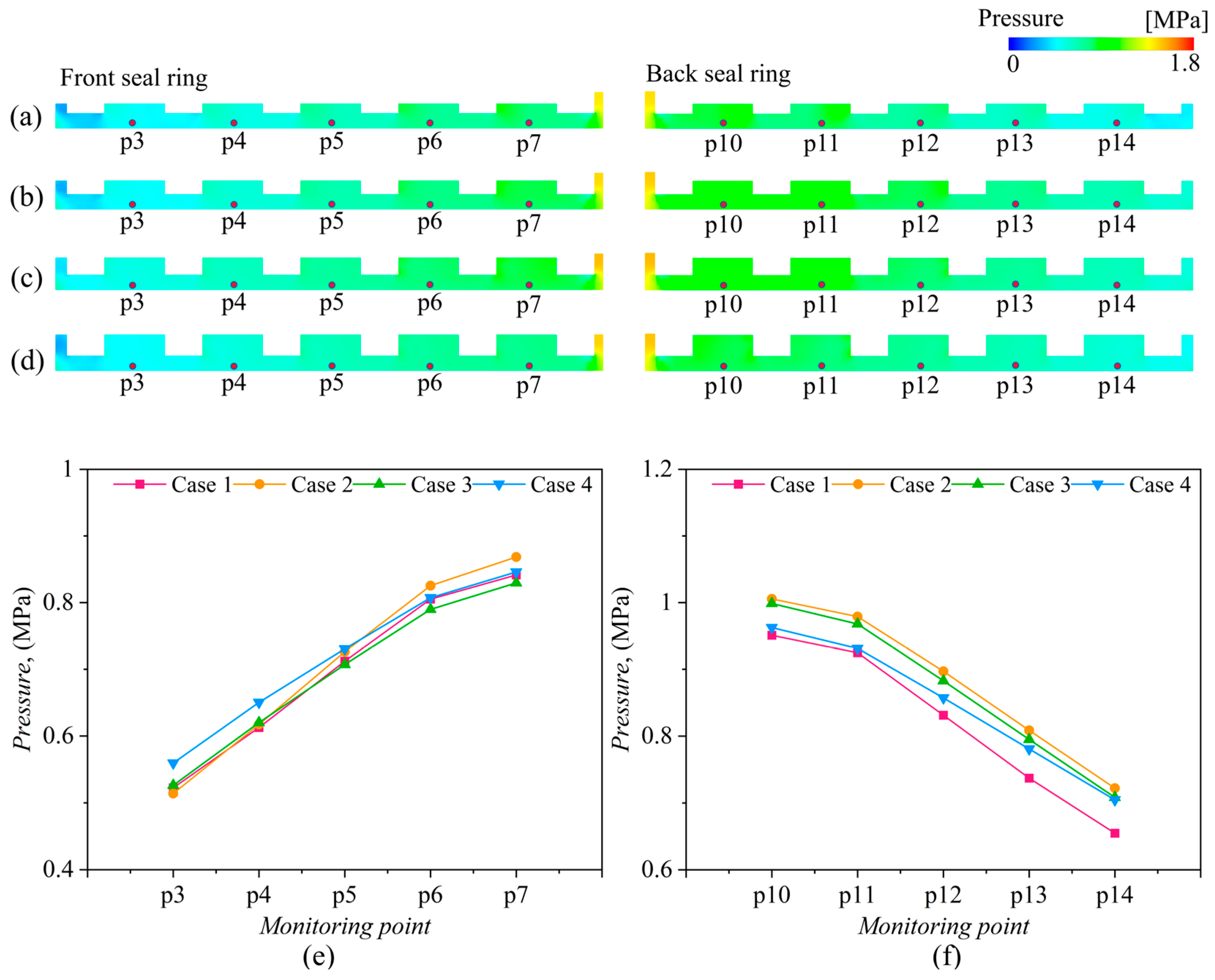
5.3. Flow Characteristics of Seal Rings
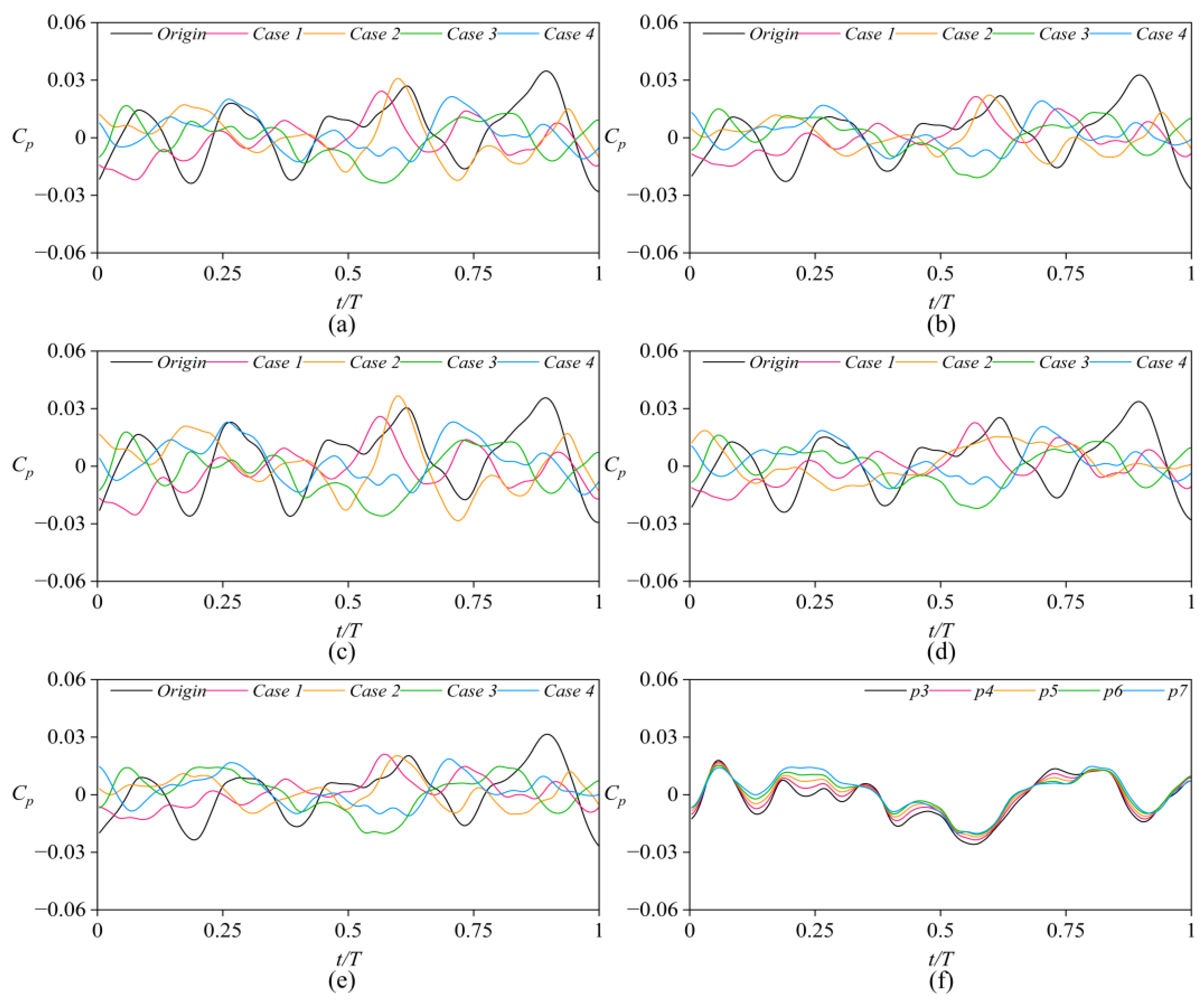
5.4. Analysis of Pressure Pulsation
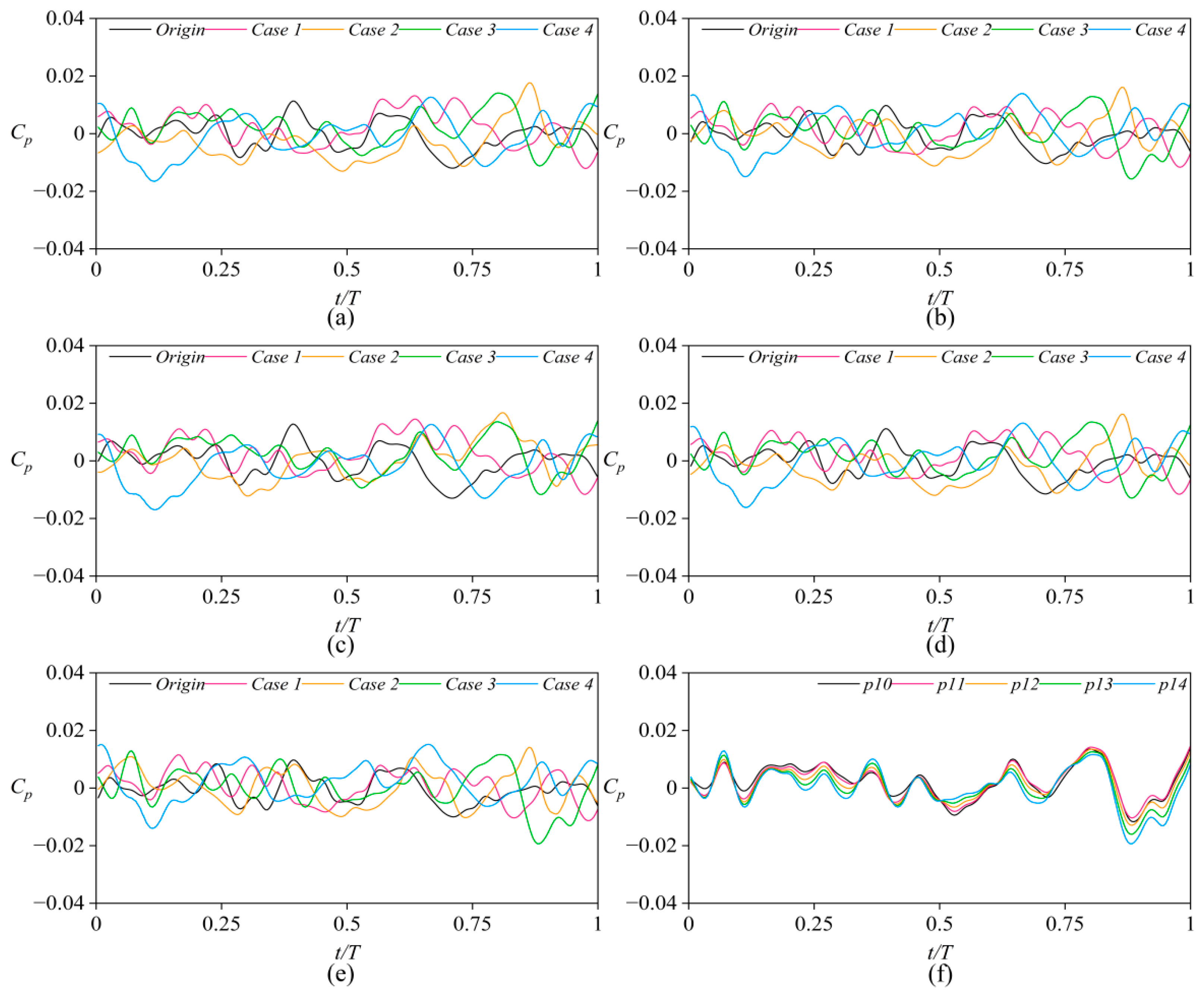
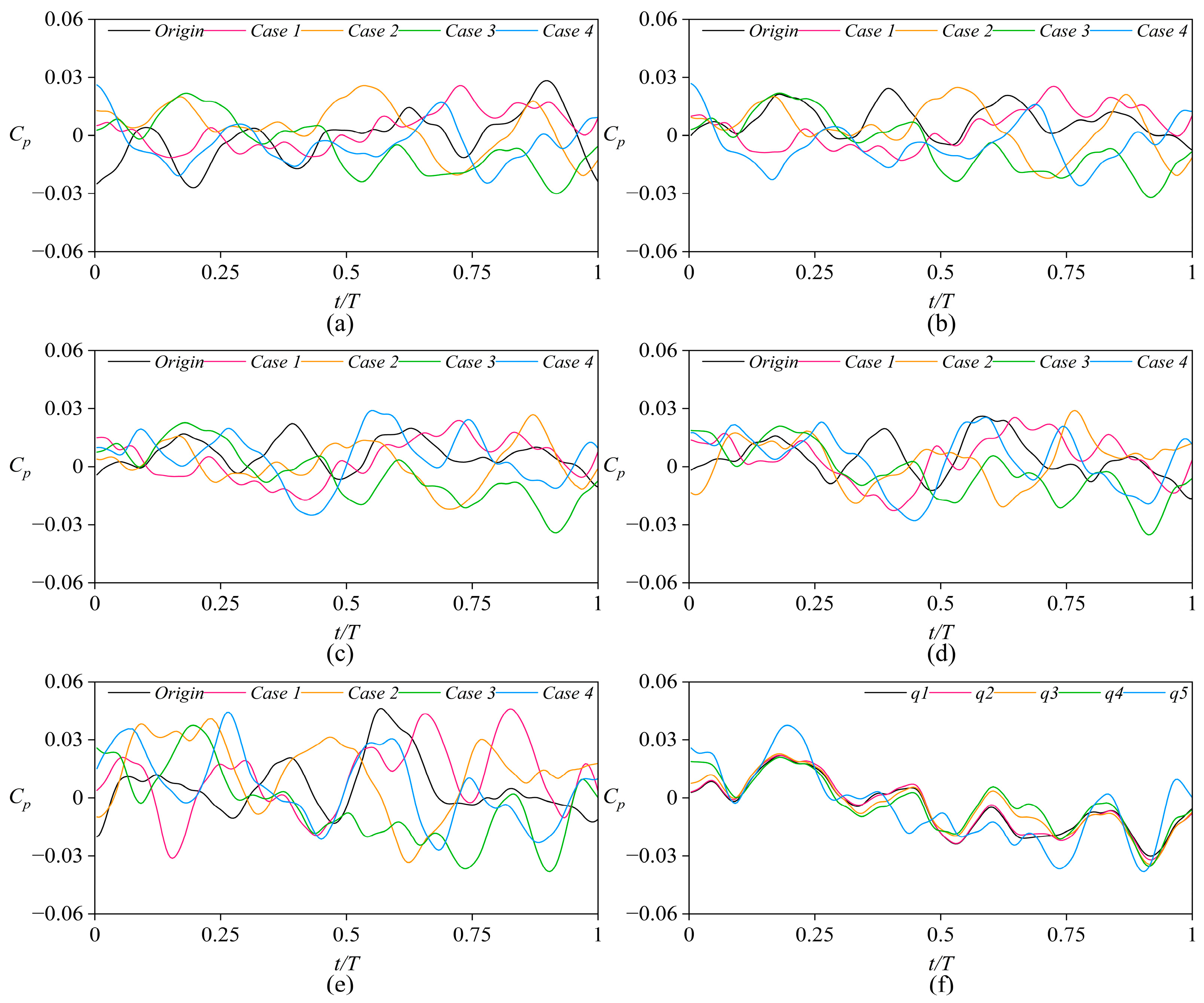
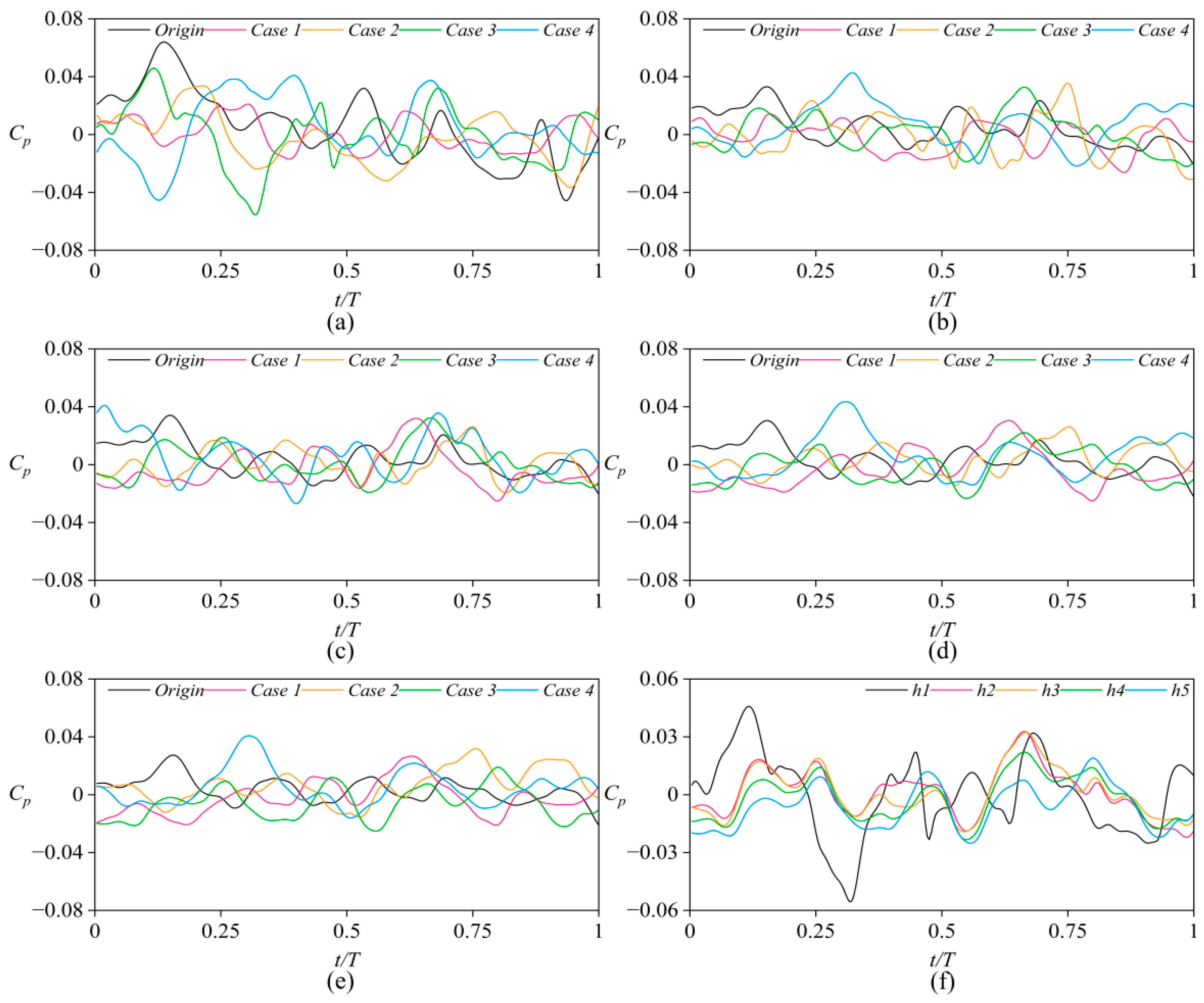
5.4.1. Pressure Pulsation in Seal Rings
5.4.2. Pressure Pulsation in Leakage Chambers
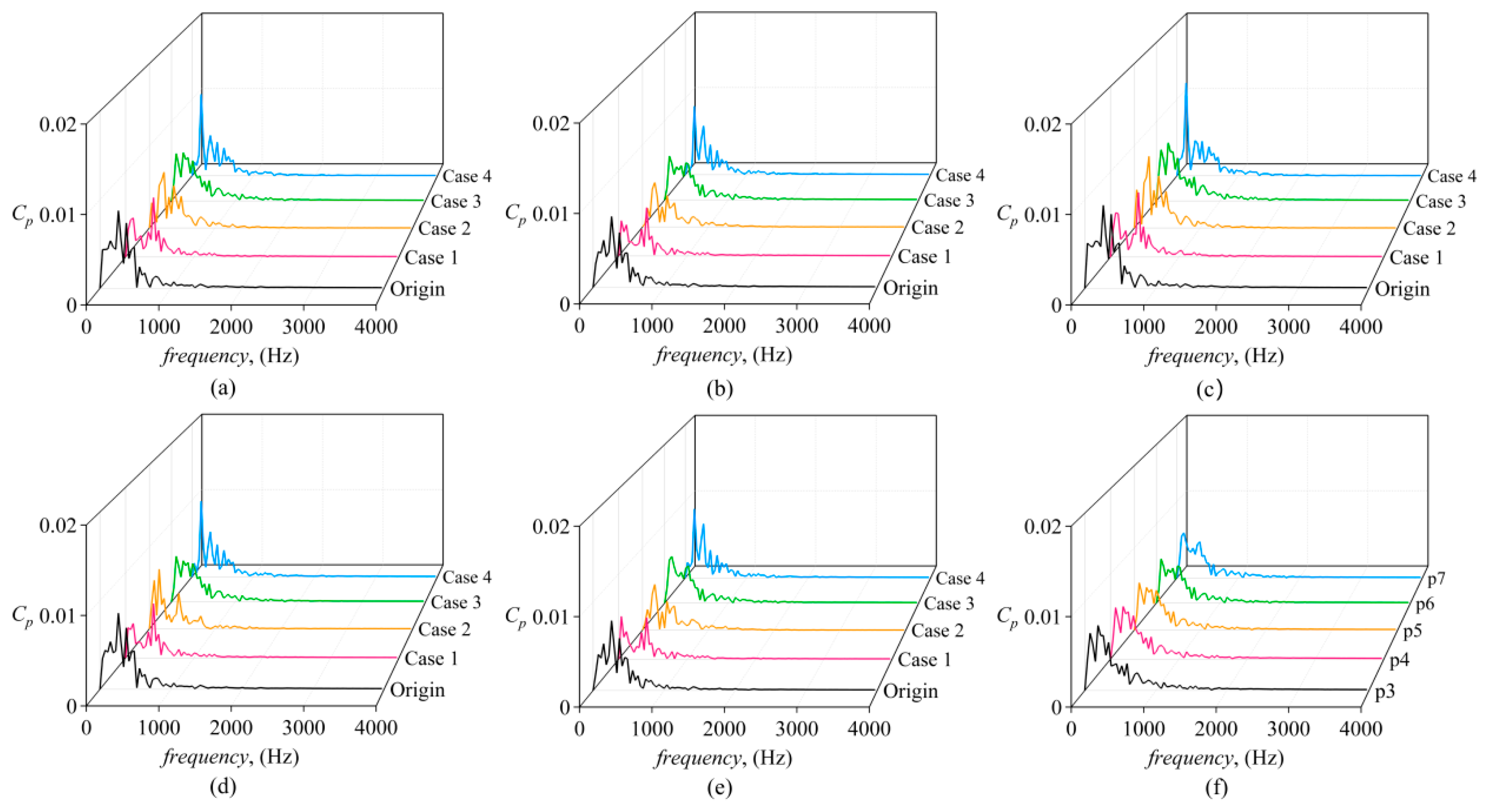
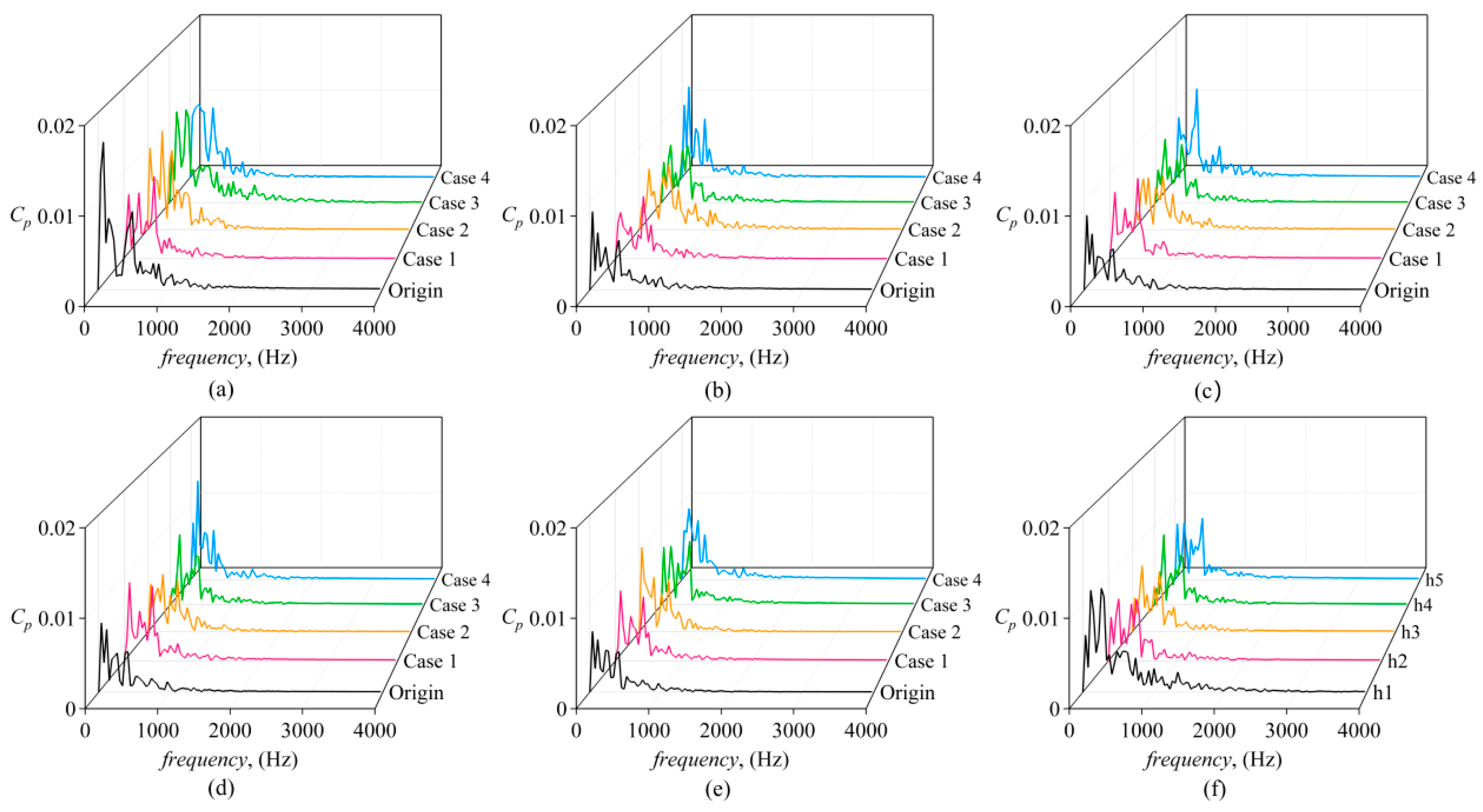
5.5. Pressure Pulsation Intensity in Leakage Chambers
6. Conclusions
- (1)
- The pressure pulsation in the leakage chambers of high-speed centrifugal pumps will increase first and then decrease with the increase in the tooth height of the labyrinth seal ring. For the Case 3 structure with a labyrinth tooth height of 0.23 mm, the pressure pulsation in the leakage chambers can reach a maximum reduction of 30.3%.
- (2)
- The use of labyrinth seal rings can also reduce the leakage rate of pump chambers. For the Case 2 structure, the leakage rate can be reduced by 41.1%, while for the Case 3 structure, the value is 40.6%.
- (3)
- The use of labyrinth seal rings significantly reduces the pressure pulsation intensity of the impeller surfaces, which improves the force stability of the high-speed centrifugal pump impeller.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| n | nominal rotating speed (9685 r/min) |
| Qd | nominal flow rate (130 m3/h) |
| H | designed head (400 m) |
| D1 | impeller inlet diameter (98 mm) |
| D2 | impeller outlet diameter (172 mm) |
| W | impeller outlet width (10 mm) |
| Z1 | impeller blade number (6) |
| Z2 | inducer blade number (3) |
| p | static pressure at inlet (101,325 Pa) |
| β2 | blade outlet angle (37°) |
| h | tooth height |
| b | cavity width |
| a | tooth width |
| N | number of teeth |
| m | gap width |
| Pout | outlet pressure |
| Pin | inlet pressure |
| T | time of one impeller revolution period (s) |
| ρ | density (998.2 kg/m3) |
| Δz | height difference |
| η | efficiency |
| μ | viscosity (0.895 × 10−3 Pa·s) |
| k | turbulence kinetic energy (m2·s−2) |
| Cp | pressure pulsation coefficient (=) |
| fr | shaft frequency |
| fBPF | blade passing frequency |
| Cpsd | pressure pulsation intensity coefficient |
References
- Yang, H.; Hao, J.; Zuchao, Z.; Xianghui, S.; Wenqi, L.; Gruszczynski, M.; Qiangmin, D.; Panlong, G. Review of the Hydraulic and Structural Design of High-Speed Centrifugal Pumps. Front. Energy Res. 2022, 10, 899093. [Google Scholar] [CrossRef]
- Algieri, A.; Zema, D.A.; Nicotra, A.; Zimbone, S.M. Potential Energy Exploitation in Collective Irrigation Systems Using Pumps as Turbines: A Case Study in Calabria (Southern Italy). J. Clean. Prod. 2020, 257, 120538. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, H.; Ma, Z.; Li, Y. Unsteady Flow and Pressure Pulsation Characteristics in Centrifugal Pump Based on Dynamic Mode Decomposition Method. Phys. Fluids 2022, 34, 117107. [Google Scholar] [CrossRef]
- Gülich, J.F. Centrifugal Pumps, 4th ed.; Springer Nature: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Gülich, J.F.; Bolleter, U. Pressure Pulsations in Centrifugal Pumps. J. Fluids Eng. 1992, 114, 459–465. [Google Scholar] [CrossRef]
- Barzdaitis, V.; Mažeika, P.; Vasylius, M.; Kartašovas, V.; Tadžijevas, A. Investigation of Pressure Pulsations in Centrifugal Pump System. J. Vibroengineering 2016, 18, 1849–1860. [Google Scholar] [CrossRef][Green Version]
- Jia, X.Q.; Chu, Q.; Zhang, L.; Zhu, Z.C. Experimental Study on Operational Stability of Centrifugal Pumps of Varying Impeller Types Based on External Characteristic, Pressure Pulsation and Vibration Characteristic Tests. Front. Energy Res. 2022, 10, 866037. [Google Scholar] [CrossRef]
- Kim, T.S.; Cha, K.S. Comparative Analysis of the Influence of Labyrinth Seal Configuration on Leakage Behavior. J. Mech. Sci. Technol. 2009, 23, 2830–2838. [Google Scholar] [CrossRef]
- Yan, J.R.; Zuo, Z.T.; Guo, W.B.; Hou, H.C.; Zhou, X.; Chen, H.S. Influences of wear-ring clearance leakage on performance of a small-scale pump-turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 454–469. [Google Scholar] [CrossRef]
- Zhao, W.G.; Li, Y.B.; Wang, X.Y.; Sun, J.P.; Wu, G.X. Research on the Effect of Wear-Ring Clearances to the Performance of Centrifugal Pump. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2012; Volume 15, p. 072018. [Google Scholar] [CrossRef]
- Wang, W.Z.; Liu, Y.Z.; Jiang, P.N.; Chen, H.P. Numerical Analysis of Leakage Flow Through Two Labyrinth Seals. J. Hydrodyn. 2007, 19, 107–112. [Google Scholar] [CrossRef]
- Matros, M.; Ziegler, A.; Nordmann, R. Fluid Structure Interactions in Annular Seals of Centrifugal Pumps. Tribol. Trans. 1995, 38, 353–363. [Google Scholar] [CrossRef]
- DaqiqShirazi, M.; Torabi, R.; Riasi, A.; Nourbakhsh, S.A. The Effect of Wear Ring Clearance on Flow Field in the Impeller Sidewall Gap and Efficiency of a Low Specific Speed Centrifugal Pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 3062–3073. [Google Scholar] [CrossRef]
- Chen, S.X.; Pan, Z.Y.; Wu, Y.L.; Zhang, D.Q. Simulation and Experiment of the Effect of Clearance of Impeller Wear-Rings on the Performance of Centrifugal Pump. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 072017. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, J.-B.; Peng, X.-D.; Ni, Z.-G. Experimental and Numerical Simulation Study on the Influence of Structural Factors on the Leakage Characteristics of Clearance Seals. Flow Meas. Instrum. 2023, 94, 102465. [Google Scholar] [CrossRef]
- Zhou, W.J.; Yang, Y.C.; Xing, G.K.; Wang, L.Q. Numerical Investigation of Nonlinear Vibration for Rotor-Seal System of Centrifugal Pump. IOP Conf. Ser. Mater. Sci. Eng. 2013, 52, 032006. [Google Scholar] [CrossRef]
- Dong, W.; Chu, W.L. Numerical Investigation of Fluid Flow Mechanism in the Back Shroud Cavity of a Centrifugal Pump. J. Appl. Fluid Mech. 2018, 11, 709–719. [Google Scholar] [CrossRef]
- Cui, B.; Zhang, Y.; Huang, Y. Analysis of the Pressure Pulsation and Vibration in a Low-Specific-Speed Centrifugal Pump. J. Fluids Eng. 2021, 143, 021201. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, M.; Gao, B.; Li, Z.; Ni, D. Investigation of Rotor-Stator Interaction and Flow Unsteadiness in a Low Specific Speed Centrifugal Pump. Stroj. Vestn. J. Mech. Eng. 2016, 62, 21–31. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, X.; Qu, J.; Ma, X. A Review of Pressure Fluctuations in Centrifugal Pumps Without or With Clearance Flow. Processes 2023, 11, 856. [Google Scholar] [CrossRef]
- Liu, H.; Ding, J.; Dai, H.; Tan, M. Investigation into Transient Flow in a Centrifugal Pump with Wear Ring Clearance Variation. Adv. Mech. Eng. 2014, 6, 693097. [Google Scholar] [CrossRef]
- Gao, B.; Wang, Z.; Yang, L.; Du, W.Q. Analysis and Test of Performance and Hydraulic Excitation Characteristics of Centrifugal Pump with Different Seal Ring Clearances. Trans. Chin. Soc. Agric. Eng. 2016, 32, 79–85. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, F.; Wang, C.; Ye, C.; Qu, Q.; Xu, J. Investigation on the Influence of Seal Clearance Leakage on the Rotating Stall Characteristics for a Centrifugal Pump. Phys. Fluids 2024, 36, 025176. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Q.; Liu, X.; Zhu, B.; Yuan, S. Investigation on Pressure Fluctuations Induced by Flow Instabilities in a Centrifugal Pump. Ocean Eng. 2022, 258, 111805. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, X.; Dou, H.S.; Zhang, W.; Zhu, Z.C.; Cheng, X. Effects of Clearance Flow on the Characteristics of Centrifugal Pump Under Low Flow Rate. J. Mech. Sci. Technol. 2020, 34, 189–200. [Google Scholar] [CrossRef]
- Chalghoum, I.; Elaoud, S. Transient Analysis of the Dynamic Flow Characteristics of the Centrifugal Pump at Different Operating Points. Nav. Eng. J. 2019, 131, 113–122. [Google Scholar]
- Babayigit, O.; Ozgoren, M.; Aksoy, M.H.; Kocaaslan, O. Experimental and CFD investigation of a multistage centrifugal pump including leakages and balance holes. Desalination Water Treat. 2018, 67, 28–40. [Google Scholar] [CrossRef]
- Si, Q.; Yuan, J.; Yuan, S.; Wang, W.; Zhu, L. Numerical Investigation of Pressure Fluctuation in Centrifugal Pump Volute Based on SAS Model and Experimental Validation. Adv. Mech. Eng. 2014, 6, 972081. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization Group Analysis of Turbulence. I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef] [PubMed]












| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Nominal rotating speed n (r/min) | 9685 | Impeller inlet diameter D1 (mm) | 98 |
| Nominal flow rate Qd (m3/h) | 130 | Impeller outlet diameter D2 (mm) | 172 |
| Designed head H (m) | 400 | Impeller outlet width W (mm) | 10 |
| Diameter of inlet pipe (m) | 100 | Impeller blade number Z1 | 6 |
| Diameter of outlet pipe (m) | 80 | Inducer blade number Z2 | 3 |
| Static pressure at inlet (Pa) | 101,325 | Blade outlet angle β2 (°) | 37 |
| Tooth Height h (mm) | Cavity Width b (mm) | Tooth Width a (mm) | Number of Teeth N | Gap Width m (mm) | |
|---|---|---|---|---|---|
| Case 1 | 0.13 | 0.8 | 0.5 | 6 | 0.2 |
| Case 2 | 0.18 | 0.8 | 0.5 | 6 | 0.2 |
| Case 3 | 0.23 | 0.8 | 0.5 | 6 | 0.2 |
| Case 4 | 0.28 | 0.8 | 0.5 | 6 | 0.2 |
| Parameter | Uncertainty | Parameter | Uncertainty |
|---|---|---|---|
| Flow rate (m3/h) | ±0.29% | Motor speed (r/min) | ±0.12% |
| Pressure (Pa) | ±0.12% | Power factor | ±0.06% |
| Electric current (A) | ±0.12% | Efficiency | ±0.36% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Xu, J.; Lian, J.; Lin, Y.; Zhu, Z. Research on the Impact of Labyrinth Seal Ring Tooth Profile on the Pressure Pulsation of Leakage Chambers in High-Speed Centrifugal Pumps. Lubricants 2025, 13, 308. https://doi.org/10.3390/lubricants13070308
Zhao G, Xu J, Lian J, Lin Y, Zhu Z. Research on the Impact of Labyrinth Seal Ring Tooth Profile on the Pressure Pulsation of Leakage Chambers in High-Speed Centrifugal Pumps. Lubricants. 2025; 13(7):308. https://doi.org/10.3390/lubricants13070308
Chicago/Turabian StyleZhao, Guodong, Jiahao Xu, Jie Lian, Yanpi Lin, and Zuchao Zhu. 2025. "Research on the Impact of Labyrinth Seal Ring Tooth Profile on the Pressure Pulsation of Leakage Chambers in High-Speed Centrifugal Pumps" Lubricants 13, no. 7: 308. https://doi.org/10.3390/lubricants13070308
APA StyleZhao, G., Xu, J., Lian, J., Lin, Y., & Zhu, Z. (2025). Research on the Impact of Labyrinth Seal Ring Tooth Profile on the Pressure Pulsation of Leakage Chambers in High-Speed Centrifugal Pumps. Lubricants, 13(7), 308. https://doi.org/10.3390/lubricants13070308




