Dynamic Characteristics of ‘Floating’ Valve Plate for Internal Curve Hydraulic Motor

Abstract

The internal curve hydraulic motor valve plate has a clearance self-compensation performance that can effectively improve the working efficiency of the valve plate. However, the dynamic characteristics of the valve plates require further investigation. This study considers the self-compensating ‘floating’ valve plate as the research object, proposes a dynamic characteristic analysis method for the internal curve hydraulic motor valve plate, and explores the changing rule of oil film thickness and surplus pressing force of the valve plate. The results showed that an increase in the inlet pressure and oil temperature led to an increase in the thickness of the oil film, and the amplitude of the oil film thickness was larger, whereas the rotational speed of the oil film thickness of the valve plate pair was not obvious. When the inlet pressure is lower than 8 MPa, and the oil temperature is in the range of 20–30 °C, the oil film is mainly subjected to the squeezing effect of the valve plate, and the displacement of the valve plate decreased with increasing rotational speed. The inlet pressure is the main factor affecting the displacement of the ‘floating’ valve plate, and when the inlet pressure reaches 8.7 MPa, the valve plate is in hydrostatic balance support. In addition, the surplus pressing force coefficient of the valve plate decreased with increasing inlet pressures. This study provides theoretical support for the design of variable pressing force valve plates for internal curve hydraulic motors by investigating the dynamic characteristics of “floating” valve plates.

1. Introduction

Multi-action internal curve radial piston hydraulic motors (internal curve hydraulic motors) feature good low-speed stability and high-power density [1,2,3,4], and are widely used in the fields of construction, chemical industry, agriculture, mining, and materials processing. The internal curve hydraulic motor (ICHM) is mainly composed of a cylinder block, stator ring, valve plate, piston, roller, and other components, as shown in Figure 1. When the high-pressure oil enters the piston chamber through the flow channel in the cylinder block, the hydraulic power pushes the roller to move on the stator guide, and the contact pressure between the stator guide and roller can be decomposed into the radial and tangential forces acting on the piston group, which the radial force accelerates the discharge of oil from the piston chamber, and the torque generated by the tangential force drives the cylinder block to rotate, such that the ICHM continuously outputs speed and torque. The ICHM adopts a ‘floating’ valve plate (VP) with a self-compensating mechanism. There are 20 balance chambers and oil holes evenly distributed on the VP, and the balance chambers generate a pressing force on the VP under the action of hydraulic power. When the pressing force of the VP and the separation force are balanced, the valve plate pair (composed of cylinder block end face and valve plate end face friction) will be in a hydrostatic balance support state [5,6], and the VP will achieve ‘floating.’ The ‘floating’ VP can not only form an ideal macro-stable oil film (dynamic balance oil film), but also actively compensate for the clearance of the valve plate pair (VVP), thus ensuring that the oil film of the VPP is in a good lubrication and sealing state, and effectively avoiding the wear and leakage of the VPP [7,8,9]. However, when the hydrostatic support of the VP is unbalanced, the ‘floating’ state of the VP is destroyed, and the thickness of the oil film of the VPP is squeezed until the hydrostatic support is balanced again. If the oil film thickness becomes thin, the VP will wear out; conversely, if the film thickness increases, the leakage of the VPP will also increase, resulting in a reduction in the mechanical efficiency and volumetric efficiency of the motor [10,11]. In addition, the calculation of the pressing force and separation forces of the ‘floating’ VP usually relies on empirical parameters [12,13], which makes it difficult to accurately reflect the actual working conditions of the VP. Therefore, it is important to study the dynamic characteristics of the ‘floating’ VP of the ICHM to improve the working performance of the VP.

Hydraulic pumps and motors usually use an end-face flow distribution structure, which is divided into fixed and ‘floating’ valve plates. The fixed and ‘floating’ valve plates have similar structures and the same flow distribution principle. Therefore, in this paper, the study of force and leakage on the VP of an ICHM will draw on the research results related to axial piston pumps. Previous studies have focused on the axial piston pump as the object of study, the establishment of the numerical model of the axial piston pump, and the characteristics of the thickness of the oil film of the VPP, pressure distribution, and leakage [14,15,16]. Ma et al. proposed a calculation method based on the leakage of the VPP of the ICHM, analyzed the leakage of the VPP under different operating conditions, and investigated the main influencing factors of the leakage of the VPP and its rule of action [17]. Other scholars have studied the flow field characteristics of the ICHM and analyzed the thickness of the oil film of the VP and the leakage characteristics of the motor under different working conditions [18,19]. Wang et al. established a lubrication model of the oil film of the VPP of a swash plate axial piston pump and analyzed the oil film thickness, elastic deformation, pressure distribution, and temperature change rule [20]. Xia et al. studied the friction and wear of the VPP of axial piston pumps with three types of texture-weaving VPs [21]. Zhang et al. used the finite element method to establish a dynamic model of an axial piston pump, deduced the numerical model of the oil film of the VPP, and studied the time-varying characteristics of the cylinder block inclination angle on the oil film bearing capacity of the VPP [22]. Vivek et al. based on the optimal design of the VP of a bi-directional axial piston pump, analyzed the lubricating state of the oil film of the VP and analyzed the leakage characteristics of the VPP [23]. Wang et al. proposed a numerical model to predict the dynamic characteristics of the ‘floating’ VP and investigated the dynamics and oil film lubrication characteristics of the ‘floating’ VP under different operating conditions [24]. Wang et al. studied the wedge-shaped oil film thickness, pressure, and temperature distribution of the axial piston pump VPP and performed a comparative analysis of the lubrication characteristics under different operating conditions, cylinder block tilting, and non-tilting states [25]. Zheng et al. used the ultrasonic method to perform a thermal compensation test on the VP to achieve the non-destructive measurement of the VPP oil film and investigated the changes in the VPP oil film under different operating conditions [26]. The above study is an important guideline for the research of ‘floating’ VPs for ICHMs.

In summary, the current research on axial piston motor/pump VPPs mainly focuses on the leakage and noise of the VPP, the thickness and pressure distribution of the oil film, and the force. Numerous theoretical analyses and experimental studies have been conducted on the dimensions of the sealing bands of the VP, the structure outline, and the weaving textures. However, there are relatively few studies on self-compensating ‘floating’ VPs for ICHMs, and the dynamic characteristics of the VP in the ‘floating’ state are unclear. Therefore, in this study, the leakage amount of the VPP was determined, the thickness of the oil film of the VPP was calculated through the test, and the pressure of the balance chamber was obtained through a transient simulation of the flow field of the ICHM, the force of the VP and micro-displacement equations were analyzed, the oil film thickness of the VPP and the maximum displacement of the VP under motor working conditions were investigated, and the trend of the surplus pressing force coefficient of the VP was analyzed. This study provides theoretical support for improving the adaptability of the VP and designing a variable pressing force.

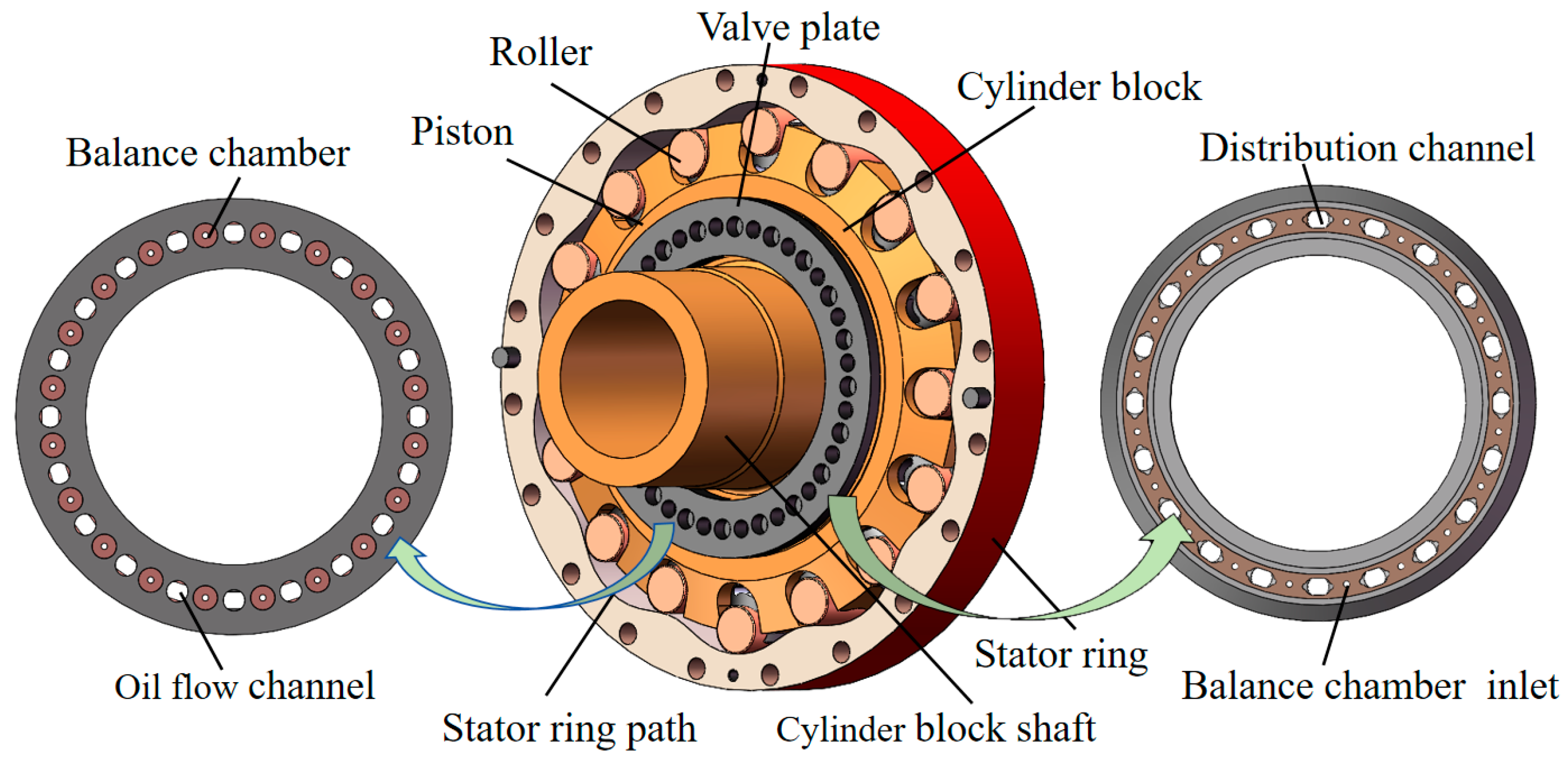
2. Mathematical Modelling

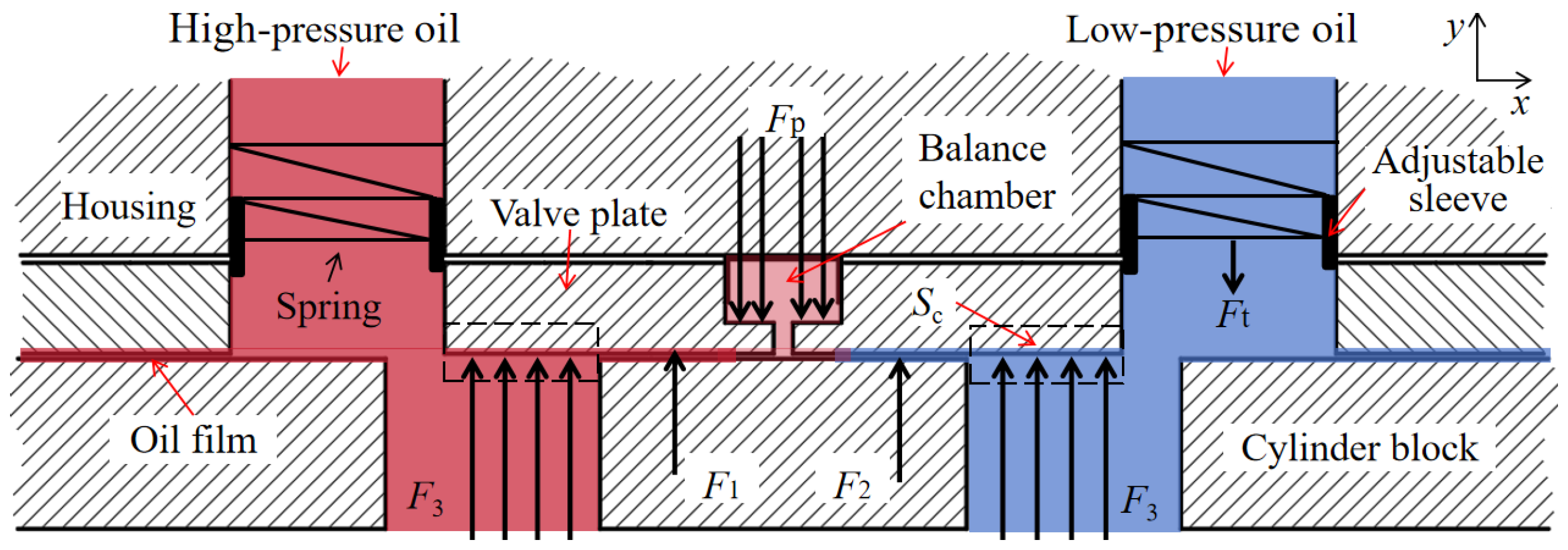
2.1. Mathematical Modelling of the Pressing Force on the VP

The ICHM ‘floating’ VP adopts the design principle of hydrostatic oil film support balance. When the VP pressing force and separation force achieve hydrostatic balance, the VPP oil film is in a fully lubricated state, and the VP achieves ‘floating’, which not only reduces the friction and wear between the VP and the cylinder block but also ensures that the VPP has good lubrication; the force of the VP is shown in Figure 2.

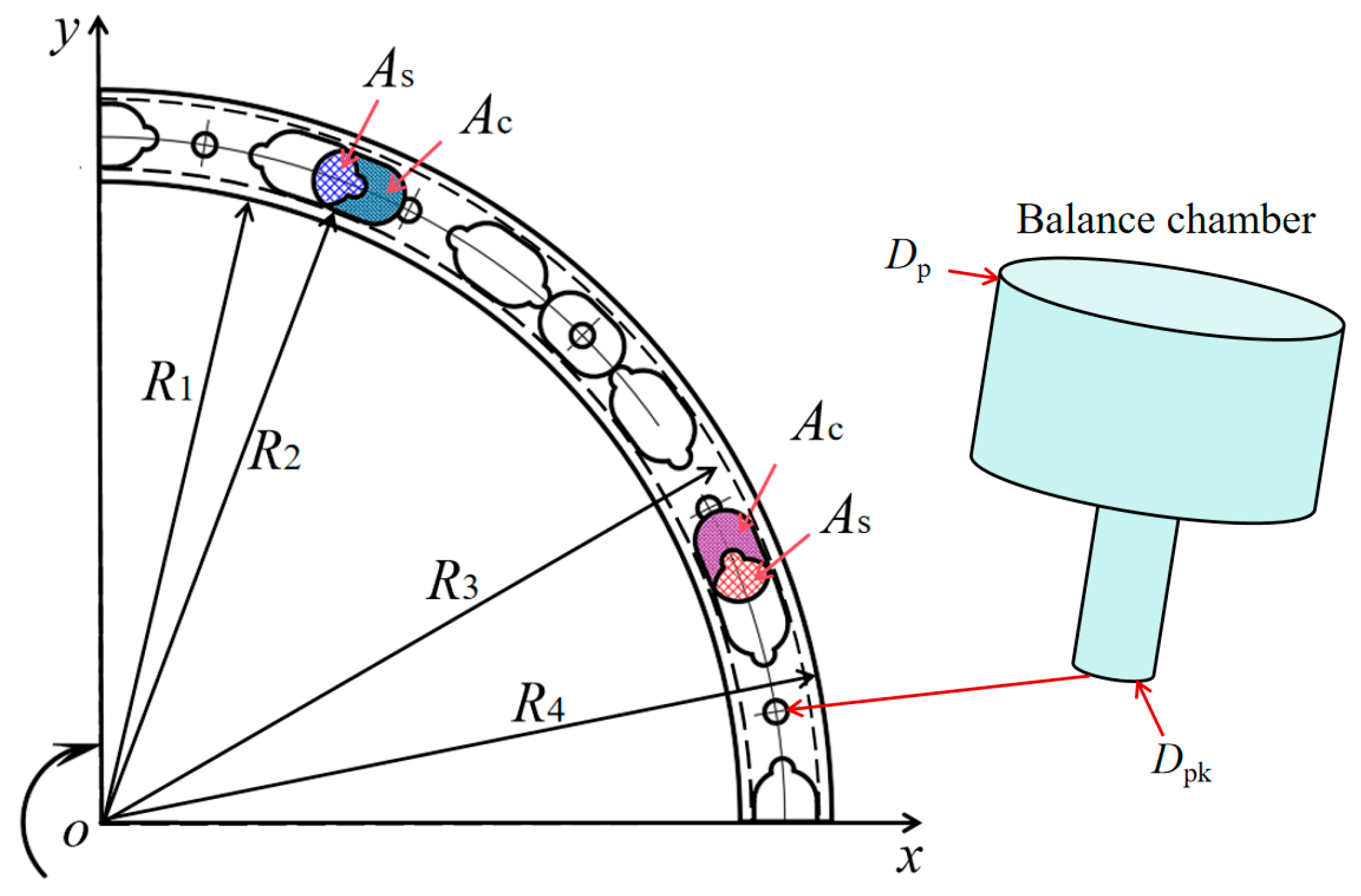
2.1.1. VP Balance Chamber Pressing Force

There are 20 balance chamber inlets evenly distributed on the VP. When the balance chamber inlet is connected to the cylinder block flow window, the hydraulic power in the balance chamber generates a pressing force. The pressure in the balance chamber changes with the cylinder block rotational angle, and the number of balance chambers connected to the cylinder block changes periodically within the motor’s periodic angle. Owing to the symmetrical structure of the VP, the pressing force in the balance chamber is also symmetrical and uniformly distributed; therefore, the pressing force does not generate a moment that causes the VP to overturn. Therefore, the pressing force of the VP can be expressed as follows:

$$\begin{array}{cc}\hfill F_{\mathrm{p}}& =ApX\hfill \\ & ={\displaystyle \sum _{i=1}^{20}{A}_{\mathrm{fb}}{p}_i}{X}_{\mathrm{n}}\hfill \end{array}$$

(1)

where A_fb is the area of action of the pressure in the balance chamber of the VP; P_i is the instantaneous pressure in the balance chamber; X_n is the number of the balance chamber connected to the cylinder block.

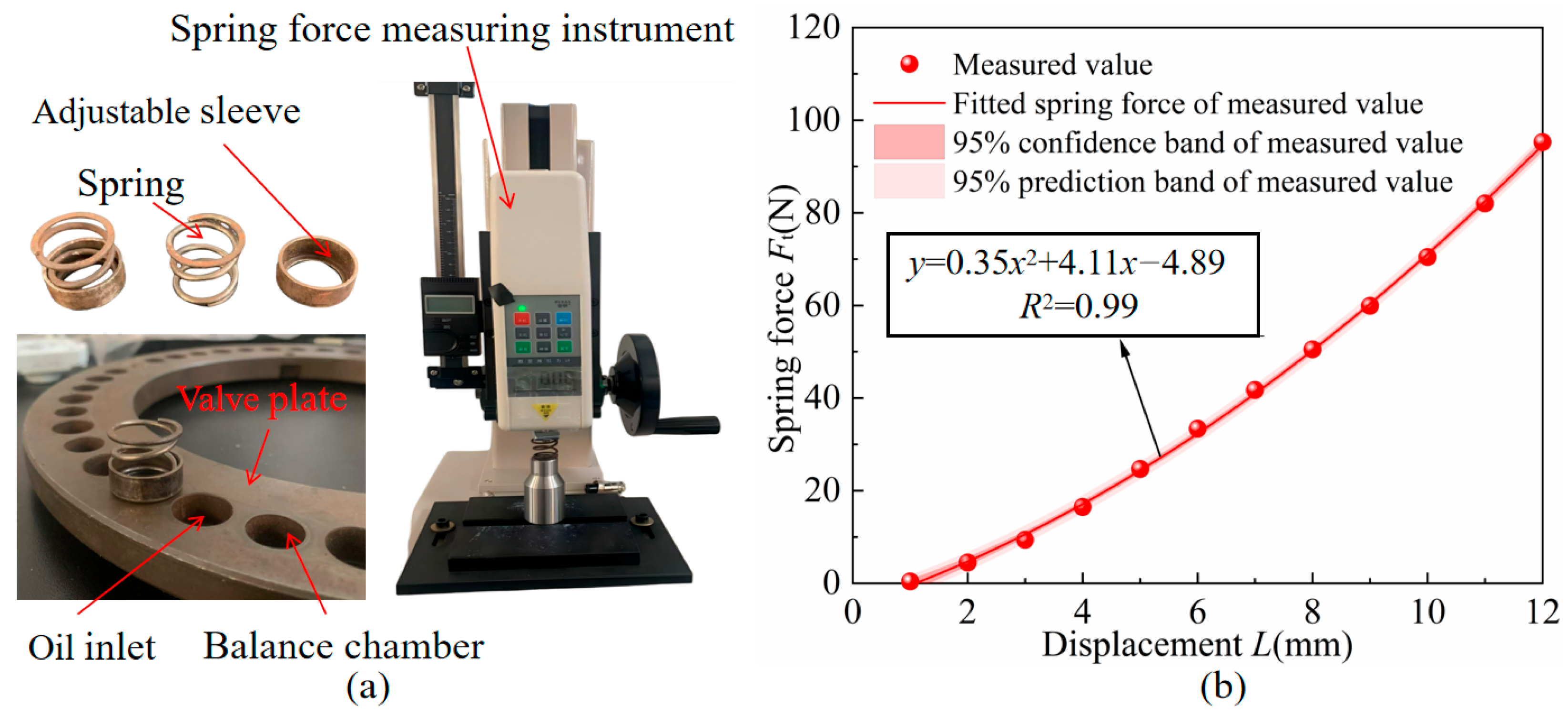
2.1.2. Telescopic Sleeve Spring Pressing Force

As shown in Figure 2, the ‘floating’ VP of the ICHM is connected to the housing bore using a telescopic sleeve. The telescopic sleeve is evenly distributed between the VP and the housing. The pressing force generated by the spring inside the telescopic sleeve ensures that the telescopic sleeve is always connected to the flow path between the motor housing and VP, which facilitates the entry of oil into the piston chamber and at the same time ensures that when the inlet pressure of the motor is small, the end face of the VP and cylinder block are always close to each other. Therefore, the pressing force of the telescopic sleeve can be expressed as follows:

$$F_{\mathrm{t}}=nKL$$

(2)

where n (n = 20) is the number of telescopic sleeve springs; K is the elasticity coefficient of the spring; L is the pressing displacement of the spring.

2.2. Mathematical Modelling of the Separation Force of VP

The ICHM ‘floating’ VP separation force includes not only the oil film squeezing effect produced by the oil film bearing force, and differential pressure flow produced by the oil film separation force, but also the cylinder block fluid pressure in the flow channel on the VP thrust. In this paper, this combined force will be collectively referred to as the VP separation force. The bearing force produced by the oil film squeezing effect is a passive force, and it only occurs when there is surplus pressing force for the VP, causing the oil film to be squeezed by the pressing force. The bearing force, oil film thickness, and pressing force action time are related. The separation force generated by the differential flow of pressure is the active force, which is directly related to the inlet pressure but not to the thickness of the oil film [27]. The thrust force on the VP owing to the hydraulic power in the flow channel varies with the flow window area of the VP. The VP separation force changes transiently with the cylinder block rotational angle, which has a direct impact on the dynamic characteristics of the VP. Because the VP structure is symmetrical, one quarter of the structure was considered for the study. The structure is shown in Figure 3, and the key calculation parameters are listed in

Table 1. Key calculation parameters for VP.

Symbol	Value	Symbol	Value
R1	111.2 mm	Dpk	3.8 mm
R2	113.3 mm	M	3.4 kg
R3	125.5 mm	Cd	51.5 MPa·S·m
R4	127.4 mm	μ	0.043 Pa·S
Dp	15.5 mm	C	0.8

.

2.2.1. Bearing Force Generated by Squeezing the Oil Film on the VP

The oil film with an initial thickness exists between the VPP, and under the action of the pressing force, the thickness of the oil film becomes thinner, while the oil between the VPP is squeezed out, and a pressure field is formed. The combined force of the pressure field was balanced with the pressing force. Based on the integral method of the micrometric ring of the VP, the bearing force formed by the oil film pressure field can be deduced. Therefore, the bearing force of the oil film squeezing effect of the VP can be expressed as follows:

$$F_1={\displaystyle \frac{3C\pi \mu }{2h^3}}\left({R_4}^2-{R_1}^2-{\displaystyle \frac{{\left({R_4}^2-{R_1}^2\right)}^2}{\ln \left(R_4/R_1\right)}}\right){\displaystyle \frac{dh}{dt}}$$

(3)

where C is the correction factor for the pressure envelope angle; $\mu$ is the oil viscosity; $h$ is the oil film thickness; and $R_i$ (i = 1, 2, 3, 4) is the radius of the sealing band of the VP.

2.2.2. Separation Force of the Oil Film on the VP

The pressure difference between the two sides of the ring-shaped sealing band of the VP causes the oil to flow radially in the sealing clearance. The oil film formed by the differential pressure flow has a certain separation force, which can offset part of the pressing force of the VP. Based on the integral method of the micrometric ring of the VP, the separation force generated by the differential flow field can be deduced. Therefore, the separation force of the oil film on the VP can be expressed as follows:

$$F_2={\displaystyle \frac{1}{4}}(A_i+A_e)p_i$$

(4)

$$A_i={\displaystyle \frac{C\pi }{2}}\left({\displaystyle \frac{{R_4}^2-{R_3}^2}{\ln R_4/R_3}}-2{R_3}^2\right);$$

$$A_e={\displaystyle \frac{\mathrm{C}\pi }{2}}\left(2{R_2}^2-{\displaystyle \frac{{R_2}^2-{R_1}^2}{\ln R_2/R_1}}\right)$$

where $A_i$ is equivalent support area of the sealing band along the inner edge of the VP; $A_e$ is equivalent support area of the sealing band along the outer edge of the VP; C is the correction factor for the pressure envelope angle (the ratio of the pressure envelope angle to 2π); and $R_i$ (i = 1, 2, 3, 4) is the radius of the sealing band of the VP.

2.2.3. Thrust of Hydraulic Power on the VP

The oil channel of the VP and piston chamber forms an irregular sealed chamber, and the hydraulic power generates a thrust force on the VP in a direction perpendicular to the pressing force. The thrust can offset part of the pressing force of the VP, and the area of the hydraulic power is the difference between the cylinder block bore and the flow area of the VP. Pang et al. [28] described the process of calculating the fluid domain area of the VP in detail, and it will not be repeated in this paper. Therefore, the thrust force of the hydraulic power on the VP can be expressed as follows:

$$F_3=A_{\mathrm{s}}{p}_i$$

(5)

where $A_{\mathrm{s}}$ is the projected area of the force on the cylinder block bore; and $p_i$ is the pressure in the balance chamber.

2.3. Mathematical Modelling of the Micro-Motion of the VP

2.3.1. Force Analysis of VP

The VP was used as the research object, and a mechanical analysis was performed, as shown in Figure 2. The VP is mainly subjected to the pressing force $F_{\mathrm{p}}$ generated by 20 balance chambers, the pressing force $F_{\mathrm{t}}$ generated by 20 telescopic sleeves, the oil film bearing force $F_1$ generated by the pressing force squeezing the oil film, the oil film separating force $F_2$ generated by the inner and outer sealing bands of the VP, and the thrust force $F_3$ generated by the pressure oil of the flow channel on the VP. The mechanical balance equations of the VP are established as follows by establishing a Cartesian coordinate system on the VP:

$$\begin{array}{l}{F}_x=F_f\\ F_y=F_{\mathrm{p}}+F_{\mathrm{t}}+F_1+F_2+F_3\end{array}$$

(6)

In the x-direction, the rotational speed of the cylinder block is low, the friction force is very small and negligible, and there is no moment in the y-direction to overturn; therefore, the displacement is only considered in the y-direction, and the VP is in a state of hydrostatic balance support when the combined force of $F_y$ is 0. We specify that the direction of the pressing force is positive and the direction of the separation force is negative.

2.3.2. Equation of Dynamic Characteristics of the VP

When the pressure of the VP is balanced with the separation force of the oil film, the VP can be in a ‘floating’ state. According to the relationship between the hydrostatic balance support of the VP along the direction of the VP, vertical to the oil film, the micro-motion equation of the VP is established in time. Therefore, under the condition of not considering the deformation of the VP and cylinder block, the micro-displacement equation of the VP can be deduced from Equation (6):

$$M{\displaystyle \frac{d^{2}y}{d{t}^2}}+{\displaystyle \frac{\mu A}{{(h_0-y)}^3}}{\displaystyle \frac{dy}{dt}}+C_{\mathrm{d}}{\displaystyle \frac{dy}{dt}}+Jy+F_2+F_3+F_{\mathrm{p}}+F_{\mathrm{t}}=0$$

(7)

where M is the mass of the VP; $\mu$ is the oil viscosity; $C_{\mathrm{d}}$ is the viscous damping coefficient of the oil; and J is the stiffness coefficient of the oil film.

2.3.3. Dynamic Thickness Equation for the Oil Film of the VPP

The oil film of the VPP not only adapts to the change in the pressing force through oil film pressure feedback but also ensures that the oil film is always in a fully lubricated state. The essence of oil film pressure feedback lies in balancing the pressing and separation forces so that the VP reaches the state of hydrostatic balance support, and the oil film of the VPP maintains the state of full lubrication, with the thermal deformation being negligible relative to the valve plate pair clearance. Therefore, the dynamic thickness h of the oil film can be expressed as follows:

$$h=h_0+y$$

(8)

$$h_0={\left(6{\displaystyle \frac{\mu C\ln (R_m/R_n)}{\alpha p_{si}}}Q\right)}^{{\displaystyle \frac{1}{3}}};$$

where $h_0$ is the average oil film thickness calculated after the leakage of the VPP, and is the initial thickness of the oil film; y is the micro-motion displacement of the VP; $\mu$ is the viscosity of the oil; $C$ is the correction coefficient for the pressure envelope angle; $R_n$ (n = 1, 2) is the radius of the sealing along the inside of the VP; $R_m$ (m = 3, 4) is the radius of the sealing along the outside of the VP; $\alpha$ is the pressure envelope angle; $p_{si}$ is the pressure of the piston chamber; and $Q$ is the amount of leakage of the VPP.

2.3.4. Equation for the Surplus Pressing Force of the VP

The surplus pressing force directly influences the optimum lubrication of the oil film, the minimum power loss, and the optimal operating conditions [29], whereas the oil film is fully lubricated in the hydrostatic balance. The balanced state of the VP can be defined by the surplus pressing force coefficient. When the surplus pressing force coefficient is greater, the pressing force is sufficient, the thickness of the oil film is thin, and the cylinder block and VP experience friction, resulting in a reduction in the mechanical efficiency of the motor. When the coefficient of the surplus pressing force is less, the pressing force is insufficient, the thickness of the oil film increases, and the leakage of the VPP increases, resulting in a reduction in the volumetric efficiency of the motor. The VP can achieve hydrostatic balance support, and the oil film is fully lubricated only when the pressing force is balanced with the separation, and the surplus pressing force is close to 0. Therefore, the surplus pressing force coefficient is usually used to measure the relationship between the pressing force of the VP and the oil film separation force, and the surplus pressing force coefficient is defined as follows:

$$\epsilon ={\displaystyle \frac{F_{pr}-F_{sp}}{F_{pr}}}\times 100\%$$

(9)

where $F_{pr}$ is the combined force of the VP pressing force and $F_{sp}$ is the combined force of the oil film separation force.

3. Simulation and Testing

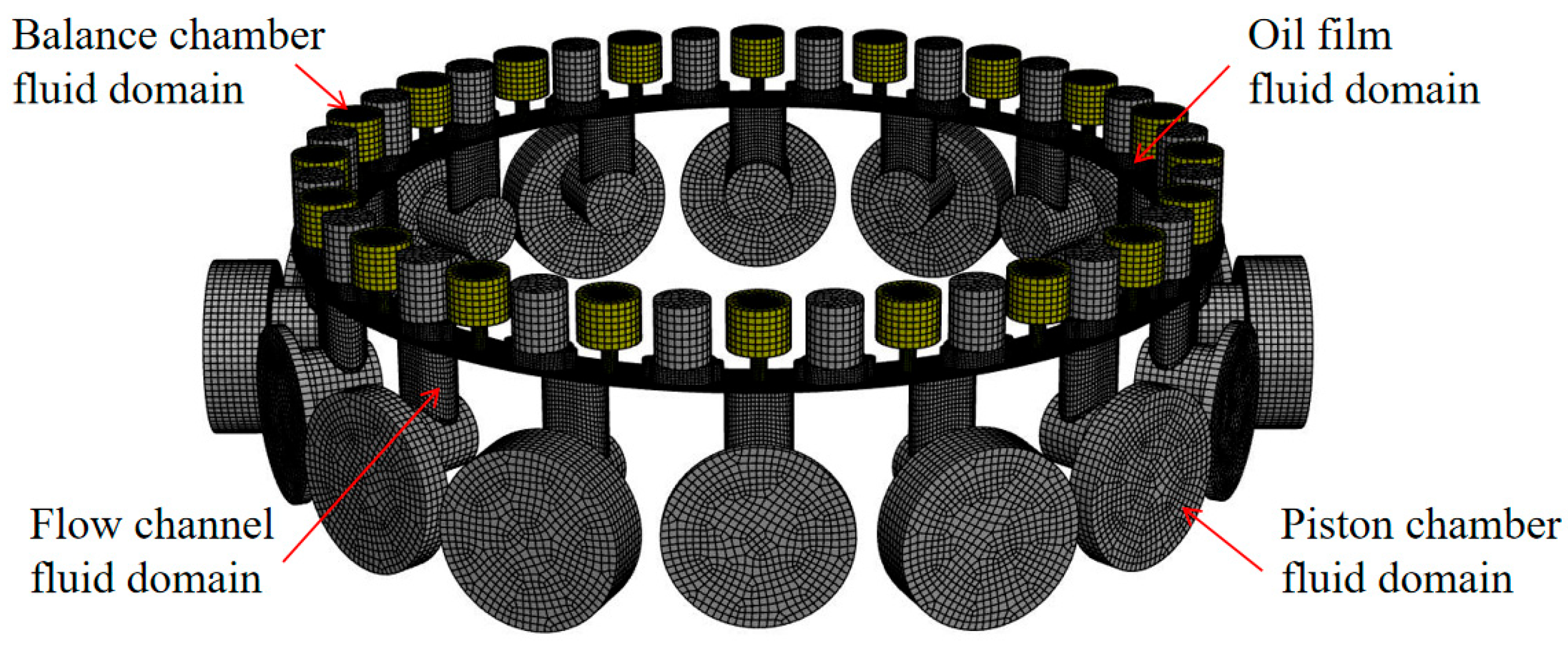
3.1. Fluid Domain Simulation of ICHM

3.1.1. Computational Domain Modelling of Fluids in ICHM

As shown in Figure 4, the fluid computational domain of the ICHM consists of the following parts: balance chamber and inlet/outlet channel, VPP oil film, piston chamber, and connecting flow channel, which the balance chamber and inlet/outlet channel are 20 independent computational domains, and the oil film computational domain is connected to 16 piston chamber computational domains. In this study, the fluid domain model of the motor adopted a structured mesh, employed a double-precision solver in Ansys Fluent software, and performed transient simulation in PISO format and second-order implicit discrete format. A user-defined function (UDF) was used to match the position of the piston with the movement of the cylinder block and to make the piston domain perform composite motion, that is, axial rotation and radial reciprocating motion, to simulate the transient changes in the internal flow field of the ICHM.

3.1.2. Fluid Modelling Simulation of ICHM

In this study, the fluid domain simulation model adopted dynamic mesh and slip mesh techniques and set reasonable simulation parameters (see

Table 2. Simulation setting.

Parameters	Value
Inlet pressure p	10 MPa
Outlet pressure ps	0.8 MPa
Rotation speed n	30 r/min
Oil	LHM-46# Hydraulic Oil
Viscosity μ	0.043 Pa·S
Turbulence model	Realizable k-ε

) while monitoring the pressure transient changes in the balance chamber. As shown in Figure 5, the numerical results of the fluid domain simulation of the ICHM converged, and there was no distortion in the mesh of the fluid domain model, which is due to the working principle of the balance chamber of the ICHM [19]. As the cylinder block rotates, the balance chamber is connected to the pressure oil, which leads to a change in the pressure of the balance chamber. According to Figure 5a–f, it can be seen that the pressure in the balance chamber varies cyclically with a periodic angle, and the number of balance chambers connected to the piston chambers is presented alternately in six or eight. Through the transient simulation of the flow field of the ICHM, the transient pressure variation of each balance chamber can be obtained, which provides data support for calculating the pressing force of the VP.

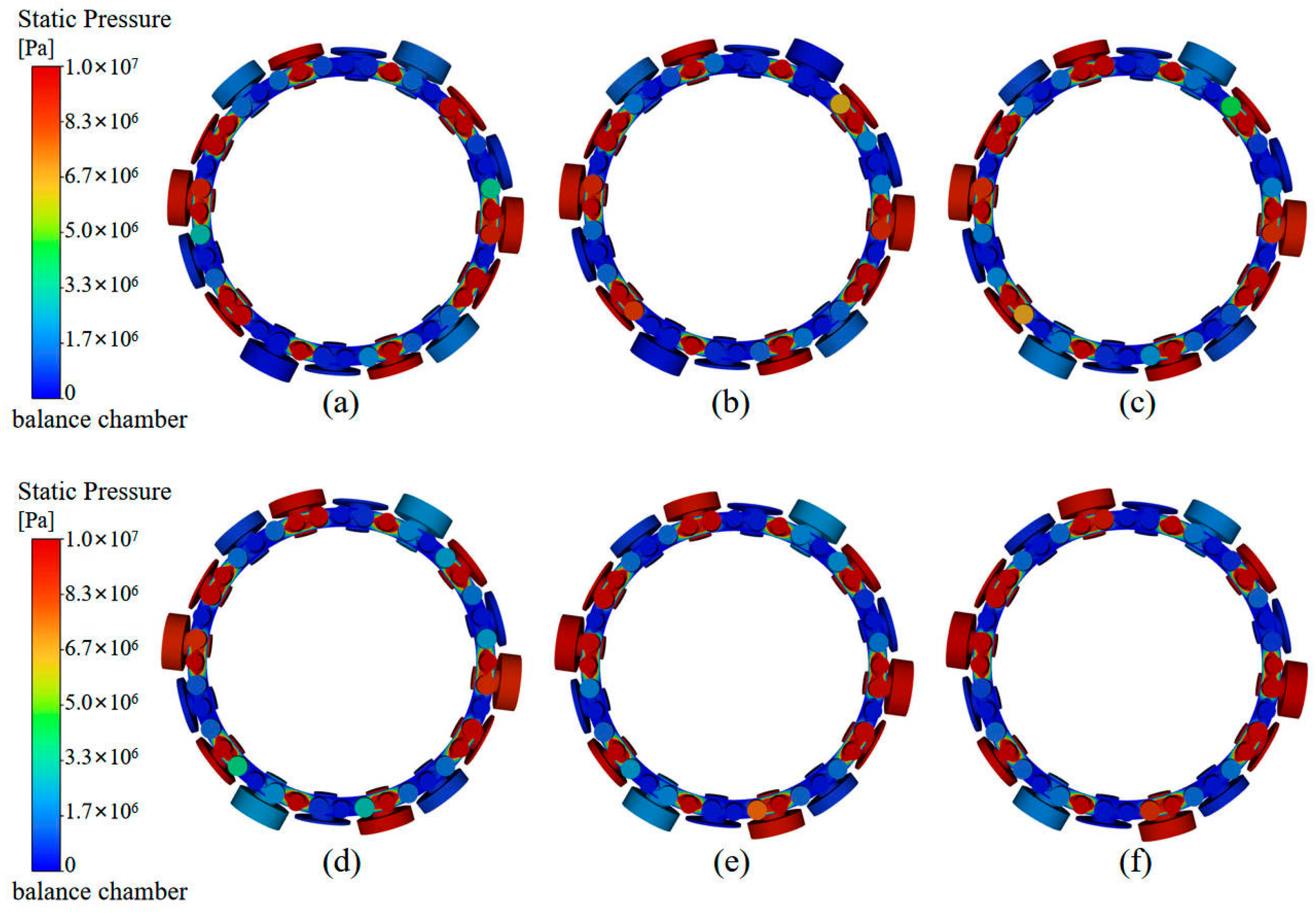
3.1.3. Validation of Numerical Mesh Grid Independence in the Fluid Domain of the Balance Chamber

To verify the stability and reliability of the simulation results of the balance chamber of the ICHM, this study adopts mesh densities of 300 K (coarse), 600 K (medium), 1200 K (fine), and 2400 K (ultrafine) resolutions for the numerical simulation of the ICHM. As shown in Figure 6, in the phase angle of the balance chamber, with an increase in the grid density, the pressure in the balance chamber gradually tended to a stable value, and the error of the numerical calculation results under the 600 K, 1200 K, and 2400 K grid densities was less than 3%, which indicated that the simulation results converged and the results were reliable, and the conditions of the grid-independence of the numerical simulation were satisfied. Therefore, the 600 K grid density model was used to analyze the balance chamber pressure change rule of the ICHM.

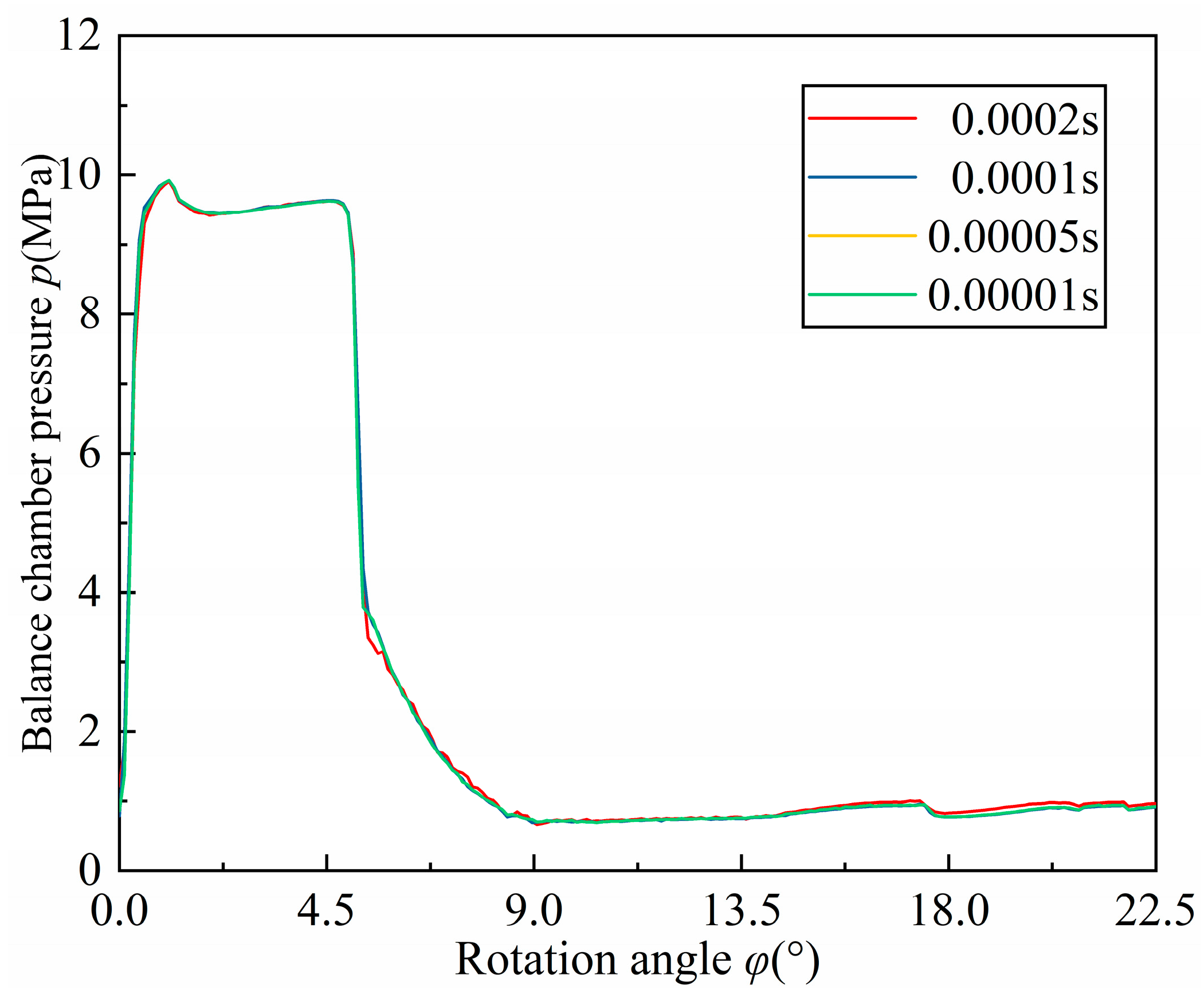
3.1.4. Verification of Simulation Time-Step Independence in the Fluid Domain of Balance Chamber

During the sliding process of the fluid domain, if the mesh on the interface appears to be spanned, the simulation results will be dispersed. The minimum simulation time step was calculated based on the size of the mesh and the rotational speed of the motor, and four step times were set as 0.0002 s, 0.0001 s, 0.00005 s, and 0.00001 s, respectively. The change in pressure in the balance chamber with the time step is shown in Figure 7. The simulation results were dispersed when the time step was less than 0.0002 s. When the time step was 0.0001 s, 0.00005 s, and 0.00001 s, the pressure in the balance chamber remained consistent, indicating that the time step did not affect the simulation results. Therefore, the transient simulation of the internal curve hydraulic motor was calculated with a time step of 0.0001 s.

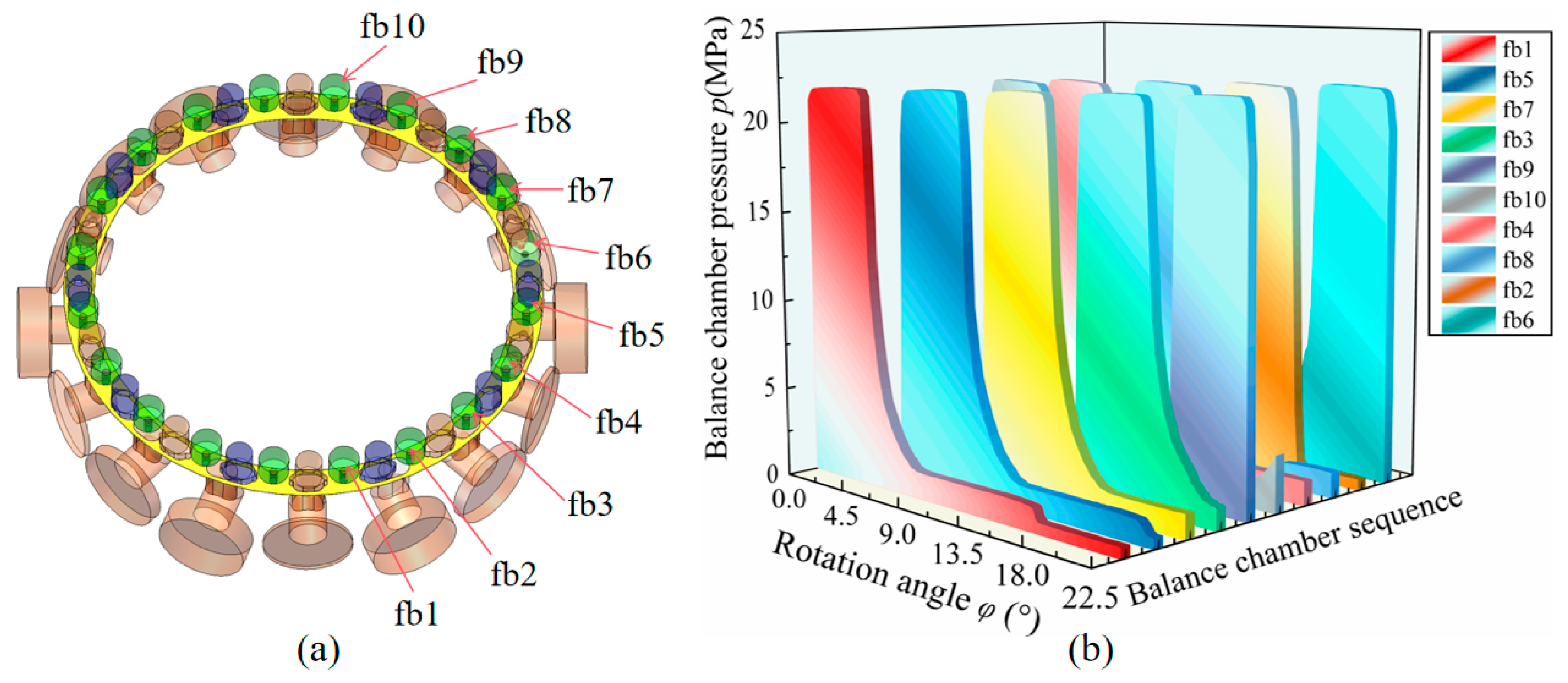
3.1.5. Balance Chamber Pressure Change Rule

The pressure change rule in the phase angle of the balance chamber is shown in Figure 8. When the balance chamber pressure is switched from high to low, it presents a high-pressure area, a pressure release area, a pressure holding area, and a low-pressure area. When the cylinder block flow distribution window connects the piston chamber with the oil inlet, the balance chamber exhibits a high-pressure state. When the balance chamber inlet is completely covered by the cylinder block, the oil in the balance chamber leaks slowly through the clearance of the VPP, resulting in a slow decline in the pressure inside the chamber, which is the pressure release area. When the pressure inside the balance chamber is equal to the pressure of the oil film the pressure in the balance chamber is maintained at a stable level, which is the pressure maintenance area. When the flow distribution window of the cylinder block connects the piston chamber with the oil outlet, the pressure in the balance chamber drops to the back pressure of the motor, presenting a low-pressure state.

As shown in Figure 9, the position and pressure change the rules of the balance chamber in the phase angle. Because the stator curve of the ICHM is a symmetrical structure, the position of the piston group is the same at the cylinder block rotational angle of n $\Delta \phi$, and the position of the cylinder block connected to the inlet of the balance chamber is also the same. Therefore, in this study, only the balance chamber with half of the VP was investigated, and the balance chambers were numbered sequentially, as shown in Figure 9a. As shown in Figure 9b, the pressure changes in fb1, fb5, fb7, fb3, and fb9 were from high-pressure to low-pressure transitions, and they showed different pressure trends. The pressures in the balance chamber cycle through the high-pressure area, pressure release area, pressure holding area, and low-pressure area, and the positional difference in the pressures in each of the balance chambers is a periodic angle. The pressure changes in fb10, fb4, fb8, fb2, and fb6 changed from low pressure to high pressure, which was exactly the opposite.

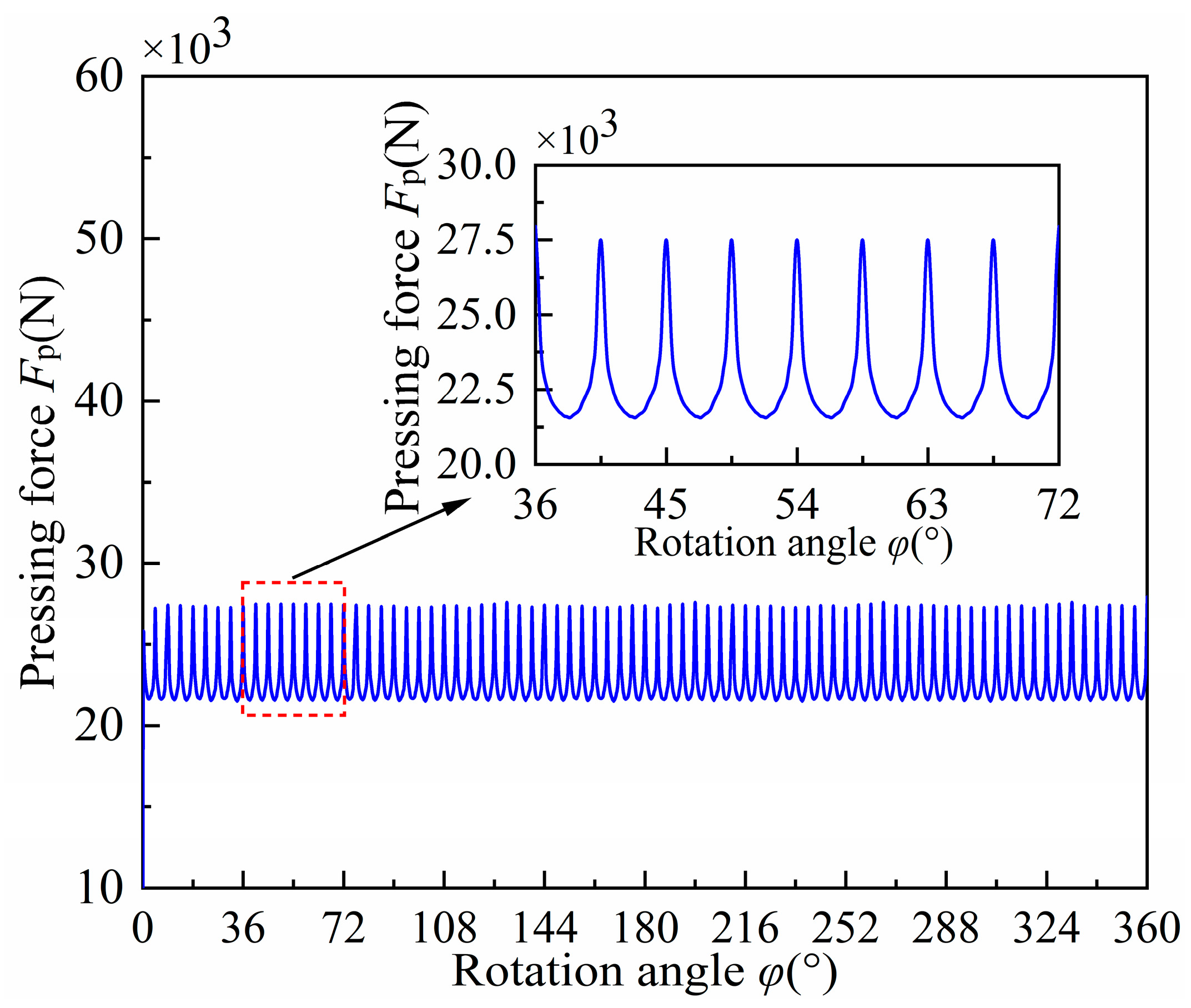
3.2. Pressing Force of the VP

Based on Equation (1) and Table 1, the change rule of the pressing force of the VP can be obtained when the cylinder block rotates for a round, as shown in Figure 10. When the cylinder block rotates at an action amplitude angle ${\phi }_x$ (${\phi }_x$ = 36°), the pressing force appears in eight peaks and low points. At each periodic angle $\Delta \phi$ ($\Delta \phi$ = 4.5°), there are eight balance chambers connected to the high-pressure oil, at which time the VP has the maximum pressing force; whereas at rotational angle 1/2$\Delta \phi$, there are six balance chambers connected to the high-pressure oil, and the VP is subjected to the minimum pressing force. The difference between the maximum and minimum pressing forces is the sum of the pressing forces generated by the two balance chambers.

3.3. Telescopic Sleeve Pressing Force

The telescopic sleeve is fixed between the VP and housing, which has the function of diversion and pre-pressing force. The telescopic sleeve spring of the pressing force measurement, as shown in Figure 11, can obtain the change rule of the telescopic sleeve pressing force. As shown in Figure 11a, one end of the telescopic sleeve was inserted into the motor housing, and the other end was inserted into the oil inlet of the VP. The internal tower-type spring makes the VP and cylinder block close to the use of an elastic force measuring instrument to determine the spring elasticity, which can be calculated to obtain the pre-pressing force of the telescopic sleeve. For the spring force test of the telescopic sleeve spring, the ZQ-21B-6 spring instrument was used, with a range of 2–500 N, an accuracy of ±0.5%, and a displacement accuracy of 0.01 mm. As shown in Figure 11b, through repeated measurements of the spring elasticity and fitting the test data of the spring force, the equation of the fit curve of the spring force with a coefficient of determination of R² = 0.99 was obtained, and the confidence interval for the fitted equations was increased. Owing to the small displacement caused by the change in oil film thickness, the effect on the spring force is negligible, and the pressing deformation of the telescopic sleeve spring is 4 mm. Therefore, the pressing force of the telescopic sleeve on the VP is calculated to be 343 N based on Equation (2).

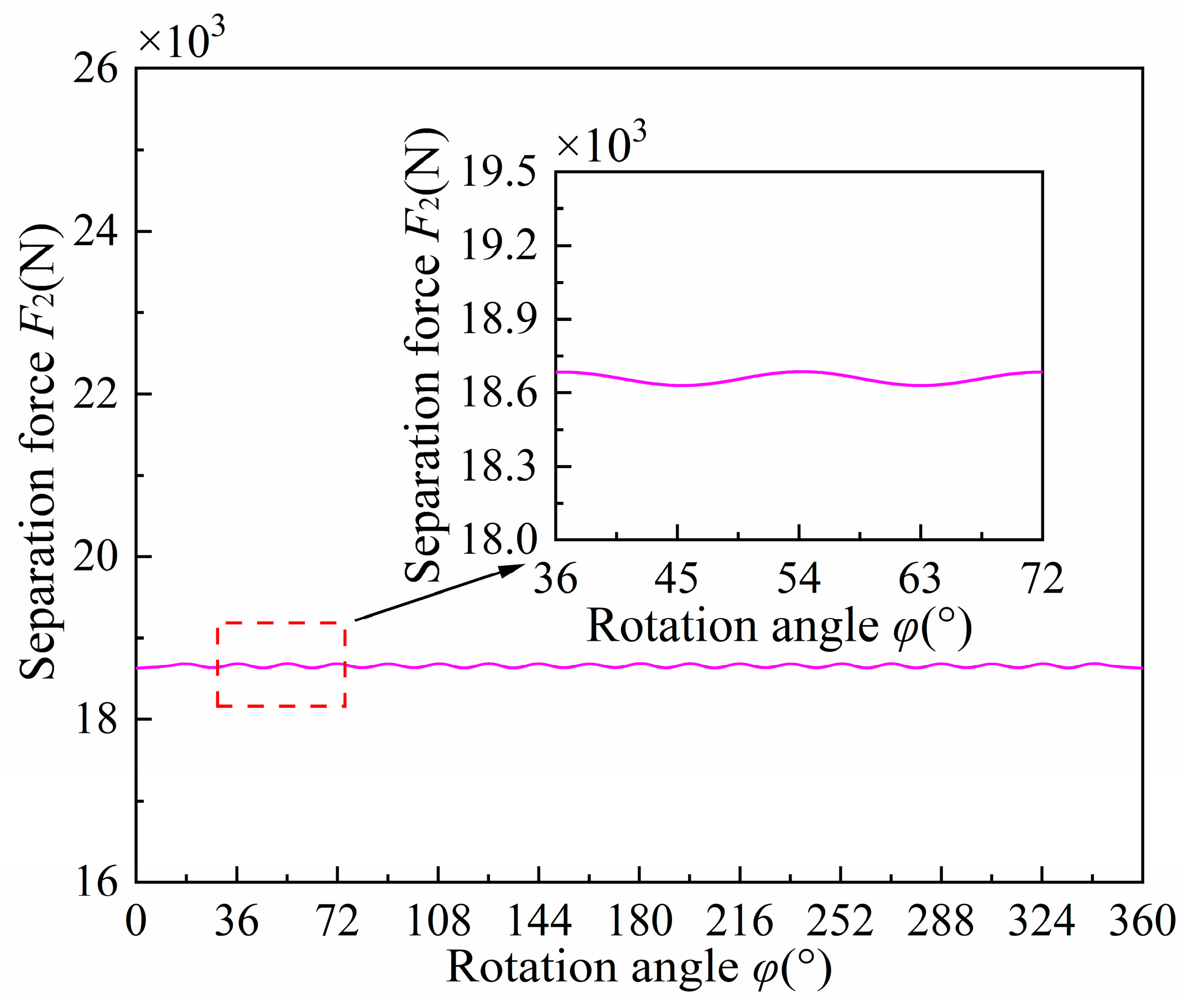
3.4. Separation Force of Oil Film

Based on Equation (4) and Table 1, the separation force of the oil film of the VPP can be obtained with the change rule of the cylinder block rotational angle, as shown in Figure 12. When the cylinder block rotational angle ${\phi }_i$ = 1/2${\phi }_x$, the separation force of the oil film reaches the maximum value; when the cylinder block rotational angle ${\phi }_i$ = 1/2${\phi }_x$, the separation force of the oil film has the minimum value; the separation force of the oil film circulates with 1/2 the action amplitude angle ${\phi }_x$ as a cycle period. From Equation (4), it can be seen that the oil film separation force of the VP is affected by the pressure envelope angle α, and the change in the separation force of the oil film seal is relatively smooth.

3.5. Thrust of Hydraulic Power

Based on Equation (5), the change rule of the hydraulic force on the VP with the cylinder block rotational angle can be obtained, as shown in Figure 13. When the cylinder block rotational angle ${\phi }_i$, the hydraulic thrust will appear with eight peaks and cycle with periodic angle $\Delta \phi$. When the cylinder block rotational angle ${\phi }_i$ = ${\Delta }_{\phi }$, the flow area of the VP is the smallest, and the hydraulic thrust reaches the maximum value; when the cylinder block rotational angle ${\phi }_i$ = 1/2$\Delta \phi$, the flow area of the VP is the largest, and the hydraulic thrust reaches the minimum value.

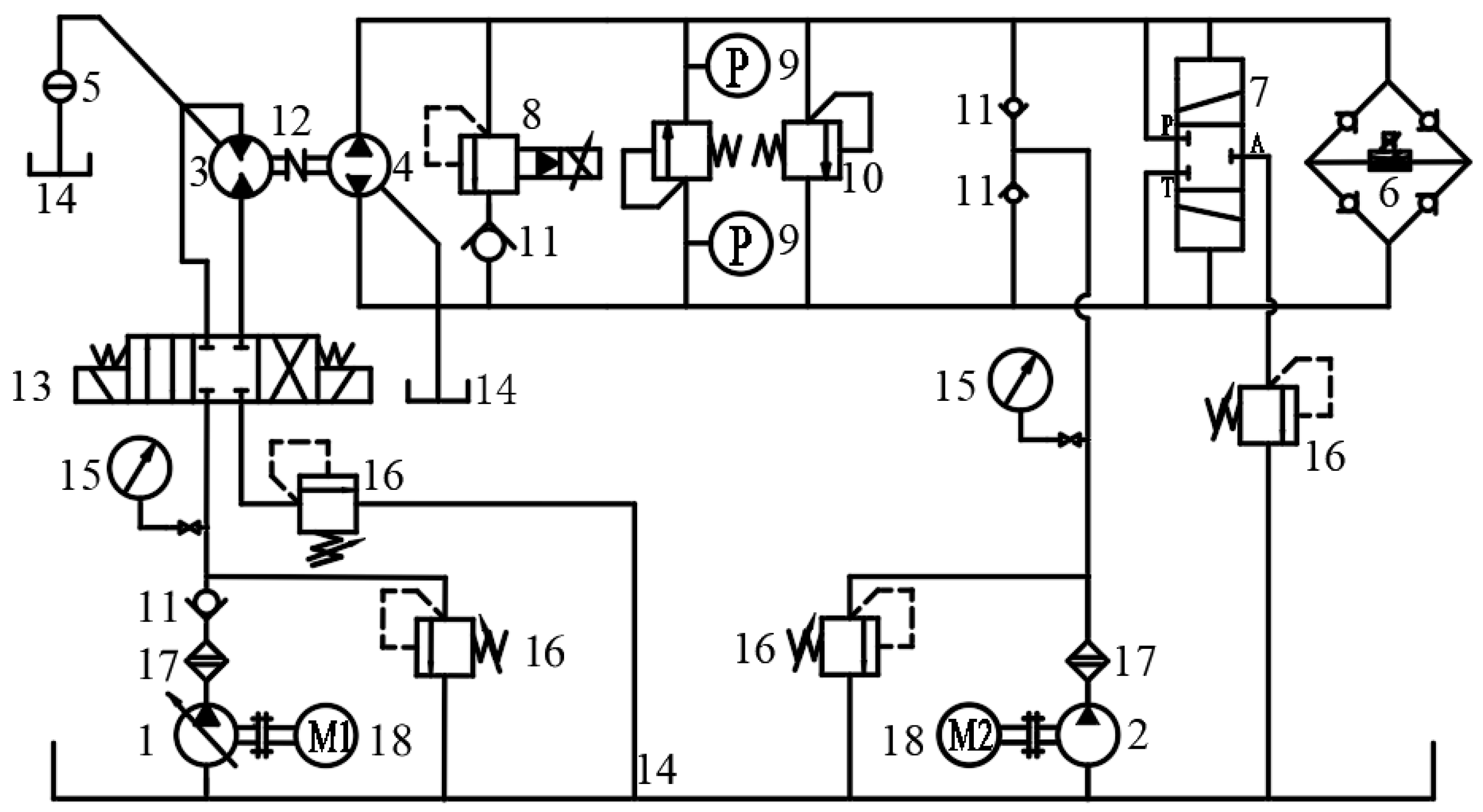
3.6. Leakage Test of VPP

3.6.1. Experimental Setup

To obtain the oil film thickness of the VPP, the internal leakage of the ICHM was calculated using an internal leakage test bench, and the thickness of the oil film was calculated, which can provide data support for the dynamic characteristic analysis of the VP, the principle of the internal leakage test bench of the ICHM is shown in Figure 14. The test system includes a drive unit, load pump, test motor, control system, and data acquisition unit. The electric motor drives the hydraulic pump to provide a pressure oil source, the pressure of the load pump is generated by the closed loop of the oil supply, and the rotational speed of the test motor can be controlled by adjusting the flow rate in the load loop. The pressure of the loop is controlled by adjusting the proportional relief valve, which plays the role of setting the working pressure of the test motor, and it can simulate the actual working conditions of the test motor. The test data were collected and recorded through the sensors so that the motor could be tested at different working pressures, oil temperatures, and operating pressures, as well as data acquisition units. It can simulate the actual working conditions of the test motor and collect and record the test data through each sensor so that the internal leakage under different working pressures, oil temperatures, and rotational speeds can be tested, and the thickness of the oil film of the VPP under different working conditions can be calculated. The test bench is illustrated in Figure 15. The main sensor parameters of the hydraulic system are shown in

Table 3. The main sensor used in the hydraulic system.

No.	Description	Parameters
1	Pressure sensor	PT5401, range 0–40 MPa, accuracy ± 0.05
2	Flowmeter	FGR200, range 0.05–7 L/min, accuracy 0.5%
3	Torque speed sensor	ZH07, range 20,000 N·m, 0–500 r/min
4	Temperature sensor	SBWZ-2460, range −50–150 °C, accuracy 0.2%
5	Pressure gauge	Range 0–40 MPa, accuracy 0.025%
6	PLC	SIMATIC S7-1200, Siemens, Munich, Germany

.

3.6.2. Test Results and Analysis

As shown in Figure 16, the leakage of the VPP of the ICHM under different working conditions was tested, and the thickness of the oil film was calculated. The results show that when the oil temperature is 40 °C and the rotational speed is 1 r/min, the influence of the inlet pressure on the oil film thickness is obvious, and the oil film thickness calculation results are shown in Figure 16a. When the inlet pressure is 4 MPa and the rotational speed is 1 r/min, the oil temperature is directly proportional to the oil film thickness of the VPP, and the influence of the oil temperature on the oil film thickness is smaller; the oil film thickness calculation results are shown in Figure 16b. However, in a previous study on hydraulic motors, under high-pressure and high-speed conditions, the thickness of the valve plate pair oil film decreased with an increase in the fluid temperature. When the inlet pressure was 24 MPa and the oil temperature was 40 °C, the change in the oil film thickness with an increase in the rotational speed was insignificant, and the oil film thickness calculation results are shown in Figure 16c. In summary, the inlet pressure has a large influence on the oil film thickness of the VPP, whereas the influence of the oil temperature and rotational speed is relatively small.

In the simulation of the dynamic characteristics of the VP, the average oil film thickness of the VPP was used as the initial oil film thickness, and the VP used the initial oil film thickness as the reference position. The VP was subjected to micro-motion owing to the pressing force, which changed the position of the VP and led to a change in the oil film thickness. Therefore, the initial film thickness of the VPP is a key factor in studying the dynamic characteristics of the VP.

4. Results and Discussion

By studying the dynamic characteristics of the VP, the micro-motion under the action of the inlet pressure of the VP, oil temperature, and rotational speed was analyzed. The dynamic displacement of the VP is expressed by the thickness of the oil film, and through the maximum displacement of the VP, the main factors causing the change in the pressing force of the VP are determined, and the influence on the surplus pressing force is analyzed to provide a theoretical basis for the study of the ‘floating’ variable surplus pressing force VP.

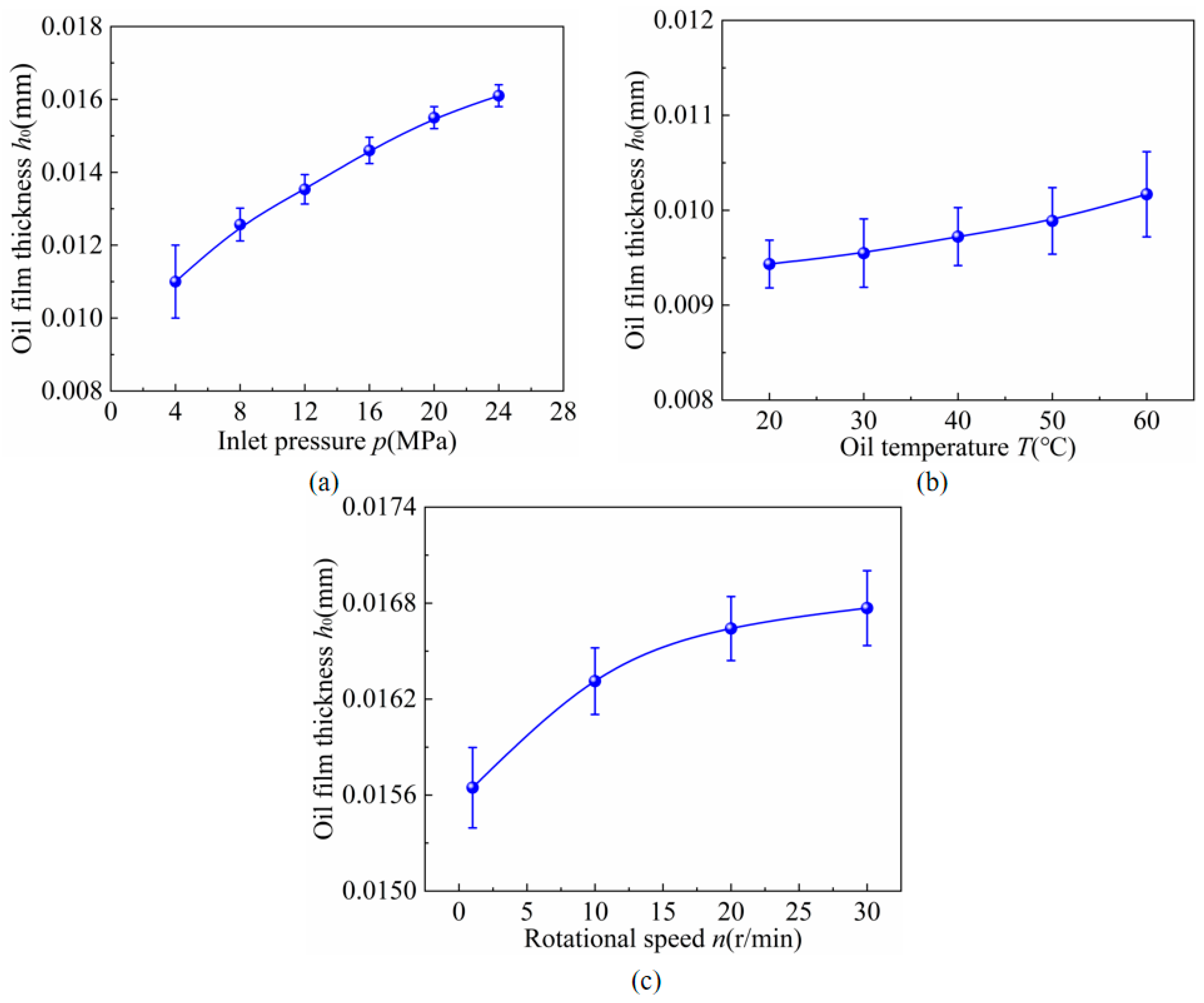
4.1. Thickness of the Oil Film of the VPP Under Different Working Conditions

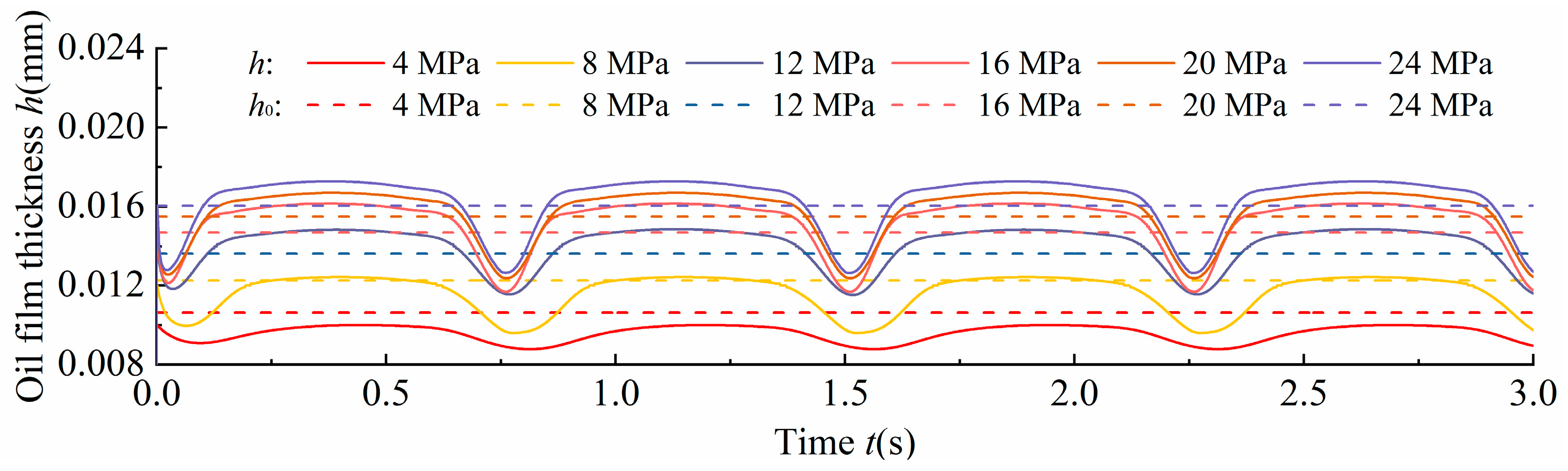
4.1.1. Oil Film Thickness at Different Inlet Pressures

As shown in Figure 17, the change in the oil film thickness of the VPP varies under different inlet pressures. When the oil temperature is 40 °C and the rotational speed is 1 r/min, the thickness of the oil film increases with the increase in the inlet pressure, and the pressing force of the VP reaches the maximum value and squeezes the oil film to make it thinner when the simulation time is n 0.75 s (the location at 0.75 s is the position of the period angle, and n is an integer). During the stage of constant pressing force, the oil film thickness also maintained a stable thickness. When the inlet pressure is lower than 8 MPa, the oil film thickness is lower than the initial oil film thickness, indicating that the pressing force acting on the VP is greater than the separation force of the oil film, and the oil film is continuously in the state of being squeezed. When the inlet pressure was higher than 8 MPa, the oil film thickness was higher than the initial oil film thickness at the stage of constant pressing force, indicating that the pressing force on the VP was smaller than the separation force of the oil film, resulting in the oil film becoming thicker. When the inlet pressure was 8 MPa, the oil film thickness was equal to the initial oil film thickness, which indicated that the valve plate was in a hydrostatic balance support condition, and the pressing force was balanced with the separation force. In conclusion, when the oil temperature and rotational speed are unchanged, with the increase in inlet pressure, the thickness change of the oil film is more obvious, and when the inlet pressure is 8 MPa, the stable oil film thickness is the same as that of the initial oil film thickness.

4.1.2. Oil Film Thickness at Different Oil Temperatures

As shown in Figure 18, the oil film thickness of the VPP changes under different oil temperatures. Under an inlet pressure of 4 MPa and rotational speed of 1 r/min, the oil film thickness was lower than the initial oil film thickness with an increase in oil temperature, and the vibration VPP of oil film thickness was also larger. This is because the pressing force generated by the VP is greater than the separation force of the oil film, resulting in the oil film being squeezed. When the oil temperature increased and the oil viscosity decreased, the flow rate of the oil film increased, and the oil film was squeezed and thinned. In addition, the lower the oil temperature, the more the position of the minimum film thickness lagged. This is because the lower the oil temperature, the greater the oil viscosity, the stronger the damping effect, and the slower the oil film on the pressing force of the squeeze response. In conclusion, when the inlet pressure and rotational speed are constant, as the oil temperature increases, the more obvious amplitude of the film thickness, and the stable thickness of the film is maintained for a shorter duration.

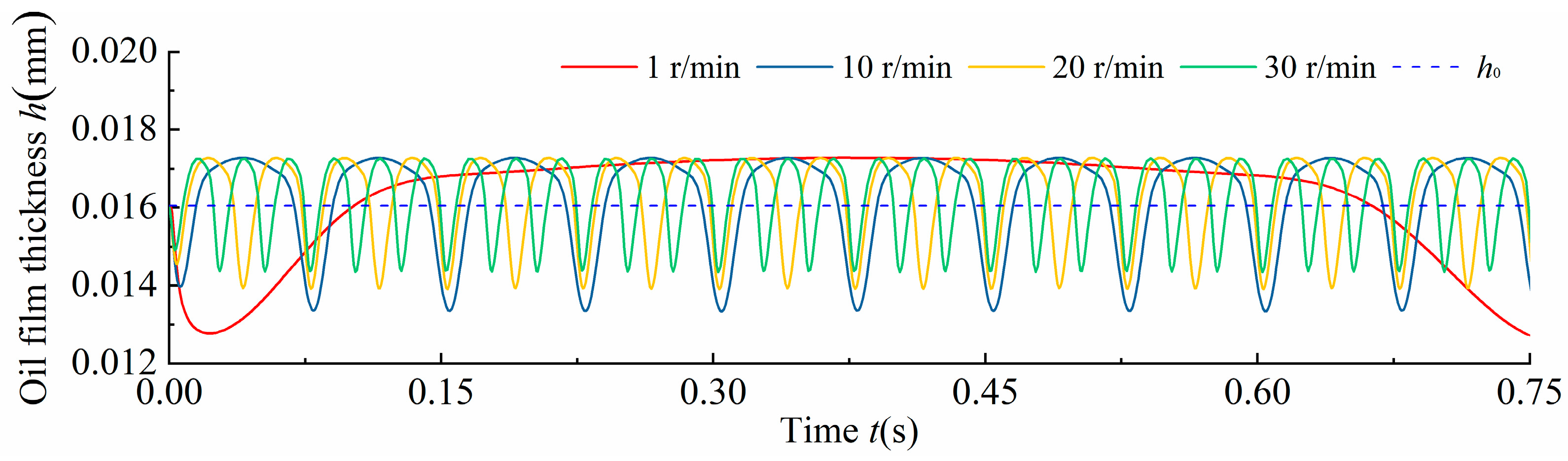
4.1.3. Oil Film Thickness at Different Rotational Speeds

In Figure 19 we present the change rule of the oil film thickness of the VPP under different rotational speeds. Under the conditions of an inlet pressure of 24 MPa and oil temperature of 40 °C, with an increase in rotational speed, the maximum thickness of the oil film remained unchanged, whereas the minimum thickness of the oil film gradually decreased. This is because, when the inlet pressure is certain, the pressing force of the VP and the separation force of the oil film remain relatively constant. When the rotational speed is low, the pressing force acts on the VP for a longer time, resulting in more oil being squeezed out between the VPP, and the displacement of the VP is larger, which reduces the thickness of the oil film. In contrast, when the rotational speed is increased, the pressing force acts on the VP for a shorter period, and the pressing and separating forces tend to be in dynamic balance. The amount of oil being squeezed out is also lower, and the thickness of the oil film is relatively stable.

In summary, under different inlet pressures, the initial oil film thickness of the VPP is different, and with an increase in the inlet pressure, the oil film thickness of the VPP also increases. When the inlet pressure reached 8 MPa and the pressing force was in the stable stage, the thickness of the oil film of the VPP was the same as the initial oil film thickness. When the oil temperature increased, the response time of the oil film squeezing effect advanced, and the oil film thickness was smaller. When the rotational speed was increased, the frequency of the squeezing effect of the oil film increased, and the amplitude of the oil film thickness decreased. The shorter the time the oil film is squeezed, the smoother the change in the oil film thickness.

4.2. Characteristics of the Maximum Displacement of the VP Under Different Working Conditions

4.2.1. Characteristics of the Maximum Displacement of the VP at Different Inlet Pressures

The maximum displacement characteristics of the VP at six inlet pressures when the ICHM was at an oil temperature of 40 °C and a rotational speed of 1 r/min are shown in Figure 20. As the inlet pressure increases, the maximum upward displacement of the VP y(+) (the increase in the VP at the position of the initial film thickness +Δy, which indicates that the film thickness will become thicker) and the maximum downward displacement of the VP y(−) (the decrease in the VP at the position of the initial film thickness −Δy, which indicates that the film thickness will be squeezed and thinned) is increased. When the inlet pressure was lower than 8 MPa, the y(+) value was 0, indicating that the VP was always close to the cylinder block, and the oil film of the VPP oil film was continuously squeezed by the pressing force. When the inlet pressure was higher than 8 MPa, the y(+) value gradually increased, indicating that the oil film of the VP would thicken at the minimum pressing force. In conclusion, under conditions of constant oil temperature and rotational speed, as the inlet pressure increases, the y(+) and y(−) values of the VP increase. When the inlet pressure was lower than 8 MPa, the VP squeezed the oil film. When the inlet pressure was higher than 8 MPa, the VP had an insufficient pressing force, which led to the thickening of the oil film.

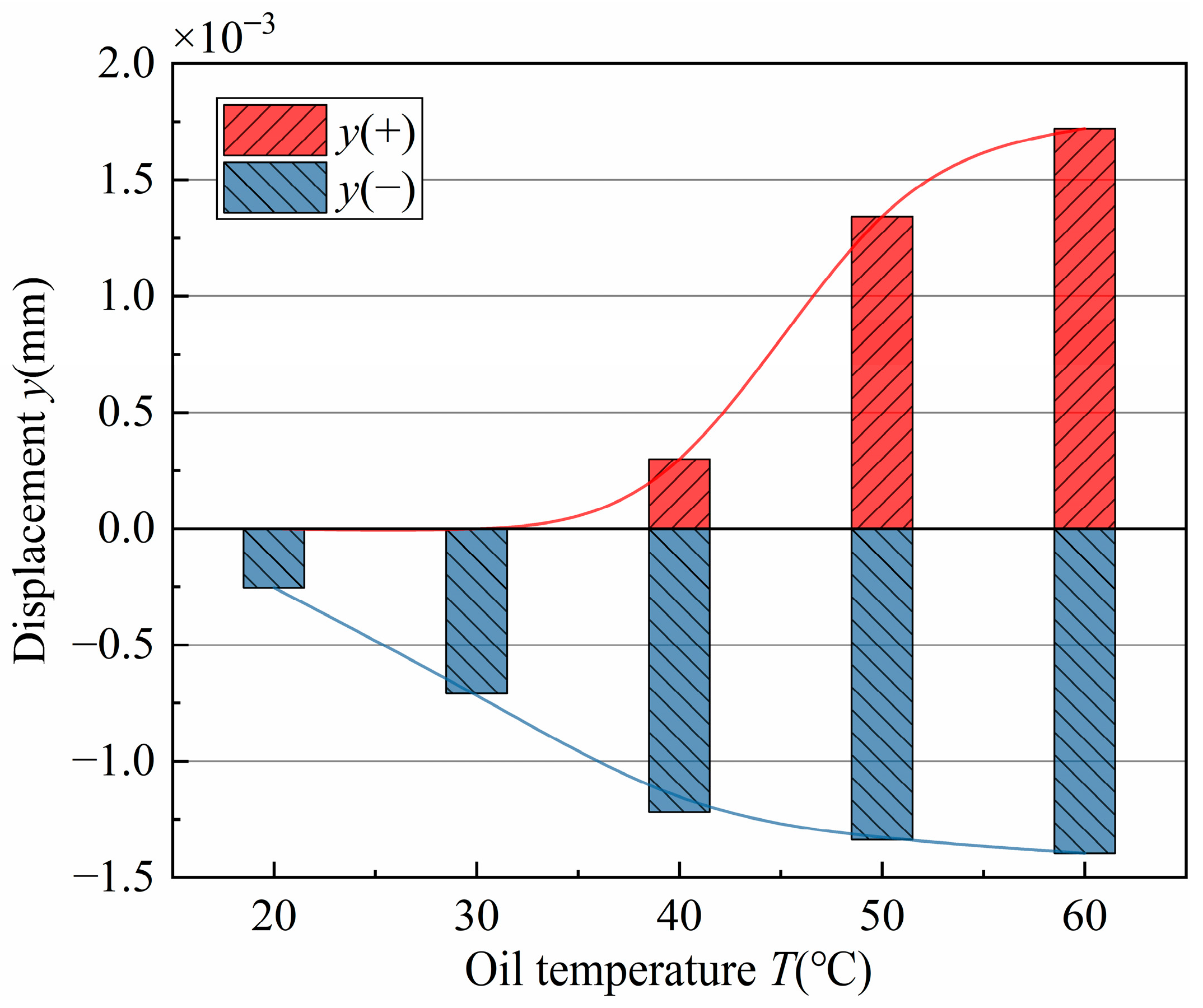
4.2.2. Characteristics of the Maximum Displacement of the VP at Different Oil Temperatures

The maximum displacement characteristics of the VP at five oil temperatures when the inlet pressure of the ICHM was 4 MPa and the rotational speed was 1 r/min are shown in Figure 21. When the oil temperature is 20–30 °C, the y(+) value is very small, which is due to the lower oil temperature, resulting in a larger oil viscosity, a larger damping effect of the oil film, and a weaker tendency of the movement of the VP. When the oil temperature is 40–60 °C, the y(+) value increases because the increase in oil temperature causes the oil viscosity to decrease, the fluidity of the oil is enhanced, and the damping effect of the oil film is reduced, which enhances the motion tendency of the VP. With the increase in oil temperature, the y(−) value will also increase, because under the action of pressing force, which will lead to an increase in the displacement of the VP. In conclusion, when the inlet pressure and rotational speed are unchanged, the amplitude of the thickness of the oil film increases; in the oil temperature range of 20–30 °C, the VP has only a squeezing effect on the oil film.

4.2.3. Characteristics of the Maximum Displacement of the VP at Different Rotational Speeds

The maximum displacement characteristics of the VP at four rotational speeds when the inlet pressure of the ICHM was 24 MPa and the oil temperature was 40 °C are shown in Figure 22. As the rotational speed increased, the y(+) value remained constant, indicating that the rotational speed did not obviously affect the pressing force generated by the VP. With the increase in rotational speed, the y(−) value decreases gradually, which is due to the following reasons: when the rotational speed is lower, the pressing force acts on the oil film for a longer time, resulting in more volume of the oil film being squeezed out, and the displacement of the VP increases accordingly; when the rotational speed increases, the pressing force acts on the oil film for a shorter period, and thus the displacement of the VP is smaller. In conclusion, at a certain inlet pressure and oil temperature, the rotational speed has less influence on the surplus pressing force of the VP, and an increase in the rotational speed reduces the displacement of the VP.

In summary, with an increase in the inlet pressure, the amplitude of the oil film thickness of the VPP increases, and when the inlet pressure is less than 8 MPa, the surplus pressing force of the VP squeezes the oil film. When the oil temperature is lower than 30 °C, the displacement of the oil film squeezed by the surplus pressing force of the VP is small. When the oil temperature increased, the amplitude of the oil film thickness also increased. When the rotational speed increased, the change in the surplus pressing force was less, the displacement of the VP decreased, and the effect of the rotational speed on the surplus pressing force of the VP was not obvious. Therefore, when the inlet pressure of the motor is smaller, the oil temperature is lower, and the rotational speed is slower, the VP will have excess pressing force, and the thickness of the oil film will become thinner, which is not conducive to full lubrication of the oil film of the VPP. In contrast, when the inlet pressure of the motor is larger, the oil temperature is higher, and the rotational speed is faster, the VP will have insufficient pressing force, the thickness of the oil film will increase, and the VPP will increase the amount of leakage.

4.3. Surplus Pressing Force of ‘Floating’ VP for the ICHM

From the change rule of oil film thickness and the maximum displacement characteristics of the VPP under different working conditions, it can be seen that there will be a hydrostatic support imbalance phenomenon of the VP under different working conditions. Compared with the oil temperature and rotational speed, the inlet pressure had the most significant influence on the oil film thickness and displacement of the VP. The inlet pressure is not only the main factor that causes the hydrostatic imbalance but also the key parameter of the VP design. The oil temperature and rotational speed, on the other hand, are secondary factors and have no obvious influence on the surplus pressing force. Therefore, considering the inlet pressure as the main research parameter, the coefficient of surplus pressing force defines the state of hydrostatic balance support of the VP, which can reveal the reasons for the hydrostatic support imbalance of the ‘floating’ VP of the ICHM.

As shown in Figure 23, when the inlet pressure was 8.7 MPa, the VP was in a state of hydrostatic balance support, which was also the balance point of hydrostatic support. At this time, the oil film of the VPP is also in the range of the ideal thickness, and the volumetric efficiency of the motor and mechanical efficiency will reach the best degree of cooperation. When the inlet pressure is higher than 8.7 MPa, there is an insufficient pressing force of the VP, and the surplus pressing force coefficient decreases with an increase in pressure, which leads to an increase in leakage of VPP and a decrease in sealing. When the inlet pressure is lower than 8.7 MPa, the VP will exhibit excess pressing force, and the surplus pressing force coefficient will increase with the decrease in inlet pressure, which will lead to the oil film being over squeezed, resulting in increased wear of the VP, and the lubrication of the VPP decreases. In short, the surplus pressing force coefficient of the ICHM ‘floating’ VP becomes larger with the decrease in inlet pressure.

5. Conclusions

In this study, the dynamic characteristics of the ‘floating’ valve plate of an internal curve hydraulic motor were studied. Based on the leakage test of the valve plate pair of the internal curve hydraulic motor and the principle of hydrostatic balance of the valve plate, a transient simulation model of the flow field in the balance chamber of the internal curve hydraulic motor and a dynamic characteristics model of the valve plate were developed. Through the model analysis, the change rule of the oil film thickness of the valve plate pair and the maximum displacement characteristics of the valve plate under different working conditions were described, and the change rule of the surplus pressing force coefficient of the valve plate under different inlet pressures was analyzed. The following conclusions were drawn.

• As the inlet pressure increased, the thickness of the oil film on the valve plate pair increased. At the cylinder block rotational angle $\Delta \phi$ (periodic angle), the oil film is squeezed, and the oil film thickness is minimal. The higher the oil temperature, the larger the amplitude of the film thickness, and the more obvious the response of the valve plate to squeezing the film. With an increase in the rotational speed, the amplitude of the oil film thickness decreased, and the change in the oil film thickness was not obvious.
• When the inlet pressure is lower than 8 MPa, the valve plate squeezes the oil film; when the inlet pressure is more than 8 MPa, the thickness of the oil film of the valve plate pair increases. In the oil temperature range of 20–30 °C, the valve plate produced a squeezing effect on the oil film, resulting in a decrease in the thickness of the oil film. An increase in the rotational speed reduces the squeezing effect of the valve plate on the oil film, and the displacement of the valve plate is inversely proportional to the rotational speed.
• When the inlet pressure was 8.7 MPa, the valve plate was in a hydrostatic balance support state. When the inlet pressure exceeded 8.7 MPa, the surplus pressing force of the valve plate was insufficient. When the inlet pressure was lower than 8.7 MPa, the surplus pressing force of the valve plate was excessive. The coefficient of the surplus pressing force of the valve plate decreased with increasing inlet pressure.

In summary, this study adopted a combination of experimental and numerical calculation methods to study the dynamic characteristics of the ‘floating’ valve plate of internal curve hydraulic motors and analyzed the trend of the surplus pressing force coefficient of the valve plate. This will provide theoretical support for improving the adaptability of the valve plate and designing a variable pressing force valve plate.