Investigating Resulting Surface Topography and Residual Stresses in Bending DC01 Sheet Under Tension Friction Test
Abstract
1. Introduction
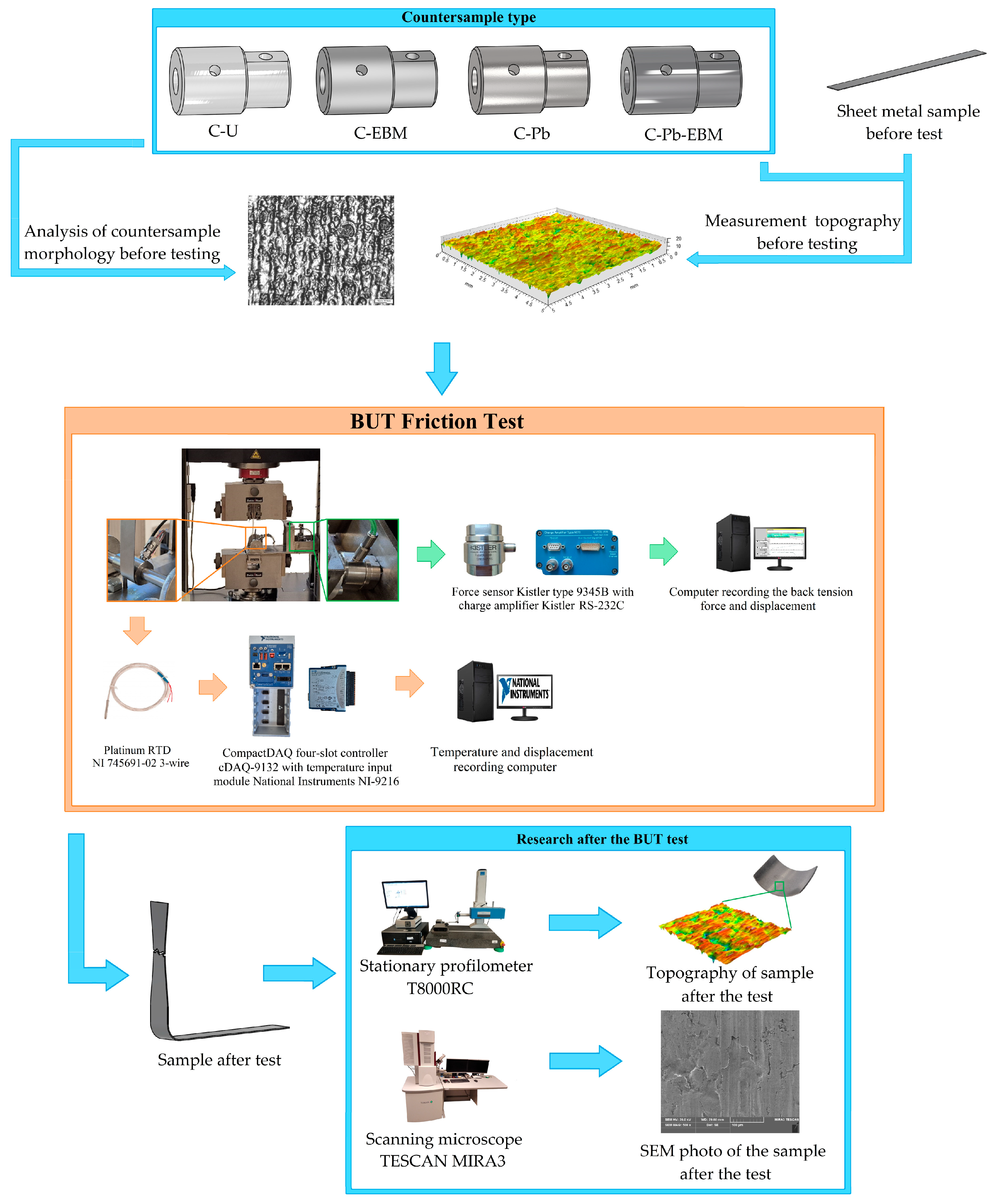
2. Materials and Methods
2.1. Material
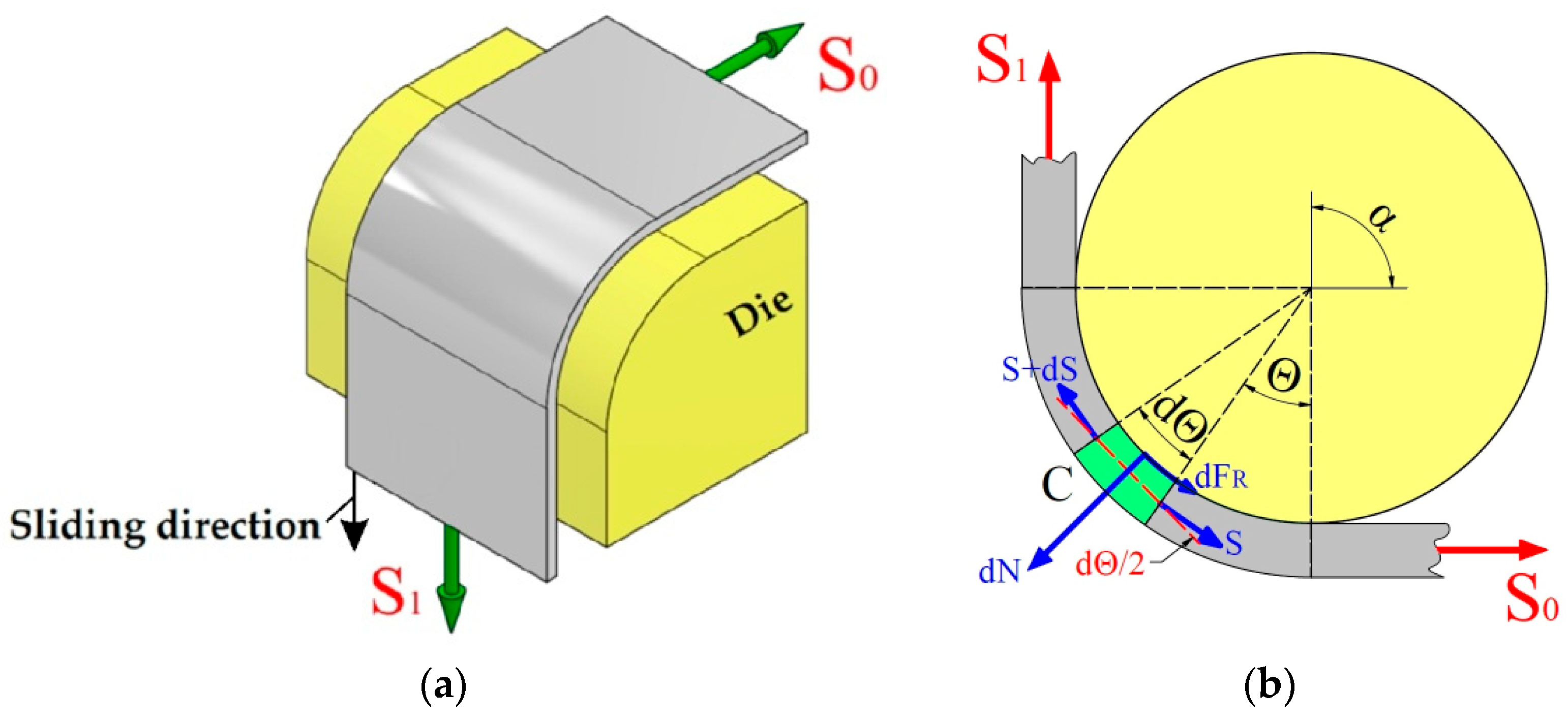
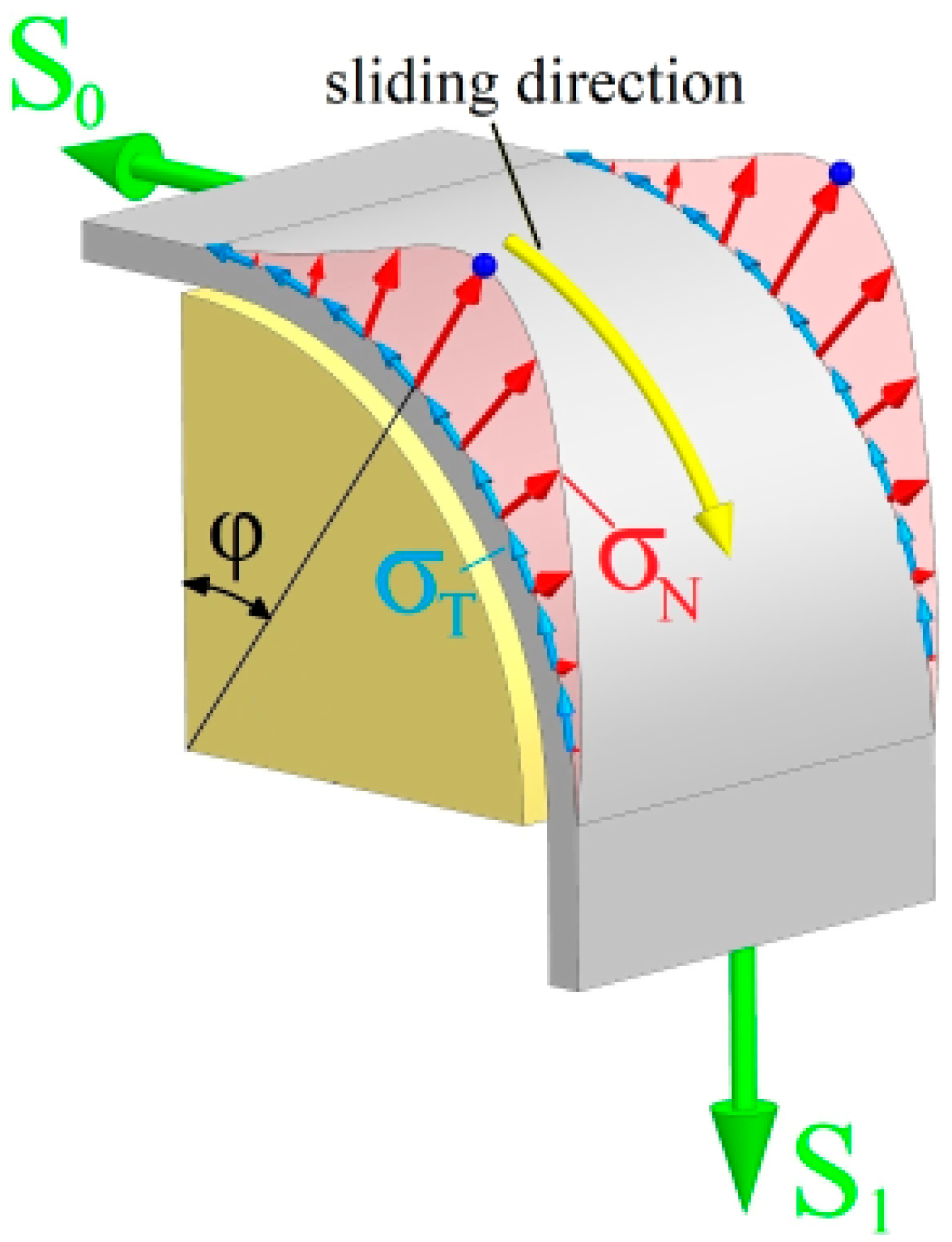
2.2. Determination of the CoF
2.3. Preparation and Characterisation of Countersamples
2.3.1. Modification of the Surface Layer of Countersamples
- (1)
- The ion implantation of lead;
- (2)
- The ion implantation of lead and pulse electron annealing;
- (3)
- The pulse electron annealing.
- -
- The implanted fluence/dose of Pb ions: 6.3·1017 cm−2 for each implanted side;
- -
- The current of the ion beam: 100 mA;
- -
- The acceleration voltage: 60 kV;
- -
- The pulse duration (FWHM): 400 µs;
- -
- The pulse frequency: 10 Hz;
- -
- The maximum measured temperature: below 120 °C.
- -
- Working gas: Ar of 99.999% purity;
- -
- Number of pulses: 1 for each annealed side;
- -
- Pulse duration: 2 µs;
- -
- Acceleration voltage in peak/electron energy: 25 kV/25 keV;
- -
- Pulse energy density: in the range from 2.27 to 3.34 J/cm2.
2.3.2. Modelling of Ion Implantation and Electron Introduction
2.3.3. Surface Topography of Countersamples
3. Results
3.1. CoF
3.2. Temperature in Contact Zone
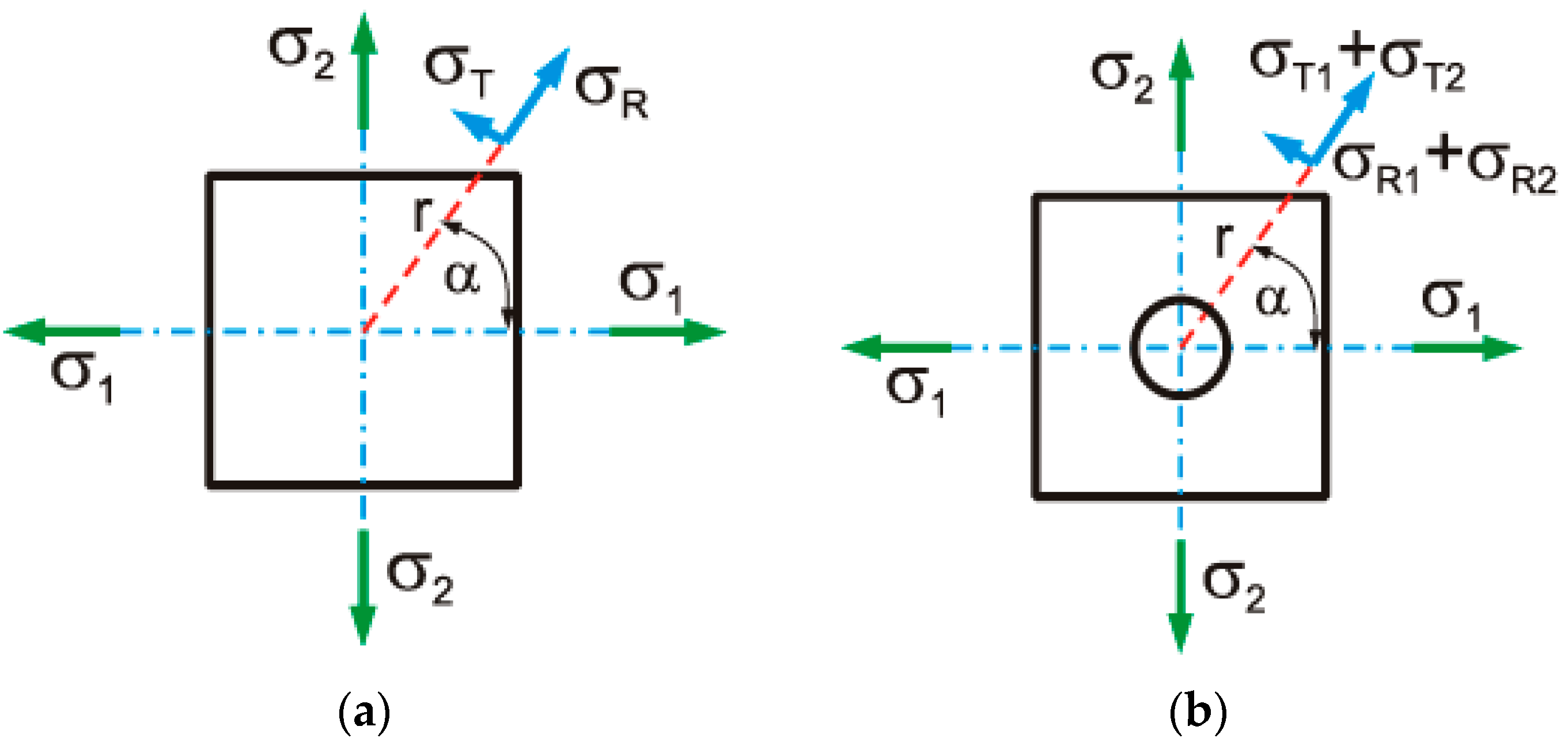
3.3. Residual Stress
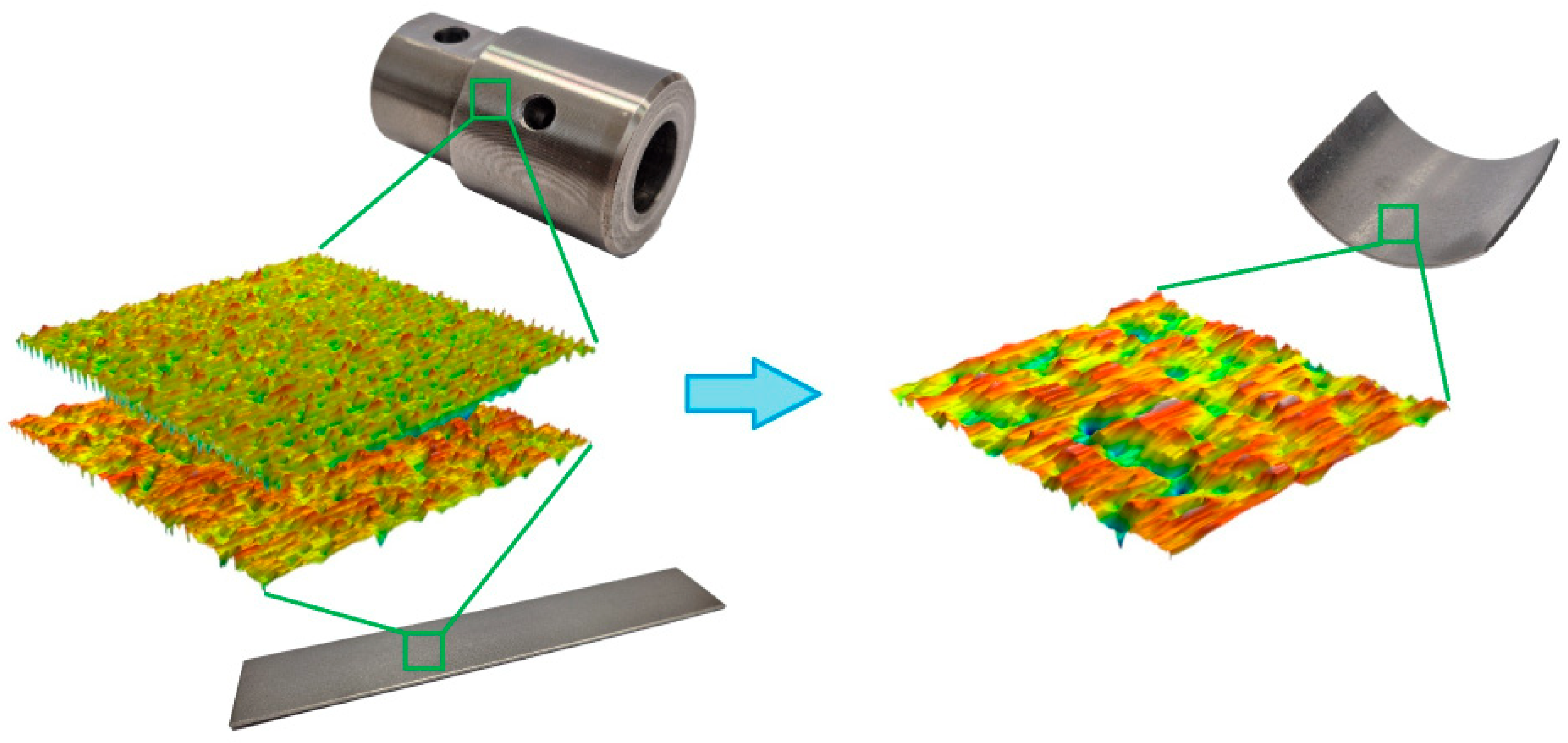
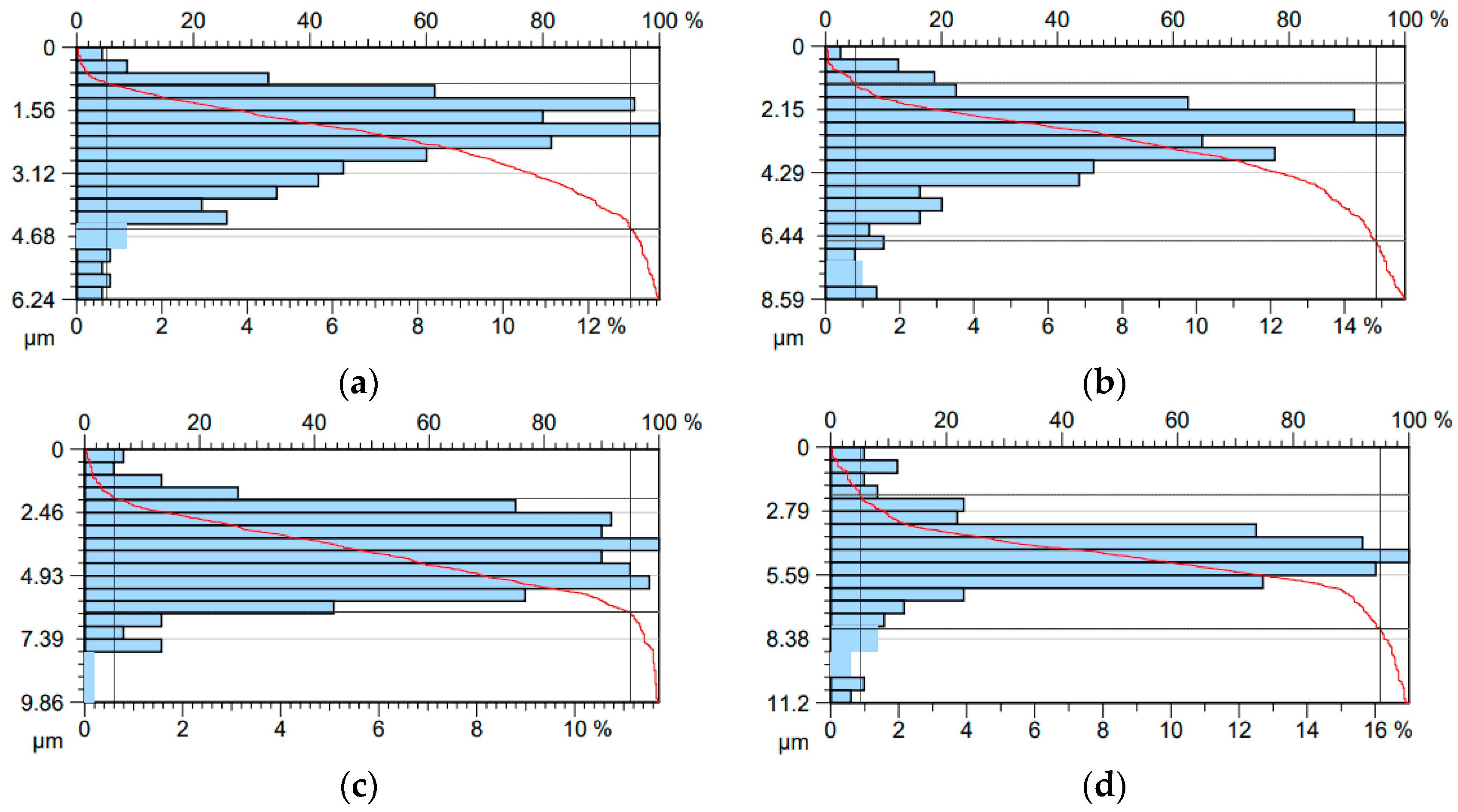
3.4. Friction-Induced Change in Surface Topography of Samples
4. Conclusions
- A significant increase in the CoF was observed with the elongation of the samples between 0% and about 6% for all the analysed types of countersamples. After exceeding this strain value, the value of the CoF stabilises. The maximum value of the CoF, about 0.31, was found for the C-EBM and C-U countersamples. For the remaining countersamples, the value of the COF was about 0.27.
- Due to the limited sample elongations to fracture in the BUT test, the recorded temperature increase was between 0.34 °C (DC01/C-Pb friction pair) and 0.58 °C (DC01/C-EBM friction pair). The increase in the surface temperature of the countersample was related to the phenomenon of external friction and the transfer of heat generated through internal friction.
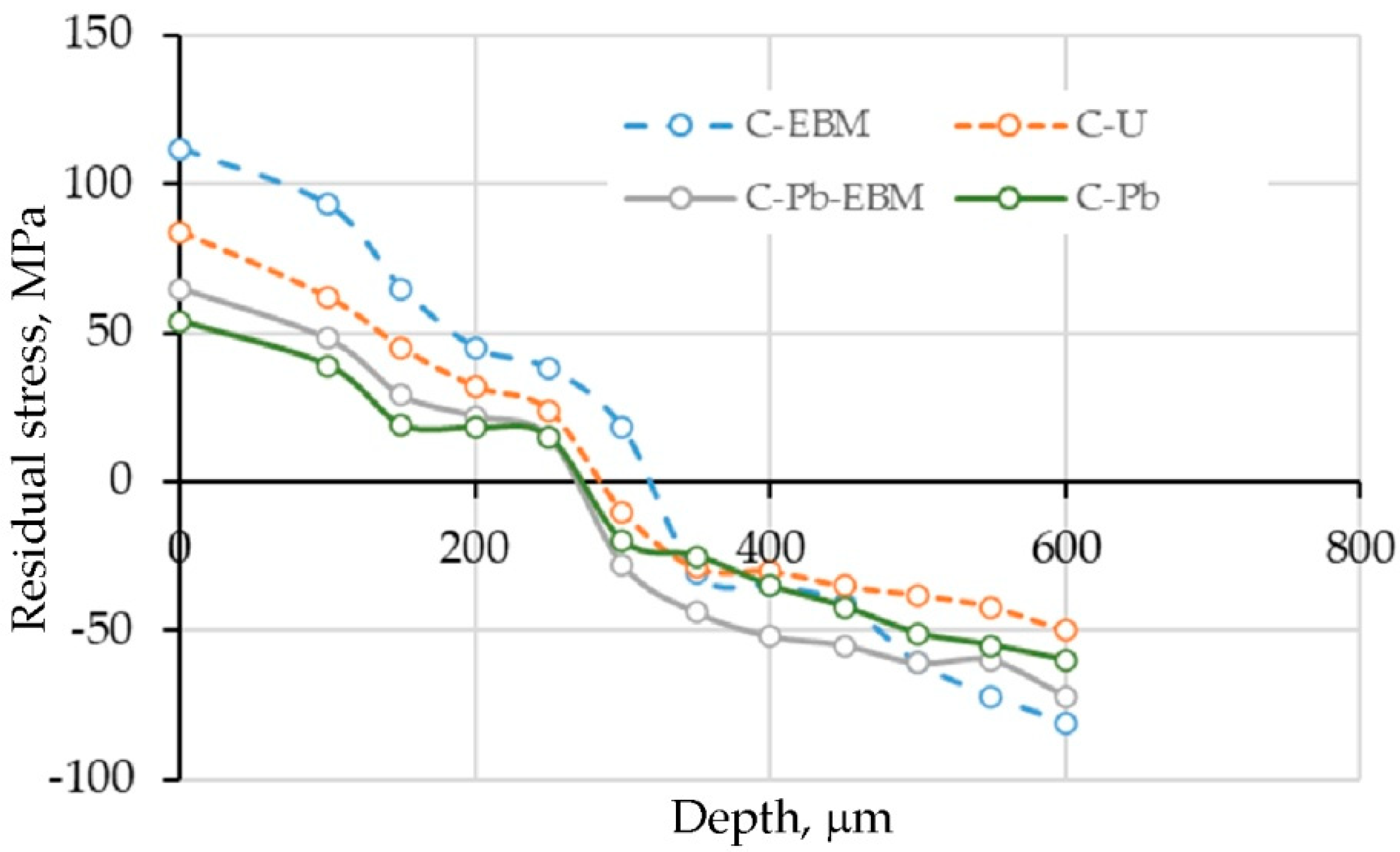
- For all the analysed friction pairs, the occurrence of residual tensile stresses was observed near the contact surface of the sheet strip with the countersample. These stresses amounted to between 55 MPa (DC01/C-Pb friction pair) and 112 MPa (DC01/C-EBM friction pair). With the increase in the considered depth of residual stress measurement, the residual tensile stresses were transformed into compressive stresses with a value between −75 and −50 MPa, depending on the type of friction pair. It was observed that the residual stresses depend on the CoF. The higher the CoF value, the higher the value of residual tensile stresses in the subsurface layer.
- Analysis using SEM allowed us to identify adhesion and abrasive wear as the main mechanisms of surface topography change of the sheets as a result of the friction process. High contact pressures and strain-induced change of surface topography of the sheets cooperating with all analysed types of countersamples led to an intensive flattening of the surface asperities of the sheet strips. The friction process caused a decrease in the parameters Sa, Sq, and Sp in relation to the base sheet metal.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luiz, V.D.; Rodrigues, P.C.M. Design of a tribo-simulator for investigation of the tribological behavior of stainless-steel sheets under different contact conditions. Mater. Res. 2022, 25, e20210220. [Google Scholar] [CrossRef]
- Trzepiecinski, T.; Lemu, H.G. Recent developments and trends in the friction testing for conventional sheet metal forming and incremental sheet forming. Metals 2020, 10, 47. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Szwajka, K.; Szewczyk, M.; Zielińska-Szwajka, J.; Slota, J.; Kaščák, Ľ. The Effect of the addition of silicon dioxide particles on the tribological performance of vegetable oils in HCT600X+Z/145Cr46 steel contacts in the deep-drawing process. Materials 2025, 18, 73. [Google Scholar] [CrossRef]
- Slota, J.; Kaščák, Ľ.; Lăzărescu, L. Frictional characteristics of EN AW-6082 aluminium alloy sheets used in metal forming. Adv. Mech. Mater. Eng. 2024, 41, 79–87. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Najm, S.M.; Ibrahim, O.M.; Kowalik, M. Analysis of the frictional performance of AW-5251 aluminium alloy sheets using the random forest machine learning algorithm and multilayer perceptron. Materials 2023, 16, 5207. [Google Scholar] [CrossRef]
- Sigvant, M.; Pilthammar, J.; Hol, J.; Wiebenga, J.H.; Chezan, T.; Carleer, B.; van den Boogaard, T. Friction in sheet metal forming: Influence of surface roughness and strain rate on sheet metal forming simulation results. Procedia Manuf. 2019, 29, 512–519. [Google Scholar] [CrossRef]
- Szewczyk, M.; Mezher, M.T.; Jaber, T.A. The use of artificial neural networks to the analysis of lubricating performance of vegetable oils for plastic working applications. Adv. Mech. Mater. Eng. 2025, 42, 5–15. [Google Scholar] [CrossRef]
- Nielsen, C.V.; Bay, N. Overview of friction modelling in metal forming processes. Procedia Eng. 2017, 207, 2257–2262. [Google Scholar] [CrossRef]
- Fum, X.J.; Li, J.J.; Liu, Q. Friction behavior under different forming speed for sheet metal forming. Adv. Mater. Res. 2012, 472–475, 662–665. [Google Scholar] [CrossRef]
- Dohda, K.; Boher, C.; Rezai-Aria, F.; Mahayotsanun, N. Tribology in metal forming at elevated temperatures. Friction 2015, 3, 1–27. [Google Scholar] [CrossRef]
- Luiz, V.D.; Santos, A.J.d.; Câmara, M.A.; Rodrigues, P.C.d.M. Influence of different contact conditions on friction properties of AISI 430 steel sheet with deep drawing quality. Coatings 2023, 13, 771. [Google Scholar] [CrossRef]
- Barros, T.H.C.; Gonzaga, I.A.D.; Neto, A.S.; Amaral, E.C.; Gonçalves, K.A.M.B.; de Matos Rodrigues, P.C.; Luiz, V.D. Influence of multi-pass forming on the tribological performance of AISI 430 steel sheet in deep drawing process. Adv. Mech. Mater. Eng. 2025, 42, 59–69. [Google Scholar] [CrossRef]
- Zwicker, M.F.R.; Bay, N.; Nielsen, C.V. A new test for sheet metal asperity flattening under varying subsurface strain conditions. Tribol. Int. 2023, 180, 108249. [Google Scholar] [CrossRef]
- Hol, J.; Cid Alfaro, M.V.; de Rooij, M.B.; Meinders, T. Advanced friction modeling for sheet metal forming. Wear 2012, 286–287, 66–78. [Google Scholar] [CrossRef]
- Peng, L.F.; Mao, M.Y.; Fu, M.W.; Lai, X.M. Effect of grain size on the adhesive and ploughing friction behaviours of polycrystalline metals in forming process. Int. J. Mech. Sci. 2016, 117, 197–209. [Google Scholar] [CrossRef]
- Pujante, J.; Pelcastre, L.; Vilascena, M.; Casellas, D.; Prakash, B. Investigations into wear and galling mechanism of aluminium alloy-tool steel tribopair at different temperatures. Wear 2013, 308, 193–198. [Google Scholar] [CrossRef]
- Hanson, M. On Adhesion and Galling in Metal Forming; Uppsala Universitet: Uppsala, Sweden, 2008; Available online: https://www.diva-portal.org/smash/get/diva2:171318/FULLTEXT01.pdf (accessed on 1 April 2024).
- Trzepieciński, T.; Szwajka, K.; Szewczyk, M.; Zielińska-Szwajka, J.; Barlak, M.; Nowakowska-Langier, K.; Okrasa, S. Analysis of influence of coating type on friction behaviour and surface topography of DC04/1.0338 steel sheet in bending under tension friction test. Materials 2024, 17, 5650. [Google Scholar] [CrossRef]
- Folle, L.; Schaeffer, L. New proposal to calculate the friction in sheet metal forming through bending under tension test. Mater. Res. 2019, 22, e20190523. [Google Scholar] [CrossRef]
- Wu, Y.; Recklin, V.; Groche, P. Strain induced surface change in sheet metal forming: Numerical prediction, influence on friction and tool wear. J. Manuf. Mater. Process. 2021, 5, 29. [Google Scholar] [CrossRef]
- Simon, N.; Erdle, H.; Walzer, S.; Gimbeier, J.; Böhlke, T.; Liewald, M. Residual stresses in deep-drawn cups made of duplex stainless steel X2CrNiN23-4. Forscung Im Ingenieurwesen 2021, 85, 795–806. [Google Scholar] [CrossRef]
- Mousavi, A.; Brosius, A. Improving the springback behavior of deep drawn parts by macro-structured tools. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012105. [Google Scholar] [CrossRef]
- Kubiak, K.J.; Liskiewicz, T.W.; Mathia, T.G. Surface morphology in engineering applications: Influence of roughness on sliding and wear in dry fretting. Tribol. Int. 2011, 44, 1427–1432. [Google Scholar] [CrossRef]
- Littlewood, M.; Wallace, J.F. Effect of surface finish and lubrication on frictional variations involved in sheet-metal-forming process Sheet Met. Ind. 1964, 41, 925–930. [Google Scholar]
- Wilson, W.R.D.; Malkani, H.G.; Saha, P.K. Boundary friction measurements using a new sheet metal forming simulator. Trans. NAMRI/SME 1991, 18, 37–42. [Google Scholar]
- Saha, P.K.; Wilson, W.R.D. Influence of plastic strain on friction in sheet metal forming. Wear 1994, 172, 167–173. [Google Scholar] [CrossRef]
- Nanayakkara, N.K.B.M.P.; Kelly, G.; Hodgson, P. Application of bending under tension test to determine the effect of tool radius and the contact pressure on the coefficient of friction in sheet metal forming. Mater. Forum 2005, 29, 114–118. [Google Scholar]
- Fratini, L.; Lo Casto, S.; Lo Valvo, E. A technical note on an experimental device to measure friction coefficient in sheet metal forming. J. Mater. Process. Technol. 2006, 172, 16–21. [Google Scholar] [CrossRef]
- Berglund, J.; Brown, C.A.; Rosén, B.G.; Bay, N. Milled die steel surface roughness correlation with steel sheet friction. CIRP Ann.—Manuf. Technol. 2010, 59, 577–580. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Szwajka, K.; Szewczyk, M.; Barlak, M.; Zielińska-Szwajka, J. Effect of countersample coatings on the friction behaviour of DC01 steel sheets in bending-under-tension friction tests. Materials 2024, 17, 3631. [Google Scholar] [CrossRef]
- Folle, L.F.; Schaeffer, L. Evaluation of contact pressure in bending under tension test by a pressure sensitive film. J. Surf. Eng. Mater. Adv. Technol. 2016, 6, 201–214. [Google Scholar] [CrossRef][Green Version]
- Nielsen, C.V.; Legarth, B.N.; Niordson, C.F.; Bay, N. A correction to the analysis of bending under tension tests. Tribol. Int. 2022, 173, 107625. [Google Scholar] [CrossRef]
- EN 10130:2009; Cold Rolled Low Carbon Steel Flat Products for Cold Forming—Technical Delivery Conditions. British Standards Institution: London, UK, 2009.
- ISO 6892-1:2020; Metallic Materials—Tensile Testing-Part 1: Method of Test at Room Temperature. Beuth-Verlag: Berlin, Germany, 2020.
- EN ISO 25178-2:2022; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. International Organization for Standardization: Geneva, Switzerland, 2022.
- EN ISO 16610-21:2013; Geometrical Product Specifications (GPS)—Filtration—Part 21: Linear Profile Filters: Gaussian Filters. International Organization for Standardization: Geneva, Switzerland, 2012.
- EN ISO 13565-2:1999; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method, Surfaces Having Stratified Functional Properties—Part 2: Height Characterization Using the Linear Material Ratio Curve. International Organization for Standardization: Geneva, Switzerland, 1996.
- Betlej, I.; Barlak, M.; Krajewski, K.; Andres, B.; Werner, Z.; Jankowska, A.; Zakaria, S.; Boruszewski, P. Effect of Cu, Zn and Ag ion implantation on the surface modification of bacterial cellulose films. Coatings 2023, 13, 254. [Google Scholar] [CrossRef]
- Barlak, M.; Wilkowski, J.; Szymanowski, K.; Czarniak, P.; Podziewski, P.; Werner, Z.; Zagórski, K.; Staszkiewicz, B. Influence of the ion implantation of nitrogen and selected metals on the lifetime of WC-Co indexable knives during MDF machining. Ann. WULS—SGGW. For. Wood Technol. 2019, 108, 45–52. [Google Scholar] [CrossRef]
- Szewczyk, M.; Szwajka, K. Assessment of the tribological performance of bio-based lubricants using analysis of variance. Adv. Mech. Mater. Eng. 2023, 40, 31–38. [Google Scholar] [CrossRef]
- Tayebi, N.; Polycarpou, A.A. Modeling the effect of skewness and kurtosis on the static friction coefficient of rough surfaces. Tribol. Int. 2004, 37, 491–505. [Google Scholar] [CrossRef]
- Durejko, T.; Zarański, Z.; Sulej, S. Surface layer of FeAl + Al2O3 composites constitued by electrical discharge machining. Kompozyty 2008, 8, 190–194. [Google Scholar]
- Shisode, M.; Hazrati, J.; Mishra, T.; de Rooij, M.; ten Horn, C.; van Beeck, J.; van den Boogaard, T. Modeling boundary friction of coated sheets in sheet metal forming. Tribol. Int. 2021, 153, 106554. [Google Scholar] [CrossRef]
- Zwicker, M.; Bay, N.; Nielsen, C.V. A discussion of model asperities as a method to study friction in metal forming. Discov. Mech. Eng. 2023, 2, 3. [Google Scholar] [CrossRef]
- Filzek, J.; Keil, D.; Schröder, H. Temperature Induced Friction Increase in Friction Test and Forming Demonstrator for Sheet Metal Forming. 2021. Available online: https://popups.uliege.be/esaform21/index.php?id=3732 (accessed on 1 April 2024).
- Hol, J.; Meinders, V.T.; de Rooij, M.B.; van den Boogaard, A.H. Multi-scale friction modeling for sheet metal forming: The boundary lubrication regime. Tribol. Int. 2015, 81, 112–118. [Google Scholar] [CrossRef]
- Popov, V.L. Contact Mechanics and Friction: Physical Principles and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Wu, L.; Zhao, C.; Cao, M.; Han, X. Effect of ultrasonic and low frequency vibrations on friction coefficient at die radius in deep drawing process. J. Manuf. Process. 2021, 71, 56–69. [Google Scholar] [CrossRef]
- Groche, P.; Kloepsch, C.; Moeller, N. Numerical analysis of the potential of deep drawing processes with hydrostatic pressure lubrication. Prod. Eng. 2012, 6, 157–167. [Google Scholar] [CrossRef]
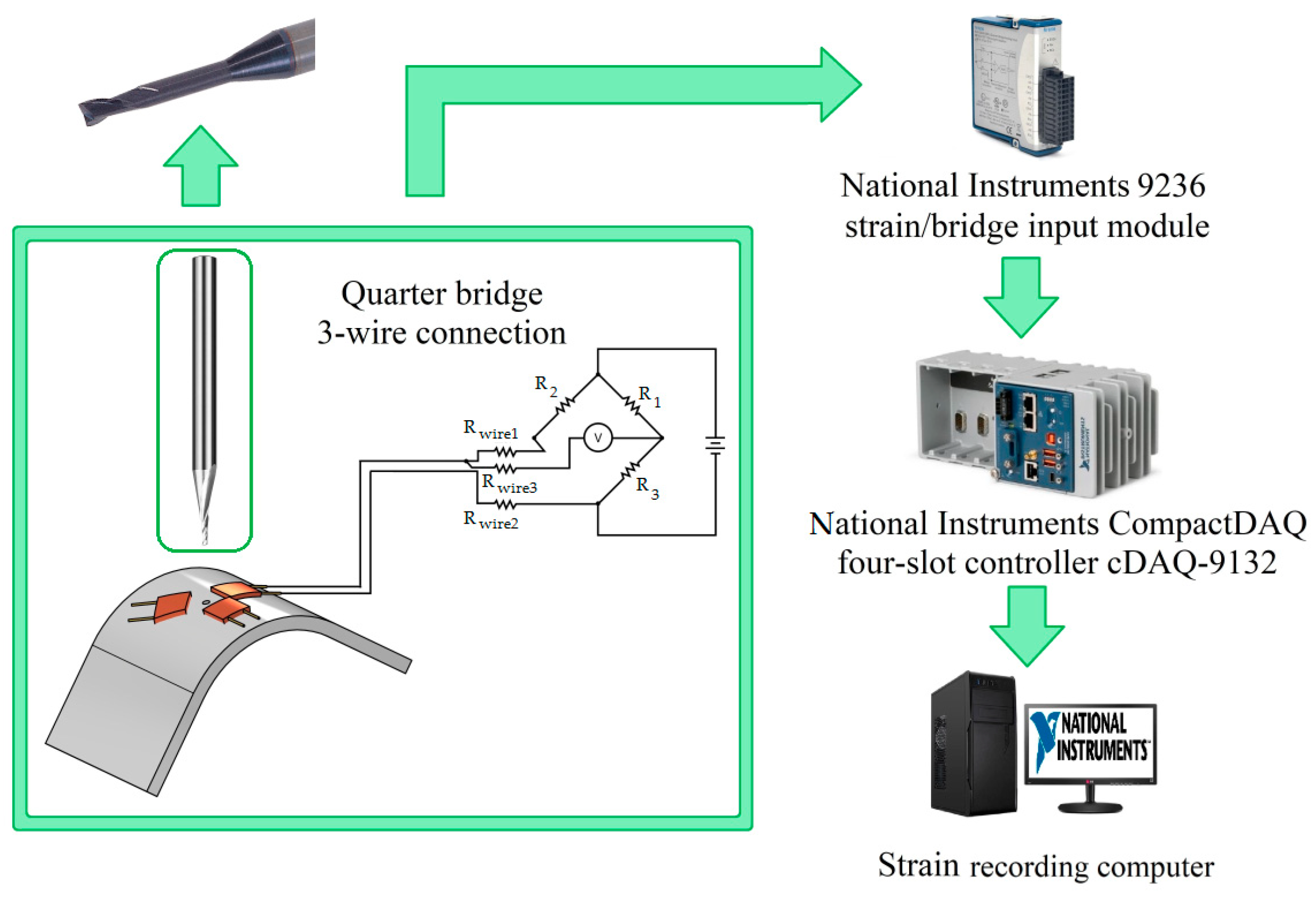
- Popov, A.L.; Kozintsev, V.M.; Chelyubeev, D.A.; Levitin, A.L. Hole-drilling method in residual stress diagnostics. Mech. Solids 2021, 56, 1320–1339. [Google Scholar] [CrossRef]
- ASTM E837-20:2020; Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. American Society for Testing and Materials: West Conshohocken, PA, USA, 2020.
- Tabatabaeian, A.; Ghasemi, A.R.; Shokrieh, M.M.; Marzbanrad, B.; Baraheni, M.; Fotouhi, M. Residual stress in engineering materials: A review. Adv. Eng. Mater. 2022, 24, 2100786. [Google Scholar] [CrossRef]
- Grzesik, W. Effect of the machine parts surface topography features on the machine service. Mechanik 2015, 8–9, 587–593. [Google Scholar] [CrossRef]
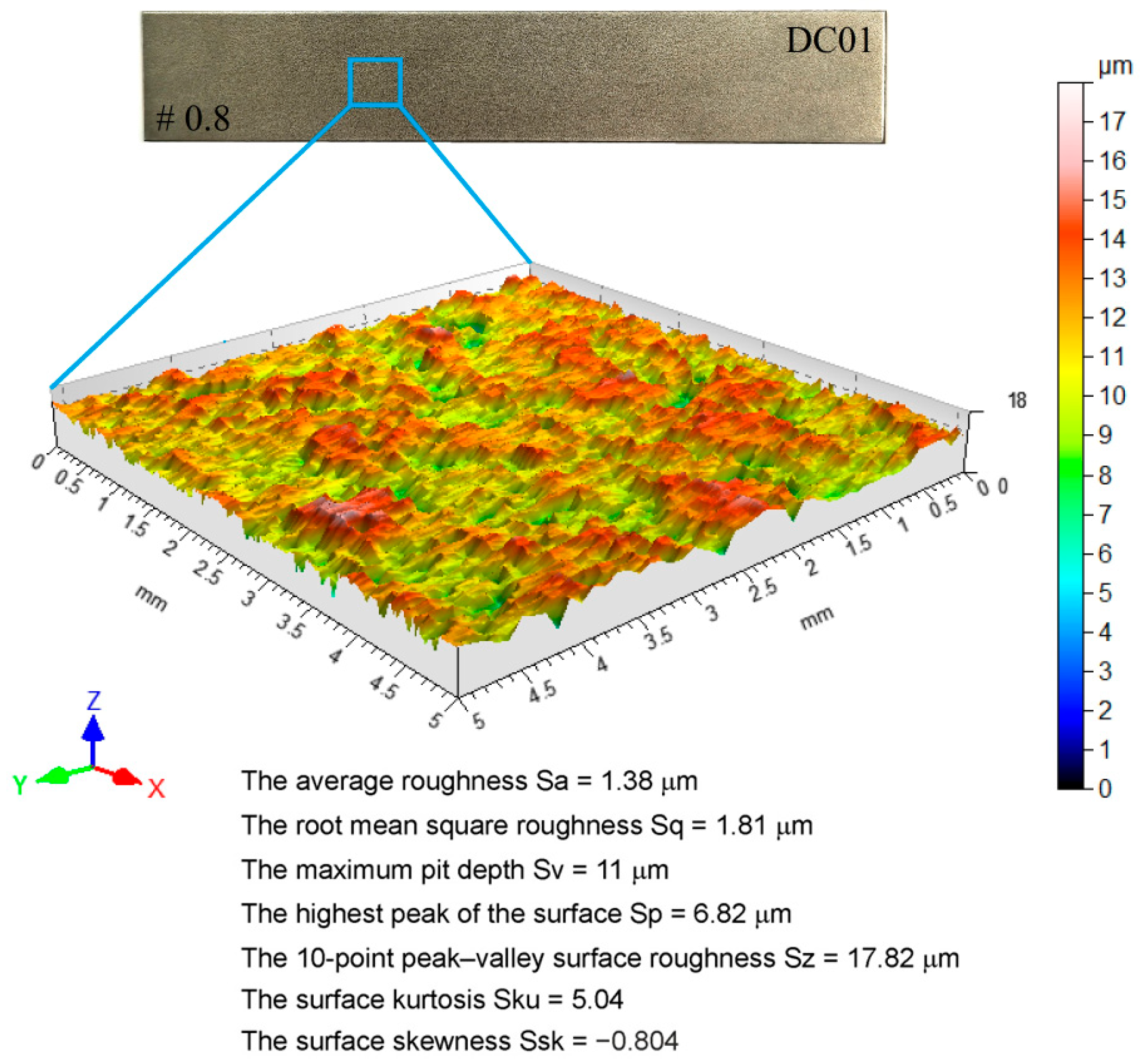













| C | Mn | S | P | Fe |
|---|---|---|---|---|
| ≤0.06 | ≤0.35 | ≤0.025 | ≤0.025 | balance |
| Parameter | Description/Value |
|---|---|
| P-R-W profile filter | Dual Gaussian filter for calculating areal material ratio curve parameters with variably adjustable cut-offs (EN ISO 16610-21:2013 [36]) |
| RK profile filter | Digital Gaussian filter with standard cut-off stages and with variably adjustable cut-offs (EN ISO 13565-1:1999 [37]) |
| cut-off wavelength λc | 0.8 mm |
| cut-off wavelength λs | 0.0027 mm |
| shortwave cut-off | 300 |
| scanning speed | 0.5 mm/s |
| measuring tip radius | 5 μm |
| Countersample | Method of Preparation | Hardness, HV |
|---|---|---|
| C-U | Unmodified | 293 |
| C-EBM | EBM (energy density 3.13 J/cm2) | 294 |
| C-Pb | LI (dose: 6.3 × 1017 cm−2, accelerating voltage: 60 kV) | 293 |
| C-Pb-EBM | LI (dose: 6.3 × 1017 cm−2, accelerating voltage: 60 kV) and EBM (energy density in the range from 2.27 to 3.34 J/cm2) | 294 |
| Parameter | Pb+ + Pb2+ Ions | Electrons | |
|---|---|---|---|
| 2.27 J/cm2 | 3.34 J/cm2 | ||
| Peak volume dopant/electron concentration, Nmax (cm−3) | 4.37·1023 (5.06·1023) | 3.79·1018 | 5.56·1018 |
| Projected range, Rp (nm) | 16.6 (16.7) | 527.04 | 527.04 |
| Range straggling, ΔRp (nm) | 12.2 (10.2) | 1376.5 | 1198.6 |
| Skewness | 0.6889 (0.4779) | No data | |
| Kurtosis | 3.3535 (3.1792) | ||
| Sputtering yield (atoms/ion) | 10.21 (10.32) | - | |
| CS | Sq μm | Ssk | Sku | Sp μm | Sv μm | Sz μm | Sa μm |
|---|---|---|---|---|---|---|---|
| C-EBM | 0.933 | 0.293 | 3.41 | 7.87 | 5.99 | 13.9 | 0.742 |
| C-U | 2.01 | 0.572 | 2.21 | 6.1 | 4.13 | 10.2 | 1.7 |
| C-Pb-EBM | 2.14 | −0.0307 | 2.22 | 8.48 | 6.82 | 15.3 | 1.81 |
| C-Pb | 2.03 | 0.504 | 1.99 | 5.18 | 3.88 | 9.06 | 1.75 |
| Denotation of Countersample | BAC Parameter | ||||
|---|---|---|---|---|---|
| Rpk, μm | Rvk, μm | Rk, μm | Mr1, % | Mr2, % | |
| C-U | 1.29 | 1.01 | 6.41 | 5 | 95 |
| C-EBM | 1.68 | 0.61 | 3.39 | 5 | 95 |
| C-Pb | 0.79 | 1.06 | 6.53 | 5 | 95 |
| C-Pb-EBM | 2.42 | 2.23 | 7.31 | 5 | 95 |
| Countersample | Temperature Increase, °C |
|---|---|
| C-U | 0.42 ± 0.02 |
| C-EBM | 0.58 ± 0.02 |
| C-Pb | 0.34 ± 0.02 |
| C-Pb-EBM | 0.39 ± 0.03 |
| Denotation of Countersample | Sq μm | Ssk | Sku | Sp μm | Sv μm | Sz μm | Sa μm |
|---|---|---|---|---|---|---|---|
| C-EBM | 1.18 | −1.57 | 7.74 | 3.60 | 11.1 | 14.7 | 0.864 |
| C-U | 1.47 | −1.57 | 9.01 | 5.86 | 13.1 | 19.0 | 1.05 |
| C-Pb-EBM | 1.52 | −0.563 | 4.78 | 6.13 | 11.1 | 17.3 | 1.13 |
| C-Pb | 1.61 | −0.718 | 4.32 | 6.16 | 9.84 | 16.0 | 1.24 |
| Denotation of Countersample | BAC Parameter | ||||
|---|---|---|---|---|---|
| Rpk, μm | Rvk, μm | Rk, μm | Mr1, % | Mr2, % | |
| C-EBM | 0.879 | 4.5 | 3.62 | 5 | 95 |
| C-U | 1.24 | 6.61 | 5.37 | 5 | 95 |
| C-Pb-EBM | 2.07 | 7.92 | 5.85 | 5 | 95 |
| C-Pb | 1.90 | 6.34 | 4.44 | 5 | 95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szwajka, K.; Trzepieciński, T.; Szewczyk, M.; Zielińska-Szwajka, J.; Barlak, M. Investigating Resulting Surface Topography and Residual Stresses in Bending DC01 Sheet Under Tension Friction Test. Lubricants 2025, 13, 255. https://doi.org/10.3390/lubricants13060255
Szwajka K, Trzepieciński T, Szewczyk M, Zielińska-Szwajka J, Barlak M. Investigating Resulting Surface Topography and Residual Stresses in Bending DC01 Sheet Under Tension Friction Test. Lubricants. 2025; 13(6):255. https://doi.org/10.3390/lubricants13060255
Chicago/Turabian StyleSzwajka, Krzysztof, Tomasz Trzepieciński, Marek Szewczyk, Joanna Zielińska-Szwajka, and Marek Barlak. 2025. "Investigating Resulting Surface Topography and Residual Stresses in Bending DC01 Sheet Under Tension Friction Test" Lubricants 13, no. 6: 255. https://doi.org/10.3390/lubricants13060255
APA StyleSzwajka, K., Trzepieciński, T., Szewczyk, M., Zielińska-Szwajka, J., & Barlak, M. (2025). Investigating Resulting Surface Topography and Residual Stresses in Bending DC01 Sheet Under Tension Friction Test. Lubricants, 13(6), 255. https://doi.org/10.3390/lubricants13060255








