Abstract
The modification of surface geometries to reduce friction is an omnipresent topic of research. In nature, different low-friction surfaces, such as fish skins, exist. To transfer this knowledge to technical applications, for example, to journal or plain bearings, many numerical and experimental studies of textured surfaces have been performed. In this work, the influence of the geometric parameters (texture length , width , angle and start position of a wedge-shaped texture on three different convergent oil film gaps was analyzed in full-film lubrication and compared with untextured oil film gaps. With the aid of a CFD (computational fluid dynamics) model, a comprehensive variation study was conducted, and the best-performing wedge-shaped texture was determined. The results show that an open texture at the inlet provides the largest improvement. Furthermore, it can be observed that the optimal relative texture width and absolute inlet height for the three investigated oil film gaps are similar. In contrast to the volume flow of the untextured geometry, the volume flow of the textured one is significantly higher, especially that perpendicular to the movement direction.
1. Introduction
To achieve climate targets, it is necessary to save energy and resources. One opportunity is a reduction in friction. Holmberg et al. [1] reported that 20% of all energy consumption is used to overcome friction. So, the reduction in friction is an omnipresent topic of research. In particular, nature demonstrates perfectly shaped surfaces, such as shark and fish skins [2] and bird wings [3], for drag reduction. Many researchers have tried to transfer these bio-inspired surfaces to technical applications and add additional indentations, called texture, to the surface, which should improve the tribological performance. The limiting factor for the geometry of the texture is the manufacturing process. Hence, simplified geometries, such as dimples, pockets, chevrons and so on, are used. Different surface texture manufacturing techniques exist, and according to [4], these methods can be divided into the following categories:
- Melting/vaporization (for example, electric discharge machining);
- Ablation (for example, laser surface texturing);
- Forced material removal (for example, micro-grinding);
- Dissolution (for example, chemical etching);
- Solidification (for example, micro-casting);
- Material addition (for example, chemical vapor deposition).
The advantages, disadvantages and applications of these methods are discussed in [4]. The quality of the generated surface is strongly influenced by the variable parameters of the manufacturing technique. In [5], the influence of the surface-texturing laser’s pulse duration on the surface topography is depicted. Too long a pulse duration leads to micro-cracks, high-heat-affected zones and quite irregular surface profiles [5]. Another efficient manufacturing process is milling, and this process can be further optimized for texture manufacturing, for instance, by implementing spindle speed modulation, which leads to low costs for texture generation [6].
In [7,8], different textured surfaces for a parallel sliding contact were studied, and a significant drag reduction could be detected. Nevertheless, many technical applications are not parallel. Hence, Bei et al. and Rosenkranz et al. [9,10] examined the tribological performance of a pocket-, dot- and line-cross-like-shaped, textured convergent oil film gap and showed that the geometry of the oil film gap had a significant influence on the load-carrying capacity. Sharma et al. [11] performed a numerical study on a partially textured journal bearing and reported that texturing can enhance the performance for low and average journal eccentricities. The application of this knowledge to a convergent oil film gap demonstrated that partial surface texturing significantly enhances the performance of parallel sliding contacts, which is described in [7,8,12] and, for a convergent oil film gap with a low pitch angle , in [10].
Different mechanisms underlying the operating principles of textured surfaces are discussed in the literature. Grützmacher et al. [13] published five different hypotheses about the performance enhancement of textured surfaces:
- Increase the hydrodynamic pressure;
- Supply the surfaces with additional lubricant;
- Store lubricant;
- Trap wear particles;
- Reduce the real contact area.
Besides these hypotheses, Hamilton et al. [14] reported that additional hydrodynamic pressure is a consequence of the existence of cavitation.
However, Babu et al. and Hu et al. [15,16] performed a detailed numerical and experimental analysis of different texture shapes and found that the geometrical parameters of every texture, such as the area density and texture height, have a strong influence on the enhancement of a textured surface. Besides the geometry itself, the position of the texture affects the tribological performance. According to Rosenkranz et al. [10], textures that are located at the inlet lead to a friction reduction when the pitch angle of a convergent oil film gap is low. Furthermore, Yagi et al. [17] found that an opened dimple on the inlet side increased the load-carrying capacity more than an enclosed dimple at the inlet position. Similar results can be observed for a journal bearing. The load-carrying capacity can be increased when the texture is located in a certain region in the convergent region, whereas textures that are placed in the region with the maximum pressure can only impair the performance [18].
As mentioned at the beginning, the surfaces of animals can inspire the development of surface texture. In [2] and Figure 1, a fish skin is depicted. The skin itself consists of different scales. The height profile of such a scale is also visualized in Figure 1. A simplification of the measured height profile, presented in the blue graph, leads to two wedges, presented in the dot-dashed turquoise graph. These simplified profiles served as inspiration for the development of a wedge-shaped texture.

Figure 1.
European seabass’ skin—an inspirational source for textures.
The current paper focuses on a comprehensive study of such a texture on a convergent oil film gap. In [19,20], a wedge-shaped texture, among others, was examined under mixed lubrication. In contrast to van Liem et al. [19], who focused on the size and distribution of textures in mixed lubrication, Maier et al. [20] concentrated on the wear simulation of wedge-shaped surfaces. In both publications, specific geometries were chosen and analyzed. This leads to the question of the influence that the geometric parameters of a wedge-shaped texture have and which geometry will best enhance the performance. As in many technical applications, full-film lubrication is present, and this was not determined for wedge-shape textures by [19,20]. In this study, such a lubrication regime will be analyzed.
2. Simulation Model
This section focuses on the methodical approach of the simulation model and its validation.
2.1. Mathematical Formulation of a Multiphase Flow
Numerical methods have the advantage, compared to experimental methods, of achieving time- and cost-efficient results. More than half of the research methods published in the field of surface texturing are simulation models [21]. In 77 % of cases, the Reynolds differential equation is solved [21]. Dobrica et al. [22] published a paper discussing the validity of the Reynolds equation in detail. This differential equation is valid for low Reynolds numbers , high dimple aspect ratios (the ratio between texture length and texture height ) and small variations in lubricant thickness. The Reynolds number is the product of density , velocity and untextured oil film gap height divided by the kinematic viscosity [22]. In [23], the influence of inertia effects in textured lubricated sliding contacts was discussed noting that these effects become more pronounced at high Reynolds numbers. For this study, a maximum Reynolds number of about is expected, so the influence of inertia effects should be small. This means that the multiphase Stokes flow, which is presented in Equation (1), is applicable to this tribological system.
In this equation, represents the velocity, the pressure field, represents the body force, the kinematic viscosity, the second viscosity, the identity matrix and the density of the fluid. In the case of multiphase flow, , and are scalar fields. In addition to this equation, the continuity equation (cf. Equation (2)) is needed for time-independent density . In [24], the mathematical inequality for the viscosity coefficients and is presented. Both coefficients were set to the same values using this inequality and an existing simulation model, which is used for validation (cf. Section 2.2). For numerical implementation, the software package Netgen/NGsolve, based on a 3D finite element method (FEM), is used [25].
The multiphase Stokes flow (cf. Equation (1)) only needs to be solved if cavitation occurs; otherwise, the incompressible Stokes flow presented in Equation (3) can be solved numerically. Cavitation is determined by finding the minimum pressure and comparing it with the vapor pressure . If the minimum pressure is less than , cavitation occurs.
In [26], the Merkle [27] cavitation model, among others, for a journal bearing was compared with the measured results in [28] and yielded favorable outcomes. This cavitation algorithm is also used in this study and presented in Equations (4)–(9). In this application, the stationary state is of interest, so the time derivative, which is generally a part of the transport equation (Equation (4)), is not required.
The source term, located on the right hand side of the transport equation (cf. Equation (4)), describes the vaporization and condensation process. represents the vapor volume fraction and represents the liquid volume fraction. The sum of both fractions must be 1, and the vapor and liquid volume fractions describe the volume of vapor or liquid , relative to the total volume (cf. Equation (7)).
The vaporization and the condensation term (cf. Equations (5) and (6)) depend on the condensation constant , the vaporization constant , vapor density , liquid density , input velocity , reference time and vapor pressure .
In addition to the previously discussed equations, it is essential to incorporate Equation (8) to compute the density field and Equation (9) to characterize the kinematic viscosity field (ν) when dealing with a multiphase flow.
2.2. Comparison of Different Simulation Models
To compare the self-programmed simulation model implemented in this study with an established software tool, OpenFOAM-8 [29] and its interPhaseChangeFoam solver were used. Since mesh generation for a wedge-shaped texture in OpenFOAM is quite complex, the geometry of a block-shaped texture on a convergent oil film gap, as depicted in Figure 2, was created. The bottom surface of the geometry is moving with a velocity , while the top surface and the texture surface are static. A Dirichlet boundary condition of was applied to the lateral surfaces. Additional boundary conditions for the liquid volume fraction were required. The lateral surface has a pressure of , resulting in a liquid volume fraction of 1 at these surfaces. The fluid parameters and parameters for the Merkle cavitation algorithm are presented in Section 2.3. A grid study was conducted for both models, and the results in the equilibrium state were analyzed. Figure 3 depicts the pressure distribution for different y-coordinate positions for both simulation models. Despite the differences in mathematical approach (finite volume method (FVM) in OpenFOAM and finite element method (FEM) in NGSolve) and element types (hexahedrons in OpenFOAM and tetrahedrons in NGSolve), similar results can be achieved. The comparison of the lifting and drag forces, calculated according to Section 2.3, showed a difference of about . These small deviations between the different simulation models can be explained by different numerical methods and potentially by the fact that the NGSolve model does not include the inertia effects of the multiphase flow. Nevertheless, the use of this simulation model is valid because this variational study requires a large number of simulations (more than 50,000) to understand the various influencing geometric parameters. Neglecting the inertia effects significantly reduces computational times, as the nonlinear term of the Navier–Stokes equation is disregarded. As shown in the Results section, the improvement in tribological performance is much greater than the difference between both simulation models.
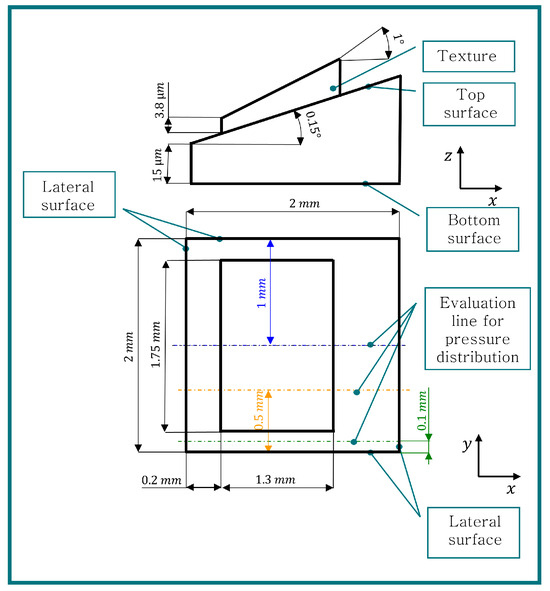
Figure 2.
Geometry for validating the simulation model (unscaled).
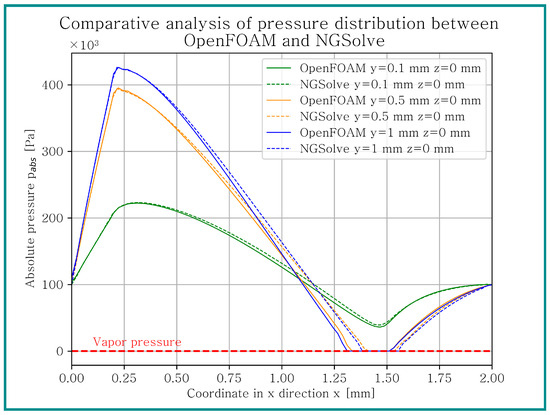
Figure 3.
Comparative analysis between OpenFOAM and NGSolve.
2.3. Simulation Methodology for Wedge-Shaped Textured Surfaces
In Figure 4, the oil film with a global length , width and pitch angle is visible. It was assumed that the surface was smooth, and the roughness of a surface was not included in this simulation model, unlike [30,31], who used flow factors to describe the real surface topography. Within this study, the performance of the texture geometry parameters themselves should be analyzed in detail and the effects of surface roughness should be neglected.
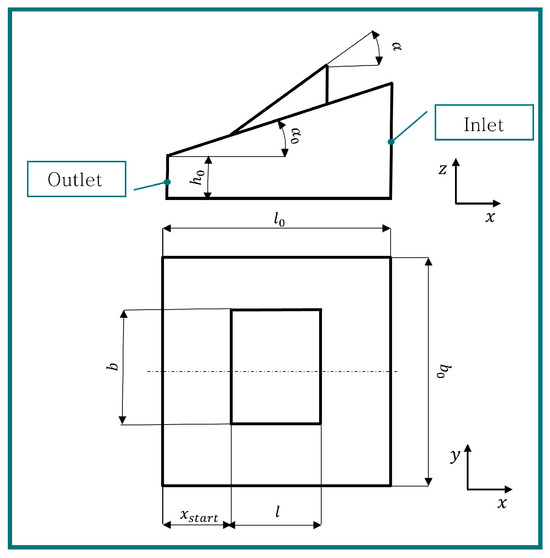
Figure 4.
Geometry of textured surface (unscaled).
Three different global geometries were analyzed in detail, and the parameters themselves are presented in Table 1. Two criteria were important for the selection of these parameters. On the one hand, the tribological performance should be enhanced, and on the other hand, the computation time has to be quite short, so that it is possible to conduct a huge number of simulations in an adequate time. Therefore, a low and a small global geometry were selected (cf. [10]). The parameters and were kept constant to vary as few parameters as possible and to focus this study on the influencing parameters of the texture parameters themselves.

Table 1.
Geometry parameters.
The geometrical parameters of the texture, length , width angle and start position were varied in a defined interval, with the requirement that the texture does not overlap the oil film gap. The texture angle was varied between 0.2° and 2.2°. The step size of the geometry parameters between each simulation was or for and , depending on the width and length of the oil film gap. A step size of for and for was selected. For only a few diagrams, some additional simulations, where a smaller step size was chosen, were added. The texture start position was varied in a defined interval for all geometries. So, all in all, 9000 simulations for geometry I, 20,000 for geometry II and 20,000 for geometry III were conducted.
In Figure 5, the boundary conditions of an unscaled model are depicted. A constant sliding velocity of is defined on the bottom surface. This velocity is typical for technical applications in hydrodynamic lubrication and can also be tested on a pin-on-disc test rig, as can be observed in [32]. The lateral surface of the texture, the top surface of the oil film gap and the texture itself are stationary. On the lateral surface of the oil film gap, the ambient pressure is applied. Additionally, a liquid volume fraction of is defined on this surface. The boundary condition of zero gradient is applied to all the other surfaces that are not mentioned. Table 2 shows the oil and cavitation parameters used for the simulation model, as presented in [33,34].
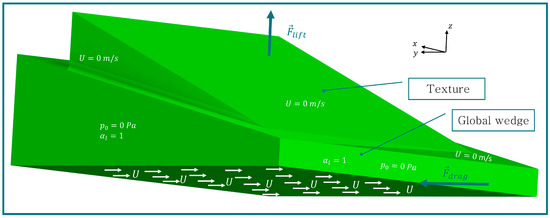
Figure 5.
Boundary conditions for velocity , pressure and liquid volume fraction of simulation model, as well as lifting force and drag force (unscaled).

Table 2.
Fluid and cavitation model parameters.
The geometry was discretized using second order 3D tetrahedron-shaped elements. To achieve sufficient precision, simulations with different maximum mesh sizes were conducted. These analyses were used to identify an adequate mesh size where only small changes, less than 1%, could be detected in the results. Based on these results, a maximum mesh size of 0.025 mm was selected for discretizing the geometries. A direct solver called the unsymmetric multi-frontal package UMFPACK was used to solve the partial differential equations.
In postprocessing, the lifting force , which is equivalent to the load that can be absorbed by the oil film gap, can be calculated by integrating the pressure field on the bottom surface (cf. Equation (10)). To calculate the drag force , the shear stresses are integrated over the bottom surface. To validate the model, an analytical solution according to [35] for an untextured convergent oil film gap was used to calculate the lifting force and the drag force . The comparison showed similar results.
Within this model, the lifting force and drag force can be calculated for different textured geometries. Since different geometries result in different lifting— and friction forces —it is necessary to combine these two physical quantities for comparison with an untextured convergent oil film gap. This leads to the performance enhancement ratio (PER) according to Sharma et al. [11] (cf. Equation (11)). The two parameters are combined into one to simplify the visualization. If PER is greater than one, the performance is enhanced; otherwise, it is impaired. However, it should be noted that a reduction in friction- and lifting force can lead to a performance enhancement ratio PER greater than one.
3. Results
Overall, numerous simulations were conducted to provide an overview of the results. Scatter plots are quite useful for this purpose, while standard plots are commonly used to investigate the influence of different parameters. This section will also focus on a detailed analysis of the velocity and pressure fields of selected texture geometries.
3.1. Analysis of Variation Parameters Depending on PER
Figure 6a–h depict the results of geometry I for different start values . Each point in each plot represents one simulation for a specific texture geometry with the parameters , , and . The color of each point indicates the performance enhancement ratio (PER). The lower limit of the color bar for Figure 6, Figure 7 and Figure 8 was set as one, allowing the visualization to focus on geometries that improve tribological performance, by increasing lifting force , reducing friction or both. The upper limit for these colored plots was determined by finding the maximum PER. For geometry I, it is 2.65, which is achievable at a texture length , width , angle and at a start position . Figure 7 and Figure 8 present the same information as Figure 6, but for geometry II and III. The maximum improvement for geometry II can be achieved with a texture length , width , angle and a start position . For geometry III, the maximal PER is 1.67 at a texture length , width , angle and a start position . All geometries were simulated with the same start positions, and a selection of these results is visible in Figure 6, Figure 7 and Figure 8. The simulation effort for geometry II and III is higher, compared to geometry I. The results show that the best performance is achieved with low texture start positions , and consequently for geometry II’s start positions and a smaller step size of for texture length and width was defined (cf. Figure 7a) in contrast to Figure 7b–d with a step size of .
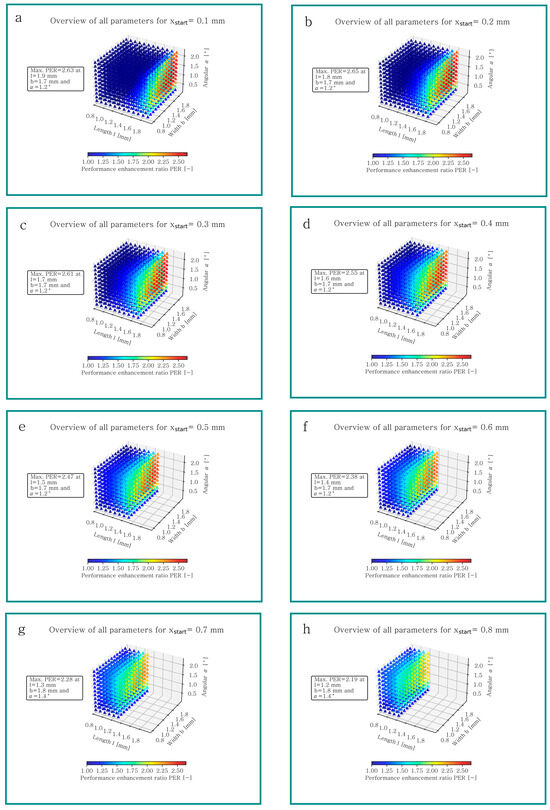
Figure 6.
Overview of all simulations of geometry I for (a) , (b) , (c) , (d) , (e) , (f) , (g) and (h) .
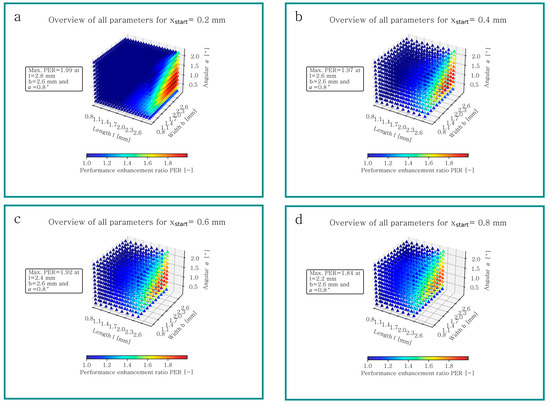
Figure 7.
Overview of all simulations of geometry II for (a) xstart = 0.2 mm, (b) xstart = 0.4 mm, (c) xstart = 0.6 mm and (d) xstart = 0.8 mm.
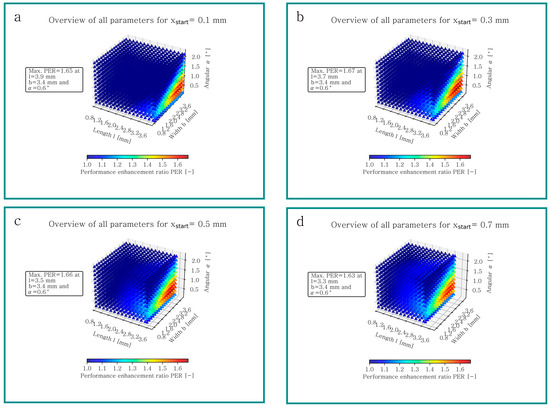
Figure 8.
Overview of all simulations of geometry III for (a) , (b) , (c) and (d) .
In Table 3, the performance enhancement ratio (PER) for the best operating textures for each geometry is shown. Additionally, the ratio, describing the improvement in lifting and drag force is illustrated. It is evident for all geometries that the lifting force increases in comparison to the untextured convergent oil film gap. Furthermore, the drag force of these textured geometries decreases compared to the untextured geometry. Additionally, it is noticeable that as the global length and width increase, in particular decreases.

Table 3.
Maximal performance enhancement ratios of best operating geometries.
Although the maximum PER for all geometries is different, similar trends can be observed. The best performance for every geometry can be achieved, with textures where the sum of texture length and start position is equivalent to the global length , resulting in an open configuration at the inlet side. An investigation of the texture width shows that tribological performance can be enhanced with increasing texture width to a local maximum, beyond which the PER decreases. The influence of the texture angle is also depicted in Figure 6, Figure 7 and Figure 8. As the global length and width increase, the optimum texture angle decreases and the range for performance enhancement becomes smaller.
The detailed influence of the different parameters is illustrated in Figure 9, Figure 10 and Figure 11. In each figure, three parameters were held constant while one was varied. The constant parameters were based on the values of the simulation model that yielded the maximum enhancement.
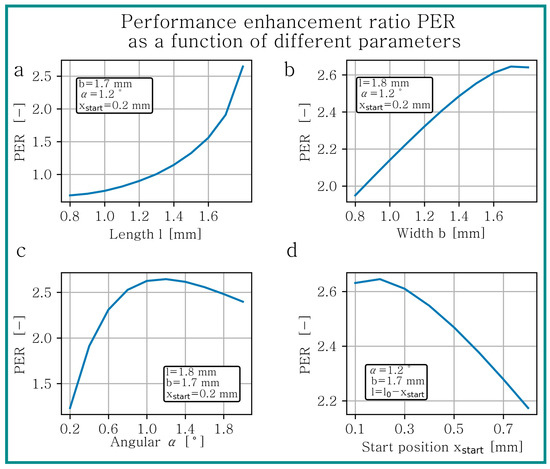
Figure 9.
Performance enhancement ratio (PER) for geometry I as a function of texture (a) length , (b) width , (c) angle and (d) start position .
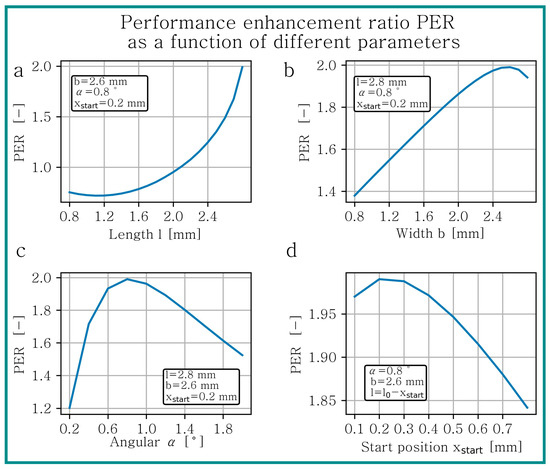
Figure 10.
Performance enhancement ratio PER for geometry II as a function of texture (a) length , (b) width , (c) angle and (d) start position .
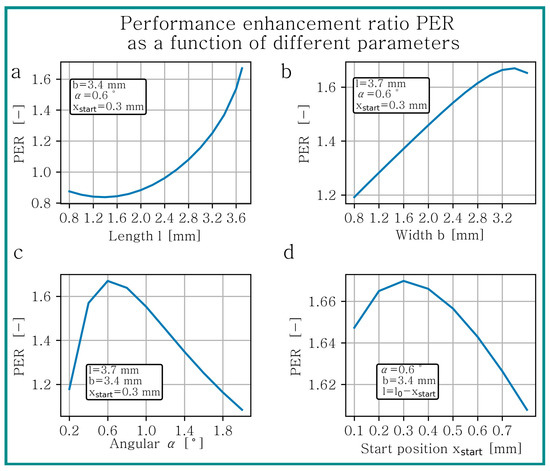
Figure 11.
Performance enhancement ratio PER for geometry III as a function of texture (a) length , (b) width , (c) angle and (d) start position .
Although the absolute values of the PER are different, the same trends for geometry I, II and III can be observed. As already mentioned, an open texture against the movement direction improves the performance the most. An increasing texture length leads to a rising PER, as shown in Figure 9a, Figure 10a and Figure 11a. For small texture lengths a significant deterioration can be noticed. In Figure 9a, it is visible that for texture lengths the performance is enhanced. This corresponds to a percentage length of . Similar analogies can be observed for geometry II and III. For (geometry II) and (geometry III), the PER is greater than one, which corresponds to a percentage length of and .
The PER depending on texture width is presented in Figure 9b, Figure 10b and Figure 11b. For all geometries, the curve progression is similar and the maximal PER can be achieved at a related width of , for geometry I, II and III. An analysis of the influence of showed that with increasing global geometry, the maximum enhancement is located at a lower texture angle (cf. Figure 9c, Figure 10c and Figure 11c). For geometry I, the best improvement can be achieved with a texture angle , for geometry II and for geometry III .
In Figure 9d, Figure 10d and Figure 11d, the PER as a function of the start position is presented. In these figures, the texture length of each simulation point is different, because it was assumed that the texture is open at the inlet side. So, the texture length was calculated by subtracting from . An optimum relative start position can be reached at , and for geometry I, II and III.
In summary, as can be seen from the figures discussed, small variations in texture geometry parameters have a significant effect on tribological performance.
For additional analysis, the pressure and velocity field of the best performing texture geometries were investigated.
3.2. Pressure and Velocity Field Analysis
In Figure 12, Figure 13 and Figure 14, the pressure distribution and the calculated volume flow for an untextured and best performing textured oil film gap are presented. The small variations that violate volume continuity can be attributed to rounding and numerical errors. The qualitative characteristic of the pressure field for all textured and untextured geometries is similar. Compared to the untextured geometry, the maximum pressure of the textured geometry is located closer to the outlet. Additionally, the texture increases the pressure, as shown in Figure 12b, Figure 13b and Figure 14b. In addition to the pressure field, the volume flow between the textured and untextured geometries differs, especially the volume flow perpendicular to the direction of movement is significantly larger, which is visually represented by the width of the arrows. This means that , and of the inlet flow are flowing out there for the textured geometry I, II and III. In contrast, only , and of the inlet flow exit on the faces perpendicular to the movement direction for the untextured geometries I, II and III.
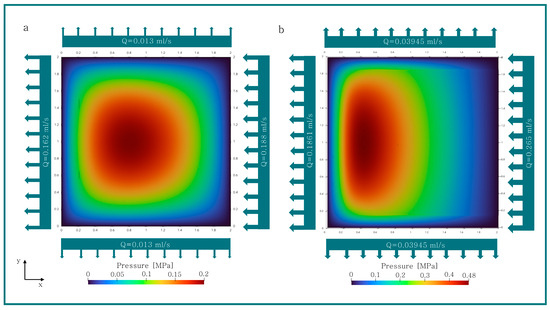
Figure 12.
Pressure distribution and volume flow of geometry I (a) untextured and (b) textured (.
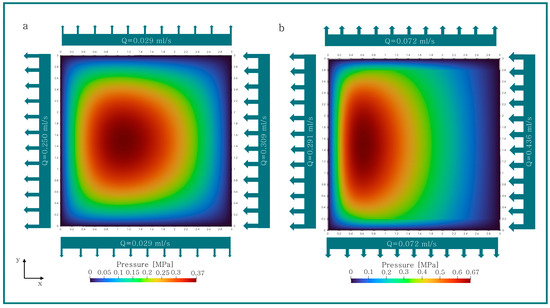
Figure 13.
Pressure distribution and volume flow of geometry II (a) untextured and (b) textured (.
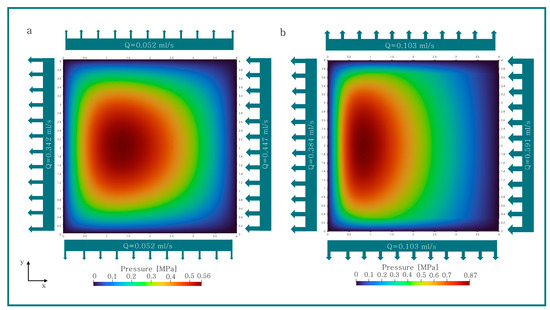
Figure 14.
Pressure distribution and volume flow of geometry III (a) untextured and (b) textured (.
In Figure 15, Figure 16 and Figure 17, the velocity field of the untextured geometries I, II, III and the best performing textures of these convergent oil film gaps are visible. The texture depicted in these pictures had the highest performance enhancement ratio of all conducted simulations. Since the real height of an oil film gap in comparison to its horizontal and vertical size is small, the z-coordinates of these figures were scaled by a factor of eight. The size of the flow vectors is constant, and the magnitude of the velocity is represented by the color. It is apparent in all slices B-B that the velocity magnitude is larger on the right side. Since all slices were created parallel to the bottom surface with a displacement of 10 μm, the velocity increases towards the right side where the oil film gap is higher. This can be explained by the simple shear case, where the velocity is linear over the oil film gap height and the flow due to pressure is not present. An increasing height consequently leads to a higher velocity for the same vertical position. This can also be observed in the outer regions of the textured geometry, where there is a sudden change in velocity between the crossover of the textured and untextured region. Compared to the untextured geometries, the magnitude of the velocity of the textured geometries is significantly higher, as seen in Figure 15b, Figure 16b and Figure 17b, due to the increased oil film gap height caused by the texture. Additionally, the y-coordinates of the textured flow vectors are higher compared to the untextured geometry, causing an increase in volume flow on the faces normal to the directional movement (cf. Figure 12b, Figure 13b and Figure 14b). Slice A-A of Figure 15a, Figure 16a and Figure 17a shows an expected velocity contribution where the fluid on the bottom surface is moving with , while the top surface is stagnant. On the right side of the textured geometry slices (cf. Figure 15b, Figure 16b and Figure 17b), a backstreaming of the oil with a low magnitude can be observed. As the global geometry increases, the length of the backstreaming region decreases.
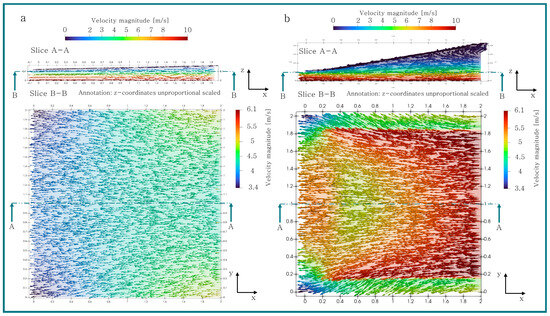
Figure 15.
Velocity field of geometry I (a) untextured and (b) textured (.
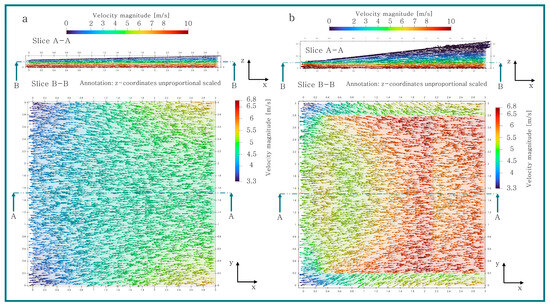
Figure 16.
Velocity field of geometry II (a) untextured and (b) textured (.
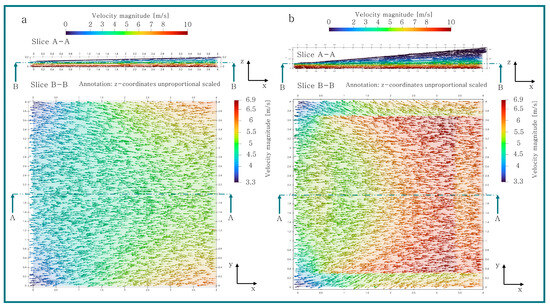
Figure 17.
Velocity field of geometry III (a) untextured and (b) textured (.
4. Discussion
The principal mechanisms of textured surfaces, such as the increase in hydrodynamical pressure and the supply of surfaces with additional lubricant as published by Grützmacher et al. [13], were also observed in this study. The increase in pressure and volume flow can be seen in Figure 12, Figure 13 and Figure 14. The volume flow also increases, when the texture is not open against the movement of direction, probably due to an increasing velocity at the inlet. This phenomenon is illustrated in Figure 18, which shows an untextured convergent oil film gap in the center, surrounded by different textures. It is qualitatively presented that the volume flow at the inlet for all four textures increases compared to the untextured oil film gap. For an open texture, the relative inlet surface area is higher compared to closed textures or untextured lubrication gaps. The average velocity magnitude on this surface is lower than the average magnitude of a smooth oil film cap, resulting in an increased volume flow at the inlet due to the larger surface area . These observations for an opened texture are presented in Figure 13 and Figure 14. The three principal mechanisms of surface textures, trap wear particles, reduce the real contact area and store lubricant, according to Grützmacher et al. [13], and so cannot be described with this simulation model.
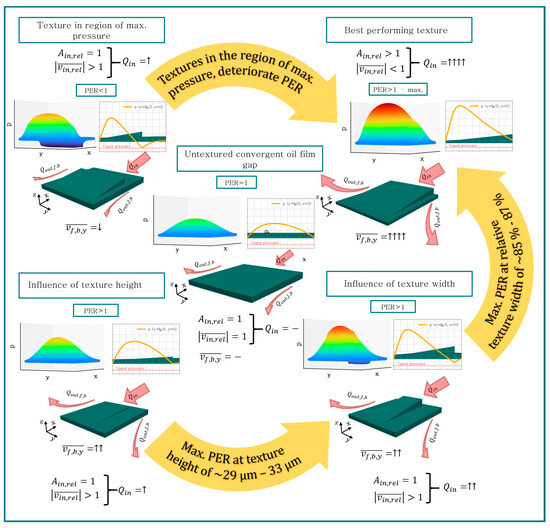
Figure 18.
Qualitative visualization of influencing parameters in wedge-shaped textures.
The hypothesis that cavitation is the reason for additional pressure in some cases [14], or that cavitation can increase the load-carrying-capacity [36], is disproved for the best performing texture geometries, as the minimum pressure for these textures and many others was not lower than the vapor pressure . In Figure 18, the pressure distribution for different textures is qualitatively presented and it can be observed that for an at-the-inlet opened texture, the minimal pressure is not lower than the ambient pressure. Additionally, it is evident that in some cases, cavitation can negatively impact performance by decreasing the lifting force , when the pressure falls below the ambient pressure. However, it is important to note that textures where cavitation occurs and enhance tribological performance do exist. For the texture, which is analyzed in detail in this study, the highest performing enhancement ratio (PER) can be achieved and cavitation does not occur.
In Figure 12, Figure 13 and Figure 14, it is depicted that textures increase the volume flow perpendicular to the movement direction. Figure 18 similarly presents this qualitatively, showing that the average magnitude of the velocity on the front and back surface can be increased, compared to the untextured lubricant gap. This results in an increasing volume flow perpendicular to the movement direction. However, it should be noted that this is not a universally valid mechanism, because an infinitely expanded untextured oil film gap is also providing a higher lifting force, in contrast to a finitely expanded one [35]. Therefore, the additional inflow of the textured oil film gaps potentially improves performance, which is one operational principle according to Grützmacher et al. [13].
As can be seen in Figure 9a, Figure 10a and Figure 11a and Figure 18, an open texture at the inlet noticeably increases the PER. Similarly, in [17], a parallel sliding surface with multiple dimples exhibits a similar behavior. This open texture may be providing additional lubrication, thereby enhancing the tribological performance.
In Figure 9a, Figure 10a and Figure 11a, it can be observed that for texture lengths less than (geometry I), (geometry II) and (geometry III), the performance enhancement ratio is less than one. When compared to the pressure field of the untextured geometries, cf. Figure 12a, Figure 13a and Figure 14a, it is evident that the area of maximum pressure is located within these lengths. This suggests that textures located only in the area of maximum pressure negatively impact performance (cf. Figure 12, Figure 13 and Figure 14). This phenomenon is also illustrated in the top left corner of Figure 18, showing the pressure distribution of an oil film gap, where the texture is located in the region of the maximal pressure of a smooth lubrication gap. Due to cavitation, the lifting force is reduced, despite the higher maximal pressure compared to a smooth wedge. In summary, it can be concluded that textures located in the region of maximal pressure have a negative impact on tribological performance. Liang et al. [18] also published similar results for partially textured journal bearings.
Bei et al. [9] published that a maximal load-carrying capacity for a convergent oil film gap and pocket-shaped textures could be achieved at a dimensionless texture width = , which is not very different from the values found in this study. Here, the optimal related width is between and (cf. Figure 18). In [9], the texture is defined through the parameters length, width and height. In this work, the texture height , (also referred to as texture depth in the literature) is not constant over the texture length . This led to the conclusion that for this variation study, a texture angle was used instead of a texture height .
According to Bei et al. [9], the load-carrying capacity first decreases, then increases and finally decreases over the texture width and depth. Within this work, it was observed that there is an initial increase followed by a decrease in performance, depending on texture width and angle .
In [37], the influence of square-shaped dimple depths is discussed in detail and the best performance could be achieved with a dimple depth of . In [37], nearly the same density and doubled dynamic viscosity as in this study were used. To compare this value with the results of this variation study, trigonometric calculations are necessary to calculate the maximal height of the texture. For geometry I, the highest PER could be acquired for a maximal texture height of , for geometry II and for geometry III , as visualized in Figure 18. These values are in the same range as those mentioned by Ullah et al. [37]. Another interesting observation regarding the texture height could be made in this study. The absolute oil film gap height at the inlet, which is the sum of the maximal texture height and the maximal height of the untextured convergent oil film gap, is nearly equivalent for all geometries ( for geometry I, for geometry II and for geometry III). The conclusion of Ullah et al. [37] that a decreasing texture height improves performance cannot be observed at all in this study. It can be shown that with increasing texture height, the PER first increases and then decreases. One possible reason why this behavior was detected in this study is that in comparison to Ullah et al. [37], simulations with a very small texture angle , which corresponds to small heights, were also conducted.
In general, it can be observed that the geometry parameters of the texture strongly influence the performance of a lubricated sliding oil film gap. A comparison with the general tolerances outlined in ISO 2768 reveals that for nominal lengths less than , a deviation of for the medium class and for the fine class is acceptable [38]. For angle dimension deviations for nominal lengths up to a deviation of is permissible [38]. Comparing these tolerances with Figure 9, Figure 10 and Figure 11 shows that the texture angle and the start position would change significantly with these tolerances, while the texture length and width would not be as strongly influenced.
5. Conclusions
Within this work, a comprehensive numerical study of a wedge-shaped texture on three different convergent oil film gaps was conducted and the influence of the geometry parameters was analyzed in detail. The following conclusion for the already mentioned global geometries can be summarized:
- The performance of a wedge-shaped texture is strongly influenced by the geometry parameters. An increasing texture length improves the tribological behavior and the maximal PER can be achieved with an open texture at the inlet. This means that the texture increases the area of the face where the fluid advects.
- Depending on the dimensions of the oil film gap, a relative texture width of to leads to the best performance.
- With increasing dimensions of the oil film gap, the optimum texture angle decreases. The best performance can be achieved if the oil film gap at the inlet side has an absolute height of about , more or less independent of the geometry of the oil film gap.
- A relative start position of the texture , referring to the length of the oil film gap between and enhances the performance in the best way.
- The texture increases the fluid velocity perpendicular to the movement direction, leading to an increasing volume flow perpendicular to the movement direction.
- The texture also induces additional pressure.
- Textures that are only located in the area of maximal pressure deteriorate the tribological performance.
Author Contributions
Conceptualization, R.S., M.M. and M.P.; methodology, R.S.; software, R.S.; validation, R.S. and M.P.; formal analysis, R.S.; investigation, R.S.; resources, R.S.; data curation, R.S.; writing—original draft preparation, R.S.; writing—review and editing, M.M., M.P. and F.G. visualization, R.S.; supervision, M.P. and F.G.; project administration, F.G.; funding acquisition, F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Holmberg, K.; Erdemir, A. The impact of tribology on energy use and CO2 emission globally and in combustion engine and electric cars. Tribol. Int. 2019, 135, 389–396. [Google Scholar] [CrossRef]
- Tian, G.; Zhang, Y.; Feng, X.; Hu, Y. Focus on Bioinspired Textured Surfaces toward Fluid Drag Reduction: Recent Progresses and Challenges. Adv. Eng. Mater. 2022, 24, 2100696. [Google Scholar] [CrossRef]
- Dutta, P.; Nagar, O.P.; Sahu, S.K.; Savale, R.R.; Raj, R.G. Aerodynamic analysis of bionic winglet- slotted wings. Mater. Today Proc. 2022, 62, 6701–6707. [Google Scholar] [CrossRef]
- Arslan, A.; Masjuki, H.H.; Kalam, M.A.; Varman, M.; Mufti, R.A.; Mosarof, M.H.; Khuong, L.S.; Quazi, M.M. Surface Texture Manufacturing Techniques and Tribological Effect of Surface Texturing on Cutting Tool Performance: A Review. Crit. Rev. Solid State Mater. Sci. 2016, 41, 447–481. [Google Scholar] [CrossRef]
- Pou-Álvarez, P.; Riveiro, A.; Nóvoa, X.; Fernández-Arias, M.; del Val, J.; Comesaña, R.; Boutinguiza, M.; Lusquiños, F.; Pou, J. Nanosecond, picosecond and femtosecond laser surface treatment of magnesium alloy: Role of pulse length. Surf. Coat. Technol. 2021, 427, 127802. [Google Scholar] [CrossRef]
- Huang, F.; Jin, X. Surface texture generation using high-feed milling with spindle speed modulation. Precis. Eng. 2021, 72, 13–24. [Google Scholar] [CrossRef]
- Bijani, D.; Deladi, E.L.; Akchurin, A.; de Rooij, M.B.; Schipper, D.J. The Influence of Surface Texturing on the Frictional Behaviour of Parallel Sliding Lubricated Surfaces under Conditions of Mixed Lubrication. Lubricants 2018, 6, 91. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Dai, S.; Dong, G. Designing a bioinspired scaly textured surface for improving the tribological behaviors of starved lubrication. Tribol. Int. 2022, 173, 107594. [Google Scholar] [CrossRef]
- Bei, G.; Ma, C.; Wang, X.; Sun, J.; Ni, X. Study on Tribological Characteristics of Textured Surface under Convergent Oil Film Gap. Lubricants 2022, 10, 183. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Costa, H.L.; Profito, F.; Gachot, C.; Medina, S.; Dini, D. Influence of surface texturing on hydrodynamic friction in plane converging bearings—An experimental and numerical approach. Tribol. Int. 2019, 134, 190–204. [Google Scholar] [CrossRef]
- Sharma, S.; Jamwal, G.; AWASTHI, R.K. Numerical study on steady state performance enhancement of partial textured hydrodynamic journal bearing. Ind. Lubr. Tribol. 2019, 71, 1055–1063. [Google Scholar] [CrossRef]
- Dobrica, M.B.; Fillon, M.; Pascovici, M.D.; Cicone, T. Optimizing surface texture for hydrodynamic lubricated contacts using a mass-conserving numerical approach. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 737–750. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Profito, F.J.; Rosenkranz, A. Multi-Scale Surface Texturing in Tribology—Current Knowledge and Future Perspectives. Lubricants 2019, 7, 95. [Google Scholar] [CrossRef]
- Hamilton, D.B.; Walowit, J.A.; Allen, C.M. A Theory of Lubrication by Microirregularities. J. Basic Eng. 1966, 88, 177–185. [Google Scholar] [CrossRef]
- Babu, P.V.; Ismail, S.; Ben, B.S. Experimental and numerical studies of positive texture effect on friction reduction of sliding contact under mixed lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 360–375. [Google Scholar] [CrossRef]
- Hu, D.; Guo, Z.; Xie, X.; Yuan, C. Effect of spherical-convex surface texture on tribological performance of water-lubricated bearing. Tribol. Int. 2019, 134, 341–351. [Google Scholar] [CrossRef]
- Yagi, K.; Sugimura, J. Performance of Balancing Wedge Action in Textured Hydrodynamic Pad Bearings. J. Lubr. Technol. 2017, 139, 248. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Wang, H.; Zhou, X.; Zhou, X. Hydrodynamic lubrication of partial textured sliding journal bearing based on three-dimensional CFD. Ind. Lubr. Tribol. 2016, 68, 106–115. [Google Scholar] [CrossRef]
- van Liem, N.; Zhenpeng, W.; Renqiang, J. Effect of shape/size and distribution of microgeometries of textures on tribo-performance of crankpin bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 421–433. [Google Scholar] [CrossRef]
- Maier, M.; Pusterhofer, M.; Grün, F. Multiscale Wear Simulation in Textured, Lubricated Contacts. Coatings 2023, 13, 697. [Google Scholar] [CrossRef]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- Dobrica, M.B.; Fillon, M. About the validity of Reynolds equation and inertia effects in textured sliders of infinite width. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 69–78. [Google Scholar] [CrossRef]
- Cupillard, S.; Glavatskih, S.; Cervantes, M.J. Inertia effects in textured hydrodynamic contacts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 751–756. [Google Scholar] [CrossRef]
- Shibata, Y.; Enomoto, Y. Global Existence of Classical Solutions and Optimal Decay Rate for Compressible Flows via the Theory of Semigroups. In Handbook of Mathematical Analysis in Mechanics of Viscous Fluids; Giga, Y., Novotný, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 2085–2181. [Google Scholar]
- Netgen/NGSolve Finite Element Tool. Available online: https://docu.ngsolve.org/latest/index.html (accessed on 10 January 2024).
- Concli, F. Equilibrium of a journal bearing: A simplified CFD-analytical coupled approach. In Advances in Fluid Mechanics XIII; WIT Transactions on Engineering Sciences: Southampton, UK, 2020; pp. 13–25. [Google Scholar]
- Merkle, C.L.; Feng, J.; Buelow, P.E. Computational modeling of sheet cavitation. In Proceedings of the 3rd International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Gao, G.; Yin, Z.; Jiang, D.; Zhang, X. Numerical analysis of plain journal bearing under hydrodynamic lubrication by water. Tribol. Int. 2014, 75, 31–38. [Google Scholar] [CrossRef]
- OpenFoam. Available online: https://www.openfoam.com/ (accessed on 8 October 2023).
- Pusterhofer, M.; Bergmann, P.; Summer, F.; Grün, F.; Brand, C. A Novel Approach for Modeling Surface Effects in Hydrodynamic Lubrication. Lubricants 2018, 6, 15. [Google Scholar] [CrossRef]
- Maier, M.; Pusterhofer, M.; Summer, F.; Grün, F. Validation of statistic and deterministic asperity contact models using experimental Stribeck data. Tribol. Int. 2021, 165, 107329. [Google Scholar] [CrossRef]
- Chen, Y.M.; Rigaut, B.; Armanet, F. Wear behaviour of partially stabilized zirconia at high sliding speed. J. Eur. Ceram. Soc. 1990, 6, 383–390. [Google Scholar] [CrossRef]
- Savio, A.; Cianferra, M.; Armenio, V. Analysis of Performance of Cavitation Models with Analytically Calculated Coefficients. Energies 2021, 14, 6425. [Google Scholar] [CrossRef]
- Hong, B.; Lv, S.; Liu, Q.; Hou, J.; Ji, Y.; Gao, Z.; Gao, J.; Hu, J. A Simple Method to Evaluate the Vapor Pressure of Transformer Oil at Various Temperatures. In Proceedings of the 2018 7th International Conference on Energy and Environmental Protection (ICEEP 2018), Shenzhen, China, 14–15 July 2018; Advances in Engineering Research. Atlantis Press: Amsterdam, The Netherlands, 2018; Volume 2018. [Google Scholar]
- Lang, O.R.; Steinhilper, W. Gleitlager: Berechnung und Konstruktion von Gleitlagern Mit Konstanter und Zeitlich Veränderlicher Belastung; mit 6 Arbeitsblättern, 1978th ed.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Meng, F.M. On influence of cavitation in lubricant upon tribological performances of textured surfaces. Opt. Laser Technol. 2013, 48, 422–431. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Rizwan, M.; Raza, A.; Ahmed, A.; Abid, M. Effect of dimple shape and depth on tribological performance of textured surface. In Proceedings of the 2021 International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, 12–16 January 2021; IEEE: Piscataway Township, NJ, USA, 2021; pp. 719–725. [Google Scholar]
- DIN ISO 2768-1:1991-06; General Tolerances; Tolerances for Linear and Angular Dimensions without Individual Tolerance Indications. Identical with ISO 2768-1:1989; International Organization for Standardization: Geneva, Switzerland, 1991.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).