The Effects of Splayed Lipid Molecules on Lubrication by Lipid Bilayers
Abstract
1. Introduction
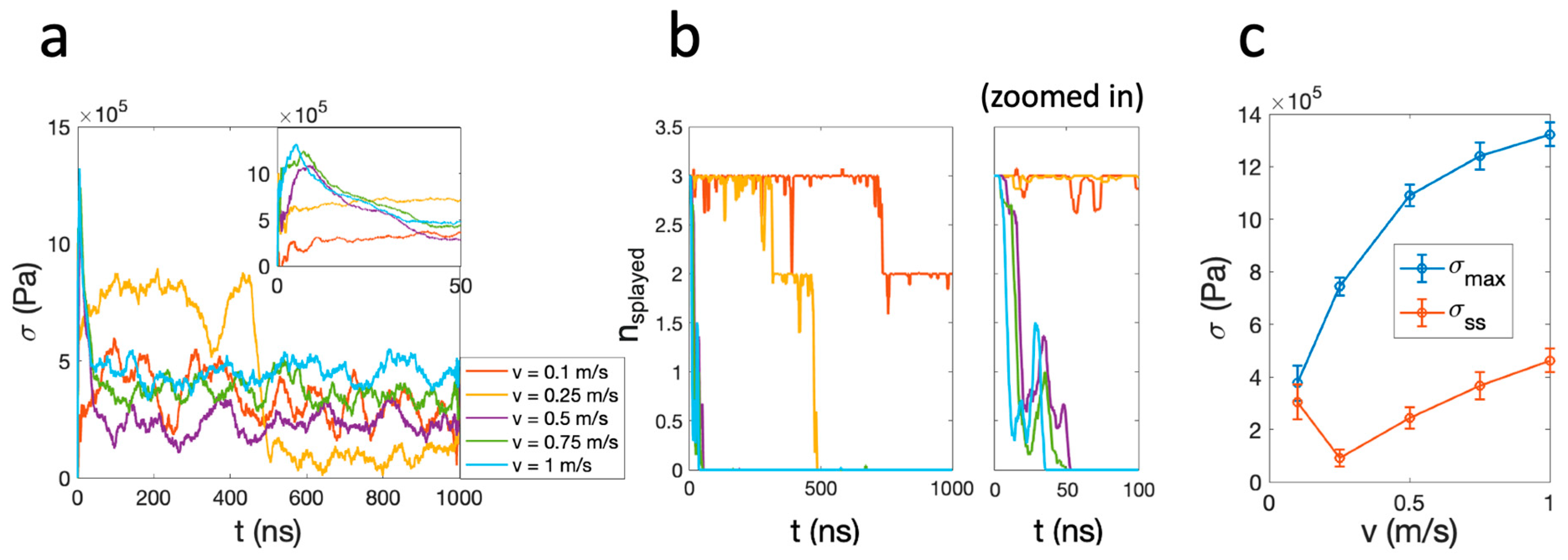
2. Results and Discussion
3. Conclusions
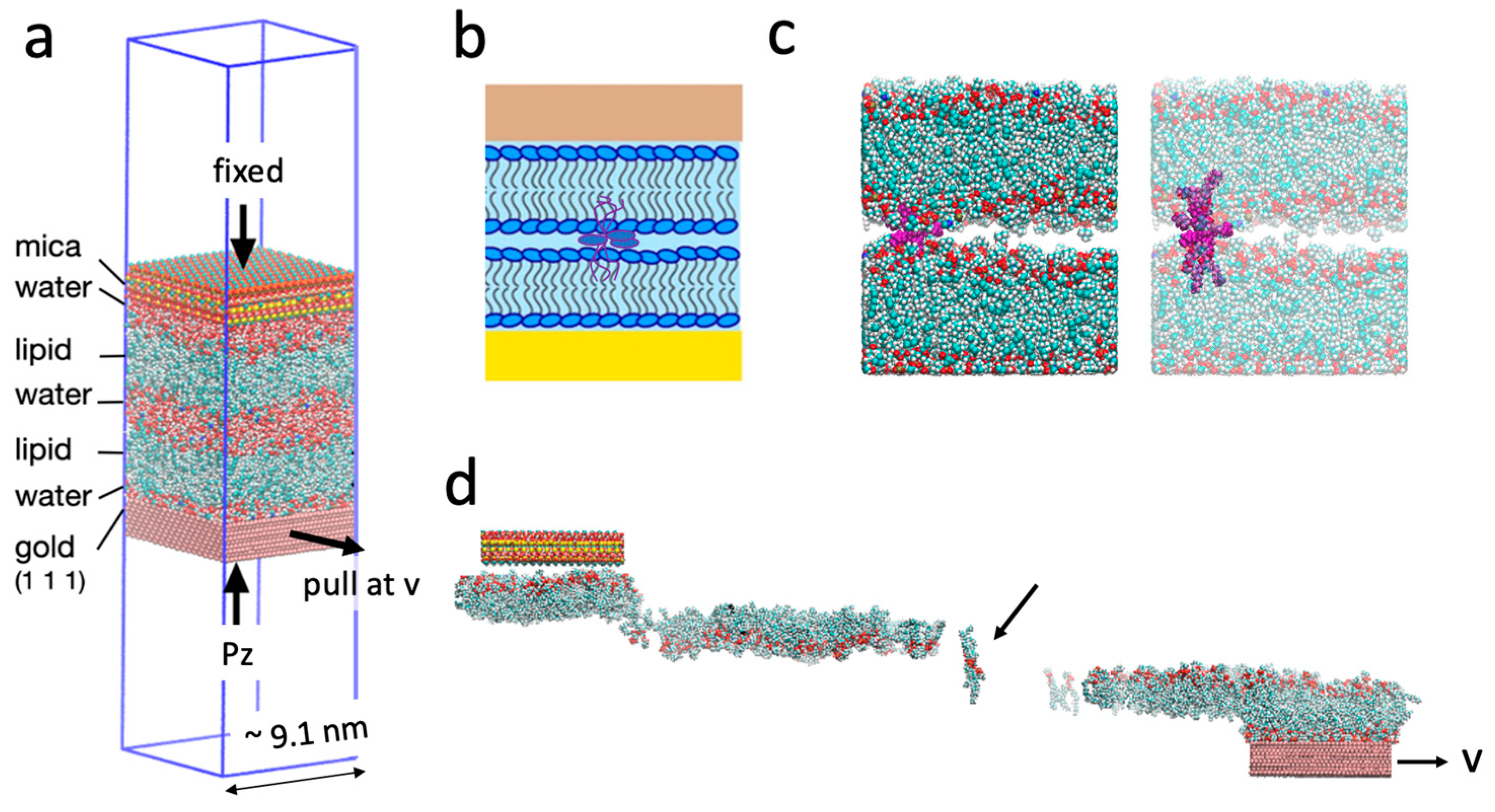
4. Materials and Methods
4.1. Equilibrium Simulations
4.2. Non-Equilibrium Simulations
4.3. Estimating the Number of Splayed Lipids
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Loeser, R.F. The Role of Aging in the Development of Osteoarthritis. Trans. Am. Clin. Climatol. Assoc. 2017, 128, 44–54. [Google Scholar] [PubMed]
- Jahn, S.; Seror, J.; Klein, J. Lubrication of Articular Cartilage. Annu. Rev. Biomed. Eng. 2016, 18, 235–258. [Google Scholar] [CrossRef]
- Yuan, H.; Mears, L.L.E.; Wang, Y.; Su, R.; Qi, W.; He, Z.; Valtiner, M. Lubricants for osteoarthritis treatment: From natural to bioinspired and alternative strategies. Adv. Colloid Interface Sci. 2023, 311, 102814. [Google Scholar] [CrossRef]
- Hunter, D.J.; Schofield, D.; Callander, E. The individual and socioeconomic impact of osteoarthritis. Nat. Rev. Rheumatol. 2014, 10, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Klein, J. Hydration Lubrication in Biomedical Applications: From Cartilage to Hydrogels. Acc. Mater. Res. 2022, 3, 213–223. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Klein, J. Recent Progress in Cartilage Lubrication. Adv. Mater. 2021, 33, e2005513. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Gaisinskaya-Kipnis, A.; Kampf, N.; Klein, J. Origins of hydration lubrication. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef]
- Kosinska, M.K.; Mastbergen, S.C.; Liebisch, G.; Wilhelm, J.; Dettmeyer, R.B.; Ishaque, B.; Rickert, M.; Schmitz, G.; Lafeber, F.P.; Steinmeyer, J. Comparative lipidomic analysis of synovial fluid in human and canine osteoarthritis. Osteoarthr. Cartil. 2016, 24, 1470–1478. [Google Scholar] [CrossRef]
- Sarma, A.V.; Powell, G.L.; LaBerge, M. Phospholipid composition of articular cartilage boundary lubricant. J. Orthop. Res. 2001, 19, 671–676. [Google Scholar] [CrossRef]
- Lin, W.; Liu, Z.; Kampf, N.; Klein, J. The Role of Hyaluronic Acid in Cartilage Boundary Lubrication. Cells 2020, 9, 1606. [Google Scholar] [CrossRef]
- Sorkin, R.; Kampf, N.; Dror, Y.; Shimoni, E.; Klein, J. Origins of extreme boundary lubrication by phosphatidylcholine liposomes. Biomaterials 2013, 34, 5465–5475. [Google Scholar] [CrossRef] [PubMed]
- Sorkin, R.; Kampf, N.; Zhu, L.; Klein, J. Hydration lubrication and shear-induced self-healing of lipid bilayer boundary lubricants in phosphatidylcholine dispersions. Soft Matter 2016, 12, 2773–2784. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, R.; Schroeder, A.; Silbert, G.; Turjeman, K.; Barenholz, Y.; Klein, J. Boundary Lubricants with Exceptionally Low Friction Coefficients Based on 2D Close-Packed Phosphatidylcholine Liposomes. Adv. Mater. 2011, 23, 3517–3521. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Kampf, N.; Kosinska, M.K.; Steinmeyer, J.; Klein, J. Interactions Between Bilayers of Phospholipids Extracted from Human Osteoarthritic Synovial Fluid. Biotribology 2021, 25, 100157. [Google Scholar] [CrossRef]
- Cao, Y.; Klein, J. Lipids and lipid mixtures in boundary layers: From hydration lubrication to osteoarthritis. In Current Opinion in Colloid and Interface Science; Elsevier Ltd.: Amsterdam, The Netherlands, 2022; Volume 58. [Google Scholar]
- Schneck, E.; Sedlmeier, F.; Netz, R.R. Hydration repulsion between biomembranes results from an interplay of dehydration and depolarization. Proc. Natl. Acad. Sci. USA 2012, 109, 14405–14409. [Google Scholar] [CrossRef] [PubMed]
- Foglia, F.; Lawrence, M.J.; Lorenz, C.D.; McLain, S.E. On the hydration of the phosphocholine headgroup in aqueous solution. J. Chem. Phys. 2010, 133, 145103. [Google Scholar] [CrossRef]
- Gawrisch, K.; Gaede, H.C.; Mihailescu, M.; White, S.H. Hydration of POPC bilayers studied by 1H-PFG-MAS-NOESY and neutron diffraction. Eur. Biophys. J. 2007, 36, 281–291. [Google Scholar] [CrossRef] [PubMed]
- Arnold, K.; Lobel, E.; Volke, F.; Gawrisch, K. 31P-NMR investigations of phospholipids. Stud. Biophys. 1981, 82, 207–214. [Google Scholar]
- Arnold, K.; Pratsch, L.; Gawrisch, K. Effect of poly(ethyl- eneglycol) on phospholipid hydration and polarity of the external phase. Biochim. Biophys. Acta 1983, 728, 121–128. [Google Scholar] [CrossRef]
- Murzyn, K.; Róg, T.; Jezierski, G.; Takaoka, Y.; Pasenkiewicz-Gierula, M. Effects of phospholipid unsaturation on the membrane/water interface: A molecular simulation study. Biophys. J. 2001, 81, 170–183. [Google Scholar] [CrossRef]
- Cao, Y.; Kampf, N.; Klein, J. Boundary Lubrication, Hemifusion, and Self-Healing of Binary Saturated and Monounsaturated Phosphatidylcholine Mixtures. Langmuir 2019, 35, 15459–15468. [Google Scholar] [CrossRef] [PubMed]
- Kinnunen, P.K.J. Fusion of lipid bilayers: A model involving mechanistic connection to HII phase forming lipids. Chem. Phys. Lipids 1992, 63, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Tahir, M.A.; Van Lehn, R.C.; Choi, S.H.; Alexander-Katz, A. Solvent-exposed lipid tail protrusions depend on lipid membrane composition and curvature. Biochim. Biophys. Acta 2016, 1858, 1207–1215. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, Y.G.; Marrink, S.J.; Lipowsky, R.; Knecht, V. Solvent-exposed tails as prestalk transition states for membrane fusion at low hydration. J. Am. Chem. Soc. 2010, 132, 6710–6718. [Google Scholar] [CrossRef] [PubMed]
- Scheidt, H.A.; Kolocaj, K.; Veje Kristensen, J.; Huster, D.; Langosch, D. Transmembrane Helix Induces Membrane Fusion through Lipid Binding and Splay. J. Phys. Chem. Lett. 2018, 9, 3181–3186. [Google Scholar] [CrossRef] [PubMed]
- Chernomordik, L.V.; Kozlov, M.M. Mechanics of membrane fusion. Nat. Struct. Mol. Biol. 2008, 15, 675–683. [Google Scholar] [CrossRef]
- Fuhrmans, M.; Marelli, G.; Smirnova, Y.G.; Müller, M. Mechanics of membrane fusion/pore formation. Chem. Phys. Lipids 2015, 185, 109–128. [Google Scholar] [CrossRef] [PubMed]
- Iwata, A.; Sano, Y.; Wanaka, H.; Kobayashi, S.; Okamoto, K.; Yamahara, J.; Inaba, M.; Konishi, Y.; Inoue, J.; Kanayama, A.; et al. Maximum knee extension velocity without external load is a stronger determinant of gait function than quadriceps strength in the early postoperative period following total knee arthroplasty. PLoS ONE 2022, 17, e0276219. [Google Scholar] [CrossRef]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D.; Pastor, R.W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef]
- Lee, J.; Cheng, X.; Swails, J.M.; Yeom, M.S.; Eastman, P.K.; Lemkul, J.A.; Wei, S.; Buckner, J.; Jeong, J.C.; Qi, Y.; et al. CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. J. Chem. Theory Comput. 2016, 12, 405–413. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. Software News and Updates CHARMM-GUI: A Web-Based Graphical User Interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L.; Mackerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Wu, E.L.; Cheng, X.; Jo, S.; Rui, H.; Song, K.C.; Dávila-Contreras, E.M.; Qi, Y.; Lee, J.; Monje-Galvan, V.; Venable, R.M.; et al. CHARMM-GUI membrane builder toward realistic biological membrane simulations. J. Comput. Chem. 2014, 35, 1997–2004. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A Linear Constraint Solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- den Otter, W.K.; Shkulipa, S.A. Intermonolayer Friction and Surface Shear Viscosity of Lipid Bilayer Membranes. Biophys. J. 2007, 93, 423–433. [Google Scholar] [CrossRef]
- Benazieb, O.; Loison, C.; Thalmann, F. Rheology of sliding leaflets in coarse-grained DSPC lipid bilayers. Phys. Rev. E 2021, 104, 054802. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, D.; Klein, J. The Effects of Splayed Lipid Molecules on Lubrication by Lipid Bilayers. Lubricants 2024, 12, 120. https://doi.org/10.3390/lubricants12040120
Jin D, Klein J. The Effects of Splayed Lipid Molecules on Lubrication by Lipid Bilayers. Lubricants. 2024; 12(4):120. https://doi.org/10.3390/lubricants12040120
Chicago/Turabian StyleJin, Di, and Jacob Klein. 2024. "The Effects of Splayed Lipid Molecules on Lubrication by Lipid Bilayers" Lubricants 12, no. 4: 120. https://doi.org/10.3390/lubricants12040120
APA StyleJin, D., & Klein, J. (2024). The Effects of Splayed Lipid Molecules on Lubrication by Lipid Bilayers. Lubricants, 12(4), 120. https://doi.org/10.3390/lubricants12040120




