Abstract
In this paper, we extend the work of Freundlich et al. 2020 who showed how to obtain a Dekel–Zhao density profile with mass dependent shape parameters in the case of galaxies. In the case of Freundlich et al. 2020, the baryonic dependence was obtained using the NIHAO set of simulations. In our case, we used simulations based on a model of ours. Following Freundlich et al. 2020, we obtained the dependence from baryon physics of the two shape parameters, obtaining in this way a mass dependent Dekel–Zhao profile describing the dark matter profiles from galaxies to clusters of galaxies. The extension to the Dekel–Zhao mass dependent profile to clusters of galaxies is the main result of the paper. In the paper, we show how the Dekel–Zhao mass dependent profile gives a good description of the density profiles of galaxies, already shown by Freundlich et al. 2020, but also to a set of clusters of galaxies.
1. Introduction
As shown by a series of observations and gravitational effects at the cosmological level [1], together with effects at astrophysical scales [2,3], we know that the Universe cannot only be constituted of baryonic matter but should contain a non-baryonic mass/energy component with the property of clustering and which is dubbed dark matter (DM). Similarly, the galaxies appear constituted by an amount of baryons that make them visible, and a large halo of DM in which the baryonic component is embedded. Many studies have been performed to describe the DM halo density profiles. Some have showed that, from dwarf galaxy haloes to galaxy clusters, the density profile can be described by the Navarro–Frenk–White (NFW) profile [4,5], characterized by a double power law at small masses (), and large masses (). Further studies found a different kind of profile whose slope decreases going toward the center of the halo, e.g., [6,7,8,9]. These kinds of profiles are well described by the so-called Einasto profile of which we will speak later. The cuspy behavior of the NFW in the central region of the halo disagrees with observations of low-surface-brightness (LSB), dwarf satellite galaxies, and even to a small extent with galaxy clusters, which show flatter cores, e.g., [10,11,12,13,14,15,16,17,18]. In other words, the smallest of the inner slope of the density profile value predicted by dissipationless N-body simulations is larger than the values obtained by observations [19,20,21,22,23,24], in SPH (Smooth Particle Hydrodynamics) simulations [25,26], or in semi-analytical models [27,28,29,30,31].
This issue presents problems for the CDM model at small scales and is called the Cusp/Core problem [10,11] (other problems often mentioned are (a) the missing satellite problem, namely the discrepancy between the number of subhaloes that N-body simulations predict, e.g., [32] and observations; (b) and the Too-Big-To-Fail (TBTF) problem, characterized by too many and too dense simulated sub-haloes with respect to observations [33,34]).
As mentioned, apart from the case of dwarf galaxies and LSBs, the cusp/core problem is also present at the scales of clusters of galaxies, mainly in their central part (10 kpc [16,17]).
As found by kinematics and lensing constraints in galaxies located in the center of relaxed clusters (cD galaxies, Brightest Central Galaxy, hereafter BCG), while the total mass profile, namely the sum of DM and baryons, is in agreement with the NFW predictions, the cluster’s DM profile is flatter than an NFW profile [16,17,35,36].
Several ideas have been proposed to solve that discrepancy: broadly, they are cosmological or astrophysical.
The first approach is based on cosmological solutions to the Cusp/Core problem, namely different DM types of particles are considered rather than, for example, the WIMPS (Weakly Interacting Massive Particles) [37,38,39,40,41,42]. Some solutions introduced modification in the spectrum at small scales e.g., [43]. Other solutions modified theories of gravity used, such as [44,45], see [46,47,48,49] and MOND (MOdified Newtonian Dynamics) [50,51].
The main idea at the root of astrophysics solutions resides in the existence of a “heating mechanism” that produces an expansion of the DM component of a galaxy. This, in turn, produces a reduction of the inner density. In the “supernovae feedback flattening” mechanism, supernovae explosions and/or AGN (Active Galactic Nucleus) outflows produce potential fluctuations that can heat the DM, producing a flattening of the cusp [25,26,52,53,54,55,56].
A different mechanism is based on the exchange of angular momentum and energy between infalling gas clumps, and DM, with the result of “heating” of the DM [27,57,58,59,60,61,62,63,64,65].
The NFW, Einasto, and related density profiles are independent of the mass scale. In [66], it was shown that the inner slope of the density profile depends on the halo mass. This result was later confirmed by several simulations both in the case of galaxies and clusters e.g., [67,68,69,70,71,72,73,74].
Some papers [67,71,72,75] showed that the inner slope in SPH simulations displays regions with values similar to or larger than the NFW slope, and others that are much flatter, reaching a minimum for masses down to , in the case of [67]. This minimum is due to the fact that mass outflows of explosive events overcome halo gravity, giving rise to an expansion of the halo. For larger masses, the slope steepens and reaches values larger than the NFW slope when the stellar mass exceeds . At those masses, baryon accumulation gives rise to adiabatic contraction. The latter effect can be counteracted in the presence of AGN feedback [74,76].
In order to fit the density profiles, several parameterizations have been used. The Einasto profile [6,77,78,79,80] presents two free shape parameters. Leaving free in the fit these two parameters, one can get good fits to DM cusps. Moreover, analytic expressions for the mass, the surface density, the gravitational potential, and quantities important for lensing can be provided. Unfortunately, the Einasto profile does not give a good fit to the innermost part of the density profile for galaxies [81]. Another profile often used is the generalized NFW (gNFW) model that performs in a similar way to the Einasto profile. Other density profiles used have adopted the averaged form.
as in Zhao [82], where , with , a characteristic radius and , a typical density Note that the non-averaged DZ density profile coincides with gNFW profiles for the choice ). This is also the functional form of the gNFW density profile. Considering this form for the actual density profile, if and , where n and k can be any natural numbers, and one can obtain analytically the gravitational potential, the mass, and the velocity dispersion. This family of density profiles is able to provide one which yields very good fits to DM simulations even when baryons are present and is able to follow the profile even when cusps or cores are present. This profile, as shown by Dekel et al. [81], corresponds to and , i.e., and in Equation (1). It remains with two free parameters, namely, a and c, is usually referred to as the Dekel–Zhao (DZ) profile, and captures cores better than other profiles [83]. In order to improve the fit to the density profiles of galaxies and clusters, a new approach has been introduced. The parameters of each fitting profile are expressed in terms of stellar mass, , and virial mass, , or their ratio. For example, Ref. [84] proposed a modified Einasto profile, and Ref. [85] a modified NFW. Unfortunately, their results are obtained at the expense of analyticity. Similarly, Ref. [86] obtained a density profile giving the functional form of the parameters and the concentration parameter, c, in terms of . Their result is a mass-dependent density profile ([86] hereafter Di Cintio et al.) for the haloes. Their corresponding gravitational potential, velocity dispersion, and lensing properties do not possess any analytic forms.
Recently, a mass dependent profile based on the DZ profile was obtained by Freundlich et al. [83]. Similarly to Di Cintio et al. [86], they used the NIHAO project to obtain the functional form of the two parameters of the DZ density profile. The validity of Freundlich et al. [83], Di Cintio et al. [86], and all the mass dependent profiles obtained in the literature is limited to galaxies because the simulations at their base do not take account of AGN feedback. Therefore, their mass dependent profile cannot be built up to the clusters of galaxy mass range. In this paper, our goal is to extend the DZ profile to clusters of galaxies.
The NIHAO project is based on SPH simulations, whose core formation base mechanism focuses on “supernovae feedback”. We previously mentioned the alternative core formation mechanism based on the exchange of energy and angular momentum between infalling gas clumps and DM. We used it in several papers, and describe the model in the next section. Generating structures of different size with it, we seek in this paper to find a relation between the parameters of the DZ density profile, from galaxies to clusters. The paper is organized as follows: In Section 2. we describe the model used. In Section 3, we summarize the steps in which the model works. In Section 4, we describe the DZ profile in general and in Section 5 the DZ mass dependent profile. In Section 6, we apply the previous profile to clusters of galaxies. Section 7 is devoted to conclusions.
2. Description of the Semi-Analytic Model
We employ the semi-analytic model of [27,87]. This scheme significantly improves on the classical spherical collapse models [88,89,90,91,92,93] by taking into account the impact of
- ◇
- tidal torque induced ordered angular momentum e.g., [94,95,96],
- ◇
- random angular momentum caused by random motion in the halo collapse phase e.g., [91,93],
- ◇
- adiabatic contraction AC, e.g., [97,98,99,100],
- ◇
- DM’s dynamical friction with baryonic stellar clumps and gas [27,57,58,59,61,62,63,64,65],
- ◇
- feedback from baryonic-radiation interactions, such as gas cooling, star formation, photoionization, supernova, and AGN feedback [101,102,103] and
- ◇
- dark energy (DE), described by the cosmological constant, as can be seen in Equation A14 in [27], giving the equation of motion of a generic shell [104,105,106],
and by further refinements [31,107,108,108]. These enhancements allowed for accurate and improved results on
- ⤙
- density profiles universality [66,109],
- ⤙
- distinct density profiles details in
- ⪧
- galaxies [3,29] and
- ⪧
- clusters [3,30],
- ⤙
- inner galactic surface-density [110].
While focused on the dynamical friction mechanism (DFBC), the semi-analytic scheme includes contributions from each of the effects listed above, including supernova explosions feedback (SNF) that each impact results to the order of a few percent.
The scheme is implemented according to the following stages:
- (i)
- Expansion of the diffuse gas and DM proto-structure in the linear phase, reaching a maximum radius before re-collapse of DM, forming a potential well for baryons to fall;
- (ii)
- Formation of stars from baryons radiative clumping in the halo center;
- (iii)
- Four parallel processes then follow;
- (a)
- baryon AC increases the DM central cusp, e.g., for galaxies, at , see [27],
- (b)
- baryon-DM dynamical friction (DF) collapses clumps to the galactic center,
- (c)
- the halo central density reduces [57,58] from the transfer to DM, and stars [54,70,111] of DF energy and angular momentum (AM), contrary to the effect of AC;
- (d)
- DF and AC balance, opening the possibility for cusps to heat up, some up to core formation, as in spirals and dwarf spheroidals, while others, like giant galaxies, retains their steeper profile and cusp because of their deeper potential wells;
- (iv)
- Tidal torques (ordered AM), and random AM join their similar effects to DF.
- (v)
- Finally, the disruption of the smallest gas clumps, due to their partial conversion to stars, and the supernovae explosions repeated gas expulsion decrease stellar density, resulting in an additional slight core enlargement; see [65].
2.1. Density Profile Generation
We model the emergence of the density profile in the framework of the spherical model. From an initial, linear Hubble expansion, the expanding density perturbations eventually reaches a maximum turn-around, marking the onset of its recollapse [112,113]. A particle-based Lagrangian approach is used to compute the final density profile, noting the particle’s initial and turn-around radii and , its turnaround density and its collapse factor , in order to obtain
In this approach, one computes the turn-around radius from the density parameter and the DM and baryon shell’s average overdensity
Baryons start entirely in gas form, denoted by the “universal baryon fraction” [114], set to 0.167 in [115] over the total mass and set to , before stars form as discussed below (Section 2.2.2 and Section 2.3).
The profile is then modified by the effects of “specific ordered angular momentum”, h, computed from Tidal torque theory (TTT) that describes how larger scales’ tidal torques induce smaller scales’ angular momentum [94,116,117,118,119], as well as from “random angular momentum”, j, which can be computed from particle orbits, specified by their orbital eccentricity, encoded in the ratio [120], using their pericentric and apocentric radii, resp. and . The dynamical state of the system induces a correction to the eccentricity [92], computed from the halo maximum and spherically averaged turnaround radii, and , as
These effects, as well as DFs, as described by the DF force equation of motion, see Equation A14 in [27], and AC’s steepening, following [98], result in the final density profile.
2.2. Inclusion of the Baryonic Discs and Clumps Effects
In spiral galaxies, the baryon gas halo evolves into a rotationally supported, stable disk, following the equation of motion to obtain a realistic disc size and mass that also solves the angular momentum catastrophe (AMC) problem, Section 3.2, Figures 3 and 4 of [3].
2.2.1. Clump Size Calculation
When disks grow denser, instability appears due to Jean’s criterion in spite of shear effect stabilization. This instability leads to clump formation, whose condition was described by [121], defining a limit criterion composed with (≃20–80 km/s, for most galaxies hosting a clump), the 1D disk’s velocity dispersion, , its surface density, connected to its adiabatic sound speed , , its angular velocity and , its epicyclic frequency
The dispersion relation for perturbations, , yields solutions with the mode that grows fastest [122]
for (Equation 6 in [65]) that leads to obtain the galaxies clump radii [123]
The total mass of maximal–velocity–dispersion, marginally unstable discs () reaches 3 times that of the cold disc and can convert % of their disk mass into clumps [124].
The main properties of clumps found by [125] reflect the general case. For instance, at , haloes harbor objects of order that remain marginally unstable for Gyr.
Smaller haloes have their profiles more efficiently flattened by clumps to DM transfer of AM and energy, as found by [27,59,60,61,62,63,64,65,126].
2.2.2. Clump Life-Time Calculation
Clumps are proven to exist in both simulations, e.g., [127,128,129,130,131,132,133] and observations, as, for instance, the clusters of clumps or clumpy structures detected in high redshift galaxies, thus dubbed chain galaxies e.g., [134,135,136], or the massive star-forming clumps found in HST (Hubble Space Telescope) Ultra Deep Field galaxies [137,138], of which several have been observed at lower redshift [139], and a few at deeper redshift [140].
Very gas-rich discs are expected to give birth, through self-gravitation instability from the accreting dense gas radiative cooling, to those clumpy structures e.g., [125,127,141,142,143]. Clump lifetime is central to their impact on halo central density: they can flatten a cusp into a core if they survive stellar feedback disruption long enough to sink to the galactic center. The assessment of a stellar clump’s bound state can be obtained through , its mass fraction loss by stellar feedback, and , its stellar mass fraction. Then, a threshold at marks the limit for most of the stellar clump’s mass to remain bound, as confirmed by simulations and analytical models [144]. The efficiency of stellar radiation feedback is evaluated from the expulsion fraction [123], with
- (i)
- , the dimensionless reduced surface density
- (ii)
- , the dimensionless reduced mass and
- (iii)
- , the dimensionless reduced efficiency rate of the star-formation, with simply obtained from the ratio between free-fall time, and the stellar mass depletion time.
A large sample of densities, sizes, environments, and scales were used in Ref. [145] to obtain . As typical clumps, having masses , exhibit and , their mass loss after reaching the galactic halo center should remain small. The expulsion fraction method and this conclusion are unfortunately valid in smaller galaxies, for smaller, more compact clumps, for which no clump can be disrupted before reaching the center.
An alternative method produces clump disruption as a result of a comparison between clump migration time to the structure center and their lifetime. The latter has been studied extensively. In their hydrodynamical simulations exhibiting rotational supported clumps in Jean’s equilibrium, Ceverino et al. deduced long lifetimes (≃ Myr) for them, in agreement with several studies: Ref. [123] found such lifetimes in local systems with Kennicutt–Schmidt law star formation. Such long lifetimes can be explained by a long enough clump galactic center migration time to allow them to retain gas, and form bound star groups, as confirmed by simulations from [146]. Galactic center reaching, long-lived clumps were also produced in other simulations, properly accounting for stellar feedback, e.g., radiative and non-thermal feedback, SNF, radiation pressure, etc., in [129,130,132], also presented by [128], for any reasonable feedback efficiency. Clump ages estimated through metal enrichment, expansion, and gas expulsion time scales, ≃200 Myr, >100 Myr and 170–1600 Myr, respectively, in [136] also favors strongly long-lived clumps. Finally, clump stability also emerges from similar clump observations, in radius, mass, and in [147,148,149] between low and high redshifts.
DF and TTT balance off to produce migration time; see Equations 1 and 18 of [65,136], obtaining ≃200 Myr for a clump. The Sedov–Taylor solution, Equations 8 and 9 in [136], produced similar migration and expansion timescales.
2.3. Feedback and Star Formation Procedure
The model’s stellar feedback proceeds from the prescriptions of Section 2.2.2 and 2.2.3 in [101,102] for gas cooling, reionisation, star formation, SNF and AGN feedback.
- Gas cooling
- is modeled with a cooling flow, e.g., see Section 2.2.2 in [102,150].
- Reionisation
- decreases the baryon fraction, during the epoch , asRef. [102], where is the virial mass and , the “filtering mass”; see [151].
- Star formation
- occurs when gas converts into stars, after settling in a disk. Over a given time interval that can be set to , the disc dynamical time, the amount of gas mass converted into stars can be computed aswith , the star formation rate, obtained from the mass of gas measured at a density above the threshold , fixed as in [67] as follows, see [101], for more details:
- SNF
- explosions inject energy into the halo hot gas, following [152]. The computation of this injected energy is prescribed from a Chabrier IMF [153], consisting of
- ∴
- , the energy efficiency of disc gas reheating;
- ∴
- , the available mass within stars;
- ∴
- , the number of SN, created from conversion of into SN, per solar mass, and
- ∴
- erg, the typical energy released per SN explosion,
into the total SN injected energyThis SN released energy into a reheated disk gas and then compared itself with the reheating energy which that same amount of gas should acquire if its injection in the halo should keep its specific energy constant, that is, if the new gas would remain at equilibrium with the halo hot gas. The amount of disk gas the SN and stellar radiation have reheated, , since it is all produced from radiation of stellar origin, is proportional to the stellar massSince the halo hot gas specific energy corresponds to the Virial equilibrium specific kinetic energy , keeping this energy constant under the addition of that reheated gas leads to defining the equilibrium reheating energy asThe comparison with the actual energy of the gas injected from the disk into the halo by SNs gives the threshold (), beyond which gas is expelled, the available energy to expel the reheated gas, and thus the amount of gas ejected from that extra energyContrary to SNF based models such as [67], our mechanism for cusp flattening initiates before the star formation epoch. Since it uses a gravitational energy source, it is thus less limited in available time and energy. Only after DF shapes the core can Stellar and SN feedback occur, which then disrupts gas clouds in the core, similarly to [65]. - AGN feedback
- points to the effects and the formation of a central Super-Massive-Black-Hole (SMBH). Our approach adopts the SMBH mass accretion, and subsequent AGN feedback models of Booth and Schaye [154], modified by the Martizzi et al. [103], Martizzi et al. [155] prescriptions. When the thresholds , and 100 , for stellar density and reduced gas density (), and 3D velocity dispersion, are exceeded, the formation of a seed SMBH occurs and it starts accreting. It has been shown [156] that, above , significant AGN quenching occurs.
2.4. Confirmations of the Semi-Analytic Model’s Robustness
The semi-analytic model’s robustness and accuracy was established in several confrontations with observations and previous converging models:
- α
- Thegalaxy and cluster cusp flattening predicted by the model from collapsing baryonic clump DM heating agrees with previous studies [57,58,61,62,63,64,65], as shown in its, Figure 4 in [109] comparison with SPH simulations from [25];
- β
- The model predicted, in advance of competing groups in the field, the halo cusp inner slope mass dependence, Figure 2a solid line in [66], in terms of rotation , given as [157], well in advance of the similar conclusion that one can extrapolate from Figure 6 in [67];
- γ
- The inner slope dependence on the ratio between baryonic and total mass of the halo was also predicted by the model; see [30] well before its more publicized claim [67];
- δ
- The correct galaxy density profiles were also obtained by the model [27,87] previous to the [25,26] SPH simulations, while that for clusters was predicted in [30], before the results of [69]. Note that these results from the model were obtained with its different dominant mechanism from those of [25,26,69];
- ε
- The Tully–Fisher and Faber–Jackson, , relationships were compared with simulations from the model (Figures 4 and 5 in [107,108]).
- ζ
- Finally, the model’s inner slope evolution with mass (Figure 1 in [107,108]) agrees with [67]’s simulations.
3. Outline of the Semi-Analytic Model’s Main Steps
The semi-analytic approach of our model is much less computing intensive than hydrodynamical and/or N-body simulations, such as NIHAO. Recall that the NIHAO simulation is based on the GASOLINE2 hydrodynamical simulation that includes effects such as [74] photoionisation, Compton cooling, metal cooling, heating from the ultraviolet background, chemical enrichment, star formation, and feedback from massive stars and from SN.
Our model therefore offers a simpler scheme to construct galaxy samples and a faster parameter space exploration. Semi-analytic and N-body/hydro simulations’ comparisons have shown good agreement in the studied cases, see [158] and references therein. Our cosmological parameters follow, Section 2 in [74], while the system’s baryons start in gas form, with “universal baryon fraction” [114] set as , set to 0.167 in [115]. Initial conditions, set from the power spectrum, and evolution follow the description from Appendix B in [27]. The onset, when the system’s nonlinear regime is reached, and subsequent evolution of tidal interaction with neighbours is detailed in Appendix C [27]. The generation of random angular momentum during the collapse phase is calculated in Appendix D [27], while the baryonic dissipative collapse is treated in Appendix E [27], when spiral structure or a spheroid shape are generated, as described in Appendix A5 [107]. The depiction of the model’s clumps characteristics and formation can be found in Section 2.2 in [107], its star formation is specified in Section 2.3 in [107], while its AGN feedback and BH formation are portrayed in Section 2.3, the final part in [107].
4. The Dekel–Zhao Profile
By means of simulated haloes using the NIHAO suite of simulations [159], Dekel et al. [81] showed that the functional form of Equation (1) with and gives very good fits to haloes characterized by cores or cusps. As already reported, this parameterization is dubbed DZ. It can be characterized by better fits to simulated profiles with respect to the NFW and the Einasto profile, and better capture of the cores of density profiles. Moreover, the DZ parameterization allows for analytic expressions of the velocity dispersion, the density, the mass, and the gravitational potential. We now recall several important relations.
The functional form of the DZ profile is
with , , , and , determined by the two shape parameters a and .
The inner logarithmic slope, at scale , is given by [83]
and the concentration parameter smoothed at the same scale, by
The condition that the density is positive yields the condition , while, from the condition that the inner slope is positive, we obtain the extra condition . The parameters are related to . Both a and c can be expressed in terms of and as
and
As in [83], (a, c) are used to express analytic expressions, and (, ) are used in numerical tests.
The analytic expression for the gravitational potential, the velocity dispersion, and the lensing properties are given in Equation (18), Equation (21), and Section 2.3 of [83], respectively.
Freundlich et al. [83] compared the DZ, the gNFW, and the Einasto profiles using the results of the NIHAO suite of SPH simulations. The authors used some profiles from the NIHAO suite, plotted in their Figure 3, and fitted the NIHAO profiles using the gNFW, DZ, and Einasto profiles. The parameters for each profile were considered free. Freundlich et al. [83] showed that the DZ performs better than the other two parameterizations, and in particular, significantly better than the Einasto profile, and marginally better than the gNFW profile.
5. The Dekel–Zhao Mass Dependent Profile
As already discussed, Ref. [86] fitted a profile, similar to Equation (1), to SPH simulations, finding the functional form of the three parameters in terms of , and Ref. [84] proceeded similarly with the Einasto profile. The result provided a density profile with parameters depending on mass. Freundlich et al. [83] did the same with the DZ profile. In summary, they fitted the logarithm of the density profile of the simulated haloes given by NIHAO, according to the DZ parameterization through a least-square minimization in the range 0.01 . Given the mass of a profile, one can easily find , and then one remains with two free parameters a, and c. One can proceed similarly with and . The profile radii r were spaced logarithmically, with radii in the indicated range (0.01 –). As we already discussed, the parameters and are related to a and c. The quality of the fit was evaluated using the rms of the residuals between the simulated , and the model
With the procedure described above, one can obtain the best fit , and , in terms of , , and . In Figure 8 of [83], the dependence of and is plotted in terms of , , and , derived from the DZ density profile fits.
To capture the behavior of and in terms of , , and , Freundlich et al. [83] assumed two functions
where , , , and are adjustable parameters whose values are reproduced in Table 1 of [83]. Concerning , they used
where again , , and are adjustable parameters.
With this procedure, the DZ becomes a mass-dependent profile, displaying some advantages over competing profiles. For example, compared with that of Di Cintio et al. [86], it requires less free parameters and has analytic expressions for dispersion velocity, gravitational potential, and lensing properties.
Until now, we have described how [83] obtained a mass-dependent profile. In our case, we followed a similar procedure, with the difference that, while the simulated haloes’ logarithm of the density profile was fitted by Freundlich et al. [83] from the NIHAO simulations, according to the DZ parameterization, we used the results given by our model. The procedures are identical, except for the forms of the functions that capture the behavior of , and in terms of , , and . From our model, we used the functions
while
and
The parameters of the fit can be found in Table 1.
Figure 1 shows the dependence of and on and . The shaded gray region represents the rms of the residuals. As described in Section 3.3.1 in [83], it is obtained by means of an iterative process excluding points beyond 3 . and are obtained from the fits to the density profile of and . The slope is obtained using Equations (22) and (23). The black solid line represents the best-fit curve, while the dashed lines represent Equations (45) and (46) of [83]. Similarly, parameter is obtained using Equations (22) and (24). The best-fit curve is again represented by the black solid line. The relations of or in terms of are not plotted, since it is directly related to the previous two relations (dependence on and ). For a fixed value of , one can obtain , and , and consider their ratio. Moreover, the relation between , , and , because of AGN feedback, is characterized by a two-branch relation, as that shown in Figure 3 in [74]. In order to obtain the DZ DM profile relative to each halo, one can follow the prescription given in the following, also proposed in Section 4.1 in [83].
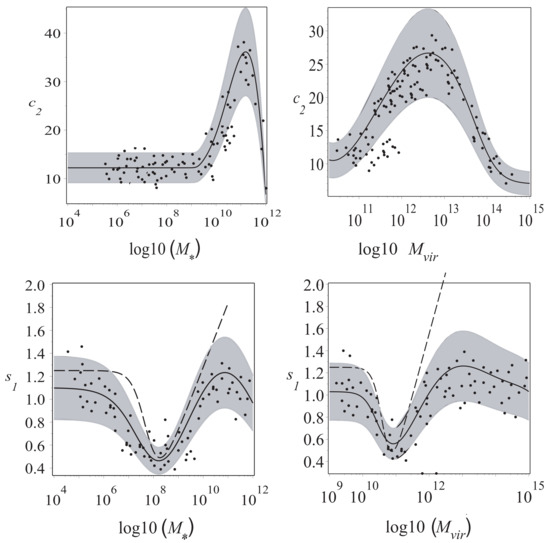
Figure 1.
Mass dependence of the DZ parameters and on and . The parameters and are obtained from the fits to the density profile of and . The stellar-to-halo mass ratio can be obtained from the other two profiles, as written in the text. The slope is obtained using Equations (22) and (23). The best-fit curve is represented by the black solid line, while the dashed lines represent Equations (45) and (46) of [83]. The parameters of the fit are given in Table 1. The parameter is obtained using Equations (22) and (24).The best-fit curve is represented by the black solid line. The rms in gray is obtained, as discussed in Section 5, by means of an iterative process excluding points beyond 3.
- (1)
- and the stellar mass constitute the input parameters. These two quantities are related by abundance matching the relation [160,161,162].
- (2)
- The virial radius can be obtained using the relationwhere , with . As is well known, the critical density is given by . Using Planck Collaboration et al. [163] parameters, and .
- (3)
- (4)
- (5)
- The scaling parameter is given by the following relations: , , and , where .
- (6)
- Finally, the DZ mass-dependent density profile is given by Equation (14). The corresponding circular velocity profile can be obtained from Equations 4 and 6 of [83] with , , and .
An application of the method is shown in Figure 2. The plot shows the density profiles for given values of the masses (, , and ) taken from the NIHAO suite. The red lines are the profiles from NIHAO, the short dashed lines those obtained by [83] with the DZ mass-dependent profile, the dotted ones the result from Di Cintio et al. [86], and the long-dashed lines are the density profiles that we obtained. Similarly to [83], is obtained from Equations (22)–(23), while , and are allowed to vary, and is constrained from the halo mass . In the case of low masses, our density profiles are flatter at low radii. This is due to the fact that, in the NIHAO simulations, the role of the supernovae feedback is larger than in our model. As we discussed in Section 2, in our case, the flattening of the profiles is mainly due to the interaction of gas clumps with DM through dynamical friction.
6. Clusters of Galaxies’ Density Profiles
In Figure 2, we showed the DZ density profile in the case of galaxy types from dwarfs to the Milky Way. Freundlich et al. [83] dedicated their papers to show how the DZ mass dependent profile can be used to describe density profiles in better detail than the gNFW and Einasto, and furthermore compared it with [86]. The main goal of the present paper is to extend [83] to the mass regime of galaxy clusters. To this aim, in Figure 1, we obtained the and parameters in terms of , , up to masses of the order of . In the following, we show how the DZ mass dependent profile can fit the density profile of clusters of galaxies. We choose the [16,17] clusters. As shown in Figure 3 of [17], the mass distribution was studied combining information from weak and strong lensing, and stellar kinematics, allowing the reconstruction of the mass distribution in baryons in the BCG. As shown in Figure 3, the total mass of the clusters studied (MS2137, A963, A383, A611, A2537, A2667, and A2390) is fitted by an NFW profile, while the DM distribution has profiles flatter than the NFW profile, as seen in Figure 5 of [17]. The baryons usually dominate inside a radius of 10 kpc. Concerning the baryon content, Table 3 of [16] gives the luminosity and Table 4 the ratio between stellar mass and luminosity, . The product of by yields the stellar mass. Table 8, of the same paper, describes the characteristics of the total mass density profile, the virial mass, and radius, given , and . The results obtained by means of X-ray observations are also given. We summarize in Table 2 the characteristic of the clusters, starting with the inner slope calculated around 1 kpc, which corresponds to 0.1 % of the virial radius. We then report , , the stellar mass, the virial mass, the ratio between stellar and virial mass, and finally the values of and obtained for each cluster with the method described in the previous sections. In Figure 3, we compared the DM density profile with DZ mass dependent profile calculated as described in the previous sections. The DM density profile obtained by [16,17] is represented in blue, while the mass dependent DZ prediction is plotted in black. The width of the blue bands represents the uncertainty, including the 1 uncertainties for isotropic models, see [16,17], and a systematic component obtained as described in Section 4.3 of [17]. As shown, there is a good agreement between the DM density profile and the mass dependent DZ profile.

Table 2.
Parameters of the clusters studied. Column 2 summarizes the inner DM slope, Column 3 the visual luminosity, Column 4 the mass-to-light ratio, Column 5 the baryon mass content, Column 6 the DM content, and Columns 7 and 8 the parameters and .
Table 2.
Parameters of the clusters studied. Column 2 summarizes the inner DM slope, Column 3 the visual luminosity, Column 4 the mass-to-light ratio, Column 5 the baryon mass content, Column 6 the DM content, and Columns 7 and 8 the parameters and .
| MS2137 | |||||||
| A963 | 1 | ||||||
| A383 | |||||||
| A611 | |||||||
| A2537 | |||||||
| A2667 | |||||||
| A2390 |
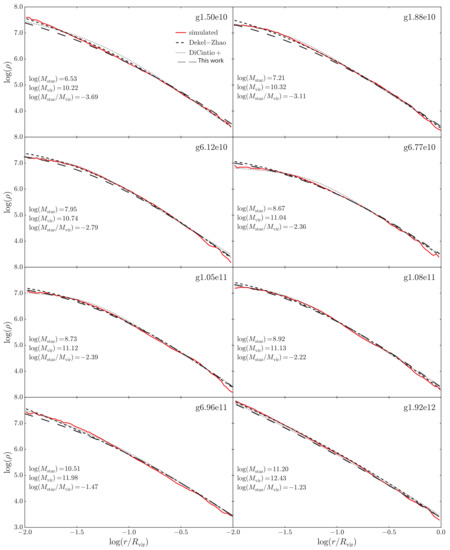
Figure 2.
Comparison of the NIHAO simulated density profile (red lines) with the DZ profile (short dashed line) of [83], the Di Cintio et al. [86] density profile (dotted line), and the DZ profile of our study (long dashed line). Similarly to [83], is obtained from Equations (22)–(23), , an are allowed to vary, and is constrained from the halo mass . , and the simulation galaxies’ names are indicated. is obtained by the ration of and .
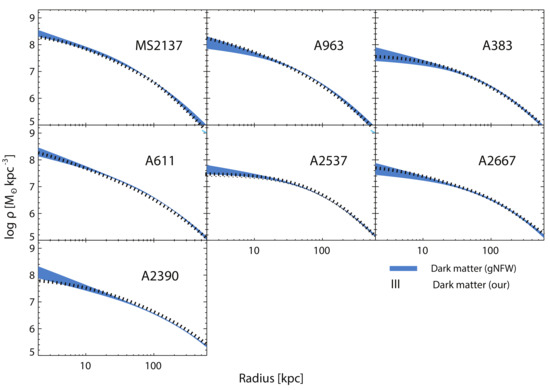
Figure 3.
Comparison of the DM density profile obtained by [16,17] and the density profile predicted by the mass dependent DZ density profile. The width of the blue bands represents the 1 uncertainty plus a systematic component (Section 4.3 of [17]). The black bands represent the DZ mass dependent profile, and the 1 uncertainty.
7. Conclusions
In the present paper, we extended the work of Freundlich et al. [83] related to the DZ density profile. By means of the NIHAO suite of simulations [159], Dekel et al. [81] showed that the functional form of Equation (1) with and gives very good fits to haloes characterized by cores or cusps. This parameterization is dubbed DZ. This function depends on two parameters: Freundlich et al. [83] fitted the DZ profile to SPH simulations expressing the two parameters in terms of stellar mass, , virial mass , and their ratio. To capture the behavior of the two parameters, and , in terms of the quoted masses, two peculiar functions for , and were assumed. In this way, the DZ profile acquires a dependence on halo mass. While Freundlich et al. [83] obtained a mass dependent DZ profile for the case of galaxies, we extended his work to clusters of galaxies. Freundlich et al. [83] used the NIHAO simulations to obtain the mass dependence of the two parameters of the profile, while we used our own analytical model. In this model, baryonic clumps moving inside structures exchange angular momentum and energy with DM through dynamical friction. Following Freundlich et al. [83], we obtained the dependence from baryon physics of the two shape parameters. In this way, we obtained a mass dependent DZ profile describing the DM profiles from galaxies to clusters of galaxies. After obtaining the mass dependent DZ profile, we compared our model’s simulated profiles with the results of [83,86]. The results from our model are in good agreement with simulations and the corresponding profiles. As already reported, the main goal of the present paper is to extend [83] up to the mass of clusters. To reach this goal, we obtained the and parameters in terms of , , up to masses of the order of . In order to see how the DZ mass dependent profile fit the density profile of clusters of galaxies, we choose the [16,17] clusters. The mass distribution in these clusters was obtained combining several techniques, such as weak and strong lensing, and stellar kinematics. We studied the clusters MS2137, A963, A383, A611, A2537, A2667, and A2390. The DM distribution displays profiles flatter than the NFW profile, as shown in Figure 5 of [17]. Given the parameters of the clusters obtained by [16,17], we obtained values of and for each cluster with the method described in the previous sections. We compared the DM density profile obtained by [16,17] with those obtained with our model. As shown, there is a good agreement between the DM density profile and our mass dependent DZ profile.
Author Contributions
A.D.P. and M.L.D. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
MLeD acknowledges the financial support by the Lanzhou University starting fund, the Fundamental Research Funds for the Central Universities (Grant No. lzujbky-2019-25), the National Science Foundation of China (Grant No. 12047501), and the 111 Project under Grant No. B20063.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Planck Collaboration; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Del Popolo, A. Nonbaryonic Dark Matter in Cosmology. Int. J. Mod. Phys. D 2014, 23, 30005. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Navarro, J.F.; Hayashi, E.; Power, C.; Jenkins, A.R.; Frenk, C.S.; White, S.D.M.; Springel, V.; Stadel, J.; Quinn, T.R. The inner structure of ΛCDM haloes - III. Universality and asymptotic slopes. Mon. Not. R. Astron. Soc. 2004, 349, 1039–1051. [Google Scholar] [CrossRef]
- Navarro, J.F.; Ludlow, A.; Springel, V.; Wang, J.; Vogelsberger, M.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Helmi, A. The diversity and similarity of simulated cold dark matter haloes. Mon. Not. R. Astron. Soc. 2010, 402, 21–34. [Google Scholar] [CrossRef]
- Gao, L.; Navarro, J.F.; Cole, S.; Frenk, C.S.; White, S.D.M.; Springel, V.; Jenkins, A.; Neto, A.F. The redshift dependence of the structure of massive Λ cold dark matter haloes. Mon. Not. R. Astron. Soc. 2008, 387, 536–544. [Google Scholar] [CrossRef]
- Springel, V.; Wang, J.; Vogelsberger, M.; Ludlow, A.; Jenkins, A.; Helmi, A.; Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Aquarius Project: The subhaloes of galactic haloes. Mon. Not. R. Astron. Soc. 2008, 391, 1685–1711. [Google Scholar] [CrossRef]
- Flores, R.A.; Primack, J.R. Observational and theoretical constraints on singular dark matter halos. Astrophys. J. Lett. 1994, 427, L1–L4. [Google Scholar] [CrossRef]
- Moore, B. Evidence against dissipation-less dark matter from observations of galaxy haloes. Nature 1994, 370, 629–631. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- De Blok, W.J.G. The Core-Cusp Problem. Adv. Astron. 2010, 2010, 789293. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; Spekkens, K. Do Baryons Alter the Halos of Low Surface Brightness Galaxies? Astrophys. J. Lett. 2011, 741, L29. [Google Scholar] [CrossRef]
- Oh, S.H.; Hunter, D.A.; Brinks, E.; Elmegreen, B.G.; Schruba, A.; Walter, F.; Rupen, M.P.; Young, L.M.; Simpson, C.E.; Johnson, M.C.; et al. High-resolution Mass Models of Dwarf Galaxies from LITTLE THINGS. Astron. J. 2015, 149, 180. [Google Scholar] [CrossRef]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J.; Nipoti, C.; Richard, J.; Jullo, E. The Density Profiles of Massive, Relaxed Galaxy Clusters. I. The Total Density Over Three Decades in Radius. Astrophys. J. 2013, 765, 24. [Google Scholar] [CrossRef]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J. The Density Profiles of Massive, Relaxed Galaxy Clusters. II. Separating Luminous and Dark Matter in Cluster Cores. Astrophys. J. 2013, 765, 25. [Google Scholar] [CrossRef]
- Adams, J.J.; Simon, J.D.; Fabricius, M.H.; van den Bosch, R.C.E.; Barentine, J.C.; Bender, R.; Gebhardt, K.; Hill, G.J.; Murphy, J.D.; Swaters, R.A.; et al. Dwarf Galaxy Dark Matter Density Profiles Inferred from Stellar and Gas Kinematics. Astrophys. J. 2014, 789, 63. [Google Scholar] [CrossRef]
- Burkert, A. The Structure of Dark Matter Halos in Dwarf Galaxies. Astrophys. J. Lett. 1995, 447, L25. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Bosma, A.; McGaugh, S. Simulating observations of dark matter dominated galaxies: Towards the optimal halo profile. Mon. Not. R. Astron. Soc. 2003, 340, 657–678. [Google Scholar] [CrossRef]
- Swaters, R.A.; Madore, B.F.; van den Bosch, F.C.; Balcells, M. The Central Mass Distribution in Dwarf and Low Surface Brightness Galaxies. Astrophys. J. 2003, 583, 732–751. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; Kaufmann, T. Recovering cores and cusps in dark matter haloes using mock velocity field observations. Mon. Not. R. Astron. Soc. 2011, 414, 3617–3626. [Google Scholar] [CrossRef]
- Oh, S.H.; de Blok, W.J.G.; Brinks, E.; Walter, F.; Kennicutt, R.C., Jr. Dark and Luminous Matter in THINGS Dwarf Galaxies. Astron. J. 2011, 141, 193. [Google Scholar] [CrossRef]
- Oh, S.H.; Brook, C.; Governato, F.; Brinks, E.; Mayer, L.; de Blok, W.J.G.; Brooks, A.; Walter, F. The Central Slope of Dark Matter Cores in Dwarf Galaxies: Simulations versus THINGS. Astron. J. 2011, 142, 24. [Google Scholar] [CrossRef]
- Governato, F.; Brook, C.; Mayer, L.; Brooks, A.; Rhee, G.; Wadsley, J.; Jonsson, P.; Willman, B.; Stinson, G.; Quinn, T.; et al. Bulgeless dwarf galaxies and dark matter cores from supernova-driven outflows. Nature 2010, 463, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Governato, F.; Zolotov, A.; Pontzen, A.; Christensen, C.; Oh, S.H.; Brooks, A.M.; Quinn, T.; Shen, S.; Wadsley, J. Cuspy no more: How outflows affect the central dark matter and baryon distribution in Λ cold dark matter galaxies. Mon. Not. R. Astron. Soc. 2012, 422, 1231–1240. [Google Scholar] [CrossRef]
- Del Popolo, A. The Cusp/Core Problem and the Secondary Infall Model. Astrophys. J. 2009, 698, 2093–2113. [Google Scholar] [CrossRef]
- Cardone, V.F.; Del Popolo, A. Newtonian acceleration scales in spiral galaxies. Mon. Not. R. Astron. Soc. 2012, 427, 3176–3187. [Google Scholar] [CrossRef]
- Del Popolo, A. Density profile slopes of dwarf galaxies and their environment. Mon. Not. R. Astron. Soc. 2012, 419, 971–984. [Google Scholar] [CrossRef]
- Del Popolo, A. On the density-profile slope of clusters of galaxies. Mon. Not. R. Astron. Soc. 2012, 424, 38–51. [Google Scholar] [CrossRef]
- Del Popolo, A.; Hiotelis, N. Cusps and cores in the presence of galactic bulges. J. Cosmol. Astropart. Phys. 2014, 1, 47. [Google Scholar] [CrossRef]
- Moore, B.; Quinn, T.; Governato, F.; Stadel, J.; Lake, G. Cold collapse and the core catastrophe. Mon. Not. R. Astron. Soc. 1999, 310, 1147–1152. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. Too big to fail? The puzzling darkness of massive Milky Way subhaloes. Mon. Not. R. Astron. Soc. 2011, 415, L40–L44. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. The Milky Way’s bright satellites as an apparent failure of ΛCDM. Mon. Not. R. Astron. Soc. 2012, 422, 1203–1218. [Google Scholar] [CrossRef]
- Sand, D.J.; Treu, T.; Ellis, R.S. The Dark Matter Density Profile of the Lensing Cluster MS 2137-23: A Test of the Cold Dark Matter Paradigm. Astrophys. J. Lett. 2002, 574, L129–L133. [Google Scholar] [CrossRef]
- Sand, D.J.; Treu, T.; Smith, G.P.; Ellis, R.S. The Dark Matter Distribution in the Central Regions of Galaxy Clusters: Implications for Cold Dark Matter. Astrophys. J. 2004, 604, 88–107. [Google Scholar] [CrossRef]
- Colín, P.; Avila-Reese, V.; Valenzuela, O. Substructure and Halo Density Profiles in a Warm Dark Matter Cosmology. Astrophys. J. 2000, 542, 622–630. [Google Scholar] [CrossRef]
- Goodman, J. Repulsive dark matter. New Astron. 2000, 5, 103–107. [Google Scholar] [CrossRef]
- Hu, W.; Barkana, R.; Gruzinov, A. Fuzzy Cold Dark Matter: The Wave Properties of Ultralight Particles. Phys. Rev. Lett. 2000, 85, 1158. [Google Scholar] [CrossRef]
- Kaplinghat, M.; Knox, L.; Turner, M.S. Annihilating Cold Dark Matter. Phys. Rev. Lett. 2000, 85, 3335. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Fluid Dark Matter. Astrophys. J. Lett. 2000, 534, L127–L129. [Google Scholar] [CrossRef] [PubMed]
- Sommer-Larsen, J.; Dolgov, A. Formation of Disk Galaxies: Warm Dark Matter and the Angular Momentum Problem. Astrophys. J. 2001, 551, 608–623. [Google Scholar] [CrossRef]
- Zentner, A.R.; Bullock, J.S. Halo Substructure and the Power Spectrum. Astrophys. J. 2003, 598, 49–72. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s other gravity and the acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Dent, J.B.; Dutta, S.; Saridakis, E.N. f(T) gravity mimicking dynamical dark energy. Background and perturbation analysis. J. Cosmol. Astropart. Phys. 2011, 1, 9. [Google Scholar] [CrossRef]
- Zheng, R.; Huang, Q.G. Growth factor in f(T) gravity. J. Cosmol. Astropart. Phys. 2011, 3, 2. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics—Implications for galaxies. Astrophys. J. 1983, 270, 371–389. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Navarro, J.F.; Eke, V.R.; Frenk, C.S. The cores of dwarf galaxy haloes. Mon. Not. R. Astron. Soc. 1996, 283, L72–L78. [Google Scholar] [CrossRef]
- Gelato, S.; Sommer-Larsen, J. On DDO 154 and cold dark matter halo profiles. Mon. Not. R. Astron. Soc. 1999, 303, 321–328. [Google Scholar] [CrossRef][Green Version]
- Read, J.I.; Gilmore, G. Mass loss from dwarf spheroidal galaxies: The origins of shallow dark matter cores and exponential surface brightness profiles. Mon. Not. R. Astron. Soc. 2005, 356, 107–124. [Google Scholar] [CrossRef]
- Mashchenko, S.; Couchman, H.M.P.; Sills, A. Formation of Minigalaxies in Defunct Cosmological H II Regions. Astrophys. J. 2006, 639, 633–643. [Google Scholar] [CrossRef][Green Version]
- Mashchenko, S.; Wadsley, J.; Couchman, H.M.P. Stellar Feedback in Dwarf Galaxy Formation. Science 2008, 319, 174. [Google Scholar] [CrossRef]
- El-Zant, A.; Shlosman, I.; Hoffman, Y. Dark Halos: The Flattening of the Density Cusp by Dynamical Friction. Astrophys. J. 2001, 560, 636–643. [Google Scholar] [CrossRef]
- El-Zant, A.A.; Hoffman, Y.; Primack, J.; Combes, F.; Shlosman, I. Flat-cored Dark Matter in Cuspy Clusters of Galaxies. Astrophys. J. Lett. 2004, 607, L75–L78. [Google Scholar] [CrossRef]
- Ma, C.P.; Boylan-Kolchin, M. Are Halos of Collisionless Cold Dark Matter Collisionless? Phys. Rev. Lett. 2004, 93, 021301. [Google Scholar] [CrossRef]
- Nipoti, C.; Treu, T.; Ciotti, L.; Stiavelli, M. Galactic cannibalism and cold dark matter density profiles. Mon. Not. R. Astron. Soc. 2004, 355, 1119–1124. [Google Scholar] [CrossRef]
- Romano-Díaz, E.; Shlosman, I.; Hoffman, Y.; Heller, C. Erasing Dark Matter Cusps in Cosmological Galactic Halos with Baryons. Astrophys. J. Lett. 2008, 685, L105–L108. [Google Scholar] [CrossRef]
- Romano-Díaz, E.; Shlosman, I.; Heller, C.; Hoffman, Y. Dissecting Galaxy Formation. I. Comparison Between Pure Dark Matter and Baryonic Models. Astrophys. J. 2009, 702, 1250–1267. [Google Scholar] [CrossRef]
- Cole, D.R.; Dehnen, W.; Wilkinson, M.I. Weakening dark matter cusps by clumpy baryonic infall. Mon. Not. R. Astron. Soc. 2011, 416, 1118–1134. [Google Scholar] [CrossRef]
- Inoue, S.; Saitoh, T.R. Cores and revived cusps of dark matter haloes in disc galaxy formation through clump clusters. Mon. Not. R. Astron. Soc. 2011, 418, 2527–2531. [Google Scholar] [CrossRef]
- Nipoti, C.; Binney, J. Early flattening of dark matter cusps in dwarf spheroidal galaxies. Mon. Not. R. Astron. Soc. 2015, 446, 1820–1828. [Google Scholar] [CrossRef]
- Del Popolo, A. On the universality of density profiles. Mon. Not. R. Astron. Soc. 2010, 408, 1808–1817. [Google Scholar] [CrossRef]
- Di Cintio, A.; Brook, C.B.; Macciò, A.V.; Stinson, G.S.; Knebe, A.; Dutton, A.A.; Wadsley, J. The dependence of dark matter profiles on the stellar-to-halo mass ratio: A prediction for cusps versus cores. Mon. Not. R. Astron. Soc. 2014, 437, 415–423. [Google Scholar] [CrossRef]
- Zolotov, A.; Brooks, A.M.; Willman, B.; Governato, F.; Pontzen, A.; Christensen, C.; Dekel, A.; Quinn, T.; Shen, S.; Wadsley, J. Baryons Matter: Why Luminous Satellite Galaxies have Reduced Central Masses. Astrophys. J. 2012, 761, 71. [Google Scholar] [CrossRef]
- Martizzi, D.; Teyssier, R.; Moore, B. Cusp-core transformations induced by AGN feedback in the progenitors of cluster galaxies. Mon. Not. R. Astron. Soc. 2013, 432, 1947–1954. [Google Scholar] [CrossRef]
- Teyssier, R.; Pontzen, A.; Dubois, Y.; Read, J.I. Cusp-core transformations in dwarf galaxies: Observational predictions. Mon. Not. R. Astron. Soc. 2013, 429, 3068–3078. [Google Scholar] [CrossRef]
- Chan, T.K.; Kereš, D.; Oñorbe, J.; Hopkins, P.F.; Muratov, A.L.; Faucher-Giguère, C.A.; Quataert, E. The impact of baryonic physics on the structure of dark matter haloes: The view from the FIRE cosmological simulations. Mon. Not. R. Astron. Soc. 2015, 454, 2981–3001. [Google Scholar] [CrossRef]
- Tollet, E.; Macciò, A.V.; Dutton, A.A.; Stinson, G.S.; Wang, L.; Penzo, C.; Gutcke, T.A.; Buck, T.; Kang, X.; Brook, C.; et al. NIHAO - IV: Core creation and destruction in dark matter density profiles across cosmic time. Mon. Not. R. Astron. Soc. 2016, 456, 3542–3552. [Google Scholar] [CrossRef]
- Peirani, S.; Dubois, Y.; Volonteri, M.; Devriendt, J.; Bundy, K.; Silk, J.; Pichon, C.; Kaviraj, S.; Gavazzi, R.; Habouzit, M. Density profile of dark matter haloes and galaxies in the HORIZON-AGN simulation: The impact of AGN feedback. Mon. Not. R. Astron. Soc. 2017, 472, 2153–2169. [Google Scholar] [CrossRef]
- Macciò, A.V.; Crespi, S.; Blank, M.; Kang, X. NIHAO-XXIII: Dark Matter density shaped by Black Hole feedback. Mon. Not. R. Astron. Soc. 2020. [Google Scholar] [CrossRef]
- Dutton, A.A.; Macciò, A.V.; Dekel, A.; Wang, L.; Stinson, G.; Obreja, A.; Di Cintio, A.; Brook, C.; Buck, T.; Kang, X. NIHAO IX: The role of gas inflows and outflows in driving the contraction and expansion of cold dark matter haloes. Mon. Not. R. Astron. Soc. 2016, 461, 2658–2675. [Google Scholar] [CrossRef]
- Del Popolo, A.; Le Delliou, M.; Deliyergiyev, M. Cluster density slopes from dark matter-baryons energy transfer. Phys. Dark Univ. 2021, 33, 100847. [Google Scholar] [CrossRef]
- Einasto, J. On the Construction of a Composite Model for the Galaxy and on the Determination of the System of Galactic Parameters. Trudy Astrofizicheskogo Instituta Alma-Ata 1965, 5, 87–100. [Google Scholar]
- Mamon, G.A.; Biviano, A.; Murante, G. The universal distribution of halo interlopers in projected phase space. Bias in galaxy cluster concentration and velocity anisotropy? Astron. Astrophys. 2010, 520, A30. [Google Scholar] [CrossRef]
- Retana-Montenegro, E.; van Hese, E.; Gentile, G.; Baes, M.; Frutos-Alfaro, F. Analytical properties of Einasto dark matter haloes. Astron. Astrophys. 2012, 540, A70. [Google Scholar] [CrossRef]
- An, J.; Zhao, H. Fitting functions for dark matter density profiles. Mon. Not. R. Astron. Soc. 2013, 428, 2805–2811. [Google Scholar] [CrossRef]
- Dekel, A.; Ishai, G.; Dutton, A.A.; Maccio, A.V. Dark-matter halo profiles of a general cusp/core with analytic velocity and potential. Mon. Not. R. Astron. Soc. 2017, 468, 1005–1022. [Google Scholar] [CrossRef]
- Zhao, H. Analytical models for galactic nuclei. Mon. Not. R. Astron. Soc. 1996, 278, 488–496. [Google Scholar] [CrossRef]
- Freundlich, J.; Jiang, F.; Dekel, A.; Cornuault, N.; Ginzburg, O.; Koskas, R.; Lapiner, S.; Dutton, A.; Macciò, A.V. The Dekel-Zhao profile: A mass-dependent dark-matter density profile with flexible inner slope and analytic potential, velocity dispersion, and lensing properties. Mon. Not. R. Astron. Soc. 2020, 499, 2912–2933. [Google Scholar] [CrossRef]
- Lazar, A.; Bullock, J.S.; Boylan-Kolchin, M.; Chan, T.K.; Hopkins, P.F.; Graus, A.S.; Wetzel, A.; El-Badry, K.; Wheeler, C.; Straight, M.C.; et al. A dark matter profile to model diverse feedback-induced core sizes of ΛCDM haloes. Mon. Not. R. Astron. Soc. 2020, 497, 2393–2417. [Google Scholar] [CrossRef]
- Read, J.I.; Agertz, O.; Collins, M.L.M. Dark matter cores all the way down. Mon. Not. R. Astron. Soc. 2016, 459, 2573–2590. [Google Scholar] [CrossRef]
- Di Cintio, A.; Brook, C.B.; Dutton, A.A.; Macciò, A.V.; Stinson, G.S.; Knebe, A. A mass-dependent density profile for dark matter haloes including the influence of galaxy formation. Mon. Not. R. Astron. Soc. 2014, 441, 2986–2995. [Google Scholar] [CrossRef]
- Del Popolo, A.; Kroupa, P. Density profiles of dark matter haloes on galactic and cluster scales. Astron. Astrophys. 2009, 502, 733–747. [Google Scholar] [CrossRef]
- Gunn, J.E.; Gott, J.R., III. On the Infall of Matter Into Clusters of Galaxies and Some Effects on Their Evolution. Astrophys. J. 1972, 176, 1. [Google Scholar] [CrossRef]
- Bertschinger, E. Self-similar secondary infall and accretion in an Einstein-de Sitter universe. Astrophys. J. Suppl. 1985, 58, 39–65. [Google Scholar] [CrossRef]
- Hoffman, Y.; Shaham, J. Local density maxima - Progenitors of structure. Astrophys. J. 1985, 297, 16–22. [Google Scholar] [CrossRef]
- Ryden, B.S.; Gunn, J.E. Galaxy formation by gravitational collapse. Astrophys. J. 1987, 318, 15–31. [Google Scholar] [CrossRef]
- Ascasibar, Y.; Yepes, G.; Gottlöber, S.; Müller, V. On the physical origin of dark matter density profiles. Mon. Not. R. Astron. Soc. 2004, 352, 1109–1120. [Google Scholar] [CrossRef]
- Williams, L.L.R.; Babul, A.; Dalcanton, J.J. Investigating the Origins of Dark Matter Halo Density Profiles. Astrophys. J. 2004, 604, 18–39. [Google Scholar] [CrossRef]
- Ryden, B.S. Galaxy formation—The role of tidal torques and dissipational infall. Astrophys. J. 1988, 329, 589–611. [Google Scholar] [CrossRef]
- Del Popolo, A.; Gambera, M. Substructure effects on the collapse of density perturbations. Astron. Astrophys. 1997, 321, 691–695. [Google Scholar]
- Del Popolo, A.; Gambera, M. Non radial motions and the shapes and the abundance of clusters of galaxies. Astron. Astrophys. 2000, 357, 809–815. [Google Scholar]
- Blumenthal, G.R.; Faber, S.M.; Flores, R.; Primack, J.R. Contraction of dark matter galactic halos due to baryonic infall. Astrophys. J. 1986, 301, 27–34. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Kravtsov, A.V.; Klypin, A.A.; Nagai, D. Response of Dark Matter Halos to Condensation of Baryons: Cosmological Simulations and Improved Adiabatic Contraction Model. Astrophys. J. 2004, 616, 16–26. [Google Scholar] [CrossRef]
- Klypin, A.; Zhao, H.; Somerville, R.S. ΛCDM-based Models for the Milky Way and M31. I. Dynamical Models. Astrophys. J. 2002, 573, 597–613. [Google Scholar] [CrossRef]
- Gustafsson, M.; Fairbairn, M.; Sommer-Larsen, J. Baryonic pinching of galactic dark matter halos. Phys. Rev. D 2006, 74, 123522. [Google Scholar] [CrossRef]
- De Lucia, G.; Helmi, A. The Galaxy and its stellar halo: Insights on their formation from a hybrid cosmological approach. Mon. Not. R. Astron. Soc. 2008, 391, 14–31. [Google Scholar] [CrossRef]
- Li, Y.S.; De Lucia, G.; Helmi, A. On the nature of the Milky Way satellites. Mon. Not. R. Astron. Soc. 2010, 401, 2036–2052. [Google Scholar] [CrossRef]
- Martizzi, D.; Teyssier, R.; Moore, B.; Wentz, T. The effects of baryon physics, black holes and active galactic nucleus feedback on the mass distribution in clusters of galaxies. Mon. Not. R. Astron. Soc. 2012, 422, 3081–3091. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Lima, J.A.S. Extended Spherical Collapse and the Accelerating Universe. Int. J. Mod. Phy. D 2013, 22, 50038. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Lima, J.A.S. Spherical collapse model with shear and angular momentum in dark energy cosmologies. Mon. Not. R. Astron. Soc. 2013, 430, 628–637. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Maydanyuk, S.P.; Lima, J.A.S.; Jesus, J.F. Shear and rotation in Chaplygin cosmology. Phys. Rev. D 2013, 87, 043527. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F. The Cusp/Core problem: Supernovae feedback versus the baryonic clumps and dynamical friction model. Astrophys. Space Sci. 2016, 361, 162. [Google Scholar] [CrossRef]
- Del Popolo, A. On the dark matter haloes inner structure and galaxy morphology. Astrophys. Space Sci. 2016, 361, 222. [Google Scholar] [CrossRef]
- Del Popolo, A. Non-power law behavior of the radial profile of phase-space density of halos. J. Cosmol. Astropart. Phys. 2011, 7, 14. [Google Scholar] [CrossRef]
- Del Popolo, A.; Cardone, V.F.; Belvedere, G. Surface density of dark matter haloes on galactic and cluster scales. Mon. Not. R. Astron. Soc. 2013, 429, 1080–1087. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. How supernova feedback turns dark matter cusps into cores. Mon. Not. R. Astron. Soc. 2012, 421, 3464–3471. [Google Scholar] [CrossRef]
- Gunn, J.E. Massive galactic halos. I - Formation and evolution. Astrophys. J. 1977, 218, 592–598. [Google Scholar] [CrossRef]
- Fillmore, J.A.; Goldreich, P. Self-similar gravitational collapse in an expanding universe. Astrophys. J. 1984, 281, 1–8. [Google Scholar] [CrossRef]
- Komatsu, E.; Dunkley, J.; Nolta, M.R. Five-Year Wilkinson Microwave Anisotropy Probe Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2009, 180, 330–376. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Hoyle, F. On the Fragmentation of Gas Clouds Into Galaxies and Stars. Astrophys. J. 1953, 118, 513. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Origin of the Angular Momentum of Galaxies. Astrophys. J. 1969, 155, 393. [Google Scholar] [CrossRef]
- White, S.D.M. Angular momentum growth in protogalaxies. Astrophys. J. 1984, 286, 38–41. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Loeb, A. An analytical model for the triaxial collapse of cosmological perturbations. Astrophys. J. 1995, 439, 520–541. [Google Scholar] [CrossRef]
- Avila-Reese, V.; Firmani, C.; Hernández, X. On the Formation and Evolution of Disk Galaxies: Cosmological Initial Conditions and the Gravitational Collapse. Astrophys. J. 1998, 505, 37–49. [Google Scholar] [CrossRef]
- Toomre, A. On the gravitational stability of a disk of stars. Astrophys. J. 1964, 139, 1217–1238. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic dynamics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Krumholz, M.R.; Dekel, A. Survival of star-forming giant clumps in high-redshift galaxies. Mon. Not. R. Astron. Soc. 2010, 406, 112–120. [Google Scholar] [CrossRef]
- Dekel, A.; Sari, R.; Ceverino, D. Formation of Massive Galaxies at High Redshift: Cold Streams, Clumpy Disks, and Compact Spheroids. Astrophys. J. 2009, 703, 785–801. [Google Scholar] [CrossRef]
- Ceverino, D.; Dekel, A.; Mandelker, N.; Bournaud, F.; Burkert, A.; Genzel, R.; Primack, J. Rotational support of giant clumps in high-z disc galaxies. Mon. Not. R. Astron. Soc. 2012, 420, 3490–3520. [Google Scholar] [CrossRef]
- Del Popolo, A.; Le Delliou, M. A unified solution to the small scale problems of the ΛCDM model II: Introducing parent-satellite interaction. J. Cosmol. Astropart. Phys. 2014, 12, 51. [Google Scholar] [CrossRef]
- Ceverino, D.; Dekel, A.; Bournaud, F. High-redshift clumpy discs and bulges in cosmological simulations. Mon. Not. R. Astron. Soc. 2010, 404, 2151–2169. [Google Scholar] [CrossRef]
- Perez, J.; Valenzuela, O.; Tissera, P.B.; Michel-Dansac, L. Clumpy disc and bulge formation. Mon. Not. R. Astron. Soc. 2013, 436, 259–265. [Google Scholar] [CrossRef]
- Perret, V.; Renaud, F.; Epinat, B.; Amram, P.; Bournaud, F.; Contini, T.; Teyssier, R.; Lambert, J.C. Evolution of the mass, size, and star formation rate in high redshift merging galaxies - MIRAGE—A new sample of simulations with detailed stellar feedback. Astron. Astrophys. 2014, 562, A1. [Google Scholar] [CrossRef]
- Ceverino, D.; Klypin, A.; Klimek, E.; Trujillo-Gomez, S.; Churchill, C.W.; Primack, J. Radiative feedback and the low efficiency of galaxy formation in low-mass haloes at high redshift. Mon. Not. Royal Astron. Soc. 2014, 442, 1545–1559. [Google Scholar] [CrossRef]
- Ceverino, D.; Dekel, A.; Tweed, D.; Primack, J. Early formation of massive, compact, spheroidal galaxies with classical profiles by violent disc instability or mergers. Mon. Not. Royal Astron. Soc. 2015, 447, 3291. [Google Scholar] [CrossRef]
- Bournaud, F.; Perret, V.; Renaud, F.; Dekel, A.; Elmegreen, B.G.; Elmegreen, D.M.; Teyssier, R.; Amram, P.; Daddi, E.; Duc, P.A.; et al. The Long Lives of Giant Clumps and the Birth of Outflows in Gas-rich Galaxies at High Redshift. Astrophys. J. 2014, 780, 57. [Google Scholar] [CrossRef]
- Behrendt, M.; Burkert, A.; Schartmann, M. Clusters of Small Clumps Can Explain the Peculiar Properties of Giant Clumps in High-redshift Galaxies. Astrophys. J. Lett. 2016, 819, L2. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G.; Hirst, A.C. Discovery of Face-on Counterparts of Chain Galaxies in the Tadpole Advanced Camera for Surveys Field. Astrophys. J. Lett. 2004, 604, L21–L23. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G.; Marcus, M.T.; Shahinyan, K.; Yau, A.; Petersen, M. Clumpy Galaxies in Goods and Gems: Massive Analogs of Local Dwarf Irregulars. Astrophys. J. 2009, 701, 306–329. [Google Scholar] [CrossRef]
- Genzel, R.; Newman, S.; Jones, T.; Förster Schreiber, N.M.; Shapiro, K.; Genel, S.; Lilly, S.J. The Sins Survey of z ~ 2 Galaxy Kinematics: Properties of the Giant Star-forming Clumps. Astrophys. J. 2011, 733, 101. [Google Scholar] [CrossRef]
- Guo, Y.; Giavalisco, M.; Ferguson, H.C.; Cassata, P.; Koekemoer, A.M. Multi-wavelength View of Kiloparsec-scale Clumps in Star-forming Galaxies at z ~ 2. Astrophys. J. 2012, 757, 120. [Google Scholar] [CrossRef]
- Wuyts, S.; Förster Schreiber, N.M.; Nelson, E.J.; van Dokkum, P.G.; Brammer, G.; Chang, Y.Y.; Faber, S.M.; Ferguson, H.C.; Franx, M.; Fumagalli, M.; et al. A CANDELS-3D-HST synergy: Resolved Star Formation Patterns at 0.7 < z < 1.5. Astrophys. J. 2013, 779, 135. [Google Scholar] [CrossRef]
- Guo, Y.; Ferguson, H.C.; Bell, E.F.; Koo, D.C.; Conselice, C.J.; Giavalisco, M.; Kassin, S.; Lu, Y.; Lucas, R.; Mandelker, N.; et al. Clumpy Galaxies in CANDELS. I. The Definition of UV Clumps and the Fraction of Clumpy Galaxies at 0.5 < z < 3. Astrophys. J. 2015, 800, 39. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G.; Ravindranath, S.; Coe, D.A. Resolved Galaxies in the Hubble Ultra Deep Field: Star Formation in Disks at High Redshift. Astrophys. J. 2007, 658, 763–777. [Google Scholar] [CrossRef]
- Noguchi, M. Clumpy star-forming regions as the origin of the peculiar morphology of high-redshift galaxies. Nature 1998, 392, 253. [Google Scholar] [CrossRef]
- Noguchi, M. Early Evolution of Disk Galaxies: Formation of Bulges in Clumpy Young Galactic Disks. Astrophys. J. 1999, 514, 77–95. [Google Scholar] [CrossRef]
- Aumer, M.; Burkert, A.; Johansson, P.H.; Genzel, R. The Structure of Gravitationally Unstable Gas-rich Disk Galaxies. Astrophys. J. 2010, 719, 1230–1243. [Google Scholar] [CrossRef]
- Baumgardt, H.; Kroupa, P. A comprehensive set of simulations studying the influence of gas expulsion on star cluster evolution. Mon. Not. R. Astron. Soc. 2007, 380, 1589–1598. [Google Scholar] [CrossRef]
- Krumholz, M.R.; Tan, J.C. Slow Star Formation in Dense Gas: Evidence and Implications. Astrophys. J. 2007, 654, 304–315. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Bournaud, F.; Elmegreen, D.M. Bulge Formation by the Coalescence of Giant Clumps in Primordial Disk Galaxies. Astrophys. J. 2008, 688, 67–77. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Elmegreen, D.M.; Sánchez Almeida, J.; Muñoz-Tuñón, C.; Dewberry, J.; Putko, J.; Teich, Y.; Popinchalk, M. Massive Clumps in Local Galaxies: Comparisons with High-redshift Clumps. Astrophys. J. 2013, 774, 86. [Google Scholar] [CrossRef]
- Garland, C.A.; Pisano, D.J.; Mac Low, M.M.; Kreckel, K.; Rabidoux, K.; Guzmán, R. Nearby Clumpy, Gas Rich, Star-forming Galaxies: Local Analogs of High-redshift Clumpy Galaxies. Astrophys. J. 2015, 807, 134. [Google Scholar] [CrossRef]
- Mandelker, N.; Dekel, A.; Ceverino, D.; DeGraf, C.; Guo, Y.; Primack, J. Giant Clumps in Simulated High-z Galaxies: Properties, Evolution and Dependence on Feedback. Mon. Not. Royal Astron. Soc. 2017, 464, 635–665. [Google Scholar] [CrossRef]
- White, S.D.M.; Frenk, C.S. Galaxy formation through hierarchical clustering. Astrophys. J. 1991, 379, 52–79. [Google Scholar] [CrossRef]
- Kravtsov, A.V.; Gnedin, O.Y.; Klypin, A.A. The Tumultuous Lives of Galactic Dwarfs and the Missing Satellites Problem. Astrophys. J. 2004, 609, 482–497. [Google Scholar] [CrossRef]
- Croton, D.J.; Springel, V.; White, S.D.M.; De Lucia, G.; Frenk, C.S.; Gao, L.; Jenkins, A.; Kauffmann, G.; Navarro, J.F.; Yoshida, N. The many lives of active galactic nuclei: Cooling flows, black holes and the luminosities and colours of galaxies. Mon. Not. R. Astron. Soc. 2006, 365, 11–28. [Google Scholar] [CrossRef]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Publ. Astron. Soc. Pac. 2003, 115, 763–795. [Google Scholar] [CrossRef]
- Booth, C.M.; Schaye, J. Cosmological simulations of the growth of supermassive black holes and feedback from active galactic nuclei: Method and tests. Mon. Not. R. Astron. Soc. 2009, 398, 53–74. [Google Scholar] [CrossRef]
- Martizzi, D.; Teyssier, R.; Moore, B. The formation of the brightest cluster galaxies in cosmological simulations: The case for active galactic nucleus feedback. Mon. Not. R. Astron. Soc. 2012, 420, 2859–2873. [Google Scholar] [CrossRef]
- Cattaneo, A.; Dekel, A.; Devriendt, J.; Guiderdoni, B.; Blaizot, J. Modelling the galaxy bimodality: Shutdown above a critical halo mass. Mon. Not. R. Astron. Soc. 2006, 370, 1651–1665. [Google Scholar] [CrossRef]
- Klypin, A.A.; Trujillo-Gomez, S.; Primack, J. Dark Matter Halos in the Standard Cosmological Model: Results from the Bolshoi Simulation. Astrophys. J. 2011, 740, 102. [Google Scholar] [CrossRef]
- Benson, A.J. G ALACTICUS: A semi-analytic model of galaxy formation. New Astron. 2012, 17, 175–197. [Google Scholar] [CrossRef]
- Wang, L.; Dutton, A.A.; Stinson, G.S.; Macciò, A.V.; Penzo, C.; Kang, X.; Keller, B.W.; Wadsley, J. NIHAO project - I. Reproducing the inefficiency of galaxy formation across cosmic time with a large sample of cosmological hydrodynamical simulations. Mon. Not. R. Astron. Soc. 2015, 454, 83–94. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. Galactic star formation and accretion histories from matching galaxies to dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 428, 3121–3138. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Wechsler, R.H.; Conroy, C. The Average Star Formation Histories of Galaxies in Dark Matter Halos from z = 0-8. Astrophys. J. 2013, 770, 57. [Google Scholar] [CrossRef]
- Behroozi, P.; Wechsler, R.H.; Hearin, A.P.; Conroy, C. UNIVERSEMACHINE: The correlation between galaxy growth and dark matter halo assembly from z = 0–10. Mon. Not. R. Astron. Soc. 2019, 488, 3143–3194. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; et al.; Planck Collaboration Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).