Impact of the Magnetic Gap in Submerged Axial Flux Motors on Centrifugal Pump Hydraulic Performance and Internal Flow
Abstract
1. Introduction
2. Numerical Simulation
2.1. Pump Parameters
2.2. Control Equations
2.3. Boundary Conditions
2.4. Computational Grids
2.5. Mesh Sensitivity
3. Experimental Setup and Validation
3.1. Experimental Setup
3.2. Comparisons of Experimental and Numerical Energy Performances
4. Results and Discussion
4.1. Analysis of Energy Conversion and Loss Characteristics
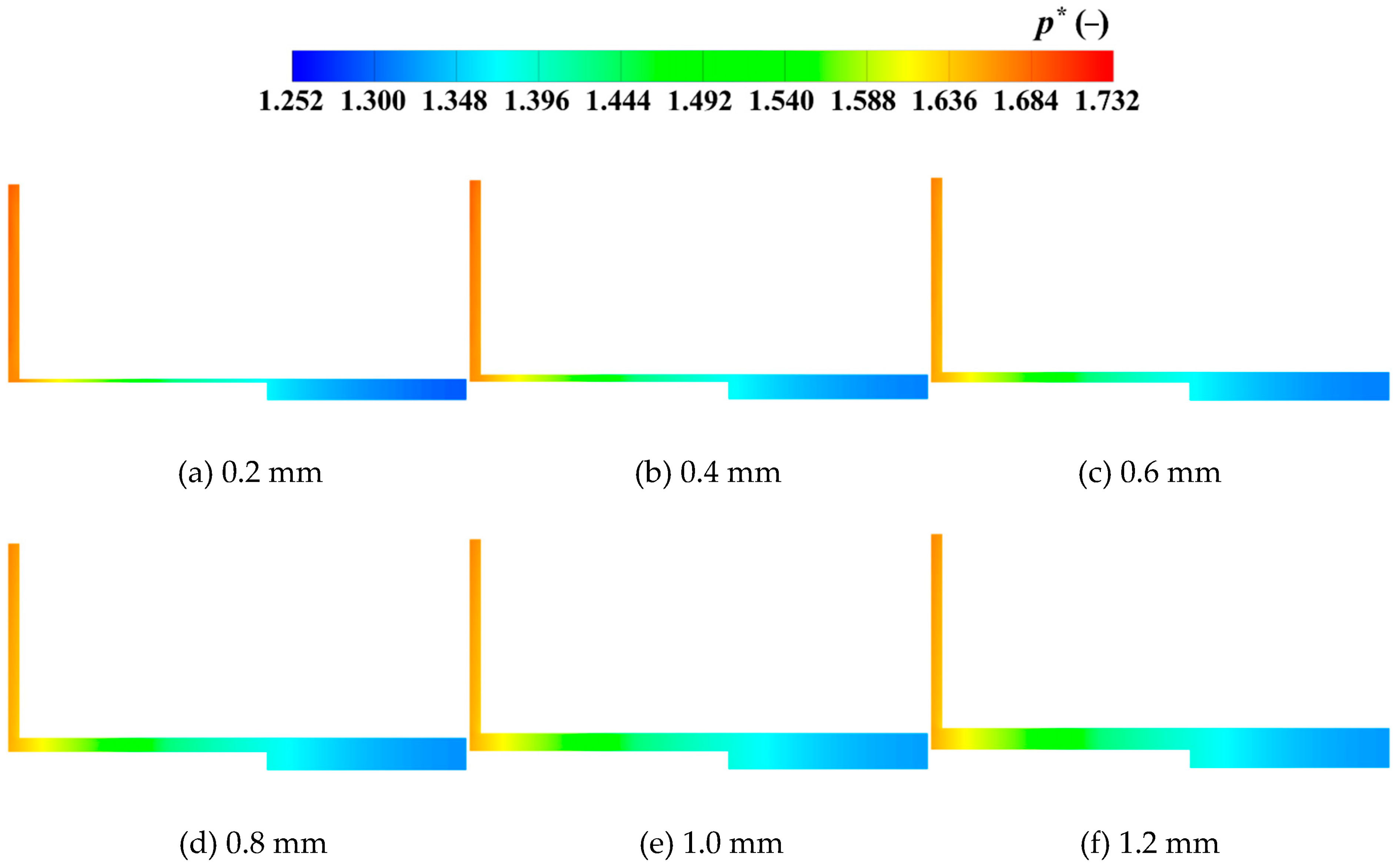
4.2. Analysis of Pressure
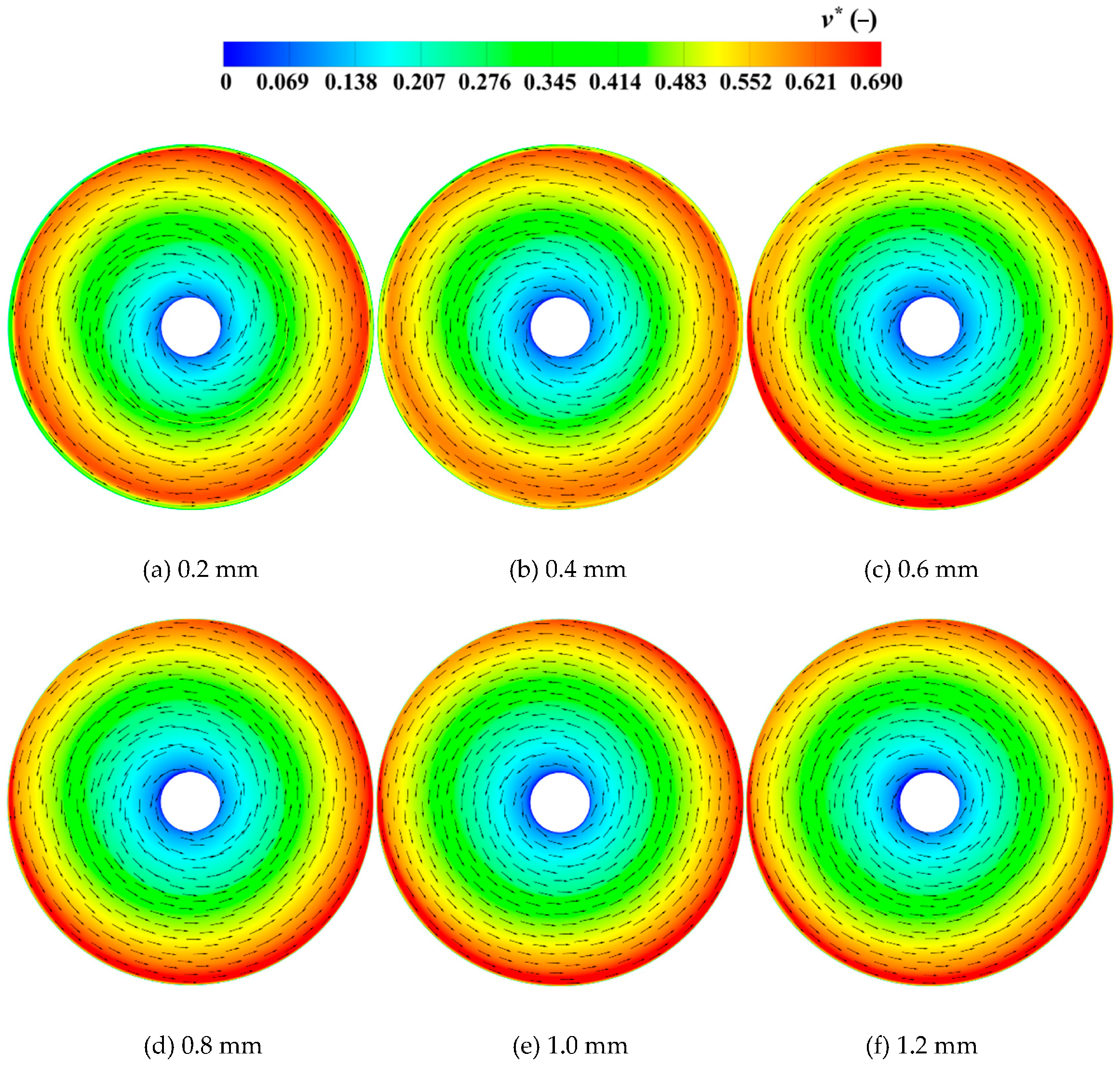
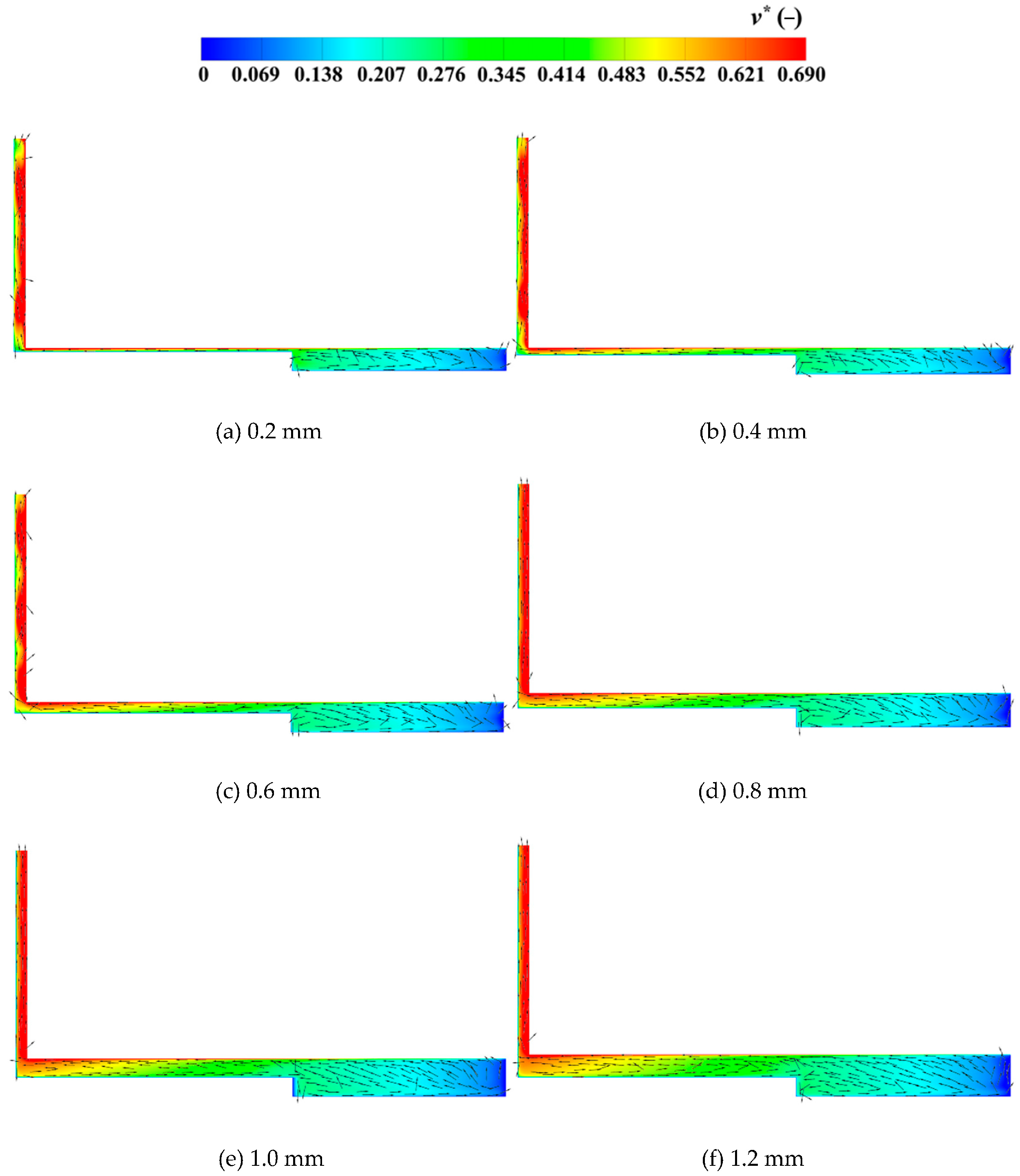
4.3. Analysis of Velocity
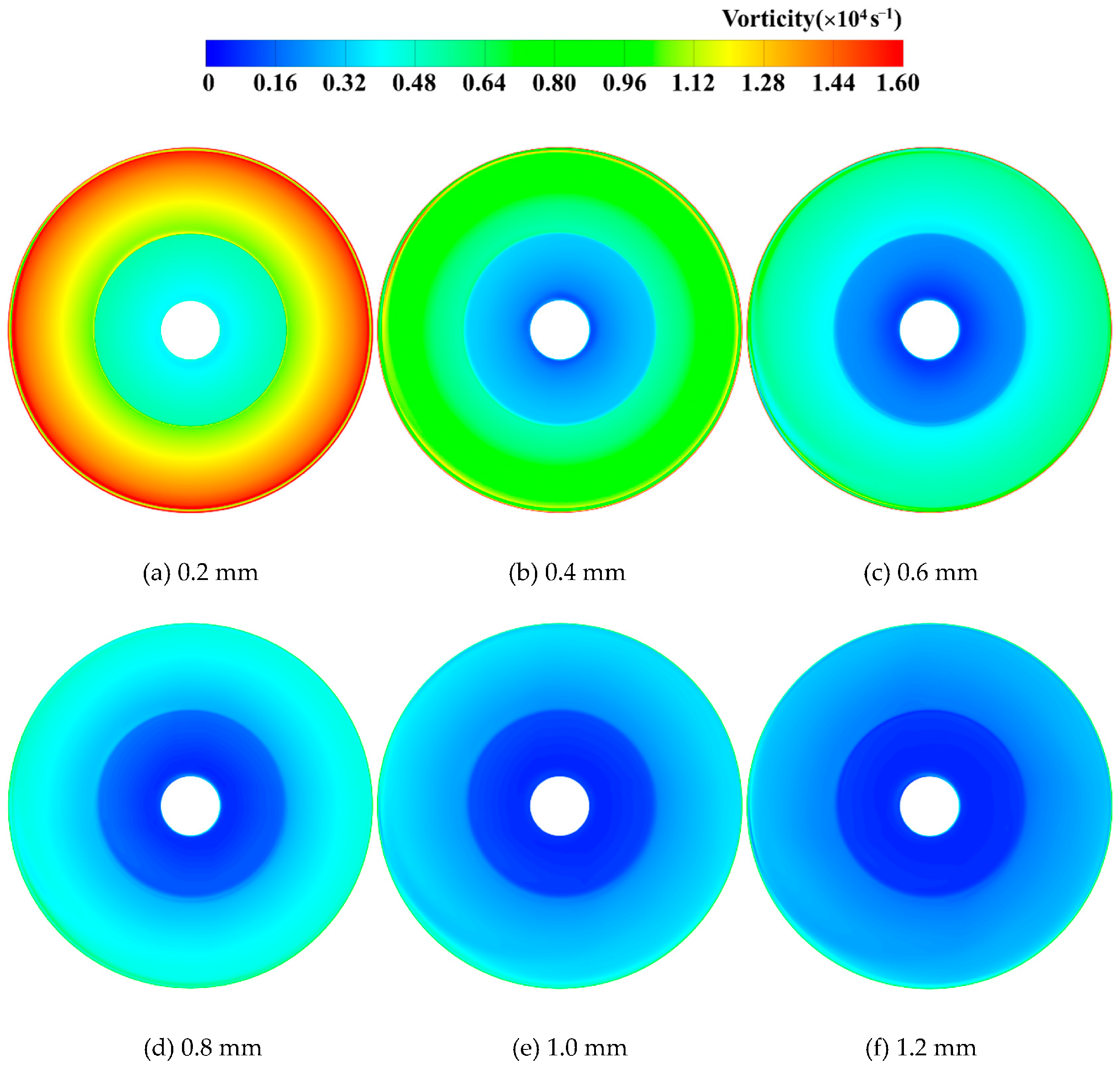
4.4. Analysis of Vortex Distribution
4.5. Analysis of Entropy Production
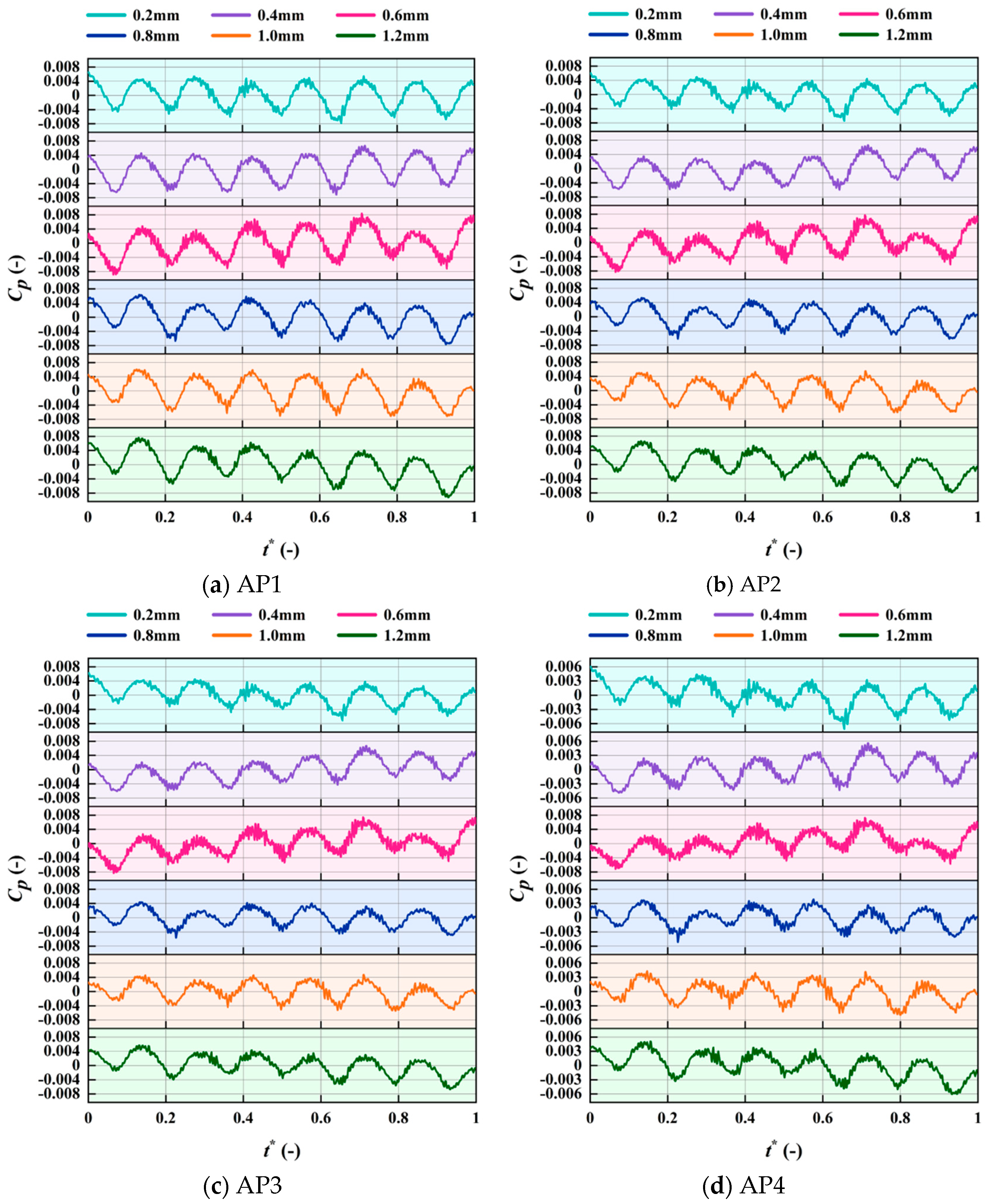
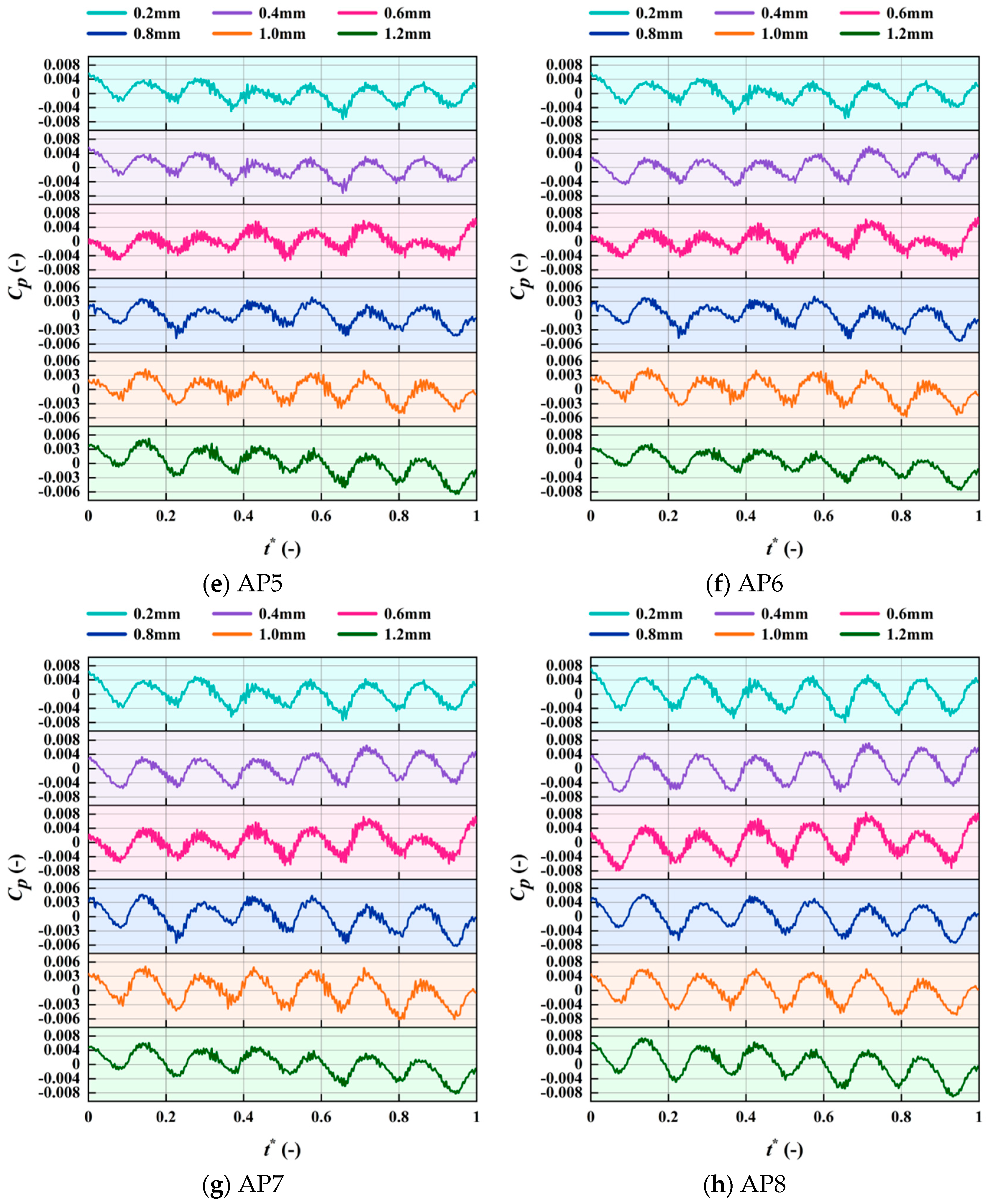
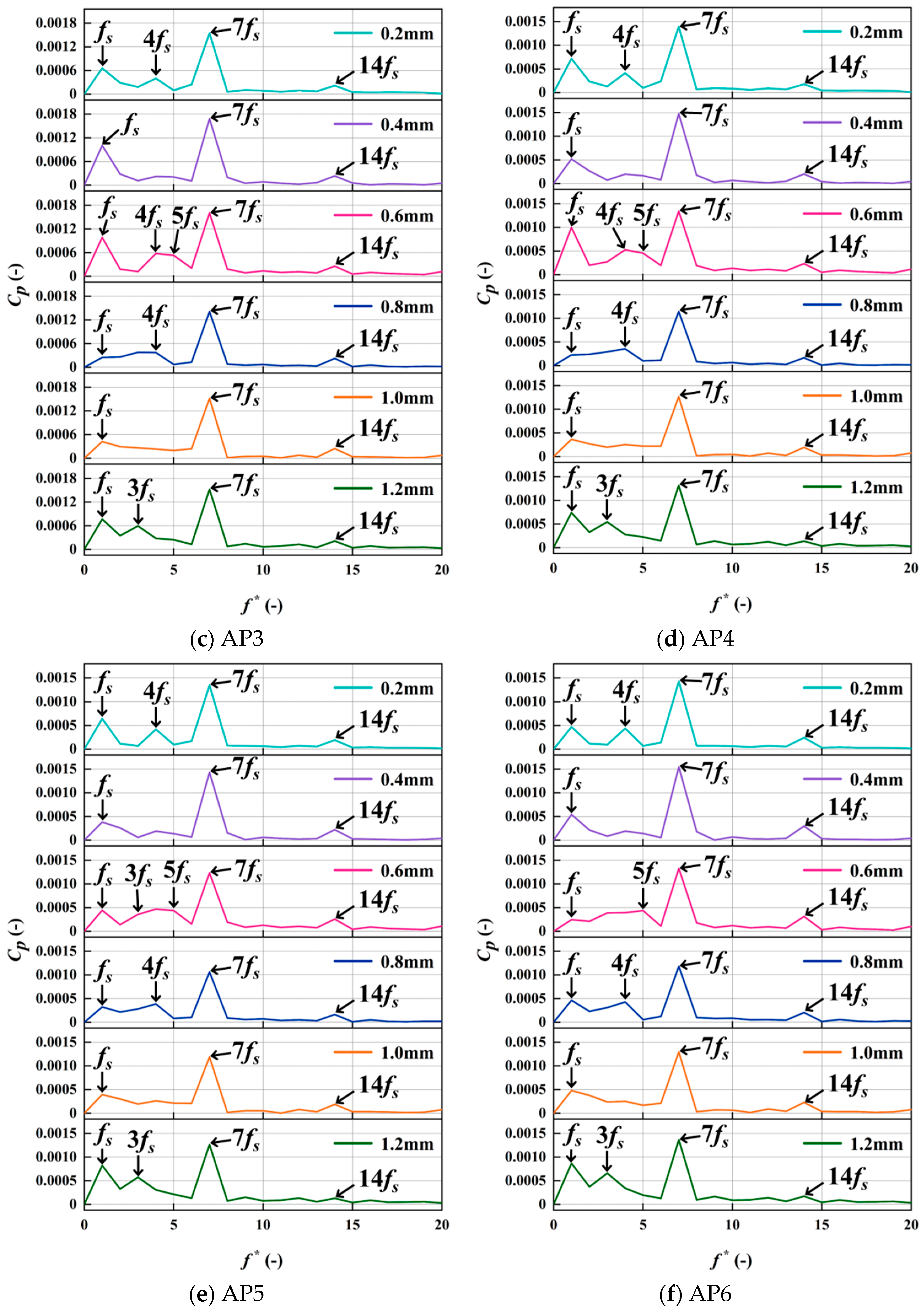
4.6. Analysis of Pressure Fluctuations
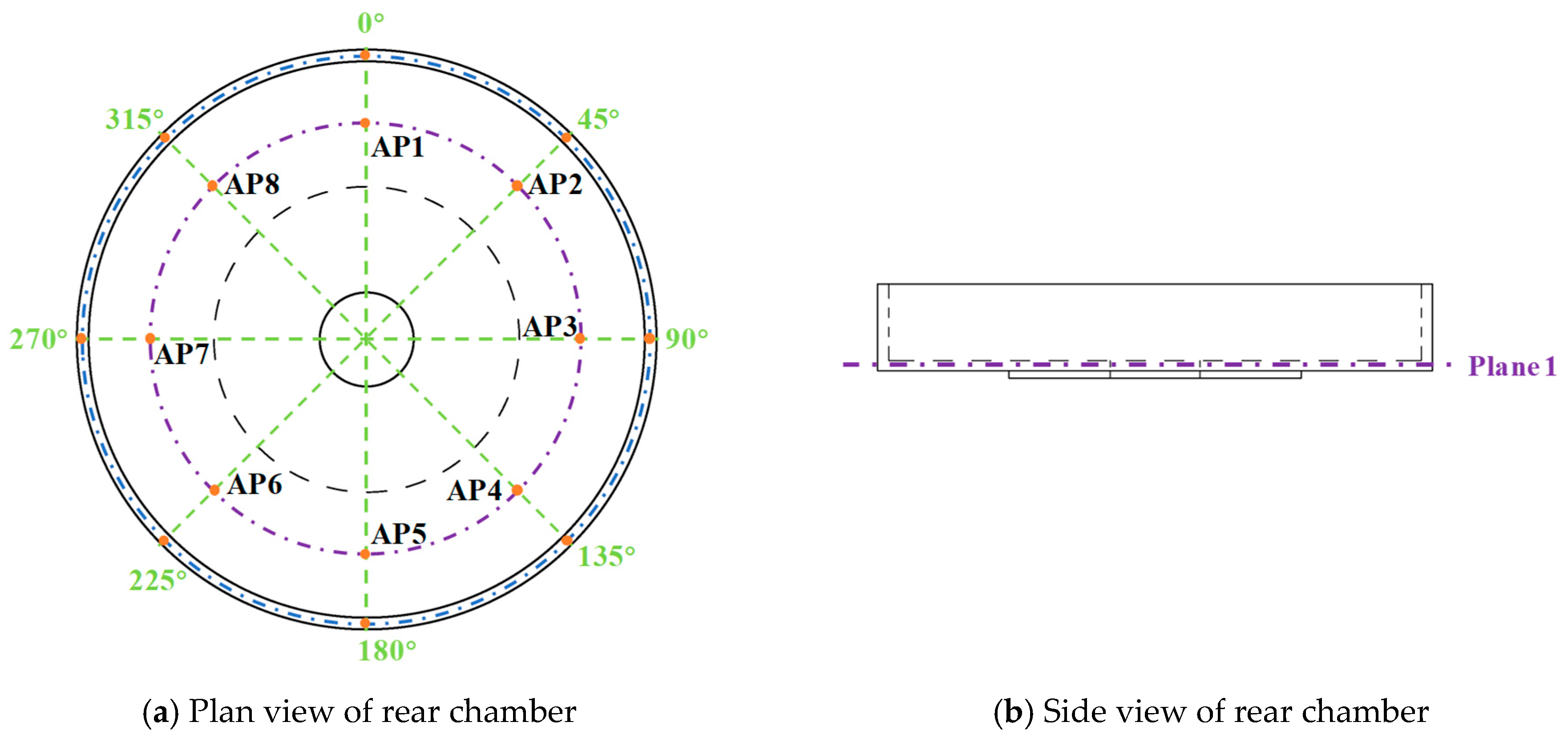
4.6.1. Monitoring Point Locations
4.6.2. Pressure Fluctuations in Rear Chamber
5. Conclusions
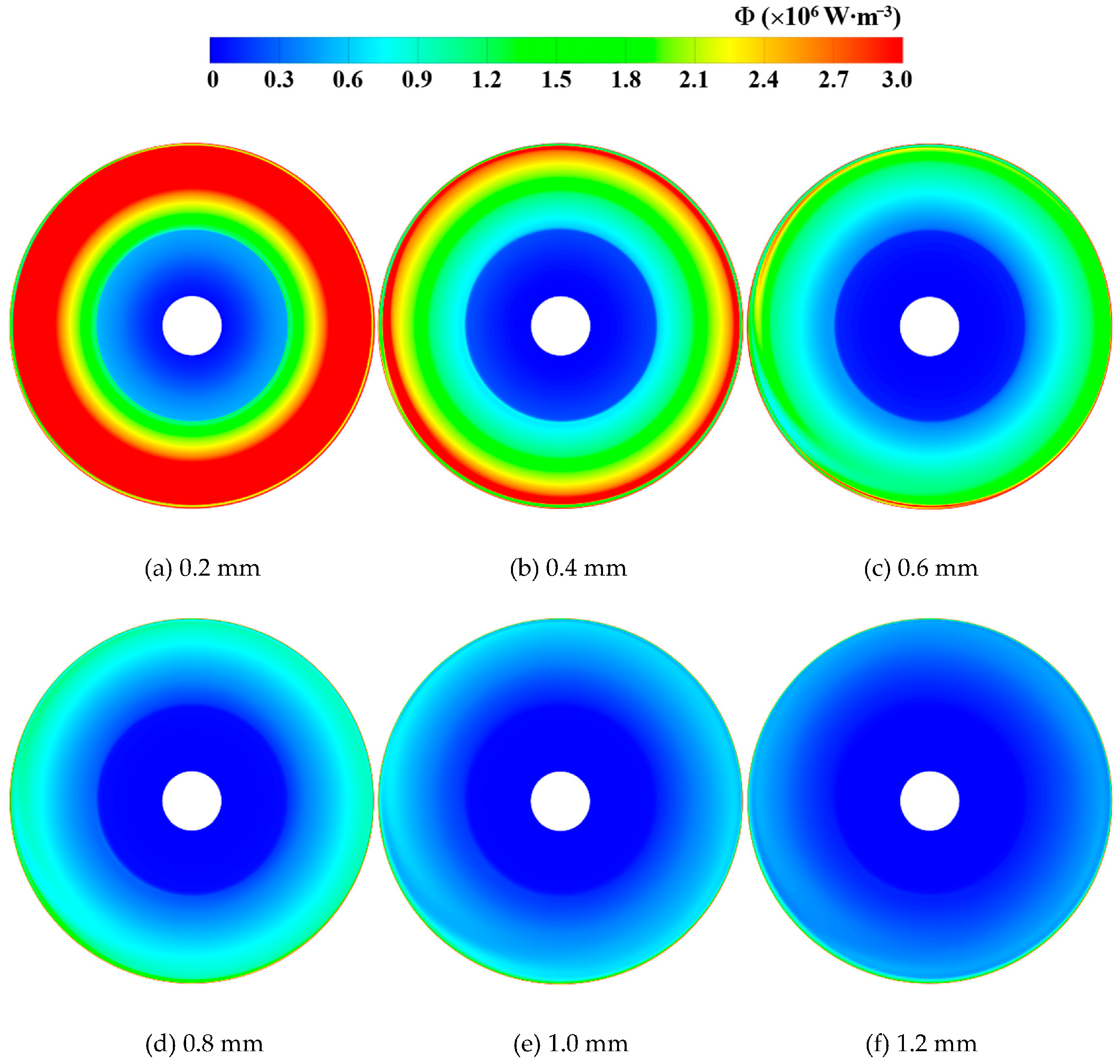
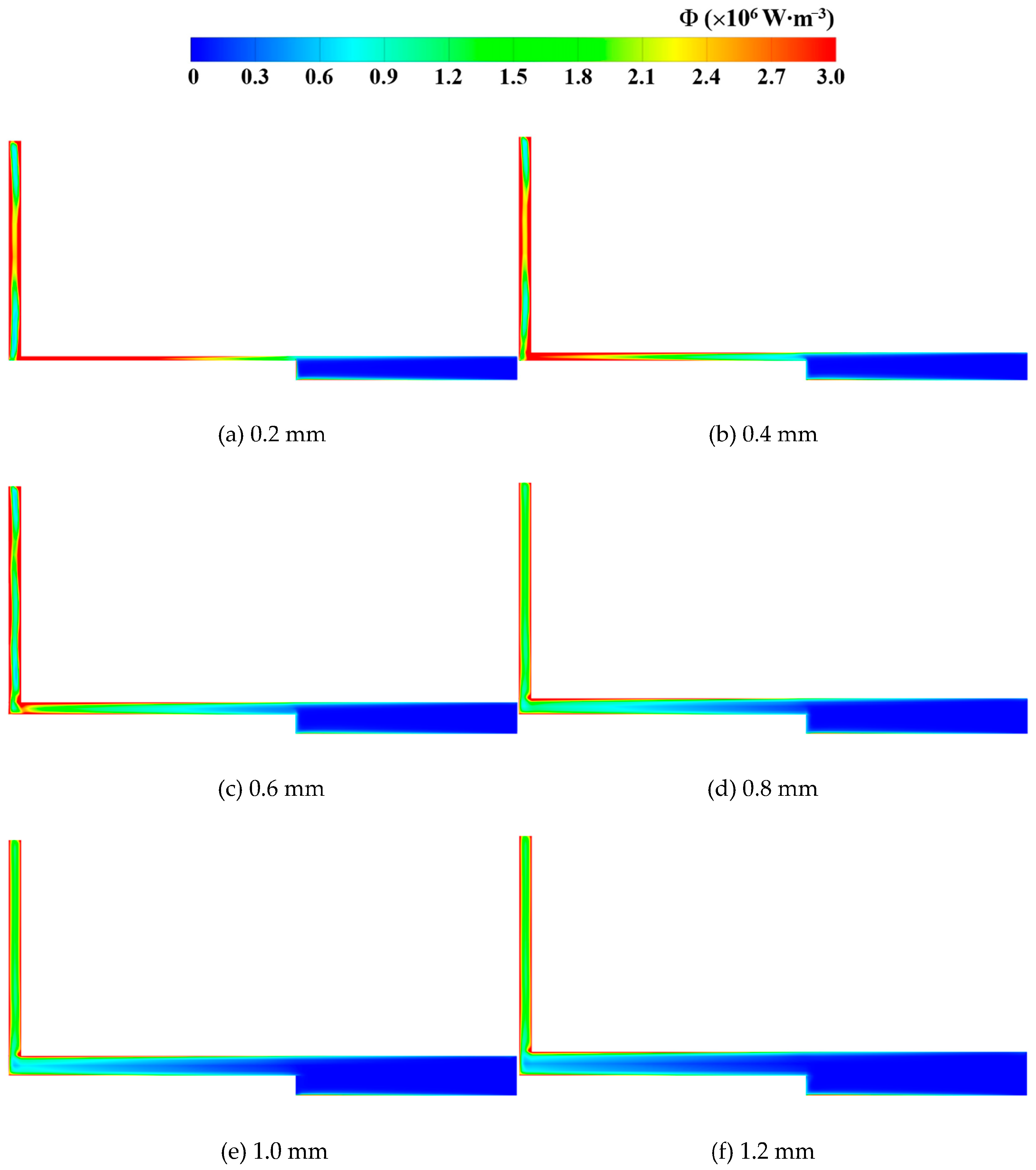
- The energy performance exhibits a significant non-linear response, with different optimal gaps for different performance indicators. The head coefficient peaks at a 0.4 mm gap, while maximum efficiency occurs at 1.0 mm. For a 0.2 mm magnetic gap, strong viscous shear effects in the confined space dominate, causing disk friction power loss to surge by nearly 10% and severely undermining efficiency. Notably, disk friction loss reaches its minimum at the 0.8 mm magnetic gap, indicating an optimal magnetic gap that balances shear and leakage effects. This finding provides crucial practical guidance for optimizing the hydraulic design of axial flux canned motor pumps.
- Both the pressure distribution and fluctuation intensity are highly sensitive to the magnetic gaps. For small gaps (0.2–0.6 mm), viscous dissipation dominates, causing the circumferential high-pressure ring to contract radially. For the magnetic gap of 0.8 mm to 1.2 mm, the effect of mainstream inertial forces becomes prominent, and the high-pressure zone tends to stabilize. The Blade Passing Frequency is the dominant frequency, with high fluctuations concentrated near the tongue and the diffuser inlet. For the 0.8 mm magnetic gap, the pressure fluctuation amplitude is lowest.
- The internal flow reflects the competitive mechanism between viscous and inertial forces. For small magnetic gaps (0.2–0.6 mm), strong shear action forms a continuous low-velocity, high-vorticity band at the circumferential periphery and induces secondary flows at abrupt geometric changes, leading to flow disorder. For the magnetic gap of 0.8 mm to 1.2 mm, mainstream inertial forces gradually dominate, causing the flow pattern to become more ordered. The high-velocity annular zone remains stable, and the vorticity accumulation near the rotor and casing walls is significantly weakened.
- Enlarging the magnetic gap attenuates viscosity-dominated momentum dissipation, thereby significantly reducing the entropy production. For small magnetic gaps (0.2–0.6 mm), the synergistic effect of strong viscous shear and geometric discontinuities forms a high entropy production zone. For the magnetic gap of 0.8 mm to 1.2 mm, viscosity-dominated momentum dissipation is effectively suppressed. The primary region of energy loss degenerates into a localized, near-wall dissipation band, while the mainstream region exhibits efficient, low-dissipation transport characteristics. This perfectly corresponds with the macroscopic phenomenon of higher efficiency observed at larger magnetic gaps.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| b2 | Blade outlet width, mm |
| b3 | Volute inlet width, mm |
| Cp | Dimensionless pressure coefficient |
| D1 | Blade inlet diameter, mm |
| D2 | Blade outlet diameter, mm |
| D3 | Volute inlet diameter, mm |
| Dd | Volute outlet diameter, mm |
| Dr | Motor rotor diameter, mm |
| fi | External force, N/m3 |
| fs | Shaft frequency, Hz |
| f* | Dimensionless frequency |
| g | Gravitational acceleration, m/s2 |
| H | Head for pumps, m |
| Lr | Motor rotor axial width |
| n | Rotating speed of impeller, rpm |
| p | Pressure, Pa |
| pout | Static pressures at the outlet, Pa |
| pin | Static pressures at the inlet, Pa |
| pi | Prompt pressure, Pa |
| Average pressure, Pa | |
| p* | Dimensionless pressure |
| P | Shaft power, W |
| Q | Flow rate for pumps, L/min |
| Qd | Design flow rate for pumps, L/min |
| Q* | Dimensionless flow rate |
| t | Time, s |
| t* | Dimensionless time |
| T | Shaft torque, N·m |
| T0 | Unloaded shaft torque, N·m |
| u2 | Circumferential velocity at blade outlet, m/s |
| v* | Dimensionless velocity |
| x | Cartesian coordinates |
| Zb | Number of blades |
| β1 | Blade inlet angle, ° |
| β2 | Blade outlet angle, ° |
| ΔZ | Vertical distance between the inlet and outlet pressure sensors, m |
| η | Efficiency, % |
| μ | Viscosity, kg/(m·s) |
| ρ | Density, kg/m3 |
| Dissipation, W/m3 | |
| Viscous dissipation, W/m3 | |
| Turbulent dissipation, W/m3 | |
| φ0 | Tongue angle, ° |
| Reynolds stress tensor | |
| Subscripts | |
| i | Free index |
| j, k | Dummy index |
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| Exp. | Experimental |
| GCI | Grid Convergence Index |
| Num. | Numerical |
| RANS | Reynolds-Averaged Navier–Stokes |
| SST | Shear Stress Transport |
References
- Gu, Y.; Yang, A.; Bian, J.; Shariff, A.M.; Stephen, C.; Wang, Q.; Cheng, L. Investigation of energy performance and unsteady flow characteristics of a multi-stage centrifugal pump under various seal wear conditions for renewable energy pumping systems. Renew. Energy 2025, 256, 123998. [Google Scholar] [CrossRef]
- Si, Q.; Xu, H.; Deng, F.; Xia, X.; Ma, W.; Guo, Y.; Wang, P. Study on performance improvement of low specific speed multistage pumps by applying full channel hydraulic optimization. J. Energy Storage 2024, 99, 113238. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, X.; Yang, Z.; Cai, Y.; Lei, G.; Zhu, J.; Lee, C.H.T. Design Optimization of a Spoke-Type Axial-Flux PM Machine for In-Wheel Drive Operation. IEEE Trans. Transp. Electrif. 2024, 10, 3770–3781. [Google Scholar] [CrossRef]
- Zhu, X.; El Shahat, S.A.; Lai, F.; Jiang, W.; Li, G. Numerical investigation of rotor–stator interaction for canned motor pump under partial load condition. Mod. Phys. Lett. B 2020, 34, 2050039. [Google Scholar] [CrossRef]
- Tinni, A.; Knittel, D.; Nouari, M.; Sturtzer, G. Electrical–thermal modeling of a double-canned induction motor for electrical performance analysis and motor lifetime determination. Electr. Eng. 2021, 103, 103–114. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, L.; Ni, Y.; Lei, H.; Gao, G. Control method analysis with high performance and stability for permanent magnet motor based on canned structure. Int. J. Electr. Power Energy Syst. 2022, 143, 108441. [Google Scholar] [CrossRef]
- Zhou, G.H.; Qiao, M.Z.; Wu, D.; Hao, Q.; Zhang, X.; Shi, P.; Tan, B. Low Noise Optimization Design of Integrated Permanent Magnet Synchronous Motor Based on Multi-Physical Field Coupling. IEEE Trans. Appl. Supercond. 2024, 34, 5207004. [Google Scholar] [CrossRef]
- Kanyolo, T.N.; Oyando, H.C.; Chang, C. Acceleration Analysis of Canned Motors for SMR Coolant Pumps. Energies 2023, 16, 5733. [Google Scholar] [CrossRef]
- Pang, D.-C.; Wang, C.-T. A Wireless-Driven, Micro, Axial-Flux, Single-Phase Switched Reluctance Motor. Energies 2018, 11, 2772. [Google Scholar] [CrossRef]
- Eker, M.; Zöhra, B.; Akar, M. Experimental performance verification of radial and axial flux line start permanent magnet synchronous motors. Electr. Eng. 2024, 106, 1693–1704. [Google Scholar] [CrossRef]
- Ai, L.; Ma, P.; Miao, S.; Jiang, S.; Xu, X. Modelling and analysis of a superconducting magnetic coupler used for cryogenic pump. IET Electr. Power Appl. 2024, 18, 1131–1141. [Google Scholar] [CrossRef]
- Ai, L.; Zhang, G.; Jing, L.; Xu, X.; Si, J. Behaviors of Axial and Radial Electromagnetic Force for Cryogenic Disk Motor. IEEE Trans. Energy Convers. 2021, 36, 874–882. [Google Scholar] [CrossRef]
- Ai, L.; Zhang, G.; Li, W.; Liu, G.; Song, N.; Xiao, L.; Lin, L. Research on a Superconducting Magnetic Bearing System for Submerged Cryogenic Disk Motor-Pump. IEEE Trans. Appl. Supercond. 2018, 28, 5202505. [Google Scholar] [CrossRef]
- Gadiyar, N.; Bohach, G.; Nahin, M.M.; Van de Ven, J.; Severson, E.L. Development of an Integrated Electro-Hydraulic Machine to Electrify Off-highway Vehicles. IEEE Trans. Ind. Appl. 2022, 58, 6163–6174. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Yan, W.; Chng, C.-B.; Chui, C.-K.; Yang, X.; Zhao, S. Advancing energy efficiency in electric vehicles: Design and performance analysis of innovative axial-flux PM motor-driven coolant pumps. Energy 2024, 313, 134112. [Google Scholar] [CrossRef]
- Fan, R.; Liang, Z.; Fan, B.; Chen, S.; Lv, W.; Xu, W.; Zheng, J.; Wang, D. Numerical analysis of internal flow characteristics and energy consumption assessment in full flow field of multi-stage centrifugal pump considering clearance flow. Adv. Mech. Eng. 2022, 14, 16878132221123423. [Google Scholar] [CrossRef]
- Gu, Y.; Bian, J.; Wang, C.; Sun, H.; Wang, M.; Ge, J. Transient numerical investigation on hydraulic performance and flow field of multi-stage centrifugal pump with floating impellers under sealing gasket damage condition. Phys. Fluids 2023, 35, 107123. [Google Scholar] [CrossRef]
- Zhan, P.; Wei, L.; Liu, R.; Liang, M.; Qiang, Y. Flow Field Modeling and Simulation of High-Speed Gear Pump Considering Optimal Radial and End Clearance. IEEE Access 2023, 11, 64725–64737. [Google Scholar] [CrossRef]
- Hou, X.; Cheng, Y.; Yang, Z.; Liu, K.; Zhang, X.; Liu, D. Influence of Clearance Flow on Dynamic Hydraulic Forces of Pump-Turbine during Runaway Transient Process. Energies 2021, 14, 2830. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, X.; Qu, J.; Ma, X. A Review of Pressure Fluctuations in Centrifugal Pumps without or with Clearance Flow. Processes 2023, 11, 856. [Google Scholar] [CrossRef]
- Guang, W.-L.; Liu, Q.; Jin, F.-Y.; Tao, R.; Xiao, R.-F. Analysis of clearance flow of a fuel pump based on dynamical mode decomposition. J. Hydrodyn. 2024, 36, 781–795. [Google Scholar] [CrossRef]
- Li, Q.; Li, S.; Wu, P.; Huang, B.; Wu, D. Investigation on Reduction of Pressure Fluctuation for a Double-Suction Centrifugal Pump. Chin. J. Mech. Eng. 2021, 34, 12. [Google Scholar] [CrossRef]
- Liang, S.; Pang, S.; Liu, J.; Chen, Z.; Sun, D.; Li, C. Unsteady internal flow characteristics study of a hydrogen circulation pump under different pressure differential conditions. Int. J. Hydrogen Energy 2024, 60, 1147–1156. [Google Scholar] [CrossRef]
- Li, L.; Yan, D.; Liu, X.; Zhao, W.; Wang, Y.; Pang, J.; Wang, Z. Numerical Study on the Effect of Crown Clearance Thickness on High-Head Pump Turbines. Water 2023, 15, 3397. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.; Meng, F.; Wang, M.; Li, Y. Numerical simulation on the influence of root clearance on the hydraulic performance of axial flow pump device. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 161. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, C.; Bai, L.; Agarwal, R. Numerical and Experimental Analysis of Vortex Pump with Various Axial Clearances. Water 2024, 16, 1602. [Google Scholar] [CrossRef]
- Jia, X.; Yu, Y.; Li, B.; Wang, F.; Zhu, Z. Effects of incident angle of sealing ring clearance on internal flow and cavitation of centrifugal pump. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2024, 238, 2867–2882. [Google Scholar] [CrossRef]
- Oro, J.F.; Perotti, R.B.; Vega, M.G.; González, J. Effect of the radial gap size on the deterministic flow in a centrifugal pump due to impeller-tongue interactions. Energy 2023, 278, 127820. [Google Scholar] [CrossRef]
- Liu, J.; Xi, W.; Lu, W. Optimization Design of Radial Clearance between Stator and Rotor of Full Cross-Flow Pump Units. J. Mar. Sci. Eng. 2024, 12, 1124. [Google Scholar] [CrossRef]
- Gu, Y.; Zhu, Q.; Bian, J.; Wang, Q.; Cheng, L. Novel sealing design for high-speed coolant pumps: Impact on energy performance, axial thrust and flow field. Energy 2025, 321, 135511. [Google Scholar] [CrossRef]
- Chang, H.; Yang, J.; Wang, Z.; Peng, G.; Lin, R.; Lou, Y.; Shi, W.; Zhou, L. Efficiency optimization of energy storage centrifugal pump by using energy balance equation and non-dominated sorting genetic algorithms-II. J. Energy Storage 2025, 114, 115817. [Google Scholar] [CrossRef]
- Huang, X.; Jin, G.; Guo, Q.; Liu, X.; Lu, J. A method for evaluating the effect induced by vortices on the moment and efficiency of the fluid machinery. Phys. Fluids 2024, 36, 115165. [Google Scholar] [CrossRef]
- Wang, D.; Gu, Y.; Stephen, C.; Ji, Q. Blade number effects on performance and internal flow dynamics in high-speed coolant pumps. Phys. Fluids 2025, 37, 015240. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, S.; Zhang, T.; Zhang, H.; Li, M. Study of a Companion Trajectory Kinematics Analysis Method for the Five-Blade Rotor Swing Scraper Pump. Machines 2024, 12, 877. [Google Scholar] [CrossRef]
- Wang, H.; Wu, X.; Xu, X.; Bian, S.; Meng, F. Size Effect on Energy Characteristics of Axial Flow Pump Based on Entropy Production Theory. Machines 2025, 13, 252. [Google Scholar] [CrossRef]
- Wang, T.; Yu, H.; Xiang, R.; Chen, X.; Zhang, X. Performance and unsteady flow characteristic of forward-curved impeller with different blade inlet swept angles in a pump as turbine. Energy 2023, 282, 128890. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Chang, H.; Yang, Z. Energy characteristics of mixed-flow pump under different tip clearances based on entropy production analysis. Energy 2020, 199, 117447. [Google Scholar] [CrossRef]
- Gu, Y.; Bian, J.; Wang, Q.; Stephen, C.; Liu, B.; Cheng, L. Energy performance and pressure fluctuation in multi-stage centrifugal pump with floating impellers under various axial oscillation frequencies. Energy 2024, 307, 132691. [Google Scholar] [CrossRef]
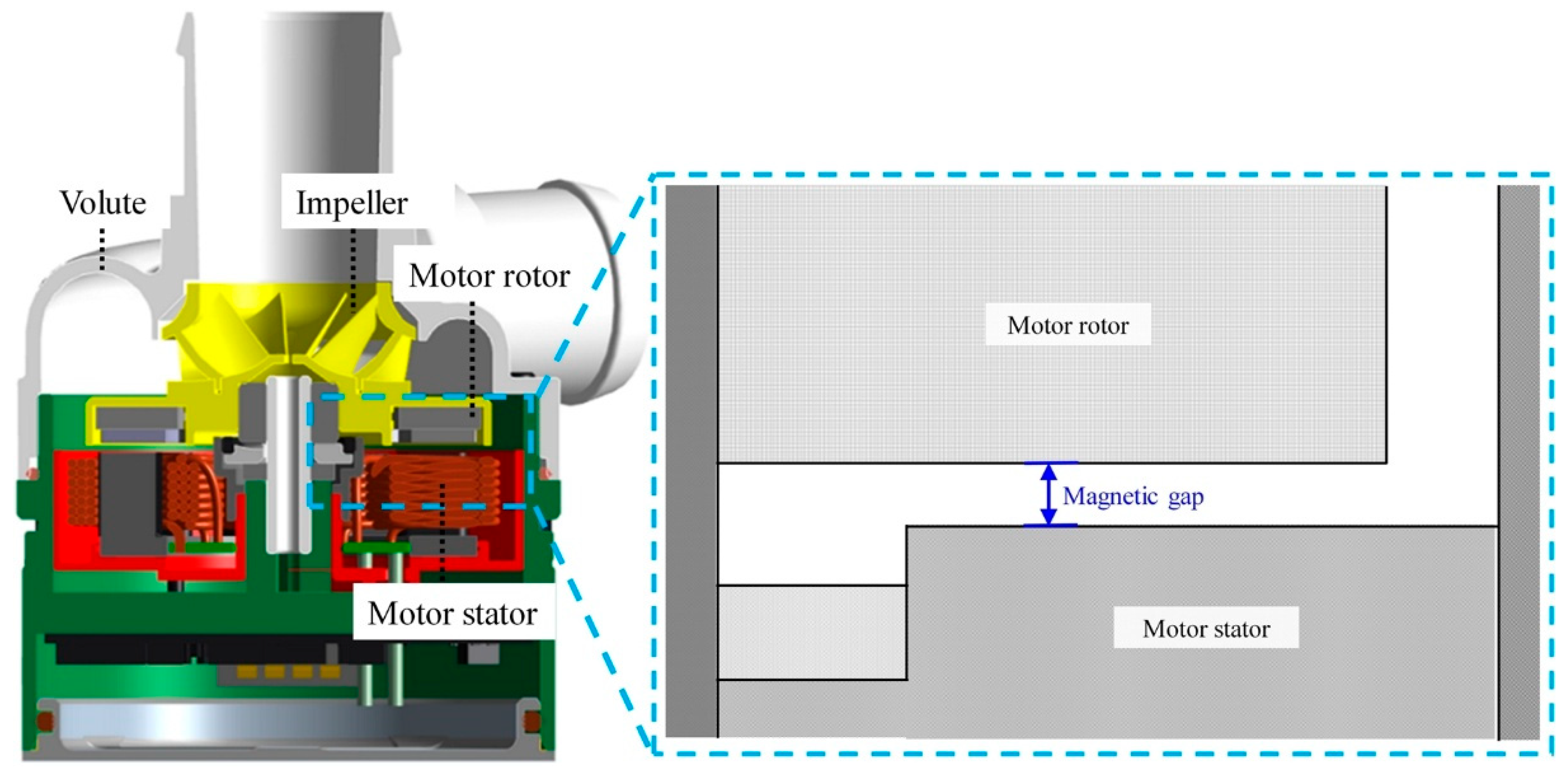

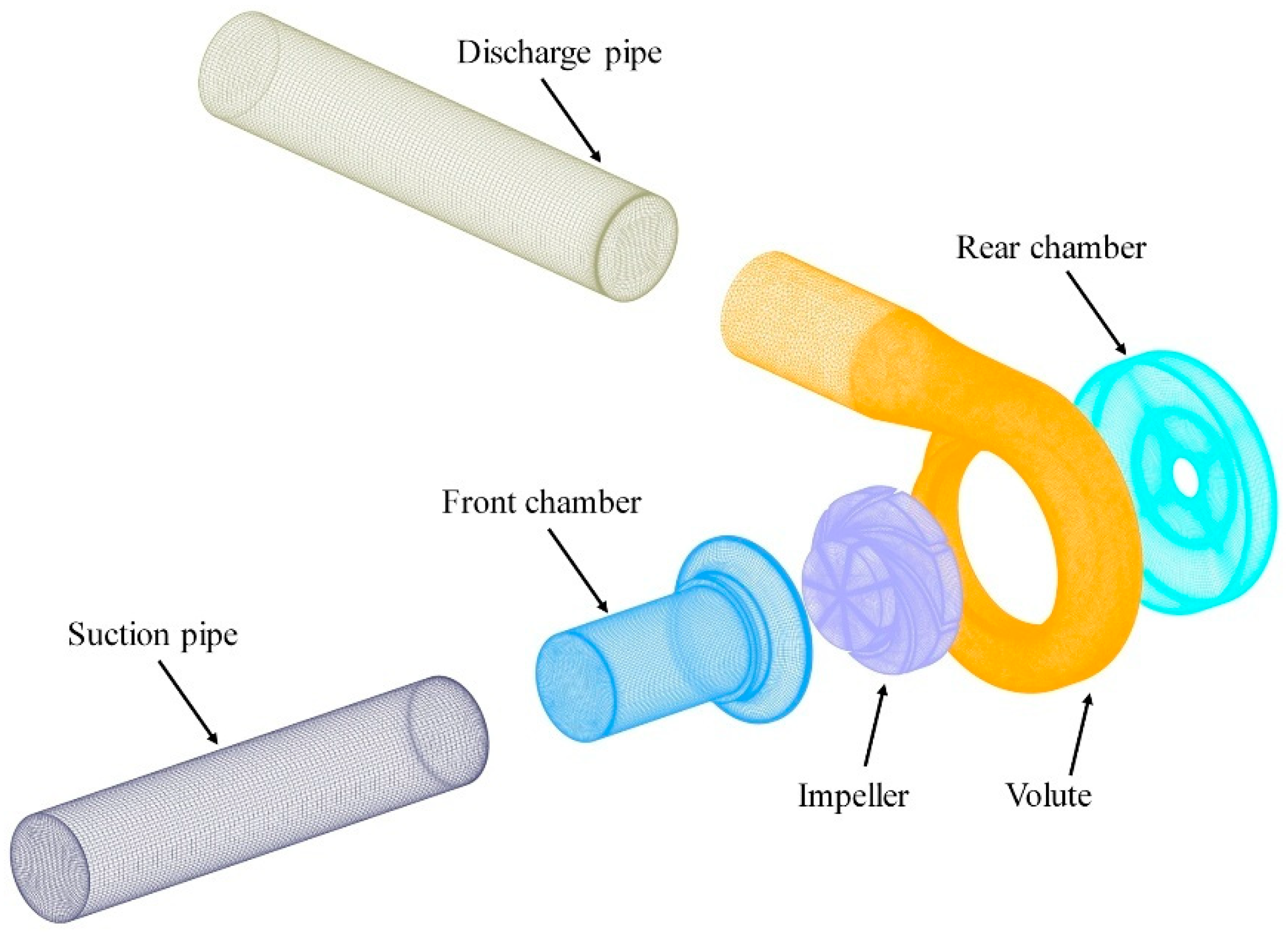


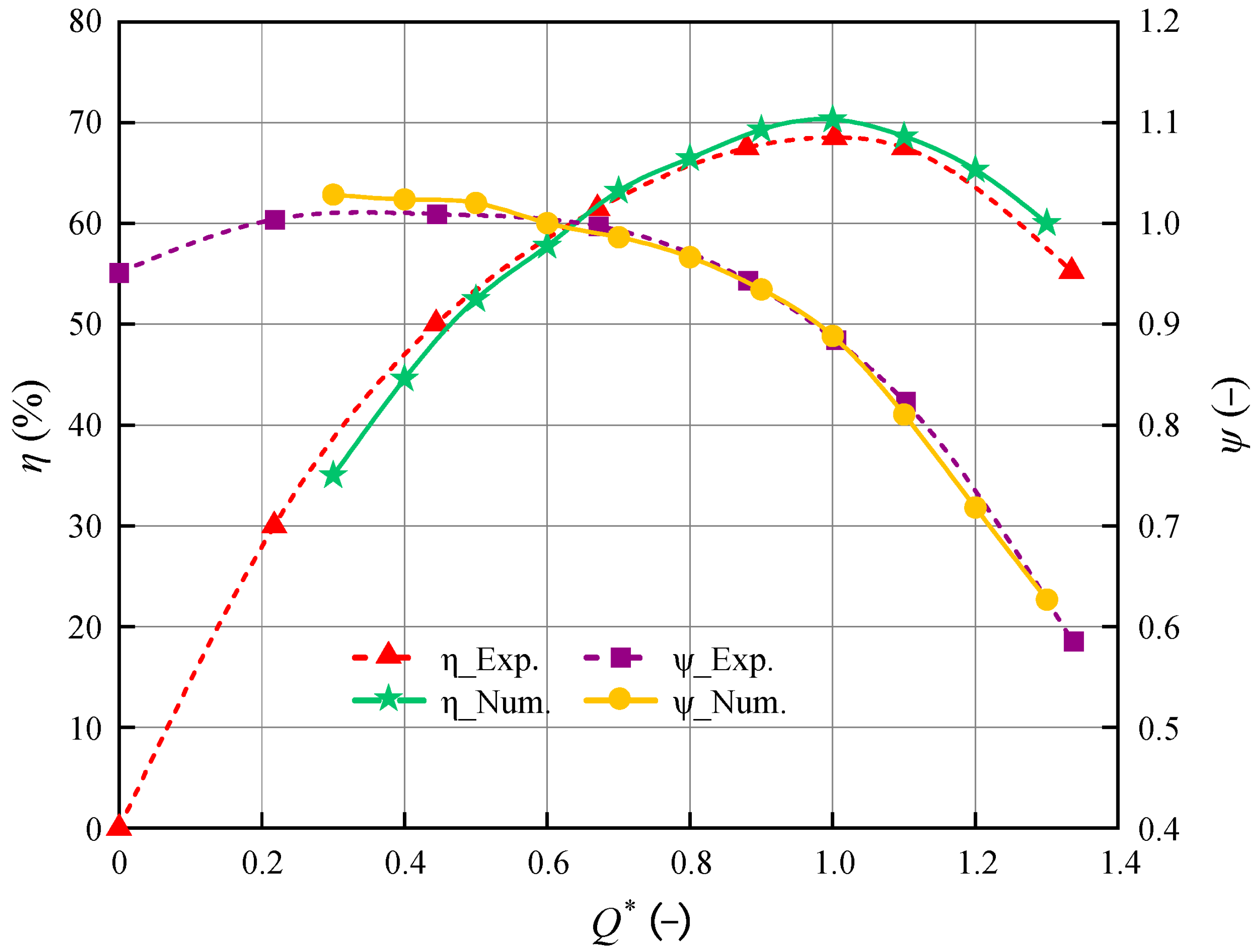

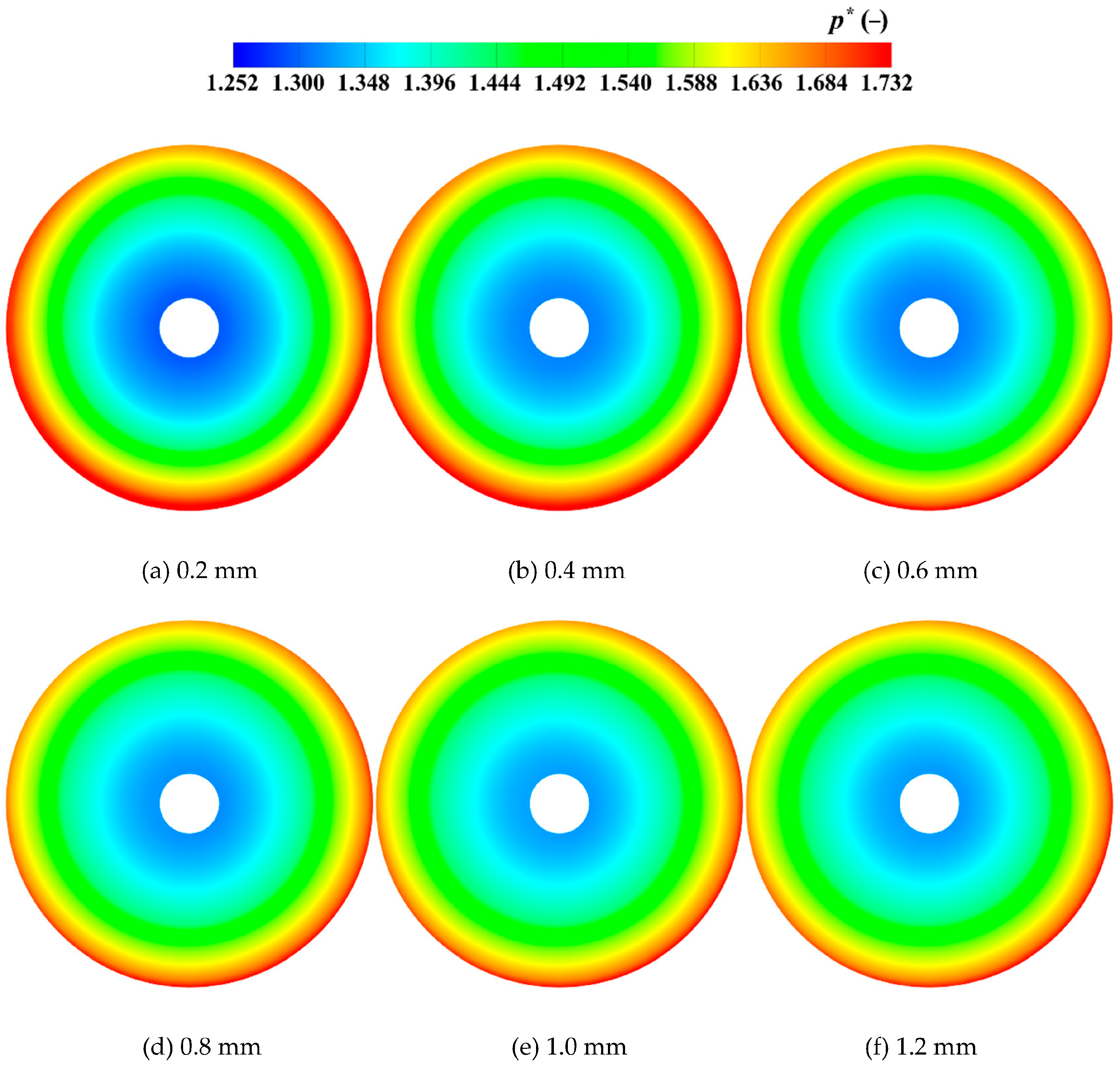



| Component | Parameter | Value |
|---|---|---|
| Impeller | Blade inlet diameter D1 (mm) | 32 |
| Blade outlet diameter D2 (mm) | 53 | |
| Blade outlet width b2 (mm) | 7.8 | |
| Blade inlet angle β1 (°) | 28.5 | |
| Blade outlet angle β2 (°) | 31 | |
| Blade wrap angle φ (°) | 88 | |
| Number of Blades Zb | 7 | |
| Motor rotor diameter Dr (mm) | 72.5 | |
| Motor rotor axial width Lr (mm) | 11 | |
| Volute | Volute inlet diameter D3 (mm) | 55 |
| Volute inlet width b3 (mm) | 12 | |
| Volute outlet diameter Dd (mm) | 32 |
| Magnetic Gap (mm) | Disk Friction Loss Power (W) | Front Cover | Rear Cover and Rotor | ||
|---|---|---|---|---|---|
| Loss Power (W) | Proportion (%) | Loss Power (W) | Proportion (%) | ||
| 0.2 | 43.1 | 3.9 | 8.9 | 39.2 | 91.1 |
| 0.4 | 41.9 | 3.8 | 9.2 | 38.0 | 90.8 |
| 0.6 | 42.0 | 4.1 | 9.8 | 37.9 | 90.2 |
| 0.8 | 39.5 | 3.5 | 8.9 | 36.0 | 91.1 |
| 1.0 | 39.9 | 3.5 | 8.9 | 36.3 | 91.1 |
| 1.2 | 40.1 | 3.5 | 8.8 | 36.6 | 91.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Gu, Y.; Bian, J. Impact of the Magnetic Gap in Submerged Axial Flux Motors on Centrifugal Pump Hydraulic Performance and Internal Flow. Machines 2025, 13, 721. https://doi.org/10.3390/machines13080721
Zhu Q, Gu Y, Bian J. Impact of the Magnetic Gap in Submerged Axial Flux Motors on Centrifugal Pump Hydraulic Performance and Internal Flow. Machines. 2025; 13(8):721. https://doi.org/10.3390/machines13080721
Chicago/Turabian StyleZhu, Qiyuan, Yandong Gu, and Junjie Bian. 2025. "Impact of the Magnetic Gap in Submerged Axial Flux Motors on Centrifugal Pump Hydraulic Performance and Internal Flow" Machines 13, no. 8: 721. https://doi.org/10.3390/machines13080721
APA StyleZhu, Q., Gu, Y., & Bian, J. (2025). Impact of the Magnetic Gap in Submerged Axial Flux Motors on Centrifugal Pump Hydraulic Performance and Internal Flow. Machines, 13(8), 721. https://doi.org/10.3390/machines13080721






