Abstract
Accurate oil debris analysis and wear monitoring of a gearbox are essential to ensure its stable and reliable operation. Element types of wear debris and their changes in the lubrication oil of the gearbox can be monitored by spectral analysis. However, it is still difficult to identify wear parts of the gearbox due to the complex composition of elements of wear debris. An improved multi-variable grey prediction model by incorporating a multi-objective genetic algorithm (MOGA-GM(1, N)) is proposed to evaluate weight coefficients of element concentrations of wear debris in the lubrication oil of the gearbox. Moreover, a wear growth rate of each element in the lubrication oil is proposed as an index for oil debris analysis to analyze the multi-variable correlation between the common element of iron (Fe) and other related elements of wear parts of the gearbox. Oil debris analysis of the gearbox is conducted on optimal weight coefficients of related elements to the common element Fe using the MOGA-GM(1, N) model. Wear experiment results verify feasibility of the proposed oil debris analysis method.
1. Introduction
Gearboxes, as main power conversion components of automotives [1], wind turbines [2], marine devices [3], and mining equipment [4], are prone to wear failure due to their complex structures and poor working conditions. Gearbox failures are multifaceted and can stem from diverse causes [5,6,7]. These failures might emerge due to factors, e.g., inadequate lubrication, which can escalate friction between gear teeth, leading to wear and eventual damage. Wear and tear on gear teeth or bearings over time due to cyclic loading, misalignment, or overloading can also contribute significantly to gearbox failures. Moreover, issues like fatigue failure arising from repeated stress on gear components or the presence of contaminants within the gearbox can compromise its efficiency and functionality. Each factor, alone or in combination, can precipitate gearbox failures, emphasizing the importance of regular maintenance, proper lubrication, alignment checks, and operational care to mitigate such risks.
Fatigue wear phenomenon in gearboxes generally occurs in combined rolling and sliding friction under elastohydrodynamic lubrication (EHL) or mix EHL/boundary lubrication conditions [8,9]. Some operation conditions of gearboxes, such as loads, speeds, film thickness, and flash temperatures, also have influences on their wear phenomenon [10,11]. More than 80% of scrap parts in gearboxes are caused by severe wear. Therefore, prediction and monitoring of worn parts of gearboxes in real time are important to evaluate the reliability and lifespans of gearboxes. To minimize wear failures in gearboxes, it is important to follow proper maintenance practices, including regular inspection, lubrication, and alignment checks [12]. Additionally, using high-quality lubricants, ensuring proper load distribution, and addressing any operational issues promptly can help extend lifespans of gearboxes. The wear phenomenon of gearboxes has been studied from several perspectives [13], including vibration-based condition monitoring [14,15,16], tribo-dynamic behaviors [17,18], metallurgy [19], surface finish [20,21], sliding friction [22], assembly [23], transmission error [24,25], and lubrication [26,27,28,29]. Mechanisms of the wear phenomenon are not completely understood, but it appears clear that it is affected by operation conditions, surface roughness, and lubricants.
Oil-related condition monitoring technologies are common solutions to identify gearbox faults, evaluate operation conditions, and define oil maintenance intervals, including oil debris analysis and oil condition monitoring (OCM) [30]. Oil debris analysis is mainly performed by using oil sampling or sensors that measure some parameters, e.g., wear particle counting and oil contaminant elements [31]. Other studies of OCM focused on sensor validation of oil analysis methods to identify gearbox faults based on valid data on additive depletion and oil degradation due to oxidation, oil contamination, temperature, and viscosity changes [32]. In addition, several OCM methods of gearboxes based on multi-variable oil analysis methods, e.g., fluorescence spectroscopy, and oil viscosity measurements, were developed to improve analysis accuracy and measurement sensitivity of oil-based condition monitoring systems of gearboxes [32,33].
An oil debris analysis method of wear evaluation was developed to monitor wear conditions of engines by analyzing wear particles in engine lubrication oil [34]. This oil debris analysis method exhibited strong sensitivity to identification of engine wear failure. Spectral analysis [35] is one of the main solutions for oil debris analysis for mechanical equipment. This technique is used to monitor variations in wear element concentrations to predict wear conditions of mechanical equipment. For many years, numerous failure analysis methods have been proposed to evaluate equipment wear failure based on spectral analysis. Huang et al. [36] evaluated dynamic performances of a hypoid gear pair in a tidal energy converter using a coupled torsional vibration model across diverse tidal speed profiles. developed a two-stage residual grey model to predict spectral data of wear particles in lubrication oil of marine engines, which improved the accuracy of failure prediction with large fluctuations of wear conditions. A remaining useful life prediction model of power-shift steering transmission systems was developed to analyze wear failure by monitoring the oil spectral data [37]. Zhang et al. [38] proposed an unequal interval GM(1, 1) model and used a lead (Pb) element as the wear characteristic index to predict wear failure of marine diesel engines. Valis et al. [39] used Wiener failure model for iron (Fe) and Pb elements in lubrication oil to enhance wear failure identification of vehicle engines. To improve the prediction accuracy of wear failure analysis based on spectral analysis, some works studied oil debris analysis with multi-variable wear elements. Lara et al. [40] combined principal component and sequential discriminant analyses to investigate multi-variable wear elements. A subspace reconstruction-based robust kernel principal component analysis model was developed [41] for fault detection of wind turbines using supervisory control and data acquisition (SCADA) data to extract nonlinear features under discontinuous interference. However, only the overall wear conditions of gearboxes can be obtained based on the above oil debris analysis methods with the Fe element as the main component, and the specific wear parts of gearboxes remained obscured.
Multi-variable gray prediction models can identify correlations among N variables [42]. The GM(0, N) and GM(1, N) models are multi-variable gray prediction models for the zero- and first-order equations, respectively. The GM(1, N) model can identify correlations between independent variables and a dependent variable by using the first-order non-derivative series [43]. The principle of the GM(1, N) model is to accumulate and generate the first-order accumulated generating operation (1-AGO) sequence with increasing regularity based on the original sequence with unstable and irregular original sequence data [44]. Consequently, the GM(1, N) model can effectively describe regular changes in correlations among multiple variables. To improve the prediction accuracy of the GM(1, N) model, Tien [45] proposed an optimized GM(1, N) model with an improved analysis structure. A multi-variable GM(1, N) model was proposed in [46], incorporating additional terms, e.g., dependent variable lag term and linear correction term. Li et al. [47] developed a time-lagged logistic grey prediction model with harvesting terms.
Wear debris and elements in lubrication oil of gearboxes come from wear behaviors of meshing gear tooth surfaces, friction couplings, and bearings, and components of each wear part are complex and different [48]. Therefore, this study aims to predict wear parts of a gearbox by studying multi-variable relationships among different wear elements in lubrication oil. An oil debris analysis method is developed based on a multi-objective genetic algorithm-GM(1, N) (MOGA-GM(1, N)) model, which combines the reliability of describing multi-variable parameter relations of the GM(1, N) model [42], and a multi-objective optimization function of the MOGA, to predict wear locations with the Fe element. The main source of the Fe element was examined based on the weight coefficient of each related element to the Fe element. Wear experimental results of a gearbox verifies feasibility and accuracy of the proposed oil debris analysis method.
The remaining part of the paper is organized as follows: the oil debris analysis method of the gearbox is introduced in Section 2. The MOGA-GM(1, N) model is developed to evaluate correlations between the Fe element and other elements of parts of the gearbox in Section 3. Wear experiments and discussions of the proposed oil debris analysis method with the MOGA-GM(1, N) model of a gearbox are presented in Section 4. Finally, some conclusions from this study are presented in Section 5.
2. Oil Debris Analysis Method
Main wear parts in a gearbox consist of gears, bearings, shafts, friction plates, seals, gear pumps, and other friction parts. Identifying varied element compositions of different parts in the gearbox is crucial for analyzing its wear conditions. Material and element compositions of parts in the gearbox are listed in Table 1. According to Table 1, most parts in the gearbox contain the Fe element, i.e., planetary gear sets, planet carriers, external teeth friction plates, bearings, ring gears, and the housing. Few parts in the gearbox do not contain the Fe element, i.e., internal toothed friction plates, bearing needle roller diaphragms, and gasket rings.

Table 1.
Material and element compositions of parts in the gearbox with element content percentages.
Since percentages of elements of material composition of parts in the gearbox are constant, the wear condition of the Fe element is always accompanied by other related elements of oil debris or particles, such as copper (Cu), nickel (Ni), chromium (Cr), molybdenum (Mo), aluminum (Al), and manganese (Mn), in the corresponding proportion, excluding carbon (C), and silicon (Si) elements that can be greatly affected by external pollution. Therefore, changes in the concentration of the Fe element in the lubrication oil can be analyzed by concentrations of other related elements. Since contents of different elements of the same part in the gearbox are different, it is difficult to obtain the correlation between the concentration of the Fe element and concentrations of other related elements in the lubrication oil. In this study, the wear growth rate (WGR) of each element in an oil sample is used to serve as the wear characteristic index of the element for oil debris analysis. The WGR of an element in the oil sample can be represented as
where y is the concentration of the element, and the subscript i is the index of the oil sample.
If the wear phenomenon occurs on any part of the gearbox, the WGR of each element increases with wear progression in the gearbox. While there are multiple worn parts in the gearbox and contents of elements of different parts are different, the WGR of each element of the same part is constant. This constancy principle is fundamentally attributed to the invariant elemental composition percentages within each component’s metallurgical matrix, ensuring that wear debris liberation occurs in proportional accordance with the predetermined material stoichiometry. To analyze multivariate relationships between the concentration of the Fe element and those of other related elements, an oil debris analysis method based on the MOGA-GM(1, N) model is proposed to analyze wear conditions of main parts of the gearbox using weight coefficients of other related elements to the WGR of the Fe element. The WGR of the Fe element of a ring gear in the gearbox can be represented as
where is the proportion of the Fe element content of the ring gear, and is the wear degree of the ring gear in the oil sample. The geometric factor represents the sectoral wear analysis approach, where denotes the effective radius reduction from the original unworn state, and the equivalence relationship validates that co-located elements exhibit identical wear progression rates within the same component.
3. Multi-Objective Genetic Algorithm
Considering the limited number of oil samples and nonlinear distribution of oil monitoring data, the GM(1, N) model is more practical and accurate than other traditional multi-variable linear methods for analyzing the relationship between multivariate parameters of small data samples. The MOGA has high adaptability to solve multi-objective optimization problems with enhanced parallelism and stability [49]. Therefore, the oil debris analysis method is proposed for multi-objective and multi-variable optimization based on a MOGA-GM(1, N) model. Detailed procedures of the oil debris analysis method are shown in Figure 1. The MOGA-GM(1, N) model is developed, in which the concentration of a common element of Fe serves as a dependent variable, and concentrations of other related elements, i.e., Ni, Cr, Al, Mn, and Mo, serve as independent variables. An optimal weight coefficient of the concentration of each related element to the Fe element can be obtained by the MOGA with the minimum posterior difference ratio C and the maximum small error probability P as optimization objectives.
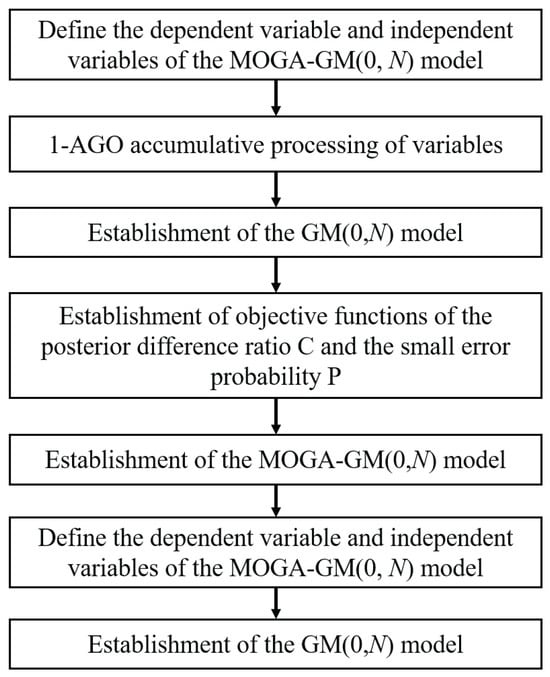
Figure 1.
Flowchart of oil debris analysis based on the MOGA-GM(1, N) model.
3.1. GM(1, N) Model
The system characteristic sequence of the GM(1, N) model can be represented as
where is a sequence of dependent variables, are sequences of independent variables, and n is the number of data samples. The 1-AGO sequence of can be represented as
The GM(1, N) model can be represented as
where is the weight coefficient of the ith independent variable to the dependent variable, and a is a non-random constant. Equation (5) can be rewritten as
where , , and
Using the least square method, weight coefficients of independent variables in the GM(1, N) model can be obtained by
Based on Equation (5), the GM(1, N) model of the oil debris analysis method, in which the concentration of the Fe element serves as the dependent variable, and concentrations of Ni, Cr, Mo, Al, and Mn elements serve as independent variables, can be represented as
3.2. MOGA-GM(1, N) Model
The genetic algorithm (GA) is an objective optimization method, which is developed based on the theory of biological evolution and genetics [50]. The MOGA is an improved multi-objective optimization method based on the GA. The posterior difference ratio C and the small error probability P are two key indicators for the accuracy test of the GM(1, N) model. Therefore, the posterior difference ratio C and the small error probability P work as objective functions to realize effective oil debris analysis. A weighting method for the MOGA is used here to transform multi-objective optimization functions into a single-objective optimization problem. To improve the optimization efficiency and accuracy of weight coefficients of the MOGA, an adaptive crossover and a mutation operator are used in this study. Moreover, an elite strategy for the MOGA is added to ensure the population diversity of the MOGA and accelerate the convergence rate. The flowchart of the MOGA for oil debris analysis is shown in Figure 2. Algorithm 1 presents the systematic implementation procedure for the MOGA-GM(1,N) model applied to oil debris analysis, outlining the sequential steps from variable definition through optimization convergence.
| Algorithm 1 MOGA-GM(1, N) model for oil debris analysis |
|
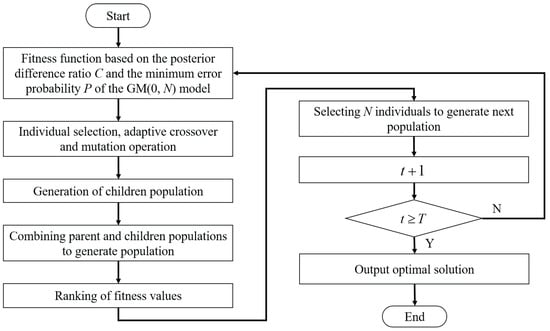
Figure 2.
Flowchart of the multi-objective genetic algorithm for oil debris analysis.
(1) Adaptive crossover-mutation probability: selection ranges of the crossover and the mutation probability in the GA model are (0.4, 0.9) and (0.001, 0.1), respectively. An adaptive crossover-mutation probability p is proposed for adaptive target search to improve the searching capability of MOGA and ensure the diversity of population evolution. If the individual fitness is greater than the average fitness value, a large adaptive crossover-mutation probability p enables individuals to search in the direction near the optimal fitness value. Suppose the individual fitness is less than the average fitness value. In that case, the search trend is reasonable, and the adaptive crossover-mutation probability p can be selected to improve the local search accuracy of the MOGA. The adaptive crossover-mutation probability can be represented as
where and are the maximum and the minimum probabilities of crossover and mutation factors, respectively, is the fitness value of the current individual, and are the maximum and the minimum fitness values, respectively, and is the average fitness value.
(2) Optimization variables: weight coefficients of concentrations of Ni, Mn, Al, Cr, and Mo elements to the concentration of the Fe element need to be optimized, which serve as optimization variables of the MOGA-GA(1, N) model. The constraint of each weight coefficient of the concentration of any other element to the concentration of the Fe element is .
(3) Fitness function: the least squares method is used to analyze relationships of weight coefficients between the concentration of the Fe element and concentrations of other elements in the GM(1, N) model. However, the accuracy is insufficient to guarantee that the posterior difference ratio C and the small error probability posterior P of the GM(1, N) model are of the first-order accuracies. Weight coefficients of the MOGA for oil debris analysis are also unconstrained. Therefore, negative values of these weight coefficients may occur. The proposed MOGA-GM(1, N) model aims to ensure that the posterior difference ratio C and the small error probability posterior P exhibit first-order accuracies, as shown in Figure 3.
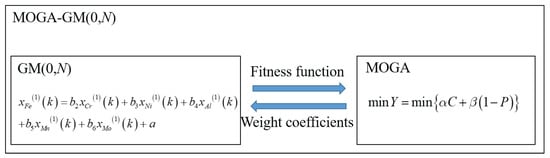
Figure 3.
MOGA-GM(1, N) model for the oil debris analysis method of gearboxes.
The GM(1, N) model selects the minimum posterior difference ratio C and the maximum small error probability posterior P as fitness functions and uses MOGA instead of the least squares algorithm to obtain the optimal multi-variable relationship between the concentration of the common element of Fe and those of other elements. According to optimization constraints, the main wear sources of the Fe element are examined by their weight coefficients.
The posterior difference ratio C can be represented as
where is the residual variance of the concentration of the Fe element, is the variance of the concentration of the Fe element, is the residual mean value of residual errors that is
is the residual error of the concentration of the Fe element that can be represented as
is the sequence of the concentration of the Fe element, is the simulated sequence of the concentration of the Fe element, and is the mean value that is
Based on Equations (11) and (12), the small error probability P can be represented as
The fitness function Y of the MOGA-GM(1, N) model can be represented as
where and are weight coefficients of the posterior difference ratio and the small error probability, respectively.
4. Experiments and Discussion
4.1. Wear Experiments of a Gearbox
To verify the effectiveness of the proposed oil debris analysis method of gearboxes, wear experiments of an SD16 bulldozer gearbox were conducted on a gear transmission reliability test rig, as shown in Figure 4. Wear experiments are performed under the thermal conditions of bulldozers to ensure that the collected oil samples can reliably represent actual wear states of the gearbox. Settings of wear tests are shown in Table 2. The input speed of the gearbox was 2000 rpm with Gear oil VG100 at 100 °C. The gearbox was initially tested with an input load of 160 Nm for running cycles of the input shaft of the gearbox to assess the adhesion of the coating of tooth surfaces in the running-in period. Each round of wear tests was then carried out with an input load of 400 Nm for running cycles of the input shaft of the gearbox. After each round of wear tests, about 200 mL of lubrication oil was extracted. To reduce the influence of lubrication oil extraction on lubrication, the same amount of lubricating oil was added to the gearbox for replenishment before the gearbox was further tested for the next round. The distance between the lubrication oil extraction position and the bottom of the gearbox is half of the depth of the lubrication oil, so that there is enough distance to prevent inhalation of a large number of abrasive particles, paint film, and sludge at the bottom of the gearbox.

Figure 4.
SD16 bulldozer gearbox for wear testing.

Table 2.
Experimental conditions of wear tests for the gearbox.
The spectral data of wear elements of the gearbox in oil samples were obtained by using a SPECTROIL Atomic Emission Spectrometer, as shown in Figure 5. The spectral data of the wear experiment of the gearbox are listed in Table 3. The variation tendency of element concentration demonstrates that concentrations of Cu and Fe elements are larger than others in oil samples, as shown in Figure 6. Oil samples from 1 to 9 in Table 3 are extracted after the gearbox operates with running cycles of its input shaft of , , , , , , , , and , respectively.

Figure 5.
Spectroil M/N type deployable atomic emission oil analysis spectrometer.

Table 3.
Concentrations of different elements in oil samples of the gearbox.
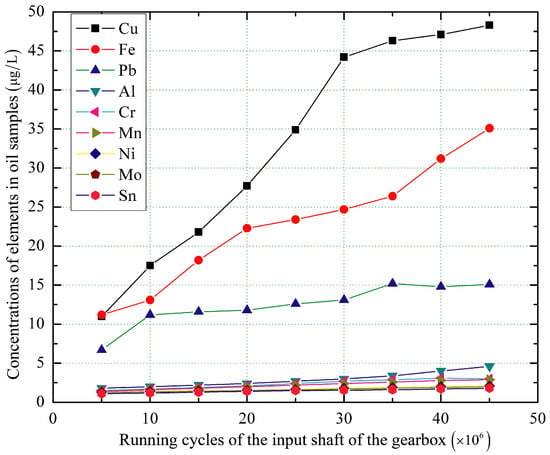
Figure 6.
Variation tendency of different elements in oil samples of the gearbox.
4.2. Oil Debris Analysis Results of the Fe Element Based on MOGA-GM(1, N) Model
Considering the complexity of wear element composition, this work uses the MOGA-GM(1, N) model to realize wear location analysis of the Fe element by analyzing the contribution of related elements Cr, Ni, Al, Mn, and Mo to the common element Fe. Table 4 shows the wear characteristic index of oil debris analysis.

Table 4.
WGRs of different elements in oil samples.
The 1-AGO sequences of wear growth rates of elements in oil samples are
Hence, the MOGA-GM(1, N) model of the Fe element for oil debris analysis is
Through iterative search, the MOGA-GM(1, N) model demonstrates that the corresponding weight coefficients of concentrations of other related elements of Cr, Ni, Al, Mn, and Mo to that of the common element of Fe are 0.44, 0.18, 0.49, 0.04, and 0.02, respectively. According to weight coefficients in Equation (16), weight coefficients of concentrations of Al, Cr, and Ni elements are larger than those of other elements. The posterior difference ratio C and the small error probability P of the MOGA-GM(1, N) model are 0.06 and 0.99, respectively, which are both first-class accuracies, as shown in Table 5. The numerical analysis results of the MOGA-GM(1, N) model show that wear faults occur on the gear pump and some slight wear occurs on the sun gear, planetary gears, and their gear shafts according to element compositions of different parts in the gearbox in Table 1.

Table 5.
Model test accuracy level of the posterior different ratio and the small error probability.
4.3. Oil Debris Analysis Results of the Cu Element Based on Grey Relational Analysis
According to the element composition of parts of the gearbox in Table 1, the Cu element in the gearbox mainly exists in internal toothed friction plates, bearing needle roller diaphragms, and gasket rings. Since the concentration of the Pb element is high and that of the Sn element is very low, the Cu element in oil samples comes from wear of internal toothed friction plates and bearing needle roller diaphragms. The grey relational analysis method [51] is used to analyze the grey relevancy between the concentration of the Cu element and that of the Pb element for predicting the main wear part of the Cu element, which can be represented as
where is the resolution coefficient, which is 0.5 in the study, is the relative difference sequence concentrations of Cu and Pb elements in oil samples, and are the minimum and the maximum components of the part of the gearbox, respectively. The grey relevancy between the concentration of the Cu element and that of the Pb element is 0.75. The analysis result of indicates that the main wear source of the Cu element is internal tooth friction plates. Hence, there is some wear on the internal tooth friction plate of the gearbox. Experimental results of the gearbox show that serious wear was on the external tooth friction plate of the gearbox, including both a macroscopic view of the wear pattern and a detailed micrograph of the affected region, as shown in Figure 7. The wear fault on the external tooth friction plate can seriously reduce the reliability and the life of the gearbox. Figure 8 shows wear results for the gear pump, again offering both an overall view of the wear condition and a microscopic examination of the wear region.

Figure 7.
Gear wear experimental results of external toothed friction plate: (a) wear condition with green frame highlighting the analyzed wear region and (b) micrograph showing detailed surface morphology of the wear region.

Figure 8.
Gear wear experimental results of the gear pump: (a) wear condition with green frame highlighting the analyzed wear region and (b) micrograph showing detailed surface morphology of the wear region.
The microscopic examination results presented in Figure 7 and Figure 8 provide critical validation of the MOGA-GM(1,N) model predictions and reveal the underlying wear mechanisms responsible for element release into the lubrication oil. Figure 7b demonstrates severe abrasive wear on the external toothed friction plate surface, characterized by parallel grooves and material removal patterns consistent with sliding friction under high contact pressures during clutch engagement cycles. The observed surface topology exhibits plastic deformation zones and material transfer indicative of boundary lubrication conditions, which explains the elevated manganese concentrations detected in the oil samples, as the 65Mn steel composition releases both iron and manganese particles proportionally during wear progression. Figure 8b reveals fatigue-induced degradation on the gear pump surface, displaying micro-pitting formations and subsurface crack propagation patterns typical of cyclic loading under elastohydrodynamic lubrication conditions. The crater-like surface irregularities and spalling characteristics observed in the micrograph correspond directly to the aluminum alloy composition breakdown, resulting in the simultaneous release of aluminum, iron, and chromium elements detected through spectral analysis. These morphological findings confirm that the weight coefficients obtained from the MOGA-GM(1, N) model accurately reflect the dominant wear sources, with the gear pump showing the highest correlation to iron element concentration changes due to its severe fatigue wear condition, while the friction plate wear contributes secondary but measurable element concentrations consistent with its abrasive wear mechanism.
4.4. Discussion
A case study of gearbox wear testing was compared with the GM(1, N) model to verify the accuracy of the oil debris analysis method for gearboxes based on the MOGA-GM(1, N) model. The GM(1, N) model demonstrated that weight coefficients of concentrations of other related elements, i.e., Cr, Ni, Al, Mn, and Mo, to the common element Fe are 0.69, 0.03, 0.42, 0.04, and −0.17, respectively. The weight coefficients of concentrations of Cr and Al elements to the common element Fe are much larger than other elements. It concludes that the gear pump has obvious wear failure. The posterior difference ratio C of the GM(1, N) model is 0.27, which is larger than the posterior difference ratio C of the MOGA-GM(1, N) model. The small error probability P of the GM(1, N) model is 0.71, which is smaller than the small error probability P of the MOGA-GM(1, N). Hence, the accuracy of the MOGA-GM(1, N) is higher than that of the GM(1, N) model.
Table 6 shows analysis results of oil debris analysis between the GM(1, N) model and the MOGA-GM(1, N) model. The weight coefficient of the Mo element in the GM(1, N) model is −0.17, which has negative effects on the concentration of the Fe element. According to Table 1, the Mo element only exists in ring gears in the gearbox, which also contains the Fe element. The concentration of the Fe element increases with the increase in the concentration of the Mo element. Thus, the weight coefficient of the Mo element in the GM(1, N) model cannot predict the variation tendency of the concentration of the Mo element in oil samples. The analysis accuracy of wear location analysis based on the MOGA-GM(1, N) model is significantly higher than that of the GM(1, N) model.

Table 6.
Analysis results of the GM(1, N) model and the MOGA-GM(1, N) model.
Wear experimental results of the gearbox indicated that the gear pump has a relatively serious wear fault and the sun gear has a slight wear. Wear experimental results of the gearbox are consistent with analysis results of wear location analysis based on the MOGA-GM(1, N) model, and verify the validity of the MOGA-GM(1, N) model for wear location analysis of the gearbox. The proposed wear location analysis method based on the MOGA-GM(1, N) model can be used to real-time monitor the serious wear parts with multiple materials in the gearbox.
The wear experimental results in Table 6 provide comprehensive validation of the MOGA-GM(1,N) model’s predictive capabilities. The model’s identification of the gear pump as the primary wear source, based on weight coefficients of Al (0.49), Cr (0.44), and Ni (0.18) elements, was directly confirmed by physical examination revealing serious wear fault in the gear pump. Similarly, the Cu element analysis correctly predicted friction plate wear, which was validated through microscopic examination of the external tooth friction plate showing significant wear patterns. The quantitative accuracy metrics (C = 0.06, P = 0.99) achieving first-class accuracy levels, combined with the precise correlation between predicted and observed wear locations, demonstrate that the MOGA-GM(1,N) model can reliably translate complex multi-element oil debris data into accurate wear location predictions for real-time gearbox condition monitoring.
5. Conclusions
This work presents an oil debris analysis method based on the MOGA-GM(1, N) model for gearboxes to predict their wear conditions by using lubrication oil spectral analysis. The proposed MOGA-GM(1, N) model provides a new approach for the wear location analysis of parts of the gearbox. The MOGA-GM(1, N) model can analyze wear conditions of parts, including different materials with multiple elements. Based on prediction results obtained by the proposed MOGA-GM(1, N) model for oil debris analysis of gearboxes, some meaningful conclusions are drawn below.
(1) Wear growth rates of concentrations of elements in lubrication oil of the gearbox are used for wear prediction of the gearbox. Wear location analysis of parts is realized by studying weight coefficients between the concentration of the common element and those of other related elements.
(2) The MOGA-GM(1, N) model is developed to analyze complex relationships between the concentration of the Fe element and those of other elements in oil samples. The posterior difference ratio and the small error probability of the accuracy test of the GM(1, N) model are used as objective functions of the MOGA-GM(1, N) model.
(3) According to the oil debris analysis method based on the MOGA-GM(1, N) model, numerical results show that the main wear part of the Fe element is the gear pump of the gearbox, and some slight wear also occurs on the sun gear, planetary gears, and the gear shaft. Wear experimental results verify the feasibility and accuracy of the MOGA-GM(1, N) model. By comparing prediction results of the MOGA-GM(1, N) model and the GM(1, N) model, the MOGA-GM(1, N) model can improve the accuracy of oil debris analysis, and describe complex relationships of WGRs of multiple elements of the gearbox.
Author Contributions
Conceptualization, Y.W.; methodology, B.W.; software, B.W.; validation, B.W.; formal analysis, B.W.; investigation, B.W.; resources, Y.W.; data curation, B.W.; writing—original draft preparation, B.W.; writing—review and editing, B.W.; visualization, B.W.; supervision, Y.W.; project administration, Y.W.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Bo Wang was employed by Shenzhen Intelligent Offshore Manufacturing Innovation Center Co., Ltd. Other author declare no conflict of interest.
References
- Barathiraja, K.; Devaradjane, G.; Paul, J.; Rakesh, S.; Jamadade, G. Analysis of automotive transmission gearbox synchronizer wear due to torsional vibration and the parameters influencing wear reduction. Eng. Fail. Anal. 2019, 105, 427–443. [Google Scholar] [CrossRef]
- Wang, T.; Han, Q.; Chu, F.; Feng, Z. Vibration based condition monitoring and fault diagnosis of wind turbine planetary gearbox: A review. Mech. Syst. Signal Process. 2019, 126, 662–685. [Google Scholar] [CrossRef]
- Li, G.; Zhu, W. A review on up-to-date gearbox technologies and maintenance of tidal current energy converters. Energies 2022, 15, 9236. [Google Scholar] [CrossRef]
- Kumar, A.; Ghosh, S.K. Size distribution analysis of wear particles in the transmission system of mining equipment. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018, 232, 921–926. [Google Scholar] [CrossRef]
- Kubo, A. Cause of Failure Beyond Conjugate Theory of Gear Meshing. In Theory and Practice of Gearing and Transmissions: In Honor of Professor Faydor L. Litvin; Springer International Publishing: Cham, Switzerland, 2016; pp. 67–96. [Google Scholar]
- Sait, A.S.; Sharaf-Eldeen, Y.I. A Review of Gearbox Condition Monitoring Based on Vibration Analysis Techniques Diagnostics and Prognostics. In Rotating Machinery, Structural Health Monitoring, Shock and Vibration; Proulx, T., Ed.; Springer: New York, NY, USA, 2011; Volume 5, pp. 307–324. [Google Scholar]
- Smith, J.D. Gear Noise and Vibration; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Huang, D.; Wang, Z.; Li, G.; Zhu, W. Conjugate approach for hypoid gears frictional loss comparison between different roughness patterns under mixed elastohydrodynamic lubrication regime. Tribol. Int. 2019, 140, 105884. [Google Scholar] [CrossRef]
- Huang, D.; Wang, Z.; Kubo, A. Hypoid gear integrated wear model and experimental verification design and test. Int. J. Mech. Sci. 2020, 166, 105228. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; Zuo, M.J.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Zhu, W. Prediction of surface wear of involute gears based on a modified fractal method. ASME J. Tribol. 2019, 141, 031603. [Google Scholar] [CrossRef]
- del Álamo, J.R.; Duran, M.J.; Muñoz, F.J. Analysis of the gearbox oil maintenance procedures in wind energy. Energies 2020, 13, 3414. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. A review of gear fault diagnosis using various condition indicators. Procedia Eng. 2016, 144, 253–263. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.; Ni, Q.; Beer, M. A review of vibration-based gear wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, Z.; Lin, J.; Lu, F. Phenomenological models of vibration signals for condition monitoring and fault diagnosis of epicyclic gearboxes. J. Sound Vib. 2016, 369, 266–281. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J. Vibration signal models for fault diagnosis of planetary gearboxes. J. Sound Vib. 2012, 331, 4919–4939. [Google Scholar] [CrossRef]
- Huangfu, Y.; Dong, X.; Chen, K.; Tu, G.; Long, X.; Peng, Z. A tribo-dynamic based pitting evolution model of planetary gear sets: A topographical updating approach. Int. J. Mech. Sci. 2022, 220, 107157. [Google Scholar] [CrossRef]
- Huangfu, Y.; Dong, X.; Chen, K.; Peng, Z. Coupling mechanism between systematic elastic deformation and gear surface damage. Int. J. Mech. Sci. 2023, 238, 107850. [Google Scholar] [CrossRef]
- Li, X.; Olofsson, U. A study on friction and wear reduction due to porosity in powder metallurgic gear materials. Tribol. Int. 2017, 110, 86–95. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Zhu, W.; Kubo, A. A function-oriented active form-grinding method for cylindrical gears based on error sensitivity. Int. J. Adv. Manuf. Technol. 2017, 92, 3019–3031. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Kubo, A. The modeling approach of digital real tooth surfaces of hypoid gears based on non-geometric-feature segmentation and interpolation algorithm. Int. J. Precis. Eng. Manuf. 2016, 17, 281–292. [Google Scholar] [CrossRef]
- Luo, W.; Qiao, B.; Shen, Z.; Yang, Z.; Cao, H.; Chen, X. Investigation on the influence of spalling defects on the dynamic performance of planetary gear sets with sliding friction. Tribol. Int. 2021, 154, 106639. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Kubo, A. Error-sensitivity analysis for hypoid gears using a real tooth surface contact model. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 507–521. [Google Scholar] [CrossRef]
- Chin, Z.Y.; Borghesani, P.; Smith, W.A.; Randall, R.B.; Peng, Z. Monitoring gear wear with transmission error. Wear 2023, 523, 204803. [Google Scholar] [CrossRef]
- Park, S.; Kim, S.; Choi, J.H. Gear fault diagnosis using transmission error and ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2018, 108, 262–275. [Google Scholar] [CrossRef]
- Krantz, T.L.; Kahraman, A. An experimental investigation of the influence of the lubricant viscosity and additives on gear wear. Tribol. Trans. 2004, 47, 138–148. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Zhu, C.; Parker, R.G. Effects of lubrication on gear performance: A review. Mech. Mach. Theory 2020, 145, 103701. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, C.; Lei, Y.; Liu, Z. An adhesive wear model for helical gears in line-contact mixed elastohydrodynamic lubrication. Wear 2019, 426, 896–909. [Google Scholar] [CrossRef]
- Wang, H.; Tang, L.; Zhou, C.; Shi, Z. Wear life prediction method of crowned double helical gear drive in point contact mixed elastohydrodynamic lubrication. Wear 2021, 484, 204041. [Google Scholar] [CrossRef]
- Pan, Y.; Liang, B.; Yang, L.; Liu, H.; Wu, T.; Wang, S. Spatial-temporal modeling of oil condition monitoring: A review. Reliab. Eng. Syst. Saf. 2024, 248, 110182. [Google Scholar] [CrossRef]
- Sheng, S. Monitoring of wind turbine gearbox condition through oil and wear debris analysis: A full-scale testing perspective. Tribol. Trans. 2016, 59, 149–162. [Google Scholar] [CrossRef]
- Mauntz, M.R.; Peuser, J. Condition based maintenance of wind turbines by 24/7 monitoring of oil quality and additive consumption: Identification of critical operation conditions and determination of the next oil change. In Proceedings of the Conference for Wind Power Drives 2017: Tagungsband zur Konferenz; BoD–Books on Demand: Norderstedt, Germany, 2017; Volume 3, p. 391. [Google Scholar]
- Coronado, D.; Wenske, J. Monitoring the oil of wind-turbine gearboxes: Main degradation indicators and detection methods. Machines 2018, 6, 25. [Google Scholar] [CrossRef]
- Fan, B.; Feng, S.; Che, Y.; Mao, J.; Xie, Y. An oil monitoring method of wear evaluation for engine hot tests. Int. J. Adv. Manuf. Technol. 2018, 94, 3199–3207. [Google Scholar] [CrossRef]
- Aucélio, R.Q.; de Souza, R.M.; de Campos, R.C.; Miekeley, N.; da Silveira, C.L.P. The determination of trace metals in lubricating oils by atomic spectrometry. Spectrochim. Acta Part B At. Spectrosc. 2007, 62, 952–961. [Google Scholar] [CrossRef]
- Huang, D.; Li, Y.; Zheng, X.; Li, G. Study on dynamic behaviors of hypoid gears under variable tidal current energy harvesting conditions. Machines 2025, 13, 178. [Google Scholar] [CrossRef]
- Yan, S.F.; Ma, B.; Zheng, C.S. Remaining useful life prediction for power-shift steering transmission based on fusion of multiple oil spectra. Adv. Mech. Eng. 2018, 10, 1687814018784201. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Chen, Z. Application of grey modeling method to fitting and forecasting wear trend of marine diesel engines. Tribol. Int. 2003, 36, 753–756. [Google Scholar] [CrossRef]
- Vališ, D.; Žák, L.; Pokora, O. Contribution to system failure occurrence prediction and to system remaining useful life estimation based on oil field data. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2015, 229, 36–45. [Google Scholar] [CrossRef]
- Lara, R.F.; Azcarate, S.M.; Cantarelli, M.Á.; Orozco, I.M.; Caroprese, M.E.; Savio, M.; Camiña, J.M. Lubricant quality control: A chemometric approach to assess wear engine in heavy machines. Tribol. Int. 2015, 86, 36–41. [Google Scholar] [CrossRef]
- Zhang, K.; Tang, B.; Deng, L.; Yu, X. Fault detection of wind turbines by subspace reconstruction-based robust kernel principal component analysis. IEEE Trans. Instrum. Meas. 2021, 70, 3515711. [Google Scholar] [CrossRef]
- Wang, N.; Cha, K.C. Multi-objective optimization of air bearings using hypercube-dividing method. Tribol. Int. 2010, 43, 1631–1638. [Google Scholar] [CrossRef]
- Wu, H.H. Applying grey model to prioritise technical measures in quality function deployment. Int. J. Adv. Manuf. Technol. 2006, 29, 1278–1283. [Google Scholar] [CrossRef]
- Zeng, B.; Luo, C.; Liu, S.; Bai, Y.; Li, C. Development of an optimization method for the GM (1, N) model. Eng. Appl. Artif. Intell. 2016, 55, 353–362. [Google Scholar] [CrossRef]
- Tien, T.L. A research on the grey prediction model GM (1, n). Appl. Math. Comput. 2012, 218, 4903–4916. [Google Scholar] [CrossRef]
- Zeng, B.; Duan, H.; Zhou, Y. A new multivariable grey prediction model with structure compatibility. Appl. Math. Model. 2019, 75, 385–397. [Google Scholar] [CrossRef]
- Li, H.; Wang, G.; Duan, H. A novel time-lagged logistic grey model and its application in forecasting energy production volume. Eng. Appl. Artif. Intell. 2024, 127, 107352. [Google Scholar] [CrossRef]
- Zhu, X.; Zhong, C.; Zhe, J. Lubricating oil conditioning sensors for online machine health monitoring—A review. Tribol. Int. 2017, 109, 473–484. [Google Scholar] [CrossRef]
- Cámara, M.; Ortega, J.; de Toro, F. Approaching dynamic multi-objective optimization problems by using parallel evolutionary algorithms. In Advances in Multi-Objective Nature Inspired Computing; Springer: Berlin/Heidelberg, Germany, 2010; pp. 63–86. [Google Scholar]
- Mirjalili, S.; Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Ying, Y.; Cao, Y.; Li, S.; Li, J.; Guo, J. Study on gas turbine engine fault diagnostic approach with a hybrid of gray relation theory and gas-path analysis. Adv. Mech. Eng. 2016, 8, 1687814015627769. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).