Drastically Accelerating Fatigue Life Assessment: A Dual-End Multi-Station Spindle Approach for High-Throughput Precision Testing
Abstract
1. Introduction
2. Materials and Methods
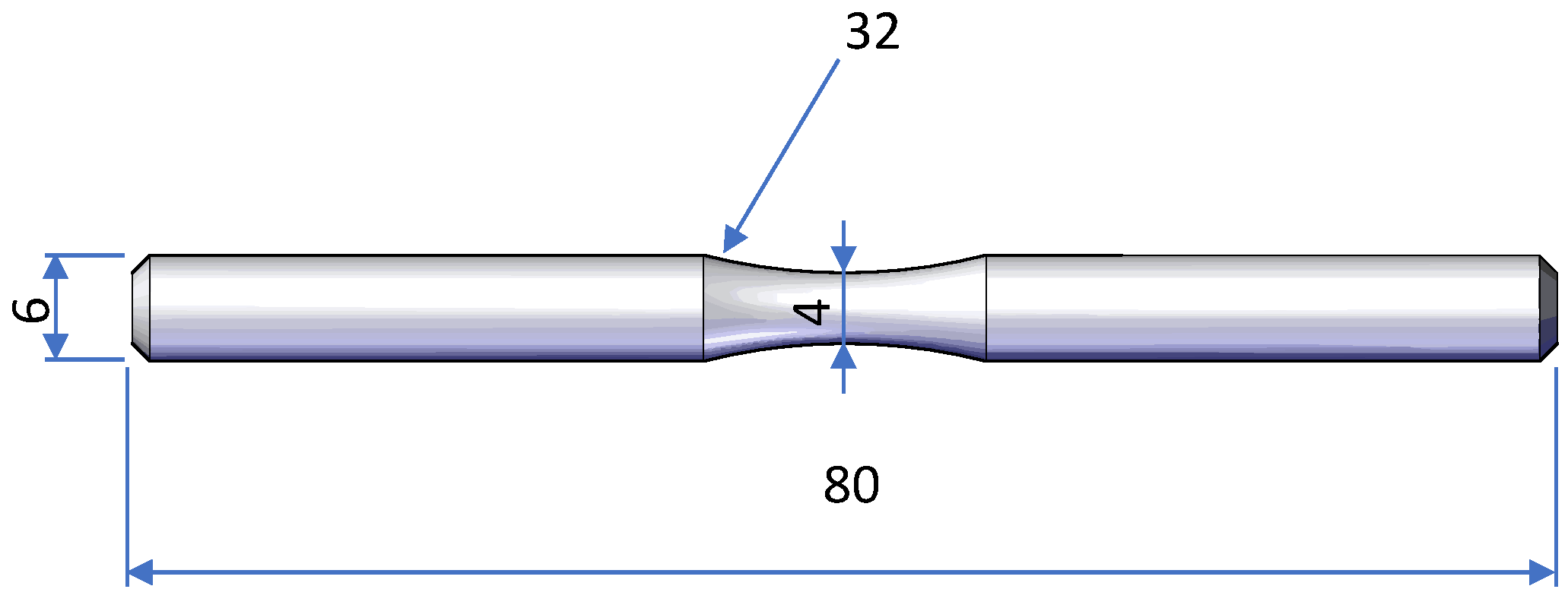
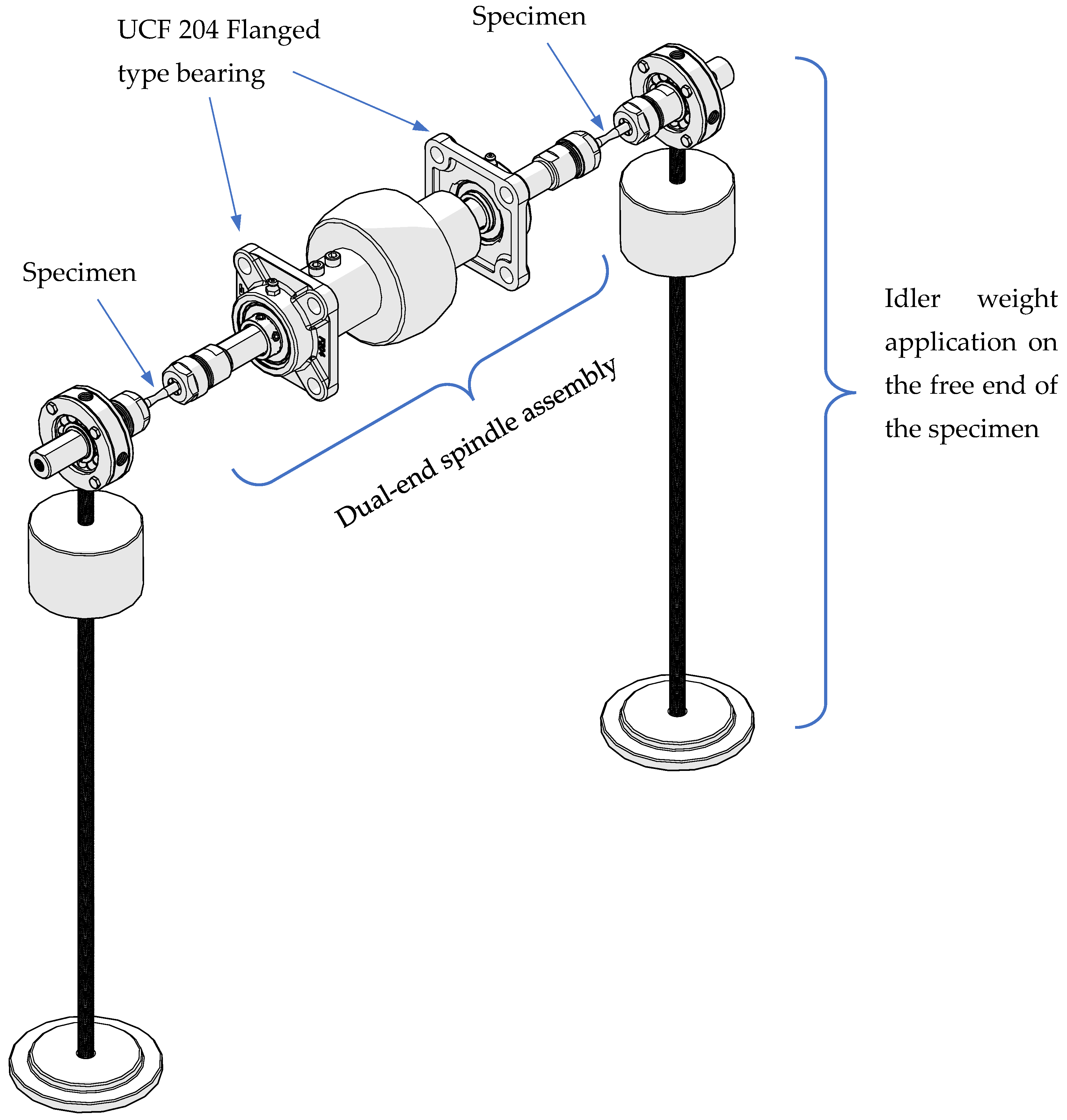
2.1. Specimen Design
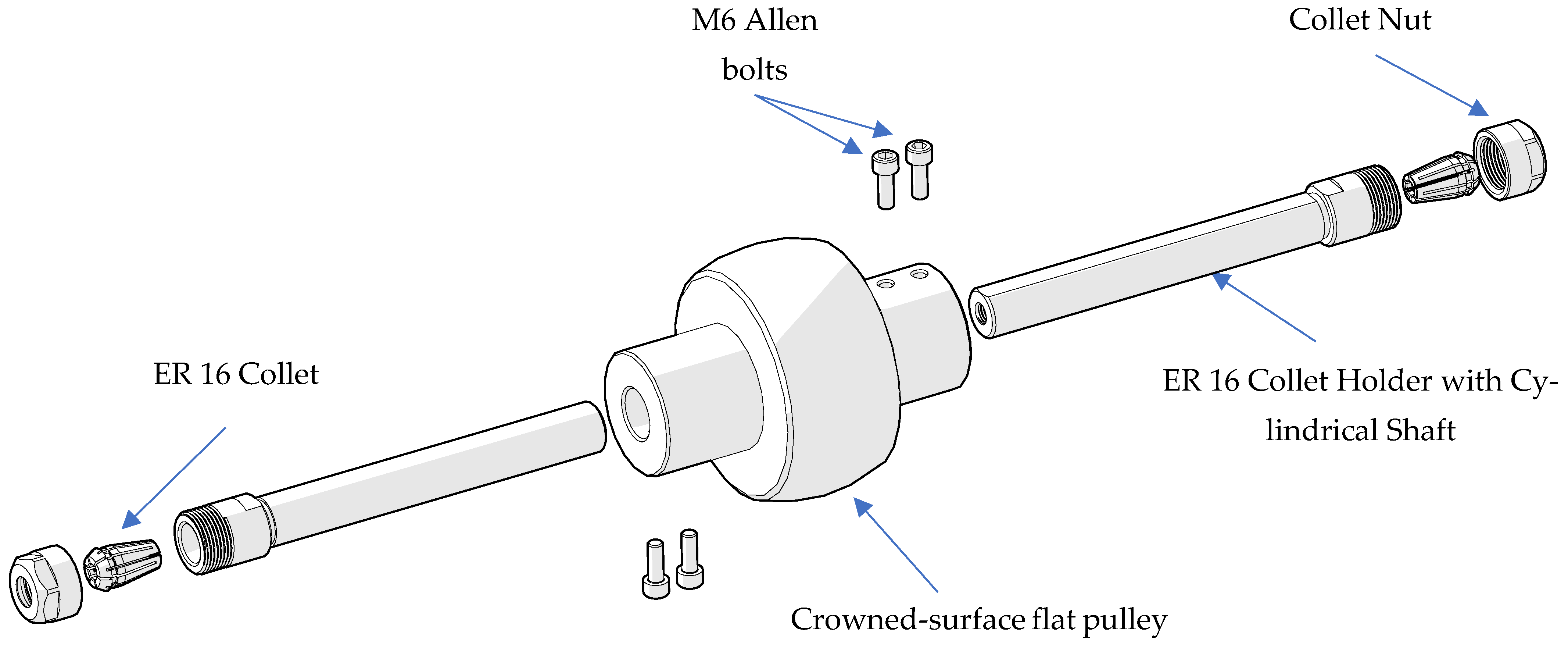
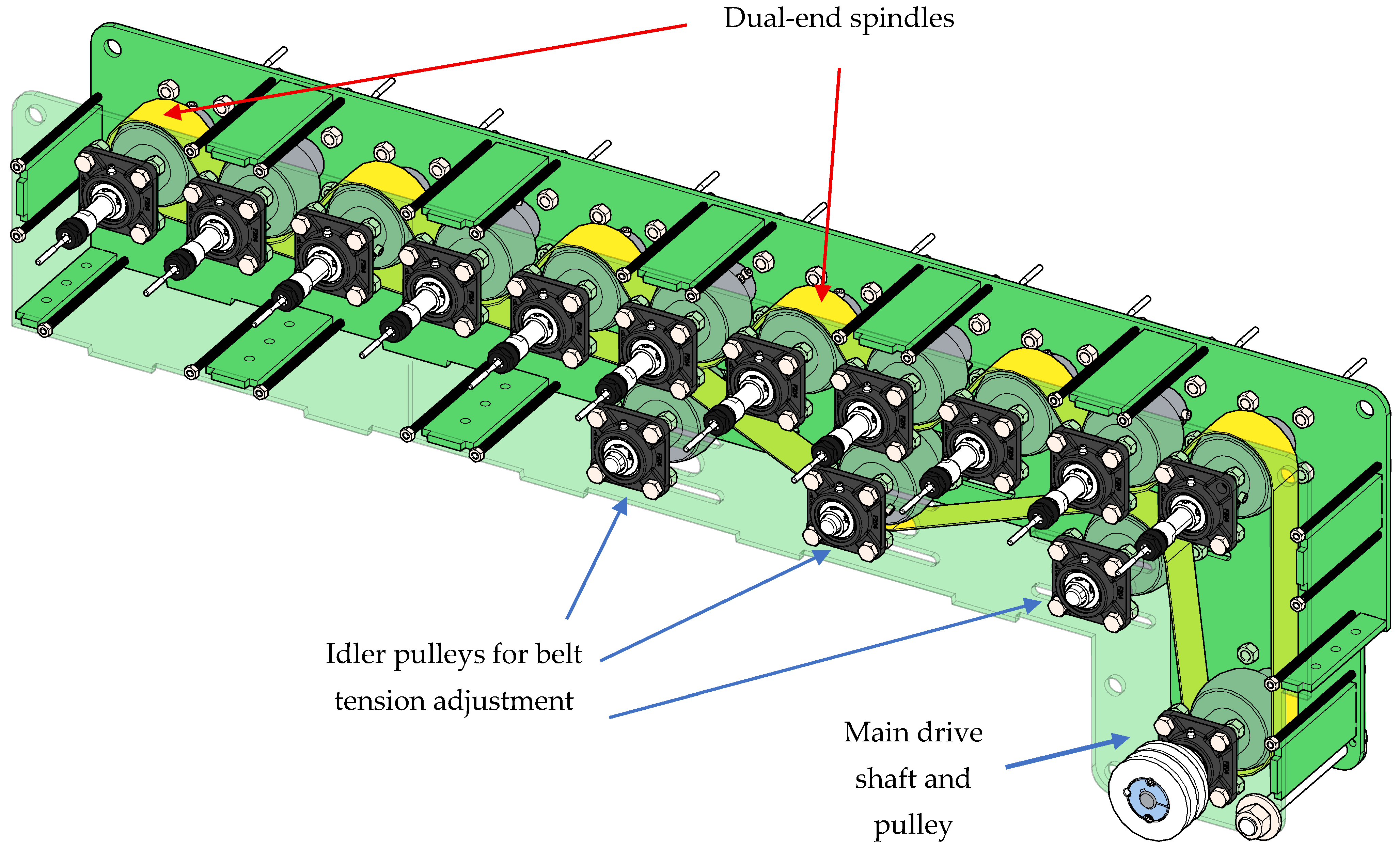
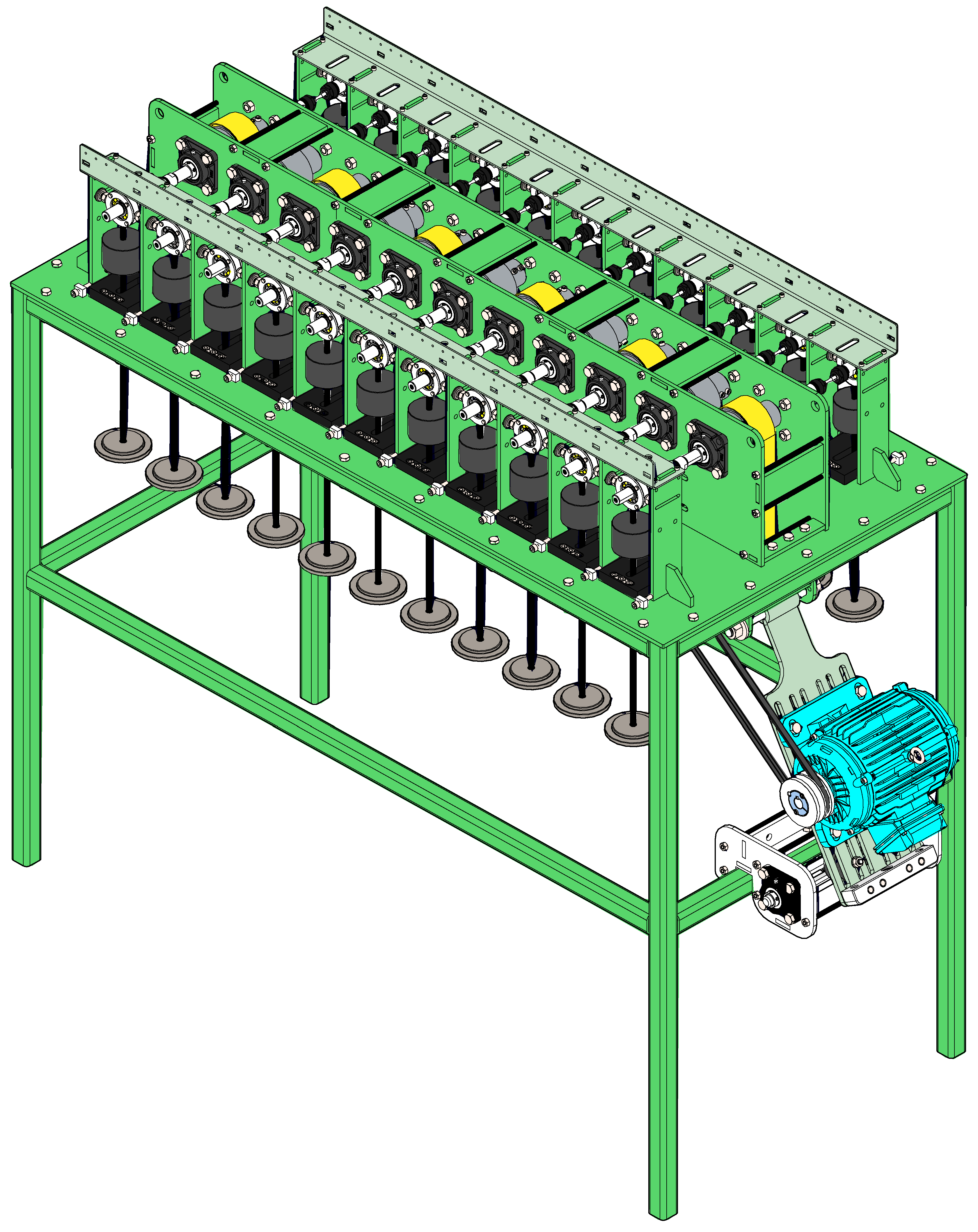
2.2. Machine Design and Assembly
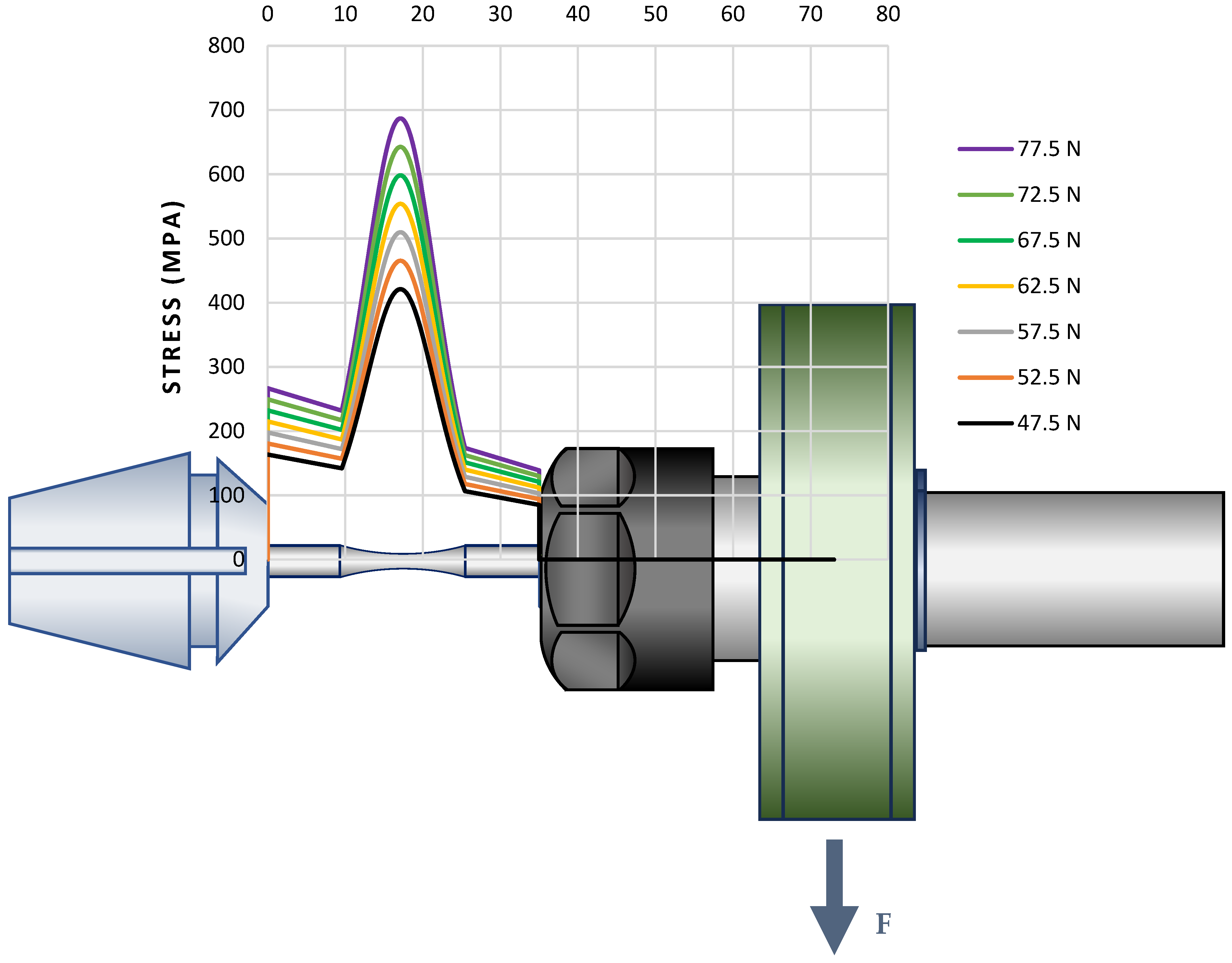
2.3. Scientific Basis and Calculation
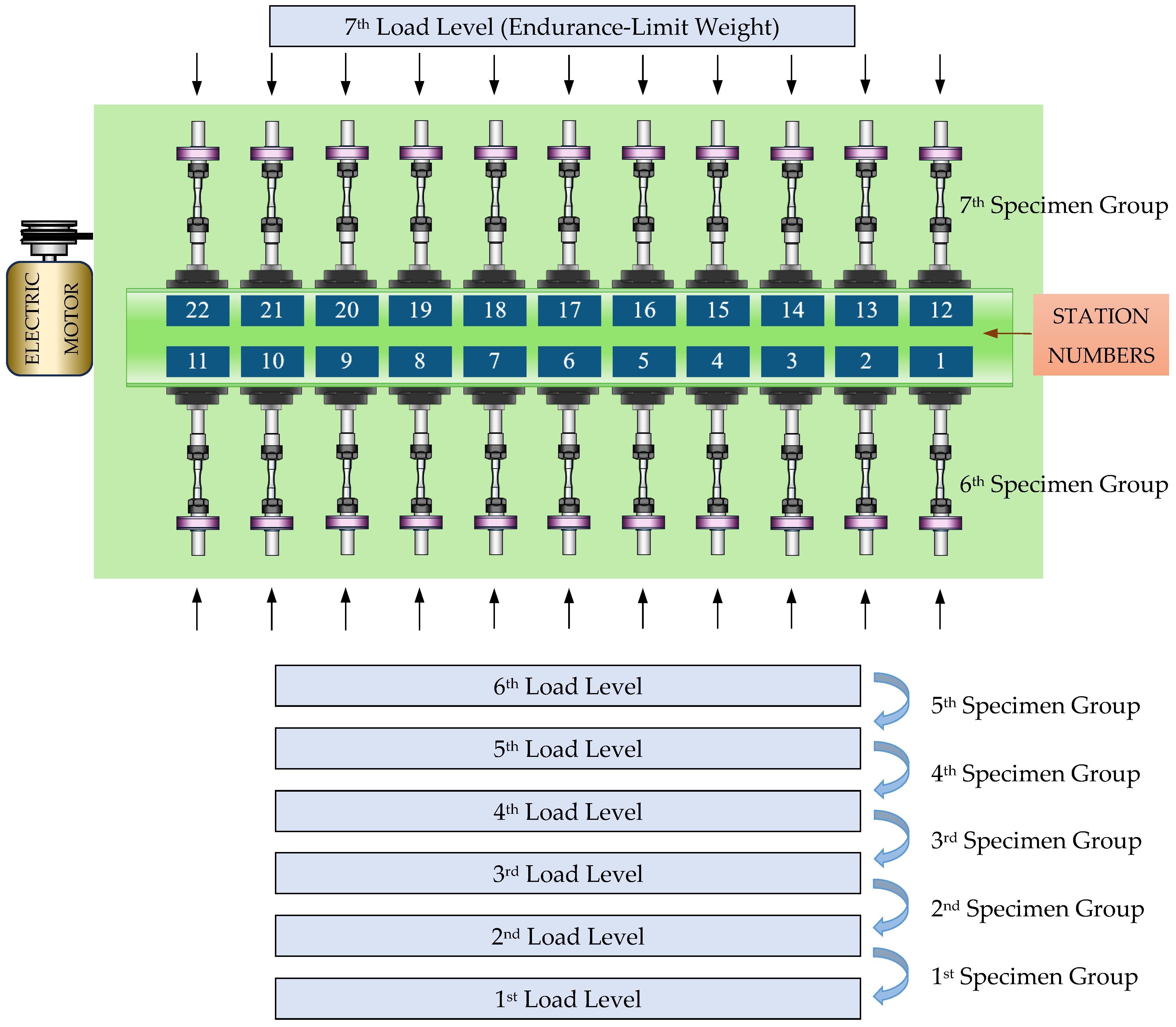
2.4. Design Considerations Behind the Number of Test Stations
3. Experimental Results
4. Discussion
4.1. Comparative Analysis of the Mechanical Design
4.1.1. Multi-Specimen Testing Efficiency
4.1.2. Transmission System
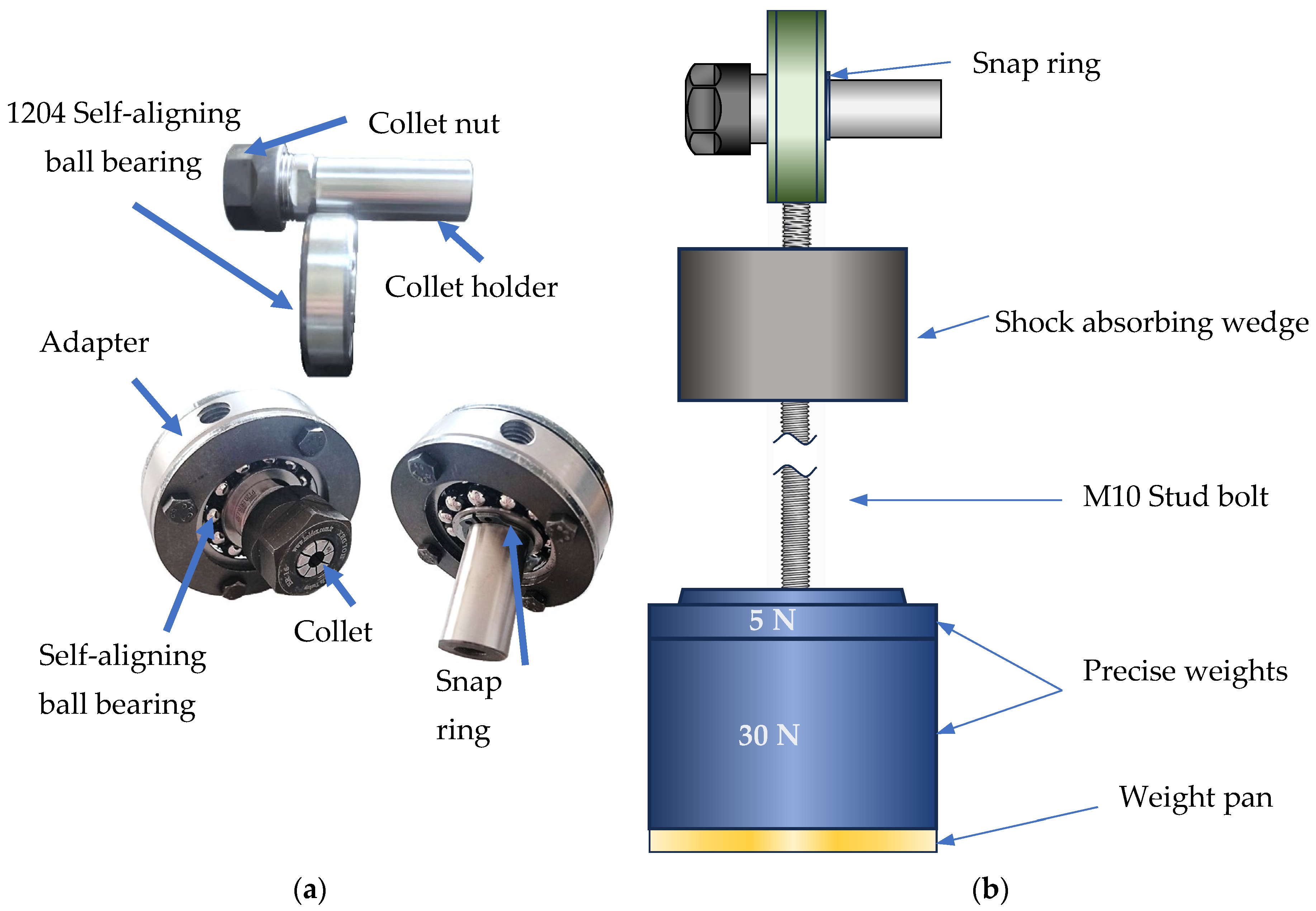
4.1.3. Specimen Fixation and Alignment
4.1.4. Ease of Load Application
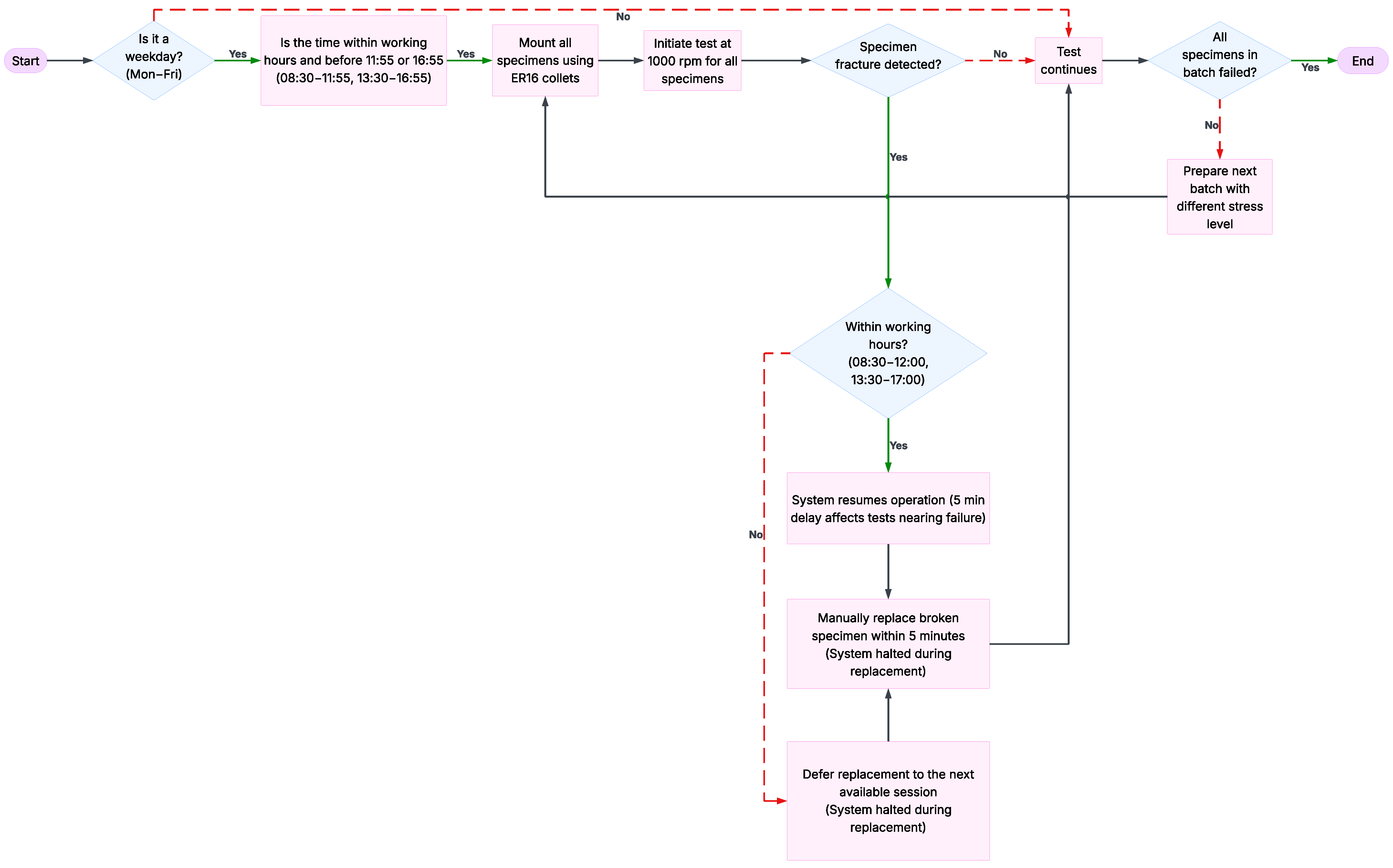
4.1.5. Integration of Real-Time Monitoring and PLC Control
- Automated failure detection through real-time sensor feedback enables the immediate identification of fracture events.
- The automation unit maintains a uniform rotational speed across all specimens, ensuring a consistent cycle frequency. Since this speed can be adjusted via the control interface, the loading frequency for each specimen can be precisely set. This functionality ensures highly uniform and repeatable fatigue loading across all test conditions.
- Real-time logging of the fatigue cycles allows uninterrupted data acquisition throughout the experiment.
- User-friendly operation through an HMI-based control interface that facilitates intuitive command input and system oversight.
- An autonomous system is shut down, wherein the machine continuously monitors all test stations and automatically stops operating once fatigue failure has been detected across all specimens.
- Automated data preservation ensures that all critical test parameters, failure events, and operational logs are securely stored without requiring manual intervention.
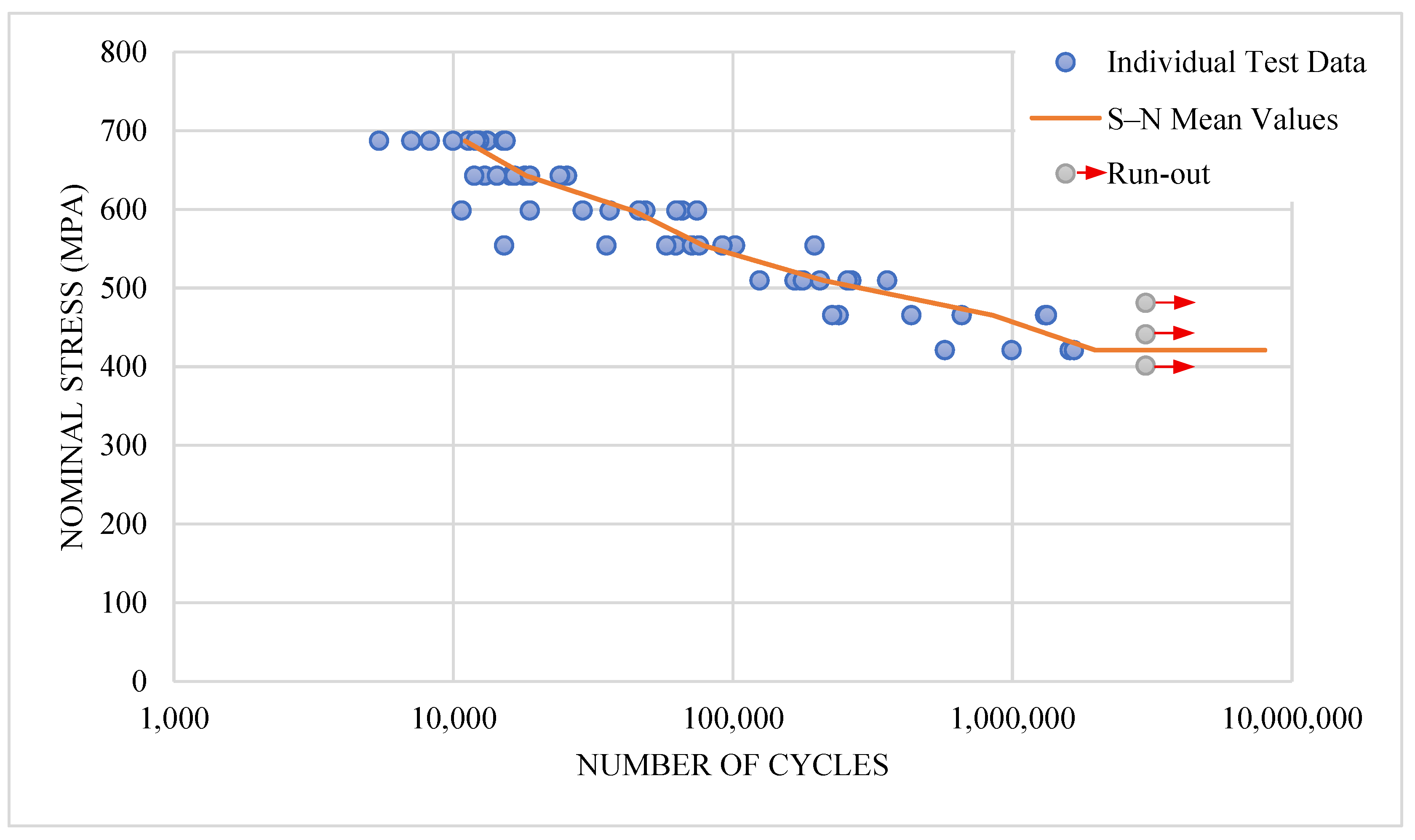
4.2. Analysis of the Fit of the Experimental Data at a Defined Interval
4.2.1. Surface Roughness Analysis of the Specimens
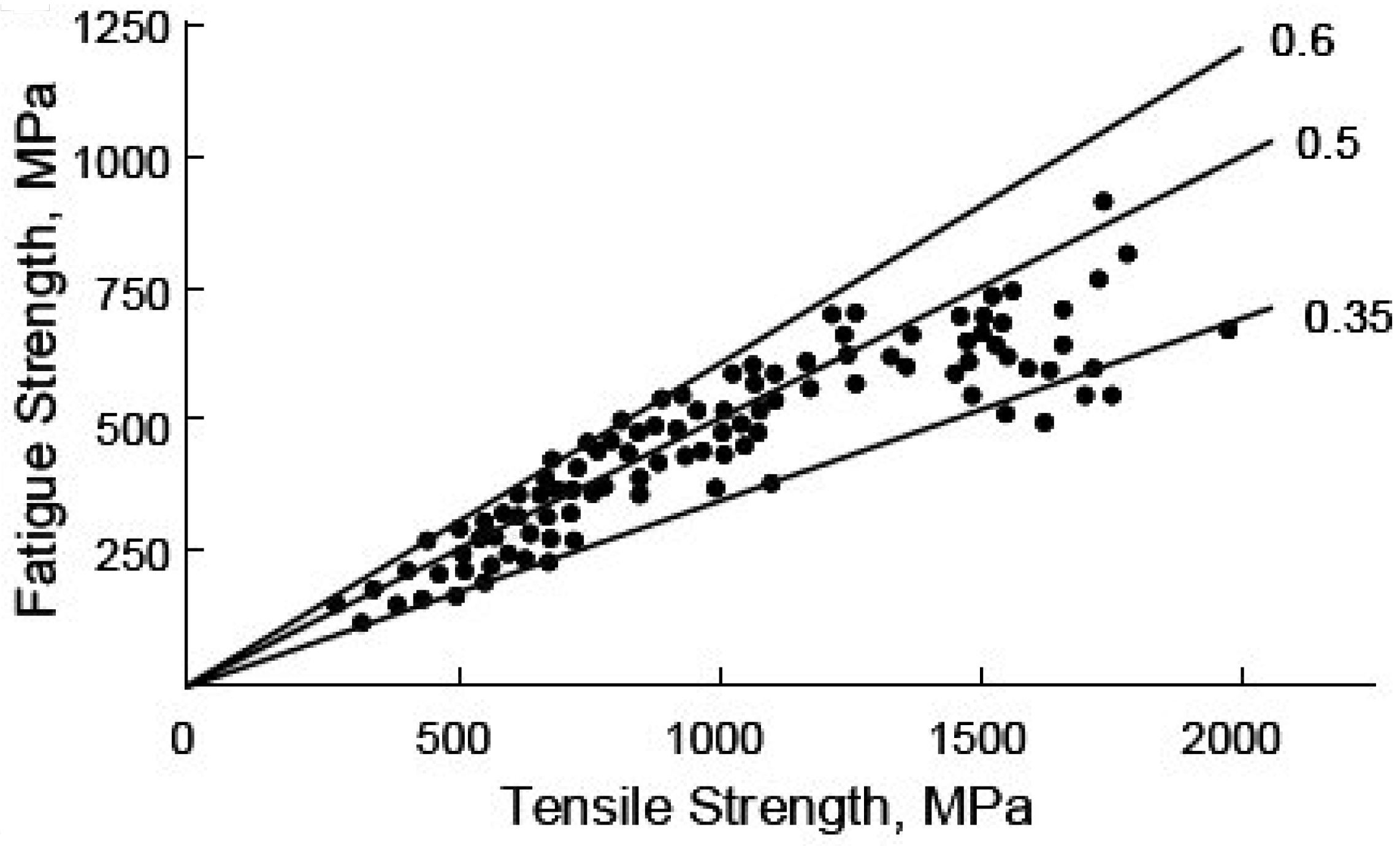
4.2.2. Endurance-Limit Analysis
- The ASM Metals Handbook, Volume 19: Fatigue and Fracture [5] states that the endurance limit for 10% CW AISI 304 stainless steel in rotating bending fatigue tests is 60 ksi (≈413.7 MPa); the present study corresponds to a 1.76% higher endurance limit.
- Behvar et al. [25] reported an endurance limit of 405 MPa for hourglass-type AISI 304 stainless steel specimens tested at room temperature. Compared with this result, the endurance limit found in the present study is 3.95% greater.
- Maximov et al. [28] reported that the endurance-limit value of 304 stainless steel material was 440 MPa. The present study’s endurance limit is 4.32% lower than this reference.
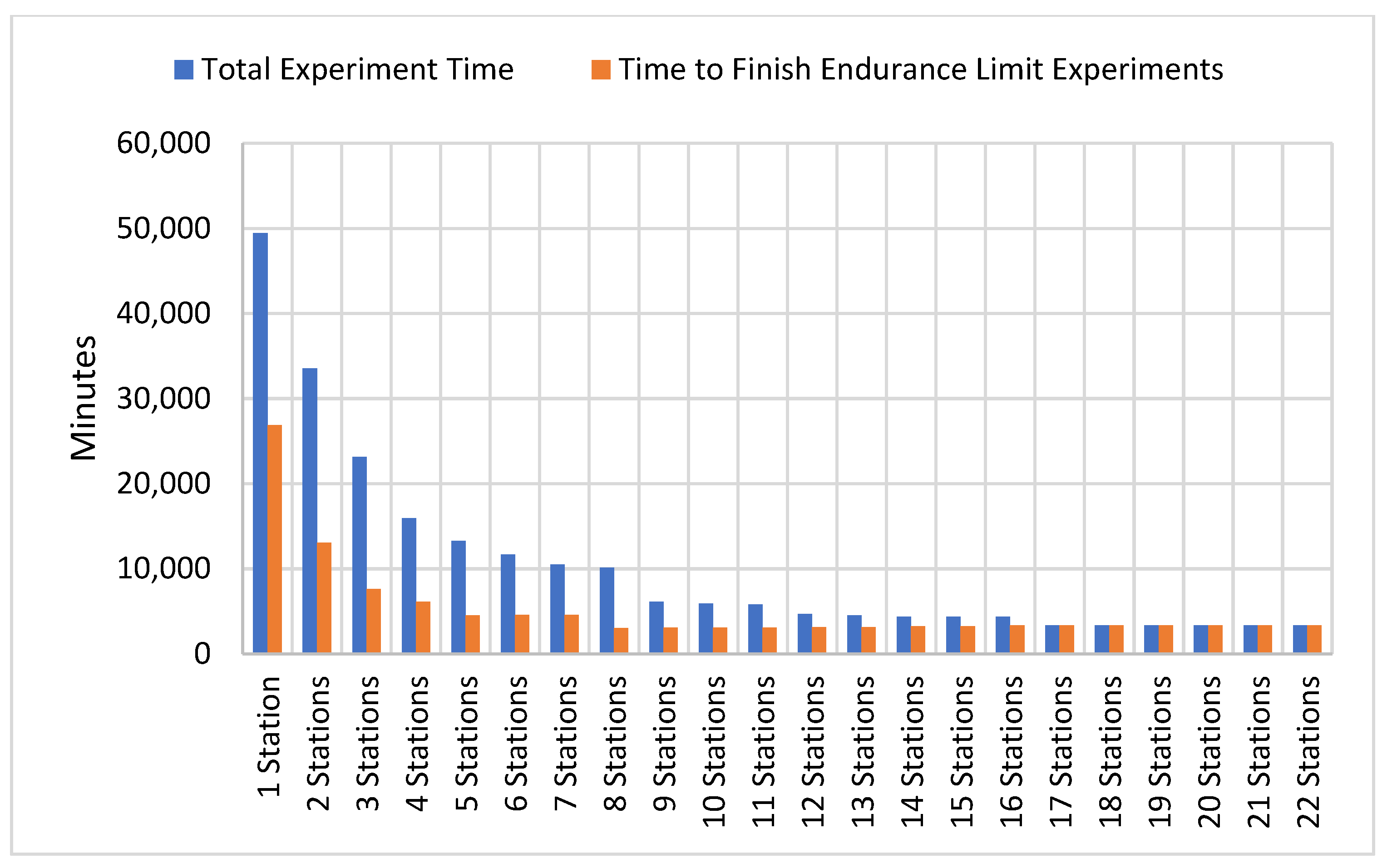
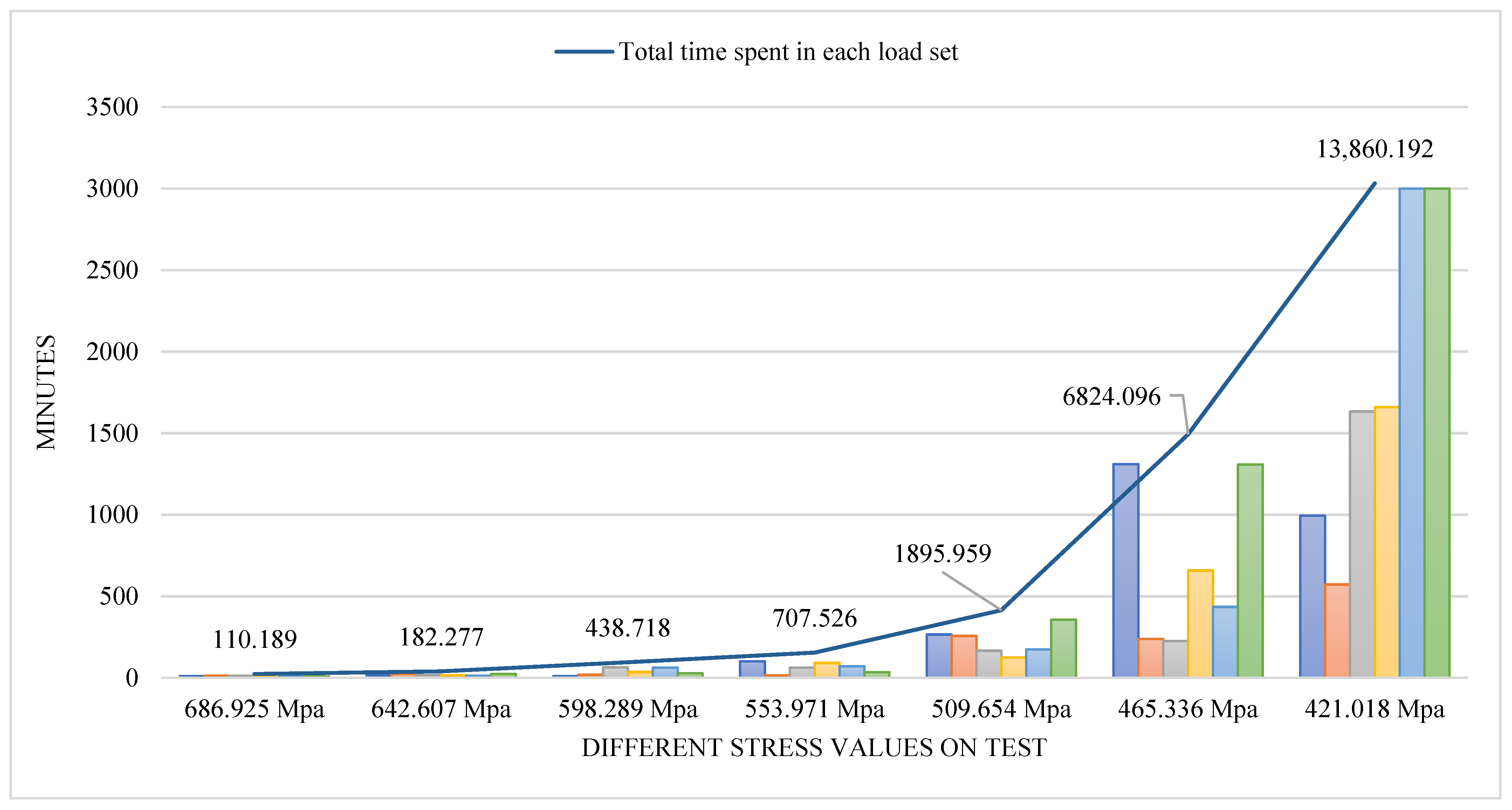
4.3. Quantitative Assessment of Experimental Time Efficiency: Theoretical Projections and Empirical Outcomes
4.3.1. Theoretical Time Efficiency Modeling
4.3.2. Experimentally Observed Time Savings
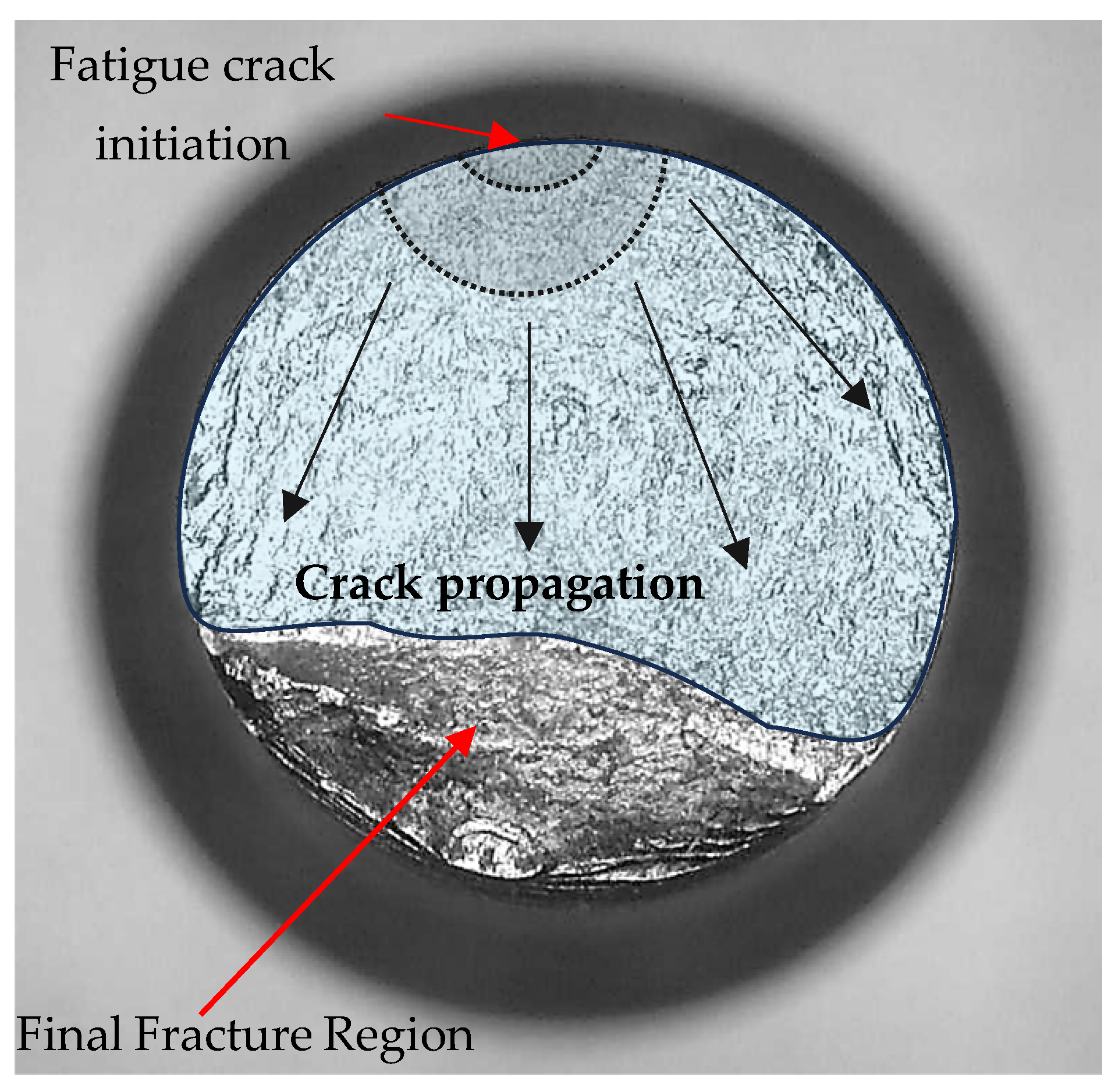
4.4. Fracture Surface Observations
5. Conclusions
- Substantial Time Efficiency: Theoretical modeling predicted a maximum time reduction of 93.2% with full utilization of all 22 stations, whereas experimental validation demonstrated a real-world efficiency gain of 87.5%. Notably, this result was achieved without operating the system at full capacity, indicating that even greater reductions are attainable under fully loaded conditions. These findings confirm the system’s potential to dramatically accelerate fatigue testing workflows.
- Optimized Resource Allocation: The analytical results identified 18 stations as the optimal configuration, balancing throughput with diminishing returns beyond this point. This finding offers a strategic reference for laboratories aiming to maximize efficiency with minimal redundancy.
- Validated Endurance Limit and Structural Reliability: Testing of AISI 304 stainless steel established an endurance limit of 421 MPa, with deviations within ±5.25% of the published literature, confirming the mechanical fidelity of the test system.
- Seamless Automation and Modularity: Integrated with a previously validated PLC-controlled automation unit Doğan et al. [23], the system offers robust control, real-time monitoring, and flexible scalability to accommodate varying experimental demands.
- Strategic Test Planning Model: A forward-looking scheduling model prioritized long-life specimens (e.g., endurance-limit tests) at the outset, ensuring synchronized test completion and minimized idle time, especially under constrained working-hour scenarios.
- Maintenance-Oriented Design for Industrial Usability: The dual-end spindle unit was designed with maintenance efficiency and field serviceability in mind. A standard ER16 cylindrical-shank collet holder, readily available in industrial supply markets, was employed to ensure ease of replacement in cases of damage or wear. Furthermore, the entire spindle module is engineered for rapid disassembly, enabling complete replacement or repair in approximately one minute, significantly minimizing downtime.
- Microscopic examination of fractured specimens revealed distinct crack initiation and propagation zones. Under light loads, the propagation regions appeared smooth and bright, whereas heavier loads resulted in plastically deformed, rougher textures. These consistent features across all load levels confirmed the validity and reliability of the fatigue life measurements.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marijančević, A.; Braut, S.; Žigulić, R.; Skoblar, A. Fatigue Assessment of Marine Propulsion Shafting Due to Cyclic Torsional and Bending Stresses. Machines 2025, 13, 384. [Google Scholar] [CrossRef]
- Rivas, C.E.; Malo, G.D.; Minchala, L.I.; Probst, O. Self-Optimizing Control System to Maximize Power Extraction and Minimize Loads on the Blades of a Wind Turbine. Machines 2023, 11, 601. [Google Scholar] [CrossRef]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering; Wiley: New York, NY, USA, 2000; p. 496. [Google Scholar]
- Fukami, M.; Oguma, N.; Guennec, B.; Horikawa, N.; Sakai, T. Effects of Loading Modes on Fatigue Limit Estimation in Terms of Rotating Bending Fatigue and Rate Process Theory. Appl. Sci. 2024, 14, 477. [Google Scholar] [CrossRef]
- AIH Committee. ASM Handbook: Fatigue and Fracture; ASM International: Metals Park, OH, USA, 1996; Volume 19, p. 2592. [Google Scholar]
- Budynas, R.; Nisbett, K. Shigley’s Mechanical Engineering Design, 10th ed.; McGraw-Hill Education: New York City, NY, USA, 2014; p. 1106. [Google Scholar]
- AIH Committee. ASM Handbook: Mechanical Testing and Evaluation; ASM International: Materials Park, OH, USA, 2000; Volume 8, p. 2235. [Google Scholar]
- Marin, J. Mechanical Behavior of Engineering Materials; Prentice-Hall: Englewood Cliffs, NJ, USA, 1962; p. 502. [Google Scholar]
- Esin, A. Properties of Materials for Mechanical Design; M.E.T.U. Printing Office: Gaziantep, Turkey, 1981. [Google Scholar]
- Gentile, D.; Martorelli, M. Design and realization of a multisamples rotating high cycle fatigue machine. Frat. Ed Integrità Strutt. 2012, 6, 85–92. [Google Scholar] [CrossRef]
- Yamamoto, T.; Kokubu, A.; Sakai, T.; Kiyama, I.; Nakamura, Y. Development and fundamental preformance of dual-spindle rotating bending fatigue testing machine with special device providing corrosive environments. In Proceedings of the Asia Pacific Conference on Fracture and Strength–Mechanics and Materials (APCFS-MM2012), Busan, Republic of Korea, 13–16 May 2012. [Google Scholar]
- Yamamoto, T.; Benning, L.; Gotoh, K. Relationship between temperature property and loading frequency of rotating bending fatigue testing machine of cantilever type. In Proceedings of the International Conference on Very High Cycle Fatigue (VHCF), Dresden, Germany, 3–5 July 2017. [Google Scholar]
- Chauhan, S.J.; Misal, A.; Jadhav, A.; Jadhav, R.; Bhalavi, A.; Jagdale, R. Design and Fabrication of Rotating Bending Fatigue Testing Machine–A Laboratory Development Project. Int. Res. J. Eng. Technol. 2016, 3, 816–819. [Google Scholar]
- Banavasi, S.M.; Ravishankar, K.S.; Naik, P.S. Review on Design and Fabrication of Fatigue Testing Machine. Int. J. Nov. Res. Dev. 2018, 3, 5–14. [Google Scholar]
- Mali, P.R.; Chavan, U.S. Design and development of rotating bending fatigue test rig. J. Emerg. Technol. Innov. Res. 2018, 5, 578–586. [Google Scholar]
- Isakov, M.; Rantalainen, O.; Saarinen, T.; Lehtovaara, A. Large-Scale Fatigue Testing Based on the Rotating Beam Method. Exp. Tech. 2022, 47, 553–563. [Google Scholar] [CrossRef]
- Çipil, M.; Karabudak, F.; Zamanlou, H. Design and manufacturing of rotating bending fatigue test machine. Eur. J. Res. Dev. 2024, 4, 77–95. [Google Scholar] [CrossRef]
- Alaneme, K.K. Design of a Cantilever-Type Rotating Bending Fatigue Testing Machine. J. Miner. Mater. Characterisation Eng. 2011, 10, 1027–1039. [Google Scholar] [CrossRef]
- Ali, S.; Tahir, M.H.; Saeed, M.A.; Zaffar, N.; Khan, M.K. Design and Development of Fatigue Machine: Rotating Bending Fatigue Testing of different Materials. Int. J. Adv. Eng. Manag. 2019, 4, 8–15. [Google Scholar] [CrossRef]
- Kattimani, M.A.; Khatib, M.I.; Ghori, M.M.; Sajjad, M.A.; Jahangir, S.; Baqtaiyan, H.; Sadiq, M. Design and Fabrication of Fatigue Testing Machine. Int. J. Sci. Res. Sci. Eng. Technol. 2020, 7, 295–304. [Google Scholar] [CrossRef]
- Pilkey, W.D.; Pilkey, D.F. Peterson’s Stress Concentration Factors, 3rd ed.; Wiley: Hoboken, NJ, USA, 2007; p. 560. [Google Scholar]
- Doğan, A.; Göv, K.; Göv, İ. Modular and Service Orientated Design with Dual-End Spindle: A New Approach for Multi-Statıon Fatigue Test Systems. In Proceedings of the 5th Bilsel International Çatalhoyuk Scientific Researches Congress, Konya, Türkiye, 19–20 April 2025. [Google Scholar]
- Dogan, A.; Göv, K.; Göv, İ. Automation of a Multi-Station Rotary Bending Fatigue Test Machine with PLC Control System. Adıyaman Univ. J. Eng. Sci. 2025, 12, 143–158. [Google Scholar] [CrossRef]
- ASTM E466-07; Standard Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials. ASTM International: Conshohocken, PA, USA.
- Behvar, A.; Scott-Emuakpor, O.; James, K.; Crannell, B.; Haghshenas, M. Rotating Bending Fatigue Durability of Wrought 304 Stainless Steel: A Comparative Study of Surface-Treated vs. Untreated Specimen. J. Des. Against Fatigue 2024, 2, 1–12. [Google Scholar] [CrossRef]
- Zagielski, M. What Is the Difference Between a Chuck and a Collet? Available online: https://www.foredom.net/2024/06/what-is-the-difference-between-a-chuck-and-a-collet (accessed on 17 June 2025).
- Forrest, P.G. Fatigue of Metals; Pergamon: Bergama, Turkey, 1962; p. 436. [Google Scholar]
- Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Argirov, Y. Effect of Diamond Burnishing on Fatigue Behaviour of AISI 304 Chromium-Nickel Austenitic Stainless Steel. Materials 2022, 15, 4768. [Google Scholar] [CrossRef] [PubMed]
- Nahm, S.-H.; Shim, H.-B.; Baek, U.-B.; Suh, C.-M. Very High Cycle Fatigue Behaviors and Surface Crack Growth Mechanism of Hydrogen-Embrittled AISI 304 Stainless Steels. Mater. Sci. Appl. 2018, 09, 393–411. [Google Scholar] [CrossRef][Green Version]
- Strzelecki, P.; Mazurkiewicz, A.; Musial, J.; Tomaszewski, T.; Slomion, M. Fatigue Life for Different Stress Concentration Factors for Stainless Steel 1.4301. Materials 2019, 12, 3677. [Google Scholar] [CrossRef] [PubMed]
- Schijve, J. Fatigue of Structures and Materials, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; p. 623. [Google Scholar]







| C% | S% | Si% | Mo% | P% | Mn% | Cr% | Cu% | Ni% |
|---|---|---|---|---|---|---|---|---|
| 0.072 | 0.011 | 0.395 | 0.276 | 0.041 | 1.421 | 17.820 | 0.425 | 7.946 |
| Ultimate Tensile Strength | Yield Strength | Young’s Modulus | Poison’s Ratio |
|---|---|---|---|
| 734 MPa | 432 MPa | 193 GPa | 0.27–0.30 |
(Between Holding Point and Beginning of the Arc) | (Between Start and Center of the Arc) | (Between Center and the End of the Arc) | (Between End of the Arc and Collet) | (In Idle Weight Collet) |
|---|---|---|---|---|
| Load Sets in Experiments | Weight Pan | Additional Weight | Total Load |
|---|---|---|---|
| 1 | 17.5 N | 60 N | 77.5 |
| 2 | 17.5 N | 55 N | 72.5 |
| 3 | 17.5 N | 50 N | 67.5 |
| 4 | 17.5 N | 45 N | 62.5 |
| 5 | 17.5 N | 40 N | 57.5 |
| 6 | 17.5 N | 35 N | 52.5 |
| 7 | 17.5 N | 30 N | 47.5 |
| 8 | 17.5 N | 25 N | 42.5 |
| Feature | Previous Studies | Present Study |
|---|---|---|
| Test Capacity | Max. 5 specimens [10] | 22 specimens (4.4× increase) |
| Drive System | Multimotor [11,12] | Centralized high-power motor |
| Fixture Design | Drill chuck [19] or collet holder [10] | ER16 collet holder |
| Frame Structure | Welded mild steel [19,20] | Rigid laser-cut steel (8 mm) |
| Bearing Type | Standard ball bearings [10,13] | Flanged type ball bearings (UCF 204) |
| Time Efficiency | 4× reduction [11,12] | 7× reduction (87.5% faster) |
| Load Consistency | Moderate [10] | High (centralized load balancing) |
| Automation | Limited or none [10,19] | PLC-based real-time monitoring with HMI interface |
| Load Application Type | Dead Weight in kg | Precision Weights in N (5 N or 30 N) |
| Study | Endurance Limit (MPa) | This Study (MPa) | Deviation of This Study from the Literature (%) | Surface Finish | Testing Method |
|---|---|---|---|---|---|
| Behvar et al. [25] | 405 | 421 | 3.95% | Turning | Rotating Bending Fatigue |
| ASM Metals Handbook [5] | 413.7 | 421 | 1.76% | Not Specified | Rotating Bending Fatigue |
| Maximov et al. [28] | 440 | 421 | 4.32% | Turning + Polishing Ra = 0.32 μm | Rotating Bending Fatigue |
| Nahm et al. [29] | 400 | 421 | 5.25% | Turning + Polishing | Rotating Bending Fatigue |
| Strzelecki et al. [30] | 400 | 421 | 5.25% | Turning Ra = 1.25 μm | Rotating Bending Fatigue |
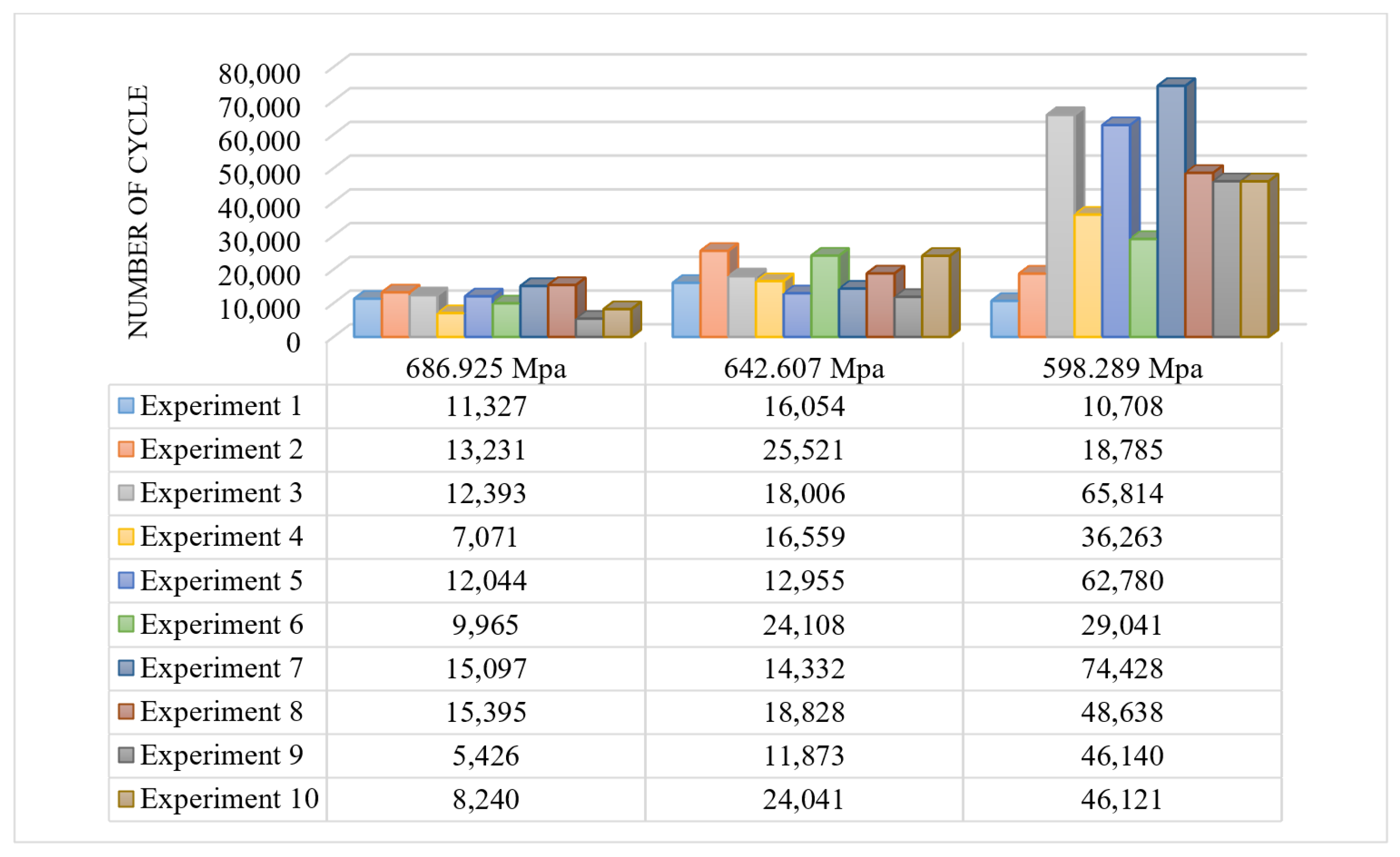
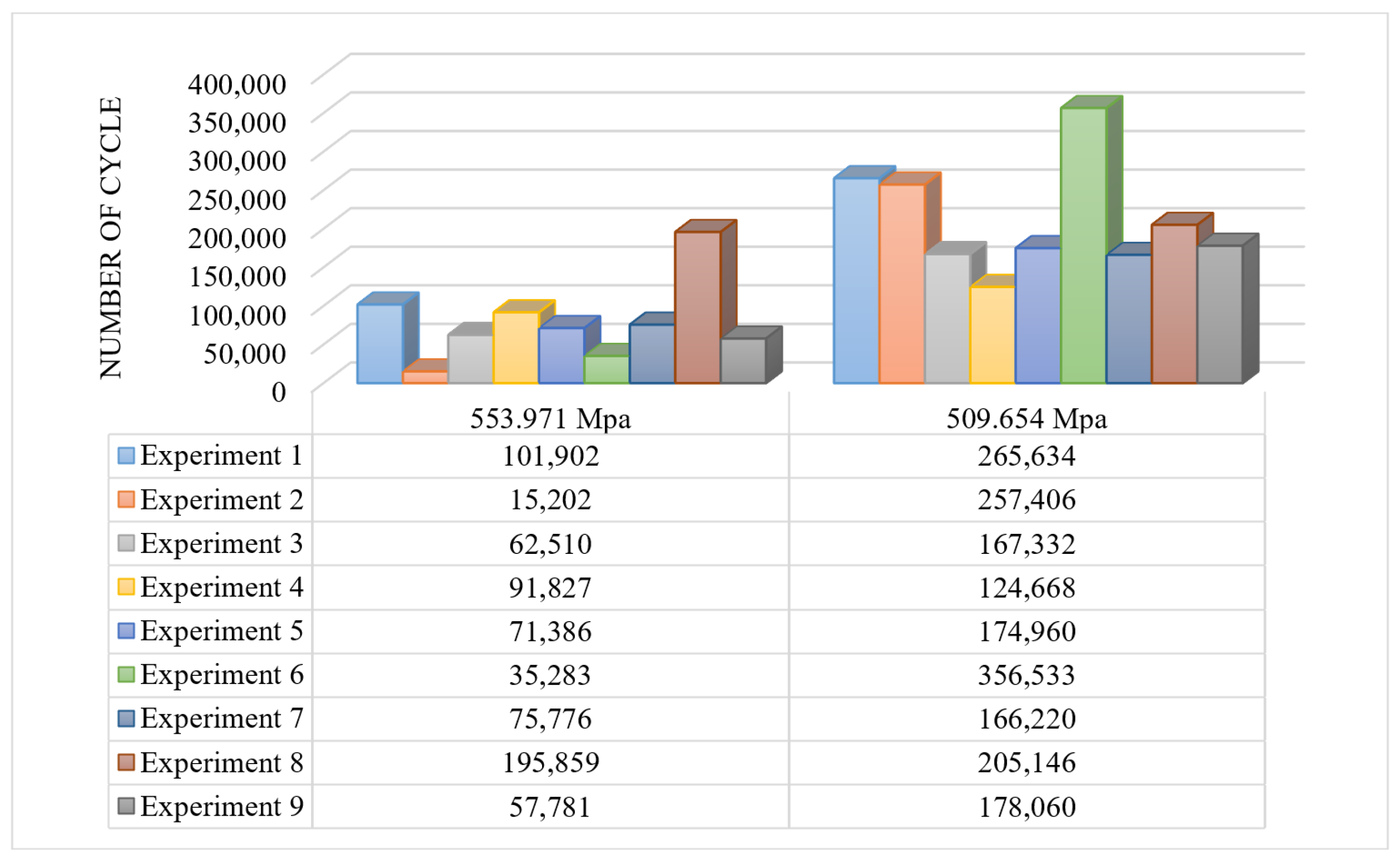
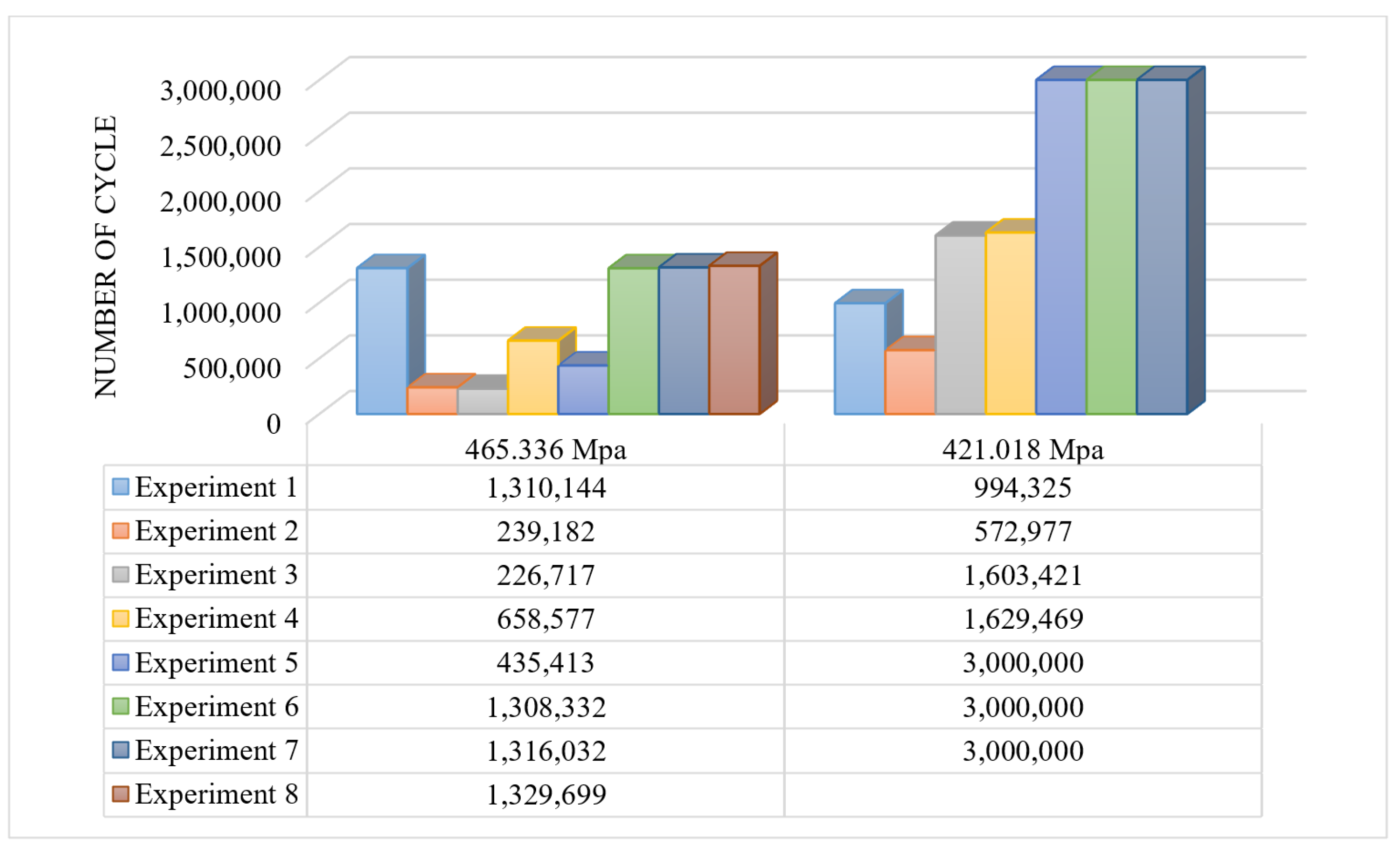
| Stress (MPa) | Life (Approx.) | Test Duration (min) | # of Specimen |
|---|---|---|---|
| 421 | 3 × 106 | 3000 | 5 |
| 421 | 1.5 × 106 | 1500 | 5 |
| 465 | 6 × 105 | 600 | 10 |
| 510 | 3 × 105 | 300 | 10 |
| 555 | 1.5 × 105 | 150 | 10 |
| 600 | 80,000 | 80 | 10 |
| 640 | 50,000 | 50 | 10 |
| 685 | 15,000 | 15 | 10 |
| Parameter | Description |
|---|---|
| Working Days | Monday to Friday |
| Working Hours (Human Access) | 08:30–12:00 and 13:30–17:00 |
| Lunch Break (No Human Access) | 12:00–13:30 (no specimen replacement allowed) |
| Weekend Access | Not allowed |
| Machine Operation During Off-Hours | Allowed (machine continues running but no specimen replacement) |
| Specimen Replacement Allowed Hours | Only during working hours |
| Latest Replacement Time (Morning) | 11:55 (last mount before lunch break) |
| Latest Replacement Time (Afternoon) | 16:55 (last mount before end of day) |
| Specimen Replacement Duration | 5 min per specimen |
| System-Wide Interruption During Replacement | All stations pause during specimen change; total interruption duration equals 5 min × number of replaced specimens |
| Deferred Replacement Rule | If replacements exceed shift time, they are postponed to the next work period |
| Testing Frequency | 1000 rpm (60,000 cycles/h) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doğan, A.; Göv, K.; Göv, İ. Drastically Accelerating Fatigue Life Assessment: A Dual-End Multi-Station Spindle Approach for High-Throughput Precision Testing. Machines 2025, 13, 665. https://doi.org/10.3390/machines13080665
Doğan A, Göv K, Göv İ. Drastically Accelerating Fatigue Life Assessment: A Dual-End Multi-Station Spindle Approach for High-Throughput Precision Testing. Machines. 2025; 13(8):665. https://doi.org/10.3390/machines13080665
Chicago/Turabian StyleDoğan, Abdurrahman, Kürşad Göv, and İbrahim Göv. 2025. "Drastically Accelerating Fatigue Life Assessment: A Dual-End Multi-Station Spindle Approach for High-Throughput Precision Testing" Machines 13, no. 8: 665. https://doi.org/10.3390/machines13080665
APA StyleDoğan, A., Göv, K., & Göv, İ. (2025). Drastically Accelerating Fatigue Life Assessment: A Dual-End Multi-Station Spindle Approach for High-Throughput Precision Testing. Machines, 13(8), 665. https://doi.org/10.3390/machines13080665






