Abstract
Optimizing mine fan operations in underground coal mines is important for ensuring proper ventilation, enhancing safety, and improving operational efficiency. A single main ventilation fan is insufficient to meet the ventilation demands of the entire mine. Therefore, it is necessary to consider the addition of booster fans to ensure effective ventilation. However, the selection of booster fans involves multiple influencing factors, and the complex interrelationships among fans remain unclear, making solution selection and risk assessment more challenging. To address this issue, this study proposes an optimization and risk analysis method for booster fan selection based on an improved analytic hierarchy process. This method leverages spherical fuzzy sets to handle uncertainty in the ventilation parameters and cloud models to facilitate probabilistic decision making. Through this model, the important relationships of the influencing factors for fan selection can be systematically determined, allowing for a rational assessment of the performance scores of candidate solutions. It provides a ranking of the alternatives based on their superiority, along with the risk indicators and optimization potentials of the selected solution. Ultimately, the reliability of the chosen model was verified through comparison and validation. This method not only enhances the scientific and rational basis for booster fan selection, reducing the complexity of the selection process, but also provides theoretical support for the optimization of coal mine ventilation systems. This study demonstrates the model’s effectiveness at improving ventilation safety and cost efficiency, making it a valuable tool for modern underground mining operations.
1. Introduction
The method of coal mining is generally divided into open-pit mining and underground mining. Compared to underground mining, open-pit mining involves the direct exchange with surface air and lacks roof control [1,2], among other factors, leading to differences in the engineering complexity and associated risks [3,4]. For example, open-pit coal mining requires the consideration of the slope stability, ecological damage, and waste rock and water management [5,6,7,8]. In contrast, underground coal mining requires attention to the safety of the ventilation systems, gas management, mine pressure, and strata control, as well as water hazard prevention [9,10,11,12]. Among these, mine ventilation plays an indispensable role throughout the entire lifecycle of underground coal mine operations.
Mine ventilation provides essential functions, such as supplying fresh air to the underground, regulating temperature, diluting harmful gases, and removing hazardous dust. The surface airflow is introduced into the underground mine through the main ventilation fan. Booster fans are ventilation devices used in conjunction with the main surface fan to supplement the insufficient air pressure in certain areas of the mine [13]. In multi-layer coal seam designs, booster fans can effectively resolve ventilation challenges [14]. However, an unreasonable booster fan solution design may lead to risks, such as the spontaneous combustion of residual coal [15,16], the accumulation of pollutants [17], and gas explosions caused by local airflow turbulence. Therefore, the reliable optimization of alternative booster fan solutions and necessary risk analysis are key measures to ensure the safety of the mine ventilation and production efficiency [18].
The traditional booster fan solution designs face challenges due to varying tunnel layouts and production risks in different underground mines. When considering booster fan solutions for specific mines, it is necessary to rely on engineers’ experience, reference ventilation-related technical standards, and influencing factors to propose a solution, which should then be verified. This approach relies too heavily on subjective experience, which may lead to incomplete consideration and decision-making errors due to personal preferences. Additionally, the decision-making process often requires extensive trial and error, ultimately resulting in only feasible solutions without the ability to assess their superiority.
With the advancement of the research on fan-related behaviors and solution optimization theories, many potentially feasible approaches have been proposed. In fan behavior studies, the conclusions drawn from numerous research efforts have simplified the process of fan selection. Bayomi et al. suggested adding a straightener at the fan inlet to eliminate deformation, increase airflow, and reduce noise [19]. Bredel discussed the impact of the fan pressure and selection on the outcomes during the fan selection process [20]. De Villiers et al. evaluated the performances of underground fan systems and found that the total efficiency of the auxiliary fan system was 5%, concluding that a greater number of auxiliary fan combinations would lead to decreased energy efficiency, providing a valuable reference for fan selection [21]. Related studies provide conclusions that can serve as references during the selection of booster fans [22], helping to reduce the research and testing process and alleviate the challenges associated with the booster fan selection.
In related research on solution optimization, many theories have been applied in relevant engineering projects with certain effectiveness. Kursunoglu and Onder introduced the analytic hierarchy process (AHP) for fan selection, specifically for choosing a main fan for underground coal mines in Turkey [23]. Jiu et al. used a mixed-integer linear-programming (MILP) model to formulate the problem and employed a hybrid genetic algorithm (HGA) to calculate the solution, achieving nearly optimal results for scheduling equipment in coal production systems [24]. Li and Ding applied the fuzzy DEMATEL method to open-pit mining, discussing the relevant evaluation indicators and methods [25]. Mulumba et al. used an optimized PSO-BP neural network model to establish a safety risk assessment model for underground coal mines, evaluating and predicting the safety risk factors [26]. Can [27] applied failure mode effect analysis and Pareto analysis to assess risks in coal mine production and exploration measurements.
Although the research on fan-related behaviors and solution optimization theories [28,29,30,31] has advanced the progress of fan selection work, the studies on fan behavior tend to focus on the in-depth analysis of single indicators, resulting in scattered research outcomes. Related solution optimization theories, while achieving good results, are still limited by the insufficient expression of fuzzy information and the quality and scale of reference data (cases) for neural networks [32], leaving room for improvement in the efficiency and superiority of fan selection. Furthermore, the use of complex spherical fuzzy theory to rank multi-criteria, decision-making solutions based on the expression of two-dimensional fuzzy information has been widely discussed and is considered a reliable approach for multi-criteria decision making [33,34,35,36,37]. Moreover, the cloud model theory, with its rich information embedded in cloud droplets, has attracted significant attention in solution evaluation, risk analysis, and optimization potential research [38,39,40].
In summary, this study focused on the design of the booster fan solution for the Okaba coal mine. Based on the AHP, an evaluation system was established, and relevant experts were consulted to assess and create a judgment matrix to determine the weight of each indicator. Fuzzy theory was applied to conduct fuzzy evaluations of the indicators, and the qualitative fuzzy assessments were converted into quantitative superiority scores using the complex spherical fuzzy function. This allowed for the ranking of the alternative booster fan solutions based on their superiority. A reference cloud model for the solution was established using the cloud model theory, and the indicator cloud model for the solution was constructed based on the expert evaluation parameter data, revealing the risk associated with each indicator and completing the optimization of the solution. Finally, the validity of the proposed solution was confirmed by a comparison with other research theories. This study not only provides scientific decision-making support for the optimization and selection of the booster fan in the Okaba coal mine but also offers a transferable methodological framework for multi-criteria decision making in similar complex engineering systems.
2. Methodology Framework
This study aimed to improve and extend the AHP by integrating complex spherical fuzzy numbers and the cloud model theory to optimize the selection of booster fan alternatives for the Okaba coal mine and perform the corresponding risk analysis and optimization of the selected solutions. The AHP method served as the primary framework of this study, effectively decomposing multi-criteria decision-making problems into hierarchical levels and determining the weight of each factor through consistency judgments, thereby constructing a clear and structured decision system. The introduction of the hybrid spherical fuzzy membership function enhanced the capability of the fuzzy representation, improving the distinguishability and boundary clarity of the evaluation results. Furthermore, the integration of the cloud model theory not only bridged qualitative and quantitative analyses but also captured uncertainty through its cloud drop generator, offering strong visualization features and interpretability. The basic approach (Figure 1) was as follows: First, the evaluation indicators and their evaluation criteria were established through the AHP, and the weights of the indicators were obtained from the judgment matrix. Further, the fuzzy theory was applied to establish the evaluation criteria for the alternative solutions. Based on these criteria and the indicator weights, the superiority ranking of the alternative booster fan solutions was completed using the complex spherical fuzzy function, ultimately achieving the optimal selection of the booster fan solution. Finally, the cloud model theory was used to present the risks associated with each indicator of the selected solutions and identify any gaps, completing the analysis and optimization of the solutions’ risks.
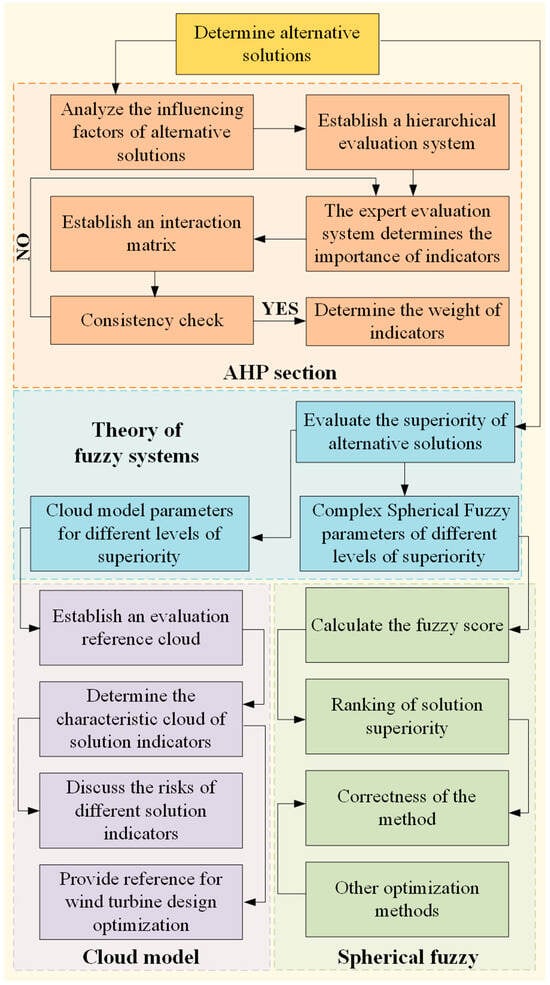
Figure 1.
Research design.
2.1. Analytic Hierarchy Process
The AHP was proposed by Satty in 1971 as a quantitative analysis method to solve complex decision-making problems [41,42,43]. By breaking down complex issues into multiple levels, the AHP uses mathematical models to quantitatively evaluate and rank different decision alternatives, thereby assisting decisionmakers in making informed choices [44]. The specific process is outlined as follows:
- (1)
- Establishing the hierarchical structure
The first step in the analytic hierarchy process (AHP) is the establishment of a scientific and comprehensive evaluation system. The AHP is a method that integrates qualitative judgments with quantitative analysis to provide systematic and rational support for complex decision-making problems. The AHP evaluation system is generally divided into several levels, where an upper-level indicator typically encompasses several lower-level indicators;
- (2)
- Expert system evaluation
The expert evaluation system was designed to obtain the pairwise relationships of the relative importances between different indicators at the same level. The interaction matrix is a method used to determine the relative importances of evaluation criteria. At the same hierarchical level, the relative importances among different criteria are typically established through the interaction matrix, which is constructed based on pairwise comparisons made by experts. This results in a judgment matrix that reflects the expert knowledge and opinions.
The mutual importance relationship between two indicators is represented using the 1–9 scale proposed by Saaty [45]. The correspondence between the mutual importance relationship between the two indicators and the scale are shown in Table 1.

Table 1.
The 1–9 scale.
- (3)
- Constructing the judgment matrix
After establishing the evaluation system and evaluation criteria (Table 1), we invited researchers and engineering professionals closely related to the design field of the alternative solutions to participate in the evaluation. First, the importance of all the indicators in the evaluation system were compared pairwise to obtain qualitative evaluation information. Using Table 1, the qualitative language provided by the experts regarding the importance of each indicator was converted into quantitative scale data, and the judgment matrix was constructed as follows:
where A represents the expert judgment matrix; n denotes the total number of indicators in the established evaluation system, which also represents the order of the matrix; represents the importance of the j-th indicator relative to the i-th indicator;
- (4)
- Calculation of the weight vector
First, the maximum eigenvalue of the judgment matrix is calculated:
where represents the eigenvalue; max represents the maximum eigenvalue of the matrix.
Then, the weight vector is obtained by normalizing the eigenvector:
where represents the weight of the i-th indicator; represents the value of the i-th eigenvector; represents the weight vector of the evaluation matrix;
- (5)
- Consistency test
A consistency test is performed on the obtained judgment matrix to ensure its rationality. First, the consistency index () is calculated:
where represents the largest eigenvalue of the matrix, and n represents the order of the matrix.
Then, the consistency ratio () is calculated:
where represents the random consistency index (selected from Table 2); represents the consistency index; represents the consistency ratio.

Table 2.
Values of the random consistency index.
- (6)
- Obtainment of the overall weights of the indicators
First, assume there are m experts. After performing the consistency check, the expert judgment matrices are merged to form a comprehensive judgment matrix:
where m represents the number of expert matrices that passed the consistency check; n represents the number of indicators involved in the evaluation.
Next, based on the professional background and work experience of each expert, a reliability coefficient matrix for each expert is provided:
where R is the reliability coefficient matrix; represents the reliability coefficient of the m-th expert, i.e., the weight of the judgment matrix provided by the i-th expert.
Finally, the comprehensive indicator weight is obtained by calculating the expert weight through a comprehensive evaluation:
where B represents the comprehensive indicator weight vector; represents the weight of the n-th indicator.
2.2. Complex Spherical Fuzzy Number
The complex spherical fuzzy number is a further extension of the spherical fuzzy number, designed to handle more complex fuzzy information, particularly suitable for multi-criteria decision-making problems with multiple fuzzy dimensions and intricate uncertainties. By introducing higher-dimensional fuzzy information, the complex spherical fuzzy number allows for a more precise representation of the relationships between different fuzzy factors [46]:
- (1)
- Basic concepts
In the domain Z, the complex spherical fuzzy set (C) can be represented as follows:
where for , and there exists and . The membership degree (), neutrality degree (), and non-membership function () are all confined within a unit circle. If exists, and there are corresponding and , then is referred to as a complex spherical fuzzy number;
- (2)
- Scoring function
Although the complex spherical fuzzy number contains higher-level mathematical information, which can significantly enhance the extraction of fuzzy information features, its complexity makes the representation results difficult to interpret. In this context, referring to relevant research [47], the scoring function is defined as follows:
2.3. Cloud Model
The cloud model is a mathematical model used to handle uncertainty and fuzziness [48,49]. It is intuitive, easy to understand, and exhibits strong fault tolerance and robustness, making it effective at simplifying the fuzzy reasoning process. It has been widely applied in fields such as fuzzy systems, pattern recognition, and decision support. The core idea is to model the fuzziness of the objects being processed using the concept of a cloud, which is represented by numerous cloud droplets.
For the forward cloud model, the generation of cloud droplets is primarily controlled by three parameters (see Figure 2): Expectation (Ex), Entropy (En), and Hyperentropy (He). The Ex controls the symmetry axis of the cloud model and is often considered the evaluator’s assessment opinion. The En controls the width (degree of dispersion) of the cloud model, while the He controls the thickness (uncertainty) of the cloud layer. These two parameters are typically regarded as reflecting the concentration and clarity of the decisionmakers’ assessment opinions.
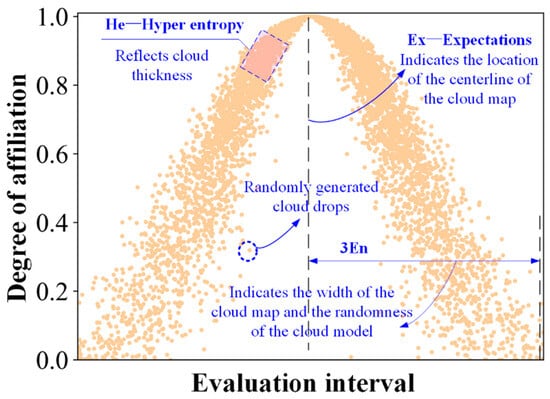
Figure 2.
The cloud model.
The generator function for the cloud drops based on eigenvalues is defined as follows:
where x represents the value of a cloud drop generated from a normal distribution; y represents the membership degree of x belonging to the concept center.
2.4. Expert Decision Making Based on Fuzzy Theory
By combining the characteristics of both the complex spherical fuzzy theory and the cloud model theory, qualitative languages divided into five levels were organized, and quantitative information was then mapped to these levels through the fuzzy theory, converting the expert’s fuzzy qualitative assessments into complex spherical fuzzy parameters and cloud model parameters, respectively (Table 3).

Table 3.
Expert opinion correspondence.
3. Introduction to the Study Area
The validation project selected for the application of the improved hierarchical analysis method optimized by the complex spherical fuzzy and cloud models in the selection and risk analysis of booster fan solutions was the booster fan optimization and risk analysis at the Okaba coal mine. The Okaba coal mine is located in one of Nigeria’s key coal production regions, with production commencing as early as the 1950s. The mine primarily extracts bituminous coal and high-rank coal. Situated at a latitude of 7°20′ N and a longitude of 7°25′ E (see Figure 3), the region’s underlying strata are predominantly composed of sedimentary rocks, with some folds and faults present. The groundwater geological conditions are relatively complex [50,51].
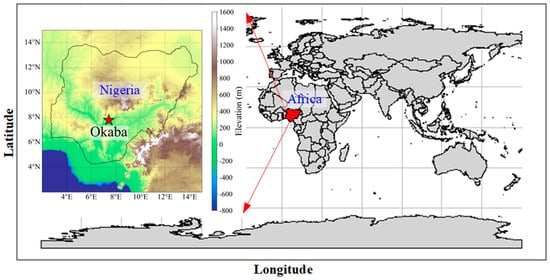
Figure 3.
Geographical location of Okaba coal mine.
The main shaft diameter of the Okaba underground coal mine (see Figure 4) is 3 m and is responsible for the transportation of personnel and related equipment, with fresh air flowing into the mine through this shaft. The shaft also functions to transport fresh air from the surface to the underground, where four booster fans (denoted as BF1, BF2, BF3, and BF4) are installed. These booster fans further deliver air from the lower part of the ventilation shaft to various working faces and other air-using locations. The circulated exhaust air is discharged through the ventilation shaft, with the airflow powered by the fans [52]. Due to the different positions of the four booster fans (BF1, BF2, BF3, and BF4), the airflow experiences varying degrees of loss before reaching each fan. Therefore, under different influencing conditions, the relative importance of each fan varies accordingly.
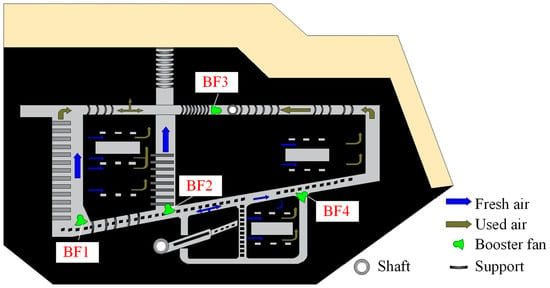
Figure 4.
Layout of booster fans at Okaba underground coal mine [52].
4. Case Application of the Method
4.1. Determining Indicator Weights (AHP)
- (1)
- Establishing the hierarchical structure
Based on the basic information about the Okaba coal mine described in Section 3, based on the relevant literature [52,53] and expert opinions, an evaluation indicator system for the selection of fan solutions was established. The system consists of three levels (see Figure 5). The first level is the solution layer, which includes information on the four fans: BF1, BF2, BF3, and BF4. The second level comprises the main criteria, which include technical (M1), operational (M2), environmental (M3), and economical (M4) indicators. These four criteria cover all aspects that need to be considered in the decision-making process and provide a comprehensive reflection of the actual situation of the alternative solutions. The third level is the sub-criteria, which include the air quality (S1), pressure (S2), air power (S3), and efficiency (S4) under the technical (M1) criterion; production (S5), safety (S6), and flexibility (S7) under the operational (M2) criterion; noise (S8) and vibration (S9) under the environmental (M3) criterion; and operation cost (S10) under the economical (M4) criterion. The experts’ evaluations of the importances of these indicators are conducted at the third (sub-criteria) level, which contains a total of 10 indicators. The solution selection is based on the first-level solutions.
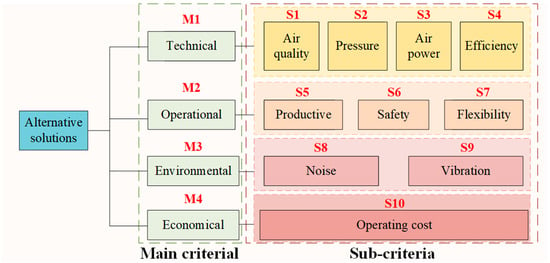
Figure 5.
Hierarchical structure.
This study conducted a comprehensive evaluation of the optimal layout scheme for mine booster fans through the establishment of four main criteria (M1–M4), which were graded across multiple dimensions [54,55]. M1 was used to assess the core performance of the fan, serving as the fundamental and crucial criterion. S1 reflects the fan’s impact on the air quality improvement, ensuring compliance with the air standards in the mine; S2 determines the fan’s ability to overcome tunnel resistance, ensuring effective airflow transmission; S3 represents the power consumption of the fan, reflecting the power requirements; and S4 influences the fan’s energy efficiency and economic viability. M2 focuses on the stability and adaptability of the fan during actual operation. S5 reflects whether the fan can stably meet the production needs of the mine, S6 assesses the fan’s reliability under extreme operating conditions, and S7 measures the fan’s ability to adapt to different working conditions. M3 addresses the impact of the fan on the working environment. S8 and S9 focus on the noise and vibration generated by the fan during operation, which affect the health of the miners and the working environment and require careful attention. M4 focuses on S10, which evaluates the economic performance of the equipment throughout its lifecycle, ensuring that the selected fan offers not only a good performance and favorable working environment but also sustainable economic advantages. Through the comprehensive consideration of these indicators, the optimal fan layout scheme can be scientifically assessed to meet the overall requirements of the mine ventilation system [56,57].
- (2)
- Obtaining the expert judgment matrix
Based on the standards in Table 1, two research-oriented experts (E1 and E2) and one technical expert (E3) were invited to evaluate the 10 sub-criteria indicators (S1–S10) in the sub-criterion layer of the hierarchical structure shown in Figure 5.
To fully account for the evaluation opinions and areas of expertise of the different experts, and to enhance the scientific validity and rationality of the assessment results, this study considered that the research-oriented experts possessed stronger theoretical judgment capabilities in comprehensive analyses compared to front-line technical personnel. Accordingly, the reliability coefficients were set at 0.35 for the two research experts and at 0.30 for the technical personnel. Based on these values, the expert reliability matrix was constructed as follows:
Based on the Expert System Evaluation Form (Table A6) developed, three experts were invited to fill it out. According to the feedback from Expert E1, the expert judgment matrix 1 is organized as follows:
Based on the opinions of E2, expert judgment matrix 2 is organized as follows:
Based on the opinions of E3, expert judgment matrix 3 is organized as follows:
- (3)
- Calculation of indicator weights
Referring to Equations (2)–(4) and using the judgment matrices provided by the three experts in Matrices (14–16), the expert weights (EWs) were calculated and are presented in Table 4. Based on the obtained indicator weights from the three experts and the expert reliability coefficients (Matrix (13)), the comprehensive indicator weights (CIWs) were then calculated and are presented in Table 4.

Table 4.
The indicator weights.
- (4)
- Consistency test
Based on Equations (5) and (6) and Table 3, the consistency parameters (CI, RI, ) corresponding to the three matrices provided by the experts were calculated. The final consistency ratio (CR) was then determined. As shown in Table 5, the CR for E1 is 0.015, that for E2 is 0.007, and that for E3 is 0.002. Since the consistency ratios for all three experts are less than 0.1, the results pass the consistency test. Therefore, the indicator weights obtained from the three experts (Table 5) are considered reliable.

Table 5.
The consistency parameters.
- (5)
- Analysis of comprehensive indicator weights
Based on the indicator weights obtained in Table 5, the distribution of the comprehensive indicator weights for the sub-criterion layer was analyzed, and the weights for the main criterion layer were further calculated (Figure 6). For the sub-criterion layer, the weight of S7 (flexibility) reached 0.143, and the weight of S1 (quality) was 0.141. This shows that, according to the invited experts, the quality of the booster fan and its impact on the complexity of the ventilation system are highly valued. This is because the ventilation system must remain stable over the long term, and frequent damage to the booster fan or an overly complex ventilation system could lead to airflow short-circuiting, which could damage equipment and personnel, affecting the safe production of the mine. Additionally, the weights for S2 (pressure), S4 (efficiency), and S10 (operation costs) are all above 0.1, indicating their relative importances, as they influence mine production from the technical, production efficiency, and economic perspectives. In the main criterion layer, M1 (technical) is the most important indicator. This is because the technical parameters represent the essential requirements that the fan must meet to satisfy production needs, and they serve as the decisive indicators to ensure the feasibility of the plan.
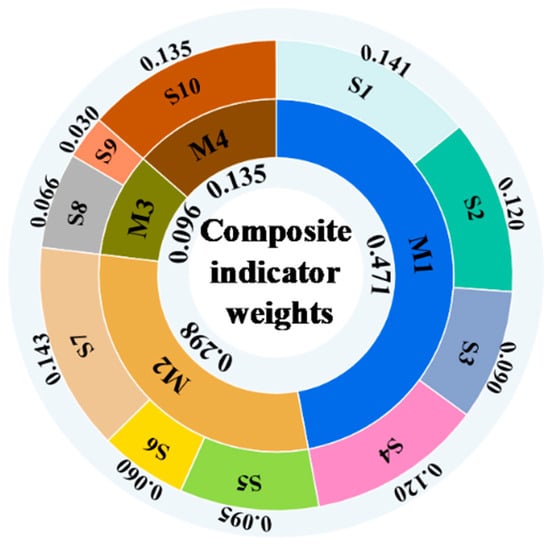
Figure 6.
Comprehensive indicator weights.
4.2. Fan Solution Selection Based on Complex Spherical Fuzzy Theory
- (1)
- Solution evaluation based on expert system
Similarly, these three experts provided evaluations of the effectiveness of the alternative fan configurations for the four booster fan locations (see Figure 4) based on the expert opinion reference table in Table 3. The evaluation results are shown in Table A1;
- (2)
- Fuzzy information transformation
The complex spherical fuzzy parameters from Table 3 were computed using Equations (10) and (11) to obtain the fuzzy scores corresponding to the evaluation levels (Table 6). It should be noted that the levels from I to V represent a classification of the indicator importances, ranging from the most important to the least important, with the scores corresponding accordingly from high to low.

Table 6.
Correspondence between evaluation levels and fuzzy scores.
Based on the correspondence between the levels and scores in Table 6, the qualitative evaluations provided by the experts in Table A1 were converted into quantitative evaluation results (Table A2);
- (3)
- Solution selection
The complex spherical fuzzy scores for each indicator corresponding to each solution (Table A2) were multiplied by the comprehensive indicator weights (Table 5) to obtain the final scores for each solution. Further, the average of the three experts’ opinions was taken as the final complex spherical fuzzy score for each solution (Table 7).

Table 7.
The complex spherical fuzzy scores for different solutions.
To ensure the validity of the evaluation verification method and assess the stability of the model, a comparative study was conducted with the fuzzy TOPSIS (FT) method, which was also applied in the selection of booster fans for the Okaba mine [58]. It was observed that the hybrid spherical fuzzy scores exhibited a similar trend to that of the FT-based scheme (see Figure 7a). Whether considering the individual experts’ complex spherical score rankings, the comprehensive score ranking, or the rankings from other related studies [58], the order remained consistent: BF4 > BF3 > BF2 > BF1. This high consistency validates the effectiveness of the method. It indicates that when considering different booster fan solutions, BF4 should be prioritized, followed by BF3, BF2, and, finally, BF1 (see Figure 7b).
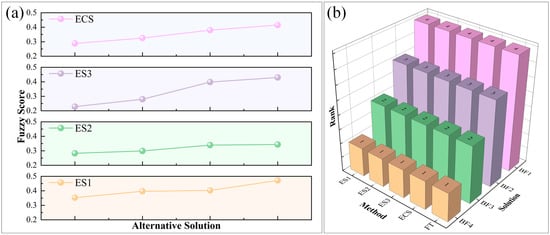
Figure 7.
Ranking of the superiorities of alternatives: (a) trend of fuzzy score changes for the different solutions, and (b) solution ranking.
4.3. Analysis of Alternative Indicators Based on Cloud Model Theory
- (1)
- Evaluation reference cloud
Based on the expert evaluation opinions and the corresponding relationship of the cloud model parameters (Table 3), the cloud droplet generation for the different levels was calculated using Equation (12) (see Figure 8). This served as the reference cloud for the indicator analysis.
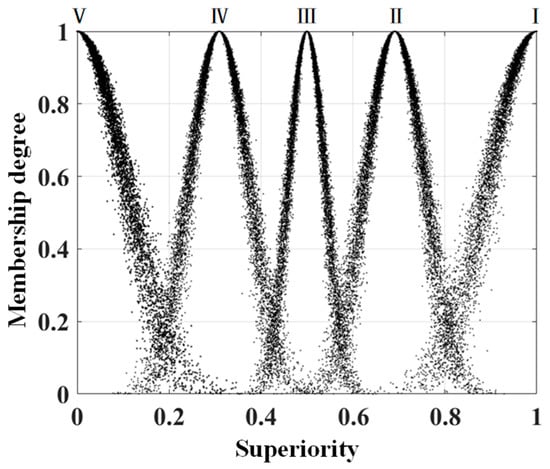
Figure 8.
The reference cloud model.
- (2)
- Analysis of solution indicators
The corresponding information on the most superior booster fan solution (BF4) for solution indicator analysis was selected. Based on the expert evaluation opinions and the correspondence of the cloud model parameters (Table 3), the cloud parameters for the evaluation of different indicators by three experts (E1, E2, E3) were organized (Table A3, Table A4 and Table A5);
Combining Expert Opinions:
Based on Equation (12), Matrix (13), and Table 8, a large number of cloud droplets were generated (Figure 9), and the superiority of each indicator for the BF4 solution was then analyzed.

Table 8.
Final cloud model parameters for the BF4 solution indicator evaluation.
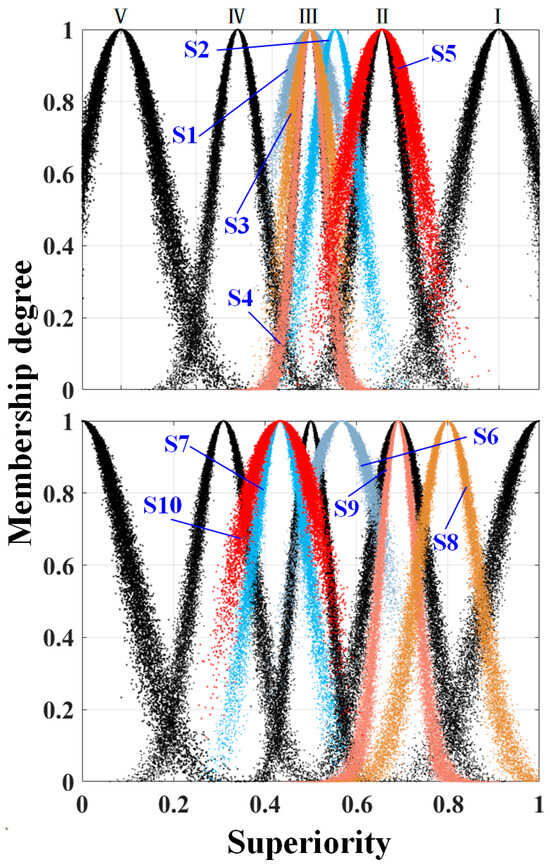
Figure 9.
Indicator superiority of the BF4 solution.
The results shown in Figure 9 reveal significant differences in the performance of the BF4 booster fan solution across the various indicators. Firstly, the cloud plots of the eight indicators (S1–S6, S8, S9) have symmetry axes greater than or equal to 0.5, indicating a high success rate for these indicators. This means that the BF4 booster fan solution performs prominently in these areas, demonstrating strong competitiveness. However, the symmetry axes of indicators S7 and S10 are less than 0.5, suggesting that the superiority of these two indicators is lower, with significant differences in their expert evaluations. There is considerable potential for optimization in these areas, and further exploration of their improvement space may be required.
Another noteworthy observation is the larger thicknesses and widths of the cloud plots for S5 and S10, indicating substantial disagreement and inconsistency among the experts when evaluating these indicators. The thickness and width of the cloud plots typically reflect the degree of dispersion in the expert evaluations. The greater the thickness and width, the larger the differences in the expert opinions, suggesting significant variation in the evaluation criteria and emphasis. To address these inconsistencies, further expert discussions or data support may be necessary to clarify and unify the evaluations of S5 and S10. The complexity of S5 and S10 may arise from multiple factors. Therefore, resolving these issues requires a multi-faceted approach, addressing data, technology, or process aspects to further refine the evaluation criteria for these indicators and reduce the evaluation discrepancies among the experts, ultimately improving the overall consistency and accuracy of the assessment.
In summary, further optimization should focus on the potential improvements of S7 and S10, particularly by refining the evaluation standards and methods for S5 and S10 to reduce discrepancies among the experts and enhance the overall performance of the solution.
5. Conclusions
This paper establishes a scientific fuzzy qualitative evaluation language system for indicators and solutions, along with the corresponding quantitative parameters, based on an improved AHP and the complex spheroidal fuzzy and cloud model theories. A new method for selecting the optimal underground booster fan solution and conducting risk assessment and optimization in coal mines is proposed. By referring to the Okaba booster fan arrangement solution, a fuzzy language system for evaluation was established using the AHP, and through fuzzy functions, it was transformed into quantitative parameters, further determining the weights of the indicators involved in the evaluation. The complex spheroidal fuzzy theory was used to complete the superiority ranking of the four alternative solutions, and a comparison with relevant studies demonstrated the validity of the superiority. The cloud model theory is applied to present the risk and superiority of the solution’s indicators through cloud droplets, thereby analyzing and optimizing the layout of underground booster fans in coal mines. The main conclusions are as follows.
- (1)
- A booster fan solution evaluation system based on the improved AHP was established, further determining the weights of the indicators involved in the evaluation and extracting the decision preferences of the experts;
- (2)
- A booster fan solution optimization model based on the complex spherical fuzzy theory was established, and the effectiveness of the model was validated through a comparison with related studies;
- (3)
- A risk analysis and optimization model for booster fan solution indicators based on the cloud model theory was established. The model visually presented the rich risk information and optimization potential of the solution indicators through cloud droplets, providing valuable insights for solution optimization.
The scalability of the designed method remains one of the main challenges when optimizing and risk managing the underground booster fans in coal mines. Although this paper aims to extract the implicit information of the solutions primarily using fuzzy logic and compares the conclusions with other studies under the same conditions to verify the effectiveness of the proposed model, the generalization capability of the model still requires further exploration under more complex and variable engineering conditions.
Author Contributions
S.Y.: Methodology, Formal analysis, Validation, Resources, Visualization, Writing—original draft. J.Z.: Conceptualization, Methodology, Validation, Investigation, Visu-alization, Writing—review & editing, Supervision, Funding acquisition. M.K.: Formal analysis, Investigation, Writing—review & editing, Data curation. A.I.L.: Investigation, Writing—review & editing. C.L.: Formal analysis, Writing—review & editing. M.O.: Formal analysis, Investigation, Writing—review & editing. S.K.: Formal analysis, Visualization, Writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the National Natural Science Foundation Project of China (52474121 and 42177164).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A. Expert Evaluation Data

Table A1.
Evaluation of alternative solutions based on expert system.
Table A1.
Evaluation of alternative solutions based on expert system.
| Indicator | Solutions | E1 | E2 | E2 |
|---|---|---|---|---|
| S1 | BF1 | V | IV | IV |
| BF2 | IV | IV | IV | |
| BF3 | III | III | III | |
| BF4 | III | III | III | |
| S2 | BF1 | III | V | V |
| BF2 | III | IV | III | |
| BF3 | III | III | III | |
| BF4 | II | III | III | |
| S3 | BF1 | II | III | IV |
| BF2 | III | IV | III | |
| BF3 | I | III | III | |
| BF4 | II | IV | III | |
| S4 | BF1 | III | IV | V |
| BF2 | III | IV | IV | |
| BF3 | III | III | II | |
| BF4 | III | III | III | |
| S5 | BF1 | III | III | III |
| BF2 | III | III | IV | |
| BF3 | III | III | II | |
| BF4 | II | II | II | |
| S6 | BF1 | III | II | II |
| BF2 | II | II | II | |
| BF3 | III | III | IV | |
| BF4 | III | II | III | |
| S7 | BF1 | V | III | III |
| BF2 | III | III | IV | |
| BF3 | V | IV | IV | |
| BF4 | III | IV | III | |
| S8 | BF1 | II | II | V |
| BF2 | I | II | III | |
| BF3 | II | II | II | |
| BF4 | II | II | II | |
| S9 | BF1 | I | II | II |
| BF2 | I | II | II | |
| BF3 | I | II | II | |
| BF4 | I | II | II | |
| S10 | BF1 | III | V | IV |
| BF2 | III | III | III | |
| BF3 | III | IV | III | |
| BF4 | III | IV | III |

Table A2.
The complex spherical fuzzy scores for each indicator.
Table A2.
The complex spherical fuzzy scores for each indicator.
| Indicator | Solutions | E1 | E2 | E2 |
|---|---|---|---|---|
| S1 | BF1 | 0.113 | 0.131 | 0.131 |
| BF2 | 0.131 | 0.131 | 0.131 | |
| BF3 | 0.395 | 0.395 | 0.395 | |
| BF4 | 0.395 | 0.395 | 0.395 | |
| S2 | BF1 | 0.395 | 0.113 | 0.113 |
| BF2 | 0.395 | 0.131 | 0.395 | |
| BF3 | 0.395 | 0.395 | 0.395 | |
| BF4 | 0.578 | 0.395 | 0.395 | |
| S3 | BF1 | 0.578 | 0.395 | 0.131 |
| BF2 | 0.395 | 0.131 | 0.395 | |
| BF3 | 0.691 | 0.395 | 0.395 | |
| BF4 | 0.578 | 0.131 | 0.395 | |
| S4 | BF1 | 0.395 | 0.131 | 0.113 |
| BF2 | 0.395 | 0.131 | 0.131 | |
| BF3 | 0.395 | 0.395 | 0.578 | |
| BF4 | 0.395 | 0.395 | 0.395 | |
| S5 | BF1 | 0.395 | 0.395 | 0.395 |
| BF2 | 0.395 | 0.395 | 0.131 | |
| BF3 | 0.395 | 0.395 | 0.578 | |
| BF4 | 0.578 | 0.578 | 0.578 | |
| S6 | BF1 | 0.395 | 0.578 | 0.578 |
| BF2 | 0.578 | 0.578 | 0.578 | |
| BF3 | 0.395 | 0.395 | 0.131 | |
| BF4 | 0.395 | 0.578 | 0.395 | |
| S7 | BF1 | 0.113 | 0.395 | 0.395 |
| BF2 | 0.395 | 0.395 | 0.131 | |
| BF3 | 0.113 | 0.131 | 0.131 | |
| BF4 | 0.395 | 0.131 | 0.395 | |
| S8 | BF1 | 0.578 | 0.578 | 0.113 |
| BF2 | 0.691 | 0.578 | 0.395 | |
| BF3 | 0.578 | 0.578 | 0.578 | |
| BF4 | 0.578 | 0.578 | 0.578 | |
| S9 | BF1 | 0.691 | 0.578 | 0.578 |
| BF2 | 0.691 | 0.578 | 0.578 | |
| BF3 | 0.691 | 0.578 | 0.578 | |
| BF4 | 0.691 | 0.578 | 0.578 | |
| S10 | BF1 | 0.395 | 0.113 | 0.131 |
| BF2 | 0.395 | 0.395 | 0.395 | |
| BF3 | 0.395 | 0.131 | 0.395 | |
| BF4 | 0.395 | 0.131 | 0.395 |
Appendix B. Cloud Model Evaluation Process Data
The evaluation results of E1:

Table A3.
Cloud model parameters for E1’s evaluation of the BF4 solution indicators.
Table A3.
Cloud model parameters for E1’s evaluation of the BF4 solution indicators.
| Indicator | Ex1 | En1 | He1 |
|---|---|---|---|
| S1 | 0.5 | 0.0394 | 0.005 |
| S2 | 0.691 | 0.0637 | 0.008 |
| S3 | 0.691 | 0.0637 | 0.008 |
| S4 | 0.5 | 0.0394 | 0.005 |
| S5 | 0.691 | 0.0637 | 0.008 |
| S6 | 0.5 | 0.0394 | 0.005 |
| S7 | 0.5 | 0.0394 | 0.005 |
| S8 | 0.691 | 0.0637 | 0.008 |
| S9 | 1 | 0.1031 | 0.013 |
| S10 | 0.5 | 0.0394 | 0.005 |
The evaluation results of E2:

Table A4.
Cloud model parameters for E2’s evaluation of the BF4 solution indicators.
Table A4.
Cloud model parameters for E2’s evaluation of the BF4 solution indicators.
| Indicator | Ex2 | En2 | He2 |
|---|---|---|---|
| S1 | 0.5 | 0.0394 | 0.005 |
| S2 | 0.5 | 0.0394 | 0.005 |
| S3 | 0.309 | 0.0637 | 0.008 |
| S4 | 0.5 | 0.0394 | 0.005 |
| S5 | 0.691 | 0.0637 | 0.008 |
| S6 | 0.691 | 0.0637 | 0.008 |
| S7 | 0.309 | 0.0637 | 0.008 |
| S8 | 0.691 | 0.0637 | 0.008 |
| S9 | 0.691 | 0.0637 | 0.008 |
| S10 | 0.309 | 0.0637 | 0.008 |
The evaluation results of E3:

Table A5.
Cloud model parameters for E3’s evaluation of the BF4 solution indicators.
Table A5.
Cloud model parameters for E3’s evaluation of the BF4 solution indicators.
| Indicator | Ex3 | En3 | He3 |
|---|---|---|---|
| S1 | 0.5 | 0.0394 | 0.005 |
| S2 | 0.5 | 0.0394 | 0.005 |
| S3 | 0.5 | 0.0394 | 0.005 |
| S4 | 0.5 | 0.0394 | 0.005 |
| S5 | 0.691 | 0.0637 | 0.008 |
| S6 | 0.5 | 0.0394 | 0.005 |
| S7 | 0.5 | 0.0394 | 0.005 |
| S8 | 0.691 | 0.0637 | 0.008 |
| S9 | 0.691 | 0.0637 | 0.008 |
| S10 | 0.5 | 0.0394 | 0.005 |
Appendix C. Expert Questionnaire

Table A6.
Expert system evaluation form.
Table A6.
Expert system evaluation form.
| No. | Comparison | Which Is More Important? | Importance Level (1–9) |
|---|---|---|---|
| 1 | Operating Cost vs. Air Quality | ||
| 2 | Operating Cost vs. Pressure | ||
| 3 | Operating Cost vs. Air Power | ||
| 4 | Operating Cost vs. Efficiency | ||
| 5 | Operating Cost vs. Productivity | ||
| 6 | Operating Cost vs. Safety | ||
| 7 | Operating Cost vs. Flexibility | ||
| 8 | Operating Cost vs. Noise | ||
| 9 | Operating Cost vs. Vibration | ||
| 10 | Air Quality vs. Pressure | ||
| 11 | Air Quality vs. Air Power | ||
| 12 | Air Quality vs. Efficiency | ||
| 13 | Air Quality vs. Productivity | ||
| 14 | Air Quality vs. Safety | ||
| 15 | Air Quality vs. Flexibility | ||
| 16 | Air Quality vs. Noise | ||
| 17 | Air Quality vs. Vibration | ||
| 18 | Pressure vs. Air Power | ||
| 19 | Pressure vs. Efficiency | ||
| 20 | Pressure vs. Productivity | ||
| 21 | Pressure vs. Safety | ||
| 22 | Pressure vs. Flexibility | ||
| 23 | Pressure vs. Noise | ||
| 24 | Pressure vs. Vibration | ||
| 25 | Air Power vs. Efficiency | ||
| 26 | Air Power vs. Productivity | ||
| 27 | Air Power vs. Safety | ||
| 28 | Air Power vs. Flexibility | ||
| 29 | Air Power vs. Noise | ||
| 30 | Air Power vs. Vibration | ||
| 31 | Efficiency vs. Productivity | ||
| 32 | Efficiency vs. Safety | ||
| 33 | Efficiency vs. Flexibility | ||
| 34 | Efficiency vs. Noise | ||
| 35 | Efficiency vs. Vibration | ||
| 36 | Productivity vs. Safety | ||
| 37 | Productivity vs. Flexibility | ||
| 38 | Productivity vs. Noise | ||
| 39 | Productivity vs. Vibration | ||
| 40 | Safety vs. Flexibility | ||
| 41 | Safety vs. Noise | ||
| 42 | Safety vs. Vibration | ||
| 43 | Flexibility vs. Noise | ||
| 44 | Flexibility vs. Vibration | ||
| 45 | Noise vs. Vibration |
References
- Zhang, Y.; Zhang, H.; Gao, K.; Zeng, Q.; Meng, F.; Cheng, J. Research on Intelligent Control System of Hydraulic Support Based on Position and Posture Detection. Machines 2023, 11, 33. [Google Scholar] [CrossRef]
- Zeng, Q.; Hu, Y.; Meng, Z.; Wan, L. Research on Velocity Feedforward Control and Precise Damping Technology of a Hydraulic Support Face Guard System Based on Displacement Feedback. Machines 2024, 12, 676. [Google Scholar] [CrossRef]
- Malyshev, Y.N. Strategy for the Development of the Russian Coal Industry. J. Min. Sci. 2000, 36, 57–65. [Google Scholar] [CrossRef]
- Kazanin, O.; Sidorenko, A.; Drebenstedt, C. Intensive Underground Mining Technologies: Challenges and Prospects for the Coal Mines in Russia. Acta. Montan. Slovaca. 2021, 26, 60–69. [Google Scholar] [CrossRef]
- Kortelev, O.B.; Cheskidov, V.I.; Norri, V.K. Effect of Highwall Parameters on the Open Pit Operation and Limits. J. Min. Sci. 2011, 47, 587–592. [Google Scholar] [CrossRef]
- Yuan, M.; Ouyang, J.; Zheng, S.; Tian, Y.; Sun, R.; Bao, R.; Li, T.; Yu, T.; Li, S.; Wu, D.; et al. Research on Ecological Effect Assessment Method of Ecological Restoration of Open-Pit Coal Mines in Alpine Regions. Int. J. Environ. Res. Public. Health 2022, 19, 7682. [Google Scholar] [CrossRef]
- Wang, S.; Ma, C.; Ma, Y.; Li, T. Monitoring and Evaluation of Ecological Restoration in Open-Pit Coal Mine Using Remote Sensing Data Based on a OM-RSEI Model. Int. J. Min. Reclam. Environ. 2025, 1–23. [Google Scholar] [CrossRef]
- Shi, S.; Guo, Z.; Ding, P.; Tao, Y.; Mao, H.; Jiao, Z. Failure Mechanism and Stability Control Technology of Slope during Open-Pit Combing Underground Extraction: A Case Study from Shanxi Province of China. Sustainability 2022, 14, 8939. [Google Scholar] [CrossRef]
- Dursun, A.E. Statistical Analysis of Methane Explosions in Turkey’s Underground Coal Mines and Some Recommendations for the Prevention of These Accidents: 2010–2017. Nat. Hazards 2020, 104, 329–351. [Google Scholar] [CrossRef]
- Karacan, C.O.; Ruiz, F.A.; Cote, M.; Phipps, S. Coal Mine Methane: A Review of Capture and Utilization Practices with Benefits to Mining Safety and to Greenhouse Gas Reduction. Int. J. Coal Geol. 2011, 86, 121–156. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Chen, M.; Jing, H.-W.; Chen, K.-F.; Meng, B. A Case Study on Large Deformation Failure Mechanism of Deep Soft Rock Roadway in Xin’An Coal Mine, China. Eng. Geol. 2017, 217, 89–101. [Google Scholar] [CrossRef]
- Tiwary, R.K. Environmental Impact of Coal Mining on Water Regime and Its Management. Water Air Soil. Pollut. 2001, 132, 185–199. [Google Scholar] [CrossRef]
- Gillies, S.; Slaughter, C.; Calizaya, F.; Wu, H.W. Booster Fans—Some Considerations for Their Usage in Underground Coal Mines. In Proceedings of the 13th United States/North American Mine Ventilation Symposium, Sudbury, ON, Canada, 13–16 June 2010. [Google Scholar]
- Mishra, D.; Mohalik, N.K.; Mishra, D.P.; Ray, S.K.; Pandey, J.K. Improving Workplace Environment of a Deep Underground Coal Mine with Multiseam Workings: An Alternative Approach. Mining Metall. Explor. 2022, 39, 1429–1443. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, J.; Ren, T.; Wang, Z.; Song, S. Application of Ventilation Simulation to Spontaneous Combustion Control in Underground Coal Mine: A Case Study from Bulianta Colliery. Int. J. Min. Sci. Technol. 2018, 28, 231–242. [Google Scholar] [CrossRef]
- Sahay, N.; Ray, S.K.; Ahmed, I.; Varma, N.K.; Singh, R.P.; Singh, A.K. Improvement in Ventilation in a Fire Affected Mine. J. S. Afr. Inst. Min. Metall. 2003, 103, 465–475. [Google Scholar]
- Shriwas, M.; Calizaya, F. Automation in Detection of Recirculation in a Booster Fan Ventilation Network. Int. J. Min. Sci. Technol. 2018, 28, 513–517. [Google Scholar] [CrossRef]
- Wempen, J.M. Characterization of Air Recirculation in Multiple Fan Ventilation Systems. Master’s Thesis, The University of Utah, Salt Lake City, UT, USA, 2012. [Google Scholar]
- Bayomi, N.N.; Hafiz, A.A.; Osman, A.M. Effect of Inlet Straighteners on Centrifugal Fan Performance. Energy Conv. Manag. 2006, 47, 3307–3318. [Google Scholar] [CrossRef]
- Brendel, M. Selecting Fans for Minimum Energy Consumption. ASHRAE J. 2015, 57, 52. [Google Scholar]
- de Villiers, D.J.; Mathews, M.J.; Mare, P.; Kleingeld, M.; Arndt, D. Evaluating the Impact of Auxiliary Fan Practices on Localised Subsurface Ventilation. Int. J. Min. Sci. Technol. 2019, 29, 933–941. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Li, X.; Gao, S.; Guo, K.; Wei, Y. Fault Diagnosis of Mine Ventilator Bearing Based on Improved Variational Mode Decomposition and Density Peak Clustering. Machines 2023, 11, 27. [Google Scholar] [CrossRef]
- Kursunoglu, N.; Onder, M. Selection of an Appropriate Fan for an Underground Coal Mine Using the Analytic Hierarchy Process. Tunn. Undergr. Space Technol. 2015, 48, 101–109. [Google Scholar] [CrossRef]
- Jiu, S.; Zhou, Z.; Liu, J. The Equipment Maintenance Scheduling Problem in a Coal Production System. Int. J. Prod. Res. 2013, 51, 5309–5336. [Google Scholar] [CrossRef]
- Li, J.; Ding, R. Research on Comprehensive Evaluation Indicators and Methods of World-Class Open-Pit Coal Mines. Sustainability 2024, 16, 8134. [Google Scholar] [CrossRef]
- Mulumba, D.M.; Liu, J.; Hao, J.; Zheng, Y.; Liu, H. Application of an Optimized PSO-BP Neural Network to the Assessment and Prediction of Underground Coal Mine Safety Risk Factors. Appl. Sci. 2023, 13, 5317. [Google Scholar] [CrossRef]
- Can, E. Assessment of Risks Relevant to Underground Measurements for Coal Mining Production and Exploration. Nat. Resour. Res. 2020, 29, 1773–1785. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Khandelwal, M.; Tao, M.; Li, C. Novel Approach to Evaluate Rock Mass Fragmentation in Block Caving Using Unascertained Measurement Model and Information Entropy with Flexible Credible Identification Criterion. Eng. Comput. 2021, 38, 1–21. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, J.; Zhou, T.; Yong, W. Evaluation of Vertical Shaft Stability in Underground Mines: Comparison of Three Weight Methods with Uncertainty Theory. Nat. Hazards 2021, 109, 1457–1479. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Du, K.; Jahed Armaghani, D.; Li, C. A New Hybrid Model of Information Entropy and Unascertained Measurement with Different Membership Functions for Evaluating Destressability in Burst-Prone Underground Mines. Eng. Comput. 2022, 38, 1–19. [Google Scholar] [CrossRef]
- Chen, C.; Yao, S.; Zhou, J. Comparison of Rock Spalling Evaluation in Underground Openings: Uncertainty-Based Mathematical Model and Empirical Method. Deep. Resour. Eng. 2025, in press. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, X. A Lightweight CNN for Wind Turbine Blade Defect Detection Based on Spectrograms. Machines 2023, 11, 99. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Yang, M.-S. TOPSIS Method Based on Complex Spherical Fuzzy Sets with Bonferroni Mean Operators. Mathematics 2020, 8, 1739. [Google Scholar] [CrossRef]
- Akram, M.; Kahraman, C.; Zahid, K. Group Decision-Making Based on Complex Spherical Fuzzy VIKOR Approach. Knowl.-Based Syst. 2021, 216, 106793. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, G.; Chen, X. SF-GRA Method Based on Cumulative Prospect Theory for Multiple Attribute Group Decision Making and Its Application to Emergency Supplies Supplier Selection. Eng. Appl. Artif. Intell. 2022, 110, 104679. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, G. Location Selection of Electric Vehicles Charging Stations by Using the Spherical Fuzzy CPT–CoCoSo and D-CRITIC Method. Comp. Appl. Math. 2023, 42, 60. [Google Scholar] [CrossRef]
- Thanh-Tuan, D.; Ngoc-Ai-Thy, N.; Van-Thanh-Tien, N.; Le-Thanh-Hieu, D. A Two-Stage Multi-Criteria Supplier Selection Model for Sustainable Automotive Supply Chain under Uncertainty. Axioms 2022, 11, 228. [Google Scholar] [CrossRef]
- Gong, S.; Yao, S.; Xi, F.; Liu, J.; Ren, X.; Niu, D.; Ding, J.; Zhang, H.; Wang, J.; Wang, S. A Comparison of Research Methods to Determine the Sustainability of Mineral Resources in Henan Province Based on Cloud Analysis. Sustainability 2022, 14, 15834. [Google Scholar] [CrossRef]
- Liu, H.-C.; Wang, L.-E.; Li, Z.; Hu, Y.-P. Improving Risk Evaluation in FMEA With Cloud Model and Hierarchical TOPSIS Method. IEEE Trans. Fuzzy Syst. 2019, 27, 84–95. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Xu, F. Comprehensive Stability Evaluation of Rock Slope Using the Cloud Model-Based Approach. Rock. Mech. Rock. Eng. 2014, 47, 2239–2252. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process (AHP). J. Oper. Res. Soc. 1980, 41, 1073–1076. [Google Scholar]
- Saaty, T.L. Axiomatic Foundation of the Analytic Hierarchy Process. Manag. Sci. 1986, 32, 841–855. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision-Making with the AHP: Why Is the Principal Eigenvector Necessary. Eur. J. Oper. Res. 2003, 145, 85–91. [Google Scholar] [CrossRef]
- Saaty, T.L. Highlights and Critical Points in the Theory and Application of the Analytic Hierarchy Process. Eur. J. Oper. Res. 1994, 74, 426–447. [Google Scholar] [CrossRef]
- Saaty, T.L. The Modern Science of Multicriteria Decision Making and Its Practical Applications: The AHP/ANP Approach. Oper. Res. 2013, 61, 1101–1118. [Google Scholar] [CrossRef]
- Akram, M.; Kahraman, C.; Zahid, K. Extension of TOPSIS Model to the Decision-Making under Complex Spherical Fuzzy Information. Soft Comput. 2021, 25, 10771–10795. [Google Scholar] [CrossRef]
- Su, Y.; Mao, J.; Sun, X.; Wang, X. The Construction and Application of a Preference Extraction Model under the Environment of Complex. Spherical Fuzzy. 2024, 37, 416–424. [Google Scholar] [CrossRef]
- Li, D.; Liu, C.; Gan, W. A New Cognitive Model: Cloud Model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
- Li, D. Comparative Study on Mathematical Foundations of Type-2 Fuzzy Set, Rough Set and Cloud Model. In Rough Set and Knowledge Technology; Yu, J., Greco, S., Lingras, P., Wang, G., Skowron, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; p. 1. [Google Scholar]
- Okeme, I.C.; Scott, T.B.; Martin, P.G.; Satou, Y.; Ojonimi, T.I.; Olaluwoye, M.O. Assessment of the Mode of Occurrence and Radiological Impact of Radionuclides in Nigerian Coal and Resultant Post-Combustion Coal Ash Using Scanning Electron Microscopy and Gamma-Ray Spectroscopy. Minerals 2020, 10, 241. [Google Scholar] [CrossRef]
- Gu, Y.-G.; Li, H.-B.; Lu, H.-B. Polycyclic Aromatic Hydrocarbons (PAHs) in Surface Sediments from the Largest Deep Plateau Lake in China: Occurrence, Sources and Biological Risk. Ecol. Eng. 2017, 101, 179–184. [Google Scholar] [CrossRef]
- Akande, J.M.; Onifade, M. Modelling of Okaba Underground Coal Mine Ventilation System. Int. J. Eng. Technol. 2013, 3, 766–772. [Google Scholar]
- Akande, J.M.; Onifade, M.; Aladejare, A. Determination of Airflow Distributions in Okaba Underground Coal Mine. J. Min. World Express 2013, 2, 40–44. [Google Scholar]
- Liang, W.; Zhao, G.; Luo, S. Selecting the Optimal Mine Ventilation System via a Decision Making Framework under Hesitant Linguistic Environment. Symmetry 2018, 10, 283. [Google Scholar] [CrossRef]
- Shang, W.; Jia, J. Theoretical Knowledge Enhanced Genetic Algorithm for Mine Ventilation System Optimization Considering Main Fan Adjustment. Complex. Intell. Syst. 2024, 11, 16. [Google Scholar] [CrossRef]
- Kursunoglu, N. Fuzzy Multi-Criteria Decision-Making Framework for Controlling Methane Explosions in Coal Mines. Environ. Sci. Pollut. Res. 2024, 31, 9045–9061. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Shao, L.; Yang, C. Fuzzy Prediction of the Mine’s Ventilation Structure’s Tunnel Air Volume. Expert Syst. Appl. 2023, 231, 120843. [Google Scholar] [CrossRef]
- Lawal, A.I.; Onifade, M.; Kwon, S.; Khandelwal, M. Enhancing Gas Drainage and Ventilation Efficiency in Underground Coal Mines: A Hybrid Expert Decision Approach for Booster Fan Prioritization. Tunn. Undergr. Space Technol. 2025, 155, 106153. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).