Abstract
In recent years, the powerful feature extraction capabilities of deep learning have attracted widespread attention in the field of bearing fault diagnosis. To address the limitations of single-modal and single-channel feature extraction methods, which often result in incomplete information representation and difficulty in obtaining high-quality fault features, this paper proposes a dual-channel parallel multimodal feature fusion model for bearing fault diagnosis. In this method, the one-dimensional vibration signals are first transformed into two-dimensional time-frequency representations using continuous wavelet transform (CWT). Subsequently, both the one-dimensional vibration signals and the two-dimensional time-frequency representations are fed simultaneously into the dual-branch parallel model. Within this architecture, the first branch employs a combination of a one-dimensional convolutional neural network (1DCNN) and a bidirectional gated recurrent unit (BiGRU) to extract temporal features from the one-dimensional vibration signals. The second branch utilizes a dilated convolutional to capture spatial time–frequency information from the CWT-derived two-dimensional time–frequency representations. The features extracted by both branches were are input into the feature fusion layer. Furthermore, to leverage fault features more comprehensively, a channel attention mechanism is embedded after the feature fusion layer. This enables the network to focus more effectively on salient features across channels while suppressing interference from redundant features, thereby enhancing the performance and accuracy of the dual-branch network. Finally, the fused fault features are passed to a softmax classifier for fault classification. Experimental results demonstrate that the proposed method achieved an average accuracy of 99.50% on the Case Western Reserve University (CWRU) bearing dataset and 97.33% on the Southeast University (SEU) bearing dataset. These results confirm that the suggested model effectively improves fault diagnosis accuracy and exhibits strong generalization capability.
1. Introduction
Rolling element bearings are critical mechanical components that significantly influence the safe and stable operation of engineering equipment. The health of bearings ensures operational stability and system safety. These bearings frequently operate under harsh conditions such as high temperature, high humidity, high speed, and heavy load. Consequently, they exhibit high failure rates. Bearings failures can lead not only to substantial economic losses but also pose serious threats to personnel safety and property, particularly given the rapid development of modern industry in recent years, which demands higher levels of intelligent fault diagnosis.
In recent years, data-driven diagnostic methods have demonstrated significant potential across various rotating machinery systems [1,2,3], with deep learning’s powerful feature extraction capabilities garnering particularly extensive attention in the field of mechanical fault diagnosis. Diagnostic methods based on convolutional neural network (CNN) and recurrent neural network (RNN) have achieved significant success in this domain, gradually becoming a focal point in intelligent fault diagnosis. To fully leverage one-dimensional time-domain signals, Baoye Song et al. [4] proposed an optimized CNN combined with the strengths of CNN and RNN, designing a convolutional neural network–bidirectional long short-term memory (CNN-BiLSTM) model that achieved precise fault features and high detection accuracy through feature extraction from raw vibration signals. Linshan Jia et al. [5] presented a novel end-to-end Gramian-noise-reduction-(GNR)-based CNN model, termed the Gramian Time Frequency Enhancement Network (GTFE-Net) for bearing fault diagnosis, with experimental results demonstrating significantly improved classification performance.
Converting one-dimensional time-domain signals into images [6] is also a highly useful technique in fault diagnosis, leveraging powerful computer vision and deep learning models for signal data processing. Current mainstream methods for transforming time-domain signals into images include short-time Fourier transform (STFT) [7,8], continuous wavelet transform (CWT), Stockwell transform (ST) [9], Gramian angular field (GAF) [10,11], and Markov transition field (MTF) [10,12]. These methods are widely applied in fault diagnosis. Ge Xin et al. [13] achieved high diagnostic accuracy by using logarithmic-scaled short-time Fourier transform (log-STFT) and improved self-calibrated convolutions. Ronny Francis Ribeiro Junior et al. [14] proposed a precise and robust deep learning method based on STFT and CNN for motor fault diagnosis, validating its effectiveness under seven different conditions. Rongrong Zhang et al. [15] introduced a bearing fault diagnosis model based on short-time Fourier transform–symmetric wavelet transform (STFT-SWT) and a two-stream convolutional neural network–K-nearest neighbors (CNN-KNN), enhancing diagnostic accuracy. Zhenzhen Tian et al. [16] proposed a two-dimensional image–CNN method combining GAF, wavelet transform (WT) images, and CNN. The two-dimensional images were input into a ResNet34 model for fault recognition, achieving a high fault diagnosis rate. Chengyu Yang et al. [17] proposed a rolling bearing fault diagnosis method fusing GAF, MTF, and a deep residual network (ResNet), utilizing the neural network’s advantages in image classification and recognition to classify different bearing fault types. Lijin Guo et al. [18] proposed a composite processing method based on GAF, MTF, and ResNet for fault identification. After converting one-dimensional time-domain signals into image datasets, ResNet was used for feature extraction, enabling the network to learn more fault features from the images, resulting in good fault identification accuracy. Lijin Guo et al. [19] also introduced a technique for diagnosing rolling bearing faults that integrates MTF with a 34-layer transfer learning residual network (TLResNet34). This approach employs two-dimensional feature maps as inputs to the TLResNet34 architecture, thereby enhancing data usage and facilitating accurate fault categorization. Jie Liu et al. [20] proposed a rolling bearing fault diagnosis method based on adaptive maximum second-order cyclostationarity blind deconvolution (ACYCRD) combined with MTF and mobile vision transformer (MobileViT), demonstrating high anti-interference capability and generalization performance. Linlin Xue et al. [21] proposed a rolling bearing fault diagnosis method based on a self-calibrated coordinate attention mechanism and multi-scale CNN (SC-MSCNN). It used MTF to convert raw vibration signals into MTF images with temporal correlation, which were then input into the proposed spatial-channel multi-scale convolutional neural network (SC-MSCNN) model for efficient classification.
However, due to the complexity of real-world bearing operating conditions, accurately extracting fault features remains challenging. Relying solely on processing features from a single time-domain or time–frequency domain modality inadequately reflects the full fault state. Composite processing, which leverages correlations between different data modalities, enables networks to learn more comprehensive fault features, leading to better fault identification accuracy. CWT is a powerful signal analysis tool providing detailed information simultaneously in time and frequency. Its adaptive window, achieved through scalable and translatable wavelet basis functions, allows it to adaptively match different frequency components of a signal. This overcomes the limitation of STFT, which uses a fixed window length. The localization properties of wavelet basis functions make CWT highly sensitive to detecting and locating singularities, discontinuities, edges, and transient events (such as spikes, pulses, and fault signatures) within signals, producing significant coefficients at corresponding times and scales. Therefore, this paper proposes using CWT to process one-dimensional time-domain signals. The time-frequency images generated by CWT contain rich spatio-temporal feature patterns that serve as powerful inputs to the proposed deep learning model for bearing fault diagnosis classification.
Building on this analysis, this paper proposes a dual-channel parallel multimodal feature fusion method for bearing fault diagnosis. The method first employs the continuous wavelet transform (CWT) to convert one-dimensional vibration signals into two-dimensional time–frequency images. Both the original one-dimensional vibration signal and the generated two-dimensional time–frequency image are then concurrently input into the proposed dual-channel parallel model. The first channel utilizes a 1DCNN combined with a BiGRU to extract temporal features from the one-dimensional vibration signal. The second channel employs a dilated convolution to extract spatio-temporal information from the CWT time-frequency image. Subsequently, the deep-level fault features extracted by both channels are fused within a feature fusion layer. Furthermore, to more comprehensively utilize the fault features, a channel attention mechanism is embedded after the fusion layer. This mechanism enables the network to focus more effectively on salient features within each channel and suppress interference from redundant features, thereby enhancing the performance and accuracy of the dual-channel network. Finally, the fused fault features are input into a softmax classifier for fault classification.
Experimental findings demonstrated that the proposed method attained a mean accuracy of 99.50% on the Case Western Reserve University (CWRU) bearing dataset and 97.33% on the Southeast University (SEU) bearing dataset. These findings confirm that the developed model effectively improves the precision of fault detection and possesses robust generalizability. When subjected to intricate noise conditions, the model showcases outstanding diagnostic efficacy relative to conventional neural network architectures, highlighting its resilience against noise interference.
The key advancements presented in this paper include the following:
- 1.
- A dual-channel parallel-architecture-based multi-modal feature fusion method is proposed for bearing fault diagnosis. This framework simultaneously processes raw one-dimensional vibration signals and two-dimensional time–frequency representations through dedicated channels to extract complementary fault features. The parallel integration of heterogeneous modal data enhances feature complementarity and significantly improves the model’s generalization capability.
- 2.
- A channel attention mechanism is incorporated to recalibrate feature channel weights, maximizing utilization of extracted sample features and enhancing the model’s focus on discriminative characteristics.
- 3.
- Comprehensive experimental validation was conducted across multiple benchmark datasets, including comparative analysis, noise robustness tests, and ablation studies. These experiments conclusively demonstrate the validity and efficacy of the proposed dual-channel parallel multi-modal feature fusion method for bearing fault diagnosis, confirming its superiority in this domain.
The remainder of this paper is structured as follows. Section 2 introduces the theoretical background relevant to this research. Section 3 explores the rationale behind the study and details the design of the proposed dual-channel parallel multimodal feature fusion method for bearing fault diagnosis. Section 4 presents the comparative experiments. Finally, Section 5 presents the conclusion and future work.
2. Theoretical Background
2.1. CWT
The continuous wavelet transform (CWT) [22,23] is a signal processing method that utilizes wavelet functions to analyze raw vibration signals and provides effective time and frequency information. CWT enables the observation of local features within vibration signals by adaptively scaling the wavelet to transform a one-dimensional vibration signal into a two-dimensional time–frequency image. Yang Xu et al. [24] combined CWT with a hybrid deep learning model integrating CNN and gcForest classifiers; Ningkun Diao et al. [25] integrated CWT with a residual neural network (T-ResNet); Guanwei Jia et al. [26] input CWT time–frequency maps into a ResNet-18 network for fault signal identification and diagnosis; Yuan Guo et al. [27] proposed a fault diagnosis method based on multi-resolution singular-value decomposition (MRSVD), continuous wavelet transform (CWT), an improved CNN enhanced with convolutional block attention modules, and long short-term memory (LSTM). All these approaches leverage the advantages of CWT to enhance feature extraction, thereby improving the accuracy of fault diagnosis. A key advantage of the CWT lies in its ability to automatically adjust the temporal resolution according to the frequency characteristics of the signal, thereby providing superior analysis results across different frequency ranges. In the high-frequency regions of a signal, CWT captures more transient features and finer details, while in the low-frequency regions, it provides a broader overview of the signal’s characteristics. The mathematical expression for the CWT is given in Equation (1):
In the equation, represents the input signal, denotes the selected wavelet function, is the complex conjugate of the wavelet function, a is the scale factor, and is the shift factor. The key to continuous wavelet transform lies in selecting the wavelet basis function. Different modern features of the signal will be suppressed in other parts due to this selection. Due to the symmetry and smoothness characteristics of the complex Morlet wavelet, this study selected the complex Morlet wavelet as the basis function for the wavelet transform. A center frequency Hz and bandwidth parameter Hz were adopted for the complex Morlet wavelet to perform time–frequency transformation on the signal. The expression for the complex Morlet wavelet is given by Equation (2).
Here, is the central frequency, and is the bandwidth parameter.
2.2. CNN
Convolutional neural networks (CNNs) are a class of deep feedforward neural network models characterized by local connectivity and weight sharing. Recognized as one of the most effective deep learning algorithms for fault diagnosis, the CNN architecture is inspired by the connection patterns of biological neurons in the visual cortex. This design enables CNN to effectively mimic the human visual system for recognizing patterns and structures within images, establishing them as a predominant technique in modern image recognition and processing. Lingli Jiang et al. [28] proposed a lightweight CNN and applied it to fault diagnosis; Xiaohan Chen et al. [29] combined two CNNs with different kernel sizes and long short-term memory networks to identify fault types; Xin Wang et al. [30] input vibration signals and acoustic signals into a 1DCNN, achieving more accurate and robust bearing fault diagnosis; Sinitsin V et al. [31] proposed a diagnostic method based on a novel hybrid CNN-MLP model, successfully detecting and locating bearing faults. These studies by scholars demonstrate the effectiveness of CNN in fault diagnosis. A typical CNN framework primarily consists of an input layer, convolutional layers, pooling layers, fully connected layers, and an output layer.
Input Layer: The input layer receives data or images for classification. If the input data is an image, its dimensions are typically set to a width-to-height ratio of (e.g., 64 × 64, 128 × 128). In this work, one channel utilizes a continuous wavelet transform (CWT) time–frequency image as input, resized to pixels. The other channel accepts the raw one-dimensional vibration signal.
Convolutional Layer: Within a CNN, convolutional layers play a crucial role in feature extraction. They operate by applying learnable filters (with shared weights) to perform a weighted summation over local regions of the input data. This process captures local features from the input (images or data) and maps local signal representations from one layer to the next. The mathematical operation of a convolutional layer is formally described by Equation (3).
Here, represents the weight of the i-th convolution kernel in the l-th layer, denotes the receptive field of that convolution kernel, is the bias of that convolution kernel, and is the input to the j-th convolution kernel in the (l + 1)-th layer.
To mitigate the spatial resolution loss associated with using standard convolutional layers for processing CWT two-dimensional time–frequency images, this work employs dilated convolution. Dilated convolution expands the receptive field without sacrificing resolution. This is achieved by controlling the dilation rate, a key parameter of the dilated convolution operation. With different dilation rates being set, the receptive field size varies, enabling the extraction of multi-scale information from the input. Figure 1 depicts a schematic comparison between standard convolution and dilated convolution.
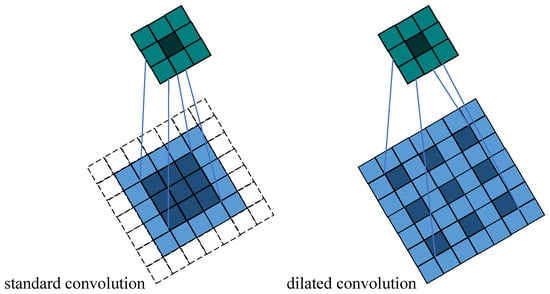
Figure 1.
Comparison between standard convolution and dilated convolution.
Pooling Layer: A pooling layer is typically appended after each convolutional layer to reduce the spatial dimensions of the data while preserving essential feature information. This operation decreases parameters in subsequent layers and enhances model robustness against input variations. Common pooling strategies include average pooling and max pooling. This work employs max pooling, which outputs the maximum value within the receptive field region, enabling the network to learn more representative features. The mathematical operation of pooling is formalized in Equation (4).
Here, represents the value of the i-th feature at the t-th neuron in the l-th layer, where , and H is the width of the pooling region; and is the input value to the j-th neuron in the (l + 1)-th layer.
Fully Connected Layer: Positioned at the terminal stage of the network architecture, the fully connected layer (FC layer) features interconnected nodes between all inputs and outputs. In CNN, the FC layer aggregates features extracted by convolutional and pooling layers, flattening them into a one-dimensional feature vector. This vector may propagate to subsequent fully connected layers, establishing comprehensive connections between inputs and outputs.
Output Layer: The output layer propagates the consolidated features from the final FC layer to an activation function (e.g., Softmax). This generates probability distributions across target classes, ultimately determining the fault category of the input data.
2.3. BiGRU
Recurrent neural networks (RNNs) [32,33] represent a specialized neural network architecture designed for processing sequential data. They play a significant role in analyzing time-series vibration signals for bearing fault diagnosis. The core principle of an RNN is to integrate information from the current element in the sequence with information processed from preceding elements. However, when handling long sequences, RNN is susceptible to the vanishing gradient or exploding gradient problems. These issues arise because gradients are multiplied repeatedly during backpropagation through time, making it difficult for the model to learn long-range dependencies and limiting its effectiveness on long sequence data.
The gated recurrent unit (GRU) [34,35], an improved variant of the RNN, addresses these limitations by introducing update gates and reset gates. These gates control the degree to which information from the previous hidden state is retained or updated, effectively mitigating the aforementioned problems.
Further extending the capabilities of the GRU, the bidirectional gated recurrent unit (BiGRU) processes sequences simultaneously in both forward and reverse directions. This bidirectional processing enables the capture of richer sequential feature information, leading to significantly improved performance in bearing fault diagnosis applications using time-series signals.
The bidirectional information flow mechanism inherent in the BiGRU model enhances its contextual awareness, allowing it to better understand and utilize long-range dependency information within lengthy sequences. Within a BiGRU neural network, each timestep employs two separate GRU units operating in parallel: one processes information from the sequence start to the current timestep (forward direction), while the other processes information from the current timestep to the sequence end (reverse direction). The outputs from these two GRU units are then combined to form the final output for each timestep. This architecture endows the BiGRU model with greater robustness and higher performance when processing long sequence data. The structure of the BiGRU is illustrated in Figure 2.
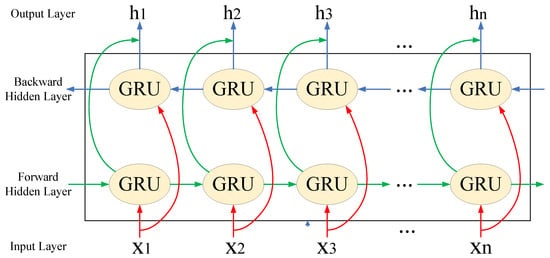
Figure 2.
BiGRU schematic diagram.
2.4. Channel Attention
Currently, enhancing feature extraction capability represents an effective approach for improving fault diagnosis models. This is frequently achieved by integrating attention mechanisms such as the convolutional block attention module (CBAM), squeeze-and-excitation network (SENet), efficient channel attention network (ECANet), and channel attention into the model architecture. In this work, channel attention is incorporated to augment feature extraction performance, enabling the network to adaptively focus on and select the essential components of features. The structure of the channel attention module is depicted in Figure 3 [36].
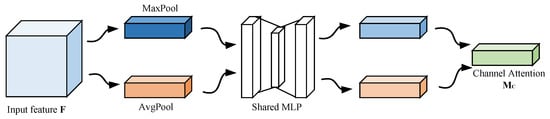
Figure 3.
Channel attention module [36].
The purpose of the channel attention module is to weight different channels within the feature maps. It employs global average pooling to capture global information from each channel’s feature map. The computational procedure is expressed in Equation (5):
Here, signifies the input feature matrix. The terms and refer to the global average pooling and maximum pooling processes, respectively. is an abbreviation for multilayer perceptron, while denotes the Sigmoid activation function.
3. Model Construction
3.1. Data Preprocessing
The multi-modal feature fusion bearing fault diagnosis model based on a dual-channel parallel structure proposed in this paper first converts the original one-dimensional vibration signals into two-dimensional time–frequency images with continuous wavelet transform (CWT). Then, both the one-dimensional vibration signals and the two-dimensional time–frequency images are input into the model. The data preprocessing is as follows: the original one-dimensional vibration signals of the bearing are segmented, with each sample set to a length of 1024 data points. Overlapping sampling is used for data augmentation, with an overlap length of 512 data points between consecutive samples. The height and width of the two-dimensional time–frequency images are set to , forming RGB color images with three color channels and a resolution of pixels. Following this step, the dataset is divided into training, validation, and testing subsets with a distribution of 60%, 20%, and 20% respectively. The resulting two-dimensional time–frequency visualizations for both categories of data post-CWT processing are illustrated in Figure 4 and Figure 5.
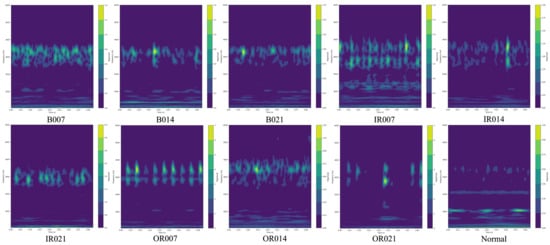
Figure 4.
CWT Time–frequency representation of the CWRU dataset.

Figure 5.
CWT Time–frequency representation of the SEU dataset.
3.2. Model Construction
3.2.1. Model Construction
This paper proposes a multimodal feature fusion bearing fault diagnosis model based on a dual-channel parallel architecture. The schematic diagram of the proposed dual-channel parallel multimodal feature fusion bearing fault diagnosis model is presented in Figure 6. The network architecture parameters are shown in Table 1. The overall diagnostic approach operates as follows: First, one-dimensional vibration signals are transformed into two-dimensional time–frequency representations using the continuous wavelet transform (CWT). Subsequently, both the raw one-dimensional vibration signals and the generated two-dimensional time-frequency representations are fed simultaneously into the dual-channel parallel model.
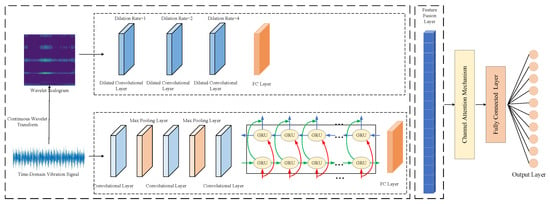
Figure 6.
Architecture of the proposed dual-channel parallel multimodal feature fusion model for bearing fault diagnosis.

Table 1.
The network architecture parameters of the proposed dual-channel parallel multimodal feature fusion model for bearing fault diagnosis.
In the first channel (processing the one-dimensional vibration signals), a one-dimensional convolutional neural network (1DCNN) combined with a bidirectional gated recurrent unit (BiGRU) extracts temporal features. The 1DCNN comprises three convolutional layers and two pooling layers. The convolutional layers employ kernel widths of 3, 3, and 4 with 8, 16, and 8 filters respectively, utilizing rectified linear unit (ReLU) activation functions. Max pooling layers with a kernel size of are applied. The GRU layer contains 32 units, resulting in a total of 64 units for the BiGRU (32 units per direction).
The second channel processes the CWT-derived two-dimensional time–frequency images using a dilated convolutional neural network (DCNN) to extract spatio-temporal features. This channel incorporates three dilated convolutional layers with dilation rates of 1, 2, and 4, utilizing 32, 64, and 64 filters respectively, also using ReLU activation.
Features indicative of faults from both channels are subsequently integrated in a specialized feature amalgamation layer. Furthermore, to comprehensively leverage the fault features, a channel attention mechanism is embedded after the fusion layer. This mechanism adaptively weights features across channels, directing the network’s focus towards the most discriminative features while suppressing redundant information, thereby enhancing the effectiveness and classification accuracy of the dual-channel network. Ultimately, the enhanced features are channeled into a softmax classifier to determine fault categories.
3.2.2. Diagnostic Workflow
The diagnostic workflow of the proposed dual-channel parallel multimodal feature fusion bearing fault diagnosis model is illustrated in Figure 7. The model is trained using the training dataset. In the “Optimize model parameters” module, the discrepancy between the model’s current predictions and the true labels is evaluated using a loss function, and the model’s internal weights and biases are adjusted via the Adam optimization algorithm to improve the model’s performance in subsequent predictions. This training process is continued until the model achieves the desired diagnostic accuracy. Then, the test dataset is input into the trained model, the evaluation metrics such as diagnostic accuracy and diagnostic loss are computed, and the final diagnostic results are obtained.
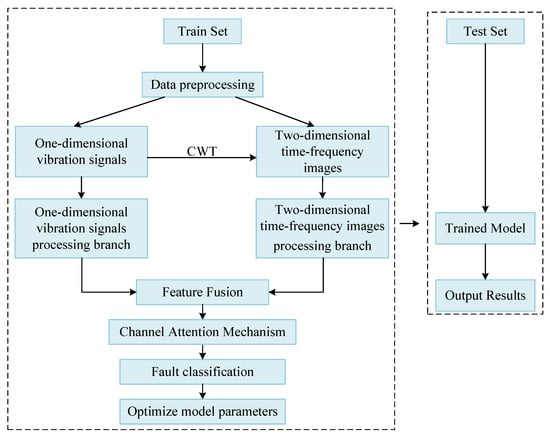
Figure 7.
Flowchart of the proposed dual-channel parallel multimodal feature fusion model for bearing fault diagnosis.
4. Experimental Results
4.1. Dataset
- (1)
- CWRU: In order to assess the effectiveness of the suggested approach for diagnosing faults in rolling bearings, experiments were conducted using the bearing dataset from Case Western Reserve University (CWRU). The CWRU bearing fault dataset is widely adopted in fault diagnosis and prognosis research, containing vibration data under various fault modes and operating conditions. The experimental platform comprises a three-phase induction motor, torque transducer, dynamometer, and SKF6205 drive-end bearings.
All tested deep-groove ball bearings contained artificially induced faults via electro-discharge machining (EDM). This study utilized drive-end bearing data acquired at a 12 kHz sampling frequency under a 1772 r/min rotational speed with a 1 hp motor load. The dataset encompasses four health conditions: faults in the inner raceway, faults in the outer raceway, ball faults, and healthy bearings. Each fault type includes three severity levels corresponding to fault diameters of 0.1778 mm, 0.3556 mm, and 0.5334 mm. The experimental dataset description and classification labels are detailed in Table 2.

Table 2.
Specifications and classification labels of the CWRU dataset.
Among these, 200 samples were allocated for each of the ten fault types, yielding a total of 2000 samples. Each sample comprises 1024 data points, acquired through overlap sampling with an overlap length of 512 points. The data collection was divided into three subsets—training, testing, and validation—with a distribution ratio of 6:2:2. This allocation led to 1200 samples allocated for training purposes, 400 samples reserved for testing, and an additional 400 samples dedicated to validation.
- (2)
- SEU: The Southeast University (SEU) test rig was equipped with an electric motor, a motor controller, a speed reducer, a planetary gearbox, a brake, and a brake controller. This study utilized a bearing vibration dataset acquired under the operating condition of a 30 Hz (1800 rpm) rotational speed and a 2 V (7.32 Nm) load, with a sampling frequency of 5120 Hz. This dataset encompasses data representing five distinct states: ball fault, inner ring fault, outer ring fault, compound fault, and healthy working state. Specifications for the SEU fault categories are detailed in Table 3.
 Table 3. SEU fault categories.
Table 3. SEU fault categories.
The dataset comprises samples representing five distinct fault types, with 300 samples per type, yielding a total of 1500 samples. Each sample has a length of 1024 data points. Samples were acquired using an overlapping sampling method with an overlap length of 512 points between consecutive segments. The data collection was divided into three subsets—training, testing, and validation–with a distribution ratio of 6:2:2. This allocation led to 900 samples allocated for training purposes, 300 samples reserved for testing, and an additional 300 samples dedicated to validation.
4.2. Comparative Methods and Experimental Results
4.2.1. Comparative Methods
In practical operating scenarios, data signals typically exhibit varying levels of noise. To validate the model’s diagnostic performance under noisy conditions, additive white Gaussian noise (AWGN) was injected into the original signals at different signal-to-noise ratios (SNRs). It should be noted that this simplified noise model is primarily used to verify the model’s basic stability under stationary and random noise interference. However, real industrial operating environments are far more complex, with disturbances often exhibiting non-stationary and non-Gaussian characteristics and may include strong structural resonances, modulation effects related to operational conditions (such as speed and load), and other unknown impulsive interferences. Therefore, the experiments described in this section were aimed to provide a baseline analysis of the model’s noise robustness, and the generalizability of the conclusions to broader industrial scenarios requires further validation. Following this approach, AWGN was systematically introduced across a range of SNR levels. Specifically, AWGN was added to the raw signal data at SNRs of −6 dB, −4 dB, 0 dB, 4 dB, and 6 dB. The specific SNRs used are defined by Equation (6).
where denotes the signal power, and denotes the noise power. To validate the effectiveness of the proposed model, it was compared against several benchmark models: the back propagation (BP) neural network, support vector machine (SVM), gated recurrent unit (GRU), long short-term memory (LSTM), and convolutional neural network (CNN). The performance evaluation of our suggested approach and the benchmark methods across different signal-to-noise ratios are summarized in Table 4, including accuracy and standard deviation. The first row of data shows the experimental results obtained on the CWRU dataset, while the second row presents the results on the SEU dataset. To mitigate experimental variability and enhance the accuracy and reliability of the results, every test was performed five separate times. The reported values represent the average over these trials.

Table 4.
Accuracy under different signal-to-noise ratio conditions.
Among the comparative models, the BP network possesses a simple structure and limited learning capability. Noise within the training data can readily perturb the network weights, leading to model instability; distortion becomes likely once the data is corrupted by noise interference. While GRU and LSTM networks exhibit a degree of inherent noise resistance, their performance degrades significantly under high-noise conditions. CNN can effectively capture local feature relationships within time-series data and attenuate certain levels of noise, yet they fall short of achieving the desired denoising effectiveness.
The proposed algorithm addresses these limitations by integrating a dual-branch architecture for hybrid-domain fault feature extraction, combining CNN and bidirectional gated recurrent unit (BiGRU). This design simultaneously exploits the CNN’s feature extraction prowess and leverages the BiGRU’s enhanced noise resilience, thereby significantly augmenting the overall noise resistance of the algorithm.
As evident from the experimental results, reducing the SNR amplifies the noise interference, which further accentuates the noise-suppression advantages of the proposed model. As a result, our proposed solution exhibited enhanced diagnostic precision in noise-resilience tests when contrasted with alternative reference models.
4.2.2. Case 1
To offer a clearer understanding of the fault classification results, the accuracy variation curve, confusion matrix, and t-distributed stochastic neighbor embedding (t-SNE) visualization for the model’s performance on the CWRU dataset for one of the experiments are also presented, as visualized in Figure 8.
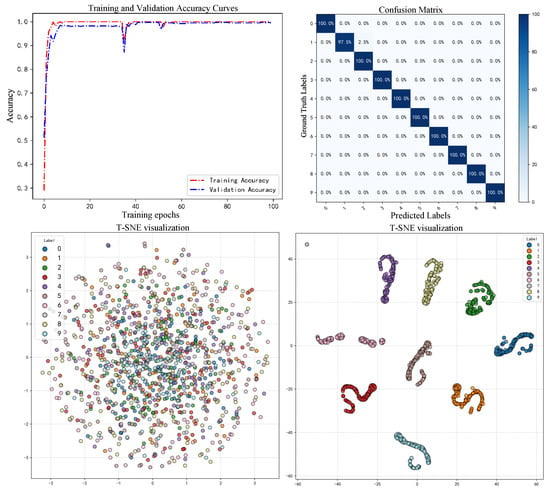
Figure 8.
Experimental results on the CWRU dataset. (From top to bottom and from left to right: accuracy curves, confusion matrix, initial t-SNE, and final t-SNE).
From the accuracy variation curves shown in Figure 8, one can see that the proposed multi-modal feature fusion bearing fault diagnosis model based on a dual-channel parallel structure achieved remarkable performance on the CWRU bearing fault classification task. The accuracy metrics for both training and validation phases display a steady increase, maintaining high levels throughout the training process. After eight epochs, the accuracies of both sets surpassed 95%. Although there was some fluctuation around the 35th epoch, overall stability was restored thereafter, with the accuracy stabilizing above 99% after the 55th epoch, indicating model convergence. The ultimate fault diagnosis accuracy on the test set reached 99.75%.
As depicted by the confusion matrix in Figure 8, which presents an intuitive tabular representation of the model’s classification performance on the CWRU fault test dataset, nearly all faults were accurately identified, with one exception: a rolling element fault characterized by a 0.3556 mm damage diameter was incorrectly categorized as having a 0.5334 mm diameter. This resulted in a classification accuracy of 99.75% for this experiment, with an overall average classification accuracy of 99.50% across five experiments.
Figure 8 shows the t-SNE visualization results, illustrating the high-level abstract features from the model’s feature fusion layer. t-SNE is a nonlinear dimensionality reduction technique that maps high-dimensional features into a two-dimensional space while preserving the local similarity relationships among samples. Furthermore, the t-SNE visualization outcomes shown in Figurereveal significant clustering effects among the ten types of fault data processed by the model. Similar feature points are densely clustered, while different categories form distinct clusters with clear boundaries between them. This observation confirms the model’s efficacy in distinguishing various types of faults, demonstrating its robust fault diagnosis and classification capabilities.
4.2.3. Case 2
To offer a clearer understanding of the fault classification results, the accuracy variation curve, confusion matrix, and t-distributed stochastic neighbor embedding (t-SNE) visualization for the model’s performance on the SEU dataset for one of the experiments are also presented, as visualized in Figure 9.
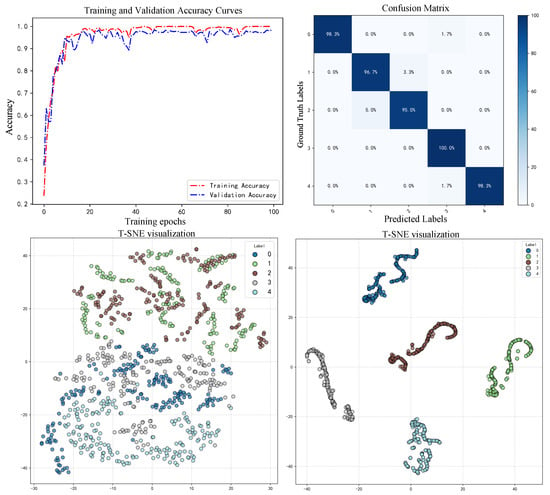
Figure 9.
Experimental results on the SEU Dataset. (From top to bottom and from left to right: accuracy curves, confusion matrix, initial t-SNE, and final t-SNE).
From the accuracy variation curves shown in Figure 9, one can see that the proposed multi-modal feature fusion bearing fault diagnosis model based on a dual-channel parallel structure demonstrated excellent performance on the CWRU bearing fault classification task. The accuracy metrics for both training and validation phases display a steady increase, maintaining high levels throughout the training process with only minor differences between them. After ten epochs, both sets achieved relatively high accuracy levels, subsequently fluctuating around 95% and eventually stabilizing near 97%. The overall trend indicates model convergence, with the final fault diagnosis accuracy on the test set reaching 97.66%.
As depicted by the confusion matrix in Figure 9, which presents an intuitive tabular representation of how well the model performs in classifying faults within the CWRU fault test dataset, misclassifications occurred in all classes except for the fourth fault type. However, the overall diagnostic accuracy shows a significant improvement, with a classification accuracy of 97.66% for this experiment and an overall average classification accuracy of 97.33% across five experiments.
Figure 9 shows the t-SNE visualization results, illustrating the high-level abstract features from the model’s feature fusion layer. t-SNE is a nonlinear dimensionality reduction technique that maps high-dimensional features into a two-dimensional space while preserving the local similarity relationships among samples. Furthermore, the t-SNE visualization results presented in Figure 9 reveal notable clustering effects among the five types of fault data processed by the model. Similar feature points are densely clustered, while different categories form distinct and well-separated clusters, indicating clear boundaries between clusters. This observation confirms the model’s effectiveness in distinguishing various types of faults, demonstrating its robust fault diagnosis and classification capabilities.
4.3. Ablation Experiments
To assess the importance of each component within our proposed dual-channel parallel multi-modal feature fusion framework for diagnosing bearing faults, an ablation analysis was performed. The results from these experiments are illustrated in Figure 10. We conducted four distinct sets of ablation tests to evaluate their individual contributions: (a) one-dimensional vibration signals were input into a one-dimensional convolutional neural network and a bidirectional gated recurrent unit, (b) time–frequency images in two-dimension were processed using a dilated convolutional neural network, and (c) both the one-dimensional vibration signals and the two-dimensional time–frequency images were input into the model without channel attention weighting and (d) the proposed model in this study.
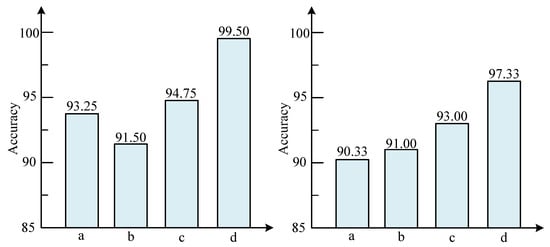
Figure 10.
Ablation experimental results on the CWRU dataset (left) and SEU dataset (right). (a) One-dimensional vibration signals were input into a one-dimensional convolutional neural network and a bidirectional gated recurrent unit. (b) Time–frequency images in two-dimension were processed using a dilated convolutional neural network. (c) Both the one-dimensional vibration signals and the two-dimensional time–frequency images were input into the model without channel attention weighting. (d) The proposed model in this study.
Every set of experiments was conducted five times, with the mean outcomes being documented. The findings depicted in Figure 10 indicate that our suggested framework outperformed all other comparative models in terms of accuracy, thereby highlighting its efficacy and advanced capabilities.
Based on the comparison results of the ablation experiments, the feasibility of the dual-channel parallel module and the attention mechanism module proposed in this paper has been demonstrated. By simultaneously processing one-dimensional vibration signals and two-dimensional time-frequency diagrams through two channel models and subsequently performing feature-weighted fusion, the classification accuracy is successfully improved. This is because the one-dimensional vibration signals and two-dimensional time-frequency diagrams provide complementary fault information with different granularities. The role of the dual-channel parallel module and the attention mechanism module is to maximize the mining and fusion of this information. Specifically, when the features of the two channels converge at the fusion layer, they form a richer, higher-dimensional joint feature space. Within this space, the patterns of faults become more linearly separable. However, the importance of the vast number of features extracted by the dual-channel parallel module is not equal. For different fault types, or even different samples, the value contributed by the one-dimensional signals and the time–frequency diagrams varies. The channel attention mechanism first “summarizes” the feature vectors extracted from the two channels, obtaining a descriptor that represents the overall information of each channel. Then, through a small neural network, it analyzes these two descriptors and outputs two weight values. For faults with particularly prominent periodic impacts, the model may assign a higher weight to the one-dimensional vibration signal channel, as the impact sequences in the raw waveform are the most direct evidence. For faults with complex modulation phenomena that require observation of specific frequency bands, the model may assign a higher weight to the two-dimensional time–frequency diagram channel, as the time–frequency diagram can more clearly reveal modulation sidebands.
5. Conclusions and Future Work
5.1. Conclusions
This study proposes a dual-channel parallel multi-modal feature fusion model for bearing fault diagnosis. The method extracts temporal features from one-dimensional vibration signals and spatial features from two-dimensional time–frequency images generated by continuous wavelet transform (CWT), enabling comprehensive feature representation by leveraging complementary information from different modalities. Experimental results demonstrate the following:
- 1.
- The proposed dual-channel parallel multi-modal feature fusion model converts the input data into time–frequency images and employs dilated convolution for feature extraction. This approach capitalizes on the strong capability of two-dimensional dilated convolution in capturing image features, where dilated convolution expands the receptive field without reducing spatial resolution, thereby preserving fine-grained image details effectively. In processing one-dimensional signals, a one-dimensional convolutional neural network (1DCNN) is employed for effective local feature identification, succeeded by a bidirectional gated recurrent unit (BiGRU) to analyze intricate time-based relationships within the sequence. The parallel dual-channel architecture effectively exploits both temporal and spatial characteristics of the data, significantly enriching feature representation and achieving high diagnostic accuracy while maintaining strong generalization ability.
- 2.
- The incorporation of a channel attention mechanism after the feature fusion layer enhances the model’s ability to focus on critical fault-related features. By adaptively reweighting channel-wise features, the attention mechanism suppresses interference from redundant or irrelevant features, thereby further improving diagnostic accuracy.
Although the model proposed in this paper can greatly leverage its advantages in practical engineering applications—such as dual-channel information fusion for complementary feature extraction and an attention mechanism to focus on critical features—enabling accurate diagnosis, this study still has several limitations that need to be acknowledged. The primary limitation concerns the validation methodology employed. Our evaluation was conducted exclusively on two widely used benchmark datasets, CWRU and SEU, which contain artificially induced faults under controlled laboratory conditions. While the use of these established benchmarks allows for direct comparison with existing methods and represents a common practice in the field, it inherently restricts the generalizability of our findings to real-world industrial scenarios.
The laboratory-controlled nature of these datasets presents an idealized environment that may not fully capture the complexities encountered in practical applications. Real-world rotating machinery often operates under variable working conditions, including fluctuating loads, changing rotational speeds, varying environmental factors, and diverse noise interference. Furthermore, the fault patterns in benchmark datasets are typically well-defined and isolated, whereas real industrial faults often manifest as compound defects with complex interactions.
5.2. Future Work
To address these limitations, our future research will focus on several key directions:
- 1.
- Real-World Data Collection and Validation. We plan to establish collaborations with industrial partners to collect vibration data from operational machinery in real industrial environments. This will include data from various types of rotating equipment operating under diverse working conditions, with natural fault progression being captured rather than artificially induced defects.
- 2.
- Variable Operating Condition Adaptation. A major focus will be on developing adaptive mechanisms that can handle variable operating conditions. We intend to investigate domain adaptation techniques and transfer learning approaches to enhance the model’s robustness when faced with changing rotational speeds, varying loads, and different operational regimes.
By pursuing these research directions, we aim to bridge the gap between laboratory-based validation and real-world industrial application, ultimately developing more robust and practical solutions for rotating machinery fault diagnosis.
Author Contributions
Methodology, W.L. and H.C.; writing—original draft preparation, W.L.; writing—reviewing and editing, H.C., X.Y., Y.X., J.Y., and X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Longmen Laboratory Frontier Exploration Project (LMQYT367SKT022).
Data Availability Statement
All data that support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Z.; Wang, S.; Cheng, Y. Fault feature extraction of parallel-axis gearbox based on IDBO-VMD and t-SNE. Appl. Sci. 2023, 14, 289. [Google Scholar] [CrossRef]
- Jyothi, R.; Holla, T.; Uma, R.K.; Jayapal, R. Machine learning based multi class fault diagnosis tool for voltage source inverter driven induction motor. Int. J. Power Electron. Drive Syst. 2021, 12, 1205. [Google Scholar] [CrossRef]
- Ambrozkiewicz, B.; Litak, G.; Georgiadis, A.; Syta, A.; Meier, N.; Gassner, A. Effect of radial clearance on ball bearing’s dynamics using a 2-DOF model. Int. J. Simul. Model. 2021, 20, 513–524. [Google Scholar] [CrossRef]
- Song, B.; Liu, Y.; Fang, J.; Liu, W.; Zhong, M.; Liu, X. An optimized CNN-BiLSTM network for bearing fault diagnosis under multiple working conditions with limited training samples. Neurocomputing 2024, 574, 127284. [Google Scholar] [CrossRef]
- Jia, L.; Chow, T.W.S.; Yuan, Y. GTFE-Net: A gramian time frequency enhancement CNN for bearing fault diagnosis. Eng. Appl. Artif. Intell. 2023, 119, 105794. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnostics—A Review. In Proceedings of the 2019 IEEE 12th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Toulouse, France, 27–30 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 257–263. [Google Scholar] [CrossRef]
- Gabor, D. Theory of communication. Part 1: The analysis of information. J. Inst. Electr. Eng. Part III 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Schafer, R.W. Digital Process. Speech Signal; Prentice Hall: Englewood Cliffs, NJ, USA, 1978; pp. 121–123. [Google Scholar] [CrossRef]
- Xu, Y.G.; Wang, L.; Hu, A.J.; Yu, G. Time-extracting S-transform algorithm and its application in rolling bearing fault diagnosis. Sci. China Technol. Sci. 2022, 65, 93–942. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Imaging Time-Series to Improve Classification and Imputation. arXiv 2015, arXiv:1506.00327. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A New Deep Transfer Learning Based on Sparse Auto-Encoder for Fault Diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 136–144. [Google Scholar] [CrossRef]
- Campanharo, A.S.L.O.; Sirer, M.I.; Malmgren, R.D.; Ramos, F.M.; Amaral, L.A.N. Duality between Time Series and Networks. PLoS ONE 2011, 6, e23378. [Google Scholar] [CrossRef]
- Xin, G.; Li, Z.; Jia, L.; Zhong, Q.; Dong, H.; Hamzaoui, N.; Antoni, J. Fault Diagnosis of Wheelset Bearings in High-Speed Trains Using Logarithmic Short-Time Fourier Transform and Modified Self-Calibrated Residual Network. IEEE Trans. Ind. Inform. 2021, 18, 7285–7295. [Google Scholar] [CrossRef]
- Ribeiro Junior, R.F.; dos Santos Areias, I.A.; Campos, M.M.; Teixeira, C.E.; da Silva, L.E.B.; Gomes, G.F. Fault Detection and Diagnosis in Electric Motors Using Convolution Neural Network and Short-Time Fourier Transform. J. Vib. Eng. Technol. 2022, 10, 2531–2542. [Google Scholar] [CrossRef]
- Zhang, R.; Zeng, X. Bearing Fault Diagnosis Based on STFT-SWT and Two-Flow CNN-KNN. In Proceedings of the International Conference on Electronics, Electrical and Information Engineering (ICEEIE 2024), Xi’an, China, 4–6 January 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13445, pp. 430–436. [Google Scholar] [CrossRef]
- Tian, Z.; Zhang, X.; Yan, W.; Wang, J. Bearing Fault Diagnosis and Interpretation Based on 2D Images and Convolutional Neural Network. In Proceedings of the 2023 Asia Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Taipei, Taiwan, 31 October–3 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 2155–2162. [Google Scholar] [CrossRef]
- Yang, C.; Zheng, L.; Zheng, G.; Wang, J. Rolling Bearing Fault Diagnosis Method Based on GAF-MTF and Deep Residual Network. In Proceedings of the 2024 IEEE International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Taiyuan, China, 2–4 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 106–111. [Google Scholar] [CrossRef]
- Guo, L.; Tang, J. Fault Diagnosis of Rolling Bearings Based on MTF-TLResNet34. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 4714–4719. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, L.; Huang, Q. Bearing Fault Diagnosis Based on Multi-Channel GAF-MTF and Res2Net. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 5321–5327. [Google Scholar] [CrossRef]
- Liu, J.; Tan, Y.; Yang, N.; Gao, Y.; Zhao, W.Q. An Anti-Noise Bearing’s Fault Diagnosis Method Using Adaptive Deconvolution and Mobile ViT. IEEE Sens. J. 2024, 24, 12345–12355. [Google Scholar] [CrossRef]
- Xue, L.; Lei, C.; Jiao, M.; Shi, J.; Li, J. Rolling Bearing Fault Diagnosis Method Based on Self-Calibrated Coordinate Attention Mechanism and Multi-Scale Convolutional Neural Network under Small Samples. IEEE Sens. J. 2023, 23, 10206–10214. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 2002, 36, 961–1005. [Google Scholar] [CrossRef]
- Peng, Z.K.; Chu, F.L. Application of the wavelet transform in machine condition monitoring and fault diagnostics: A review with bibliography. Mech. Syst. Signal Process. 2004, 18, 199–221. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Wang, S.; Li, W.; Sarkodie-Gyan, T.; Feng, S. A Hybrid Deep-Learning Model for Fault Diagnosis of Rolling Bearings. Measurement 2021, 169, 108502. [Google Scholar] [CrossRef]
- Diao, N.; Wang, Z.; Ma, H.; Yang, W. Fault Diagnosis of Rolling Bearing under Variable Working Conditions Based on CWT and T-ResNet. J. Vib. Eng. Technol. 2023, 11, 3747–3757. [Google Scholar] [CrossRef]
- Jia, G.-w.; Shi, H.-s.; Lv, H.-j.; Zhang, P.-y.; Xu, W.-q.; Cai, M. Bearing Fault Diagnosis Method Based on CWT-ResNet18. In Proceedings of the 2023 9th International Conference on Fluid Power and Mechatronics (FPM), Wuhan, China, 9–11 August 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Guo, Y.; Zhou, J.; Dong, Z.; She, H.; Xu, W. Research on Bearing Fault Diagnosis Based on Novel MRSVD-CWT and Improved CNN-LSTM. Meas. Sci. Technol. 2024, 35, 095003. [Google Scholar] [CrossRef]
- Jiang, L.; Shi, C.; Sheng, H.; Li, X.; Yang, T. Lightweight CNN architecture design for rolling bearing fault diagnosis. Meas. Sci. Technol. 2024, 35, 126142. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, B.; Gao, D. Bearing fault diagnosis base on multi-scale CNN and LSTM model. J. Intell. Manuf. 2021, 32, 971–987. [Google Scholar] [CrossRef]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Sinitsin, V.; Ibryaeva, O.; Sakovskaya, V.; Eremeeva, V. Intelligent bearing fault diagnosis method combining mixed input and hybrid CNN-MLP model. Mech. Syst. Signal Process. 2022, 180, 109454. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.; Zheng, Y.; Jiang, W.; Zhang, Y. Fault diagnosis of rolling bearings with recurrent neural network-based autoencoders. ISA Trans. 2018, 77, 167–178. [Google Scholar] [CrossRef]
- Jiang, H.; Li, X.; Shao, H.; Zhao, K. Intelligent fault diagnosis of rolling bearings using an improved deep recurrent neural network. Meas. Sci. Technol. 2018, 29, 065107. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Y.F.; Huang, H.Z.; Deng, Z.; Huang, Z. A novel method based on CNN-BiGRU and AM model for bearing fault diagnosis. J. Mech. Sci. Technol. 2024, 38, 3361–3369. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Lu, L.; Cong, S. Rolling Bearing Fault Diagnosis Based on Transfer Learning and Dual-Channel CNN and BiGRU. In Proceedings of the 2024 International Conference on Advanced Robotics and Mechatronics (ICARM), Tokyo, Japan, 8–10 July 2024; pp. 819–824. [Google Scholar] [CrossRef]
- Ren, Y.; Lu, R.; Yuan, G.; Hao, D.; Li, H. Attention-Based Spatiotemporal-Aware Network for Fine-Grained Visual Recognition. Appl. Sci. 2024, 14, 7755. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).