Rotation-Angle Solution and Singularity Handling of Five-Axis Machine Tools for Dual NURBS Interpolation
Abstract
1. Introduction
2. Rotation-Angle Solution of Five-Axis Machine Tools for Dual NURBS Interpolation
2.1. Dual NURBS Interpolation
2.2. Generic Method of Rotation-Angle Solution of Five-Axis Machine Tools
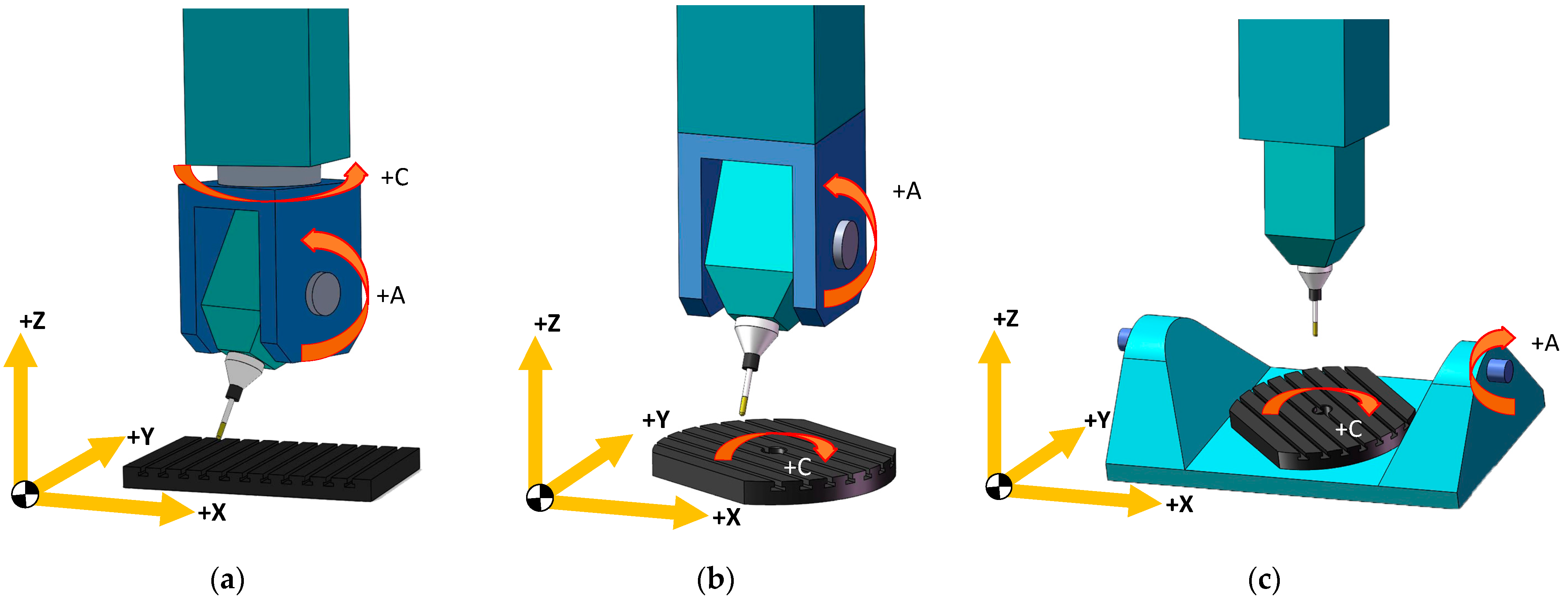
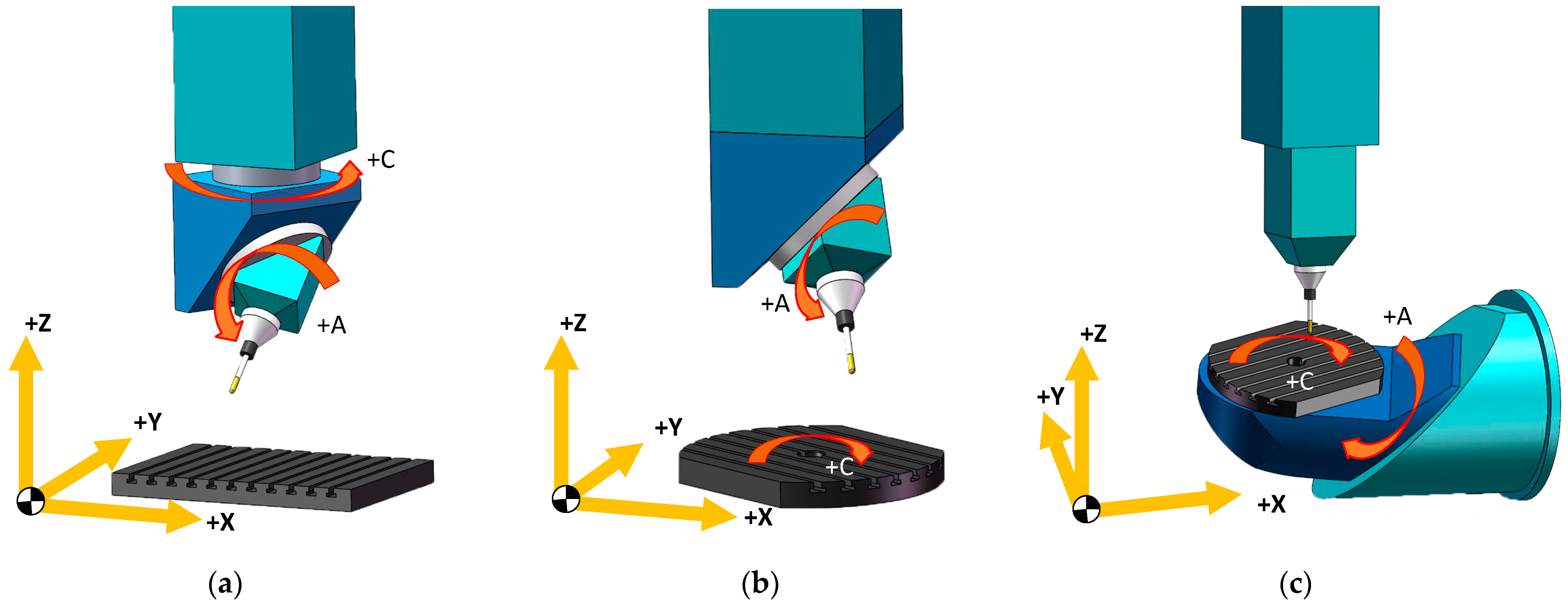
2.2.1. Typical Layouts of Rotary Axes of Five-Axis Machine Tools and Analysis
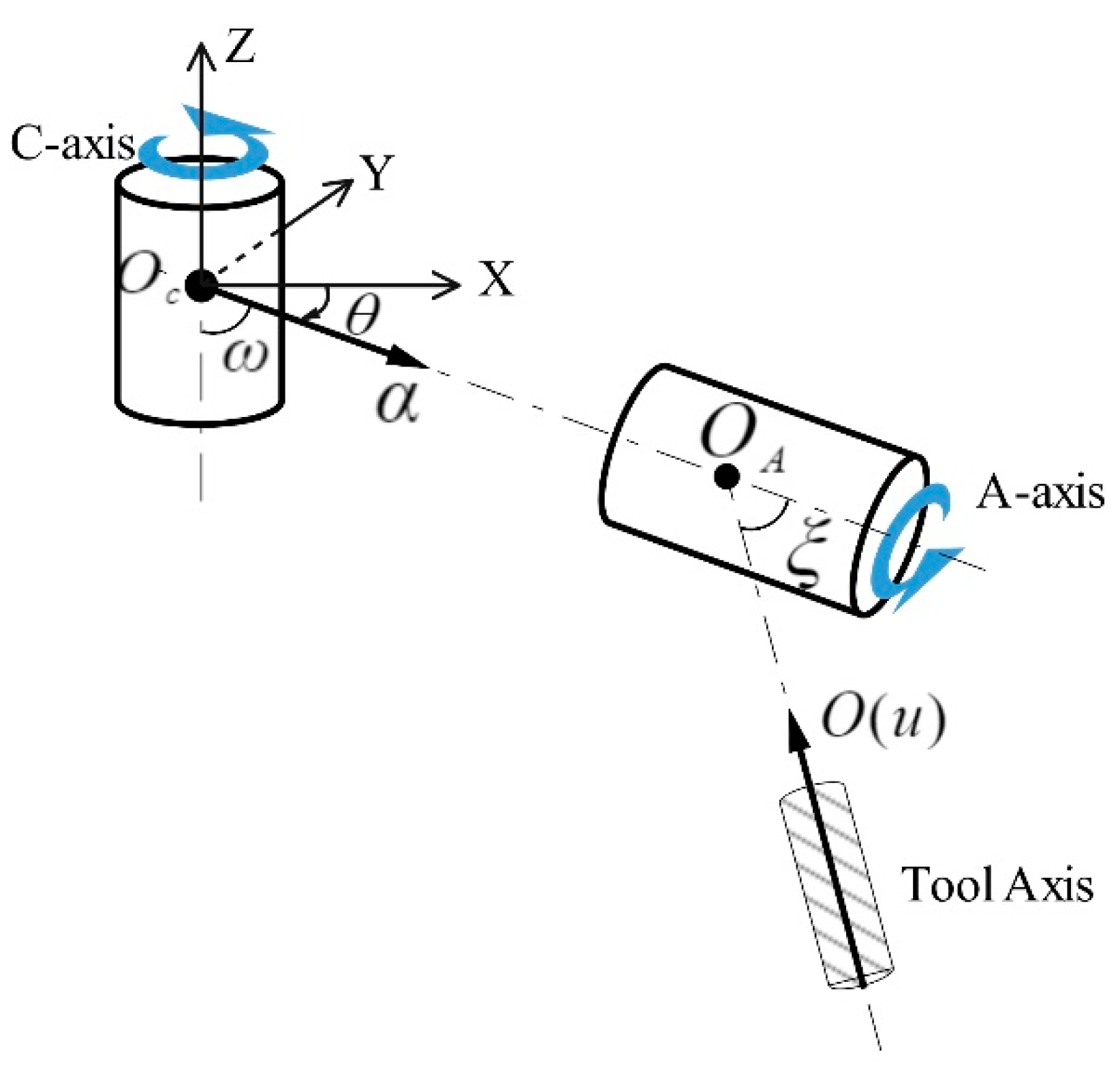
2.2.2. Generic Method for Solving the Rotation Angles of Five-Axis Machine Tools Based on the Vector Inner Product
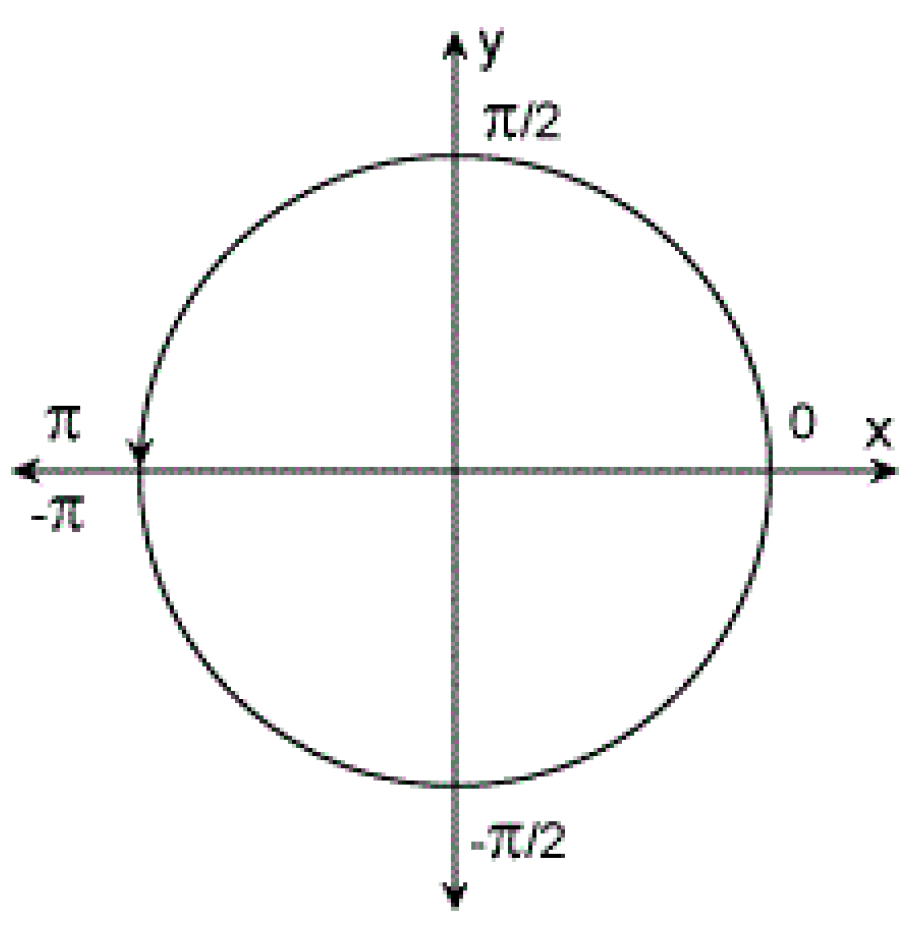
2.3. Solution Space of the Generic Method
- (a)
- No solution. The tool orientation vector cannot be realized by rotation axes as the tool orientation vector is beyond the reach of the machine tool when .
- (b)
- Finite solutions. The C-axis angle has two sets of solutions when and , as shown in Equation (13). The rotation angles are high-order continuous with respect to the parameter u, when the tool orientation vector is high-order continuous.
- (c)
- Infinite solutions. The C-axis angle has infinite sets of solutions when . The tool orientation vector is at the singularity point, which cannot be changed no matter the C-axis angle. The tool orientation and the layout of rotation axes must meet the following conditions.
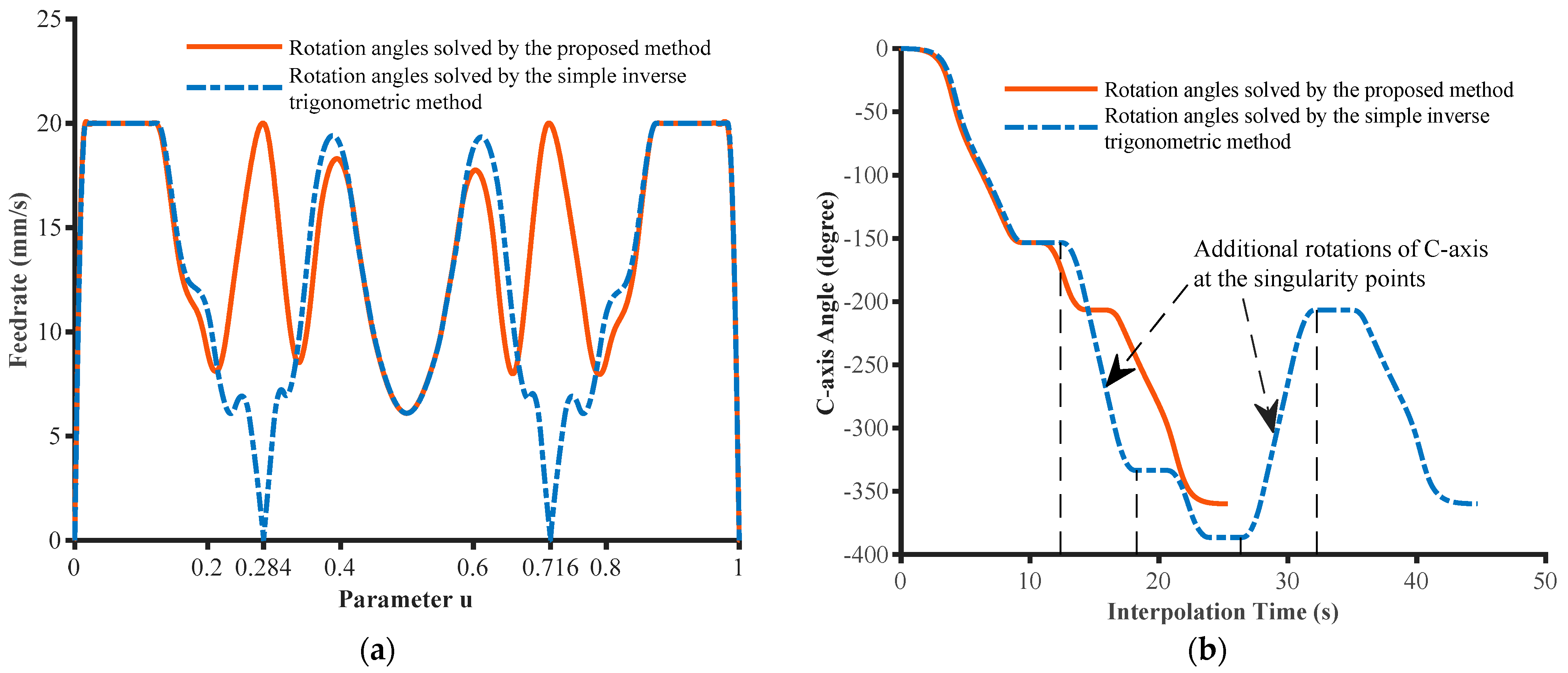
2.4. Singularity Handling
3. Experiments and Discussions
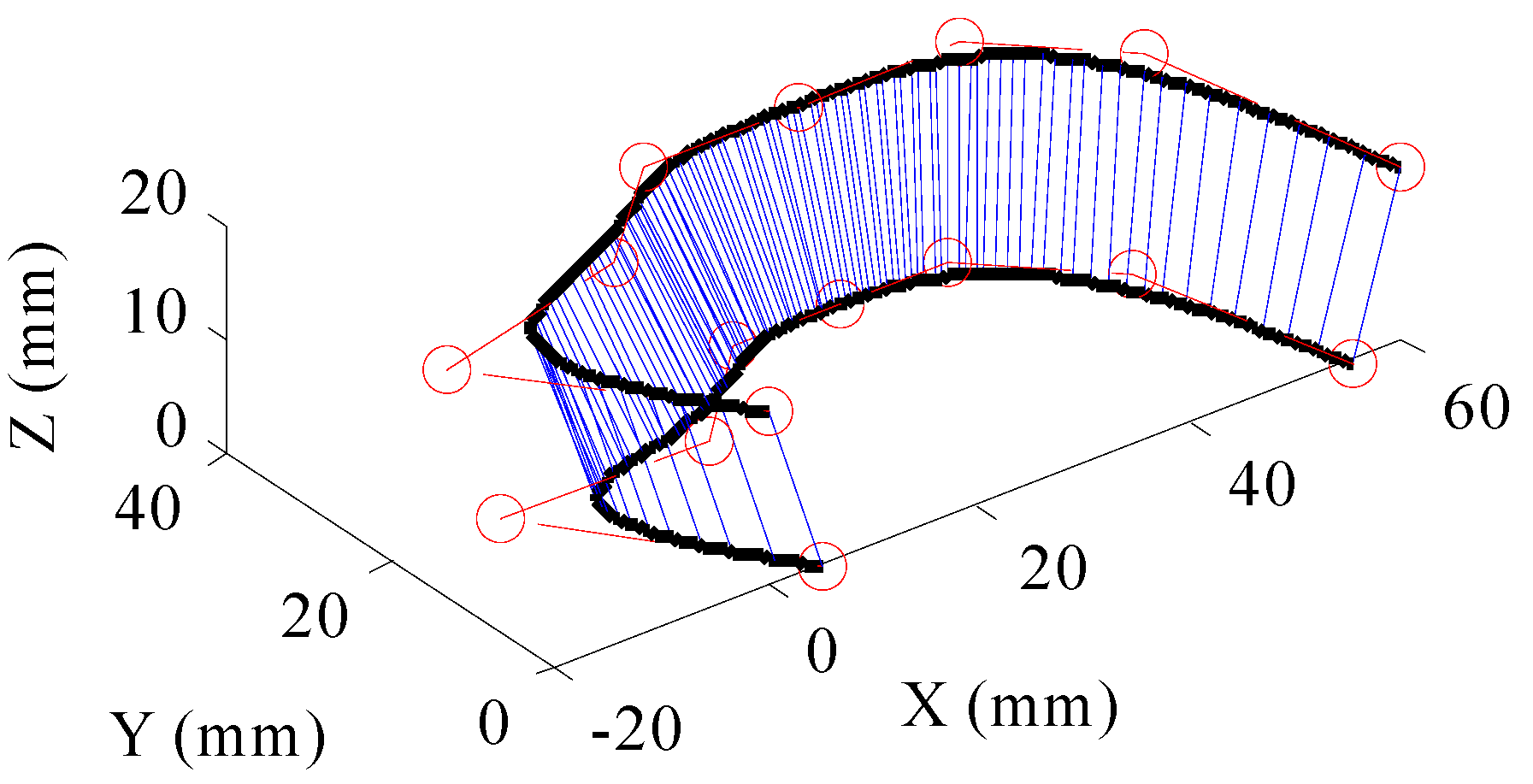
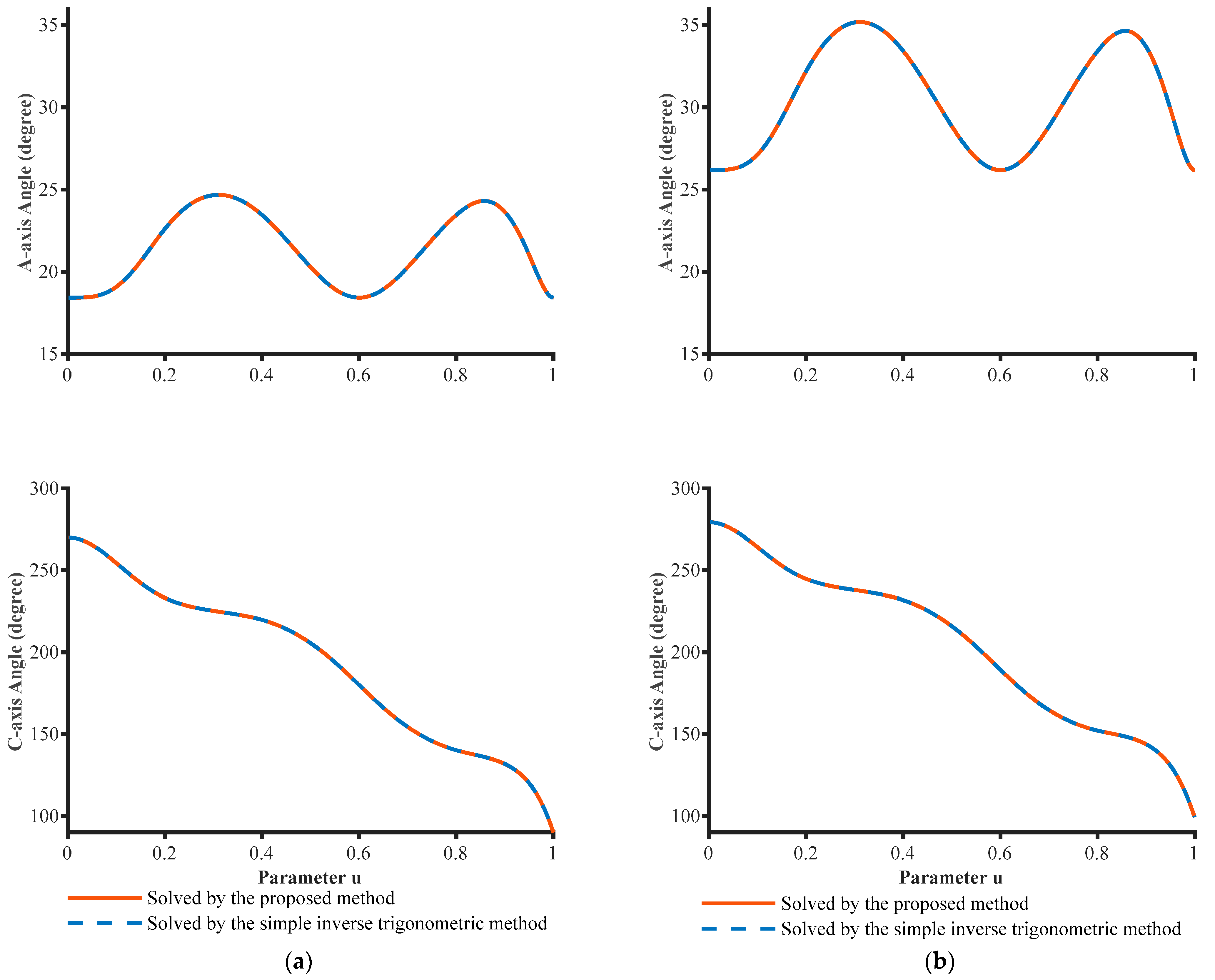
3.1. Experiment on an Open-Pocket Tool Path
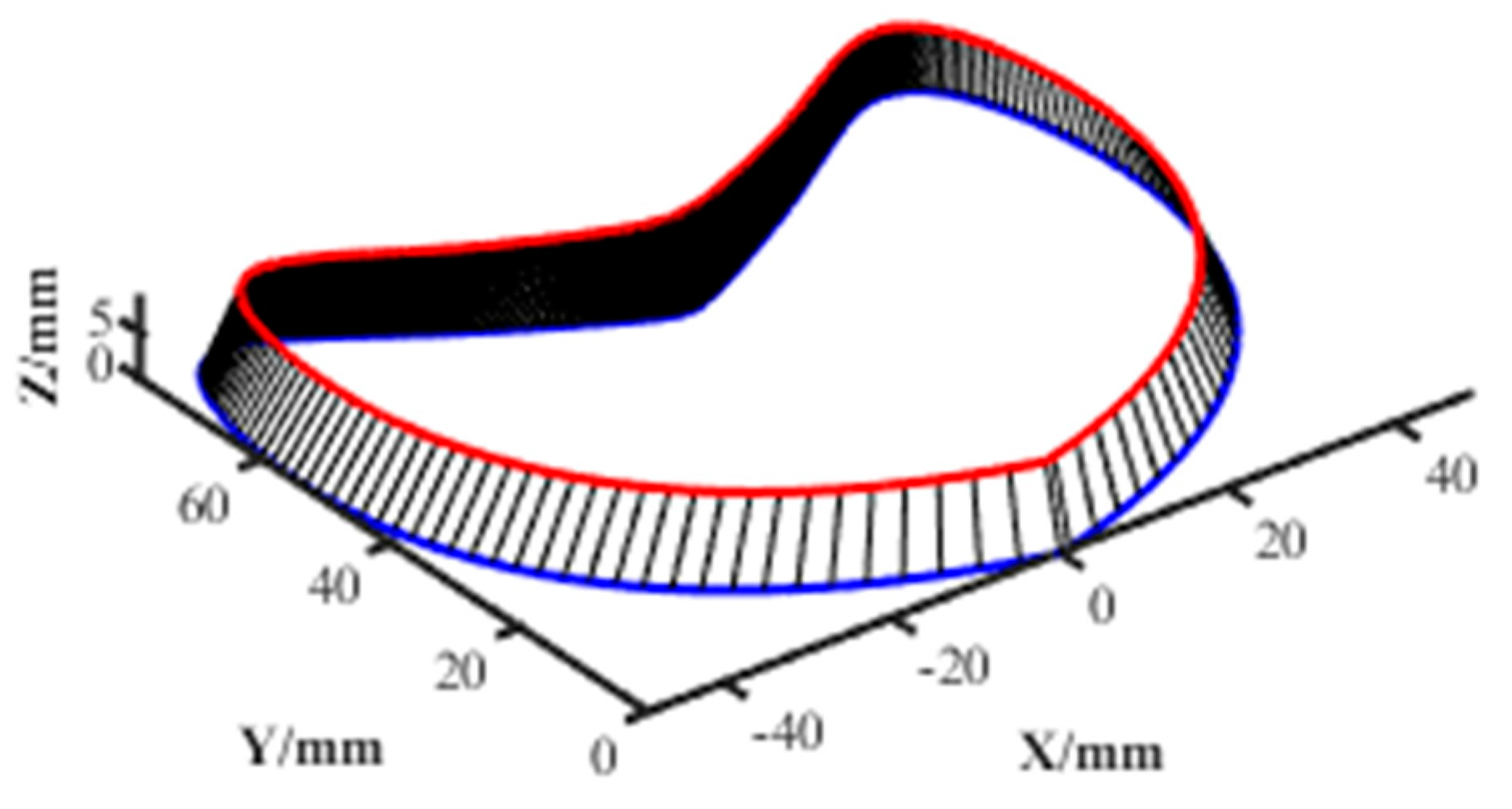
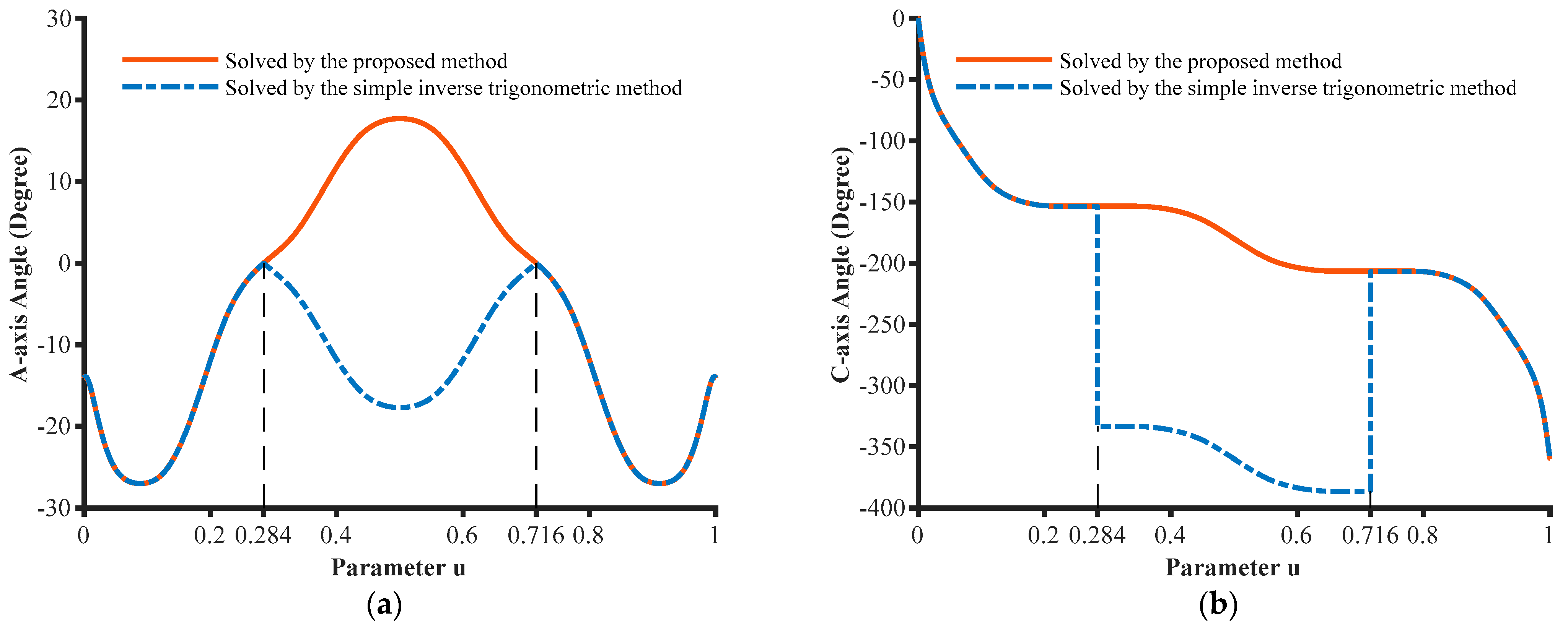
3.2. Experiment on a Cardioid Curve
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Values |
|---|---|
| NURBS Degree | 3 |
| Knot Vector | (0, 0, 0, 0, 0.2, 0.4, 0.6, 0.8, 1, 1, 1, 1) |
| Weight Vector | (1, 1, 1, 1, 1, 1, 1, 1) |
| Control Points of the Tool Tip Point Curve | (5,0,0), (−10,20,0), (10,20,0), (20,30,0), (30,30,0), (40,30,0), (50,20,0), (55,0,0) |
| Control Points of the Tool Axis Point Curve | (0,0,15), (−15,20,15), (5,25,15), (15,35,15), (30,35,15), (45,35,15), (55,25,15), (60,0,15) |
Appendix B
| Parameters | Values |
|---|---|
| NURBS Degree | 3 |
| Knot Vector | (0, 0, 0, 0, 1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, 1, 1, 1, 1) |
| Weight Vector | (1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1) |
| Control Points of the Tool Tip Point Curve | (0,0,0), (−51,13.5,0), (−51,87,0), (−30,75,0), (−22.5,69,0), (−1.5,57,0),(1.5,57,0), (22.5,69,0), (30,75,0), (51,87,0), (51,13.5,0), (0,0,0) |
| Control Points of the Tool Axis Point Curve | (0,2.25,9), (−45,15,9), (−48,81,9), (−30,75,9), (−22.5,69,9), (−3,60,9),(3,60,9), (22.5,69,9), (30,75,9), (48,81,9), (45,15,9), (0,2.25,9) |
References
- Li, D.D.; Zhang, W.M.; Zhou, W.; Shang, T.F.; Fleischer, J. Dual NURBS Path Smoothing for 5-Axis Linear Path of Flank Milling. Int. J. Precis. Eng. Man. 2018, 19, 1811–1820. [Google Scholar] [CrossRef]
- Sun, Y.; Bao, Y.; Kang, K.; Guo, D. An adaptive feedrate scheduling method of dual NURBS curve interpolator for precision five-axis CNC machining. Int. J. Adv. Manuf. Technol. 2013, 68, 1977–1987. [Google Scholar] [CrossRef]
- Xu, J.T.; Zhang, D.Y.; Sun, Y.W. Kinematics performance oriented smoothing method to plan tool orientations for 5-axis ball-end CNC machining. Int. J. Mech. Sci. 2019, 157, 293–303. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Watanabe, T. Generation of 5-axis control collision-free tool path and postprocessing for NC data. CIRP Ann. 1992, 41, 539–542. [Google Scholar] [CrossRef]
- Lee, R.; She, C. Developing a postprocessor for three types of five-axis machine tools. Int. J. Adv. Manuf. Technol. 1997, 13, 658–665. [Google Scholar] [CrossRef]
- Mahbubur, R.; Heikkala, J.; Lappalainen, K.; Karjalainen, J.A. Positioning accuracy improvement in five-axis milling by post processing. Int. J. Mach. Tools Manuf. 1997, 37, 223–236. [Google Scholar] [CrossRef]
- She, C.; Chang, C. Development of a five-axis postprocessor system with a nutating head. J. Mater Process. Tech. 2007, 187, 60–64. [Google Scholar] [CrossRef]
- She, C.; Huang, Z. Postprocessor development of a five-axis machine tool with nutating head and table configuration. Int. J. Adv. Manuf. Technol. 2008, 38, 728–740. [Google Scholar] [CrossRef]
- She, C.; Chang, C. Design of a generic five-axis postprocessor based on generalized kinematics model of machine tool. Int. J. Mach. Tools Manuf. 2007, 47, 537–545. [Google Scholar] [CrossRef]
- Peng, Y.; Ma, J.; Wang, L.; Yan, R.; Li, B. Post-processing Algorithm Based on Total Differential Method for Multi-axis Machine Tools with Arbitrary Configuration. J. Mech. Eng. 2012, 48, 121–126. [Google Scholar] [CrossRef]
- Li, Z. Research and Application on Kinematic Generic Modeling Theory for Five-Axis; Southwest Jiaotong University: Chengdu, China, 2013. [Google Scholar] [CrossRef]
- He, Y.X.; Xu, Q.H.; Zhou, Y.H. Kinematics model and its solution for NC machines of arbitrary configuration. J. Mech. Eng. 2002, 38, 31–36. [Google Scholar] [CrossRef]
- Tan, G.Z.; Chen, H.R.; Dai, Y.X. Study on Kinematics Analysis and Non-Linear Error of a TATC Five-Axis Machine Tool. Mach. Des. Manuf. 2018, 332, 229–232. [Google Scholar] [CrossRef]
- My, C.A.; Bohez, E. A novel differential kinematics model to compare the kinematic performances of 5-axis CNC machines. Int. J. Mech. Sci. 2019, 163, 105–117. [Google Scholar] [CrossRef]
- Xu, R.F.; Cheng, X.; Zheng, G.M.; Chen, Z.T. A tool orientation smoothing method based on machine rotary axes for five-axis machining with ball end cutters. Int. J. Adv. Manuf. Tech. 2017, 92, 3615–3625. [Google Scholar] [CrossRef]
- Liu, Y.; Wan, M.; Xing, W.J.; Xiao, Q.B.; Zhang, W.H. Generalized actual inverse kinematic model for compensating geometric errors in five-axis machine tools. Int. J. Mech. Sci. 2018, 145, 299–317. [Google Scholar] [CrossRef]
- Farouki, R.T.; Han, C.Y.; Li, S.Q. Inverse kinematics for optimal tool orientation control in 5-axis CNC machining. Comput. Aided. Geom. D 2014, 31, 13–26. [Google Scholar] [CrossRef]
- Lin, T.K.; Lin, A.C. Conversion CL data to NC data using an instinctive method for non-orthogonal table-type 5 axis machines. In Mechatronics and Applied Mechanics II, Pts 1 and 2; 2nd International Conference on Mechatronics and Applied Mechanics (ICMAM2012); Wang, C.K., Guo, J., Eds.; Trans Tech Publications Ltd.: Bach, Switzerland, 2013; Volume 300–301, pp. 232–235. [Google Scholar]
- Yu, D.; Yan, G.R.; Fan, Q.X.; Ding, T.; Xu, X.Y. Research on Optimization of Rotation Angle and Singular Area Handling in Five-Axis Post-Processing. J. Graph. 2016, 37, 614–619. [Google Scholar] [CrossRef]
- Hong, X.Y.; Hong, R.J.; Lin, X.C. Analysis and optimization of singular problem in five-axis machining. J. Nanjing Univ. Technol. (Nat. Sci. Ed.) 2021, 43, 58–64. [Google Scholar] [CrossRef]
- Beudaert, X.; Lavernhe, S.; Tournier, C. Feedrate interpolation with axis jerk constraints on 5-axis NURBS and G1 tool path. Int. J. Mach. Tools Manuf. 2012, 57, 73–82. [Google Scholar] [CrossRef]
- Lu, Y.A.; Wang, C.Y. Smoothing method of generating flank milling tool paths for five-axis flat-end machining considering constraints. Int. J. Adv. Manuf. Tech. 2020, 110, 3295–3309. [Google Scholar] [CrossRef]
- Castagnetti, C.; Duc, E.; Ray, P. The Domain of Admissible Orientation concept: A new method for five-axis tool path optimisation. Comput. Aided. Design 2008, 40, 938–950. [Google Scholar] [CrossRef]
- Wang, Q.R.; Feng, Y.X.; Zhang, Z.X.; Tan, J.R. Tool orientation sequence smoothing method based on the discrete domain of feasible orientations. Int. J. Adv. Manuf. Tech. 2017, 92, 4501–4510. [Google Scholar] [CrossRef]
- Hu, P.C.; Tang, K. Improving the dynamics of five-axis machining through optimization of workpiece setup and tool orientations. Comput. Aided. Design 2011, 43, 1693–1706. [Google Scholar] [CrossRef]
- Sorby, K. Inverse kinematics of five-axis machines near singular configurations. Int. J. Mach. Tools Manuf. 2007, 47, 299–306. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Q.; Sun, P.P.; Liu, Q.T.; Yuan, S.M. The optimal feedrate planning on five-axis parametric tool path with geometric and kinematic constraints for CNC machine tools. Int. J. Prod. Res. 2017, 55, 3715–3731. [Google Scholar] [CrossRef]



| Conditions of the Tool Orientation | Equation of the Rotation Angle | Solutions |
|---|---|---|
| … | … | … |
| Axis | Maximum Velocity (Unit/s) | Maximum Acceleration (Unit/s2) | Maximum Jerk (Unit/s3) |
|---|---|---|---|
| X/Y/Z (mm) | 100 | 500 | 3000 |
| A (degree) | 22.9 | 28.6 | 85.9 |
| C (degree) | 45.8 | 28.6 | 85.9 |
| Maximum Chord Error (mm) | 0.125 | ||
| Interpolation Cycle Time (s) | 0.002 | ||
| Feedrate (mm/s) | Spindle Speed (rpm) | Cutting Depth (mm) | Cutting Width (mm) |
|---|---|---|---|
| 20 | 6000 | 9 | 0.2 |
| Method | Ra (μm) | Rq (μm) | Rz (μm) |
|---|---|---|---|
| The proposed method | 1.26 | 1.55 | 6.89 |
| The simple inverse trigonometric method | 5.67 | 7.48 | 33.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Liu, Q.; Wang, J.; Yin, Z.; Wang, L. Rotation-Angle Solution and Singularity Handling of Five-Axis Machine Tools for Dual NURBS Interpolation. Machines 2023, 11, 281. https://doi.org/10.3390/machines11020281
Sun P, Liu Q, Wang J, Yin Z, Wang L. Rotation-Angle Solution and Singularity Handling of Five-Axis Machine Tools for Dual NURBS Interpolation. Machines. 2023; 11(2):281. https://doi.org/10.3390/machines11020281
Chicago/Turabian StyleSun, Pengpeng, Qiang Liu, Jian Wang, Zhenshuo Yin, and Liuquan Wang. 2023. "Rotation-Angle Solution and Singularity Handling of Five-Axis Machine Tools for Dual NURBS Interpolation" Machines 11, no. 2: 281. https://doi.org/10.3390/machines11020281
APA StyleSun, P., Liu, Q., Wang, J., Yin, Z., & Wang, L. (2023). Rotation-Angle Solution and Singularity Handling of Five-Axis Machine Tools for Dual NURBS Interpolation. Machines, 11(2), 281. https://doi.org/10.3390/machines11020281





