A Novel Rolling Bearing Fault Diagnosis Method Based on BLS and CNN with Attention Mechanism
Abstract
:1. Introduction
2. Related Work
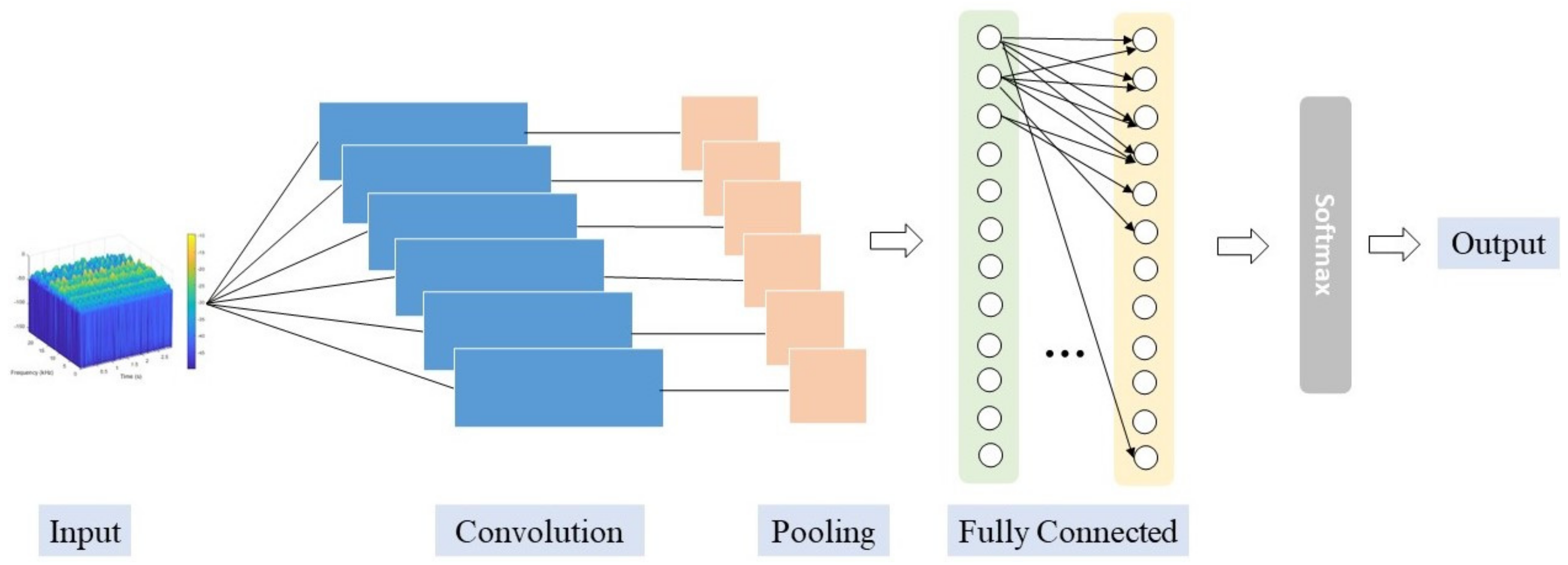
2.1. Convolutional Neural Network (CNN)
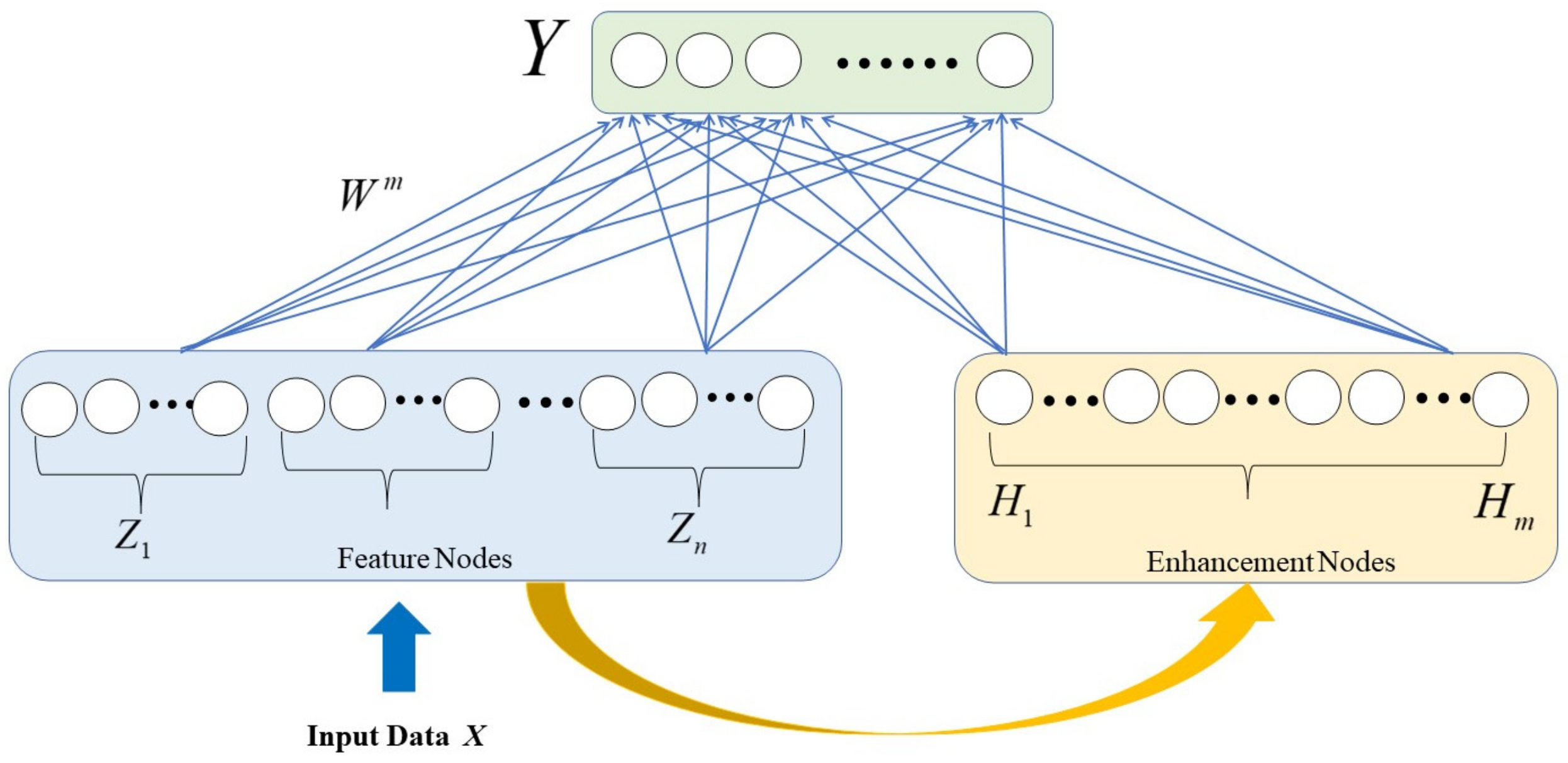
2.2. Broad Learning System (BLS)
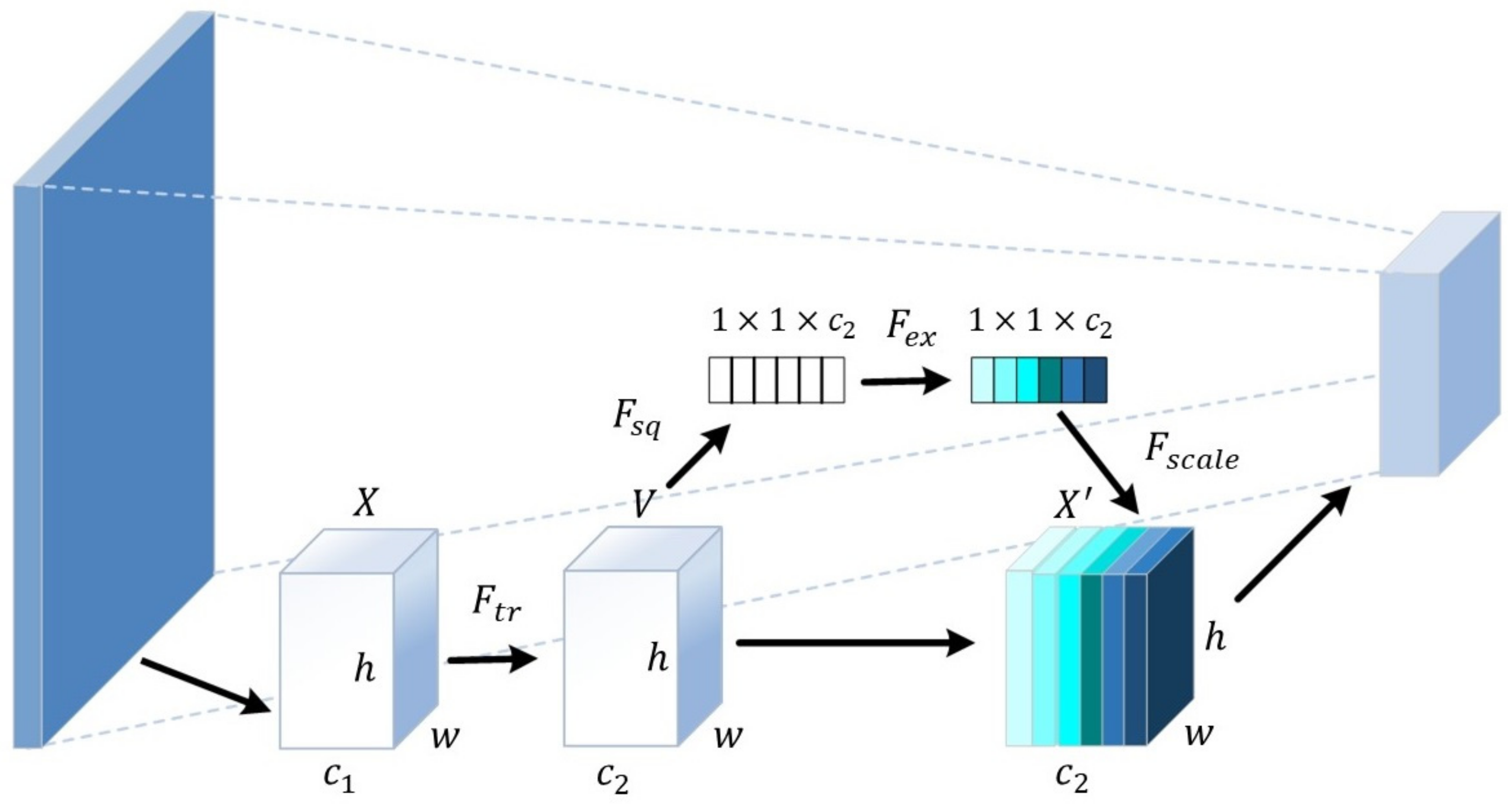
2.3. Attention Mechanism
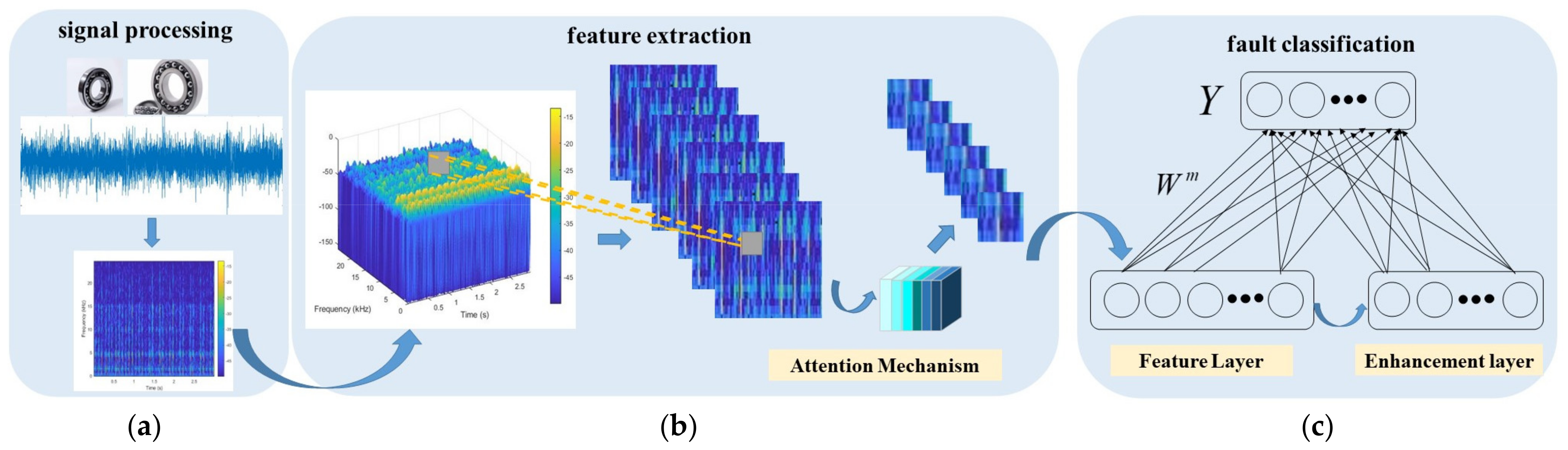
3. The Proposed SECNN–BLS Framework
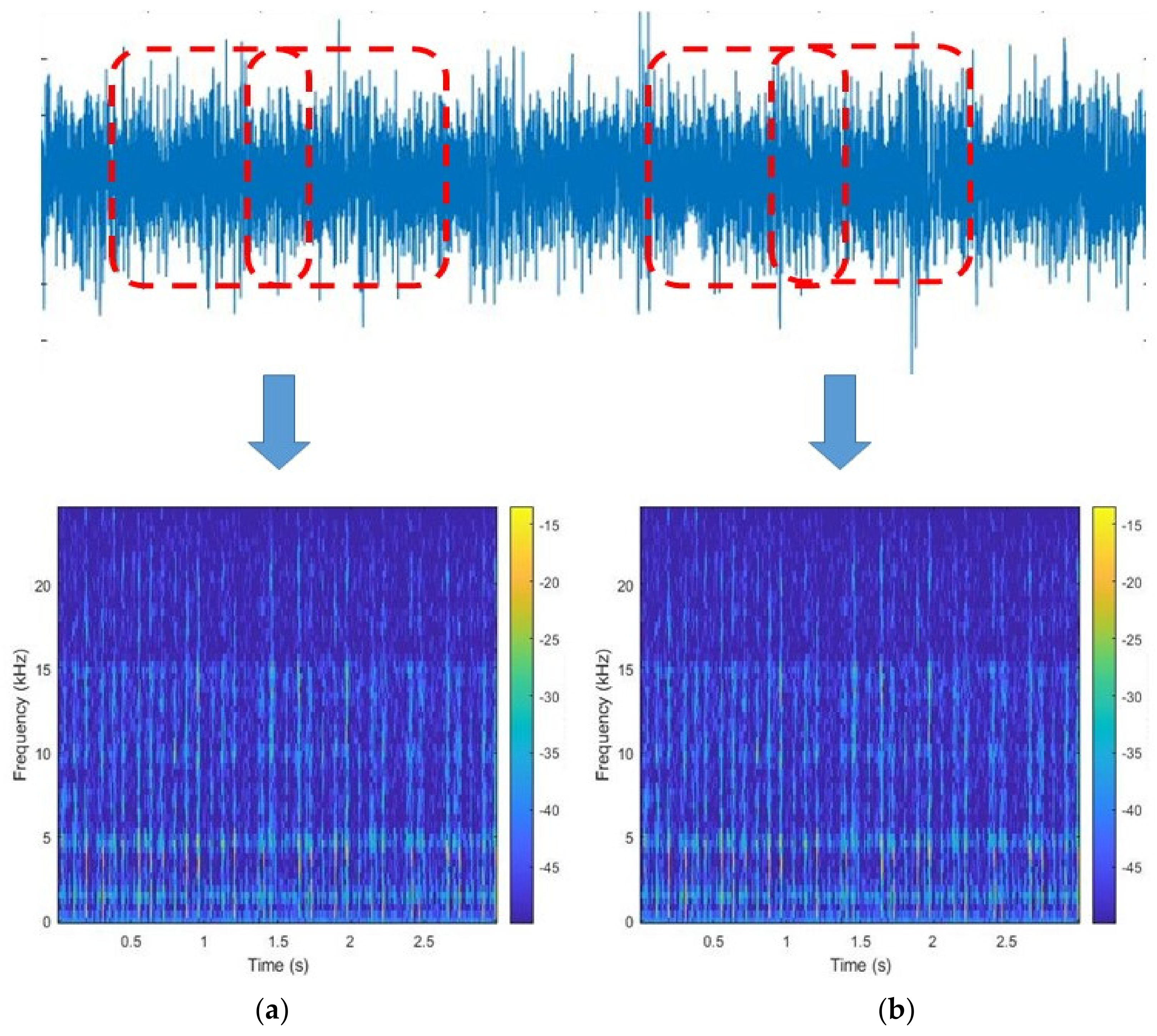
3.1. Vibration Signal Processing
3.2. Feature Extraction Based on the SECNN
3.3. Fault Diagnosis Based on the SECNN–BLS
4. Experiment
4.1. Data Description
4.2. Analysis of Experimental Results
4.3. Performance under Additional Noise Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, G.; Hu, Z. Bearing fault diagnosis based on multi-scale mean permutation entropy and parametric optimization SVM. J. Vib. Shock. 2022, 41, 221–228. [Google Scholar]
- Zhang, J.; Wu, J.; Hu, B. Intelligent fault diagnosis of rolling bearings using variational mode decomposition and self-organizing feature map. J. Vib. Control. 2020, 26, 1886–1897. [Google Scholar] [CrossRef]
- Tang, S.; He, J.; Ren, J. Research on fault diagnosis of rolling bearing based on the improved EWT method of spectral envelope. Renew. Energy 2022, 40, 825. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, Y.; Yi, C. Sparsity guided empirical wavelet transform for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2018, 101, 292–308. [Google Scholar] [CrossRef]
- Guo, T.; Deng, Z. An improved EMD method based on the multi-objective optimization and its application to fault feature extraction of rolling bearing. Appl. Acoust. 2017, 127, 46–62. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Miao, Q. Complete ensemble local mean decomposition with adaptive noise and its application to fault diagnosis for rolling bearings. Mech. Syst. Signal Process. 2018, 106, 24–39. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Xiong, J.; Xiao, M.; Sun, G.; He, J. Fault Diagnosis of a Rolling Bearing Using Wavelet Packet Denoising and Random Forests. IEEE Sens. J. 2017, 17, 5581–5588. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, B.; Yang, T.; Yu, D.; Gao, W. Multitask Convolutional Neural Network with Information Fusion for Bearing Fault Diagnosis and Localization. IEEE Trans. Ind. Electron. 2020, 67, 8005–8015. [Google Scholar] [CrossRef]
- Gao, S.; Shi, S.; Zhang, Y. Rolling Bearing Compound Fault Diagnosis Based on Parameter Optimization MCKD and Convolutional Neural Network. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Peng, D.; Qin, Y. Understanding and Learning Discriminant Features based on Multiattention 1DCNN for Wheelset Bearing Fault Diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 5735–5745. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault diagnosis of rolling bearings using an Improved Multi-Scale Convolutional Neural Network with Feature Attention mechanism. ISA Trans. 2021, 110, 379–393. [Google Scholar] [CrossRef]
- Chen, L.P.; Liu, Z.L. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Han, M.; Chen, L.P.; Qiu, T. Recurrent Broad Learning Systems for Time Series Prediction. IEEE Trans. Cybern. 2020, 50, 1405–1417. [Google Scholar] [CrossRef]
- Yu, W.K.; Zhao, C.H. Broad Convolutional Neural Network Based Industrial Process Fault Diagnosis with Incremental Learning Capability. IEEE Trans. Ind. Electron. 2020, 67, 5081–5091. [Google Scholar] [CrossRef]
- Chen, L.P.; Liu, Z.L.; Feng, S. Universal Approximation Capability of Broad Learning System and Its Structural Variations. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1191–1204. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Cao, H.; Chen, X. Adaptive Broad Learning System for High-Efficiency Fault Diagnosis of Rotating Machinery. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, W.J.; Chen, H.T.; Zhang, B.C.; Shao, J.J.; Teng, W.X. Enhanced Fault Diagnosis Using Broad Learning for Traction Systems in High-Speed Trains. IEEE Trans. Power Electron. 2021, 36, 7461–7469. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the 2018 IEEE CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Yu, S.-S.; Zhou, N.-R.; Gong, L.-H.; Nie, Z. Optical image encryption algorithm based on phase-truncated short-time fractional Fourier transform and hyper-chaotic system. Opt. Lasers Eng. 2020, 124, 105816. [Google Scholar] [CrossRef]
- Sun, G.; Gao, Y.; Lin, K.; Hu, Y. Fine-grained fault diagnosis method of rolling bearing combining multisynchrosqueezing transform and sparse feature coding based on dictionary learning. Shock. Vib. 2019, 2019, 1531079. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, S.; Geng, B. Refined composite multiscale fluctuation-based dispersion Lempel–Ziv complexity for signal analysis. ISA Trans. 2022, in press. [Google Scholar] [CrossRef]
- Verstraete, D.; Ferrada, A.; Lopez Droguett, E.; Meruane, V.; Modarres, M. Deep learning enabled fault diagnosis using time-frequency image analysis of rolling element bearings. Shock Vib. 2017, 2017, 5067651. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, J.; Gu, X.; Ling, D.; Yu, H. Multi-scale attention mechanism residual neural network for fault diagnosis of rolling bearings. Proc. Inst. Mech. Eng. 2022, 236, 10615–10629. [Google Scholar] [CrossRef]
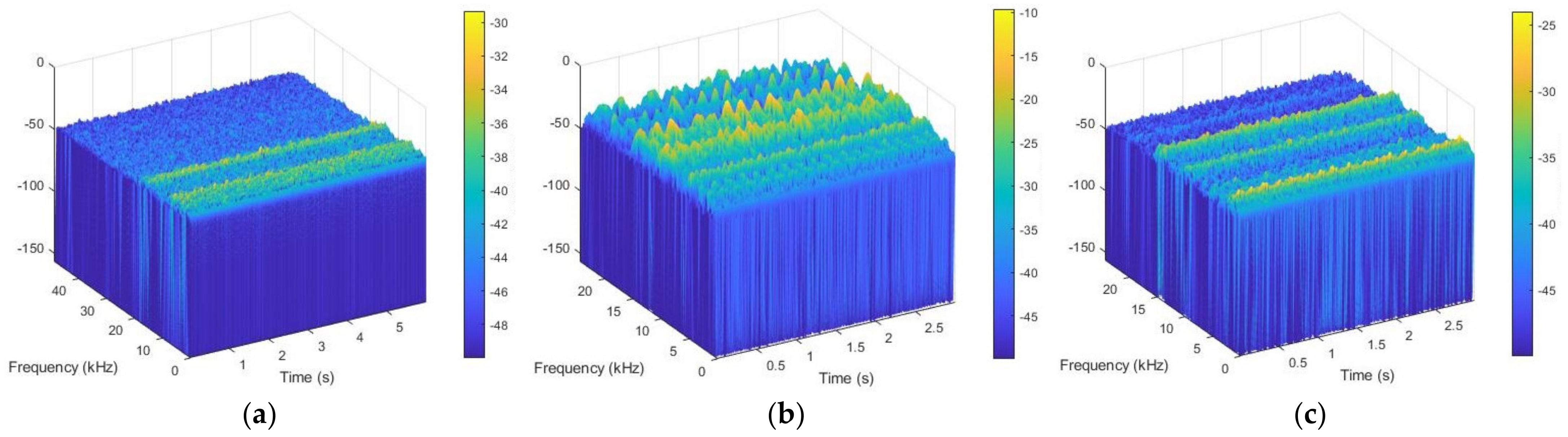

| Fault Condition | Label | Load (lbs) | Input Shaft Rate (Hz) | Sample Rate (sps) | Time (s) | Number of Data Points | Number of Training Samples | Number of Testing Samples |
|---|---|---|---|---|---|---|---|---|
| Baseline | B-1, B-2, B-3 | 270 | 25 | 97,656 | 6 | 585,936 | 194 | 97 |
| Outer Race Fault | O-1, O-2, O-3 | 270 | 25 | 97,656 | 6 | 585,936 | 534 | 267 |
| O-4, O-5, O-6, O-7, O-8, O-9, O-10 | 25, 50, 100, 150, 200, 250, 300 | 25 | 48,828 | 3 | 146,484 × 7 | |||
| Inner Race Fault | I-1, I-2, I-3, I-4, I-5, I-6, I-7 | 0, 50, 100, 150, 200, 250, 300 | 25 | 48,828 | 3 | 146,484 × 7 | 340 | 170 |
| Label | Precision | Recall | F1-Score | AU-ROC | Accuracy |
|---|---|---|---|---|---|
| O-1 | 99.74% | 90.65% | 94.98% | 95.50% | 99.74% |
| O-2 | 96.51% | 97.66% | 97.08% | 95.15% | 96.51% |
| O-3 | 97.17% | 97.43% | 97.30% | 95.15% | 97.17% |
| O-4 | 99.92% | 94.21% | 96.98% | 95.30% | 99.92% |
| O-5 | 97.90% | 93.39% | 95.59% | 95.35% | 97.90% |
| O-6 | 98.94% | 95.60% | 97.24% | 95.25% | 98.94% |
| O-7 | 97.17% | 97.50% | 97.34% | 95.15% | 97.17% |
| O-8 | 96.20% | 96.13% | 96.17% | 95.20% | 96.20% |
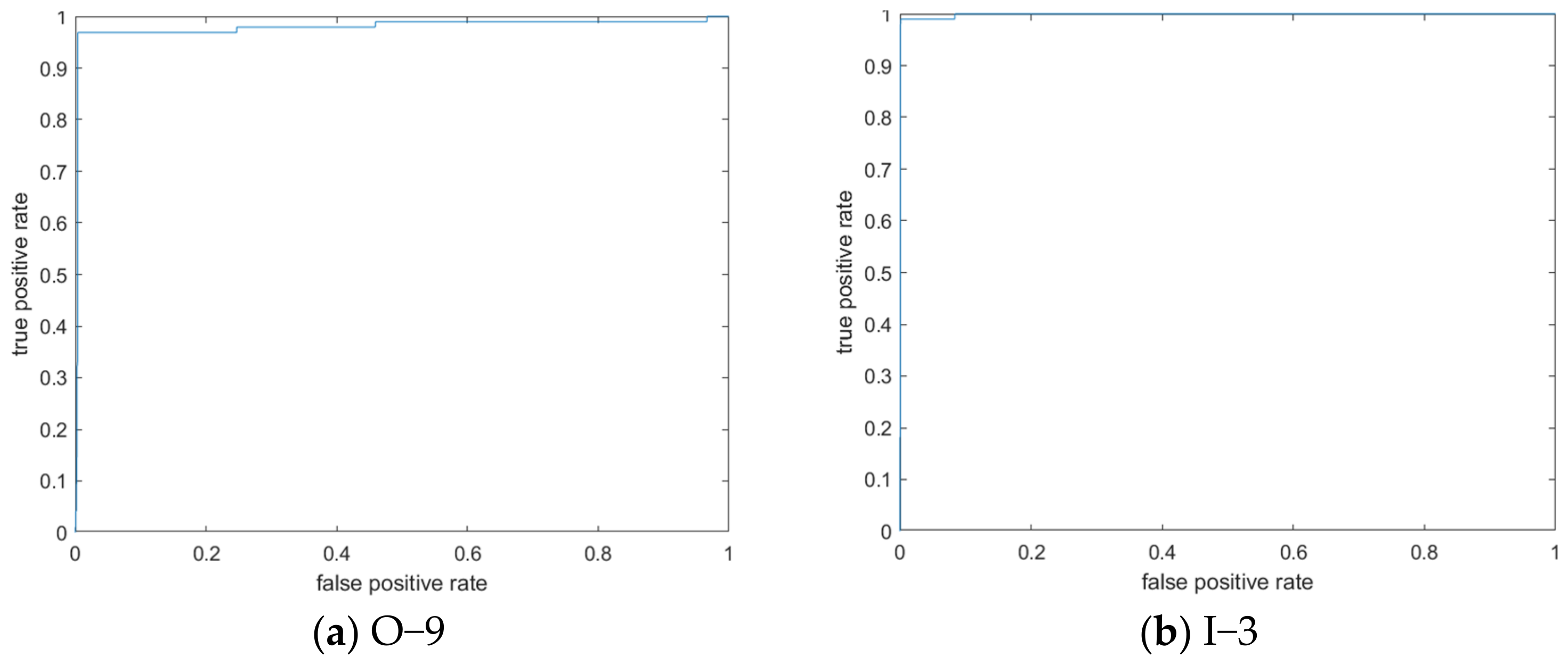
| O-9 | 99.88% | 93.49% | 96.58% | 95.35% | 99.88% |
| O-10 | 98.10% | 97.04% | 97.57% | 95.15% | 98.10% |
| I-1 | 99.97% | 96.65% | 98.28% | 95.20% | 99.97% |
| I-2 | 98.17% | 97.67% | 97.92% | 95.15% | 98.17% |
| I-3 | 99.99% | 98.85% | 99.42% | 95.10% | 99.99% |
| I-4 | 96.62% | 95.22% | 95.92% | 95.25% | 96.62% |
| I-5 | 97.26% | 97.86% | 97.56% | 95.15% | 97.26% |
| I-6 | 98.95% | 94.24% | 96.54% | 95.30% | 98.95% |
| I-7 | 98.79% | 91.33% | 94.92% | 95.45% | 98.79% |
| Literature | Feature Extraction | Fault Identification | Fault Types | Average Accuracy (%) |
|---|---|---|---|---|
| [20] | MSST+SFC-DL | LSVM | 3 | 95.83 |
| [21] | RCMFDLZC | DAC | 3 | 96.05 |
| [22] | CNN | HHT | 3 | 92.90 |
| [23] | SAE | Softmax | 3 | 90.11 |
| [23] | CNN | Fully Connected Layer, Softmax | 3 | 94.33 |
| [23] | ResNet | Fully Connected Layer, Softmax | 3 | 96.83 |
| [23] | Attention Mechanism ResNet | Fully Connected Layer, Softmax | 3 | 97.87 |
| This paper | SECNN | BLS | 3 | 98.31 |
| Method | Accuracy (%) under Different SNR (dB) | ||||
|---|---|---|---|---|---|
| −4 | 0 | 4 | 8 | 12 | |
| SAE | 55.39 | 69.32 | 81.22 | 87.33 | 89.27 |
| CNN | 61.57 | 77.13 | 83.89 | 91.25 | 92.95 |
| ResNet | 64.44 | 80.49 | 89.73 | 94.84 | 96.03 |
| A−ResNet | 75.05 | 86.54 | 92.86 | 96.47 | 97.52 |
| CWT−ResNet | 72.86 | 85.07 | 92.47 | 96.28 | 98.06 |
| SECNN–BLS | 81.22 | 92.08 | 95.76 | 97.83 | 98.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Hua, T.; Xu, S.; Zhao, X. A Novel Rolling Bearing Fault Diagnosis Method Based on BLS and CNN with Attention Mechanism. Machines 2023, 11, 279. https://doi.org/10.3390/machines11020279
Wang X, Hua T, Xu S, Zhao X. A Novel Rolling Bearing Fault Diagnosis Method Based on BLS and CNN with Attention Mechanism. Machines. 2023; 11(2):279. https://doi.org/10.3390/machines11020279
Chicago/Turabian StyleWang, Xiaojia, Tong Hua, Sheng Xu, and Xibin Zhao. 2023. "A Novel Rolling Bearing Fault Diagnosis Method Based on BLS and CNN with Attention Mechanism" Machines 11, no. 2: 279. https://doi.org/10.3390/machines11020279
APA StyleWang, X., Hua, T., Xu, S., & Zhao, X. (2023). A Novel Rolling Bearing Fault Diagnosis Method Based on BLS and CNN with Attention Mechanism. Machines, 11(2), 279. https://doi.org/10.3390/machines11020279






