On a Viscosity Iterative Method for Solving Variational Inequality Problems in Hadamard Spaces

Abstract

In this paper, we propose and study an iterative algorithm that comprises of a finite family of inverse strongly monotone mappings and a finite family of Lipschitz demicontractive mappings in an Hadamard space. We establish that the proposed algorithm converges strongly to a common solution of a finite family of variational inequality problems, which is also a common fixed point of the demicontractive mappings. Furthermore, we provide a numerical experiment to demonstrate the applicability of our results. Our results generalize some recent results in literature.

1. Introduction

The classical variational inequality problem (VIP) is defined in a real Hilbert space setting as: find $x\in D$ such that

$$⟨Tx,y-x⟩\ge 0 \forall y\in D,$$

(1)

where T is a nonlinear operator defined on D and D is a nonempty subset of the Hilbert space. The theory of VIP combines concepts of nonlinear operators and convex analysis in such a way that it generalizes both and is used to model nonlinear problems of physical phenomena in economics, sciences and engineering (see [1] for details). The VIP (1) was first introduced in finite dimensional spaces by Stampacchia [2], and since then researchers have devoted a lot of attention to VIP in finite and infinite dimensional spaces (see [3,4,5,6,7,8] and other references therein). Another form of the VIP widely studied in real Hilbert space settings (see [9,10] and the references therein) is defined as: find $x\in D$ such that

$$⟨x-Tx,y-x⟩\ge 0 \forall y\in D.$$

(2)

Several algorithms have been developed for solving VIP and related optimization problems in Hilbert and Banach spaces (see [3,7,11,12,13,14,15,16] and other references therein). It is well known that many of the problems in practical applications of optimization are constrained optimization problems, where the constraints are nonlinear, non-convex and non-smooth. Hence, it is pertinent to extend the study of these optimization problems to the nonlinear space settings, due to its ability to see non-convex and non-smooth constrained optimization problems as convex, smooth and unconstrained problems. For this reason, Németh [17] introduced and generalized the existence and uniqueness results of the classical VIP from Euclidean spaces to complete Riemannian manifolds. This development led to increasing interest from researchers in the study of VIPs and their generalizations in nonlinear spaces (see [18,19,20,21,22,23,24,25,26,27] and other references therein). Despite the increasing attention of researchers in this direction, little attention has been given to other more general nonlinear spaces apart from the Riemannian manifolds. In 2015, Khatibzadeh and Ranjbar [28] extended the study of VIP (2) to the framework of complete CAT(0) spaces. They formulated the VIP as follows:

$$\mathrm{Find} x\in D \mathrm{such} \mathrm{that} ⟨\overrightarrow{Txx},\overrightarrow{xy}⟩\ge 0 \forall y\in D,$$

(3)

where D is a nonempty, closed and convex subset of an Hadamard space X and T is a nonexpansive mapping. They established the existence of solutions for the VIP (3) and also employed an inexact proximal point algorithm to approximate a fixed point of the nonexpansive mapping which is also a solution of (3). They obtained convergence result for the algorithm under suitable conditions on the control sequences. Very recently, Alizadeh-Dehghan-Moradlou [29] introduced the notion of inverse strongly monotone mappings in metric spaces as follows: Let D be a nonempty subset of a metric space X and $T:D\to X$ be a mapping. T is called $\alpha$-inverse strongly monotone if there exists $\alpha >0$ such that

$$d^2(x,y)-⟨\overrightarrow{TxTy},\overrightarrow{xy}⟩\le \alpha {\mathrm{\Phi }}_T(x,y), \forall x,y\in D,$$

(4)

where ${\mathrm{\Phi }}_T(x,y)=d^2(x,y)+d^2(Tx,Ty)-2⟨\overrightarrow{TxTy},\overrightarrow{xy}⟩$.

Additionally, in [29], the authors studied the VIP (3) in an Hadamard space, where T is an inverse strongly monotone mapping. They established the existence of solutions for the VIP (3) associated with an inverse strongly monotone mapping. Furthermore, they introduced the following iterative algorithm to solve the VIP (3): for arbitrary $x_1\in D,$ the sequence $\left\{x_n\right\}$ is generated by

$$\left\{\begin{array}{c}{y}_n=P_D[{\beta }_n{x}_n\oplus (1-{\beta }_n)T{x}_n],\hfill \\ x_{n+1}=P_D[{\alpha }_n{x}_n\oplus (1-{\alpha }_n)S{x}_n],n\ge 1,\hfill \end{array}\right.$$

(5)

where $\left\{{\beta }_n\right\} \mathrm{and} \left\{{\alpha }_n\right\}\in (0,1)$, $P_D$ is a metric projection, T is inverse strongly monotone and S is nonexpansive mapping. They obtained that Algorithm (5) $\mathrm{\Delta }$-converges to a solution of the VIP (3), which is also a fixed point of the nonexpansive mapping $S$.

Very recently, Osisiogu et al. [30] proposed and studied the following Halpern-type algorithm in Hadamard spaces for approximating a common solution of a finite family of the VIP (3):

$$\left\{\begin{array}{c}{y}_n=\underset{i=1}{\overset{N}{\oplus }}{\beta }_i{P}_D{T}_{{\lambda }_i}{x}_n,\hfill \\ x_{n+1}={\alpha }_{n}u\oplus {\beta }_n{x}_n\oplus {\gamma }_{n}S{y}_n \forall n\ge 1,\hfill \end{array}\right.$$

(6)

where $T_{{\lambda }_i}=(1-{\lambda }_i)x\oplus {\lambda }_{i}Tx, 0<{\lambda }_i<2{\alpha }_i,$ for each $i=1,2,\cdots ,N$, $\left\{{\beta }_n\right\},\left\{{\alpha }_n\right\} \mathrm{and} \left\{{\gamma }_n\right\}\in (0,1),$ T is an inverse strongly monotone mapping and S is a nonexpansive mapping. They obtained a strong convergence result of Algorithm (6) under some suitable conditions.

Motivated by the results of Khatibzadeh and Ranjbar [28], Alizadeh-Dehghan-Moradlou [29] and Osisiogu et al. [30], we propose and study a viscosity iterative algorithm (from the fact that viscosity-type algorithms converge faster than Halpern-type algorithms and also Halpern-type algorithms are particular cases of viscosity-type algorithms, see [31,32]) that comprises of a finite family of inverse strongly monotone mappings (3) and a finite family of Lipchitz demicontractive mappings in an Hadamard space. Additionally, we establish that the proposed algorithm converges strongly to a common solution of a finite family of VIPs, which is also a common fixed point of a finite family of Lipchitz demicontractive mappings in the framework of Hadamard spaces. Furthermore, we provide a numerical experiment to demonstrate the applicability of our results. Our result generalizes the works of Alizadeh-Dehghan-Moradlou [29] and Osisiogu et al. [30] and other similar works in literature.

2. Preliminaries

Let $(X,d)$ be a metric space, $x,y\in X$ and $I=[0,d(x,y\left)\right]$ be an interval. A curve c (or simply a geodesic path) joining x to y is an isometry $c:I\to X$ such that $c\left(0\right)=x$, $c\left(d\right(x,y\left)\right)=y$ and $d(c\left(t\right),c\left(t^{\prime }\right))=|t-t^{\prime }|$ for all $t,t^{\prime }\in I$. The image of a geodesic path is called the geodesic segment, which is denoted by $[x,y]$ whenever it is unique. We say that a metric space X is a geodesic space if for every pair of points $x,y\in X$, there is a minimal geodesic from x to y. A geodesic triangle $\mathrm{\Delta }(x_1,x_2,x_3)$ in a geodesic metric space $(X,d)$ consists of three vertices (points in X) with geodesic segments between each pair of vertices. For any geodesic triangle, there is a comparison (Alexandrov) triangle $\overline{\mathrm{\Delta }}\subset {\mathbb{R}}^2$ such that $d(x_i,x_j)=d_{{\mathbb{R}}^2}({\overline{x}}_i,{\overline{x}}_j)$ for $i,j\in \{1,2,3\}$. A geodesic space X is a CAT(0) space if the distance between arbitrary pair of points on a geodesic triangle $\mathrm{\Delta }$ does not exceed the distance between its pair of corresponding points on its comparison triangle $\overline{\mathrm{\Delta }}$. If $\mathrm{\Delta }$ is a geodesic triangle and $\overline{\mathrm{\Delta }}$ is its comparison triangle in X, then $\mathrm{\Delta }$ is said to satisfy the CAT(0) inequality for all points $x,y$ of $\mathrm{\Delta }$ and $\overline{x},\overline{y}$ of $\overline{\mathrm{\Delta }}$, if

$$d(x,y)=d_{{\mathbb{R}}^2}(\overline{x},\overline{y}).$$

(7)

Let $x,y,z$ be points in X and $y_0$ be the midpoint of the segment $[y,z]$; then the CAT(0) inequality implies

$$d^2(x,y_0)\le \frac{1}{2}{d}^2(x,y)+\frac{1}{2}{d}^2(x,z)-\frac{1}{4}d(y,z).$$

(8)

Inequality (8) is known as CN inequality of Bruhat and Tits [33]. A geodesic space X is said to be a CAT(0) space if all geodesic triangles satisfy the CN inequality. Equivalently, X is called a CAT(0) space if and only if it satisfies the CN inequality. Examples of CAT(0) spaces includes Hadamard manifold, $\mathbb{R}$-trees [34], pre-Hilbert spaces [35], hyperbolic metric [36] and Hilbert balls [37].

Let D be a nonempty subset of a metric space $(X,d).$ A point $x\in X$ is called a fixed point of a nonlinear mapping $T:D\to X,$ if $x=Tx.$ We denote by $F\left(T\right)$ the set of fixed points of T. The mapping T is said to be:

• L-Lipschitz, if there exists $L>0$ such that

  $$d(Tx,Ty)\le Ld(x,y), \forall x,y\in X;$$

  if $L=1,$ then T is called nonexpansive;
• Firmly nonexpansive (see [38]), if

  $$d^2(Tx,Ty)\le ⟨\overrightarrow{TxTy},\overrightarrow{xy}⟩ \forall x,y\in X;$$
• Quasi-nonexpansive, if $F\left(T\right)\ne \varnothing$ and

  $$d(Tx,p)\le d(x,p) \forall x\in X \mathrm{and} p\in F\left(T\right);$$
• k-demicontractive, if $F\left(T\right)\ne \varnothing$ and there exists $k\in [0,1)$ such that

  $$d^2(Tx,p)\le d^2(x,p)+k{d}^2(x,Tx) \forall x,y\in X, \mathrm{and} p\in F\left(T\right).$$

Obviously, the class of quasi-nonexpansive are k-demicontractive mappings. However, the converse is not true (see [39] Example 1.1).

Definition 1.

[40] Let a pair$(a,b)\in X\times X$, denoted by$\overrightarrow{ab},$be called a vector in$X\times X$. The quasilinearization map$⟨.,.⟩:(X\times X)\times (X\times X)\to \mathbb{R}$is defined by

$$⟨\overrightarrow{ab},\overrightarrow{cd}⟩=\frac{1}{2}(d^2(a,d)+d^2(b,c)-d^2(a,c)-d^2(b,d)),\forall a,b,c,d\in X.$$

(9)

It is easy to see that$⟨\overrightarrow{ba},\overrightarrow{cd}⟩=-⟨\overrightarrow{ab},\overrightarrow{cd}⟩, ⟨\overrightarrow{ab},\overrightarrow{cd}⟩=⟨\overrightarrow{ae},\overrightarrow{cd}⟩+⟨\overrightarrow{eb},\overrightarrow{cd}⟩$and$⟨\overrightarrow{ab},\overrightarrow{cd}⟩=⟨\overrightarrow{cd},\overrightarrow{ab}⟩$for all$a,b,c,d,e\in X$. Furthermore, a geodesic space X is said to satisfy the Cauchy–Schwarz inequality if

$$⟨\overrightarrow{ab},\overrightarrow{cd}⟩\le d(a,b)d(c,d), \forall a,b,c,d\in X.$$

It is known from [41] that a geodesically connected metric space is a CAT(0) space if and only if it satisfies the Cauchy–Schwarz inequality.

We state some known and useful results which will be needed in the proof of our main results. In the sequel, we denote strong and $\mathrm{\Delta }$-convergence by “$\to$” and “$\rightharpoonup$” respectively.

Let $\left\{x_n\right\}$ be a bounded sequence in X and $r(.,\left\{x_n\right\}):X\to [0,\infty )$ be a continuous mapping defined by $r(x,\left\{x_n\right\})=\underset{n\to \infty }{\lim \sup }d(x,x_n)$. The asymptotic radius of $\left\{x_n\right\}$ is given by $r\left(\left\{x_n\right\}\right):=\inf \{r(x,\left\{x_n\right\}):x\in X\}$ while the asymptotic center of $\left\{x_n\right\}$ is the set $A\left(\left\{x_n\right\}\right)=\{x\in X:r(x,\left\{x_n\right\})=r\left(\left\{x_n\right\}\right)\}$. It is known that in an Hadamard space X, $A\left(\left\{x_n\right\}\right)$ consists of exactly one point. A sequence $\left\{x_n\right\}$ in X is said to be $\mathrm{\Delta }$-convergent to a point $x\in X,$ if $A\left(\left\{x_{n_k}\right\}\right)=\left\{x\right\}$ for every subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$. In this case, we write $\mathrm{\Delta }$-$\underset{n\to \infty }{\lim }{x}_n=x$ (see [42,43]).

Definition 2.

Let D be a nonempty, closed and convex subset of an Hadamard space$X.$The metric projection is a mapping$P_D:X\to D$which assigns to each$x\in X,$the unique point$P_{D}x\in D$such that

$$d(x,P_{D}x)=\inf \{d(x,y):y\in D\}.$$

Lemma 1.

[44] Let D be a nonempty, closed convex subset of an Hadamard space$X, x\in X$and$u\in D.$Then$u=P_{D}x$if and only if$⟨\overrightarrow{xu},\overrightarrow{uy}⟩\ge 0,$for all$y\in D.$

Lemma 2.

[29] Let D be a nonempty convex subset of an Hadamard space X and$T:D\to X$be an α-inverse strongly monotone mapping. Assume$\lambda \in [0,1]$and define$T_{\lambda }:D\to X$by$T_{\lambda }x=(1-\lambda )x\oplus \lambda Tx.$If$0<\lambda <2\alpha ,$then$T_{\lambda }$is nonexpansive and$F\left(T_{\lambda }\right)=F\left(T\right).$

Lemma 3.

[29] Let D be a nonempty convex subset of an Hadamard space X and $T:D\to X$ be a mapping. Then

$$VI(D,T)=VI(D,T_{\lambda }),$$

where $\lambda \in (0,1]$ and $T_{\lambda }:D\to X$ is a mapping defined by $T_{\lambda }x=(1-\lambda )x\oplus \lambda Tx,$ for all $x\in D.$

Remark 1.

Observe from Lemma 2 that

$$F\left(P_{D}T\right)=VI(D,T)=VI(D,T_{\lambda })=F\left(P_D{T}_{\lambda }\right).$$

Lemma 4.

[29] Let D be a nonempty bounded closed convex subset of an Hadamard space X and $T:D\to X$ be an α-inverse-strongly monotone mapping. Then $VI(D,T)$ is nonempty, closed and convex.

Lemma 5.

[41,45] Let X be an Hadamard space. Then for all $x,y,z\in X$ and all $t,s\in [0,1],$ we have

(i) 

$d(tx\oplus (1-t)y,z)\le td(x,z)+(1-t)d(y,z),$

(ii) 

$d^2(tx\oplus (1-t)y,z)\le t{d}^2(x,z)+(1-t)d^2(y,z)-t(1-t)d^2(x,y),$

(iii) 

$d^2(z,tx\oplus (1-t)y)\le t^2{d}^2(z,x)+{(1-t)}^2{d}^2(z,y)+2t(1-t)⟨\overrightarrow{zx},\overrightarrow{zy}⟩.$

Lemma 6.

[46] Let X be a CAT(0) space and $z\in X$. Let $x_1,\cdots ,x_N\in X$ and ${\gamma }_1,\cdots ,{\gamma }_N$ be real numbers in $[0,1]$ such that ${\displaystyle \sum _{i=1}^N}{\gamma }_i=1$. Then the following inequality holds:

$$d^2(\sum _{i=1}^N\oplus {\gamma }_i{x}_i,z)\le \sum _{i=1}^N{\gamma }_i{d}^2(x_i,z)-\sum _{i,j=1,i\ne j}^N{\gamma }_i{\gamma }_j{d}^2(x_i,x_j).$$

Lemma 7.

[47] Every bounded sequence in an Hadamard space has a Δ-convergent subsequence.

Lemma 8.

[48] Let X be an Hadamard space, $\left\{x_n\right\}$ be a sequence in X and $x\in X.$ Then $\left\{x_n\right\}$ Δ-converges to x if and only if

$$\underset{n\to \infty }{\lim \sup }⟨\overrightarrow{x_{n}x},\overrightarrow{yx}⟩\le 0, \forall y\in X.$$

Definition 3.

Let D be a nonempty, closed and convex subset of an Hadamard space $X$. A mapping $T:D\to D$ is said to be Δ-demiclosed, if for any bounded sequence $\left\{x_n\right\}$ in $X,$ such that $\mathrm{\Delta }-\underset{n\to \infty }{\lim }{x}_n=x$ and $\underset{n\to \infty }{\lim }d(x_n,T{x}_n)=0,$ then $x=Tx$.

Lemma 9.

[49] Let X be an Hadamard space and $T:X\to X$ be a nonexpansive mapping. Then T is Δ-demiclosed.

Lemma 10.

[50,51] Let $\left\{a_n\right\}$ be a sequence of non-negative real numbers satisfying

$$a_{n+1}\le (1-{\alpha }_n)a_n+{\delta }_n, n\ge 0,$$

where $\left\{{\alpha }_n\right\}$ and $\left\{{\delta }_n\right\}$ satisfy the following conditions:

(i) 

$\left\{{\alpha }_n\right\}\subset [0,1], {\displaystyle \sum _{n=0}^{\infty }}{\alpha }_n=\infty$,

(ii) 

$\underset{n\to \infty }{\lim \sup }\frac{{\delta }_n}{{\alpha }_n}\le 0$or${\displaystyle \sum _{n=0}^{\infty }}\left|{\delta }_n\right|\le \infty .$

Then${\lim }_{n\to \infty }{a}_n=0.$

Lemma 11.

[52] Let $\left\{a_n\right\}$ be a sequence of non-negative real numbers such that there exists a subsequence $\left\{n_j\right\}$ of $\left\{n\right\}$ with $a_{n_j}<a_{n_j+1}$ $for all j\in \mathbb{N}$. Then there exists a nondecreasing sequence $\left\{m_k\right\}\subset \mathbb{N}$ such that $m_k\to \infty$ and the following properties are satisfied by all (sufficiently large) numbers $k\in \mathbb{N}$:

$$a_{m_k}\le a_{m_k+1} and a_k\le a_{m_k+1}.$$

In fact, $m_k=\max \{i\le k:a_i<a_{i+1}\}$.

3. Main Results

In this section, we present our strong convergence results.

Theorem 1.

Let X be an Hadamard space and D be a nonempty, closed and convex subset of $X$. Let $S_i:D\to D$ be a finite family of $L_i$-Lipschitz $k_i$-demicontractive mappings and Δ-demiclosed such that $L>0, L=\max \{L_i, i=1,2,\cdots ,N\},$$k\in [0,1), k=\max \{k_i, i=1,2,\cdots ,N\}, k_i\in [0,1),i=1,2,\cdots ,N.$ Let $T_i:D\to X$ be a finite family of ${\alpha }_i$-inverse strongly monotone mappings and f be a contraction on D with coefficient $\theta \in (0,1).$ Suppose that $\mathrm{\Gamma }:={\cap }_{i=1}^{N}VI(D,T_i)\cap {\cap }_{i=1}^{N}F\left(S_i\right)\ne \varnothing .$ For arbitrary $x_1\in D,$ let the sequence $\left\{x_n\right\}$ be generated by

$$\left\{\begin{array}{c}{w}_n={\gamma }_{n}f\left(x_n\right)\oplus (1-{\gamma }_n)x_n,\hfill \\ y_n={\beta }_{n,0}{w}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\beta }_{n,i}{P}_D{T}_{{\lambda }_i}{w}_n,\hfill \\ x_{n+1}={\alpha }_{n,0}{y}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\alpha }_{n,i}{S}_i{y}_n, \forall n\ge 1,\hfill \end{array}\right.$$

(10)

where $T_{{\lambda }_i}=(1-{\lambda }_i)x\oplus {\lambda }_i{T}_{i}x, 0<{\lambda }_i<2{\alpha }_i,$ for each $i=1,2,\cdots ,N,$$\left\{{\gamma }_n\right\},\left\{{\beta }_{n,i}\right\} and \left\{{\alpha }_{n,i}\right\}\in (0,1)$ such that the following conditions are satisfied:

(A1) 

$\underset{n\to \infty }{\lim }{\gamma }_n=0;$

(A2) 

${\displaystyle \sum _{n=1}^{\infty }}{\gamma }_n=\infty ,$

(A3) 

$0<a\le {\beta }_{n,i},{\alpha }_{n,i}\le b<1;$${\displaystyle \sum _{i=0}^N}{\alpha }_{n,i}=1 and {\displaystyle \sum _{i=0}^N}{\beta }_{n,i}=1;$

(A4) 

$0<c\le {\alpha }_{n,0}-k\le d<1.$

Then, the sequence $\left\{x_n\right\}$ converges strongly to an element $\overline{z}=P_{\mathrm{\Gamma }}f\left(\overline{z}\right),$ where $P_{\mathrm{\Gamma }}$ is the metric projection of X onto $\mathrm{\Gamma }.$

Proof. 

Let $p\in \mathrm{\Gamma };$ then by (10), condition (A3), Lemma 6 and the fact that $P_D{T}_{\lambda }$ is nonexpansive, we have

$$\begin{array}{cc}\hfill d^2(y_n,p)& =d^2({\beta }_{n,0}{w}_n\sum _{i=1}^N\oplus {\beta }_{n,i}{P}_D{T}_{{\lambda }_i}{w}_n,p)\hfill \\ & \le {\beta }_{n,0}{d}^2(w_n,p)+\sum _{i=1}^N{\beta }_{n,i}{d}^2(P_D{T}_{{\lambda }_i}{w}_n,p)-\sum _{i=1}^N{\beta }_{n,0}{\beta }_{n,i}{d}^2(P_D{T}_{{\lambda }_i}{w}_n,w_n)\hfill \\ & \le d^2(w_n,p)-\sum _{i=1}^N{\beta }_{n,0}{\beta }_{n,i}{d}^2(P_D{T}_{{\lambda }_i}{w}_n,w_n).\hfill \end{array}$$

(11)

Additionally, since $S_i$ is demicontractive, we have from (10) and Lemma 6 that

$$\begin{array}{cc}\hfill d^2(x_{n+1},p)& \le {\alpha }_{n,0}{d}^2(y_n,p)+\sum _{i=1}^N{\alpha }_{n,i}{d}^2(S_i{y}_n,p)-\sum _{i=1}^N{\alpha }_{n,0}{\alpha }_{n,i}{d}^2(y_n,S_i{y}_n)\hfill \\ & \le {\alpha }_{n,0}{d}^2(y_n,p)+\sum _{i=1}^N{\alpha }_{n,i}\left[d^2(y_n,p)+k{d}^2(S_i{y}_n,y_n)\right]-\sum _{i=1}^N{\alpha }_{n,0}{\alpha }_{n,i}{d}^2(y_n,S_i{y}_n)\hfill \\ & =d^2(y_n,p)-\sum _{i=1}^N{\alpha }_{n,i}\left({\alpha }_{n,0}-k\right)d^2(y_n,S_i{y}_n).\hfill \end{array}$$

(12)

From (11), (12) and condition (A4), we have

$$\begin{array}{cc}\hfill d(x_{n+1},p)& \le {\gamma }_{n}d(f\left(x_n\right),p)+(1-{\gamma }_n)d(x_n,p)\hfill \\ & \le {\gamma }_n\theta d(x_n,p)+{\gamma }_{n}d(f\left(p\right),p)+(1-{\gamma }_n)d(x_n,p)\hfill \\ & \le (1-{\gamma }_n(1-\theta ))d(x_n,p)+{\gamma }_{n}d(f\left(p\right),p).\hfill \\ & \le \max \{d(x_n,p),\frac{1}{1-\theta }d(f\left(p\right),p)\}\hfill \\ & ⋮\hfill \\ & \le \max \{d(x_1,p),\frac{1}{1-\theta }d(f\left(p\right),p)\}.\hfill \end{array}$$

Thus, $\left\{x_n\right\}$ is bounded. Consequently, $\left\{w_n\right\},$$\left\{y_n\right\},$$\left\{S{y}_n\right\}$ and $\left\{P_D{T}_{{\lambda }_i}{w}_n\right\}$ are also bounded.

Now we divide the rest of the proof into two cases:

Case 1: Assume that $\left\{d^2(x_n,p)\right\}$ is a monotonically non-increasing sequence. Then, $\left\{d^2(x_n,p)\right\}$ is convergent and

$$d^2(x_n,p)-d^2(x_{n+1},p)\to 0, as n\to \infty .$$

Hence, from (11) and (12), we have

$$\begin{array}{cc}\hfill d^2(x_{n+1},p)& \le d^2(w_n,p)-\sum _{i=1}^N{\beta }_{n,0}{\beta }_{n,i}{d}^2(P_D{T}_{{\lambda }_i}{w}_n,w_n)-\sum _{i=1}^N{\alpha }_{n,i}\left({\alpha }_{n,0}-k\right)d^2(y_n,S_i{y}_n)\hfill \\ & \le {\gamma }_n{d}^2(f\left(x_n\right),p)+(1-{\gamma }_n)d^2(x_n,p)-\sum _{i=1}^N{\beta }_{n,0}{\beta }_{n,i}{d}^2(P_D{T}_{{\lambda }_i}{w}_n,w_n)-\sum _{i=1}^N{\alpha }_{n,i}\left({\alpha }_{n,0}-k\right)d^2(y_n,S_i{y}_n),\hfill \end{array}$$

(13)

which implies

$$\sum _{i=1}^N{\beta }_{n,0}{\beta }_{n,i}{d}^2(P_D{T}_{{\lambda }_i}{w}_n,w_n)\le {\gamma }_n(d^2(f\left(x_n\right),p)-d^2(x_n,p))+d^2(x_n,p)-d^2(x_{n+1},p).$$

By conditions (A1) and (A3), we obtain that

$$\underset{n\to \infty }{\lim }d(P_D{T}_{{\lambda }_i}{w}_n,w_n)=0, i=0,1,2,\cdots ,N.$$

(14)

Similarly, from (13) and condition (A1), we have

$$\underset{n\to \infty }{\lim }d(S_i{y}_n,y_n)=0, i=0,1,2,\cdots ,N.$$

(15)

Additionally,

$$\begin{array}{cc}\hfill d(w_n,x_n)& \le {\gamma }_{n}d(f\left(x_n\right),x_n)\to 0 as n\to \infty .\hfill \end{array}$$

(16)

Again from (10) and Lemma 6, we have

$$\begin{array}{cc}\hfill d^2(y_n,x_n)& \le {\beta }_{n,0}{d}^2(w_n,x_n)+\sum _{i=1}^N{\beta }_{n,i}{d}^2(P_D{T}_{{\lambda }_i}{w}_n,x_n)\hfill \\ & \le {\beta }_{n,0}{d}^2(w_n,x_n)+\sum _{i=1}^N{\beta }_{n,i}{\left[d(P_D{T}_{{\lambda }_i}{w}_n,w_n)+d(w_n,x_n)\right]}^2.\hfill \end{array}$$

Hence, from (14) and (16), we obtain

$$d(y_n,x_n)\to 0 as n\to \infty .$$

(17)

Additionally, from (15) and (17), we have

$$d(S_i{y}_n,x_n)\le d(S_i{y}_n,y_n)+d(y_n,x_n)\to 0, as n\to \infty , i=0,1,2,\cdots ,N.$$

(18)

Since $S_i$ is Lipschitz, then from (17) and (18), we have that

$$\begin{array}{cc}\hfill d(S_i{x}_n,x_n)& \le d(S_i{x}_n,S_i{y}_n)+d(S_i{y}_n,x_n)\hfill \\ \hfill & \le Ld(x_n,y_n)+d(S_i{y}_n,x_n)\to 0, as n\to \infty , i=0,1,2,\cdots ,N.\hfill \end{array}$$

(19)

Hence, from (14), (16) and Lemma 2, we obtain that

$$\begin{array}{cc}\hfill d(P_D{T}_{{\lambda }_i}{x}_n,x_n)& \le d(P_D{T}_{{\lambda }_i}{x}_n,P_D{T}_{{\lambda }_i}{w}_n)+d(P_D{T}_{{\lambda }_i}{w}_n,w_n)+d(w_n,x_n)\hfill \\ \hfill & \le d(x_n,w_n)+d(P_D{T}_{{\lambda }_i}{w}_n,w_n)+d(w_n,x_n)\to 0, \mathrm{as} n\to \infty , i=0,1,2,\cdots ,N.\hfill \end{array}$$

(20)

Since $\left\{x_n\right\}$ is bounded, by Lemma 7 there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $\mathrm{\Delta }-\underset{k\to \infty }{\lim }{x}_{n_k}=z$ for some $z\in D.$ Then, it follows from (16) that there exists a subsequence $\left\{w_{n_k}\right\}$ of $\left\{w_n\right\},$ such that $\mathrm{\Delta }$-$\underset{k\to \infty }{\lim }{w}_{n_k}=z.$ Additionally, from (17), we have that $\mathrm{\Delta }$-$\underset{k\to \infty }{\lim }{y}_{n_k}=z.$ Since $S_i$ is $\mathrm{\Delta }$-demiclosed for each $i=1,2,\cdots ,N,$ it follows from (19) that $z\in {\cap }_{i=0}^{N}F\left(S_i\right).$ Additionally, $P_D{T}_{{\lambda }_i}$ is nonexpansive (by Lemma 2) for each $i=1,2,\cdots ,N,$ thus we obtain from (20) and Remark 1 that $z\in {\cap }_{i=0}^{N}F\left(P_D{T}_{{\lambda }_i}\right)={\cap }_{i=0}^{N}F\left(P_D{T}_i\right).$ Hence, $z\in \mathrm{\Gamma }$.

Next we show that $\left\{x_n\right\}$ converges strongly to $\overline{z}=P_{\mathrm{\Gamma }}f\left(\overline{z}\right).$ Since $\left\{x_n\right\}$ is bounded, we may choose without loss of generality, a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $\left\{x_{n_k}\right\}$$\mathrm{\Delta }$-converges to z and

$$\underset{n\to \infty }{\lim \sup }⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_n\overline{z}}⟩=\underset{k\to \infty }{\lim }⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_{n_k}\overline{z}}⟩.$$

(21)

Thus, by (21) and Lemma 1, we obtain that

$$\underset{k\to \infty }{\lim \sup }⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_n\overline{z}}⟩=⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{z\overline{z}}⟩\le 0.$$

(22)

From (12), Lemma 5 (iii) and quasilinearization properties in Definition 1, we have that

$$\begin{array}{cc}\hfill d^2(x_{n+1},\overline{z})& \le {\gamma }_n^2{d}^2(f\left(x_n\right),\overline{z})+{(1-{\gamma }_n)}^2{d}^2(x_n,\overline{z})+2{\gamma }_n(1-{\gamma }_n)⟨\overrightarrow{f\left(x_n\right)\overline{z}},\overrightarrow{x_n\overline{z}}⟩\hfill \\ & \le {\gamma }_n^2{d}^2(f\left(x_n\right),\overline{z})+{(1-{\gamma }_n)}^2{d}^2(x_n,\overline{z})+2{\gamma }_n(1-{\gamma }_n)\left[⟨\overrightarrow{f\left(x_n\right)f\left(\overline{z}\right)},\overrightarrow{x_n\overline{z}}⟩+⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_n\overline{z}}⟩\right]\hfill \\ & \le {\gamma }_n^2{d}^2(f\left(x_n\right),\overline{z})+{(1-{\gamma }_n)}^2{d}^2(x_n,\overline{z})+2{\gamma }_n(1-{\gamma }_n)\left[\theta d^2(x_n,\overline{z})+⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_n\overline{z}}⟩\right]\hfill \\ & \le (1-2{\gamma }_n+2{\gamma }_n\theta )d^2(x_n,\overline{z})+2{\gamma }_n(1-{\gamma }_n)⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_n\overline{z}}⟩+{\gamma }_n^2\left(d^2(f\left(x_n\right),\overline{z})+d^2(x_n,\overline{z})\right)\hfill \\ & =1-2{\gamma }_n(1-\theta )d^2(x_n,\overline{z})+2{\gamma }_n(1-\theta )\left[\frac{1-{\gamma }_n}{1-\theta }⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_n\overline{z}}⟩+\frac{{\gamma }_n}{2(1-\theta )}\left(d^2(f\left(x_n\right),\overline{z})+d^2(x_n,\overline{z})\right)\right].\hfill \end{array}$$

That is,

$$\begin{array}{c}\hfill d^2(x_{n+1},\overline{z})\le 1-2{\gamma }_n(1-\theta )d^2(x_n,\overline{z})+2{\gamma }_n(1-\theta )M_n,\end{array}$$

(23)

where

$$M_n=\left[\frac{1-{\gamma }_n}{1-\theta }⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_n\overline{z}}⟩+\frac{{\gamma }_n}{2(1-\theta )}\left(d^2(f\left(x_n\right),\overline{z})+d^2(x_n,\overline{z})\right)\right].$$

Thus from (22), (23) and condition (A1), we conclude by Lemma 10 that $\left\{x_n\right\}$ converges strongly to $\overline{z}=P_{\mathrm{\Gamma }}f\left(\overline{z}\right).$

Case 2: Suppose there exists a subsequence $\left\{n_k\right\}$ of $\left\{n\right\}$ such that $d^2(x_{n_k},p)\le d^2(x_{k+1},p)$ for all $k\in \mathbb{N}.$ Then by Lemma 11, there exists a nondecreasing sequence $\left\{m_k\right\}\subset \mathbb{N}$ such that $m_k\to \infty :$

$$\begin{array}{c}\hfill d(x_{m_k},p)<d(x_{m_{k+1}},p), \mathrm{and} d(x_k,p)<d(x_{k+1},p) \forall k\in \mathbb{N}.\end{array}$$

(24)

Therefore

$$\begin{array}{cc}\hfill 0& \le \underset{k\to \infty }{\lim }\left(d(x_{m_{k+1}},p)-d(x_{m_k},p)\right)\hfill \\ \hfill & \le \underset{n\to \infty }{\lim \sup }\left(d(x_{n+1},p)-d(x_n,p)\right)\hfill \\ \hfill & \le \underset{n\to \infty }{\lim \sup }\left({\gamma }_{n}d(f\left(x_n\right),p)+(1-{\gamma }_n)d(x_n,p)-d(x_n,p)\right)\hfill \\ \hfill & =\underset{n\to \infty }{\lim \sup }\left({\gamma }_n\left(d(f\left(x_n\right),p)-d(x_n,p)\right)\right)=0.\hfill \end{array}$$

This implies that

$$\underset{k\to \infty }{\lim }\left(d(x_{m_{k+1}},p)-d(x_{m_k},p)\right)=0.$$

(25)

Following the arguments as in Case 1, we get

$$\underset{k\to \infty }{\lim }⟨\overrightarrow{f\left(\overline{z}\right)\overline{z}},\overrightarrow{x_{m_k}\overline{z}}⟩\le 0.$$

(26)

Hence, from (23), we obtain that

$$d^2(x_{m_{k+1}},\overline{z})\le 1-2{\gamma }_{m_k}(1-\theta )d^2(x_{m_k},\overline{z})+2{\gamma }_{m_k}(1-\theta )M_{m_k}.$$

Additionally, from (24), we have that

$$d^2(x_{m_k},\overline{z})\hspace{1em}\le M_{m_k},$$

which implies that

$$\underset{k\to \infty }{\lim }{d}^2(x_{m_k},\overline{z})=0.$$

Thus, from cases 1 and 2, we conclude that $\left\{x_n\right\}$ converges to $\overline{z}=P_{\mathrm{\Gamma }}f\left(\overline{z}\right)$ which is an element of $\mathrm{\Gamma }.$

We present some consequences of our main results.

Now, by setting $S_i$ to be a family of quasi-nonexpansive mappings in Theorem 1, we obtain the following result:

Corollary 2.

Let X be an Hadamard space and D be a nonempty, closed and convex subset of $X.$ Let $S_i:D\to D$ be a finite family of quasi-nonexpansive mappings, $T_i:D\to X$ be a finite family of ${\alpha }_i$-inverse strongly monotone mappings and f be a contraction on D with coefficient $\theta \in (0,1).$ Suppose that $\mathrm{\Gamma }:={\cap }_{i=1}^{N}VI(D,T_i)\cap {\cap }_{i=1}^{N}F\left(S_i\right)\ne \varnothing .$ For arbitrary $x_1,\in D,$ let the sequence $\left\{x_n\right\}$ be generated by

$$\left\{\begin{array}{c}{w}_n={\gamma }_{n}f\left(x_n\right)\oplus (1-{\gamma }_n)x_n,\hfill \\ y_n={\beta }_{n,0}{w}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\beta }_{n,i}{P}_D{T}_{{\lambda }_i}{w}_n,\hfill \\ x_{n+1}={\alpha }_{n,0}{y}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\alpha }_{n,i}{S}_i{y}_n, \forall n\ge 1,\hfill \end{array}\right.$$

(27)

where $T_{{\lambda }_i}=(1-{\lambda }_i)x\oplus {\lambda }_i{T}_{i}x, 0<{\lambda }_i<2{\alpha }_i,$ for each $i=1,2,\cdots ,N,$$\left\{{\gamma }_n\right\},\left\{{\beta }_{n_i}\right\} and \left\{{\alpha }_{n_i}\right\}\in (0,1)$ such that conditions (A1)–(A3) of Theorem 1 are satisfied. Then, the sequence $\left\{x_n\right\}$ converges strongly to an element $\overline{z}=P_{\mathrm{\Gamma }}f\left(\overline{z}\right),$ where $P_{\mathrm{\Gamma }}$ is the metric projection of X onto $\mathrm{\Gamma }$.

Proof. 

The proof follows from the proof of Theorem 1. □

By setting $N=1$ in Corollary 2, we obtain the following result:

Corollary 3.

Let X be an Hadamard space and D be a nonempty, closed and convex subset of $X.$ Let $S:D\to D$ be a quasi-nonexpansive mapping, $T:D\to X$ be an α-inverse strongly monotone mapping and f be a contraction on D with coefficient $\theta \in (0,1).$ Suppose that $\mathrm{\Gamma }:=VI(D,T)\cap F\left(S\right)\ne \varnothing .$ For arbitrary $x_1\in D,$ let the sequence $\left\{x_n\right\}$ be generated by

$$\left\{\begin{array}{c}{w}_n={\gamma }_{n}f\left(x_n\right)\oplus (1-{\gamma }_n)x_n,\hfill \\ y_n={\beta }_{n,0}{w}_n\oplus {\beta }_{n,1}{P}_D{T}_{\lambda }{w}_n,\hfill \\ x_{n+1}={\alpha }_{n,0}{y}_n\oplus {\alpha }_{n,1}S{y}_n, \forall n\ge 1,\hfill \end{array}\right.$$

(28)

where $T_{\lambda }=(1-\lambda )x\oplus \lambda Tx, 0<\lambda <2\alpha ,$ $\left\{{\gamma }_n\right\}$ and $\left\{{\alpha }_n\right\}\in (0,1)$ such that $0<a\le {\beta }_{n,i},{\alpha }_{n,i}\le b<1, for i=0,1,$ ${\displaystyle \sum _{i=0}^1}{\alpha }_{n,i}=1, {\displaystyle \sum _{i=0}^1}{\beta }_{n,i}=1$ and conditions (A1)–(A2) of Theorem 1 are satisfied. Then, the sequence $\left\{x_n\right\}$ converges strongly to an element $\overline{z}=P_{\mathrm{\Gamma }}f\left(\overline{z}\right),$ where $P_{\mathrm{\Gamma }}$ is the metric projection of X onto $\mathrm{\Gamma }.$

Suppose $u=f\left(x\right)$ for arbitrary but fixed $u\in X$ and for all $x\in X$ in Theorem 1, we obtain the following result:

Corollary 4.

Let X be an Hadamard space and D be a nonempty, closed and convex subset of $X.$ Let $S_i:D\to D$ be a finite family of $L_i$-Lipschitz demicontractive mappings and Δ-demiclosed such that $L>0, L=\max \{L_i, i=1,2,\cdots ,N\},$ $k\in [0,1), k=\max \{k_i, i=1,2,\cdots ,N\}, k_i\in [0,1),i=1,2,\cdots ,N.$ Let $T_i:D\to X$ be a finite family of ${\alpha }_i$-inverse strongly monotone mappings and suppose that $\mathrm{\Gamma }:={\cap }_{i=1}^{N}VI(D,T_i)\cap {\cap }_{i=1}^{N}F\left(S_i\right)\ne \varnothing .$ For arbitrary $x_1, u\in D,$ let the sequence $\left\{x_n\right\}$ be generated by

$$\left\{\begin{array}{c}{w}_n={\gamma }_{n}u\oplus (1-{\gamma }_n)x_n,\hfill \\ y_n={\beta }_{n,0}{w}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\beta }_{n,i}{P}_D{T}_{{\lambda }_i}{w}_n,\hfill \\ x_{n+1}={\alpha }_{n,0}{y}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\alpha }_{n,i}{S}_i{y}_n, \forall n\ge 1,\hfill \end{array}\right.$$

(29)

where $T_{{\lambda }_i}=(1-{\lambda }_i)x\oplus {\lambda }_i{T}_{i}x, 0<{\lambda }_i<2{\alpha }_i,$ for each $i=1,2,\cdots ,N,$$\left\{{\gamma }_n\right\},\left\{{\beta }_{n_i}\right\} and \left\{{\alpha }_{n_i}\right\}\in (0,1)$ such that conditions (A1)–(A4) of Theorem 1 are satisfied. Then, the sequence $\left\{x_n\right\}$ converges strongly to an element $\overline{z}\in \mathrm{\Gamma }$ which is the nearest point to $u.$

By setting $S_i\equiv I$ for all $i=1,2,\cdots ,N$ in Theorem 1, we obtain the following result:

Corollary 5.

Let X be an Hadamard space and D be a nonempty, closed and convex subset of $X.$ Let $T_i:D\to X$ be a finite family of ${\alpha }_i$-inverse strongly monotone mappings and f be a contraction on D with coefficient $\theta \in (0,1).$ Suppose that $\mathrm{\Gamma }:={\cap }_{i=1}^{N}VI(D,T_i)\ne \varnothing .$ For arbitrary $x_1\in D,$ let the sequence $\left\{x_n\right\}$ be generated by

$$\left\{\begin{array}{c}{w}_n={\gamma }_{n}f\left(x_n\right)\oplus (1-{\gamma }_n)x_n,\hfill \\ y_n={\beta }_{n,0}{w}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\beta }_{n,i}{P}_D{T}_{{\lambda }_i}{w}_n\hfill \\ x_{n+1}={\alpha }_{n,0}{y}_n\oplus {\displaystyle \sum _{i=i}^N}\oplus {\alpha }_{n,i}{y}_n \forall n\ge 1,\hfill \end{array}\right.$$

(30)

where $T_{{\lambda }_i}=(1-{\lambda }_i)x\oplus {\lambda }_i{T}_{i}x, 0<{\lambda }_i<2{\alpha }_i,$ for each $i=1,2,\cdots ,N,$$\left\{{\gamma }_n\right\},\left\{{\beta }_{n_i}\right\} and \left\{{\alpha }_{n_i}\right\}\in (0,1)$ such that conditions (A1)–(A3) of Theorem 1 are satisfied. Then, the sequence $\left\{x_n\right\}$ converges strongly to an element $\overline{z}=P_{\mathrm{\Gamma }}f\left(\overline{z}\right),$ where $P_{\mathrm{\Gamma }}$ is the metric projection of X onto $\mathrm{\Gamma }$.

4. Numerical Example

In this section, we give a numerical experiment to show the applicability of our result.

Example 1.

[29] Let $X={\mathbb{R}}^2$ be an R-tree with radial metric $d_r,$ where $d_r(x,y)=d(x,y)$ if x and y are situated on a Euclidean straight line passing through the origin and $d_r(x,y)=d(x,\mathbf{0})+d(y,\mathbf{0})$ otherwise. We put $p=(0,1),q=(1,0)$ and $D=A\cup B\cup C,$ where

$$A=\left\{\right(0,t):t\in [2/3,1\left]\right\},\hspace{1em}B=\left\{\right(t,0):t\in [2/3,1\left]\right\},\hspace{1em}C=\left\{\right(t,s):t+s=1,t\in (0,1\left)\right\}.$$

Define $T:D\to X$ by

$$Tx=\left\{\begin{array}{c}q if x\in A,\hfill \\ p if x\in B,\hfill \\ x if x\in C,\hfill \end{array}\right.$$

(31)

then T is $\frac{1}{4}$-inverse strongly monotone in $(X,d_r).$

Now, define $S:D\to D$ by $Sx=\frac{5}{8}x.$ We make the following choices of parameters: $\lambda =\frac{1}{4}, {\gamma }_n=\frac{1}{n+1},$${\alpha }_{n,0}=\frac{2n}{5n+7}, {\alpha }_{n,1}=\frac{3n+7}{5n+7}, {\beta }_{n,0}=\frac{n}{3n+2},{\beta }_{n,1}=\frac{2n+2}{3n+2} \forall n\ge 1$ and $f\left(x\right)=\frac{1}{2}x \forall x\in X;$ then the conditions (A1)–(A3) of Theorem 2 are satisfied. Therefore, for $x_1\in X,$ Algorithm (28) becomes

$$\left\{\begin{array}{c}{w}_n=\frac{1}{n+1}f\left(x_n\right)\oplus (1-\frac{1}{n+1})x_n,\hfill \\ y_n={\beta }_{n,0}{w}_n\oplus {\beta }_{n,1}{P}_D{T}_{\lambda }{w}_n,\hfill \\ x_{n+1}={\alpha }_{n,0}{y}_n\oplus {\alpha }_{n,1}S{y}_n \forall n\ge 1.\hfill \end{array}\right.$$

(32)

We now consider the following 3 cases for our numerical experiments given in Figure 1 above.

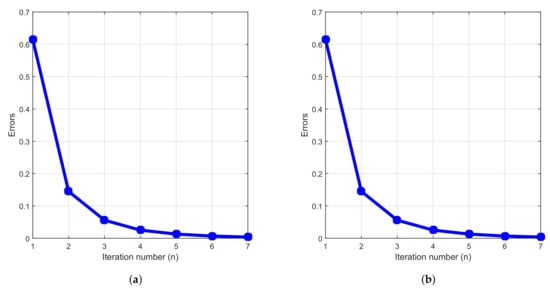
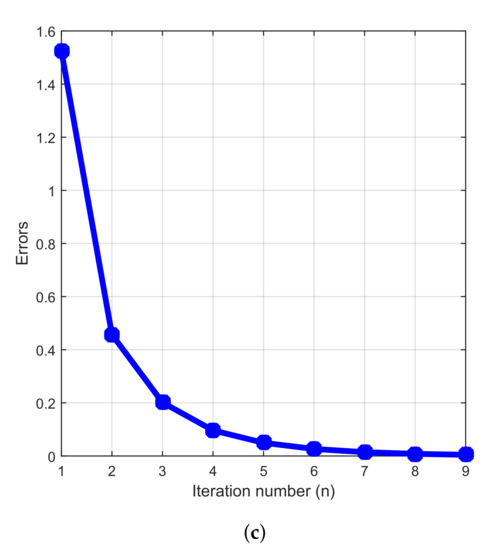
Figure 1. Errors vs. iteration numbers (n) for Example 1: case 1 (a); case 2 (b); case 3 (c).

• Case 1:$x_1={(-0.5,0.5)}^T$.
• Case 2:$x_1={(0.5,-0.5)}^T$.
• Case 2:$x_1={(1,2)}^T$.