On a Viscosity Iterative Method for Solving Variational Inequality Problems in Hadamard Spaces
Abstract
1. Introduction
2. Preliminaries
- L-Lipschitz, if there exists such thatif then T is called nonexpansive;
- Firmly nonexpansive (see [38]), if
- Quasi-nonexpansive, if and
- k-demicontractive, if and there exists such that
- (i)
- ,
- (ii)
- orThen
3. Main Results
- (A1)
- (A2)
- (A3)
- (A4)
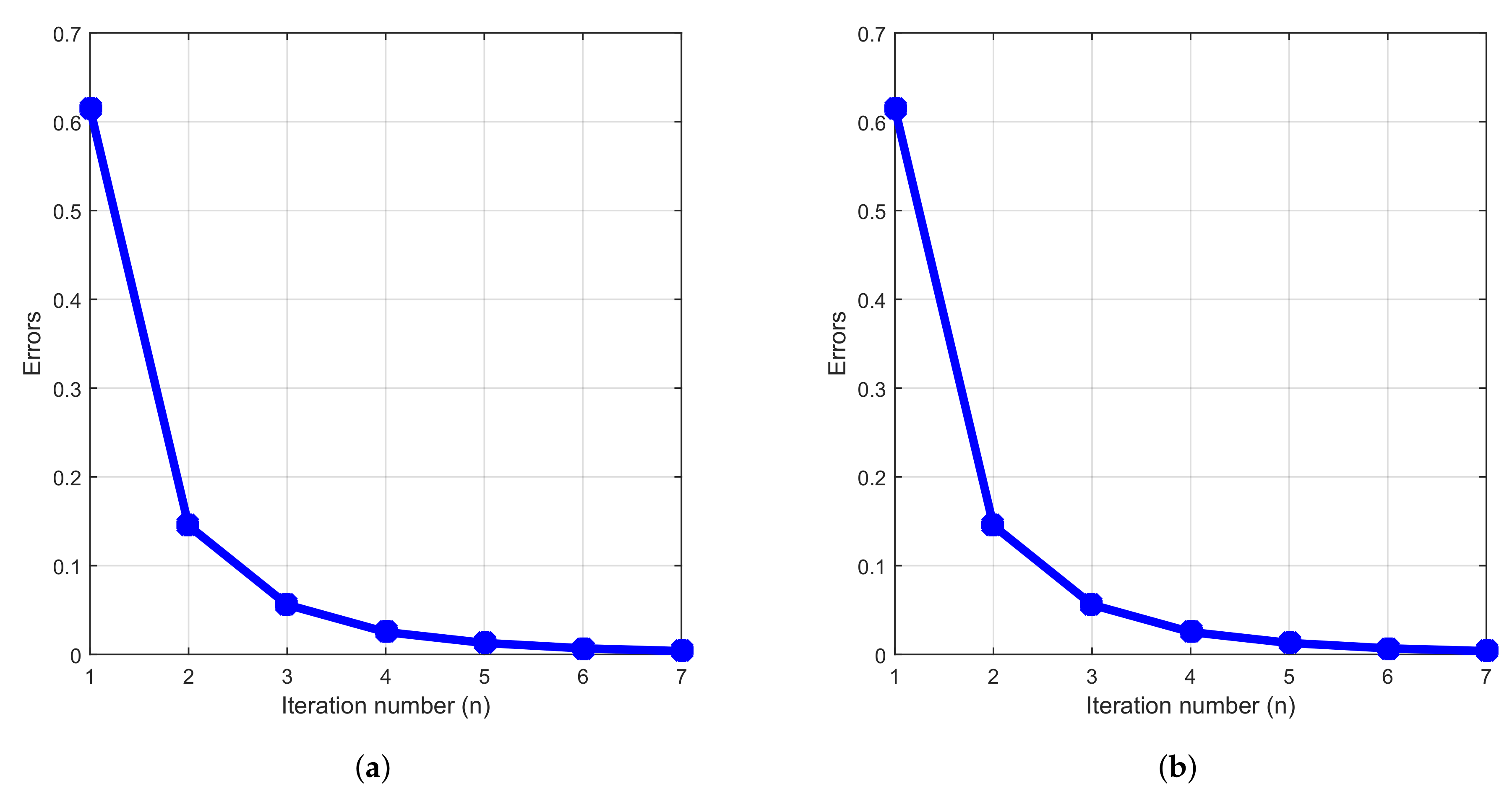
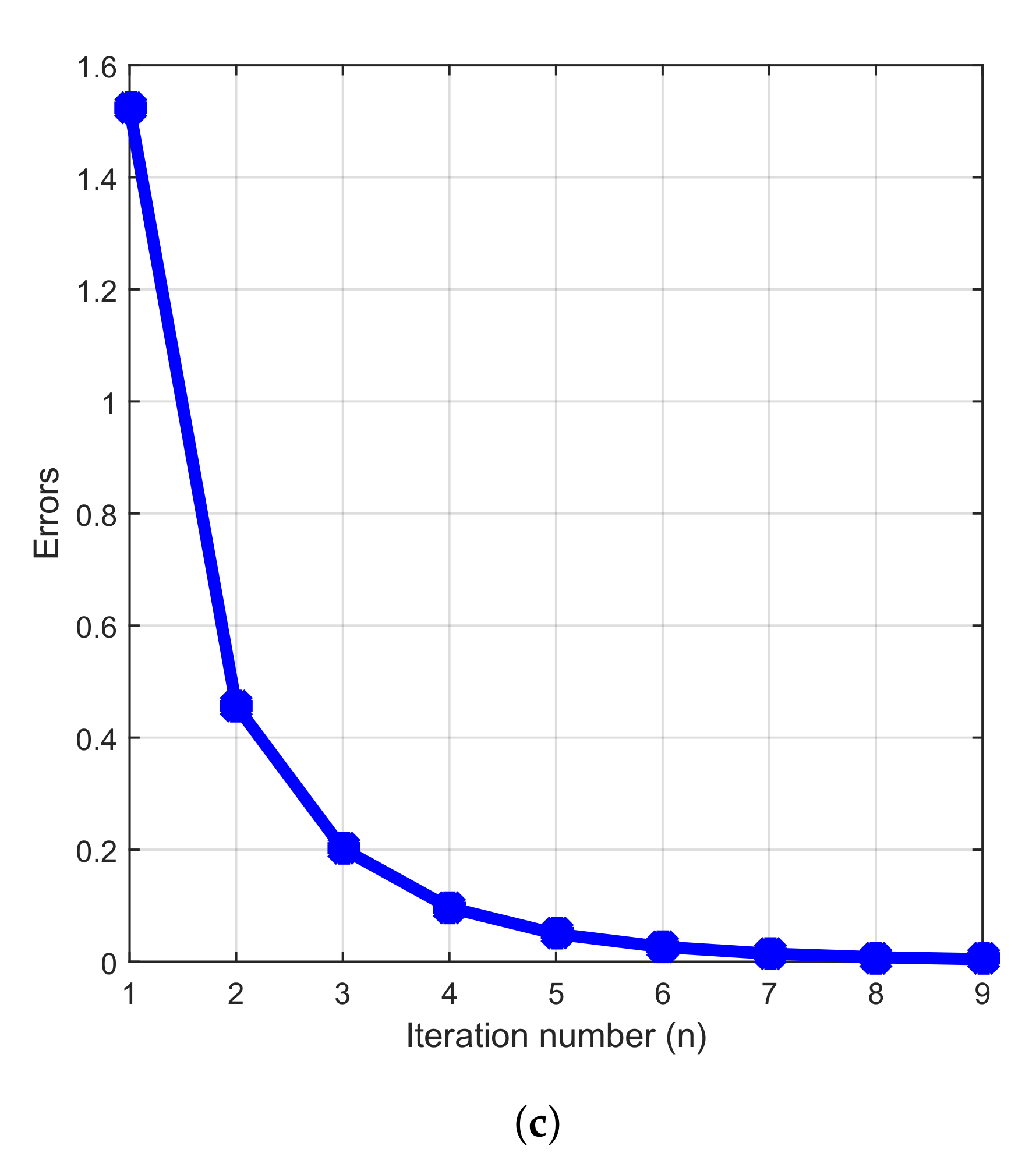
4. Numerical Example
- Case 1:.
- Case 2:.
- Case 2:.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oden, J.T.; Kikuchi, N. Theory of variational inequalities with applications to problems of flow through porous media. Int. J. Eng. Sci. 1980, 18, 1173–1284. [Google Scholar] [CrossRef]
- Stampacchia, G. Variational inequalities. In Theory and Applicalions of Monotone Operators; Ghizzetti, A., Ed.; Edizioni Oderisi: Gubbio, Italy, 1969; pp. 102–192. [Google Scholar]
- Alakoya, T.O.; Jolaoso, L.O.; Mewomo, O.T. Modified inertia subgradient extragradient method with self adaptive stepsize for solving monotone variational inequality and fixed point problems. Optimization 2020. [Google Scholar] [CrossRef]
- Alakoya, T.O.; Jolaoso, L.O.; Mewomo, O.T. Two modifications of the inertial Tseng extragradient method with self-adaptive step size for solving monotone variational inequality problems. Demonstr. Math. 2020, 53, 208–224. [Google Scholar] [CrossRef]
- Allen, G. Variational inequalities, complementarity problems, and duality theorems. J. Math. Anal. Appl. 1977, 58, 1–10. [Google Scholar] [CrossRef]
- Izuchukwu, C.; Mebawondu, A.A.; Mewomo, O.T. A New Method for Solving Split Variational Inequality Problems without Co-coerciveness. J. Fixed Point Theory Appl. 2020, 22, 1–23. [Google Scholar] [CrossRef]
- Jolaoso, L.O.; Taiwo, A.; Alakoya, T.O.; Mewomo, O.T. Strong convergence theorem for solving pseudo-monotone variational inequality problem using projection method in a reflexive Banach space. J. Optim. Theory Appl. 2020, 185, 744–766. [Google Scholar] [CrossRef]
- Khan, S.H.; Alakoya, T.O.; Mewomo, O.T. Relaxed projection methods with self-adaptive step size for solving variational inequality and fixed point problems for an infinite family of multivalued relatively nonexpansive mappings in Banach spaces. Math. Comput. Appl. 2020, 25, 54. [Google Scholar] [CrossRef]
- Marino, G.; Xu, H.K. Explicit hierarchical fixed point approach to variational inequalities. J. Optim. Theory. Appl. 2011, 149, 61–78. [Google Scholar] [CrossRef]
- Moudafi, A. Viscosity approximation methods for fixed-point problems. J. Math. Anal. Appl. 2000, 241, 46–55. [Google Scholar] [CrossRef]
- Alakoya, T.O.; Jolaoso, L.O.; Mewomo, O.T. A self adaptive inertial algorithm for solving split variational inclusion and fixed point problems with applications. J. Ind. Manag. Optim. 2020. [Google Scholar] [CrossRef]
- Gibali, A.; Jolaoso, L.O.; Mewomo, O.T.; Taiwo, A. Fast and simple Bregman projection methods for solving variational inequalities and related problems in Banach spaces. Results Math. 2020, 75, 1–36. [Google Scholar] [CrossRef]
- Izuchukwu, C.; Ogwo, G.N.; Mewomo, O.T. An Inertial Method for solving Generalized Split Feasibility Problems over the solution set of Monotone Variational Inclusions. Optimization 2020. [Google Scholar] [CrossRef]
- Jolaoso, L.O.; Alakoya, T.O.; Taiwo, A.; Mewomo, O.T. Inertial extragradient method via viscosity approximation approach for solving Equilibrium problem in Hilbert space. Optimization 2020. [Google Scholar] [CrossRef]
- Oyewole, O.K.; Abass, H.A.; Mewomo, O.T. A Strong convergence algorithm for a fixed point constrainted split null point problem. Rend. Circ. Mat. Palermo II 2020. [Google Scholar] [CrossRef]
- Taiwo, A.; Owolabi, A.O.-E.; Jolaoso, L.O.; Mewomo, O.T.; Gibali, A. A new approximation scheme for solving various split inverse problems. Afr. Mat. 2020. [Google Scholar] [CrossRef]
- Németh, S.Z. Variational inequalities on Hadamard manifolds. Nonlinear Anal. 2003, 52, 1491–1498. [Google Scholar] [CrossRef]
- Aremu, K.O.; Abass, H.A.; Izuchukwu, C.; Mewomo, O.T. A viscosity-type algorithm for an infinitely countable family of (f,g)-generalized k-strictly pseudononspreading mappings in CAT(0) spaces. Analysis 2020, 40, 19–37. [Google Scholar] [CrossRef]
- Aremu, K.O.; Izuchukwu, C.; Ogwo, G.N.; Mewomo, O.T. Multi-step Iterative algorithm for minimization and fixed point problems in p-uniformly convex metric spaces. J. Ind. Manag. Optim. 2020. [Google Scholar] [CrossRef]
- Aremu, K.O.; Izuchukwu, C.; Ugwunnadi, G.C.; Mewomo, O.T. On the proximal point algorithm and demimetric mappings in CAT(0) spaces. Demonstr. Math. 2018, 51, 277–294. [Google Scholar] [CrossRef]
- Bento, G.C.; Ferreira, O.P.; Oliveira, P.R. Proximal point method for a special class of non convex functions on Hadamard manifolds. Optimization 2015, 64, 289–319. [Google Scholar] [CrossRef]
- Chen, S.L.; Huang, N.J. Vector variational inequalities and vector optimization problems on Hadamard manifolds. Optim. Lett. 2016, 10, 753–767. [Google Scholar] [CrossRef]
- Dehghan, H.; Izuchukwu, C.; Mewomo, O.T.; Taba, D.A.; Ugwunnadi, G.C. Iterative algorithm for a family of monotone inclusion problems in CAT(0) spaces. Quaest. Math. 2020, 43, 975–998. [Google Scholar] [CrossRef]
- Ogwo, G.N.; Izuchukwu, C.; Aremu, K.O.; Mewomo, O.T. A viscosity iterative algorithm for a family of monotone inclusion problems in an Hadamard space. Bull. Belg. Math. Soc. Simon Stevin 2020, 27, 127–152. [Google Scholar] [CrossRef]
- Ogwo, G.N.; Izuchukwu, C.; Aremu, K.O.; Mewomo, O.T. On θ-generalized demimetric mappings and monotone operators in Hadamard spaces. Demonstr. Math. 2020, 53, 95–111. [Google Scholar] [CrossRef]
- Taiwo, A.; Jolaoso, L.O.; Mewomo, O.T. Viscosity approximation method for solving the multiple-set split equality common fixed-point problems for quasi-pseudocontractive mappings in Hilbert Spaces. J. Ind. Manag. Optim. 2017. [Google Scholar] [CrossRef]
- Ugwunnadi, G.C.; Izuchukwu, C.; Mewomo, O.T. Strong convergence theorem for monotone inclusion problem in CAT(0) spaces. Afr. Mat. 2019, 31, 151–169. [Google Scholar] [CrossRef]
- Khatibzadeh, H.; Ranjbar, S. A variational inequality in complete CAT(0) spaces. J. Fixed Point Theory Appl. 2015, 17, 557–574. [Google Scholar] [CrossRef]
- Alizadeh, S.; Dehghan, H.; Moradlou, F. Δ-convergence theorem for inverse strongly monotone mapping in CAT(0) spaces. Fixed Point Theory 2018, 19, 45–56. [Google Scholar] [CrossRef]
- Osisiogu, U.A.; Adum, F.L.; Efor, T.E. Strong convergence results for variational inequality problem in CAT(0) spaces. Adv. Nonlinear Var. Inequal. 2020, 23, 84–101. [Google Scholar]
- Izuchukwu, C.; Okeke, C.C.; Isiogugu, F.O. Viscosity iterative technique for split variational inclusion problem and fixed point problem between Hilbert space and Banach space. J. Fixed Point Theory Appl. 2018, 20, 1–25. [Google Scholar] [CrossRef]
- Song, Y.; Liu, X. Convergence comparison of several iteration algorithms for the common fixed point problems. Fixed Point Theory Appl. 2009, 2009, 824374. [Google Scholar] [CrossRef][Green Version]
- Bruhat, F.; Tits, J. Groupes réductits sur un cor local. In Donnee´s Radicielles Valuee´s; Institut des Hautes E´tudes Scientifiques: Bures-sur-Yvette, France, 1972; Volume 41. [Google Scholar]
- Kirk, W.A. Fixed point theorems in CAT(0) spaces and R-trees. Fixed Point Theory Appl. 2004, 2004, 309–316. [Google Scholar] [CrossRef]
- Bridson, M.R.; Haefliger, A. Metric Spaces of Non-Positive Curvature. In Fundamental of Mathematical Sciences; Springer: Berlin, Germany, 1999; Volume 319. [Google Scholar]
- Reich, S.; Shafrir, I. Nonexpansive iterations in hyperbolic spaces. Nonlinear Anal. 1990, 15, 537–558. [Google Scholar] [CrossRef]
- Goebel, K.; Reich, S. Uniform Convexity, Hyperbolic Geometry and Nonexpansive Mappings; Marcel Dekker: New York, NY, USA, 1984. [Google Scholar]
- Khatibzadeh, H.; Ranjbar, S. Monotone operators and the proximal point algorithm in complete CAT(0) metric spaces. J. Aust. Math. Soc. 2017, 103, 70–90. [Google Scholar] [CrossRef]
- Aremu, K.O.; Jolaoso, L.O.; Izuchukwu, C.; Mewomo, O.T. Approximation of common solution of finite family of monotone inclusion and fixed point problems for demicontractive mappings in CAT(0) spaces. Ric. Mat. 2020, 69, 13–34. [Google Scholar] [CrossRef]
- Berg, I.D.; Nikolaev, I.G. Quasilinearization and curvature of Alexandrov spaces. Geom. Dedicata 2008, 133, 195–218. [Google Scholar] [CrossRef]
- Dhompongsa, S.; Panyanak, B. On Δ-convergence theorems in CAT(0) spaces. Comp. Math. Appl. 2008, 56, 2572–2579. [Google Scholar] [CrossRef]
- Dhompongsa, S.; Kirk, W.A.; Sims, B. Fixed points of uniformly Lipschitzian mappings. Nonlinear Anal. 2006, 65, 762–772. [Google Scholar] [CrossRef]
- Kirk, W.A.; Panyanak, B. A concept of convergence in geodesic spaces. Nonlinear Anal. 2008, 68, 3689–3696. [Google Scholar] [CrossRef]
- Dehghan, H.; Rooin, J. A characterization of metric projection in CAT(0) spaces. arXiv 2013, arXiv:1311.4174VI. [Google Scholar]
- Dehghan, H.; Rooin, J. Metric projection and convergence theorems for nonexpansive mapping in Hadamard spaces. arXiv 2014, arXiv:1410.1137VI. [Google Scholar]
- Chidume, C.E.; Bello, A.U.; Ndambomve, P. Strong and Δ-convergence theorems for common fixed points of a finite family of multivalued demicontractive mappings in CAT(0) soaces. Abstr. Appl. Anal. 2014, 2014, 805168. [Google Scholar] [CrossRef]
- Leustean, L. Nonexpansive iterations in uniformly convex W-hyperbolic spaces. arXiv 2013, arXiv:0810.4117. [Google Scholar]
- Kakavandi, B.A.; Amini, M. Duality and subdifferential for convex functions on complete CAT(0) metric spaces. Nonlinear Anal. 2010, 73, 3450–3455. [Google Scholar] [CrossRef]
- Dhompongsa, S.; Kirk, W.A.; Panyanak, B. Nonexpansive set-valued mappings in metric and Banach spaces. J. Nonlinear Convex Anal. 2007, 8, 35–45. [Google Scholar]
- Taiwo, A.; Alakoya, T.O.; Mewomo, O.T. Halpern-type iterative process for solving split common fixed point and monotone variational inclusion problem between Banach spaces. Numer. Algorithms 2020. [Google Scholar] [CrossRef]
- Xu, H.K. Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 2002, 66, 240–256. [Google Scholar] [CrossRef]
- Taiwo, A.; Jolaoso, L.O.; Mewomo, O.T.; Gibali, A. On generalized mixed equilibrium problem with α-β-μ bifunction and μ-τ monotone mapping. J. Nonlinear Convex Anal. 2020, 21, 1381–1401. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aremu, K.O.; Izuchukwu, C.; Abass, H.A.; Mewomo, O.T. On a Viscosity Iterative Method for Solving Variational Inequality Problems in Hadamard Spaces. Axioms 2020, 9, 143. https://doi.org/10.3390/axioms9040143
Aremu KO, Izuchukwu C, Abass HA, Mewomo OT. On a Viscosity Iterative Method for Solving Variational Inequality Problems in Hadamard Spaces. Axioms. 2020; 9(4):143. https://doi.org/10.3390/axioms9040143
Chicago/Turabian StyleAremu, Kazeem Olalekan, Chinedu Izuchukwu, Hammed Anuolwupo Abass, and Oluwatosin Temitope Mewomo. 2020. "On a Viscosity Iterative Method for Solving Variational Inequality Problems in Hadamard Spaces" Axioms 9, no. 4: 143. https://doi.org/10.3390/axioms9040143
APA StyleAremu, K. O., Izuchukwu, C., Abass, H. A., & Mewomo, O. T. (2020). On a Viscosity Iterative Method for Solving Variational Inequality Problems in Hadamard Spaces. Axioms, 9(4), 143. https://doi.org/10.3390/axioms9040143





