Abstract
In this paper, we consider some paraconsistent calculi in a Hilbert-style formulation with the rule of detachment as the sole rule of interference. Each calculus will be expected to contain all axiom schemas of the positive fragment of classical propositional calculus and respect the principle of gentle explosion.
1. Introduction
The principle of explosion states that from any set of contradictory formulas any other formula follows. Paraconsistent logic can be described as a logic in which the principle does not hold. The ‘definition’ is very simple, but it is also very broad. This may lead to some ambiguity and cause interpretive problems, especially if we aim to draw a sharp distinction between paraconsistent and some other nonclassical logics. In this paper, we discuss some possible consequences of the definition. We examine several paraconsistent calculi that respect the so-called principle of gentle explosion, according to which from any set of formulas any other formula follows. The calculi (of paraconsistent logic) that admit the principle will be called gently paraconsistent.
Let denote a denumerable set of all propositional variables: , , , etc. The set of formulas is defined in the standard way using propositional variables from and the symbols ¬, ∨, ∧ and → for negation, disjunction, conjunction and implication, respectively. The connective of equivalence, , is treated as an abbreviation for , and hence it will be omitted. We say that a formula is atomic, if ; otherwise will be called complex. By literals we mean the set of all formulas of the form , where , and (if , then ; if , then ; etc.). We use lowercase Greek letters for formulas and uppercase Greek letters for subsets of .
In , we will consider axiomatic propositional calculi in a Hilbert-style formulation with the rule of detachment, (MP) , , as the sole rule of interference. Each calculus discussed in this paper is expected to have all axiom schemas of the positive fragment of classical propositional calculus (, for short), that is, all instances of the following schemas:
- ()
- ()
- ()
- ()
- ()
- ()
- ()
- ()
- () ,
and include the law of gentle explosion: () .
Definition 1.
For , any and any , we say that α is provable from within (in symbols: ) if, and only if there is a finite sequence of formulas, , , ⋯, such that and for each , either , or is an axiom of , or for some , we have . A formula α is a thesis of (in symbols: ) iff α is provable from within (henceforth, we will use iff as shorthand for if, and only if).
Notice that each calculus may be identified with a triple , but it is determined by its set of axioms which is included in . Moreover, it can be verified that is a finitary consequence relation satisfying the so-called Tarskian properties (viz. reflexivity, monotonicity and transitivity).
Lemma 1.
Let and , then we have
- (1)
- iff for some finite ,
- (2)
- If , then
- (3)
- If and , then
- (4)
- If , and for every it is true that , then
- (5)
- If and , then ; in particular,
if and , then .
Proof.
We refer the reader to [1] and [2] for details. □
The deduction theorem holds for any calculus having (MP) as the sole rule of inference, and (), () as its axiom schemas. Thus we have
Theorem 1.
For any and : iff .
It follows from (), the deduction theorem and (MP) that the following lemma holds as well:
Lemma 2.
For any and : if and , then .
Remark 1.
The following formulas are provable in :
- .
The formulas will be useful for proving the results presented below.
2. Gently Paraconsistent Calculi
The set of axiom schemas of enriched with () and () yields the axiom system of classical propositional calculus (in short: ). From the viewpoint of paraconsistency, neither () nor () seems to be controversial, and therefore they could be generally accepted. There is a problem, however, in admitting () and () simultaneously. This is because the pair of formulas is equivalent, on the grounds of , to () . The latter, being viewed as a highly contentious logical law, should be rejected. Not surprisingly then, () cannot be universally accepted either. On the other hand, the formula () appears to be more applicable than (), in the sense that its application does not need to be limited, for example, to certain complex formulas (cf. Section 2.2 and Section 2.5).
2.1. The Calculus
The basic gently paraconsistent calculus is . The calculus is defined by the axioms of , () and (MP) as the sole rule of inference. It is a proper subsystem of the paracomplete logic . The , as proposed in [3], is axiomatized by , () and (MP). The calculus may be seen as an example of a paranormal calculus (in Miró Quesada’s terminology), that is, a calculus which is both paraconsistent and paracomplete. Some other examples of the paranormal calculi are given in [4,5].
Definition 2.
An -valuation is any function that satisfies, for any , the following conditions:
- (∧) = 1 iff = 1 and = 1
- (∨) = 1 iff = 1 or = 1
- (→) = 1 iff = 0 or = 1
- () if = = 1, then = 0.
Definition 3.
A formula α is an -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
Theorem 2.
For every and : if then .
The proof of soundness proceeds by induction on the length of a derivation in . To prove the completeness, we apply the method which is based on the notion of maximal nontrivial sets of formulas (see [6,7]). To begin with, let us recall some important definitions and results.
Definition 4.
Let be a calculus (satisfying Tarskian properties) and . We say that is a closed theory of iff for any , we have iff . We say that is maximal nontrivial with respect to in iff (i) and (ii) for every , if then .
Lemma 3
([6], Lemma 2.2.5). Every maximal nontrivial set with respect to some formula is a closed theory.
Observe that the lemma holds for . Additionally, we have
Lemma 4.
For any maximal nontrivial set with respect to α in , any , the mapping defined as (): = 1 iff , is an -valuation.
Proof.
We need to prove that the mapping v is an -valuation. The proof splits into a number of cases. The case (∧) follows directly from the definition of (), the axioms – and Lemma 1; the case (∨) from (), – and Lemma 1.
Case (→): (if–then) Assume, for a contradiction, that = 1, ) = 1 and ) = 0. Then, by (), we have that , and . Now, by Lemma 1, we get , , that is, . The formula () is a thesis of and the deduction theorem holds, so . Since the relation is transitive (see Lemma 1), then , which means that . However, . This entails a contradiction.
(then–if) There are two subcases to consider. Subcase (i): Suppose, for a contradiction, that ) = 0 and = 0. This implies that and , by (). Since is a maximal nontrivial set with respect to , then and . Hence, , , by the deduction theorem, and consequently, . Observe that () is a thesis of , so , by the deduction theorem. The relation is transitive, and therefore . Since is deductively closed, then . However, , by the main assumption. This yields a contradiction. Subcase (ii): Suppose that ) = 1. Then, by (), we get . This implies, by Lemma 1, that . Since is an axiom schema of , then, by the deduction theorem, we have . The relation is transitive, and hence . If , then , which means that = 1.
Case (): Assume, for a contradiction, that = 1, = 1 and = 1. Then by (), we have , and . By Lemma 1, we obtain , and . This implies that . Since () is an axiom schema of , then , by the deduction theorem. The relation is transitive, so . Observe that is deductively closed, then . However, by the main assumption, . This entails a contradiction. □
Notice that the so-called Lindenbaum–oś theorem holds, for any finitary calculus = .
Lemma 5
([2], Theorem 3.31; [6], Theorem 2.2.6). For any and such that , there is a maximal nontrivial set with respect to α in such that .
Thus, the completeness of follows
Theorem 3.
For all and : if , then .
Proof.
Assume that and let be a maximal nontrivial set with respect to in such that . Then, . Because Lemma 4 holds, there is an -valuation v such that = 0 and, for any , = 1. Hence, . □
Though the calculus is very weak and does not provide any adequate grounds for practical inference, it offers a good starting point for further research. In the subsequent paragraphs, we will discuss various paraconsistent extensions of .
2.2. The Calculus
The calculus is defined by , (), () , where , and (MP). There are only few paraconsistent calculi in which () is provable. One of them is Sette’s calculus . Anticipating what comes next in Section 2.5, Sette’s calculus will be the top paraconsistent extension of the calculi admitting () and (), simultaneously.
Definition 5.
An -valuation is any function that, for any , satisfies all the conditions of -valuation and, additionally: () if = 1, then = 0, where .
Definition 6.
A formula α is an -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
Theorem 4.
For every and : iff .
The proof of soundness is by induction on the structure of proofs in . The completeness proof strategy is exactly the same as that of the proof of Theorem 3. The key point is to show that the following lemma holds:
Lemma 6.
For any maximal nontrivial set with respect to α in , any , the mapping defined as (): = 1 iff , is an -valuation.
Proof.
Case (∧), (∨), (→) and (): The proof proceeds analogously to that of Lemma 4. Case (): Assume, for a contradiction, that = 1 and = 1, where . Then by (), we have and . It follows from Lemma 1 that and , which results in . By () and the deduction theorem, we easily show that . The relation is transitive, so . Since is deductively closed, then . However, (the main assumption). This entails a contradiction. □
Definition 7.
Let be the set of all theses of . For any calculi and in , we say that is an extension of iff . We say that is a proper subsystem of (in symbols: ) iff and .
Remark 2.
.
There is an alternative way to extend so that the resulting calculus preserves () as provable. Let be the calculus defined by , (), () , where , and (MP). It then follows from the deduction theorem, (), () and (MP) that () is a thesis of . Note that of the form () is not an -tautology. So, by completeness, it is not provable in , either. This suggests that the new calculus is strictly stronger than , i.e., .
Another example is the paranormal logic . The logic was considered in [4,8,9,10]. It is characterized by the four-valued matrix
where and are the sets of logical values and designated values, respectively; the connectives are defined in the following way:
|
|
|
|
An -valuation is any function compatible with the above truth tables. An -tautology is a formula which under every valuation v takes on the designated values .
All axioms of are -tautologies, and (MP) preserves tautologicality. However, the formula , being an -tautology, is unprovable in . This yields that .
A slightly different example is with . The logic, as proposed in [5,11], is axiomatizable by (), (), ()–(), () , where , and (MP). The formula of the form () is unprovable in , and neither is of the form () provable in , then we have that 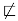 and
and 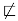 .
.
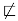 and
and 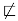 .
.2.3. The Calculus
The calculus is obtained from by adding the formula () as a new axiom schema, which indicates that is axiomatizable by , (), () and (MP). Since the law of excluded middle is unprovable in , we obviously have that . The calculus was considered in [12,13] as the strongest in the hierarchy of -calculi ().
Definition 8.
A -valuation is any function that satisfies, for any , the following conditions:
- (∧) = 1 iff = 1 and = 1
- (∨) = 1 iff = 1 or = 1
- (→) = 1 iff = 0 or = 1
- () if = 0, then = 1
- () if = 1, then = 0 or = 0.
Definition 9.
A formula α is a -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
Theorem 5.
For every and : iff .
The completeness proof is carried out similarly as for the calculus . In addition to Lemmas 3 and 5 given in Section 2.1, the following lemma is of particular importance:
Lemma 7.
For any maximal nontrivial set with respect to α in , any , the mapping defined as (): = 1 iff , is a -valuation.
Proof.
Case (∧), (∨), (→) and (): We proceed analogously to the proof of Lemma 4. Case (): Assume, for a contradiction, that = 0 and = 0. Then by (), we obtain and . Since is a maximal nontrivial set with respect to , then and . By Lemma 2, we get . Since () is a thesis of and Lemma 1 holds, then . Recall that is a closed theory, so . However, . This entails a contradiction.
Case (): Suppose, for a contradiction, that = 1, = 1 and = 1. The remaining part of the proof is similar to the case () of Lemma 4 and thus omitted. □
As of the form () is not a thesis of and of the form () is not provable in , it follows that 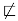 and
and 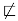 .
.
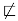 and
and 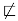 .
.2.4. The Calculi and
The calculus comprises the axioms of , (), (), () and (MP), which clearly yields that both and . The is an example of calculus which is paraconsistent only at the level of literals: a pair of the formulas and yields any iff is not a propositional variable nor is its iterated negation.
Definition 10.
A -valuation is any function that satisfies, for any , all the conditions of -valuation and additionally: () if = 1, then = 0, where .
Definition 11.
A formula α is a -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
Theorem 6.
For every and : iff .
Proof.
The proof proceeds as in Theorems 2–4. □
The calculus was introduced in [14]. It arose as a result of the extension of with the law of double negation () , which suggests that . Moreover, we have
Remark 3.
The calculus is axiomatizable by , (), () and (MP).
Proof.
See op. cit., p. 227, for details. □
Definition 12.
A -valuation is any function that satisfies, for any , the following conditions:
- (∧) = 1 iff = 1 and = 1
- (∨) = 1 iff = 1 or = 1
- (→) = 1 iff = 0 or = 1
- () if = 0, then = 1.
- () if = 1, then = 0.
Definition 13.
A formula α is a -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
Theorem 7.
For every and : iff .
Proof.
We refer the reader to op. cit., pp. 230–231, for details. □
Since of the form () is not a thesis of and of the form () is not provable in , it follows that and . There exists, however, some paraconsistent calculi in which () does not fail (see [15], for discussion on the topic). The example of such a calculus is .
2.5. Sette’s Calculus
The calculus , proposed in [16], is defined in the language with negation and implication as primitives by (), (), () , () , () . The sole rule of inference is (MP). Some alternative axiomatizations of have been developed since then (see e.g., [9,17,18,19,20,21,22]).
Sette’s calculus is sound and complete with respect to the matrix , where and are the sets of logical and designated values, respectively. The connectives of → and ¬ are determined by the following truth tables (cit. per [16], p. 176):
|
|
A -valuation is any function v from the set of formulas to the set of logical values, i.e., , compatible with the above truth tables. A -tautology is a formula which under every valuation v takes on the designated values . Conjunction and disjunction are definable connectives: ; (cit. per [9,20]).
Remark 4.
The calculus is axiomatizable by , (), (), (), where , and (MP).
Proof.
The proof splits into two steps. To show that the axioms ()–(), (), () and () are -tautologies, and (MP) preserves tautologicality, it suffices to apply the three-valued semantics for (plus the definitions of ‘missing’ connectives). Next we need to demonstrate that (), () and () are provable in the proposed axiomatization. This in turn follows from the results of [17], pp. 270–272, and [19], pp. 1111–1113. □
Sette’s calculus is maximal with respect to (see [16], pp. 179–180). Consequently, it is the top extension of all gently paraconsistent calculi discussed in this paper.
3. Final Remarks
We considered several paraconsistent calculi that admitted the principle of gentle explosion, namely
- = + () + (MP)
- = + () + () + (MP)
- = + () + () + (MP)
- = + () + () + () + (MP)
- = + () + () + (MP)
- = + () + () + () + (MP).
They all form together the lattice structure shown in Figure 1.
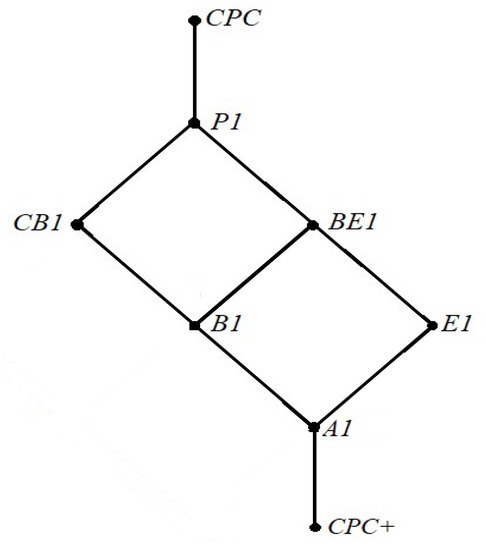
Figure 1.
Gently paraconsistent calculi.
It is noteworthy that some well-known (not-gently) paraconsistent logics can be obtained by eliminating () from the axiom schemas. For instance, dropping () from results in obtaining the logic (see [3], for details); dropping () from results in obtaining in the logic (see [23]). The calculi form together the lattice structure shown in Figure 2.
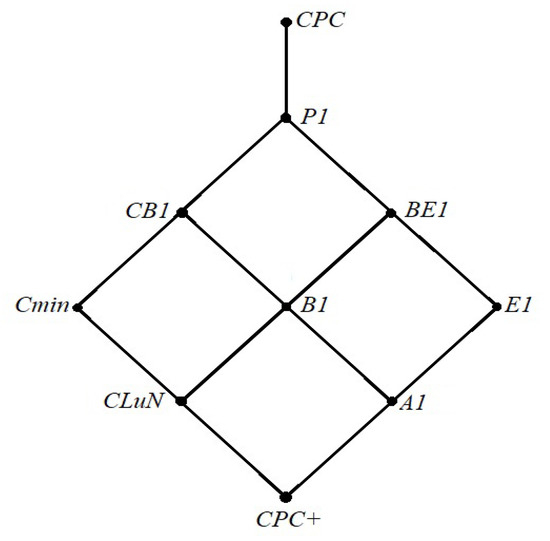
Figure 2.
Paraconsistent extensions of .
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wójcicki, R. Theory of Logical Calculi. Basic Theory of Consequence Operations. In Synthese Library; Springer: Dutch, The Netherlands, 1988; Volume 199. [Google Scholar]
- Pogorzelski, W.A.; Wojtylak, P. Completeness Theory for Propositional Logics; Studies in Universal Logic: Birkhäuser Basel, Switzerland, 2008. [Google Scholar]
- Batens, D.; Clercq, K.D.; Kurtonina, N. Embedding and interpolation for some paralogics. The propositional case. Rep. Math. Log. 1999, 33, 29–44. [Google Scholar]
- Karpenko, A.S.; Tomova, N. Bochvar’s three-valued logic and literal paralogics: Their lattice and functional equivalence. Log. Log. Philos. 2017, 26, 207–235. [Google Scholar] [CrossRef]
- Lewin, R.A.; Mikenberg, I.F. Literal-paraconsistent and literal-paracomplete matrices. Math. Log. Quart. 2006, 52, 478–493. [Google Scholar] [CrossRef]
- Carnielli, W.; Coniglio, M.E. Paraconsistent Logic: Consistency, Contradiction and Negation, Logic, Epistemology, and the Unity of Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; Volume 40. [Google Scholar]
- da Costa, N.C.A.; Alves, E.H. A semantical analysis of the calculi Cn. Notre Dame J. Form. Log. 1977, 18, 621–630. [Google Scholar] [CrossRef]
- Devyatkin, L.Y. Many-Valued paraconsistent extensions of Classical Positive Propositional Calculus. J. Appl. Log. 2019, 6, 229–253. [Google Scholar]
- Fernández, V.L.; Coniglio, M.E. Combining Valuations with Society Semantics. J. Appl. Non Class. Log. 2003, 13, 21–46. [Google Scholar] [CrossRef]
- Tomova, N.E. On properties of a class of four-valued paranormal logics. Log. Investig. 2018, 24, 75–89. [Google Scholar]
- Puga, L.Z.; da Costa, N.C.A. On the imaginary logic of N. A. Vasiliev. Math. Log. Q. 1988, 34, 205–211. [Google Scholar] [CrossRef]
- Ciuciura, J. Paraconsistent heap. A Hierarchy of mbCn-systems. Bull. Sect. Log. 2014, 43, 173–182. [Google Scholar]
- Ciuciura, J. Paraconsistency and Paracompleteness. Log. Investig. 2019, 25, 46–60. [Google Scholar] [CrossRef]
- Ciuciura, J. On the System CB1 and a Lattice of the Paraconsistent Calculi. Log. Log. Philos. 2020, 29, 223–237. [Google Scholar] [CrossRef]
- Karpenko, A.S. Atomic and molecular paraconsistent logics. Log. Anal. 2002, 177, 31–37. [Google Scholar]
- Sette, A.M. On the propositional calculus P1. Math. Jpn. 1973, 18, 89–128. [Google Scholar]
- Ciuciura, J. Paraconsistency and Sette’s calculus P1. Log. Log. Philos. 2015, 24, 265–273. [Google Scholar] [CrossRef]
- Ciuciura, J. A Note on Fernández–Coniglio’s Hierarchy of Paraconsistent Systems. Axioms 2020, 9, 35. [Google Scholar] [CrossRef]
- Ciuciura, J. Sette’s calculus P1 and some hierarchies of paraconsistent systems. J. Log. Comput. 2020, 30, 1109–1124. [Google Scholar] [CrossRef]
- Marcos, J. On a problem of da Costa. In Essays on the Foundations of Mathematics and Logic; Sica, G., Ed.; Polimetrica: Monza, Italy, 2005; Volume 2, pp. 53–69. [Google Scholar]
- Popov, V.M. On a three-valued paracomplete logic. Log. Investig. 2002, 9, 175–178. (In Russian) [Google Scholar]
- Sette, A.M.; Alves, E.H. On the equivalence between two systems of paraconsistent logic. Bull. Sect. Log. 1995, 24, 155–157. [Google Scholar]
- Carnielli, W.; Marcos, J. Limits for paraconsistent calculi. Notre Dame J. Form. Log. 1999, 40, 375–390. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).