A Two Dimensional Discrete Mollification Operator and the Numerical Solution of an Inverse Source Problem

Abstract

We consider a two-dimensional time fractional diffusion equation and address the important inverse problem consisting of the identification of an ingredient in the source term. The fractional derivative is in the sense of Caputo. The necessary regularization procedure is provided by a two-dimensional discrete mollification operator. Convergence results and illustrative numerical examples are included.

1. Introduction

The mollification method has been known since the 1980s as a regularization procedure for ill-posed problems [1,2]. Later on, it was implemented as an accelerator of explicit schemes [2,3,4] and there are a variety of implementations and variations. Among the most recent, Reference [5] presents a new and very close method, called the convolution regularization method.

Applications of one-dimensional mollification methods are found, for instance, in References [6,7,8]. Mollification in two dimensions is less common and it is worth mentioning that it serves as a smoothing operator in Reference [9], appears as an accelerator of explicit schemes in Reference [4], and is a regularization tool for an identification problem in Reference [10].

In this paper, we deal with the two-dimensional discrete mollification operator defined in Section 3.2 of Reference [4]. This operator, which we call a 2DDM operator, will be defined shortly. Based on this operator, we propose the stable solution of a challenging inverse problem consisting of the identification of an ingredient in a source term for a time fractional diffusion equation, where the fractional derivative is defined in the sense of Caputo.

This inverse problem was solved in References [11,12,13]. The first two papers implemented the Tikhonov method as the required regularization procedure. The third one introduced a modified quasi-boundary regularization method. Our main original contribution is the implementation of two-dimensional discrete mollification as a regularization method for the numerical solution of this inverse source problem. It is important to have alternatives and this is the case with regularization. We offer an alternative that has not been considered before for the stable solution of this inverse problem.

The solution of the inverse problem requires the solution of the corresponding direct problem. In Reference [12], there are no details on the numerical solution, although the authors provide abundant numerical results. In Reference [11], the numerical solution is obtained by a finite difference scheme, but the only examples are one-dimensional. In our numerical solution of the direct problem, we make use of the implicit scheme defined in Reference [14] for a more general equation.

Problems based on time fractional diffusion equations are useful in the description of anomalous diffusion in highly heterogeneous porous media. There are a variety of time fractional inverse source problems. According to the number of fractional differentiation orders, they are classified as single-term and multi-term problems. This paper deals with a single-term problem that is ill-posed in the Hadamard sense. However, there are other situations, for instance in Reference [15], where the problem is single-term and depends on a parameter. For some values of this parameter, it is a well-posed problem in the Hadamard sense. Finally, we mention that in Reference [16], there is a theoretical analysis and some numerical results for a fairly general multiterm time fractional inverse source problem.

The paper is organized as follows: Section 2 is devoted to the 2DDM operator. Section 3 deals with the convergence analysis for the solution of the inverse problem, and Section 4 includes the numerical experiments. After this section, there are some final comments and conclusions.

2. The 2D Discrete Mollification Operator (2DDM Operator)

2.1. One-Dimensional Discrete Mollification

The one-dimensional mollification of a discrete function [1,2,4] is defined as follows: Let $\mathit{y}={\left\{y_j\right\}}_{j\in \mathbb{Z}}$ be a discrete function, which can, for example, be the evaluations or cell averages of a real function $y=y\left(x\right)$ at equidistant grid points on:

$$X=\left\{x_j:x_j=x_0+jh,j\in \mathbb{Z}\right\}.$$

The discrete mollification of $\mathit{y}$, denoted $J_{\eta }y$, is:

$${\left(J_{\eta }\mathit{y}\right)}_j:=\sum _{i=-\eta }^{\eta }{w}_i{y}_{j+i},$$

(1)

where $\eta$ is the integer support parameter.

2.2. Mollification Weights

The weights are defined as integrals over cells. Given positive real numbers p and h, compute:

$$\delta =\frac{\left(\eta +1/2\right)h}{p}.$$

(2)

This is the continuous mollification parameter. The weights are obtained by numerical integration of the truncated Gaussian kernel:

$${\kappa }_{p\delta }\left(t\right)=\left\{\begin{array}{cc}{A}_p{\delta }^{-1}exp(-t^2/{\delta }^2),& \left|t\right|\le p\delta \\ 0,& \left|t\right|>p\delta ,\end{array}\right.$$

where the normalization constant:

$$A_p={\left({\displaystyle \underset{-p}{\overset{p}{\int }}}exp(-s^2)ds\right)}^{-1}$$

is chosen in such a way that ${\int }_{\mathbb{R}}{\kappa }_{p\delta }=1.$ Thus, the mollification weights are obtained by integrations of this kernel over cells, namely,

$$w_i={\displaystyle \underset{t_i}{\overset{t_{i+1}}{\int }}}{\kappa }_{p\delta }\left(s\right)ds,$$

(3)

where:

$$t_j=\left(j-1/2\right)h,j\in \mathbb{Z}.$$

(4)

We usually take $p=3$. Chosen in this way, the weights $w_i$ satisfy:

$$w_i=w_{-i},0\le w_i\le w_{i-1},i=1,\cdots ,\eta ;\sum _{i=-\eta }^{\eta }{w}_i=1,\sum _{i=-\eta }^{\eta }i{w}_i=0.$$

(5)

The set of weights has a feature worth mentioning: Independence of the step size h.

$$\begin{array}{cc}\hfill w_i& ={\displaystyle \underset{t_i}{\overset{t_{i+1}}{\int }}}{\kappa }_{\delta p}\left(s\right)ds=A_p{\delta }^{-1}{\displaystyle \underset{t_i}{\overset{t_{i+1}}{\int }}}exp(-\frac{s^2}{{\delta }^2})ds\hfill \\ & =A_p{\displaystyle \underset{t_i/\delta }{\overset{t_{i+1}/\delta }{\int }}}exp(-s^2)ds\hfill \end{array}$$

and

$$\frac{t_i}{\delta }=p\frac{\left(i-1/2\right)h}{\left(\eta +1/2\right)h}=p\frac{\left(i-1/2\right)}{\left(\eta +1/2\right)},$$

then the $w_i$s depend only on p and $\eta$. Some weights are shown in Table 1.

Table 1. Mollification weights.

$\mathit{\eta }$	${\mathit{w}}_0$	${\mathit{w}}_1$	${\mathit{w}}_2$	${\mathit{w}}_3$	${\mathit{w}}_4$	${\mathit{w}}_5$
1	8.4272 $\times {10}^{-1}$	7.8640 $\times {10}^{-2}$
2	6.0387 $\times {10}^{-1}$	1.9262 $\times {10}^{-1}$	5.4438 $\times {10}^{-3}$
3	4.5556 $\times {10}^{-1}$	2.3772 $\times {10}^{-1}$	3.3291 $\times {10}^{-2}$	1.2099 $\times {10}^{-3}$
4	3.6266 $\times {10}^{-1}$	2.4003 $\times {10}^{-1}$	6.9440 $\times {10}^{-2}$	8.7275 $\times {10}^{-3}$	4.7268 $\times {10}^{-4}$
5	3.0028 $\times {10}^{-1}$	2.2625 $\times {10}^{-1}$	9.6723 $\times {10}^{-2}$	2.3430 $\times {10}^{-2}$	3.2095 $\times {10}^{-3}$	2.4798 $\times {10}^{-4}$

2.3. Two-Dimensional Discrete Mollification

Likewise [4], two-dimensional discrete mollification requires a uniform bidimensional grid of the form $(x_i,y_j)$ where $x_i=x_0+i{h}_x$ and $y_j=y_0+j{h}_y$. Let Y be a discrete function defined by $Y(x_i,y_j)=Y_{ij}$. For each positive integer $\eta$, the two dimensional discrete mollification of Y is:

$$\begin{array}{c}\hfill {\left[J_{\eta }^{2}Y\right]}_{ij}=\sum _{k=-\eta }^{\eta }\sum _{m=-\eta }^{\eta }{w}_k{w}_m{Y}_{i+m,j+k}.\end{array}$$

(6)

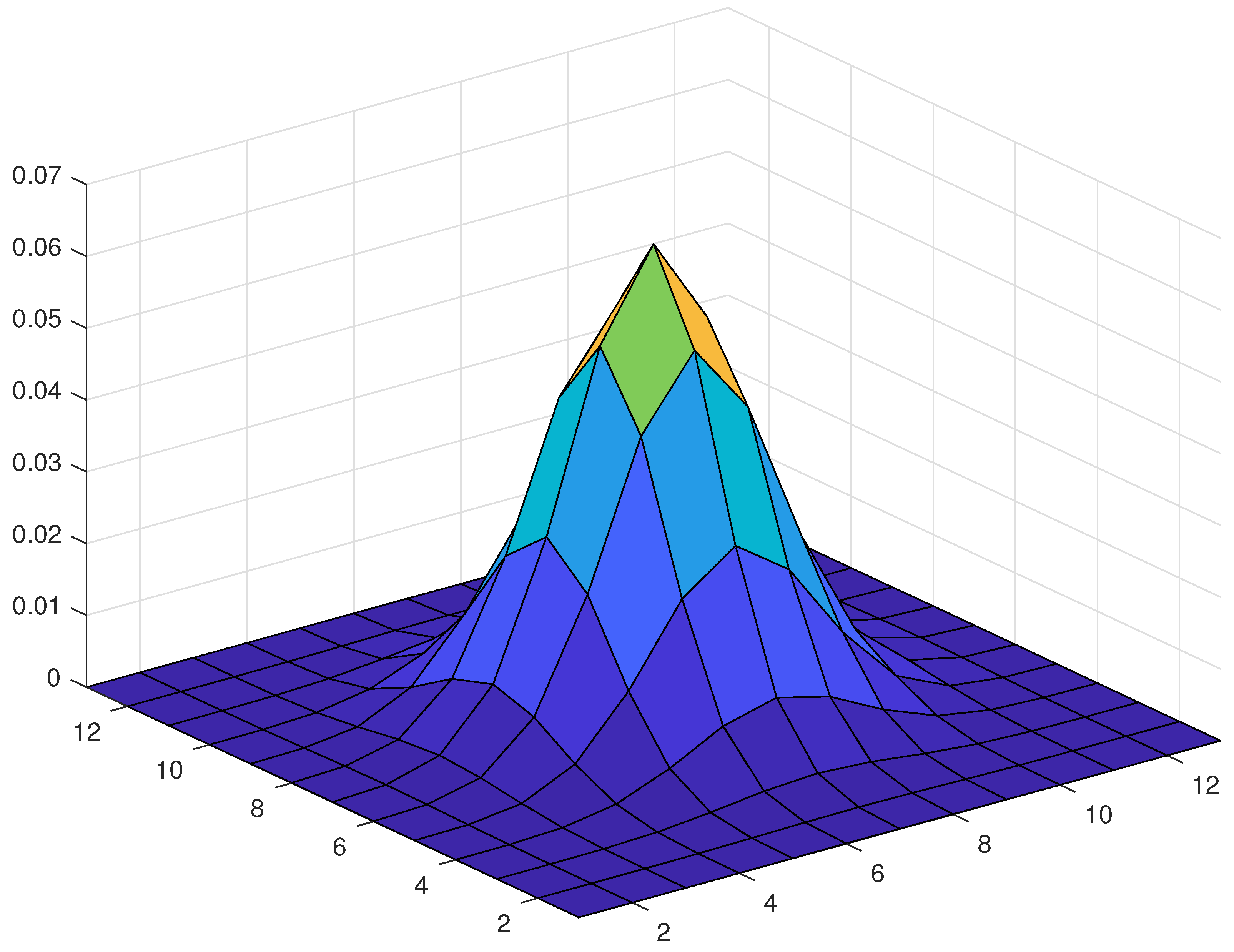
The weights of this two dimensional convolution are denoted by $w_{km}=w_k{w}_m$. If $h_x=h_y=h$ and $\delta$ is given by Equation (2), the shape of a weight is shown in Figure 1.

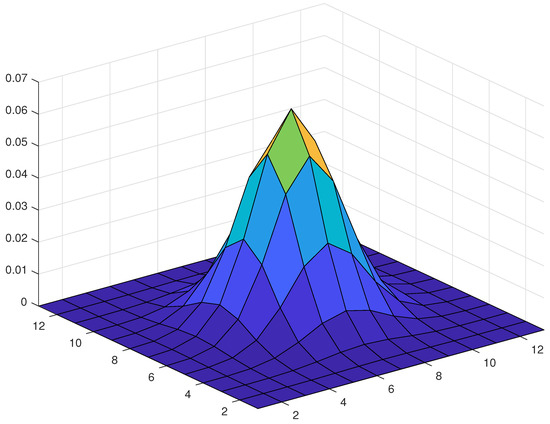
Figure 1. A weight for $\delta =0.015$ and $\eta =4$.

The main relation with one dimensional mollification is [4]:

$$\begin{array}{c}\hfill {\left[J_{\eta }^{2}Y\right]}_{ij}=\sum _{k=-\eta }^{\eta }\sum _{m=-\eta }^{\eta }{w}_k{w}_m{Y}_{i+m,j+k}=\sum _{k=-\eta }^{\eta }{w}_k\sum _{m=-\eta }^{\eta }{w}_m{Y}_{i+m,j+k}=\sum _{k=-\eta }^{\eta }{w}_k{\left[J_{\eta }^{x}Y\right]}_{i,j+k}=J_{\eta }^y{\left[J_{\eta }^{x}Y\right]}_{ij}.\end{array}$$

2.4. Abstract Setting

The discrete convolutions that define mollification in one and two dimensions have their counterparts in infinite dimensions. It is true that in numerical computations, one deals with discrete functions, but what about the error estimates? They relate the abstract model based on differential equations with the discretized problem.

Convolutions are troublesome near borders; thus, whenever a convolution is mentioned, some kind of domain restriction is in order. Our presentation of the abstract setting follows Reference [17]. Let $I=[0,1]\times [0,1],I_p=[-p,p]\times [-p,p],I_{p\delta }=[-p\delta ,p\delta ]\times [-p\delta ,p\delta ]$ and $I_{\delta }=[p\delta ,1-p\delta ]\times [p\delta ,1-p\delta ].$ If $s=(s_1,s_2),$ the two-dimensional truncated Gaussian kernel is defined by multiplication of the known one dimensional kernels, that is:

$${\varphi }_{\delta p}(s_1,s_2)={\kappa }_{\delta p}^x\left(s_1\right){\kappa }_{\delta p}^y\left(s_2\right)=\left\{\begin{array}{cc}{\mathbf{A}}_p{\delta }^{-2}exp(-(s_1^2+s_2^2)/{\delta }^2),& \hfill s\in I_{p\delta }\\ 0,& \hfill otherwise\end{array}\right.$$

(7)

where ${\mathbf{A}}_p={\left({\int }_{I_p}{exp(-\parallel s\parallel }_2^2)ds\right)}^{-1}.$ This kernel satisfies:

• $\varphi \ge 0$,
• $\varphi \equiv 0$ outside $I_{p\delta }$,
• ${\int }_{{\mathbb{R}}^2}{\varphi }_{\delta p}=1$.

Definition 1.

A function $g:{\mathbb{R}}^2\to \mathbb{R}$ is called Lipschitz continuous, if there exists a constant $C_{Lip}$ such that:

$$|g\left(x_1\right)-g\left(x_2\right)|\le C_{Lip}{\parallel x_1-x_2\parallel }_{\infty }$$

(8)

The next lemma establishes the consistency and stability of the two-dimensional discrete mollification.

Lemma 1.

Suppose g is a Lipschitz continuous function with Lipschitz constant L defined on I and $G=G_{ij}$ is the associated discrete function defined on a uniform grid covering $I_{\delta }$ with step size h in both directions. Then, there exists a constant C such that:

1. 

Consistency

$$\parallel J_{\eta }^2{G-g\parallel }_{\infty ,I_{\delta }}\le C\left(\delta +h\right).$$

(9)

Proof. 

This is Lemma 3.1 Part (1) of Reference [17]. □

Remark 1.

Notice that due to Equation (2), we may say that the right hand side bound is of the form $C\delta$, where C depends on $L,p$, and η.

2. 

Stability: If $g^{ϵ}$ is a Lipschitz continuous approximation of g so that $\parallel g^{ϵ}{-g\parallel }_{\infty ,I}\le ϵ$, then:

$$\parallel J_{\eta }^2{g}^{ϵ}{-g\parallel }_{2,I_{\delta }}\le C\left(\delta +ϵ\right).$$

(10)

Remark 2.

Actually, the right hand side bound is of the form $C(h+\delta +ϵ)$, according to the previous remark.

Proof. 

It follows from Part 1 that since:

$$\begin{array}{ccc}\hfill \parallel J_{\eta }^2{g}^{ϵ}{-g\parallel }_2^2& =& {\int }_{I_{\delta }}{|J_{\eta }^2{g}^{ϵ}-g|}^{2}dxdy\hfill \\ & \le & \parallel J_{\eta }^2{g}^{ϵ}{-g\parallel }_{\infty ,I_{\delta }}^2\mu \left(I_{\delta }\right)\hfill \\ & \le & {\left(\parallel J_{\eta }^2{g}^{ϵ}-g^{ϵ}{\parallel }_{\infty ,I_{\delta }}+{\parallel g^{ϵ}-g\parallel }_{\infty ,I_{\delta }}\right)}^2\hfill \\ & \le & C^{\prime }{\left(\delta +ϵ\right)}^2,\hfill \end{array}$$

where μ stands for measure. Notice that this estimate is valid in any other square subset of ${\mathbb{R}}^2$. Only the constant may change. □

3. The Inverse Source Problem

Fractional derivatives have been known since the seventeenth century, but only recently have they become the subject of attention due in part to a variety of interesting applications. Podlubny [18] says: “Fractional derivatives provide an excellent instrument for the description of memory and hereditary properties of various materials and processes.” We mention only two examples: For materials, we chose the damage evolution of brain tissue modeled in Reference [19] by a model in which the time derivative is a Caputo–Almeida fractional derivative. For processes, we selected the anomalous diffusion of a contaminant in fractured porous rocks modeled in Reference [20]. The model is based on fractional differentiation in the sense of Caputo.

3.1. Direct Problem

Our concern is a time fractional diffusion equation. More precisely, we are interested in an initial/boundary value problem, in which the time derivative is a Caputo fractional derivative of order $\alpha ,0<\alpha <1.$ The Caputo fractional derivative of order $\alpha$ of a differentiable function v is:

$$D_t^{\alpha }v\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma (1-\alpha )}{\int }_0^t\frac{v^{\prime }\left(\xi \right)}{{(t-\xi )}^{\alpha }}d\xi ,}\hfill & 0<\alpha <1,\hfill \\ v^{\prime }\left(t\right),\hfill & \alpha =1,\hfill \end{array}\right.$$

(11)

where $\Gamma$ is the Gamma function given by:

$$\Gamma \left(z\right)={\int }_0^{\infty }{x}^{z-1}{e}^{-x}dx.$$

(12)

We are interested in the following initial/boundary value problem:

$$\left.\begin{array}{cccc}{D}_t^{\alpha }u(z,t)-\left(Lu\right)(z,t)\hfill & =p\left(t\right)f\left(z\right),\hfill & z\in \Omega \hfill & \hfill t\in (0,T)\\ u(z,t)\hfill & =0,\hfill & z\in \partial \Omega \hfill & \hfill t\in (0,T)\\ u(z,0)\hfill & =0,\hfill & z\in \overline{\Omega }\hfill \end{array}\right\}$$

(13)

where $\Omega \subset {\mathbb{R}}^d$ and:

$$\begin{array}{ccc}\hfill Lu\left(z\right)& =& \sum _{i=1}^d\frac{\partial }{\partial z_i}\left(\sum _{j=1}^d{a}_{ij}\left(z\right)\frac{\partial }{\partial z_j}u\left(z\right)\right)+c\left(z\right)u\left(z\right),z\in \Omega .\hfill \end{array}$$

(14)

The coefficients satisfy $a_{ij}=a_{ji}\in C^1\left(\overline{\Omega }\right)$, ${\sum }_{i,j=1}^d{a}_{ij}{\zeta }_i{\zeta }_j>\theta {\sum }_{i=1}^d{\left|{\zeta }_i\right|}^2$ ($\theta >0$), $c\left(z\right)\le 0$, $c\in C\left(\overline{\Omega }\right)$. The theoretical analysis that follows is from References [11,13,21]. The operator $-L$ is a symmetric uniformly elliptic operator defined on $D(-L)=H^2(\Omega )\cap H_0^1(\Omega )$.

The direct problem is to find u that safisfies Equation (13), with p and f known functions and $\alpha$ a known fractional order of differentiation. If we think of this problem as the model for a contaminant diffusion in groundwater, then $f\left(z\right)$ plays the role of contaminant discharge intensity and $p\left(t\right)$ is an attenuation coefficient.

Let $0<{\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_n\le \cdots$ be the eigenvalues of $-L$, with associated eigenfunctions ${\left\{{\chi }_n\right\}}_{n\in \mathbb{N}}$. It is known that $li{m}_{n\to \infty }{\lambda }_n=\infty$ and ${\left\{{\chi }_n\right\}}_{n\in \mathbb{N}}$ is an orthonormal basis of $L^2(\Omega ).$

The first step is the consideration of a fractional power operator ${(-L)}^{\gamma },\gamma \in \mathbb{R}$ and the space:

$$D\left({(-L)}^{\gamma }\right)=\left\{\psi \in L^2(\Omega ):\sum _{n=1}^{\infty }{\lambda }_n^{2\gamma }{\left|(\psi ,{\chi }_n)\right|}^2<\infty \right\},$$

(15)

where $(·,·)$ is the inner product in $L^2(\Omega )$. It is a Hilbert space with the norm:

$$\begin{array}{c}\hfill {\parallel \psi \parallel }_{D\left({(-L)}^{\gamma }\right)}={\left(\sum _{n=1}^{\infty }{\lambda }_n^{2\gamma }{\left|(\psi ,{\chi }_n)\right|}^2\right)}^{\frac{1}{2}}.\end{array}$$

(16)

The Mittag–Leffler function is a generalization of the exponential function and is very useful when dealing with fractional derivatives.

Definition 2.

A two-parameter function of the Mittag–Leffler type is defined by:

$$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\alpha k+\beta )},$$

(17)

where $\alpha >0,\beta >0$ are real constants and Γ is the Gamma function defined by Equation (12).

The formal solution of the direct problem (13) can be written in terms of a Mittag–Leffler function. It is:

$$u(z,t)=\sum _{n=1}^{\infty }{f}_n{\int }_0^{t}p\left(\tau \right){\left(t-\tau \right)}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\lambda }_n{\left(t-\tau \right)}^{\alpha }\right)d\tau {\chi }_n\left(z\right),$$

(18)

where $f_n=(f,{\chi }_n).$

From Equation (18):

$$\begin{array}{ccc}\hfill u(z,T)& =& \sum _{n=1}^{\infty }{f}_n{\int }_0^{T}p\left(\tau \right){\left(T-\tau \right)}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\lambda }_n{\left(T-\tau \right)}^{\alpha }\right)d\tau {\chi }_n\left(z\right),\hfill \\ & =& q\left(z\right).\hfill \end{array}$$

Denote:

$$\begin{array}{c}\hfill Q_n\left(t\right)={\int }_0^{t}p\left(\tau \right){\left(t-\tau \right)}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\lambda }_n{\left(t-\tau \right)}^{\alpha }\right)d\tau .\end{array}$$

Thus:

$$\begin{array}{ccc}\hfill q\left(z\right)& =& \sum _{n=1}^{\infty }{f}_n{Q}_n\left(T\right){\chi }_n\left(z\right),\hfill \end{array}$$

and its Fourier coefficients are $q_n=f_n{Q}_n\left(T\right).$ We conclude $f_n={\displaystyle \frac{q_n}{Q_n\left(T\right)}}.$

3.2. Inverse Problem

We are interested in the inverse problem of determining the unknown source ingredient $f\left(z\right)$ in Equation (13) based on the overposed data $u(z,T)=q\left(z\right).$ Time T is a final time and the data $q\left(t\right)$ are not known exactly; what is known is a measurement $q^{ϵ}$ so that $\parallel q-q^{ϵ}{\parallel }_{\infty }<ϵ.$

As in Reference [11], the identification of f can be formulated as the operator equation:

$$\begin{array}{ccc}\hfill \left(Kf\right)\left(z\right)& =& \sum _{n=1}^{\infty }{f}_n{\int }_0^{T}p\left(\tau \right){\left(T-\tau \right)}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\lambda }_n{\left(T-\tau \right)}^{\alpha }\right)d\tau {\chi }_n\left(z\right)=q\left(z\right).\hfill \end{array}$$

The operator K is a linear self-adjoint compact operator and Problem (19) is ill-posed.

Our aim is to obtain a function $f_{\delta }^{ϵ}$ that minimizes the functional:

$$Hf=\parallel q-J_{\eta }^2{q}^{ϵ}{\parallel }_2^2,$$

where $J_{\eta }^2{q}^{ϵ}$ is the mollification of a discrete version of the noisy data $q^{ϵ}$. Since K is a self-adjoint compact operator, there exists a minimizer of H, $f_{\delta }^{ϵ}$, given by:

$$\begin{array}{ccc}\hfill f_{\delta }^{ϵ}\left(z\right)=\sum _{n=1}^{\infty }\frac{{\left(J_{\eta }^2{q}^{ϵ}\right)}_n}{Q_n\left(T\right)}{\chi }_n\left(z\right),& where& {\left(J_{\eta }^2{q}^{ϵ}\right)}_n=\left(J_{\eta }^2{q}^{ϵ},{\chi }_n\right).\hfill \end{array}$$

Theorem 1.

([13] Remark 3.1) If $p\left(t\right)\in C[0,T]$ satisfying $p\left(t\right)\ge p_0>0$ for all $t\in [0,T]$, set ${\parallel p\parallel }_{C[0,T]}={sup}_{t\in [t\in [0,T\left]\right]}\left|p\left(t\right)\right|$. Then, we have:

$$\frac{p_0\underline{C}}{{\lambda }_n}\le Q_n\left(T\right)={\int }_0^{T}p\left(\tau \right){(T-\tau )}^{\alpha -1}{E}_{\alpha ,\alpha }(-{\lambda }_n{(T-\tau )}^{\alpha })d\tau \le \frac{{\parallel p\parallel }_{C[0,T]}}{{\lambda }_n},$$

(19)

where $\underline{C}=1-E_{\alpha ,1}(-{\lambda }_1{T}^{\alpha }).$

Theorem 2.

Suppose $p\in C[0,T]$ satisfies $p\left(t\right)\ge p_0>0,t\in [0,T]$. Moreover, suppose $\parallel q^{ϵ}{-q\parallel }_{\infty }<ϵ$ and there exist $m\in {\mathbb{R}}^{+}$ and E, a constant such that ${\parallel f\parallel }_{\mathcal{D}\left({(-L)}^{\frac{m}{2}}\right)}\le E$, then:

$$\parallel f_{\delta }^{ϵ}{-f\parallel }_2\le C_1{\left(\delta +ϵ\right)}^{m/(m+2)},$$

(20)

where $C_1$ depends on $\alpha ,T,{\lambda }_1,\mu (\Omega )$.

Proof. 

$$\begin{array}{ccc}\hfill \parallel f_{\delta }^{ϵ}{\parallel }_{\mathcal{D}\left({(-L)}^{\frac{m}{2}}\right)}^2& =& \left|\sum _{n=1}^{\infty }{\lambda }_n^m{(f_{\delta }^{ϵ},{\chi }_n\left(z\right))}^2\right|\hfill \\ & =& \left|\sum _{n=1}^{\infty }{\lambda }_n^m{\left(f_{\delta }^{ϵ}\right)}_n^2\right|\hfill \\ & =& \left|\sum _{n=1}^{\infty }{\lambda }_n^m\frac{{\left(J_{\eta }^2{q}^{ϵ}\right)}_n^2}{Q_n{\left(T\right)}^2}\right|\hfill \\ & \le & \left|\sum _{n=1}^{\infty }\frac{{\lambda }_n^{m+2}}{{\underline{C}}^2{p}_0^2}{(J_{\eta }^2{q}^{ϵ},{\chi }_n\left(z\right))}^2\right|\hfill \\ & =& \frac{1}{{\underline{C}}^2{p}_0^2}\left|\sum _{n=1}^{\infty }{\lambda }_n^{m+2}{(J_{\eta }^2{q}^{ϵ},{\chi }_n(x,y))}^2\right|\hfill \\ & =& \frac{1}{{\underline{C}}^2{p}_0^2}{∥J_{\eta }^2{q}^{ϵ}∥}_{\mathcal{D}\left({(-L)}^{\frac{m}{2}+1}\right)}^2.\hfill \end{array}$$

The inequality follows from Theorem 1. However, $J_{\eta }^2{q}^{ϵ}\in C^{\infty }(\Omega )$, which implies $f_{\delta }^{ϵ}\in \mathcal{D}\left({(-L)}^{\frac{m}{2}}\right)$. Taking $M=max\{{∥J_{\eta }^2{q}^{ϵ}∥}_{\mathcal{D}\left({(-L)}^{\frac{m}{2}+1}\right)},E\}$, we obtain:

$$\begin{array}{ccc}\hfill \parallel K{f}_{\delta }^{ϵ}{-q\parallel }_2& \le & \parallel K{f}_{\delta }^{ϵ}-J_{\eta }^2{q}^{ϵ}{\parallel }_2+{\parallel J_{\eta }^2{q}^{ϵ}-q\parallel }_2\hfill \\ & \le & \parallel Kf-J_{\eta }^2{q}^{ϵ}{\parallel }_2+\parallel J_{\eta }^2{q}^{ϵ}{-q\parallel }_2=2{\parallel J_{\eta }^2{q}^{ϵ}-q\parallel }_2\hfill \\ & \le & C\left(\delta +ϵ\right).\hfill \\ \hfill \parallel f_{\delta }^{ϵ}{-f\parallel }_{\mathcal{D}\left({(-L)}^{m/2}\right)}& \le & |f_{\delta }^{ϵ}{\parallel }_{\mathcal{D}\left({(-L)}^{m/2}\right)}+{\parallel f\parallel }_{\mathcal{D}\left({(-L)}^{m/2}\right)}\hfill \\ & \le & M\left(1+\frac{1}{\underline{C}{p}_0}\right).\hfill \end{array}$$

Following Reference [11] and taking into consideration Lemma 1, Part 1, we conclude:

$$\begin{array}{ccc}\hfill \parallel f_{\delta }^{ϵ}{-f\parallel }_2& \le & {\left(\underline{C}{p}_0\right)}^{-\frac{m}{m+2}}\parallel K{f}_{\delta }^{ϵ}{-q\parallel }_2^{m/(m+2)}{\parallel f_{\delta }^{ϵ}-f\parallel }_{\mathcal{D}\left({(-L)}^{m/2}\right)}^{2/(m+2)}\hfill \\ & \le & {\left(\underline{C}{p}_0\right)}^{-\frac{m}{m+2}}{\left(M\left(1+\frac{1}{\underline{C}{p}_0}\right)\right)}^{2/(m+2)}{\left(C\left(\delta +ϵ\right)\right)}^{m/(m+2)}\hfill \end{array}$$

□

4. Numerical Results

There are many alternatives for the numerical solution of a time fractional diffusion problem. If we restrict our attention to methods based on finite difference discretizations, we mention Reference [22], in which Caputo fractional derivatives are computed by the so-called Caputo fractional derivative rule, which in turn depends on a modified trapezoidal rule. This method is successfully implemented in Reference [23] for plane strain/stress elasticity in the presence of nonlocal elasticity.

Our finite difference method for the solution of the time fractional diffusion equation is taken from Reference [14], which in turn is inspired by Reference [24]. The method is implicit and its properties about stability and convergence are discussed in Reference [14].

We consider the following time fractional diffusion problem:

$$\left.\begin{array}{cccc}{D}_t^{\alpha }u(z,t)-\left(Lu\right)(z,t)\hfill & =p\left(t\right)f\left(z\right),\hfill & z\in \Omega \hfill & \hfill t\in (0,T)\\ u(z,t)\hfill & =0,\hfill & z\in \partial \Omega \hfill & \hfill t\in (0,T)\\ u(z,0)\hfill & =0,\hfill & z\in \overline{\Omega }\hfill & \hfill t\in (0,T)\end{array}\right\}$$

(21)

where:

$$\begin{array}{c}\hfill Lu(x,y)=\frac{\partial }{\partial x}\left(a_{11}(x,y)\frac{\partial }{\partial x}u(x,y)\right)+\frac{\partial }{\partial y}\left(a_{22}(x,y)\frac{\partial }{\partial y}u(x,y)\right).\end{array}$$

(22)

After discretization, operator L leads to a matrix l, whose eigenvectors and eigenvalues play the roles of the eigenfunctions and eigenvalues of the differential operator.

The $Q_n$s are approximated according to Reference [11] by:

$$Q_n=-\frac{1}{{\lambda }_n}\left(E_{\alpha ,1}(-{\lambda }_n{\tau }^{\alpha })p(T-\tau ){|}_{\tau =T}-p(T-t){|}_{\tau =0}-{\int }_0^T{E}_{\alpha ,1}(-{\lambda }_n{\tau }^{\alpha })p^{\prime }(T-\tau )d\tau \right).$$

(23)

The integrals are approximated by composite trapezoidal rule.

The errors are measured by the root mean square (rms) norm given by:

$$\begin{array}{ccc}\hfill \parallel f-f_{\delta }^{ϵ}{\parallel }_{rms}& =& {\left(\frac{1}{NM}\sum _{n=1}^N\sum _{m=1}^M{(f_{nm}-{\left(f_{\delta }^{ϵ}\right)}_{nm})}^2\right)}^{1/2}.\hfill \end{array}$$

(24)

The particular examples considered here are for:

$$\begin{array}{ccc}\hfill f(x,y)& =& sin\left(3\pi x\right)sin\left(3\pi y\right)\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill p\left(t\right)& =& 1+exp(-(t+\alpha \left)\right).\hfill \end{array}$$

(26)

The space step size $h=1/32$ is used for both coordinates, x and y. Final time is $T=1$ and $\Delta t=1/10$.

Example 1

Let $a_{11}(x,y)=x^2+1,a_{22}(x,y)=y^2+1$. The relative $l_2$ norms of the identification are shown in Table 2 and Table 3.

Table 2. Error norms, $ϵ=0.025$ and $\eta =5$.

$\mathit{\alpha }$	0.1	0.5	0.7	0.9
$\parallel f-f_{\delta }^{ϵ}{\parallel }_{rms}$	0.11237258	0.11341573	0.11482934	0.11338589

Table 3. Error norms, $\alpha =0.7$.

$\mathit{ϵ}$	0.005	0.01	0.025	0.05
$\eta$	3	4	5	6
$\parallel f-f_{\delta }^{ϵ}{\parallel }_{rms}$	0.05634342	0.11141561	0.17683141	0.24996681

Example 2

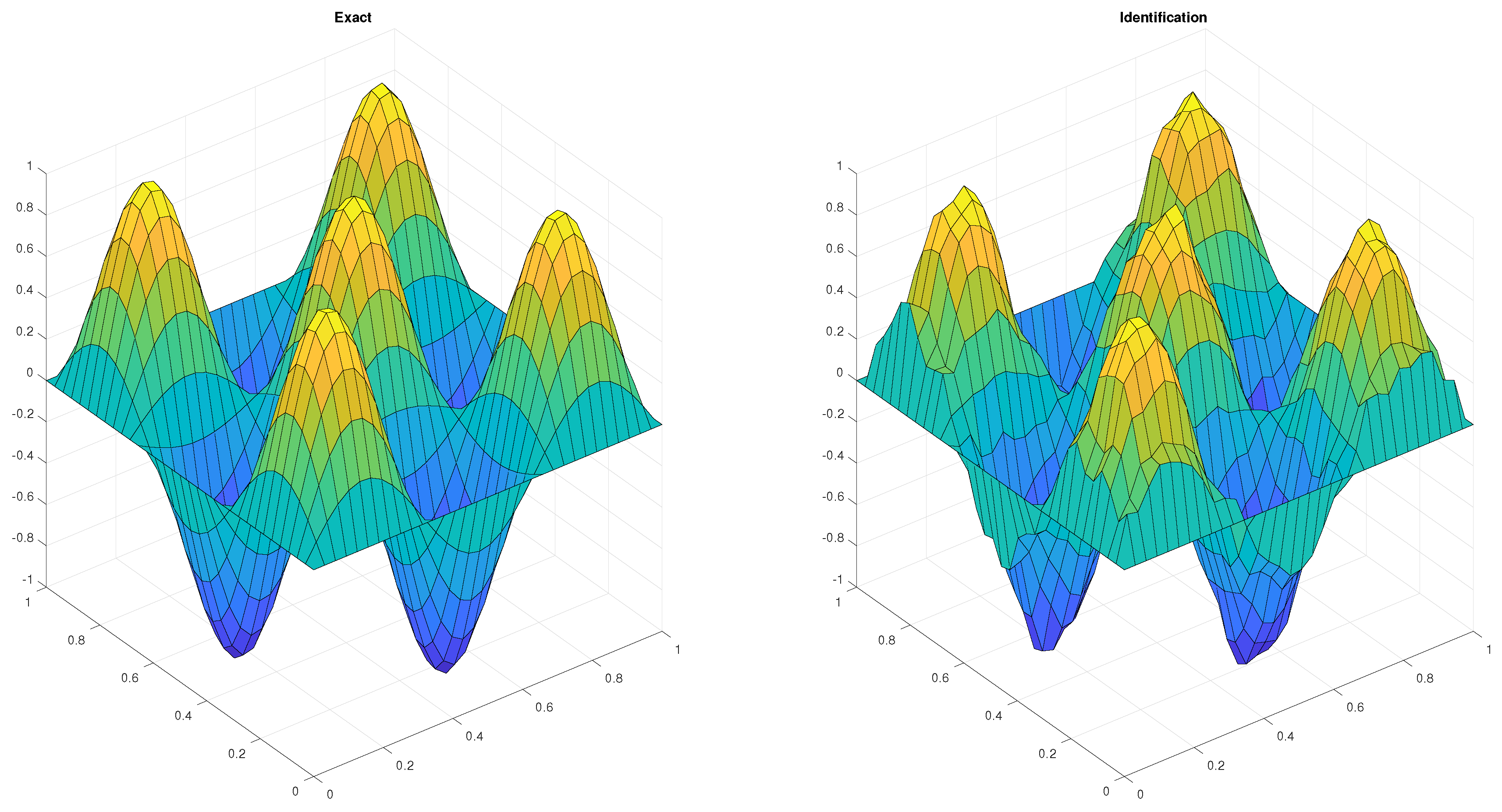
Let $a_{11}(x,y)\equiv 1$ and $a_{22}(x,y)\equiv 1$. Relative $l_2$ errors for the identification of the source term are shown in Table 4 and Table 5. Figure 2 gives an idea of the quality of the identification.

Table 4. Error norms, $ϵ=0.025$ and $\eta =5$.

$\mathit{\alpha }$	0.1	0.5	0.7	0.9
$\parallel f-f_{\delta }^{ϵ}{\parallel }_{rms}$	0.18679846	0.18330355	0.19129097	0.19253567

Table 5. Error norms, $\alpha =0.7$.

$\mathit{ϵ}$	0.005	0.01	0.025	0.05
$\eta$	3	4	5	6
$\parallel f-f_{\delta }^{ϵ}{\parallel }_{rms}$	0.0715818	0.12090887	0.19295488	0.26167402

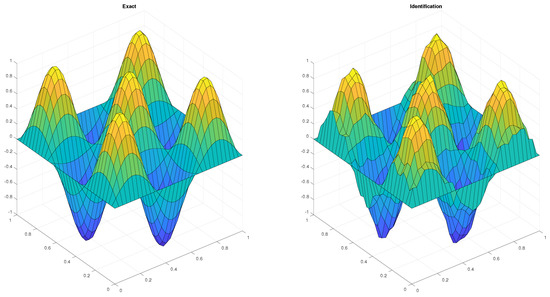
Figure 2. Identification of f for $h=1/32,ϵ=0.025$ and $\eta =3$.

5. Discussion and Final Comments

The 2DDM operator is a useful regularization procedure when dealing with inverse source problems for time fractional diffusion equations. It is also appropriate for surface and gradient fitting as shown in Reference [17], but we do not pursue this objective here. There are more applications of this operator and we hope to master some of them; for instance, we would like to modify our identification problem and deal with the factor $p\left(t\right)$ as unknown and the factor $f(x,y)$ as data.