Assigning Numerical Scores to Linguistic Expressions

Abstract

In this paper, we study different methods of scoring linguistic expressions defined on a finite set, in the search for a linear order that ranks all those possible expressions. Among them, particular attention is paid to the canonical extension, and its representability through distances in a graph plus some suitable penalization of imprecision. The relationship between this setting and the classical problems of numerical representability of orderings, as well as extension of orderings from a set to a superset is also explored. Finally, aggregation procedures of qualitative rankings and scorings are also analyzed.

1. Introduction

Let U stand for a nonempty set, called universe. It is clear that comparing the elements of U through some sort of binary relation $\mathcal{R}$ such that $u\mathcal{R}v$ is immediately understood as “the element u is not worse than the element v” gives less information than assigning scores to each element of U. A scoring function is a real-valued function $S:U\to \mathbb{R}$. The interpretation is obvious: if the score $S\left(u\right)$ of the element $u\in U$ is not smaller than the score $S\left(v\right)$ of the element v, then the above conclusion, namely, “the element u is not worse than the element v” is also achieved. However, if an ordering given on U through a binary relation $\mathcal{R}$ is also represented by a scoring function, say $S:U\to \mathbb{R}$, the composition of $f\circ S$ of the map S with no matter what strictly increasing function $f:\mathbb{R}\to \mathbb{R}$ also represents the same ordering $\mathcal{R}$ on U. In other words: $u\mathcal{R}v\iff S\left(u\right)\ge S\left(v\right)\iff f\left(S\right(u\left)\right)\ge f\left(S\right(v\left)\right)$ holds true for all $u,v\in U$.

Despite the ordering being the same, the scores have important consequences and collateral meanings. A typical example corresponds to a firm that wants to hire people, and prepares a test or exam consisting of one hundred tasks to be done. Suppose the scores of two candidates u and v have been just $S\left(u\right)=1$ and $S\left(v\right)=2$ (out of 100). Obviously, we would say that v is better than u, but both of them having such poor results, the firm would reject hiring anyone among them. If, instead, the scores were $S\left(u\right)=99$ and $S\left(v\right)=100$, again we would say that v is better than u, but now, quite probably, the firm would be willing to hire both candidates.

The most typical scoring procedures consist of numerical scales. Nevertheless, due to the vagueness and imprecision involved in a wide variety of practical situations in which some sort of evaluation is made, sometimes the use of finite measurement scales based on linguistic terms or expressions seems to be more suitable than just using numerical scales. In this case, if L is a set of linguistic terms (also known as labels), such as {very bad, bad, poor, fair, good, very good, excellent}, a scoring function on U taking values on L is a function $S:U\to L$ that can obviously be interpreted as a qualitative scale of measurement.

From a pure mathematical point of view, whenever L is given a linear order ${\succcurlyeq }_L$, a scoring procedure on U taking values on L can equivalently be understood through a numerical scoring function $f:U\to \mathbb{R}$, which is obviously a quantitative scale of measurement. Indeed, if $L=\{l_1,l_2,\dots ,l_g\}$ denotes the set of linguistic terms and we understand that $l_h{\succcurlyeq }_L{l}_k$ holds true if and only if $h\ge k$, then a scoring function $S:U\to L$ can be immediately interpreted by means of the numerical scoring function $T\circ S:U\to \mathbb{R}$, where $T:L\to \mathbb{R}$ is given by $T\left(l_h\right)=h,h\in \{1,\dots ,g\}$. In this situation, namely when L is given a linear order, the use of a scoring function taking values on L or an equivalent numerical scoring function is, perhaps, a matter of taste (see García-Lapresta et al. [1]).

However, sometimes, in a higher degree of vagueness or imprecision, and even in the case of using a set $L=\{l_1,l_2,\dots ,l_g\}$ of linguistic terms, it could happen that the agents that assign scores to the elements of a nonempty set U may hesitate when, given an element $u\in U$, the score $S\left(u\right)$ needs to be determined. A typical example is an approximation (based on data as climate, composition of soil, amount of rain water per year, etc.) of the quality of the wine produced in a vineyard. An expert could hesitate here, and instead of saying “no doubt, it will be very good”, she/he could declare something as “from good to excellent”, so using a linguistic expression instead of just a linguistic term.

Our approach concerning the imprecision is based on an adaptation of the absolute order of magnitude spaces introduced by Travé-Massuyès and Dague [2] and Travé-Massuyès and Piera [3]; more specifically in the extensions devised by Roselló et al. [4,5,6] (see also Agell et al. [7] and Falcó et al. [8,9]).

At this stage, several mathematical problems appear, namely

(i)

If a set $L=\{l_1,l_2,\dots ,l_g\}$ of linguistic terms has been endowed with a linear order ${\succcurlyeq }_L$, try to define a linear order on the set of linguistic expressions based on L. Needless to say, this “extended” order should preserve or be compatible with ${\succcurlyeq }_L$ when acting on the labels of L considered as special cases of linguistic expressions.

(ii)

Compare different linear orders (when available) defined on a set of linguistic expressions, trying to explain which is the most suitable one to be used in some practical concrete situation.

(iii)

Study problems of aggregation of a finite number of scorings based on linguistic terms and expressions.

Having in mind these questions, the structure of the paper goes as follows. After the Introduction (Section 1) and a compulsory Section 2 of preliminaries, previous results and necessary background, in Section 3, we study sets of linguistic expressions and define suitable orderings on these kinds of sets. In Section 4, we analyze some questions relative to the aggregation of rankings and scorings based on qualitative scales. A final Section 5 of concluding remarks, suggestions for further research and open questions closes the paper.

2. Previous Concepts and Results

Intuitively, a ranking on a universe U is some kind of ordering defined on U, usually defined through a binary relation $\mathcal{R}$ on U, such that $u\mathcal{R}v$ means “the element u is at least as good as the element v”. A scoring function on U is a map $S:U\to \mathbb{R}$. Notice that a scoring function S immediately defines a ranking $\mathcal{R}$ on U, by declaring $u\mathcal{R}v\iff S\left(u\right)\ge S\left(v\right)$, for all $u,v\in U$. For finite sets, a sort of converse is also true, namely, each ranking can be represented by a scoring function (see e.g., the first three chapters in Bridges and Mehta [10] for further details).

Let us formalize all this through some definitions.

Definition 1.

Let U denote a universe. A preorder $\succcurlyeq$ on U is a binary relation on U which is reflexive and transitive.

An antisymmetric preorder is said to be a partial order. A total preorder $\succcurlyeq$ on U is a preorder such that $u\succcurlyeq v$ or $v\succcurlyeq u$ holds true for all $u,v\in U$. A total order is also called a linear order.

If $\succcurlyeq$ is a preorder on U, then the associated asymmetric relation is denoted by $\succ$, whereas $\sim$ stands for the associated equivalence relation. These relations are respectively defined by $u\succ v\iff \left(\right(u\succcurlyeq v)$ and not $(v\succcurlyeq u))$, and $u\sim v\iff \left(\right(u\succcurlyeq v)$ and $(v\succcurlyeq u))$, for all $u,v\in U$. Notice that if $\succcurlyeq$ is a linear order, then $u\succ v\iff \left(\right(u\succcurlyeq v)$ and $(u\ne v))$.

Definition 2.

Let U denote a universe. Let ≽ stand for a total preorder defined on U. We say that ≽ is representable if there exists a real-valued function $S:U\to \mathbb{R}$ such that $u\succcurlyeq v\iff S\left(u\right)\ge S\left(v\right)$ holds true for all $u,v\in U$.

As commented before, it happens that, provided that U is finite, any total preorder defined on U is representable (see Bridges and Mehta [10]). A function S that represents a total preorder ≽ defined on U is usually said to be a utility function for ≽.

Remark 1.

Notice that a ranking (e.g., a total preorder) on a universe U is a qualitative scale of measurement, whereas a scoring function is a quantitative scale. Other typical sorts of qualitative scales are those based on labels and linguistic expressions (see next Definition 3). If S is a utility function that represents a total preorder ≽ on a universe U, and $T:\mathbb{R}\to \mathbb{R}$ is a strictly increasing function, it is straightforward to see that the composition $T\circ S:U\to \mathbb{R}$ is also a utility function that represents ≽. Consequently, there are infinitely many utility functions that represent a given total preorder $\succcurlyeq$ on a finite universe U.

Definition 3.

Let $L=\{l_1,l_2,\dots ,l_g\}$ denote a finite nonempty set of linguistic terms (labels), with $g\ge 3$. The set of linguistic expressions associated with L is defined as

$$\mathbb{L}=\{[l_h,l_k]\mid l_h,l_k\in L,1\le h\le k\le g\},$$

where $[l_h,l_k]=\{l_h,l_{h+1},\cdots ,l_k\}$. Since the linguistic expression $[l_h,l_h]$ is the singleton $\left\{l_h\right\}$, by convention, it can be replaced by the label $l_h$. In this way, $L\subset \mathbb{L}$.

Remark 2.

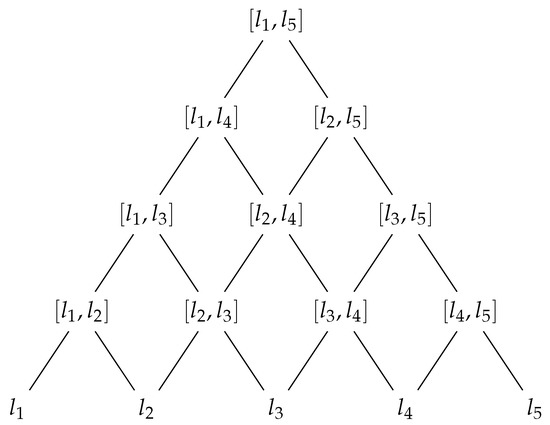
The set of linguistic expressions can be represented by a graph $G_{\mathbb{L}}$. In the graph, the lowest layer represents the linguistic terms $l_h\in L\subset \mathbb{L}$, the second layer represents the linguistic expressions created by two consecutive labels $[l_h,l_{h+1}]$, the third layer represents the linguistic expressions generated by three consecutive labels $[l_h,l_{h+2}]$, and so on up to last layer, where we represent the linguistic expression $[l_1,l_g]$. As a result, the higher an element of the graph $G_{\mathbb{L}}$ is, the more imprecise it becomes.

The vertices in $G_{\mathbb{L}}$ are the elements of $\mathbb{L}$ and the edges $\mathcal{E}-\mathcal{F}$, where $\mathcal{E}=[l_h,l_k]$ and $\mathcal{F}=[l_h,l_{k+1}]$, or $\mathcal{E}=[l_h,l_k]$ and $\mathcal{F}=[l_{h+1},l_k]$. Figure 1 shows the graph representation for $g=5$.

Figure 1. Graph representation of the linguistic expressions for $g=5$.

3. Defining Orderings on Sets of Linguistic Expressions

Suppose that the set $L=\{l_1,l_2,\dots ,l_g\}$ of linguistic terms is endowed with the linear order ≽ given by $l_h\succcurlyeq l_k\iff h\ge k$, for all $h,k\in \{1,\cdots ,g\}$.

We want now to extend the linear order ≽ to a new linear order defined on the whole set $\mathbb{L}$ of linguistic expressions on L. This problem has several positive solutions.

Remark 3.

To extend the linear order ≽ on L to a new linear order defined on $\mathbb{L}$, first, we may consider a partial order ${\succcurlyeq }_1$ defined on $\mathbb{L}$ as follows: $[l_h,l_k]{\succcurlyeq }_1[l_h,l_k]$ (reflexivity), and also $\left\{l_h\right\}=[l_h,l_h]{\succcurlyeq }_1[l_k,l_k]=\left\{l_k\right\}\iff h\ge k$, for all $h,k\in \{1,\cdots ,g\}$ (compatibility with ≽ on L).

Then, we may apply the well-known Szpilrajn’s theorem ([11]) that ensures that any partial order on a given set can be extended to a linear order on that set.

3.1. Constructive Extensions: The Lexicographic Order and the Canonical Order

Instead of using a powerful result as Szpilrajn’s theorem as commented in Remark 3, when $L=\{l_1,l_2,\dots ,l_g\}$, we can directly furnish some extensions in a constructive way, as stated in Proposition 1 and Proposition 2, whose straightforward proofs are omitted for the sake of brevity.

Proposition 1.

The binary relation ${\succcurlyeq }_{\ell }$ on $\mathbb{L}$ defined as

$$[l_h,l_k]{\succcurlyeq }_{\ell }[l_{h^{\prime }},l_{k^{\prime }}]\iff \left\{\begin{array}{c}h>h^{\prime }\hfill \\ or\hfill \\ h=h^{\prime }andk\ge k^{\prime }\hfill \end{array}\right.$$

is a linear order that preserves the given order ≽ on $L\subset \mathbb{L}$. It is called the lexicographic order on $\mathbb{L}$.

Notice that the real valued function $S:\mathbb{L}\to \mathbb{R}$ given by $S\left([l_h,l_k]\right)=(g·h)+k$ is a utility representation for ${\succcurlyeq }_{\ell }$.

Proposition 2.

([8]) The binary relation ${\succcurlyeq }_c$ on $\mathbb{L}$ defined as

$$[l_h,l_k]{\succcurlyeq }_c[l_{h^{\prime }},l_{k^{\prime }}]\iff \left\{\begin{array}{c}h+k>h^{\prime }+k^{\prime }\hfill \\ or\hfill \\ h+k=h^{\prime }+k^{\prime }andk-h\le k^{\prime }-h^{\prime }\hfill \end{array}\right.$$

is a linear order, and it is called the canonical order on $\mathbb{L}$. It also preserves the given order $\succcurlyeq$ on $L\subset \mathbb{L}$.

Example 1.

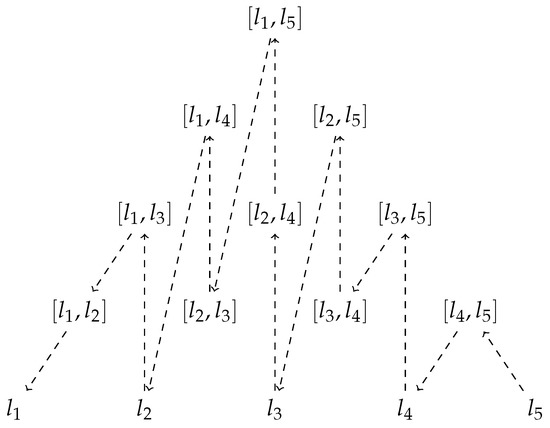
For $g=5$, the elements of $\mathbb{L}$ are ordered as follows with respect to the lexicographic order:

$$\begin{array}{c}{l}_5{\succ }_{\ell }[l_4,l_5]{\succ }_{\ell }{l}_4{\succ }_{\ell }[l_3,l_5]{\succ }_{\ell }[l_3,l_4]{\succ }_{\ell }{l}_3{\succ }_{\ell }[l_2,l_5]{\succ }_{\ell }[l_2,l_4]{\succ }_{\ell }\hfill \\ {\succ }_{\ell }[l_2,l_3]{\succ }_{\ell }{l}_2{\succ }_{\ell }[l_1,l_5]{\succ }_{\ell }[l_1,l_4]{\succ }_{\ell }[l_1,l_3]{\succ }_{\ell }[l_1,l_2]{\succ }_{\ell }{l}_1.\hfill \end{array}$$

Moreover, through the canonical order (see also Figure 2), we get:

$$\begin{array}{c}{l}_5{\succ }_c[l_4,l_5]{\succ }_c{l}_4{\succ }_c[l_3,l_5]{\succ }_c[l_3,l_4]{\succ }_c[l_2,l_5]{\succ }_c{l}_3{\succ }_c[l_2,l_4]{\succ }_c\hfill \\ {\succ }_c[l_1,l_5]{\succ }_c[l_2,l_3]{\succ }_c[l_1,l_4]{\succ }_c{l}_2{\succ }_c[l_1,l_3]{\succ }_c[l_1,l_2]{\succ }_c{l}_1.\hfill \end{array}$$

Figure 2. Canonical order in $\mathbb{L}$ for $g=5$.

3.2. Numerical Representation of the Canonical Order Based on the Geodesic Metric

The canonical order on $\mathbb{L}$ can be represented by utility functions $u:\mathbb{L}⟶\mathbb{R}$ in such a way that $\mathcal{E}{\succ }_c\mathcal{F}\iff u\left(\mathcal{E}\right)>u\left(\mathcal{F}\right)$, for all $\mathcal{E},\mathcal{F}\in \mathbb{L}$.

Among the infinite possible utility representations of the canonical order on $\mathbb{L}$, we are interested in those based on distances. In addition, concerning metrics on a graph, perhaps the most typical one is the so-called geodesic metric.

Definition 4.

The geodesic metric $d_G:{\mathbb{L}}^2\to \mathbb{R}$ is defined as

$$d_G\left([l_h,l_k],[l_{h^{\prime }},l_{k^{\prime }}]\right)=|h-h^{\prime }|+|k-k^{\prime }|$$

(1)

for all $\mathcal{E}=[l_h,l_k],\mathcal{F}=[l_h^{\prime },l_k^{\prime }]\in \mathbb{L}$.

Remark 4.

Notice that $d_G(l_h,l_{h+1})=2$ for every $h\in \{1,\cdots ,g\}$, so that $\mathbb{L}$ becomes uniform, in the sense that adjacent linguistic terms are equidistant (see e.g., Herrera et al. [12] and García-Lapresta and Pérez-Román [13,14] for dealing with non uniform qualitative scales).

Given $\mathcal{E}=[l_h,l_k]\in \mathbb{L}$, with $\#\mathcal{E}$, we denote the cardinality of $\mathcal{E}$, i.e., the number of labels in the interval $[l_h,l_k]$: $\#\mathcal{E}=k+1-h$.

In the following result, we establish that the canonical order on $\mathbb{L}$ introduced in Proposition 2 can be defined through the geodesic distances to the highest possible assessment and the cardinality of the linguistic expressions.

Proposition 3.

For all $\mathcal{E},\mathcal{F}\in \mathbb{L}$, it holds

$$\mathcal{E}{\succ }_c\mathcal{F}\iff \left\{\begin{array}{c}{d}_G(\mathcal{E},l_g)<d_G(\mathcal{F},l_g),\hfill \\ or\hfill \\ d_G(\mathcal{E},l_g)=d_G(\mathcal{F},l_g)and\#\mathcal{E}<\#\mathcal{F}.\hfill \end{array}\right.$$

Proof. 

It follows from Proposition 2 and Equation (1). ☐

Remark 5.

To distinguish between elements $\mathcal{E},\mathcal{F}\in \mathbb{L}$, the second condition that appears in the statement of Proposition 3, namely the one that reads “or $d_G(\mathcal{E},l_g)=d_G(\mathcal{F},l_g)$ and $\#\mathcal{E}<\#\mathcal{F}$” is crucial. In fact, suppose that on $\mathbb{L}$ we use only a scoring function S based on the geodesic metric, and given by $S\left(\mathcal{E}\right)=d_G(\mathcal{E},l_g)$. Then, it is straightforward to see that two nodes $\mathcal{E},\mathcal{F}$ that appear in the same vertical in the graph $G_{\mathbb{L}}$ are assigned the same score, which is $S\left(\mathcal{E}\right)=d_G(\mathcal{E},l_g)=d_G(\mathcal{F},l_g)=S\left(\mathcal{F}\right)$. This scoring function S defines an ordering ${\succcurlyeq }^{*}$ on $\mathbb{L}$ by declaring $\mathcal{E}{\succcurlyeq }^{*}\mathcal{F}\iff S\left(\mathcal{E}\right)\ge S\left(\mathcal{F}\right)$, for all $\mathcal{E},\mathcal{F}\in \mathbb{L}$. However, since $g\ge 3$, it happens that ${\succcurlyeq }^{*}$ is a total preorder, but not a linear order. In other words, the geodesic distance is, so-to-say, miopic since it cannot detect the difference between two elements in the same vertical in $G_{\mathbb{L}}$. For instance, if $L=${very bad, bad, poor, fair, good, very good, excellent}, the linguistic expressions “very good” and “from good to excellent” would be assigned the same score through the geodesic metric.

3.3. GeodesIc Metric Matching Penalization of Imprecision

Another important feature that carries the second condition in the statement of Proposition 3 and says “or $d_G(\mathcal{E},l_g)=d_G(\mathcal{F},l_g)$ and $\#\mathcal{E}<\#\mathcal{F}$” is warning us about the role played by imprecision. If a linguistic expression $\mathcal{F}$ consists of more labels than another one $\mathcal{E}$, we understand that “$\mathcal{F}$ is more imprecise than $\mathcal{E}$” or, equivalently, “$\mathcal{E}$ is more accurate than $\mathcal{F}$”. Taking this fact into account, it seems interesting to search for measurements or scoring methods that, someway, penalize the imprecision when comparing terms in $\mathbb{L}$, as next Proposition 4 does.

Proposition 4.

For every $\alpha \ge 0$, the function $d_{\alpha }:{\mathbb{L}}^2⟶\mathbb{R}$, defined as

$$d_{\alpha }(\mathcal{E},\mathcal{F})=d_G(\mathcal{E},\mathcal{F})+\alpha |\#\mathcal{E}-\#\mathcal{F}|,$$

i.e.,

$$d_{\alpha }\left([l_h,l_k],[l_{h^{\prime }},l_{k^{\prime }}]\right)=|h-h^{\prime }|+|k-k^{\prime }|+\alpha |h^{\prime }-h+k-k^{\prime }|$$

(2)

for all $\mathcal{E}=[l_h,l_k],\mathcal{F}=[l_h^{\prime },l_k^{\prime }]\in \mathbb{L}$, is a metric, and it is called the metric associated with α.

Proof. 

Since $d_{\alpha }$ is a positive linear combination of the geodesic metric $d_G$ and the pseudometric $d:{\mathbb{L}}^2⟶\mathbb{R}$ defined as $d(\mathcal{E},\mathcal{F})=|\#\mathcal{E}-\#\mathcal{F}|$, then $d_{\alpha }$ is a metric. ☐

Proposition 5.

Given $\alpha \ge 0$, the following statements are equivalent:

• $\forall \mathcal{E},\mathcal{F}\in \mathbb{L}\left(\mathcal{E}{\succ }_c\mathcal{F}\iff d_{\alpha }(\mathcal{E},l_g)<d_{\alpha }(\mathcal{F},l_g)\right)$.
• $\alpha \in I_g$, where $I_g=\left(0,\frac{1}{g-2}\right)$, if g is odd, and $I_g=\left(0,\frac{1}{g-1}\right)$, if g is even.

Proof. 

$1\Rightarrow 2$) Consider g is odd. By Proposition 2, we have

$$[l_1,l_g]{\succ }_c\left[l_{\frac{g-1}{2}},l_{\frac{g+1}{2}}\right].$$

Then, by hypothesis, we have

$$d_{\alpha }\left([l_1,l_g],l_g\right)<d_{\alpha }\left(\left[l_{\frac{g-1}{2}},l_{\frac{g+1}{2}}\right],l_g\right).$$

(3)

Taking into account Equation (2),

$$d_{\alpha }\left([l_1,l_g],l_g\right)=|1-g|+|g-g|+\alpha |g-1+g-g|=g-1+\alpha (g-1)$$

and

$$\begin{array}{c}{d}_{\alpha }\left(\left[l_{\frac{g-1}{2}},l_{\frac{g+1}{2}}\right],l_g\right)=\hfill \\ \left|\frac{g-1}{2}-g\right|+\left|\frac{g+1}{2}-g\right|+\alpha \left|g-\frac{g-1}{2}+\frac{g+1}{2}-g\right|=g+\alpha .\hfill \end{array}$$

Then, from Inequality (3), we obtain $g-1+\alpha (g-1)<g+\alpha$, i.e.,

$$\alpha <\frac{1}{g-2}.$$

In order to prove that $\alpha >0$, suppose by way of contradiction that $\alpha =0$. By Proposition 2, we have

$$l_{\frac{g+1}{2}}{\succ }_c[l_1,l_g].$$

Then, by hypothesis, we have

$$d_{\alpha }\left(l_{\frac{g+1}{2}},l_g\right)<d_{\alpha }([l_1,l_g],l_g).$$

Taking into account Equation (2),

$$d_{\alpha }\left(l_{\frac{g+1}{2}},l_g\right)=g-1=d_{\alpha }([l_1,l_g],l_g),$$

which is a contradiction. Consequently, $\alpha \in I_g=\left(0,\frac{1}{g-2}\right)$.

We now consider that g is even. By Proposition 2, we have

$$\left[l_{\frac{g}{2}},l_{\frac{g}{2}+1}\right]{\succ }_c[l_1,l_g].$$

Then, by hypothesis, we have

$$d_{\alpha }\left(\left[l_{\frac{g}{2}},l_{\frac{g}{2}+1}\right],l_g\right)<d_{\alpha }\left([l_1,l_g],l_g\right).$$

(4)

Taking into account Equation (2),

$$d_{\alpha }\left(\left[l_{\frac{g}{2}},l_{\frac{g}{2}+1}\right],l_g\right)=\left|\frac{g}{2}-g\right|+\left|\frac{g}{2}+1-g\right|+\alpha \left|g-\frac{g}{2}+\frac{g}{2}+1-g\right|=g.$$

Then, from Inequality (4), we obtain $g-1+\alpha (g-1)<g$, i.e.,

$$\alpha <\frac{1}{g-1}.$$

In order to prove that $\alpha >0$, suppose by way of contradiction that $\alpha =0$. As mentioned above, we have

$$d_{\alpha }\left(\left[l_{\frac{g}{2}},l_{\frac{g}{2}+1}\right],l_g\right)<d_{\alpha }([l_1,l_g],l_g).$$

However, taking into account Equation (2),

$$d_{\alpha }\left(\left[l_{\frac{g}{2}},l_{\frac{g}{2}+1}\right],l_g\right)=g-1=d_{\alpha }([l_1,l_g],l_g),$$

we obtain a contradiction. Consequently, $\alpha \in I_g=\left(0,\frac{1}{g-1}\right)$.

$2\Rightarrow 1$) It is a routine. ☐

Definition 5.

Given $\alpha \in I_g$, the scoring function $S_{\alpha }:\mathbb{L}⟶\mathbb{R}$ is defined as

$$S_{\alpha }\left(\mathcal{E}\right)=d_{\alpha }(l_1,l_g)-d_{\alpha }(\mathcal{E},l_g),$$

for every $\mathcal{E}\in \mathbb{L}$.

It is easy to see that, for every $[l_h,l_k]\in \mathbb{L}$, it holds

$$S_{\alpha }\left([l_h,l_k]\right)=h+k-2-\alpha (k-h).$$

(5)

Proposition 6.

Given $\alpha \in I_g$, for all $\mathcal{E},\mathcal{F}\in \mathbb{L}$, it holds

$$\mathcal{E}{\succ }_c\mathcal{F}\iff S_{\alpha }\left(\mathcal{E}\right)>S_{\alpha }\left(\mathcal{F}\right).$$

Proof. 

By Proposition 5. ☐

Example 2.

Taking into account the condition appearing in Proposition 5 for $g=5$, i.e., $0<\alpha <\frac{1}{3}$, and Equation (5), we have

$$\begin{array}{c}{S}_{\alpha }\left(l_5\right)=8>S_{\alpha }\left([l_4,l_5]\right)=7-\alpha >S_{\alpha }\left(l_4\right)=6>S_{\alpha }\left([l_3,l_5]\right)=6-2\alpha >\hfill \\ S_{\alpha }\left([l_3,l_4]\right)=5-\alpha >S_{\alpha }\left([l_2,l_5]\right)=5-3\alpha >S_{\alpha }\left(l_3\right)=4>\hfill \\ S_{\alpha }\left([l_2,l_4]\right)=4-2\alpha >S_{\alpha }\left([l_1,l_5]\right)=4-4\alpha >S_{\alpha }\left([l_2,l_3]\right)=3-\alpha >\hfill \\ S_{\alpha }\left([l_1,l_4]\right)=3-3\alpha >S_{\alpha }\left(l_2\right)=2>S_{\alpha }\left([l_1,l_3]\right)=2-2\alpha >\hfill \\ S_{\alpha }\left([l_1,l_2]\right)=1-\alpha >S_{\alpha }\left(l_1\right)=0.\hfill \end{array}$$

3.4. Extensions Based on Different Criteria

As we have already seen, both the lexicographic and the canonical linear orders on $\mathbb{L}$ extend the given order on L. Although it is always possible to extend a linear order from a given finite set U to its power set, a typical question that, as a matter of fact, gave rise to a battery of classical papers from the 1970s (see e.g., Gärdenfors [15], Kannai and Peleg [16], Barberà and Pattanaik [17], Fishburn [18], Bossert [19] and Bossert et al. [20]) is whether or not it is possible to perform an extension that follows a list of criteria imposed a priori.

Sometimes, the extension is not possible because the criteria used are, so-to-say, contradictory. However, perhaps surprisingly, there are other situations in which the extension is not possible because of a combinatorial explosion, which, due to the much bigger cardinality $2^{\#U}$ of the power set of U, does not leave room to accommodate all terms of the power set, in an extended linear order, accomplishing all the criteria. Perhaps the most famous result in this direction is the so-called theorem of impossibility of extension due to Kannai and Peleg [16] (for a detailed account, see Barberà et al. [21]).

Consider the following example.

Example 3.

Let $U=\{u_1,u_2,\dots ,u_p\}$ be a finite universe. Assume that U is endowed with a linear order ≽ such that $u_i\succcurlyeq u_j\iff i\ge j$. Consider the following two criteria for an extension, say ${\succcurlyeq }_{ext}$ of ≽ to the power set of U.

(i)

A criterion [M] based on the idea of a mean value, so that if $u_i\succ u_j$ in U, then $\left\{u_i\right\}{\succ }_{\mathrm{ext}}\{u_i,u_j\}{\succ }_{\mathrm{ext}}\left\{u_j\right\}$ holds true.

(ii)

A criterion [C] based on the idea of cardinality, in the sense “the bigger, the better”, so that given $u_i,u_j\in U$ such that $u_i\ne u_j$, then $\{u_i,u_j\}{\succ }_{\mathrm{ext}}\left\{u_i\right\}$ and also $\{u_i,u_j\}{\succ }_{\mathrm{ext}}\left\{u_j\right\}$ hold true.

In this example, it is clear that these two criteria are contradictory. Unless the set U is a singleton, no extension ${\succcurlyeq }_{ext}$ can at the same time satisfy [M] and [C].

By the way, suppose that we use the criterion [C], jointly with a rule [B] that pays attention to the best elements of the corresponding subsets, as follows: when two subsets $A,B\subset U$ have the same cardinality, pay attention to the best elements $maxA,maxB$ as regards ≽. If $maxA=maxB=u_i$, then pay attention to $max(A\setminus \left\{u_i\right\})$ and $max(B\setminus \left\{u_i\right\})$, and so on. We proceed this way until we declare $A\succ B$ or $B\succ A$.

Starting with the set of labels $L=\{l_1,l_2,\dots ,l_g\}$, we extend the usual ordering not to the whole power set of L, but to the set of linguistic expressions $\mathbb{L}$, and accomplishing the criteria [C] and [B], and it is well understood that [C] is accomplished in this context if, for every $[l_h,l_k]\in \mathbb{L}$ such that $k<g$ it holds $[l_h,l_{k+1}]{\succ }_{\mathrm{ext}}[l_h,l_k]$, and for every $[l_h,l_k]\in \mathbb{L}$ such that $h>1$, it holds that $[l_{h-1},l_k]{\succ }_{\mathrm{ext}}[l_h,l_k]$.

Calling ${\succcurlyeq }_{\mathrm{cm}}$ to the extended linear order on $\mathbb{L}$, for $g=5$, we get:

$$\begin{array}{c}[l_1,l_5]{\succ }_{\mathrm{cm}}[l_2,l_5]{\succ }_{\mathrm{cm}}[l_1,l_4]{\succ }_{\mathrm{cm}}[l_3,l_5]{\succ }_{\mathrm{cm}}[l_2,l_4]{\succ }_{\mathrm{cm}}\hfill \\ [l_1,l_3]{\succ }_{\mathrm{cm}}[l_4,l_5]{\succ }_{\mathrm{cm}}[l_3,l_4]{\succ }_{\mathrm{cm}}[l_2,l_3]{\succ }_{\mathrm{cm}}[l_1,l_2]{\succ }_{\mathrm{cm}}\hfill \\ l_5{\succ }_{\mathrm{cm}}{l}_4{\succ }_{\mathrm{cm}}{l}_3{\succ }_{\mathrm{cm}}{l}_2{\succ }_{\mathrm{cm}}{l}_1.\hfill \end{array}$$

The linear order ${\succcurlyeq }_{\mathrm{cm}}$ is said to be the cardinality-maximality extension of ≽.

Remark 6.

The canonical order ${\succcurlyeq }_c$ on $\mathbb{L}$ only satisfies the criterion [M], well understood that [M] is accomplished in this context if, for every $l_h\in L$ such that $h<g$, it holds that $\left\{l_{h+1}\right\}{\succ }_{ext}[l_h,l_{h+1}]{\succ }_{ext}\left\{l_h\right\}$.

The lexicographic order ${\succcurlyeq }_{\ell }$ fails to satisfy both [M] and [C].

The cardinality-maximality extension ${\succcurlyeq }_{cm}$ satisfies [C], but not [M].

Taking into account the last ideas in Example 3, in which an extended order was defined on $\mathbb{L}$ but not necessarily on the whole power set of L, we may realize that, at this stage, an interesting question appears. Suppose that we are given a set of criteria for extension of a linear order from a set U to its power set. Assume also that, as it is the case of Kannai–Peleg’s theorem ([16]), such set of criteria provokes an impossibility result. Even if this happens, when we try to extend the ordering ≽ defined on the set $L=\{l_1,l_2,\dots ,l_g\}$ of labels, to its corresponding set $\mathbb{L}$ of linguistic expressions, it may still happen that an extension that accomplishes the criteria is possible. The reason is that $\mathbb{L}$ is much smaller than the whole power set of L. Sometimes, due to this restriction of domain, the extension could still be obtained. Similar questions, namely impossibility theorems in which the intrinsic impossibility actually disappears when a suitable restriction of domain is done, have been analyzed in depth in the contexts of Social Choice (see e.g., Gaertner [22]).

Let us explore this fact in more detail. Given a finite set $U=\{u_1,u_2,\dots ,u_p\}$ endowed with a linear order ≽ such that $u_i\succcurlyeq u_j\iff i\ge j$, suppose that we want to define an extension ${\succcurlyeq }_{\mathrm{ext}}$ on the power set of U. We say that ${\succcurlyeq }_{\mathrm{ext}}$ satisfies:

(i)

The Gärdenfors principle [G] (see Gärdenfors [15]) if, for all $A\subseteq U$ and $u_i\in U$, it holds that $u_i\succ max\left(A\right)\Rightarrow A\cup \left\{u_i\right\}{\succ }_{\mathrm{ext}}A$ and $min\left(A\right)\succ u_i\Rightarrow A{\succ }_{\mathrm{ext}}A\cup \left\{u_i\right\}$.

(ii)

The weak monotonicity principle [W] if, for all $A,B\subseteq U$ and $u_i\notin A\cup B$, it holds that $A{\succ }_{\mathrm{ext}}B\Rightarrow A\cup \left\{u_i\right\}{\succcurlyeq }_{\mathrm{ext}}B\cup \left\{u_i\right\}$.

A version of the key Kannai–Peleg impossibility theorem (see Kannai and Peleg [16], Fishburn [18], Barberà et al. [17] and Bossert [19]) reads as follows.

Theorem 1.

Let $U=\{u_1,u_2,\dots ,u_p\}$ be a finite set with at least six elements $(p\ge 6)$, endowed with the linear order ≽ defined as $u_i\succcurlyeq u_j\iff i\ge j$. Then, there is no extension ${\succcurlyeq }_{ext}$ that satisfies both [G] and [W] and is a total preorder on the power set of U.

However, after a suitable restriction of domain, the impossibility stated in the Kannai–Peleg theorem could actually disappear, if built in our context of linguistic terms and expressions, as the next Remark 7 clearly shows.

Remark 7.

When we consider the set of labels $L=\{l_1,l_2,\dots ,l_6\}$ endowed with the usual linear order ≽, we may observe that the canonical order ${\succcurlyeq }_c$ on $\mathbb{L}$ satisfies both [G] and [W], well understood that here in this context where a restriction of domain plays a crucial role, [G] and [W] should read as follows:

(i)

[G] is accomplished in this context if, for every $[l_h,l_k]\in \mathbb{L}$, the following conditions hold:

• $[l_h,l_{k+1}]{\succ }_{\mathrm{ext}}[l_h,l_k]$, whenever $k<g$,
• $[l_h,l_k]{\succ }_{\mathrm{ext}}[l_{h-1},l_k]$, whenever $h>1$.

(ii)

[W] is satisfied in this context if for all $[l_h,l_k],[l_h,l_{k^{\prime }}]\in \mathbb{L}$, the following conditions hold:

• $[l_h,l_k]{\succ }_{\mathrm{ext}}[l_h,l_{k^{\prime }}]\Rightarrow [l_{h-1},l_k]{\succcurlyeq }_{\mathrm{ext}}[l_{h-1},l_k]$, whenever $h>1$,
• $[l_h,l_k]{\succ }_{\mathrm{ext}}[l_{h^{\prime }},l_k]\Rightarrow [l_h,l_{k+1}]{\succcurlyeq }_{\mathrm{ext}}[l_{h^{\prime }},l_{k+1}]$, whenever $k<g$.

The extension ${\succcurlyeq }_{\mathrm{ext}}$ is a total preorder order because it is indeed a linear order. Therefore, Kannai–Peleg impossibility theorem is no longer valid when we extend linear orders from L to $\mathbb{L}$, that, obviously, is much smaller than the power set of L.

Another classical question in this approach consists in, starting from a finite set U endowed with a linear order, in order to characterize orderings on the power set of U (but not necessarily extensions of the given order on U) that satisfy a set of criteria imposed a priori.

Let us see an example of this situation.

Example 4.

Suppose that a total preorder ≽, defined directly on the power set of a finite set U, satisfies the following conditions:

(i) 

$\left\{u_i\right\}\sim \left\{u_j\right\}$ and also $\{u_i,u_j\}\succ \left\{u_i\right\}$ hold true for all $u_i,u_j\in U$ such that $u_i\ne u_j$.

(ii) 

For all $A,B\subset U$ and $u_i\notin A\cup B$, it holds that $A\succcurlyeq B\Rightarrow A\cup \left\{u_i\right\}\succcurlyeq B\cup \left\{u_i\right\}$.

Then, it can be straightforwardly proved that ≽ is, exactly, the so-called cardinal ordering on the power set of U, namely $A\succcurlyeq B\iff \#A\ge \#B$ holds true for all $A,B\subseteq U$ (see Pattanaik and Xu [23] for a proof of this last fact).

Having these ideas in mind, and coming back to our context of labels and linguistic expressions, we may see that the lexicographic extension ${\succcurlyeq }_{\ell }$ on $\mathbb{L}$ is characterized as follows.

Proposition 7.

Consider the set of labels $L=\{l_1,l_2,\dots ,l_g\}$, endowed with the usual linear order ≽. An extension ${\succcurlyeq }_{ext}$ to the set $\mathbb{L}$ of linguistic expressions satisfies the following conditions:

(i) 

For all $h,k\in \{1,\cdots ,g\}$, it holds that $\left\{l_h\right\}{\succcurlyeq }_{ext}\left\{l_k\right\}\iff h\ge k$.

(ii) 

For all $[l_h,l_k],[l_{h^{\prime }},l_{k^{\prime }}]\in \mathbb{L}$, it holds that $h>h^{\prime }\Rightarrow [l_h,l_k]{\succ }_{ext}[l_{h^{\prime }},l_{k^{\prime }}]$.

(iii) 

For all $[l_h,l_k],[l_h,l_{k^{\prime }}]\in \mathbb{L}$, it holds that $k>k^{\prime }\Rightarrow [l_h,l_k]{\succ }_{ext}[l_h,l_{k^{\prime }}]$,

if and only if ${\succcurlyeq }_{ext}={\succcurlyeq }_{\ell }$.

Proof. 

It is in immediate consequence of the mere definition of the lexicographic extension ${\succcurlyeq }_{\ell }$ on $\mathbb{L}$. ☐

The cardinality-maximality extension ${\succcurlyeq }_{\mathrm{cm}}$ can be characterized as follows.

Proposition 8.

Consider the set of labels $L=\{l_1,l_2,\dots ,l_g\}$, endowed with the usual linear order ≽. An extension ${\succcurlyeq }_{ext}$ to the set $\mathbb{L}$ of linguistic expressions satisfies the following conditions:

(i) 

For all $h,k\in \{1,\cdots ,g\}$, it holds that $\left\{l_h\right\}{\succcurlyeq }_{ext}\left\{l_k\right\}\iff h\ge k$.

(ii) 

For all $\mathcal{E}=[l_h,l_k],\mathcal{F}=[l_{h^{\prime }},l_{k^{\prime }}]\in \mathbb{L}$, it holds that $\#\mathcal{E}>\#\mathcal{F}\Rightarrow \mathcal{E}{\succ }_{ext}\mathcal{F}$.

(iii) 

For all $\mathcal{E}=[l_h,l_k],\mathcal{F}=[l_{h^{\prime }},l_{k^{\prime }}]\in \mathbb{L}$ with $\#\mathcal{E}=\#\mathcal{F}$, it holds $k>k^{\prime }\Rightarrow \mathcal{E}{\succ }_{ext}\mathcal{F}$,

if and only if ${\succcurlyeq }_{ext}={\succcurlyeq }_{cm}$.

Proof. 

It is in immediate consequence of the mere definition of the cardinality-maximality extension ${\succcurlyeq }_{\mathrm{cm}}$ on $\mathbb{L}$. ☐

We may also point out that these characterizations can reflect practical situations. In fact, they could reflect particular methods of assigning scores, perhaps discriminating between expressions that have the same score, as the next Examples 5 and 6 show. Notice that sometimes people use more than one score: first, there is one method of scoring, but if this leads to a tie, then a second method of scoring is used, and so on, using more methods of scorings if necessary, until the tie is broken.

Example 5.

Consider the set of labels $L=\{l_1,l_2,\dots ,l_g\}$, two scoring functions $S,T:\mathbb{L}\to \mathbb{R}$ and the following total preorder on $\mathbb{L}$

$$[l_h,l_k]{\succcurlyeq }_{ext}[l_{h^{\prime }},l_{k^{\prime }}]\iff \left\{\begin{array}{c}S\left([l_h,l_k]\right)>S\left([l_{h^{\prime }},l_{k^{\prime }}]\right)\hfill \\ or\hfill \\ S\left([l_h,l_k]\right)=S\left([l_{h^{\prime }},l_{k^{\prime }}]\right)andT\left([l_h,l_k]\right)\ge T\left([l_{h^{\prime }},l_{k^{\prime }}]\right).\hfill \end{array}\right.$$

(6)

(i)

If $S\left([l_h,l_k]\right)=h+k$ and $T\left([l_h,l_k]\right)=h-k$, then ${\succcurlyeq }_{\mathrm{ext}}$ is the canonical extension ${\succcurlyeq }_c$ on $\mathbb{L}$.

(ii)

If $S\left([l_h,l_k]\right)=h$ and $T\left([l_h,l_k]\right)=k$, then ${\succcurlyeq }_{\mathrm{ext}}$ is the lexicographic extension ${\succcurlyeq }_{\ell }$ on $\mathbb{L}$.

(iii)

If $S\left([l_h,l_k]\right)=k-h$ and $T\left([l_h,l_k]\right)=k$, then ${\succcurlyeq }_{\mathrm{ext}}$ is the cardinality-maximality extension ${\succcurlyeq }_{\mathrm{cm}}$ on $\mathbb{L}$.

Example 6.

An expert is forecasting the quality of the forthcoming new harvest in a piece of land. To do so, she/he uses labels as {very bad, bad, poor, fair, good, very good, excellent}. Moreover she/he can hesitate and show imprecision, so that the forecast could be an expression as, for instance, “from fair to very good”. From the point of view of the land keepers, a forecast is more positive than another one if the “average” is more favorable. Among two forecasts with identical average, it is important to avoid imprecision so that the most accurate is declared the more positive. The extension ${\succcurlyeq }_{ext}$ defined this way is the lexicographic one, ${\succcurlyeq }_{\ell }$, on $\mathbb{L}$.

4. Aggregation of Qualitative Assessments and Scorings

4.1. Some Facts about the Aggregation of Assessments and Scorings

Suppose now that a finite number of experts, agents, decision-makers or individuals show their assessments on a finite set, called universe of alternatives, $X=\{x_1,x_2,\dots ,x_n\}$. To do so, each individual could establish a qualitative ranking on X, based on linguistic terms $L=\{l_1,l_2,\dots ,l_g\}$, or perhaps they show some imprecision and use the set $\mathbb{L}$ of linguistic expressions that come from L. Once the opinions of all the individuals have been established, a typical problem consists in aggregating them into a social ranking that somewhat reflects a decision that could be shared by all the individuals, as a society or collective, following some rules of “common sense” on which all the agents could agree. To put a trivial example, if each agent has ranked the elements of X in an identical manner, it seems compulsory that the social ranking should keep this, making no changes on the label or linguistic expression assigned to each one of the alternatives, and consequently showing respect for unanimity. It could also happen that each agent has already defined a sort of numerical scoring on the alternatives, so that the problem of aggregation translates in defining some sort of average of the individual numerical scores.

Notice that any scoring function $S:X\to \mathbb{R}$ immediately defines a total preorder $\succcurlyeq$ on X by just declaring $x_i\succcurlyeq x_j\iff S\left(x_i\right)\ge S\left(x_j\right)$, for all $x_i,x_j\in X$. An important fact that comes from the aggregation problem is that, even in the case of any individual scoring function defining a linear order on X—that is, provided that ties never occur at the individual level—the final social aggregated scoring function could fail to be a linear order. Ties could appear after aggregation, so that total preorder is all the best that we may expect a priori as the ordering coming from a social scoring function.

Moreover, at this stage, it is relevant to say that even imposing mild restrictions of so-to-say “common sense” to the rules that aggregate individual preferences into a social one, the existence of a social rule in those conditions could become impossible, as proved in the famous Arrow’s impossibility theorem in Social Choice (see e.g., Arrow [24], Kelly [25], Campbell and Kelly [26] and Campión et al. [27] for further information on this topic).

In the present Section 4, we will not pay attention to these last kinds of questions. Instead, we will introduce some aggregation procedures for qualitative assessments and/or scorings over a finite set, disregarding the fact of the aggregation procedure satisfying the typical conditions (e.g., independence of irrelevant alternatives, non-dictatorship, etc.) arising in the Arrovian model or similar settings.

Let us introduce now some necessary concepts to deal with an aggregation procedure.

Definition 6.

Let $X=\{x_1,x_2,\dots ,x_n\}$ be a finite set of alternatives. Suppose that a finite set of agents $A=\{1,2,\dots ,m\}$ declare their assessments on the elements of X by means of linguistic expressions. A profile V is a matrix $\left(v_i^a\right)$ consisting of m rows and n columns (Notice that here the superindex a will correspond to a row (that depends on agents), whereas the subindex i corresponds to a column (that depends on alternatives)) of linguistic expressions, where the element $v_i^a\in \mathbb{L}$ represents the linguistic assessment given by the agent $a\in A$ to the alternative $x_i\in X$. Then,

$$V=\left(\begin{array}{ccccc}{v}_1^1& \cdots & v_i^1& \cdots & v_n^1\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ v_1^a& \cdots & v_i^a& \cdots & v_n^a\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ v_1^m& \cdots & v_i^m& \cdots & v_n^m\end{array}\right)=\left(v_i^a\right).$$

Therefore, each entry $v_i^a$ is a linguistic expression $[l_h,l_k]\in \mathbb{L}$, which corresponds to the assessment that the a-th agent or expert has done on the i-th element $x_i$ of the set X of alternatives. Both $l_h$ and $l_k$ will depend on the position in which $v_i^a$ is located in the matrix V, namely in the a-th row and i-th column.

Taking into account the interval $I_g$ appearing in Proposition 5 and the scoring function $S_{\alpha }:\mathbb{L}⟶\mathbb{R}$ introduced in Definition 5, we now define the scoring function $T_{\alpha }:X\to \mathbb{R}$ as

$$T_{\alpha }\left(x_i\right)=\frac{1}{m}\sum _{a=1}^m{S}_{\alpha }\left(v_i^a\right),$$

for each profile $V=\left(v_i^a\right)$.

We now establish the procedure for ranking the alternatives.

Proposition 9.

Given $\alpha \in I_g$ and a profile $V=\left(v_i^a\right)$, the binary relation ${\succcurlyeq }_{\alpha }$ on X defined as

$$x_i{\succcurlyeq }_{\alpha }{x}_j\iff T_{\alpha }\left(x_i\right)\ge T_{\alpha }\left(x_j\right)$$

is a total preorder on X.

Proof. 

Just notice that any scoring function $T:X\to \mathbb{R}$ immediately defines a total preorder $\succcurlyeq$ on X by declaring $x_i\succcurlyeq x_j\iff T\left(x_i\right)\ge T\left(x_j\right)$.

Consider now that agents should assess each alternative from different criteria, so that $C=\{c_1,c_2,\cdots ,c_r\}$ represents the set of criteria available to the agents. Then, we have r profiles $V^1=\left(v_i^{a,1}\right)$, $V^2=\left(v_i^{a,2}\right)$, ⋯, $V^r=\left(v_i^{a,r}\right)$, where $v_i^{a,q}\in \mathbb{L}$ is the assessment given by the agent $a\in A$ to the i-th alternative $x_i\in X$ with respect to the q-th criterion $c_q\in C$.

Since each criterion may have different importance in the decision, we will also consider a weighting vector $w=(w_1,w_2,\cdots ,w_r)\in {[0,1]}^r$, satisfying $w_1+w_2+\cdots +w_r=1$.

Given $\alpha \in I_g$, the profiles $V^1=\left(v_i^{a,1}\right)$, $V^2=\left(v_i^{a,2}\right)$, ⋯, $V^r=\left(v_i^{a,r}\right)$ and a weighting vector $\mathit{w}=(w_1,w_2,\cdots ,w_r)$ satisfying $w_1+w_2+\cdots +w_r=1$, we now define the scoring function $T_{\alpha ,\mathit{w}}:X\to \mathbb{R}$ as

$$T_{\alpha ,\mathit{w}}\left(x_i\right)=\frac{1}{r}\sum _{q=1}^r{w}_q\left(\frac{1}{m}\sum _{a=1}^m{S}_{\alpha }\left(v_i^{a,q}\right)\right).$$

Proposition 10.

Given $\alpha \in I_g$, the profiles $V^1=\left(v_i^{a,1}\right)$, $V^2=\left(v_i^{a,2}\right)$, ⋯, $V^r=\left(v_i^{a,r}\right)$ and a weighting vector $\mathit{w}=(w_1,w_2,\cdots ,w_r)$ satisfying $w_1+w_2+\cdots +w_r=1$, the binary relation ${\succcurlyeq }_{\alpha ,\mathit{w}}$ on X defined as

$$x_i{\succcurlyeq }_{\alpha ,\mathit{w}}{x}_j\iff T_{\alpha ,\mathit{w}}\left(x_i\right)\ge T_{\alpha ,\mathit{w}}\left(x_j\right)$$

is a total preorder on the set X of alternatives.

Proof. 

The proof is immediate and leans on the same fact as the proof of Proposition 9. ☐

Remark 8.

Similar constructions could also be done using, instead of the arithmetic mean, other kinds of aggregation functions as, e.g., medians, trimmed means and so on.

We note that García-Lapresta and González del Pozo [28] propose a multi-criteria decision-making procedure in the same framework, but using a purely ordinal approach.

4.2. A Field Experiment

As described with more detail in García-Lapresta et al. [1], the proposed use of qualitative rankings and scorings based on linguistic expressions, their numerical representation by means of the geodesic distance plus a penalization of imprecision, as well as the subsequent method of aggregation just described in Proposition 10, have actually been tested in a field experiment carried out in Trigo restaurant in Valladolid, Spain (30 November 2013), under appropriate conditions of temperature, light and service.

A total of six experts trained in the sensory analysis of wines and wild mushrooms were recruited through the Gastronomy and Food Academy of Castile and Leon. When the test was being carried out, there was no communication between the experts and the samples were given to them without any identification.

The six experts assessed the products included in Table 1 through the five linguistic terms of Table 2 (or the corresponding linguistic expressions, when they hesitated) under three criteria: appearance (A), smell (S) and taste (T).

Table 1. Alternatives.

$x_1$	White wine ‘Rueda Zascandil 2012’
$x_2$	Red wine ‘Toro Valdelacasa 2007’
$x_3$	Raw Boletus pinophilus
$x_4$	Raw Tricholoma portentosum
$x_5$	Cooked Boletus pinophilus
$x_6$	Cooked Tricholoma portentosum

Table 2. Linguistic terms.

$l_1$	I don’t like it at all
$l_2$	I don’t like it
$l_3$	I like it
$l_4$	I rather like it
$l_5$	I like it so much

Five of the six experts sometimes hesitated about their opinions, and they assigned linguistic expressions with two labels. This happened in 19 of the 108 ratings, i.e., $17.59\%$ of the cases. The ratings provided by the experts appear in Table 3.

Table 3. Ratings.

		Expert 1	Expert 2	Expert 3	Expert 4	Expert 5	Expert 6
$x_1$	A	$l_3$	$l_4$	$l_4$	$l_5$	$l_3$	$l_3$
	S	$[l_3,l_4]$	$l_3$	$l_4$	$l_4$	$l_4$	$l_4$
	T	$l_3$	$l_3$	$l_4$	$l_4$	$l_3$	$l_3$
$x_2$	A	$l_4$	$l_4$	$l_2$	$l_5$	$l_4$	$l_4$
	S	$[l_4,l_5]$	$l_5$	$l_2$	$l_5$	$l_3$	$l_5$
	T	$[l_4,l_5]$	$l_5$	$l_2$	$l_5$	$l_3$	$[l_4,l_5]$
$x_3$	A	$l_4$	$l_4$	$l_5$	$l_5$	$l_3$	$l_4$
	S	$[l_4,l_5]$	$l_3$	$[l_4,l_5]$	$l_5$	$l_3$	$l_5$
	T	$l_5$	$l_5$	$[l_4,l_5]$	$l_5$	$l_4$	$[l_4,l_5]$
$x_4$	A	$l_4$	$l_3$	$l_4$	$l_5$	$l_3$	$[l_2,l_3]$
	S	$l_3$	$[l_2,l_3]$	$l_4$	$l_3$	$l_2$	$[l_2,l_3]$
	T	$l_3$	$l_3$	$[l_4,l_5]$	$l_4$	$l_2$	$l_4$
$x_5$	A	$l_5$	$l_4$	$l_4$	$l_4$	$l_3$	$l_4$
	S	$l_5$	$l_5$	$l_5$	$l_4$	$l_3$	$[l_4,l_5]$
	T	$[l_4,l_5]$	$l_5$	$l_5$	$l_5$	$l_4$	$[l_4,l_5]$
$x_6$	A	$l_5$	$l_3$	$[l_4,l_5]$	$l_5$	$[l_2,l_3]$	$l_4$
	S	$l_5$	$l_3$	$l_5$	$l_3$	$[l_3,l_4]$	$l_4$
	T	$l_4$	$l_4$	$l_5$	$l_3$	$l_4$	$[l_3,l_4]$

We now show the outcomes in five cases.

• When only considering appearance, i.e., $\mathit{w}=(1,0,0)$, and the parameter $\alpha =0.3$, we obtain:

  $$\begin{array}{ccc}{T}_{\alpha ,\mathit{w}}\left(x_1\right)=5.333,& T_{\alpha ,\mathit{w}}\left(x_2\right)=5.666,& T_{\alpha ,\mathit{w}}\left(x_3\right)=6.333,\\ T_{\alpha ,\mathit{w}}\left(x_4\right)=5.116,& T_{\alpha ,\mathit{w}}\left(x_5\right)=6.000,& T_{\alpha ,\mathit{w}}\left(x_6\right)=5.900.\end{array}$$
  Then, $x_3{\succ }_{\alpha ,\mathit{w}}{x}_5{\succ }_{\alpha ,\mathit{w}}{x}_6{\succ }_{\alpha ,\mathit{w}}{x}_2{\succ }_{\alpha ,\mathit{w}}{x}_1{\succ }_{\alpha ,\mathit{w}}{x}_4$.
• When only considering smell, i.e., $\mathit{w}=(0,1,0)$, and the parameter $\alpha =0.3$, we obtain:

  $$\begin{array}{ccc}{T}_{\alpha ,\mathit{w}}\left(x_1\right)=5.450,& T_{\alpha ,\mathit{w}}\left(x_2\right)=6.116,& T_{\alpha ,\mathit{w}}\left(x_3\right)=6.233,\\ T_{\alpha ,\mathit{w}}\left(x_4\right)=3.566,& T_{\alpha ,\mathit{w}}\left(x_5\right)=6.783,& T_{\alpha ,\mathit{w}}\left(x_6\right)=5.783.\end{array}$$
  Then, $x_5{\succ }_{\alpha ,\mathit{w}}{x}_3{\succ }_{\alpha ,\mathit{w}}{x}_2{\succ }_{\alpha ,\mathit{w}}{x}_6{\succ }_{\alpha ,\mathit{w}}{x}_1{\succ }_{\alpha ,\mathit{w}}{x}_4$.
• When only considering taste, i.e., $\mathit{w}=(0,0,1)$, and the parameter $\alpha =0.3$, we obtain:

  $$\begin{array}{ccc}{T}_{\alpha ,\mathit{w}}\left(x_1\right)=4.666,& T_{\alpha ,\mathit{w}}\left(x_2\right)=5.900,& T_{\alpha ,\mathit{w}}\left(x_3\right)=7.233,\\ T_{\alpha ,\mathit{w}}\left(x_4\right)=4.783,& T_{\alpha ,\mathit{w}}\left(x_5\right)=7.233,& T_{\alpha ,\mathit{w}}\left(x_6\right)=5.783.\end{array}$$
  Then, $x_3{\sim }_{\alpha ,\mathit{w}}{x}_5{\succ }_{\alpha ,\mathit{w}}{x}_2{\succ }_{\alpha ,\mathit{w}}{x}_6{\succ }_{\alpha ,\mathit{w}}{x}_4{\succ }_{\alpha ,\mathit{w}}{x}_1$.
• Taking into account the weights (These weights are quite usual in this kind of tasting.), $w_1=0.2$ for appearance, $w_2=0.3$ for smell and $w_3=0.5$ for taste, i.e., $\mathit{w}=(0.2,0.3,0.5)$, and the parameter $\alpha =0.3$, we obtain:

  $$\begin{array}{ccc}{T}_{\alpha ,\mathit{w}}\left(x_1\right)=5.035,& T_{\alpha ,\mathit{w}}\left(x_2\right)=5.918,& T_{\alpha ,\mathit{w}}\left(x_3\right)=6.753,\\ T_{\alpha ,\mathit{w}}\left(x_4\right)=4.485,& T_{\alpha ,\mathit{w}}\left(x_5\right)=6.852,& T_{\alpha ,\mathit{w}}\left(x_6\right)=5.807.\end{array}$$
  Then, $x_5{\succ }_{\alpha ,\mathit{w}}{x}_3{\succ }_{\alpha ,\mathit{w}}{x}_2{\succ }_{\alpha ,\mathit{w}}{x}_6{\succ }_{\alpha ,\mathit{w}}{x}_1{\succ }_{\alpha ,\mathit{w}}{x}_4$.
• Taking into account the weights $w_1=0.4$ for appearance, $w_2=0.2$ for smell and $w_3=0.4$ for taste, i.e., $\mathit{w}=(0.4,0.2,0.4)$, and the parameter $\alpha =0.3$, we obtain the following outcomes:

  $$\begin{array}{ccc}{T}_{\alpha ,\mathit{w}}\left(x_1\right)=5.090,& T_{\alpha ,\mathit{w}}\left(x_2\right)=5.850,& T_{\alpha ,\mathit{w}}\left(x_3\right)=6.673,\\ T_{\alpha ,\mathit{w}}\left(x_4\right)=4.673,& T_{\alpha ,\mathit{w}}\left(x_5\right)=6.650,& T_{\alpha ,\mathit{w}}\left(x_6\right)=5.830.\end{array}$$
  Then, $x_3{\succ }_{\alpha ,\mathit{w}}{x}_5{\succ }_{\alpha ,\mathit{w}}{x}_2{\succ }_{\alpha ,\mathit{w}}{x}_6{\succ }_{\alpha ,\mathit{w}}{x}_1{\succ }_{\alpha ,\mathit{w}}{x}_4$.

Although we have considered the specific value of $\alpha =0.3$ in the previous calculations, we have to notice that in all cases the alternatives are ranked in the same way for all the values of $\alpha \in I_5=(0,1/3)$. Thus, the parameter $\alpha$ has been irrelevant in this field experiment. The reason is the low number of assessments with more than one linguistic term ($17.59\%$ of the cases). However, if applying the procedure of Proposition 9 to the field experiment presented in Agell et al. [29], where five experts assessed five fruits with respect to their suitability to combine with dark chocolate, and $40\%$ of the assessments were linguistic expressions with two or more linguistic terms, the ranking depending on the value of the parameter $\alpha$.

We may conclude that this method, based on geodesic distances on linguistic expressions, plus a penalization of imprecision, and using a weighting vector according to different criteria, could be considered as a suitable one in these practical experiments, at least in the field of sensory analysis.

5. Conclusions

The definition of ratings and/or scorings on a finite set has been associated with a wide sort of theoretical questions, namely:

(i)

The existence of a numerical representation for a total preorder on a finite set, so translating qualitative scales into quantitative (numerical) ones.

(ii)

The selection of a suitable method of scoring or numerical representation of a qualitative scale.

(iii)

The search for a compatible extension of a ranking defined on a finite set to its power set—or at least to a suitable superset of the given set—following a list of criteria established a priori.

(iv)

The implementation of aggregation procedures on profiles of individual ratings and/or scorings, in the search for a new scoring that reflects a social average.

(v)

The comparison between different ways of rating, scoring and aggregating, in the search for the most suitable one in view of some practical circumstances to be used in field experiments, and so on.

As a matter of fact, each of these questions, studied separately, could give raise to a wide sort of results in the literature. Indeed most of them have already been considered and analyzed, at least partially, by many authors.

However, many open problems remain. To provide only a few examples, we could say at this point that:

(i)

A systematic study of criteria to extend a linear order from a set to its power set, trying to classify the criteria in, so-to-say, contradictory families, so that any two criteria coming from different families give raise to an impossibility result.

(ii)

The systematic development of a standard procedure to determine which rating, scoring and/or aggregation procedure is the most suitable, maybe taking into account some previous criteria.

Needless to say, all of this leaves enough room for further research to be developed in the future.