Abstract
Recent years have seen significant advances in the study of symmetric informationally complete (SIC) quantum measurements, also known as maximal sets of complex equiangular lines. Previously, the published record contained solutions up to dimension 67, and was with high confidence complete up through dimension 50. Computer calculations have now furnished solutions in all dimensions up to 151, and in several cases beyond that, as large as dimension 844. These new solutions exhibit an additional type of symmetry beyond the basic definition of a SIC, and so verify a conjecture of Zauner in many new cases. The solutions in dimensions 68 through 121 were obtained by Andrew Scott, and his catalogue of distinct solutions is, with high confidence, complete up to dimension 90. Additional results in dimensions 122 through 151 were calculated by the authors using Scott’s code. We recap the history of the problem, outline how the numerical searches were done, and pose some conjectures on how the search technique could be improved. In order to facilitate communication across disciplinary boundaries, we also present a comprehensive bibliography of SIC research.
1. Introduction
The problem of symmetric, informationally complete quantum measurements [1,2,3,4] stands at the confluence of multiple areas of physics and mathematics. SICs, as they are known for short, tie into algebraic number theory [5,6,7,8], higher-dimensional sphere packing [9], Lie and Jordan algebras [10,11], finite groups [12,13] and quantum information theory [14,15,16,17,18,19,20,21,22,23]. Without the study of SICs, one might think that the intersection of all these subjects would have to be the empty set. Yet, for all that, a SIC is a remarkably simple mathematical structure, as structures go. Consider the complex vector space . To a physicist, this is the Hilbert space associated with a d-level quantum system. Let be a set of exactly unit vectors in such that
whenever . The set , which can be associated with a set of pairwise equiangular lines through the origin, is a SIC.
One can prove that no more than vectors in a d-dimensional Hilbert space can be equiangular. That is, if is a set of vectors, and for every , then that set can have at most elements. In addition, for a maximal set the value of is fixed by the dimension; it must be . So, a SIC is a maximal equiangular set in ; the question is whether they can be constructed for all values of the dimension. Despite a substantial number of exact solutions, as well as a longer list of high-precision numerical solutions [4,8,24], the problem remains open.
Exact solutions, found by hand in a few cases and by computer algebra software in others, are known in the following dimensions:
The historical record of exact solutions is spread over a sequence of publications [4,8,25,26]. For several years, the most extensive published set of numerical results went as high as dimension [4]. Now, numerical solutions are known in all dimensions up to and including , as well as a handful of other dimensions up to . These numerical solutions were found using code designed and written by Scott, who extended the results of [4] through using his personal computer over several years of dedicated effort. In addition, Scott found solutions in a set of dimensions (, 143, 147, 168, 172, 195, 199, 228, 259, 323) by taking advantage of particular simplifying assumptions that are applicable in those dimensions [24]. Further close study of these properties led to a solution for [26]. Because dimension was pushing the limits of what was computationally feasible without those simplifying assumptions, the authors calculated solutions in dimensions 122 through 151 by running Scott’s code on the Chimera supercomputer at UMass Boston. In turn, Scott was able to employ another algorithm (outlined below) to refine the numerical precision of these results.
The solutions from all of these search efforts are available together at the website of the QBism Research Group at UMass Boston [27].
An intriguing feature of the SIC problem is that some numerical solutions, if extracted to sufficiently high precision, can be converted to exact ones [8,25]. Most recently, this technique was used to derive an exact solution in dimension . Another interesting aspect is that the number of distinct SIC constructions varies from one dimension to another (The sense in which two SICs can be equivalent will be discussed in detail below). One reason computational research is valuable, beyond extending the list of dimensions in which SICs are known, is that it provides what is likely a complete picture for many values of the dimension. This is important for understanding the subtle connection between SICs and algebraic number theory [5], a connection that brings a new angle of illumination to Hilbert’s twelfth problem [6,7].
SICs are so called because, thanks to the rules of quantum theory, a SIC in specifies a measurement procedure that can, in principle, be applied to a d-level quantum system. For example, a SIC in is a set of four equiangular lines, and it is a mathematical model of a measurement that a physicist can perform on a single qubit. The term “informationally complete”—the “IC” in “SIC”—means that if one has a probability distribution for the possible outcomes of a SIC experiment, one can compute the probabilities for the possible outcomes of any other experiment carried out on the target system [17]. So, while one can pose the question of their existence using pure geometry, SICs are relevant to applied physics. Indeed, SIC measurements have recently been performed or approximated in the laboratory [28,29,30,31,32,33,34,35], and they are known to be optimal measurements for quantum-state tomography [36].
A SIC provides a frame—more specifically, an equiangular tight frame—for the vector space . Given a finite-dimensional Hilbert space with an inner product , a frame for is a set of vectors such that for any vector ,
for some positive constants A and B. The frame is equal-norm if all the vectors have the same norm, and the frame is tight if the “frame bounds” A and B are equal. The ratio of the number of vectors to the dimension of the space is known as the redundancy of the frame [37]. For more on this terminology and its history, we refer to Kovačević and Chebira [38,39]. In our experience, the language of frames is more common among those who come to SICs from pure mathematics or from signal processing than among those motivated by quantum physics.
Any vector in can be represented by its inner products with all the SIC vectors. In quantum physics, one also considers the set of Hermitian operators on . This set in fact forms a Hilbert space itself, with a dimension of , and the inner product given by the Hilbert–Schmidt formula
Rewriting the SIC vectors as rank-1 projection operators,
we construct a nonorthogonal basis for the Hilbert space of Hermitian operators. Because the inner products of these projectors are uniform, given by
then it is straightforward to find a shifting and rescaling that orthogonalizes the basis , at the cost of making the operators non-positive-semidefinite. In fact, there are two choices:
The bases have interesting properties with regard to Lie algebra theory [11] and the study of quantum probability [20,40].
2. Generating SICs with Groups
All known SICs have an additional kind of symmetry, above and beyond their definition: They are group covariant. Each SIC can be constructed by starting with a single vector, known as a fiducial vector, and acting upon it with the elements of some group. It is not known in general whether a SIC must be group covariant. Because such an assumption greatly reduces the search space [4,5], it has been the only method used so far: The fact that we only know of group-covariant SICs could potentially be an artifact of this. (However, we do have a proof that all SICs in and are group covariant [41].)
In all cases but one, the group that generates a SIC from a fiducial is an instance of a Weyl–Heisenberg group. We can define this group as follows. First, fix a value of d, and let . Let be an orthonormal basis for the Hilbert space . Then, construct the shift and phase operators
where the shift is modulo d. These operators satisfy the Weyl commutation relation,
In a sense, the operators X and Z come as close as possible to commuting, without actually doing so: The only cost to exchanging their order is a phase factor determined by the dimension.
The Weyl–Heisenberg displacement operators in dimension d are defined by
The product of two displacement operators is, up to a phase factor, a third:
Therefore, by allowing the generators to be multiplied by phase factors, we can define a group, known as the Weyl–Heisenberg group in dimension d. This group dates back to the early days of quantum physics. Weyl introduced the generators X and Z as long ago as 1925 in order to define what one might mean by the quantum theory of discrete degrees of freedom [42,43,44] (see also [45] (pp. 2055–2056)). This group, and structures derived from it, are critically important in quantum information and computation; for example, this is the basic prerequisite for the Gottesman–Knill theorem, which indicates when a quantum computation can be efficiently simulated classically [46]. The close relationship between SICs and the Weyl–Heisenberg group suggests that SICs are a kind of structure that quantum physics should have been studying all along.
Zhu has proved that in prime dimensions, group covariance implies Weyl–Heisenberg covariance [47]. The one known exception to the rule of Weyl–Heisenberg covariance is the Hoggar SIC [48,49], which lives in a prime-power dimension, . As in all other dimensions, there is a Weyl–Heisenberg SIC, but there is also the Hoggar SIC. Like many other exceptions to mathematical classifications, it is related to the octonions [9,13].
One example of a Weyl–Heisenberg SIC can be constructed by taking the orbit of the following two-dimensional vector under the Weyl–Heisenberg displacement operators:
This orbit is a set of four vectors. In the Bloch sphere representation, they form the vertices of a regular tetrahedron inscribed within the sphere.
An example in dimension , one which is remarkable for the further subtle symmetries it possesses beyond even group covariance, is the orbit of
under the Weyl–Heisenberg displacements. This set of vectors is known as the Hesse SIC [41,50,51], thanks to its relation with the Hesse configuration familiar from design theory and the study of cubic curves, specifically nonsingular cubic curves in complex projective two-space [12,16,52,53].
3. Historical Overview
In order to understand the current state of SIC research, one must grasp how people came to the SIC question, what other structures they think are related, what tools they suspect are applicable, and so forth. A physicist, motivated by quantum information theory, is apt to have a different mental context than a pure mathematician driven by the abstract appeal of geometry. To attempt to foster an interdisciplinary discussion, we provide in this section a brief historical overview.
The Hesse SIC can be extracted from a 1940 article by H. S. M. Coxeter [54], which discusses what he later called the “Hessian polyhedron” [52]. This polyhedron lives in three-dimensional complex vector space and has 27 vertices (which correspond to the 27 lines on a cubic surface [55]). The vectors in the Hesse SIC are a subset of those vertices. Mathematicians were studying SICs in and more explicitly as early as the 1970s, in the terminology of complex equiangular lines [56]. Stuart Hoggar found a SIC in dimension a few years later [48], by considering the diagonals of a quaternionic polytope and converting their coordinates to complex numbers. The SICs in and , together with the Hoggar lines in , still stand out among the known SICs; various unusual attributes they possess have led them to be designated the sporadic SICs [7,9]. (Other investigations in this time period, before SICs became a physics subject, are recorded in references [57,58,59,60].)
In a 1987 article, Richard Feynman used a construction that is in retrospect a SIC to study the probability theory of a qubit. SICs entered quantum theory more generally starting with the work of Gerhard Zauner, who began to consider the problem in the 1990s [45] (p. 1941). By 1999, Zauner had found the connection with the Weyl–Heisenberg group and proven SIC existence up to [1]. He also posed a conjecture that the search for Weyl–Heisenberg SICs could be simplified by considering a particular unitary operator [1], a conjecture we will describe in detail below.
Independently of Zauner, Carlton Caves developed the idea of a SIC as representing a quantum measurement [2], motivated originally by attempts to prove the “quantum de Finetti theorem” [61]. SICs turned out to have more symmetry than was necessary for that proof, but they soon took on a life of their own in quantum information theory [23]. The term “SIC” (first pronounced as “sick,” and later like “seek”) dates to this period. A 2004 paper, “Symmetric Informationally Complete Quantum Measurements” [3], introduced them to the mainstream of the quantum information community, and reported numerical solutions for dimensions up to . In a later survey, Andrew Scott and Markus Grassl extended these numerical results up to dimension [4]. Further work by Scott established Weyl–Heisenberg SICs in all cases up to without exception. Moreover, these results together are probably a complete catalogue of all distinct Weyl–Heisenberg SICs up to dimension [24]. In later sections, we will give an overview of how these searches were done.
Exact solutions were found more slowly. Having exact expressions for SIC fiducial vectors allowed Appleby et al. to discover a connection with Galois theory [62]. In turn, this led to further relations with algebraic number theory, a frankly mysterious development that is still under active investigation [5,6,7,8].
An exhaustive treatment of SIC research would require transgressing many disciplinary boundaries, and would doubtless grow to an intimidating length. In order to provide at least a helpful ordering on the literature, we have made our bibliography as comprehensive as possible. Table 1 lists references by topic. We note in particular the significant number of student theses written in whole or in part on the SIC problem [1,18,25,63,64,65,66,67,68,69,70].

Table 1.
References classified by the topics to which they give significant coverage.
Before moving on, we note that the real analogue of the SIC problem, i.e., finding maximal sets of equiangular lines in real vector spaces, has also been of considerable interest to mathematicians [191,192,193]. The maximal number of equiangular lines in a d-dimensional vector space is not , but only . That is, if we have a set of N unit vectors in a d-dimensional vector space, such that
then the size N of the set cannot exceed . Moreover, while the complex bound of has been saturated in every dimension that we have been able to check, it is known that the real bound of is not even attained for all values of d. For example, in , one can construct a set of equiangular lines, but this is also the best that can be done in . In fact, the only known instances where the bound of can be attained are dimensions 2, 3, 7 and 23 [193].
There is a sign freedom in this definition of the angle, since Equation (14) is satisfied if the inner product is either or . The presence of this discrete choice means that investigations of real equiangular lines often have a rather combinatorial flavor. In contrast, when we take the magnitude of a complex inner product, we discard a continuous quantity, a phase that in principle can be anywhere from 0 to . Generally speaking, the “feel” of the real and complex problems differ, as is evidenced by the different areas of mathematical expertise brought to bear upon them. However, subtle and unanticipated points of contact between the real and complex cases do exist [13].
4. How to Search for SICs Numerically
As before, let be an orthonormal basis for the Hilbert space . In this basis, the fiducial vector can be written
for some set of coefficients .
Acting with the Weyl–Heisenberg operator on the fiducial vector produces a new vector, whose squared innner product with the fiducial vector is
The right-hand side has the form of the magnitude squared of a Fourier coefficient, i.e., of a power spectrum. Specifically, the set of squared inner products between and for any given value of l is the power spectrum of the sequence
By the Wiener–Khinchin theorem, we know that the power spectrum of a sequence is the Fourier transform of the autocorrelation of that sequence [194]. Therefore, the autocorrelation of the sequence , when put through the Fourier transform, will yield the sequence . The set of autocorrelation sequences for all values of l forms a matrix. Using ★ to denote the correlation of two sequences, we can write the elements of this matrix as
The matrix is in many situations more convenient to work with than the original matrix , because lacks phase factors and treats both of its indices on equal footing. For example, it is apparent from the definition of that
This is equivalent to a property of the matrix that is less obvious to the eye:
If we take the Fourier transform of the columns of the matrix ,
we recover the squared inner products between the candidate SIC vectors and the fiducial. This means that if the vectors really do comprise a SIC, then the matrix must take a very specific form. Every entry in must equal , except for the element at , which equals 1. Recalling that a constant sequence is the discrete Fourier transform of a Kronecker delta function, we can deduce the desired values of .
The result is that if is a Weyl–Heisenberg fiducial vector, then
This implication also works in reverse, thanks to the transitivity of the group action.
The basic idea of finding SICs numerically is to use standard optimization methods to find a fiducial vector that makes as close to the desired form as possible. Note that, when is constructed from a SIC fiducial,
One can prove [123] that this is a lower bound. In general,
and the inequality is saturated if and only if the input vector is truly a SIC fiducial.
This naturally suggests a way to find SIC fiducial vectors: Minimize the LHS of the inequality in Equation (24), aiming for the lower bound given on the RHS. During our time investigating the SIC question, we have at various points implemented this idea in Mathematica, in Python and in C++ using the GNU Scientific Library. We find in general that numerical optimization finds a local minimum quickly, but a local minimum might only imply inner products between the vectors that are correct to a few decimal digits. A way around this problem is to repeat the optimization many times, starting from different points in the search space. Since these trials can run concurrently, the problem is amenable to parallelization. This is the approach we followed when using the Chimera supercomputer to obtain solutions in dimensions 122 through 151. Scott’s implementation, which we employed on Chimera, uses a C++ code for a limited-memory quasi-Newton optimization algorithm, L-BFGS, due to Liu [195].
As is evident from Figure 1, the time required to obtain solutions did not increase steadily with the dimension. For example, took eleven days of computer time and required twelve days, but took only 18 hours. Likewise, Chimera spent 28 days trying to find a solution before succeeding, but it found a SIC in in only two hours. (These figures are all for “wall clock” elapsed time. The number of processor-hours devoted was greater, since we ran Scott’s code in parallel on 96 of Chimera’s cores.) We suspect the variation is due to different numbers of inequivalent solutions existing in different dimensions: The more solutions, the easier it is to hit upon one of them.
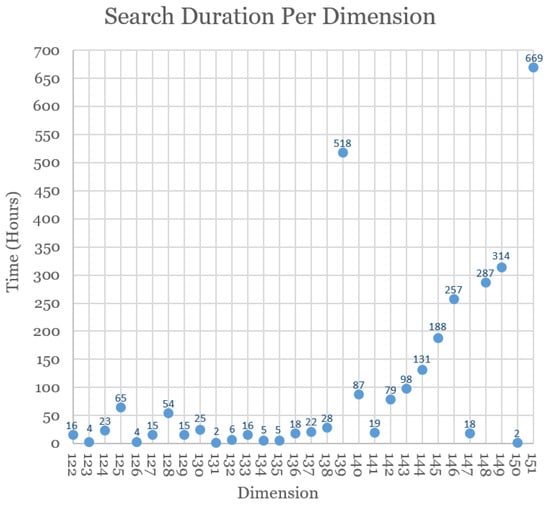
Figure 1.
Time (in hours) spent searching for a Weyl–Heisenberg SIC in dimensions 122 through 151.
Once we have a numerical result in hand, we can refine its precision. This requires a code that uses multi-precision arithmetic, which will run more slowly than the optimization in the first step [24]. The fiducial vectors available at [24] and at the website referenced above were obtained in this way and are accurate to 150 digits.
Before moving on, we note a conjecture, based on numerical evidence, that hints at additional hidden structure in the SIC problem. Note that the definition of implies
Here, indices are to be interpreted modulo d. Because any autocorrelation attains its maximum at zero offset, we also know immediately that the elements of cannot be larger in the middle of the matrix than they are on the edges:
The Fourier transform of over the index k is, by the Wiener–Khinchin theorem, the power spectrum of . Because power spectra are nonnegative, we can say that
Are there additional symmetries or redundancies, not so apparent from the definition? By happenstance, one of the authors (CAF) observed that imposing a subset of the constraints in Equation (22) was sufficient to find a SIC fiducial vector [45] (pp. 1252–1259). Specifically, by finding a solution to the simultaneous equations
one finds a solution to all the equations in (22). The redundancies in Equation (25) are sufficient to imply that this holds up to . We call the idea that it remains true in all dimensions the “ conjecture.” It has been verified numerically up to dimension [123]. If the conjecture is indeed true, it would reduce the complexity of the problem, as measured by the number of simultaneous equations to solve, from quadratic in the dimension to linear.
5. Zauner Symmetry
Is there any way to narrow the search space for SIC fiducial vectors? To see how to answer this in the affirmative, we must elaborate upon the group theory we discussed in the previous sections. The Clifford group for dimension d is the “normalizer” of the Weyl–Heisenberg group: It is the set of all unitary operators that, acting by conjugation, map the set of Weyl–Heisenberg operators in dimension d to itself. We saw earlier how the orbit of a vector under the Weyl–Heisenberg group can be a SIC; likewise, we can study the orbit of a vector under the entire Clifford group.
For our purposes in this note, the important point is that if we conjugate a Weyl–Heisenberg operator by a Clifford unitary U, we obtain a Weyl–Heisenberg operator , possibly with an additional phase. Details on the construction and representation of the Clifford group in any finite dimension d can be found in Appleby [102].
It was conjectured by Zauner [1], and independently by Appleby, that in every dimension , a Weyl–Heisenberg SIC fiducial exists that is an eigenvector of a certain order-3 Clifford unitary, which is now known as the Zauner unitary. Acting on the Weyl–Heisenberg generators, the Zauner unitary effects the change
up to an overall phase factor (See Equation (3.10b) of Zauner [1], or Equation (127) of Appleby [102]). Applying this again yields
and a third iteration gives
confirming that this operation has order 3.
How might assuming the Zauner conjecture simplify the search for SICs? First, we will make some remarks on this from an algebraic perspective, and then we will address the point in a way suited to numerical optimization. Let be a candidate fiducial vector, and suppose that it is an eigenvector of the Zauner unitary U with unit eigenvalue:
Consequently,
As U is a Clifford unitary, requiring that is an eigenvector of U implies degeneracies among the elements of the matrix .
Because
the Zauner unitary sends the left edge of to the top edge and then to the main diagonal. More generally, specifying a column of (which is equivalent to fixing a column of ) and imposing the Zauner condition means that the same constraint also simultaneously fixes a row and a diagonal.
Earlier, in Equation (20), we saw that a symmetry of implied a Fourier-type relation among the elements of . We have expressed the Zauner condition as a degeneracy within , but what does it imply for ? The result can be found straightforwardly, and it closely resembles Equation (20):
This the expression of Zauner symmetry in the matrix. A special case of note: If we set , then
We note that the assumption that the fiducial is a Zauner eigenvector is enough to prove some additional cases of the conjecture, up to dimension , in a straightforward way. In dimension , the basic symmetries of imply that the constraints automatically specify the entire matrix , and thus also fix to have the desired form for a SIC. By imposing the condition that our initial vector is a Zauner eigenvector, we can extend this up to dimension . This can be seen directly by drawing an grid and shading in the appropriate squares.
In fact, we can carry this argument a little further. We obtain by Fourier transforming the columns of . Therefore, if we specify , we automatically fix , and by Equation (25), we set the values of as well. Imposing the Zauner condition fixes in terms of . Specifically, for , we have
Recalling that
we therefore find that
In other words, the Zauner condition implies that if we add up the entries in a column, leaving out the entry on the top row, they must all cancel out and leave zero. We knew already, thanks to the Wiener–Khinchin theorem and Equation (27), that the imaginary parts will sum to zero. Now we can establish this for the real parts as well.
The left-most column of is also its top row, which tells us the averages of each column of . So, if the Zauner orbits leave only one element in a column unspecified, then we can fill in that element, because we know the average over the whole column vector. This proves the conjecture in dimension .
We now turn to the simplification that the Zauner conjecture provides for numerical search efforts. By postulating that the SIC fiducial we are looking for is a Zauner eigenvector, we can significantly reduce the effective size of the search space. First, suppose that U is a unitary of order n, so that
and the eigenvalues of U can all be written
with m an integer. The projector onto the eigenspace with this eigenvalue is
We can restrict our numerical search to this subspace by projecting our vectors into it,
at each iteration of the optimization algorithm.
Most of the known solutions were found by postulating Zauner symmetry. Scott has also found several solutions by assuming that the fiducial was an eigenvector of another Clifford unitary. For an in-depth exposition of these variations, see [24].
6. Exhaustive Searches
Suppose that is a vector in a Weyl–Heisenberg SIC, and let U be a Clifford unitary. Applying U to the vector will yield some vector,
The Weyl–Heisenberg orbit of is a SIC, so what about the orbit of under the same group? We define
and we consider the squared magnitudes of the inner products
Because U is a Clifford unitary, it maps to some Weyl–Heisenberg operator , with any phase factor dropping out when we take the magnitude of the inner product. So,
meaning that the image of our original SIC under the mapping U is also a SIC. One way in which the Hesse SIC is remarkable is that it is invariant under the entire Clifford group. For contrast, we can take the vector
which differs from the Hesse SIC fiducial in Equation (13) by a sign. The orbit of this vector under the Clifford group is a set of four separate SICs, comprising 36 vectors in all—the so-called Norrell states, which are significant in the theory of quantum computation [53,182].
We consider two SICs equivalent if they can be mapped into each other by a Clifford unitary. In fact, it is convenient to extend the Clifford group by including the anti-unitary operation of complex conjugation. The extended Clifford group for dimension d, , is the set of all unitary and anti-unitary operators that send the Weyl–Heisenberg group to itself. For (extensive) details, we again refer to Appleby [102,104].
In order to search the space as exhaustively as possible and create a catalogue of all essentially unique SICs, Scott’s code chooses initial vectors at random under the unitarily invariant Haar measure on the complex projective space . Once enough solutions are found—generally, this means hundreds of them—the code then refines their precision, as described above. Then, we must identify unique orbits under the extended Clifford group. This last step is computationally demanding, because we must translate each solution vector by each element in the extended Clifford group . However, in the process, Scott’s algorithm also finds the stabilizer group of each fiducial, which is important information. The task of determining when two SICs are equivalent up to a unitary or anti-unitary transformation has been discussed in depth by Zhu [18], and we expect that additional theoretical insights may lead to an improved algorithm for this step.
Following this procedure, Scott has carried out exhaustive searches in dimensions up to . We strongly expect his catalogue of solutions to be complete up to that point: All Weyl–Heisenberg SICs in those dimensions are equivalent to the ones tabulated, up to equivalence under the extended Clifford group.
7. Discussion
In the preceding sections, we have described the process of finding SIC fiducial vectors numerically. However, some patterns among SICs have only become apparent when exact solutions were studied carefully. Suppose we refrain from taking the magnitude-squared in our definition of a SIC, Equation (1). Then
for some set of phases . (In fact, one can reconstruct the SIC from knowing the phases [10]). It was recently discovered that when , for all the known Weyl–Heisenberg SICs, these phases have a remarkable meaning in algebraic number theory: They are units in ray class fields and extensions thereof [5]. This is a topic to which we can hardly do justice here, and indeed, treatments accessible to anyone who is not already an algebraic number theorist have only recently been attempted [6,7]. For now, we content ourselves with the observation that this area of number theory is the territory of Hilbert’s twelfth problem, one of the still outstanding questions on history’s most influential list of mathematical challenges [196] (Specialists may recall that according to the Kronecker–Weber theorem, any abelian extension of the rationals is contained in a cyclotomic field. When we instead consider abelian extensions of real quadratic fields, the analogue of the cyclotomic fields are the ray class fields. The phases of Weyl–Heisenberg SICs appear to be playing a role regarding ray class fields much like the role that roots of unity play with cyclotomic fields. Moreover, recalling Equation (14), it is intriguing that in the real-vector-space version of equiangular lines, we discard a phase factor that is a unit among the ordinary integers, while in the complex Weyl–Heisenberg case, the phases turn out to be units among algebraic integers). From Hilbert space to Hilbert’s twelfth problem! What physicist would ever have anticipated that? In addition, who could turn down the opportunity to intermingle two subjects that had seemed so widely separated?
Many open questions remain, foremost of which is whether SICs exist in all dimensions. Also, as we mentioned in Section 2, it is not yet known whether SICs are necessarily group covariant. One can search for SICs without presuming group covariance, at the cost of having to minimize a function involving many more terms. This has been done for dimensions up through , without finding any additional SICs [18].
SICs have found relevance, not just in quantum computation, but in signal-processing tasks like high-precision radar [75] and speech recognition [77]. In February 2016, our colleague Marcus Appleby attended a conference in Bonn, Germany on uses of the Weyl–Heisenberg group. Many participants were engineers, including representatives from the automotive and cell-phone industries. Appleby was told that if he managed to construct a SIC in dimension 2048, he should patent it [197]. At the moment, dimension 2048 is beyond our abilities for algebraic or numerical solutions, but this may not always be the case.
Acknowledgments
We are deeply indebted to Andrew J. Scott, the guru of SIC numerical solutions, for code and for discussions. We also thank Marcus Appleby for many conversations, and Gary McConnell for email feedback on the original arXiv version of this article. This research was supported in part by MCH’s Oracle Undergraduate Research Fellowship at UMass Boston.
Author Contributions
Michael C. Hoang ran the calculations on Chimera to find SICs in dimensions 122 through 151. Blake C. Stacey wrote the paper. Christopher A. Fuchs directed the research, contributed to the bibliography and worked with Blake C. Stacey in revising the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zauner, G. Quantendesigns. Grundzüge einer nichtkommutativen Designtheorie [Quantum designs: Foundations of a noncommutative design theory]. Ph.D. Thesis, University of Vienna, Vienna, Austria, 1999. Published in English translation as Int. J. Quantum Inf. 2011, 9, 445–508. [Google Scholar]
- Caves, C.M. Symmetric Informationally Complete POVMs. 2002. Available online: http://info.phys.unm.edu/~caves/reports/infopovm.pdf (accessed on 17 July 2017).
- Renes, J.M.; Blume-Kohout, R.; Scott, A.J.; Caves, C.M. Symmetric Informationally Complete Quantum Measurements. J. Math. Phys. 2004, 45, 2171–2180. [Google Scholar] [CrossRef]
- Scott, A.J.; Grassl, M. Symmetric informationally complete positive-operator-valued measures: A new computer study. J. Math. Phys. 2010, 51, 042203. [Google Scholar] [CrossRef]
- Appleby, M.; Flammia, S.; McConnell, G.; Yard, J. Generating Ray Class Fields of Real Quadratic Fields via Complex Equiangular Lines. arXiv 2016, arXiv:1604.06098. [Google Scholar]
- Bengtsson, I. The Number behind the Simplest SIC-POVM. Found. Phys. 2016, arXiv:1611.09087. [Google Scholar] [CrossRef]
- Appleby, M.; Flammia, S.; McConnell, G.; Yard, J. SICs and Algebraic Number Theory. Found. Phys. 2017, arXiv:1701.05200. [Google Scholar] [CrossRef]
- Appleby, M.; Chien, T.Y.; Flammia, S.; Waldron, S. Constructing Exact Symmetric Informationally Complete Measurements from Numerical Solutions. arXiv 2017, arXiv:1703.05981. [Google Scholar]
- Stacey, B.C. Sporadic SICs and the Normed Division Algebras. Found. Phys. 2017, arXiv:1605.0142647, 1–5. [Google Scholar]
- Appleby, D.M.; Flammia, S.T.; Fuchs, C.A. The Lie Algebraic Significance of Symmetric Informationally Complete Measurements. J. Math. Phys. 2011, arXiv:1001.000452, 022202. [Google Scholar] [CrossRef]
- Appleby, D.M.; Fuchs, C.A.; Zhu, H. Group theoretic, Lie algebraic and Jordan algebraic formulations of the SIC existence problem. Quantum Inf. Comput. 2015, arXiv:1312.055515, 61–94. [Google Scholar]
- Zhu, H. Super-symmetric informationally complete measurements. Ann. Phys. 2015, arXiv:1412.1099362, 311–326. [Google Scholar]
- Stacey, B.C. Geometric and Information-Theoretic Properties of the Hoggar Lines. arXiv 2016, arXiv:1609.03075. [Google Scholar]
- Fuchs, C.A. QBism, the Perimeter of Quantum Bayesianism. arXiv 2010, arXiv:1003.5209. [Google Scholar]
- Tabia, G.N.M. Experimental scheme for qubit and qutrit symmetric informationally complete positive operator-valued measurements using multiport devices. Phys. Rev. A 2012, arXiv:1207.603586, 062107. [Google Scholar]
- Tabia, G.N.M.; Appleby, D.M. Exploring the geometry of qutrit state space using symmetric informationally complete probabilities. Phys. Rev. A 2013, 88, 012131. [Google Scholar] [CrossRef]
- Fuchs, C.A.; Schack, R. Quantum-Bayesian coherence. Rev. Mod. Phys. 2013, arXiv:1301.327485, 1693–1715. [Google Scholar]
- Zhu, H. Quantum State Estimation and Symmetric Informationally Complete POMs. Ph.D. Thesis, National University of Singapore, Singapore, 2012. [Google Scholar]
- Graydon, M.A.; Appleby, D.M. Quantum conical designs. J. Phys. A 2016, arXiv:1507.0532349, 085301. [Google Scholar]
- Zhu, H. Quasiprobability Representations of Quantum Mechanics with Minimal Negativity. Phys. Rev. Lett. 2016, arXiv:1604.06974117, 120404. [Google Scholar] [PubMed]
- Szymusiak, A.; Słomczyński, W. Informational power of the Hoggar symmetric informationally complete positive operator-valued measure. Phys. Rev. A 2015, arXiv:1512.0173594, 012122. [Google Scholar]
- Appleby, M.; Fuchs, C.A.; Stacey, B.C.; Zhu, H. Introducing the Qplex: A Novel Arena for Quantum Theory. arXiv 2016, arXiv:1612.03234. [Google Scholar]
- Fuchs, C.A.; Stacey, B.C. QBism: Quantum Theory as a Hero’s Handbook. arXiv 2016, arXiv:1612.07308. [Google Scholar]
- Scott, A.J. SICs: Extending the list of solutions. arXiv 2017, arXiv:1703.03993. [Google Scholar]
- Chien, T.Y. Equiangular Lines, Projective Symmetries and Nice Error Frames. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2015. [Google Scholar]
- Grassl, M.; Scott, A. Fibonacci-Lucas SIC-POVMs. arXiv 2017, arXiv:1707.02944. [Google Scholar]
- DeBrota, J.B.; Fuchs, C.A.; Hoang, M.C.; Stacey, B.C. QBism Research Group. 2017. Available online: http://www.physics.umb.edu/Research/QBism (accessed on 17 July 2017).
- Du, J.; Sun, M.; Peng, X.; Durt, T. Realization of Entanglement Assisted Qubit-covariant Symmetric Informationally Complete Positive Operator Valued Measurements. Phys. Rev. A 2006, 74, 042341. [Google Scholar] [CrossRef]
- Durt, T.; Kurtsiefer, C.; Lamas-Linares, A.; Ling, A. Wigner Tomography of Two-Qubit States and Quantum Cryptography. Phys. Rev. A 2008, 78, 042338. [Google Scholar] [CrossRef]
- Medendorp, Z.E.D.; Torres-Ruiz, F.A.; Shalm, L.K.; Tabia, G.N.M.; Fuchs, C.A.; Steinberg, A.M. Experimental characterization of qutrits using symmetric informationally complete positive operator-valued measurements. Phys. Rev. A 2011, arXiv:1006.490583, 051801(R). [Google Scholar]
- Pimenta, W.M.; Marques, B.; Maciel, T.O.; Vianna, R.O.; Delgado, A.; Saavedra, C.; Pádua, S. Minimum tomography of two entangled qutrits using local measurements of one-qutrit symmetric informationally complete positive operator-valued measure. Phys. Rev. A 2013, arXiv:1312.111988, 012112. [Google Scholar]
- Bian, Z.; Li, J.; Qin, H.; Zhan, X.; Xue, P. Experimental realization of a single qubit SIC POVM on via a one-dimensional photonic quantum walk. arXiv 2014, arXiv:1412.2355. [Google Scholar]
- Zhao, Y.Y.; Yu, N.K.; Kurzyński, P.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Experimental realization of generalized qubit measurements based on quantum walks. Phys. Rev. A 2015, arXiv:1501.0509691, 042101. [Google Scholar]
- Bent, N.; Qassim, H.; Tahir, A.A.; Sych, D.; Leuchs, G.; Sánchez-Soto, L.L.; Karimi, E.; Boyd, R.W. Experimental Realization of Quantum Tomography of Photonic Qudits via Symmetric Informationally Complete Positive Operator-Valued Measures. Phys. Rev. X 2015, 5, 041006. [Google Scholar] [CrossRef]
- Sosa-Martinez, H.; Lysne, N.K.; Baldwin, C.H.; Kalev, A.; Deutsch, I.H.; Jessen, P.S. Experimental study of optimal measurements for quantum state tomography. arXiv 2017, arXiv:1706.03137. [Google Scholar]
- Scott, A.J. Tight Informationally Complete Quantum Measurements. J. Phys. A 2006, arXiv:quant-ph/060404939, 13507–13530. [Google Scholar]
- Et-Taoui, B. Complex Conference Matrices, Complex Hadamard Matrices and Complex Equiangular Tight Frames. In Convexity and Discrete Geometry Including Graph Theory; Adiprasito, K., Bárány, I., Vilcu, C., Eds.; Springer: Basel, Switzerland, 2016; pp. 181–191. [Google Scholar]
- Kovačević, J.; Chebira, A. Life Beyond Bases: The Advent of Frames (Part 1). IEEE Signal Process. Mag. 2007, 24, 86–104. [Google Scholar] [CrossRef]
- Kovačević, J.; Chebira, A. Life Beyond Bases: The Advent of Frames (Part 2). IEEE Signal Process. Mag. 2007, 24, 115–125. [Google Scholar] [CrossRef]
- DeBrota, J.B.; Fuchs, C.A. Negativity Bounds for Weyl–Heisenberg Quasiprobability Representations. Found. Phys. 2017, arXiv:1703.08272. [Google Scholar] [CrossRef]
- Hughston, L.P.; Salamon, S.M. Surveying points in the complex projective plane. Adv. Math. 2016, arXiv:1410.5862286, 1017–1052. [Google Scholar] [CrossRef]
- Weyl, H. The Theory of Groups and Quantum Mechanics; Dover: Mineola, NY, USA, 1931. [Google Scholar]
- Scholz, E. Introducing groups into quantum theory (1926–1930). Hist. Math. 2006, arXiv:math/040957133, 440–490. [Google Scholar]
- Scholz, E. Weyl entering the ‘new’ quantum mechanics discourse. In Proceedings of the Conference on the History of Quantum Physics, Berlin, Germany, 2–6 July 2007; Volume 2. [Google Scholar]
- Fuchs, C.A. My Struggles with the Block Universe. arXiv 2014, arXiv:1405.2390. [Google Scholar]
- Gottesman, D. The Heisenberg representation of quantum computers. In Group22: Proceedings of the XXII International Colloquium on Group Theoretical Methods in Physics; Corney, S.P., Delbourgo, R., Jarvis, P.D., Eds.; International Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Zhu, H. SIC POVMs and Clifford Groups in Prime Dimensions. J. Phys. A 2010, arXiv:1003.359143, 305305. [Google Scholar]
- Hoggar, S.G. Two quaternionic 4-polytopes. In The Geometric Vein: The Coxeter Festschrift; Davis, C., Grünbaum, B., Sherk, F.A., Eds.; Springer: New York, NY, USA, 1981. [Google Scholar]
- Hoggar, S.G. 64 lines from a quaternionic polytope. Geom. Dedicata 1998, 69, 287–289. [Google Scholar] [CrossRef]
- Hughston, L. d = 3 SIC-POVMs and Elliptic Curves. PIRSA Video Lecture 2007. PIRSA:07100040. [Google Scholar]
- Dang, H.B.; Blanchfield, K.; Bengtsson, I.; Appleby, D.M. Linear Dependencies in Weyl–Heisenberg Orbits. Quantum Inf. Process. 2013, arXiv:1211.021512, 3449–3475. [Google Scholar]
- Coxeter, H.S.M. Regular Complex Polytopes, 2nd ed.; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Stacey, B.C. SIC-POVMs and Compatibility among Quantum States. Mathematics 2016, arXiv:1404.37744, 36. [Google Scholar]
- Coxeter, H.S.M. The polytope 221 whose twenty-seven vertices correspond to the lines on the general cubic surface. Am. J. Math. 1940, arXiv:237146662, 457–486. [Google Scholar]
- Baez, J.C. 27 Lines on a Cubic Surface. 2016. Available online: http://blogs.ams.org/visualinsight/2016/02/15/27-lines-on-a-cubic-surface/ (accessed on 17 July 2017).
- Delsarte, P.; Goethels, J.M.; Seidel, J.J. Bounds for systems of lines and Jacobi polynomials. Philips Res. Rep. 1975, 30, 91–105. [Google Scholar]
- König, H.; Tomczak-Jaegermann, N. Norms of Minimal Projections. J. Funct. Analysis 1994, arXiv:math.FA/9211211119, 253–280. [Google Scholar]
- König, H. Cubature formulas on spheres. Math. Res. 1999, 107, 201–212. [Google Scholar]
- Et-Taoui, B. Equiangular lines in Cr. Indag. Math. 2000, 11, 201–207. [Google Scholar] [CrossRef]
- Et-Taoui, B. Equiangular lines in Cr (part II). Indag. Math. 2002, 13, 483–486. [Google Scholar] [CrossRef]
- Caves, C.M.; Fuchs, C.A.; Schack, R. Unknown quantum states: The quantum de Finetti representation. J. Math. Phys. 2002, arXiv:quant-ph/010408843, 4537–4559. [Google Scholar]
- Appleby, D.M.; Yadsan-Appleby, H.; Zauner, G. Galois automorphisms of a symmetric measurement. Quantum Inf. Comput. 2013, arXiv:1209.181313, 672–720. [Google Scholar]
- Renes, J.M. Frames, Designs, and Spherical Codes in Quantum Information Theory. Ph.D. Thesis, The University of New Mexico, Albuquerque, NM, USA, 2004. [Google Scholar]
- Khatirinejad, M. Regular Structures of Lines in Complex Spaces. Ph.D. Thesis, Simon Fraser University, Vancouver, BC, Canada, 2008. [Google Scholar]
- Yadsan-Appleby, H. Gaussian and Covariant Processes In Discrete And Continuous Variable Quantum Information. Ph.D. Thesis, University College London, London, UK, 2012. [Google Scholar]
- Tabia, G.N.M. Geometry of Quantum States from Symmetric Informationally Complete Probabilities. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2013. [Google Scholar]
- Andersson, D. An Enthusiast’s Guide to SICs in Low Dimensions. Master’s Thesis, Stockholm University, Stockholm, Sweden, 2014. [Google Scholar]
- Blanchfield, K. Geometry and Foundations of Quantum Mechanics. Ph.D. Thesis, Stockholm University, Stockholm, Sweden, 2014. [Google Scholar]
- Dang, H.B. Studies of Symmetries That Give Special Quantum States the “Right to Exist”. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. [Google Scholar]
- Stacey, B.C. Multiscale Structure in Eco-Evolutionary Dynamics. Ph.D. Thesis, Brandeis University, Waltham, MA, USA, 2015. [Google Scholar]
- Zhu, H. Tomographic and Lie algebraic significance of generalized symmetric informationally complete measurements. Phys. Rev. A 2014, arXiv:1408.056090, 032309. [Google Scholar]
- Appleby, M. Galois calculations using Magma. PIRSA Video Lecture 2012. PIRSA:12020149. [Google Scholar]
- Graydon, M. Conical Designs and Categorical Jordan Algebraic Post-Quantum Theories. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2017. [Google Scholar]
- Van de Wetering, J. Quantum theory is a quasi-stochastic process theory. arXiv 2017, arXiv:1704.08525. [Google Scholar]
- Howard, S.D.; Calderbank, A.R.; Moran, W. The Finite Heisenberg–Weyl Groups in Radar and Communications. EURASIP J. Appl. Signal Process. 2006, 2006, 1–11. [Google Scholar] [CrossRef]
- Herman, M.A.; Strohmer, T. High-Resolution Radar via Compressed Sensing. IEEE Trans. Signal Process. 2009, 57, 2275–2284. [Google Scholar] [CrossRef]
- Balan, R.; Bodmann, B.G.; Casazza, P.G.; Edidin, D. Painless Reconstruction from Magnitudes of Frame Coefficients. J. Fourier Anal. Appl. 2009, 15, 488–501. [Google Scholar] [CrossRef]
- Mixon, D. Sparse Signal Processing with Frame Theory. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2012. [Google Scholar]
- Hulek, K. Projective geometry of elliptic curves. In Algebraic Geometry—Open Problems; Ciliberto, C., Ghione, F., Orecchia, F., Eds.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1983; Volume 997, pp. 228–266. [Google Scholar]
- Bengtsson, I. From SICs and MUBs to Eddington. In Quantum Groups, Quantum Foundations, and Quantum Information: A Festschrift for Tony Sudbery, York, 29–30 September 2008; IOP Publishing: Bristol, UK, 2010. [Google Scholar]
- Grassl, M. Computing equiangular lines in complex space. In Mathematical Methods in Computer Science: Essays in Memory of Thomas Beth; Calmet, J., Geiselmann, W., Müller-Quade, J., Eds.; Springer: Berlin, Germany, 2008; pp. 89–104. [Google Scholar]
- Khatirinejad, M. On Weyl–Heisenberg Orbits of Equiangular Lines. J. Algebraic Comb. 2008, 28, 333–349. [Google Scholar] [CrossRef]
- Wootters, W.K. Symmetric informationally complete measurements: Can we make big ones out of small ones? PIRSA Video Lecture 2009. PIRSA:09120023. [Google Scholar]
- McConnell, G. Some non-standard ways to generate SIC-POVMs in dimensions 2 and 3. arXiv 2014, arXiv:1402.7330. [Google Scholar]
- Jedwab, J.; Wiebe, A. A simple construction of complex equiangular lines. In Algebraic Design Theory and Hadamard Matrices; Springer: Cham, Switzerland, 2015; pp. 159–169. [Google Scholar]
- Bruzda, W.; Goyeneche, D.; Życzkowski, K. Quantum measurements with prescribed symmetry. arXiv 2017, arXiv:1704.04609. [Google Scholar]
- Bos, L.; Waldron, S. Some remarks on Heisenberg frames and sets of equiangular lines. N. Z. J. Math. 2007, 36, 113–137. [Google Scholar]
- Bodmann, B.G.; Casazza, P.G.; Edidin, D.; Balan, R. Frames for Linear Reconstruction without Phase. In Proceedings of the 42nd Annual Conference on Information Sciences and Systems (CISS 2008), Princeton, NJ, USA, 19–21 March 2008; pp. 721–726. [Google Scholar]
- Ferrie, C.; Emerson, J. Frame representations of quantum mechanics and the necessity of negativity in quasi-probability representations. J. Phys. A 2008, 41, 352001. [Google Scholar] [CrossRef]
- Ferrie, C.; Emerson, J. Framed Hilbert space: Hanging the quasi-probability pictures of quantum theory. New J. Phys. 2009, 11, 063040. [Google Scholar] [CrossRef]
- Bengtsson, I.; Granström, H. The Frame Potential, on Average. Open Syst. Inf. Dyn. 2009, 16, 145–156. [Google Scholar] [CrossRef]
- Fickus, M. Maximally Equiangular Frames and Gauss Sums. J. Fourier Anal. Appl. 2009, 15, 413–427. [Google Scholar] [CrossRef]
- Bodmann, B.G.; Elwood, H.J. Complex equiangular Parseval frames and Seidel matrices containing pth roots of unity. Proc. AMS 2010, 138, 4387–4404. [Google Scholar] [CrossRef]
- Waldron, S. Frames for vector spaces and affine spaces. Linear Algebra Appl. 2011, 435, 77–94. [Google Scholar] [CrossRef]
- Fickus, M.; Mixon, D.G.; Tremain, J.C. Steiner equiangular tight frames. Linear Algebra Appl. 2012, 436, 1014–1027. [Google Scholar] [CrossRef]
- Chien, T.Y.; Waldron, S. A characterisation of projective unitary equivalence of finite frames. arXiv 2013, arXiv:1312.5393. [Google Scholar]
- Waldron, S. Group frames. In Finite Frames: Theory and Applications; Casazza, P.G., Kutyniok, G., Eds.; Springer: New York, NY, USA, 2013; pp. 171–191. [Google Scholar]
- Chien, T.Y.; Flynn, V.; Waldron, S. Tight frames for cyclotomic fields and other rational vector spaces. Linear Algebra Appl. 2015, 476, 98–123. [Google Scholar] [CrossRef]
- Goyeneche, D.; Turek, O. Equiangular tight frames and unistochastic matrices. J. Phys. A 2017, 50, 245304. [Google Scholar] [CrossRef]
- Malikiosis, R.D. Spark deficient Gabor frames. arXiv 2016, arXiv:1602.09012. [Google Scholar]
- Chien, T.Y.; Waldron, S. Nice error frames, canonical abstract error groups and the construction of SICs. Linear Algebra Appl. 2017, 516, 93–117. [Google Scholar] [CrossRef]
- Appleby, D.M. Symmetric informationally complete-positive operator valued measures and the extended Clifford group. J. Math. Phys. 2005, arXiv:quant-ph/041200146, 052107. [Google Scholar]
- Flammia, S. On SIC-POVMs in prime dimensions. J. Phys. A 2006, 39, 13483–13493. [Google Scholar] [CrossRef]
- Appleby, D.M. Properties of the Extended Clifford Group with Applications to SIC-POVMs and MUBs. arXiv 2009, arXiv:0909.5233. [Google Scholar]
- Larsson, J.Å. SIC POVMs and the Discrete Affine Fourier Transform (the Linear Canonical Transform). 2010. Available online: http://www.akademietraunkirchen.com/wp-content/uploads/2010/06/SIC-POVMs-and-the-Discrete-Affine-Fourier-Transform.pdf (accessed on 17 July 2017).
- Appleby, M.; Bengtsson, I.; Brierley, S.; Grassl, M.; Gross, D.; Larsson, J.Å. Monomial representations of the Clifford group. Quantum Inf. Comput. 2012, arXiv:1102.126812, 0404–0431. [Google Scholar]
- Bengtsson, I. A remarkable representation of the Clifford group. arXiv 2012, arXiv:1202.3559. [Google Scholar]
- Klappenecker, A.; Rötteler, M.; Shparlinski, I.E.; Winterhof, A. On approximately symmetric informationally complete positive operator-valued measures and related systems of quantum states. J. Math. Phys. 2005, 46, 082104. [Google Scholar] [CrossRef]
- Appleby, D.M. Symmetric informationally complete measurements of arbitrary rank. Opt. Spectrosc. 2007, arXiv:quant-ph/0611260103, 416–428. [Google Scholar]
- Gour, G.; Kalev, A. Construction of all general symmetric informationally complete measurements. J. Phys. A 2014, 47, 335302. [Google Scholar] [CrossRef]
- Rastegin, A.E. Notes on general SIC-POVMs. Phys. Scr. 2014, 89, 085101. [Google Scholar] [CrossRef]
- Chen, B.; Li, T.; Fei, S.M. General SIC measurement-based entanglement detection. Quantum Inf. Process. 2015, 14, 2281–2290. [Google Scholar] [CrossRef]
- Shen, S.Q.; Li, M.; Duan, X.F. Entanglement detection via some classes of measurements. Phys. Rev. A 2015, 91, 012326. [Google Scholar] [CrossRef]
- Graydon, M.A.; Appleby, D.M. Entanglement and designs. J. Phys. A 2016, arXiv:1507.0788149, 33LT02. [Google Scholar]
- Cao, X.; Mi, J.; Xu, S. Two constructions of approximately symmetric informationally complete positive operator-valued measures. J. Math. Phys. 2017, 58, 062201. [Google Scholar] [CrossRef]
- Planat, M.; Gedik, Z. Magic informationally complete POVMs with permutations. arXiv 2017, arXiv:1704.02749. [Google Scholar]
- Fuchs, C.A. Notwithstanding Bohr, the Reasons for QBism. arXiv 2017, arXiv:1705.03483. [Google Scholar]
- Khrennikov, A.; Stacey, B.C. Aims and Scope of the Special Issue, “Quantum Foundations: Informational Perspective”. Found. Phys. 2017. [Google Scholar] [CrossRef]
- Oreshkov, O.; Calsamiglia, J.; Muñoz-Tapia, R.; Bagan, E. Optimal Signal States for Quantum Detectors. New J. Phys. 2011, 13, 073032. [Google Scholar] [CrossRef]
- Dall’Arno, M.; D’Ariano, G.M.; Sacchi, M.F. Informational power of quantum measurements. Phys. Rev. A 2011, 83, 062304. [Google Scholar] [CrossRef]
- Dall’Arno, M. Accessible information and informational power of quantum 2-designs. Phys. Rev. A 2014, 90, 052311. [Google Scholar] [CrossRef]
- Dall’Arno, M.; Buscemi, F.; Ozawa, M. Tight bounds on accessible information and informational power. J. Phys. A Math. Theor. 2014, 47, 235302. [Google Scholar] [CrossRef]
- Appleby, D.M.; Dang, H.B.; Fuchs, C.A. Symmetric Informationally-Complete Quantum States as Analogues to Orthonormal Bases and Minimum-Uncertainty States. Entropy 2014, 16, 1484–1492. [Google Scholar] [CrossRef]
- Słomczyński, W.; Szymusiak, A. Highly symmetric POVMs and their informational power. Quantum Inf. Process. 2014, arXiv:1402.037515, 505–606. [Google Scholar]
- Szymusiak, A. Maximally informative ensembles for SIC-POVMs in dimension 3. J. Phys. A 2014, arXiv:1405.005247, 445301. [Google Scholar]
- Dall’Arno, M. Hierarchy of bounds on accessible information and informational power. Phys. Rev. A 2015, 92, 012328. [Google Scholar] [CrossRef]
- Brandsen, S.; Dall’Arno, M.; Szymusiak, A. Communication capacity of mixed quantum t-designs. Phys. Rev. A 2016, arXiv:1603.0632094, 022335. [Google Scholar]
- Słomczyński, W.; Szczepanek, A. Quantum dynamical entropy, chaotic unitaries and complex Hadamard matrices. arXiv 2016, arXiv:1612.03363. [Google Scholar]
- Szymusiak, A. Pure states that are ‘most quantum’ with respect to a given POVM. arXiv 2017, arXiv:1701.01139. [Google Scholar]
- König, R.; Renner, R. A de Finetti Representation for Finite Symmetric Quantum States. J. Phys. A 2005, arXiv:quant-ph/041022946, 122108. [Google Scholar]
- Carmeli, C.; Heinosaari, T.; Toigo, A. Sequential measurements of conjugate observables. J. Phys. A 2011, arXiv:1105.497644, 285304. [Google Scholar]
- Carmeli, C.; Heinosaari, T.; Toigo, A. Informationally complete joint measurements on finite quantum systems. Phys. Rev. A 2012, arXiv:1111.350985, 012109. [Google Scholar]
- Kalev, A.; Shang, J.; Englert, B.G. Experimental proposal for symmetric minimal two-qubit state tomography. Phys. Rev. A 2012, 85, 052115. [Google Scholar] [CrossRef]
- Kalev, A.; Shang, J.; Englert, B.G. Symmetric Minimal Quantum Tomography by Successive Measurements. Phys. Rev. A 2012, 85, 052116. [Google Scholar] [CrossRef]
- Fuchs, C.A.; Stacey, B.C. Some Negative Remarks on Operational Approaches to Quantum Theory. In Quantum Theory: Informational Foundations and Foils; Chiribella, G., Spekkens, R.W., Eds.; Springer: Dordrecht, The Netherlands, 2016; pp. 283–305. [Google Scholar]
- Oszmaniec, M.; Guerini, L.; Wittek, P.; Acín, A. Simulating positive-operator-valued measures with projective measurements. arXiv 2016, arXiv:1609.06139. [Google Scholar]
- Fuchs, C.A.; Sasaki, M. Squeezing Quantum Information Through a Classical Channel: Measuring the Quantumness of a Set of Quantum States. Quantum Inf. Comput. 2003, arXiv:quant-ph/03020923, 377–404. [Google Scholar]
- Englert, B.G.; Kaszlikowski, D.; Ng, H.K.; Chua, W.K.; Řeháček, J.; Anders, J. Efficient and Robust Quantum Key Distribution with Minimal State Tomography. arXiv 2004, arXiv:quant-ph/0412075. [Google Scholar]
- Fuchs, C.A. On the Quantumness of a Hilbert Space. Quantum Inf. Comput. 2004, arXiv:quant-ph/04041224, 467–478. [Google Scholar]
- Řeháček, J.; Englert, B.G.; Kaszlikowski, D. Minimal qubit tomography. Phys. Rev. A 2004, 70, 052321. [Google Scholar] [CrossRef]
- Renes, J.M. Equiangular Spherical Codes in Quantum Cryptography. Quantum Inf. Comput. 2005, arXiv:quant-ph/04090435, 81–92. [Google Scholar]
- Kim, I.H. Quantumness, Generalized Spherical 2-design and Symmetric Informationally Complete POVM. Quantum Inf. Comput. 2007, arXiv:quant-ph/06080247, 730–737. [Google Scholar]
- Matthews, W.; Wehner, S.; Winter, A. Distinguishability of quantum states under restricted families of measurements with an application to quantum data hiding. Commun. Math. Phys. 2009, arXiv:0810.2327291, 813–843. [Google Scholar]
- Feynman, R.P. Negative probability. In Quantum Implications: Essays in Honour of David Bohm; Routledge: Abingdon-on-Thames, UK, 1987; pp. 235–248. [Google Scholar]
- Bengtsson, I.; Blanchfield, K.; Cabello, A. A Kochen-Specker Inequality from a SIC. Phys. Lett. A 2012, arXiv:1109.6514376, 374–376. [Google Scholar]
- Cabello, A. Minimal proofs of state-independent contextuality. arXiv 2012, arXiv:1201.0374. [Google Scholar]
- Andersson, D.; Bengtsson, I.; Blanchfield, K.; Dang, H.B. States that are far from being stabilizer states. J. Phys. A 2014, arXiv:1412.818148, 345301. [Google Scholar]
- Xu, Z.P.; Chen, J.L.; Su, H.Y. State-independent contextuality sets for a qutrit. Phys. Lett. A 2015, arXiv:1501.01746379, 1868–1870. [Google Scholar]
- Howard, M.; Campbell, E.T. Application of a resource theory for magic states to fault-tolerant quantum computing. Phys. Rev. Lett. 2017, arXiv:1609.07488118, 090501. [Google Scholar] [PubMed]
- Ahmadi, M.; Dang, H.B.; Gour, G.; Sanders, B.C. Quantification and manipulation of magic states. arXiv 2017, arXiv:1706.03828. [Google Scholar]
- Andersson, O.; Badziag, P.; Bengtsson, I.; Dumitru, I.; Cabello, A. Self-testing properties of the elegant Bell inequality. arXiv 2017, arXiv:1706.02130. [Google Scholar]
- Bodmann, B.G.; Kribs, D.W.; Paulsen, V.I. Decoherence-Insensitive Quantum Communication by Optimal C*-Encoding. IEEE Trans. Inf. Theory 2007, 53, 4738–4749. [Google Scholar] [CrossRef]
- Kayser, J.; Luoma, K.; Strunz, W.T. Geometric Characterization of True Quantum Decoherence. arXiv 2015, arXiv:1508.04027. [Google Scholar]
- Zhu, H.; Teo, Y.S.; Englert, B.G. Two-Qubit Symmetric Informationally Complete Positive Operator Valued Measures. Phys. Rev. A 2010, arXiv:1008.113882, 042308. [Google Scholar]
- Grassl, M. Tomography of quantum states in small dimensions. Electron. Notes Discret. Math. 2005, 20, 151–164. [Google Scholar] [CrossRef]
- Ballester, M.A. Optimal Estimation of SU(d) Using Exact and Approximate 2-designs. arXiv 2005, arXiv:quant-ph/0507073. [Google Scholar]
- Belovs, A. Welch Bounds and Quantum State Tomography. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2008. [Google Scholar]
- Goyeneche, D.; de la Torre, A.C. Quantum state reconstruction from dynamical systems theory. arXiv 2011, arXiv:1103.3213. [Google Scholar]
- Zhu, H.; Englert, B.G. Quantum State Tomography with Fully Symmetric Measurements and Product Measurements. Phys. Rev. A 2011, arXiv:1105.456184, 022327. [Google Scholar]
- Petz, D.; Ruppert, L. Efficient quantum tomography needs complementary and symmetric measurements. Rep. Math. Phys. 2012, 69, 161–177. [Google Scholar] [CrossRef]
- Petz, D.; Ruppert, L. Optimal quantum-state tomography with known parameters. J. Phys. A 2012, 45, 085306. [Google Scholar] [CrossRef]
- Goyeneche, D.; de la Torre, A.C. Quantum tomography meets dynamical systems and bifurcations theory. J. Math. Phys. 2014, 55, 062103. [Google Scholar] [CrossRef]
- Petz, D.; Ruppert, L.; Szanto, A. Conditional SIC-POVMs. IEEE Trans. Inf. Theory 2014, 60, 351–356. [Google Scholar] [CrossRef]
- Baldwin, C.H. Efficient and robust methods for quantum tomography. Ph.D. Thesis, University of New Mexico, Albuquerque, NM, USA, 2016. [Google Scholar]
- Chaparro Sogamoso, E.C.; Angulo, D.; Fonseca-Romero, K.M. Single plane minimal tomography of double slit qubits. arXiv 2017, arXiv:1703.04260. [Google Scholar]
- Graydon, M.A. Quaternionic quantum dynamics on complex Hilbert spaces. Found. Phys. 2013, 43, 656–664. [Google Scholar] [CrossRef]
- Cohn, H.; Kumar, A.; Minton, G. Optimal simplices and codes in projective spaces. Geom. Topol. 2016, arXiv:1308.318820, 1289–1357. [Google Scholar]
- Fuchs, C.A.; Schack, R. A Quantum-Bayesian route to quantum state space. Found. Phys. 2011, 41, 345–356. [Google Scholar] [CrossRef]
- Fuchs, C.A. Charting the Shape of Quantum-State Space. In Quantum Communication, Measurement and Computing (QCMC): The Tenth International Conference; Ralph, T., Lam, P.K., Eds.; American Institute of Physics: Melville, NY, USA, 2011; AIP Conference Proceedings Volume 1363, pp. 305–314. [Google Scholar]
- Rosado, J.I. Representation of quantum states as points in a probability simplex associated to a SIC-POVM. Found. Phys. 2011, arXiv:1007.071541, 1200–1213. [Google Scholar]
- Appleby, D.M.; Ericsson, Å.; Fuchs, C. Properties of QBist State Spaces. Found. Phys. 2011, arXiv:0910.275041, 564–579. [Google Scholar]
- Rosado, J.I. Probing the geometry of quantum states with symmetric POVMs. arXiv 2013, arXiv:1309.7309. [Google Scholar]
- Grassl, M. On SIC-POVMs and MUBs in dimension 6. arXiv 2004, arXiv:quant-ph/0406175. [Google Scholar]
- Colin, S.; Corbett, J.; Durt, T.; Gross, D. About SIC POVMs and discrete Wigner distributions. J. Opt. B Quantum Semiclass. Opt. 2005, 7, S778–S785. [Google Scholar] [CrossRef]
- Wootters, W.K. Quantum measurements and finite geometry. Found. Phys. 2006, arXiv:quant-ph/040603236, 112–126. [Google Scholar]
- Albouy, O.; Kibler, M.R. A unified approach to SIC-POVMs and MUBs. J. Russ. Laser Res. 2007, 28, 429–438. [Google Scholar] [CrossRef]
- Godsil, C.; Roy, A. Equiangular Lines, Mutually Unbiased Bases, and Spin Models. Eur. J. Comb. 2009, 30, 246–262. [Google Scholar] [CrossRef]
- Appleby, D.M. SIC-POVMs and MUBs: Geometrical Relationships in Prime Dimension. arXiv 2009, arXiv:0905.1428. [Google Scholar]
- Rastegin, A.E. Uncertainty relations for MUBs and SIC-POVMs in terms of generalized entropies. Eur. Phys. J. D 2013, 67, 269. [Google Scholar] [CrossRef]
- Beneduci, R.; Bullock, T.; Busch, P.; Carmeli, C.; Heinosaari, T.; Toigo, A. An operational link between MUBs and SICs. Phys. Rev. A 2013, arXiv:1306.600288, 032312. [Google Scholar]
- Jedwab, J.; Wiebe, A. Constructions of complex equiangular lines from mutually unbiased bases. arXiv 2014, arXiv:1408.5169. [Google Scholar]
- Veitch, V.; Mousavian, S.A.H.; Gottesman, D.; Emerson, J. The resource theory of stabilizer computation. New J. Phys. 2014, arXiv:1307.717116, 013009. [Google Scholar]
- Zhu, H. Mutually unbiased bases as minimal Clifford covariant 2-designs. Phys. Rev. A 2015, arXiv:1505.0112391, 060301. [Google Scholar]
- Bengtsson, I.; Życzkowski, K. On discrete structures in finite Hilbert spaces. arXiv 2017, arXiv:1701.07902. [Google Scholar]
- Aravind, P.K. MUBs and SIC-POVMs of a spin-1 system from the Majorana approach. arXiv 2017, arXiv:1707.02601. [Google Scholar]
- Casazza, P.G.; Cheng, D. Associating vectors in with rank 2 projections in : With applications. arXiv 2017, arXiv:1703.02657. [Google Scholar]
- Bar-On, T. The probability interpretation of Wigner function by SIC-POVM. Eur. Phys. J. D 2009, 54, 137–138. [Google Scholar] [CrossRef]
- Bar-On, T. Discrete Wigner function by symmetric informationally complete positive operator valued measure. J. Math. Phys. 2009, 50, 072106. [Google Scholar] [CrossRef]
- Filippov, S.N.; Man’ko, V.I. Symmetric Informationally Complete Positive Operator Valued Measure and Probability Representation of Quantum Mechanics. J. Russ. Laser Res. 2010, 31, 211–231. [Google Scholar] [CrossRef]
- Saraceno, M.; Ermann, L.; Cormick, C. Phase-space representations of SIC-POVM fiducial states. Phys. Rev. A 2016, arXiv:1612.0235195, 032102. [Google Scholar]
- Sloane, N.J.A. A002853: Maximal size of a set of equiangular lines in n dimensions. In On-Line Encyclopedia of Integer Sequences; The OEIS Foundation: Highland Park, NJ, USA, 2015. [Google Scholar]
- Greaves, G.; Koolen, J.H.; Munemasa, A.; Szöllősi, F. Equiangular lines in Euclidean spaces. J. Comb. Theory Ser. A 2016, arXiv:1403.2155138, 208–235. [Google Scholar]
- Balla, I.; Dräxler, F.; Keevash, P.; Sudakov, B. Equiangular Lines and Spherical Codes in Euclidean Space. arXiv 2016, arXiv:1606.06620. [Google Scholar]
- Wiener, N. Time Series; MIT Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Liu, Y. 2012. Available online: https://sourceforge.net/projects/hlbfgs/ (accessed on 17 July 2017).
- Gray, J. The Hilbert Challenge; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Appleby, M. Email communication, 2016.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).