Abstract
In this paper, we obtain the extended genus field of a finite abelian extension of a global rational function field. We first study the case of a cyclic extension of prime power degree. For the general case, we use the fact that the extended genus fields of a composition of two cyclotomic extensions of a global rational function field is the same as the composition of their corresponding extended genus fields. In the main result of the paper, we give the extended genus field of finite abelian extensions of a global rational function field explicitly in terms of the field and extended genus field of its “cyclotomic projection”.
MSC:
11R58; 11R60; 11R29
1. Introduction
The concepts of genus field and extended (or narrow) genus field depend on the respective concepts of Hilbert class field (HCF) and extended (or narrow) Hilbert class field. The theory of the genus goes back to Gauss. The HCF concept is much more recent. The first to translate Gauss’ genus theory into genus to “modern terms” was Hilbert. Currently, it may be used to study the “easy” part of the HCF of a finite extension of the field of rational numbers.
The notion of genus field for number fields was first introduced by H. Hasse, who defined the genus field of a quadratic extension of . Since the genus field is related to the HCF, one natural way to study genus fields is by means of class field theory. However, we may study genus fields of abelian extensions of the rational field by using Dirichlet characters.
For number fields, the definition of Hilbert and extended Hilbert class field are canonically given as the maximal abelian unramified and the maximal abelian unramified at the finite primes of the field, respectively. The definition of the genus field is not absolute, as is the HCF, but depends on an extension of the base field. A. Fröhlich gave a general definition of genus fields for any number field K as follows: , where F is the maximal abelian extension of the field of the rational numbers contained in the Hilbert class field of K. Fröhlich’s definition is also canonical.
We are interested in global function fields. In this context, there are several different definitions of the HCF of a global field K depending on which aspect we are interested in. In this paper, we study the extended genus field of a finite abelian extension , where is a global rational function field. Let be the infinite prime of k. Then we define the HCF of K as the maximal unramified abelian extension of K such that the infinite primes of K (those above ) decompose fully in . B. Anglès and J.-F. Jaulent [1] give the same concept by means of the idèle norm subgroup corresponding to . They also define the extended HCF of any global field K by means of the norm subgroup of in the idèle group of K. We use the definitions of Anglès and Jaulent of and to define the genus field and the extended genus field of K with respect to the extension , by means of their corresponding idéle subgroups. We compare our findings with the concepts of extended genus fields given by Ramírez–Rzedowski–Villa and by R. Clement in [2].
The definition of the extended genus field of a finite abelian extension given by Ramírez–Rzedowski–Villa differs from the one defined by Anglès and Jaulent. In the general case, we have that .
In this paper, we explicitly describe the extended genus field via Anglès and Jaulent’s approach. This result reinforces the connection between these two approaches and highlights the robustness of genus field theory, since we obtain that . We explore the implications of this equality in the context of algebraic number theory and its applications to the study of class field theory.
We first study the case of a cyclic extension of k of prime power degree . We consider four possible types of primes l: (1) , the characteristic of k (Artin–Schreier–Witt case); (2) , ; (3) (Kummer case); and (4) , and (“semi-Kummer” case).
Our main results are Theorems 11 and 12. We obtain that , where E is the cyclotomic projection of K (see (1) below) and is the maximal abelian extension of E contained in a cyclotomic extension field unramified at the finite primes.
The main tools used in this paper are the Carlitz theory of cyclotomic function fields and class field theory, particularly the concepts of HCF and genus fields developed by Anglès and Jaulent.
2. Notations and General Results
For the general Carlitz–Hayes theory of cyclotomic function fields, we refer to [3]. For local and global class field theory, we refer to [4,5], respectively.
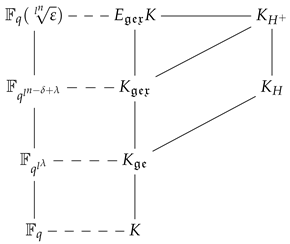
We will be using the following notation. Let be a global rational function field, where is the finite field of q elements. Let and let denote the set of monic irreducible elements of . For , denotes the Nth cyclotomic function field where is the Nth torsion of the Carlitz module. For a , we define . The relevance of is that in the case .
We will call a field F a cyclotomic function field if there exists such that . In this way, in the case and , we have that is a cyclotomic function field.
Let . The Dirichlet characters are the group homomorphisms . Given a group X of Dirichlet characters modulo N, the field associated to X is the fixed field , where . We say that F corresponds to the group X and that X corresponds to F. We have that . When X is a cyclic group generated by , we have that the field associated to X is equal to , and we say that F corresponds to .
Let , and let be its decomposition as a product of irreducible polynomials. Then . Then, if is a Dirichlet character , we have that , where is a character .
Given a cyclotomic function field F with Dirichlet group characters X, we have that the ramification index of in equals , where and is the Pth component of . The maximum cyclotomic extension of F, unramified at the finite prime divisors, is the field that corresponds to This field is denoted as .
We denote the infinite prime of k by . That is, is the pole divisor of T, and is a uniformizer for .
Given a finite extension , a definition of HCF , and a definition of extended HCF of K, the respective genus field and extended genus field of K with respect to k are the extensions such that L is the maximal abelian extension of k contained in and in , respectively.
We will use both notations or to denote the ramification index of the prime P of k in F. For the place we use the notation .
When is a finite abelian extension, it follows from the Kronecker–Weber–Hayes Theorem that there exist , , and such that , where, for any F, , for any , , and is the maximum subfield of where is totally and wildly ramified. Then we define
where . We call E the “cyclotomic projection of K”, since E is a cyclotomic function field with similar arithmetic properties as K, except for wild ramification of the infinite prime.
When is a Kummer extension, where , and is free of ℓ- powers, then we have that if and only if . If , we have that where is the cyclotomic projection of K.
Let H be the decomposition group of the infinite primes in , and . Since , from the Galois correspondence, we have that . The group is also the decomposition group of the infinite primes of K in . Furthermore, , where denotes the inertia group of . Therefore, is a cyclic group and . We have that .
For any global function field L, denotes the set of all places of L.
For , denotes the valuation of x at l. That is, if and . We write .
3. Basic Results
One result of ramification of tamely ramified extensions, used frequently, is the following theorem.
Theorem 1
(Abhyankar’s Lemma). Let be a separable extension of global function fields. Assume that with , . Let be a prime divisor of K and a prime divisor in L above . Let , . If at least one of the extensions is tamely ramified at , then
where denotes the ramification index.
Next, we present some basic facts on finite cyclic groups and we apply them to the case of a finite field.
Let G be a cyclic group of order n, say . Let be the unique subgroup of G of order m where . We have . Let and let . We have , where is given by .
Note that if and , then , namely, if are such that , we have
Conversely, let with . Then .
We also have that since, if , then so that . Conversely, if and if , then .
Now, if , then because we have the exact sequence
obtaining and, if , there exists such that that implies so that . Thus .
We apply the previous basic results to the multiplicative group of the finite field , which is a cyclic group of elements.
Lemma 1.
Let l be a prime number and , with . Let with . Then for some .
Proof.
Let . Then . Set s, , to be the minimal non-negative integer such that . If , then and is irreducible.
For any s, we will see that is an irreducible polynomial. We have , where denotes a primitive m-th root of unity. Let . Let , and let , where , with . We choose an element such that b is minimal.
We have . Let be such that . Then . This is a cyclic group of order and
Hence . Therefore , , and is irreducible.
It follows that and . □
Remark 1.
We have , where s is the minimal non-negative integer such that , with .
Corollary 1.
With the above notations, if , we have .
Proof.
Set , then , and . Clearly is minimal. □
Next, we consider , with and for some . Set , . Hence , where .
In case that there would exist such that , it would imply that and thus . Therefore, would have as a root. It would follow that , contrary to our hypothesis. Therefore, .
Conversely, if , then where is not an l-power. Therefore
hence . In the case that , it would follow that contrary to our hypothesis.
We have proved:
Theorem 2.
We have that if and only if .
A basic result on cyclic groups of prime power degree that we need is the following.
Proposition 1.
Let G be a cyclic group of order , with l a prime number. Given , then or . In particular, with or and if and , then .
Proof.
By cyclicity, G has a unique subgroup of each of the divisors of . These subgroups are with . The result follows. □
4. Extended Genus Fields and Class Field Theory
First, we establish the definition of extended genus fields according to Anglès and Jaulent [1].
We have that is the completion of k at . Let . Then x is written uniquely as
where is the group of one units of . We write , which is a uniformizer at .
The sign function is defined as given by for .
We have that is an epimorphism and .
For a finite separable extension L of , we define the sign of by the morphism . We have .
For a global function field L, let be the set of places of L dividing . We define the following subgroups of the group of idèles as
where we denote if and if . The groups and are open subgroups of , the idèle group of L.
Definition 1.
Let be a finite abelian extension. Then the Hilbert class field (HCF) and the extended HCF of K are the fields corresponding to the idèle subgroups and of , respectively. By class field theory, the respective genus and extended genus fields with respect to the extension correspond to the idèle subgroups and of , respectively.
By class field theory, we have
We have that is an unramified extension at the finite prime divisors of K, and
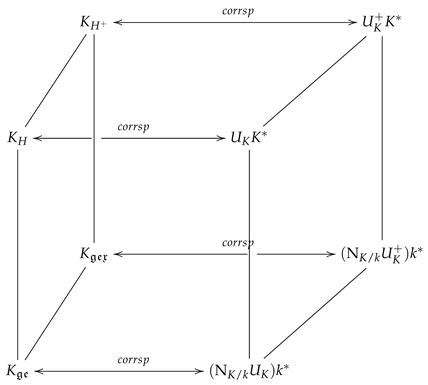
Let be a finite abelian extension. Then, with the notation given above, if , we have for some subfield for some decomposition group . In most cases, we have . In this case, and .
In this paper, we particularly study the case . A general result is the following.
Proposition 2.
Let be a finite abelian extension and let E be given by (1). Then, if are the finite primes of k ramified in K and
for all , it follows that .
Proof.
The group of Dirichlet characters associated with is
where X is the group of Dirichlet characters associated with E. Each is cyclic of order . The field associated with is the subfield of of degree over k. It follows that
Let Z be the group of Dirichlet characters associated to . The only finite primes of k possibly ramified in are . The group of Dirichlet characters associated to is . By hypothesis, for all . Therefore . □
Corollary 2.
We have there exists such that .
Proof.
It follows from Proposition 2 and from the facts that is not ramified at any finite prime and that is fully ramified in . □
In the rest of the section, we will focus on the cases .
Definition 2.
For a finite abelian extension , we define , where E is given by (1).
In this paper, we will prove that it always happens
where is any finite abelian extension.
Ramírez–Rzedowski–Villa defined for a finite abelian extension . In general, we have .
We recall the following theorem from class field theory.
Theorem 3.
Let F be a global function field. Let be a finite abelian extension, and let be the subgroup of the idèle class group of F corresponding to N. Then, if is the field of constants of F, is the field of constants of N, where
Remark 2.
Hereafter, κ is given by (3).
Remark 3.
Note that if F is any global function field, then the fields of the constants of and of are the same. Therefore, in the special case , if we obtain that if the field of constants of is contained in the one of then, because is an extension of constants of , say and and , it follows that and therefore . Since , we obtain .
Consider a finite abelian extension . The idèle class subgroup B of the idèle class group , the idèle class group of K, associated to is
where
We denote .
On the one hand, if , then , for , so that for . On the other hand, if and are two infinite primes, . It follows that if we fix an infinite prime of K, then
Lemma 2.
We have
5. Cyclic Extensions of Prime Power Degree
In this section, we study the extended genus field of a finite cyclic extension of degree with l a prime number and . We will assume that the extension is geometric, that is, the field of constants of K is . We consider four types of primes l:
- (1)
- , where p is the characteristic of k, the Artin–Schreier–Witt case,
- (2)
- and ,
- (3)
- , the Kummer case,
- (4)
- with and , the “semi-Kummer” case.
5.1. The Artin–Schreier–Witt Case:
Since is a subgroup of the inertia group of in and the order of this last group is a divisor of , the order of is relatively prime to p. Hence, . It follows that .
5.2. Case and
By the same reason as in Section 5.1, the order of is relatively prime to l. Thus and .
5.3. The Kummer Case:
5.3.1. The Genus Field in the Cyclotomic Case
Let , with , be a Kummer cyclic extension of k. Let be the group of Dirichlet characters associated to F. Note that for any relatively prime to l, the field associated to is F since . The above corresponds to the fact that .
When , we have that the character associated to F is , the Legendre symbol that is defined as follows: if P is of degree d, then for any with , . Then is defined as the unique element of such that . We have that is the character associated to . Let us denote . Then is the character associated to .
Hence, if is the character associated to , then .
Remark 4.
Let l be a prime number different from p, the characteristic of K, such that , . We have that for all l and all κ except when and .
Proof.
If l is odd, for all . Let . If , contains a primitive th root of unity . Let . Then and . Thus .
On the other hand, if , . Now, if we had for some , then is a primitive th root of unity, contrary to our hypothesis. □
Corollary 3.
For any prime number l such that , with and , we have , except when is odd, , and . We also have that if and , then with the same exception.
Proof.
If is even, . If is odd, except when and . The same argument works for and . □
In general, for a radical extension, we have:
Theorem 4.
Let be a geometric separable extension of k, , and let . Then
As a consequence, we obtain the following result for a cyclic cyclotomic Kummer extension . Let X be the group of Dirichlet characters associated to F and let be the group associated to M, the maximal cyclotomic extension of F unramified at the finite primes.
Let , , and let be the field associated to . Then, is cyclotomic, P is the only ramified prime in , and P is tamely ramified in . This implies that and with . Therefore, is the only field of degree over k. Since is a Kummer extension, it follows that .
Theorem 5.
The maximal unramified cyclotomic extension of at the finite primes is . In other words,
Proof.
The field M corresponds to the group of Dirichlet characters and the field associated to is , for each . The result follows. □
Remark 5.
Let with and . Then and
with , .
Another proof of Theorem 5 is obtained using Abhyankar’s Lemma. On the one hand, we have that
On the other hand, if , from Abyankar’s Lemma, is unramified at every finite prime, so is unramified at the finite primes and . Hence and . Therefore, .
The following theorem gives the genus field of a cyclic extension.
Theorem 6.
Let , with , , with , , different monic irreducible polynomials with , , . We order the polynomials so that .
Let with , . Let
Let , , be such that and for . For we have , and therefore there exist such that . For , we have . Let . For , let .
Then
where with if , i.e, , and if , then
Remark 6.
When , we may also use the description of given in the case .
5.3.2. The Genus Field in the General Case
The following theorem gives the genus field of a general cyclic extension.
Theorem 7.
Let , with , , , with , , different polynomials and some . We order the polynomials so that . Let , t as in Theorem 6, and . Let . Then , where are given in (4) for all j. Thus
Further, if , we have
The general structure of when is a finite l–Kummer extension for a prime number l, is given by with D a field satisfying .
With notations given above, particularly in Theorem 6, we consider first the case .
Proposition 3.
If then and there exists such that .
Proof.
First, assume that . Suppose that for all we have .
We have that for all , . Thus
We have
Hence . It follows that
Therefore, , contrary to our assumption. Thus, there exists with .
The same argument shows that if , then . □
From Theorems 6 and 7, we have that for all , we have . In case there exists such that we obtain that
Hence
From the above, the following result is immediate.
Proposition 4.
If there exists such that , in particular when , then .
The first main result on extended genus fields is the following:
Theorem 8.
With the above notations, we have that , except possibly in the following case:
- (a)
- ,
- (b)
- ,
- (c)
- ,
- (d)
- for all .
Proof.
If , the result follows. If , K is cyclotomic and therefore . If , then, from Proposition 3, we have that for all and therefore . If for some , then for all and therefore . If , we have that is unramified in so that . □
The above result shows that, outside of the special case given in Theorem 8, we have .
5.3.3. The Special Case
We now consider the special case, that is, the exception mentioned in Theorem 8. We will prove that, also in this case, the equality holds.
Let be a geometric separable extension of k, with and let , with distinct, , . Let , , , . We assume that we have the exception given in Theorem 8. Let , and with . Then , so that .
Since , we have and for all . We also have that .
Lemma 3.
We have . It also holds that and are extensions of constants and . That is,
We also have that and are extensions of constants. Furthermore, and .
Proof.
The extension is fully ramified at the infinite prime . Since and since , it follows that .
Now, .
We also have . Therefore
□
Corollary 4.
The field of constants of is .
Theorem 9.
In the exceptional case given in Theorem 8, we have that , the field of constants of is , and the field of constants of is .
Proof.
Since , we have . □
Later on, we will see that the field of constants of is .
We fix an infinite prime of K, and we denote .
Since , with , we have
We have that , and, since l is different from the characteristic, it follows that . Therefore
Since , there exists such that . Thus
Now, . Set . We have that and . Therefore, is fully ramified in .
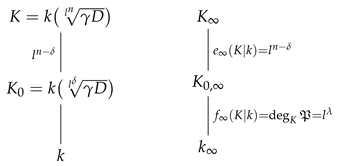
We have and
Lemma 4.
The field of constants of are .
Next, we will prove that the field of constants of and of are the same.
Let
We also have
Then, is an extension of constants and, since , it follows that
Now, . The field of constants of are and the field of constants of are . We have . Therefore . From Theorem 2, we obtain that .
Let , with and . Then
The element satisfies , that is, is a root of . Since , the polynomial
is irreducible. We also have and is fully ramified at .
Set . Then and
Hence, and is a prime element of . We also have
Now, . Let be a primitive th root of unity and set . We have
Thus
Now we consider a generic element :
Then
It follows that
Therefore, such that
Now, , thus and . Hence, .
Next, we break our study in two cases: and .
5.3.4. Case
This case was considered in Theorem 3.5 [6].
5.3.5. Case
We now assume that . We always have, since , that because and therefore (see Remark 4). Hence, . That is, .
Because , it follows that
and that the field of constants of is .
We have that , so that, from Theorem 2, we obtain
On the other hand, the field of constants of is and . Again, from Theorem 2, we obtain that
We have so that and . Therefore, . Hence, . It follows from (6) that and .
Thus, . Since , . Therefore, , so that and . In particular, .
It follows that the field of constants of is . In short, the field of constants of both and , is .
Thus, and . Therefore, . Since , we finally obtain that .
Theorem 10.
For Kummer extensions satisfying the special case described in Theorem 8, we have .
Corollary 5.
For any cyclic Kummer extension of k, we have .
5.4. Semi-Kummer Case: , and
Recall that we only need to consider the case , or, equivalently, there exists a finite prime ramified in . The prime is fully ramified in .
We have that , the inertia group of in the extension .
It follows that , and we have that is a cyclic group of order a power of l. Set , an l–cyclic group. Furthermore .
Using Proposition 1, we obtain:
Proposition 5.
.
Proof. 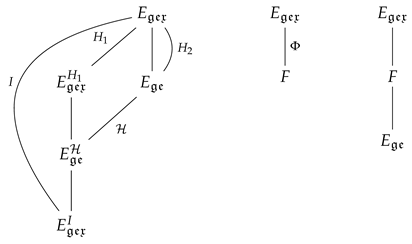
Let , and . By hypothesis, we have . Set and .

Then, is fully ramified in and . Therefore is fully ramified and non-ramified in . Hence and . Finally, it follows that and that . □
Lemma 5.
We have that .
Proof.
Since the extension is geometric, and , we have . □
We use the following notation. Let . Since is a quotient of I, it follows that because . In particular, .
Set . We have
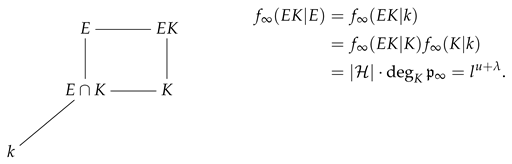
Since eP(K|k) = eP(E|k) for all P ∈ ∪ {∞}, from Abhyankar’s Lemma, we obtain that eP(EK|E) = 1 for all P ∈ ∪ {∞}, that is, EK/E is an unramified extension. We will show that it is an extension of constants.
It is easy to see that . We have, on the one hand
On the other hand
Therefore
Because and are unramified extensions,
We have that is an extension of constants of degree . We also have that the field of constants of is . Hence, the field of constants of is , where .
Let us see that the field of constants of is also , the same as that of .
Since is tamely ramified, the conductor of constants is the minimum such that . We have that , where , , and . Therefore
Furthermore, we have
We have
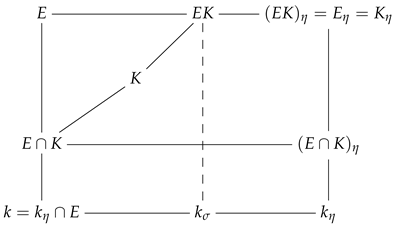
If , then . Since is minimum, it follows that , and . Therefore, the field of constants of is .
Proposition 6.
The field of constants of either or is , where and .
Furthermore, .
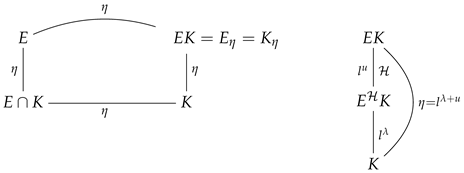
We have that is an extension of constants of degree , and the same is true for the extension . The field of constants of is , that is, the same as for the field .
Let be a prime above and denote , . Let , that is, and . We have
Let be the inertia field of , that is, and . We have that is unramified.
For each local field, there exists a unique unramified extension of each degree. Therefore, , that is, is an “extension of constants” of degree . More precisely,
where is a prime element of .
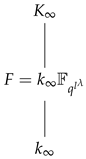
Let where is a prime element of . Now, we have
Hence .
We have

It follows that is a Kummer extension, say for some .
Let , with , , and . Since , we have . We write , where . Then, if , we have
Let , with and . Set . Thus is unramified, , and is totally ramified. It follows that and that , that is, .
Therefore, for some . Set . Then, . Hence
It follows that . Therefore, we may take as a prime element of F.
Now we consider for some . We have
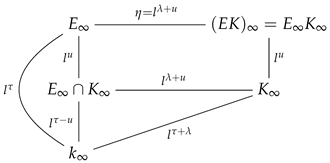
Because is cyclotomic, the field of constants of is also .
As before, is a prime element of . We have
Hence
Thus
Since the field of constants of is , from Theorem 3, there exists an element of degree 1 in satisfying
Set with . Since , it follows that . Furthermore, and . Therefore
where . Therefore, and, since , it follows that . Thus and .
We obtain
The field of constants of is , therefore, . From Theorem 2 we have that .
In short, with , , and .
The irreducible polynomial of over F is . Then and
Now, . Therefore, .
Let us see the norm of an arbitrary element X of . Let with , , and . Then
Therefore
and
Now
In other words,
Since with and , we have . Thus . Therefore, . Since , it follows that and that is the minimum positive integer with this property. For such X, we have
Therefore, the field of constants of is , the same as for .
We have obtained our first main result:
Theorem 11.
Let be a geometric cyclic extension of degree with l a prime number and . Then, if E is given by(1), we have
6. General Finite Abelian Extensions
The following theorem is the main key to obtain the extended genus field of a finite abelian extension.
Lemma 6.
Let and be two finite cyclotomic extensions of k, and let . Then .
As a consequence, we obtain our final main result.
Theorem 12.
Proof.
Let , where each is a cyclic extension of prime power degree. Let with each given in (1). Then, from Lemma 6, we obtain
Therefore, from Theorem 11, it follows that
Hence . □
We obtain some consequences from Theorem 12. We consider a geometric abelian finite extension. We have and . Let , , and . For any finite abelian extension and any prime of J, we denote by the tame ramification index of the prime in the extension , namely, if with , then . The set of tame ramification indexes is multiplicative.
Lemma 7.
We have .
Proof. 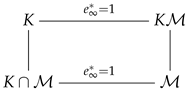
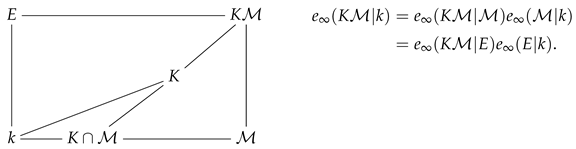
First, note that if , then . Now we consider

Since , it follows that . Therefore, .
We have

It follows that
Now
□
Theorem 13.
We have . In particular . It also holds
Furthermore, the field of constants of is , , and the field of constants of both and is , and we have .
Proof. 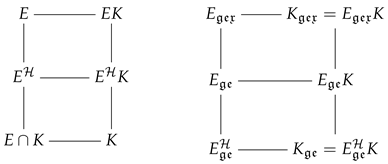
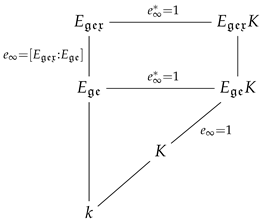
We have

It follows that .
Now, since is an extension of constants of degree, in fact, , we will see that the extension is totally ramified.

We have that . Hence . Similarly, we obtain .
Therefore, and is totally ramified.
Since and is geometric, we obtain that . We know that the field of constants of is .
Finally, is an extension of constants of degree . Hence, the field of constants of both and is . □
7. Discussion
In this paper, it is shown that the notion of the extended genus field of an abelian finite extension of the field of rational functions given by B. Anglès and J.F. Jaulent by means of class field theory is the same as the one given by E. Ramírez-Ramírez, M. Rzedowski-Calderón, and G. Villa-Salvador using Dirichlet characters.
Author Contributions
Investigation, J.C.H.-B. and G.V.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We thank the anonymous referees for the careful reading and helpful suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Anglès, B.; Jaulent, J.-F. Théorie des genres des corps globaux. Manuscripta Math. 2000, 101, 513–532. [Google Scholar] [CrossRef]
- Clement, R. The genus field of an algebraic function field. J. Number Theory 1992, 40, 359–375. [Google Scholar] [CrossRef][Green Version]
- Hayes, D.R. Explicit class fields theory for rational function fields. Trans. AMS 1974, 189, 77–91. [Google Scholar] [CrossRef]
- Iwasawa, K. Local Class Field Theory; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Artin, E.; Tate, J. Class Field Theory; W. A. Benjamin Inc.: London, UK, 1967. [Google Scholar]
- Hernandez–Bocanegra, J.C.; Villa–Salvador, G. Genus Field and Extended Genus Field of an Elementary Abelian Extension of Global Fields. Bull. Braz. Math. Soc. New Ser. 2023, 54, 20. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).