Construction of Inequalities for Network Quantum Steering Detection

Abstract

Quantum network correlations are crucial for long-distance quantum communication, quantum cryptography, and distributed quantum computing. Detecting network steering is particularly challenging in complex network structures. We have studied the steering inequality criteria for a 2-forked 3-layer tree-shaped network. Assuming the first and third layers are trusted and the second layer is untrusted, we derived a steering inequality criterion using the correlation matrix between trusted and untrusted observables. In particular, we apply the steering criterion to three classes of measurements which are of special significance: local orthogonal observables, mutually unbiased measurements, and general symmetric informationally complete measurements. We further illustrate the effectiveness of our method through an example.

1. Introduction

Quantum steering, initially proposed by Einstein, Podolsky, and Rosen in 1935 [1,2], was formalized by Wiseman, Jones, and Doherty in 2007 as the ability to remotely generate quantum ensembles that cannot be explained by a local hidden state (LHS) model [3]. Quantum steering is regarded as a subtle form of quantum correlation that lies between entanglement and nonlocality. In quantum communication, the application of quantum entanglement usually requires a certain degree of device reliability, that is, the devices of all parties involved need to be trusted. In contrast, quantum nonlocality provides a fully device-independent communication method. However, as a semi-device-independent communication method, quantum steering is considered to have the potential to bridge the gap between information security and practicality, offering advantages for multiple applications, including one-sided device-independent quantum key distribution [4,5,6], subchannel discrimination [7] and quantum teleportation [8].

One of the most fundamental problems in quantum steering is to identify whether a given quantum state is steerable. Several criteria for detecting bipartite steering have been proposed to date from different points of view, including linear and nonlinear steering inequalities [9,10,11,12,13], uncertainty relations [14,15,16], moment matrix approaches [17], and all-versus-nothing methods [18]. Beyond bipartite systems, genuine multipartite steering has garnered significant interest, with several approaches now available for its characterization [19,20,21,22,23]. In addition, the proposal of steering criteria for arbitrary-dimensional bipartite systems also provides methods for detecting high-dimensional bipartite steering, and these criteria are experimentally testable [24,25].

In recent years, quantum communication networks have witnessed remarkable progress and play a pivotal role in long-distance quantum communication [26,27]. Jones et al. firstly defined chain-shaped (especially entanglement-swapping) network steering by the corresponding network local hidden state model with trusted endpoints and untrusted intermediate ones [28]. Recently, Refs. [29,30] extended the study of network steering to star networks, deriving linear and nonlinear inequalities for detecting network steering when the center party is trusted and when the center party is untrusted, respectively. Since any noncyclic quantum network can be regarded as a tree-shaped network, which has been shown to emerge in various application scenarios, such as quantum simulations [31,32,33,34], entanglement transitions [35], and quantum-assisted machine learning [36]. Therefore, in this paper, we define a kind of quantum steering in two-forked 3-layer tree-shaped networks with the first and the last layers being trusted while the intermediate layer being untrusted. Meanwhile, we propose a steering criterion based on the correlation matrix between the observables of trusted and untrusted parties, and this criterion does not restrict the dimension of the bipartite states distributed in the network. Specifically, we apply this method to three specific and important types of local measurements, namely Local Orthogonal Observables (LOOs) [37], Mutually Unbiased Measurements (MUMs) [38], and General Symmetric Informationally Complete positive operator-valued measures (GSICs) [39], to provide some operational criteria.

The paper is organized as follows. Section 2 briefly reviews the fundamental theory of quantum steering and network steering in the context of entanglement swapping. In Section 3, we define quantum steering in a 2-forked 3-layer tree-shaped network by building a local hidden state model of the tree-shaped network. In Section 4, we propose a steering criterion based on correlation matrices between local observables of trusted and untrusted parties and establish some operational steering criteria by employing three classes of important measurements, that is, LOOs, MUMs, and GSICs. Finally, we summarize our results in Section 5.

2. Preliminaries

In this section, we lay the foundation for the results of this work by introducing the notations and reviewing the framework of quantum network steering.

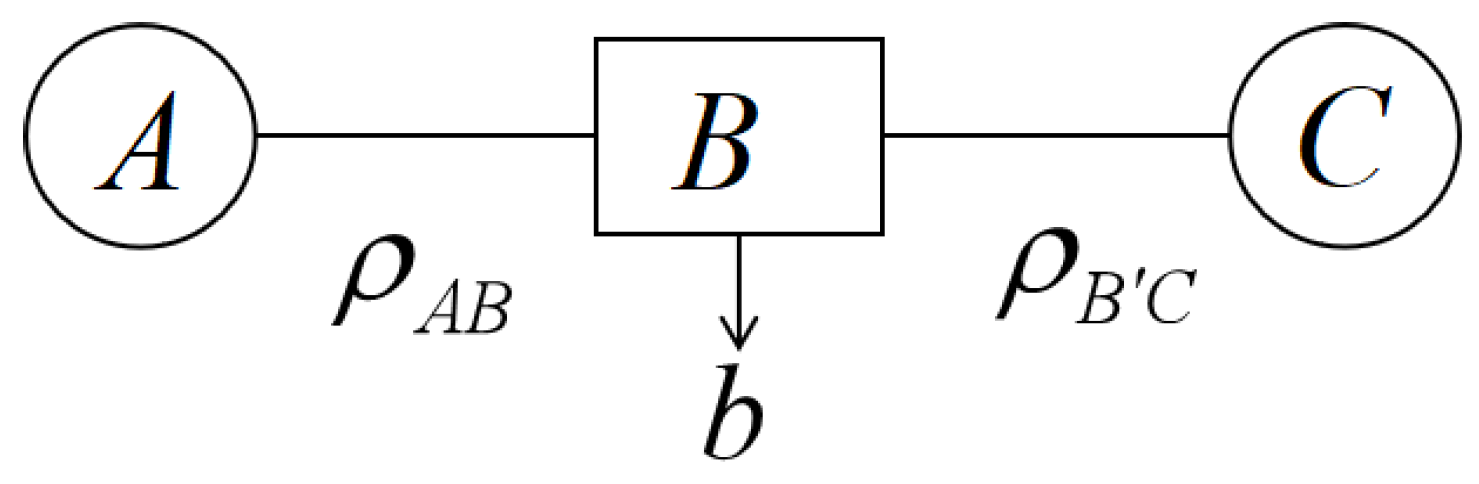
2.1. Bipartite Steering

Consider a scenario in which Alice (A) and Bob (B) share a quantum state ${\rho }_{AB}$. Suppose that A is untrusted while B is trusted. Alice generates a random input $x\in \{1,\dots ,m\}$ to select a measurement from the set of a positive operator-valued measure (POVM) ${\left\{M_{a|x}^A\right\}}_{a=1}^n$. Then the collection of Bob’s subnormalized states consists of ${\sigma }_{a|x}^B={\mathrm{tr}}_A\left[(M_{a|x}^A\otimes I){\rho }_{AB}\right]$, which is referred to as an assemblage. We say that this assemblage admits an LHS model if it can be written as ${\sigma }_{a|x}^B={\sum }_{\lambda }p\left(\lambda \right)p\left(a\right|x,\lambda ){\sigma }_{\lambda }^B$, where $\lambda$ is a hidden variable obeying the probability distribution $p\left(\lambda \right)$, ${\sigma }_{\lambda }^B$ represents the hidden state of Bob and $p\left(a\right|x,\lambda )$ is the local response function of Alice. Then we say that it does not demonstrate steering. Conversely, if there exist measurements such that ${\sigma }_{a|x}^B$ does not admit such an LHS model, we say that the state ${\rho }_{AB}$ is steerable from A to B.

2.2. Network Quantum Steering

The pursuit of long-distance and large-scale quantum communication has led to a focus on network correlations. The notions of network steering and network local hidden state models were first introduced in Ref. [28], in which Jones et al. focused on the entanglement-swapping network with the end point parties being trusted and the intermediate party being untrusted (see Figure 1). This is a network of three parties consisting of Alice (A), Bob (B), and Charlie (C) and two independent bipartite sources ${\rho }_{AB}$, ${\rho }_{B^{\prime }C}$. This network state is of the form ${\rho }_{AB}\otimes {\rho }_{B^{\prime }C}$. Assume that the two sources ${\rho }_{AB}$ and ${\rho }_{B^{\prime }C}$ are characterized by independent hidden variables ${\lambda }_1$ and ${\lambda }_2$, respectively.

If the intermediate party Bob performs one fixed measurement $M_b^{B{B}^{\prime }}$ with the corresponding output b, then the subnormalized state between A and C obtained from the measurement is ${\sigma }_b^{AC}={\mathrm{tr}}_{B{B}^{\prime }}\left[(I^A\otimes M_b^{B{B}^{\prime }}\otimes I^C)({\rho }_{AB}\otimes {\rho }_{B^{\prime }C})\right]$. ${\rho }_{AB}\otimes {\rho }_{B^{\prime }C}$ is network unsteerable if ${\sigma }_b^{AC}$ admits a network local hidden state (NLHS) model, i.e., ${\sigma }_b^{AC}={\sum }_{{\lambda }_1,{\lambda }_2}p\left({\lambda }_1\right)p\left({\lambda }_2\right)p\left(b\right|{\lambda }_1,{\lambda }_2){\sigma }_{{\lambda }_1}^A\otimes {\sigma }_{{\lambda }_2}^C$, where ${\sigma }_{{\lambda }_1}^A$ and ${\sigma }_{{\lambda }_2}^C$ are given hidden states, respectively, and $p\left(b\right|{\lambda }_1,{\lambda }_2)$ is the local response function of Bob. Otherwise, ${\rho }_{AB}\otimes {\rho }_{B^{\prime }C}$ is network steerable. However, unlike the quantum state steering that requires multiple measurements, the network framework permits even a single fixed measurement $M_b^{B{B}^{\prime }}$ to expose a violation of the NLHS model and confirm the network’s steerability [28].

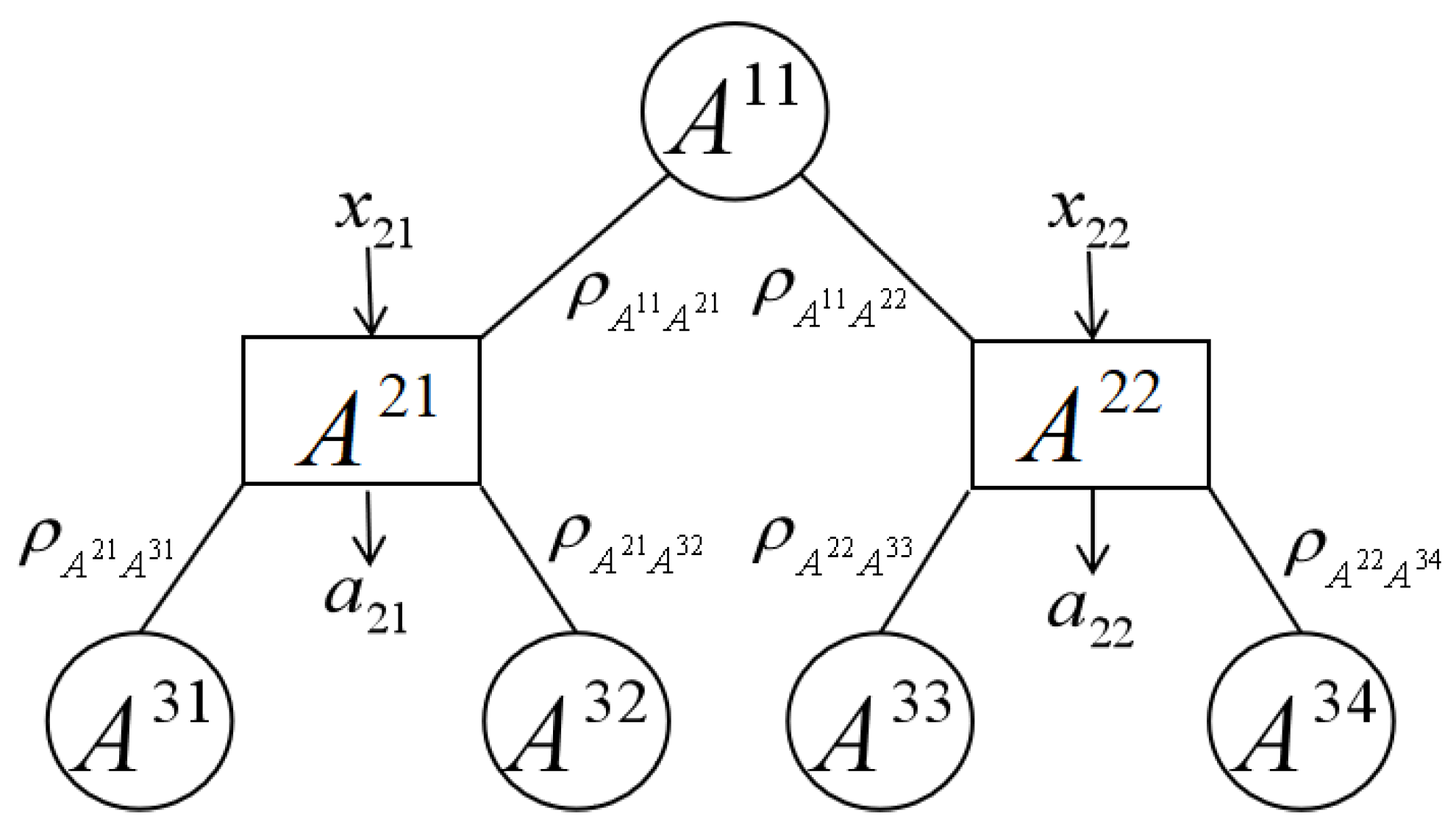
3. Definition of Network Steering in a 3-Layer Tree-Shaped Network

In this section, we present the formulaic definition of tree-shaped network steering shown in Figure 2. To do this, we use ${\mathcal{H}}_X$ to denote the finite dimensional complex Hilbert space, which describes quantum systems X, and we use $\mathcal{S}\left({\mathcal{H}}_X\right)$ to denote the set of all quantum states of the system X described by a Hilbert space ${\mathcal{H}}_X$.

This 3-layer tree-shaped network consists of seven parties $A^{11}$, $A^{21}$, …, $A^{34}$ and six independent bipartite states ${\rho }_{A^{11}{A}^{21}}$, ${\rho }_{A^{11}{A}^{22}}$ …, ${\rho }_{A^{22}{A}^{34}}$ characterized by independent hidden variables ${\lambda }_i$$(i=1,2,\dots ,6)$, respectively (see Figure 2). Assume that the parties in the second layer are distributed as untrusted parties and the remaining parties are trusted. The state space of the untrusted parties $A^{21}$ and $A^{22}$ are ${\mathcal{H}}_{A^{21}}={\mathcal{H}}_{A^{21\left(1\right)}}\otimes {\mathcal{H}}_{A^{21\left(2\right)}}\otimes {\mathcal{H}}_{A^{21\left(3\right)}}$ and ${\mathcal{H}}_{A^{22}}={\mathcal{H}}_{A^{22\left(1\right)}}\otimes {\mathcal{H}}_{A^{22\left(2\right)}}\otimes {\mathcal{H}}_{A^{22\left(3\right)}}$, respectively. The state space of the trusted parties $A^{11}$ and ${\left\{A^{3i}\right\}}_{i=1}^4$ are ${\mathcal{H}}_{A^{11}}={\mathcal{H}}_{A^{11\left(1\right)}}\otimes {\mathcal{H}}_{A^{11\left(2\right)}}$ and ${\mathcal{H}}_{A^{3s}}$ (for $s=1,2,3,4$), respectively. Here the 3-layer tree-shaped network state is $\rho ={\rho }_{A^{11}{A}^{21}}\otimes {\rho }_{A^{11}{A}^{22}}\otimes \dots \otimes {\rho }_{A^{22}{A}^{34}}$.

Definition 1.

In the 3-layer tree-shaped quantum network in Figure 2, let ${\mathcal{M}}_{A^{ij}}=\{{\left\{M_{a_{ij}|x_{ij}}\right\}}_{a_{ij}=1}^{o_{A^{ij}}}:x_{ij}=1,2,\dots ,m_{A^{ij}}\}$ be a POVM assemblage of $A^{ij}$ for $i=2$ and $j=1,2$, where $x_{ij}$ and $a_{ij}$ represent inputs and outputs, respectively, $m_{A^{ij}}$ and $o_{A^{ij}}$ indicate the number of measurement inputs and outputs, respectively.

$\left(1\right)$ The 3-layer tree-shaped network state ρ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable with ${\mathcal{M}}_{A^{21}}$ and ${\mathcal{M}}_{A^{22}}$ if there exists a set of probability distributions (PDs) $\left\{p\left({\lambda }_t\right)\right\}$ for $t=1,2,\dots ,6$ and a set of states ${\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\subset \mathcal{S}\left({\mathcal{H}}_{A^{11\left(1\right)}}\right)$, ${\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}}\subset \mathcal{S}\left({\mathcal{H}}_{A^{11\left(2\right)}}\right)$, $\left\{{\sigma }_{{\lambda }_s}^{A^{3s}}\right\}\subset \mathcal{S}\left({\mathcal{H}}_{A^{3s}}\right)$ for $s=1,2,3,4$ such that

$$\begin{array}{cc}\hfill & {\mathrm{tr}}_{A^{21}{A}^{22}}\left[(I^{A^{11}}\otimes M_{a_{21}|x_{21}}\otimes M_{a_{22}|x_{22}}\otimes I^{A^{31}}\otimes I^{A^{32}}\otimes I^{A^{33}}\otimes I^{A^{34}})\rho \right]\hfill \\ \hfill =& \sum _{{\lambda }_1\dots {\lambda }_6}p\left({\lambda }_1\right)p\left({\lambda }_2\right)\dots p\left({\lambda }_6\right)p\left(a_{21}\right|x_{21},{\lambda }_1,{\lambda }_3,{\lambda }_4)p\left(a_{22}\right|x_{22},{\lambda }_2,{\lambda }_5,{\lambda }_6)\hfill \\ \hfill & \times {\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}}\otimes {\sigma }_{{\lambda }_3}^{A^{31}}\otimes {\sigma }_{{\lambda }_4}^{A^{32}}\otimes {\sigma }_{{\lambda }_5}^{A^{33}}\otimes {\sigma }_{{\lambda }_6}^{A^{34}},\forall x_{ij},a_{ij},i=2,j=1,2,\hfill \end{array}$$

(1)

where ${\left\{p\left(a_{21}\right|x_{21},{\lambda }_1,{\lambda }_3,{\lambda }_4)\right\}}_{a_{21}=1}^{o_{A^{21}}}$ and ${\left\{p\left(a_{22}\right|x_{22},{\lambda }_2,{\lambda }_5,{\lambda }_6)\right\}}_{a_{22}=1}^{o_{A^{22}}}$ are PDs for each inputs $x_{21}$ and $x_{22}$. In this case, we also say that Equation (1) is a 3-layer tree-shaped NLHS model of ρ with respect to ${\mathcal{M}}_{A^{ij}}$.

$\left(2\right)$ ρ is said to be $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ steerable with ${\mathcal{M}}_{A^{ij}}$ if it does not satisfy Equation (1).

$\left(3\right)$ ρ is said to be $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable if for any ${\mathcal{M}}_{A^{ij}}$, ρ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable with ${\mathcal{M}}_{A^{ij}}$.

$\left(4\right)$ ρ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ steerable if there exist at least one ${\mathcal{M}}_{A^{ij}}$ such that it is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ steerable with ${\mathcal{M}}_{A^{ij}}$.

It is worth noting that if the quantum state $\rho$ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable, then using the 3-layer tree-shaped NLHS model one has

$$\begin{array}{cc}\hfill & \sum _{a_{21}}\sum _{a_{22}}{\mathrm{tr}}_{A^{21}{A}^{22}}\left[(I^{A^{11}}\otimes M_{a_{21}|x_{21}}\otimes M_{a_{22}|x_{22}}\otimes I^{A^{31}}\otimes I^{A^{32}}\otimes I^{A^{33}}\otimes I^{A^{34}})\rho \right]\hfill \\ \hfill =& \sum _{a_{21}}\sum _{a_{22}}\sum _{{\lambda }_1\dots {\lambda }_6}p\left({\lambda }_1\right)p\left({\lambda }_2\right)\dots p\left({\lambda }_6\right)p\left(a_{21}\right|x_{21},{\lambda }_1,{\lambda }_3,{\lambda }_4)p\left(a_{22}\right|x_{22},{\lambda }_2,{\lambda }_5,{\lambda }_6)\hfill \\ \hfill & \times {\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}}\otimes {\sigma }_{{\lambda }_3}^{A^{31}}\otimes {\sigma }_{{\lambda }_4}^{A^{32}}\otimes {\sigma }_{{\lambda }_5}^{A^{33}}\otimes {\sigma }_{{\lambda }_6}^{A^{34}}\hfill \\ \hfill =& \sum _{{\lambda }_1\dots {\lambda }_6}p\left({\lambda }_1\right)p\left({\lambda }_2\right)\dots p\left({\lambda }_6\right){\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}}\otimes {\sigma }_{{\lambda }_3}^{A^{31}}\otimes {\sigma }_{{\lambda }_4}^{A^{32}}\otimes {\sigma }_{{\lambda }_5}^{A^{33}}\otimes {\sigma }_{{\lambda }_6}^{A^{34}}\hfill \end{array}$$

(2)

and

$$\begin{array}{cc}\hfill & \sum _{a_{21}}\sum _{a_{22}}{\mathrm{tr}}_{A^{21}{A}^{22}}[(I^{A^{11}}\otimes M_{a_{21}|x_{21}}\otimes M_{a_{22}|x_{22}}\otimes I^{A^{31}}\otimes I^{A^{32}}\otimes I^{A^{33}}\otimes I^{A^{34}})\rho ]\hfill \\ \hfill =& {\mathrm{tr}}_{A^{21}{A}^{22}}[(I^{A^{11}}\otimes \sum _{a_{21}}{M}_{a_{21}|x_{21}}\otimes \sum _{a_{22}}{M}_{a_{22}|x_{22}}\otimes I^{A^{31}}\otimes I^{A^{32}}\otimes I^{A^{33}}\otimes I^{A^{34}})\rho ]\hfill \\ \hfill =& {\mathrm{tr}}_{A^{21}{A}^{22}}\left(\rho \right)\hfill \\ \hfill =& {\mathrm{tr}}_{A^{21}}\left({\rho }_{A^{11}{A}^{21}}\right)\otimes {\mathrm{tr}}_{A^{22}}\left({\rho }_{A^{11}{A}^{22}}\right)\otimes {\mathrm{tr}}_{A^{21}}\left({\rho }_{A^{21}{A}^{31}}\right)\otimes {\mathrm{tr}}_{A^{21}}\left({\rho }_{A^{21}{A}^{32}}\right)\hfill \\ \hfill & \otimes {\mathrm{tr}}_{A^{22}}\left({\rho }_{A^{22}{A}^{33}}\right)\otimes {\mathrm{tr}}_{A^{22}}\left({\rho }_{A^{22}{A}^{34}}\right)\hfill \\ \hfill =& {\rho }^{11\left(1\right)}\otimes {\rho }^{11\left(2\right)}\otimes {\rho }^{31}\otimes {\rho }^{32}\otimes {\rho }^{33}\otimes {\rho }^{34}\hfill \end{array}$$

(3)

where we let ${\rho }^{11\left(1\right)}={\mathrm{tr}}_{A^{21}}\left({\rho }_{A^{11}{A}^{21}}\right)$, ${\rho }^{11\left(2\right)}={\mathrm{tr}}_{A^{22}}\left({\rho }_{A^{11}{A}^{22}}\right)$, ${\rho }^{31}={\mathrm{tr}}_{A^{21}}\left({\rho }_{A^{21}{A}^{31}}\right)$, ${\rho }^{32}={\mathrm{tr}}_{A^{21}}\left({\rho }_{A^{21}{A}^{32}}\right)$, ${\rho }^{33}={\mathrm{tr}}_{A^{22}}\left({\rho }_{A^{22}{A}^{33}}\right)$ and ${\rho }^{34}={\mathrm{tr}}_{A^{22}}\left({\rho }_{A^{22}{A}^{34}}\right)$. It follows from Equations (2) and (3) that we can obtain

$$\begin{array}{cc}\hfill & {\rho }^{11\left(1\right)}\otimes {\rho }^{11\left(2\right)}\otimes {\rho }^{31}\otimes {\rho }^{32}\otimes {\rho }^{33}\otimes {\rho }^{34}\hfill \\ \hfill =& \sum _{{\lambda }_1\dots {\lambda }_6}p\left({\lambda }_1\right)p\left({\lambda }_2\right)\dots p\left({\lambda }_6\right){\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}}\otimes {\sigma }_{{\lambda }_3}^{A^{31}}\otimes {\sigma }_{{\lambda }_4}^{A^{32}}\otimes {\sigma }_{{\lambda }_5}^{A^{33}}\otimes {\sigma }_{{\lambda }_6}^{A^{34}}.\hfill \end{array}$$

(4)

4. Inequality Criteria for the 3-Layer Tree-Shaped Network Steerability

4.1. Detecting 3-Layer Tree-Shaped Network Steering via Correlation Matrices

Let ${\left\{A_{i_0}^{11}\right\}}_{i_0=1}^{m_{A^{11}}},{\left\{A_{j_1}^{21}\right\}}_{j_1=1}^{m_{A^{21}}},{\left\{A_{j_2}^{22}\right\}}_{j_2=1}^{m_{A^{22}}},{\left\{A_{i_1}^{31}\right\}}_{i_1=1}^{m_{A^{31}}},{\left\{A_{i_2}^{32}\right\}}_{i_2=1}^{m_{A^{32}}},{\left\{A_{i_3}^{33}\right\}}_{i_3=1}^{m_{A^{33}}},{\left\{A_{i_4}^{34}\right\}}_{i_4=1}^{m_{A^{34}}}$ be a POVM assemblage of parties $A^{11},A^{21},\dots ,A^{34}$, where $A_{i_0}^{11}={\sum }_{a_{11}=1}^{o_{A^{11}}}{a}_{11}{M}_{a_{11}|i_0}$, and the rest are similar. For simplicity, we use i to index all possible values of $(i_0,i_1,i_2,i_3,i_4)$ and j to index all possible values of $(j_1,j_2)$. While we let $n=m_{A^{11}}\times m_{A^{31}}\times \dots \times m_{A^{34}}$ and $m=m_{A^{21}}\times m_{A^{22}}$. Then we define

$$\mathcal{N}={\left\{{\mathcal{N}}_i\right\}}_{i=1}^n={\{A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34}\}}_{i_0=1,i_1=1,\dots ,i_4=1}^{m_{A^{11}},m_{A^{31}},\dots ,m_{A^{34}}},$$

$$\mathcal{M}={\left\{{\mathcal{M}}_j\right\}}_{j=1}^m={\{A_{j_1}^{21}\otimes A_{j_2}^{22}\}}_{j_1=1,j_2=1}^{m_{A^{21}},m_{A^{22}}}.$$

Then for the states in the 3-layer tree-shaped network, the correlation matrix associated with these data is defined as

$$\mathcal{C}(\mathcal{N},\mathcal{M}|\rho )=\left(c_{ij}\right)$$

(5)

with the entries

$$c_{ij}=\mathrm{tr}\left[({\mathcal{N}}_i\otimes {\mathcal{M}}_j)(\rho -\tilde{\rho })\right],$$

(6)

where

$$\begin{array}{cc}\hfill \tilde{\rho }=& {\rho }^{11\left(1\right)}\otimes {\rho }^{11\left(2\right)}\otimes {\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\hfill \\ \hfill & \otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)}\otimes {\rho }^{31}\otimes {\rho }^{32}\otimes {\rho }^{33}\otimes {\rho }^{34}.\hfill \end{array}$$

Note that some of the states that make up $\tilde{\rho }$ have already been defined in Equation (3), and the remaining ones are ${\rho }^{21\left(1\right)}={\mathrm{tr}}_{A^{11}}\left({\rho }_{A^{11}{A}^{21}}\right)$, ${\rho }^{21\left(2\right)}={\mathrm{tr}}_{A^{31}}\left({\rho }_{A^{21}{A}^{31}}\right)$, ${\rho }^{21\left(3\right)}={\mathrm{tr}}_{A^{32}}\left({\rho }_{A^{21}{A}^{32}}\right)$, ${\rho }^{22\left(1\right)}={\mathrm{tr}}_{A^{11}}\left({\rho }_{A^{11}{A}^{22}}\right)$, ${\rho }^{22\left(2\right)}={\mathrm{tr}}_{A^{33}}\left({\rho }_{A^{22}{A}^{33}}\right)$, ${\rho }^{22\left(3\right)}={\mathrm{tr}}_{A^{34}}\left({\rho }_{A^{22}{A}^{34}}\right)$.

Now we can construct a useful network steering criterion in terms of the above correlation matrix. In the following, for any matrix C, we denote by ${\parallel C\parallel }_{\mathrm{tr}}$ and $\parallel C\parallel$ the trace norm (i.e., the sum of singular values) and the spectral norm (i.e., the maximum singular values), respectively.

Theorem 1.

Using the above notation, if ρ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable, then

$${\parallel \mathcal{C}(\mathcal{N},\mathcal{M}|\rho )\parallel }_{\mathrm{tr}}\le \sqrt{{\Lambda }_{A^{21}{A}^{22}}{\Lambda }_{A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}}},$$

(7)

where

$${\Lambda }_{A^{21}{A}^{22}}=\sum _{j=1}^{m}V({\mathcal{M}}_j,{\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)}),$$

(8)

$${\Lambda }_{A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}}={\max }_{\xi }\{\sum _{i=1}^n{\left[\mathrm{tr}\left({\mathcal{N}}_i\sigma \right)\right]}^2\}-\sum _{i=1}^n{\left[\mathrm{tr}\left({\mathcal{N}}_i{\mathrm{tr}}_{A^{21}{A}^{22}}\left(\rho \right)\right)\right]}^2$$

(9)

with the maximum being over all state sets $\xi =\{{\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}},{\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}},{\sigma }_{{\lambda }_3}^{A^{31}},{\sigma }_{{\lambda }_4}^{A^{32}}{\sigma }_{{\lambda }_5}^{A^{33}},{\sigma }_{{\lambda }_6}^{A^{34}}\}$ on trusted parties, and $\sigma ={\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}}\otimes {\sigma }_{{\lambda }_3}^{A^{31}}\otimes {\sigma }_{{\lambda }_4}^{A^{32}}\otimes {\sigma }_{{\lambda }_5}^{A^{33}}\otimes {\sigma }_{{\lambda }_6}^{A^{34}}$. Here V denotes the variance, specifically denoted as

$$\begin{array}{cc}\hfill & V({\mathcal{M}}_j,{\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})\hfill \\ \hfill =& \mathrm{tr}\left[{\left({\mathcal{M}}_j\right)}^2({\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})\right]\hfill \\ \hfill & -{\left[\mathrm{tr}\left({\mathcal{M}}_j({\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})\right)\right]}^2,\hfill \end{array}$$

Proof. 

If $\rho$ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable, then there must be a 3-layer tree-shaped NLHS model (1) of $\rho$, then by using Equation (4), we can obtain

$$\begin{array}{cc}\hfill & \mathrm{tr}\left[({\mathcal{N}}_i\otimes {\mathcal{M}}_j)\rho \right]\hfill \\ \hfill =& \sum _{a_{11}}\sum _{a_{21}}\dots \sum _{a_{34}}{a}_{11}{a}_{21}\dots a_{34}p(a_{11},a_{21},\dots ,a_{34}|A_{i_0}^{11},A_{j_1}^{21},A_{j_2}^{22},A_{i_1}^{31},A_{i_2}^{32},A_{i_3}^{33},A_{i_4}^{34},\rho )\hfill \\ \hfill =& \sum _{a_{11}}\sum _{a_{21}}\dots \sum _{a_{34}}{a}_{11}{a}_{21}\dots a_{34}\sum _{{\lambda }_1\dots {\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)p_Q\left(a_{11}\right|x_{11},{\lambda }_1,{\lambda }_2)\hfill \\ \hfill & p\left(a_{21}\right|x_{21},{\lambda }_1,{\lambda }_3,{\lambda }_4)p\left(a_{22}\right|x_{22},{\lambda }_2,{\lambda }_5,{\lambda }_6)p_Q\left(a_{31}\right|x_{31},{\lambda }_3)p_Q\left(a_{32}\right|x_{32},{\lambda }_4)\hfill \\ \hfill & p_Q\left(a_{33}\right|x_{33},{\lambda }_5)p_Q\left(a_{34}\right|x_{34},{\lambda }_6)\hfill \\ \hfill =& \sum _{{\lambda }_1\dots {\lambda }_6}(p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right))(\sum _{a_{11}}{a}_{11}{p}_Q\left(a_{11}\right|x_{11},{\lambda }_1,{\lambda }_2))(\sum _{a_{21}}{a}_{21}p\left(a_{21}\right|x_{21},{\lambda }_1,{\lambda }_3,{\lambda }_4))\hfill \\ \hfill & (\sum _{a_{22}}{a}_{22}p\left(a_{22}\right|x_{22},{\lambda }_2,{\lambda }_5,{\lambda }_6))(\sum _{a_{31}}{a}_{31}{p}_Q\left(a_{31}\right|x_{31},{\lambda }_3))(\sum _{a_{32}}{a}_{32}{p}_Q\left(a_{32}\right|x_{32},{\lambda }_4))\hfill \\ \hfill & (\sum _{a_{33}}{a}_{33}{p}_Q\left(a_{33}\right|x_{33},{\lambda }_5))(\sum _{a_{34}}{a}_{34}{p}_Q\left(a_{34}\right|x_{34},{\lambda }_6))\hfill \\ \hfill =& \sum _{{\lambda }_1\dots {\lambda }_6}(\prod _{t=1}^{6}p\left({\lambda }_t\right))({\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}{\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6})\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})\sigma \right]\right\}\hfill \end{array}$$

(10)

Notice that

$$\begin{array}{cc}\hfill c_{ij}=& \mathrm{tr}\left[({\mathcal{N}}_i\otimes {\mathcal{M}}_j)(\rho -\tilde{\rho })\right]\hfill \\ \hfill =& \sum _{{\lambda }_1,\dots ,{\lambda }_6}(\prod _{t=1}^{6}p\left({\lambda }_t\right))({\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}{\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6})\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})\sigma \right]\right\}\hfill \\ \hfill & -\mathrm{tr}\left[A_{j_1}^{21}({\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)})\right]\mathrm{tr}\left[A_{j_2}^{22}({\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})\right]\hfill \\ \hfill & \times \mathrm{tr}\left[A_{i_0}^{11}({\rho }^{11\left(1\right)}\otimes {\rho }^{11\left(2\right)})\right]\mathrm{tr}\left(A_{i_1}^{31}{\rho }^{31}\right)\mathrm{tr}\left(A_{i_2}^{32}{\rho }^{32}\right)\mathrm{tr}\left(A_{i_3}^{33}{\rho }^{33}\right)\mathrm{tr}\left(A_{i_4}^{34}{\rho }^{34}\right)\hfill \\ \hfill =& \sum _{{\lambda }_1,\dots ,{\lambda }_6}(\prod _{t=1}^{6}p\left({\lambda }_t\right))({\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}{\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6})\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})\sigma \right]\right\}\hfill \\ \hfill & -(\sum _{{\lambda }_1,{\lambda }_3,{\lambda }_4}p\left({\lambda }_1\right)p\left({\lambda }_3\right)p\left({\lambda }_4\right){\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4})(\sum _{{\lambda }_2,{\lambda }_5,{\lambda }_6}p\left({\lambda }_2\right)p\left({\lambda }_5\right)p\left({\lambda }_6\right){\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6})\hfill \\ \hfill & \times (\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})\sigma \right]\right\})\hfill \\ \hfill =& \sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)X_{{\lambda }_1,\dots ,{\lambda }_6}^j{Y}_{{\lambda }_1,\dots ,{\lambda }_6}^i-(\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)X_{{\lambda }_1,\dots ,{\lambda }_6}^j)\hfill \\ \hfill & \times (\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)Y_{{\lambda }_1,\dots ,{\lambda }_6}^i)\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\sum _{{\lambda }_1,\dots ,{\lambda }_6}\sum _{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}(\prod _{t=1}^{6}p\left({\lambda }_t\right))(\prod _{t=1}^{6}p\left({\lambda }_t^{\prime }\right))(X_{{\lambda }_1,\dots ,{\lambda }_6}^j-X_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^j)(Y_{{\lambda }_1,\dots ,{\lambda }_6}^i-Y_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^i)\hfill \end{array}$$

(11)

with ${\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}{\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6}=X_{{\lambda }_1,\dots ,{\lambda }_6}^j$ and $\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})\sigma \right]=Y_{{\lambda }_1,\dots ,{\lambda }_6}^i$. Using the results above, we can get

$$\mathcal{C}(\mathcal{N},\mathcal{M}|\rho )={\displaystyle \frac{1}{2}}\sum _{{\lambda }_1,\dots ,{\lambda }_6}\sum _{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}(\prod _{t=1}^{6}p\left({\lambda }_t\right))(\prod _{t=1}^{6}p\left({\lambda }_t^{\prime }\right)){\eta }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}{\gamma }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^T$$

(12)

with

$${\eta }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}=\left(\begin{array}{c}{Y}_{{\lambda }_1,\dots ,{\lambda }_6}^1-Y_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^1\\ Y_{{\lambda }_1,\dots ,{\lambda }_6}^2-Y_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^2\\ ⋮\\ Y_{{\lambda }_1,\dots ,{\lambda }_6}^n-Y_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^n\end{array}\right)$$

and

$${\gamma }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}=\left(\begin{array}{c}{X}_{{\lambda }_1,\dots ,{\lambda }_6}^1-X_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^1\\ X_{{\lambda }_1,\dots ,{\lambda }_6}^2-X_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^2\\ ⋮\\ X_{{\lambda }_1,\dots ,{\lambda }_6}^m-X_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^m\end{array}\right).$$

Thus,

$$\begin{array}{cc}\hfill & {\parallel \mathcal{C}(\mathcal{N},\mathcal{M}|\rho )\parallel }_{\mathrm{tr}}\hfill \\ \hfill \le & {\displaystyle \frac{1}{2}}\sum _{{\lambda }_1,\dots ,{\lambda }_6}\sum _{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)p\left({\lambda }_1^{\prime }\right)\dots p\left({\lambda }_6^{\prime }\right){\parallel {\eta }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}{\gamma }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^T\parallel }_{\mathrm{tr}}\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\sum _{{\lambda }_1,\dots ,{\lambda }_6}\sum _{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)p\left({\lambda }_1^{\prime }\right)\dots p\left({\lambda }_6^{\prime }\right)\parallel {\gamma }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}\parallel \parallel {\eta }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}\parallel \hfill \\ \hfill \le & {\displaystyle \frac{1}{2}}\sqrt{\sum _{{\lambda }_1,\dots ,{\lambda }_6}\sum _{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)p\left({\lambda }_1^{\prime }\right)\dots p\left({\lambda }_6^{\prime }\right){\parallel {\gamma }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}\parallel }^2}\hfill \\ \hfill & \times \sqrt{\sum _{{\lambda }_1,\dots ,{\lambda }_6}\sum _{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)p\left({\lambda }_1^{\prime }\right)\dots p\left({\lambda }_6^{\prime }\right){\parallel {\eta }_{{\lambda }_1,\dots ,{\lambda }_6,{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}\parallel }^2}\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\sqrt{\sum _{{\lambda }_1,\dots ,{\lambda }_6}\sum _{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)p\left({\lambda }_1^{\prime }\right)\dots p\left({\lambda }_6^{\prime }\right)\sum _{j=1}^m{(X_{{\lambda }_1,\dots ,{\lambda }_6}^j-X_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^j)}^2}\hfill \\ \hfill & \times \sqrt{\sum _{{\lambda }_1,\dots ,{\lambda }_6}\sum _{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)p\left({\lambda }_1^{\prime }\right)\dots p\left({\lambda }_6^{\prime }\right)\sum _{i=1}^m{(Y_{{\lambda }_1,\dots ,{\lambda }_6}^i-Y_{{\lambda }_1^{\prime },\dots ,{\lambda }_6^{\prime }}^i)}^2}\hfill \\ \hfill =& \sqrt{\sum _{j=1}^m[\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right){\left(X_{{\lambda }_1,\dots ,{\lambda }_6}^j\right)}^2-{(\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)X_{{\lambda }_1,\dots ,{\lambda }_6}^j)}^2]}\hfill \\ \hfill & \times \sqrt{\sum _{i=1}^n[\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right){\left(Y_{{\lambda }_1,\dots ,{\lambda }_6}^i\right)}^2-{(\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)Y_{{\lambda }_1,\dots ,{\lambda }_6}^i)}^2]}\hfill \end{array}$$

(13)

with

$$\begin{array}{cc}\hfill & \sum _{j=1}^m[\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right){(X_{{\lambda }_1,\dots ,{\lambda }_6}^j)}^2-{(\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)X_{{\lambda }_1,\dots ,{\lambda }_6}^j)}^2]\hfill \\ \hfill =& \sum _{j=1}^m[\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right){({\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}{\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6})}^2-(\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)\hfill \\ \hfill & \times {\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}{\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6}{)}^2]\hfill \\ \hfill \le & \sum _{j=1}^m[\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)({\langle {(A_{j_1}^{21})}^2\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}{\langle {(A_{j_2}^{22})}^2\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6})-(\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)\hfill \\ \hfill & \times {\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}{\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6}{)}^2]\hfill \\ \hfill =& \sum _{j=1}^m[(\sum _{{\lambda }_1,{\lambda }_3,{\lambda }_4}p\left({\lambda }_1\right)p\left({\lambda }_3\right)p\left({\lambda }_4\right){\langle {(A_{j_1}^{21})}^2\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4})(\sum _{{\lambda }_1,{\lambda }_3,{\lambda }_4}p\left({\lambda }_2\right)p\left({\lambda }_5\right)p\left({\lambda }_6\right){\langle {(A_{j_2}^{22})}^2\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6})]\hfill \\ \hfill & -\sum _{j=1}^m{[(\sum _{{\lambda }_1,{\lambda }_3,{\lambda }_4}p\left({\lambda }_1\right)p\left({\lambda }_3\right)p\left({\lambda }_4\right){\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4})(\sum _{{\lambda }_1,{\lambda }_3,{\lambda }_4}p\left({\lambda }_2\right)p\left({\lambda }_5\right)p\left({\lambda }_6\right){\langle A_{j_2}^{22}\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6})]}^2\hfill \\ \hfill =& \sum _{j=1}^m\{\mathrm{tr}({\left(A_{j_1}^{21}\right)}^2{\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)})\mathrm{tr}({\left(A_{j_2}^{22}\right)}^2{\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})-\left[\mathrm{tr}\right(A_{j_1}^{21}{\rho }^{21\left(1\right)}\hfill \\ \hfill & \otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)})\times \mathrm{tr}(A_{j_2}^{22}{\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)}){]}^2\}\hfill \\ \hfill =& {\Lambda }_{A^{21}{A}^{22}}\hfill \end{array}$$

(14)

and

$$\begin{array}{cc}\hfill & \sum _{i=1}^n[\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right){(Y_{{\lambda }_1,\dots ,{\lambda }_6}^i)}^2-{(\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)Y_{{\lambda }_1,\dots ,{\lambda }_6}^i)}^2]\hfill \\ \hfill =& \sum _{i=1}^n\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right){\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})\sigma \right]\right\}}^2\hfill \\ \hfill & -\sum _{i=1}^n{\{\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right)\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})\sigma \right]\}}^2\hfill \\ \hfill =& \sum _{i=1}^n\sum _{{\lambda }_1,\dots ,{\lambda }_6}p\left({\lambda }_1\right)\dots p\left({\lambda }_6\right){\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})\sigma \right]\right\}}^2\hfill \\ \hfill & -\sum _{i=1}^n{\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34}){\mathrm{tr}}_{A^{21}{A}^{22}}\left(\rho \right)\right]\right\}}^2\hfill \\ \hfill \le & {\Lambda }_{A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}}.\hfill \end{array}$$

(15)

Here we use the relations ${\sum }_{{\lambda }_s}p\left(s\right)=1$ for $s=1,2,\dots ,6$,

$${({\langle A_{j_1}^{21}\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4})}^2\le {\langle {(A_{j_1}^{21})}^2\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4},$$

$$\mathrm{tr}({(A_{j_1}^{21})}^2{\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)})=\sum _{{\lambda }_1,{\lambda }_3,{\lambda }_4}p\left({\lambda }_1\right)p\left({\lambda }_3\right)p\left({\lambda }_4\right){\langle {(A_{j_1}^{21})}^2\rangle }_{{\lambda }_1,{\lambda }_3,{\lambda }_4}$$

and

$$\mathrm{tr}({(A_{j_2}^{22})}^2{\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})=\sum _{{\lambda }_2,{\lambda }_5,{\lambda }_6}p\left({\lambda }_2\right)p\left({\lambda }_5\right)p\left({\lambda }_6\right){\langle {(A_{j_2}^{22})}^2\rangle }_{{\lambda }_2,{\lambda }_5,{\lambda }_6}$$

Combining inequalities (13), (14), and (15), the proof can be completed. □

Next, we consider the special case, i.e., adding constants as coefficients and obtain the following corollary.

Corollary 1.

If ρ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable, then

$$\sum _{j=1}^m\left|\mathrm{tr}\left[(g_j{\mathcal{N}}_j\otimes {\mathcal{M}}_j)\right]\right|\le \sqrt{{\Lambda }_{A^{21}{A}^{22}}\left(g\right){\Lambda }_{A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}}},$$

(16)

where

$${\Lambda }_{A^{21}{A}^{22}}=\sum _{j=1}^m{g}_j^{2}V({\mathcal{M}}_j,{\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})$$

(17)

for any real number $g_i$ and ${\Lambda }_{A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}}$ is defined as in Equation (9).

Here the main use of ${\sum }_{i=1}^m|c_{ii}{|\le \parallel C\parallel }_{\mathrm{tr}}$ for any matrix $C=\left(c_{ij}\right)\in {\mathbb{C}}^m\otimes {\mathbb{C}}^m$ and $g_i$ as flexible coefficients to form a more efficient inequality criterion.

4.2. Detecting via Some Classes of Measurements

In this section, we specify the observables in the 3-layer tree-shaped network steering criteria (Theorem 1) to three important classes of measurements: LOOs, MUMs, and GSICs.

The set of local operations $\{Q_i:i=1,2,\dots ,d^2\}$ constitutes the orthogonal bases of the Hermitian operator space on ${\mathbb{C}}^d$. Specifically, these bases span the entire operator space and satisfy the orthogonality condition $\mathrm{tr}\left(Q_i{Q}_j\right)={\delta }_{ij}$. Moreover, for any quantum state $\rho$ on ${\mathbb{C}}^d$, the following relations hold: ${\sum }_i\mathrm{tr}\left(Q_i^2\rho \right)=d$ and ${\sum }_i{\left(\mathrm{tr}{Q}_i\rho \right)}^2=\mathrm{tr}\left({\rho }^2\right)$. Furthermore, an important property of LOOs is that if $\{O_i:i=1,2,\dots ,d_1^2\}$ and $\{T_j:j=1,2,\dots ,d_2^2\}$ are LOOs on ${\mathbb{C}}^{d_1}$ and ${\mathbb{C}}^{d_2}$, respectively, then the set ${\{O_i\otimes T_j\}}_{i=1,j=1}^{d_1^2,d_2^2}$ also forms a set of LOOs and the number of orthogonal bases is $d_1^2{d}_2^2$.

Proposition 1.

Suppose that ${\left\{A_{i_0}^{11}\right\}}_{i_0=1}^{d_1^2},{\left\{A_{j_1}^{21}\right\}}_{j_1=1}^{d_2^2},{\left\{A_{j_2}^{22}\right\}}_{j_2=1}^{d_3^2},{\left\{A_{i_1}^{31}\right\}}_{i_1=1}^{d_4^2},{\left\{A_{i_2}^{32}\right\}}_{i_2=1}^{d_5^2},{\left\{A_{i_3}^{33}\right\}}_{i_3=1}^{d_6^2}$ and ${\left\{A_{i_4}^{34}\right\}}_{i_4=1}^{d_7^2}$ are any seven sets of LOOs on ${\mathbb{C}}^{d_1}$, ${\mathbb{C}}^{d_2}$, ${\mathbb{C}}^{d_3}$, ${\mathbb{C}}^{d_4}$, ${\mathbb{C}}^{d_5}$, ${\mathbb{C}}^{d_6}$ and ${\mathbb{C}}^{d_7}$, respectively. With this notation, if the state ρ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable, then

$$\begin{array}{c}\hfill {\parallel \mathcal{C}(\mathcal{N},\mathcal{M}|\rho )\parallel }_{\mathrm{tr}}\le \sqrt{(d_2{d}_3-\mathrm{tr}\left[{({\rho }^{21}\otimes {\rho }^{22})}^2\right])(1-\mathrm{tr}\left[{({\rho }^{11}\otimes {\rho }^{31}\otimes {\rho }^{32}\otimes {\rho }^{33}\otimes {\rho }^{34})}^2\right])}.\end{array}$$

(18)

Proof. 

By using Equations (8) and (9) in Theorem 1 and the properties of LOOs, we can obtain

$$\begin{array}{cc}\hfill & {\Lambda }_{A^{21}{A}^{22}}\hfill \\ \hfill =& \sum _{j=1}^{d_2^2{d}_3^2}V({\mathcal{M}}_j,{\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})\hfill \\ \hfill =& \sum _{j=1}^{d_2^2{d}_3^2}\mathrm{tr}\left[{\left({\mathcal{M}}_j\right)}^2({\rho }^{21}\otimes {\rho }^{22})\right]-\sum _{j=1}^{d_2^2{d}_3^2}{\left\{\mathrm{tr}\left[{\mathcal{M}}_j({\rho }^{21}\otimes {\rho }^{22})\right]\right\}}^2\hfill \\ \hfill =& d_2{d}_3-\mathrm{tr}\left[{({\rho }^{21}\otimes {\rho }^{22})}^2\right],\hfill \end{array}$$

(19)

and

$$\begin{array}{cc}\hfill & {\Lambda }_{A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}}\hfill \\ \hfill =& {\max }_{\xi }\{\sum _{i=1}^{d_1^2{d}_4^2{d}_5^2{d}_6^2{d}_7^2}{\left[\mathrm{tr}\left({\mathcal{N}}_i\sigma \right)\right]}^2\}-\sum _{i=1}^{d_1^2{d}_4^2{d}_5^2{d}_6^2{d}_7^2}{\left[\mathrm{tr}\left({\mathcal{N}}_i{\mathrm{tr}}_{A^{21}{A}^{22}}\left(\rho \right)\right)\right]}^2\hfill \\ \hfill =& {\max }_{\xi }\left\{\mathrm{tr}\left[{\sigma }^2\right]\right\}-\mathrm{tr}\left[{\left({\mathrm{tr}}_{A^{21}{A}^{22}}\left(\rho \right)\right)}^2\right]\hfill \\ \hfill =& 1-\mathrm{tr}\left[{({\rho }^{11}\otimes {\rho }^{31}\otimes {\rho }^{32}\otimes {\rho }^{33}\otimes {\rho }^{34})}^2\right].\hfill \end{array}$$

(20)

Combining Equations (19) and (20), we have completed the proof. □

Next, we consider the choice of MUMs to construct the steering inequality criterion for the network. A set $\mathcal{P}=\{{\left\{P_i^{\left(\mu \right)}\right\}}_{i=1}^d:\mu =1,2,\dots ,m\}$ of measurements (POVM) with ${\left\{P_i^{\left(\mu \right)}\right\}}_{i=1}^d$ on ${\mathbb{C}}^d$ is called mutually unbiased if $\mathrm{tr}\left(P_i^{\left(\mu \right)}\right)=1$ and $\mathrm{tr}\left(P_i^{\left(\mu \right)}{P}_{i^{\prime }}^{\left({\mu }^{\prime }\right)}\right)={\delta }_{i{i}^{\prime }}{\delta }_{\mu {\mu }^{\prime }}\kappa +(1-{\delta }_{i{i}^{\prime }}){\delta }_{\mu {\mu }^{\prime }}{\displaystyle \frac{1-\kappa }{d-1}}+(1-{\delta }_{\mu {\mu }^{\prime }}){\displaystyle \frac{1}{d}}$, where ${\displaystyle \frac{1}{d}}<\kappa \le 1$. $\mathcal{P}$ is considered to be a complete set of MUMs on ${\mathbb{C}}^d$ when $m=d+1$. In the seminal paper Ref. [38], a general construction of $d+1$ MUMs (a complete set of MUMs) in arbitrary dimension d has been presented.

When all parties in this tree-shaped network implement complete MUMs, that means $A^{11}$ implements MUMs ${\{A_{i_0}^{11}=P_i^{\left({\mu }_1\right)},i_0=({\mu }_1-1)d_1+i\}}_{i_0}^{d_1(d_1+1)}$ with the parameter ${\kappa }_1$. The remaining parties $A^{21}$, $A^{22}$, $A^{31}$, $A^{32}$, $A^{33}$, and $A^{34}$ also implement complete MUMs, with corresponding dimensions of $d_2$, $d_3$, $d_4$, $d_5$, $d_6$, and $d_7$, and parameters ${\kappa }_2$, ${\kappa }_3$, ${\kappa }_4$, ${\kappa }_5$, ${\kappa }_6$, and ${\kappa }_7$, respectively. We then obtain the following conclusions.

Proposition 2.

With the above notation, if the state ρ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable, then

$$\begin{array}{c}\hfill {\parallel \mathcal{C}(\mathcal{N},\mathcal{M}|\rho )\parallel }_{\mathrm{tr}}\le \sqrt{\{\left[(d_2+1){\kappa }_2\right]\left[(d_3+1){\kappa }_3\right]-R_1\}[(1+{\kappa }_1)\prod _{p=4}^7(1+{\kappa }_p)-R_2]},\end{array}$$

(21)

where

$$R_1=[1+{\displaystyle \frac{1-{\kappa }_2+({\kappa }_2{d}_2-1)\mathrm{tr}\left[{\left({\rho }^{21}\right)}^2\right]}{d_2-1}}][1+{\displaystyle \frac{1-{\kappa }_3+({\kappa }_3{d}_3-1)\mathrm{tr}\left[{\left({\rho }^{22}\right)}^2\right]}{d_3-1}}]$$

and

$$R_2=(1+{\displaystyle \frac{1-{\kappa }_1+({\kappa }_1{d}_1-1)\mathrm{tr}\left[{\left({\rho }^{11}\right)}^2\right]}{d_1-1}})\prod _{p=4}^7(1+{\displaystyle \frac{1-{\kappa }_p({\kappa }_p{d}_p-1)\mathrm{tr}\left[{\left({\rho }^{3(p-3)}\right)}^2\right]}{d_p-1}}).$$

Proof. 

By using Equations (8) and (9) in Theorem 1 and the properties of MUMs, we can obtain

$$\begin{array}{cc}\hfill & {\Lambda }_{A^{21}{A}^{22}}\hfill \\ \hfill =& \sum _{j=1}^{d_2(d_2+1)d_3(d_3+1)}V({\mathcal{M}}_j,{\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(3\right)})\hfill \\ \hfill =& \sum _{j=1}^{d_2(d_2+1)d_3(d_3+1)}\mathrm{tr}\left[{\left({\mathcal{M}}_j\right)}^2({\rho }^{21}\otimes {\rho }^{22})\right]-\sum _{j=1}^{d_2(d_2+1)d_3(d_3+1)}{\left\{\mathrm{tr}\left[{\mathcal{M}}_j({\rho }^{21}\otimes {\rho }^{22})\right]\right\}}^2\hfill \\ \hfill =& \sum _{j_1=1}^{d_2(d_2+1)}\sum _{j_2=1}^{d_3(d_3+1)}\mathrm{tr}\left[{(A_{j_1}^{21}\otimes A_{j_2}^{22})}^2({\rho }^{21}\otimes {\rho }^{22})\right]-\sum _{j_1=1}^{d_2(d_2+1)}\sum _{j_2=1}^{d_3(d_3+1)}{\left\{\mathrm{tr}\left[(A_{j_1}^{21}\otimes A_{j_2}^{22})({\rho }^{21}\otimes {\rho }^{22})\right]\right\}}^2\hfill \\ \hfill =& \sum _{j_1=1}^{d_2(d_2+1)}\mathrm{tr}\left[{\left(A_{j_1}^{21}\right)}^2{\rho }^{21}\right]\sum _{j_2=1}^{d_3(d_3+1)}\mathrm{tr}\left[{\left(A_{j_2}^{22}\right)}^2{\rho }^{22}\right]-\sum _{j_1=1}^{d_2(d_2+1)}{\left[\mathrm{tr}\left(A_{j_1}^{21}{\rho }^{21}\right)\right]}^2\sum _{j_2=1}^{d_3(d_3+1)}{\left[\mathrm{tr}\left(A_{j_2}^{22}{\rho }^{22}\right)\right]}^2\hfill \\ \hfill =& \left[(d_2+1){\kappa }_2\right]\left[(d_3+1){\kappa }_3\right]-[1+{\displaystyle \frac{1-{\kappa }_2+({\kappa }_2{d}_2-1)\mathrm{tr}\left[{\left({\rho }^{21}\right)}^2\right]}{d_2-1}}]\hfill \\ \hfill & \times [1+{\displaystyle \frac{1-{\kappa }_3+({\kappa }_3{d}_3-1)\mathrm{tr}\left[{\left({\rho }^{22}\right)}^2\right]}{d_3-1}}]\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill & {\Lambda }_{A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}}\hfill \\ \hfill =& {\max }_{\xi }\{\sum _{i=1}^n{\left[\mathrm{tr}\left({\mathcal{N}}_i\sigma \right)\right]}^2\}-\sum _{i=1}^n{\left[\mathrm{tr}\left({\mathcal{N}}_i{\mathrm{tr}}_{A^{21}{A}^{22}}\left(\rho \right)\right)\right]}^2\hfill \\ \hfill =& {\max }_{\xi }\{\sum _{i=1}^n{\left[\mathrm{tr}(A_{i_0}^{11}{\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}})\right]}^2{\left[\mathrm{tr}\left(A_{i_1}^{31}{\sigma }_{{\lambda }_3}^{A^{31}}\right)\right]}^2{\left[\mathrm{tr}\left(A_{i_2}^{32}{\sigma }_{{\lambda }_4}^{A^{32}}\right)\right]}^2{\left[\mathrm{tr}\left(A_{i_3}^{33}{\sigma }_{{\lambda }_5}^{A^{33}}\right)\right]}^2{\left[\mathrm{tr}\left(A_{i_4}^{34}{\sigma }_{{\lambda }_6}^{A^{34}}\right)\right]}^2\}\hfill \\ \hfill & -\sum _{i=1}^n{\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})({\rho }^{11}\otimes {\rho }^{31}\otimes {\rho }^{32}\otimes {\rho }^{33}\otimes {\rho }^{34})\right]\right\}}^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill =& {\max }_{\xi }\{\sum _{i_0}^{d_1(d_1+1)}{\left[\mathrm{tr}(A_{i_0}^{11}{\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}})\right]}^2\sum _{i_1}^{d_4(d_4+1)}{\left[\mathrm{tr}\left(A_{i_1}^{31}{\sigma }_{{\lambda }_3}^{A^{31}}\right)\right]}^2\sum _{i_2}^{d_5(d_5+1)}{\left[\mathrm{tr}\left(A_{i_2}^{32}{\sigma }_{{\lambda }_4}^{A^{32}}\right)\right]}^2\hfill \\ \hfill & \sum _{i_3}^{d_6(d_6+1)}{\left[\mathrm{tr}\left(A_{i_3}^{33}{\sigma }_{{\lambda }_5}^{A^{33}}\right)\right]}^2\sum _{i_4}^{d_7(d_7+1)}{\left[\mathrm{tr}\left(A_{i_4}^{34}{\sigma }_{{\lambda }_6}^{A^{34}}\right)\right]}^2\}-\sum _{i_0}^{d_1(d_1+1)}{\left[\mathrm{tr}\left(A_{i_0}^{11}{\rho }^{11}\right)\right]}^2\sum _{i_1}^{d_4(d_4+1)}{\left[\mathrm{tr}\left(A_{i_1}^{31}{\rho }^{31}\right)\right]}^2\hfill \\ \hfill & \sum _{i_2}^{d_5(d_5+1)}{\left[\mathrm{tr}\left(A_{i_2}^{32}{\rho }^{32}\right)\right]}^2\sum _{i_3}^{d_6(d_6+1)}{\left[\mathrm{tr}\left(A_{i_3}^{33}{\rho }^{33}\right)\right]}^2\sum _{i_4}^{d_7(d_7+1)}{\left[\mathrm{tr}\left(A_{i_4}^{34}{\rho }^{34}\right)\right]}^2\hfill \\ \hfill =& (1+{\kappa }_1)(1+{\kappa }_4)(1+{\kappa }_5)(1+{\kappa }_6)(1+{\kappa }_7)-(1+{\displaystyle \frac{1-{\kappa }_1+({\kappa }_1{d}_1-1)\mathrm{tr}\left[{\left({\rho }^{11}\right)}^2\right]}{d_1-1}})\hfill \\ \hfill & \times \prod _{p=4}^7(1+{\displaystyle \frac{1-{\kappa }_p({\kappa }_p{d}_p-1)\mathrm{tr}\left[{\left({\rho }^{3(p-3)}\right)}^2\right]}{d_p-1}}),\hfill \end{array}$$

(23)

where $n=d_1(d_1+1)d_4(d_4+1)d_5(d_5+1)d_6(d_6+1)d_7(d_7+1)$. Therefore, when the measurements on each system are taken as MUMs, combining Equations (22) and (23), we can obtain the conclusion in Proposition 2. □

In the following, we consider the case that each party performs measurement is a GSICs. Concretely, a POVM $\{M_i:i=1,2,\dots d^2\}$ with $d^2$ operators on ${\mathbb{C}}^d$ is said to be GSICs if $\mathrm{tr}\left(M_i^2\right)=\eta$ and $\mathrm{tr}\left(M_i{M}_j\right)={\displaystyle \frac{1-d\eta }{d(d^2-1)}}$, $i\ne j$, where the parameter $\eta$ satisfies ${\displaystyle \frac{1}{d^3}}<\eta \le {\displaystyle \frac{1}{d^2}}$.

Proposition 3.

Suppose that ${\left\{A_{i_0}^{11}\right\}}_{i_0=1}^{d_1^2},{\left\{A_{j_1}^{21}\right\}}_{j_1=1}^{d_2^2},{\left\{A_{j_2}^{22}\right\}}_{j_2=1}^{d_3^2},{\left\{A_{i_1}^{31}\right\}}_{i_1=1}^{d_4^2},{\left\{A_{i_2}^{32}\right\}}_{i_2=1}^{d_5^2},{\left\{A_{i_3}^{33}\right\}}_{i_3=1}^{d_6^2}$ and ${\left\{A_{i_4}^{34}\right\}}_{i_4=1}^{d_7^2}$ are any seven sets of GSICs on ${\mathbb{C}}^{d_1}$, ${\mathbb{C}}^{d_2}$, ${\mathbb{C}}^{d_3}$, ${\mathbb{C}}^{d_4}$, ${\mathbb{C}}^{d_5}$, ${\mathbb{C}}^{d_6}$, and ${\mathbb{C}}^{d_7}$, respectively, with their parameters being ${\eta }_1$, ${\eta }_2$, ${\eta }_3$, ${\eta }_4$, ${\eta }_5$, ${\eta }_6$, and ${\eta }_7$, respectively. If the state ρ is $A^{21}{A}^{22}\to A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}$ unsteerable, then

$$\begin{array}{c}\hfill {\parallel \mathcal{C}(\mathcal{N},\mathcal{M}|\rho )\parallel }_{\mathrm{tr}}\le \sqrt{(d_2{\eta }_2{d}_3{\eta }_3-E_1)({\displaystyle \frac{{\eta }_1{d}_1^2+1}{d_1(d_1+1)}}\prod _{q=4}^7{\displaystyle \frac{{\eta }_q{d}_q^2+1}{d_q(d_q+1)}}-E_2)},\end{array}$$

(24)

where

$$E_1=[{\displaystyle \frac{({\eta }_2{d}_2^3-1)\mathrm{tr}\left[{\left({\rho }^{21}\right)}^2\right]+d_2(1-{\eta }_2{d}_2)}{d_2(d_2^2-1)}}][{\displaystyle \frac{({\eta }_3{d}_3^3-1)\mathrm{tr}\left[{\left({\rho }^{22}\right)}^2\right]+d_3(1-{\eta }_3{d}_3)}{d_3(d_3^2-1)}}]$$

and

$$E_2={\displaystyle \frac{({\eta }_1{d}_1^3-1)\mathrm{tr}\left[{\left({\rho }^{11}\right)}^2\right]+d_1(1-{\eta }_1{d}_1)}{d_1(d_1^2-1)}}\prod _{q=4}^7{\displaystyle \frac{({\eta }_q{d}_q^3-1)\mathrm{tr}\left[{\left({\rho }^{3(q-3)}\right)}^2\right]+d_q(1-{\eta }_q{d}_q)}{d_q(d_q^2-1)}}.$$

Proof. 

The proof of Proposition 3 is almost the same as the proof of the Proposition 2. The main use of the property of GSICs.

$$\begin{array}{cc}\hfill & {\Lambda }_{A^{21}{A}^{22}}\hfill \\ \hfill =& \sum _{j=1}^{d_2^2{d}_3^2}V({\mathcal{M}}_j,{\rho }^{21\left(1\right)}\otimes {\rho }^{21\left(2\right)}\otimes {\rho }^{21\left(3\right)}\otimes {\rho }^{22\left(1\right)}\otimes {\rho }^{22\left(2\right)}\otimes {\rho }^{22\left(1\right)})\hfill \\ \hfill =& \sum _{j=1}^{d_2^2{d}_3^2}\mathrm{tr}\left[{\left({\mathcal{M}}_j\right)}^2({\rho }^{21}\otimes {\rho }^{22})\right]-\sum _{j=1}^{d_2^2{d}_3^2}{\left\{\mathrm{tr}\left[{\mathcal{M}}_j({\rho }^{21}\otimes {\rho }^{22})\right]\right\}}^2\hfill \\ \hfill =& \sum _{j_1=1}^{d_2^2}\sum _{j_2=1}^{d_3^2}\mathrm{tr}\left[{(A_{j_1}^{21}\otimes A_{j_2}^{22})}^2({\rho }^{21}\otimes {\rho }^{22})\right]-\sum _{j_1=1}^{d_2^2}\sum _{j_2=1}^{d_3^2}{\left\{\mathrm{tr}\left[(A_{j_1}^{21}\otimes A_{j_2}^{22})({\rho }^{21}\otimes {\rho }^{22})\right]\right\}}^2\hfill \\ \hfill =& \sum _{j_1=1}^{d_2^2}\mathrm{tr}\left[{\left(A_{j_1}^{21}\right)}^2{\rho }^{21}\right]\sum _{j_2=1}^{d_3^2}\mathrm{tr}\left[{\left(A_{j_2}^{22}\right)}^2{\rho }^{22}\right]-\sum _{j_1=1}^{d_2^2}{\left[\mathrm{tr}\left(A_{j_1}^{21}{\rho }^{21}\right)\right]}^2\sum _{j_2=1}^{d_3^2}{\left[\mathrm{tr}\left(A_{j_2}^{22}{\rho }^{22}\right)\right]}^2\hfill \\ \hfill =& d_2{\eta }_2{d}_3{\eta }_3-[{\displaystyle \frac{({\eta }_2{d}_2^3-1)\mathrm{tr}\left[{\left({\rho }^{21}\right)}^2\right]+d_2(1-{\eta }_2{d}_2)}{d_2(d_2^2-1)}}][{\displaystyle \frac{({\eta }_3{d}_3^3-1)\mathrm{tr}\left[{\left({\rho }^{22}\right)}^2\right]+d_3(1-{\eta }_3{d}_3)}{d_3(d_3^2-1)}}]\hfill \end{array}$$

(25)

and

$$\begin{array}{cc}\hfill & {\Lambda }_{A^{11}{A}^{31}{A}^{32}{A}^{33}{A}^{34}}\hfill \\ \hfill =& {\max }_{\xi }\{\sum _{i=1}^n{\left[\mathrm{tr}\left({\mathcal{N}}_i\sigma \right)\right]}^2\}-\sum _{i=1}^n{\left[\mathrm{tr}\left({\mathcal{N}}_i{\mathrm{tr}}_{A^{21}{A}^{22}}\left(\rho \right)\right)\right]}^2\hfill \\ \hfill =& {\max }_{\xi }\{\sum _{i=1}^n{\left[\mathrm{tr}(A_{i_0}^{11}{\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}})\right]}^2{\left[\mathrm{tr}\left(A_{i_1}^{31}{\sigma }_{{\lambda }_3}^{A^{31}}\right)\right]}^2{\left[\mathrm{tr}\left(A_{i_2}^{32}{\sigma }_{{\lambda }_4}^{A^{32}}\right)\right]}^2{\left[\mathrm{tr}\left(A_{i_3}^{33}{\sigma }_{{\lambda }_5}^{A^{33}}\right)\right]}^2{\left[\mathrm{tr}\left(A_{i_4}^{34}{\sigma }_{{\lambda }_6}^{A^{34}}\right)\right]}^2\}\hfill \\ \hfill & -\sum _{i=1}^n{\left\{\mathrm{tr}\left[(A_{i_0}^{11}\otimes A_{i_1}^{31}\otimes A_{i_2}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34})({\rho }^{11}\otimes {\rho }^{31}\otimes {\rho }^{32}\otimes {\rho }^{33}\otimes {\rho }^{34})\right]\right\}}^2\hfill \\ \hfill =& {\max }_{\xi }\{\sum _{i_0}^{d_1^2}{\left[\mathrm{tr}(A_{i_0}^{11}{\sigma }_{{\lambda }_1}^{A^{11\left(1\right)}}\otimes {\sigma }_{{\lambda }_2}^{A^{11\left(2\right)}})\right]}^2\sum _{i_1}^{d_4^2}{\left[\mathrm{tr}\left(A_{i_1}^{31}{\sigma }_{{\lambda }_3}^{A^{31}}\right)\right]}^2\sum _{i_2}^{d_5^2}{\left[\mathrm{tr}\left(A_{i_2}^{32}{\sigma }_{{\lambda }_4}^{A^{32}}\right)\right]}^2\sum _{i_3}^{d_6^2}{\left[\mathrm{tr}\left(A_{i_3}^{33}{\sigma }_{{\lambda }_5}^{A^{33}}\right)\right]}^2\hfill \\ \hfill & \sum _{i_4}^{d_7^2}{\left[\mathrm{tr}\left(A_{i_4}^{34}{\sigma }_{{\lambda }_6}^{A^{34}}\right)\right]}^2\}-\sum _{i_0}^{d_1^2}{\left[\mathrm{tr}\left(A_{i_0}^{11}{\rho }^{11}\right)\right]}^2\sum _{i_1}^{d_4^2}{\left[\mathrm{tr}\left(A_{i_1}^{31}{\rho }^{31}\right)\right]}^2\sum _{i_2}^{d_5^2}{\left[\mathrm{tr}\left(A_{i_2}^{32}{\rho }^{32}\right)\right]}^2\sum _{i_3}^{d_6^2}{\left[\mathrm{tr}\left(A_{i_3}^{33}{\rho }^{33}\right)\right]}^2\sum _{i_4}^{d_7^2}{\left[\mathrm{tr}\left(A_{i_4}^{34}{\rho }^{34}\right)\right]}^2\hfill \\ \hfill =& {\displaystyle \frac{{\eta }_1{d}_1^2+1}{d_1(d_1+1)}}\prod _{q=4}^7{\displaystyle \frac{{\eta }_q{d}_q^2+1}{d_q(d_q+1)}}-{\displaystyle \frac{({\eta }_1{d}_1^3-1)\mathrm{tr}\left[{\left({\rho }^{11}\right)}^2\right]+d_1(1-{\eta }_1{d}_1)}{d_1(d_1^2-1)}}\hfill \\ \hfill & \times \prod _{q=4}^7{\displaystyle \frac{({\eta }_q{d}_q^3-1)\mathrm{tr}\left[{\left({\rho }^{3(q-3)}\right)}^2\right]+d_q(1-{\eta }_q{d}_q)}{d_q(d_q^2-1)}}\hfill \end{array}$$

(26)

where $n=d_1^2{d}_4^2{d}_5^2{d}_6^2{d}_7^2$. Therefore, when the measurements on each system are taken as GSICs, combining Equations (25) and (26), we can obtain the conclusion in Proposition 3. □

4.3. Example

In what follows, we work out an example in order to illustrate the effectiveness of our steering criteria. Consider the 3-layer tree-shaped network, where all states are a two-qubit Werner state

$$\rho \left(v_i\right)=v_i|{\Phi }^{+}\rangle \langle {\Phi }^{+}|+{\displaystyle \frac{1-v_i}{4}}{I}_2,i=1,2,\cdots ,6,$$

where $0\le v_i\le 1$, and $|{\Phi }^{+}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|00\rangle +|11\rangle )$ is the singlet state. The Werner states are entangled when $v_i>{\displaystyle \frac{1}{3}}$, and separable when $v_i\le {\displaystyle \frac{1}{3}}$. It is easy to see that the reduced states of $\rho \left(v_i\right)$ for each subsystem are all ${\displaystyle \frac{1}{2}}{I}_2$. The Bloch-Fano decomposition of Werner state is of the form

$$\rho \left(v_i\right)={\displaystyle \frac{1}{4}}[I_2\otimes I_2+v_i{\sigma }_x\otimes {\sigma }_x-v_i{\sigma }_y\otimes {\sigma }_y+v_i{\sigma }_z\otimes {\sigma }_z].$$

We use Proposition 1 to detect the steerability of $\rho ={⨂}_{i=1}^6\rho \left(v_i\right)$ with LOOs as input for all parties. Specifically, $A_{i_0}^{11}=A_{i_0^{\prime }}^{11\left(1\right)}\otimes A_{i_0^{″}}^{11\left(2\right)}$ with $\left\{A_{i_0^{\prime }}^{11\left(1\right)}\right\}=\left\{A_{i_0^{\prime \prime }}^{11\left(25\right)}\right\}=\{{\displaystyle \frac{1}{\sqrt{2}}}{I}_2,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_x,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_y,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_z\}$; $A_{j_1}^{21}=A_{j_1^{\prime }}^{21\left(1\right)}\otimes A_{j_1^{″}}^{21\left(2\right)}\otimes A_{j_1^{\prime \prime \prime }}^{21\left(3\right)}$ with $\left\{A_{j_1^{\prime }}^{21\left(1\right)}\right\}=\left\{A_{j_1^{\prime \prime }}^{21\left(2\right)}\right\}=\left\{A_{j_1^{\prime \prime \prime }}^{21\left(3\right)}\right\}=\{{\displaystyle \frac{1}{\sqrt{2}}}{I}_2,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_x,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_y,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_z\}$, and the same to $A_{j_2}^{22}$; $A_{i_s}^{3s}=\{{\displaystyle \frac{1}{\sqrt{2}}}{I}_2,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_x,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_y,{\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_z\}$ for $s=1,2,3,4$. According to the properties of LOOs, $A_{i_0}^{11}$, $A_{j_1}^{21}$, and $A_{j_2}^{22}$ are all LOOs. At this point,

$${\mathcal{N}}_i=A_{i_0^{\prime }}^{11\left(1\right)}\otimes A_{i_0^{″}}^{11\left(2\right)}\otimes A_{i_1}^{31}\otimes A_{i_4}^{32}\otimes A_{i_3}^{33}\otimes A_{i_4}^{34},$$

$${\mathcal{M}}_j=A_{j_1^{\prime }}^{21\left(1\right)}\otimes A_{j_1^{″}}^{21\left(2\right)}\otimes A_{j_1^{\prime \prime \prime }}^{21\left(3\right)}\otimes A_{j_2^{\prime }}^{22\left(1\right)}\otimes A_{j_2^{\prime \prime }}^{22\left(2\right)}\otimes A_{j_2^{\prime \prime \prime }}^{22\left(3\right)}.$$

It is worth noting that for the joint measurement of each Werner state $\rho \left(v_i\right)$, when the measurement of one party is determined, the other party must be consistent to ensure that the measurement value is non-zero. Taking $\rho \left(v_1\right)$ as an example, we have provided the form of the joint measurement and the measurement results in

Table 1. Four measurements performed by parties $A^{11\left(1\right)}$ and $A^{21\left(1\right)}$.

${\mathit{A}}_{{\mathit{j}}_1^{\prime }}^{21\left(1\right)}$	${\mathit{A}}_{{\mathit{i}}_0^{\prime }}^{11\left(1\right)}$	$\mathbf{tr}\left[({\mathit{A}}_{{\mathit{i}}_0^{\prime }}^{11\left(1\right)}\otimes {\mathit{A}}_{{\mathit{j}}_1^{\prime }}^{21\left(1\right)})\mathit{\rho }\left({\mathit{v}}_1\right)\right]$
${\displaystyle \frac{1}{\sqrt{2}}}{I}_2$	${\displaystyle \frac{1}{\sqrt{2}}}{I}_2$	${\displaystyle \frac{1}{2}}$
${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_x$	${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_x$	${\displaystyle \frac{1}{2}}{v}_1$
${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_y$	${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_y$	$-{\displaystyle \frac{1}{2}}{v}_1$
${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_z$	${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_z$	${\displaystyle \frac{1}{2}}{v}_1$

. Therefore, the measurement results for the entire network state are non-zero only when ${\mathcal{N}}_i$ and ${\mathcal{M}}_j$ are consistent. In this way, $\mathcal{C}(\mathcal{N},\mathcal{M}|\rho )$ is actually a diagonal matrix. We have listed all the measurements and their corresponding results in

Table 2. The measurements performed by parties ${\left\{A^{21\left(i\right)}\right\}}_{i=1}^3$ and ${\left\{A^{22\left(i\right)}\right\}}_{i=1}^3$, and the corresponding measurement results.

	$\mathit{\rho }\left({\mathit{v}}_1\right)$	$\mathit{\rho }\left({\mathit{v}}_2\right)$	$\mathit{\rho }\left({\mathit{v}}_3\right)$	$\mathit{\rho }\left({\mathit{v}}_4\right)$	$\mathit{\rho }\left({\mathit{v}}_5\right)$	$\mathit{\rho }\left({\mathit{v}}_6\right)$
${\displaystyle \frac{1}{\sqrt{2}}}{I}_2$	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{1}{2}}$
${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_x$	${\displaystyle \frac{1}{2}}{v}_1$	${\displaystyle \frac{1}{2}}{v}_2$	${\displaystyle \frac{1}{2}}{v}_3$	${\displaystyle \frac{1}{2}}{v}_4$	${\displaystyle \frac{1}{2}}{v}_5$	${\displaystyle \frac{1}{2}}{v}_6$
${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_y$	$-{\displaystyle \frac{1}{2}}{v}_1$	$-{\displaystyle \frac{1}{2}}{v}_2$	$-{\displaystyle \frac{1}{2}}{v}_3$	$-{\displaystyle \frac{1}{2}}{v}_4$	$-{\displaystyle \frac{1}{2}}{v}_5$	$-{\displaystyle \frac{1}{2}}{v}_6$
${\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_z$	${\displaystyle \frac{1}{2}}{v}_1$	${\displaystyle \frac{1}{2}}{v}_2$	${\displaystyle \frac{1}{2}}{v}_3$	${\displaystyle \frac{1}{2}}{v}_4$	${\displaystyle \frac{1}{2}}{v}_5$	${\displaystyle \frac{1}{2}}{v}_6$

.

We illustrate how to utilize the results in Table 2 through an example. When

$$A_{j_1^{\prime }}^{21\left(1\right)}=A_{j_1^{\prime \prime }}^{21\left(2\right)}=A_{j_1^{\prime \prime \prime }}^{21\left(3\right)}={\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_x,A_{j_1^{\prime }}^{22\left(1\right)}=A_{j_1^{″}}^{22\left(2\right)}=A_{j_1^{\prime \prime \prime }}^{22\left(3\right)}={\displaystyle \frac{1}{\sqrt{2}}}{\sigma }_y.$$

Then the corresponding $\mathrm{tr}\left[({\mathcal{N}}_i\otimes {\mathcal{M}}_j)\rho \right]={\displaystyle \frac{v_1}{2}}(-{\displaystyle \frac{v_2}{2}}){\displaystyle \frac{v_3}{2}}{\displaystyle \frac{v_4}{2}}(-{\displaystyle \frac{v_5}{2}})(-{\displaystyle \frac{v_6}{2}})=-{\left({\displaystyle \frac{1}{2}}\right)}^6{v}_1{v}_2{v}_3{v}_4{v}_5{v}_6$. Furthermore, since $\tilde{\rho }={⨂}_{i=1}^{12}\left({\displaystyle \frac{1}{2}}{I}_2\right)$, so $\mathrm{tr}\left[({\mathcal{N}}_i\otimes {\mathcal{M}}_j)\tilde{\rho }\right]={\displaystyle \frac{1}{64}}$ only when ${\mathcal{N}}_i={\mathcal{M}}_j={⨂}_{i=1}^6\left({\displaystyle \frac{1}{\sqrt{2}}}{I}_2\right)$, and all the others are 0. Therefore, combining Equations (5) and (6), we can conclude that

$${\parallel \mathcal{C}(\mathcal{N},\mathcal{M}|\rho )\parallel }_{\mathrm{tr}}={\left({\displaystyle \frac{1}{2}}\right)}^6(1+3v_1)(1+3v_2)\dots (1+3v_6)-{\left({\displaystyle \frac{1}{2}}\right)}^6.$$

On the other hand, according to Proposition 1, it is easy to see that the corresponding upper bound

$$\sqrt{(d_2{d}_3-\mathrm{tr}\left[{({\rho }^{21}\otimes {\rho }^{22})}^2\right])(1-\mathrm{tr}\left[{({\rho }^{11}\otimes {\rho }^{31}\otimes {\rho }^{32}\otimes {\rho }^{33}\otimes {\rho }^{34})}^2\right])}={\displaystyle \frac{63\sqrt{65}}{64}}.$$

Therefore, when $(1+3v_1)(1+3v_2)\dots (1+3v_6)>63\sqrt{65}+1\approx 508.9222$, the entire network is steerable. In particular, when $v_1=v_2=v_3=v_4=v_5=v_6=v$, that is, when the network is populated with identical Werner states, it can be shown that the entire network is steerable when $v>0.60822$.

Furthermore, we explore the maximum number of separable Werner states that can be distributed in this network while retaining steerability. Let $f(v_1,v_2,\dots ,v_6)=(1+3v_1)(1+3v_2)\dots (1+3v_6)$. In

Table 3. When there are 5 separable states in the network, even if the remaining one is a maximally entangled state, it is equivalent to having 5 states with $v_i\le {\displaystyle \frac{1}{3}}$, and the remaining one with $v_i=1$. In this case, $f(v_1,v_2,\dots ,v_6)\le 4\times 2^5=128$.

The Number of Separable States	${\mathit{f}}_{\mathbf{max}}({\mathit{v}}_1,{\mathit{v}}_2,\dots ,{\mathit{v}}_6)$
5	128
4	256
3	512

, we list the maximum values that $f(v_1,v_2,\dots ,v_6)$ can achieve when different numbers of separable states are distributed.

According to the results in Table 3, when the network is populated with four separable Werner states, since $f_{\max }(v_1,v_2,\dots ,v_6)=256<508.9222$, it always holds that $f(v_1,v_2,\dots ,v_6)<508.9222$, and thus the network is not steerable. When the network is populated with three separable states, since $f_{\max }(v_1,v_2,\dots ,v_6)=512>508.9222$, there exists $f(v_1,v_2,\dots ,v_6)>508.9222$. In summary, at most three separable Werner states can be distributed in the network to ensure that it is steerable.

5. Conclusions

Based on the steering inequality criterion for detecting bipartite states presented in Ref. [28], we have investigated the steering inequality criterion for a 2-forked 3-layer tree-shaped network. Assuming that the first and third layers are trusted parties while the second layer is an untrusted party, we have derived a steering inequality criterion based on the correlation matrix between the observables of trusted and untrusted parties. To derive some practical criteria, we have specifically employed the following three types of observables: LOOs, MUMs, and GSICs. For any given network state, we can detect whether it is steerable by finding appropriate measurement schemes that satisfy certain conditions and then calculating the conditions under which the steering inequality criteria are violated. Of course, due to the joint measurement involving three subsystems, the measurement dimension required for the second layer is relatively large; nevertheless, such measurement schemes always exist in arbitrary-dimensional spaces. To demonstrate the effectiveness of the proposed criteria, we provide a simple example for illustration.

This paper considers a class of tree-shaped networks. In principle, the different quantities and locations of trusted and untrusted parties in such networks result in discriminative definition and properties of network quantum steering. It would be interesting to address the problems of network steering with different choices of trusted and untrusted parties. Moreover, the optimal choice of measurement values will be a challenge in the application of inequality criteria, as a better selection of measurement values helps us collect more network steerable states.