An Innovative Analytical Approach for the Solution of Fractional Differential Equations Using the Integral Transform

Abstract

In this study, we suggest a straightforward analytical/semi-analytical method based on the Elzaki transform (ET) method to find the solution to a number of differential fractional boundary value problems with initial conditions (ICs). The suggested approach not only resolves the issue of some equation nonlinearity but also transforms the issue into a simpler algebraic recurrence problem. In science and engineering, fractional differential equations (FDEs) can be solved with the help of this basic but effective concept. Some illustrative cases are used to demonstrate the efficacy and value of the suggested technique.

1. Introduction

Although fractional derivatives have a lengthy mathematical history, science disciplines did not employ them for a very long time. The fact that there are numerous non-equivalent definitions of a fractional derivative could be one reason for its unpopularity [1]. One area of mathematics that was formerly regarded to be esoteric was fractional calculus. Fractional calculus may be broadly defined as an extension of the traditional differentiation and integration to any order. Numerous academics and mathematicians have contributed to its advancement since its start. Liouville, Riemann, Leibniz, Weyl, Abel, Grünwald, Letnikov, Caputo, Riesz, Hadamard, Marchaud, Machado, Chen, Pichaghchi, Katugampola, Coimbra, Davidson, Erdélyi, Kober, and Feller are among the mathematicians that spring to mind.

An extension of classical calculus that deals with derivatives and integrals of non-integer orders is called fractional calculus. Since its inception more than three centuries ago, the idea has undergone substantial development, influencing a number of fields, including anomalous diffusion, control theory, and viscoelasticity.

Another issue is that due to their nonlocal nature, fractional derivatives lack a clear geometrical interpretation [2]. However, over the past ten years, mathematicians and engineers have begun to pay much greater attention to fractional calculus. It was discovered that fractional derivatives can be used to clearly simulate a variety of applications, notably interdisciplinary ones. For instance, fractional derivatives can be used to describe the nonlinear oscillation of earthquakes [3] and the flaw introduced by the assumption of continuous traffic flow in the fluid-dynamic traffic model [4]. Both differential equations with fractional order phenomena and FPDEs for seepage flow in porous media are proposed in [5,6], respectively, based on experimental evidence. Mainardi [7] provides an overview of a few fractional derivative applications in statistical mechanics and continuous mechanics. Many authors have looked into the analytical findings regarding the existence and distinctiveness of solutions to the FDEs [1,8]. A number of techniques, including Adomian decomposition, differential transform method, Variational Iteration, method Homotopy Analysis, First Integral, and many others, have been utilized in recent years to solve FDEs, FPDEs, FIDEs, and dynamic systems involving fractional derivatives [9,10,11,12,13,14,15,16].

This work focuses on solving FPDEs using a novel approach known as the ET approach. Initial and boundary value issues are solved using the ET and its variants. The recommended approach [17] gives the solution in a finite series form that is straightforward to calculate, but the actual process offers better precision because different starting approximations are employed in any iteration. This paper provides a few examples to support this claim.

Some instances of the listed problems are addressed by the general explanation of the suggested technique. The analytical solutions of FPDEs with ICs and BCs pose a highly challenging set of issues. The current work provides closed-form answers by using a comparatively easy and basic method to derive the analytical solutions of FPDEs.

The newly developed method has two distinguishing features: it is simple to use and requires minimal processing complexity. This paper discusses the value of a special analytical technique combined with the ET for solving FPDEs. This technique is a powerful tool for solving functional equations produced by mathematically modeling diverse processes.

Definition 1.

A real function  $f(u),$$u>0$  is said to be in the space  $C_{\mathsf{\mu }},\hspace{0.17em}\hspace{0.17em}\mathsf{\mu }\in \Re$ if there exists a real number $p>\mathsf{\mu },$ such that $f(u)=u^p{f}_1(u),$ where $f_1(B)\in C(0,\infty ),$ and it is said to be in the space $C_{\mathsf{\mu }}^n$ if and only if $f^n\in C_{\mathsf{\mu }},\hspace{0.17em}\hspace{0.17em}n\in N.$

Definition 2.

The Riemann-Liouville (R-L) fractional integral operator, of the order $\mathsf{\alpha }>0,$ of $f\in C_{\mathsf{\mu }},\hspace{0.17em}\hspace{0.17em}\mathsf{\mu }\ge -1,$ is defined as follows

$$J^{\mathsf{\alpha }}f(u)={\displaystyle \frac{1}{\mathsf{\Gamma }(\mathsf{\alpha })}}{\displaystyle \underset{0}{\overset{u}{\int }}{(u-v)}^{\mathsf{\alpha }-1}f(v)dv,\hspace{0.17em}\hspace{0.17em}\mathsf{\alpha }>0.}{J}^{0}f(u)=f(u)$$

Some properties of $J^{\mathsf{\alpha }},$

For $f^n\in C_{\mathsf{\mu }},\hspace{0.17em}\hspace{0.17em}n\in N,\hspace{0.17em}\hspace{0.17em}\mathsf{\alpha },\mathsf{\beta }\ge 0$ and $\mathsf{\gamma }\ge -1:$

(a)

$J^{\mathsf{\alpha }}{J}^{\mathsf{\beta }}f(u)=J^{\mathsf{\alpha }+\mathsf{\beta }}f(u)$

(b)

$J^{\mathsf{\alpha }}{u}^{\mathsf{\gamma }}={\displaystyle \frac{\mathsf{\Gamma }(\mathsf{\gamma }+1)}{\mathsf{\Gamma }(\mathsf{\gamma }+\mathsf{\alpha }+1)}}{u}^{\mathsf{\alpha }+\mathsf{\gamma }}$

Definition 3.

According to Caputo, the fractional derivative (FD) of $f(u),$ is as follows:

$$D^{\mathsf{\alpha }}f(u)=J^{m-\mathsf{\alpha }}{D}^{m}f(u)$$

For $m-1<\mathsf{\alpha }\le m,$ $m\in N,$ $u>0,$ and $f\in C_{-1}^m.$

Caputo’s FD computes an ordinary derivative first, followed by a fractional integral, to generate the desired order of an FD. Similar to the integer-order integration, the R-L fractional integral operator is a linear operation:

$$J^{\mathsf{\alpha }}\left({\displaystyle \sum _{i=1}^n{c}_i{f}_i(u)}\right)={\displaystyle \sum _{i=1}^n{c}_i{J}^{\mathsf{\alpha }}{f}_i(u)}$$

 where ${\left\{c_i\right\}}_{i=1}^n$ are constants.

We can find the justification for utilizing the Caputo concept in [10].

2. Elzaki Transform (ET)

The modified Sumudu transform, also known as the ET of the function $\mathsf{\Phi }(u)$, has some basic explanations, which are provided below.

$$E[\mathsf{\Phi }](p)=p{\displaystyle \underset{0}{\overset{\infty }{\int }}\mathsf{\Phi }(u)e^{-\frac{u}{p}}du},u>0,$$

(1)

where p is a complex value.

The application of the modified Sumudu transform, or the ET, to PDEs, ODEs, systems of ODEs and PDEs, and integral equations was demonstrated by Elzaki et al. in [1,2,3,4,18,19,20]. The ET can be utilized efficiently when Sumudu and Laplace transformations fail to solve DEs with variable coefficients [21], and in [22,23], some engineering and biological problems were studied using the ET, and it demonstrated good effectiveness in finding exact solutions.

Theorem 1

([2]). The partial derivatives are transformed by the ET as follows:

$$\begin{gathered} E\left[{\displaystyle \frac{\partial \mathsf{\Phi }(u,v)}{\partial v}}\right]={\displaystyle \frac{1}{p}}T(u,p)-p\mathsf{\Phi }(u,0),E\left[{\displaystyle \frac{\partial \mathsf{\Phi }(u,v)}{\partial u}}\right]={\displaystyle \frac{d}{du}}[T(u,p)] \\ E\left[{\displaystyle \frac{{\partial }^2\mathsf{\Phi }(u,v)}{\partial v^2}}\right]={\displaystyle \frac{1}{p^2}}T(u,p)-\mathsf{\Phi }(u,0)-p{\displaystyle \frac{\partial \mathsf{\Phi }(u,0)}{\partial v}}, \\ E\left[{\displaystyle \frac{{\partial }^2\mathsf{\Phi }(u,v)}{\partial u^2}}\right]={\displaystyle \frac{d^2}{d{u}^2}}[T(u,p)] \end{gathered}$$

The ET of some functions:

$\Phi (u)$	$E[\Phi (u)]=T(p)$
1	p2
U	p3
un	$n!p^{n+2}$
eau	${\displaystyle \frac{p^2}{1-ap}}$
sin au	${\displaystyle \frac{a{p}^3}{1+a^2{p}^2}}$
cos au	${\displaystyle \frac{p^2}{1+a^2{p}^2}}$

Now, we will show you a few lemmas that can be used to deduce the function from its ET.

Lemma 1.

ET of R-L operator of order $\alpha \hspace{0.17em}>\hspace{0.17em}0$ is;

$$E[J^{\mathsf{\alpha }}\mathsf{\Phi }(u)]=p^{\mathsf{\alpha }}T(p)$$

Proof. 

Applying the ET on the R-L fractional operator for $\mathsf{\alpha }>0$ yields the following:

$$E[J^{\mathsf{\alpha }}\mathsf{\Phi }(u)]=E\left[{\displaystyle \frac{1}{\mathsf{\Gamma }(\mathsf{\alpha })}}{\displaystyle \underset{0}{\overset{A}{\int }}{(u-\mathsf{\alpha })}^{\mathsf{\alpha }-1}}\mathsf{\Phi }(v)dv\right]={\displaystyle \frac{1}{\mathsf{\Gamma }(\mathsf{\alpha })}}{\displaystyle \frac{1}{p}}T(p)G(p)=p^{\mathsf{\alpha }}T(p)$$

where $G(p)=E[u^{\mathsf{\alpha }-1}]=p^{\mathsf{\alpha }+1}\mathsf{\Gamma }(\mathsf{\alpha })$. □

Lemma 2.

Let α be defined such that $m-1<\mathsf{\alpha }\le m,$ $m\in IN,$ we obtain with the Caputo FD.

$$E[D_v^{\mathsf{\alpha }}\mathsf{\Phi }(u,v)]=p^{m-\mathsf{\alpha }}\left[{\displaystyle \frac{T(u,p)}{p^m}}-{\displaystyle \frac{\mathsf{\Phi }(u,0)}{p^{m-2}}}-{\displaystyle \frac{\frac{\partial \mathsf{\Phi }(u,0)}{\partial v}}{p^{m-3}}}-\cdots -p{\displaystyle \frac{{\partial }^{m-1}\mathsf{\Phi }(u,0)}{\partial v^{m-1}}}\right]$$

Or,

$$\begin{gathered} E[D_v^{\mathsf{\alpha }}\mathsf{\Phi }(u,v)]={\displaystyle \frac{1}{p^{\mathsf{\alpha }}}}E[\mathsf{\Phi }(u,v)]-{\displaystyle \sum _{k=0}^{m-1}\frac{{\partial }^k\mathsf{\Phi }(u,0)}{\partial v^k}}{p}^{2-\mathsf{\alpha }+k}, \\ m-1<\mathsf{\alpha }\le m \end{gathered}$$

The definition of the typical and generalized Mittag–Leffler functions is as follows:

$${\in }_{\mathsf{\alpha },\mathsf{\beta }}(u)={\displaystyle \sum _{n=0}^{\infty }\frac{u^n}{\mathsf{\Gamma }(n\mathsf{\alpha }+\mathsf{\beta })}}$$

Especially for ${\in }_{\mathsf{\alpha }}(u)=\hspace{0.17em}\hspace{0.17em}{\in }_{\mathsf{\alpha },1}(u).$

Lemma 3.

If, $\mathsf{\alpha },\mathsf{\beta }>0,$ $a\in C$ and ${\displaystyle \frac{1}{p^{\mathsf{\alpha }}}}>\left|a\right|,$ the inverse ET formula is as follows:

$$E^{-1}\left[{\displaystyle \frac{p^{\mathsf{\beta }+1}}{1+a{p}^{\mathsf{\alpha }}}}\right]=u^{\mathsf{\beta }-1}{\in }_{\mathsf{\alpha },\mathsf{\beta }}(-a{u}^{\mathsf{\alpha }})$$

Proof. 

$${\displaystyle \frac{p^{\mathsf{\beta }+1}}{1+b{p}^{\mathsf{\alpha }}}}=p^{\mathsf{\beta }+1}{\displaystyle \frac{1}{1+b{p}^{\mathsf{\alpha }}}}=p^{\mathsf{\beta }+1}{\displaystyle \sum _{j=0}^{\infty }{(-b)}^j{(p^{\mathsf{\alpha }})}^j}={\displaystyle \sum _{j=0}^{\infty }{(-b)}^j}{p}^{j\mathsf{\alpha }+\mathsf{\beta }+1},$$

Then

$$\begin{gathered} E^{-1}\left[{\displaystyle \frac{p^{\mathsf{\beta }+1}}{1+b{p}^{\mathsf{\alpha }}}}\right]=E^{-1}\left[{\displaystyle \sum _{j=0}^{\infty }{(-b)}^j{p}^{j\mathsf{\alpha }+\mathsf{\beta }+1}}\right]={\displaystyle \sum _{j=0}^{\infty }\frac{{(-b)}^j{u}^{j\mathsf{\alpha }+\mathsf{\beta }-1}}{\mathsf{\Gamma }(j\mathsf{\alpha }+\mathsf{\beta })}} \\ =u^{\mathsf{\beta }-1}{\displaystyle \sum _{j=0}^{\infty }\frac{{(-b{u}^{\mathsf{\alpha }})}^j}{\mathsf{\Gamma }(j\mathsf{\alpha }+\mathsf{\beta })}=u^{\mathsf{\beta }-1}{\in }_{\mathsf{\alpha },\mathsf{\beta }}(-b{u}^{\mathsf{\alpha }}).} \end{gathered}$$

□

3. The Proposed Method

To further explain the fundamental idea of the suggested strategy, we provide the following FPDE:

$$\begin{gathered} D_t^{\mathsf{\alpha }}\mathsf{\Phi }(z,t)+R[\mathsf{\Phi }(z,t)]+N[\mathsf{\Phi }(z,t)]=g(z,t); 0<\mathsf{\alpha }\le 2, 0<t<M; \\ M,z>0 \end{gathered}$$

(2)

With the ICs and BCs,

$$\mathsf{\Phi }(z,0)=h_1(z),{\mathsf{\Phi }}_t(z,0)=h_2(z),\mathsf{\Phi }(0,t)=k_1(t),\mathsf{\Phi }(1,t)=k_2(t)$$

(3)

where R and N are linear and nonlinear operators and g is the inhomogeneous term.

Using the newly suggested approach below to calculate the new solution ${\mathsf{\Phi }}_j^{*}(z,t)$,

$${\mathsf{\Phi }}_n^{*}={\mathsf{\Phi }}_n+(1-z)(k_1(t)-{\mathsf{\Phi }}_n(0,t))+z(k_2(t)-{\mathsf{\Phi }}_n(1,t))$$

(4)

where $n=0,1,2,\dots .$

It is clear that the new solution ${\mathsf{\Phi }}_n^{*}$ will satisfy both ICs and BCs.

It is obvious that the new solution ${\mathsf{\Phi }}_n^{*}$ will meet the needs of ICs and BCs alike.

We can resolve Equation (2) by using Equation (3) and the ET to derive

$$\begin{gathered} E[D_t^{\mathsf{\alpha }}\mathsf{\Phi }]+E\{R[\mathsf{\Phi }]+N[\mathsf{\Phi }]\}=E[g], \\ E(\mathsf{\Phi })=p^2{h}_1+p^3{h}_2-p^{\mathsf{\alpha }}E\{R[\mathsf{\Phi }]+N[\mathsf{\Phi }]-g\} \end{gathered}$$

(5)

Presumably, the solution to Equation (2) has a series form that reads as follows:

$$\mathsf{\Phi }={\displaystyle \sum _{n=0}^{\infty }{\mathsf{\Phi }}_n}$$

(6)

Now, we apply the inverse of the ET to Equation (5) and use Equation (6) to obtain

$${\displaystyle \sum _{n=0}^{\infty }\mathsf{\Phi }=G-E^{-1}\{p^{\mathsf{\alpha }}E[R[\mathsf{\Phi }]+N[\mathsf{\Phi }]\}}$$

(7)

$G$ is give an explanation of the term that comes from all or part of the function $g$ and the ICs.

The choice of the initial iteration Φ₀ is very important as it can activate the convergence of the method and succeed in calculating the exact solution in a finite number of steps.

This approach is dependent on how we select the initial iteration Φ₀ that results in precise solutions in a few steps. For illustration, if we decide, ${\mathsf{\Phi }}_0=G$.

We can select Φ₀ all or a portion of the function $g$ if the ICs are equal to zero. If the ICs are equal to zero, we can choose Φ₀ the entire function or just a portion of it. The solution Φ can then be found iteratively using the following relations:

$${\mathsf{\Phi }}_{n+1}=E^{-1}\{p^{\mathsf{\alpha }}E[R[{\mathsf{\Phi }}_n^{*}]+N[{\mathsf{\Phi }}_n^{*}]]\},{\mathsf{\Phi }}_0=G$$

(8)

From Equations (4) and (8), we can locate ${\mathsf{\Phi }}_0,{\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2,\dots .$

Equation (6) can then be used to determine the solution. We show that the recommended method can be used to resolve FPDEs that arise under the ICs, BCs, and the ET.

Convergence Analysis

This section describes how to find the exact solution for FPDEs using the ET approach.

Theorem 2.

If $B$  is a Banach space, then ${\displaystyle \sum _{n=0}^{\infty }{Q}_n},$ in Equation (6) converges, if

$$\exists \left(0\le \omega <1\right), \mathrm{s}.\mathrm{t}.\forall \varpi \in \mathbb{N}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}‖Q_i‖\le \omega ‖Q_{i-1}‖, \mathit{to} \varpi \in B$$

Proof. 

The definition of the partial sum sequence is ${\left\{{\varpi }_i\right\}}_{i=0}^{\infty }$

$$\begin{array}{c}{\varpi }_0=Q_0\\ {\varpi }_1=Q_0+Q_1\\ {\varpi }_2=Q_0+Q_1+Q_2\\ ⋮\\ {\varpi }_{\tau }=Q_0+Q_1+\dots +Q_i.\end{array}$$

The next step is to demonstrate that ${\left\{{\varpi }_i\right\}}_{i=0}^{\infty }$ is a Cauchy series in B space

$$‖{\varpi }_{i+1}-{\varpi }_i‖=‖{\displaystyle \sum _{n=0}^{i+1}{Q}_n}-{\displaystyle \sum _{n=0}^i{Q}_n}‖=‖Q_{i+1}‖\le \eta ‖Q_i‖\le \dots \le {\eta }^{i+1}‖Q_n‖,$$

for all $i,\eta \in \mathbb{N}\hspace{0.17em}\hspace{0.17em}as i\ge \eta ,$

$$\begin{array}{l}‖{\varpi }_i-{\varpi }_{\eta }‖=‖\left({\varpi }_i-{\varpi }_{i-1}\right)+\left({\varpi }_{i-1}-{\varpi }_{i-2}\right)+\dots +\left({\varpi }_{\eta +1}-{\varpi }_{\eta }\right)‖\le \\ ‖{\varpi }_i-{\varpi }_{i-1}‖+‖{\varpi }_{i-1}-{\varpi }_{i-2}‖+\dots .+‖\left({\varpi }_{\eta +1}-{\varpi }_{\eta }\right)‖\le {\omega }^i‖Q_0‖+{\omega }^{i-1}‖Q_0‖+\dots +{\omega }^{\eta +1}‖Q_0‖\\ \le {\omega }^{\eta +1}‖w_0‖\left({\omega }^{i-\eta -1}+{\omega }^{i-\eta -2}+\dots +\omega \right)={\displaystyle \frac{1-{\omega }^{i-\eta }}{1-\omega }}{\omega }^{\eta +1}‖Q_0‖.\end{array}$$

Since $\left({\omega }^{i-\eta -1}+{\omega }^{i-\eta -2}+\dots +\omega \right)$ is a geometric series and $0\le \omega <1,$ then $\underset{i,\eta \to \infty }{\lim }{\varpi }_i-{\varpi }_{\eta }=0,$

This means that $Q={\displaystyle \sum _{n=0}^{\infty }{Q}_n},$ converges and then ${\left\{{\varpi }_i\right\}}_{i=0}^{\infty }$ is Cauchy in B space. □

4. Illustrative Examples

Here, we applied the method outlined in this study to offer an exact solution to a few FPDEs.

Example 1.

Let us examine the linear fractional heat equation:

$$D_t^{\mathsf{\alpha }}\mathsf{\Phi }(z,t)={\displaystyle \frac{1}{2}}{z}^2{\mathsf{\Phi }}_{zz}(z,t), 0<\mathsf{\alpha }<1, 0<z\le 1, t>0$$

(9)

Regarding the IC and BCs,

$$\mathsf{\Phi }(z,0)=z^2, \mathsf{\Phi }(0,t)=0, \mathsf{\Phi }(1,t)=e^t$$

(10)

Employing the ET of (9), with the IC, we obtain the following outcome:

$$E[\mathsf{\Phi }(z,t)]=z^2{p}^2+p^{\mathsf{\alpha }}E\left[{\displaystyle \frac{1}{2}}{z}^2{\mathsf{\Phi }}_{zz}\right]$$

The inverse ET suggests that $\mathsf{\Phi }(z,t)=z^2+E^{-1}\left\{p^{\mathsf{\alpha }}E\left[{\displaystyle \frac{1}{2}}{z}^2{\mathsf{\Phi }}_{zz}\right]\right\}$

The following is the iteration formula using an initial approximation ${\mathsf{\Phi }}_n^{*}(z,t):$

$${\mathsf{\Phi }}_{n+1}(z,t)=E^{-1}\left\{p^{\mathsf{\alpha }}E\left[{\displaystyle \frac{1}{2}}{z}^2{({\mathsf{\Phi }}_n^{*})}_{zz}\right]\right\}$$

(11)

With ${\mathsf{\Phi }}_0(z,t)=z^2$

Utilize the BCs in (4) with $n=0$  to establish ${\mathsf{\Phi }}_0^{*}(z,t)=z^2+z{e}^t-z$

Secondly, using (11), we obtain

$${\mathsf{\Phi }}_1=E^{-1}\left\{p^{\mathsf{\alpha }}E[z^2]\right\}=E^{-1}[z^2{p}^{\mathsf{\alpha }+2}]={\displaystyle \frac{z^2{t}^{\mathsf{\alpha }}}{\mathsf{\Gamma }(\mathsf{\alpha }+1)}}$$

When $n=1$, (4) give, ${\mathsf{\Phi }}_1^{*}={\displaystyle \frac{z^2{t}^{\mathsf{\alpha }}}{\mathsf{\Gamma }(\mathsf{\alpha }+1)}}+z{e}^t-{\displaystyle \frac{z{t}^{\mathsf{\alpha }}}{\mathsf{\Gamma }(\mathsf{\alpha }+1)}},$ and with (11) we obtain

$${\mathsf{\Phi }}_2=E^{-1}\left\{p^{\mathsf{\alpha }}E\left[{\displaystyle \frac{z^2{t}^{\mathsf{\alpha }}}{\mathsf{\Gamma }(\mathsf{\alpha }+1)}}\right]\right\}=E^{-1}[z^2{p}^{2\mathsf{\alpha }+2}]={\displaystyle \frac{z^2{t}^{2\mathsf{\alpha }}}{\mathsf{\Gamma }(2\mathsf{\alpha }+1)}}$$

${\mathsf{\Phi }}_2^{*}={\displaystyle \frac{z^2{t}^{2\mathsf{\alpha }}}{\mathsf{\Gamma }(2\mathsf{\alpha }+1)}}+z{e}^t-{\displaystyle \frac{z{t}^{2\mathsf{\alpha }}}{\mathsf{\Gamma }(2\mathsf{\alpha }+1)}},$ using (11), to obtain

$${\mathsf{\Phi }}_3=E^{-1}\left\{p^{\mathsf{\alpha }}E\left[{\displaystyle \frac{z^2{t}^{2\mathsf{\alpha }}}{\mathsf{\Gamma }(2\mathsf{\alpha }+1)}}\right]\right\}=E^{-1}[z^2{p}^{3\mathsf{\alpha }+2}]={\displaystyle \frac{z^2{t}^{3\mathsf{\alpha }}}{\mathsf{\Gamma }(3\mathsf{\alpha }+1)}}$$

And so on.

Then, the solution of (9) can be found by using (6) to find

$$\mathsf{\Phi }(z,t)={\displaystyle \sum _{n=0}^{\infty }{\mathsf{\Phi }}_n}=z^2+{\displaystyle \frac{z^2{t}^{\mathsf{\alpha }}}{\mathsf{\Gamma }(\mathsf{\alpha }+1)}}+{\displaystyle \frac{z^2{t}^{2\mathsf{\alpha }}}{\mathsf{\Gamma }(2\mathsf{\alpha }+1)}}+{\displaystyle \frac{z^2{t}^{3\mathsf{\alpha }}}{\mathsf{\Gamma }(3\mathsf{\alpha }+1)}}+\cdots$$

For $\mathsf{\alpha }=1,$

$$\mathsf{\Phi }(z,t)={\displaystyle \sum _{n=0}^{\infty }{\mathsf{\Phi }}_n}=z^2+{\displaystyle \frac{z^{2}t}{\mathsf{\Gamma }(2)}}+{\displaystyle \frac{z^2{t}^2}{\mathsf{\Gamma }(3)}}+{\displaystyle \frac{z^2{t}^3}{\mathsf{\Gamma }(4)}}+{\displaystyle \frac{z^2{t}^4}{\mathsf{\Gamma }(5)}}+\dots +{\displaystyle \frac{z^2{t}^n}{\mathsf{\Gamma }(n+1)}}+\dots$$

But $\mathsf{\Gamma }(n+1)=n!$

Hence,

$$\begin{gathered} \mathsf{\Phi }(z,t)=z^2\left(1^2+{\displaystyle \frac{t}{1!}}+{\displaystyle \frac{t^2}{2!}}+{\displaystyle \frac{t^3}{3!}}+{\displaystyle \frac{t^4}{4!}}+\dots +{\displaystyle \frac{t^n}{n!}}+\dots \right) \\ \mathsf{\Phi }(z,t)=z^2{\displaystyle \sum _{n=0}^{\infty }\frac{t^n}{n!}}=z^2{e}^t \end{gathered}$$

if $\mathsf{\alpha }=1$, we obtain the exact solution $\mathsf{\Phi }(z,t)=z^2{e}^t$.

To examine the performance of this method, we first took $\mathsf{\alpha }=1$ to compare the numerical result with the exact solution given above. By using a solution of order 11 and by choosing the domain of study $I=[0,1]\times [0,2],$ we obtain a maximum relative error of order $1.36\times {10}^{-6}.$ On the other hand, for a solution of order 11 and on a larger domain, for example, twice the previous domain (i.e.,$I=[0,1]\times [0,4]),$ the maximum relative error of order will be order $9.15\times {10}^{-4}.$

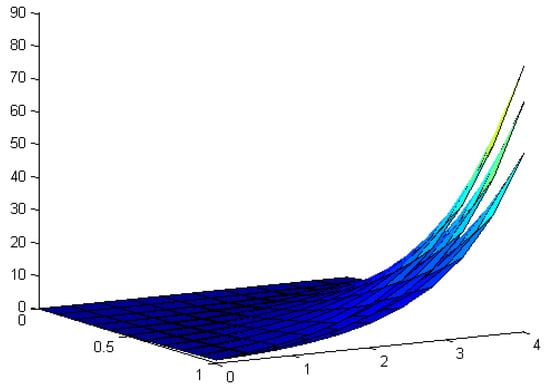
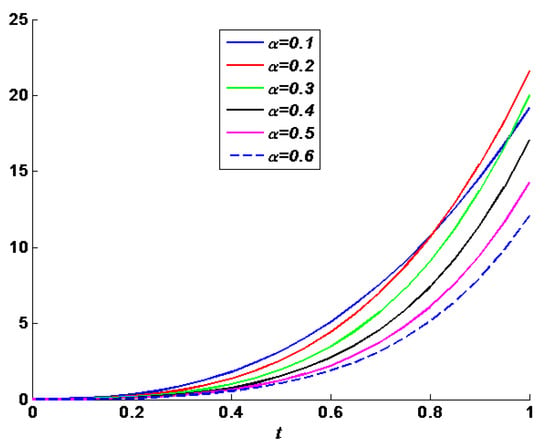
In Figure 1 and Figure 2, we present the solutions obtained for some values of α. The solutions obtained follow two stages. The first occurs when alpha varies between 0.1 and 0.2; then, the values of the solutions increase when alpha increases. The solution reaches maximum values when alpha is close to 0.2. Second, if α exceeds the value 0.2, we notice that if the alpha increases, then the maximum solution decreases.

Example 2.

Consider the inhomogeneous linear FPDE:

$$D_t^{\mathsf{\alpha }}\mathsf{\Phi }+{\displaystyle \frac{\partial \mathsf{\Phi }}{\partial z}}={\displaystyle \frac{t^{1-\mathsf{\alpha }}}{\mathsf{\Gamma }(2-\mathsf{\alpha })}}\sin z-{\displaystyle \frac{{\partial }^3\mathsf{\Phi }}{\partial z^3}}, 0<\mathsf{\alpha }\le 1, z\in [0,\pi ], \mathrm{and} t\in I{R}^{+}$$

(12)

With the IC and BCs,

$$\mathsf{\Phi }(z,0)=0, \mathsf{\Phi }(0,t)=0, \mathsf{\Phi }(\pi ,t)=0$$

(13)

Applying the Elzaki transform to (12), with the IC considered, gives

$$\begin{gathered} E(D_t^{\mathsf{\alpha }}\mathsf{\Phi })=E\left({\displaystyle \frac{t^{1-\mathsf{\alpha }}}{\mathsf{\Gamma }(2-\mathsf{\alpha })}}\sin z-{\displaystyle \frac{{\partial }^3\mathsf{\Phi }}{\partial z^3}}\right)-E{\displaystyle \frac{\partial \mathsf{\Phi }}{\partial z}} \\ {\overline{p}}^{\mathsf{\alpha }}E(\mathsf{\Phi })=\sin z\hspace{0.17em}E\left({\displaystyle \frac{t^{1-\mathsf{\alpha }}}{\mathsf{\Gamma }(2-\mathsf{\alpha })}}\right)-E\left({\displaystyle \frac{{\partial }^3\mathsf{\Phi }}{\partial z^3}}+{\displaystyle \frac{\partial \mathsf{\Phi }}{\partial z}}\right) \\ E[\mathsf{\Phi }]=p^{\mathsf{\alpha }}E\left[{\displaystyle \frac{t^{1-\mathsf{\alpha }}}{\mathsf{\Gamma }(2-\mathsf{\alpha })}}\sin z\right]-p^{\mathsf{\alpha }}E\left({\displaystyle \frac{{\partial }^3\mathsf{\Phi }}{\partial z^3}}+{\displaystyle \frac{\partial \mathsf{\Phi }}{\partial z}}\right) \end{gathered}$$

The inverse ET suggests that $\mathsf{\Phi }(z,t)=t\sin z-E^{-1}\left\{p^{\mathsf{\alpha }}E\left({\displaystyle \frac{{\partial }^3\mathsf{\Phi }}{\partial z^3}}+{\displaystyle \frac{\partial \mathsf{\Phi }}{\partial z}}\right)\right\},$

The iteration formula is as follows, starting from a rough estimate:

$${\mathsf{\Phi }}_{n+1}=-E^{-1}\left\{p^{\mathsf{\alpha }}E\left({\displaystyle \frac{{\partial }^3{\mathsf{\Phi }}_n}{\partial z^3}}+{\displaystyle \frac{\partial {\mathsf{\Phi }}_n}{\partial z}}\right)\right\}$$

(14)

With ${\mathsf{\Phi }}_0=t\sin z$.

Note: ${\mathsf{\Phi }}_0(z=0,t)=t\sin 0=0;$ ${\mathsf{\Phi }}_0(z=\pi ,t)=t\sin \pi =0;$${\mathsf{\Phi }}_1=-E^{-1}\left(p^{\mathsf{\alpha }}E(-t\cos z+{\displaystyle \frac{\partial }{\partial z}}(t\sin z)\right)$.

From (4), we have: ${\mathsf{\Phi }}_0^{*}=t\sin z$.

According to (14), we have ${\mathsf{\Phi }}_1=-E^{-1}\left\{p^{\mathsf{\alpha }}E[-t\cos z+t\cos z]\right\}=0,$

So, the exact solution is as follows: $\mathsf{\Phi }(z,t)=t\sin z$.

Example 3.

Take into account the gas dynamics equation below:

$$D_{tt}^{\mathsf{\alpha }}\mathsf{\Phi }+{\displaystyle \frac{1}{2}}{\mathsf{\Phi }}_z^2-\mathsf{\Phi }+{\mathsf{\Phi }}^2=0, 0<\mathsf{\alpha }\le 1, 0<t\le 1, \mathrm{and} z>0$$

(15)

This equation is nonlinear with the ICs and BCs:

$$\mathsf{\Phi }(z,0)=e^{-z}, \mathsf{\Phi }(0,t)=\hspace{0.17em}\hspace{0.17em}{\in }_{\mathsf{\alpha }}(t^{\mathsf{\alpha }}), \mathsf{\Phi }(1,t)=e^{-1}{\in }_{\mathsf{\alpha }}(t^{\mathsf{\alpha }})$$

(16)

The recurrence relationship will continue as previously,

$${\mathsf{\Phi }}_{n+1}=-E^{-1}\left\{{\displaystyle \frac{p^{\mathsf{\alpha }}}{1-p^{\mathsf{\alpha }}}}E\left[{\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial }{\partial z}}{({\mathsf{\Phi }}_n^{*})}^2-{({\mathsf{\Phi }}_n^{*})}^2\right]\right\}$$

(17)

With ${\mathsf{\Phi }}_0=e^{-z}{\in }_{\mathsf{\alpha }}(t^{\mathsf{\alpha }})$

Equation (4) provides ${\mathsf{\Phi }}_0^{*}=e^{-z}{\in }_{\mathsf{\alpha }}(t^{\mathsf{\alpha }})$.

According to (17), we have: ${\mathsf{\Phi }}_1=-E^{-1}\left\{{\displaystyle \frac{p^{\mathsf{\alpha }}}{1-p^{\mathsf{\alpha }}}}E[0]\right\}=0.$

As a result, the solution of (15) is $\mathsf{\Phi }(z,t)=e^{-z}{\in }_{\mathsf{\alpha }}(t^{\mathsf{\alpha }})$. If $\mathsf{\alpha }=1$, then $\mathsf{\Phi }(z,t)=e^{t-z}$.

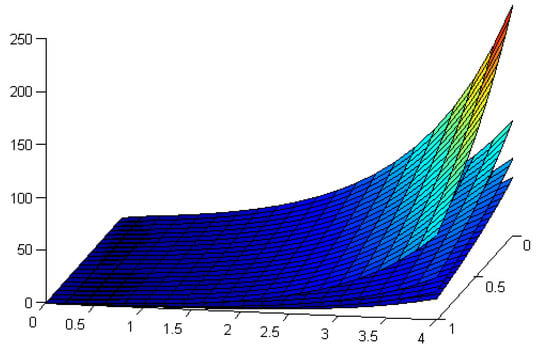
In Figure 3, we present the solutions obtained for some values of α. The solutions obtained when alpha varies between 0.25 and 1; then, the values of the solutions increase when alpha increases. The solution reaches maximum values when alpha is close to 1.

Example 4.

Consider the nonlinear FPDE shown below:

$$D_t^{\mathsf{\alpha }}\mathsf{\Phi }+\mathsf{\Phi }{\mathsf{\Phi }}_z-\mathsf{\Phi }={\displaystyle \frac{2t^{2-\mathsf{\alpha }}}{\mathsf{\Gamma }(3-\mathsf{\alpha })}}{e}^z+t^4{e}^{2z}-t^2{e}^z, 0<\mathsf{\alpha }\le 2, x,t\ge 0$$

(18)

With the ICs and BCs,

$$\mathsf{\Phi }(z,0)={\mathsf{\Phi }}_t(z,0)=0, \mathsf{\Phi }(0,t)=t^2, \mathsf{\Phi }(1,t)=e{t}^2$$

(19)

The recurrence relationship will continue in the same manner,

$${\mathsf{\Phi }}_{n+1}=E^{-1}\left\{p^{\mathsf{\alpha }}E\left[t^4{e}^{2z}-t^2{e}^z+{\mathsf{\Phi }}_n^{*}-{\mathsf{\Phi }}_n^{*}{({\mathsf{\Phi }}_n^{*})}_z\right]\right\}$$

(20)

With ${\mathsf{\Phi }}_0=t^2{e}^z$

Equation (4) provides us with

$${\mathsf{\Phi }}_0^{*}={\mathsf{\Phi }}_0(z,t)+(1-z)(t^2-{\mathsf{\Phi }}_0(0,t)+z(e{t}^2-{\mathsf{\Phi }}_0(1,t)=t^2{e}^z$$

Using (20), we obtain ${\mathsf{\Phi }}_1=E^{-1}\left\{p^{\mathsf{\alpha }}E[0]\right\}=0.$

Accordingly, the solution of (18) is $\mathsf{\Phi }(z,t)=t^2{e}^z$.

Example 5.

Consider the wave-like equation below:

$$D_t^{\mathsf{\alpha }}\mathsf{\Phi }=z^2{\displaystyle \frac{\partial }{\partial z}}[{\mathsf{\Phi }}_z{\mathsf{\Phi }}_{zz}]-z^2{[{\mathsf{\Phi }}_{zz}]}^2-\mathsf{\Phi }, 0<\mathsf{\alpha }\le 2, 0<z\le 1, t>0$$

(21)

This equation is nonlinear with the ICs and BCs,

$$\mathsf{\Phi }(z,0)=0, {\mathsf{\Phi }}_t(z,0)=z, \mathsf{\Phi }(0,t)=0, \mathsf{\Phi }(1,t)=t{e}^{-1}{\in }_{\mathsf{\alpha },2}(-t^{\mathsf{\alpha }})$$

(22)

The recurrence relation is as follows:

$${\mathsf{\Phi }}_{n+1}=E^{-1}\left\{{\displaystyle \frac{p^{\mathsf{\alpha }}}{1+p^{\mathsf{\alpha }}}}E\left[z^2{\displaystyle \frac{\partial }{\partial z}}\left[{({\mathsf{\Phi }}_n^{*})}_z{({\mathsf{\Phi }}_n^{*})}_{zz}\right]-z^2{\left[{({\mathsf{\Phi }}_n^{*})}_{zz}\right]}^2\right]\right\}$$

(23)

With ${\mathsf{\Phi }}_0=z^{2}t{\in }_{\mathsf{\alpha },2}(-t^{\mathsf{\alpha }})$.

Equation (4) gives

$${\mathsf{\Phi }}_0^{*}={\mathsf{\Phi }}_0+(1-z)(0-{\mathsf{\Phi }}_0(0,t))+z(t{\in }_{\mathsf{\alpha },2}(-t^{\mathsf{\alpha }})-{\mathsf{\Phi }}_0(1,t)=z^{2}t{\in }_{\mathsf{\alpha },2}(-t^{\mathsf{\alpha }})$$

Equation (23) gives us

$${\mathsf{\Phi }}_1=E^{-1}\left\{{\displaystyle \frac{p^{\mathsf{\alpha }}}{1+p^{\mathsf{\alpha }}}}E\left[4z^2{t}^2{({\in }_{\mathsf{\alpha },2}(-t^{\mathsf{\alpha }}))}^2-4z^2{t}^2{({\in }_{\mathsf{\alpha },2}(-t^{\mathsf{\alpha }}))}^2\right]\right\}=0$$

The solution to (21) is then $\mathsf{\Phi }(z,t)=z^{2}B{\in }_{\mathsf{\alpha },2}(-t^{\mathsf{\alpha }})$.

Consequently, if $\mathsf{\alpha }=2,$ the exact solution is $\mathsf{\Phi }(z,t)=z^2\sin t$.

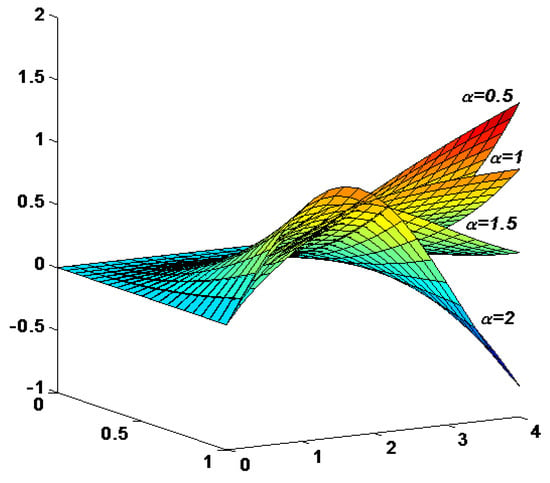
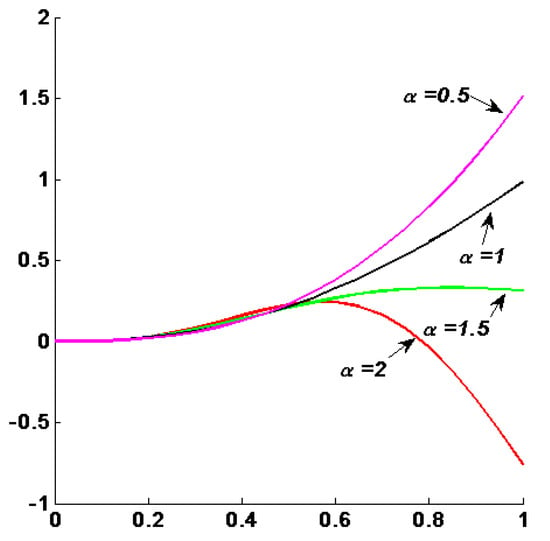
The solutions of examples 4 and 5 are represented in Figure 4 and Figure 5, according to alpha = 0.5, 1, 1.5, and 2. We notice that the branches of each solution on the interval [0, 0.5] and for these values of alpha chosen are almost equal. Then, they begin to remarkably change their gaits from point 0.5 (Figure 5).

Examples 1–5 produced using the current approaches are shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 in comparison with the exact solutions at different values of $\alpha$; then, the approximate solutions found using this method/approach are nearly similar to the exact solutions, as shown by these figures.

5. Conclusions

We have presented an analytical approach for FDEs based on an integral transform for speed and simplicity in solving some problems. We used the ET, but we can use any other integral transform method. Classically, the transformed integral is used in the restricted case when dealing with linear equations and with only an initial condition. We also discuss the convergence analysis in this article. With a simple computational technique, we were able to extend this interesting tool to nonlinear problems with both Cs and BCs. various examples are discussed to show the validity of the proposed technique. Our findings demonstrate that the existing approach works effectively for FDEs based on an integral transform, enabling its future application to more linear and nonlinear FPDEs. Additionally, one of our top priorities going forward is how to broaden the scope of this approach or integrate it with symbolic computing software or other numerical techniques to achieve a more comprehensive application that can be used in a variety of applied sciences.