Extremal Unicyclic Graphs for the Euler Sombor Index: Applications to Benzenoid Hydrocarbons and Drug Molecules

Abstract

With geometric significance, the Euler Sombor index of a graph $\Gamma$ is defined as $EP(\Gamma )={\sum }_{\left\{uv\right\}\in E(\Gamma )}\sqrt{d{\left(u\right)}^2+d{\left(v\right)}^2+d\left(u\right)d\left(v\right)}$. It originates from the mathematical distance property and has been proven to have good chemical applications in octane isomers. In this paper, the minimum and maximum of the Euler Sombor index for unicyclic graphs with given girth, as well as the corresponding extremal graphs, are determined. As an application, the experimental values of this index for some benzenoid hydrocarbons and drug molecules were compared with the boiling point. Through regression analysis, it was further demonstrated that the Euler Sombor index has excellent predictability in the physicochemical properties of compounds.

1. Introduction

Topological indices are used to indicate and predict the physical and chemical properties of compounds [1,2]. It has widespread applications in chemistry, mathematics, and other fields and has become one of the most active research areas in chemical graph theory [3,4,5]. Many types of topological indices have been studied, among which the most extensively investigated and widely applied is undoubtedly vertex-degree-based topological indices (see [6,7,8]).

A vertex-degree-based topological index (VDB topological index) of $\Gamma$ is as follows:

$$T{I}_f(\Gamma )=\sum _{\left\{uv\right\}\in E(\Gamma )}f(d\left(u\right),d\left(v\right)),$$

where $f(x,y)$ is a pertinently chosen symmetric real function with $x\ge 1$ and $y\ge 1$. In [9], motivated by geometrics, Gutman proposed a new concept for the Sombor index, which was defined by

$$SO(\Gamma )=\sum _{\left\{uv\right\}\in E(\Gamma )}\sqrt{d{\left(u\right)}^2+d{\left(v\right)}^2},$$

where $d\left(u\right)$ represents the degree of vertex u and $\left\{uv\right\}$ takes over the edges of graph $\Gamma$.

Since its proposal, this index has attracted considerable attention and research interest. Gutman [9] investigated the extremum of the Sombor index for any tree T and connected graphs. Das et al. [10] provided lower and upper bounds for the Sombor index and established some relationships between the Sombor index and the first and second Zagreb indices. Furthermore, the extremal values of this index among all molecular trees were determined by Deng and Tang [11]. In [12], the authors deduced several upper and lower bounds of the Sombor index for some uniform hypergraphs. Chen and Zhu [13] established the upper and lower bounds of the Sombor index for unicyclic graphs, as well as the extrema of chemical unicyclic graphs with a fixed girth. Cruz and Rada [14] obtained the minimal values of (chemical) unicyclic and bicyclic graphs for the Sombor index and presented an upper bound on this index for such graphs. In 2024, Das [15] completely solved these open problems and characterized the extremal graphs. In addition, the authors [16,17,18] also studied the relevant chemical properties and applications of the Sombor index. For more research on this index, refer to review paper [19,20,21,22].

Recently, a new type of Sombor index, i.e, the Euler Sombor index was proposed by Gutman [23] and Tang et al. [24], which is formulated as

$$EP(\Gamma )=\sum _{\left\{uv\right\}\in E(\Gamma )}\sqrt{d{\left(u\right)}^2+d{\left(v\right)}^2+d\left(u\right)d\left(v\right)}=f(d\left(u\right),d\left(v\right)).$$

Both articles explained that this index originates from an approximate expression of the circumference of an ellipse and is therefore a geometry-based invariant. Meanwhile, Gutman [23] determined some actual relations between the Euler Sombor index and the Sombor index. In [24], the authors determined the extremal values for this Euler Sombor index among all (molecular) trees and characterized the corresponding extremum graphs. More importantly, by studying the relevant chemical properties of octane isomers, such as the boiling point, acentric factor, entropy, SNar, HNar, etc., it has been demonstrated that the Euler Sombor index has excellent predictive applicability for physicochemical properties.

The purpose of our work was to investigate the extremum Euler Sombor index of unicyclic graphs with given girth l, with a focus on its applications for chemical and physical properties. In Section 2 and Section 3, the minimum and maximum Euler Sombor index of unicyclic graphs with given girth are identified and the corresponding extremum graphs are characterized. In Section 4, as an application of the Euler Sombor index, the experimental values of this index for some benzenoid hydrocarbons and drug molecules are compared with the boiling point. Through regression analysis, it is further demonstrated that the Euler Sombor index has excellent predictability of the physicochemical properties of compounds.

Now, we review some definitions and terms that will be used in the following text. In this article, we consider graphs as connected, simple, and undirected. A graph $\Gamma =(V,E)$, where the vertex set and edge set are denoted by $V(\Gamma )$ and $E(\Gamma )$, respectively. The degree of vertex v is denoted by $d_{\Gamma }\left(v\right)$ or $d\left(v\right)$. In particular, a vertex v is called pendant if $d\left(v\right)=1$. The neighbors of vertex v, denoted by $N_{\Gamma }\left(v\right)$ or $N\left(v\right)$, is the collection of vertices adjacent to v. An edge $\left\{uv\right\}$ is called pendant if $d\left(u\right)=1$ or $d\left(v\right)=1$. $\Gamma -\left\{uv\right\}$ represents the subgraph from $\Gamma$ by deleting the edge $\left\{uv\right\}$. Meanwhile, $\Gamma +\left\{uv\right\}$ represents the graph by joining a new edge $\left\{uv\right\}$ from $\Gamma$. Recall that a graph $\Gamma$ is unicyclic if $\left|E\right(\Gamma \left)\right|=\left|V\right(\Gamma \left)\right|$. Let ${\mathbb{U}}_{n,l}$ represent the set of unicyclic graphs with given girth l and an order of n. Clearly, if $l=n$, then ${\mathbb{U}}_{n,n}=C_n$, where $C_n$ be the cycle of n vertices.

2. The Minimal Euler Sombor Index in ${\mathbb{U}}_{n,l}$

Lemma 1.

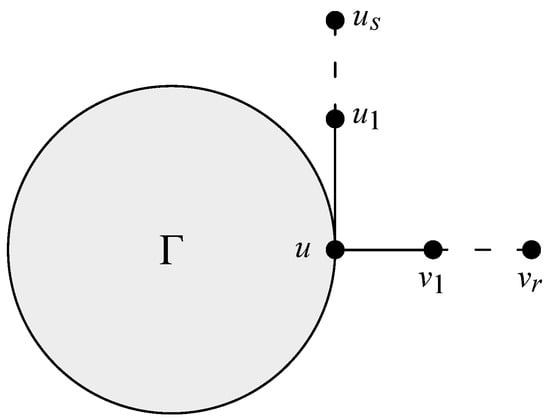
Let ${\Gamma }_1\in {\mathbb{U}}_{n,l}$ be as shown in Figure 1, where $d\left(u\right)\ge 3$, $r\ge s\ge 1$ and $\Gamma$ is a subgraph of ${\Gamma }_1$. Suppose that ${\Gamma }_2={\Gamma }_1-u{u}_1+v_r{u}_1$. Then, $EP\left({\Gamma }_2\right)<EP\left({\Gamma }_1\right)$.

Figure 1. Graph of ${\Gamma }_1$.

Proof. 

Assume that $N_{{\Gamma }_1}\left(u\right)=\{u_1,v_1,x_1,x_2,\cdots x_t\}$ and $N_{\Gamma }\left(u\right)=\{x_1,x_2,\cdots x_t\}$, where $t\ge 1$. Thus, we have $d_{{\Gamma }_1}\left(u\right)=t+2$. Now, three possibilities occur according to the values of $d_{{\Gamma }_1}\left(u_1\right)$ and $d_{{\Gamma }_1}\left(v_1\right)$.

Case 1. If $d_{{\Gamma }_1}\left(u_1\right)=d_{{\Gamma }_1}\left(v_1\right)=1$. Since $t\ge 1$, combining the structures of ${\Gamma }_1$ and ${\Gamma }_2$, we obtain

$$\begin{array}{c}EP\left({\Gamma }_1\right)-EP\left({\Gamma }_2\right)\hfill \\ ={\Sigma }_{i=1}^{t}f(t+2,d_{\Gamma }\left(x_i\right))+2f(t+2,1)-\left({\Sigma }_{i=1}^{t}f(t+1,d_{\Gamma }\left(x_i\right))+f(t+1,2)+f(2,1)\right)\hfill \\ \ge {\Sigma }_{i=1}^t\left(\sqrt{{(t+2)}^2+{x_i}^2+x_i(t+2)}-\sqrt{{(t+1)}^2+{x_i}^2+x_i(t+1)}\right)\hfill \\ +2\sqrt{t^2+5t+7}-\sqrt{t^2+4t+7}-\sqrt{7}\hfill \\ \ge 2\sqrt{t^2+5t+7}-\sqrt{t^2+4t+7}-\sqrt{7}\hfill \\ >\sqrt{13}-\sqrt{7}>0.\hfill \end{array}$$

Case 2. If $d_{{\Gamma }_1}\left(v_1\right)=2,d_{{\Gamma }_1}\left(u_1\right)=1$. Similar to Case 1, it can be concluded that

$$\begin{array}{c}EP\left({\Gamma }_1\right)-EP\left({\Gamma }_2\right)\hfill \\ ={\Sigma }_{i=1}^t\left(f(t+2,d\left(x_i\right))-f(t+1,d\left(x_i\right))\right)+f(t+2,2)-f(t+1,2)+f(t+2,1)-f(2,2)\hfill \\ >\sqrt{t^2+6t+10}-\sqrt{t^2+4t+7}+\sqrt{t^2+5t+7}-\sqrt{12}\hfill \\ >\sqrt{t^2+6t+10}-\sqrt{12}\hfill \\ \ge \sqrt{17}-\sqrt{12}>0.\hfill \end{array}$$

Case 3. If $d_{{\Gamma }_1}\left(v_1\right)=d_{{\Gamma }_1}\left(u_1\right)=2$, it follows that

$$\begin{array}{c}EP\left({\Gamma }_1\right)-EP\left({\Gamma }_2\right)\hfill \\ ={\Sigma }_{i=1}^t\left(f(t+2,d_{\Gamma }\left(x_i\right))-f(t+1,d_{\Gamma }\left(x_i\right))\right)+2f(t+2,2)+f(2,1)-f(t+1,2)-2f(2,2)\hfill \\ >2\sqrt{t^2+6t+12}+\sqrt{7}-\sqrt{t^2+4t+7}-2\sqrt{12}\hfill \\ >\sqrt{t^2+6t+12}+\sqrt{7}-2\sqrt{12}\hfill \\ \ge \sqrt{19}+\sqrt{7}-2\sqrt{12}>0.\hfill \end{array}$$

Therefore, based on the above three cases, we can conclude that $EP\left({\Gamma }_1\right)-EP\left({\Gamma }_2\right)>0$. The lemma is proven. □

Lemma 2.

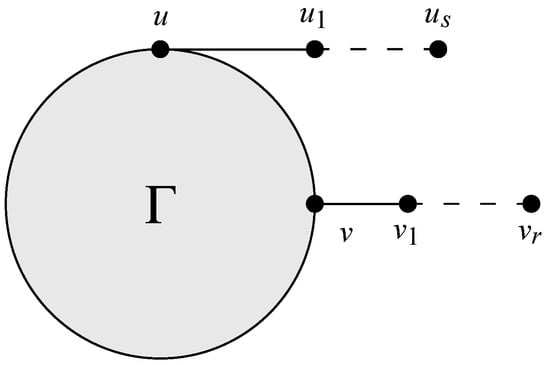
Let ${\Gamma }_3\in {\mathbb{U}}_{n,l}$ be as shown in Figure 2, where $u,v\in E\left(C_l\right)$, $d\left(u\right)=d\left(v\right)=3$ and $r\ge s\ge 1$. Assume that ${\Gamma }_4={\Gamma }_3-u{u}_1+v_r{u}_1$. Then, we have $EP\left({\Gamma }_4\right)<EP\left({\Gamma }_3\right)$.

Figure 2. Graph of ${\Gamma }_3$.

Proof. 

We assume that $N_{{\Gamma }_3}\left(u\right)=\{u_1,x_1,x_2\}$ and $N_{{\Gamma }_4}\left(v\right)=\{v_1,y_1,y_2\}$. If $uv\in C_l$, then $x_2=v$, $y_2=u$. We can use this for the following three cases.

Case 1. $d_{{\Gamma }_3}\left(u_1\right)=d_{{\Gamma }_3}\left(v_1\right)=1$. Since $\sqrt{3^2+{x_i}^2+3x_i}-\sqrt{2^2+{x_i}^2+2x_i}>0$ for $i=1$ and 2, we deduce that

$$\begin{array}{c}EP\left({\Gamma }_3\right)-EP\left({\Gamma }_4\right)\hfill \\ ={\Sigma }_{i=1}^{2}f(3,d_{{\Gamma }_3}\left(x_i\right))+2f(3,1)-\left({\Sigma }_{i=1}^{2}f(2,d_{{\Gamma }_3}\left(x_i\right))+f(3,2)+f(2,1)\right)\hfill \\ \ge {\Sigma }_{i=1}^2\left(\sqrt{3^2+{x_i}^2+3x_i}-\sqrt{2^2+{x_i}^2+2x_i}\right)+2\sqrt{13}-\sqrt{19}-\sqrt{7}\hfill \\ >2\sqrt{13}-\sqrt{19}-\sqrt{7}>0.\hfill \end{array}$$

Case 2. $d_{{\Gamma }_3}\left(u_1\right)=2,d_{{\Gamma }_3}\left(v_1\right)=1$. It follows that

$$\begin{array}{c}EP\left({\Gamma }_3\right)-EP\left({\Gamma }_4\right)\hfill \\ ={\Sigma }_{i=1}^{2}f(3,d_{{\Gamma }_3}\left(x_i\right))+f(3,1)+f(2,1)-\left({\Sigma }_{i=1}^{2}f(2,d_{{\Gamma }_3}\left(x_i\right))+f(2,2)+f(2,1)\right)\hfill \\ \ge {\Sigma }_{i=1}^2\left(\sqrt{3^2+{x_i}^2+3x_i}-\sqrt{2^2+{x_i}^2+2x_i}\right)+\sqrt{13}-\sqrt{12}\hfill \\ >\sqrt{13}-\sqrt{12}>0.\hfill \end{array}$$

Case 3. $d_{{\Gamma }_3}\left(u_1\right)=d_{{\Gamma }_3}\left(v_1\right)=2$. If $uv\in C_l$, we immediately have

$$\begin{array}{c}EP\left({\Gamma }_3\right)-EP\left({\Gamma }_4\right)\hfill \\ =f(3,d_{{\Gamma }_3}\left(x_1\right))+f(3,3)+f(3,2)+f(2,1)-\left(f(2,d_{{\Gamma }_3}\left(x_1\right))+f(3,2)+2f(2,2)\right)\hfill \\ \ge (\sqrt{3^2+{x_1}^2+3x_1}-\sqrt{2^2+{x_i}^2+2x_1})+\sqrt{27}+\sqrt{13}+\sqrt{7}-\sqrt{19}-2\sqrt{12}\hfill \\ >\sqrt{27}+\sqrt{13}+\sqrt{7}-\sqrt{19}-2\sqrt{12}>0.\hfill \end{array}$$

Similarly, if $uv\notin C_l$, then we have

$$\begin{array}{c}EP\left({\Gamma }_3\right)-EP\left({\Gamma }_4\right)\hfill \\ ={\Sigma }_{i=1}^{2}f(3,d_{{\Gamma }_3}\left(x_i\right))+f(3,2)+f(2,1)-\left({\Sigma }_{i=1}^{2}f(2,d_{{\Gamma }_3}\left(x_i\right))+2f(2,2)\right)\hfill \\ \ge {\Sigma }_{i=1}^2\left(\sqrt{3^2+{x_i}^2+3x_i}-\sqrt{2^2+{x_i}^2+2x_i}\right)+\sqrt{19}+\sqrt{7}-2\sqrt{12}\hfill \\ >\sqrt{19}+\sqrt{7}-2\sqrt{12}>0.\hfill \end{array}$$

Consequently, the above discussion implies that $EP\left({\Gamma }_3\right)-EP\left({\Gamma }_4\right)>0$. This completes the proof. □

Let $M_{n,l}\in {\mathbb{U}}_{n,l}$, and $M_{n,l}$ is obtained by attaching the path $P=v_1{v}_2\dots v_{n-l}$ to the cycle of $C_l$ via the vertex $v\in C_l$. Now, we present the main results.

Theorem 1.

Let $\Gamma \in {\mathbb{U}}_{n,l}$. Then,

$$\begin{array}{c}EP(\Gamma )\ge \left\{\begin{array}{ccc}& 2\sqrt{3}(n-4)+3\sqrt{19}+\sqrt{7},\hfill & \hfill \mathrm{if}3\le l\le n-2,\\ & 2\sqrt{3}(n-3)+2\sqrt{19}+\sqrt{13},\hfill & \hfill \mathrm{if}l=n-1,& \\ & 2\sqrt{3}n,\hfill & \hfill \mathrm{if}l=n.& \end{array}\right.\hfill \end{array}$$

equality holds if and only if $\Gamma \cong M_{n,l}$.

Proof. 

Firstly, for $l=n$ and $l=n-1$, by direct calculation, we have

$$\begin{array}{c}EP(\Gamma )=EP\left(M_{n,n}\right)=EP\left(C_n\right)=n\sqrt{2^2+2^2+2^2}=2\sqrt{3}n,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill EP(\Gamma )& =EP\left(M_{n,n-1}\right)=(n-3)\sqrt{2^2+2^2+2·2}+2\sqrt{2^2+3^2+2·3}+\sqrt{1^2+3^2+3}\hfill \\ & =2\sqrt{3}(n-3)+2\sqrt{19}+\sqrt{13}.\hfill \end{array}$$

Next, we consider the case $3\le l\le n-2$. Suppose $C=v_1{v}_2\cdots v_l{v}_1$ is the unique cycle in $\Gamma$. Consequently, $\Gamma \ncong C_n$, and there is at least a vertex $v_i$, such that $d\left(v_i\right)\ge 3$.

If there are at least two vertices in $\{v_1,v_2,\cdots ,v_l\}$ whose degrees are greater than or equal to 3, then Lemmas 1 and 2 can be applied to obtain

$$EP(\Gamma )>EP\left(M_{n,l}\right)=2\sqrt{3}(n-4)+3\sqrt{19}+\sqrt{7}.$$

If there is exactly one vertex in $\{v_1,v_2,\cdots ,v_l\}$ whose degree is greater than or equal to 3, without loss of generality, let $v_i$. If $d\left(v_i\right)\ge 4$, according to Lemma 1, we obtain

$$EP(\Gamma )>EP\left(M_{n,l}\right)=2\sqrt{3}(n-4)+3\sqrt{19}+\sqrt{7}.$$

If $d\left(v_i\right)=3$, by Lemma 1, we deduce that

$$EP(\Gamma )\ge EP\left(M_{n,l}\right)=2\sqrt{3}(n-4)+3\sqrt{19}+\sqrt{7},$$

and equality holds when $\Gamma \cong M_{n,l}$. Therefore, from the above discussion, the theorem holds. □

3. The Maximal Euler Sombor Index in ${\mathbb{U}}_{n,l}$

Let $H_{n,l}\in {\mathbb{U}}_{n,l}$ be a unicylic graph obtained by attaching $n-l$ pendant edges to the vertex $u\in V\left(C_l\right)$. In particular, $H_{n,3}$ is denoted as $S_n+e$.

Lemma 3.

Let $f(s,t)=\sqrt{{(s+t+2)}^2+s+t+3)}-\sqrt{{(s+2)}^2+s+3}-\sqrt{{(t+2)}^2+t+3}+\sqrt{12}$, where $s,t\ge 1$. Then, $f_{min}(s,t)=f(1,1)>0$.

Proof. 

Since ${\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(x+2+\frac{1}{2})}^2}}}}$ is increasing with $x\ge 1$, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial f(s,t)}{\partial s}}& ={\displaystyle \frac{(s+t+2)+\frac{1}{2}}{\sqrt{{(s+t+2)}^2+(s+t+2)+1}}}-{\displaystyle \frac{(s+2)+\frac{1}{2}}{\sqrt{{(s+2)}^2+(s+2)+1}}}\hfill \\ & ={\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(s+t+2+\frac{1}{2})}^2}}}}-{\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(s+2+\frac{1}{2})}^2}}}}\hfill \\ & >0.\hfill \end{array}$$

Similarly, it can be concluded that

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial f(s,t)}{\partial t}}& ={\displaystyle \frac{(s+t+2)+\frac{1}{2}}{\sqrt{{(s+t+2)}^2+(s+t+2)+1}}}-{\displaystyle \frac{(t+2)+\frac{1}{2}}{\sqrt{{(t+2)}^2+(t+2)+1}}}\hfill \\ & ={\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(s+t+2+\frac{1}{2})}^2}}}}-{\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(t+2+\frac{1}{2})}^2}}}}\hfill \\ & >0.\hfill \end{array}$$

Consequently, we obtain $f_{min}(s,t)=f(1,1)=\sqrt{21}+\sqrt{12}-2\sqrt{13}>0$, and Lemma 3 is finished. □

Lemma 4.

Let $f(s,t)=2\sqrt{{(s+t+2)}^2+s+t+3}+2\sqrt{{(s+t+2)}^2+2{(s+t)}^2+8}+2\sqrt{12}-\sqrt{{(s+2)}^2+s+3}-\sqrt{{(t+2)}^2+t+3}-2\sqrt{{(s+2)}^2+2s+8}-2\sqrt{{(t+2)}^2+2t+8}$, where $s,t\ge 1$. Then, $f_{min}(s,t)=f(1,1)>0$.

Proof. 

Because ${\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(x+2+\frac{1}{2})}^2}}}}$ and ${\displaystyle \frac{2}{(x+2)+2}}$ are increasing and decreasing with $x\ge 1$, respectively, we deduce that

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial f(s,t)}{\partial s}}& ={\displaystyle \frac{2(s+t+2)+1}{\sqrt{{(s+t+2)}^2+(s+t+2)+1}}}+{\displaystyle \frac{2(s+t+2)+2}{\sqrt{{(s+t+2)}^2+2(s+t+2)+4}}}\hfill \\ & -{\displaystyle \frac{(s+2)+\frac{1}{2}}{\sqrt{{(s+2)}^2+(s+2)+1}}}-{\displaystyle \frac{2(s+2)+2}{\sqrt{{(s+2)}^2+2(s+2)+4}}}\hfill \\ & >\left({\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(s+t+2+\frac{1}{2})}^2}}}}-{\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(s+2+\frac{1}{2})}^2}}}}\right)+\left({\displaystyle \frac{2}{(s+2)+2}}-{\displaystyle \frac{2}{(s+t+2)+2}}\right)\hfill \\ & >0.\hfill \end{array}$$

Similarly, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial f(s,t)}{\partial t}}& >\left({\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(s+t+2+\frac{1}{2})}^2}}}}-{\displaystyle \frac{1}{\sqrt{1+\frac{\frac{3}{4}}{{(t+2+\frac{1}{2})}^2}}}}\right)+\left({\displaystyle \frac{2}{(t+2)+2}}-{\displaystyle \frac{2}{(s+t+2)+2}}\right)\hfill \\ & >0.\hfill \end{array}$$

Therefore, we have $f_{min}(s,t)=f(1,1)=2\sqrt{21}+2\sqrt{28}+\sqrt{12}-4\sqrt{19}-2\sqrt{13}>0$, and the proof is completed. □

Lemma 5.

Let ${\Gamma }_1\in {\mathbb{U}}_{n,l}$, and T is a component of ${\Gamma }_1-C_l$, where $\left\{uv\right\}\in T$ and $u\in V\left(C_l\right)$. If $\left|T\right|\ge 2$, then the edge $\left\{uv\right\}$ is contracted to u, and joining a pendant edge $\left\{uw\right\}$ is denoted it by ${\Gamma }_2$. Thus, $EP\left({\Gamma }_1\right)<EP\left({\Gamma }_2\right)$.

Proof. 

Suppose that $N_{{\Gamma }_1}\left(u\right)=\{v,x_1,x_2,\cdots ,x_t\}$ and $N_{{\Gamma }_1}\left(v\right)=\{u,y_1,y_2,\cdots ,y_s\}$, where $s,t\ge 1$. Since $f(x,y)=\sqrt{x^2+y^2+xy}$ increases with $x\ge 1$, we have

$$\begin{array}{c}EP\left({\Gamma }_2\right)-EP\left({\Gamma }_1\right)\hfill \\ ={\Sigma }_{i=1}^t\left(f(d\left(u\right)+d\left(v\right)-1,d\left(x_i\right))-f(d\left(u\right),d\left(x_i\right))\right)\hfill \\ +{\Sigma }_{i=1}^s\left(f(d\left(u\right)+d\left(v\right)-1,d\left(x_i\right))-f(d\left(v\right),d\left(x_i\right))\right)\hfill \\ +f\left(d\right(u)+d(v)-1,1)-f\left(d\right(u),d(v\left)\right)\hfill \\ \ge \sqrt{{(t+s+1)}^2+t+s+2}-\sqrt{{(t+1)}^2+{(s+1)}^2+(t+1)(s+1)}\hfill \\ \ge \sqrt{t^2+s^2+3t+3s+3+2ts}-\sqrt{t^2+s^2+3t+3s+3+ts}\hfill \\ >0.\hfill \end{array}$$

Therefore, the lemma holds true. □

Lemma 6.

Let ${\Gamma }_3\in {\mathbb{U}}_{n,l}$; $\{u{u}_1,u{u}_2,\cdots ,u{u}_s\}$ and $\{v{v}_1,v{v}_2,\cdots ,v{v}_t\}$ are the pendant edges joining to u and v, where $u,v\in V\left(C_l\right)$ and $s,t\ge 1$. Assume that ${\Gamma }_4={\Gamma }_3-\{v{v}_1,v{v}_2,\cdots ,v{v}_t\}+\{u{v}_1,u{v}_2,\cdots ,u{v}_t\}$; then, $EP\left({\Gamma }_3\right)<EP\left({\Gamma }_4\right)$.

Proof. 

Assume that $N_{{\Gamma }_3}\left(u\right)=\{x_1,x_2,u_1,u_2,\cdots ,u_s\}$ and $N_{{\Gamma }_3}\left(v\right)=\{y_1,y_2,v_1,v_2,\cdots ,v_t\}$. If $uv\in E\left({\Gamma }_3\right)$, then $u=y_1$, $v=x_1$. We consider two cases according to whether $\left\{uv\right\}\in E\left(C_l\right)$ or not.

Case 1. $\left\{uv\right\}\in E\left(C_l\right)$. Since $f(d\left(u\right)+d\left(v\right)-2,d\left(x_2\right))-f(d\left(u\right),d\left(x_2\right))>0$, we have

$$\begin{array}{c}EP\left({\Gamma }_4\right)-EP\left({\Gamma }_3\right)\hfill \\ ={\Sigma }_{i=1}^s\left(f(d\left(u\right)+d\left(v\right)-2,d\left(x_i\right))-f(d\left(u\right),d\left(x_i\right))\right)\hfill \\ +{\Sigma }_{i=1}^t\left(f(d\left(u\right)+d\left(v\right)-2,d\left(x_i\right))-f(d\left(v\right),d\left(x_i\right))\right)+f(d\left(u\right)+d\left(v\right)-2,2)\hfill \\ -f(d\left(u\right),d\left(v\right))+f(d\left(u\right)+d\left(v\right)-2,d\left(x_2\right))-f(d\left(u\right),d\left(x_2\right))+f(2,d\left(y_2\right))-f(d\left(v\right),d\left(y_2\right))\hfill \\ >2\sqrt{{(s+t+2)}^2+s+t+3}+\sqrt{{(s+t+2)}^2+2{(s+t)}^2+8}+\sqrt{12}-\sqrt{{(s+2)}^2+s+3}\hfill \\ -\sqrt{{(t+2)}^2+t+3}-\sqrt{{(s+2)}^2+{(t+2)}^2+(s+2)(t+2)}-\sqrt{{(t+2)}^2+s^2+2t+8}.\hfill \end{array}$$

Through direct calculations, it can be concluded that

$$\sqrt{{(s+t+2)}^2+s+t+3}>\sqrt{{(t+2)}^2+s^2+2t+8},$$

$$\sqrt{{(s+t+2)}^2+2{(s+t)}^2+8}>\sqrt{{(s+2)}^2+{(t+2)}^2+(s+2)(t+2)}.$$

Consequently, based on the above two equations and Lemma 3, we have

$$\begin{array}{c}EP\left({\Gamma }_4\right)-EP\left({\Gamma }_3\right)\hfill \\ >\sqrt{{(s+t+2)}^2+s+t+3}+\sqrt{12}-\sqrt{{(s+2)}^2+s+3}-\sqrt{{(t+2)}^2+t+3}>0.\hfill \end{array}$$

Case 2. $\left\{uv\right\}\notin E\left(C_l\right)$. Note that $N_{{\Gamma }_3}\left(u\right)=\{x_1,x_2,u_1,u_2,\cdots ,u_s\}$ and $N_{{\Gamma }_3}\left(v\right)=\{y_1,y_2,v_1,v_2,\cdots ,v_t\}$. From Case 1, for $i=1,2$, $d\left(x_i\right)=d\left(y_i\right)=2$. This together with Lemma 4 implies that

$$\begin{array}{c}EP\left({\Gamma }_4\right)-EP\left({\Gamma }_3\right)\hfill \\ ={\Sigma }_{i=1}^s\left(f(d\left(u\right)+d\left(v\right)-2,d\left(x_i\right))-f(d\left(u\right),d\left(x_i\right))\right)\hfill \\ +{\Sigma }_{i=1}^t\left(f(d\left(u\right)+d\left(v\right)-2,d\left(x_i\right))-f(d\left(v\right),d\left(x_i\right))\right)\hfill \\ +2\left(f\left(d\right(u)+d(v)-2,2)-f\left(d\right(u),2)\right)+2\left(f(2,2)-f\left(d\right(v),2)\right)\hfill \\ \ge 2\sqrt{{(s+t+2)}^2+s+t+3}+2\sqrt{{(s+t+2)}^2+2{(s+t)}^2+8}+2\sqrt{12}\hfill \\ -\sqrt{{(s+2)}^2+s+3}-\sqrt{{(t+2)}^2+t+3}-2\sqrt{{(s+2)}^2+2s+8}-2\sqrt{{(t+2)}^2+2t+8}\hfill \\ >0.\hfill \end{array}$$

Therefore, the proof is finished. □

With the help of the above two lemmas, we can deduce the maximal Euler Sombor index in ${\mathbb{U}}_{n,l}$.

Theorem 2.

Let $\Gamma \in {\mathbb{U}}_{n,l}$. Then,

$$EP(\Gamma )\le (n-3)\sqrt{n^2-n+1}+2\sqrt{n^2+3}+\sqrt{12},$$

and equality occurs when $\Gamma \cong H_{n,l}$.

Proof. 

Let $C=v_1{v}_2\cdots v_l{v}_1$ be the unique cycle in $\Gamma$. Then, there is at least one vertex $v_i$ that meets with $d\left(v_i\right)\ge 3$. If there are at least two vertices in $\{v_1,v_2,\cdots ,v_l\}$ whose degrees are greater than or equal to 3, then according to Lemmas 5 and 6, we deduce that

$$EP(\Gamma )<EP\left(H_{n,l}\right)=(n-3)\sqrt{n^2-n+1}+2\sqrt{n^2+3}+\sqrt{12}.$$

If there is exactly one vertex in $\{v_1,v_2,\cdots ,v_l\}$ whose degrees are greater than or equal to 3, and $\Gamma \ncong H_{n,l}$, then, by Lemma 5, we have

$$EP(\Gamma )<EP\left(H_{n,l}\right)=(n-3)\sqrt{n^2-n+1}+2\sqrt{n^2+3}+\sqrt{12}.$$

If $\Gamma \ncong H_{n,l}$, we have

$$EP(\Gamma )=EP\left(H_{n,l}\right)=(n-3)\sqrt{n^2-n+1}+2\sqrt{n^2+3}+\sqrt{12}.$$

Therefore, considering the above cases, the theorem holds. □

4. Chemical Applications of the Euler Sombor Index

There are various types of topological indices, and they have grown rapidly in recent years. One important role of topological indices is to predict the physical and chemical properties of molecules, such as the melting point, boiling point, etc. However, current research on topological indices mostly focuses on mathematical calculations, and it is very important to calculate topological indices through experiments and compare them with chemical and physical properties. Recently, Tang et al. [24] determined the relationship between the Euler Sombor index and the structure performance for octane. As an important compound, the study of the index and properties of benzene hydrocarbons is also of great significance. Therefore, in this section, we fill this gap.

Firstly, some typical benzenoid hydrocarbons (BHs) were considered (Figure 3). The experimental values of the Euler Sombor index (EP), Sombor index (SO), Elliptic Sombor index (ESO), forgotten topological index (F), symmetric division degree index (SDD), first (M1) and second (M2) Zagreb indices, and sum connectivity index (SCI), as well as the boiling point (BP) of benzenoid hydrocarbons, are shown in Table 1. In particular, |V(BH)| represents the size of molecules (the number of vertices) in BHs.

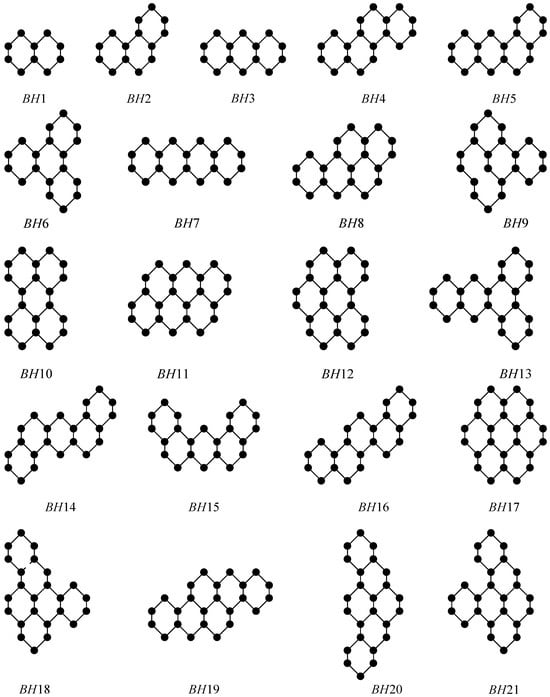
Figure 3. Molecular graphs of some BHs.

Table 1. Experimental values of some existing indices for BHs with BP.

BH	$\left|\mathit{V}\right(\mathit{BH}\left)\right|$	BP	$\mathit{EP}$	$\mathit{SO}$	$\mathit{ESO}$	F	$\mathit{SDD}$	${\mathit{M}}_1$	${\mathit{M}}_2$	$\mathit{SCI}$
BH1	10	218	43.416	35.635	165.449	90	172	50	57	6.014
BH2	14	338	65.991	54.160	252.416	170	409	76	91	7.408
BH3	14	340	66.048	54.300	263.016	180	500	76	90	7.394
BH4	18	431	88.565	72.685	362.011	280	995	102	125	9.619
BH5	18	425	88.622	72.825	361.297	284	938	102	124	9.605
BH6	18	429	88.507	72.545	362.725	246	729	102	126	9.633
BH7	18	440	88.680	72.965	360.583	298	1085	102	123	9.591
BH8	20	496	104.211	85.553	437.664	318	1080	120	151	10.830
BH9	20	493	104.153	85.413	438.379	286	862	120	152	10.844
BH10	20	497	104.153	85.413	438.379	286	862	120	152	10.844
BH11	22	547	119.857	98.421	513.318	356	1201	138	177	12.041
BH12	22	542	119.799	98.281	514.032	326	995	138	178	12.055
BH13	22	535	111.139	91.210	460.292	370	1344	128	159	11.830
BH14	22	536	111.197	91.350	459.578	424	1780	128	158	11.816
BH15	22	531	111.197	91.350	459.578	402	1584	128	158	11.816
BH16	22	519	111.139	91.210	460.292	424	1780	128	159	11.830
BH17	24	590	135.445	111.149	589.686	366	1128	156	204	13.266
BH18	24	592	126.727	103.938	536.659	411	1484	146	186	13.055
BH19	24	596	126.785	104.078	535.945	466	1926	146	185	13.041
BH20	24	594	126.785	104.078	535.945	466	1927	146	185	13.041
BH21	24	595	126.727	103.938	536.659	392	1349	146	186	13.055

To eliminate the influence of molecular size on the prediction model, we adopted the method of dividing the obtained index value with the number of vertices and then compared different graphs of BHs to obtain the true prediction potentiality. From Table 1, we constructed the scatter chart among BP and $EP$ values of BHs, as shown in Figure 4. Furthermore, we obtained the correlation coefficient (R) of various indices through regression analysis, as shown in Table 2. Therefore, the above results imply that the Euler Sombor index has important applicability in predicting the boiling point of BHs.

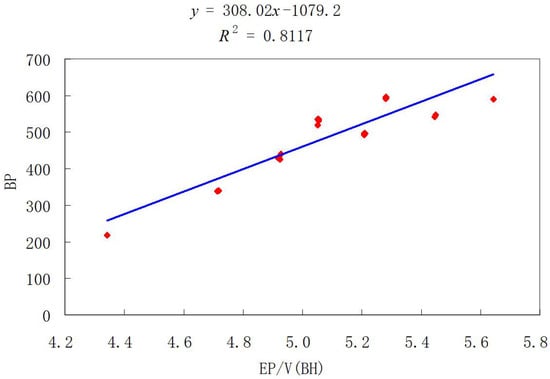
Figure 4. Linear fitting of $EP$ with BP for some BHs.

Table 2. The correlation coefficient of some existing indices for BHs with BP.

Index	$\mathit{EP}$	$\mathit{SO}$	$\mathit{ESO}$	F	$\mathit{SDD}$	${\mathit{M}}_1$	${\mathit{M}}_2$	$\mathit{SCI}$
R	0.9009	0.9012	0.9038	0.8004	0.7269	0.9007	0.8971	0.2924

We conducted the above-mentioned research on some drug designs and mainly examined the ten chemical drugs listed in Table 3, whose molecular structures can be viewed online and are thus omitted here. The experimental values of the Euler Sombor index (EP), Sombor index (SO), Elliptic Sombor index (ESO), and boiling point (BP) of some drugs are shown in Table 3.

Table 3. Experimental values of three types of Sombor index for drug molecules with BP.

Drug Molecules	$\left|\mathit{V}\right(\mathbf{\Gamma }\left)\right|$	BP	$\mathit{EP}$	$\mathit{SO}$	$\mathit{ESO}$
Carmustine	12	404.0	40.208	33.415	146.254
Convolutamydine B	16	496.7	75.512	63.265	328.024
Bunitrolol	17	414.2	70.562	59.579	286.141
Perfragilin A	17	413.5	78.841	65.774	338.283
Melatonin	17	512.8	73.336	60.810	290.423
Aspirin	20	321.4	52.642	44.042	207.560
Podophyllotoxin	29	597.9	142.744	117.694	603.003
Deguelin	31	560.1	147.033	134.880	734.123
Aminopterin	32	551.7	141.805	118.149	571.435
Minocycline	35	563.3	184.633	155.027	863.063

Similar to the operation of BHs, we eliminated the influence of molecular size on the prediction model by dividing the obtained index value with the number of vertices. Therefore, we constructed the scatter chart among BP and $EP$ values of these drug molecules, as shown in Figure 5. Moreover, we obtained the correlation coefficient (R) of three types of Sombor index through regression analysis, as shown in Table 4. Clearly, the Euler Sombor index has a good ability to distinguish drug molecules and can be widely used in compound identification and drugs design.

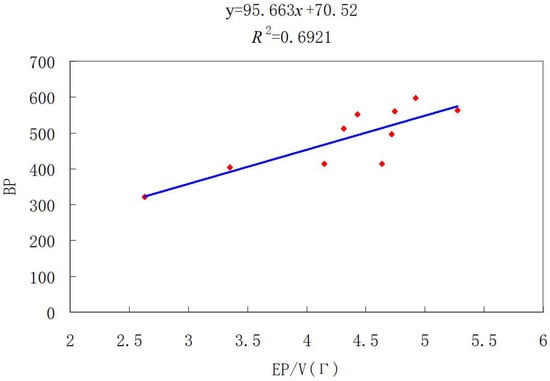
Figure 5. Linear fitting of $EP$ with BP for some drug molecules.

Table 4. The correlation coefficient of three types of Sombor index for drug molecules with BP.

Index	$\mathit{EP}$	$\mathit{SO}$	$\mathit{ESO}$
R	0.8319	0.8313	0.7911

5. Conclusions

In this paper, the minimum and maximum of the Euler Sombor index for unicyclic graphs with given girth were determined and the corresponding extremal graphs were characterized. In addition, by experimental comparison, it was confirmed that the Euler Sombor index can describe the physicochemical properties of benzene hydrocarbons and some drug structures. Through regression analysis, Figure 4 and Figure 5 show that both of the correlation coefficients (R) of the Euler Sombor index ($EP$) for benzenoid hydrocarbons and drug molecules with boiling point (BP) are greater than 0.8. This indicates that this index has good predictive ability for the physicochemical properties of compounds, especially those containing benzene rings. Therefore, it is of great significance for the design of new drugs and the development of new chemical materials.