On Sharp Coefficients and Hankel Determinants for a Novel Class of Analytic Functions

Abstract

In this article, a new subclass of starlike functions is defined by using the technique of subordination and introducing a novel generalized domain. This domain is obtained by taking the composition of trigonometric $\sin e$ function and the well known curve called lemniscate of Bernoulli which is the image of open unit disc under a function $g\left(\xi \right)=\sqrt{1+\xi }$. This domain is characterized by its pleasing geometry which exhibits symmetric about the real axis. For this newly defined subclass, we investigate the sharp upper bounds for its first four coefficients, as well as the second and third order Hankel determinants.

1. Introduction

In the theory of geometric functions, analytic and univalent functions play a significant role to investigate various important properties. Analytic functions have extensive applications due to their differentiability, and ability to be represented as a power series while, univalent functions enhance their strength by addressing certain mapping problems that require univalency. The family of all normalized analytic functions within an open unit disc $\mathfrak{D}=\left\{\xi \in \mathbb{C}:\left|\xi \right|<1\right\}$ is denoted by $\mathcal{A}$. These functions satisfy the condition of normalization that is $f\left(0\right)=0$ and $f^{\prime }\left(0\right)=1$ and having the Maclaurin’s series representation given as:

$$f(\xi )=\xi +\sum _{k=2}^{\infty }{a}_k{\xi }^k,\left(\xi \in \mathfrak{D}\right).$$

(1)

A function $f\in \mathcal{A}$ is referred to as univalent if it maps distinct points in a domain $\Omega$ to distinct values, ensuring it is one-to-one. The collection of all such univalent functions in $\mathfrak{D}$ is denoted by $\mathcal{S}$. The investigation of univalent functions has led the foundation for introducing various significant subclasses, each characterized by its unique geometric properties.

For two functions f, $g\in \mathcal{A}$, the function $f\left(\xi \right)$ is said to be subordinate to $g\left(\xi \right)$ (denoted as $f\left(\xi \right)\prec g\left(\xi \right)$), if there exists a Schwarz function $u\left(\xi \right)$ satisfying $u\left(0\right)=0$, $\left|u(\xi )\right|<1$ and $f(\xi )=g\left(u\left(\xi \right)\right),$ (see [1]). Moreover, if $g\left(\xi \right)$ is univalent in $\mathfrak{D}$ then $f\left(\xi \right)\prec g\left(\xi \right)$ if and only if

$$f\left(0\right)=g\left(0\right)\mathrm{and}f\left(\mathfrak{D}\right)\subseteq g\left(\mathfrak{D}\right).$$

By using the principle of subordination, researchers have introduced and analyzed several key subclasses of univalent functions, such as $\mathcal{C}$, ${\mathcal{S}}^{*}$, $\mathcal{K}$ and $\mathcal{R}$ which correspond to class of convex functions, starlike functions, close-to-convex functions, and functions with bounded turnings, respectively. These subclasses play a vital role in understanding the geometric and analytic behavior of univalent functions. Notably, the class of starlike functions is defined as:

$${\mathcal{S}}^{*}=\left\{f\in \mathcal{S}:{\displaystyle \frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}}\prec {\displaystyle \frac{1+\xi }{1-\xi }},\xi \in \mathfrak{D}\right\},$$

equivalently, that can be written as:

$${\mathcal{S}}^{*}=\left\{f\in \mathcal{S}:Re\left({\displaystyle \frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}}\right)>0,\xi \in \mathfrak{D}\right\}.$$

In geometrical interpretation, the class ${\mathcal{S}}^{*}$ contains all those functions f such that ${\displaystyle \frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}}$ lies in the right half-plane. For detail study (see [2]).

In 1916, Bieberbach [3] proposed the renowned coefficient conjecture for normalized univalent functions in a groundbreaking work, posing a significant challenge that remained unresolved for decades. This conjecture was finally proven by Branges [4] in 1985, making a significant milestone in the field. Over the years, extensive efforts have been devoted to exploring this conjecture and its associated coefficients problems, leading to the discovery of new subclasses of analytic and univalent functions. Among these developments, Ma and Minda [5] defined the general form of the family of starlike functions as:

$${\mathcal{S}}^{*}\left(\vartheta \right)=\left\{f\in \mathcal{A}:{\displaystyle \frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}}\prec \vartheta \left(\xi \right),\xi \in \mathfrak{D}\right\},$$

(2)

where the function $\vartheta$ is analytic having positive real part and satisfying $\vartheta \left(0\right)=1$ and ${\vartheta }^{\prime }\left(0\right)>0$. This function $\vartheta$ maps $\mathfrak{D}$ onto a symmetric, star-shaped region centered at $\vartheta \left(0\right)=1$. In recent past, several subclasses of class $\mathcal{A}$ have been explored as a special cases of the class ${\mathcal{S}}^{*}\left(\vartheta \right)$, reveling fascinating geometric properties like growth, distortion and covering results for newly defined subclasses. For instance, if $\vartheta \left(\xi \right)={\displaystyle \frac{1+\xi }{1-\xi }}$, then the class ${\mathcal{S}}^{*}\left(\vartheta \right)$ reduced to ${\mathcal{S}}^{*}$ the fundamental class of starlike functions.

Here, we enlist some important subclasses of $\mathcal{A}$ obtained by choosing special values of $\vartheta \left(\xi \right)$ in (2).

• The subclass ${\Lambda }_L^{*}$ was defined and studied by Soköl et al. [6] by setting the function $\vartheta \left(\xi \right)=\sqrt{1+\xi }$.
• The subclass ${\Lambda }_{cre}^{*}$ of starlike functions associated with a crescent-shaped region was investigated by Raina et al. [7] by taking $\vartheta \left(\xi \right)=\xi +\sqrt{1+{\xi }^2}$.
• The subclass ${\Lambda }_{cre}^{*}$ of starlike functions related to cardioid shape domain was introduced and explored by Sharma et al. [8] by taking $\vartheta \left(\xi \right)=1+{\displaystyle \frac{4}{3}}\xi +{\displaystyle \frac{2}{3}}{\xi }^2$.
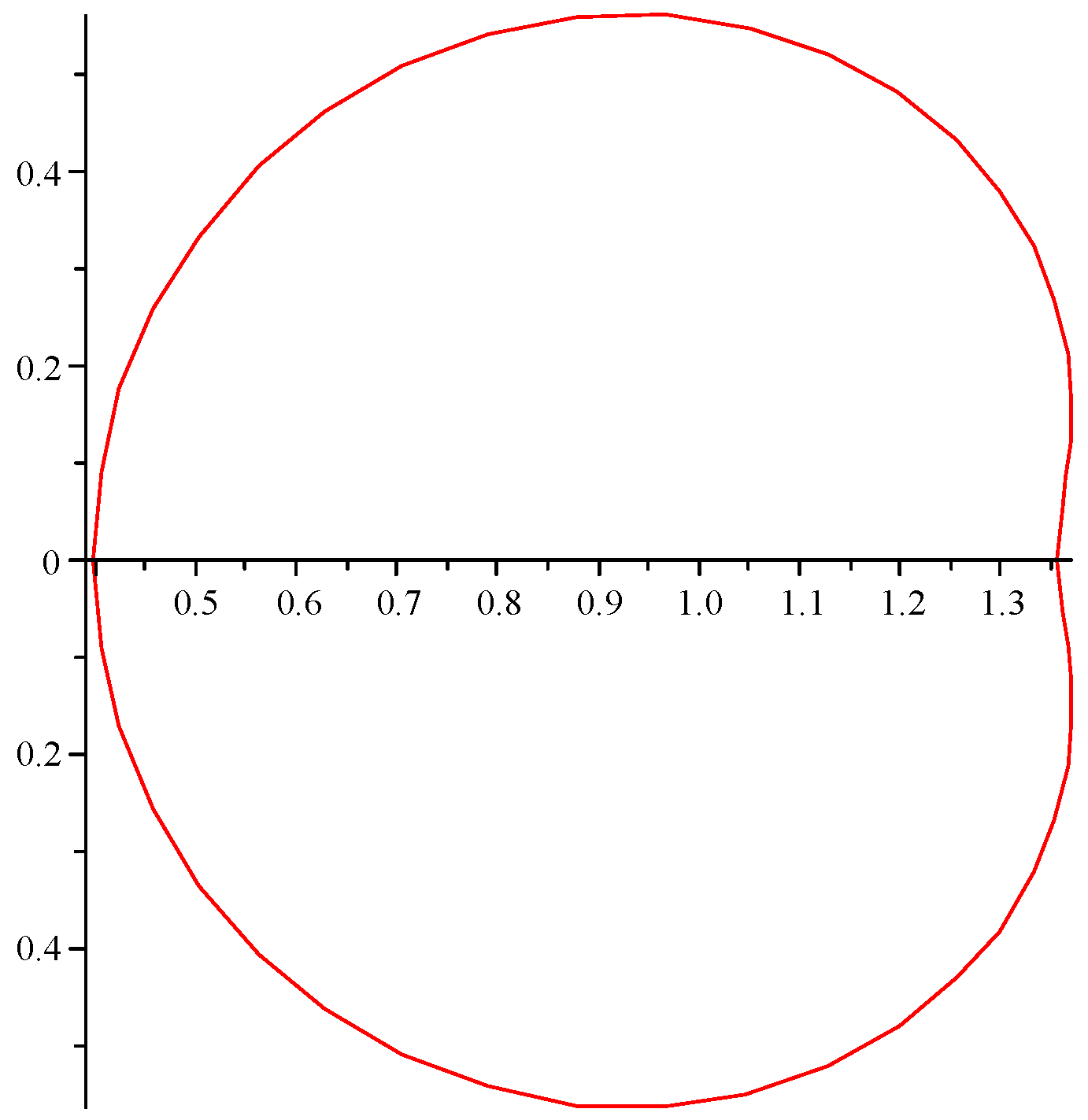
• The subclass ${\mathcal{S}}_{\sin }^{*}$, which contain the functions whose image domain is bounded by a symmetric region. This class was established and studied by Cho et al. [9] by selecting $\vartheta \left(\xi \right)=1+\sin \xi$.
• The subclass ${\mathcal{S}}_{\vartheta }^{*}$ was introduced by Kumar et al. [10] by setting the function $\vartheta \left(\xi \right)=1+{\sin }^{-1}\xi$.
• The subclass ${\mathcal{S}}_{nep}^{*}$ associated with nephroid shaped region was introduced by Wani et al. [11], by taking $\vartheta \left(\xi \right)=1+\xi -{\displaystyle \frac{1}{3}}{\xi }^3$.

Motivated by the studies referenced above, we introduce a new subclass ${\mathcal{S}}_{LP}^{*}$ which is closely related to starlike functions as follows:

Definition 1. 

Let $f\in \mathcal{A},$ given in (1). Then $f\in {\mathcal{S}}_{LP}^{*}$ if the following subordination condition holds:

$${\displaystyle \frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}}\prec \sqrt{1+\sin \xi },\xi \in \mathfrak{D}.$$

(3)

Geometrically, the class ${\mathcal{S}}_{LP}^{*}$ consists of all those functions f such that the functional ${\displaystyle \frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}}$ maps the open unit disc $\mathfrak{D}$ onto the restricted image domain of $\sqrt{1+\sin \xi }$ which lies in right half-plane as shown in the Figure 1:

For $n$, $q\ge 1$ and $f\in \mathcal{S}$ the Hankel determinant written as ${\mathcal{H}}_{q,n}\left(f\right)$ was defined by Pommerenke [12] as:

$${\mathcal{H}}_{q,n}\left(f\right)=\left|\begin{array}{cccc}{a}_n& a_{n+1}& \cdots & a_{n+q-1}\\ a_{n+1}& a_{n+2}& \cdots & a_{n+q}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n+q-1}& a_{n+q}& \cdots & a_{n+2q-2}\end{array}\right|.$$

(4)

For $a_1=1$, and some particular values of q and n, we get the second and third order Hankel determinants as:

$${\mathcal{H}}_{2,1}\left(f\right)=\left|\begin{array}{cc}{a}_1& a_2\\ a_2& a_3\end{array}\right|=a_3-a_2^2,{\mathcal{H}}_{2,2}\left(f\right)=\left|\begin{array}{cc}{a}_2& a_3\\ a_3& a_4\end{array}\right|=a_2{a}_4-a_3^2,$$

(5)

and

$${\mathcal{H}}_{3,1}\left(f\right)=\left|\begin{array}{ccc}1& a_2& a_3\\ a_2& a_3& a_4\\ a_3& a_4& a_5\end{array}\right|=2a_2{a}_3{a}_4-a_2^2{a}_5-a_3^3+a_3{a}_5-a_4^2.$$

(6)

Hankel determinants are important mathematical tools extensively used to study the geometric properties of analytic functions, including power series, singularities and coefficient bounds. They provide key insights into function behavior, such as growth, distortion, area and length of geometric curves. Also, restrictions on coefficients bounds can be used to derive the sufficient conditions for a function to belong in a particular functions class. Additionally, they play a crucial role in Random Matrix Theory, where they are linked to special functions like perturbed Gaussian, Laguerre, and Jacobi weights representing partition functions that help describe and analyze random matrices. For the applications of Hankel determinants (see [13,14,15]).

Hayman [16] was the first to explore the Hankel determinants for univalent functions, where he established the best possible upper bounds for $f\in \mathcal{S}$ that is $\left|{\mathcal{H}}_{2,n}\left(f\right)\right|\le \lambda \sqrt{n}$ where $\lambda >0$. This foundational work has inspired subsequent research, leading to refinements and extension of such estimates across various subclasses of analytic and univalent functions. over the years, several authors have estimated second order Hankel determinants but not much work have done on third and higher order determinants. In 2010, Babalola [17] was the first to compute non-sharp bounds of $\left|{\mathcal{H}}_{3,1}\left(f\right)\right|$ for several subfamilies of analytic functions. Zaprawa [18] later advanced Babalola’s work by obtaining improved upper bounds, though these were still not the best possible. Further progress was made by Kwon et al. [19], who enhanced the bounds for third-order Hankel determinant, specifically for the class of starlike functions, marking a significant step forward in this area of research. Following the methodology introduced in [19], Raza et al. [20] investigated the upper bounds for coefficients and Hankel determinants for a subclass of analytic functions related with Bernoulli’s lemniscate. Mishra et al. [21] explored the bounds of Hankel determinants for the subclasses of starlike and convex functions with respect to symmetric points. Additionally, Zhang et al. [22] calculated the upper bounds of the coefficients and Hankel determinants for a subclass of analytic functions. Murugusundaramoorthy et al. [23] contributed by estimating important coefficients bounds for a subclass of analytic functions related with a shell-shaped domain. Moreover, Zaparwa et al. [24] studied the Hankel determinant problems for certain subclass of univalent starlike functions. For more details on Hankel determinants we refer to see [25,26,27,28,29,30]. In recent years, estimating the sharp upper bounds for the Hankel determinants $\left|{\mathcal{H}}_{q,n}\left(f\right)\right|$ for specific values of q and n in certain subclasses of analytic and univalent functions has become an important area of research.

Initially, janteng et al. [31] determined the sharp bounds of $\left|{\mathcal{H}}_{2,2}\left(f\right)\right|$ for the classes of convex functions $\mathcal{C}$, starlike functions ${\mathcal{S}}^{*}$ and functions with bounded turnings $\mathcal{R}$ yielding the following results

$$\left|{\mathcal{H}}_{2,2}\left(f\right)\right|\le \left\{\begin{array}{ccc}{\displaystyle \frac{1}{8}},& \mathrm{for}& f\in \mathcal{C},\\ 1,& \mathrm{for}& f\in {\mathcal{S}}^{*},\\ {\displaystyle \frac{4}{9}},& \mathrm{for}& f\in \mathcal{R}.\end{array}\right.$$

The estimation of sharp bounds for third and higher-order Hankel determinants is significantly more challenging compared to the bounds of $\left|{\mathcal{H}}_{2,1}\left(f\right)\right|$ and $\left|{\mathcal{H}}_{2,2}\left(f\right)\right|$. Kowalezyk et al. [32] were the first to estimated the sharp bounds of third-order Hankel determinant for a subclass of convex functions. Following a similar approach, Lecko et al. [33] investigated the sharp upper bounds for $\left|{\mathcal{H}}_{3,1}\left(f\right)\right|$ for a class of starlike functions defined in order terminology. Later, Ullah et al. [34] explored sharp coefficient and Hankel determinant problems for a subclass of starlike functions. Additionally, Arif et al. [35] derived sharp bounds for certain coefficients and Hankel determinants of a subclass of analytic functions related to a three-leaf domain. Shi et al. [36] proved sharp bounds of the third-order Hankel determinants for a specific subclass of analytic functions associated with an eight-shaped domain. Sumthrayuth et al. [37] addressed sharp coefficients problems, important inequalities and Hankel determinants for a subclass of functions with bounded turnings, connected to a four-leaf type domain. Similarly, Tang et al. [38] studied sharp coefficient and Hankel determinant problems for a subclass of convex functions defined within a symmetric domain.

Furthermore, Raza et al. [39] investigated the Hankel determinants and provided the coefficient estimates for subclass of starlike functions associated to a symmetric booth lemniscate domain. Kumar et al. [40] calculated the sharp bounds of the third Hankel determinants for the class which involves the inverse of bounded turning function, while Ahmad et al. [41] examined the sharpness of coefficients and Hankel determinants for a subclass of analytic functions which is defined by considering a balloon-shaped domain. Recently, Kumar et al. [42] addressed the sharp Hankel determinants problems for a subclass of starlike functions connected with hyperbolic secant function.

This work primarily aims to derive sharp coefficient estimates and to establish sharp upper bounds for the second and third Hankel determinants associated with the coefficients of functions in the class ${\mathcal{S}}_{LP}^{*}$.

To obtain our main results, the subsequent Lemmas play a fundamental role. Their application provides the necessary mathematical framework for deriving the sharp estimates.

2. Set of Lemmas

Let $\mathcal{P}$ denote the class of all analytic functions, which has the series representation given as:

$$p\left(\xi \right)=1+\sum _{k=1}^{\infty }{p}_k{\xi }^k,\left(\xi \in \mathfrak{D}\right).$$

(7)

Geometrically, the class $\mathcal{P}$ contain all those functions whose real parts is positive in $\mathfrak{D}$ that is $Rep\left(\xi \right)>0$, $\left(\xi \in \mathfrak{D}\right)$. The functions in class $\mathcal{P}$, can be expressed as:

$$p\left(\xi \right)={\displaystyle \frac{1+u\left(\xi \right)}{1-u\left(\xi \right)}},\left(\xi \in \mathfrak{D}\right),$$

where $u\left(\xi \right)$ is Schwarz function, satisfying $u\left(0\right)=0$ and $\left|u\left(\xi \right)\right|<1$. The given relation is a Möbius transformation that maps the open unit disc $\mathfrak{D}$ to right half plane, establishing a one-to-one correspondence between the functions in class $\mathcal{P}$ and Schwarz functions. Conversely, if $p\left(\xi \right)\in \mathcal{P}$ then $u\left(\xi \right)$ can be written as:

$$u\left(\xi \right)={\displaystyle \frac{p\left(\xi \right)-1}{p\left(\xi \right)+1}},\left(\xi \in \mathfrak{D}\right).$$

Lemma 1 

([12]). Let $p\in \mathcal{P}$, be given in (7). Then

$$\begin{array}{ccc}\hfill \left|p_k\right|& \le & 2k\ge 1,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \left|p_{k+n}-\nu p_k{p}_n\right|& \le & 2,0\le \nu \le 1,\hfill \end{array}$$

(9)

Lemma 2 

([43]). Let $p\in \mathcal{P}$, be given in (7). Then for $0\le T\le 1$ and $T\left(2T-1\right)\le L\le T$ the following inequality hold true

$$\left|p_3-2T{p}_1{p}_2+L{p}_1^3\right|\le 2.$$

(10)

Lemma 3. 

Let $p\in \mathcal{P}$, be given in (7). Then there exist $r$, α and $\nu \in \mathbb{C}$ with $\left|r\right|\le 1$, $\left|\alpha \right|\le 1$ and $\left|\nu \right|\le 1$ such that

$$\begin{array}{cc}\hfill p_2& ={\displaystyle \frac{1}{2}}\left(p_1^2+r\left(4-p_1^2\right)\right),\hfill \\ \hfill p_3& ={\displaystyle \frac{1}{4}}\left(p_1^3+2p_{1}r\left(4-p_1^2\right)-\left(4-p_1^2\right)p_1{r}^2+2\left(4-p_1^2\right)\left(1-{\left|r\right|}^2\right)\alpha \right),\hfill \end{array}$$

and

$$p_4={\displaystyle \frac{1}{8}}\left[\begin{array}{c}{p}_1^4+r\left(4-p_1^2\right)\left(4r+\left(r^2-3r+3\right)p_1^2\right)\\ -4\left(4-p_1^2\right)\left(1-{\left|r\right|}^2\right)\left(p\left(r-1\right)\alpha -\nu \left(1-{\left|\alpha \right|}^2\right)+\overline{r}{\alpha }^2\right)\end{array}\right],$$

where the values $p_2$, $p_3$ and $p_4$ are taken from [44], [43] and [10], respectively.

Lemma 4 

([45]). Let $\eta$, $\delta$, κ and χ satisfying the conditions $0<\eta <1$, $0<\chi <1$, and

$$8\chi \left(1-\chi \right)\left[{\left(\eta \delta -2\kappa \right)}^2+{\left(\eta \left(\chi +\eta \right)-\delta \right)}^2\right]+\eta \left(1-\eta \right){\left(\delta -2\chi \eta \right)}^2\le 4{\eta }^2{\left(1-\eta \right)}^2\chi \left(1-\chi \right),$$

then for $p\in \mathcal{P}$, be given in (7). we have

$$\left|\kappa p_1^4+\chi p_2^2+2\eta p_1{p}_3-{\displaystyle \frac{3}{2}}\delta p_1^2{p}_2-p_4\right|\le 2.$$

(11)

3. Main Results

Theorem 1. 

Let$f\in {\mathcal{S}}_{LP}^{*}$ having the series representation given in (1). Then we have

$$\left|a_2\right|\le {\displaystyle \frac{1}{2}},\left|a_3\right|\le {\displaystyle \frac{1}{4}},\left|a_4\right|\le {\displaystyle \frac{1}{6}}\mathit{and}\left|a_5\right|\le {\displaystyle \frac{1}{8}}.$$

(12)

These inequalities are sharp. The equalities can be obtained by the normalized extremal function $f_n\left(\xi \right)$ defined as:

$$f_n\left(\xi \right)=exp\underset{0}{\overset{\xi }{\int }}{\displaystyle \frac{1}{t}}\left(\sqrt{1+\sin t^n}\right)dt,\xi \in \mathfrak{D}.$$

In particular, for the coefficients bounds in Equation (12), we consider $n=1,2,3,4$ and obtained their respective extremal functions as:

$$\begin{array}{ccc}\hfill f_1\left(\xi \right)& =& exp\underset{0}{\overset{\xi }{\int }}{\displaystyle \frac{1}{t}}\left(\sqrt{1+\sin t}\right)dt=\xi +{\displaystyle \frac{1}{2}}{\xi }^2+{\displaystyle \frac{1}{16}}{\xi }^3+\dots ,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill f_2\left(\xi \right)& =& exp\underset{0}{\overset{\xi }{\int }}{\displaystyle \frac{1}{t}}\left(\sqrt{1+\sin t^2}\right)dt=\xi +{\displaystyle \frac{1}{4}}{\xi }^3-{\displaystyle \frac{1}{128}}{\xi }^7+\dots ,\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill f_3\left(\xi \right)& =& exp\underset{0}{\overset{\xi }{\int }}{\displaystyle \frac{1}{t}}\left(\sqrt{1+\sin t^3}\right)dt=\xi +{\displaystyle \frac{1}{6}}{\xi }^4-{\displaystyle \frac{1}{144}}{\xi }^7+\dots ,\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill f_4\left(\xi \right)& =& exp\underset{0}{\overset{\xi }{\int }}{\displaystyle \frac{1}{t}}\left(\sqrt{1+\sin t^4}\right)dt=\xi +{\displaystyle \frac{1}{8}}{\xi }^5-{\displaystyle \frac{1}{128}}{\xi }^9+\dots .\hfill \end{array}$$

(16)

Proof. 

Let $f\in {\mathcal{S}}_{LP}^{*}$ then by (3), we have

$${\displaystyle \frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}}=\sqrt{1+\sin u\left(\xi \right)},$$

(17)

where $u\left(\xi \right)$ is known as Schwarz function. Let $p\in \mathcal{P}$, then

$$p\left(\xi \right)={\displaystyle \frac{1+u\left(\xi \right)}{1-u\left(\xi \right)}}=1+p_1\xi +p_2{\xi }^2+p_3{\xi }^3+p_4{\xi }^4+\dots ,$$

and

$$u\left(\xi \right)={\displaystyle \frac{p\left(\xi \right)-1}{p\left(\xi \right)+1}}={\displaystyle \frac{p_1\xi +p_2{\xi }^2+p_3{\xi }^3+p_4{\xi }^4+\dots }{2+p_1\xi +p_2{\xi }^2+p_3{\xi }^3+p_4{\xi }^4+\dots }},$$

which on simplifications, gives

$$\begin{array}{ccc}\hfill u\left(\xi \right)& =& {\displaystyle \frac{1}{2}}{p}_1\xi +\left({\displaystyle \frac{1}{2}}{p}_2-{\displaystyle \frac{1}{4}}{p}_1^2\right){\xi }^2+\left({\displaystyle \frac{1}{8}}{p}_1^3-{\displaystyle \frac{1}{2}}{p}_1{p}_2+{\displaystyle \frac{1}{2}}{p}_3\right){\xi }^3+\hfill \\ & & \left({\displaystyle \frac{1}{2}}{p}_4-{\displaystyle \frac{1}{2}}{p}_1{p}_3-{\displaystyle \frac{1}{4}}{p}_2^2-{\displaystyle \frac{1}{16}}{p}_1^4+{\displaystyle \frac{3}{8}}{p}_1^2{p}_2\right){\xi }^4+\dots .\hfill \end{array}$$

As

$$\begin{array}{c}\hfill \sqrt{1+\sin \xi }=1+{\displaystyle \frac{1}{2}}\xi -{\displaystyle \frac{1}{8}}{\xi }^2-{\displaystyle \frac{1}{48}}{\xi }^3+{\displaystyle \frac{1}{384}}{\xi }^4+\dots .\end{array}$$

(18)

Putting the value of $u\left(\xi \right)$ in Equation (18) and adjusting the like terms, we have

$$\begin{array}{ccc}\hfill \sqrt{1+\sin u\left(\xi \right)}& =& 1+{\displaystyle \frac{1}{4}}{p}_1\xi +\left({\displaystyle \frac{1}{2}}{p}_2-{\displaystyle \frac{5}{32}}{p}_1^2\right){\xi }^2+\left({\displaystyle \frac{35}{384}}{p}_1^3-{\displaystyle \frac{5}{16}}{p}_1{p}_2+{\displaystyle \frac{1}{4}}{p}_3\right){\xi }^3+\hfill \\ & & \left({\displaystyle \frac{1}{4}}{p}_4-{\displaystyle \frac{5}{16}}{p}_1{p}_3-{\displaystyle \frac{5}{32}}{p}_2^2+{\displaystyle \frac{35}{128}}{p}_1^2{p}_2-{\displaystyle \frac{311}{6144}}{p}_1^4\right){\xi }^4+\dots .\hfill \end{array}$$

(19)

From (1) and some simple calculations, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}}& =& 1+a_2\xi +\left(2a_3-a_2^2\right){\xi }^2+\left(3a_4-3a_2{a}_3+a_2^3\right){\xi }^3\hfill \\ & & +\left(4a_5-2a_3^2-4a_2{a}_4+4a_2^2{a}_3-a_2^4\right){\xi }^4+\dots .\hfill \end{array}$$

(20)

From the comparison of (19) and (20), we get

$$\begin{array}{ccc}\hfill a_2& =& {\displaystyle \frac{1}{4}}{p}_1,\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill a_3& =& {\displaystyle \frac{1}{8}}{p}_2-{\displaystyle \frac{3}{64}}{p}_1^2,\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill a_4& =& {\displaystyle \frac{31}{2304}}{p}_1^3-{\displaystyle \frac{7}{96}}{p}_1{p}_2+{\displaystyle \frac{1}{12}}{p}_3,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill a_5& =& -{\displaystyle \frac{79}{18432}}{p}_1^4+{\displaystyle \frac{7}{192}}{p}_1^2{p}_2-{\displaystyle \frac{11}{192}}{p}_1{p}_3-{\displaystyle \frac{1}{32}}{p}_2^2+{\displaystyle \frac{1}{16}}{p}_4.\hfill \end{array}$$

(24)

From (21) and (22) and applying (8) and (9) of Lemma 1 respectively, we have

$$\left|a_2\right|\le {\displaystyle \frac{1}{2}}\mathrm{and}\left|a_3\right|\le {\displaystyle \frac{1}{4}}.$$

From (23), we can write

$$\left|a_4\right|={\displaystyle \frac{1}{12}}\left|p_3-2\left({\displaystyle \frac{7}{16}}\right)p_1{p}_2+{\displaystyle \frac{31}{192}}{p}_1^3\right|.$$

By (10), we have $T={\displaystyle \frac{7}{16}}=0.4375$ and $L={\displaystyle \frac{31}{192}}=0.1614$, clearly, $L<T$ and also simple calculation shows $T(2T-1)<L$. Then by Lemma 2, we obtain

$$\left|a_4\right|\le {\displaystyle \frac{1}{6}}.$$

From (24), we have

$$\left|a_5\right|={\displaystyle \frac{1}{16}}\left|{\displaystyle \frac{79}{1152}}{p}_1^4+{\displaystyle \frac{1}{2}}{p}_2^2+2\left({\displaystyle \frac{11}{24}}\right)p_1{p}_3-{\displaystyle \frac{3}{2}}\left({\displaystyle \frac{7}{18}}\right)p_1^2{p}_2-p_4\right|,$$

comparing right hand side with (11), we have $\kappa ={\displaystyle \frac{79}{1152}}$, $\chi ={\displaystyle \frac{1}{2}}$, $\eta ={\displaystyle \frac{11}{24}}$ and $\delta ={\displaystyle \frac{7}{18}}$. It can be seen that $0<\eta <1$, $0<\chi <1$, and simple calculations shows

$$8\chi \left(1-\chi \right)\left[{\left(\eta \delta -2\kappa \right)}^2+{\left(\eta \left(\chi +\eta \right)-\delta \right)}^2\right]+\eta \left(1-\eta \right){\left(\delta -2\chi \eta \right)}^2\le 4{\eta }^2{\left(1-\eta \right)}^2\chi \left(1-\chi \right),$$

then by Lemma 4, we get

$$\left|a_5\right|\le {\displaystyle \frac{1}{8}}.$$

□

Theorem 2. 

Let $f\in {\mathcal{S}}_{LP}^{*}.$ Then we have

$$\left|{\mathcal{H}}_{2,1}\left(f\right)\right|\le {\displaystyle \frac{1}{4}}.$$

(25)

This result is sharp. The sharpness of the inequality presented in (25), can be obtained by the $f_2\left(\xi \right)$ given in (14).

Proof. 

Let $f\in {\mathcal{S}}_{LP}^{*}$ then by (21) and (22), we have

$$\left|{\mathcal{H}}_{2,1}\left(f\right)\right|=\left|a_3-a_2^2\right|={\displaystyle \frac{1}{8}}\left|p_2-{\displaystyle \frac{7}{8}}{p}_1^2\right|.$$

Now by the application of relation (9) of Lemma 1, we obtain

$$\left|{\mathcal{H}}_{2,1}\left(f\right)\right|\le {\displaystyle \frac{1}{4}}.$$

□

Theorem 3. 

Let $f\in {\mathcal{S}}_{LP}^{*}.$ Then we have

$$\left|{\mathcal{H}}_{2,2}\left(f\right)\right|\le {\displaystyle \frac{1}{16}}.$$

(26)

This result is sharp. The sharpness of the inequality presented in (26), can be obtained by (14).

Proof. 

Let $f\in {\mathcal{S}}_{LP}^{*}$ then by (21)–(23), we have

$$\left|a_2{a}_4-a_3^2\right|=\left|{\displaystyle \frac{43}{36864}}{p}_1^4-{\displaystyle \frac{5}{768}}{p}_1^2{p}_2+{\displaystyle \frac{1}{48}}{p}_3{p}_1-{\displaystyle \frac{1}{64}}{p}_2^2\right|.$$

Using Lemma 3, we have

$$\left|a_2{a}_4-a_3^2\right|={\displaystyle \frac{1}{36864}}\left|\begin{array}{c}-144{\left(4-p_1^2\right)}^2{r}^2-29p_1^4-24p_1^2\left(4-p_1^2\right)r-192p_1^2\left(4-p_1^2\right)r^2\\ +384p_1\left(4-p_1^2\right)\left(1-{\left|r\right|}^2\right)\alpha \end{array}\right|.$$

Let $\left|p_1\right|=p\in \left[0,2\right]$, $\left|r\right|=b\in \left[0,1\right]$ and $\left|\alpha \right|\le 1$, then by using triangular inequality, we obtain

$$\left|a_2{a}_4-a_3^2\right|\le {\displaystyle \frac{1}{36864}}\left[\begin{array}{c}144\left(4-p^2\right)b^2+29p^4+24p^2\left(4-p^2\right)b+192p^2\left(4-p^2\right)b^2\\ +384p\left(4-p^2\right)\left(1-b^2\right)\end{array}\right].$$

Consider

$$F\left(p,b\right)={\displaystyle \frac{1}{36864}}\left[\begin{array}{c}144\left(4-p^2\right)b^2+29p^4+24p^2\left(4-p^2\right)b+192p^2\left(4-p^2\right)b^2\\ +384p\left(4-p^2\right)-384p\left(4-p^2\right)b^2\end{array}\right],$$

then for all $b\in \left[0,1\right]$, $p\in \left[0,2\right]$, we have

$${\displaystyle \frac{\partial F}{\partial b}}={\displaystyle \frac{1}{36864}}\left(24p^2\left(4-p^2\right)+\left(4-p^2\right)b\{\left(4-p^2\right)288+384p^2-768p\}\right)\ge 0,$$

which show that the maximum of $F\left(p,b\right)$ occurs at $b=1$, therefore

$$maxF\left(p,b\right)=F\left(p,1\right)={\displaystyle \frac{1}{36864}}\left(144{\left(4-p^2\right)}^2+29p^4+24p^2\left(4-p^2\right)+192p^2\left(4-p^2\right)\right).$$

Let

$$H\left(p\right)={\displaystyle \frac{1}{36864}}\left(-43p^4-288p^2+2304\right).$$

Differentiating $H\left(p\right)$ twice we get $p=0$ as the maximum point and the corresponding maximum value is

$$maxH\left(p\right)=H\left(0\right)={\displaystyle \frac{1}{16}}.$$

From all above discussion, we conclude that

$$\left|{\mathcal{H}}_{2,2}\left(f\right)\right|\le {\displaystyle \frac{1}{16}}.$$

□

Theorem 4. 

Let $f\in {\mathcal{S}}_{LP}^{*}.$ Then we have

$$\left|{\mathcal{H}}_{3,1}\left(f\right)\right|\le {\displaystyle \frac{1}{36}}.$$

(27)

This result is sharp. The sharpness of the inequality presented in (27), can be obtained by the $f_3\left(\xi \right)$ given in (15).

Proof. 

From (6), we have

$$\left|{\mathcal{H}}_{3,1}\left(f\right)\right|=2a_2{a}_3{a}_4-a_2^2{a}_5-a_3^3+a_3{a}_5-a_4^2.$$

(28)

Using (21)–(24), we have

$$\left|{\mathcal{H}}_{3,1}\left(f\right)\right|={\displaystyle \frac{1}{21233664}}\left[\begin{array}{c}-145152p_1^2{p}_4+43968p_1^3{p}_3-17736p_1^4{p}_2-124416p_2^3-147456p_3^2\\ +1601p_1^6+6336p^2{p}_2^2+165888p_2{p}_4+216576p_1{p}_2{p}_3\end{array}\right].$$

(29)

By Lemma 3, and letting $p_1=p$, $\left(4-p^2\right)=t$, we have

$$\begin{array}{cc}\hfill -145152p^2{p}_4& =-18144p^6-18144t{p}^4{r}^3+54432t{p}^4{r}^2-54432t{p}^4{r+72576t(1-|r|}^2)p^{3}r\alpha \hfill \\ \hfill & {-72567t(1-|r|}^2)p^3\alpha -72576t{p}^2{r}^2{+72576t(1-|r|}^2)p^{2}r{\alpha }^2\hfill \\ \hfill & {-72576t(1-|r|}^2\left)\right(1-{\left|\alpha \right|}^2)\nu p^2,\hfill \\ \hfill 43968p^3{p}_3& =10992p^6-10992t{p}^4{r}^2+21984t{p}^4{r+21984(1-|r|}^2)t\alpha p^3,\hfill \\ \hfill -17736p^4{p}_2& =-8868p^6-8868p^{4}rt,\hfill \\ \hfill -124416p_2^3& =-15552p^6-46656p^{4}rt-46656p^2{r}^2{t}^2-155552r^3{t}^3,\hfill \\ \hfill -147456p_3^2& =-9216p^6+18432p^4{r}^{2}t-36864p^{4}rt-36864\left(1-{\left|r\right|}^2\right)p^{3}t\alpha -9216p^2{r}^4{t}^2\hfill \\ \hfill & +36864p^2{r}^3{t}^2-36864p^2{r}^2{t}^2+36864p\left(1-{\left|r\right|}^2\right)r^2{t}^2\alpha -73728p\left(1-{\left|r\right|}^2\right)r{t}^2\alpha \hfill \\ \hfill & -36864{\left(1-{\left|r\right|}^2\right)}^2{t}^2{\alpha }^2,\hfill \\ \hfill 6336p^2{p}_2^2& =1584p^6+3168p^{4}rt+1584p^2{r}^2{t}^2,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill 165888p_2{p}_4& =& 10368p^6+10368p^4{r}^{3}t-31104p^4{r}^{2}t+41472p^{4}rt-41472\left(1-{\left|r\right|}^2\right)p^{3}rt\alpha \hfill \\ & & +41472\left(1-{\left|r\right|}^2\right)p^{3}t\alpha +10368p^2{r}^4{t}^2-31104p^2{r}^3{t}^2+31104p^2{r}^2{t}^2\hfill \\ & & +41472p^2{r}^{2}t-41472\left(1-{\left|r\right|}^2\right)p^{2}rt{\alpha }^2+41472\left(1-{\left|r\right|}^2\right)\left(1-{\left|\alpha \right|}^2\right)\nu p^{2}t\hfill \\ & & -41472\left(1-{\left|r\right|}^2\right)p{r}^2{t}^2\alpha +41472\left(1-{\left|r\right|}^2\right)pr{t}^2\alpha +41472r^3{t}^2\hfill \\ & & -41472\left(1-{\left|r\right|}^2\right)r^2{t}^2{\alpha }^2+41472\left(1-{\left|r\right|}^2\right)\left(1-{\left|\alpha \right|}^2\right)\nu r{t}^2,\hfill \\ \hfill 216576p{p}_2{p}_3& =& 27072p^6-27072p^4{r}^{2}t+81216p^{4}rt+54144\left(1-{\left|r\right|}^2\right)\alpha p^{3}t\hfill \\ & & -27072p^2{r}^3{t}^2+54144p^2{r}^2{t}^2+54144\left(1-{\left|r\right|}^2\right)\alpha pr{t}^2.\hfill \end{array}$$

Using these values in (29), we get

$${\mathcal{H}}_{3,1}\left(f\right)={\displaystyle \frac{1}{21233664}}\left(\begin{array}{c}-163p^6-7776p^{4}t{r}^3+3696p^{4}t{r}^2+1020p^{4}tr-31104p^{2}t{r}^2\hfill \\ +1152p^2{t}^2{r}^4-21312p^2{t}^2{r}^3+3312p^2{t}^2{r}^2-15552t^3{r}^3+41472t^2{r}^3\hfill \\ +31104p^3\left(1-{\left|r\right|}^2\right)tr\alpha +8160p^3\left(1-{\left|r\right|}^2\right)t\alpha -4608p\left(1-{\left|r\right|}^2\right)r^2{t}^2\alpha \hfill \\ +21888p\left(1-{\left|r\right|}^2\right)r{t}^2\alpha +31104p^2\left(1-{\left|r\right|}^2\right)rt{\alpha }^2\hfill \\ -41472\left(1-{\left|r\right|}^2\right)r^2{t}^2{\alpha }^2-36864{\left(1-{\left|r\right|}^2\right)}^2{t}^2{\alpha }^2\hfill \\ +41472\left(1-{\left|r\right|}^2\right)\left(1-{\left|\alpha \right|}^2\right)r{t}^2\nu -31104\left(1-{\left|r\right|}^2\right)\left(1-{\left|\alpha \right|}^2\right)p^{2}t\nu \hfill \end{array}\right).$$

Since $t=\left(4-p^2\right)$, then we can write

$$\left|{\mathcal{H}}_{3,1}\left(f\right)\right|={\displaystyle \frac{1}{21233664}}\left[w_1\left(p,r\right)+w_2\left(p,r\right)\alpha +w_3\left(p,r\right){\alpha }^2+\epsilon \left(p,r,\alpha \right)\nu \right],$$

where

$$\begin{array}{ccc}\hfill w_1\left(p,r\right)& =& -163p^6-\left(4-p^2\right)r\left(\begin{array}{c}7776p^4{r}^2-3696p^{4}r-1020p^4+31104p^{2}r\hfill \\ +\left(4-p^2\right)r\left(-1152p^2{r}^2+5760p^{2}r-3312p^2+20736r\right)\hfill \end{array}\right),\hfill \\ \hfill w_2\left(p,r\right)& =& -4p\left(4-p^2\right)\left(1-{\left|r\right|}^2\right)\left(\left(4-p^2\right)r\left(1152r-547\right)-24p^2\left(324r+85\right)\right),\hfill \\ \hfill w_3\left(p,r\right)& =& -128\left(4-p^2\right)\left(1-{\left|r\right|}^2\right)\left(36\left(4-p^2\right)\left(r^2+8\right)-243p^{2}r\right),\hfill \\ \hfill \epsilon \left(p,r,\alpha \right)& =& 10368\left(4-p^2\right)\left(1-{\left|r\right|}^2\right)\left(1-{\left|\alpha \right|}^2\right)\left(4r\left(4-p^2\right)-3p^2\right).\hfill \end{array}$$

Let $\left|\alpha \right|=s$ and $\left|\nu \right|\le 1$, then

$$\begin{array}{ccc}\hfill \left|{\mathcal{H}}_{3,1}\left(f\right)\right|& \le & {\displaystyle \frac{1}{21233664}}\left[\left|w_1\left(p,r\right)\right|+\left|w_2\left(p,r\right)\right|s+\left|w_3\left(p,r\right)\right|s^2+\left|\epsilon \left(p,r,\alpha \right)\right|\right]\hfill \\ & \le & {\displaystyle \frac{1}{21233664}}\left|Q\left(p,r,s\right)\right|,\hfill \end{array}$$

(30)

where

$$Q\left(p,r,s\right)=u_1\left(p,r\right)+u_2\left(p,r\right)s+u_3\left(p,r\right)s^2+u_4\left(p,r\right)\left(1-s^2\right),$$

(31)

with

$$\begin{array}{ccc}\hfill u_1\left(p,r\right)& =& 163p^6+\left(4-p^2\right)r\left(\begin{array}{c}7776p^4{r}^2+3696p^{4}r+1020p^4+31104p^{2}r\\ +\left(4-p^2\right)r\left(1152p^2{r}^2+5760p^{2}r+3312p^2+20736r\right)\end{array}\right),\hfill \\ \hfill u_2\left(p,r\right)& =& 4p\left(4-p^2\right)\left(1-{\left|r\right|}^2\right)\left(\left(4-p^2\right)r\left(1152r+547\right)+24p^2\left(324r+85\right)\right),\hfill \\ \hfill u_3\left(p,r\right)& =& 128\left(4-p^2\right)\left(1-{\left|r\right|}^2\right)\left(36\left(4-p^2\right)\left(r^2+8\right)+243p^{2}r\right),\hfill \\ \hfill u_4\left(p,r\right)& =& 10368\left(4-p^2\right)\left(1-{\left|r\right|}^2\right)\left(1-{\left|\alpha \right|}^2\right)\left(4r\left(4-p^2\right)+3p^2\right).\hfill \end{array}$$

To determine the maximum value of $Q\left(p,r,s\right)$ over the closed cuboid $\Delta :\left[0,2\right]\times \left[0,1\right]\times \left[0,1\right]$, it is necessary to examine the behavior of $Q\left(p,r,s\right)$ within the closed cuboid, across all six faces and along the twelve edges of the cuboid. For clarity, the investigation is divided into the following three cases:

(1) 

Interior points of cuboid

Initially, we will examine maximum value of the function Q within the interior of $\Delta$. Let $\left(p,r,s\right)\in \left(0,2\right)\times \left(0,1\right)\times \left(0,1\right)$ then differentiating partially with respect to s, we have

$${\displaystyle \frac{\partial Q}{\partial s}}=\left[\begin{array}{c}4p\left(4-p^2\right)\left(1-{\left|r\right|}^2\right)\left[\left(4-p^2\right)r\left(1152r+547\right)+24p^2\left(324r+85\right)\right]\\ +2s\left(4-p^2\right)\left(1-{\left|r\right|}^2\right)\left[\left(4-p^2\right)\left(4608\left(r-8\right)\right)+31104p^2\right]\left(r-1\right)\end{array}\right],$$

by establishing ${\displaystyle \frac{\partial Q}{\partial s}}=0,$ we get

$$s={\displaystyle \frac{2p\left[\left(4-p^2\right)r\left(1152r+547\right)+24p^2\left(324r+85\right)\right]}{\left[\left(4-p^2\right)\left(4608\left(8-r\right)\right)-31104p^2\right]\left(r-1\right)}}=s_1.$$

If “$s_1$” is a critical point inside $\Delta$, it must lie in the range $s_1\in \left(0,1\right)$, a situation that only occurs if

$$p^3\left(31104r+8160\right)+pr\left(4-p^2\right)\left(4608r+2188\right)+9126\left(4-p^2\right)\left(8-r\right)<31104\left(1-r\right)p^2,$$

(32)

and

$$p^2>{\displaystyle \frac{16\left(8-r\right)}{59-4r}}.$$

(33)

To identify the critical point inside the cuboid, we must determine a solution that satisfies the inequalities (32) and (33). Let $k\left(r\right)={\displaystyle \frac{16\left(r-8\right)}{\left(4r-59\right)}},$ where $k^{\prime }\left(r\right)=-{\displaystyle \frac{432}{{\left(4r-59\right)}^2}}<0$ in $\left(0,1\right)$ which confirms that $k\left(r\right)$ is a decreasing function. Thus

$$p^2>{\displaystyle \frac{112}{55}}.$$

It follows from the straightforward computation that (32) is not held for $r\in [{\displaystyle \frac{77}{486}},1).$ Therefore, it can be deduced that the function $Q\left(p,r,s\right)$ does not exhibit any critical points in the specified interior of the cuboid $\left[0,2\right)\times [{\displaystyle \frac{77}{486}},1)\times \left(0,1\right).$ Assume $\left(p,r,s\right)$ represents a critical point of “Q” in the interior of the cuboid, where $r\in [0,{\displaystyle \frac{77}{486}})$ and $s\in \left(0,1\right)$. This assumption implies that $p^2>g\left({\displaystyle \frac{77}{486}}\right)={\displaystyle \frac{30488}{14183}}$. It can also be observed that

$$u_1\left(p,r\right)\le u_1\left(p,{\displaystyle \frac{77}{486}}\right)={\phi }_1\left(p\right).$$

Since $1-r^2\le 1$ and $0<r<{\displaystyle \frac{77}{486}}$, we have

$$\begin{array}{ccc}\hfill u_2\left(p,r\right)& \le & 4\left(4-p^2\right)\left[\left(4-p^2\right)\left(1152p{\left({\displaystyle \frac{77}{486}}\right)}^2+547p\left({\displaystyle \frac{77}{486}}\right)\right)+\left(7776\left({\displaystyle \frac{77}{486}}\right)+2040\right)p^3\right],\hfill \\ & =& {\displaystyle \frac{236196}{230267}}{u}_2\left(p,{\displaystyle \frac{77}{486}}\right)={\phi }_2\left(p\right).\hfill \end{array}$$

Similarly, we acquire

$$u_j\left(p,r\right)\le {\displaystyle \frac{236196}{230267}}{u}_j\left(p,{\displaystyle \frac{77}{486}}\right)={\phi }_j\left(p\right),\left(j=3,4\right).$$

It can be deduced that

$$Q\left(p,r,s\right)\le {\phi }_1\left(p\right)+{\phi }_4\left(p\right)+{\phi }_2\left(p\right)s+\left({\phi }_3\left(p\right)-{\phi }_4\left(p\right)\right)s^2=\Psi \left(p,s\right),$$

differentiating with respect to “s” we have

$${\displaystyle \frac{\partial \Psi }{\partial s}}={\phi }_2\left(p\right)+2\left({\phi }_3\left(p\right)-{\phi }_4\left(p\right)\right)s.$$

Consider

$${\phi }_3\left(p\right)-{\phi }_4\left(p\right)=\left({\displaystyle \frac{371254208}{6561}}-{\displaystyle \frac{798053888}{6561}}\right)\left(4-p^2\right)\le 0,p\in \left(\sqrt{{\displaystyle \frac{30488}{14183}}},2\right),$$

then for all $p\in \left(\sqrt{{\displaystyle \frac{30488}{14183}}},2\right)$ and $s\in \left(0,1\right)$ we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial \Psi }{\partial s}}& =& {\phi }_2\left(p\right)+2\left({\phi }_3\left(p\right)-{\phi }_4\left(p\right)\right)s,\hfill \\ & \ge & {\phi }_2\left(p\right)+2\left({\phi }_3\left(p\right)-{\phi }_4\left(p\right)\right),\hfill \\ & =& \left(4-p^2\right)\left({\displaystyle \frac{82837030}{6561}}{p}^3-{\displaystyle \frac{742508416}{6561}}{p}^2+{\displaystyle \frac{12133352}{6561}}p+{\displaystyle \frac{1596107776}{6561}}\right),\hfill \\ & \ge & 0,\hfill \end{array}$$

Thus we acquire

$$\Psi \left(p,s\right)=\Psi \left(p,1\right)={\phi }_1\left(p\right)+{\phi }_2\left(p\right)+{\phi }_3\left(p\right)=\Lambda \left(p\right),$$

where

$$\begin{array}{ccc}\hfill \Lambda \left(p\right)& =& -{\displaystyle \frac{6018966931}{387420489}}{p}^6-{\displaystyle \frac{82837030}{6561}}{p}^5+{\displaystyle \frac{12385947808040}{387420489}}{p}^4+{\displaystyle \frac{319214768}{6561}}{p}^3\hfill \\ & & -{\displaystyle \frac{106382822840128}{387420489}}{p}^2+{\displaystyle \frac{48533408}{6561}}p+{\displaystyle \frac{105982126592}{177147}}.\hfill \end{array}$$

For $p\in \left(\sqrt{{\displaystyle \frac{30488}{14183}}},2\right)$ it is evident that ${\Lambda }^{\prime }\left(p\right)\ne 0$. Additionally, computations reveal that $\Lambda \left(p\right)$ is a decreasing function, with the maximum value of 234230 occurring at $p\approx 1.466156$.

(2) 

On the six faces of the cuboid

In the subsequent step, we assess the maximum value of $Q\left(p,r,s\right)$ over the six individual faces of $\Delta$.

$\left(\mathrm{i}\right)$ On the face $p=0$, $Q\left(0,r,s\right)$ gives

$$m_1\left(r,s\right)=663552r^3+\left(73728\left(r-1\right)\left(r-8\right)s^2+2654208r\right)\left(1-r^2\right),$$

then

$${\displaystyle \frac{\partial m_1}{\partial s}}=-147456s\left(r^2-1\right)\left(r-1\right)\left(r-8\right)\ne 0\mathrm{for}s\in \left(0,1\right),$$

this indicates that $m_1$ has no optimal points within the interval $\left(0,1\right)\times \left(0,1\right).$

$\left(\mathrm{ii}\right)$ On the face $p=2,Q\left(2,r,s\right)$ becomes

$$Q\left(2,r,s\right)=10432.$$

(34)

$\left(\mathrm{iii}\right)$ On the face $r=0$, $Q\left(p,0,s\right)$ turns into

$$m_2\left(p,s\right)=163p^6+8160p^{3}s\left(4-p^2\right)+67968p^4{s}^2-31104p^4-419328p^2{s}^2+124416p^2+589824s^2,$$

putting ${\displaystyle \frac{\partial m_2}{\partial s}}=0$, gives

$$s={\displaystyle \frac{85p^3}{1416p^2-3072}}=s_0.$$

For the provided range of “s” $s_0\in \left(0,1\right),$ if $p>p_0\approx 1.472919.$ Consider ${\displaystyle \frac{\partial m_2}{\partial p}}=0$, then we have

$$6p\left(163p^4-6800p^{3}s+4532p^2{s}^2-20736p^2+16320ps-139776s^2+41472\right)=0,$$

(35)

putting value of s in (35), we obtain

$$114720043p^9+10066228992p^7-65207918592p^5+139122966528p^3-97844723712p=0.$$

Upon solving for p within the interval $\left(0,2\right)$ we obtain $p\approx 1.4396$, implying that an optimal solution for $Q\left(p,0,s\right)$ does not exist.

$\left(\mathrm{iv}\right)$ On the face $r=1$, $Q\left(p,1,s\right)$ becomes

$$m_3\left(p,s\right)=-2105p^6-42192p^4+122112p^2+331776,$$

by solving ${\displaystyle \frac{\partial m_3}{\partial p}}=0$ we find a critical point at $p\approx 1.1477,$ where $m_3$ achieve its maximum value, which is

$$m_3\left(p,s\right)\le 414610.$$

$\left(\mathrm{v}\right)$ On the face $s=1$, $Q\left(p,r,1\right)$ provides

$$\begin{array}{ccc}\hfill m_4\left(p,s\right)& =& 1152p^6{r}^4-2016p^6{r}^3-384p^6{r}^2-1020p^{6}r+163p^6-4608p^5{r}^4+28916p^5{r}^3\hfill \\ & & +12768p^5{r}^2-28916p^{5}r-8160p^5-13824p^4{r}^4+36864p^4{r}^3-75072p^4{r}^2\hfill \\ & & -27024p^{4}r+36864p^4+36864p^3{r}^4-106912p^3{r}^3-69504p^3{r}^2+106912p^{3}r\hfill \\ & & +32640p^3+55296p^2{r}^4-198144p^2{r}^3+435456p^2{r}^2+124416p^{2}r-294912p^2\hfill \\ & & -73728p{r}^4-35008p{r}^3+73728p{r}^2+35008pr-73728r^4+331776r^3\hfill \\ & & -516096r^2+589824.\hfill \end{array}$$

Differentiating, we get

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial m_4}{\partial p}}& =& 6912p^5{r}^4-12096p^5{r}^3-2304p^5{r}^2-6120p^{5}r+978p^5\hfill \\ & & -23040p^4{r}^4+144580p^4{r}^3+63840p^4{r}^2-144580p^{4}r-40800p^4\hfill \\ & & -55296p^3{r}^4+147456p^3{r}^3-300288p^3{r}^2-108096p^{3}r+147456p^3\hfill \\ & & +110592p^2{r}^4-320736p^2{r}^3-208512p^2{r}^2+320736p^{2}r+97920p^2\hfill \\ & & +110592p{r}^4-396288p{r}^3+870912p{r}^2+248832pr-589824p\hfill \\ & & -73728r^4-35008r^3+73728r^2+35008r\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial m_4}{\partial r}}& =& 4608p^6{r}^3-6048p^6{r}^2-768p^{6}r-1020p^6-18432p^5{r}^3+86748p^5{r}^2+25536p^{5}r\hfill \\ & & -28916p^5-55296p^4{r}^3+110592p^4{r}^2-150144p^{4}r-27024p^4+147456p^3{r}^3\hfill \\ & & -320736p^3{r}^2-139008p^3+106912p^3+221184p^2{r}^3-594432p^2{r}^2+870912p^{2}r\hfill \\ & & +124416p^2-294912p{r}^3-105024p{r}^2+147456pr+35008p+995328r^2-1032192r.\hfill \end{array}$$

It is clear from the analysis that the system of equations ${\displaystyle \frac{\partial m_4}{\partial p}}=0$ and ${\displaystyle \frac{\partial m_4}{\partial r}}=0$ does not have any solution in $\left(0,2\right)\times \left(0,1\right)$.

$\left(\mathrm{vi}\right)$ On the face $s=0:Q\left(p,r,0\right)$ becomes

$$\begin{array}{ccc}\hfill m_5\left(p,r\right)& =& 1152p^6{r}^4-2016p^6{r}^3-384p^6{r}^2-1020p^{6}r+163p^6-9216p^4{r}^4-35712p^4{r}^3\hfill \\ & & -11712p^4{r}^2+45552p^{4}r-31104p^4+18432p^2{r}^4+258048p^2{r}^3+52992p^2{r}^2\hfill \\ & & -331776p^{2}r+124416p^2-331776r^3+663552r.\hfill \end{array}$$

Differentiating, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial m_5}{\partial p}}& =& 6912p^5{r}^4-12096p^5{r}^3-2304p^5{r}^2-6120p^{5}r+978p^5-\hfill \\ & & 36864p^3{r}^4-142848p^3{r}^3-46848p^3{r}^2+182208p^{3}r-124416p^3\hfill \\ & & +36864p{r}^4+516096p{r}^3+105984p{r}^2-663552pr+248832p,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial m_5}{\partial r}}& =& 4608p^6{r}^3-6048p^6{r}^2-768p^{6}r-1020p^6-36864p^4{r}^3\hfill \\ & & -107136p^4{r}^2-23424p^{4}r+45552p^4+73728p^2{r}^3\hfill \\ & & +774144p^2{r}^2+105984p^{2}r-331776p^2-995328r^2+663552.\hfill \end{array}$$

It is observed by the calculations that for values in the interval $\left(0,2\right)\times \left(0,1\right)$, the system of equations ${\displaystyle \frac{\partial m_5}{\partial p}}=0$ and ${\displaystyle \frac{\partial m_5}{\partial r}}=0$ has no solution.

(3) 

On the twelve edges of the cuboid

Finally, we evaluate the maximum value of $Q\left(p,r,s\right)$ across the twelve edges.

$\left(\mathrm{i}\right)$ On $r=0$ and $s=0:Q\left(p,0,0\right)$ becomes

$$m_6\left(p\right)=163p^6-31104p^4+124416p^2,$$

solving ${\displaystyle \frac{\partial m_6}{\partial p}}=0$ leads us to the critical point $p\approx 1.4256,$ at which the maximum value is achieved, given as

$$m_6\left(p\right)\le 125750.$$

(36)

$\left(\mathrm{ii}\right)$ On $r=0$ and $s=1:Q\left(p,0,1\right)$ gives

$$m_7\left(p\right)=163p^6-8160p^5+36864p^4+32640p^3-29412p^2+589824,$$

since ${\displaystyle \frac{\partial m_7}{\partial p}}\le 0,$ for all $p\in \left[0,2\right]$, it follows that $m_7\left(p\right)$ is a decreasing function with its maximum value occurring at $p=0$, given by

$$m_7\left(p\right)\le 589824.$$

(37)

$\left(\mathrm{iii}\right)$ On $r=0$ and $p=0:Q\left(0,0,s\right)$ gives

$$m_8\left(s\right)=589808s^2+16,$$

as, ${\displaystyle \frac{\partial m_8}{\partial s}}>0$ for $s\in \left[0,1\right]$, this indicates that $m_8\left(s\right)$ is an increasing function and achieve its maximum value at $s=1$, given as

$$m_8\left(s\right)\le 589824.$$

(38)

$\left(\mathrm{iv}\right)$ On $r=1$ and $s=0,1$ we have

$$m_9\left(p\right)=Q\left(p,1,0\right)=Q\left(p,1,1\right)=-2105p^6-42192p^4+122112p^2+331776,$$

putting ${\displaystyle \frac{\partial m_9}{\partial p}}=0$ we find a critical points $p\approx 1.1477,$ where $m_9$ attains its maximum value that is

$$m_9\left(p\right)\le 414610.$$

(39)

$\left(\mathrm{v}\right)$ On $r=1$ and $p=0$, we have

$$m_{10}\left(s\right)=Q\left(0,1,s\right)=331776.$$

(40)

$\left(\mathrm{vi}\right)$ On $p=2$, we get

$$Q\left(2,0,s\right)=Q\left(2,1,s\right)=Q\left(2,r,1\right)=Q\left(2,r,1\right)=10432.$$

$\left(\mathrm{vii}\right)$ On $p=0$ and $s=0:Q\left(0,r,0\right)$ becomes

$$m_{11}\left(r\right)=-331776r\left(2r^2-r-2\right),$$

from the calculation, it follows that ${\displaystyle \frac{\partial m_{11}}{\partial r}}\le 0$ for all $r\in \left[0,1\right]$ which indicates $m_{11}\left(r\right)$ is a decreasing function. Consequently, its maximum value is achieved at $r=0$, yielding

$$m_{11}\left(r\right)\le 0.$$

(41)

$\left(\mathrm{viii}\right)$ On $p=0$ and $s=1:Q\left(0,r,1\right)$ provides

$$m_{12}\left(r\right)=-73728r^4+1658880r^3+-516096r^2+589824.$$

By setting ${\displaystyle \frac{\partial m_{12}}{\partial r}}=0,$ the critical point $r=0,$ is obtained at which the functions $m_{12}\left(r\right)$ attains its maximum value, leading to

$$m_{12}\left(r\right)\le 589824.$$

(42)

Therefore, we conclude that

$$Q\left(p,r,s\right)\le 589824.$$

Hence

$$\left|{\mathcal{H}}_{3,1}\left(f\right)\right|\le {\displaystyle \frac{1}{36}}.$$

□

4. Conclusions

In this article, a new geometric image domain is introduced which is generated by the composition of $\sqrt{1+\xi }$ and $\sin \xi$. The transformation of open unit disc under this newly defined domain has a nice geometric appearance, which lies in the right-half plane and is symmetric about the real axis. This image domain was utilized to define a new subclass ${\mathcal{S}}_{LP}^{*}$ of starlike functions within the open unit disc $\mathfrak{D}$. For this subclass, the sharp upper bounds for the first four Maclaurin’s coefficients were derived, and the sharp estimates for the second and third-order Hankel determinants were established. The methodologies developed in this study can be extended to explore related problems such as logarithmic coefficients and higher- order Hankel determinants, including the fourth and fifth orders, as discussed in [46,47,48]. This work not only advances the field of geometric function theory, but also provides a framework for future investigations into the sharp bounds and structural properties of analytic functions.