Exploring the Embedding of the Extended Zero-Divisor Graph of Commutative Rings

Abstract

${\mathfrak{R}}_{\mathfrak{c}}$ represents commutative rings that have unity elements. The collection of all zero-divisor elements in ${\mathfrak{R}}_{\mathfrak{c}}$ are represented by $D\left({\mathfrak{R}}_{\mathfrak{c}}\right)$. We denote an extended zero-divisor graph by the notation ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ of ${\mathfrak{R}}_{\mathfrak{c}}.$ This graph has a set of vertices in $D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$. The graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ illustrates interactions among the zero-divisor elements of ${\mathfrak{R}}_{\mathfrak{c}}.$ Specifically, two different vertices u and y are connected in ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ iff $u{\mathfrak{R}}_{\mathfrak{c}}\cap Ann\left(y\right)$ is non-null or $y{\mathfrak{R}}_{\mathfrak{c}}\cap Ann\left(u\right)$ is non-null. The main idea for this work is to systematically analyze the ring ${\mathfrak{R}}_{\mathfrak{c}}$ which is finite for the unique aspect of their extended zero-divisor graph. This study particularly focuses on instances where the extended zero-divisor graph has a genus or crosscap of two. Furthermore, this work aims to thoroughly characterize finite ring ${\mathfrak{R}}_{\mathfrak{c}}$ wherein the extended zero-divisor graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has an outerplanarity index of two. Finally, we determine the book thickness of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ for genus at most one.

1. Introduction

The exploration of different graphs linked to algebraic systems is extensive and is an emerging trend in modern research. The focus of the present work is based on the classification of the graphs of the theoretical ring structure and vice versa. Special attention is paid to understanding the correspondence through the algebraic system for known entities with graphical properties of the associated structures. When a combinatorial entity is assigned to an algebraic system, this gives rise to algebraic and combinatorial problems. Consequently, this is an important area for the investigation of graph structures related to rings with commutativity. Let ${\mathfrak{R}}_{\mathfrak{c}}$ denote a commutative ring that has a non-null unit element. $D\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is assumed to represent a collection of all zero-divisor elements. Innovative concepts on zero-divisor graphs were introduced and investigated by Beck [1] in commutative rings with unity element, considering elements of this ring as vertices of the graph and examining the dynamics of the coloring of the graph. Taking this concept, Anderson and Livingston [2] defined $\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$, where vertices are non-null zero-divisors and connected if the product of the vertices are zero (see [3,4,5,6,7,8] for more details). Adding this mathematical development, Badawi [9] introduced the annihilator graph $AG\left({\mathfrak{R}}_{\mathfrak{c}}\right)$, with a set of vertices $D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$, where two different vertices, u and y, are connected iff $Ann\left(uv\right)\ne Ann\left(u\right)\cup Ann\left(y\right)$.

A more recent work by Bakhtyiari et al. [10,11] presented the extended zero-divisor graph for ${\mathfrak{R}}_{\mathfrak{c}}$, given by ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$, that is, the undirected graph with a set of vertices $D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$, where two different vertices, u and y, are connected iff $u{\mathfrak{R}}_{\mathfrak{c}}\cap Ann\left(y\right)\ne 0$ or $y{\mathfrak{R}}_{\mathfrak{c}}\cap Ann\left(u\right)\ne 0$. In [10], the authors investigated properties based on the extended zero-divisor graph and given the relationships between ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ and $\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$.

Rehman et al. [12] characterized rings that are finite and commutative with an extended zero-divisor graph that is isomorphic in accordance with existing graphs in the literature with the classification of rings that are finite and commutative with an extended zero-divisor graph that is planar, projective, or toroidal. Ali et al. [13] computed eccentric topological indices of zero-divisor graphs. Recently, Mohd et al. [14] investigated the genus and crosscap-two annihilator graph of commutative rings.

Motivated by the above research, we consider ${\mathfrak{R}}_{\mathfrak{c}}$ as a ring that is finite and commutative containing an identity element. It is characterized by sets, such as $D\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ that denote the collection of zero-divisor elements, $U\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ represents the collection of all unit elements, $M\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ encompasses the collection of minimal prime ideals, and $N\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ shows the collection of nilpotent elements. The notation ${\mathbb{A}}_n$ denotes the ring over integer modulo n. ${\mathbb{K}}_q$ stands for the field with q elements. Notably, $T^{*}=T\setminus \left\{0\right\}$ of ${\mathfrak{R}}_{\mathfrak{c}}.$ For $b\in {\mathfrak{R}}_{\mathfrak{c}}$, $Ann\left(b\right)$ stands for the annihilators of $b.$ For more details regarding theoretical ring terminologies, readers can review [15].

This paper extends the investigation by categorizing finite commutative rings ${\mathfrak{R}}_{\mathfrak{c}}$ with ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$, which have a genus and crosscap two. In addition, an identification is provided for ${\mathfrak{R}}_{\mathfrak{c}}$, where ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has an outerplanarity index of 2. A determination of the minimally non-outerplanar graph is also given. Finally, we determine the book thickness of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ for a genus of, at most, one.

2. Preliminaries

This section contains a short overview of symbols, principles, and results related to the genus of graphs, establishing the foundation for the following sections.

We consider a simple graph H that is undirected and has V as the vertex set and E as the edge set. ${\mathcal{K}}_m$ stands for a complete graph characterized by a tuple of vertices linked with an edge. A partite graph is a graph with vertex sets that are partitioned into different subsets so that no two vertices are linked within the same set. In general, an s-partite graph is partitioned into s subsets so that none of two vertices are connected within the same set. Next to the s-partite, we have a complete s-partite graph that has vertices connected to another vertex not in the same set. ${\mathcal{K}}_{p,q}$ is a special case of the 2-partite graph with a part size that is ($p,$q), with each vertex from one part connected to every vertex in the other part. For more details on graph theory, readers refer to [16,17].

We represent a given graph on a surface in topological graph theory. In that sense, consider $S_h$ represents a sphere where h stands for handles, which is a positive integer, indicating genus h for its oriented surface. $\daleth \left(H\right)$, refers genus which is smallest integer h allowing H for embedding in $S_h$.

In a visual sense, H is considered as embedded on a surface if H depicts on the surface with edges divided on a vertex that is shared by a pair of vertices. A planar graph has 0 genus, while a toroidal graph has $1.$ Furthermore, it is worth noting that $\gamma \left(H\right)\ge \gamma \left(J\right)$ indicates that H is a subgraph of J. In graph theory based on topology, using Euler’s formula, we determine that the relationship for a finite connected graph H is written as $n+f-e=2-2\gamma$, where $n=$ no. of vertices, $e=$ no. of edges, $\gamma =$ genus, and $f=$ no. of faces due to cellular embedded process of H on $S_{\gamma }$. For the combined combinatorial identities and various inequalities, this formula plays the role of a powerful tool for exploring and demonstrating the existence of concerned graph embeddings. To search more thoroughly for embedded graphs on a surface, refer to [17]. Some more details on genus one for zero-divisor graphs, readers can refer to [18,19]. The zero-divisor planar graph is given in [20], whereas computations on radio labeling associated with the zero-divisor graph of a commutative ring is given in [21], and further eccentric topological indices based on the edges of zero-divisor graphs are studied in [22].

Some results and bounds based on genus are presented below.

Proposition 1

([10], Lemma 2.2). With ${\mathfrak{R}}_{\mathfrak{c}}$ as a commutative ring, we have the following:

(i.)

$\varrho \sim \varsigma$ being the edge of $\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$ for $\varrho ,\varsigma \in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*},$ we obtain $\varrho \sim \varsigma$, which is an edge of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$.

(ii.)

$\varrho \sim \varsigma$ being not an edge of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ for $\varrho ,\varsigma \in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$, we obtain $Ann\left(\varrho \right)=Ann\left(\varsigma \right)$. The indirect part is true only if ${\mathfrak{R}}_{\mathfrak{c}}$ is a reduced ring.

(iii.)

$Ann\left(\varsigma \right)⊉Ann\left(\varrho \right)$ or $Ann\left(\varrho \right)⊉Ann\left(\varsigma \right)$ for $\varrho ,\varsigma \in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$, we obtain $\varrho \sim \varsigma$ as an edge of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$.

(iv.)

$\varrho {\mathfrak{R}}_{\mathfrak{c}}\cap Ann\left(\varrho \right)$ being non-null for $\varrho \in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$, we obtain ϱ, which is connected to all other vertices in ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$. Specifically, $\varrho \in N{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$, we obtain ϱ, which is connected to the rest of the vertices in ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$.

(v.)

${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\left[N{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}\right]$ is a complete subgraph.

The following example shows that graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ and graph $\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$ are not identical.

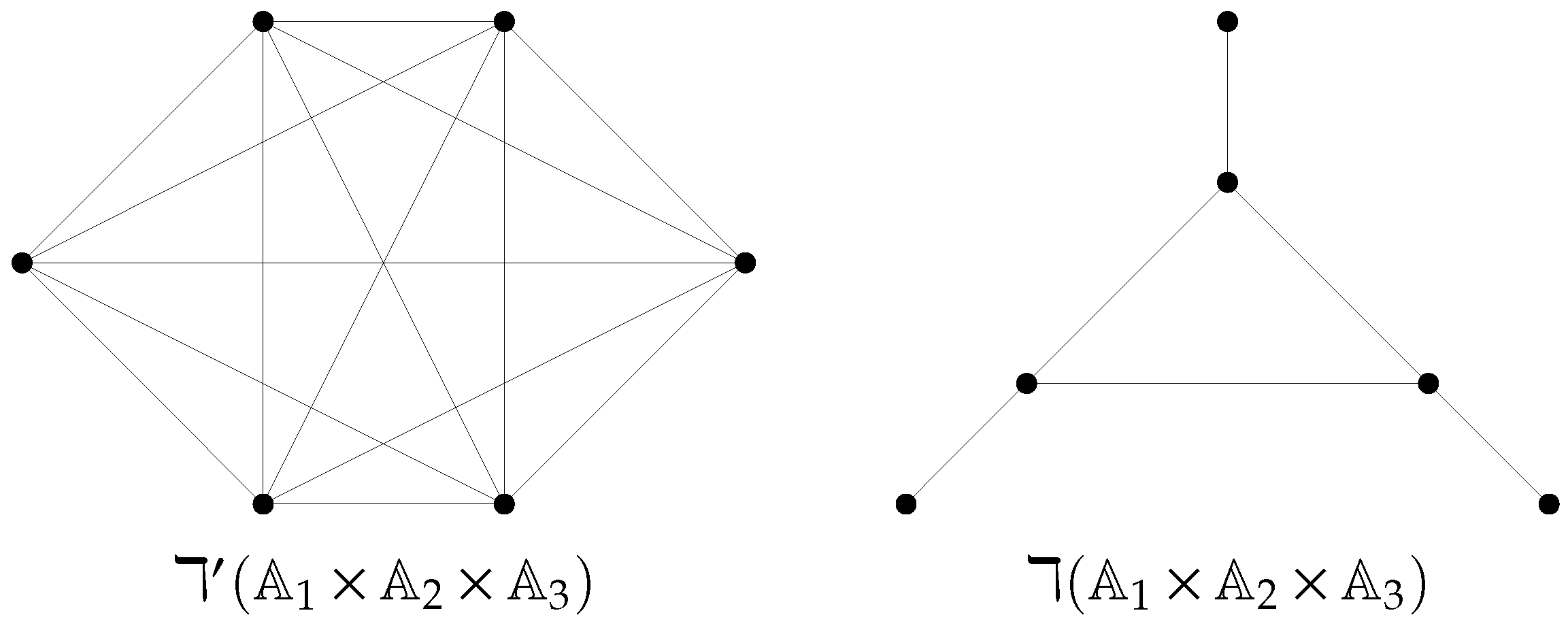
Theorem 1

([12]). With $({\mathfrak{R}}_{\mathfrak{c}},\xi )$ as a commutative local ring, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is a complete graph.

The following are some known results of the genus of complete graphs and complete bipartite graphs.

Lemma 1

([17]). Let $p,q\ge 2$. Then,

$$\gamma \left({\mathcal{K}}_{p,q}\right)=⌈{\displaystyle \frac{1}{4}}(p-2)(q-2)⌉.$$

Specifically, $\gamma \left({\mathcal{K}}_{4,4}\right)=\gamma \left({\mathcal{K}}_{3,q}\right)=1$ if $q=3,\dots ,6$ and $\gamma \left({\mathcal{K}}_{5,4}\right)=\gamma \left({\mathcal{K}}_{6,4}\right)=\gamma \left({\mathcal{K}}_{3,p}\right)=2$, if $p=7,\dots ,10.$

Lemma 2

([17]). Let $p\ge 3$. Then,

$$\gamma \left({\mathcal{K}}_p\right)=⌈{\displaystyle \frac{1}{12}}(p-3)(p-4)⌉.$$

Specifically, $\gamma \left({\mathcal{K}}_p\right)=1$ if $p=5,6,7$ and $\gamma \left({\mathcal{K}}_8\right)=2,$

Lemma 3

([23]). H being connected graph and e being its edges with vertices $y\ge 3$, the following formula holds:

$$\gamma \left(H\right)\ge ⌈{\displaystyle \frac{e}{6}}-{\displaystyle \frac{v}{2}}+1⌉.$$

3. Genus of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$

Finite commutative rings ${\mathfrak{R}}_{\mathfrak{c}}$ with an identity element are thoroughly examined where graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has a genus of two. Using the Euler characteristic equation and deletion–insertion method, we eliminate some steps that lead to yielding a higher genus.

Theorem 2

([12], Theorems 3.2, 3.3, 3.5). ${\mathfrak{R}}_{\mathfrak{c}}$ being a finite commutative ring, we obtain ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$, which is planar, iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent to one of the rings listed below:

$$\begin{gathered} {\mathbb{A}}_4,{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_9,{\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_8,{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3,x^2-2⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨2x,x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,xy,y^2⟩}},{\displaystyle \frac{{\mathbb{K}}_4\left[x\right]}{⟨x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2+x+1⟩}},{\mathbb{A}}_{25},{\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_4\times \\ {\mathbb{A}}_2,{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2,{\mathbb{A}}_2\times F\mathit{or}{\mathbb{A}}_3\times F, \mathit{for} \mathit{finite} F. \end{gathered}$$

Theorem 3

([12], Theorem 4.1). $(A,\xi )$ being a finite commutative local ring, we obtain $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=1$ iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent amongst the following:

$$\begin{gathered} {\mathbb{A}}_{49},{\displaystyle \frac{{\mathbb{A}}_7\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_{16},{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^4⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2-2,x^4⟩}},{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3-2,x^4⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3+x^2-2,x^4⟩}},{\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^3,xy,y^2-x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3,x^2-2x⟩}},{\displaystyle \frac{{\mathbb{A}}_8\left[x\right]}{⟨x^2-4,2x⟩}}, \\ {\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^3,x^2-2,xy,y^2-2,y^3⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^2,y^2,xy-2⟩}},{\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,y^2⟩}},{\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,y^2,xy⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3,2x⟩}},{\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^3,x^2-2,xy,y^2⟩}},{\displaystyle \frac{{\mathbb{A}}_8\left[x\right]}{⟨x^2,2x⟩}}, \\ {\displaystyle \frac{{\mathbb{K}}_8\left[x\right]}{⟨x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3+x+1⟩}},{\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨2x,2y,x^2,y^2,xy⟩}} \mathit{or} {\displaystyle \frac{{\mathbb{A}}_2[x,y,z]}{{⟨x,y,z⟩}^2}}. \end{gathered}$$

Theorem 4

([12], Theorems 4.2, 4.4). Let ${\mathfrak{R}}_{\mathfrak{c}}$ be a finite commutative non-local ring. Then, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=1$ iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent to one of the rings listed below:

$${\mathbb{K}}_4\times {\mathbb{K}}_4,{\mathbb{K}}_4\times {\mathbb{A}}_5,{\mathbb{A}}_5\times {\mathbb{A}}_5,{\mathbb{K}}_4\times {\mathbb{A}}_7,{\mathbb{A}}_2\times {\mathbb{A}}_2\times {\mathbb{A}}_2,{\mathbb{A}}_4\times {\mathbb{A}}_3, \mathit{or} {\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_3.$$

Theorem 5.

Let $({\mathfrak{R}}_{\mathfrak{c}},\xi )$ be a finite local commutative ring. Then, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent to one of the rings listed below:

$${\mathbb{A}}_{27},{\displaystyle \frac{{\mathbb{A}}_9\left[x\right]}{⟨3x,x^2-3⟩}},{\displaystyle \frac{{\mathbb{A}}_9\left[x\right]}{⟨3x,x^2-6⟩}},{\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^3⟩}},{\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{{⟨x,y⟩}^2}},{\displaystyle \frac{{\mathbb{A}}_9\left[x\right]}{{⟨3,x⟩}^2}},{\displaystyle \frac{{\mathbb{K}}_9\left[x\right]}{⟨x^2⟩}} \mathit{or} {\displaystyle \frac{{\mathbb{A}}_9\left[x\right]}{⟨x^2+1⟩}}.$$

Proof. 

We have that ${\mathfrak{R}}_{\mathfrak{c}}$ is local. Next, graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is completed using Theorem 1. Thus, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ iff $|D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}|=8$. □

In the Theorem given below, we calculate all finite reduced non-local rings ${\mathfrak{R}}_{\mathfrak{c}}$ for which ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has a genus of two.

Theorem 6.

With ${\mathfrak{R}}_{\mathfrak{c}}$ being finite commutative rings that are non-local and reduced, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent to one of the rings listed below:

$${\mathbb{K}}_4\times {\mathbb{K}}_8,{\mathbb{K}}_4\times {\mathbb{K}}_9,{\mathbb{K}}_4\times {\mathbb{K}}_{11}, \mathit{or} {\mathbb{A}}_5\times {\mathbb{A}}_7.$$

Proof. 

Consider $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$. Since ${\mathfrak{R}}_{\mathfrak{c}}$ is a finite reduced non-local commutative ring, $A\cong F_1\times F_2\times \cdots \times F_n$, with each $F_i$ a field having the property of $n\ge 2$. Let $n=4,5,6,\dots$. Let $x_1=(1,0,\dots ,0)$, $x_2=(0,1,0\dots ,0)$, $x_3=(0,0,1,0,\dots ,0)$, $x_4=(0,0,0,1,0,\dots ,0)$, $y_1=(1,1,0,\dots ,0)$, $y_2=(1,0,1,0,\dots ,0)$, $y_3=(0,1,1,0,\dots ,0)$, $y_4=(1,0,0,1,0,\dots ,0)$, $y_5=(0,1,0,1,0,\dots ,0)$, $y_6=(0,0,1,1,0,\dots ,0)$ and $y_7=(0,1,1,1,0,\dots ,0)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$. Since $Ann\left(x_1\right)⊈Ann\left(y_1\right)$, $Ann\left(x_1\right)⊈Ann\left(y_2\right)$, $x_1{y}_3=0$, $Ann\left(x_1\right)⊈Ann\left(y_4\right)$, $x_1{y}_5=0$, $x_1{y}_6=0$, $x_1{y}_7=0$, $Ann\left(x_2\right)⊈Ann\left(y_1\right)$, $x_2{y}_2=0$, $Ann\left(x_2\right)⊈Ann\left(y_3\right)$, $x_2{y}_4=0$, $Ann\left(x_2\right)⊈Ann\left(y_5\right)$, $x_2{y}_6=0$, $Ann\left(x_2\right)⊈Ann\left(y_7\right)$, $x_3{y}_1=0$, $Ann\left(x_3\right)⊈Ann\left(y_2\right)$, $Ann\left(x_3\right)⊈Ann\left(y_3\right)$, $x_3{y}_4=0$, $x_3{y}_5=0$, $Ann\left(x_3\right)⊈Ann\left(y_6\right)$, $Ann\left(x_3\right)⊈Ann\left(y_7\right)$, $x_4{y}_1=0$, $x_4{y}_2=0$, $x_4{y}_3=0$, $Ann\left(x_4\right)⊈Ann\left(y_4\right)$, $Ann\left(x_4\right)⊈Ann\left(y_5\right)$, $Ann\left(x_4\right)⊈Ann\left(y_6\right)$ and $Ann\left(x_4\right)⊈Ann\left(y_7\right)$. Using Lemma 1, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_{4,7}$ induced by the set $\{x_1,x_2,x_3,x_4\}\cup \{y_1,y_2,\dots ,y_7\}$ with Lemma 1. This shows that $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 1 is contradictory. Hence, $3\ge n$.

• Let $n=3$. Our claim is $|F_i|=2$ for every $1\le i\le 3$. Conversely, $|F_1|\ge 3$ with $1\ne \alpha \in F_1^{*}$. Let $a_1=(1,0,0)$, $a_2=(\alpha ,0,0)$, $a_3=(0,1,0)$, $a_4=(1,1,0)$, $a_5=(\alpha ,1,0)$, $a_6=(0,0,1)$, $a_7=(1,0,1)$, $a_8=(\alpha ,0,1)$, and $a_9=(0,1,1)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$. The set $\{a_1,a_2,\dots ,a_9\}$ inducing the subgraph has a minimum of 33 edges with 9 vertices. Using Lemma 3, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)\ge 3$ is contradictory. This shows that ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_2\times {\mathbb{A}}_2\times {\mathbb{A}}_2$. Using Theorem 4, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=1$, which again contradicts.

Now, let $n=2\Rightarrow \left|M\right({\mathfrak{R}}_{\mathfrak{c}}\left)\right|=2$ and using ([10], Theorem 4.2), ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)=\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$. Using ([24], Theorem 4), $A\cong {\mathbb{K}}_4\times {\mathbb{K}}_9,$${\mathbb{K}}_4\times {\mathbb{K}}_8$, ${\mathbb{A}}_5\times {\mathbb{A}}_7$, or ${\mathbb{K}}_4\times {\mathbb{K}}_{11}$.

Conversely, if $A\cong {\mathbb{K}}_4\times {\mathbb{K}}_9,$${\mathbb{K}}_4\times {\mathbb{K}}_8$, ${\mathbb{A}}_5\times {\mathbb{A}}_7$, or ${\mathbb{K}}_4\times {\mathbb{K}}_{11}$, then by ([10], Theorem 4.2), ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)=\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$. Hence, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ by ([24], Theorem 4). □

Theorem 7.

Let ${\mathfrak{R}}_{\mathfrak{c}}$ be a finite non-local non-reduced commutative ring. Then, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)\ne 2$.

Proof. 

The ring ${\mathfrak{R}}_{\mathfrak{c}}$ is non-infinite, non-reduced, and non-local, so $A\cong {\mathfrak{R}}_{\mathfrak{c}1}\times {\mathfrak{R}}_{\mathfrak{c}2}\times \cdots \times {\mathfrak{R}}_{\mathfrak{c}n}\times F_1\times F_2\times F_3\times \cdots \times F_m,$ where every $({\mathfrak{R}}_{\mathfrak{c}i},{\xi }_i)$ is local, having the maximal ideal ${\xi }_i,$ with field $F_i$ for each i with $n,m\ge 1.$ Consider n is greater than or equal to $2.$ Since ${\xi }_i\ne 0,\exists a_i\in {\xi }_i^{*}\in Ann\left(a_i\right)={\xi }_i$ for every $i.$ Consider $x_1=(1,0,0,\dots ,0), x_2=(u_1,0,0,\dots ,0), x_3=(a_1,0,\dots ,0), x_4=(0,a_2,0,\dots ,0)$, $y_1=(a_1,1,0,\dots ,0), y_2=(a_1,u_1,0,\dots ,0), y_3=(a_1,a_2,0,\dots ,0), y_4=(u_1,a_2,0,\dots ,0)$, $y_5=(1,a_2,0,\dots ,0)$, $y_6=(0,u_2,0,\dots ,0), y_7=(0,1,0,\dots ,0)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$, where $1\ne u_i\in U\left({\mathfrak{R}}_{\mathfrak{c}i}\right).$

Since $$\begin{gathered} Ann\left(x_1\right)⊈Ann\left(y_1\right), Ann\left(x_1\right)⊈Ann\left(y_2\right), Ann\left(x_1\right)⊈Ann\left(y_3\right), Ann\left(x_1\right)⊈Ann\left(y_4\right), Ann\left(x_1\right)⊈Ann\left(y_5\right), x_1{y}_6=0, x_1{y}_7=0, Ann\left(x_2\right)⊈Ann\left(y_1\right), Ann\left(x_2\right)⊈Ann\left(y_2\right), Ann\left(x_2\right)⊈Ann\left(y_3\right), Ann\left(x_2\right)⊈Ann\left(y_4\right), \\ Ann\left(x_2\right)⊈Ann\left(y_5\right), x_2{y}_6=0 \end{gathered}$$, $x_2{y}_7=0, Ann\left(x_3\right)⊈Ann\left(y_1\right), Ann\left(x_3\right)⊈Ann\left(y_2\right), Ann\left(x_3\right)⊈Ann\left(y_3\right), Ann\left(x_3\right)⊈Ann\left(y_4\right)$, $Ann\left(x_3\right)⊈Ann\left(y_5\right), x_3{y}_6=0, x_3{y}_7=0, Ann\left(x_4\right)⊈Ann\left(y_1\right), Ann\left(x_4\right)⊈Ann\left(y_2\right), Ann\left(x_4\right)⊈Ann\left(y_3\right), Ann\left(x_4\right)⊈Ann\left(y_4\right)$.

$Ann\left(x_4\right)⊈Ann\left(y_5\right), x_4{y}_6=0,x_4{y}_7=0,{\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains a subgraph of ${\mathcal{K}}_{4,7}$ induced by the set $\{x_1,x_2,x_3,x_4\}\cup \{y_1,y_2,\dots ,y_7\}.$ Hence, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 1.

Now, suppose that $m\ge 2.$ Consider $w_1=(1,0,0,\dots ,0), w_2=(0,1,0,\dots ,0)$, $w_3=(0,0,1,0,\dots ,0), w_4=(a_1,0,0,\dots ,0), z_1=(1,1,0,\dots ,0), z_2=(1,0,1,0,\dots ,0)$, $z_3=(u_1,1,0,\dots ,0), z_4=(u_1,0,1,0,\dots ,0), z_5=(a_1,1,0,\dots ,0), z_6=(a_1,0,1,0,\dots ,0)$, and $z_7=(a_1,1,1,0,\dots ,0)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}.$

Since $$\begin{gathered} Ann\left(w_1\right)⊈Ann\left(z_1\right), Ann\left(w_1\right)⊈Ann\left(z_2\right), Ann\left(w_1\right)⊈Ann\left(z_3\right), Ann\left(w_1\right)⊈Ann\left(z_4\right), Ann\left(z_5\right)⊈Ann\left(w_1\right), Ann\left(w_1\right)⊈Ann\left(z_6\right), Ann\left(z_7\right)⊈Ann\left(w_1\right), Ann\left(w_2\right)⊈Ann\left(z_1\right), w_2{z}_2=0, Ann\left(w_2\right)⊈Ann\left(z_3\right), \\ w_2{z}_4=0, Ann\left(w_2\right)⊈Ann\left(z_5\right), Ann\left(w_2\right)⊈Ann\left(z_6\right), Ann\left(w_2\right)⊈Ann\left(z_7\right), w_3{z}_1=0, Ann\left(w_3\right)⊈Ann\left(z_2\right), Ann\left(w_3\right)⊈Ann\left(z_3\right) \end{gathered}$$, $Ann\left(w_3\right)⊈Ann\left(z_4\right), w_3{z}_5=0, Ann\left(w_3\right)⊈Ann\left(z_6\right), w_3{z}_7=0, Ann\left(w_4\right)⊈Ann\left(z_1\right)$, $Ann\left(w_4\right)⊈Ann\left(z_2\right), Ann\left(w_4\right)⊈Ann\left(z_3\right), Ann\left(w_4\right)⊈Ann\left(z_4\right), Ann\left(w_4\right)⊈Ann\left(z_5\right)$, $Ann\left(w_4\right)⊈Ann\left(z_6\right)$, and $Ann\left(w_4\right)⊈Ann\left(z_7\right),$ then using Lemma 1, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains a subgraph of ${\mathcal{K}}_{4,7}$ induced by the set $\{w_1,w_2,w_3,w_4\}\cup \{z_1,z_2,\dots ,z_7\}$. Hence, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 1.

Suppose that $m=n=1$ and $|{\xi }_1^{*}|=2.$ Then, ${\mathfrak{R}}_{\mathfrak{c}1}\cong {\mathbb{A}}_9$ or ${\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^2⟩}}$, and hence, $\left|U\right({\mathfrak{R}}_{\mathfrak{c}1}\left)\right|=6.$ Let $a,b\in {\xi }_1^{*}\in ab=0$ and $Ann\left(a\right)={\xi }_1.$ Consider $r_1=(1,0), r_2=(u_1,0), r_3=(u_2,0),$ $r_4=(u_3,0), s_1=(0,1), s_2=(a,0), s_3=(b,0), s_4=(a,1), s_5=(b,1)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*},$ where $u_i\in U\left({\mathfrak{R}}_{\mathfrak{c}1}\right).$ Since $r_i\sim s_j$ for every $i,j,{\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_{5,5}.$ Hence, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 1. Hence, $|{\xi }_1^{*}|\ne 2.$

Suppose that $m=n=1$ and $|{\xi }_1^{*}|\ge 3,$ then $\left|U\right({\mathfrak{R}}_{\mathfrak{c}1}\left)\right|\ge 4.$ Assume $a,b,c$ as members of ${\xi }_1^{*}$, which is a member of $ab=bc=0$, with $Ann\left(a\right)={\xi }_1.$ Let $d_1=(u_1,0), d_2=(u_2,0),$ $d_3=(u_3,0), d_4=(u_4,0), e_1=(a,0), e_2=(b,0), e_3=(c,0), e_4=(a,1), e_5=(b,1),$ $e_6=(c,1)$, and $e_7=(0,1)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*},$ where $u_i\in U\left({\mathfrak{R}}_{\mathfrak{c}1}\right).$ Since $d_i\sim e_j$ for every $i,j,$${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_{4,7},$ using Lemma 1. Hence, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 1.

Now, suppose that $n=m=1,|{\xi }_1^{*}|=1$ and $|F_1|\ge 5$ and $x\in {\xi }_1^{*}\in x^2=0.$ Consider $a_1=(0,1), a_2=(0,x_1), a_3=(0,x_2), a_4=(0,x_3), b_1=(1,0), b_2=(x,0), b_3=(u,0),$ $b_4=(x,1),b_5=(x,x_1), b_6=(x,x_2), b_7=(x,x_3)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*},$ where $1\ne x_1,x_2,x_3\in F_1^{*}$ and $1\ne u\in U\left({\mathfrak{R}}_{\mathfrak{c}1}\right).$ Since $a_i\sim b_j$ for every $i,j,{\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_{4,7}.$ Hence, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 1.

Now, suppose that $n=m=1,|{\xi }_1^{*}|=1$ and $|F_1|=2$ or $|F_1|=3,$ then, with Theorems 2 and 4, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)\ne 2$.

Finally, suppose that $n=m=1,|{\xi }_1^{*}|=1$ and $|F_1|=4.$ Then, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains 32 edges and 9 vertices. Hence, $\gamma \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 3. □

4. Crosscap of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$

In this section, we classify the finite commutative rings ${\mathfrak{R}}_c$ for which the extended zero-divisor graph ${\daleth }^{\prime }\left({\mathfrak{R}}_c\right)$ is a Klein bottle.

For $0\ne k,$$N_k$ refers to a sphere having k crosscaps. It is worth noting that a connected compact surface could be matched topologically with $N_k$ for $0\ne k$. $\overline{\gamma }\left(H\right)$ or the non-orientable genus is the least positive integer k that is written for crosscap numbers and embedded to H in $N_k$. The projective graph has a crosscap of 1, and a Klein bottle graph has a crosscap of 2.

The results given below provide crosscap numbers for complete and bipartite graphs. The ceiling function $\lceil x\rceil$ signifies the least positive integer that is ≥x, for x as a real number.

Lemma 4

([17]). For $n\ge 3$,

$$\overline{\gamma }\left({\mathcal{K}}_n\right)=\left\{\begin{array}{cc}⌈{\displaystyle \frac{(n-3)(n-4)}{6}}⌉\hfill & \mathit{if}n\ge 3\mathit{and}n\ne 7;\hfill \\ 3\hfill & \mathit{if}n=7.\hfill \end{array}\right.$$

Lemma 5

([17]). For $n\ge 2$ and $m\ge 2$,

$$\overline{\gamma }\left({\mathcal{K}}_{m,n}\right)=⌈{\displaystyle \frac{(m-2)(n-2)}{2}}⌉.$$

Theorem 8

([12]). Let ${\mathfrak{R}}_{\mathfrak{c}}$ be a finite commutative ring. Then, $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=1$ iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent to one of the rings listed below:

$${\mathbb{A}}_{49},{\displaystyle \frac{{\mathbb{A}}_7\left[x\right]}{⟨x^2⟩}},{\mathbb{K}}_4\times {\mathbb{K}}_4,{\mathbb{K}}_4\times {\mathbb{A}}_5, \mathit{or} {\mathbb{A}}_2\times {\mathbb{A}}_2\times {\mathbb{A}}_2.$$

Now, we classify the finite ring ${\mathfrak{R}}_{\mathfrak{c}}$ as having $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$.

Theorem 9.

Let ${\mathfrak{R}}_{\mathfrak{c}}$ be a finite commutative ring. Then, $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent to one of the rings listed below:

$${\mathbb{K}}_4\times {\mathbb{A}}_7,{\mathbb{A}}_5\times {\mathbb{A}}_5,{\mathbb{A}}_4\times {\mathbb{A}}_3, \mathit{or} {\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_3.$$

Proof. 

Consider $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$. Since ${\mathfrak{R}}_{\mathfrak{c}}$ is finite, ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathfrak{R}}_{\mathfrak{c}1}\times {\mathfrak{R}}_{\mathfrak{c}2}\times \cdots \times {\mathfrak{R}}_{\mathfrak{c}m}$, where $({\mathfrak{R}}_{\mathfrak{c}i},{\xi }_i)$ is a local ring for every i and $m=1,2,3,\dots .$ Let $m=4,5,\dots .$ Consider $p_1=(1,0,0,0,0,\dots ,0), p_2=(0,1,0,0,0,\dots ,0), p_3=(1,1,0,0,\dots ,0), p_4=(1,0,1,0,0,0,\dots ,0), q_1=(0,0,1,0,0,0,\dots ,0), q_2=(0,0,0,1,0,0,0,\dots ,0), q_3=(1,0,0,1,$$0,0,0,\dots ,0), q_4=(0,1,1,0,0,0\dots ,0), q_5=(0,0,1,1,0,0,\dots ,0)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}.$ Since $Ann\left(p_1\right)⊈Ann\left(q_1\right)$, $Ann\left(p_1\right)⊈Ann\left(q_2\right)$, $Ann\left(p_1\right)⊈Ann\left(q_3\right), Ann\left(p_1\right)⊈Ann\left(q_4\right),$ $Ann\left(p_1\right)⊈Ann\left(q_5\right), Ann\left(p_2\right)⊈Ann\left(q_1\right), Ann\left(p_2\right)⊈Ann\left(q_2\right), Ann\left(p_2\right)⊈Ann\left(q_3\right),$ $Ann\left(p_2\right)⊈Ann\left(q_4\right), Ann\left(p_2\right)⊈Ann\left(q_5\right), Ann\left(p_3\right)⊈Ann\left(q_1\right), Ann\left(p_3\right)⊈Ann\left(q_2\right),$ $Ann\left(p_3\right)⊈Ann\left(q_3\right), Ann\left(p_3\right)⊈Ann\left(q_4\right), Ann\left(p_3\right)⊈Ann\left(q_5\right), Ann\left(p_4\right)⊈Ann\left(q_1\right),$ $Ann\left(p_4\right)⊈Ann\left(q_1\right), Ann\left(p_4\right)⊈Ann\left(q_2\right), Ann\left(p_4\right)⊈Ann\left(q_3\right), Ann\left(p_4\right)⊈Ann\left(q_4\right),$ $Ann\left(p_4\right)⊈Ann\left(q_5\right),$ then using Lemma 1, $p_i\sim q_j$ for every $i,j.$ Hence, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_{4,5}$ induced by the set $\{p_1,p_2,p_3,p_4\}\cup \{q_1,q_2,\dots ,q_5\}.$ This shows that $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 5, which is contradictory. Thus, $m\le 3.$

Case 1.

Let $m=3.$ If ${\mathfrak{R}}_{\mathfrak{c}1}$ is not a field with a maximal ideal ${\xi }_1$ that is non-null, then ∃$a_1\in {\xi }_1^{*}\in Ann\left(a_1\right)={\xi }_1.$ Consider $r_1=(1,0,0), r_2=(0,1,0), r_3=(0,0,1)$, $r_4=(a_1,0), s_1=(1,1,0), s_2=(1,0,1), s_3=(u_1,1,0), s_4=(u_1,0,1)$, and $s_5=(a_1,1,0)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*}$. Since $Ann\left(r_1\right)⊈Ann\left(s_1\right), Ann\left(r_1\right)⊈Ann\left(s_2\right), Ann\left(r_1\right)⊈Ann\left(s_3\right), Ann\left(r_1\right)⊈Ann\left(s_4\right), Ann\left(s_5\right)⊈Ann\left(r_1\right), Ann\left(r_2\right)⊈Ann\left(s_1\right), r_2{s}_2=0, Ann\left(r_2\right)⊈Ann\left(s_3\right), r_2$$s_4=0, Ann\left(r_2\right)⊈Ann\left(s_5\right), r_1{s}_1=0, Ann$$\left(r_3\right)⊈Ann\left(s_2\right), Ann\left(r_3\right)⊈Ann\left(s_3\right), Ann\left(r_3\right)⊈Ann\left(s_4\right), r_3{s}_5=0, Ann\left(r_4\right)⊈Ann\left(s_1\right), Ann\left(r_4\right)⊈Ann\left(s_2\right), Ann\left(r_4\right)⊈Ann\left(s_3\right), Ann\left(r_4\right)⊈Ann\left(s_4\right), Ann\left(r_4\right)⊈Ann\left(s_5\right)$, then using Lemma 1, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains a subgraph of ${\mathcal{K}}_{4,5}$ induced by the set $\{r_1,r_2,r_3,r_4\}\cup \{s_1,s_2,\dots ,s_5\}.$ Hence, $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 5, which contradicts. Hence, ${\mathfrak{R}}_{\mathfrak{c}1}$ is a field. Similarly, one can show that both ${\mathfrak{R}}_{\mathfrak{c}2},{\mathfrak{R}}_{\mathfrak{c}3}$ are fields.

Let $|{\mathfrak{R}}_{\mathfrak{c}1}|\ge 3$. Consider $w_1=(1,0,0), w_2=(0,1,0), w_3=(0,0,1)$, $w_4$$=(a,1,0), w_4=(1,0,1), w_5=(0,1,1), z_6=(a,0,0), w_7=(a,0,1)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*},$ where $1\ne a\in {\mathfrak{R}}_{\mathfrak{c}}{1}^{*}$. Since $w_i\sim w_j$ for every $i,j$, then ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_7$ that is a subgraph and implies that $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)\ge 3$ using Lemma 4, which contradicts. Hence, $|{\mathfrak{R}}_{\mathfrak{c}1}|=2$. Similarly, we can show that $|{\mathfrak{R}}_{\mathfrak{c}2}|=|{\mathfrak{R}}_{\mathfrak{c}3}|=2$. Hence, ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_2\times {\mathbb{A}}_2\times {\mathbb{A}}_2$, which contradicts Theorem 8.

Case 2.

Let $m=2$. If ${\mathfrak{R}}_{\mathfrak{c}i}$ is a local ring with non-null maximal ideals ${\xi }_i$ for every $i=1,2$, then $\exists a_i\in {\xi }_i^{*}\in Ann\left(a_i\right)={\xi }_i$ with $i=1,2.$ Let $p_1=(1,0),p_2=(u_1,0),p_3=(a_1,0),$$p_4=(0,a_2),q_1=(a_1,1),q_2=(a_1,u_1),q_3=(a_1,a_2),q_4=(u_1,a_2),q_5=(1,a_2)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*},$ where $1\ne u_i\in U\left({\mathfrak{R}}_{\mathfrak{c}}i\right).$ Since $Ann\left(p_1\right)⊈Ann\left(q_1\right)$, $$\begin{gathered} Ann\left(p_1\right)⊈Ann\left(q_2\right), Ann\left(p_1\right)⊈Ann\left(q_3\right), Ann\left(p_1\right)⊈Ann\left(q_4\right), Ann\left(p_1\right)⊈Ann\left(q_5\right), Ann\left(p_2\right)⊈Ann\left(q_1\right), Ann\left(p_2\right)⊈Ann\left(q_2\right), Ann\left(p_2\right)⊈Ann\left(q_3\right), Ann\left(p_2\right)⊈Ann\left(q_4\right), Ann\left(p_2\right)⊈Ann\left(q_5\right), \\ Ann\left(p_3\right)⊈Ann\left(q_1\right), Ann\left(p_3\right)⊈Ann\left(q_2\right), Ann\left(p_3\right)⊈Ann\left(q_3\right), Ann\left(p_3\right)⊈Ann\left(q_4\right), Ann\left(p_3\right)⊈Ann\left(q_5\right) \end{gathered}$$, $Ann\left(p_4\right)⊈Ann\left(q_1\right), Ann\left(p_4\right)⊈Ann\left(q_2\right), Ann\left(p_4\right)⊈Ann\left(q_3\right), Ann\left(p_4\right)⊈Ann\left(q_4\right), Ann\left(p_4\right)⊈Ann\left(q_5\right),\daleth \left(A\right)$ contains a subgraph of ${\mathcal{K}}_{4,5}$ induced by the set $\{p_1,p_2,p_3,p_4\}\cup \{q_1,q_2,\dots ,q_5\}$. Thus, $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)>2$ using Lemma 5, which contradicts. Hence, ${\mathfrak{R}}_{\mathfrak{c}1}$ or ${\mathfrak{R}}_{\mathfrak{c}2}$ is a field.

If ${\mathfrak{R}}_{\mathfrak{c}1}$ and ${\mathfrak{R}}_{\mathfrak{c}2}$ both are fields, then $\left|M\right({\mathfrak{R}}_{\mathfrak{c}}\left)\right|=2$ and by ([10], Theorem 4.2), ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)=\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$. Using ([25], Theorem 3.11), $A\cong {\mathbb{K}}_4\times {\mathbb{A}}_7$ or ${\mathbb{A}}_5\times {\mathbb{A}}_5$.

Suppose that ${\mathfrak{R}}_{\mathfrak{c}1}$ is not a field with ${\xi }_1\ne 0$ and that ${\mathfrak{R}}_{\mathfrak{c}2}$ is a field. Let $|{\xi }_1^{*}|=2.$ Then, ${\mathfrak{R}}_{\mathfrak{c}1}\cong {\mathbb{A}}_9$ or ${\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^2⟩}}$, and hence, $\left|U\right({\mathfrak{R}}_{\mathfrak{c}1}\left)\right|=6.$ Let $a,b\in {\xi }_1^{*}\in ab=0$ and $Ann\left(a\right)={\xi }_1.$ Consider $x_1=(1,0),x_2=(u_1,0),x_3=(u_2,0),x_4=(u_3,0),y_1=(0,1),y_2=(a,0),y_3=(b,0),$$y_4=(a,1),y_5=(b,1)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*},$ where $u_i\in U\left({\mathfrak{R}}_{\mathfrak{c}1}\right).$ Since $x_i\sim s_j$ for every $i,j,{\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_{4,5},$ which contradicts when Lemma 5 is used. Hence, $|{\xi }_1^{*}|\ne 2.$

Suppose that $|{\xi }_1^{*}|\ge 3$, then $\left|U\right({\mathfrak{R}}_{\mathfrak{c}1}\left)\right|\ge 4.$ Let $a,b,c\in {\xi }_1^{*}\in ab=bc=0$ and $Ann\left(a\right)={\xi }_1.$ Consider $d_1=(u_1,0),d_2=(u_2,0),d_3=(u_3,0),d_4=(u_4,0),e_1=(a,0),e_2=(b,0),$$e_3=(c,0),e_4=(a,1)$, and $e_5=(b,1)\in D{\left({\mathfrak{R}}_{\mathfrak{c}}\right)}^{*},$ where $u_i\in U\left({\mathfrak{R}}_{\mathfrak{c}}1\right).$ Since $d_i\sim e_j$ for every $i,j,{\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_{4,5},$ which again contradicts when using Lemma 5. Hence, $|{\xi }_1^{*}|=1,$ which implies that ${\mathfrak{R}}_{\mathfrak{c}1}\cong {\mathbb{A}}_4$ or ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}.$

Now, suppose that $|{\mathfrak{R}}_{\mathfrak{c}2}|\ge 4$ with $x,y,z\in {{\mathfrak{R}}_{\mathfrak{c}2}}^{*}$ and $a\in {\xi }_1^{*}\in a^2=0.$ Then, the set $\left\{\right(1,0),(u,0),(0,x),(0,y),(0,z\left)\right\}\cup \left\{\right(a,0),(a,x),(a,y),(a,z\left)\right\},$ where $1\ne u\in U\left({\mathfrak{R}}_{\mathfrak{c}1}\right),$ induces a copy of ${\mathcal{K}}_{4,5}$ in ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right),$ which contradicts when using Lemma 5. Hence, $|{\mathfrak{R}}_{\mathfrak{c}2}|\le 3.$ According to Theorem 2, $|{\mathfrak{R}}_{\mathfrak{c}2}|\ne 2$. Hence, ${\mathfrak{R}}_{\mathfrak{c}2}\cong {\mathbb{A}}_3$.

Case 3.

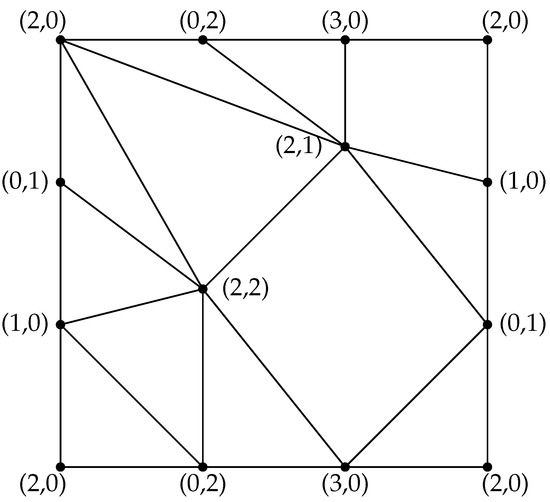
Suppose that $m=1$. Then, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is a complete graph in accordance with Theorem 1. Using Lemma 4, $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)\ne 2$, which contradicts.

Conversely, if ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{K}}_4\times {\mathbb{A}}_7$ or ${\mathbb{A}}_5\times {\mathbb{A}}_5,$ then, according to ([10] Theorem 4.2), ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)=\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right).$ Hence, $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ by ([25] Theorem 3.11), Also, if ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_4\times {\mathbb{A}}_3$ or ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_3$, then $\overline{\gamma }\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ by Figure 1. □

Figure 1. The embedding of ${\daleth }^{\prime }({\mathbb{A}}_4\times {\mathbb{A}}_3)\cong {\daleth }^{\prime }({\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_3)$ on $N_2$.

5. Outerplanarity of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$

If an embedding $\varphi$ of a planar graph exhibits outerplanarity, meaning that every vertex in the embedding is connected to the outer face, it is designated as 1-outerplanar. This concept is expanded to identify an embedding as k-outerplanar if it is a $(k-1)$-outerplanar embedding after eliminating all of the vertices on the outer face together with incident edges. If such a k-outerplanar embedding is possible on a graph, it is categorized as k-outerplanar. For a given graph G, the outerplanarity index is the lowest value of k for a G that is k-outerplanar. For a planar graph G, $i\left(G\right)$ is known as the inner vertex number which is the lowest number of vertices in any plane embedding of G that are not part of the boundary of the exterior region. When $i\left(G\right)$ = 1, graph G is considered minimally non-outerplanar. To gain a deeper understanding of k-outerplanarity, readers can refer to [26,27]. Establishing the findings given in this section is made possible from the Theorem given below:

Theorem 10

([16]). The graph G is outerplanar iff it contains no subgraph that is a subdivision of either ${\mathcal{K}}_4$ or ${\mathcal{K}}_{2,3}$.

Theorem 11

([12], Theorem 2.6). Let ${\mathfrak{R}}_{\mathfrak{c}}$ be a finite commutative ring. Then, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is outerplanar iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent to one of the rings listed below:

$${\mathbb{A}}_4,{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_9,{\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_8,{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3,x^2-2⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨2x,x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,xy,y^2⟩}},{\displaystyle \frac{{\mathbb{K}}_4\left[x\right]}{⟨x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2+x+1⟩}},{\mathbb{A}}_2\times F,{\mathbb{A}}_3\times {\mathbb{A}}_3,$$

where F is a finite field.

Theorem 12.

Let ${\mathfrak{R}}_{\mathfrak{c}}$ is finite commutative ring. Then, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has an outerplanarity index of 2 iff ${\mathfrak{R}}_{\mathfrak{c}}$ is equivalent to one of the rings listed below:

$${\mathbb{A}}_{25},{\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_4\times {\mathbb{A}}_2,{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2 \mathit{or} {\mathbb{A}}_3\times {\mathbb{K}}_m, \mathit{where} m\ge 4.$$

Proof. 

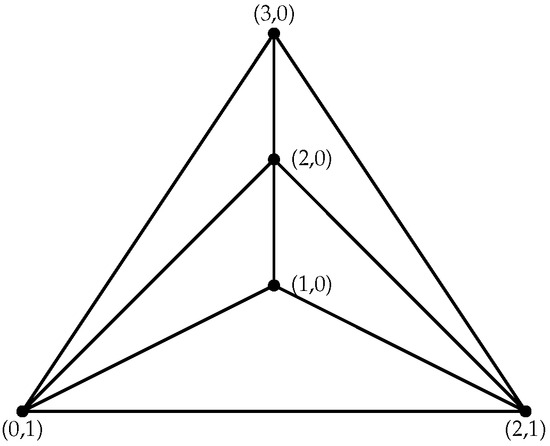
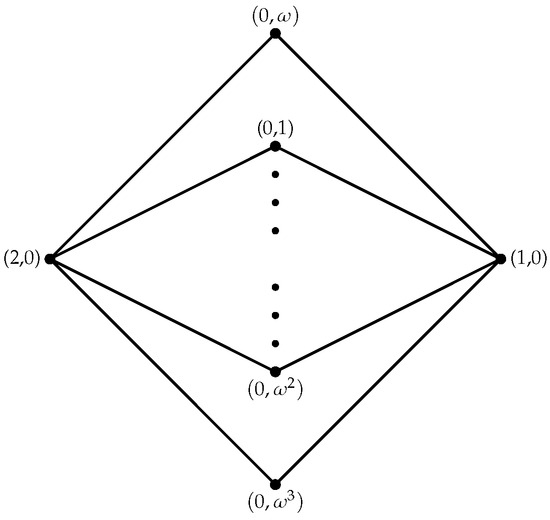
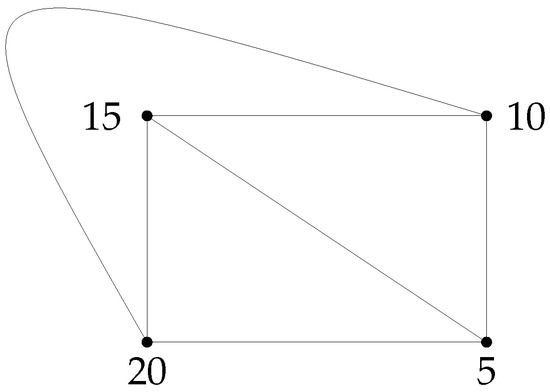
Suppose that ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has an outerplanarity index of 2, meaning ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is a planar graph. Using Theorem 2, ring ${\mathfrak{R}}_{\mathfrak{c}}$ can be determined to be isomorphic to one of the subsequent rings:

$$\begin{gathered} {\mathbb{A}}_4,{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_9,{\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_8,{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3,x^2-2⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨2x,x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,xy,y^2⟩}},{\displaystyle \frac{{\mathbb{K}}_4\left[x\right]}{⟨x^2⟩}},{\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2+x+1⟩}},{\mathbb{A}}_{25},{\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}},{\mathbb{A}}_4\times {\mathbb{A}}_2, \\ {\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2,{\mathbb{A}}_2\times \mathbb{K},\mathrm{or}{\mathbb{A}}_3\times \mathbb{K}, \end{gathered}$$

where $\mathbb{K}$ is a finite field.

All that is left to do is determine whether or not these rings are minimal and 2-outerplanar. But, in the case of ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_4$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_9$, ${\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_8$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3,x^2-2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨2x,x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,xy,y^2⟩}}$, ${\displaystyle \frac{{\mathbb{K}}_4\left[x\right]}{⟨x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2+x+1⟩}}$, ${\mathbb{A}}_2\times \mathbb{K}$ or ${\mathbb{A}}_3\times {\mathbb{A}}_3$, where $\mathbb{K}$ is a finite field, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is a 1-outerplanar graph by Theorem 11. Since ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has an outerplanarity index of 2, ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{25}$, ${\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_4\times {\mathbb{A}}_2$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2$, or ${\mathbb{A}}_3\times {\mathbb{K}}_m$, where $m\ge 4$.

Conversely, if ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{25}$, ${\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_4\times {\mathbb{A}}_2$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2$, or ${\mathbb{A}}_3\times {\mathbb{K}}_m$, where $m\ge 4$, then ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ contains ${\mathcal{K}}_4$ or ${\mathcal{K}}_{2,3}$ as subgraphs (Figure 2, Figure 3 and Figure 4). Thus, it is proved that ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is not 1-outerplanar, according to Theorem 10. The resulting graph is ${\mathcal{K}}_1$, ${\mathcal{K}}_2$, or fully disconnected after deleting vertices from the outside face; these three graphs are clearly 1-outerplanar (see Figure 2, Figure 3 and Figure 4). From the definition, we can infer that ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is 2-outerplanar for all rings, with 2 being the minimum. For this reason, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has an outerplanarity index of 2. □

Figure 2. ${\daleth }^{\prime }({\mathbb{A}}_4\times {\mathbb{A}}_2)\cong {\daleth }^{\prime }({\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2)$.

Figure 3. ${\daleth }^{\prime }({\mathbb{A}}_3\times {\mathbb{K}}_m),m\ge 4$.

Figure 4. ${\daleth }^{\prime }\left({\mathbb{A}}_{25}\right)\cong {\daleth }^{\prime }\left({\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}\right)$.

Corollary 1.

Consider ${\mathfrak{R}}_{\mathfrak{c}}$ as a finite commutative ring. Then, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has an outerplanarity index of, at most, two.

Theorem 13.

Let ${\mathfrak{R}}_{\mathfrak{c}}$ be a finite commutative ring. Then, $i\left(G\right)$ of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is given by the following:

$$i\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=\left\{\begin{array}{cc}m-3\hfill & \mathit{if}{\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_3\times {\mathbb{K}}_m,m\ge 6;\hfill \\ 2& \mathit{if}{\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_4\times {\mathbb{A}}_2\mathrm{or}{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2\mathrm{or}{\mathbb{A}}_3\times {\mathbb{K}}_5;\\ 1& \mathit{if}{\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{25}\mathrm{or}{\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}\mathrm{or}{\mathbb{A}}_3\times {\mathbb{K}}_4;\\ 0& \mathit{otherwise}.\end{array}\right.$$

Proof. 

Using Theorem 11 and Figure 2, Figure 3 and Figure 4, the proof is completed. □

Corollary 2.

Consider ${\mathfrak{R}}_{\mathfrak{c}}$ as a finite commutative ring. Then, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is minimally non-outerplanar iff ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_3\times {\mathbb{K}}_4$, ${\mathbb{A}}_{25}$, or ${\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}$.

6. Book Thickness of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$

In this section, we explore the book thickness of the graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ with a genus of, at most, one. Initially, we calculate the book thickness of the planar ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ associated with the rings described in Theorem 2 and demonstrate that the book thickness of all planar ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is bounded above by two.

An n-book embedding consists of a set of n half-planes called pages, with boundaries that are bound together along a single line called the spine. If the vertices of a graph can be embedded on the spine of a book, and the edges can be placed in r pages such that every edge lies in exactly one page, and no two edges cross within a given page, then the embedding is called an r-book embedding. The book thickness of a graph H, denoted by $bt\left(H\right)$, is the smallest integer n for which H has an n-book embedding. For details on the notion of embedding of graphs in a surface and book embedding, readers can refer to [17,28].

The results presented in [28] will assist us in proving the main results of this section.

Lemma 6

([28], Theorem 2.5). For a connected graph H, the following equivalences are valid:

• H has a book thickness of zero iff it is a path.
• H has a book thickness that is less than or equal to 1 iff it is outerplanar.

Lemma 7

([28], Theorems 3.4, 3.5, 3.6).

• $bt\left({\mathcal{K}}_p\right)$ is given by $⌈{\displaystyle \frac{p}{2}}⌉$, where $p\ge 3$.
• $bt\left({\mathcal{K}}_{p,q}\right)=p$, where $p\le q$ with $q\ge p^2-p+1$.
• $bt\left({\mathcal{K}}_{3,3}\right)=3$ and $bt\left({\mathcal{K}}_{p,p}\right)=p-1$, where $p\ge 4$.

Theorem 14.

Let ${\mathfrak{R}}_{\mathfrak{c}}$ be an Artinian commutative ring for which ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is a planar graph. The following conditions must then be satisfied:

• $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=0$ iff ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_4$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_9$, ${\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_2\times {\mathbb{A}}_2$, or ${\mathbb{A}}_2\times {\mathbb{A}}_3$.
• $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=1$ iff ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_8$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3,x^2-2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨2x,x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,xy,y^2⟩}}$, ${\displaystyle \frac{{\mathbb{K}}_4\left[x\right]}{⟨x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2+x+1⟩}}$, ${\mathbb{A}}_2\times {\mathbb{K}}_m$, where $m\ge 4$ or ${\mathbb{A}}_3\times {\mathbb{A}}_3$.
• $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ iff ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{25}$, ${\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_4\times {\mathbb{A}}_2$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2$ or ${\mathbb{A}}_3\times {\mathbb{K}}_m$, where $m\ge 4$.

Proof. 

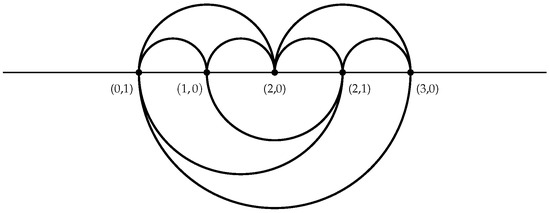
The proof of parts (1) and (2) follows from Theorem 11 and Lemma 6.

For the proof of part (3), we have to discuss the following rings ${\mathfrak{R}}_{\mathfrak{c}}$ for which ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is planar but not an outerplanar graph:

${\mathbb{A}}_{25}$, ${\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_4\times {\mathbb{A}}_2$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2$, or ${\mathbb{A}}_3\times {\mathbb{K}}_m$, where $m\ge 4$

Since the graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ for the above rings is not outerplanar, $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)\ge 2$.

If ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{25}$, ${\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}$, then ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\cong {\mathcal{K}}_4$. Thus, by using Lemma 7(1), $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$. If ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_3\times {\mathbb{K}}_m$, where $m\ge 4$, ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)=\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$ by ([10], Theorem 4.2), then $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=2$ by using ([29], Theorem 6). If ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_4\times {\mathbb{A}}_2$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2$, then the 2-book embedding of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is as shown in Figure 5. □

Figure 5. Two-book embedding of ${\daleth }^{\prime }({\mathbb{A}}_4\times {\mathbb{A}}_2)\cong {\daleth }^{\prime }({\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2)$.

Theorem 15.

Let ${\mathfrak{R}}_{\mathfrak{c}}$ be a finite $CRU$. If $\lambda \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=1$, then the following holds:

• $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=3$ iff ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{49}$, ${\displaystyle \frac{{\mathbb{A}}_7\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{K}}_4\times {\mathbb{K}}_4$, ${\mathbb{K}}_4\times {\mathbb{A}}_5$, ${\mathbb{A}}_5\times {\mathbb{A}}_5$, ${\mathbb{K}}_4\times {\mathbb{A}}_7$ or ${\mathbb{A}}_2\times {\mathbb{A}}_2\times {\mathbb{A}}_2$.
• $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=4$ iff ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{16}$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^4⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2-2,x^4⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3-2,x^4⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3+x^2-2,x^4⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^3,xy,y^2-x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3,x^2-2x⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_8\left[x\right]}{⟨x^2-4,2x⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^3,x^2-2,xy,y^2-2,y^3⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^2,y^2,xy-2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,y^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,y^2,xy⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3,2x⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^3,x^2-2,xy,y^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_8\left[x\right]}{⟨x^2,2x⟩}}$, ${\displaystyle \frac{{\mathbb{K}}_8\left[x\right]}{⟨x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3+x+1⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨2x,2y,x^2,y^2,xy⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y,z]}{{⟨x,y,z⟩}^2}}$, ${\mathbb{A}}_4\times {\mathbb{A}}_3$ or ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_3$.

Proof. 

Since $\lambda \left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=1$, we have to consider the rings given in Theorems 3 and 4.

• If ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{49}$, ${\displaystyle \frac{{\mathbb{A}}_7\left[x\right]}{⟨x^2⟩}}$, or ${\mathbb{A}}_2\times {\mathbb{A}}_2\times {\mathbb{A}}_2$, then ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)={\mathcal{K}}_6$. Thus, by using Lemma 7(1), $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=3$. If ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{16}$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^4⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2-2,x^4⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3-2,x^4⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3+x^2-2,x^4⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^3,xy,y^2-x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^3,x^2-2x⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_8\left[x\right]}{⟨x^2-4,2x⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^3,x^2-2,xy,y^2-2,y^3⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^2,y^2,xy-2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,y^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_2[x,y]}{⟨x^2,y^2,xy⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3,2x⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨x^3,x^2-2,xy,y^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_8\left[x\right]}{⟨x^2,2x⟩}}$, ${\displaystyle \frac{{\mathbb{K}}_8\left[x\right]}{⟨x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4\left[x\right]}{⟨x^3+x+1⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_4[x,y]}{⟨2x,2y,x^2,y^2,xy⟩}}$, or ${\displaystyle \frac{{\mathbb{A}}_2[x,y,z]}{{⟨x,y,z⟩}^2}}$, then ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)={\mathcal{K}}_7$. Thus, $bt\left(\Gamma \left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=4$ by using Lemma 7(1). If ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{K}}_4\times {\mathbb{K}}_4$, ${\mathbb{K}}_4\times {\mathbb{A}}_5$, ${\mathbb{A}}_5\times {\mathbb{A}}_5$ or ${\mathbb{K}}_4\times {\mathbb{A}}_7$, then ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)=\daleth \left({\mathfrak{R}}_{\mathfrak{c}}\right)$ by using ([10], Theorem 4.2). Thus, by using ([29], Theorem 11), $bt\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=3$. If ${\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_4\times {\mathbb{A}}_3$ or ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_3$, then the 4-book embedding of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is as shown in Figure 6. □
  

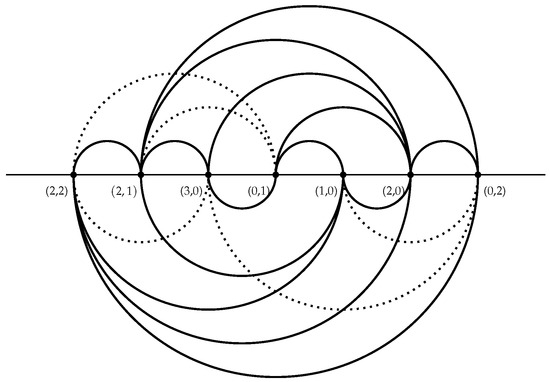  Figure 6. Four-book embedding of ${\daleth }^{\prime }({\mathbb{A}}_4\times {\mathbb{A}}_3)\cong {\daleth }^{\prime }({\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_3)$.

7. Conclusions

In conclusion, this paper successfully achieved a systematic classification of finite rings ${\mathfrak{R}}_{\mathfrak{c}}$ through the unique properties of their extended zero-divisor graphs ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$. By focusing on cases when the extended zero-divisor graph has a genus or crosscap of two, we were able to elucidate several key characteristics of these rings.

Our findings can be summarized as follows:

• For a finite commutative ring ${\mathfrak{R}}_{\mathfrak{c}}$, the genus of the extended zero-divisor graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ equals 2 iff ${\mathfrak{R}}_{\mathfrak{c}}$ is isomorphic to any one rings from the following: ${\mathbb{A}}_{27}$, ${\displaystyle \frac{{\mathbb{A}}_9\left[x\right]}{⟨3x,x^2-3⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_9\left[x\right]}{⟨3x,x^2-6⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{⟨x^3⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_3\left[x\right]}{{⟨x,y⟩}^2}}$, ${\displaystyle \frac{{\mathbb{A}}_9\left[x\right]}{{⟨3,x⟩}^2}}$, ${\displaystyle \frac{{\mathbb{K}}_9\left[x\right]}{⟨x^2⟩}}$, ${\displaystyle \frac{{\mathbb{A}}_9\left[x\right]}{⟨x^2+1⟩}}$, ${\mathbb{K}}_4\times {\mathbb{K}}_8$, ${\mathbb{K}}_4\times {\mathbb{K}}_9$, ${\mathbb{K}}_4\times {\mathbb{K}}_{11}$, or ${\mathbb{A}}_5\times {\mathbb{A}}_7$.
• The extended zero-divisor graph ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ has a crosscap of 2 if and only if ${\mathfrak{R}}_{\mathfrak{c}}$ is isomorphic to ${\mathbb{K}}_4\times {\mathbb{A}}_7$, ${\mathbb{A}}_5\times {\mathbb{A}}_5$, ${\mathbb{A}}_4\times {\mathbb{A}}_3$, or ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_3$.
• The outerplanarity index of ${\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)$ is 2 if and only if ${\mathfrak{R}}_{\mathfrak{c}}$ is isomorphic to ${\mathbb{A}}_{25}$, ${\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}}$, ${\mathbb{A}}_4\times {\mathbb{A}}_2$, ${\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2$, or ${\mathbb{A}}_3\times {\mathbb{K}}_m$, where $m\ge 4$.
• The $i\left(G\right),$ of $i\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)$ is
  $i\left({\daleth }^{\prime }\left({\mathfrak{R}}_{\mathfrak{c}}\right)\right)=\left\{\begin{array}{cc}2\hfill & \mathrm{if}{\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_4\times {\mathbb{A}}_2\mathrm{or}{\displaystyle \frac{{\mathbb{A}}_2\left[x\right]}{⟨x^2⟩}}\times {\mathbb{A}}_2;\hfill \\ m-3\hfill & \mathrm{if}{\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_3\times {\mathbb{K}}_m,m\ge 4;\hfill \\ 1\hfill & \mathrm{if}{\mathfrak{R}}_{\mathfrak{c}}\cong {\mathbb{A}}_{25}\mathrm{or}{\displaystyle \frac{{\mathbb{A}}_5\left[x\right]}{⟨x^2⟩}};\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

These results offer a comprehensive understanding of the structural aspects of finite rings ${\mathfrak{R}}_{\mathfrak{c}}$ via the lens of their extended zero-divisor graphs. This classification not only enriches the theory of zero-divisor graphs but also opens new avenues for exploring the linkup with ring-theoretical properties and graph-theoretical characteristics.