Abstract
In this paper, locally nearly uniformly convex is studied in Banach space. Furthermore, the implication relationship between and the Kadec–Klee property , the fixed–point property are investigated in Banach space. Finally, the relationship between the uniform Kadec−Klee property , the coordinate-wise uniform Kadec–Klee property , the coordinate-wise Kadec–Klee property and conditions are investigated in Orlicz sequence spaces equipped with the Orlicz norm, meanwhile we get a criteria that Orlicz sequence spaces equipped with the Orlicz norm are .
Keywords:
locally nearly uniformly convex; Kadec–Klee property; uniform Kadec−Klee; fixed–point property; Orlicz sequence spaces MSC:
46B10; 46B20; 46B22
1. Introduction
Let be a Banach space and be its dual space. By and denoted the closed unit ball and the unit sphere of Banach space , respectively.
By and denoted the closed unit ball and the closed unit sphere of the dual space of , respectively. , and represent the , and norm topologies, respectively. By and , we denote the convex hull and the closed convex hull of the set , respectively. By we denote converging to , and denotes converging to Let us define the following:
In 1973, M. M. Day [1] introduced the concept of the property (also called property).
We say that a Banach space has the Kadec−Klee property if for any , , and , then .
In 1980, Huff [2] introduced the concepts of spaces and spaces.
We say that a Banach space has the uniform Kadec−Klee property if for every , there exists such that , and , then .
A Banach space is called a Nearly Uniform Convex space if for every , there exists such that with , then there is an and scalars with such that .
Huff showed that a Banach space is if and only if is and reflexive.
It is widely recognized that the condition equivalent to nearly uniformly convex was separately articulated in [3,4].
A mapping defined on a subset of a Banach space is said to be non-expansive if for all .
For the fixed–point theory of nonexpansive mappings is referred to Kirk [5,6], he also proved that if a weakly compact subset of that has a normal structure, then any nonexpansive mapping on has a fixed point.
Many research have focused on ; for example A. Granas [7] covers topology, functional analysis, operator theory, and other related fields, focusing on the classical fixed point theory for continuous mappings, as well as the theoretical achievements of scholars such as Poincaré and Brouwer and their modern extensions. A. Górniewicz, L. [8] systematically elaborates on the relevant achievements and methods of the topological fixed point theory for multivalued mappings, and also incorporates the applications of this theory in fields such as differential inclusions, convex analysis, game theory, and mathematical economics., and D. van Dulst [9] researched equivalent norms and the fixed–point property for non-expansive mappings.
Jean Saint Raymond studied the relationship between the Kadec-Klee property, the Dual Kadec-Klee property and the fixed point property (see [10,11]).
In 1999, P. Foralewski H. and Hudzik [12] introduced a new property the coordinate-wise Kadec–Klee property .
Let be a Köthe sequence space. Say that has the coordinate-wise Kadec–Klee property if for every and every sequence such that and for all , then we have .
In 2003, T. Zhang [13] introduced a new property the coordinate-wise uniform Kadec–Klee property for a Banach space and studied it in the Orlicz sequence space.
Let Köthe sequence space. Say that has the coordinate-wise uniform Kadec–Klee property if for every there exists such that , , and implies .
In 1932, W. Orlicz [14] introduced the Orlicz space, and in 1936, he introduced the Orlicz norm in Orlicz space [15]. In 1955, W. A. Luxemburg [16] introduced the Luxemburg norm in Orlicz space.
One aim of this study is to give the sufficient and necessary condition of in the Orlicz sequence space. We next recall some basic facts about Orlicz spaces.
A mapping is called a Orlicz function provided that is even, convex on and .
Let stand for the right derivative of at and is left inverse of . Then and be a pair of complementary functions in the sense of Young.
A Orlicz function is said to be function if it also satisfies and .
Let denote the space of all real sequence. Given any Orlicz function , we define on the convex modular by
for any .
For following details on Orlicz space please see [17].
The Orlicz sequence space is defined as the set
The spaces and endowed with the following norm
or the Orlicz norm is defined, respectively, by
are Banach spaces. It is well known that if and only if , where
We say that the Orlicz function satisfies the -condition ( for short) if there exist a constant such that . For every .
We say that the Orlicz function satisfies the -condition ( for short) if its complementary function satisfies the -condition. if and only if .
2. Materials and Methods
In this study, we introduced a new geometric property locally nearly uniformly convex in Banach space. Then the implication relationship between and the Kadec–Klee property , the fixed–point property are investigated in Banach space by using the basic theoretical knowledge of Banach space, such as the triangle inequality of norm, weak lower continuous of norm and several relative Lemmas. And the relationship between , the coordinate-wise uniform Kadec–Klee property , the coordinate-wise Kadec–Klee property , and , conditions are investigated in Orlicz sequence spaces by using the basic theoretical knowledge of Orlicz space and several relative Lemmas.
3. Result
3.1. Preliminaries
Let us recall some lemmas which will be used in the remainder of the paper.
Lemma 1 (see [17]).
Suppose that and . Then For every , there exists such that .
Lemma 2 (see [10]).
Let be a reflexive infinite dimensional Banach space having the Kadec–Klee property . If is a compact function, then there exist some such that .
Lemma 3 (see [10]).
Let be a separable reflexive Banach space. Then there exists a linear compact mapping such that for all with .
Lemma 4 (see [10]).
Let be a separable reflexive Banach space without the Kadec–Klee property. Then there exists a compact function such that and for all .
Lemma 5 (see [11]).
Let be an infinite-dimensional Banach space having the dual Kadec–Klee property. Then there exists a compact function such that and for all .
Lemma 6 (see [13]).
Let be a function. Then the following are equivalent:
- (1)
- has the property;
- (2)
- has the property;
- (3)
- .
3.2. Results and Discussion
We present the main definitions of this section.
Definition 1.
Let be a Banach space. Say that has the locally nearly uniformly convex property if for every , there exists such that , , then there hold and for which
Below, we present the main theorem of this section.
Theorem 1.
If Banach space has the property, then has the .
Proof of Theorem 1.
Suppose does not have the property, then there exists and such that although , we still have
In other words, the sequence is not a Cauchy sequence, thanks to , i.e.,
there exists and a subsequence for which for convenience, we may assume that . For any , , using the weak lower continuous of norm, we get
This contradicts with that is . □
By the Lemma 2–5 and Theorem 1 we can obtain the following theorems.
Theorem 2.
If Banach space has the property, then has the property.
Theorem 3.
The following statements are equivalent:
- (1)
- has the ;
- (2)
- has the ;
- (3)
- has the ;
- (4)
- .
Proof of Theorem 3.
So, for any with , we have . Consequently,
Without loss of generality, we may assume that there exists satisfy
. By Lemma 6 we get that .
is obviously.
. Since is convex and , thus whenever Then for any , we have
Hence, exists.
Case I: .
- Then
Case II: . In this case . If , then , where . It is easy to see that if , then is a finite set. Hence,
We next consider two cases:
- (i)
- , i.e.,
- ①
- If , thenSince uniformly for . We get that there exists such thatThen , put and Hence there exists such thatHence,i.e., .
- ②
- .
In this case, there exists such that
using we get that
In virtue of that and , we get that i.e., for any , there exists such that . Using , there exists such that
Hence, for there exists a such that
Therefore,
i.e.,
- (ii)
In this case, we have
If is finite set, we may assume that where . Using , we get that for large enough, i.e.,
If is finite set, we can find a such that
Hence, we also have for large enough.
Without loss of generality, in the case of , we may assume that for each .
Suppose that , and , using for any , the set is compact, we set , where
There holds that
Since , by Lemma 1 there exists such that
using again, there exists such that
In virtue of that we get
for each .
- Thus,where .
Then there exists ,
Take such that
Hence,
Therefore,
Consequently, is .
- . We only need to prove that weak convergence implies coordinate-wise convergence in if . Suppose that , . TakeThen,Hence, converges coordinate-wise to . □
Theorem 4.
Orlicz sequence space equipped with the Orlicz norm has the property if and only if .
Proof of Theorem 4.
Necessity. Suppose that . Then there exists a sequence and such that
- Take such thatPut
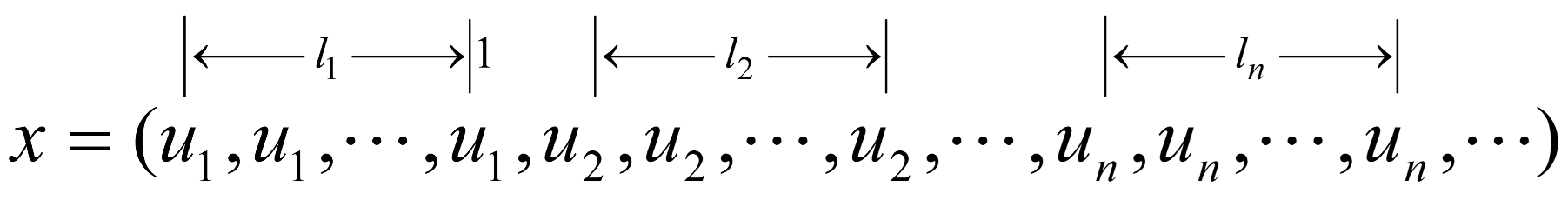 Then
Then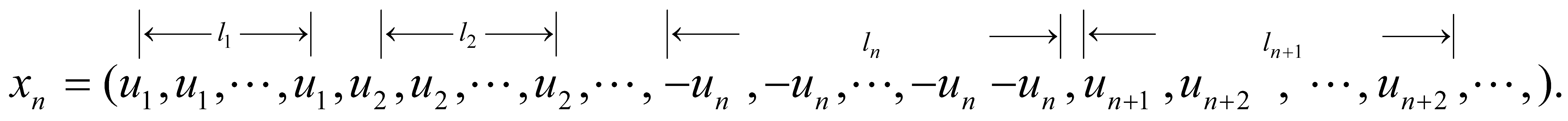 For any , there exists such thatwhenever . Hence,i.e.,Take such that , whereThen, for any with ,Thus,For any ,i.e.,a contradiction.
For any , there exists such thatwhenever . Hence,i.e.,Take such that , whereThen, for any with ,Thus,For any ,i.e.,a contradiction.
Suppose that , i.e., . We divided into infinite disjoint subsets
Based on the counter examples above, we can built a sequence such that
Take a supporting function of for each with . Without loss generality, we can assume that (If necessary, we can take a subsequence such that ) (see [17] proposition 1.84)
- PutThen and for anyi.e., , a contradiction. □
By Theorem 4 we can obtain that is . Since , thus is .
Corollary 1.
Orlicz space is if and only if is reflexive.
4. Discussion
Our study focuses on a new geometric property locally nearly uniformly convex and the classical geometric Kadec–Klee property in Banach space.
We also study , , , and five geometric properties in Orlicz sequence spaces with four theorems and a corollary, these properties indicate that they play a very significant role in some recent trends related to the geometric theory of Banach and Orlicz spaces.
5. Conclusions
In this paper, locally nearly uniformly convex is studied in Banach space. Furthermore, the implication relationship between and the Kadec–Klee property , the fixed–point property are investigated in Banach space according to the following principles: (1) if Banach space has the property, then has the property; (2) if Banach space has the property, then has the property. Finally, the relationship between the coordinate-wise uniform Kadec–Klee property , the coordinate-wise Kadec–Klee property and conditions are investigated in Orlicz sequence spaces equipped with the Orlicz norm according to the following principle: Let . Then, the following are equivalent: (i) has property; (ii) has the property; (iii) . Meanwhile we get a criteria that Orlicz sequence spaces equipped with the Orlicz norm are according to the following principles: Orlicz sequence space equippeds with Orlicz norm has the property if and only if . We also get a criteria that Orlicz sequence spaces equipped with the Orlicz norm are if and only if is reflexive.
Author Contributions
The authors contributed equally to this paper. All authors reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the China Natural Science Fund, grant number 12271121; The Science Research Project of Inner Mongolia Autonomous Region, grant number NJZY22215; and the Natural Science Foundation of Inner Mongolia, grant number 2024MS01005.
Data Availability Statement
Data sharing is not applicable—no new data were generated, and the article describes entirely theoretical research.
Acknowledgments
The authors are grateful to the referee for their comments, which improved the paper.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute. |
| DOAJ | Directory of open access journals. |
References
- Day, M.M. Normed Linear Spaces. Ergebnisse der Mathematik und Ihrer Grenzgebiete, Band 2, 3rd ed.; Springer: New York, NY, USA, 1973. [Google Scholar]
- Huff, R. Banach spaces which are nearly uniformly convex. Rocky Mt. J. Math. 1980, 10, 743–749. [Google Scholar] [CrossRef]
- Goebel, K.; Sekowski, T. The modulus of noncompact convexity. Ann. Univ. Mariae Curie-Sklodowska Sect. A 1984, 38, 41–48. [Google Scholar]
- Goebel, K.; Kirk, W.A. Topics in Metric Fixed Point Theory; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Kirk, W.A.A. Fixed point theorem for mappings which do not increase distance. Am. Math. 1965, 72, 1004–1006. [Google Scholar] [CrossRef]
- Kirk, W.A.A. Fixed point theory for non-expansive mappings. Lect. Notes Math. 1981, 886, 484–505. [Google Scholar]
- Granas, A.; Dugundji, J. Fixed Point Theory; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Górniewicz, L. Topological Fixed Point Theory of Multivalued Mappings, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Van Dulst, D. Equivalent norms and the fixed point property for non-expansive mappings. J. Lond. Math. Soc. 1982, 25, 139–144. [Google Scholar] [CrossRef]
- Saint Raymond, J. Kadec-Klee property and fixed points. J. Funct. Anal. 2014, 266, 5249–5438. [Google Scholar] [CrossRef]
- Saint Raymond, J. Dual Kadec-Klee property and fixed points. J. Funct. Anal. 2017, 272, 3825–3844. [Google Scholar] [CrossRef]
- Foralewski, P.; Hudzik, H. On some geometrical and topological properties of generalized Calderon–Lozanovskij sequence spaces. Houst. J. Math. 1999, 25, 523–542. [Google Scholar]
- Zhang, T. The coordinate-wise uniformly Kadec–Klee property in some Banach spaces. Sib. Math. J. 2003, 44, 363–365. [Google Scholar] [CrossRef]
- Orlicz, W. Uber Eine Gewisse Klasses von Raumen von Typus B. M. Bull. Inst. Acad. Pol. Sci. 1932, A, 207–220. [Google Scholar]
- Orlicz, W. Uber Raumen (). M. Bull. Acad. Pol. Sci. 1936, A, 93–107. [Google Scholar]
- Luxembur, W.A. Banach Function Space. Ph.D. Thesis, Technische Hogeschool te Delft, Delft, The Netherlands, 1955; pp. 31–206. [Google Scholar]
- Chen, S.T. Geometry of Orlicz Spaces; Dissertationes Mathematicae; Institute of Mathematics, Polish Academy of Sciences: Warsaw, Poland, 1996; Volume 356, pp. 1–204. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
