Bayesian Updating for Stochastic Processes in Infinite-Dimensional Normed Vector Spaces

Abstract

In this paper, we introduce a generalized framework for conditional probability in stochastic processes taking values in infinite-dimensional normed spaces. Classical definitions, based on measurability with respect to a conditioning $\sigma$-algebra, become inadequate when the available information is restricted to a $\sigma$-algebra generated by a finite or countable family of random variables. In such settings, many events of interest are not measurable with respect to the conditioning $\sigma$-field, preventing the standard definition of conditional probability. To overcome this limitation, we propose an extension of the coherent conditioning model through the use of Hausdorff measures. The key idea is to exploit the non-equivalence of norms in infinite-dimensional spaces, which gives rise to distinct metric structures and corresponding Hausdorff dimensions for the same events. Conditional probabilities are then defined relative to families of Hausdorff outer measures parameterized by their dimensional exponents. This geometric reformulation allows the notion of conditionality to depend explicitly on the underlying metric and topological properties of the space. The resulting model provides a flexible and coherent framework for analyzing conditioning in infinite-dimensional stochastic systems, with potential implications for Bayesian inference in functional spaces.

1. Introduction

Recent years have seen substantial advances in the theory and methodology of high- and infinite-dimensional Bayesian statistics, driven by the increasing need to model complex structures in modern data. A broad overview of these developments is provided by [1], which surveys contemporary approaches to Bayesian inference in infinite-dimensional parameter spaces and highlights both theoretical progress and emerging applications. Foundational contributions in this area are deeply rooted in nonparametric Bayesian inference, particularly in the rigorous asymptotic framework developed by [2]. Their monograph establishes the basic tools for analyzing posterior behavior in infinite-dimensional settings, with emphasis on convergence rates, concentration phenomena, and constructive prior modeling. A novel Bayesian model to handle heterogeneous data with outliers by using a two-component mixture of geometric distributions with a censoring scheme has been proposed in [3], and Bayesian estimation in life-testing (reliability) studies, where the lifetime model is a multi-component geometric distribution and the data are censored under a given scheme, has been investigated in [4].

A key line of research within nonparametric Bayesian analysis concerns Gaussian process priors, which naturally give rise to infinite-dimensional posterior distributions. Ref. [5] derives sharp posterior contraction rates for Gaussian process priors under a variety of smoothness assumptions, thereby offering insight into the adaptability and theoretical guarantees of such priors. Complementing these results, ref. [6] investigates Bayesian inference for high-dimensional nonstationary Gaussian processes, demonstrating how these models can accommodate spatially varying features in practical applications.

From a frequentist perspective, ref. [7] studies confidence bands in nonparametric density estimation, providing tools that parallel Bayesian uncertainty quantification and shedding light on the interplay between empirical processes and infinite-dimensional parameter spaces. Related geometric aspects of infinite-dimensional analysis are explored in [8], which characterizes surface measures in infinite-dimensional Banach spaces, offering insights relevant to both stochastic analysis and the geometry underlying infinite-dimensional Bayesian models.

The notion of prevalence plays a fundamental role in understanding “large” or “generic” behavior in infinite-dimensional spaces. Ref. [9] introduces prevalence as an infinite-dimensional analogue of “almost everywhere” that is invariant under translation, offering a conceptually robust measure-theoretic framework for discussing typical behavior in infinite-dimensional Bayesian settings.

A separate but increasingly influential body of work highlights challenges and potential pathologies in Bayesian inference when models are misspecified or data dependencies are ignored. Ref. [10] analyzes the dynamics of Bayesian updating under model misspecification and dependent data, demonstrating that posterior behavior can deviate substantially from classical expectations under standard assumptions. Ref. [11] further emphasizes the vulnerability of Bayesian inference in high and infinite-dimensional contexts, showing that even minimal perturbations of the model or prior can lead to dramatic changes in posterior conclusions.

This growing body of work forms the basis for contemporary research that seeks to develop reliable, flexible, and computationally tractable Bayesian methods in increasingly complex and high-dimensional settings.

In this work, we investigate stochastic processes taking values in infinite-dimensional normed spaces, where the available information is represented by the $\sigma$-algebra generated by a finite or countable sequence of random variables. This $\sigma$-algebra is properly contained in the initial $\sigma$-algebra of the underlying probability space. As a consequence, for any event that does not belong to the conditioning $\sigma$-algebra, the corresponding conditional probability cannot be defined in the standard axiomatic sense, since it fails to be measurable with respect to the conditioning $\sigma$-algebra.

In the classical framework [12], conditional probabilities are defined as measurable functions with respect to a conditioning $\sigma$-algebra, ensuring consistency with the axioms of probability. However, when dealing with stochastic processes in infinite-dimensional settings, such as in functional analysis or random fields in Banach or Hilbert spaces, this assumption becomes restrictive. The interplay between topology, norm equivalence, and $\sigma$-algebraic measurability introduces structural limitations that prevent the direct extension of classical conditional probability.

To address these limitations, we propose an extension of the coherent conditioning model based on Hausdorff measures ([13,14,15,16,17]) and its properties ([18,19]. The key idea relies on the fact that, in infinite-dimensional normed vector spaces, not all norms are equivalent. Consequently, the associated metric structures induce different Hausdorff dimensions for the same events. Each conditioned event is thus associated with a set of possible Hausdorff dimensions $s_d$, and the family of corresponding Hausdorff outer measures is used to define conditional probabilities in different metric spaces. In this approach, the fact that an event is considered rare is not an intrinsic property of the event itself but rather depends on the conditioning event, that is, on the information available and on the particular metric space being considered. The role of unexpected or rare events—represented by events with zero conditional probability—has been fundamental in the mathematical representation of the unconscious activity of the human brain ([20,21]). The model and rare events have been investigated also by considering other fractal measures ([22,23,24]). This approach allows the definition of conditional probability to depend explicitly on the underlying geometric and metric structure of the space. As a result, the notion of rare or unexpected events, those of zero probability given a certain conditioning event, becomes relative to the chosen metric and the corresponding Hausdorff dimensional measure. Such a framework provides a richer and more flexible foundation for understanding conditional structures in stochastic processes on infinite-dimensional spaces, with potential applications in infinite-dimensional Bayesian inference.

2. Motivation

In this section, it is highlighted how the axiomatic definition of conditional expectation, based on the notion of Radon–Nikodym, can lead to an incoherent posterior, because the property of being measurable with respect to the $\sigma$-field of the conditioning variables, which is required for the axiomatic definition of expectation, contradicts a necessary condition for coherence.

Let $\mathcal{B}$ be a partition of $\Omega$ in a metric space $(\Omega ,d).$ A bounded random variable is a function $X:\Omega \to \mathbb{R}$, and $L(\Omega )$ is the class of all bounded random variables defined on $\Omega$; for every $B\in \mathcal{B}$, denote by $X|B$ the restriction of X to B and by sup($X\left|B\right)$ the supremum value that X assumes on B. The class of all bounded random variables $X|B$ is $L\left(B\right)$. The indicator function $I_A$ of an event $A\in \wp \left(B\right)$, i.e., $I_A\left(\omega \right)=1$ if $\omega \in A$ and $I_A\left(\omega \right)=0$ if $\omega \in A^c$. For every $B\in \mathcal{B}$, coherent upper conditional expectations or previsions $\overline{P}(·|B)$ are functionals defined on $L\left(B\right)$ [25].

Definition 1.

Coherent upper conditional previsions are functionals $\overline{P}(·|B)$ defined on $L\left(B\right)$, such that the following axioms of coherence hold for every X and Y in $L\left(B\right)$ and every strictly positive constant λ:

(1)

$\overline{P}\left(X\right|B)\le sup\left(X\right|B)$;

(2)

$\overline{P}\left(\lambda X\right|B)=\lambda \overline{P}\left(X\right|B)$ (positive homogeneity);

(3)

$\overline{P}(X+Y|B)\le \overline{P}\left(X\right|B)+\overline{P}\left(Y\right|B)$ (subadditivity).

Assume that $\overline{P}(X\mid B)$ is a coherent upper conditional prevision on a linear space $\mathcal{K}\subseteq L\left(B\right)$. Its conjugate coherent lower conditional prevision is defined through the conjugacy relation

$$\underline{P}(X\mid B):=-\overline{P}(-X\mid B).$$

Whenever, for every $X\in \mathcal{K}\left(B\right)$, we have

$$P(X\mid B)=\underline{P}(X\mid B)=\overline{P}(X\mid B),$$

the functional $P(X\mid B)$ is called a coherent linear conditional prevision. If, in addition, $\mathcal{K}=L\left(B\right)$, then $P(·\mid B)$ is a linear, positive, and positively homogeneous functional in the sense of de Finetti [26,27] and Walley [25] (Corollary 2.8.5).

From axioms (1)–(3) and the conjugacy property, it follows that

$$1\le \underline{P}(I_B\mid B)\le \overline{P}(I_B\mid B)\le 1;$$

hence,

$$\underline{P}(I_B\mid B)=\overline{P}(I_B\mid B)=1.$$

In [25], the functionals $\overline{P}(X\mid B)$ defined for $B\in \mathcal{B}$ and $X\in L\left(B\right)$, satisfying axioms (1)–(3), and such that $\overline{P}(I_B\mid B)=1$, are termed separately coherent.

The unconditional coherent upper prevision is obtained as the special case $\overline{P}=\overline{P}(·\mid \Omega )$. Coherent upper conditional probabilities arise when only $\{0,1\}$-valued random variables are considered.

Definition 2.

Given a partition $\mathcal{B}$ and a random variable $X\in L(\Omega )$, a coherent upper conditional prevision $\overline{P}(X\mid \mathcal{B})$ is a random variable on $\Omega$ taking the value $\overline{P}(X\mid B)$ for $\omega \in B$.

Definition 3.

A bounded random variable $X\in L(\Omega )$ is called $\mathcal{B}$-measurable (or measurable with respect to the partition $\mathcal{B}$) if it is constant on each atom of the partition.

The following necessary condition for coherence holds [25] (p. 292).

Proposition 1.

If $P(X\mid B)$ is a coherent linear prevision for every B belonging to a partition $\mathcal{B}$ of $\Omega$, then

$$P(X\mid \mathcal{B})=X,$$

for all $\mathcal{B}$-measurable random variables $X\in L(\Omega )$.

Coherent Conditional Prevision and Conditional Expectation

In the axiomatic approach [12] (Section 34), conditional expectation with respect to a conditioning $\sigma$-field is defined via the Radon–Nikodym derivative.

Let $\mathcal{F}$ and $\mathcal{G}$ be two $\sigma$-fields on $\Omega$ with $\mathcal{G}\subseteq \mathcal{F}$, and let X be a positive and integrable random variable. Let P be a probability measure on $\mathcal{F}$, and define a measure $\nu$ on $\mathcal{G}$ by

$$\nu \left(G\right):={\int }_{G}XdP.$$

Then, $\nu$ is finite and absolutely continuous with respect to ${P|}_{\mathcal{G}}$; therefore, there exists a non-negative, $\mathcal{G}$-measurable, and integrable function defined on $\Omega$-the Radon–Nikodym derivative—denoted $E[X\mid \mathcal{G}]$, such that

$${\int }_{G}E[X\mid \mathcal{G}]dP={\int }_{G}XdP,G\in \mathcal{G}.$$

Although the Radon–Nikodym derivative is non-negative, this is no restriction for defining the conditional expectation of an arbitrary integrable random variable. Indeed, for X not necessarily non-negative, we write $X=X^{+}-X^{-}$, where

$$X^{+}=0\vee X,X^{-}={(-X)}^{+},$$

and define

$$E[X\mid \mathcal{G}]:=E[X^{+}\mid \mathcal{G}]-E[X^{-}\mid \mathcal{G}].$$

This function satisfies the usual properties and is unique up to P-null sets; it is a version of the conditional expectation.

The next theorem, proven in [28], shows that whenever the $\sigma$-field $\mathcal{G}$ is properly contained in $\mathcal{F}$ and contains all singletons of $[0,1]$, then the conditional prevision defined by the Radon–Nikodym derivative need not be coherent. This failure stems from the fact that one of the defining properties of the Radon–Nikodym conditional expectation is $\mathcal{G}$-measurability, which contradicts the necessary condition for the coherence of a linear conditional prevision stated in Proposition 1.

Theorem 1.

Let $\Omega ={[0,1]}^n$, and let F and G be two σ-field of subsets of $\Omega$ such that G is properly contained in F, and it contains all singletons of $\Omega$. Let B be the partition of singletons, and let X be the indicator function of an event A belonging to $\mathit{F}-\mathit{G}$. If we define the conditional prevision $P\left(X\right|\mathcal{B})$ equal to the Radon–Nikodym derivative with probability 1, that is,

$$P\left(X\right|\mathcal{B})=E[X\left|\mathcal{G}\right],$$

except on a subset N of ${[0,1]}^n$ of P-measure zero, then the conditional prevision $P\left(X\right|\mathcal{B})$ is not coherent.

3. Mathematical Preliminaries

In this section, we study the phenomenon described in Theorem 1, namely the possible incoherence of the axiomatically defined conditional expectation obtained from the Radon–Nikodym derivative. More precisely, when conditioning on a $\sigma$-field $\mathcal{G}$, the value $E(I_A\mid \mathcal{G})$ of the conditional expectation of an event A may differ from its indicator function $I_A$, despite the fact that coherence would require the equality $E(I_A\mid \mathcal{G})=I_A$ for all $\mathcal{G}$-measurable indicator functions. This mismatch reveals that Radon–Nikodym conditional expectations may fail to be coherent linear conditional previsions. We examine this issue in depth in the framework of infinite-dimensional stochastic processes, where such inconsistencies arise naturally due to the rich structure of the underlying filtrations.

3.1. Infinite Dimensional Normed Vector Spaces

Let $(\Omega ,d)$ be a metric space. The metric d induces a topology ${\tau }_d$ on $\Omega$, defined by

$${\tau }_d=\left\{U\subseteq X:\forall x\in U,\exists r>0,\mathrm{such}\mathrm{that}{B}_d(x,r)\subseteq U\right\},$$

where $B_d(x,r)$ denotes the open ball of radius r centered at x.

The Borel σ-field on the metric space $(\Omega ,d)$ is the $\sigma$-field generated by this topology:

$$\mathcal{C}\left(X\right)=\sigma \left({\tau }_d\right).$$

In other words, $\mathcal{C}$ is the smallest $\sigma$-field containing all open sets of the topology induced by the metric d. The sets in $\mathcal{C}$ are called Borel sets. Let $(\Omega ,\mathcal{F},\mathbb{P})$ be a probability space, and let $X:\Omega \to \mathbb{R}$ be a random variable. The random variable X induces a probability measure ${\mathbb{P}}_X$ on the measurable space $(\mathbb{R},\mathcal{B}(\mathbb{R}\left)\right)$, where $\mathcal{C}\left(\mathbb{R}\right)$ is the Borel $\sigma$-algebra on $\mathbb{R}$.

The induced probability measure ${\mathbb{P}}_X$ is defined by

$${\mathbb{P}}_X\left(B\right)=\mathbb{P}\left(X^{-1}\left(B\right)\right),\mathrm{for}\mathrm{all}B\in \mathcal{C}\left(\mathbb{R}\right).$$

This measure describes the distribution of X and allows us to study X as a measurable function independent of the original probability space $(\Omega ,\mathcal{F},\mathbb{P})$.

The space of real-valued random variables on $(\Omega ,\mathcal{F},\mathbb{P})$ can be endowed with a vector space structure. In particular, if we consider the space

$$L^2(\Omega ,\mathcal{F},\mathbb{P})=\left\{X:\Omega \to \mathbb{R}\left|X\mathrm{is}\mathrm{measurable}\mathrm{and}\mathbb{E}\right[X^2]<\infty \right\},$$

this becomes a Hilbert space when equipped with the inner product

$$⟨X,Y⟩=\mathbb{E}\left[XY\right].$$

Thus, probability spaces give rise to vector spaces (in particular, Hilbert spaces), where random variables can be added, scaled, and compared via inner products and norms:

$$\parallel X\parallel =\sqrt{\mathbb{E}\left[X^2\right]}.$$

A metric can be naturally defined using a norm. Let V be a vector space over $\mathbb{R}$ or $\mathbb{C}$, and let $\parallel ·\parallel :V\to \mathbb{R}$ be a norm on V. Then, the function

$$d(x,y)=\parallel x-y\parallel$$

defines a metric on V, called the metric induced by the norm.

Therefore, any normed vector space $(V,\parallel ·\parallel )$ naturally gives rise to a metric space $(V,d)$, where $d(x,y)=\parallel x-y\parallel$.

3.2. Equivalence of Norms

Let $(X,d_1)$ and $(X,d_2)$ be two metric spaces defined on the same set X.

Definition 4.

Two metrics $d_1$ and $d_2$ on X are said to be topologically equivalent if they generate the same topology on X. That is, a set $U\subseteq X$ is open in $(X,d_1)$ if and only if it is open in $(X,d_2)$.

Definition 5.

Two metrics $d_1$ and $d_2$ on X are said to be bi-Lipschitz equivalent if there exists a constant $C\ge 1$ such that for all $x,y\in X$,

$${\displaystyle \frac{1}{C}}{d}_1(x,y)\le d_2(x,y)\le C{d}_1(x,y).$$

Bi-Lipschitz equivalence implies topological equivalence, but the converse is not true in general. That is, two metrics can be topologically equivalent without being bi-Lipschitz equivalent.

Example 1.

Consider $X=\mathbb{R}$, and define the metrics

$$d_1(x,y)=|x-y|,d_2(x,y)={\displaystyle \frac{|x-y|}{1+|x-y|}}.$$

These metrics are topologically equivalent, as they generate the same open sets. However, they are not bi-Lipschitz equivalent: the ratio $d_2(x,y)/d_1(x,y)$ tends to 0 as $|x-y|\to \infty$; so, no global Lipschitz bounds exist in both directions.

In a finite-dimensional vector space, all norms are equivalent. That is, given any two norms ${\parallel ·\parallel }_1$ and ${\parallel ·\parallel }_2$ on ${\mathbb{R}}^n$, there exist constants $c,C>0$ such that for all $x\in {\mathbb{R}}^n$,

$$c·{\parallel x\parallel }_1\le {\parallel x\parallel }_2\le C·{\parallel x\parallel }_1.$$

This equivalence implies that the metrics induced by these norms, defined by $d_1(x,y)={\parallel x-y\parallel }_1$ and $d_2(x,y)={\parallel x-y\parallel }_2$, generate the same topology on ${\mathbb{R}}^n$.

Consequently, open sets, closed sets, convergence of sequences, and continuity of functions are the same with respect to both metrics. This is a fundamental result in analysis, ensuring that topological properties in finite-dimensional normed spaces do not depend on the particular choice of norm.

Example 2.

Consider the Euclidean norm ${\parallel x\parallel }_2=\sqrt{x_1^2+\cdots +x_n^2}$ and the maximum norm ${\parallel x\parallel }_{\infty }={max}_i\left|x_i\right|$ on ${\mathbb{R}}^n$. These norms are equivalent, and therefore, the metric spaces $({\mathbb{R}}^n,d_2)$ and $({\mathbb{R}}^n,d_{\infty })$ have the same topological structure.

However, in infinite-dimensional spaces, there exist norms that are not equivalent and, hence, define different topologies.

For example, consider the space $C\left(\right[0,1\left]\right)$, the set of continuous real-valued functions on the interval $[0,1]$. It can be equipped with different norms, such as

• The supremum norm: ${\parallel f\parallel }_{\infty }={sup}_{x\in [0,1]}\left|f\left(x\right)\right|;$
• The $L^1$ norm: ${\parallel f\parallel }_1={\int }_0^1\left|f\left(x\right)\right|dx.$

These norms are not equivalent. For instance, one can construct a sequence of functions that converges to zero in the $L^1$ norm but not in the supremum norm.

In general topology and functional analysis, two metrics $d_1$ and $d_2$ on a set X are called equivalent if they generate the same topology. This means that the convergence of sequences, continuity of functions, and openness of sets are the same under both metrics.

In infinite-dimensional spaces, however, in some restricted infinite-dimensional settings, equivalent metrics can still be constructed. Below are some examples.

Definition 6.

The space ${\ell }^1$ is the set of all infinite sequences of real or complex numbers

$$x=(x_1,x_2,x_3,\dots ),$$

such that the series of absolute values is convergent:

$$\sum _{n=1}^{\infty }\left|x_n\right|<\infty .$$

Formally, we write

$${\ell }^1:=\left\{x={\left(x_n\right)}_{n\in \mathbb{N}}|\sum _{n=1}^{\infty }\left|x_n\right|<\infty \right\}.$$

The norm on ${\ell }^1$, called the ${\ell }^1$ norm, is defined as

$${\parallel x\parallel }_1=\sum _{n=1}^{\infty }\left|x_n\right|.$$

${\ell }^1$ is a normed vector space over $\mathbb{R}$ or $\mathbb{C}$, it is a Banach space (i.e., it is complete with respect to the ${\ell }^1$ norm), and it is infinite-dimensional.

Example 3.

Let $c_{00}$ denote the space of sequences with only finitely many non-zero entries. On this space, consider the following norms:

$${\parallel x\parallel }_1=\sum _{i=1}^{\infty }|x_i{|,\parallel x\parallel }_2={\left(\sum _{i=1}^{\infty }{\left|x_i\right|}^2\right)}^{1/2}{,\parallel x\parallel }_{\infty }=\underset{i}{sup}\left|x_i\right|.$$

Since vectors in $c_{00}$ have finite support, all the above norms are finite and induce equivalent metrics. That is, the topologies defined by the metrics $d_i(x,y)={\parallel x-y\parallel }_i$ are the same.

Example 4.

Consider the space $X={\ell }^1\cap {\ell }^2$. Define two norms on X by

$${\parallel x\parallel }_a={\parallel x\parallel }_1+{\parallel x\parallel }_2{,\parallel x\parallel }_b={max(\parallel x\parallel }_1{,\parallel x\parallel }_2).$$

These norms are equivalent on X, since each bounds the other up to a constant factor. Therefore, the metrics they induce are also equivalent.

Example 5.

Let $C\left(\right[0,1\left]\right)$ be the space of continuous real-valued functions on the interval $[0,1]$. This space is commonly equipped with the uniform norm:

$${\parallel f\parallel }_{\infty }=\underset{x\in [0,1]}{sup}\left|f\left(x\right)\right|.$$

An alternative (bounded) metric that induces the same topology is

$$d(f,g)={\int }_0^1{\displaystyle \frac{\left|f\right(x)-g(x\left)\right|}{1+\left|f\right(x)-g(x\left)\right|}}dx.$$

Though this metric is not induced by a norm, it is equivalent to the one defined by ${\parallel ·\parallel }_{\infty }$, in the sense that both generate the same topology on $C\left(\right[0,1\left]\right)$.

These examples illustrate that while infinite-dimensional spaces may not admit globally equivalent norms in general (e.g., ${\ell }^1$ and ${\ell }^2$ are not isomorphic), it is still possible to construct equivalent metrics in restricted contexts.

3.3. Conditional Probability and Measurability in Infinite-Dimensional Spaces

Definition 7.

Let $(V,\parallel ·\parallel )$ be a normed vector space over $\mathbb{R}$ (or $\mathbb{C}$), and let $(\Omega ,\mathcal{F},\mathbb{P})$ be a probability space. A stochastic process taking values in V is a family of V-valued random variables

$${\left\{X_t\right\}}_{t\in T},$$

where $T\subseteq \mathbb{R}$ is an index set, typically representing time, and for each $t\in T$, the map $X_t:\Omega \to V$ is a measurable function.

That is, for every $t\in T$, the function $X_t$ is such that, for any Borel set $B\subseteq V$, the preimage $X_t^{-1}\left(B\right)\in \mathcal{F}$, meaning $X_t$ is $\mathcal{F}$-measurable with respect to the Borel $\sigma$-algebra on V.

If V is a Banach space (i.e., a complete normed vector space), then ${\left\{X_t\right\}}_{t\in T}$ is called a Banach space-valued stochastic process.

In the context of stochastic processes defined on infinite-dimensional spaces, conditional probability presents unique challenges. A key issue arises when the $\sigma$-algebra with respect to which we condition is generated by a topology that is strictly weaker than the topology of the ambient space.

Let $(\Omega ,\mathcal{F},\mathbb{P})$ be a probability space, and let $X={\left(X_t\right)}_{t\in T}$ be a stochastic process taking values in a product space $E={\prod }_{t\in T}{E}_t$, where T is possibly uncountable, and each $E_t$ is a measurable space. Consider the $\sigma$-algebra $\mathcal{G}=\sigma (X_s:s\in S)$ for some subset $S\subset T$, which is often taken to be countable. This $\sigma$-algebra is naturally associated with the product topology restricted to S, which is strictly weaker than the product topology on the full index set T.

Theorem 2.

Let S be a finite set, endowed with the discrete σ-algebra $\mathcal{P}\left(S\right)$. Consider the infinite product space

$$\Omega =S^{\mathbb{N}}=\{\omega =({\omega }_1,{\omega }_2,\dots ):{\omega }_i\in S\},$$

and let $X_i:\Omega \to S$ denote the coordinate projections, i.e., $X_i\left(\omega \right)={\omega }_i$.

Define, for each $n\in \mathbb{N}$,

$${\mathcal{F}}_n=\sigma (X_1,\dots ,X_n)\mathrm{and}\mathcal{F}=\sigma (X_1,X_2,\dots ),$$

so that $\mathcal{F}$ is the product σ-algebra on $\Omega$.

Then, for every $n\in \mathbb{N}$,

$${\mathcal{F}}_n⊊\mathcal{F}.$$

That is, the σ-algebra generated by finitely many coordinate random variables is strictly contained in the σ-algebra generated by the entire infinite process.

Proof. 

By definition, ${\mathcal{F}}_n=\sigma (X_1,\dots ,X_n)$ consists of all events that depend only on the first n coordinates of $\omega \in \Omega$. That is, $A\in {\mathcal{F}}_n$ if and only if there exists a subset $B\subseteq S^n$ such that

$$A=\{\omega \in \Omega :({\omega }_1,\dots ,{\omega }_n)\in B\}.$$

Therefore, each ${\mathcal{F}}_n$ is finite, since $\left|S\right|<\infty$ implies $|{\mathcal{F}}_n|\le 2^{{\left|S\right|}^n}$.

It is clear that

$${\mathcal{F}}_1\subseteq {\mathcal{F}}_2\subseteq \cdots \subseteq \mathcal{F},\mathrm{and}\mathcal{F}=\sigma \left(\bigcup _{n=1}^{\infty }{\mathcal{F}}_n\right).$$

To show that the inclusion is strict, consider the event

$$A=\{\omega \in \Omega :{\omega }_i=s_0\mathrm{for}\mathrm{infinitely}\mathrm{many}i\},$$

where $s_0\in S$ is fixed.

We can express A as

$$A=\bigcap _{n=1}^{\infty }\bigcup _{m\ge n}\{\omega :{\omega }_m=s_0\}.$$

Each set $\{\omega :{\omega }_m=s_0\}$ belongs to ${\mathcal{F}}_m\subseteq \mathcal{F}$, and hence, $A\in \mathcal{F}$ by closure of $\sigma$-algebras.

However, $A\notin {\mathcal{F}}_n$ for any finite n, since membership in A depends on infinitely many coordinates: for any two sequences $\omega ,{\omega }^{\prime }\in \Omega$ that coincide on the first n coordinates but differ afterwards, one may have infinitely many occurrences of $s_0$, while the other may not. Thus, A cannot be measurable with respect to ${\mathcal{F}}_n$.

Consequently,

$$A\in \mathcal{F}\setminus {\mathcal{F}}_n;$$

so, ${\mathcal{F}}_n⊊\mathcal{F}$. □

Under these conditions, it may happen that the conditional probability $\mathbb{P}(A\mid \mathcal{G})$, for some $A\in \mathcal{F}$, fails to be $\mathcal{G}$-measurable. The issue stems from the fact that the regular conditional probability, typically constructed as a $\mathcal{G}$-measurable function, may not be measurable with respect to the weaker topology-induced $\sigma$-algebra $\mathcal{G}$. As a result, conditional expectations or conditional distributions may not exist in the usual sense or may not be representable by a measurable function. So, the subjective definition of coherent conditional probability can be considered, which does not require that the conditional probability is measurable with respect to the $\sigma$-field of the conditioning events.

4. The Proposed Model

A new model of coherent upper previsions defined by the Choquet integral with respect to Hausdorff outer measures has been introduced.

Choquet Integral

We recall the definition of the Choquet integral [29,30] with the aim to define upper conditional previsions by the Choquet integral with respect to the dimensional Hausdorff outer measures and to prove their properties. The Choquet integral is an integral with respect to a monotone set function. Given a non-empty set $\Omega$ and, denoted by $\wp (\Omega )$, the family of all subsets of $\Omega$ a monotone set function, also called capacity, $\mu :\wp (\Omega )\to {\overline{\mathbb{R}}}_{\ge 0}={\mathbb{R}}_{\ge 0}\cup \left\{+\infty \right\}$ is such that $\mu$(⊘)=0, and if A, B∈$\wp (\Omega )$ with A⊂B, then $\mu$(A) ≤$\mu$ (B).

Let $\mathcal{F}$ be a field of subsets of $\Omega$, i.e., a collection of sets closed under finite unions, finite intersections, and relative complements.

A set function $\mu :\mathcal{F}\to [0,\infty ]$ is called a measure on the field $\mathcal{F}$ if it satisfies the following properties:

• $\mu (\varnothing )=0$.
• Countable additivity:

For any disjoint sets $A_1,A_2,\cdots \in \mathcal{F}$, and ${\bigcup }_{n=1}^{\infty }{A}_n\in \mathcal{F}$, we have

$$\mu \left(\bigcup _{n=1}^{\infty }{A}_n\right)=\sum _{n=1}^{\infty }\mu \left(A_n\right).$$

$\mu$ is a probability measure on $\mathcal{F}$ if $\mu$ is a measure such that $\mu (\Omega )=1.$ Given a monotone set function $\mu$ on $S\subset \wp (\Omega )$, the outer set function of $\mu$ is the set function ${\mu }^{*}$ defined on the whole power set $\wp (\Omega )$ by

$${\mu }^{*}\left(A\right)=inf\left\{\mu \left(B\right):B\supset A;B\in S\right\},A\in \wp (\Omega ).$$

On a field S, the outer set function ${\mu }^{*}$ of $\mu$ is sub-additive if $\mu$ is ([30] (Proposition 2.4)). So, the outer set function of a measure defined on a field S is sub-additive.

The inner set function of $\mu$ is the set function ${\mu }_{*}$ defined on the whole power set $\wp (\Omega )$ by

$${\mu }_{*}\left(A\right)=sup\left\{\mu \left(B\right)|B\subset A;B\in S\right\},A\in \wp (\Omega ).$$

Let $\mu$ be a monotone set function defined on $\wp (\Omega )$, and let $X:\Omega \to \overline{\Re }=\Re \cup \left\{-\infty ,+\infty \right\}$ be an arbitrary function on $\Omega$. Then, the set function

$$G_{\mu ,X}\left(x\right)=\mu \{\omega \in \Omega :X(\omega )>x\}$$

is decreasing, and it is called a decreasing distribution function of X with respect to $\mu$. If $\mu$ is continuous from below, then $G_{\mu ,X}\left(x\right)$ is right continuous.

A function X: $\Omega \to \overline{\Re }$ is called upper $\mu$-measurable if $G_{{\mu }^{*},X}\left(x\right)=G_{{\mu }_{*},X}\left(x\right).$ Given an upper $\mu$-measurable random variable X: $\Omega \to \overline{R}$ with decreasing distribution function $G_{\mu ,X}\left(x\right)$, the Choquet integral of X with respect to $\mu$ is defined if $\mu (\Omega )<\infty$ through

$$\int Xd\mu ={\int }_{-\infty }^0(G_{\mu ,X}\left(x\right)-\mu (\Omega ))dx+{\int }_0^{\infty }{G}_{\mu ,X}\left(x\right)dx.$$

The integral is in ℜ or can assume the values $-\infty$, ∞, and ‘non-existing’.

For upper $\mu$-measurable random variable X, we have

$$\int Xd\mu =\int Xd{\mu }^{*}=\int Xd{\mu }_{*}.$$

If X ≥ 0 or X ≤ 0, the integral always exists. In particular, for X ≥ 0, we obtain

$$\int Xd\mu ={\int }_0^{\infty }{G}_{\mu ,X}\left(x\right)dx.$$

If X is bounded and $\mu (\Omega )$ = 1, we have that

$$\int Xd\mu ={\int }_{infX}^0(G_{\mu ,X}\left(x\right)-1)dx+{\int }_0^{supX}{G}_{\mu ,X}\left(x\right)dx.$$

If $\mu$ is a $\sigma$-additive measure, the Choquet integral coincides with the Lebesgue integral except for infinite measures.

In the following example, it is shown that if conditional probability is required to be $\mathcal{G}$-measurable, and $\mathcal{G}$ is properly contained in the $\sigma$-field of the underlying probability space, then it contradicts a necessary condition for coherence.

Example 6.

Consider the product space $\Omega ={\{0,1\}}^{[0,1]}$ endowed with the product σ-algebra $\mathcal{F}$ and the product measure $\mathbb{P}=\mu ={⨂}_{t\in [0,1]}Bernoulli(1/2)$. Each coordinate projection $X_t:\Omega \to \{0,1\}$ is independent and identically distributed.

Let $\mathcal{G}=\sigma (X_r:r\in \mathbb{Q}\cap [0,1])$ be the σ-algebra generated by the values of the process on the rational points. Note that $\mathcal{G}$ is strictly smaller than $\mathcal{F}$ and corresponds to the information given by a countable dense subset of coordinates.

Define the event:

$$A:=\left\{\omega \in \Omega :\omega iscontinuouson[0,1]\right\}.$$

Note that $A\notin \mathcal{G}$, since the information in $\mathcal{G}$ (i.e., the values of ω on a countable dense set) is insufficient to determine whether a path ω is continuous on the entire interval. Continuity is a topological property that depends on the behavior of the function at all points, not just a countable subset.

Now, if we define the conditional probability in the axiomatic way, requiring it is $\mathcal{G}$-measurable, we have

$$\mathbb{P}(A\mid \mathcal{G})=\mathbb{E}[I_A\mid \mathcal{G}]\ne I_A\left(\omega \right),$$

since $A\notin \mathcal{G}$, and so, the conditional probability is not coherent in the sense of de Finetti and Walley, because it does not satisfy a necessary condition for coherence [25] (Section 6.2.6).

5. Bayesian Conditional Models Based on Hausdorff Outer Measures

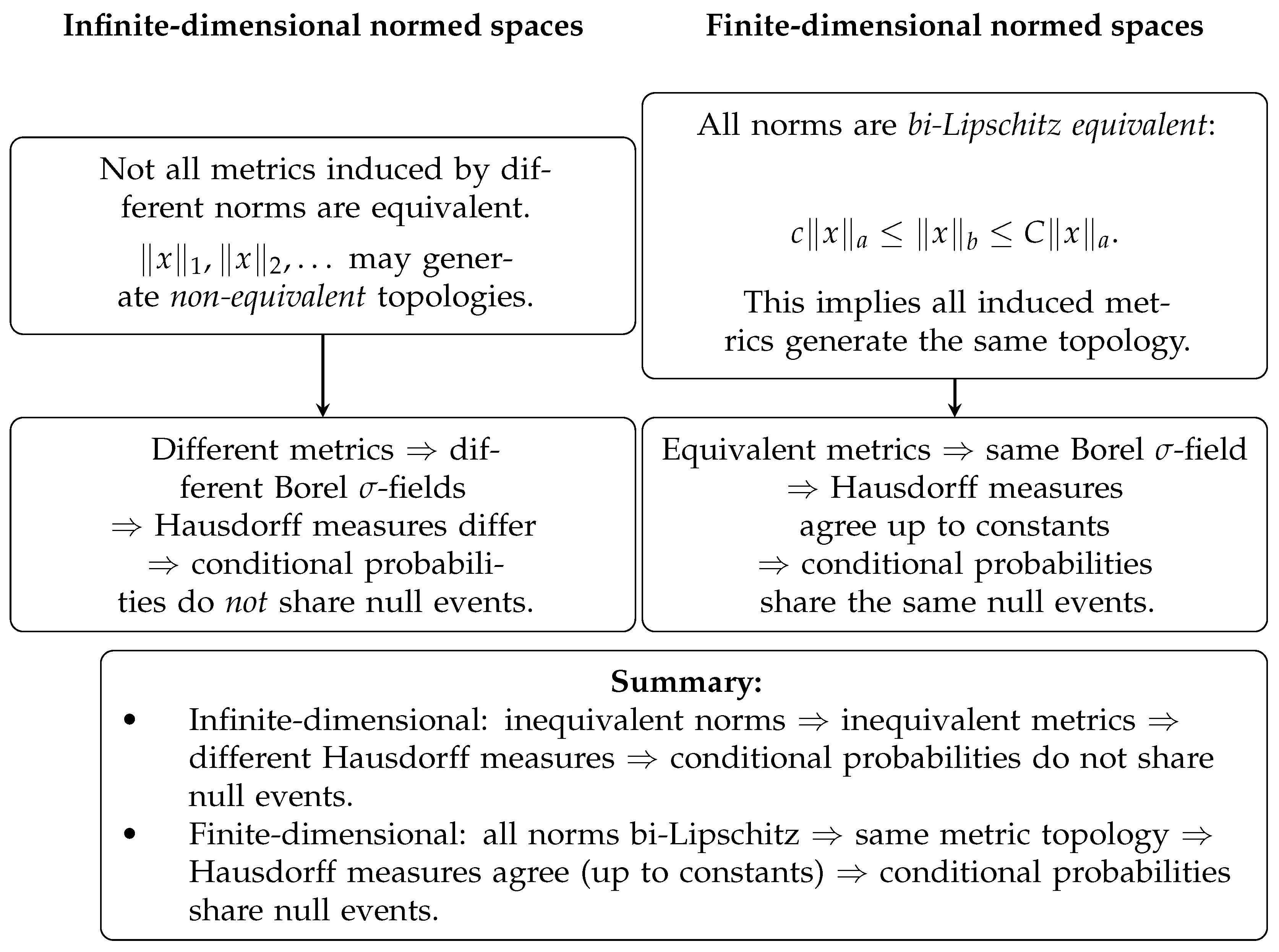
In finite-dimensional normed spaces, it is possible to adopt a unified Bayesian model of coherent conditional probability based on outer Hausdorff measures defined on the metric spaces endowed with the metrics induced by the norms. Since the Hausdorff dimension is invariant under bi-Lipschitz mappings, and all norms on a finite-dimensional vector space are bi-Lipschitz equivalent, the corresponding Hausdorff outer measures are mutually absolutely continuous. As a result, they share the same null sets, allowing for a consistent probabilistic framework across all such norm-induced metric structures.

In contrast, in infinite-dimensional normed spaces, not all norms are equivalent—hence, not all induced metrics are bi-Lipschitz equivalent. Consequently, the Hausdorff dimension of a set is not invariant, different Hausdorff outer measures may assign different null sets, and a unique Bayesian model based on a single Hausdorff outer measure cannot, in general, be consistently defined. In such settings, distinct conditional probability models based on different Hausdorff measures must be considered, as different normed structures may not agree on which sets have measure zero.

5.1. Hausdorff Outer Measures and Hausdorff Dimension

Let $(\Omega ,d)$ be a metric space. For any $s\ge 0$, we define the s-dimensional Hausdorff outer measure ${\mathcal{H}}^s$ on $\Omega$ as follows [31]. For $\delta >0$, consider all countable covers ${\left\{U_i\right\}}_{i\in I}$ of a set $A\subset X$ such that $\mathrm{diam}\left(U_i\right)\le \delta$ for all i. Define

$${\mathcal{H}}_{\delta }^s\left(A\right)=inf\left\{\sum _{i\in I}{\left(\mathrm{diam}{U}_i\right)}^s:A\subset \bigcup _{i\in I}{U}_i,\mathrm{diam}\left(U_i\right)\le \delta \right\}.$$

The s-dimensional Hausdorff outer measure is then given by the limit

$${\mathcal{H}}^s\left(A\right)=\underset{\delta \to 0}{lim}{\mathcal{H}}_{\delta }^s\left(A\right).$$

The function ${\mathcal{H}}^s$ defined above is an outer measure, i.e.,

• ${\mathcal{H}}^s(⌀)=0$,
• ${\mathcal{H}}^s\left(A\right)\le {\mathcal{H}}^s\left(B\right)$ whenever $A\subset B$,
• ${\mathcal{H}}^s\left({\bigcup }_{n=1}^{\infty }{A}_n\right)\le {\sum }_{n=1}^{\infty }{\mathcal{H}}^s\left(A_n\right)$ for any sequence $\left\{A_n\right\}$.

Moreover, ${\mathcal{H}}^s$ is a metric outer measure, meaning that for any two sets $A,B\subset \Omega$ with $d(A,B)>0$, we have

$${\mathcal{H}}^s(A\cup B)={\mathcal{H}}^s\left(A\right)+{\mathcal{H}}^s\left(B\right).$$

This property ensures that the Carathéodory construction of measurable sets relative to ${\mathcal{H}}^s$ coincides with the Borel $\sigma$-algebra on $\Omega$. Hence, the restriction of ${\mathcal{H}}^s$ to Borel sets defines a complete measure, also called the s-dimensional Hausdorff measure.

The Hausdorff dimension of a set $A\subset X$ is defined in terms of the behavior of ${\mathcal{H}}^s\left(A\right)$ as s varies:

$${dim}_H\left(A\right)=inf\{s\ge 0:{\mathcal{H}}^s\left(A\right)=0\}=sup\{s\ge 0:{\mathcal{H}}^s\left(A\right)=\infty \}.$$

Intuitively, ${\mathcal{H}}^s$ measures the “size” of A at different scales s, and the Hausdorff dimension captures the critical threshold at which the measure transitions from infinite to zero. This concept generalizes the notion of integer dimensions and provides a fundamental tool for quantifying the geometric complexity of fractal sets.

Theorem 3.

Let $(\Omega ,d)$ be a metric space, let $\mathcal{B}$ be a partition of Ω and $\mathcal{F}$ the Borel σ-field induced by the metric d. For each $B\in \mathcal{B}$, denote by $s_d$ the Hausdorff dimension of B in the metric space and denote by $m_B$ a 0–1 valued finitely additive, but not countably probability defined on B. Then, the set function defined on $\wp (\Omega )$ by

$${\overline{P}}_{s_d}(A\mid B)=\left\{\begin{array}{cc}{\displaystyle \frac{H^{s_d}(A\cap B)}{H^{s_d}\left(B\right)}}\hfill & 0<H^{s_d}\left(B\right)<\infty ,\hfill \\ m_B\hfill & H^{s_d}\left(B\right)\in \left\{0,\infty \right\}\hfill \end{array}\right.$$

is a coherent upper conditional probability.

Proof. 

For each $s_d$, the coherence of the upper conditional probability has been proven in Theorem 3 of [15]. □

Remark 1.

If, fixed $\Omega$, the metric d is allowed to vary, then every set $B\in \mathcal{B}$ is associated with a credal set $C\left(B\right)$ of coherent upper conditional probabilities defined by

$$C\left(B\right)=\left\{{\overline{P}}_{s_d}:s_d\in S\left(B\right)\right\}.$$

In particular, in infinite-dimensional normed spaces, not all norms are equivalent—hence, not all induced metrics are bi-Lipschitz equivalent. Consequently, the Hausdorff dimension of a set is not invariant, and different dimensional Hausdorff outer measures can be defined for the same set B in different metric spaces. The class $C\left(B\right)$ contains all the conditional probabilities defined by different dimensional Hausdorff measures associated with the same conditioning event B but in different metric spaces, which do not share the same null sets. In finite-dimensional normed spaces, the class $C\left(B\right)$ contains Hausdorff measures of the same dimension (since all the induced metrics are bi-Lipschitz) that share the same null sets.

If $m_B$ is of bounded variation, by the previous model we can obtain a model of coherent countably additive probability on the Borel $\sigma$-field of the metric space by using the countably additive Mobius transform ([32,33,34,35]).

5.2. Countably Additive Möbius Transform

Let $\mathcal{A}$ be an algebra of subsets of $\Omega$, properly contained in $\wp (\Omega )$, and let $\nu$ be a monotone set function. Let $\mathcal{H}\left(\mathcal{A}\right)$ denote the class of all normalized monotone set functions with values in $\{0,1\}$.

Consider the two subsets of $\mathcal{H}\left(\mathcal{A}\right)$:

$$H_p\left(\mathcal{A}\right)=\left\{\eta \in \mathcal{H}\left(\mathcal{A}\right):\eta \mathrm{is}\mathrm{supermodular}\right\},H_u\left(\mathcal{A}\right)=\left\{u_K\in \mathcal{H}\left(\mathcal{A}\right):K\in \mathcal{A},K\ne \varnothing \right\},$$

where, for a fixed $K\subseteq \Omega$, the function $u_K$ is defined on $\mathcal{A}$ by

$$u_K\left(A\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}K\subseteq A,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

It is continuous from above, whereas a general $\{0,1\}$-valued supermodular set function need not be continuous. The function $u_K$ is supermodular and is a belief function since it is totally monotone.

When $\Omega$ is finite, every filter has the form

$$\mathcal{A}=\{A:A\supseteq K\}$$

for some nonempty set K, and in this case $u_K$ is a coherent lower probability (Section 2.9.8 of [25]). In game theory, $u_K$ is called a unanimity game.

Definition 8.

Let $K\subseteq N$ be a coalition. The unanimity game on K is the game $(N,u_K)$ where

$$u_K\left(S\right)=\left\{\begin{array}{cc}1,\hfill & ifK\subseteq S,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

In other words, a coalition S has worth 1 (is winning) if it contains all players of K and 0 (is losing) otherwise.

$$H_u\left(\mathcal{A}\right)\subseteq H_p\left(\mathcal{A}\right)\subseteq \mathcal{H}\left(\mathcal{A}\right),$$

and the equality $H_u\left(\mathcal{A}\right)=H_p\left(\mathcal{A}\right)$ holds when $\Omega$ is finite.

Let us consider the tilde operator defined for any $\mathcal{A}$-measurable random variable X and any $\{0,1\}$-valued monotone set function $\eta \in \mathcal{H}\left(\mathcal{A}\right)$:

$$\tilde{X}=\int X\left(\omega \right)\eta \left(d\omega \right).$$

If X is the indicator of an event $A\in \mathcal{A}$, then

$$\widetilde{I_A}=I_{\tilde{A}},\tilde{A}=\{\eta \in \mathcal{H}\left(\mathcal{A}\right):\eta \left(A\right)=1\}.$$

Although $\mathcal{A}$ is a field, the set system

$$\tilde{\mathcal{A}}=\{\tilde{A}:A\in \mathcal{A}\}$$

is not a field in $\wp \left(\mathcal{H}\right(\mathcal{A}\left)\right)$, except in the trivial case $\tilde{\mathcal{A}}=\{Ø,\Omega \}$. Hence, we consider the field $\mathcal{D}\left(\tilde{\mathcal{A}}\right)$ generated by $\tilde{\mathcal{A}}$, i.e., the smallest field containing it.

If $(\Omega ,\mathcal{F})$ is a measurable space and $Ø\ne E\subseteq \Omega$, then

$$\{E\cap A:A\in \mathcal{F}\}$$

is a $\sigma$-field on E, called the trace σ-field.

Let ${\mathcal{D}}^{\prime }(\tilde{A})$ and ${\mathcal{D}}^{″}(\tilde{A})$ denote the trace $\sigma$-fields generated by $\tilde{A}$ in $H_p\left(\mathcal{A}\right)$ and $H_u\left(\mathcal{A}\right)$, respectively.

Definition 9.

A monotone set function $\nu :\mathcal{A}\to \mathbb{R}$ is said to be of bounded variation if there exist monotone set functions ${\nu }_1,{\nu }_2$ such that $\nu ={\nu }_1-{\nu }_2$. Let $V_b\left(\mathcal{A}\right)$ denote the class of set functions on $\mathcal{A}$ of bounded variation for which ${\nu }_1$ and ${\nu }_2$ are totally monotone.

Definition 10.

Given a monotone set function ν on $\mathcal{A}$, the additive Möbius transform ${\mu }^{\nu }$ is uniquely determined on $(H_u\left(\mathcal{A}\right),{\mathcal{D}}^{\prime \prime }(\tilde{A}))$ by

$${\mu }^{\nu }(\tilde{A})=\nu \left(A\right),A\in \mathcal{A}.$$

Moreover, as shown in [34], integrals are preserved under the Möbius transform:

$$\int Xd\nu =\int \tilde{X}d{\mu }^{\nu }.$$

Example 7.

For a fixed nonempty set $K\in \wp (\Omega )$, the Choquet integral with respect to $u_K$ on $\wp (\Omega )$ is

$$\tilde{X}=\int X\left(\omega \right)d{u}_K\left(\omega \right)=\underset{\omega \in K}{inf}X\left(\omega \right).$$

The same expression holds for the restriction of $u_K$ to a field $\mathcal{A}$ and an $\mathcal{A}$-measurable X, even when $K\notin \mathcal{A}$.

The Möbius transform of $u_K$ is given by

$${\mu }^{u_K}\left(\tilde{A}\right)=u_K\left(A\right).$$

A set function $\nu$ on an algebra $\mathcal{A}\subseteq \wp (\Omega )$ is totally monotone if and only if its Möbius transform ${\mu }^{\nu }$ is monotone (i.e., nonnegative) ([36,37]).

In Theorem 6.2 of [34], the following result is proved.

Theorem 4.

If $\nu \in V_b\left(\mathcal{A}\right)$, the Möbius transform ${\mu }^{\nu }$ can be uniquely extended to $(H_p\left(\mathcal{A}\right),{\mathcal{D}}^{\prime }(\tilde{A}))$. It is σ-additive and is called the σ-additive Möbius transform of ν. It is a signed (possibly negative) additive set function.

The theorem holds, because if ${\mathcal{D}}_n\in {\mathcal{D}}^{\prime }(\tilde{A})$ with ${\mathcal{D}}_n\downarrow Ø$, then there exists $\overline{n}\in \mathbb{N}$ such that ${\mathcal{D}}_n=Ø$ for all $n>\overline{n}$ (Lemma 6.1 of [34]). Thus, any monotone set function on ${\mathcal{D}}^{\prime }(\tilde{A})$ is trivially continuous from above at Ø; so, any additive set function is automatically $\sigma$-additive. Lemma 6.1 of [34] is proved by contradiction: assuming $D_n\ne Ø$ for all n, one constructs a sequence $E_n\downarrow Ø$ with each $E_n\ne Ø$ such that there exists $\eta \in {\mathcal{H}}^{\prime }$ satisfying $\eta \in {\bigcap }_n{E}_n$, contradicting $E_n\downarrow Ø$.

Example 8.

Let $\Omega$ be an uncountable set and fixed $a\in \Omega$ define the countable additive probability on the Borel σ-field by

$$\nu \left(A\right)=\{\begin{array}{cccc}1& if& a\in A& ,\\ \\ 0& otherwise.\end{array}$$

Then, $\tilde{X}\left(\nu \right)=X\left(a\right)$, and since

$${\int }_{B}Xd\nu ={\int }_{\tilde{B}}\tilde{X}d{\mu }^{\nu },$$

then the Möbius transform is

$${\mu }_{\tilde{B}}^{\nu }\left(\tilde{A}\right)=\{\begin{array}{cccc}1& if& a\in A& \\ \\ 0& otherwise.\end{array}$$

In the following theorems, the countably additive Möbius transform is considered to define coherent countably additive conditional probabilities and coherent conditional previsions.

Theorem 5.

Let $(\Omega ,d)$ be a metric space, let $\mathcal{B}$ be a partition of $\Omega$, and let $\mathcal{C}$ be the Borel σ-field induced by the metric d. For each $B\in \mathcal{B}$, denote by $s_d$ the Hausdorff dimension of B in the metric space, and denote by ${\mu }^{\nu }$ the countably additive Möbius transform. Then, the set function defined on $\mathcal{F}$ by

$$P_{s_d}(A\mid B)=\left\{\begin{array}{cc}{\displaystyle \frac{H^{s_d}(A\cap B)}{H^{s_d}\left(B\right)}}\hfill & if0<H^{s_d}\left(B\right)<\infty ,\hfill \\ {\mu }^{\nu }\left(\tilde{B}\right)\hfill & otherwise.\hfill \end{array}\right.$$

is a coherent countably additive conditional probability.

Proof. 

For each $s_d$, the coherence of the conditional probability has been proven in Theorem 4 of [35]. □

Theorem 6.

Let $(\Omega ,d)$ be a metric space, and let $\mathrm{\rfloor }$ be the Borel σ-field. Let $\mathcal{B}$ be a partition of Ω. For every $B\in \mathcal{B}$, denote by s the Hausdorff dimension of the conditioning event B and by ${\mathcal{H}}^s$ the Hausdorff s-dimensional outer measure. Let ${\mu }^{\nu }$ be the σ-additive Möbius transform of a finitely additive conditional probability ν of bounded variation. Then, for each $B \in$ $\mathit{B}$ with a positive and finite Hausdorff s-dimensional outer measure, the functional $\overline{P}\left(X\right|B)$ is defined on the class of all $\mathrm{\rfloor }$-measurable random variables by

$$\overline{P}\left(X\right|B)=\{\begin{array}{ccc}{\displaystyle \frac{1}{{\mathcal{H}}^s\left(B\right)}}{\int }_{B}Xd{\mathcal{H}}^s& if& 0<{\mathcal{H}}^s\left(B\right)<+\infty \\ {\int }_{\tilde{B}}\tilde{X}d{\mu }_{\tilde{B}}^{\nu }& if& {\mathcal{H}}^s\left(B\right)\in \left\{0,+\infty \right\}\end{array},$$

which is a continuous linear conditional prevision.

For each $s_d$, the coherence of the upper conditional prevision has been proven in Theorem 5 of [35].

6. Examples

In this section, some examples of stochastic processes in infinite-dimensional normed spaces are considered.

Example 9.

Consider the separable Hilbert space ${\ell }^2=\{x=(x_1,x_2,\dots ):{\sum }_{i=1}^{\infty }{x}_i^2<\infty \}$ with the standard inner product. Let μ be a probability measure on ${\ell }^2$, for instance a Gaussian measure $\mathcal{N}(0,I)$, where I is the identity operator.

Classically, conditioning on a finite-dimensional subspace, such as fixing the first coordinate $X_1=x_1$, gives the conditional probability

$$\mathbb{P}[X_2\in B\mid X_1=x_1]={\displaystyle \frac{\mathbb{P}[X_1=x_1,X_2\in B]}{\mathbb{P}[X_1=x_1]}}.$$

However, in infinite-dimensional spaces, $\mathbb{P}[X_1=x_1]=0$, making the classical definition ill-defined.

• Consider the hyperplane

$$H_{x_1}=\{x\in {\ell }^2:x_1=c\}.$$

Instead of a zero-probability event, we define a conditional probability applying Theorem 4

$$\mathbb{P}[X\in A\mid X_1=c]:={\displaystyle \frac{{\mathcal{H}}^1(A\cap H_{x_1})}{{\mathcal{H}}^1\left(H_{x_1}\right)}}={\mu }^{\nu }\left(\tilde{A}\right).$$

The conditioning event $H_{x_1}$ has a Hausdorff measure equal to infinite in its Hausdorff dimension equal to 1 (${\mathcal{H}}^1\left(H_{x_1}\right)=\infty$); then, by Theorem 4, the conditional probability can be defined by the countably additive Möbius transform of a finite additive probability of bounded variation.

This provides a non-degenerate and coherent definition of conditional probability.

Example 10.

Consider ${\ell }^2$ truncate ${\ell }^2$ to ${\mathbb{R}}^2$ with $X=(X_1,X_2)\sim \mathcal{N}(0,I_2)$. Classically, $\mathbb{P}[X_2\in B\mid X_1=c]$ is undefined, because $\mathbb{P}[X_1=c]=0$.

Using the 1-dimensional Hausdorff measure ((that is the 1-dimensional Lebesgue) along the line $H_c=\{(c,x_2):x_2\in \mathbb{R}\}$, the conditional probability is

$$\mathbb{P}[X_2\in [a,b]\mid X_1=c]={\displaystyle \frac{{\int }_a^b{e}^{-x_2^2/2}d{x}_2}{{\int }_{-\infty }^{\infty }{e}^{-x_2^2/2}d{x}_2}}={\int }_a^b{\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-x_2^2/2}d{x}_2.$$

This coincides with the classical conditional Gaussian density, but it is derived via the Hausdorff measure approach rather than dividing by a probability-zero event.

In general, in ${\ell }^2$, conditioning on $X_1=c$ or any finite set of coordinates $X_1,\dots ,X_k$ results in a zero-probability event in the classical sense. Using Hausdorff measures, we can define the hyperplane $H_{c_1,\dots ,c_k}=\{x\in {\ell }^2:x_1=c_1,\dots ,x_k=c_k\}$ and use the Hausdorff measure on this hyperplane (if it is positive and finite) to define the conditional probability. Thus, the Hausdorff measure-based conditional probability respects the geometry of infinite-dimensional spaces and resolves inconsistencies that arise with classical definitions based on Radon–Nikodym derivatives.

Example 11.

Let $(\Omega ,\mathcal{F},\mathbb{P})$ be a probability space and ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ a filtration, that is, an increasing family of sub-σ-algebras of $\mathcal{F}$.

A stochastic process ${\left\{X_t\right\}}_{t\ge 0}$ adapted to the filtration $\left\{{\mathcal{F}}_t\right\}$ is called a martingale if, for every $t\ge 0$,

• $X_t\in L^1(\Omega ,\mathcal{F},\mathbb{P})$,
• $\mathbb{E}\left[\right|X_t\left|\right]<\infty$,
• $\mathbb{E}[X_{t+s}\mid {\mathcal{F}}_t]=X_t$ for all $s\ge 0$, $\mathbb{P}$-almost surely.

This formulation captures the intuitive idea that the process $\left\{X_t\right\}$ has “fair” increments: its future value has no predictable drift given the present information encoded in ${\mathcal{F}}_t$.

Let $(\Omega ,d)$ be a separable metric space, and let ${\mathcal{H}}^s$ denote the s-dimensional Hausdorff measure on Ω for some $s\ge 0$. If ${\mathcal{H}}^s(\Omega )$ is positive and finite, we consider a random variable taking values on $(\Omega ,\mathcal{C}(\Omega \left)\right)$, where $\mathcal{C}(\Omega )$ is the Borel σ-field.

Given an integrable function $X\in L^1(\Omega ,\mathcal{B}(\Omega ),{\mathcal{H}}^s)$ and a sub-σ-algebra $\mathcal{G}\subseteq \mathcal{B}(\Omega )$, the coherent conditional expectation of X with respect to $\mathcal{G}$ and the Hausdorff measure ${\mathcal{H}}^s$ is the function (up to ${\mathcal{H}}^s$-a.e. equality) ${\mathbb{E}}_{{\mathcal{H}}^s}[X\mid \mathcal{G}]=P\left(X\right|B)$ if $\omega \in B\subseteq G$, satisfying

$${\int }_G{\mathbb{E}}_{{\mathcal{H}}^s}[X\mid \mathcal{G}]\mathrm{d}{\mathcal{H}}^s={\int }_{G}X\mathrm{d}{\mathcal{H}}^s,\forall G\in \mathcal{G}.$$

(1)

In the following example, it has shown that a set can have different Hausdorff dimensions and Hausdorff measures in different etric spaces, and so, according to the model proposed in this paper, different conditional previsions can be obtained in different metric spaces with metrics that are not bi-Lipschitz.

Example 12.

Let

$$V=C\left([0,1]\right),d_{\infty }(f,g)={\parallel f-g\parallel }_{\infty },$$

and define a non–bi-Lipschitz metric

$$d^{\prime }(f,g)=\sqrt{{\parallel f-g\parallel }_{\infty }}.$$

Consider the 1-parameter family of functions

$$B=\{f_c:f_c\left(t\right)=t^c,c\in [0,1]\}.$$

The map $c\mapsto f_c$ is injective; so, we identify B with $[0,1]$ but endowed with different metrics inherited from V.

6.1. Hausdorff Dimension Under $d_{\infty }$ and $d^{\prime }$

For $c,c^{\prime }\in [0,1]$,

$$d_{\infty }(f_c,f_{c^{\prime }})=\underset{t\in [0,1]}{sup}|t^c-t^{c^{\prime }}|=|c-c^{\prime }|.$$

Thus, $(B,d_{\infty })$ is isometric to the ordinary interval $[0,1]$, and therefore,

$$s_{d_{\infty }}={dim}_H(B,d_{\infty })=1.$$

Under the snowflake metric $d^{\prime }$,

$$d^{\prime }(f_c,f_{c^{\prime }})=\sqrt{d_{\infty }(f_c,f_{c^{\prime }})}=\sqrt{|c-c^{\prime }|},$$

and for snowflake metrics $d_{\alpha }(x,y)={|x-y|}^{\alpha }$, the Hausdorff dimension is ${\alpha }^{-1}$ (see Appendix A). Hence,

$$s_{d^{\prime }}={dim}_H(B,d^{\prime })=2.$$

6.2. Hausdorff Measures on B

For $(B,d_{\infty })$, the 1-dimensional Hausdorff measure is the Lebesgue measure:

$$d{\mathcal{H}}^1\left(c\right)=dc.$$

For $(B,d^{\prime })$, the 2-dimensional Hausdorff measure satisfies

$${\mathcal{H}}^2\left([c,c+\Delta c]\right)\asymp {(\Delta c)}^{1/2},$$

(because a length $\Delta c$ becomes diameter ${(\Delta c)}^{1/2}$, squared); hence,

$$d{\mathcal{H}}^2\left(c\right)=C{c}^{-1/2}dc,$$

where C normalizes the total measure on $[0,1]$ to a finite nonzero value. After normalizing ${\mathcal{H}}^2$ on B,

$$d{\mu }_{d^{\prime }}\left(c\right)=K{c}^{-1/2}dc,K^{-1}={\int }_0^1{c}^{-1/2}dc=2.$$

Thus,

$$d{\mu }_{d^{\prime }}\left(c\right)={\displaystyle \frac{1}{2}}{c}^{-1/2}dc.$$

In contrast, under $d_{\infty }$,

$$d{\mu }_{d_{\infty }}\left(c\right)=dc.$$

Let the gamble be

$$X\left(f\right)=f(1/2)={(1/2)}^c.$$

On B, this is simply $X\left(f_c\right)=2^{-c}$.

• Under $d_{\infty }$:

$${\overline{P}}_{d_{\infty }}(X\mid B)={\int }_0^1{2}^{-c}dc={\displaystyle \frac{1-2^{-1}}{ln2}}={\displaystyle \frac{1}{2ln2}}.$$

Under $d^{\prime }$:

$${\overline{P}}_{d^{\prime }}(X\mid B)={\int }_0^1{2}^{-c}\left({\displaystyle \frac{1}{2}}{c}^{-1/2}\right)dc={\displaystyle \frac{1}{2}}{\int }_0^1{c}^{-1/2}{2}^{-c}dc.$$

This is strictly larger than the $d_{\infty }$ value because the weight $u^{-1}$ near $c=0$ (i.e., $u=0$) increases the mass on the functions $f_c$ with the smallest c, which maximizes $2^{-c}$.

$${\overline{P}}_{d_{\infty }}(X\mid B)={\displaystyle \frac{1}{2ln2}}\approx 0.7213,$$

while

$${\overline{P}}_{d^{\prime }}(X\mid B)={\int }_0^1{2}^{-u^2}du\approx 0.8135.$$

Although the underlying set B is the same subset of V, the change from $d_{\infty }$ to the non-bi-Lipschitz metric $d^{\prime }$ changes both the Hausdorff dimension ($1\to 2$) and the associated Hausdorff measure; after normalization, this leads to a different conditional upper prevision:

$${\overline{P}}_{d_{\infty }}(X\mid B)\ne {\overline{P}}_{d^{\prime }}(X\mid B).$$

7. Discussion

In this section, we compare the results proposed in this paper with the Extreme Value Theory, one of the theories proposed in literature to manage rare events.

7.1. Extreme Value Theory

Extreme Value Theory (EVT) studies the probabilistic behavior of the extreme observations in a sequence of random variables, such as the maximum or minimum values observed in a large sample. While classical limit theorems (such as the Law of Large Numbers or the Central Limit Theorem) describe the behavior of averages or sums, EVT focuses on the tail behavior of distributions and the occurrence of rare extreme events.

Typical examples include the highest annual flood level of a river, the maximum daily wind speed, or the largest financial loss in a given period.

Let ${\left\{X_i\right\}}_{i=1}^n$ be a sequence of independent and identically distributed (i.i.d.) random variables with common distribution function $F\left(x\right)$. Define the sample maximum as

$$M_n=max(X_1,X_2,\dots ,X_n).$$

The goal of EVT is to determine the possible non-degenerate limit distributions of the normalized maxima

$${\displaystyle \frac{M_n-b_n}{a_n}},a_n>0,b_n\in \mathbb{R},$$

as $n\to \infty$.

7.2. Fisher–Tippett–Gnedenko Theorem

Theorem 7 (Fisher–Tippett–Gnedenko).

Suppose that there exist sequences of constants $a_n>0$ and $b_n\in \mathbb{R}$ such that

$$Pr\left({\displaystyle \frac{M_n-b_n}{a_n}}\le x\right)\to G\left(x\right),\mathrm{as}n\to \infty ,$$

for some non-degenerate distribution function G. Then, G must belong to one of the following three families of extreme value distributions:

• Gumbel type (light tails):

  $$G\left(x\right)=exp(-e^{-\alpha }),x\in \mathbb{R}.$$
• Fréchet type (heavy tails):

  $$G\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x\le 0,\hfill \\ exp(-{\left({\displaystyle \frac{x-\mu }{\sigma }}\right)}^{-\alpha }),\hfill & x>0,\hfill \end{array}\right.\alpha >0.$$
• Weibull type (bounded upper support):

  $$G\left(x\right)=\left\{\begin{array}{cc}exp(-{(-x)}^{\alpha }),\hfill & x\le 0,\hfill \\ 1,\hfill & x>0,\hfill \end{array}\right.\alpha >0.$$

7.3. Unified Representation: The Generalized Extreme Value Distribution

The three possible limit laws can be expressed in a unified form known as the Generalized Extreme Value (GEV) distribution:

$$G_{\xi }\left(x\right)=exp\left(-{\left[1+\xi {\displaystyle \frac{x-\mu }{\sigma }}\right]}^{-1/\xi }\right),1+\xi {\displaystyle \frac{x-\mu }{\sigma }}>0,$$

where $\mu \in \mathbb{R}$ is the location parameter, $\sigma >0$ is the scale parameter, and $\xi \in \mathbb{R}$ is the shape parameter. The three types correspond to

$$\xi =0\left(\mathrm{Gumbel}\right),\xi >0\left(\mathrm{Fr}é\mathrm{chet}\right),\xi <0\left(\mathrm{Weibull}\right).$$

EVT characterizes the limiting behavior of sample extremes and shows that, after appropriate normalization, the distribution of maxima converges to one of three universal forms (Gumbel, Fréchet, Weibull), unified in the Generalized Extreme Value family. This result provides a rigorous statistical foundation for modeling and predicting rare high-impact events.

7.4. Comparison Between Extreme Value Theory and the Bayesian Model Based on Hausdorff Measures

The Extreme Value Theory (EVT) and the Bayesian probabilistic model based on Hausdorff measures represent two fundamentally different approaches to the analysis of rare events.

In the classical framework of EVT, one begins by considering a sequence of independent and identically distributed (i.i.d.) random variables

$$X_1,X_2,\dots ,X_n,$$

with the primary goal of determining the limiting distribution of the maximum value

$$M_n=max(X_1,\dots ,X_n)$$

as the sample size n tends to infinity. The theory focuses on characterizing the asymptotic behavior of the extremes and identifying the universal limit laws (Gumbel, Fréchet, or Weibull) that govern such behavior under appropriate normalization.

In contrast, the proposed Bayesian model based on Hausdorff measures does not assume any specific probability distribution for the random variables, nor does it require them to be independent. In this framework, the conditioning information is represented by a subset of a metric space, characterized by its Hausdorff dimension $s_d$. This value $s_d$ acts as an aggregation operator, encoding the amount of information carried by the conditioning event.

It determines the corresponding Hausdorff dimensional measure ${\mathcal{H}}^{s_d}$, which is then used to define conditional probability.

Within this measure-theoretic Bayesian framework, rare events are identified as those to which the Hausdorff measure ${\mathcal{H}}^{s_d}$ assigns zero probability. Hence, while EVT derives rarity from the asymptotic behavior of maxima under the assumption of independence and identical distributions, the Hausdorff-based Bayesian model defines rarity through geometric and dimensional properties of the underlying information set, without assuming a particular probabilistic structure.

8. Conclusions

In this work, we have introduced a Bayesian updating model defined through Hausdorff measures, offering a geometric perspective on probabilistic inference. The proposed framework reveals that the notion of a rare event, understood as an event with zero probability, is not an intrinsic property of the probabilistic structure alone but rather depends on the underlying metric space in which the measure is defined. In particular, the metric itself plays a crucial role in determining which subsets of the space are assigned vanishing probability.

This observation highlights the interplay between geometry and probability: by altering the metric structure, one may effectively reshape the probabilistic characterization of events, thereby influencing the interpretation of uncertainty and the behavior of Bayesian updates. Consequently, the model provides a flexible tool for studying stochastic systems where the notion of distance and, hence, of similarity among outcomes are subject to modeling choices. Future research may further explore how different metric configurations affect convergence properties, posterior stability, and the emergence of rare events in high-dimensional or non-Euclidean settings. Such notions arise naturally in the study of stochastic processes defined on fractals.

Figure 1 shows why a single Hausdorff model of conditional probability suffices in finite dimensional normed spaces, while a family of Hausdorff models is needed in infinite-dimensional normed spaces to assess conditional probabilities.

Figure 1. Metric equivalence and conditional probabilities in normed spaces.