The Theory and Applications of Hölder Widths

Abstract

We introduce the Hölder width, which measures the best error performance of some recent nonlinear approximation methods, such as deep neural network approximation. Then, we investigate the relationship between Hölder widths and other widths, showing that some Hölder widths are essentially smaller than $n$-Kolmogorov widths and linear widths. We also prove that, as the Hölder constants grow with n, the Hölder widths are much smaller than the entropy numbers. The fact that Hölder widths are smaller than the known widths implies that the nonlinear approximation represented by deep neural networks can provide a better approximation order than other existing approximation methods, such as adaptive finite elements and $n$-term wavelet approximation. In particular, we show that Hölder widths for Sobolev and Besov classes, induced by deep neural networks, are $\mathcal{O}\left(n^{-2s/d}\right)$ and are much smaller than other known widths and entropy numbers, which are $\mathcal{O}\left(n^{-s/d}\right)$.

1. Introduction

Width theory is one of the most important topics in approximation theory because widths can be considered approximation standards that indicate the accuracy achievable for a given function class using an approximation method. They have been extensively studied and applied in various fields, providing a benchmark for the best performance of different approximation techniques. One of the earliest studies on widths was Kolmogorov’s work in 1936, where he introduced the concept of $n$-Kolmogorov widths [1]. With the development of modern science and engineering, the theory of widths has also developed rapidly, greatly promoting research into various linear and nonlinear approximation methods. Problems related to width theory have been and continue to be studied by many experts, including Pinkus, Lorentz, DeVore, Temlyakov, et al. [2,3,4,5,6,7,8,9,10,11,12]. In addition, nonlinear methods play a crucial role in understanding complex phenomena across various applications, such as compressed sensing, signal processing, and neural networks [13,14,15]. Widths such as manifold widths, nonlinear widths, and Lipschitz widths have been utilized as fundamental measures to assess the optimal convergence rate of these nonlinear methods [12,15,16,17,18].

It is known that neural networks can serve as powerful nonlinear tools. For instance, the ReLU (Rectified Linear Unit) activation function,

$$\sigma \left(t\right):=\mathrm{ReLU}\left(t\right)=max\{0,t\},t\in \mathbb{R},$$

is characterized as a Lipschitz mapping, which has led to the introduction of stable manifold widths and Lipschitz widths. In [13,17], Cohen et al. and DeVore, et al. investigated stable manifold widths to quantify error performance in nonlinear approximation methods, such as compressed sensing and neural networks. They discussed the fundamental properties of these widths and established their connections with entropy numbers. In [18,19], Petrova and Wojtaszczyk introduced Lipschitz widths and showed their relationships with other widths and entropy numbers. However, not all mappings are Lipschitz; thus, it is essential to consider weaker conditions to understand the error performance of nonlinear approximation methods. One such condition is the Hölder mapping, which we explore in this paper. We will introduce the concept of Hölder widths and investigate their relationship with other widths and entropy numbers. Our results may provide a better understanding of the effects of such nonlinear approximation methods and their potential applications in deep neural networks.

Many authors have achieved profound results for the ReLU activation function, which acts as a $Lip1$ continuous function in feed-forward deep neural networks (DNNs) [14,17,18,20,21]. It is known that the mapping $\mathsf{\Phi }:(B_{l_{\infty }^{cn}}{,\parallel ·\parallel }_{l_{\infty }^{cn}})\to C\left({[0,1]}^d\right)$ in [18] with the ReLU activation function is a $C^{\prime }n{W}^n$ Lipschitz mapping in DNNs, where the network has a width W and adepth n. Unlike the Lipschitz width, the terms ‘width’ and ‘depth’ here indicate the scale of the network. The performance of this Lipschitz mapping is discussed in [14].

We introduce a more flexible assumption. Let $(Y,d)$ and $(Z,\rho )$ be metric spaces. Moreover, we assume that the space Z is separable. Define $\mathsf{\Phi }:(Y,d)\to (Z,\rho )$ as an $\alpha$-Hölder mapping with coefficient $\gamma$ if for any $x,y\in Y$,

$$\rho \left(\mathsf{\Phi }\left(x\right),\mathsf{\Phi }\left(y\right)\right)\le \gamma d^{\alpha }\left(x,y\right),\gamma >0\mathrm{and}0<\alpha \le 1.$$

We could also say that $\mathsf{\Phi }$ satisfies the $H_{\alpha }\left(\gamma \right)$ condition [22] equivalent to

$$\underset{x,y\in Y}{sup}{\displaystyle \frac{\rho \left(\mathsf{\Phi }\left(x\right),\mathsf{\Phi }\left(y\right)\right)}{d^{\alpha }\left(x,y\right)}}\le \gamma ,\gamma >0\mathrm{and}0<\alpha \le 1.$$

We provide some remarks on Hölder mappings below.

Remark 1.

If $\alpha =1$, then Φ is Lipschitz continuous.

Remark 2.

If Y is bounded and Φ is an α-Hölder mapping, then for any $\beta \le \alpha$, Φ is a β-Hölder mapping.

Remark 3.

The minimum α-Hölder coefficient $\gamma =0$ if and only if Φ is constant.

Note that the RePU (Rectified Power Unit) activation function [23,24],

$${\sigma }_1\left(t\right):=\mathrm{RePU}\left(t\right)=max{\{0,t\}}^{\alpha },t\in \mathbb{R},$$

with $\alpha \in \mathbb{N},\alpha \ge 2$, and the GELU (Gaussian Error Linear Unit) activation function [25],

$${\sigma }_2\left(t\right):=\mathrm{GELU}\left(t\right)=0.5t\left(1+tanh\left(\sqrt{{\displaystyle \frac{2}{\pi }}}(t+0.044715t^3)\right)\right),t\in \mathbb{R}.$$

can be considered 1-Hölder mappings in bounded spaces. The performance of these mappings can be found in [14,18]. Moreover, there are various $\alpha$-Hölder activation functions with $0<\alpha <1$. In [26], Forti, Grazzini, et al. obtained global convergence results, where the neuron activations were modeled by ${\alpha }_i$-Hölder continuous functions with ${\alpha }_i\in$ (0, 1), such as

$${\sigma }_i\left(t\right)=k_i\mathrm{sign}\left(t\right){\left|t\right|}^{{\alpha }_i},$$

where $k_i>0$ and $i\in {\theta }_C$ defined in [26]. These activations can significantly increase the computational power [26,27,28]. Motivated by the above results, we mainly focus on the $\alpha$-Hölder condition with $0<\alpha <1$, which is weaker than the Lipschitz condition.

Now, we introduce Hölder widths, which measure the best error performance of some recent nonlinear approximation methods characterized by Hölder mappings. Throughout this paper, let X be a Banach space with a norm ${\parallel ·\parallel }_X$, and let $Y_n$ be an $n$-dimensional Banach space with a norm ${\parallel ·\parallel }_{Y_n}$ on ${\mathbb{R}}^n$, $n\ge 1$. Denote the unit ball of $Y_n$ by $B\left(Y_n\right):=\{y\in {\mathbb{R}}^n{:\parallel y\parallel }_{Y_n}\le 1\}$.

Let K be a bounded subset of X. For $\gamma \ge 0$, $0<\alpha <1$, we define the fixed Hölder widths

$${\delta }_n^{\gamma ,\alpha }{(K,Y_n)}_X:=\underset{{\mathsf{\Phi }}_n}{inf}\underset{f\in K}{sup}\underset{y\in B\left(Y_n\right)}{inf}{\parallel f-{\mathsf{\Phi }}_n\left(y\right)\parallel }_X,$$

(1)

where ${\mathsf{\Phi }}_n:\left(B\left(Y_n\right),{\parallel ·\parallel }_{Y_n}\right)\to X$ satisfies

$$\underset{x,y\in B\left(Y_n\right)}{sup}{\displaystyle \frac{{\parallel \mathsf{\Phi }\left(x\right)-\mathsf{\Phi }\left(y\right)\parallel }_X}{{\parallel x-y\parallel }_{Y_n}^{\alpha }}}\le \gamma .$$

Next, we define the Hölder width

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X:=\underset{{\parallel ·\parallel }_{Y_n}}{inf}{\delta }_n^{\gamma ,\alpha }{(K,Y_n)}_X,$$

(2)

where the infimum is taken over all norms ${\parallel ·\parallel }_{Y_n}$ on ${\mathbb{R}}^n$. From definition (1), we see that the error of any numerical method based on Hölder mappings will not be smaller than the Hölder widths.

We propose the Hölder widths, exploring their properties and relationships with other known widths and entropy numbers. In Section 2, we establish the fundamental properties of Hölder widths. In Section 3, we compare Hölder widths with $n$-Kolmogorov widths, linear widths, and nonlinear $(n,N)$-widths. In Section 4, we investigate the relationship between Hölder widths and entropy numbers. In Section 5, we provide some specific applications and derive the asymptotic order of Hölder widths for Sobolev classes $B{W}_p^s\left({[0,1]}^d\right)$ and Besov classes $B{B}_{p,\tau }^s\left({[0,1]}^d\right)$ using deep neural networks. In Section 6, we provide some concluding remarks. All detailed proofs for the results from Section 2, Section 3 and Section 4 are included in Appendix A, Appendix B and Appendix C, and the proofs for Theorems 10 and 15 in Section 5 are provided in Appendix D.

2. Fundamental Properties of Hölder Widths

Recall that the radius of a set $K\subset X$ is defined as

$$\mathrm{rad}\left(K\right)=:\underset{g\in X}{inf}\underset{f\in K}{sup}{\parallel f-g\parallel }_X.$$

(3)

It is known from Remark 3 that a function that satisfies the $H_{\alpha }\left(0\right)$ condition is a constant function. Then, for the $n$-dimensional space $Y_n$,

$$\mathrm{rad}\left(K\right)={\delta }_n^{0,\alpha }{(K,Y_n)}_X={\delta }_n^{0,\alpha }{\left(K\right)}_X.$$

(4)

Moreover, for a fixed constant $\alpha$, it is known from (2) that ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$ is decreasing with respect to $\gamma$ and n, that is, (i) if ${\gamma }_1\le {\gamma }_2$, then ${\delta }_n^{{\gamma }_2,\alpha }{\left(K\right)}_X\le {\delta }_n^{{\gamma }_1,\alpha }{\left(K\right)}_X\le \mathrm{rad}\left(K\right)<\infty$, and (ii) if $n_1\le n_2$, then ${\delta }_{n_2}^{\gamma ,\alpha }{\left(K\right)}_X\le {\delta }_{n_1}^{\gamma ,\alpha }{\left(K\right)}_X$.

In addition, it is easy to see that the space (${\mathbb{R}}^n$, ${\parallel ·\parallel }_{Y_n}$) in (1) and (2) can be replaced with any $n$-dimensional normed space ($Z_n$,${\parallel ·\parallel }_{Z_n}$) such that

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X=\underset{{\parallel ·\parallel }_{Z_n}}{inf}{\delta }_n^{\gamma ,\alpha }{(K,Z_n)}_X,{\delta }_n^{\gamma ,\alpha }{(K,Z_n)}_X=\underset{{\mathsf{\Phi }}_n}{inf}\underset{f\in K}{sup}\underset{z\in B\left(Z_n\right)}{inf}{\parallel f-{\mathsf{\Phi }}_n\left(z\right)\parallel }_X,$$

where $B\left(Z_n\right):=\{z\in Z_n{:\parallel z\parallel }_{Z_n}\le 1\}.$

Denote by

$${\ell }_p^n:=({\mathbb{R}}^n{,\parallel ·\parallel }_{{\ell }_p})$$

the space ${\mathbb{R}}^n$ equipped with the ${\ell }_p$ norm, that is, for $y=(y_1,y_2,\cdots ,y_n)\in {\mathbb{R}}^n$,

$${\parallel y\parallel }_{{\ell }_{\infty }^n}:=\underset{j}{max}|y_j{|,\parallel y\parallel }_{{\ell }_p^n}:={\left(\sum _{j=1}^n{\left|y_j\right|}^p\right)}^{1/p}.$$

Recall that an $\epsilon$-covering of K is a collection $\{g_1,\cdots ,g_m\}\subset X$ such that

$$K\subset \bigcup _{j=1}^{m}B(g_j,\epsilon ).$$

The minimal $\epsilon$-covering number $N_{\epsilon }\left(K\right)$ is the minimal cardinality of the $\epsilon$-covering of K. We say that a set K is totally bounded if for every $\epsilon >0$, $N_{\epsilon }\left(K\right)<\infty$.

We establish the following fundamental properties of Hölder widths.

Theorem 1.

Let K be a compact subset of X. For any $n\in \mathbb{N}$, $\gamma >0$, and $0<\alpha <1$, there exists a norm ${\parallel ·\parallel }_Y$ on ${\mathbb{R}}^n$ satisfying for $y\in {\mathbb{R}}^n$,

$${\parallel y\parallel }_{{\ell }_{\infty }^n}\le {\parallel y\parallel }_Y\le {\parallel y\parallel }_{{\ell }_1^n},$$

(5)

such that

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X={\delta }_n^{\gamma ,\alpha }{(K,Y)}_X.$$

Theorem 2.

Let K be a compact subset of X. As a function of γ, the Hölder width ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$ is continuous.

Theorem 3.

A subset K of X is totally bounded if and only if for every $n\in \mathbb{N}$,

$$\underset{\gamma \to \infty }{lim}{\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X=0.$$

Theorem 4.

Let $K\subset X$ and $0<\alpha <1$. If for every $\epsilon >0$, there exist two numbers $n\in \mathbb{N}$ and $\gamma >0$ such that ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le \epsilon$, then K is totally bounded.

It is important to delve deeper into Hölder widths since the Hölder condition offers a more flexible framework that can accommodate a broader range of functions, making it particularly suitable for analyzing and approximating complicated functions and datasets. In the forthcoming sections, we will gain deeper insights into the approximation performance measured by Hölder widths.

3. The Relationship Between Hölder Widths and Other Widths

In this section, we will demonstrate that Hölder widths are smaller than other known widths, such as $n$-Kolmogorov, linear, and nonlinear $(n,N)$-widths. In the following sections, we assume that K is a compact subset of the Banach space X, which is our main concern.

3.1. The Relationship Between Hölder Widths, $n$-Kolmogorov Widths, and Linear Widths

We recall the definition of the $n$-Kolmogorov width of K from [2], as follows:

$$d_0{\left(K\right)}_X:=\underset{f\in K}{sup}{\parallel f\parallel }_X,d_n{\left(K\right)}_X:=\underset{dim\left(X_n\right)=n}{inf}\underset{f\in K}{sup}\underset{g\in X_n}{inf}{\parallel f-g\parallel }_X,n\ge 1,$$

where the infimum is taken over all $n$-dimensional subspaces $X_n\subset X$.

It is known that the $n$-Kolmogorov width determines the optimal errors generated by approximating the ‘worst’ element of the set K using $n$-dimensional subspaces of X. We will show that some Hölder widths are essentially smaller than $n$-Kolmogorov widths.

Theorem 5.

For a compact set $K\subset X$ and $n\ge 1$, $0<\alpha <1$,

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le d_n{\left(K\right)}_X,for\gamma ={\displaystyle \frac{d_n{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}}.$$

Corollary 1.

If $K\subset X$ is compact, then for each $n_0\in \mathbb{N}$ and each $\gamma \ge {\displaystyle \frac{d_{n_0}{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}}$,

$$\underset{n\to \infty }{lim}{\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X=0.$$

Remark 4.

Recall that the linear width $d_n^L{\left(K\right)}_X$ is defined as

$$d_0^L{\left(K\right)}_X:=\underset{f\in K}{sup}{\parallel f\parallel }_X,d_n^L{\left(K\right)}_X:=\underset{L\in {\mathcal{L}}_n}{inf}\underset{f\in K}{sup}{\parallel f-L\left(f\right)\parallel }_X,n\ge 1,$$

where the infimum is taken over the class ${\mathcal{L}}_n$ of all continuous linear operators from X into itself with rank at most n. It follows from the definitions of the $n$-Kolmogorov width and linear width that $d_n{\left(K\right)}_X\le d_n^L{\left(K\right)}_X$. Thus, Theorem 5 implies that

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le d_n^L{\left(K\right)}_X,for\gamma ={\displaystyle \frac{d_n{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}}.$$

3.2. The Relationship Between Hölder Widths and Nonlinear $(n,N)$-Widths

To evaluate the performance of the best $n$-term approximation with respect to different systems, such as the trigonometric system and wavelet bases, Temlyakov introduced the nonlinear $(n,N)$-width in [16], which is defined as follows: for $N\ge 1$, $n\ge 1$,

$$d_0{(K,N)}_X:=\underset{f\in K}{sup}{\parallel f\parallel }_X,d_n{(K,N)}_X:=\underset{{\mathcal{L}}_N}{inf}\underset{f\in K}{sup}\underset{X_n\in {\mathcal{L}}_N}{inf}\mathrm{dist}{(f,X_n)}_X.$$

(6)

where the second infimum is taken over the sets ${\mathcal{L}}_N$ of N linear spaces $X_n\subset X$ of dimension n. The nonlinear $(n,N)$-width can reflect the approximation performance of greedy algorithms.

It is clear that $d_n{(K,1)}_X=d_n{\left(K\right)}_X$. The larger N is, the more flexibility we have in approximating f. Moreover, it is known from (6) and Theorem 5 that

$$d_n{(K,N)}_X\ge d_{n·N}{\left(K\right)}_X\ge {\delta }_{n·N}^{\gamma ,\alpha }{\left(K\right)}_X,\mathrm{where}\gamma =2^{2-\alpha }\mathrm{rad}\left(K\right).$$

Moreover, we obtain the following inequalities, revealing the relationship between Hölder widths and nonlinear $(n,N)$-widths.

Theorem 6.

For any $n\ge 1$, $N>1$, $0<\alpha <1$, and any compact set $K\subset X$ with $\underset{f\in K}{sup}{\parallel f\parallel }_X=1$, we have

$${\delta }_{n+1}^{4(N+1)\sqrt{n},\alpha }{\left(K\right)}_X\le d_n{(K,N)}_X,\mathrm{and}{\delta }_{n+\lceil {log}_{2}N\rceil }^{12\sqrt{n},\alpha }{\left(K\right)}_X\le d_n{(K,N)}_X.$$

4. Comparison Between Hölder Widths and Entropy Numbers

We first recall the definition of the entropy number from [29]. The entropy number ${\epsilon }_n{\left(K\right)}_X$ is defined as

$${\epsilon }_n{\left(K\right)}_X:=inf\{\epsilon >0:K\subset \bigcup _{j=1}^{2^n}B(g_j,\epsilon ),g_j\in X,j=1,2,\cdots ,2^n\},$$

which is the infimum of all $\epsilon >0$ for which $2^n$ balls of radius $\epsilon$ cover a compact set $K\subset X$, and $B(g_j,\epsilon ):=\{g\in X:\parallel g-g_j{\parallel }_X\le \epsilon \}$.

Entropy numbers have many applications in fields such as compressed sensing, statistics, and learning theory [30,31,32]. They can provide a benchmark for the best error performance of numerical recovery algorithms. Sometimes, estimating the entropy numbers ${\epsilon }_n{\left(K\right)}_X$ is more accessible than computing other known widths, such as $n$-Kolmogorov widths and nonlinear $(n,N)$-widths. For example, for some model classes K, such as unit balls in classical Sobolev and Besov spaces, the entropy numbers are known and can also be used to estimate the lower bound of these widths.

In this section, we compare the convergence rate of the Hölder widths with that of the entropy numbers. We first obtain the following general results.

Theorem 7.

For any $n\ge 1$ and $0<\alpha <1$, we have

$${\delta }_n^{2^k\mathrm{rad}\left(K\right),\alpha }{\left(K\right)}_X\le {\epsilon }_{kn}{\left(K\right)}_X,k=1,2,\cdots .$$

Specifically, if $k=n$, then

$${\delta }_n^{2^n\mathrm{rad}\left(K\right),\alpha }{\left(K\right)}_X\le {\epsilon }_{n^2}{\left(K\right)}_X.$$

Remark 5.

It is known from Theorem 7 that if $k=1$, then

$${\delta }_n^{2·\mathrm{rad}\left(K\right),\alpha }{\left(K\right)}_X\le {\epsilon }_n{\left(K\right)}_X.$$

So, by the decreasing property of ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$ with respect to γ, Hölder widths are smaller than entropy numbers for $\gamma \ge 2·\mathrm{rad}\left(K\right)$.

It follows from Theorem 7 with $k=1$ that the following corollary holds.

Corollary 2.

Let $0<\alpha <1$, and $\gamma \ge 2·\mathrm{rad}\left(K\right)$.

(i) If the following inequality holds:

$${\epsilon }_n{\left(K\right)}_X\le c_1{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}},n\ge 1,$$

where $c_1,p,q$ are some constants such that $p\in \mathbb{R}$, $c_1,q>0$, then we have

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le C{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}},n\ge 1,$$

where C is a positive constant.

(ii) If the following inequality holds:

$${\epsilon }_n{\left(K\right)}_X\le c_1{\left({log}_{2}n\right)}^{-q},n\ge 1,$$

where $c_1,q$ are two positive constants, then we have

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le C{\left({log}_{2}n\right)}^{-q},n\ge 1,$$

where C is a positive constant.

Theorem 7 and Corollary 2 state that given an upper bound on the entropy number, it can be determined that the upper bound of the Hölder width is less than it. Conversely, if we know a lower bound of the entropy number, then we can obtain a lower bound of the Hölder width. To show this, we need the following theorem.

Theorem 8.

Let $\gamma >0$, $0<\alpha <1$. If there exists $n>n_0$, where $n_0=n_0(c_0,\alpha ,p,q)$ satisfies $p\in \mathbb{R},q>0$,

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X<c_0{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}},$$

then for $m=c_{1}n{log}_{2}n$,

$${\epsilon }_m{\left(K\right)}_X<C{\displaystyle \frac{{\left({log}_{2}m\right)}^{p+q}}{m^q}},$$

where $c_1,C$ are constants that depend on $\gamma ,\alpha ,c_0,p$, and q.

Based on Theorem 8, we can obtain a lower bound of the Hölder width from that of the entropy number.

Theorem 9.

(i) If the following inequality holds:

$${\epsilon }_n{\left(K\right)}_X>c_1{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}},n\ge 1,$$

where $c_1,p,q$ are constants such that $p\in \mathbb{R}$, $c_1,q>0$, then for each $\gamma >0$ and $0<\alpha <1$, we have

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\ge C{\displaystyle \frac{{\left({log}_{2}n\right)}^{p-q}}{n^q}},n\ge 1,$$

(7)

where C is a positive constant.

(ii) If the following inequality holds:

$${\epsilon }_n{\left(K\right)}_X>c_1{\left({log}_{2}n\right)}^{-q},n\ge 1,$$

where $c_1,q$ are some positive constants, then for each $\gamma >0$ and $0<\alpha <1$, we have

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\ge C{\left({log}_{2}n\right)}^{-q},n\ge 1,$$

(8)

where C is a positive constant.

(iii) If the following inequality holds:

$${\epsilon }_n{\left(K\right)}_X>c_1{2}^{-c_2{n}^p},n\ge 1,$$

where $c_1,c_2,p$ are some constants such that $c_1,c_2>0$, and $0<p<1$, then for each

$$\gamma >{\displaystyle \frac{d_n{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}},\mathrm{and}0<\alpha <1,$$

we have

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\ge C_1{2}^{-C_2{n}^{{\displaystyle \frac{p}{1-p}}}},n\ge 1,$$

(9)

where $C_1,C_2$ are two positive constants.

Combining Corollary 2 (ii) with Theorem 9 (ii), we derive the following corollary.

Corollary 3.

For any compact set $K\subset X$, $0<\alpha <1$, $\gamma \ge max\left\{2·\mathrm{rad}\left(K\right),{\displaystyle \frac{d_{n_0}{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}}\right\}$, and $q>0$, then

$${\epsilon }_n{\left(K\right)}_X\asymp {\left({log}_{2}n\right)}^{-q}⟺{\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\asymp {\left({log}_{2}n\right)}^{-q},\mathrm{for}\mathrm{any}n\ge 1.$$

5. Some Applications

The importance of the Hölder width lies in its lower bound, which is independent of any specific algorithm. This bound not only reveals the limitations of certain approximation tools but also provides information on the order of the Hölder width without knowing the concrete algorithms. The insights from the lower bound can help us show the optimality of some existing algorithms or prompt us to design optimal algorithms that can achieve such a bound. In essence, the concept of width is independent of any specific algorithm but inspires us to design optimal algorithms.

We apply the above general theoretical results to some important function spaces and obtain the corresponding orders of Hölder widths.

First, we remark that some common neural networks are Hölder mappings. Therefore, we can obtain their asymptotic orders of Hölder widths characterized by these fully connected feed-forward neural networks. In the following discussion, we mainly consider the Banach spaces X of functions, where $C\left({[0,1]}^d\right)$ is continuously embedded in X. Let $\sigma :\mathbb{R}\to \mathbb{R}$ be an activation function. Denote by $\mathsf{\Omega }:={[0,1]}^d$ and ${\mathsf{\Phi }}_{\sigma }:\left(B_{l_{\infty }^{\tilde{n}}},{\parallel ·\parallel }_{l_{\infty }^{\tilde{n}}}\right)\to C\left(\mathsf{\Omega }\right)$.

A feed-forward neural network with width W, depth n, and activation $\sigma$ produces a family ${\mathsf{\Sigma }}_{n,\sigma }\subset C\left(\mathsf{\Omega }\right)$:

$${\mathsf{\Sigma }}_{n,\sigma }:=\left\{{\mathsf{\Phi }}_{\sigma }\left(t\right):t\in {\mathbb{R}}^{\tilde{n}},\tilde{n}=\tilde{n}(W,n)=C_{0}n\right\},$$

which generates an approximation to a target element $f\in K$. For every $t\in {\mathbb{R}}^{\tilde{n}},$ there exists a continuous function ${\mathsf{\Phi }}_{\sigma }\left(t\right)\in {\mathsf{\Sigma }}_{n,\sigma }$ on $\mathsf{\Omega }$

$${\mathsf{\Phi }}_{\sigma }\left(t\right):=T^{\left(n\right)}\circ \overline{\sigma }\circ T^{(n-1)}\circ \overline{\sigma }\circ \cdots \circ \overline{\sigma }\circ T^{\left(0\right)},$$

(10)

where the affine mappings $T^{\left(0\right)}:{\mathbb{R}}^d\to {\mathbb{R}}^W$, $T^{\left(k\right)}:{\mathbb{R}}^W\to {\mathbb{R}}^W$, $k=1,2\cdots ,n-1$, and $T^{\left(n\right)}:{\mathbb{R}}^W\to \mathbb{R}$, and the function $\overline{\sigma }:{\mathbb{R}}^W\to {\mathbb{R}}^W$

$$\overline{\sigma }(z_{j+1},\cdots ,z_{j+W}):=\left(\sigma \left(z_{j+1}\right),\cdots ,\sigma \left(z_{j+W}\right)\right).$$

Here, t is the vector whose coordinates are the entries of the matrices and biases of $T^{\left(k\right)}$, $k=0,1,\cdots ,n$. We note that the dimension of any hidden layer can naturally be expanded; thus, any fully connected network can be made to have a fixed width [13,33]. Our assumption about a fixed width W can simplify the computations and notations.

Proposition 1.

If σ is an $H_{\alpha }\left(\gamma \right)$ mapping, then ${\mathsf{\Phi }}_{\sigma }:\left(B_{l_{\infty }^{\tilde{n}}},{\parallel ·\parallel }_{l_{\infty }^{\tilde{n}}}\right)$, defined in (10), is an $H_{\alpha }\left({\mathsf{\Gamma }}_n\right)$ mapping, which means that for $t,t^{\prime }\in B_{l_{\infty }^{\tilde{n}}}$,

$$\parallel {\mathsf{\Phi }}_{\sigma }\left(t\right)-{\mathsf{\Phi }}_{\sigma }\left(t^{\prime }\right){\parallel }_{C\left(\mathsf{\Omega }\right)}\le {\mathsf{\Gamma }}_n{\parallel t-t^{\prime }\parallel }_{l_{\infty }^{\tilde{n}}}^{\alpha },$$

where ${\mathsf{\Gamma }}_n=M_{d,\alpha }{\gamma }_0^n{\left(2W\right)}^{n\alpha }$, ${\gamma }_0=max\{\gamma ,1\}$, and $M_{d,\alpha }$ is a constant.

It follows that a specific neural network can be a Hölder mapping with coefficient ${\mathsf{\Gamma }}_n=M_{d,\alpha }{\left({\left(2W\right)}^{\alpha }{\gamma }_0\right)}^n$ to approximate the target element f, where $0<\alpha <1$ and $W>1$. Then, we consider the lower bound for the Hölder width with coefficient ${\gamma }_n=M{\lambda }^n$, $M>0$, $\lambda >1$, which also implies the lower bound of the DNN approximation.

Theorem 10.

Let $0<\alpha <1$ and ${\gamma }_n=M{\lambda }^n$, where $M>0$, $\lambda >1$, $n\ge 1$.

(i) If the following inequality holds:

$${\epsilon }_n{\left(K\right)}_X>c_1{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}},n\ge 1,$$

where $c_1,p,q$ are constants such that $p\in \mathbb{R}$, $c_1,q>0$, then

$${\delta }_n^{{\gamma }_n,\alpha }{\left(K\right)}_X\ge C{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^{2q}}},n\ge 1,$$

(11)

where C is a positive constant.

(ii) If the following inequality holds:

$${\epsilon }_n{\left(K\right)}_X>c_1{\left({log}_{2}n\right)}^{-q},n\ge 1,$$

where $c_1,q$ are some positive constants, then

$${\delta }_n^{{\gamma }_n,\alpha }{\left(K\right)}_X\ge C{\left({log}_{2}n\right)}^{-q},n\ge 1,$$

(12)

where C is a positive constant.

Theorems 7 and 10 imply the following corollary, which means that if we know the asymptotic orders of some entropy numbers, we can obtain the asymptotic orders of their Hölder widths.

Corollary 4.

Let $0<\alpha <1$ and ${\gamma }_n=M{\lambda }^n$, where $M>0$, $\lambda >1$, $n\ge 1$.

(i) If the following holds:

$${\epsilon }_n{\left(K\right)}_X\asymp {\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}},n\ge 1,$$

where $p,q$ are some constants such that $p\in \mathbb{R}$, $q>0$, then we have

$${\delta }_n^{{\gamma }_n,\alpha }{\left(K\right)}_X\asymp {\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^{2q}}},n\ge 1.$$

(ii) If the following holds:

$${\epsilon }_n{\left(K\right)}_X\asymp {\left({log}_{2}n\right)}^{-q},n\ge 1,$$

where q is a positive constant, then we have

$${\delta }_n^{{\gamma }_n,\alpha }{\left(K\right)}_X\asymp {\left({log}_{2}n\right)}^{-q},n\ge 1.$$

We point out that Corollary 4 provides a tool for giving lower bounds on how well a compact set K can be approximated by a DNN, where all weights and biases are from the unit ball of some norm ${\parallel ·\parallel }_{Y_{\tilde{n}}}$. The classical model classes K for multivariate functions can be the unit balls of smoothness spaces, such as classical Lipschitz, Hölder, Sobolev, and Besov spaces. For any model class K, denote the unit ball of K by

$$BK:=\{f\in K:\parallel f{\parallel }_K\le 1\}.$$

For any $K,A\subset X$, let

$$\mathrm{dist}{\left(K,A\right)}_X:=\underset{f\in K}{sup}\underset{g\in A}{inf}{\parallel f-g\parallel }_X.$$

Many experts have investigated the performance of deep learning approximation for these function classes of the Lebesgue space $L_p$ on the cube $\mathsf{\Omega }$ [20,21,33,34].

First, we determine the exact order of the Hölder width for the classical Sobolev class. For $1\le p\le \infty$, we denote by $L_p\left(\mathsf{\Omega }\right)$ the usual Lebesgue space on $\mathsf{\Omega }$ equipped with the $L_p$ norm

$${\parallel f\parallel }_p:={\parallel f\parallel }_{L_p\left(\mathsf{\Omega }\right)}=\left\{\begin{array}{cc}& {\left({\int }_{\mathsf{\Omega }}{\left|f\left(x\right)\right|}^p\mathrm{d}\mu \left(x\right)\right)}^{1/p},1\le p<\infty ,\hfill \\ & \mathrm{ess}\underset{x\in \mathsf{\Omega }}{sup}\left|f\left(x\right)\right|,p=\infty .\hfill \end{array}\right.$$

For $s\in \mathbb{N}$, $1\le p\le \infty$, we say that function f belongs to the Sobolev space $W_p^s\left(\mathsf{\Omega }\right)$ if $f\in L_p\left(\mathsf{\Omega }\right)$, and the norm ${\parallel ·\parallel }_{W_p^s}$ of f is given by, for $\left|\mathbf{k}\right|:={\sum }_{j=1}^d\left|k_j\right|=s$,

$${\parallel f\parallel }_{W_p^s}:={\parallel f\parallel }_p+\underset{\left|\mathbf{k}\right|=s}{max}\parallel D^{\mathbf{k}}f{\parallel }_p<\infty .$$

It is known from [35] that when $s>d{(1/p-1/q)}_{+}$, $1<p,q<\infty$

$${\epsilon }_n{\left(B{W}_p^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\asymp n^{-s/d}.$$

(13)

Moreover, the approximation error rates $\mathcal{O}\left(n^{-s/d}\right)$ for Sobolev and Besov classes can be obtained using many classical methods of nonlinear approximation, such as adaptive finite elements or $n$-term wavelet approximation [13,15].

It follows from Theorem 10 and Corollary 4 that for some deep neural networks,

$$\mathrm{dist}{\left(B{W}_p^s\left(\mathsf{\Omega }\right),{\mathsf{\Sigma }}_{n,\sigma }\right)}_{L_q}\ge {\delta }_{\tilde{n}}^{{\gamma }_n,\alpha }{\left(B{W}_p^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\gg n^{-2s/d},$$

(14)

where ${\mathsf{\Sigma }}_{n,\sigma }$ is produced by some neural networks with depth n, fixed width, and $H_{\alpha }\left(\gamma \right)$ activation functions $\sigma$, $0<\alpha \le 1$. Compared with classical methods, the factor 2 in the exponent leaves open the possibility of improved approximation rates when using deep neural networks. Indeed, it is known from [33] that there exists a neural network ${\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}$ with depth n, width $25d+31$, and ReLU activation function ${\sigma }^{\prime }$ such that, for $f\in B{W}_p^s\left(\mathsf{\Omega }\right),$

$$\underset{f_n\in {\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}}{inf}\parallel f-f_n{\parallel }_q\ll {\parallel f\parallel }_{W_p^s}·n^{-2s/d},$$

(15)

The author used a novel bit-extraction technique, which gives an optimal encoding of sparse vectors, to obtain the upper bounds $\mathcal{O}\left(n^{-2s/d}\right)$.

Based on the above discussion, we obtain the Hölder widths for the Sobolev classes $B{W}_p^s\left(\mathsf{\Omega }\right)$.

Theorem 11.

Let $1<p,q<\infty$, $0<\alpha \le 1$, and $s>d{\left({\displaystyle \frac{1}{p}}-{\displaystyle \frac{1}{q}}\right)}_{+}$. Then, there exist $M>0$, $\lambda >1$ such that for ${\gamma }_n=M{\lambda }^n$,

$${\delta }_n^{{\gamma }_n,\alpha }{\left(B{W}_p^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\asymp \mathrm{dist}{\left(B{W}_p^s\left(\mathsf{\Omega }\right),{\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}\right)}_{L_q}\asymp n^{-2s/d}.$$

Proof. 

It is known from (13) and Corollary 4 that for any $M>0$, $\lambda >1$,

$${\delta }_n^{{\gamma }_n,\alpha }{\left(B{W}_p^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\gg n^{-2s/d}.$$

Moreover, it is known from (14) that

$$\mathrm{dist}{\left(B{W}_p^s\left(\mathsf{\Omega }\right),{\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}\right)}_{L_q}\gg n^{-2s/d}.$$

It follows from (15) that

$$\mathrm{dist}{\left(B{W}_p^s\left(\mathsf{\Omega }\right),{\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}\right)}_{L_q}\asymp \underset{f\in B{W}_p^s\left(\mathsf{\Omega }\right)}{sup}\underset{f_n\in {\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}}{inf}{\parallel f-f_n\parallel }_q\ll n^{-2s/d},$$

and for any $f\in B{W}_p^s\left(\mathsf{\Omega }\right),$

$$\underset{f_n\in {\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}}{inf}{\parallel f-f_n\parallel }_q\ll n^{-2s/d}.$$

Therefore, there exist constants c, $c_0>0$ such that

$${\delta }_{c_{0}n}^{c{(50d+62)}^n,1}{\left(B{W}_p^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\ll n^{-2s/d}.$$

Replacing $c_{0}n$ with n, it follows from the decreasing property of the Hölder width that there exist $M=2c>0$ and $\lambda ={(50d+62)}^{1/c_0}>1$ such that

$${\delta }_n^{{\gamma }_n,\alpha }{\left(B{W}_p^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\le {\delta }_n^{c{\lambda }^n,1}{\left(B{W}_p^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\ll n^{-2s/d}.$$

Thus, we complete the proof of Theorem 11. □

Remark 6.

Theorem 11 implies that the upper bound in inequality (15) is sharp.

For a fixed $s\in \mathbb{N}$ and $d=1$, Figure 1 compares the performance of the approximation error versus the number of elements or layers using different approximation methods, such as the classical methods represented by $n$-term wavelets, adaptive finite elements, and new tools represented by deep neural networks. The blue solid line shows the approximation error decreasing at a rate of $\mathcal{O}\left(n^{-s}\right)$ with the number of elements n for $n$-term wavelets or adaptive finite elements, while the orange dashed line indicates a faster decay of $\mathcal{O}\left(n^{-2s}\right)$ with depth n for deep neural networks. Overall, deep neural networks significantly outperform classical methods, such as $n$-term wavelets or adaptive finite elements, offering more rapid convergence and potentially higher accuracy in approximating functions. We call this phenomenon the super-convergence of deep neural networks, where the classical Hölder, Sobolev, and Besov classes on ${[0,1]}^d$ can achieve super-convergence [20,21].

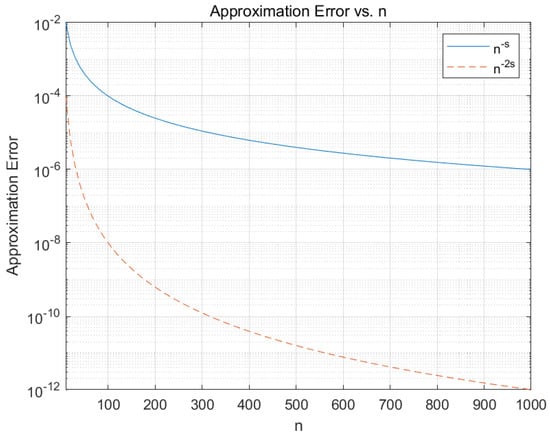
Figure 1. Approximation error and the number of elements n and depth d: classical methods ($n$-term wavelets and adaptive finite elements) vs. new tools (deep neural networks).

The results of Theorem 11 can be extended to Besov spaces, which are much more general than Sobolev spaces. It is well known that functions from Besov spaces have been widely used in approximation theory, statistics, image processing, and machine learning (see [6,36,37,38], and the references therein). Recall that for $r\in \mathbb{N}$, the modulus of smoothness of order r of $f\in L_p\left(\mathsf{\Omega }\right)$ is

$${\omega }_r{(f,t)}_p:=\underset{\left|h\right|\le t}{sup}{\parallel {▵}_h^r(f,·,\mathsf{\Omega })\parallel }_p,$$

where ${▵}_h^r(f,x)$ is the r-th order difference of f with step h, and

$${▵}_h^r(f,x,\mathsf{\Omega }):=\left\{\begin{array}{cc}& {▵}_h^r(f,x),x,x+h,\cdots ,x+rh\in \mathsf{\Omega },\hfill \\ & 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

For $0<s<r$, $1\le p,\tau \le \infty$, we say that function f belongs to the Besov space $B_{p,\tau }^s\left(\mathsf{\Omega }\right)$ if $f\in L_p\left(\mathsf{\Omega }\right)$, and the norm ${\parallel ·\parallel }_{B_{p,\tau }^s}$ of f, given by

$$\begin{array}{c}{\parallel f\parallel }_{B_{p,\tau }^s}:=\left\{\begin{array}{cc}& {\parallel f\parallel }_p+{\left({\int }_0^1{\left({\displaystyle \frac{{\omega }_r{(f,t)}_p}{t^s}}\right)}^{\tau }{\displaystyle \frac{\mathrm{d}t}{t}}\right)}^{{\displaystyle \frac{1}{\tau }}},1\le \tau <\infty ;\hfill \\ & {\parallel f\parallel }_p+\underset{t>0}{sup}{\displaystyle \frac{{\omega }_r{(f,t)}_p}{t^s}},\tau =\infty ,\hfill \end{array}\right.\end{array}$$

is finite. It is known from [15] that when $s>d{(1/p-1/q)}_{+}$, $q\ne \infty$

$${\epsilon }_n{\left(B{B}_{p,\tau }^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\asymp n^{-s/d}.$$

It follows from Theorem 10 and Corollary 4 that for some deep neural networks,

$$\mathrm{dist}{\left(B{B}_{p,\tau }^s\left(\mathsf{\Omega }\right),{\mathsf{\Sigma }}_{n,\sigma }\right)}_{L_q}\ge {\delta }_{\tilde{n}}^{{\gamma }_n,\alpha }{\left(B{B}_{p,\tau }^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\gg n^{-2s/d},$$

and it is also known from [33] that there exists a neural network ${\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}$ with depth n, width $25d+31$, and ReLU activation function ${\sigma }^{\prime }$ such that for $f\in B{B}_{p,\tau }^s\left(\mathsf{\Omega }\right),$

$$\underset{f_n\in {\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}}{inf}\parallel f-f_n{\parallel }_q\ll {\parallel f\parallel }_{B_{p,\tau }^s}·n^{-2s/d}.$$

Thus, we obtain the Hölder widths for the Besov classes $B{B}_{p,\tau }^s\left(\mathsf{\Omega }\right)$.

Theorem 12.

Let $1<p,q<\infty$, $1\le \tau \le \infty$, $0<\alpha \le 1$, and $s>d{\left({\displaystyle \frac{1}{p}}-{\displaystyle \frac{1}{q}}\right)}_{+}$. Then, there exist $M>0$, $\lambda >1$ such that for ${\gamma }_n=M{\lambda }^n$,

$${\delta }_n^{{\gamma }_n,\alpha }{\left(B{B}_{p,\tau }^s\left(\mathsf{\Omega }\right)\right)}_{L_q}\asymp \mathrm{dist}{\left(B{B}_{p,\tau }^s\left(\mathsf{\Omega }\right),{\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}\right)}_{L_q}\asymp n^{-2s/d}.$$

The proof of Theorem 12 is similar to that of Theorem 11, so we omit the details here.

Note that any numerical algorithm based on Hölder mappings will have a convergence rate that is not faster than that of the Hölder width. This characterizes the limitation of the approximation power of some deep neural networks.

Meanwhile, it is well known that spherical approximation has been widely applied in many fields, such as cosmic microwave background analysis, global ionospheric prediction for geomagnetic storms, climate change modeling, environmental governance, and other spherical signals [39].

We recall some concepts on the sphere from [40]. Let

$${\mathbb{S}}^{d-1}:=\left\{x=(x_1,\cdots ,x_d)\in {\mathbb{R}}^d:\sum _{j=1}^d{x}_j^2=1\right\}$$

be the unit sphere in ${\mathbb{R}}^d$ equipped with the rotation-invariant measure $\mathrm{d}\mu \left(x\right)$ normalized by ${\int }_{{\mathbb{S}}^{d-1}}\mathrm{d}\mu \left(x\right)=1$. For $1\le p<\infty$, denote by $L_p\left({\mathbb{S}}^{d-1}\right)$ the usual Lebesgue space on ${\mathbb{S}}^{d-1}$ endowed with the $L_p$ norm

$${\parallel f\parallel }_{L_p\left({\mathbb{S}}^{d-1}\right)}:={\left({\int }_{{\mathbb{S}}^{d-1}}{\left|f\left(x\right)\right|}^p\mathrm{d}\mu \left(x\right)\right)}^{1/p}\mathrm{for}1\le p<\infty .$$

In [41], Feng et al. studied the approximation of the Sobolev class on the sphere ${\mathbb{S}}^{d-1}$, denoted by $W_p^s\left({\mathbb{S}}^{d-1}\right)$, using convolutional neural networks with layer J. Recall that a function f belongs to the Sobolev class $W_p^s\left({\mathbb{S}}^{d-1}\right)$ if $f\in L_p\left({\mathbb{S}}^{d-1}\right)$, and the norm ${\parallel ·\parallel }_{W_p^s\left({\mathbb{S}}^{d-1}\right)}$ of f is given by

$${\parallel f\parallel }_{W_p^s\left({\mathbb{S}}^{d-1}\right)}:={\parallel f\parallel }_{L_p\left({\mathbb{S}}^{d-1}\right)}+\parallel {(-{▵}_0)}^{s/2}f{\parallel }_{L_p\left({\mathbb{S}}^{d-1}\right)}<\infty ,$$

where ${▵}_0$ is the Laplace–Beltrami operator on the sphere. The authors obtained the upper bound $\mathcal{O}\left(J^{-{\displaystyle \frac{s}{d-1}}}\right)$ of the error of such an approximation in $L_p\left({\mathbb{S}}^{d-1}\right)$.

However, it is known from [42] that when $s>(d-1){(1/p-1/q)}_{+}$, $1<p,q<\infty$

$${\epsilon }_n{\left(B{W}_p^s\left({\mathbb{S}}^{d-1}\right)\right)}_{L_q}\asymp n^{-{\displaystyle \frac{s}{d-1}}}.$$

Then, it follows from Corollary 4 that the lower bound of the Hölder width for $B{W}_p^s\left({\mathbb{S}}^{d-1}\right)$ may be $\mathcal{O}\left(n^{-{\displaystyle \frac{2s}{d-1}}}\right)$.

Theorem 13.

Let $1<p,q<\infty$, $0<\alpha \le 1$, and $s>(d-1){\left({\displaystyle \frac{1}{p}}-{\displaystyle \frac{1}{q}}\right)}_{+}$. Then, there exist $M>0$, $\lambda >1$ such that for ${\gamma }_n=M{\lambda }^n$,

$$\mathrm{dist}{\left(B{W}_p^s\left({\mathbb{S}}^{d-1}\right),{\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}\right)}_{L_q}\gg {\delta }_n^{{\gamma }_n,\alpha }{\left(B{W}_p^s\left({\mathbb{S}}^{d-1}\right)\right)}_{L_q}\gg n^{-{\displaystyle \frac{2s}{d-1}}}.$$

With the development of spherical theory [40,43,44,45] and the relationship between Hölder widths and entropy numbers, we conjecture that the approximation order of $W_p^s\left({\mathbb{S}}^{d-1}\right)$ using some fully connected feed-forward neural networks with the bit-extraction technique may be $\mathcal{O}(n^{-{\displaystyle \frac{2s}{d-1}}})$. This conjecture can be formulated as follows.

Conjecture 1.

Let $1<p,q<\infty$, $0<\alpha \le 1$, and $s>(d-1){\left({\displaystyle \frac{1}{p}}-{\displaystyle \frac{1}{q}}\right)}_{+}$. Then, there exist $M>0$, $\lambda >1$ such that for ${\gamma }_n=M{\lambda }^n$,

$${\delta }_n^{{\gamma }_n,\alpha }{\left(B{W}_p^s\left({\mathbb{S}}^{d-1}\right)\right)}_{L_q}\asymp \mathrm{dist}{\left(B{W}_p^s\left({\mathbb{S}}^{d-1}\right),{\mathsf{\Sigma }}_{n,{\sigma }^{\prime }}\right)}_{L_q}\asymp n^{-{\displaystyle \frac{2s}{d-1}}}.$$

Our results show that networks modeled by both Hölder and Lipschitz (e.g., ReLU) functions can achieve the approximation error $\mathcal{O}\left(n^{-2s/d}\right)$, which is superior to classical approximation tools such as $n$-term wavelets and adaptive finite elements. We achieve the same approximation error for networks with a weaker condition, $0<\alpha <1$, which gives us more options for neural network approximation tools. For example, if we need to solve numerically differential equations with a discontinuous right-hand side modeling neural network dynamics, we can choose networks with non-Lipschitz activation functions, using the fact that non-Lipschitz functions share the peculiar property that even small variations in the neuron state are able to produce significant changes in the neuron output [26,27,28]. The results of the Hölder widths would help us select suitable Hölder activation functions. Moreover, it is known from Appendix B.2 that the Hölder width is smaller than the Lipschitz width in the sense that

$${\delta }_n^{2\gamma ,\alpha }{\left(K\right)}_X\le {\delta }_n^{\gamma ,1}{\left(K\right)}_X.$$

Thus, from the perspective of the approximation error, the Hölder activation function performs better than the Lipschitz activation function. However, it is currently unknown what magnitude this improvement can reach. It would be interesting to study this problem.

Next, we estimate the Hölder widths for discrete Lebesgue spaces. For $1\le q<\infty$, denote by ${\ell }_q$ the set of all sequences ${\left\{x_k\right\}}_{k=1}^{\infty }$ with

$$\begin{array}{c}\hfill {\parallel x\parallel }_q:={\left(\sum _{k=1}^{\infty }{\left|x_k\right|}^q\right)}^{1/q}<\infty .\end{array}$$

Let $\tau ={\left\{t_k\right\}}_{k=1}^{\infty }$ be a sequence such that $t_k={\left({log}_2(k+1)\right)}^{-1/2}$ for $k\ge 1$. Denote by

$${\mathcal{A}}_{\tau }:=\left\{y\in {\ell }_2:y_k=t_k{x}_k,\mathrm{where}\sum _{j=1}^{\infty }\left|x_k\right|\le 1\right\},$$

where $x=(x_1,x_2,\cdots )\in {\ell }_1$, and $y=(y_1,y_2,\cdots )\in {\ell }_2$.

Theorem 14.

For the space $X={\ell }_2$ and the subset ${\mathcal{A}}_{\tau }$, its Hölder width satisfies $\gamma \ge 2·\mathrm{rad}\left({\mathcal{A}}_{\tau }\right)$ and $0<\alpha <1$,

$${\left(logn\right)}^{-1/2}{n}^{-1/2}\ll {\delta }_n^{\gamma ,\alpha }{\left({\mathcal{A}}_{\tau }\right)}_X\ll n^{-1/2}.$$

Proof. 

It is known from [46] that its entropy number satisfies

$${\epsilon }_n{\left({\mathcal{A}}_{\tau }\right)}_{{\ell }_2}\asymp n^{-1/2}.$$

It follows from Corollary 2 that there exists $C_1>0$ such that its Hölder width satisfies $\gamma \ge 2·\mathrm{rad}\left({\mathcal{A}}_{\tau }\right)$,

$${\delta }_n^{\gamma ,\alpha }{\left({\mathcal{A}}_{\tau }\right)}_{{\ell }_2}\le C_1{n}^{-1/2}.$$

It follows from Theorem 9 (i) that there exists $C_2>0$ such that its Hölder width satisfies

$${\delta }_n^{\gamma ,\alpha }{\left({\mathcal{A}}_{\tau }\right)}_{{\ell }_2}\ge C_2{\left(logn\right)}^{-1/2}{n}^{-1/2}.$$

The proof of Theorem 14 is completed. □

Remark 7.

It is known from [18] that its $n$-Kolmogorov width satisfies

$$d_n{\left({\mathcal{A}}_{\tau }\right)}_{{\ell }_2}\asymp {\left({log}_{2}n\right)}^{-1/2}.$$

Theorem 14 illustrates that the Hölder width of ${\mathcal{A}}_{\tau }$ is smaller than that of the $n$-Kolmogorov width.

Finally, we obtain the asymptotic order of the Hölder width for ${\mathbf{c}}_{\mathbf{0}}$, which is the Banach space of all sequences converging to 0, equipped with the ${\ell }_{\infty }$ norm. Let $\eta ={\left\{{\eta }_k\right\}}_{k=1}^{\infty }$ be a sequence with ${\eta }_k={\left({log}_2(k+1)\right)}^{-1}$, $k\ge 1$. Denote a compact subset of X by

$${\mathcal{K}}_{\eta }:={\left\{{\eta }_k{e}_k\right\}}_{k=1}^{\infty }\cup \left\{0\right\},$$

where the sequence ${\left\{e_k\right\}}_{k=1}^{\infty }$ is the standard basis in X. It is known from [18] that its entropy number satisfies

$${\epsilon }_n{\left({\mathcal{K}}_{\eta }\right)}_X\asymp {\displaystyle \frac{1}{n}}.$$

Theorem 15.

For the space $X={\mathbf{c}}_{\mathbf{0}}$ and the subset ${\mathcal{K}}_{\eta }$, we obtain that its Hölder width satisfies $\gamma >2$, $0<\alpha <1$,

$${\delta }_n^{\gamma ,\alpha }{\left({\mathcal{K}}_{\eta }\right)}_X\asymp {\displaystyle \frac{1}{n{log}_2(n+1)}}.$$

Theorem 15 shows the sharpness of Theorem 9 (i).

6. Concluding Remarks

We introduce the Hölder width, which measures the best error performance of some recent nonlinear approximation methods. We investigate the relationship between Hölder widths and other known widths, demonstrating that some Hölder widths are essentially smaller than $n$-Kolmogorov widths and linear widths. Moreover, we obtain that as the Hölder constants grow with n, the Hölder widths are much smaller than the entropy numbers. The significance of Hölder widths being smaller than known widths is that it implies that some nonlinear approximations, such as deep neural network approximations, may yield a better approximation order than other known classical approximation methods. In fact, we show that the asymptotic orders of Hölder widths for the Sobolev classes $B{W}_p^s\left(\mathsf{\Omega }\right)$ and the Besov classes $B{B}_{p,\tau }^s\left(\mathsf{\Omega }\right)$ are $\mathcal{O}\left(n^{-2s/d}\right)$ for $s>d{\left({\displaystyle \frac{1}{p}}-{\displaystyle \frac{1}{q}}\right)}_{+}$ using deep neural networks, while other known widths might be $\mathcal{O}\left(n^{-s/d}\right)$. This result shows that deep neural networks significantly outperform classical methods of approximation, such as adaptive finite elements and $n$-term wavelet approximation. Indeed, the Hölder width in neural networks serves two purposes. On the one hand, it demonstrates the superior approximation power of deep neural networks. On the other hand, it reveals the limitation in the approximating ability of some deep neural networks. These features are crucial for a deeper understanding and further exploration of the approximation power of deep neural networks. It would be interesting to calculate the Hölder widths for some important function classes.

Appendix A.1. Proof of Theorem 1

To prove Theorem 1, we need the following lemmas.

Lemma A1

(Auerbach lemma [47,48]). Let $X_n$ be an $n$-dimensional Banach space and $X_n^{*}$ be its dual space. Then, there exist elements $x_1,\cdots ,x_n\in X_n$ and functionals $f_1,\cdots ,f_n\in X_n^{*}$ such that for $1\le i,j\le n$,

$$\parallel x_j{\parallel }_{X_n}={\parallel f_j\parallel }_{X_n^{*}}=1,\mathrm{and}{f}_j\left(x_i\right)=\left\{\begin{array}{c}\hfill 1,i=j,\\ \hfill 0,i\ne j.\end{array}\right.$$

Lemma A2.

Let K be a bounded subset of X. For any $n\in \mathbb{N}$, $\gamma >0$, and $0<\alpha <1$, we can limit the infimum in (2) to normed spaces $({\mathbb{R}}^n,\parallel ·{\parallel }_{{\mathcal{Z}}_n})$ with the norm ${\parallel ·\parallel }_{{\mathcal{Z}}_n}$ satisfying, for $y\in {\mathbb{R}}^n$,

$${\parallel y\parallel }_{{\ell }_{\infty }^n}\le {\parallel y\parallel }_{{\mathcal{Z}}_n}\le {\parallel y\parallel }_{{\ell }_1^n}.$$

(A1)

Proof. 

According to Lemma A1, we can find vectors ${\left\{v_j\right\}}_{j=1}^n\subset {\mathbb{R}}^n$ and linear functionals ${\left\{f_j\right\}}_{j=1}^n$ on the space (${\mathbb{R}}^n$, ${\parallel ·\parallel }_{Y_n}$) satisfying

$$\parallel v_j{\parallel }_{Y_n}={\parallel f_j\parallel }_{Y_n^{*}}=1,\mathrm{and}{f}_i\left(v_j\right)=\left\{\begin{array}{c}\hfill 1,i=j,\\ \hfill 0,i\ne j,\end{array}\right.$$

(A2)

where $Y_n^{*}$ is the dual space of $Y_n$ and $i,j=1.\cdots ,n$.

For $y=(y_1,y_2,\cdots ,y_n)\in {\mathbb{R}}^n$, we can consider a new norm ${\parallel ·\parallel }_{{\mathcal{Z}}_n}$ on ${\mathbb{R}}^n$ and a mapping ${\varphi }_0:(B\left({\mathcal{Z}}_n\right){,\parallel ·\parallel }_{{\mathcal{Z}}_n})\to (B\left(Y_n\right){,\parallel ·\parallel }_{Y_n})$ as

$${\parallel y\parallel }_{{\mathcal{Z}}_n}:={∥\sum _{j=1}^n{y}_j{v}_j∥}_{Y_n},\mathrm{and}{\varphi }_0\left(y\right):=\sum _{j=1}^n{y}_j{v}_j.$$

(A3)

It is clear that ${\varphi }_0\left(B\left({\mathcal{Z}}_n\right)\right)=B\left(Y_n\right)$.

In this case, we can construct an $H_{\alpha }\left(\gamma \right)$ mapping ${\tilde{\mathsf{\Phi }}}_n:\left(B\left({\mathcal{Z}}_n\right),{\parallel ·\parallel }_{{\mathcal{Z}}_n}\right)\to X$. For any $H_{\alpha }\left(\gamma \right)$ mapping ${\mathsf{\Phi }}_n:(B\left(Y_n\right){,\parallel ·\parallel }_{Y_n})\to X$, we can define ${\tilde{\mathsf{\Phi }}}_n$ as ${\tilde{\mathsf{\Phi }}}_n:={\mathsf{\Phi }}_n\circ {\varphi }_0$. Then,

$$\parallel {\tilde{\mathsf{\Phi }}}_n\left(y^{\prime }\right)-{\tilde{\mathsf{\Phi }}}_n\left(y\right){\parallel }_X=\parallel {\mathsf{\Phi }}_n\circ {\varphi }_0\left(y^{\prime }\right)-{\mathsf{\Phi }}_n\circ {\varphi }_0\left(y\right){\parallel }_X\le \gamma {\parallel {\varphi }_0\left(y^{\prime }\right)-{\varphi }_0\left(y\right)\parallel }_{Y_n}^{\alpha }.$$

By (A2) and (A3),

$$\parallel {\tilde{\mathsf{\Phi }}}_n\left(y^{\prime }\right)-{\tilde{\mathsf{\Phi }}}_n\left(y\right){\parallel }_X\le \gamma {∥\sum _{j=1}^n\left(y_j^{\prime }-y_j\right)v_j∥}_{Y_n}^{\alpha }=\gamma {\parallel y_j^{\prime }-y_j\parallel }_{{\mathcal{Z}}_n}^{\alpha }.$$

Therefore, ${\tilde{\mathsf{\Phi }}}_n$ satisfies the $H_{\alpha }\left(\gamma \right)$ condition, and ${\tilde{\mathsf{\Phi }}}_n\left(B\left({\mathcal{Z}}_n\right)\right)={\mathsf{\Phi }}_n\left(B\left(Y_n\right)\right)$.

Moreover, we can verify that the construction (A3) satisfies the condition (A1). Indeed,

$${\parallel y\parallel }_{{\mathcal{Z}}_n}\le \sum _{j=1}^n\left|y_j\right|{∥v_j∥}_{Y_n}=\sum _{j=1}^n\left|y_j\right|={\parallel y\parallel }_{{\ell }_1^n},$$

and for $f_i\in Y_n^{*}$,

$${\parallel y\parallel }_{{\mathcal{Z}}_n}={∥\sum _{j=1}^n{y}_j{v}_j∥}_{Y_n}=\underset{{∥f∥}_{Y_n^{*}}=1}{sup}\left|f\left(\sum _{j=1}^n{y}_j{v}_j\right)\right|\ge \left|f_i\left(\sum _{j=1}^n{y}_j{v}_j\right)\right|=\left|y_i\right|,i=1,\cdots ,n.$$

Then, ${\parallel y\parallel }_{{\mathcal{Z}}_n}\ge \underset{i}{max}|y_i{|=\parallel y\parallel }_{{\ell }_{\infty }^n}$. Thus, the proof of Lemma A2 is completed. □

We also need the following $\alpha$-Hölder version of Ascoli’s theorem.

Lemma A3.

For a separable metric space $(Z,\rho )$ and a metric space $(Y,d)$ where every closed ball is compact, let ${\mathsf{\Psi }}_j:Y\to Z$ be a sequence of α-Hölder mappings such that there exist $y\in Y$ and $z\in Z$ satisfying ${\mathsf{\Psi }}_j\left(y\right)=z$ for $j\ge 1$. Then, there exists a subsequence ${\left\{{\mathsf{\Psi }}_{j_k}\right\}}_{k=1}^{\infty }$, which converges pointwise to an α-Hölder function $\mathsf{\Phi }:Y\to Z$. If $(Y,d)$ is also compact, then the convergence is uniform.

Proof. 

For $f\in Y$, we have

$$\rho \left({\mathsf{\Psi }}_j\left(f\right),z\right)=\rho \left({\mathsf{\Psi }}_j\left(f\right),{\mathsf{\Psi }}_j\left(y\right)\right)\le \gamma d^{\alpha }\left(f,y\right).$$

Fix a countable dense subset $\mathcal{M}={\left\{f_j\right\}}_{j=1}^{\infty }\in Y$, and define $B_j:=B\left(z,\gamma d^{\alpha }(f_j,y)\right)$ as the closed ball in Z with radius $\gamma d^{\alpha }(f_j,y)$ centered at z for $j\ge 1$. It follows that the Cartesian product

$$\mathcal{B}:=B_1\times B_2\times \cdots ,$$

is a compact metric space under the product topology.

Let

$${\mathcal{F}}_n:=\{{\mathsf{\Psi }}_n\left(f_1\right),{\mathsf{\Psi }}_n\left(f_2\right),\cdots ,{\mathsf{\Psi }}_n\left(f_j\right),\cdots \}\in \mathcal{B}.$$

Then, there exists a subsequence ${\left\{{\mathcal{F}}_{n_s}\right\}}_{s=1}^{\infty }$ and an element $\mathcal{F}\in \mathcal{B}$ such that

$$\mathcal{F}\left(j\right)=\underset{s\to \infty }{lim}{\mathcal{F}}_{n_s}\left(j\right)=\underset{s\to \infty }{lim}{\mathsf{\Psi }}_{n_s}\left(f_j\right),j=1,2,\cdots .$$

Thus, we obtain a function $\mathsf{\Phi }:\mathcal{M}\to Z$ satisfying

$$\mathsf{\Phi }\left(f_j\right)=\mathcal{F}\left(j\right)=\underset{s\to \infty }{lim}{\mathsf{\Psi }}_{n_s}\left(f_j\right),$$

where $\rho (\mathsf{\Phi }\left(f_j\right),\mathsf{\Phi }\left(f_i\right))\le \gamma d^{\alpha }(f_j,f_i)$ for i, $j\ge 1$. Since $\mathcal{M}$ is dense, $\mathsf{\Phi }$ can extend to an $\alpha$-Hölder function on Y, that is, $\mathsf{\Phi }:Y\to Z$. Furthermore, for every $f\in Y$, $\mathsf{\Phi }\left(f\right)=\underset{s\to \infty }{lim}{\mathsf{\Psi }}_{n_s}\left(f\right),$ which implies that ${\mathsf{\Psi }}_{n_s}$ is pointwise convergent to $\mathsf{\Phi }$.

If $(Y,d)$ is compact, then for $\epsilon >0$, we can cover Y by a finite number of ${\epsilon }^{{\displaystyle \frac{1}{\alpha }}}$-balls with centers $g_1,\cdots g_k\in Y$. Thus, for sufficiently large s, we have

$$\begin{array}{cc}\hfill \underset{f\in Y}{sup}\rho ({\mathsf{\Psi }}_{n_s}\left(f\right),\mathsf{\Phi }\left(f\right))& \le \underset{f\in Y}{sup}\rho ({\mathsf{\Psi }}_{n_s}\left(f\right),{\mathsf{\Psi }}_{n_s}\left(g_i\right))+\rho ({\mathsf{\Psi }}_{n_s}\left(g_i\right),\mathsf{\Phi }\left(g_i\right))+\underset{f\in Y}{sup}\rho (\mathsf{\Phi }\left(g_i\right),\mathsf{\Phi }\left(f\right))\hfill \\ \hfill & \le 2\gamma \epsilon +\underset{i=1,\cdots ,n}{max}\rho ({\mathsf{\Psi }}_{n_s}\left(g_i\right),\mathsf{\Phi }\left(g_i\right))\hfill \\ \hfill & \le (2\gamma +1)\epsilon ,\hfill \end{array}$$

which implies that the convergence is uniform. The proof of Lemma A3 is completed. □

Now, we are ready to prove all theorems in this section.

Proof of Theorem 1.

By (1) and (2), it is obvious that for any $n$-dimensional space Y with a norm ${\parallel ·\parallel }_Y$ on ${\mathbb{R}}^n$,

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le {\delta }_n^{\gamma ,\alpha }{(K,Y)}_X.$$

Thus, we only need to prove that

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\ge {\delta }_n^{\gamma ,\alpha }{(K,Y)}_X.$$

By Lemma A2, we can find a sequence ${\left\{{\mathsf{\Psi }}_j\right\}}_{j=1}^{\infty }$, where ${\mathsf{\Psi }}_j:(B\left(Z_j\right){,\parallel ·\parallel }_{Z_j})\to X$ satisfies the $H_{\alpha }\left(\gamma \right)$ condition and the norm ${\parallel ·\parallel }_{Z_j}$ on ${\mathbb{R}}^n$ satisfies (5), such that

$$d_j:=\underset{f\in K}{sup}\underset{y\in B\left(Z_j\right)}{inf}{\parallel f-{\mathsf{\Psi }}_j\left(y\right)\parallel }_X\to {\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X,\mathrm{as}j\to \infty .$$

According to Lemma A3, there exists a subsequence ${\parallel ·\parallel }_{Z_{j_k}}$ of the sequence of norms ${\parallel ·\parallel }_{Z_j}$ that converges pointwise on ${\mathbb{R}}^n$ and uniformly on $B_{{\ell }_{\infty }^n}$ to a norm ${\parallel ·\parallel }_Y$ on ${\mathbb{R}}^n$ satisfying (5).

Thus, there exists a number $j_0\in \mathbb{N}$ such that for every $j\ge j_0$, there is a corresponding value ${\epsilon }_j$ with $0<{\epsilon }_j<1$, $\underset{j\to \infty }{lim}{\epsilon }_j=0$ and

$${\parallel y\parallel }_{Z_j}-{\epsilon }_j\le {\parallel y\parallel }_Y\le {\parallel y\parallel }_{Z_j}+{\epsilon }_j,\mathrm{for}\mathrm{all}{\parallel y\parallel }_{{\ell }_{\infty }^n}\le 1.$$

(A4)

If $y\in (1-{\epsilon }_j)B\left(Z_j\right)$, then we have ${\parallel y\parallel }_{Z_j}\le 1-{\epsilon }_j$ and ${\parallel y\parallel }_Y\le 1-{\epsilon }_j+{\epsilon }_j\le 1.$ And if $y\in B\left(Y\right)$, then we have ${\parallel y\parallel }_{Z_j}\le 1+{\epsilon }_j$. Thus,

$$(1-{\epsilon }_j)B\left(Z_j\right)\subset B\left(Y\right)\subset (1+{\epsilon }_j)B\left(Z_j\right),j\ge j_0.$$

Next, we define the mapping ${\tilde{\mathsf{\Psi }}}_j:(1+{\epsilon }_j)B\left(Z_j\right)\to X$ as

$${\tilde{\mathsf{\Psi }}}_j:={\mathsf{\Psi }}_j\left({(1+{\epsilon }_j)}^{-1}y\right).$$

For any $y,y^{\prime }\in (1+{\epsilon }_j)B\left(Z_j\right)$, we have

$$\begin{array}{cc}\hfill \parallel {\tilde{\mathsf{\Psi }}}_j\left(y^{\prime }\right)-{\tilde{\mathsf{\Psi }}}_j\left(y\right){\parallel }_X& =\parallel {\mathsf{\Psi }}_j\left({(1+{\epsilon }_j)}^{-1}y\right)-{\mathsf{\Psi }}_j\left({(1+{\epsilon }_j)}^{-1}{y}^{\prime }\right){\parallel }_X\hfill \\ \hfill & \le {\displaystyle \frac{\gamma }{{\left(1+{\epsilon }_j\right)}^{\alpha }}}{\parallel y^{\prime }-y\parallel }_{Z_j}^{\alpha }\hfill \\ \hfill & <\gamma \parallel y^{\prime }{-y\parallel }_{Z_j}^{\alpha },\hfill \end{array}$$

so ${\tilde{\mathsf{\Psi }}}_j$ also satisfies the $H_{\alpha }\left(\gamma \right)$ condition. We could write ${\mathsf{\Phi }}_j$ as the restriction of ${\tilde{\mathsf{\Psi }}}_j$ on $B\left(Y\right)$.

Let $f\in K$ and $j\ge j_0$. Then, for each $\theta >0$, we can find an element $y=y(f,j,\theta )\in B\left(Z_j\right)$ such that $\parallel f-{\mathsf{\Psi }}_j{\left(y\right)\parallel }_X<d_j+\theta$. Taking

$$z:=(1-{\epsilon }_j)y\in (1-{\epsilon }_j)B\left(Z_j\right)\subset B\left(Y\right),$$

we have

$$\begin{array}{cc}\hfill \underset{x\in B_Y}{inf}{\parallel f-{\mathsf{\Phi }}_j\left(x\right)\parallel }_X& \le \parallel f-{\mathsf{\Phi }}_j{\left(z\right)\parallel }_X={\parallel f-{\tilde{\mathsf{\Psi }}}_j\left(z\right)\parallel }_X\hfill \\ \hfill & =\parallel f-{\mathsf{\Psi }}_j\left({(1+{\epsilon }_j)}^{-1}z\right){\parallel }_X={∥f-{\mathsf{\Psi }}_j\left({\displaystyle \frac{1-{\epsilon }_j}{1+{\epsilon }_j}}·y\right)∥}_X\hfill \\ \hfill & \le \parallel f-{\mathsf{\Psi }}_j{\left(y\right)\parallel }_X+{∥{\mathsf{\Psi }}_j\left(y\right)-{\mathsf{\Psi }}_j\left({\displaystyle \frac{1-{\epsilon }_j}{1+{\epsilon }_j}}·y\right)∥}_X\hfill \\ \hfill & <d_j+\theta +\gamma {\left(1-{\displaystyle \frac{1-{\epsilon }_j}{1+{\epsilon }_j}}\right)}^{\alpha }{\parallel y\parallel }_{Z_j}^{\alpha }\hfill \\ \hfill & \le d_j+\theta +\gamma {\left({\displaystyle \frac{2{\epsilon }_j}{1+{\epsilon }_j}}\right)}^{\alpha }.\hfill \end{array}$$

As $\theta \to 0$ and by taking the supremum over $f\in K$, we have

$${\delta }_n^{\gamma ,\alpha }{(K,Y)}_X\le \underset{f\in K}{sup}\underset{x\in B\left(Y\right)}{inf}{\parallel f-{\mathsf{\Phi }}_j\left(x\right)\parallel }_X\le d_j+\gamma {\left({\displaystyle \frac{2{\epsilon }_j}{1+{\epsilon }_j}}\right)}^{\alpha }.$$

As $j\to \infty$, we have $d_j\to {\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$ and ${\epsilon }_j\to 0$. Thus, ${\delta }_n^{\gamma ,\alpha }{(K,Y)}_X\le {\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$.

The proof of Theorem 1 is completed. □

Appendix A.2. Proofs of Theorems 2–4

Proof of Theorem 2.

We begin with the continuity of the Hölder widths ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$ at $\gamma =0$. For any $H_{\alpha }\left(\gamma \right)$ mapping $\mathsf{\Phi }:(B\left(Y_n\right),\parallel ·{\parallel }_{Y_n})\to X$, $f\in K$ and $y\in B\left(Y_n\right)$, we have

$$\begin{array}{cc}\hfill {\parallel f-\mathsf{\Phi }\left(y\right)\parallel }_X& \ge {\parallel f-\mathsf{\Phi }\left(0\right)\parallel }_X-{\parallel \mathsf{\Phi }\left(0\right)-\mathsf{\Phi }\left(y\right)\parallel }_X\hfill \\ \hfill & \ge {\parallel f-\mathsf{\Phi }\left(0\right)\parallel }_X-\gamma {\parallel y\parallel }_{Y_n}^{\alpha }\hfill \\ \hfill & \ge {\parallel f-\mathsf{\Phi }\left(0\right)\parallel }_X-\gamma .\hfill \end{array}$$

Thus, for any $H_{\alpha }\left(\gamma \right)$ mapping $\mathsf{\Phi }$,

$$\underset{f\in K}{sup}\underset{y\in B\left(Y_n\right)}{inf}{\parallel f-\mathsf{\Phi }\left(y\right)\parallel }_X\ge \underset{f\in K}{sup}{\parallel f-\mathsf{\Phi }\left(0\right)\parallel }_X-\gamma \ge \underset{g\in X}{inf}\underset{f\in K}{sup}{\parallel f-g\parallel }_X-\gamma ,$$

which implies that

$${\delta }_n^{\gamma ,\alpha }{(K,Y_n)}_X\ge \underset{g\in X}{inf}\underset{f\in K}{sup}{\parallel f-g\parallel }_X-\gamma .$$

It follows from (3), (4), and the decreasing property of ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$ with respect to $\gamma$ that

$$\mathrm{rad}\left(K\right)-\gamma \le {\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le \mathrm{rad}\left(K\right),$$

which implies that the continuity at $\gamma =0$.

Next, we prove that ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$ is continuous for $\gamma >0$ by contradiction. For convenience, denote by $F\left(\gamma \right):={\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$. We assume that F is not continuous at some ${\gamma }_0>0$. Therefore, there exists ${\xi }_0>0$ and a sequence of real numbers ${\delta }_k\to 0$, $k\ge 1$ such that

$$|F({\gamma }_0+{\delta }_k)-F({\gamma }_0-{\delta }_k)|\ge {\xi }_0.$$

(A5)

It is known from the definition of Hölder widths that for fixed ${\delta }_k$, there exists an $H_{\alpha }({\gamma }_0+{\delta }_k)$ mapping ${\mathsf{\Phi }}_n:(B\left(Y_n\right){,\parallel ·\parallel }_{Y_n})\to X$ such that

$$F({\gamma }_0+{\delta }_k)\le \underset{f\in K}{sup}\underset{y\in B\left(Y_n\right)}{inf}{\parallel f-{\mathsf{\Phi }}_n\left(y\right)\parallel }_X\le F({\gamma }_0+{\delta }_k)+{\delta }_k.$$

Let ${\lambda }_k:={\displaystyle \frac{{\gamma }_0-{\delta }_k}{{\gamma }_0+{\delta }_k}}$, and ${\tilde{\mathsf{\Phi }}}_n:={\lambda }_k{\mathsf{\Phi }}_n.$ Then, ${\tilde{\mathsf{\Phi }}}_n$ is an $H_{\alpha }({\gamma }_0-{\delta }_k)$ mapping, and

$$\begin{array}{cc}\hfill F({\gamma }_0-{\delta }_k)& \le \underset{f\in K}{sup}\underset{y\in B\left(Y_n\right)}{inf}{\parallel f-{\tilde{\mathsf{\Phi }}}_n\left(y\right)\parallel }_X\hfill \\ \hfill & \le \underset{f\in K}{sup}\underset{y\in B\left(Y_n\right)}{inf}\left({\lambda }_k\parallel f-{\mathsf{\Phi }}_n{\left(y\right)\parallel }_X+(1-{\lambda }_k){\parallel f\parallel }_X\right)\hfill \\ \hfill & \le {\lambda }_k(F({\gamma }_0+{\delta }_k)+{\delta }_k)+(1-{\lambda }_k)\underset{f\in K}{sup}{\parallel f\parallel }_X.\hfill \end{array}$$

It follows from the compactness of K and (A5) that

$$F({\gamma }_0+{\delta }_k)+{\xi }_0\le F({\gamma }_0-{\delta }_k)\le {\lambda }_k(F({\gamma }_0+{\delta }_k)+{\delta }_k)+(1-{\lambda }_k)C,$$

where $C:=\underset{f\in K}{sup}{\parallel f\parallel }_X<\infty$. As ${\delta }_k\to 0$, we have ${\lambda }_k\to 0$, and thus $F\left({\gamma }_0\right)+{\xi }_0\le F\left({\gamma }_0\right)$, which contradicts the assumption that ${\xi }_0>0$. Thus, ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X$ is continuous as a function of $\gamma \ge 0$. We complete the proof of Theorem 2. □

Proof of Theorem 3.

If $\underset{\gamma \to 0}{lim}{\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X=0,$ then for any $\delta >0$, there exists a norm ${\parallel ·\parallel }_{Y_n}$ and an $H_{\alpha }\left(\gamma \right)$ mapping ${\mathsf{\Phi }}_n$ such that

$$\underset{f\in K}{sup}\underset{y\in B\left(Y_n\right)}{inf}{\parallel f-{\mathsf{\Phi }}_n\left(y\right)\parallel }_X<{\displaystyle \frac{\delta }{2}}.$$

Thus, for a given $f\in K$, we can find $y_f\in B\left(Y_n\right)$ such that

$$\parallel f-{\mathsf{\Phi }}_n\left(y_f\right){\parallel }_X\le {\displaystyle \frac{\delta }{2}}.$$

For a compact set $B\left(Y_n\right)$, there is a finite collection ${\left\{y_j\right\}}_{j=1}^N\subset B\left(Y_n\right)$ such that

$$B_{Y_n}\subset \bigcup _{j=1}^{N}B\left(y_j,{\left({\displaystyle \frac{\delta }{2\gamma }}\right)}^{1/\alpha }\right).$$

Therefore, for $y_f\in B\left(Y_n\right)$, there exists $j_0\in \{1,\cdots ,N\}$ such that $y_f\in B\left(y_{j_0},{\left({\displaystyle \frac{\delta }{2\gamma }}\right)}^{1/\alpha }\right)$, and

$$\parallel \mathsf{\Phi }\left(y_f\right)-\mathsf{\Phi }\left(y_{j_0}\right){\parallel }_X\le \gamma {\parallel y_f-y_{j_0}\parallel }_{Y_n}^{\alpha }\le {\displaystyle \frac{\delta }{2}}.$$

Thus, for any $f\in K$, there exists $j_0\in \{1,\cdots ,N\}$ such that

$$\parallel f-\mathsf{\Phi }\left(y_{j_0}\right){\parallel }_X\le \parallel f-\mathsf{\Phi }\left(y_f\right){\parallel }_X+{\parallel \mathsf{\Phi }\left(y_f\right)-\mathsf{\Phi }\left(y_{j_0}\right)\parallel }_X\le \delta ,$$

which implies that $K\subset {\bigcup }_{j=1}^{N}B(\mathsf{\Phi }\left(y_j\right),\delta )$. By the arbitrariness of $\delta$, the set K is totally bounded.

If K is totally bounded, then for $\epsilon >0$, we can find a minimal $\delta$-covering ${\left\{f_j\right\}}_{j=1}^{N_{\epsilon }\left(K\right)}$ and a suitable $\gamma >0$ such that

$$\mathrm{diam}K·(N_{\epsilon }\left(K\right)-1)\le 2\gamma ,$$

(A6)

where $\mathrm{diam}K:=\underset{f,g\in K}{sup}{\parallel f-g\parallel }_X$. We only consider the case $n=1$ since ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le {\delta }_1^{\gamma ,\alpha }{\left(K\right)}_X$ for any $n\ge 1$. Set the points in $\left(\right[-1,1],|·\left|\right)$ satisfying

$$t_j:=-1+{\left({\displaystyle \frac{2j-2}{N_{\epsilon }\left(K\right)-1}}\right)}^{{\displaystyle \frac{1}{\alpha }}},j=1,\cdots ,N_{\epsilon }\left(K\right),$$

and the continuous piecewise linear function $\mathsf{\Phi }:\left([-1,1],|·|\right)\to X$ satisfying

$$\mathsf{\Phi }\left(t_j\right):=f_j,j=1,\cdots ,N_{\epsilon }\left(K\right).$$

Thus, it follows from (A6) that for $0<\alpha <1$,

$$\underset{j=1,\cdots ,N_{\epsilon }\left(K\right)-1}{max}{\displaystyle \frac{\parallel f_{j+1}-f_j{\parallel }_X}{|t_{j+1}-t_j{|}^{\alpha }}}\le {\displaystyle \frac{\mathrm{diam}K·(N_{\epsilon }\left(K\right)-1)}{2·{\left|j^{1/\alpha }-{(j-1)}^{1/\alpha }\right|}^{\alpha }}}\le \gamma ,$$

which implies that $\mathsf{\Phi }$ satisfies the $H_{\alpha }\left(\gamma \right)$ condition. Therefore, we have

$$\underset{f\in K}{sup}\underset{y\in [-1,1]}{inf}{\parallel f-\mathsf{\Phi }\left(y\right)\parallel }_X\le \delta ,$$

and thus $\underset{\gamma \to 0}{lim}{\delta }_1^{\gamma ,\alpha }{\left(K\right)}_X=0.$ The proof of Theorem 3 is completed. □

Proof of Theorem 4.

The proof is similar to that of Theorem 3. For any fixed $\eta >0$, there exist $n_0\in \mathbb{N}$ and ${\gamma }_0>0$ such that we can find a norm ${\parallel ·\parallel }_{Y_{n_0}}$ in ${\mathbb{R}}^{n_0}$ and an $H_{\alpha }\left({\gamma }_0\right)$ mapping $\mathsf{\Phi }$ satisfying

$$\underset{f\in K}{sup}\underset{y\in B\left(Y_{n_0}\right)}{inf}{\parallel f-\mathsf{\Phi }\left(y\right)\parallel }_X<{\displaystyle \frac{\eta }{2}}.$$

Since $B\left(Y_{n_0}\right)$ is compact, there is a finite collection ${\left\{y_j\right\}}_{j=1}^N\subset B\left(Y_{n_0}\right)$, which is a ${\left({\displaystyle \frac{\eta }{2{\gamma }_0}}\right)}^{1/\alpha }$-covering of $B\left(Y_{n_0}\right)$. Then, for any $y\in B\left(Y_{n_0}\right)$, we can find $y_{j_0}$, $j_0=\{1,\cdots ,N\}$ such that

$$\parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y_{j_0}\right){\parallel }_X\le {\gamma }_0{\parallel y-y_{j_0}\parallel }_{Y_{n_0}}^{\alpha }\le {\displaystyle \frac{\eta }{2}}.$$

Thus, for any $f\in K$, we can find $y\in B\left(Y_{n_0}\right)$ and $y_{j_0}$, $j=\{1,\cdots ,N\}$ such that

$$\parallel f-\mathsf{\Phi }\left(y_{j_0}\right){\parallel }_X\le \parallel f-\mathsf{\Phi }\left(y\right){\parallel }_X+{\parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y_{j_0}\right)\parallel }_X\le \eta ,$$

which implies that $K\subset {\bigcup }_{j=1}^{N}B(\mathsf{\Phi }\left(y_j\right),\eta )$. The proof of Theorem 4 is completed. □

Appendix B.1. Proofs of Theorem 5 and Corollary 1

Proof of Theorem 5.

We begin with

$$\gamma >{\displaystyle \frac{d_n{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}},\mathrm{and}\eta :=\gamma -{\displaystyle \frac{d_n{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}}>0.$$

Choose a number ${\eta }_1$ such that $0<{\eta }_1<\eta$. Let $X_n$ be an $n$-dimensional linear subspace of X that satisfies the inequality

$$\underset{f\in K}{sup}\underset{g\in X_n}{inf}{\parallel f-g\parallel }_X\le d_n{\left(K\right)}_X+2^{\alpha -1}{\eta }_1.$$

Then, for every $f\in K$, there is an element $h:=h\left(f\right)$ in $X_n$ such that

$${\parallel f-h\parallel }_X\le d_n{\left(K\right)}_X+2^{\alpha -1}{\eta }_1.$$

(A7)

Denote the set of all such elements as

$$\mathcal{M}:=\{h\left(f\right):f\in K\}\subset X_n.$$

Next, fix $f_0\in X$ such that

$$\underset{f\in K}{sup}\parallel f-f_0\parallel \le \mathrm{rad}\left(K\right)+2^{\alpha -1}\eta -2^{\alpha -1}{\eta }_1.$$

Then, for $f\in K$,

$$\begin{array}{cc}\hfill & \parallel h-f_0{\parallel }_X\hfill \\ \hfill & \le {\parallel h\left(f\right)-f\parallel }_X+{\parallel f-f_0\parallel }_X\hfill \\ \hfill & <d_n{\left(K\right)}_X+\mathrm{rad}\left(K\right)+2^{\alpha -1}\eta =2^{\alpha -1}\gamma .\hfill \end{array}$$

Thus, we have

$$\mathrm{rad}\left(\mathcal{M}\right)\le 2^{\alpha -1}\gamma ,\mathrm{and}\mathcal{M}\subset \{g\in X_n:\parallel g-f_0{\parallel }_X\le 2^{\alpha -1}\gamma \}=:B(f_0,2^{\alpha -1}\gamma ).$$

In addition, denote the unit ball in $X_n$ by $B\left(X_n\right)$, which is defined by

$$B\left(X_n\right):=\{g\in X_n{:\parallel g\parallel }_X=1\}.$$

Define the mapping $\mathsf{\Phi }:(B\left(X_n\right),\parallel ·{\parallel }_X)\to X$ such that

$$\mathsf{\Phi }\left(g\right):=f_0+2^{\alpha -1}\gamma g.$$

Then, for $g_1,g_2\in B\left(X_n\right)$,

$$\parallel \mathsf{\Phi }\left(g_1\right)-\mathsf{\Phi }\left(g_2\right){\parallel }_X=2^{\alpha -1}\gamma \parallel g_1-g_2{\parallel }_X\le \gamma {\parallel g_1-g_2\parallel }_X^{\alpha }.$$

Thus, $\mathsf{\Phi }$ satisfies the $H_{\alpha }\left(\gamma \right)$ condition, and $\mathsf{\Phi }\left(B\left(X_n\right)\right)=B(f_0,2^{\alpha -1}\gamma )$.

For $\mathcal{M}\subset \mathsf{\Phi }\left(B\left(X_n\right)\right)$ and (A7), we have

$$\underset{f\in K}{sup}\underset{g\in X_n}{inf}{\parallel f-\mathsf{\Phi }\left(g\right)\parallel }_X\le \underset{f\in K}{sup}\underset{h\in \mathcal{M}}{inf}{\parallel f-h\parallel }_X\le d_n{\left(K\right)}_X+2^{\alpha -1}{\eta }_1.$$

Thus,

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le d_n{\left(K\right)}_X+2^{\alpha -1}{\eta }_1.$$

Let ${\eta }_1\to 0$, then for any $\gamma >{\displaystyle \frac{d_n{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}}$,

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le d_n{\left(K\right)}_X.$$

By Theorem 3 as $\gamma \to {\displaystyle \frac{d_n{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}}$, we complete the proof of Theorem 5. □

Proof of Corollary 1.

For a compact set $K\subset X$, it is known from [2] that the sequence ${\left\{d_n{\left(K\right)}_X\right\}}_{n=1}^{\infty }$ is decreasing and tends to zero. Denote

$${\gamma }_0={\displaystyle \frac{d_{n_0}{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}}.$$

For $\gamma \ge {\gamma }_0$, it follows from Theorem 5 that

$${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\le {\delta }_n^{{\gamma }_0,\alpha }{\left(K\right)}_X.$$

Then, it is clear that Corollary 1 holds true. □

Appendix B.2. Proofs of Theorem 6

To prove Theorem 6, we use a result from [14].

Lemma A4.

For any $n\ge 1$, $N>1$, and any compact set $K\subset X$ with $\underset{f\in K}{sup}{\parallel f\parallel }_X=1$, the following inequalities hold

$${\delta }_{n+1}^{2(N+1)\sqrt{n},1}{\left(K\right)}_X\le d_n{(K,N)}_X,and{\delta }_{n+\lceil {log}_{2}N\rceil }^{6\sqrt{n},1}{\left(K\right)}_X\le d_n{(K,N)}_X.$$

Proof of Theorem 6.

By the definition of ${\delta }_n^{\gamma ,1}{\left(K\right)}_X$, there is an $\epsilon >0$ and a $Lip\gamma$ mapping $\mathsf{\Psi }:(B\left(Y_n\right),\parallel ·{\parallel }_{Y_n})\to X$ satisfying

$$\parallel f-{\mathsf{\Psi }}_n{\left(y\right)\parallel }_X\le {\delta }_n^{\gamma ,1}{(K,Y_n)}_X+\epsilon ,$$

(A8)

where, for any $y,y^{\prime }\in B\left(Y_n\right)$, the mapping $\mathsf{\Psi }$ satisfies

$$\parallel \mathsf{\Psi }\left(y\right)-\mathsf{\Psi }\left(y^{\prime }\right){\parallel }_X\le \gamma {\parallel y-y^{\prime }\parallel }_{Y_n}.$$

Then, we have

$$\parallel \mathsf{\Psi }\left(y\right)-\mathsf{\Psi }\left(y^{\prime }\right){\parallel }_X\le 2^{1-\alpha }\gamma \parallel y-y^{\prime }{\parallel }_{Y_n}^{\alpha }\le 2\gamma {\parallel y-y^{\prime }\parallel }_{Y_n}^{\alpha }.$$

Thus, $\mathsf{\Psi }$ satisfies the $\alpha$-Hölder condition, and $\mathsf{\Psi }$ is an $H_{\alpha }\left(2\gamma \right)$ mapping.

Therefore, it is known from (A8) and the definition of Hölder widths that

$${\delta }_n^{2\gamma ,\alpha }{(K,Y_n)}_X\le \underset{f\in K}{sup}\underset{y\in B\left(Y_n\right)}{inf}{\parallel f-{\mathsf{\Psi }}_n\left(y\right)\parallel }_X\le {\delta }_n^{\gamma ,1}{(K,Y_n)}_X+\epsilon .$$

Taking $\epsilon \to 0$, we obtain

$${\delta }_n^{2\gamma ,\alpha }{\left(K\right)}_X\le {\delta }_n^{\gamma ,1}{\left(K\right)}_X.$$

Thus, by Lemma A4, we complete the proof of Theorem 6. □

Appendix C.1. Proof of Theorem 7

To prove Theorem 7, we recall a result from [22].

Proposition A1

([22]). If Φ satisfies the $H_{{\alpha }_1}\left({\gamma }_1\right)$ condition, and Ψ satisfies the $H_{{\alpha }_1}\left({\gamma }_2\right)$ condition, the composition $\mathsf{\Phi }\circ \mathsf{\Psi }$ satisfies the $H_{{\alpha }_1{\alpha }_2}\left({\gamma }_1{\gamma }_2^{{\alpha }_2}\right)$ condition. In addition, if ${\alpha }_1={\alpha }_2=\alpha$, then $\mathsf{\Phi }+\mathsf{\Psi }$ satisfies the $H_{\alpha }({\gamma }_1+{\gamma }_2)$ condition.

Proof of Theorem 7.

Note that entropy numbers and Hölder widths are invariant in terms of translation, that is, for any $g\in X$,

$${\epsilon }_n{\left(K\right)}_X={\epsilon }_n{(K-g)}_X,{\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X={\delta }_n^{\gamma ,\alpha }{(K-g)}_X.$$

We only need to consider the compact set $K\subset B_X(0,r):={\{g\in X:\parallel g\parallel }_X\le r,\mathrm{where}r>0\}$.

For any $\epsilon >0$, it is known from the definition of Hölder widths that there is an element $g\in X$ satisfying

$$\underset{f\in K}{sup}{\parallel f-g\parallel }_X<\mathrm{rad}\left(K\right)+\epsilon 2^{-k}.$$

Thus, we could set $r=\mathrm{rad}\left(K\right)+\epsilon 2^{-k}$.

Let $\eta >0$ and the set ${\mathcal{S}}_{kn}:=\{h_1,h_2,\cdots h_{2^{kn}}\}\subset K$, satisfying, for any $f\in K$, that there is an element $h_j\in {\mathcal{S}}_{kn}$ such that

$$\parallel f-h_j{\parallel }_X\le {\epsilon }_{kn}{\left(K\right)}_X+\eta .$$

Next, we split the unit ball $(B_n{,\parallel ·\parallel }_{{\ell }_{\infty }^n}{)=[-1,1]}^n\subset {\mathbb{R}}^n$ into $2^{kn}$ non-overlapping open balls ${\mathcal{B}}_j$ with side length $2^{1-k}$. Denote by $y_j$ the center of ${\mathcal{B}}_j$. Let ${\varphi }_j:{\mathbb{R}}^n\to \mathbb{R}$ be the mapping such that

$${\varphi }_j\left(y\right)=max\{0,1-2^k\parallel y_j-y{\parallel }_{{\ell }_{\infty }^n}^{\alpha }\},j=1,\cdots ,2^{kn}.$$

(A9)

It is clear that $z=max\{0,x\}$, $x\in \mathbb{R}$ satisfies the $H_1\left(1\right)$ condition, and $z=x^{\alpha }$, $x\ge 0$ satisfies the $H_{\alpha }\left(1\right)$ condition. Indeed, for a constant $0<\alpha <1$, the function $\zeta \left(t\right):={\displaystyle \frac{{(1+t)}^{\alpha }}{1+t^{\alpha }}}$ on $t\ge 0$ is non-negative and has maximum 1. Set $t={\displaystyle \frac{x_1}{x_2}}$ for any $x_1,x_2>0$. Then, we have

$${\left(1+{\displaystyle \frac{x_1}{x_2}}\right)}^{\alpha }\le 1+{\left({\displaystyle \frac{x_1}{x_2}}\right)}^{\alpha },$$

which implies that $|x_1+x_2{|}^{\alpha }\le x_1^{\alpha }+x_2^{\alpha }$, and thus

$$|x_1^{\alpha }-x_2^{\alpha }|\le |x_1-x_2{|}^{\alpha }.$$

(A10)

So, $z=x^{\alpha }$, $x\ge 0$ satisfies the $H_{\alpha }\left(1\right)$ condition. It follows from Proposition A1 that ${\varphi }_j$ satisfies the $H_{\alpha }\left(2^k\right)$ condition. Denote by $Y=({\mathbb{R}}^n,\parallel ·{\parallel }_{{\ell }_{\infty }^n})$. Let the mapping $\mathsf{\Phi }:Y\to X$ satisfy

$$\mathsf{\Phi }\left(y\right):=\sum _{j=1}^{2^{kn}}{h}_j{\varphi }_j\left(y\right).$$

Then, we prove that $\mathsf{\Phi }$ satisfies the $H_{\alpha }\left(2^{k}r\right)$ condition and $\mathsf{\Phi }\left(y_j\right)=h_j$.

It is known from (A9) that if $y=y_j$, then ${\varphi }_j\left(y\right)=1$, and if $y\notin {\mathcal{B}}_j$, then ${\varphi }_j\left(y\right)=0$. Thus, $\mathsf{\Phi }\left(y_j\right)=h_j$. Moreover, for any $y,y^{\prime }\in Y$, we consider the following three cases.

Case 1: If $y,y^{\prime }\notin B_n$, then $\parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y^{\prime }\right){\parallel }_X=0\le 2^k{max}_j\parallel h_j{\parallel }_X{\parallel y-y^{\prime }\parallel }_Y^{\alpha }$.

Case 2: If $y^{\prime }\notin B_n$ and $y\in B_n$, then there is a $j_0$ such that $y\in {\mathcal{B}}_{j_0}$. Thus,

$$\begin{array}{cc}\hfill & \parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y^{\prime }\right){\parallel }_X={\parallel h_{j_0}{\varphi }_{j_0}\left(y\right)-0\parallel }_X\hfill \\ \hfill & \le \underset{j}{max}{\parallel h_j\parallel }_X·\left|{\varphi }_{j_0}\left(y\right)-{\varphi }_{j_0}\left(y^{\prime }\right)\right|\hfill \\ \hfill & \le 2^k\underset{j}{max}\parallel h_j{\parallel }_X·{\parallel y-y^{\prime }\parallel }_Y^{\alpha }.\hfill \end{array}$$

Case 3: If $y,y^{\prime }\in B_n$, then there exist two numbers $j_0$, $j_1$ such that $y\in {\mathcal{B}}_{j_0}$ and $y^{\prime }\in {\mathcal{B}}_{j_1}$. Therefore,

$$\parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y^{\prime }\right){\parallel }_X\le \underset{j}{max}\parallel h_j{\parallel }_X·|{\varphi }_{j_0}\left(y\right)-{\varphi }_{j_1}\left(y^{\prime }\right)|.$$

(A11)

We divide it into the following cases.

Case 3.1: If $j_0=j_1$, it follows from ${\varphi }_{j_0}$ satisfying the $H_{\alpha }\left(2^k\right)$ condition that

$$\parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y^{\prime }\right){\parallel }_X\le \underset{j}{max}\parallel h_j{\parallel }_X·|{\varphi }_{j_0}\left(y\right)-{\varphi }_{j_0}\left(y^{\prime }\right)|\le 2^k\underset{j}{max}\parallel h_j{\parallel }_X·{\parallel y-y^{\prime }\parallel }_Y^{\alpha }.$$

Case 3.2: If $j_0\ne j_1$, we have

$$|{\varphi }_{j_0}\left(y\right)-{\varphi }_{j_1}\left(y^{\prime }\right)|=2^k·\left|\parallel y_{j_0}{-y\parallel }_{{\ell }_{\infty }^n}^{\alpha }-{\parallel y_{j_1}-y^{\prime }\parallel }_{{\ell }_{\infty }^n}^{\alpha }\right|.$$

(A12)

Due to the arbitrariness of $y,y^{\prime }$ and $j_0,j_1$, we can assume that $\parallel y_{j_0}{-y\parallel }_{{\ell }_{\infty }^n}^{\alpha }\ge {\parallel y_{j_1}-y^{\prime }\parallel }_{{\ell }_{\infty }^n}^{\alpha }$. Then,

$$\begin{array}{cc}\hfill & \left|\parallel y_{j_0}{-y\parallel }_{{\ell }_{\infty }^n}^{\alpha }-{\parallel y_{j_1}-y^{\prime }\parallel }_{{\ell }_{\infty }^n}^{\alpha }\right|\hfill \\ \hfill & =\parallel y_{j_0}{-y\parallel }_{{\ell }_{\infty }^n}^{\alpha }-{\parallel y_{j_1}-y^{\prime }\parallel }_{{\ell }_{\infty }^n}^{\alpha }\hfill \\ \hfill & \le \parallel y_{j_1}{-y\parallel }_{{\ell }_{\infty }^n}^{\alpha }-{\parallel y_{j_1}-y^{\prime }\parallel }_{{\ell }_{\infty }^n}^{\alpha }\hfill \\ \hfill & \le \parallel y-y^{\prime }{\parallel }_{{\ell }_{\infty }^n}^{\alpha },\hfill \end{array}$$

where the last inequality uses (A10). Otherwise,

$$\begin{array}{cc}\hfill \left|\parallel y_{j_0}{-y\parallel }_{{\ell }_{\infty }^n}^{\alpha }-{\parallel y_{j_1}-y^{\prime }\parallel }_{{\ell }_{\infty }^n}^{\alpha }\right|& =\parallel y_{j_1}-y^{\prime }{\parallel }_{{\ell }_{\infty }^n}^{\alpha }-{\parallel y_{j_0}-y\parallel }_{{\ell }_{\infty }^n}^{\alpha }\hfill \\ \hfill & \le \parallel y_{j_0}-y^{\prime }{\parallel }_{{\ell }_{\infty }^n}^{\alpha }-{\parallel y_{j_0}-y\parallel }_{{\ell }_{\infty }^n}^{\alpha }\hfill \\ & \le \parallel y-y^{\prime }{\parallel }_{{\ell }_{\infty }^n}^{\alpha }.\hfill \end{array}$$

Thus, by combining (A11) with (A12), we have

$$\parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y^{\prime }\right){\parallel }_X\le 2^k\underset{j}{max}\parallel h_j{\parallel }_X·{\parallel y-y^{\prime }\parallel }_Y^{\alpha }.$$

Therefore, $\mathsf{\Phi }$ satisfies the $H_{\alpha }\left(2^{k}r\right)$ condition, where $r=\mathrm{rad}\left(K\right)+\epsilon 2^{-k}>\underset{j}{max}{\parallel h_j\parallel }_X$.

Then, we have

$${\delta }_n^{2^{k}r,\alpha }{\left(K\right)}_X={\delta }_n^{2^k\mathrm{rad}\left(K\right)+\epsilon ,\alpha }{\left(K\right)}_X\le {\epsilon }_{kn}{\left(K\right)}_X+\eta .$$

Let $\eta \to 0$ and $\epsilon \to 0$. We obtain

$${\delta }_n^{2^k\mathrm{rad}\left(K\right),\alpha }{\left(K\right)}_X\le {\epsilon }_{kn}{\left(K\right)}_X.$$

We complete the proof of Theorem 7. □

Appendix C.2. Proof of Theorem 8

To prove Theorem 8, we recall some definitions and lemmas.

An $\epsilon$-packing of K is a collection $\{f_1,\cdots ,f_l\}\subset K$, there is

$$\underset{i\ne j}{min}{\parallel f_i-f_j\parallel }_X>\epsilon .$$

The maximal $\epsilon$-packing number $P_{\epsilon }\left(K\right)$ is the cardinality of the largest $\epsilon$-packing of K.

It is known ([3], Chapter 15) that $P_{2\epsilon }\left(K\right)\le N_{\epsilon }\left(K\right)\le P_{\epsilon }\left(K\right)$, and Lemma A5 holds.

Lemma A5

([3]). For the ball $B_r:=\{x\in Y_n{:\parallel x\parallel }_{Y_n}\le r\}$ and $0\le \epsilon \le r$, we have

$$2^{-n}{\left({\displaystyle \frac{r}{\epsilon }}\right)}^n\le P_{\epsilon }\left(B_r\right)\le 3^n{\left({\displaystyle \frac{r}{\epsilon }}\right)}^n,$$

(A13)

and

$$2^{-n}{\left({\displaystyle \frac{r}{\epsilon }}\right)}^n\le N_{\epsilon }\left(B_r\right)\le 3^n{\left({\displaystyle \frac{r}{\epsilon }}\right)}^n,$$

(A14)

Lemma A6.

If ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X<\epsilon$, then

$$\gamma \ge 3^{-\alpha }\epsilon N_{2\epsilon }^{{\displaystyle \frac{\alpha }{n}}}\left(K\right).$$

(A15)

Specifically, if ${\delta }_n^{\gamma ,\alpha }{\left(B_{Z_m}\right)}_X\le \epsilon$, then

$$\gamma \ge 3^{-\alpha }{2}^{-{\displaystyle \frac{2m\alpha }{n}}}{\epsilon }^{1-{\displaystyle \frac{m\alpha }{n}}},$$

where $B_{Z_m}$ is an m-dimensional unit ball of X.

Proof. 

For ${\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X<\epsilon$, there exists an $H_{\alpha }\left(\gamma \right)$ mapping $\mathsf{\Phi }$ and a norm ${\parallel ·\parallel }_{Y_n}$ such that $\mathsf{\Phi }\left(B\left(Y_n\right)\right)$ can approximate K with an accuracy of $\epsilon$. That is, for any $y\in B\left(Y_n\right)$ and $z\in K$,

$${\parallel z-\mathsf{\Phi }\left(y\right)\parallel }_X<\epsilon .$$

Then, we consider a collection $\{y_1,y_2,\cdots ,y_N\}\subset B\left(Y_n\right)$ such that $\{\mathsf{\Phi }\left(y_1\right),\mathsf{\Phi }\left(y_2\right),\cdots ,\mathsf{\Phi }\left(y_N\right)\}$ is a maximal $\epsilon$-packing of ${\mathsf{\Phi }}_{B\left(Y_n\right)}$. By the definition of the maximal packing number and Hölder widths, for any $i\ne j,i,j=1,\cdots ,N$, we obtain

$$\epsilon <\parallel \mathsf{\Phi }\left(y_i\right)-\mathsf{\Phi }\left(y_j\right){\parallel }_X\le \gamma {\parallel y_i-y_j\parallel }_{Y_n}^{\alpha },$$

and thus

$$\parallel y_i-y_j{\parallel }_{Y_n}>{\left({\displaystyle \frac{\epsilon }{\gamma }}\right)}^{{\displaystyle \frac{1}{\alpha }}}.$$

(A16)

In addition, if we add an element $y\in B\left(Y_n\right)$, then the set $\{\mathsf{\Phi }\left(y\right),\mathsf{\Phi }\left(y_1\right),\mathsf{\Phi }\left(y_2\right),\cdots ,\mathsf{\Phi }\left(y_N\right)\}$ is not an $\epsilon$-packing of ${\mathsf{\Phi }}_{B\left(Y_n\right)}$. Therefore, there exists a $j_0\in [1,N]$ satisfying

$$\parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y_{j_0}\right){\parallel }_X<\epsilon ,$$

which implies that

$$\parallel z-\mathsf{\Phi }\left(y_{j_0}\right){\parallel }_X\le \parallel z-\mathsf{\Phi }\left(y\right){\parallel }_X+{\parallel \mathsf{\Phi }\left(y\right)-\mathsf{\Phi }\left(y_{j_0}\right)\parallel }_X<2\epsilon .$$

(A17)

By the definition of the maximal packing number and (A16),

$$N\le P_{{\left(\epsilon {\gamma }^{-1}\right)}^{1/\alpha }}\left(B\left(Y_n\right)\right).$$

Thus, by (A13), we have

$$N\le {\left(3^{\alpha }\gamma {\epsilon }^{-1}\right)}^{{\displaystyle \frac{n}{\alpha }}}.$$

It follows from (A17) that $\{\mathsf{\Phi }\left(y_1\right),\mathsf{\Phi }\left(y_2\right),\cdots ,\mathsf{\Phi }\left(y_N\right)\}$ is a $2\epsilon$-covering of K. Therefore,

$${\left(3^{\alpha }\gamma {\epsilon }^{-1}\right)}^{{\displaystyle \frac{n}{\alpha }}}\ge N\ge N_{2\epsilon }\left(K\right).$$

Then, we obtain

$${\gamma }^{{\displaystyle \frac{n}{\alpha }}}\ge 3^{-n}{\epsilon }^{{\displaystyle \frac{n}{\alpha }}}{N}_{2\epsilon }\left(K\right),$$

(A18)

which means that (A15) holds true.

When $K=B_{Z_m}$, by (A14), we have $N_{2\epsilon }\left(K\right)\ge 2^{-2m}{\epsilon }^{-m}.$ It follows from (A18) that

$$\gamma \ge 3^{-\alpha }\epsilon N_{2\epsilon }^{{\displaystyle \frac{\alpha }{n}}}\left(K\right)\ge 3^{-\alpha }{2}^{-{\displaystyle \frac{2m\alpha }{n}}}{\epsilon }^{1-{\displaystyle \frac{m\alpha }{n}}}.$$

The proof of Lemma A6 is completed. □

Proof of Theorem 8.

By Lemma A6 with $\epsilon =c_0{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}}$, we have

$$\begin{array}{cc}\hfill N_{2\epsilon }\left(K\right)& \le {\left(3^{\alpha }\gamma {\epsilon }^{-1}\right)}^{{\displaystyle \frac{n}{\alpha }}}={\left(3^{\alpha }\gamma c_0^{-1}{\left({log}_{2}n\right)}^{-p}{n}^q\right)}^{{\displaystyle \frac{n}{\alpha }}}\hfill \\ \hfill & \le 2^{{\displaystyle \frac{n}{\alpha }}\{{log}_2\left(3^{\alpha }\gamma c_0^{-1}\right)-p{log}_2\left({log}_{2}n\right)+q{log}_{2}n\}}\hfill \\ \hfill & <2^{c_{1}n{log}_{2}n},\hfill \end{array}$$

where $c_1$ is a constant depending on $\gamma ,\alpha ,c_0,p$, and q. It follows from the definitions of the minimal covering number and entropy number that

$${\epsilon }_{c_{1}n{log}_{2}n}{\left(K\right)}_X\le 2\epsilon =2c_0{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}}.$$

(A19)

If we take $m=c_{1}n{log}_{2}n$, then

$${log}_{2}m={log}_2{c}_1+{log}_{2}n+{log}_2\left({log}_{2}n\right).$$

Thus, for sufficiently large n, we obtain $2^{-1}{log}_{2}n<{log}_{2}m<3{log}_{2}n$. By using (A19) and $n={\displaystyle \frac{m}{c_1{log}_{2}n}}$, we obtain

$${\epsilon }_m{\left(K\right)}_X\le 2c_0{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{{\left(\frac{m}{c_1{log}_{2}n}\right)}^q}}=2c_0{c}_1^q{\displaystyle \frac{{\left({log}_{2}n\right)}^{p+q}}{m^q}}\le C{\displaystyle \frac{{\left({log}_{2}m\right)}^{p+q}}{m^q}}.$$

We complete the proof of Theorem 8. □

Appendix C.3. Proof of Theorem 9

To prove Theorem 9, we need the following lemma.

Lemma A7.

Suppose that the sequence ${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ of real numbers is decreasing to zero. Moreover, if

$${\epsilon }_n\left(K\right)\ge {\eta }_n,n\ge 1,$$

(A20)

and there exist $m\in \mathbb{N}$ and $\theta >0$ satisfying

$${\delta }_m^{\gamma ,\alpha }{\left(K\right)}_X<\theta ,$$

then

$${\eta }_{{\displaystyle \frac{m}{\alpha }}{log}_2\left(3^{\alpha }\gamma {\theta }^{-1}\right)}<2\theta .$$

Proof. 

By using Lemma A6 with $\epsilon =\theta$, we have

$$N_{2\theta }\left(K\right)\le {\left(3^{\alpha }\gamma {\theta }^{-1}\right)}^{{\displaystyle \frac{m}{\alpha }}}=2^{{\displaystyle \frac{m}{\alpha }}{log}_2\left(3^{\alpha }\gamma {\theta }^{-1}\right)}.$$

Then, by the definition of the entropy number and (A20), we obtain

$$2\theta \ge {\epsilon }_{{\alpha }^{-1}m{log}_2\left(3^{\alpha }\gamma {\theta }^{-1}\right)}>{\eta }_{{\alpha }^{-1}m{log}_2\left(3^{\alpha }\gamma {\theta }^{-1}\right)}.$$

The proof of Lemma A7 is completed. □

Proof of Theorem 9.

We prove all statements of the theorem by contradiction.

To prove Theorem 9 (i), we assume that (7) is false, meaning there exists a strictly increasing sequence of integers ${\left\{n_k\right\}}_{k=1}^{\infty }$ such that

$$a_k:={\delta }_{n_k}^{\gamma ,\alpha }{\left(K\right)}_X{n}_k^q{\left({log}_2{n}_k\right)}^{q-p}\to 0,\mathrm{as}k\to \infty .$$

Thus, we have

$${\delta }_{n_k}^{\gamma ,\alpha }{\left(K\right)}_X={\displaystyle \frac{a_k{\left({log}_2{n}_k\right)}^{p-q}}{n_k^q}}\le {\displaystyle \frac{2a_k{\left({log}_2{n}_k\right)}^{p-q}}{n_k^q}}=:{\theta }_k.$$

(A21)

Set ${\eta }_n:=c_1{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}}$. It is known that ${\eta }_n$ is decreasing to zero as $n\to \infty$. Therefore, by Lemma A7,

$${\eta }_{{\alpha }^{-1}{n}_k{log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)}\le 2{\theta }_k.$$

Thus,

$${\alpha }^q{c}_1{\displaystyle \frac{{\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p}{n_k^q{\left[{log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)\right]}^q}}\le {\displaystyle \frac{4a_k{\left({log}_2{n}_k\right)}^{p-q}}{n_k^q}},$$

that is,

$${\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p\le {\displaystyle \frac{4a_k}{c_1{\alpha }^q}}·{\left({log}_2{n}_k\right)}^{p-q}{\left[{log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)\right]}^q.$$

(A22)

It is known that for sufficiently large k, we have

$${log}_2{n}_k<n_k\mathrm{and}{a}_k^{-1}\to \infty .$$

(A23)

Then, by (A21), we have

$$\begin{array}{cc}\hfill {log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)& ={log}_2\left({\displaystyle \frac{3^{\alpha }\gamma n_k^q}{2a_k{\left({log}_2{n}_k\right)}^{p-q}}}\right)\hfill \\ \hfill & <\alpha {log}_{2}1.5\gamma +q{log}_2{n}_k+{log}_2{a}_k^{-1}+(q-p){log}_2\left({log}_2{n}_k\right)\hfill \\ \hfill & \le 2q{log}_2{n}_k+2{log}_2{a}_k^{-1}.\hfill \end{array}$$

(A24)

Thus, by combining (A22) with (A24), we obtain

$$\begin{array}{cc}\hfill {\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p& \le {\displaystyle \frac{2^{q+2}{a}_k}{c_1{\alpha }^q}}{\left({log}_2{n}_k\right)}^{p-q}{\left({log}_2{a}_k^{-1}+q{log}_2{n}_k\right)}^q\hfill \\ \hfill & =C_0{a}_k{\left({log}_2{n}_k\right)}^p{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{{log}_2{n}_k}}+q\right)}^q,\hfill \end{array}$$

(A25)

where $C_0=2^{q+2}{c}_1^{-1}{\alpha }^{-q}$.

Next, we use the property of $y\left(x\right)=x^p,x>0$. When $p<0$, $y\left(x\right)$ is decreasing on $x>0$; when $p>0$, $y\left(x\right)$ is increasing on $x>0$. Then, we divide it into the following three cases.

Case 1: $p=0$. For sufficiently large k, it follows from (A25) and $n_k\to \infty$ that

$$1\le C_0{a}_k{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{{log}_2{n}_k}}+q\right)}^q\le C{a}_k{\left({log}_2{a}_k^{-1}\right)}^q.$$

Therefore, $a_k^{-1}\le C{\left({log}_2{a}_k^{-1}\right)}^q$, which implies that $a_k^{-1}\to 0$, contradicting (A23).

Case 2: $p>0$. For sufficiently large k and $0<\alpha <1$, we have

$${\left({log}_2{n}_k\right)}^p\le {\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p.$$

Then, it follows from (A25) that

$$1\le C_0{a}_k{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{{log}_2{n}_k}}+q\right)}^q\le C{a}_k{\left({log}_2{a}_k^{-1}\right)}^q,$$

which also implies that $a_k^{-1}\to 0$, contradicting (A23).

Case 3: $p<0$. For sufficiently large k and $0<\alpha <1$, by (A23) and (A24), we obtain

$$\begin{array}{cc}\hfill & {\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p\hfill \\ \hfill & >{\left[{log}_2{n}_k+{log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p\hfill \\ \hfill & \ge {\left[2{log}_2{n}_k+{log}_2\left(3^{\alpha }\gamma {\theta }_k^{-1}\right)\right]}^p\hfill \\ \hfill & \ge {\left[(2q+2){log}_2{n}_k+2{log}_2{a}_k^{-1}\right]}^p.\hfill \end{array}$$

Thus, by combining these results with (A25) and multiplying both sides by ${\left({log}_2{n}_k\right)}^{-p}$, we obtain

$${\left[(2q+2)+{\displaystyle \frac{2{log}_2{a}_k^{-1}}{{log}_2{n}_k}}\right]}^p\le C_0{a}_k{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{{log}_2{n}_k}}+q\right)}^q,$$

which implies that

$$a_k^{-1}\le C_0{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{{log}_2{n}_k}}+q\right)}^q{\left[(2q+2)+{\displaystyle \frac{2{log}_2{a}_k^{-1}}{{log}_2{n}_k}}\right]}^{-p}\le C{\left({log}_2{a}_k^{-1}\right)}^{q-p}.$$

Therefore, $a_k^{-1}\to 0$ as $k\to \infty$, which contradicts (A23). We complete the proof of Theorem 9 (i).

To prove Theorem 9 (ii), we assume that (8) is false. Then, there is an increasing sequence of ${\left\{n_k\right\}}_{k=1}^{\infty }$ satisfying, for $q>0$,

$$b_k:={\delta }_{n_k}^{\gamma ,\alpha }{\left(K\right)}_X{\left({log}_2{n}_k\right)}^q\to 0,\mathrm{as}k\to \infty .$$

(A26)

Set ${\eta }_n:=c_1{\left({log}_{2}n\right)}^{-q}$ and

$${\delta }_{n_k}^{\gamma ,\alpha }{\left(K\right)}_X=b_k{\left({log}_2{n}_k\right)}^{-q}\le 2b_k{\left({log}_2{n}_k\right)}^{-q}=:{\zeta }_k.$$

Then by Lemma A7, we have

$${\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }\gamma {\zeta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^{-q}\le 2{\zeta }_k={\displaystyle \frac{4b_k}{c_1}}{\left({log}_2{n}_k\right)}^{-q}.$$

(A27)

When $q>0$, the function $y=x^{-q},x>0$ is decreasing. For sufficiently large k, it follows from (A23) and $0<\alpha <1$ that

$${\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }\gamma {\zeta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^{-q}\ge {\left[2{log}_2{n}_k+{log}_2\left(3^{\alpha }\gamma {\zeta }_k^{-1}\right)\right]}^{-q}.$$

(A28)

Moreover, it is known that

$$\begin{array}{cc}\hfill {log}_2\left(3^{\alpha }\gamma {\zeta }_k^{-1}\right)& ={log}_2\left({\displaystyle \frac{3^{\alpha }\gamma {\left({log}_2{n}_k\right)}^q}{2b_k}}\right)\hfill \\ \hfill & <\alpha {log}_{2}1.5\gamma +{log}_2{b}_k^{-1}+q{log}_2\left({log}_2{n}_k\right)\hfill \\ \hfill & \le q{log}_2{n}_k+2{log}_2{b}_k^{-1}.\hfill \end{array}$$

By combining (A27) with (A28), we obtain

$${\displaystyle \frac{4b_k}{c_1}}{\left({log}_2{n}_k\right)}^{-q}\ge {\left[(q+2){log}_2{n}_k+2{log}_2{b}_k^{-1}\right]}^{-q}.$$

Thus,

$$b_k^{-1}\le {\displaystyle \frac{4}{c_1}}{\left((q+2)+{\displaystyle \frac{2{log}_2{b}_k^{-1}}{{log}_2{n}_k}}\right)}^q\le C{\left({log}_2{b}_k^{-1}\right)}^q,$$

which implies that $b_k^{-1}\to 0$ as $k\to \infty$, contradicting (A26). We complete the proof of Theorem 9 (ii).

Finally, we prove Theorem 9 (iii). The proof is similar to those above. It is known from Corollary 1 that if

$$\gamma \ge {\displaystyle \frac{d_{n_0}{\left(K\right)}_X+\mathrm{rad}\left(K\right)}{2^{\alpha -1}}},$$

then

$${\delta }_n:={\delta }_n^{\gamma ,\alpha }{\left(K\right)}_X\to 0,\mathrm{as}n\to \infty .$$

By using Lemma A7 with $\theta =2{\delta }_{n_k}^{\gamma ,\alpha }{\left(K\right)}_X$ and ${\eta }_n=c_1{2}^{-c_2{n}^p}$, we have

$$c_1{2}^{-c_2{\left[{\displaystyle \frac{n_k}{\alpha }}{log}_2\left(2^{-1}{3}^{\alpha }\gamma {\delta }_{n_k}^{-1}\right)\right]}^p}\le 4{\delta }_{n_k}.$$

(A29)

Taking the logarithm on both sides of (A29), and using the fact that ${\delta }_{n_k}^{-1}\to \infty$ as $k\to \infty$, we have

$${log}_2\left({\displaystyle \frac{c_1}{4}}{\delta }_{n_k}^{-1}\right)\le c_2{\displaystyle \frac{n_k^p}{{\alpha }^p}}{\left[{log}_2\left(2^{-1}{3}^{\alpha }\gamma {\delta }_{n_k}^{-1}\right))\right]}^p,$$

which implies that

$${log}_2\left({\delta }_{n_k}^{-1}\right)\le C{n}_k^p{\left[{log}_2\left({\delta }_{n_k}^{-1}\right)\right]}^p.$$

Thus,

$${log}_2\left({\delta }_{n_k}^{-1}\right)\le C^{{\displaystyle \frac{1}{1-p}}}{n_k}^{{\displaystyle \frac{p}{1-p}}}.$$

Therefore, we obtain

$${\delta }_{n_k}\ge C_1{2}^{-C^{{\displaystyle \frac{1}{1-p}}}{n}_k^{{\displaystyle \frac{p}{1-p}}}}\ge C_1{2}^{-C_2{n}_k^{{\displaystyle \frac{p}{1-p}}}},$$

which contradicts ${\delta }_{n_k}\to 0$ as $k\to \infty$. The proof of Theorem 9 is completed. □

Appendix D.1. Proof of Theorem 10

Proof of Theorem 10.

The proofs are similar to those of Theorem 9. To prove Theorem 10 (i), we assume that (11) is false, that is, there is an increasing sequence of ${\left\{n_k\right\}}_{k=1}^{\infty }$ satisfying

$$a_k:={\delta }_{n_k}^{{\gamma }_{n_k},\alpha }{\left(K\right)}_X{n}_k^{2q}{\left({log}_2{n}_k\right)}^{-p}\to 0,\mathrm{as}k\to \infty .$$

Thus, we have

$${\delta }_{n_k}^{{\gamma }_{n_k},\alpha }{\left(K\right)}_X={\displaystyle \frac{a_k{\left({log}_2{n}_k\right)}^p}{n_k^{2q}}}\le {\displaystyle \frac{2a_k{\left({log}_2{n}_k\right)}^p}{n_k^{2q}}}=:{\theta }_k.$$

(A30)

It follows from Lemma A7 with ${\eta }_n:=c_1{\displaystyle \frac{{\left({log}_{2}n\right)}^p}{n^q}}$ that

$${\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }{\gamma }_{n_k}{\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p\le {\displaystyle \frac{4a_k}{c_1{\alpha }^q}}·{\left({log}_2{n}_k\right)}^p{\left[{log}_2\left(3^{\alpha }{\gamma }_{n_k}{\theta }_k^{-1}\right)\right]}^q{n}_k^{-q}.$$

(A31)

Recall that for sufficiently large k,

$${log}_2{n}_k<n_k\mathrm{and}{a}_k^{-1}\to \infty .$$

(A32)

It is known from (A30) and ${\gamma }_{n_k}=M{\lambda }^{n_k}$ that there exists a constant $C_0>0$ such that

$$\begin{array}{cc}\hfill {log}_2\left(3^{\alpha }{\gamma }_{n_k}{\theta }_k^{-1}\right)& ={log}_2\left({\displaystyle \frac{3^{\alpha }{\gamma }_{n_k}{n}_k^{2q}}{2a_k{\left({log}_2{n}_k\right)}^p}}\right)\hfill \\ \hfill & <\alpha {log}_2(1.5·M{\lambda }^{n_k})+2q{log}_2{n}_k+{log}_2{a}_k^{-1}-p{log}_2\left({log}_2{n}_k\right)\hfill \\ \hfill & \le 2C_0{n}_k+2{log}_2{a}_k^{-1}.\hfill \end{array}$$

(A33)

Thus, by combining (A31) with (A33), we obtain

$$\begin{array}{cc}\hfill {\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }{\gamma }_{n_k}{\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p& \le {\displaystyle \frac{2^{q+2}{a}_k}{c_1{\alpha }^q}}{\left({log}_2{n}_k\right)}^p{\left({log}_2{a}_k^{-1}+C_0{n}_k\right)}^q{n}_k^{-q}\hfill \\ \hfill & =C_1{a}_k{\left({log}_2{n}_k\right)}^p{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{n_k}}+C_0\right)}^q,\hfill \end{array}$$

(A34)

where $C_1=2^{q+2}{c}_1^{-1}{\alpha }^{-q}$. Then, we divide it into the following two cases.

Case 1: $p\ge 0$. For sufficiently large k and $0<\alpha <1$, we have

$${\left({log}_2{n}_k\right)}^p\le {\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }{\gamma }_{n_k}{\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p.$$

It follows from (A34) and $n_k\to \infty$ that

$$1\le C_1{a}_k{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{n_k}}+C_0\right)}^q<C{a}_k{\left({log}_2{a}_k^{-1}\right)}^q.$$

Therefore, $a_k^{-1}\le C{\left({log}_2{a}_k^{-1}\right)}^q$, which implies that $a_k^{-1}\to 0$, contradicting (A32).

Case 2: $p<0$. For sufficiently large k and $0<\alpha <1$, by (A32) and (A33), we obtain

$$\begin{array}{cc}\hfill & {\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }{\gamma }_{n_k}{\theta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^p\ge {\left[2{log}_2{n}_k+{log}_2\left(2C_0{n}_k+2{log}_2{a}_k^{-1}\right)\right]}^p.\hfill \end{array}$$

Thus, by combining these results with (A34) and multiplying both sides by ${\left({log}_2{n}_k\right)}^{-p}$, we obtain

$${\left[2+{\displaystyle \frac{{log}_2\left(2C_0{n}_k+2{log}_2{a}_k^{-1}\right)}{{log}_2{n}_k}}\right]}^p\le C_1{a}_k{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{n_k}}+C_0\right)}^q,$$

which implies that

$$a_k^{-1}\le C_1{\left({\displaystyle \frac{{log}_2{a}_k^{-1}}{n_k}}+C_0\right)}^q{\left[2+{\displaystyle \frac{{log}_2\left(2C_0{n}_k+2{log}_2{a}_k^{-1}\right)}{{log}_2{n}_k}}\right]}^{-p}.$$

(A35)

Case 2.1: If $a_k^{-1}\le c{n}_k$, it follows from (A35) that $a_k^{-1}\le C,$ where c, C are constants, which contradicts (A32).

Case 2.2: If $a_k^{-1}>c{n}_k$, it follows from (A35) that

$$a_k^{-1}\le C{\left({log}_2{a}_k^{-1}\right)}^q{\left({log}_2\left({log}_2{a}_k^{-1}\right)\right)}^{-p}\le C{\left({log}_2{a}_k^{-1}\right)}^{q-p}.$$

Therefore, $a_k^{-1}\to 0$ as $k\to \infty$, which contradicts (A32). We complete the proof of Theorem 10 (i).

To prove Theorem 10 (ii), we assume that (12) is false. Then, there is an increasing sequence of ${\left\{n_k\right\}}_{k=1}^{\infty }$ satisfying, for $q>0$,

$$b_k:={\delta }_{n_k}^{{\gamma }_{n_k},\alpha }{\left(K\right)}_X{\left({log}_2{n}_k\right)}^q\to 0,\mathrm{as}k\to \infty .$$

(A36)

Set ${\eta }_n:=c_1{\left({log}_{2}n\right)}^{-q}$ and

$${\delta }_{n_k}^{{\gamma }_{n_k},\alpha }{\left(K\right)}_X=b_k{\left({log}_2{n}_k\right)}^{-q}\le 2b_k{\left({log}_2{n}_k\right)}^{-q}=:{\zeta }_k.$$

Then, by Lemma A7, we have

$${\left[{log}_2{n}_k+{log}_2\left({log}_2\left(3^{\alpha }{\gamma }_{n_k}{\zeta }_k^{-1}\right)\right)+{log}_2\left({\alpha }^{-1}\right)\right]}^{-q}\le 2{\zeta }_k={\displaystyle \frac{4b_k}{c_1}}{\left({log}_2{n}_k\right)}^{-q}.$$

(A37)

For sufficiently large k, it follows from (A32) and $0<\alpha <1$ that there exists a constant $C_0>0$ such that

$$\begin{array}{c}\hfill {log}_2\left(3^{\alpha }{\gamma }_{n_k}{\zeta }_k^{-1}\right)={log}_2\left({\displaystyle \frac{3^{\alpha }M{\lambda }^{n_k}·{\left({log}_2{n}_k\right)}^q}{2b_k}}\right)<C_0{n}_k+2{log}_2{b}_k^{-1}.\end{array}$$

By combining these results with (A37), we obtain

$${\displaystyle \frac{4b_k}{c_1}}{\left({log}_2{n}_k\right)}^{-q}\ge {\left[2{log}_2{n}_k+{log}_2\left(C_0{n}_k+2{log}_2{b}_k^{-1}\right)\right]}^{-q}.$$

Thus, we obtain

$$b_k^{-1}\le {\displaystyle \frac{4}{c_1}}{\left(2+{\displaystyle \frac{{log}_2\left(C_0{n}_k+2{log}_2{b}_k^{-1}\right)}{{log}_2{n}_k}}\right)}^q.$$

Case 2.1: If $b_k^{-1}\le c{n}_k$, then $b_k^{-1}\le C,$ where c, C are constants, which contradicts (A36).

Case 2.2: If $b_k^{-1}>c{n}_k$, it follows from (A35) that

$$b_k^{-1}\le C{\left({log}_2{b}_k^{-1}\right)}^q.$$

Therefore, $b_k^{-1}\to 0$ as $k\to \infty$, which contradicts (A36). We complete the proof of Theorem 10 (ii). □

Appendix D.2. Proof of Theorem 15

Proof of Theorem 15.

By Theorem 9 (i), it is clear that

$${\delta }_n^{\gamma ,\alpha }{\left({\mathcal{K}}_{\eta }\right)}_X\gg {\displaystyle \frac{1}{n{log}_2(n+1)}}.$$

The proof of the upper bound is similar to the proof in [18]. We give the detailed proof, using the method from the proof of Theorem 7. For $j=1,\cdots ,N$, define $l_j\in \mathbb{N}\cup \left\{0\right\}$ as

$$2^{-l_j-1}<{\displaystyle \frac{2{\eta }_j}{\gamma }}\le 2^{-l_j}.$$

(A38)

Set $N={(n+1)}^n$. We could divide the unit ball ${[-1,1]}^n\subset {\mathbb{R}}^n$ into $k_1$ non-overlapping open balls with side length $2^{-l_{k_1}}$, $(k_2-k_1)$ non-overlapping open balls with side length $2^{-l_{k_2}}$, ⋯, or $(k_s-k_{s-1})$ non-overlapping open balls with side length $2^{-l_{k_s}}$, where $k_s=N$ and

$$l_1=\cdots =l_{k_1}<l_{k_1+1}=\cdots =l_{k_2}<\cdots <l_{k_{s-1}+1}=\cdots =l_{k_s}.$$

Hence, there is a sequence of non-overlapping open balls ${\mathcal{B}}_j\subset {[-1,1]}^n$ with side length $2^{-l_j}$,

$${\mathcal{B}}_j:={\mathcal{B}}_j\left(y_j,2^{-l_j-1}\right),j=1,\cdots ,N.$$

Let ${\varphi }_j:{\mathbb{R}}^n\to \mathbb{R}$ be a mapping such that

$${\varphi }_j\left(y\right)={\eta }_{j}max\{0,1-2^{l_j+1}\parallel y_j-y{\parallel }_{{\ell }_{\infty }^n}^{\alpha }\},j=1,\cdots ,N,$$

and the mapping $\mathsf{\Phi }$ be such that

$$\mathsf{\Phi }\left(y\right):=\sum _{j=1}^N{\varphi }_j\left(y\right)·e_j.$$

It is known from the proof of Theorem 7 and (A38) that $\mathsf{\Phi }$ satisfies the $H_{\alpha }\left(\underset{j=1,\cdots ,N}{sup}\left\{2^{l_j+1}{\eta }_j\right\}\right)$ condition; thus, it satisfies the $H_{\alpha }\left(\gamma \right)$ condition. Moreover, $\mathsf{\Phi }\left(y_j\right)={\eta }_j{e}_j$, $j=1,\cdots ,N$.

For ${\mathcal{K}}_{\eta }={\left\{{\eta }_k{e}_k\right\}}_{k=1}^{\infty }\cup \left\{0\right\}$, by the decreasing property of ${\left\{{\eta }_k\right\}}_{k=1}^{\infty }$, we have

$$\begin{array}{cc}\hfill & \underset{k\ge 1}{sup}\underset{y\in B\left(Y_n\right)}{inf}{\parallel {\eta }_k{e}_k-\mathsf{\Phi }\left(y\right)\parallel }_X\hfill \\ \hfill & \le \underset{k\ge 1}{sup}\underset{j=1,\cdots ,N}{inf}{\parallel {\eta }_k{e}_k-\mathsf{\Phi }\left(y_j\right)\parallel }_{{\ell }_{\infty }^n}\hfill \\ \hfill & =\underset{k\ge 1}{sup}\underset{j=1,\cdots ,N}{inf}{\parallel {\eta }_k{e}_k-{\eta }_j{e}_j\parallel }_{{\ell }_{\infty }^n}\hfill \\ \hfill & ={\eta }_N,\hfill \end{array}$$

and

$$\underset{y\in B\left(Y_n\right)}{inf}{\parallel 0-\mathsf{\Phi }\left(y\right)\parallel }_X\le \underset{j=1,\cdots ,N}{inf}\parallel \mathsf{\Phi }\left(y_j\right){\parallel }_{{\ell }_{\infty }^n}=\underset{j=1,\cdots ,N}{inf}{\parallel {\eta }_j{e}_j\parallel }_{{\ell }_{\infty }^n}={\eta }_N.$$

Thus,

$${\delta }_n^{\gamma ,\alpha }{\left({\mathcal{K}}_{\eta }\right)}_X\le \underset{f\in {\mathcal{K}}_{\eta }}{sup}\underset{y\in B\left(Y_n\right)}{inf}{\parallel f-\mathsf{\Phi }\left(y\right)\parallel }_X\le {\eta }_N<{\displaystyle \frac{1}{n{log}_2(n+1)}}.$$

The proof of Theorem 15 is completed. □