Characterizations of Spatial Quaternionic Partner-Ruled Surfaces

Abstract

In this paper, we investigate the spatial quaternionic expressions of partner-ruled surfaces. Moreover, we formulate the striction curves and dralls of these surfaces by use of the quaternionic product. Furthermore, the pitches and angles of pitches are interpreted for the spatial quaternionic ruled surfaces that are closed. Additionally, we calculate the integral invariants of these surfaces using quaternionic formulas. Finally, the partner-ruled surfaces of a given spatial quaternionic ruled surface are demonstrated as an example, and their graphics are drawn.

1. Introduction

In 1843, William Rowan Hamilton, an Irish mathematician, first introduced the concept of quaternions [1]. Quaternions have since found numerous applications across a wide range of disciplines, including computer graphics, vision device development, animation representations, control theory, molecular dynamics, quantum theory, robot kinematics, and navigation devices. These applications have been extensively considered and documented in various sources, including references [2,3,4,5]. Quaternions have also been applied to the theory of curves and surfaces, leading to new interpretations and results. In 1987, Bharathi and Nagaraj demonstrated the use of quaternions to express the Serret–Frenet invariants of any curve [6]. Subsequently, as well as quaternionic curves, rectifying and osculating quaternionic curves were given the attention of various researchers [7,8,9,10,11,12,13]. Furthermore, modified Korteweg-de Vries equations were used to describe the motions of inextensible quaternionic curves, and these findings were presented in a research article that outlines the evolutions of inextensible quaternionic curves based on the Frenet formulae [14].

Additionally, in 2005, Chen and Li established new correlations between quaternionic transformations and minimal surfaces, resulting in novel findings [15]. Hoffman and Wang introduced a new technique that uses dual-quaternion multiplication to describe rigid transformations with dual quaternions, resulting in a family of rational surfaces in an affine 3-space. They specifically employed an approach to calculate all base points of the homogeneous tensor product parameterization of the resultant surfaces, together with three rational space curves [16].

These examples highlight the versatility and utility of quaternions in diverse areas of mathematics and beyond. Ruled surfaces are structures that can be generated by moving a straight line along a curve. There have been numerous studies conducted in various spaces and frames. The concept of partner-ruled surfaces based on the Flc frame on a polynomial curve was introduced in [17]. They investigated the requirements for two of these surfaces to be simultaneously developable and minimal. Şenyurt and Çalışkan investigated the ruled surface with the theory of quaternions and dual quaternions. They expressed integral invariants and obtained the ruled surfaces drawn by spatial quaternionic curves [18,19]. In [20], the quaternionic ruled surfaces were analyzed according to the alternative frame. During this process, some noteworthy studies on quaternions and surfaces have been presented in [21,22,23,24].

In Section 2, we present the geometric concepts regarding the basic structures of the paper mentioned in the introduction. In Section 3, we investigate the spatial quaternionic expressions of partner-ruled surfaces. Moreover, we determine the striction curves, dralls, pitches, and angles of pitches for these surfaces. Section 4 consists of a special example of the findings with graphical representations. The last section provides a summary of the article and highlights its main contributions and implications.

2. Preliminaries

In this section, we recall the concepts of quaternions [1] and spatial quaternionic curves [6]. We then explain some of the properties of spatial quaternionic ruled surfaces [18]. Understanding these preliminary concepts is crucial for comprehending the subsequent discussions on the subject.

A real quaternion can be described as the sum of a scalar $S_q=q_0$ and a vector $V_q=q_1{e}_1+q_2{e}_2+q_3{e}_3$ such that

$$q=q_0+q_1{e}_1+q_2{e}_2+q_3{e}_3,$$

where the components $q_0$, $q_1$, $q_2$, $q_3$ are real numbers, and 1, $e_1$, $e_2$, $e_3$ are quaternionic units that satisfy the multiplication rules given in Table 1.

Table 1. Multiplication table.

×	1	$e_1$	$e_2$	$e_3$
1	1	$e_1$	$e_2$	$e_3$
$e_1$	$e_1$	$-1$	$e_3$	$-e_2$
$e_2$	$e_2$	$-e_3$	$-1$	$e_1$
$e_3$	$e_3$	$e_2$	$-e_1$	$-1$

Here, the left column displays the left factor, and the top row displays the right factor.

The complex conjugate $\overline{q}$ is defined by

$$\overline{q}=S_q-V_q=q_0-q_1{e}_1-q_2{e}_2-q_3{e}_3.$$

Let Q denote the set of quaternions. The quaternion inner product is presented by the following real-valued, symmetric, and bilinear form:

$$\begin{array}{c}h:Q\times Q\to \mathbb{R}\hfill \\ \left(p,q\right)\to h\left(p,q\right)={\displaystyle \frac{1}{2}}\left(p\times \overline{q}+q\times \overline{p}\right).\end{array}$$

For $p=S_p+V_p$ and $q=S_q+V_q$, the quaternionic product is given by

$$p\times q=S_p{S}_q+S_p{V}_q+S_q{V}_p-⟨V_p,V_q⟩+V_p\wedge V_q,$$

where $⟨,⟩$ and ∧ denote the inner product and cross-product in ${\mathbb{R}}^3$. Thus, the quaternionic product satisfies

$$p\times q=-⟨V_p,V_q⟩+V_p\wedge V_q.$$

The square of the norm of a quaternion q is

$$\rho {\left(q\right)}^2=h\left(q,q\right)=q\times \overline{q}=\overline{q}\times q={q_0}^2+{q_1}^2+{q_2}^2+{q_3}^2.$$

Provided that $\rho \left(q\right)=1$, the quaternion q is called the unit quaternion. The inverse of the quaternion q is given by $q^{-1}={\displaystyle \frac{\overline{q}}{\rho \left(q\right)}}$ where $\rho \left(q\right)\ne 0$.

The space of the spatial quaternions is classified by $\left\{\left.q\in Q\right|q+\overline{q}=0\right\}$ where Q denotes the set of quaternions [6].

Definition 1. 

A spatial quaternionic curve α is defined by

$$\begin{array}{c}\alpha :I\to Q\hfill \\ s\to \alpha \left(s\right)={\displaystyle \sum _{i=1}^3}{\alpha }_i\left(s\right)e_i\hfill \end{array}$$

where I is an interval in real line $\mathbb{R}$ and $s\in I$ is the arc-length parameter [6].

Theorem 1. 

Let α be a spatial quaternionic curve with the arc-length parameter s. Then, the Serret–Frenet formulae of the spatial quaternionic curve α at any point $\alpha \left(s\right)$ are

$${\left[\begin{array}{c}T\\ N\\ B\end{array}\right]}_s=\left[\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right]\left[\begin{array}{c}T\\ N\\ B\end{array}\right]$$

(1)

such that

$$T\left(s\right)={\alpha }^{\prime }\left(s\right),N\left(s\right)={\displaystyle \frac{{\alpha }^{″}\left(s\right)}{∥{\alpha }^{″}\left(s\right)∥}},B\left(s\right)=T\left(s\right)\times N\left(s\right),$$

where the spatial quaternions $T, N$, and B are the unit tangent, unit principal normal, and unit binormal of the spatial quaternionic curve α, respectively. Moreover, the scalar functions κ and τ are the curvature and torsion of α, respectively [6].

The spatial quaternion $w=N\times N^{\prime }=\tau T+\kappa B$ is called the instantaneous Pfaffian quaternion along the motion of the Frenet frame $\left\{T,N,B\right\}$ of a spatial quaternionic curve $\alpha$ [18].

Definition 2. 

A spatial quaternionic ruled surface is represented by

$$\begin{array}{c}\phi :I\times \mathbb{R}\to Q\hfill \\ \left(s,u\right)\to \phi \left(s,u\right)=\alpha \left(s\right)+uX\left(s\right)\hfill \end{array}$$

where α is a spatial quaternionic curve and X is a spatial quaternion [18].

Lemma 1. 

The drall and the striction curve of a spatial quaternionic ruled surface φ are given by

$$P={\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(X\times X^{\prime }\right)\times \overline{{\alpha }^{\prime }}+{\alpha }^{\prime }\times \overline{\left(X\times X^{\prime }\right)}}{\rho {\left(X^{\prime }\right)}^2}}$$

(2)

and

$$r\left(s\right)=\alpha \left(s\right)-{\displaystyle \frac{1}{2}}{\displaystyle \frac{X^{\prime }\times \overline{{\alpha }^{\prime }}+{\alpha }^{\prime }\times \overline{X^{\prime }}}{\rho {\left(X^{\prime }\right)}^2}}X,$$

(3)

respectively [18].

It is known that if a ruled surface satisfies $\phi \left(s+2\pi ,u\right)=\phi \left(s,u\right)$ for all $s\in I$, then the ruled surface is called closed.

Definition 3. 

For a given closed spatial quaternionic ruled surface, the magnitude $l_x=\underset{\alpha }{\oint }h\left(d\alpha ,X\right)ds$ is called the pitch of this surface [18].

Definition 4. 

The spatial quaternions D and V defined by

$$D=\underset{\alpha }{\oint }wds=\underset{\alpha }{\oint }\left(\tau T+\kappa B\right)ds$$

(4)

and

$$V=\underset{\alpha }{\oint }d\alpha$$

(5)

are called the Steiner rotation quaternion and Steiner translation quaternion of the closed motion of the Frenet frame of a closed spatial quaternionic curve α, respectively. Here, w is the instantaneous Pfaffian quaternion [18].

Theorem 2. 

The angle of pitch and the pitch of a closed spatial quaternionic ruled surface ${\lambda }_x$ and $l_x$ are equal to

$${\lambda }_x=h\left(D,X\right)$$

(6)

and

$$l_x=h\left(V,X\right)$$

(7)

where D and V are the Steiner rotation and translation quaternions, respectively [18].

3. Characterizations of the Spatial Quaternionic Partner-Ruled Surfaces

In this section, we examine the spatial quaternionic expressions of partner-ruled surfaces. Then, we calculate the striction curves and dralls of these surfaces. Finally, our investigation focuses on closed quaternionic ruled surfaces. We analyze their pitches and pitch angles and interpret these properties. Additionally, we use quaternionic formulas to calculate the integral invariants of these surfaces.

3.1. $TN$-Spatial Quaternionic Partner-Ruled Surfaces

Definition 5. 

Consider a differentiable spatial quaternionic curve $\alpha =\alpha \left(s\right)$ that moves with a unit speed for its parameter s, and let $\left\{T,N,B\right\}$ denote the Frenet frame of this curve. The two spatial quaternionic ruled surfaces defined by

$$\left\{\begin{array}{c}{\phi }_N^T\left(s,u\right)=T\left(s\right)+uN\left(s\right),\\ {\phi }_T^N\left(s,u\right)=N\left(s\right)+uT\left(s\right),\end{array}\right.$$

are called $TN$-spatial quaternionic partner-ruled surfaces.

Theorem 3. 

Let $r_{TN}$ and $r_{NT}$ be the striction curves of any $TN$-spatial quaternionic partner-ruled surfaces ${\phi }_N^T$ and ${\phi }_T^N$. Then, the position vector of the striction curve on surface ${\phi }_N^T$ is equal to the tangent of the curve, and the position vector of the striction curve on surface ${\phi }_T^N$ is equal to the principal normal of the spatial quaternionic curve $\alpha =\alpha \left(s\right)$.

Proof. 

Let $\alpha =\alpha \left(s\right)$ be a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$. If we consider Equation (3) and employ the quaternionic inner product, we find the equation of the striction curve of a spatial quaternionic ruled surface ${\phi }_N^T$ as follows:

$$r_{TN}=T-{\displaystyle \frac{h\left(N^{\prime },T^{\prime }\right)}{\rho {\left(N^{\prime }\right)}^2}}N=T-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(N^{\prime }\times \overline{T^{\prime }}+T^{\prime }\times \overline{N^{\prime }}\right)}{\sqrt{h\left(N^{\prime },N^{\prime }\right)}}}N.$$

By taking the complex conjugate of a quaternion and applying Equation (1), we arrive at

$$r_{TN}=T+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(-\kappa T+\tau B\right)\times \kappa N+\kappa N\times \left(-\kappa T+\tau B\right)}{\sqrt{{\kappa }^2+{\tau }^2}}}N.$$

If we take the quaternionic product of the spatial quaternions, we obtain that the position vector of the striction curve corresponds to the tangent of the curve $\alpha$.

Again, we calculate the position vector of the striction curve

$$r_{NT}=N-{\displaystyle \frac{h\left(T^{\prime },N^{\prime }\right)}{\rho {\left(T^{\prime }\right)}^2}}T.$$

By a similar method, the striction curve of ${\phi }_T^N$ is found to be equal to the principal normal vector of the curve $\alpha$, and this completes the proof. □

Theorem 4. 

Let ${\phi }_N^T$ and ${\phi }_T^N$ be $TN$-spatial quaternionic partner-ruled surfaces; then, the dralls of the closed spatial quaternionic partner-ruled surfaces ${\phi }_N^T$ and ${\phi }_T^N$ are

$$P_{TN}=0,P_{NT}=\tau ,$$

respectively.

Proof. 

Assuming $\alpha =\alpha \left(s\right)$ is a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$, the drall of the closed spatial quaternionic ruled surface ${\phi }_N^T$ can be obtained by considering Equation (2) and utilizing the quaternionic inner product. Specifically, the drall can be expressed as

$$P_{TN}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(N\times N^{\prime }\right)\times \overline{T^{\prime }}+T^{\prime }\times \overline{\left(N\times N^{\prime }\right)}}{\rho {\left(N^{\prime }\right)}^2}}.$$

We obtain the drall of the surface ${\phi }_N^T$ by utilizing the quaternionic product of the spatial quaternions and the Frenet invariants. The computation is carried out as follows:

$$P_{TN}=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(\kappa B+\tau T\right)\times N+N\times \left(\kappa B+\tau T\right)}{\sqrt{{\kappa }^2+{\tau }^2}}}=0.$$

In a similar way, the drall of the surface ${\phi }_T^N$ is determined by

$$\begin{array}{c}{P}_{NT}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(T\times T^{\prime }\right)\times \overline{N^{\prime }}+N^{\prime }\times \overline{\left(T\times T^{\prime }\right)}}{\rho {\left(T^{\prime }\right)}^2}}\hfill \\ ={\displaystyle \frac{\kappa }{2}}{\displaystyle \frac{\left(\kappa B\times \left(-\kappa T+\tau B\right)+\left(-\kappa T+\tau B\right)\times \kappa B\right)}{\kappa }}\hfill \\ =\tau .\hfill \end{array}$$

□

Corollary 1. 

Let ${\phi }_N^T$ and ${\phi }_T^N$ be $TN$-spatial quaternionic partner-ruled surfaces; then, the $TN$-spatial quaternionic partner-ruled surfaces are developable surfaces if and only if the spatial quaternionic curve $\alpha =\alpha \left(s\right)$ is planar.

Proof. 

The proof is obvious by the fact that the necessary and sufficient condition for a ruled surface to be developable is having a vanishing drall at each point of the surface, and the necessary and sufficient condition for a curve to be planar is having vanishing torsion at each point of the curve. □

Theorem 5. 

Let ${\phi }_N^T$ and ${\phi }_T^N$ be $TN$-spatial quaternionic partner-ruled surfaces; then, the angles of the pitch of the closed spatial quaternionic partner-ruled surfaces are

$${\lambda }_{TN}=0,{\lambda }_{NT}=\oint \tau ds,$$

respectively.

Proof. 

Assume $\alpha =\alpha \left(s\right)$ is a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$. By taking into consideration Equation (6), we can express the angle of the pitch of the closed spatial quaternionic ruled surface ${\phi }_N^T$ as

$${\lambda }_{TN}=h\left(D,N\right)={\displaystyle \frac{1}{2}}\left(D\times \overline{N}+N\times \overline{D}\right)=-{\displaystyle \frac{1}{2}}\left(D\times N+N\times D\right).$$

Using the quaternionic product of the spatial quaternions and Equation (4), we calculate the angle of the pitch as follows:

$${\lambda }_{TN}=h\left(D,N\right)=h\left(\oint \left(\tau T+\kappa B\right)ds,N\right)=0.$$

On the other hand, the angle of the pitch ${\lambda }_{NT}$ of the ruled surface ${\phi }_T^N$ is maintained:

$$\begin{array}{c}{\lambda }_{NT}=h\left(D,T\right)={\displaystyle \frac{1}{2}}\left(D\times \overline{T}+T\times \overline{D}\right)\hfill \\ =h\left(\oint \left(\tau T+\kappa B\right)ds,T\right)\hfill \\ =\oint \tau ds.\hfill \end{array}$$

□

Theorem 6. 

Let ${\phi }_N^T$ and ${\phi }_T^N$ be $TN$-spatial quaternionic partner-ruled surfaces; then, the pitches of the closed spatial quaternionic partner-ruled surfaces ${\phi }_N^T$ and ${\phi }_T^N$ are

$$l_{TN}=\oint \kappa ds,l_{NT}=-\oint \kappa ds,$$

respectively.

Proof. 

Assume that $\alpha =\alpha \left(s\right)$ is a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$. From Equation (5) we obtain $V=\oint dT=\oint \kappa Nds$, and from Equation (7), the pitch $l_{TN}$ of the closed spatial quaternionic ruled surface ${\phi }_N^T$ is written by

$$l_{TN}=h\left(V,N\right)=h\left(\oint \kappa Nds,N\right).$$

By referring to the definition of the quaternion inner product, we find

$$l_{TN}={\displaystyle \frac{1}{2}}\left(\oint \kappa Nds\times \overline{N}+N\times \overline{\oint \kappa Nds}\right).$$

Hence, using the quaternionic product and the conjugate of a quaternion, we obtain

$$l_{TN}=\oint \kappa ds.$$

By making similar calculations, the pitch $l_{NT}$ of the closed spatial quaternionic ruled surface ${\phi }_T^N$ is found:

$$l_{NT}=h\left(V,T\right)=-\oint \kappa ds.$$

□

3.2. $TB$-Spatial Quaternionic Partner-Ruled Surfaces

Definition 6. 

Consider a spatial quaternionic curve $\alpha =\alpha \left(s\right)$ that is differentiable and moves at a unit speed for its parameter s, and let $\left\{T,N,B\right\}$ be the Frenet frame of the curve. The two spatial quaternionic ruled surfaces defined by

$$\left\{\begin{array}{c}{\phi }_B^T\left(s,u\right)=T\left(s\right)+uB\left(s\right),\\ {\phi }_T^B\left(s,u\right)=B\left(s\right)+uT\left(s\right),\end{array}\right.$$

are called $TB$-spatial quaternionic partner-ruled surfaces.

Theorem 7. 

Let the surfaces ${\phi }_B^T$ and ${\phi }_T^B$ be spatial quaternionic partner-ruled surfaces; then, the striction curves $r_{TB}$ and $r_{BT}$ of the surfaces ${\phi }_B^T$ and ${\phi }_T^B$ are

$$\left\{\begin{array}{c}{r}_{TB}=T\left(s\right)+{\displaystyle \frac{\kappa }{\tau }}B\left(s\right),\hfill \\ r_{BT}=B\left(s\right)+{\displaystyle \frac{\tau }{\kappa }}T\left(s\right),\hfill \end{array}\right.$$

where $\kappa \ne 0$ and $\tau \ne 0$, respectively.

Proof. 

Let $\alpha =\alpha \left(s\right)$ be a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$. By referring to Equation (3) and using the quaternionic inner product, the striction curve of the spatial quaternionic ruled surface ${\phi }_B^T$ can be written by

$$r_{TB}=T-{\displaystyle \frac{h\left(B^{\prime },T^{\prime }\right)}{\rho {\left(B^{\prime }\right)}^2}}B=T-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(B^{\prime }\times \overline{T^{\prime }}+T^{\prime }\times \overline{B^{\prime }}\right)}{\sqrt{h\left(B^{\prime },B^{\prime }\right)}}}B.$$

Using the complex conjugate of a quaternion and Equation (1), we arrive at

$$r_{TB}=T+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(-\tau N\right)\times \kappa N+\kappa N\times \left(-\tau N\right)}{\tau }}B.$$

Considering the quaternionic product of the spatial quaternions, the striction curve of ${\phi }_B^T$ is

$$r_{TB}=T\left(s\right)+{\displaystyle \frac{\kappa }{\tau }}B\left(s\right).$$

Similarly, from the equation $r_{BT}=B-{\displaystyle \frac{h\left(T^{\prime },B^{\prime }\right)}{\rho {\left(T^{\prime }\right)}^2}}T$, one can easily find that the striction curve of ${\phi }_T^B$ is

$$r_{BT}=B\left(s\right)+{\displaystyle \frac{\tau }{\kappa }}T\left(s\right).$$

□

Theorem 8. 

Let ${\phi }_B^T$ and ${\phi }_T^B$ be any $TB$-spatial quaternionic partner-ruled surfaces; then, the dralls of the closed spatial quaternionic partner-ruled surfaces ${\phi }_B^T$ and ${\phi }_T^B$ are

$$P_{TB}=P_{BT}=0,$$

respectively.

Proof. 

Let $\alpha =\alpha \left(s\right)$ be a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$. The drall of the closed spatial quaternionic ruled surface ${\phi }_B^T$ can be obtained by considering Equation (2) and utilizing the quaternionic inner product. Specifically, the drall is expressed as

$$P_{TB}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(B\times B^{\prime }\right)\times \overline{T^{\prime }}+T^{\prime }\times \overline{\left(B\times B^{\prime }\right)}}{\rho {\left(B^{\prime }\right)}^2}}.$$

We compute the drall of the surface ${\phi }_B^T$ by utilizing the quaternionic product of the spatial quaternions and the Frenet invariants. The computation is carried out as follows:

$$P_{TB}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(\tau T\times \kappa N\right)+\left(\kappa N\times \tau T\right)}{\tau }}=0.$$

In a similar way, the drall of the surface ${\phi }_T^B$ is determined by

$$\begin{array}{c}{P}_{BT}=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(T\times T^{\prime }\right)\times \overline{B^{\prime }}+B^{\prime }\times \overline{\left(T\times T^{\prime }\right)}}{\rho {\left(T^{\prime }\right)}^2}}\hfill \\ =-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(\kappa B\times \tau N\right)+\left(\tau N\times \kappa B\right)}{\kappa }}\hfill \\ =0.\hfill \end{array}$$

□

Corollary 2. 

Let ${\phi }_B^T$ and ${\phi }_T^B$ be any $TB$-spatial quaternionic partner-ruled surfaces; then, the $TB$-spatial quaternionic partner-ruled surfaces are developable surfaces.

Proof. 

The proof is obvious by virtue that the necessary and sufficient condition for a ruled surface to be developable is having zero drall at each point of the surface. □

Theorem 9. 

Let ${\phi }_B^T$ and ${\phi }_T^B$ be any $TB$-spatial quaternionic partner-ruled surfaces; the angles of the pitch of the closed spatial quaternionic partner-ruled surfaces are

$${\lambda }_{TB}=\oint \kappa ds,{\lambda }_{BT}=\oint \tau ds,$$

respectively.

Proof. 

Assume $\alpha =\alpha \left(s\right)$ is a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$. Taking into consideration Equation (6), the angle of pitch of the closed spatial quaternionic ruled surface ${\phi }_B^T$ is written by

$${\lambda }_{TB}=h\left(D,B\right)={\displaystyle \frac{1}{2}}\left(D\times \overline{B}+B\times \overline{D}\right)=-{\displaystyle \frac{1}{2}}\left(D\times B+B\times D\right).$$

By referring to Equation (4) and the definition of the quaternion inner product, we obtain

$${\lambda }_{TB}=h\left(D,B\right.⟩=\left.⟨\oint \left(\tau T+\kappa B\right)ds,B\right)=\oint \kappa ds.$$

In a similar manner, the angle of the pitch ${\lambda }_{BT}$ of the closed spatial quaternionic ruled surface ${\phi }_T^B$ is calculated

$${\lambda }_{BT}=h\left(D,T\right)=⟨\oint \left(\tau T+\kappa B\right)ds,T⟩=\oint \tau ds.$$

□

Theorem 10. 

Let ${\phi }_B^T$ and ${\phi }_T^B$ be $TB$-spatial quaternionic partner-ruled surfaces; then, the pitches of the closed spatial quaternionic partner-ruled surfaces ${\phi }_B^T$ and ${\phi }_T^B$ are

$$l_{TB}=0,l_{BT}=0,$$

respectively.

Proof. 

Let $\alpha =\alpha \left(s\right)$ be a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$. From Equation (5), $V=\oint dT=\oint \kappa Nds$ is found, and from Equation (7), the pitch $l_{TB}$ of the closed spatial quaternionic ruled surface ${\phi }_B^T$ is written by

$$l_{TB}=h\left(V,B\right)=h\left(\oint \kappa Nds,B\right).$$

From the definition of the quaternion inner product, it is found as

$$l_{TB}={\displaystyle \frac{1}{2}}\left(\oint \kappa Nds\times \overline{B}+B\times \overline{\oint \kappa Nds}\right).$$

So, using the cross-product and the conjugate of a quaternion, we obtain

$$l_{TB}=0.$$

By making similar calculations, the pitch $l_{BT}$ of the closed spatial quaternionic ruled surface ${\phi }_T^B$ is determined as

$$l_{BT}=h\left(V,T\right)=0,$$

where $V=\oint dB=-\oint \tau Nds$. □

Corollary 3. 

Let ${\phi }_B^T$ and ${\phi }_T^B$ be any $TB$-spatial quaternionic partner-ruled surfaces. The $TB$-spatial quaternionic partner-ruled surfaces represent cones.

Proof. 

The proof is obvious by virtue that the necessary and sufficient condition for a developable ruled surface to be a cone is having zero pitch at each point of the surface. □

3.3. $NB$-Spatial Quaternionic Partner-Ruled Surfaces

Definition 7. 

Consider a spatial quaternionic curve $\alpha =\alpha \left(s\right)$ that is differentiable and moves at a unit speed for its parameter s, and let $\left\{T,N,B\right\}$ be Frenet frame of the curve. The two spatial quaternionic ruled surfaces defined by

$$\left\{\begin{array}{c}{\phi }_B^N\left(s,u\right)=N\left(s\right)+uB\left(s\right),\\ {\phi }_N^B\left(s,u\right)=B\left(s\right)+uN\left(s\right),\end{array}\right.$$

are called $NB$-spatial quaternionic partner-ruled surfaces.

Theorem 11. 

Let the surfaces ${\phi }_B^N$ and ${\phi }_N^B$ be spatial quaternionic partner-ruled surfaces; then, the striction curves $r_{NB}$ and $r_{BN}$ of the surfaces ${\phi }_B^N$ and ${\phi }_N^B$ are

$$r_{NB}=N,r_{BN}=B,$$

respectively.

Proof. 

Let $\alpha =\alpha \left(s\right)$ be a unit-speed spatial quaternionic curve with the Frenet frame $\left\{T,N,B\right\}$. By considering Equation (3) and using the quaternionic inner product, the striction curve of the spatial quaternionic ruled surface ${\phi }_B^N$ can be written by

$$r_{NB}=N-{\displaystyle \frac{h\left(B^{\prime },N^{\prime }\right)}{\rho {\left(B^{\prime }\right)}^2}}B=N-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(B^{\prime }\times \overline{N^{\prime }}+N^{\prime }\times \overline{B^{\prime }}\right)}{\sqrt{h\left(B^{\prime },B^{\prime }\right)}}}B.$$

If we consider Equations (1) and (3), we can prove using similar methods of Theorem 3. □

Theorem 12. 

Let ${\phi }_B^N$ and ${\phi }_N^B$ be $NB$-spatial quaternionic partner-ruled surfaces; then, the dralls of the closed spatial quaternionic partner-ruled surfaces ${\phi }_B^N$ and ${\phi }_N^B$ are $P_{NB}=-\kappa$ and $P_{BN}=0$, respectively.

Proof. 

By considering Equation (2), the proof is completed in a similar way to the proof of Theorem 4. □

Corollary 4. 

Let ${\phi }_B^N$ and ${\phi }_N^B$ be any $NB$-spatial quaternionic partner-ruled surfaces; then, the spatial quaternionic partner-ruled surfaces are developable surfaces if and only if the spatial quaternionic curve $\alpha =\alpha \left(s\right)$ is a straight line.

Proof. 

The necessary and sufficient condition for a ruled surface to be developable is having zero drall at each point of the surface, and the necessary and sufficient condition for a curve to be a straight line is having zero curvature at each point of the curve. These prove the corollary. □

Theorem 13. 

Let ${\phi }_B^N$ and ${\phi }_N^B$ be any $NB$-spatial quaternionic partner-ruled surfaces; then, the angles of the pitch of the closed spatial quaternionic partner-ruled surfaces are ${\lambda }_{NB}=\oint \kappa ds$ and ${\lambda }_{BN}=0,$ respectively.

Proof. 

By considering Equations (4) and (6), the proof is completed similarly to the proof of Theorem 5. □

Theorem 14. 

Let ${\phi }_B^N$ and ${\phi }_N^B$ be $NB$-spatial quaternionic partner-ruled surfaces; then, the pitches of the closed spatial quaternionic partner-ruled surfaces ${\phi }_B^N$ and ${\phi }_N^B$ are $l_{NB}=0,l_{BN}=-\oint \tau ds,$ respectively.

Proof. 

By considering Equations (5) and (7), the proof is completed similarly to the proof of Theorem 6. □

Corollary 5. 

Let ${\phi }_B^N$ and ${\phi }_N^B$ be $NB$-spatial quaternionic partner-ruled surfaces. Then, the following expressions are satisfied:

i.

The surface ${\phi }_B^N$ is a cone if and only if the curve $\alpha =\alpha \left(s\right)$ is a straight line.

ii.

The surface ${\phi }_N^B$ is a cone if and only if the curve $\alpha =\alpha \left(s\right)$ is a planar curve.

Proof. 

The necessary and sufficient condition for a developable ruled surface to be a cone is having zero pitch at each point of the surface, and the necessary and sufficient condition a curve to be a straight line (planar) is having zero curvature (torsion) at each point of the curve. These prove the corollary. □

4. A Particular Example for Spatial Quaternionic Partner-Ruled Surfaces

Let us consider a spatial quaternionic curve given by the parametric equation

$$\alpha \left(s\right)={\displaystyle \frac{3}{4}}\left(coss+{\displaystyle \frac{cos3s}{9}},sins+{\displaystyle \frac{sin3s}{9}},{\displaystyle \frac{-2coss}{\sqrt{3}}}\right).$$

The Frenet elements of the spatial quaternionic curves $\alpha$ are

$$\begin{array}{c}T\left(s\right)=\left({\displaystyle \frac{-3sins-sin3s}{4}},{cos}^{3}s,{\displaystyle \frac{\sqrt{3}sins}{2}}\right),\hfill \\ N\left(s\right)=\left(-{\displaystyle \frac{\sqrt{3}cos2s}{2}},-{\displaystyle \frac{\sqrt{3}sin2s}{2}},{\displaystyle \frac{1}{2}}\right),\hfill \\ B\left(s\right)=\left({\displaystyle \frac{3coss-cos3s}{4}},{sin}^{3}s,{\displaystyle \frac{\sqrt{3}coss}{2}}\right),\hfill \\ \kappa =\sqrt{3}coss,\tau =-\sqrt{3}sins.\hfill \end{array}$$

and the $TN$-spatial quaternionic partner-ruled surfaces are found as

$$\left\{\begin{array}{c}{\phi }_N^T=\left({\displaystyle \frac{-2\sqrt{3}ucos2s-3sins-sin3s}{4}},{cos}^{3}s-\sqrt{3}usinscoss,{\displaystyle \frac{u+\sqrt{3}sins}{2}}\right),\hfill \\ \hfill \\ {\phi }_T^N=\left({\displaystyle \frac{-2\sqrt{3}cos2s-u\left(3sins+sin3s\right)}{4}},u{cos}^{3}s-{\displaystyle \frac{\sqrt{3}sin2s}{2}},{\displaystyle \frac{1+\sqrt{3}usins}{2}}\right).\hfill \end{array}\right.$$

Obviously, the striction curves of these $TN$-spatial quaternionic partner-ruled surfaces are

$$\left\{\begin{array}{c}{r}_{TN}=\left({\displaystyle \frac{-3sins-sin3s}{4}},{cos}^{3}s,{\displaystyle \frac{\sqrt{3}sins}{2}}\right)\\ r_{NT}=\left(-{\displaystyle \frac{\sqrt{3}cos2s}{2}},-{\displaystyle \frac{\sqrt{3}sin2s}{2}},{\displaystyle \frac{1}{2}}\right),\end{array}\right.$$

respectively; see Figure 1.

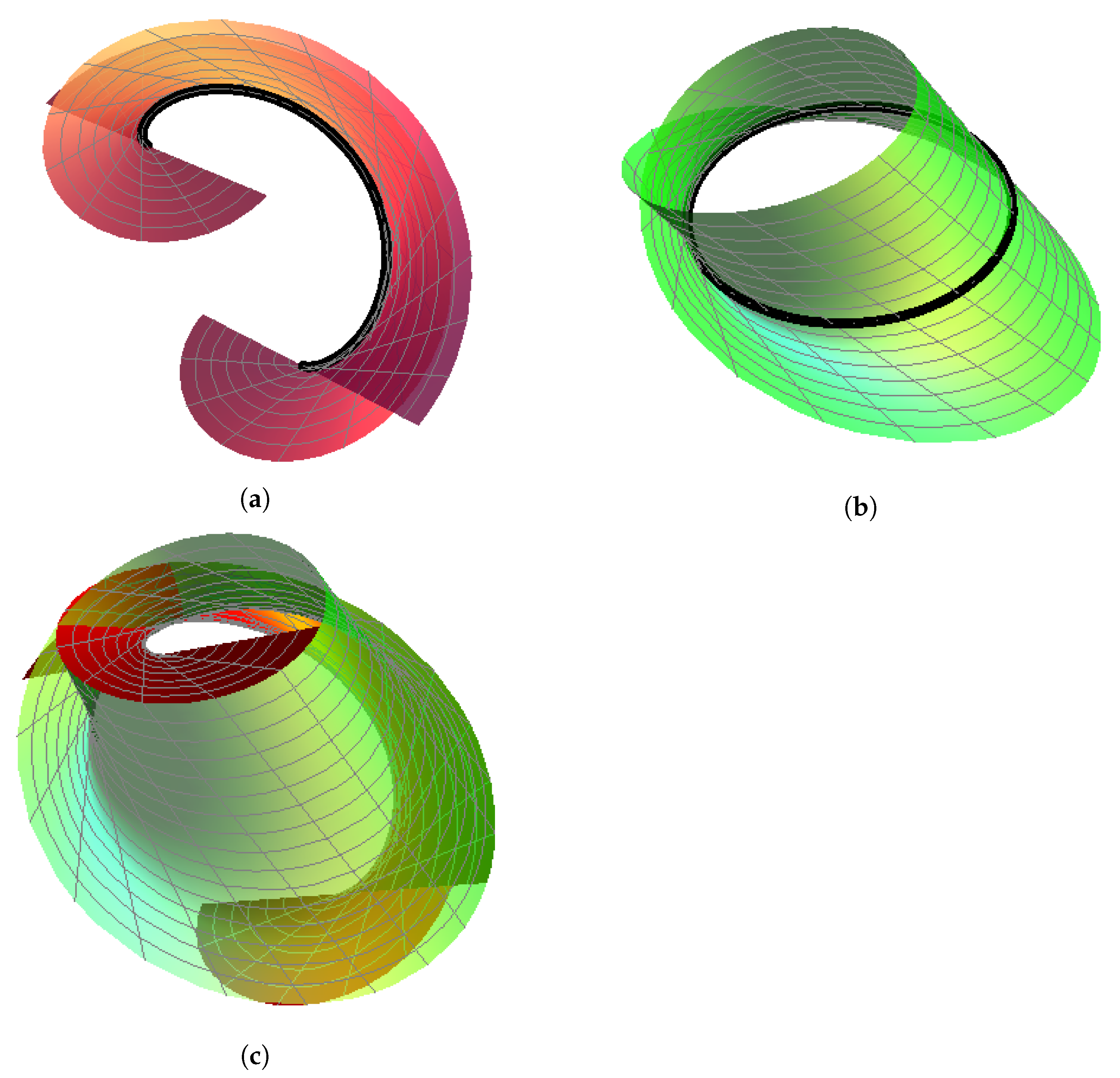
Figure 1. $TN$-spatial quaternionic partner-ruled surfaces for $s\in \left(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right)$ and $u\in \left(-1,1\right)$. (a) ${\phi }_N^T$ and its striction curve (black). (b) ${\phi }_T^N$ and its striction curve (black). (c) The surfaces ${\phi }_N^T$ (red) and ${\phi }_N^T$ (green).

In a similar manner, the parametric forms of the $TB$-spatial quaternionic partner-ruled surfaces and their striction curves are found as

$$\left\{\begin{array}{c}{\phi }_B^T=\left({\displaystyle \frac{u\left(3coss-cos3s\right)-3sins-sin3s}{4}},{cos}^{3}s+u{sin}^{3}s,{\displaystyle \frac{\sqrt{3}\left(ucoss+sins\right)}{2}}\right),\hfill \\ \hfill \\ {\phi }_T^B=\left({\displaystyle \frac{3coss-cos3s-u\left(3sins+sin3s\right)}{4}},u{cos}^{3}s+{sin}^{3}s,{\displaystyle \frac{\sqrt{3}\left(coss+usins\right)}{2}}\right),\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}{r}_{TB}=\left({\displaystyle \frac{\left(-3+cos4s\right)cscs}{4}},{\displaystyle \frac{coss+cos3s}{2}},-{\displaystyle \frac{\sqrt{3}cos2scscs}{2}}\right),\\ r_{BT}=\left({\displaystyle \frac{\left(3-cos4s\right)secs}{4}},{\displaystyle \frac{sins-sin3s}{2}},{\displaystyle \frac{\sqrt{3}cos2ssecs}{2}}\right),\end{array}\right.$$

respectively; see Figure 2.

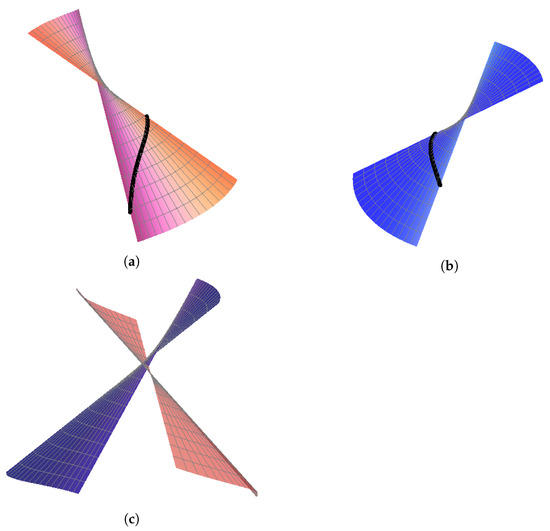
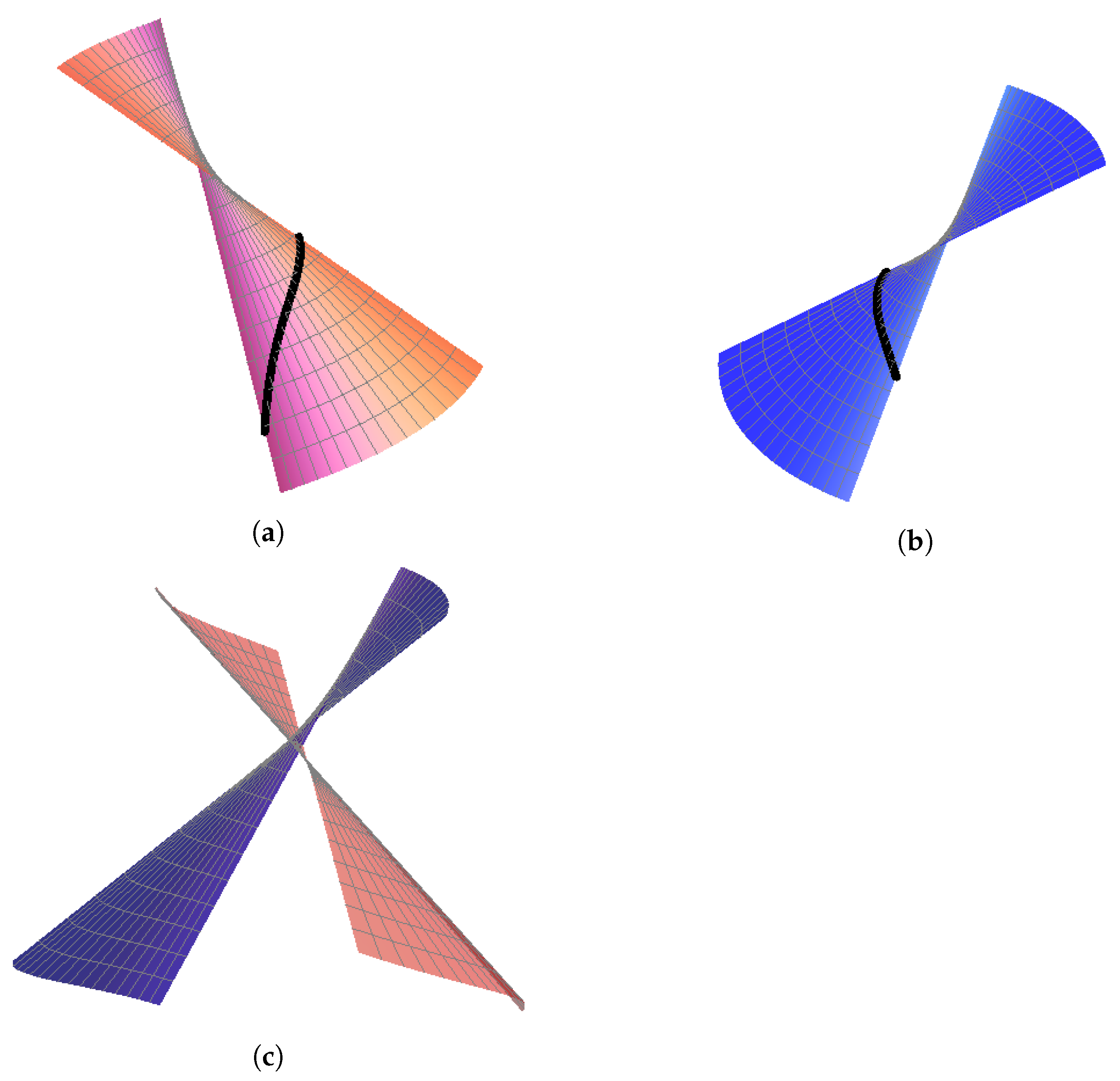
Figure 2. $TB$-spatial quaternionic partner-ruled surfaces for $s\in \left({\displaystyle \frac{\pi }{10}},{\displaystyle \frac{\pi }{3}}\right)$ and $u\in \left(-4,4\right)$. (a) ${\phi }_B^T$ and its striction curve (black). (b) ${\phi }_T^B$ and its striction curve (black). (c) The surfaces ${\phi }_B^T$ (red) and ${\phi }_T^B$ (blue).

Similarly, the parametric forms for the $NB$-spatial quaternionic partner-ruled surfaces and their striction curves are found as

$$\left\{\begin{array}{c}{\phi }_B^N=\left({\displaystyle \frac{u\left(3coss-cos3s\right)-2\sqrt{3}cos2s}{4}},{\displaystyle \frac{-\sqrt{3}sin2s}{2}}+u{sin}^{3}s,{\displaystyle \frac{1+\sqrt{3}ucoss}{2}}\right),\hfill \\ \hfill \\ {\phi }_N^B=\left({\displaystyle \frac{3coss-cos3s-2\sqrt{3}ucos2s}{4}},{\displaystyle \frac{-\sqrt{3}usin2s}{2}}+{sin}^{3}s,{\displaystyle \frac{u+\sqrt{3}coss}{2}}\right),\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}{r}_{NB}=\left(-{\displaystyle \frac{\sqrt{3}cos2s}{2}},-{\displaystyle \frac{\sqrt{3}sin2s}{2}},{\displaystyle \frac{1}{2}}\right),\\ r_{BN}=\left({\displaystyle \frac{3coss-cos3s}{4}},{sin}^{3}s,{\displaystyle \frac{\sqrt{3}coss}{2}}\right),\end{array}\right.$$

respectively; see Figure 3.

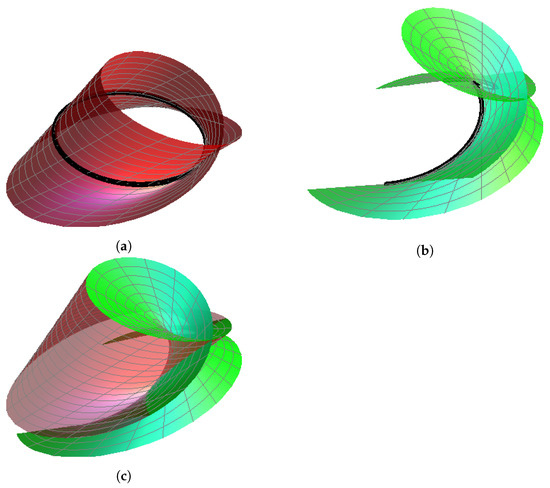
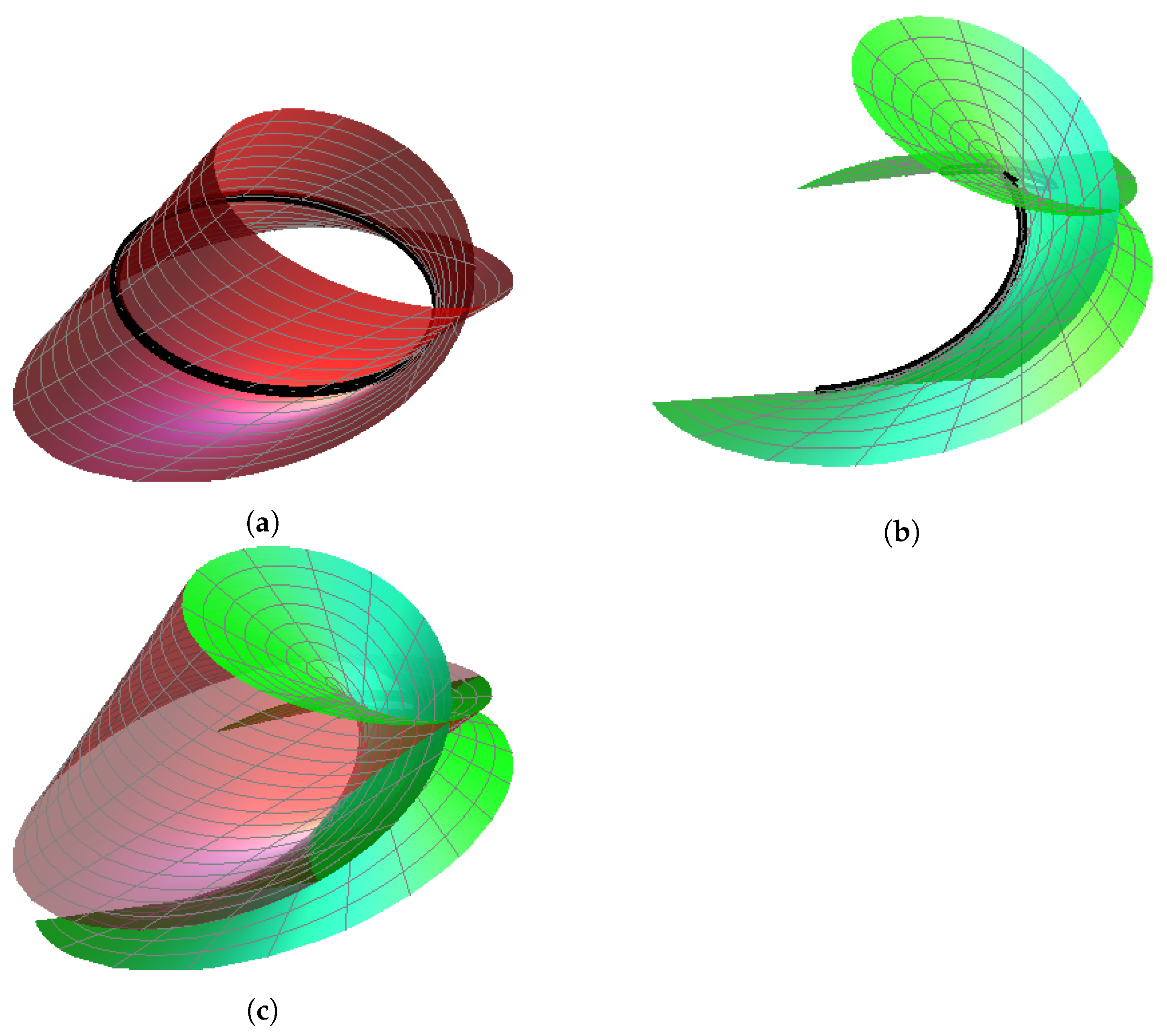
Figure 3. The $NB$-spatial quaternionic partner-ruled surfaces for $s\in \left(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right)$ and $u\in \left(-1,1\right)$. (a) ${\phi }_B^N$ and its striction curve (black). (b) ${\phi }_N^B$ and its striction curve (black). (c) The surfaces ${\phi }_B^N$ (red) and ${\phi }_N^B$ (green).

5. Conclusions

In this paper, we derived the spatial quaternionic partner-ruled surfaces formed by spatial quaternions, which are Frenet elements of a spatial quaternionic base curve. Then, we determined the striction curves and dralls of these surfaces. Additionally, the conditions of these partner-ruled surfaces to be developable were investigated. Under consideration, the quaternionic partner-ruled surfaces were closed, and the pitches and angles of pitches of them were found. The integral invariants of these partner surfaces were calculated by using quaternionic products.