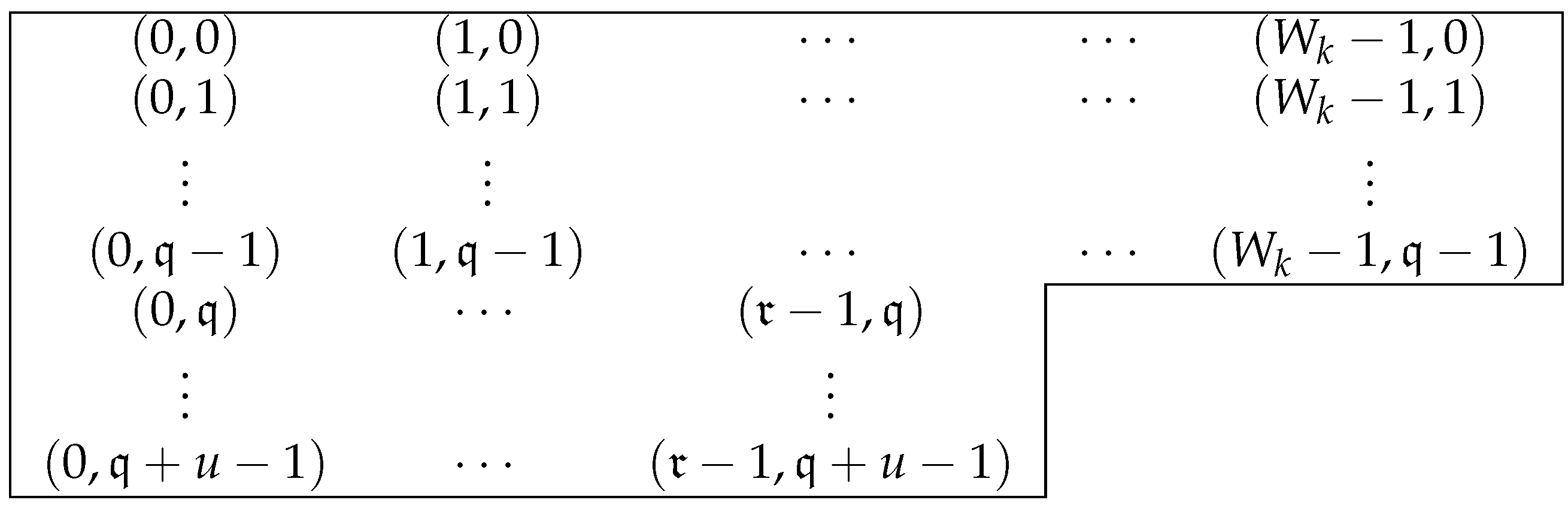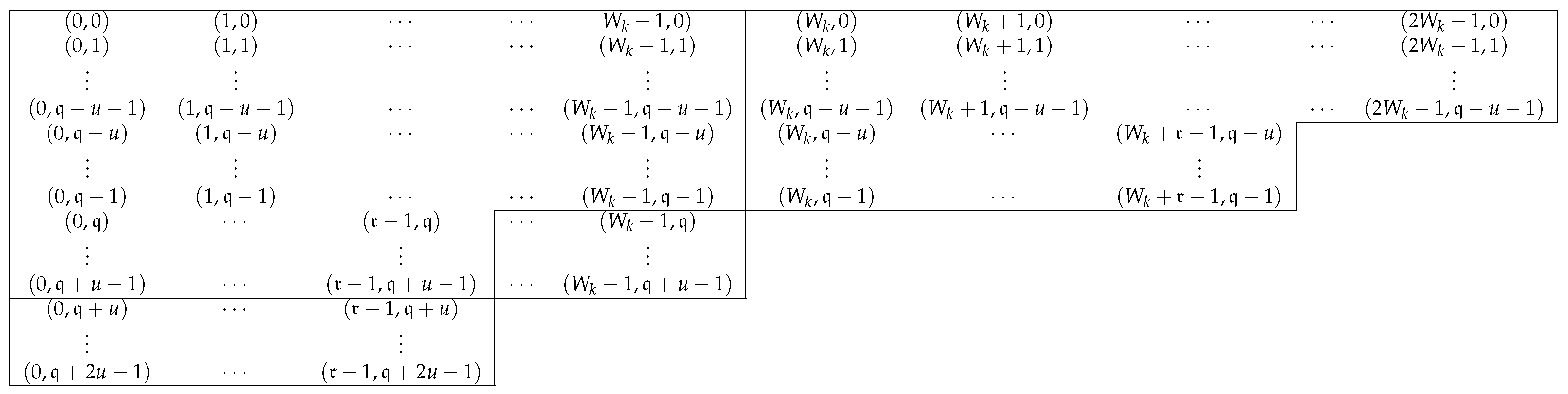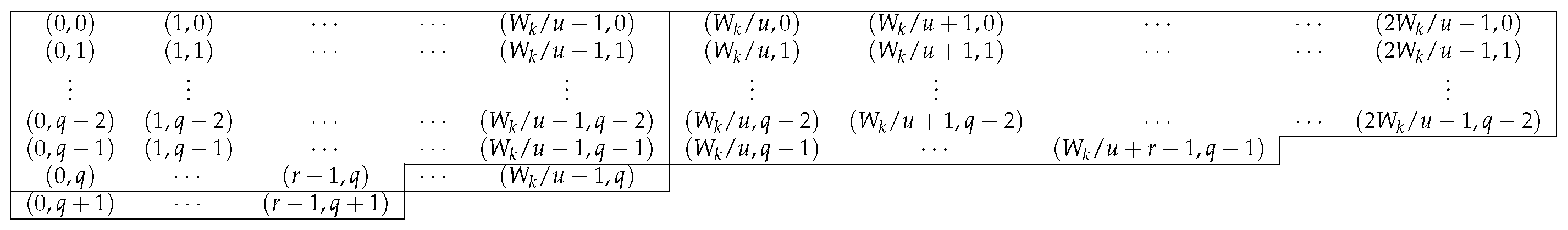p-Numerical Semigroups of Triples from the Three-Term Recurrence Relations

Abstract

Many people, including Horadam, have studied the numbers $W_n$, satisfying the recurrence relation $W_n=u{W}_{n-1}+v{W}_{n-2}$ ($n\ge 2$) with $W_0=0$ and $W_1=1$. In this paper, we study the p-numerical semigroups of the triple $(W_i,W_{i+2},W_{i+k})$ for integers $i,k(\ge 3)$. For a nonnegative integer p, the p-numerical semigroup $S_p$ is defined as the set of integers whose nonnegative integral linear combinations of given positive integers $a_1,a_2,\dots ,a_{\kappa }$ with $\gcd (a_1,a_2,\dots ,a_{\kappa })=1$ are expressed in more than p ways. When $p=0$, $S=S_0$ is the original numerical semigroup. The largest element and the cardinality of ${\mathbb{N}}_0\setminus S_p$ are called the p-Frobenius number and the p-genus, respectively.

1. Introduction

We consider the sequence ${\left\{W_n\right\}}_{n=0}^{\infty }$, satisfying:

$$W_n=u{W}_{n-1}+v{W}_{n-2}(n\ge 2)W_0=0,W_1=1,$$

(1)

where u and v are positive integers with $\gcd (u,v)=1$. The values of $W_n=W_n(u,v)$ depend on the values of u and v. If $u=v=1$, $F_n=W_n(1,1)$ is the n-th Fibonacci number [1]. If $u=1$ and $v=2$, $J_n=W_n(1,2)$ is the n-th Jacobsthal number [2,3]. If $u=2$ and $v=1$, $P_n=W_n(2,1)$ is the n-th Pell number [4]. However, for simplicity, if we do not specify the values of u or v, we will simply write $W_n$ for $W_n(u,v)$.

This type of number sequence has been well known to many people by Horadam’s series of studies ([5,6,7,8,9]) in the 1960s. Because of this fact, this sequence is sometimes called the Horadam sequence. Horadam himself used the recurrence relation $W_n=u{W}_{n-1}-v{W}_{n-2}$. However, recently more people (see, e.g., [10,11]) have used the recurrence relation $W_n=u{W}_{n-1}+v{W}_{n-2}$ and such works are still due to Horadam. In general, the initial values are arbitrary, but because of some simplifications, we set $W_0=0$ and $W_1=1$. According to [6], this sequence has long exercised interest, as seen in, for instance, Bessel-Hagen [12], Lucas [13], and Tagiuri [14], and, for historical details, Dickson [15]. However, it is deplorable that quite a few papers are publishing results that have already been obtained by these authors as new results, either because they are unaware of their or the following important results, or even if they are ignoring them.

Given the set of positive integers $A:=\{a_1,a_2,\dots ,a_{\kappa }\}$ ($\kappa \ge 2$), for a nonnegative integer p, let $S_p$ be the set of integers whose nonnegative integral linear combinations of given positive integers $a_1,a_2,\dots ,a_{\kappa }$ are expressed in more than p ways. For a set of nonnegative integers ${\mathbb{N}}_0$, the set ${\mathbb{N}}_0\setminus S_p$ is finite if and only if $\gcd (a_1,a_2,\dots ,a_{\kappa })=1$. Then, there exists the largest integer $g_p\left(A\right):=g\left(S_p\right)$ in ${\mathbb{N}}_0\setminus S_p$, called the p-Frobenius number. The cardinality of ${\mathbb{N}}_0\setminus S_p$ is called the p-genus and is denoted by $n_p\left(A\right):=n\left(S_p\right)$. The sum of the elements in ${\mathbb{N}}_0\setminus S_p$ is called the p-Sylvester sum and is denoted by $s_p\left(A\right):=s\left(S_p\right)$. This kind of concept is a generalization of the famous Diophantine problem of Frobenius since $p=0$ is the case when the original Frobenius number $g\left(A\right)=g_0\left(A\right)$, the genus $n\left(A\right)=n_0\left(A\right)$ and the Sylvester sum $s\left(A\right)=s_0\left(A\right)$ are recovered. We can call $S_p$ the p-numerical semigroup. Strictly speaking, when $p\ge 1$, $S_p$ does not include 0 since the integer 0 has only one representation, so it satisfies simple additivity, and the set $S_p\cup \left\{0\right\}$ becomes a numerical semigroup. For numerical semigroups, we refer to [16,17,18]. For the p-numerical semigroup, we refer to [19]. The recent study of the number of representation (denumerant), denoted by p in this paper, can be seen in [20,21,22]. In particular, in [23], an algorithm that computes the denumerant is shown. In [24], three simple reduction formulas for the denumerant are obtaine using the Bernoulli–Barnes polynomials. In [25], this algorithm is shown to avoid plenty of repeated computations and is, hence, faster.

We are interested in finding any closed or explicit form of the p-Frobenius number, which is even more difficult when $p>0$. For three or more variables, no concrete example had been found. Most recently, we have finally succeeded in giving the p-Frobenius number as closed-form expressions for the triangular number triplet ([26]), for repunits ([27,28]).

In this paper, we study the p-numerical semigroups of the triple $(W_i,W_{i+2},W_{i+k})$ for integers $i,k(\ge 3)$. We give explicit closed formulas of p-Frobenius numbers and p-genus of this triple. Note that the special cases for Fibonacci [1], Pell [4], and Jacobsthal triples [2,3] have already been studied.

The outline of this paper is as follows. In the next section, we introduce the concept of the p-Apéry set and show how it is used to obtain the p-Frobenius number, the p-genus and the p-Sylvester sum. In Section 3, we show the result for $p=0$. The structure is different for odd k and even k. In Section 4, we show the result for $p\ge 1$, which is yielded from that for $p=0$. In Section 5, we give an explicit form of the p-genus. The figures in Section 3 and Section 4 are helpful to find the calculation of the p-genus. In Section 6, we hint at some comments on a simple modification of the recurrence relation.

2. Preliminaries

We introduce the Apéry set (see [29]) below in order to obtain the formulas for $g_p\left(A\right)$, $n_p\left(A\right)$, and $s_p\left(A\right)$ technically. Without loss of generality, we assume that $a_1=min\left(A\right)$.

Definition 1.

Let p be a nonnegative integer. For a set of positive integers $A=\{a_1,a_2,\dots ,a_{\kappa }\}$ with $\gcd \left(A\right)=1$ and $a_1=min\left(A\right)$ we denote by:

$${\mathrm{Ap}}_p\left(A\right)={\mathrm{Ap}}_p(a_1,a_2,\dots ,a_{\kappa })=\{m_0^{\left(p\right)},m_1^{\left(p\right)},\dots ,m_{a_1-1}^{\left(p\right)}\},$$

the p-Apéry set of A, where each positive integer $m_i^{\left(p\right)}$ $(0\le i\le a_1-1)$ satisfies the conditions:

$$\left(\mathrm{i}\right)m_i^{\left(p\right)}\equiv i\left(\mathrm{mod}{a}_1\right),\left(\mathrm{ii}\right)m_i^{\left(p\right)}\in S_p\left(A\right),\left(\mathrm{iii}\right)m_i^{\left(p\right)}-a_1\notin S_p\left(A\right).$$

Note that $m_0^{\left(0\right)}$ is defined to be 0.

It follows that for each p:

$${\mathrm{Ap}}_p\left(A\right)\equiv \{0,1,\dots ,a_1-1\}\left(\mathrm{mod}{a}_1\right).$$

Even though it is hard to find any explicit form of $g_p\left(A\right)$ as well as $n_p\left(A\right)$ and $s_p\left(A\right)$$k\ge 3$, by using convenient formulas established in [30,31], we can obtain such values for some special sequences $(a_1,a_2,\dots ,a_{\kappa })$ after finding any regular structure of $m_j^{\left(p\right)}$. One convenient formula is on the power sum:

$$s_p^{\left(\mu \right)}\left(A\right):=\sum _{n\in {\mathbb{N}}_0\setminus S_p\left(A\right)}{n}^{\mu }$$

by using Bernoulli numbers $B_n$ defined by the generating function:

$$\frac{x}{e^x-1}=\sum _{n=0}^{\infty }{B}_n\frac{x^n}{n!},$$

and another convenient formula is on the weighted power sum ([32,33]):

$$s_{\lambda ,p}^{\left(\mu \right)}\left(A\right):=\sum _{n\in {\mathbb{N}}_0\setminus S_p\left(A\right)}{\lambda }^n{n}^{\mu }$$

by using Eulerian numbers $⟨\genfrac{}{}{0pt}{}{n}{m}⟩$ appearing in the generating function:

$$\sum _{k=0}^{\infty }{k}^n{x}^k=\frac{1}{{(1-x)}^{n+1}}\sum _{m=0}^{n-1}⟨\genfrac{}{}{0pt}{}{n}{m}⟩x^{m+1}(n\ge 1)$$

with $0^0=1$ and $⟨\genfrac{}{}{0pt}{}{0}{0}⟩=1$. Here, $\mu$ is a nonnegative integer and $\lambda \ne 1$. Some generalization of Bernulli numbers in connection with summation are devied in [34]. From these convenient formulas, many useful expressions are yielded as special cases. Some useful ones are given as follows. The Formulas (3) and (4) are entailed from $s_{\lambda ,p}^{\left(0\right)}\left(A\right)$ and $s_{\lambda ,p}^{\left(1\right)}\left(A\right)$, respectively. The proof of this lemma is given in [31] as a more general case.

Lemma 1.

Let κ, p, and μ be integers with $\kappa \ge 2$ and $p\ge 0$. Assume that $\gcd (a_1,a_2,\dots ,a_{\kappa })=1$. We have:

$$\begin{array}{cc}\hfill g_p(a_1,a_2,\dots ,a_{\kappa })& =\left(\underset{0\le j\le a_1-1}{\max }{m}_j^{\left(p\right)}\right)-a_1,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill n_p(a_1,a_2,\dots ,a_{\kappa })& =\frac{1}{a_1}\sum _{j=0}^{a_1-1}{m}_j^{\left(p\right)}-\frac{a_1-1}{2},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill s_p(a_1,a_2,\dots ,a_{\kappa })& =\frac{1}{2a_1}\sum _{j=0}^{a_1-1}{\left(m_j^{\left(p\right)}\right)}^2-\frac{1}{2}\sum _{j=0}^{a_1-1}{m}_j^{\left(p\right)}+\frac{a_1^2-1}{12}.\hfill \end{array}$$

(4)

Remark 1.

When $p=0$, the Formulas (2)–(4) reduce to the formulas by Brauer and Shockley [35] [Lemma 3], Selmer [36] [Theorem], and Tripathi [37] [Lemma 1] (the latter reference contained a typo, which was corrected in [38]), respectively:

$$\begin{array}{cc}\hfill g(a_1,a_2,\dots ,a_{\kappa })& =\left(\underset{0\le j\le a_1-1}{\max }{m}_j\right)-a_1,\hfill \\ \hfill n(a_1,a_2,\dots ,a_{\kappa })& =\frac{1}{a_1}\sum _{j=0}^{a_1-1}{m}_j-\frac{a_1-1}{2},\hfill \\ \hfill s(a_1,a_2,\dots ,a_{\kappa })& =\frac{1}{2a_1}\sum _{j=0}^{a_1-1}{\left(m_j\right)}^2-\frac{1}{2}\sum _{j=0}^{a_1-1}{m}_j+\frac{a_1^2-1}{12},\hfill \end{array}$$

where $m_j=m_j^{\left(0\right)}$ ($1\le j\le a_1-1$) with $m_0=m_0^{\left(0\right)}=0$.

3. The Case Where $\mathit{p}\mathbf{=}\mathbf{0}$

We use the following properties repeatedly. The proof is trivial and omitted.

Lemma 2.

For $i,k\ge 1$, we have:

$$\begin{array}{cc}\hfill & W_k|W_i\iff k|i,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \gcd (W_i,W_{i+2})=\left\{\begin{array}{cc}u\hfill & \mathit{if}\mathit{i}\mathit{is}\mathit{even};\hfill \\ 1\hfill & \mathit{if}\mathit{i}\mathit{is}\mathit{odd},\hfill \end{array}\right.\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & W_{i+k}=W_{i+1}{W}_k+v{W}_i{W}_{k-1},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & W_n\equiv \left\{\begin{array}{cc}0\left(\mathrm{mod}u\right)\hfill & \mathit{if}\mathit{n}\mathit{is}\mathit{even};\hfill \\ v^{\frac{n-1}{2}}\left(\mathrm{mod}u\right)\hfill & \mathit{if}\mathit{n}\mathit{is}\mathit{odd}.\hfill \end{array}\right.\hfill \end{array}$$

(8)

First of all, if i is odd and $3\le i\le k-1$, then by (1) and (7):

$$\begin{array}{cc}\hfill W_{i+k}-g_0(W_i,W_{i+2})& \ge W_{2i+1}-W_i{W}_{i+2}+W_i+W_{i+2}\hfill \\ \hfill & =W_{i+1}{W}_{i-1}+W_{i+2}+W_i>0.\hfill \end{array}$$

Hence, $g_0(W_i,W_{i+2},W_{i+k})=g_0(W_i,W_{i+2})$. Therefore, from now on, we consider the case only when i is even and k is odd, or when i is odd, with $i\ge k\ge 3$.

3.1. The Case Where k Is Odd

When k is odd, we choose nonnegative integers $\mathfrak{q}$ and $\mathfrak{r}$ as:

$$W_i=\mathfrak{q}{W}_k+\mathfrak{r}u,0\le \mathfrak{r}<W_k,$$

(9)

where $\mathfrak{q}=W_i/W_k$ if $k|i$ due to (5); otherwise $\mathfrak{q}$ is the largest integer, satisfying:

$$\mathfrak{q}\le \frac{W_i}{W_k}\mathrm{and}\mathfrak{q}\equiv \left\{\begin{array}{cc}0\left(\mathrm{mod}u\right)\hfill & \mathrm{if}i\mathrm{is}\mathrm{even};\hfill \\ v^{\frac{i-k}{2}}\left(\mathrm{mod}u\right)\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.$$

(10)

More directly, when i is even (and k is odd):

$$\mathfrak{q}=u⌊\frac{1}{u}⌊\frac{W_i}{W_k}⌋⌋.$$

(11)

When i is odd (and k is odd):

$$\mathfrak{q}=u⌊\frac{1}{u}\left(⌊\frac{W_i}{W_k}⌋-v^{\frac{i-k}{2}}\right)⌋+v^{\frac{i-k}{2}}.$$

(12)

Note that if $u=1$ ([2]), then always $\mathfrak{q}=⌊W_i/W_k⌋$.

In particular, if i is even and:

$$u>\frac{W_i}{W_k},\mathrm{then}\mathfrak{q}=0,\mathrm{so}\mathfrak{r}=W_i/u.$$

If $k|i$, then by (5) $W_k|W_i$. So, when i is even, by (8) $u|W_i$. Thus, we get:

$$\mathfrak{q}=\frac{W_i}{W_k},\mathrm{so}\mathfrak{r}=0.$$

When $k|i$ and i is odd, by $W_i\equiv v^{\frac{i-1}{2}}$ and $W_k\equiv v^{\frac{k-1}{2}}$, there exists an integer h such that $v^{\frac{i-1}{2}}\equiv h{v}^{\frac{k-1}{2}}\left(\mathrm{mod}u\right)$. By $\gcd (u,v)=1$, $h\equiv v^{\frac{i-k}{2}}\left(\mathrm{mod}u\right)$. Thus:

$$u\left|\left(\frac{W_i}{W_k}-v^{\frac{i-k}{2}}\right)\right.$$

Thus, we get:

$$\mathfrak{q}=\frac{W_i}{W_k},so\mathfrak{r}=0.$$

We use the following identity.

Lemma 3.

For $i,v\ge 3$, we have:

$$\mathfrak{r}{W}_{i+2}+\mathfrak{q}{W}_{i+k}=\left(W_{i+1}+v(\mathfrak{q}{W}_{k-1}+\mathfrak{r})\right)W_i.$$

Proof. 

By (1) and (7) together with (9), we get:

$$\begin{array}{cc}\hfill \mathrm{LHS}-\mathrm{RHS}& =\mathfrak{r}(u^2+v)W_i+\mathfrak{r}uvs.W_{i-1}+\mathfrak{q}(W_{i+1}{W}_k+v{W}_i{W}_{k-1})\hfill \\ \hfill & -(u{W}_i+v{W}_{i-1})W_i-\mathfrak{r}vs.W_i-\mathfrak{q}vs.W_i{W}_{k-1}\hfill \\ \hfill & =0.\hfill \end{array}$$

□

Assume that $k\nmid i$ (the case $k\mid i$ is discussed later). Then, the elements of the (0-)Apéry set are given in Figure 1. Here, we consider the expression:

$$t_{y,z}:=y{W}_{i+2}+z{W}_{i+k}(y,z\ge 0)$$

or simply the position $(y,z)$.

Figure 1. ${\mathrm{Ap}}_0(W_i,W_{i+2},W_{i+k})$ for odd k.

We shall show that all the elements in Figure 1 constitute the sequence ${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}$ in the vertical y direction. However, if i is odd and i is even, the situation of this sequence is different. In short, if i is odd, the sequence appears continuously, but if i is even, the sequence is divided into u subsequences.

First, let i be odd. Then, by $\gcd (W_i,W_{i+2})=1$, we have:

$${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}={\left\{\mathcal{l}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}.$$

By (7), we get:

$$W_{i+2}{W}_k-u{W}_{i+k}=v^2{W}_i{W}_{k-2}$$

(13)

Hence:

$$W_{i+2}{W}_k\equiv u{W}_{i+k}\left(\mathrm{mod}{W}_i\right)\mathrm{and}{W}_{i+2}{W}_k>u{W}_{i+k}.$$

(14)

Thus, the element at $(W_k,j)$ ($0\le j\le \mathfrak{q}-1$) cannot be an element of ${\mathrm{Ap}}_0\left(A\right)$ but $(0,u+j)$ as the same residue modulo $W_i$, where $A=\{W_i,W_{i+2},W_{i+k}\}$. Next, by Lemma 3, we have:

$$\mathfrak{r}{W}_{i+2}+\mathfrak{q}{W}_{i+k}\equiv 0\left(\mathrm{mod}{W}_i\right)\mathrm{and}\mathfrak{r}{W}_{i+2}+\mathfrak{q}{W}_{i+k}>0.$$

Thus, the element at $(\mathfrak{r},\mathfrak{q}+j)$ ($0\le j\le u-1$) cannot be an element of ${\mathrm{Ap}}_0\left(A\right)$ but $(0,j)$.

Therefore, the sequence ${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}$ is divided into the longer parts with length $W_k$ and the shorter parts with length $\mathfrak{r}$. Namely, the longer part is of the subsequence:

$$(0,j),(1,j),\dots ,(W_k-1,j)(j=0,1,\dots ,\mathfrak{q}-1)$$

with the next element at $(0,u+j)$. The shorter part is of the subsequence

$$(0,\mathfrak{q}+j),(1,\mathfrak{q}+j),\dots ,(\mathfrak{r}-1,\mathfrak{q}+j)(j=0,1,\dots ,u-1)$$

with the next element at $(0,j)$. Since $\gcd (W_{i+2},W_{i+k})=1$, all elements in ${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}$ are different modulo $W_i$.

Next, let i be even. Then by $\gcd (W_i,W_{i+2})=u$, we have:

$${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i/u-1}={\left\{\mathcal{l}(\mathrm{mod}{W}_i/u)\right\}}_{\mathcal{l}=0}^{W_i/u-1}.$$

Hence:

$${\left\{\mathcal{l}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}={\cup }_{\kappa =0}^{u-1}{\{\mathcal{l}{W}_{i+2}+\kappa W_{i+k}\left(\mathrm{mod}{W}_i\right)\}}_{\mathcal{l}=0}^{W_i/u-1}$$

with ${\{\mathcal{l}{W}_{i+2}+{\kappa }_1{W}_{i+k}\left(\mathrm{mod}{W}_i\right)\}}_{\mathcal{l}=0}^{W_i/u-1}\cap {\{\mathcal{l}{W}_{i+2}+{\kappa }_2{W}_{i+k}\left(\mathrm{mod}{W}_i\right)\}}_{\mathcal{l}=0}^{W_i/u-1}=\varnothing$ (${\kappa }_1\ne {\kappa }_2$). By the determination of $\mathfrak{q}$ in (11), we see that $u|\mathfrak{q}$. So, we use the relation (14). Thus, each subsequence is given as the following points. For $z=0,1,\dots ,u-1$:

$$\begin{array}{cc}\hfill & (0,z),(1,z),\dots ,(W_k-1,z),(0,u+z),(1,u+z),\dots ,(W_k-1,u+z),\hfill \\ \hfill & (0,2u+z),(1,2u+z),\dots ,(W_k-1,2u+z),\dots \dots ,\hfill \\ \hfill & (0,\mathfrak{q}-u+z),(1,\mathfrak{q}-u+z),\dots ,(W_k-1,\mathfrak{q}-u+z),\hfill \\ \hfill & (0,\mathfrak{q}+z),(1,\mathfrak{q}+z),\dots ,(\mathfrak{r}-1,\mathfrak{q}+z)\hfill \end{array}$$

with next element is at $(0,z)$, coming back to the first one, because of Lemma 3. In addition, by (8), all terms of the above subsequence are:

$$y{W}_{i+2}+z{W}_{i+k}\equiv z{v}^{\frac{i+k-1}{2}}\left(\mathrm{mod}u\right).$$

Since $\gcd (u,v)=1$, this is equivalent to $z\left(\mathrm{mod}u\right)$ ($z=0,1,\dots ,u-1$). Therefore, there is no overlapped element among all subsequences. By (9), the total number of terms in each subsequence is:

$$\frac{\mathfrak{q}}{u}{W}_k+\mathfrak{r}=\frac{W_i}{u}$$

as expected.

By Figure 1, the candidates of the largest element of ${\mathrm{Ap}}_0\left(A\right)$ are at $(\mathfrak{r}-1,\mathfrak{q}+u-1)$ or at $(W_k-1,\mathfrak{q}-1)$. Since $(\mathfrak{r}-1)W_{i+2}+(\mathfrak{q}+u-1)W_{i+k}>(W_k-1)W_{i+2}+(\mathfrak{q}-1)W_{i+k}$ is equivalent to $\mathfrak{r}{W}_{i+2}>v^2{W}_i{W}_{k-2}$, by Lemma 1 (2), if $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_0(W_i,W_{i+2},W_{i+k})=(\mathfrak{r}-1)W_{i+2}+(\mathfrak{q}+u-1)W_{i+k}-W_i.$$

If $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_0(W_i,W_{i+2},W_{i+k})=(W_k-1)W_{i+2}+(\mathfrak{q}-1)W_{i+k}-W_i.$$

• The case k is odd with $k|i$

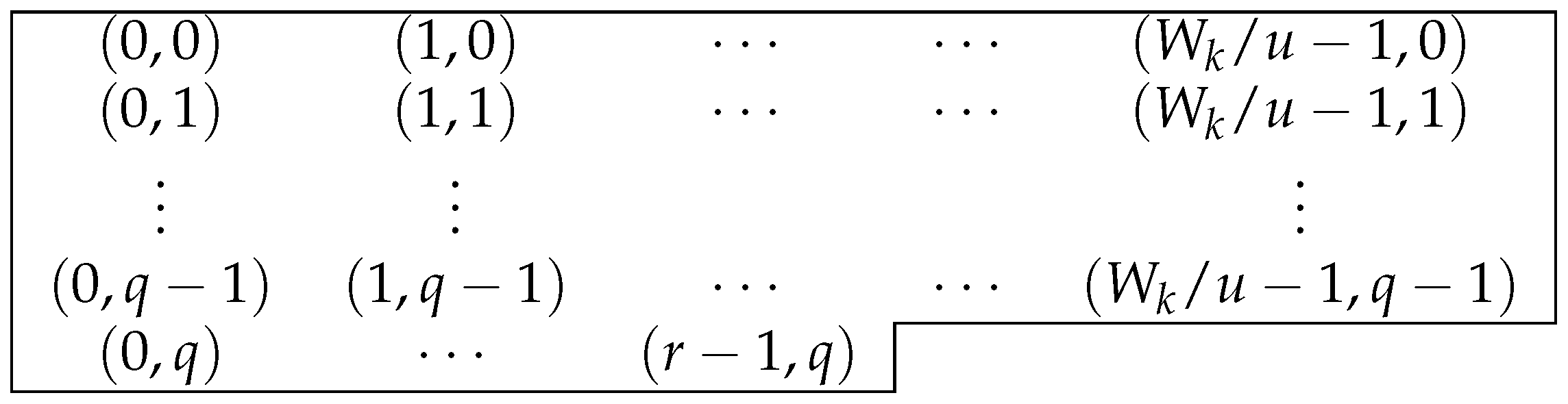
When k is odd and $k|i$, we get $\mathfrak{q}=W_i/W_k$ and $\mathfrak{r}=0$. Hence, the elements of the (0-)Apéry set are given in Figure 2.

Figure 2. ${\mathrm{Ap}}_0\left(W_i,W_{i+2},W_{i+k}\right)$ when $k|i$.

Similarly to the case $k\nmid i$, when i is odd, so $u{W}_k\nmid W_i$, the sequence ${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}$ simply becomes one sequence by combining all the subsequences with length $W_k$ and with length $\mathfrak{r}$. When i is even, so $u{W}_k\mid W_i$, the sequence ${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}$ consists of u subsequences with the same length $W_i/u$.

By Figure 2, the largest element of ${\mathrm{Ap}}_0\left(A\right)$ is at $(W_k-1,W_i/W_k-1)$. Hence:

$$g_0(W_i,W_{i+2},W_{i+k})=(W_k-1)W_{i+2}+\left(\frac{W_i}{W_k}-1\right)W_{i+k}-W_i.$$

In fact, this is included in the case where $k\nmid i$ and $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{i-2}$.

3.2. The Case Where k Is Even

When k is even (so i is odd), we choose nonnegative integers q and r as:

$$W_i=q\frac{W_k}{u}+r,0\le r<\frac{W_k}{u},$$

(15)

where $q=⌊u{W}_i/W_k⌋$. Note that $W_k/u$ is an integer for even k. Note that $k\nmid i$ because otherwise i is also even. Then, the elements of the (0-)Apéry set are given in Figure 3.

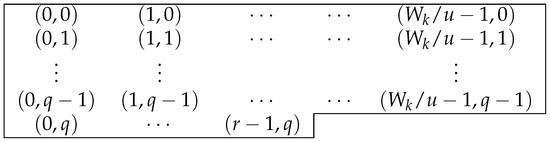
Figure 3. ${\mathrm{Ap}}_0\left(P_{2i+1}\left(u\right),P_{2i+3}\left(u\right),P_{2i+k+1}\left(u\right)\right)$ for even k.

Similarly to the case where k is odd in (14), we have:

$$W_{i+2}\frac{W_k}{u}\equiv W_{i+k}\left(\mathrm{mod}{W}_i\right)\mathrm{and}{W}_{i+2}\frac{W_k}{u}>W_{i+k}.$$

Thus, the element at $(W_k/u,j)$ ($0\le j\le q-1$) cannot be an element of ${\mathrm{Ap}}_0\left(A\right)$ but $(0,j+1)$ as the same residue modulo $W_i$. The sequence ${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}$ is divided into the longer parts with length $W_k/u$ and one shorter part with length r. Namely, the longer part is of the subsequence:

$$(0,j),(1,j),\dots ,(W_k/u-1,j)(j=0,1,\dots ,q-1)$$

with the next element at $(0,j+1)$. One shorter part is of the subsequence:

$$(0,q),(1,q),\dots ,(r-1,q)$$

with the next element at $(0,0)$. Notice that similarly to Lemma 3, we have:

$$r{W}_{i+2}+q{W}_{i+k}\equiv 0\left(\mathrm{mod}{W}_i\right).$$

Since $\gcd (W_{i+2},W_{i+k})=1$, all elements in ${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}$ are different modulo $W_i$. Then by $\gcd (W_i,W_{i+2})=1$, we have:

$${\left\{\mathcal{l}{W}_{i+2}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}={\left\{\mathcal{l}\left(\mathrm{mod}{W}_i\right)\right\}}_{\mathcal{l}=0}^{W_i-1}.$$

By Figure 3, the candidates of the largest element of ${\mathrm{Ap}}_0\left(A\right)$ are at $(r-1,q)$ or at $(W_k/u-1,q-1)$. Since $(r-1)W_{i+2}+q{W}_{i+k}>(W_k/u-1)W_{i+2}+(q-1)W_{i+k}$ is equivalent to $ru{W}_{i+2}>v^2{W}_i{W}_{k-2}$, by Lemma 1 (2), if $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_0(W_i,W_{i+2},W_{i+k})=(r-1)W_{i+2}+q{W}_{i+k}-W_i.$$

If $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_0(W_i,W_{i+2},W_{i+k})=\left(\frac{W_k}{u}-1\right)W_{i+2}+(q-1)W_{i+k}-W_i.$$

Notice that $ru{W}_{i+2}=v^2{W}_i{W}_{k-2}$ may occur in some cases. For example, $(i,k,u,v)=(9,2,6,133)$. In this case, both of the two formulas are valid, yielding the Frobenius number $g_0\left(A\right)=5949962315313983$.

4. The Case Where $\mathit{p}\mathbf{>}\mathbf{0}$

It is important to see that the elements of ${\mathrm{Ap}}_p\left(A\right)$ are determined from those of ${\mathrm{Ap}}_{p-1}\left(A\right)$.

4.1. When k Is Odd

• When $p=1$

The corresponding relations from ${\mathrm{Ap}}_0\left(A\right)$ to ${\mathrm{Ap}}_1\left(A\right)$ are as follows, see Figure 4.

Figure 4. ${\mathrm{Ap}}_p(W_i,W_{i+2},W_{i+k})$ ($p=0,1$) for odd k.

[The first u rows]

$$\begin{array}{cc}\hfill & (y,z)\to (y+\mathfrak{r},z+\mathfrak{q})(0\le y\le W_k-\mathfrak{r}-1,0\le z\le u-1),\hfill \\ \hfill & (y,z)\to (y-W_k+\mathfrak{r},z+\mathfrak{q}+u)(W_k-\mathfrak{r}\le y\le W_k-1,0\le z\le u-1)\hfill \end{array}$$

by Lemma 3 and

$$\begin{array}{cc}\hfill (-W_k+\mathfrak{r})W_{i+2}+(\mathfrak{q}+u)W_{i+k}=(W_{i+1}+v(\mathfrak{q}{W}_{k-1}+\mathfrak{r})-v^2{W}_{k-2})W_i& \\ \hfill \left(\mathrm{Lemma}3\mathrm{and}\left(13\right)\right)& ,\hfill \end{array}$$

respectively. Note that when $\mathfrak{r}=0$, the second corresponding relation does not exist. This also implies that all the elements at $(y+\mathfrak{r},z+\mathfrak{q})$ and $(y-W_k+\mathfrak{r},z+\mathfrak{q}+u)$ can be expressed in terms of $(W_i,W_{i+2},W_{i+k})$ in at least two ways.

[Others]

$$\begin{array}{cc}\hfill (y,z)\to (y+W_k,z-u)& (0\le y\le W_k-1,u\le z\le \mathfrak{q}-1;\hfill \\ \hfill & 0\le y\le \mathfrak{r}-1,\mathfrak{q}\le z\le \mathfrak{q}+u-1)\hfill \end{array}$$

by the identity (13). This also implies that all the elements at $(y+W_k,z-u)$ can be expressed in at least two ways.

By Figure 4, there are four candidates to take the largest value of ${\mathrm{Ap}}_1\left(A\right)$. Namely, the values at:

$$\begin{array}{cc}\hfill & (\mathfrak{r}-1,\mathfrak{q}+2u-1),(W_k-1,\mathfrak{q}+u-1),\hfill \\ \hfill & (W_k+\mathfrak{r}-1,\mathfrak{q}-1),(2W_k-1,\mathfrak{q}-u-1).\hfill \end{array}$$

If $2u{W}_{i+k}>W_k{W}_{i+2}$, one of the elements at $(\mathfrak{r}-1,\mathfrak{q}+2u-1)$ and at $(W_k-1,\mathfrak{q}+u-1)$ is the largest. In this case, if $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_1(W_i,W_{i+2},W_{i+k})=(\mathfrak{r}-1)W_{i+2}+(\mathfrak{q}+2u-1)W_{i+k}-W_i.$$

If $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_1(W_i,W_{i+2},W_{i+k})=(W_k-1)W_{i+2}+(\mathfrak{q}+u-1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$, one of the elements at $(W_k+\mathfrak{r}-1,\mathfrak{q}-1)$ and at $(2W_k-1,\mathfrak{q}-u-1)$ is the largest. In this case, if $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_1(W_i,W_{i+2},W_{i+k})=(W_k+\mathfrak{r}-1)W_{i+2}+(\mathfrak{q}-1)W_{i+k}-W_i.$$

If $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_1(W_i,W_{i+2},W_{i+k})=(2W_k-1)W_{i+2}+(\mathfrak{q}-u-1)W_{i+k}-W_i.$$

Example 1.

When $(i,k,u,v)=(5,3,4,3)$, the first identity is applied:

$$\begin{array}{cc}\hfill g_1(W_5,W_7,W_8)& =g_1(409,8827,41008)\hfill \\ \hfill & =11W_7+26W_8-W_5=1162896.\hfill \end{array}$$

Indeed, there are two representations in terms of $W_5,W_7,W_8$ as:

$$11W_7+26W_8=2155W_5+18W_7+3W_8,$$

which is the largest element of ${\mathrm{Ap}}_1(W_5,W_7,W_8)$. In fact, the second, the third and the fourth identities yield the smaller values:

$$\begin{array}{cc}\hfill 1060653& =18W_7+22W_8-W_5(=2164W_5+6W_7+3W_8-W_5),\hfill \\ \hfill 1002545& =30W_7+18W_8-W_5(=9W_5+11W_7+22W_8-W_5),\hfill \\ \hfill 900302& =37W_7+14W_8-W_5(=9W_5+18W_7+18W_8-W_5),\hfill \end{array}$$

respectively.

When $(i,k,u,v)=(5,3,2,7)$, the second identity is applied:

$$\begin{array}{cc}\hfill & g_1(W_5,W_7,W_8)=g_1(149,2143,8136)\hfill \\ \hfill & =10W_7+14W_8-W_5(=753W_5+7W_7+W_8-W_5)=135185.\hfill \end{array}$$

In fact, the first, the third, and the fourth identities yield the smaller values:

$$134313,125342,126214,$$

respectively.

When $(i,k,u,v)=(5,3,1,4)$, the third identity is applied:

$$\begin{array}{cc}\hfill & g_1(W_5,W_7,W_8)=g_1(29,181,441)\hfill \\ \hfill & =8W_7+4W_8-W_5(=16W_5+3W_7+5W_8-W_5)=3183.\hfill \end{array}$$

In fact, the first, the second, and the fourth identities yield the smaller values:

$$3160,2900,2923,$$

respectively.

When $(i,k,u,v)=(5,3,3,35)$, the fourth identity is applied:

$$\begin{array}{cc}\hfill & g_1(W_5,W_7,W_8)=g_1(2251,123929,898467)\hfill \\ \hfill & =87W_7+46W_8-W_5(=1225W_5+43W_7+49W_8-W_5)=521090543.\hfill \end{array}$$

In fact, the first, the second, and the third identities yield the smaller values:

$$51396298,52046980,51458372,$$

respectively.

• When $p\ge 2$

The similar corresponding relations to the case $p=1$ are also applied for $p\ge 2$. When $p=2$, the elements of the first u rows of the main area (the second block from the left) correspond to fill the gap below the left-most block:

$$\begin{array}{cc}\hfill & (y,z)\to (y-W_k+\mathfrak{r},z+\mathfrak{q}+u)(W_k\le y\le 2W_k-\mathfrak{r}-1,0\le z\le u-1),\hfill \\ \hfill & (y,z)\to (y-2W_k+\mathfrak{r},z+\mathfrak{q}+2u)(2W_k-\mathfrak{r}\le y\le 2W_k-1,0\le z\le u-1)\hfill \end{array}$$

The other elements of the main area correspond to those in the block immediately to the right to go up the u row:

$$\begin{array}{cc}\hfill (y,z)\to (y+W_k,z-u)& (W_k\le y\le 2W_k-1,u\le z\le \mathfrak{q}-u-1;\hfill \\ \hfill & W_k\le y\le W_k+\mathfrak{r}-1,\mathfrak{q}-u\le z\le \mathfrak{q}-1).\hfill \end{array}$$

The elements of the stair areas correspond to those in the block immediately to the right in the form as it is to go up the $2u$ row:

$$\begin{array}{cc}\hfill (y,z)\to (y+W_k,z-2u)& (\mathfrak{r}\le y\le W_k-1,\mathfrak{q}+u\le z\le \mathfrak{q}+2u-1;\hfill \\ \hfill & 0\le y\le \mathfrak{r}-1,\mathfrak{q}+2u\le z\le \mathfrak{q}+3u-1).\hfill \end{array}$$

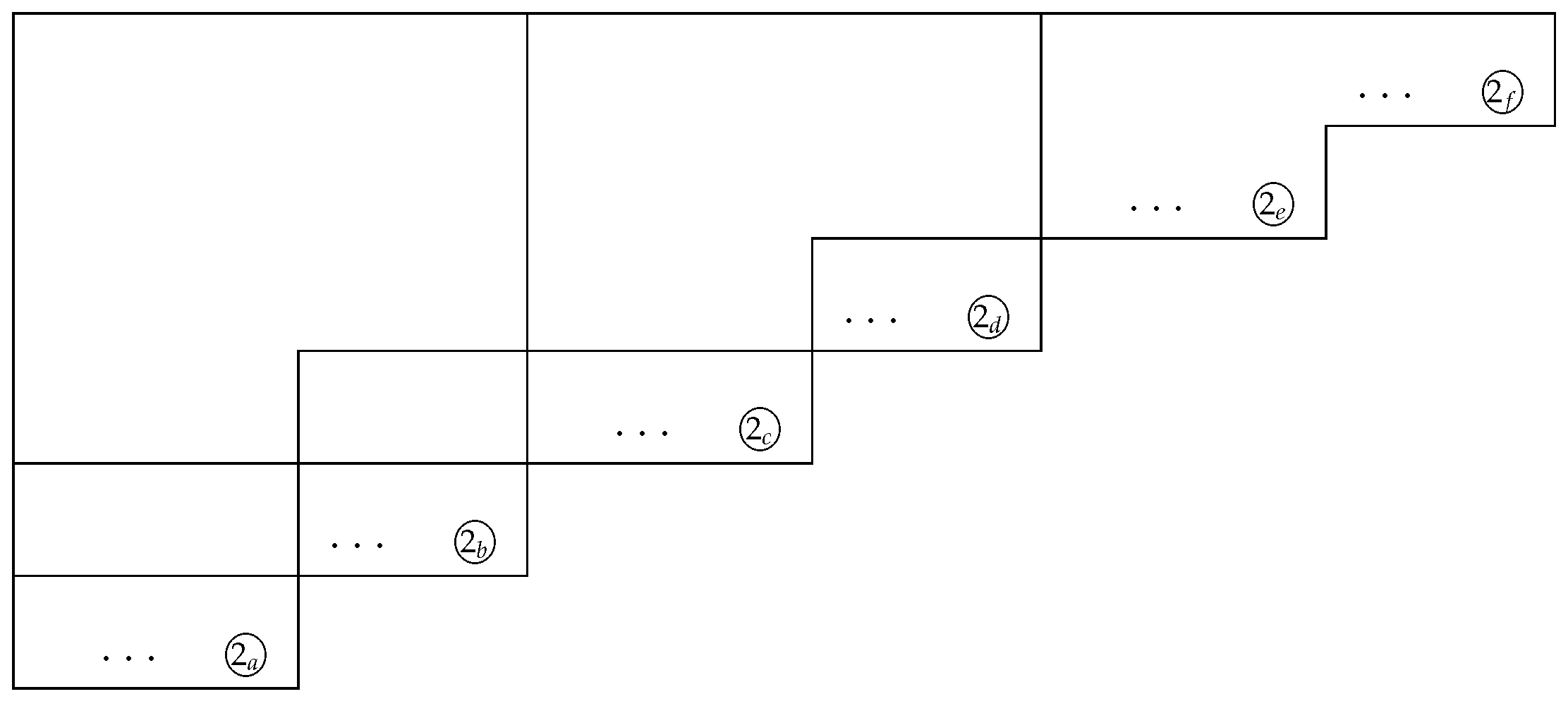
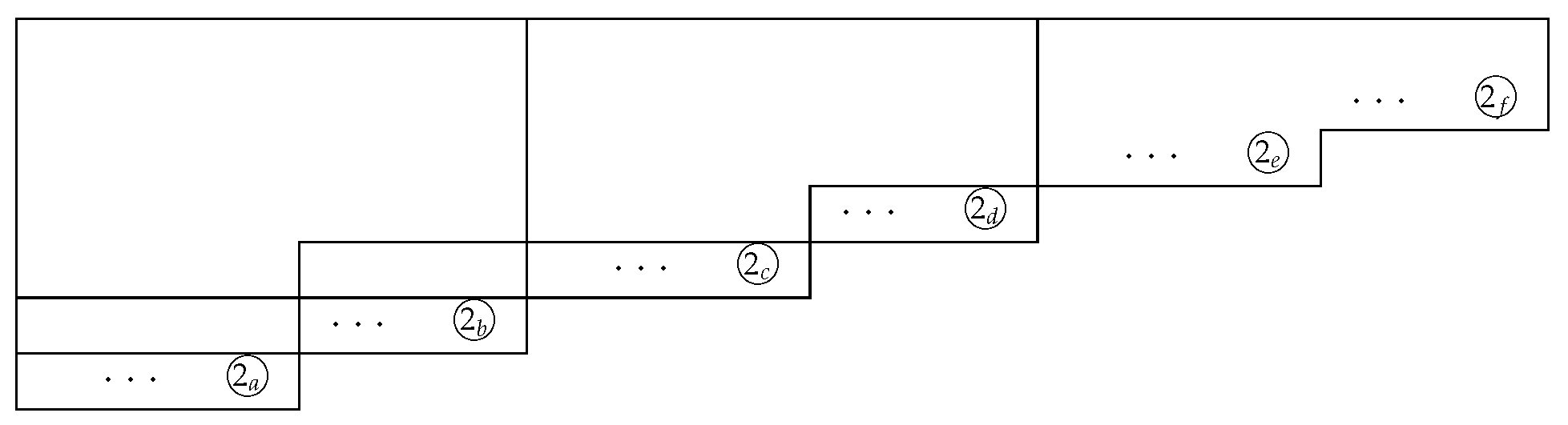
Figure 5 shows the areas in which the elements of p-Apéry set exist for $p=0,1,2$. The outermost lower right area is the area where the elements of the 2-Apéry set exist. We can also show that all the elements of the 2-Apéry set have at least three distinct representations in terms of $W_i,W_{i+2},W_{i+k}$.

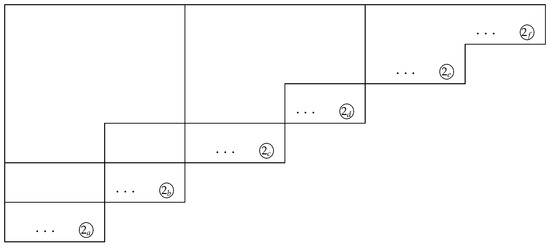
Figure 5. ${\mathrm{Ap}}_p\left(W_i,W_{i+2},W_{i+k}\right)$ ($p=0,1,2$) for odd k.

From Figure 5, there are six candidates to take the largest element of ${\mathrm{Ap}}_2\left(A\right)$. These elements are indicated as follows:

If $u{W}_{i+k}>(W_k-\mathfrak{r})W_{i+2}$ (or $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$), one of those at , , and is the largest. Otherwise, one of those at , , and is the largest. However, it is clear that one of the values at or (respectively, or ) is larger than at (respectively, ). Hence, if $2u{W}_{i+k}>W_k{W}_{i+2}$, then the element at (respectively, ) is the largest. Otherwise, the element at (respectively, ) is the largest.

In conclusion, if $2u{W}_{i+k}>W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_2(W_i,W_{i+2},W_{i+k})=(\mathfrak{r}-1)W_{i+2}+(\mathfrak{q}+3u-1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}>W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_2(W_i,W_{i+2},W_{i+k})=(W_k-1)W_{i+2}+(\mathfrak{q}+2u-1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_2(W_i,W_{i+2},W_{i+k})=(2W_k+\mathfrak{r}-1)W_{i+2}+(\mathfrak{q}-u-1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_2(W_i,W_{i+2},W_{i+k})=(3W_k-1)W_{i+2}+(\mathfrak{q}-2u-1)W_{i+k}-W_i.$$

In general, for an integer $p>0$, it is sufficient to compare two elements at both ends, see Figure 6. If $2u{W}_{i+k}>W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=(\mathfrak{r}-1)W_{i+2}+\left(\mathfrak{q}+(p+1)u-1\right)W_{i+k}-W_i.$$

Figure 6. ${\mathrm{Ap}}_p\left(W_i,W_{i+2},W_{i+k}\right)$ for odd k.

If $2u{W}_{i+k}>W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=(W_k-1)W_{i+2}+(\mathfrak{q}+pu-1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=(p{W}_k+\mathfrak{r}-1)W_{i+2}+\left(\mathfrak{q}-(p-1)u-1\right)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=\left((p+1)W_k-1\right)W_{i+2}+(\mathfrak{q}-pu-1)W_{i+k}-W_i.$$

The positions of the elements of ${\mathrm{Ap}}_p\left(A\right)$ below the left-most block and the positions of ${\mathrm{Ap}}_p\left(A\right)$ in the right-most block are arranged as shown in Figure 6.

This situation is continued as long as $z=\mathfrak{q}-pu\ge 0$. However, when $p>\mathfrak{q}/u-1$, the shape of the block on the right side collapses. Thus, the regularity of taking the maximum value of ${\mathrm{Ap}}_p\left(A\right)$ is broken. Hence, the fourth case holds until $p\le ⌊\mathfrak{q}/u⌋-1$ and other cases hold for $p\le ⌊\mathfrak{q}/u⌋$.

In conclusion, when k is odd, the p-Frobenius number is given as follows.

Theorem 1.

Let i be an integer and k be odd with $3\le k\le i$. Let $\mathfrak{q}$ and $\mathfrak{r}$ be determined as (9) and (10). For $0\le p\le \mathfrak{q}/u$, if $2u{W}_{i+k}>W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=(\mathfrak{r}-1)W_{i+2}+\left(\mathfrak{q}+(p+1)u-1\right)W_{i+k}-W_i.$$

If $2u{W}_{i+k}>W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=(W_k-1)W_{i+2}+(\mathfrak{q}+pu-1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=(p{W}_k+\mathfrak{r}-1)W_{i+2}+\left(\mathfrak{q}-(p-1)u-1\right)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $\mathfrak{r}{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then for $p\le q/u-1$:

$$g_p(W_i,W_{i+2},W_{i+k})=\left((p+1)W_k-1\right)W_{i+2}+(\mathfrak{q}-pu-1)W_{i+k}-W_i.$$

Example 2.

When $(i,k,u,v)=(5,3,3,7)$, the first identity is applied. Since $\mathfrak{q}=19$ and $\mathfrak{r}=5$, for $0\le p\le ⌊19/3⌋=6$ we have:

$$\begin{array}{c}{\left\{g_p(W_5,W_7,W_8)\right\}}_{p=0}^6={\left\{g_p(319,6553,29739)\right\}}_{p=0}^6\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=650412,739629,828846,918063,1007280,1096497,1185714.\end{array}$$

Namely, the corresponding element for each integer is at $(4,3p+21)$ ($p=0,1,\dots ,6$). However, for $p\ge 7$, the p-Frobenius numbers can be computed neither by the above formula nor by any other closed formulas. Namely, the real value is $g_7\left(A\right)=1218479$, corresponding to $(9,39)$, though the formula gives 1274931, corresponding to $(4,42)$.

4.2. When k Is Even

• When $p=1$

Similarly to the odd case where k is odd, the elements of ${\mathrm{Ap}}_p\left(A\right)$ can be determined from those of ${\mathrm{Ap}}_{p-1}\left(A\right)$. When $p=1$, there are corresponding relations as follows.

[The first row $z=0$]

$$\begin{array}{cc}\hfill & (y,0)\to (y+r,z+q)(0\le y\le W_k/u-r-1),\hfill \\ \hfill & (y,0)\to (y-W_k/u+r,z+q+1)(W_k/u-r\le y\le W_k/u-1)\hfill \end{array}$$

with

$$\begin{array}{c}\hfill r{W}_{i+2}+q{W}_{i+k}=(W_{i+1}+v(q{W}_{k-1}+r))W_i\end{array}$$

due to (15). Note that when $r=0$ the second corresponding relation does not exist. This also implies that all the elements at $(y+r,z+q)$ and $(y-W_k/u+r,z+q+1)$ can be expressed in terms of $(W_i,W_{i+2},W_{i+k})$ in at least two ways.

[Others]

$$\begin{array}{cc}\hfill (y,z)\to (y+W_k/u,z-1)& (0\le y\le W_k/u-1,1\le z\le q-1;\hfill \\ \hfill & 0\le y\le r-1,z=q)\hfill \end{array}$$

by the identity (13). This also implies that all the elements at $(y+W_k/u,z-1)$ can be expressed in at least two ways.

By Figure 7, there are four candidates to take the largest value of ${\mathrm{Ap}}_1\left(A\right)$. Namely, the values at:

$$\begin{array}{cc}\hfill & (r-1,q+1),(W_k/u-1,q),\hfill \\ \hfill & (W_k/u+r-1,q-1),(2W_k/u-1,q-2).\hfill \end{array}$$

Figure 7. ${\mathrm{Ap}}_p(W_i,W_{i+2},W_{i+k})$ ($p=0,1$) for even k.

If $2u{W}_{i+k}>W_k{W}_{i+2}$, one of the elements at $(r-1,q+1)$ and at $(W_k/u-1,q)$ is the largest. In this case, if $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_1(W_i,W_{i+2},W_{i+k})=(r-1)W_{i+2}+(q+1)W_{i+k}-W_i.$$

If $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then

$$g_1(W_i,W_{i+2},W_{i+k})=\left(\frac{W_k}{u}-1\right)W_{i+2}+q{W}_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$, one of the elements at $(W_k/u+r-1,q-1)$ and at $(2W_k/u-1,q-2)$ is the largest. In this case, if $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_1(W_i,W_{i+2},W_{i+k})=\left(\frac{W_k}{u}+r-1\right)W_{i+2}+(q-1)W_{i+k}-W_i.$$

If $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_1(W_i,W_{i+2},W_{i+k})=\left(\frac{2W_k}{u}-1\right)W_{i+2}+(q-2)W_{i+k}-W_i.$$

• When $p\ge 2$

The situation is similar for $p\ge 2$. From Figure 8, there are six candidates to take the largest element of ${\mathrm{Ap}}_2\left(A\right)$. These elements are indicated as follows:

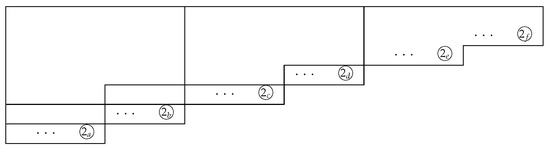
Figure 8. ${\mathrm{Ap}}_p(W_i,W_{i+2},W_{i+k})$ ($p=0,1,2$) for even k.

Similarly to the case where k is odd, middle element at and at cannot take the largest value. Hence, if $2u{W}_{i+k}>W_k{W}_{i+2}$, then the element at (respectively, ) is the largest. Otherwise, the element at (respectively, ) is the largest.

In conclusion, if $2u{W}_{i+k}>W_k{W}_{i+2}$ and $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_2(W_i,W_{i+2},W_{i+k})=(r-1)W_{i+2}+(q+2)W_{i+k}-W_i.$$

If $2u{W}_{i+k}>W_k{W}_{i+2}$ and $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_2(W_i,W_{i+2},W_{i+k})=\left(\frac{W_k}{u}-1\right)W_{i+2}+(q+1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_2(W_i,W_{i+2},W_{i+k})=\left(\frac{2W_k}{u}+r-1\right)W_{i+2}+(q-2)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_2(W_i,W_{i+2},W_{i+k})=\left(\frac{3W_k}{u}-1\right)W_{i+2}+(q-3)W_{i+k}-W_i.$$

In general, for an integer $p>0$, it is sufficient to compare two elements at both ends, see Figure 9. If $2u{W}_{i+k}>W_k{W}_{i+2}$ and $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=(r-1)W_{i+2}+(q+p)W_{i+k}-W_i.$$

If $2u{W}_{i+k}>W_k{W}_{i+2}$ and $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=\left(\frac{W_k}{u}-1\right)W_{i+2}+(q+p-1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=\left(\frac{p{W}_k}{u}+r-1\right)W_{i+2}+(q-p)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=\left(\frac{(p+1)W_k}{u}-1\right)W_{i+2}+(q-p-1)W_{i+k}-W_i.$$

Figure 9. ${\mathrm{Ap}}_p(W_i,W_{i+2},W_{i+k})$ for even k.

The positions of the elements of ${\mathrm{Ap}}_p\left(A\right)$ below the left-most block and the positions of ${\mathrm{Ap}}_p\left(A\right)$ in the right-most block are arranged as shown in Figure 6.

This situation is continued as long as $z=q-p-1\ge 0$. However, when $p=q$, the shape of the block on the right side collapses. Namely, we cannot take the value at $\left((p+1)W_k/u-1,q-p-1\right)$. Thus, the regularity of taking the maximum value of ${\mathrm{Ap}}_p\left(A\right)$ is broken. Hence, the fourth case holds until $p\le q-1$, and other cases hold for $p\le q$.

In conclusion, when k is even, the p-Frobenius number is given as follows.

Theorem 2.

Let i be an integer and k be even with $3\le k\le i$. Let q and r be determined as (15). For $0\le p\le q$, if $2u{W}_{i+k}>W_k{W}_{i+2}$ and $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=(r-1)W_{i+2}+(q+p)W_{i+k}-W_i.$$

If $2u{W}_{i+k}>W_k{W}_{i+2}$ and $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=\left(\frac{W_k}{u}-1\right)W_{i+2}+(q+p-1)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $ru{W}_{i+2}\ge v^2{W}_i{W}_{k-2}$, then:

$$g_p(W_i,W_{i+2},W_{i+k})=\left(\frac{p{W}_k}{u}+r-1\right)W_{i+2}+(q-p)W_{i+k}-W_i.$$

If $2u{W}_{i+k}<W_k{W}_{i+2}$ and $ru{W}_{i+2}\le v^2{W}_i{W}_{k-2}$, then for $0\le p\le q-1$:

$$g_p(W_i,W_{i+2},W_{i+k})=\left(\frac{(p+1)W_k}{u}-1\right)W_{i+2}+(q-p-1)W_{i+k}-W_i.$$

Example 3.

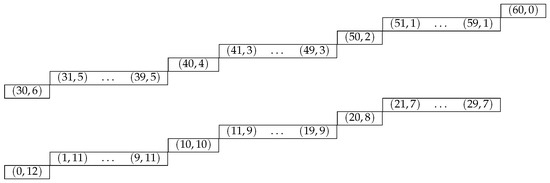
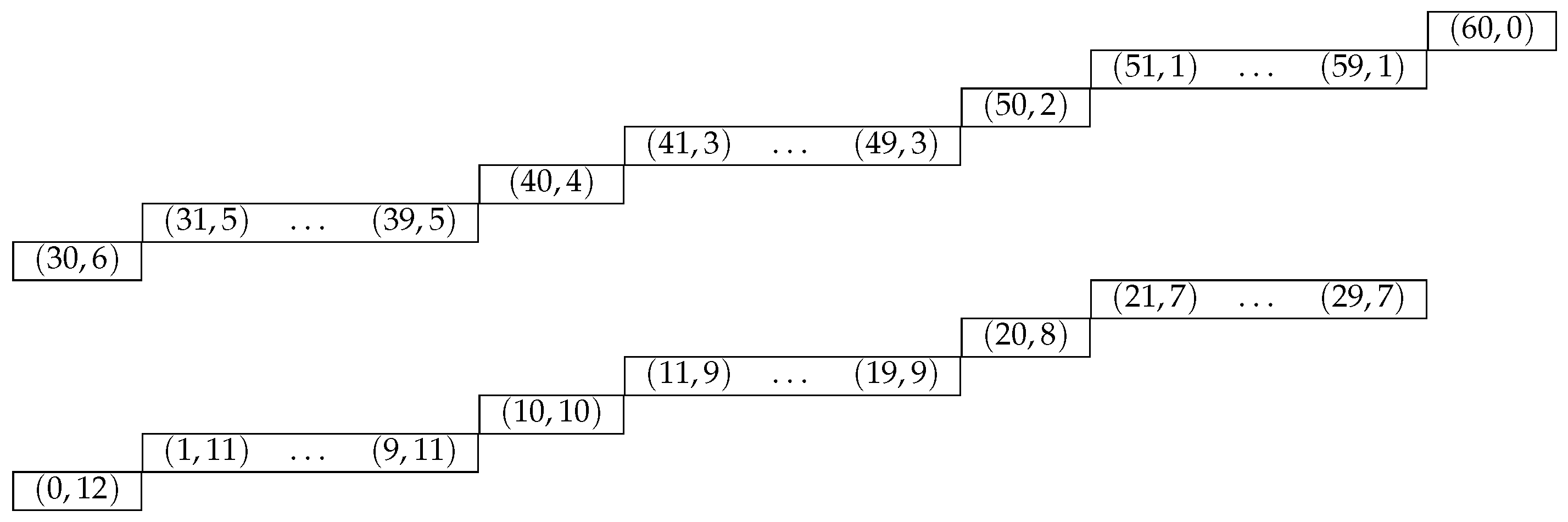
When $(i,k,u,v)=(5,4,2,3)$, we have $q=6$ and $r=1$. So, the elements of ${\mathrm{Ap}}_6(W_5,W_7,W_9)$, where $(W_5,W_7,W_9)=(61,547,4921)$, are given as in Figure 10. The largest element is at $(W_k/u-1,q+p-1)=(9,11)$, which comes from the second identity. Thus:

$$g_6(W_5,W_7,W_9)=9W_7+11W_9-W_5=58993.$$

Figure 10. ${\mathrm{Ap}}_6(W_5,W_7,W_9)$ for $(u,v)=(2,3)$.

Notice that the right-most element is at $(p{W}_k/u+r-1,q-p)=(60,0)$ and the block of the right side is empty. Therefore, the formula does not hold for $p=7$. In fact, $g_7\left(A\right)=59542$, corresponding to $(19,10)$, though the formula gives 63,914, corresponding to $(9,12)$.

5. $\mathit{p}$-Genus

5.1. The Case Where k Is Odd

Let k be odd. For a nonnegative integer p, the areas of the p-Apéry set can be divided into three parts: the stairs part (left), the stairs part (right), and the main part. By referring to Figure 6 (with Figure 4 and Figure 5), we can compute:

$$\begin{array}{cc}\hfill & \sum _{w\in {\mathrm{Ap}}_p\left(A\right)}w\hfill \\ \hfill & =\sum _{l=0}^p\sum _{z=\mathfrak{q}+(p-2l)u}^{\mathfrak{q}+(p-2l+1)u-1}\sum _{y=l{W}_k}^{l{W}_k+\mathfrak{r}-1}(y{W}_{i+2}+z{W}_{i+k})\hfill \\ \hfill & +\sum _{l=0}^p\sum _{z=\mathfrak{q}+(p-2l-1)u}^{\mathfrak{q}+(p-2l)u-1}\sum _{y=l{W}_k+\mathfrak{r}}^{(l+1)W_k-1}(y{W}_{i+2}+z{W}_{i+k})\hfill \\ \hfill & +\sum _{z=0}^{\mathfrak{q}-pu-1}\sum _{y=p{W}_k}^{p{W}_k+\mathfrak{r}-1}(y{W}_{i+2}+z{W}_{i+k})+\sum _{z=0}^{\mathfrak{q}-(p+1)u-1}\sum _{y=p{W}_k+\mathfrak{r}}^{(p+1)W_k-1}(y{W}_{i+2}+z{W}_{i+k})\hfill \\ \hfill & =\frac{W_i}{2u}((W_i-u)W_{i+2}+u(u-1)W_{i+k}-\mathfrak{q}{v}^2(2W_i-u{W}_k)W_{k-2}\hfill \\ \hfill & +{\mathfrak{q}}^2{v}^2{W}_k{W}_{k-2})\hfill \\ \hfill & +\frac{p{W}_i}{2}{W}_k(2W_{i+2}-u{v}^2{W}_{k-2})-\frac{p^2{W}_i}{2}u{v}^2{W}_k{W}_{k-2}.\hfill \end{array}$$

Here, we used the relation (9) to simplify the expression. In addition, by $qvs.W_{k-2}\equiv q{W}_k\equiv W_i\left(\mathrm{mod}u\right)$, we have:

$$\begin{array}{cc}\hfill & (W_i-u)W_{i+2}+u(u-1)W_{i+k}-\mathfrak{q}{v}^2(2W_i-u{W}_k)W_{k-2}+{\mathfrak{q}}^2{v}^2{W}_k{W}_{k-2}\hfill \\ \hfill & \equiv vs.W_i^2-2vs.W_i^2+v{W}_i^2\equiv 0\left(\mathrm{mod}u\right).\hfill \end{array}$$

By Lemma 1 (3), we have:

$$\begin{array}{cc}\hfill & n_p(W_i,W_{i+2},W_{i+k})\hfill \\ \hfill & =\frac{1}{2u}((W_i-u)W_{i+2}+u(u-1)W_{i+k}-\mathfrak{q}{v}^2(2W_i-u{W}_k)W_{k-2}\hfill \\ \hfill & +{\mathfrak{q}}^2{v}^2{W}_k{W}_{k-2})\hfill \\ \hfill & +\frac{p}{2}{W}_k(2W_{i+2}-u{v}^2{W}_{k-2})-\frac{p^2}{2}u{v}^2{W}_k{W}_{k-2}-\frac{W_i-1}{2}\hfill \\ \hfill & =\frac{1}{2u}((W_i-u)(W_{i+2}-u)+u(u-1)(W_{i+k}-1)-\mathfrak{q}{v}^2(2W_i-u{W}_k)W_{k-2}\hfill \\ \hfill & +{\mathfrak{q}}^2{v}^2{W}_k{W}_{k-2})\hfill \\ \hfill & +\frac{p}{2}{W}_k(2W_{i+2}-u{v}^2{W}_{k-2})-\frac{p^2}{2}u{v}^2{W}_k{W}_{k-2}.\hfill \end{array}$$

Since the z value of the right-most side must be nonnegative, $\mathfrak{q}-pu-1\ge 0$. Namely, the above formula is valid for $p\le (\mathfrak{q}-1)/u$.

Example 4.

When $(i,k,u,v)=(5,3,3,7)$, by:

$$\mathfrak{q}=3⌊\frac{1}{3}\left(⌊\frac{319}{16}⌋-7^{\frac{5-3}{2}}\right)⌋+7^{\frac{5-3}{2}}=19,$$

for $0\le p\le (\mathfrak{q}-1)/u=6$ we have for $0\le p\le ⌊\mathfrak{q}/u⌋=6$

$$\begin{array}{cc}\hfill {\left\{n_p(W_5,W_7,W_8)\right\}}_{p=0}^6& =\{n_p{(319,6553,29739)}_{p=0}^6\hfill \\ \hfill & =330327,432823,532967,630759,726199,819287,910023.\hfill \end{array}$$

However, for $p\ge 7$, the p-genus cannot be obtained by the above formula. The real values are given by:

$${\left\{n_p(W_5,W_7,W_8)\right\}}_{p=7}^9=965215,1021448,1067956,$$

though the formula gives:

$$998407,1084439,1168119.$$

5.2. The Case Where k Is Even

Similarly to the case for k is odd, when k is even, by referring to Figure 9 (with Figure 7 and Figure 8), we can compute:

$$\begin{array}{cc}\hfill & \sum _{w\in {\mathrm{Ap}}_p\left(A\right)}w\hfill \\ \hfill & =\sum _{l=0}^p\sum _{y=l{W}_k/u}^{l{W}_k/u+r-1}\left(y{W}_{i+2}+(q+p-2l)W_{i+k}\right)\hfill \\ \hfill & +\sum _{l=0}^p\sum _{y=l{W}_k/u+r}^{(l+1)W_k/u-1}(y{W}_{i+2}+(q+p-2l-1)W_{i+k})\hfill \\ \hfill & +\sum _{z=0}^{q-p-1}\sum _{y=p{W}_k/u}^{p{W}_k/u+r-1}(y{W}_{i+2}+z{W}_{i+k})+\sum _{z=0}^{q-p-2}\sum _{y=p{W}_k/u+r}^{(p+1)W_k/u-1}(y{W}_{i+2}+z{W}_{i+k})\hfill \\ \hfill & (\mathrm{When}p=q-1,\mathrm{the}\mathrm{fourth}\mathrm{term}\mathrm{is}\mathrm{empty},\mathrm{and}\hfill \\ \hfill & \mathrm{when}p=q,\mathrm{the}\mathrm{third}\mathrm{and}\mathrm{the}\mathrm{fourth}\mathrm{terms}\mathrm{are}\mathrm{empty}.)\hfill \\ \hfill & =\frac{1}{2u^2}{W}_i(u^2{W}_{i+2}(W_i-1)-q{v}^2{W}_{k-2}(2u{W}_i-W_k)\hfill \\ \hfill & +q^2{v}^2{W}_k{W}_{k-2})\hfill \\ \hfill & +\frac{p}{2u^2}{W}_i{W}_k(2u{W}_{i+2}-v^2{W}_{k-2})-\frac{p^2}{2u^2}{v}^2{W}_i{W}_k{W}_{k-2}.\hfill \end{array}$$

Here, we used the relation (15) to simplify the expression. In addition:

$$\begin{array}{cc}\hfill & \frac{W_{k-2}(2u{W}_i-W_k)}{u^2}=\frac{W_{k-2}}{u}\left(2W_i-\frac{W_k}{u}\right),\hfill \\ \hfill & \frac{v^2{W}_k{W}_{k-2}}{u^2}=v^2\frac{W_k}{u}\frac{W_{k-2}}{u},\hfill \\ \hfill & \frac{W_k(2u{W}_{i+2}-v^2{W}_{k-2})}{u^2}=\frac{W_k}{u}\left(2W_{i+2}-v^2\frac{W_{k-2}}{u}\right),\hfill \\ \hfill & \frac{v^2{W}_i{W}_k{W}_{k-2}}{u^2}=v^2{W}_i\frac{W_k}{u}\frac{W_{k-2}}{u}\hfill \end{array}$$

are all positive integers. By Lemma 1 (3), we have:

$$\begin{array}{cc}\hfill & n_p(W_i,W_{i+2},W_{i+k})\hfill \\ \hfill & =\frac{1}{2u^2}(u^2{W}_{i+2}(W_i-1)-q{v}^2{W}_{k-2}(2u{W}_i-W_k)\hfill \\ \hfill & +q^2{v}^2{W}_k{W}_{k-2})\hfill \\ \hfill & +\frac{p}{2u^2}{W}_k(2u{W}_{i+2}-v^2{W}_{k-2})-\frac{p^2}{2u^2}{v}^2{W}_k{W}_{k-2}-\frac{W_i-1}{2}\hfill \\ \hfill & =\frac{1}{2u^2}(u^2(W_i-1)(W_{i+2}-1)-q{v}^2{W}_{k-2}(2u{W}_i-W_k)\hfill \\ \hfill & +q^2{v}^2{W}_k{W}_{k-2})\hfill \\ \hfill & +\frac{p}{2u^2}{W}_k(2u{W}_{i+2}-v^2{W}_{k-2})-\frac{p^2}{2u^2}{v}^2{W}_k{W}_{k-2}.\hfill \end{array}$$

In conclusion, the p-genus is explicitly given as follows.

Theorem 3.

Let i and k be integers with $\gcd (i,k)=1$ and $i\ge k\ge 3$. When k is odd, for $0\le p\le \mathfrak{q}/u$ we have:

$$\begin{array}{cc}\hfill & n_p(W_i,W_{i+2},W_{i+k})\hfill \\ \hfill & =\frac{1}{2u}((W_i-u)(W_{i+2}-u)+u(u-1)(W_{i+k}-1)-\mathfrak{q}{v}^2(2W_i-u{W}_k)W_{k-2}\hfill \\ \hfill & +{\mathfrak{q}}^2{v}^2{W}_k{W}_{k-2})\hfill \\ \hfill & +\frac{p}{2}{W}_k(2W_{i+2}-u{v}^2{W}_{k-2})-\frac{p^2}{2}u{v}^2{W}_k{W}_{k-2},\hfill \end{array}$$

where $\mathfrak{q}$ and $\mathfrak{r}$ are given in (9). When k is even (and i is odd), for $0\le p\le q$ we have:

$$\begin{array}{cc}\hfill & n_p(W_i,W_{i+2},W_{i+k})\hfill \\ \hfill & =\frac{1}{2u^2}(u^2(W_i-1)(W_{i+2}-1)-q{v}^2{W}_{k-2}(2u{W}_i-W_k)\hfill \\ \hfill & +q^2{v}^2{W}_k{W}_{k-2})\hfill \\ \hfill & +\frac{p}{2u^2}{W}_k(2u{W}_{i+2}-v^2{W}_{k-2})-\frac{p^2}{2u^2}{v}^2{W}_k{W}_{k-2},\hfill \end{array}$$

where q and r are given in (15).

Example 5.

Let $(i,k,u,v)=(5,4,2,3)$. So, $q=⌊2W_5/W_4⌋=⌊2·61/20⌋=6$. Then, for $0\le p\le 6$ by the formula we have:

$$\begin{array}{cc}\hfill {\left\{n_p(W_5,W_7,W_9)\right\}}_{p=0}^6& ={\left\{n_p(61,547,4921)\right\}}_{p=0}^6\hfill \\ \hfill & =14976,20356,25646,30846,35956,40976,45906.\hfill \end{array}$$

However, contrary to the fact that $n_7(W_5,W_7,W_9)=46885$, the formula gives 50746.

6. Final Comments

The original numbers studied by Horadam satisfy the recurrence relation $W_n=u{W}_{n-1}-v{W}_{n-2}$. From this point of view, almost all the above identities hold by replacing v by $-v$, though the condition $u>\left|v\right|$ is necessary. For example, the identities of (7) and (8) are replaced by:

$$\begin{array}{cc}\hfill & W_{i+k}=W_{i+1}{W}_k-v{W}_i{W}_{k-1},\hfill \\ \hfill & W_n\equiv \left\{\begin{array}{cc}0\left(\mathrm{mod}u\right)\hfill & \mathrm{if}n\mathrm{is}\mathrm{even};\hfill \\ {(-v)}^{\frac{n-1}{2}}\left(\mathrm{mod}u\right)\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.\hfill \end{array}$$

respectively. For example, when $(i,k,u,v)=(8,5,4,-3)$, by $\mathfrak{q}=24$ for $0\le p\le 6=24/4$ by the first identity of Theorem 1, we have:

$$\begin{array}{c}{\left\{g_p(W_5,W_7,W_9)\right\}}_{p=0}^6=24265799,27454443,30643087,\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}33831731,37020375,40209019,43397663.\end{array}$$

When $(i,k,u,v)=(5,4,3,-2)$, by $q=6$ for $0\le p\le 6$ by the first identity of Theorem 2, we have:

$${\left\{g_p(W_5,W_7,W_9)\right\}}_{p=0}^6=3035,3546,4057,4568,5079,5590,6101.$$

7. Conclusions

In this paper, we give explicit formulas of the p-Frobenius number and the p-genus of triplet $(W_i,W_{i+2},W_{i+k})$ for integers $i,k(\ge 3)$, where $W_n$’s are the so-called Horadam numbers, satisfying the recurrence relation $W_n=u{W}_{n-1}+v{W}_{n-2}$ ($n\ge 2$) with $W_0=0$ and $W_1=1$. We give explicit closed formulas of p-Frobenius numbers and p-genus of this triple. When $u=v=1$, $v=1$ or $u=1$, the results for Fibonacci, Pell, and Jacobsthal triples are recovered.

Horadam also studied the number $W_n$ with arbitrary initial values $W_0$ and $W_1$. However, with arbitrary initial values, many identities (e.g., (7)) do not hold as they are. Hence, the situation becomes too complicated. An approach to get some recurrences to a wide class of polynomials in [39] may be useful for future works.