$\mathcal{I}$-Symmetric Spaces and the π-Images of Metric Spaces

Abstract

Symmetric spaces and $sn$-symmetric spaces, as a generalization of metric spaces, have many important properties and have been widely discussed. We consider characterizations and mapping properties of $sn$-symmetric spaces under ideal convergence. $\mathcal{I}$-symmetric spaces and $\mathcal{I}$-$sn$-symmetric spaces are defined and studied. These not only generalize some classical results on symmetric spaces but also provide new directions to study generalized metric spaces using the notion of ideal convergence. As an application of $\mathcal{I}$-$sn$-symmetric spaces, some relevant properties of statistical convergence are obtained. Some unanswered questions in this field are raised.

1. Introduction

Spaces and mappings have become a frontier research subject in general topology and have achieved rich results in the past half century [1]. Symmetric spaces introduced by Arhangel’skiǐ [2] are an important class of generalized metric spaces and play a special role in this field [1,3]. It is particularly prominent in metrizability and in the quotient and $\pi$-images of metric spaces.

Externally, a symmetric space is a topological space that is compatible with a symmetric distance [2]. In fact, the characteristic difficulty with studying symmetric spaces lies in the concept of weak bases, which is a network having a certain base-like property. One of the ways to overcome this difficulty was to introduce the concept of $sn$-networks [1]; this is a natural generalization of weak bases and has better properties compared to weak bases [1] and thus to defined $sn$-symmetric spaces [4]. It is known that, in Hausdorff sequential spaces, $gf$-countable spaces are equivalent to $snf$-countable spaces [1], and symmetric spaces are equivalent to $sn$-symmetric spaces [4]. It can be seen that the further development of symmetric spaces involves deeper research into $sn$-symmetric spaces and sequential spaces [1].

The following are some basic results on symmetric spaces.

Theorem 1

([5]). A topological space X is a symmetric space if and only if it has a sequence ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ of covers such that the family ${\left\{st(x,{\mathcal{P}}_n)\right\}}_{n\in \mathbb{N}}$ is a weak base at x for each $x\in X$, where each $st(x,{\mathcal{P}}_n)=\bigcup \{P\in {\mathcal{P}}_n:x\in P\}$.

Theorem 2

([6]). The following are equivalent for a Hausdorff space X:

(1) 

X is a quotient and π-image of a metric space.

(2) 

X is a symmetric space with a weak Cauchy condition.

Theorem 3

([6]). The following are equivalent for a Hausdorff space X:

(1) 

X is a quotient, sequence-covering, and π-image of a metric space.

(2) 

X is a symmetric space with a Cauchy condition.

The above results all involve the convergence of sets or sequences in symmetric spaces. In recent years, the ideal convergence of sequences in topological spaces has become an active topic [7,8,9,10]. Although the usual convergence of sequences in topological spaces is ideally convergent, the situation becomes more complex for specific topological spaces.

Question 1

(Question 5.10, [10]). Is every $gf$-countable space an $\mathcal{I}$-$snf$-countable space for some admissible ideal $\mathcal{I}$ on $\mathbb{N}$?

Existing research has rarely related to the properties of generalized metric spaces determined by the ideal convergence of sequences. Thus, we discuss some properties of spaces and mappings with respect to symmetric spaces under ideal convergence and provide an application to statistical convergence. In addition, we also provide several examples to illustrate the non-implicative relationship between certain spaces and provide a negative answer to Question 1.

The following main results are obtained in this article.

Theorem 4.

Let $\mathcal{I}$ be an admissible ideal on $\mathbb{N}$. The following are equivalent for a $T_1$-space X:

(1) 

X is an $\mathcal{I}$-$sn$-symmetric space.

(2) 

X has a point-star $\mathcal{I}$-$sn$-network.

(3) 

X is an FU-${\mathcal{I}}_{sn}$ and $sn$-symmetric space.

Theorem 5.

Let $\mathcal{I}$ be an admissible ideal on $\mathbb{N}$. The following are equivalent for a $T_1$-space X:

(1) 

X is an $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition.

(2) 

X has a point-star network consisting of $\mathcal{I}$-$cs$-covers.

(3) 

X is an $\mathcal{I}$-covering and π-image of a metric space.

Theorem 6.

Let $\mathcal{I}$ be an asymptotic density zero ideal. The following are equivalent for a $T_1$-space X:

(1) 

X is a 1-$\mathcal{I}$-covering and π-image of a metric space.

(2) 

X is an $\mathcal{I}$-covering and π-image of a metric space.

(3) 

X has a point-star network consisting of $\mathcal{I}$-$sn$-covers.

(4) 

X has a point-star network consisting of $\mathcal{I}$-$cs$-covers.

(5) 

X is an $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition.

These not only generalize some classical results on symmetric spaces [1,4,5,6,10,11] but also provide new directions to study generalized metric spaces in the sense of ideal convergence, and we obtain some applications to statistical convergence.

2. Preliminaries

In this section, we mainly recall the ideal convergence of sequences, generalized sequential spaces determined by ideal convergence, and symmetric spaces. Afterwards, some relationships among spaces defined by these notions are given. Readers may refer to [12] for some terminology unstated here. In this article, all spaces are assumed to be $T_1$, all mappings are continuous and surjective, and $\mathbb{N}$ is the set of all positive integers.

A family $\mathcal{I}$ of subsets of $\mathbb{N}$ is called an $\mathit{ideal}$ on $\mathbb{N}$ (p. 670, [8]), provided that the following are satisfied: if $B\subseteq A\in \mathcal{I}$, then $B\in \mathcal{I}$; if $A,B\in \mathcal{I}$, then $A\cup B\in \mathcal{I}$. An ideal $\mathcal{I}$ on $\mathbb{N}$ is called $\mathit{admissible}$ if $\mathbb{N}\notin \mathcal{I}\ne \varnothing$, and $\mathcal{I}$ covers $\mathbb{N}$. The ideal ${\mathcal{I}}_{fin}$ of all finite subsets of $\mathbb{N}$ is the smallest admissible ideal on $\mathbb{N}$. Next, we always assume that $\mathcal{I}$ is an admissible ideal on $\mathbb{N}$.

Recalling that a sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in a topological space X is said to be $\mathcal{I}$-$\mathit{convergent}$ to a point $x\in X$ provided for any neighborhood U of x, we have $\{n\in \mathbb{N}:x_n\notin U\}\in \mathcal{I}$, which is denoted by $x_n\stackrel{\mathcal{I}}{\to }x$ (Definition 3.1, [8]).

Let P be a subset of a topological space X. A sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in X is said to be $\mathcal{I}$-eventually in P if the set $\{n\in \mathbb{N}:x_n\notin P\}\in \mathcal{I}$ (p. 1982, [9]). The set P is said to be an $\mathcal{I}$-sequential neighborhood of a point $x\in X$ if each sequence that is $\mathcal{I}$-convergent to x is $\mathcal{I}$-eventually in P (Definition 2.5, [13]). The set P is said to be an ${\mathcal{I}}_{sn}$-open set of X if P is an $\mathcal{I}$-sequential neighborhood of x for each $x\in P$ (p. 4, [9]). ${\mathcal{I}}_{fin}$-sequential neighborhoods of x or ${\left({\mathcal{I}}_{fin}\right)}_{sn}$-open sets are called sequential neighborhoods of x [14] or sequentially open sets, respectively (p. 108, [15]). It is known that every open subset is ${\mathcal{I}}_{sn}$-open, and every ${\mathcal{I}}_{sn}$-open subset is sequentially open (Lemma 2.1, [9]).

Put

$$\begin{array}{cc}\hfill {\left(P\right)}_{seq}=& \{x\in X:P \mathrm{is} \mathrm{a}\mathrm{sequential} \mathrm{neighborhood} \mathrm{of}x \mathrm{in} X\},\hfill \\ \hfill {\left(P\right)}_{{\mathcal{I}}_{sn}}=& \{x\in X:P \mathrm{is} \mathrm{an}\mathcal{I}\mathrm{-sequential} \mathrm{neighborhood} \mathrm{of} x \mathrm{in} X\}.\hfill \end{array}$$

Then, $P^{\circ }\subseteq {\left(P\right)}_{{\mathcal{I}}_{sn}}\subseteq {\left(P\right)}_{seq}\subseteq P$ (Lemma 2.6, [9]).

Definition 1.

Let X be a topological space.

(1) 

X is called a sequential space if any sequentially open subset of X is open [15].

(2) 

X is called an ${\mathcal{I}}_{sn}$-sequential space if any ${\mathcal{I}}_{sn}$-open subset of X is open (Definition 3.1, [10]).

(3) 

X is called a Fréchet–Urysohn space if ${\left(P\right)}_{seq}\subseteq P^{\circ }$ for each $P\subseteq X$ [15].

(4) 

X is called an ${\mathcal{I}}_{sn}$-FU-space if ${\left(P\right)}_{{\mathcal{I}}_{sn}}\subseteq P^{\circ }$ for each $P\subseteq X$ (Definition 3.1, [10]).

(5) 

X is called an FU-${\mathcal{I}}_{sn}$-space if ${\left(P\right)}_{seq}\subseteq {\left(P\right)}_{{\mathcal{I}}_{sn}}$ for each $P\subseteq X$.

Sequential spaces and Fréchet–Urysohn spaces in the sense of ideal convergence were first defined by Pal [16] and Renukadevi and Prakash [17], respectively. It is obvious that every Fréchet–Urysohn space is an ${\mathcal{I}}_{sn}$-FU, FU-${\mathcal{I}}_{sn}$, and sequential space and that each sequential space and each ${\mathcal{I}}_{sn}$-FU-space is an ${\mathcal{I}}_{sn}$-sequential space.

The concept of networks is important to topological spaces [2]. Let $\mathcal{P}$ be a family of subsets of a topological space X and $x\in X$. $\mathcal{P}$ is called a network at x in X, if $x\in \bigcap \mathcal{P}$ and, whenever $x\in U$ with U open in X, then $P\subseteq U$ for some $P\in \mathcal{P}$ [2].

Definition 2.

Let $\mathcal{P}={\bigcup }_{x\in X}{\mathcal{P}}_x$ be a family of subsets of a topological space X. $\mathcal{P}$ is called an $\mathcal{I}$-$sn$-network of X provided that, for each $x\in X$, ${\mathcal{P}}_x$ is a network at x in X satisfying the following conditions: (1) each $P\in {\mathcal{P}}_x$ is an $\mathcal{I}$-sequential neighborhood of x; (2) for each $P,Q\in {\mathcal{P}}_x$, there is $W\in {\mathcal{P}}_x$ such that $W\subseteq P\cap Q$. The family ${\mathcal{P}}_x$ is called an $\mathcal{I}$-$sn$-network at x in X (Definition 5.1, [10]).

X is called an $\mathcal{I}$-$snf$-countable space if X has a countable $\mathcal{I}$-$sn$-network at each point in X (Definition 4.1, [10]). An ${\mathcal{I}}_{fin}$-$sn$-network is called an $sn$-network (Definition 1.1.8, [1]), and an ${\mathcal{I}}_{fin}$-$snf$-countable space is called an $snf$-countable space (Definition 1.1.8, [1]).

Let X be a set. A function $d:X\times X\to [0,+\infty )$ is called a d-function on X if, for each $x,y\in X$: (1) $d(x,y)=0\iff x=y$; (2) $d(x,y)=d(y,x)$ (p. 4, [1]). For each $x\in X$ and $\epsilon >0$, put $B(x,\epsilon )=\{y\in X:d(x,y)<\epsilon \}$.

Definition 3.

Let d be a d-function on a topological space X. The space $(X,d)$ is called a semi-metric space [2] if, whenever $x\in X$, ${\left\{B(x,1/n)\right\}}_{n\in \mathbb{N}}$ is a neighborhood base at x in X. The space $(X,d)$ is called a symmetric space [2] if a subset U in X is open if and only if, for each $x\in U$, there exists $n\in \mathbb{N}$ such that $B(x,1/n)\subseteq U$.

A topological space X is called $gf$-countable [2] if, for each $x\in X$, there is a countable and decreasing family ${\mathcal{B}}_x$ of subsets of X satisfying that a subset U in X is open if and only if, for each $x\in U$, there exist $n\in \mathbb{N}$ and $B\in {\mathcal{B}}_x$ such that $x\in B\subseteq U$.

Remark 1.

If ${\left\{B_n\right\}}_{n\in \mathbb{N}}$ is a decreasing network at a point x in X, then for each sequential neighborhood U of x in X, there exists $n\in \mathbb{N}$ such that $B_n\subseteq U$. Otherwise, there is a sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ such that each $x_n\in B_n\setminus U$, and then the sequence $x_n\to x$ in X contradicts U being a sequential neighborhood of x.

It is obvious that every symmetric space is $gf$-countable, and it follows from Remark 1 that every $gf$-countable space is sequential [2].

Remark 2.

In the sense of ideal convergence, $\mathcal{I}$-open sets in topological spaces are one of the first concepts proposed. Every ${\mathcal{I}}_{sn}$-open set in a topological space is $\mathcal{I}$-open, and every $\mathcal{I}$-open set is sequentially open (Lemma 2.1, [9]). In this article, we chose the ${\mathcal{I}}_{sn}$-open sets instead of the $\mathcal{I}$-open sets for the following two main reasons:

(1) 

The family of ${\mathcal{I}}_{sn}$-open sets in a topological space forms a topology, while the family of $\mathcal{I}$-open sets forms a generalized topology [9].

(2) 

In $\mathcal{I}$-$snf$-countable spaces, each $\mathcal{I}$-open set is ${\mathcal{I}}_{sn}$-open (Corollary 5.2, [18]).

3. $\mathcal{I}$-Symmetric Spaces

In this section, we define and study some properties of $\mathcal{I}$-symmetric spaces and $\mathcal{I}$-$sn$-symmetric spaces, answer Question 1 in the negative, and obtain some relationships among $\mathcal{I}$-symmetric spaces, $\mathcal{I}$-$sn$-symmetric spaces, and $sn$-symmetric spaces.

As a generalization of symmetric spaces, $sn$-symmetric spaces were introduced in the sense of the usual convergence of sequences. Next, we discuss the ideal convergence versions of these types of generalized metric spaces. A subset U of a topological space X is called an ${\mathcal{I}}_{sn}$-open neighborhood of a point x in X if $x\in V\subseteq U$ for some ${\mathcal{I}}_{sn}$-open subset V of X.

Definition 4.

Let d be a d-function on a topological space X.

(1) 

The space $(X,d)$ is called an $\mathcal{I}$-semi-metric space, in which d is called an $\mathcal{I}$-semi-metric on X if, for each $x\in X$, ${\left\{B(x,1/n)\right\}}_{n\in \mathbb{N}}$ is a network at x in X consisting of ${\mathcal{I}}_{sn}$-open neighborhoods of x.

(2) 

The space $(X,d)$ is called an $\mathcal{I}$-symmetric space, in which d is called an $\mathcal{I}$-symmetric on X, if a subset U in X is ${\mathcal{I}}_{sn}$-open if and only if, for each $x\in U$, there exists $n\in \mathbb{N}$ such that $B(x,1/n)\subseteq U$.

(3) 

The space $(X,d)$ is called an $\mathcal{I}$-$sn$-symmetric space, in which d is called an $\mathcal{I}$-$sn$-symmetric on X if, for each $x\in X$, ${\left\{B(x,1/n)\right\}}_{n\in \mathbb{N}}$ is an $\mathcal{I}$-$sn$-network at x in X.

An ${\mathcal{I}}_{fin}$-$sn$-symmetric space is called an $sn$-symmetric space (Definition 2.6, [4]).

Lemma 1.

Let X be a Hausdorff space.

(1) 

X is an $\mathcal{I}$-symmetric space if and only if X is an $sn$-symmetric space and each sequentially open subset of X is ${\mathcal{I}}_{sn}$-open.

(2) 

X is a $gf$-countable space if and only if X is an $snf$-countable sequential space (Corollary 1.3.10, [1]).

Proof. 

We only prove that part (1) holds.

Sufficiency. Suppose that each sequentially open set of X is ${\mathcal{I}}_{sn}$-open and d is $sn$-symmetric on X. We prove that d is $\mathcal{I}$-symmetric on X. If U is ${\mathcal{I}}_{sn}$-open in X and $x\in U$, it follows from Remark 1 that there exists $n\in \mathbb{N}$ such that $B(x,1/n)\subseteq U$. On the other hand, if a subset V of X satisfies that, for each $x\in V$, there exists $n\in \mathbb{N}$ such that $B(x,1/n)\subseteq V$, then V is sequentially open because each $B(x,1/n)$ is a sequential neighborhood of x in X. Thus, V is ${\mathcal{I}}_{sn}$-open. Consequently, d is $\mathcal{I}$-symmetric on X.

Necessity. Let d be $\mathcal{I}$-symmetric on X. Then, for each $x\in X$, the family ${\left\{B(x,1/n)\right\}}_{n\in \mathbb{N}}$ is a network at x in X. If U is sequentially open in X, it follows from Remark 1 that, for each $x\in U$, there exists $n\in \mathbb{N}$ such that $B(x,1/n)\subseteq U$; thus, U is ${\mathcal{I}}_{sn}$-open. Next, we just need to prove that, for each $x\in X$ and $n\in \mathbb{N}$, the set $B(x,1/n)$ is a sequential neighborhood of x in X. Otherwise, there is a sequence ${\left\{x_m\right\}}_{m\in \mathbb{N}}$ such that $x_m\to x$ and each $x_m\notin B(x,1/n)$. Let $U=X\setminus \{x_m:m\in \mathbb{N}\}$. Then, $B(x,1/n)\subseteq U$. Since X is Hausdorff, if $u\in U\setminus \left\{x\right\}$, then $u\in X\setminus \overline{\{x_m:m\in \mathbb{N}\}}$; thus, there exists $k\in \mathbb{N}$ such that $B(u,1/k)\subseteq X\setminus \overline{\{x_m:m\in \mathbb{N}\}}\subset U$. Therefore, U is ${\mathcal{I}}_{sn}$-open, which contradicts $x_m\to x\in U$. □

A non-trivial relationship for weak first-countability is as follows.

Lemma 2.

Every $\mathcal{I}$-$snf$-countable space is an FU-${\mathcal{I}}_{sn}$-space.

Proof. 

Let X be an $\mathcal{I}$-$snf$-countable space and $A\subseteq X$. For each $x\in {\left(A\right)}_{seq}$, let ${\left\{P_m\right\}}_{m\in \mathbb{N}}$ be an $\mathcal{I}$-$sn$-network at x in X. For each $k\in \mathbb{N}$, put $Q_k={\bigcap }_{m\le k}{P}_m$. Since the intersection of finitely many $\mathcal{I}$-sequential neighborhoods of x is still an $\mathcal{I}$-sequential neighborhood of x, it is easy to see that the set $Q_k$ is also an $\mathcal{I}$-sequential neighborhood of x. Then, some $Q_k\subseteq A$. Otherwise, there is $x_k\in Q_k\setminus A$ for each $k\in \mathbb{N}$. Then, $x_k\to x$ in X, which is a contradiction because A is a sequential neighborhood of x. Therefore, some $Q_k\subseteq A$, and $x\in {\left(A\right)}_{{\mathcal{I}}_{sn}}$. Thus, X is an FU-${\mathcal{I}}_{sn}$-space. □

The following result is direct by means of Remark 1.

Lemma 3.

A topological space X is a symmetric space if and only if it is an $\mathcal{I}$-symmetric and ${\mathcal{I}}_{sn}$-sequential space.

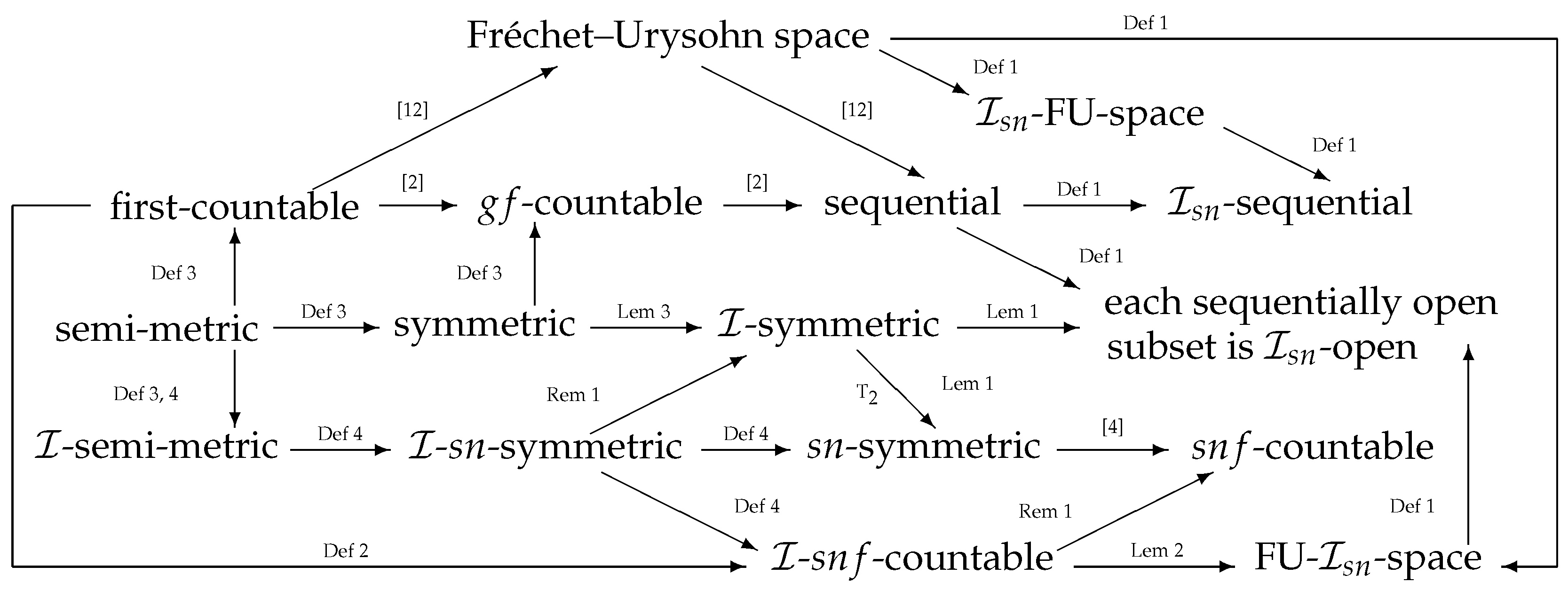
Figure 1 illustrates some relationships among these spaces in Definitions 1–4.

The following example gives a negative answer to Question 1. It shows that the Hausdorff space in Lemma 1 cannot be weakened to a $T_1$-space.

Example 1.

There is a Fréchet–Urysohn and symmetric space that is not an $\mathcal{I}$-$snf$-countable space for each admissible ideal $\mathcal{I}$ on $\mathbb{N}$.

Proof. 

Let X be the space consisting of the countable ordinals with cofinite topology. Then, X is a symmetric space (Example 2.13, [19]). Next, we show that X is not an $snf$-countable space. If $A\subseteq X$ and $x\in {\left(A\right)}_{seq}$, then $X\setminus A$ is a finite set. Otherwise, take a non-trivial sequence S in $X\setminus A$. Then, the sequence S converges to x in X; thus, it is eventually in A, which is a contradiction. Since $X\setminus A$ is finite, A is open in X. Hence, ${\left(A\right)}_{seq}=A^{\circ }=A$. This implies that X is a Fréchet–Urysohn space and that no point in X is $snf$-countable; thus, X is not an $\mathcal{I}$-$snf$-countable space for each admissible ideal $\mathcal{I}$ on $\mathbb{N}$. □

Example 2.

There is an $sn$-symmetric space that is neither an $\mathcal{I}$-symmetric space nor an $\mathcal{I}$-$snf$-countable space.

Proof. 

There is a maximal ideal $\mathcal{I}$ on $\mathbb{N}$ and an ${\mathcal{I}}_{sn}$-FU-space X such that it is neither an $\mathcal{I}$-$snf$-countable space nor contains no non-trivial convergent sequence (Examples 3.4 and 5.8, [10]). Define a function $d:X\times X\to [0,+\infty )$ by

$$d(x,y)=\left\{\begin{array}{cc}0,\hfill & x=y,\hfill \\ 1,\hfill & x\ne y.\hfill \end{array}\right.$$

Then, it is a d-function, and each $B(x,1/n)=\left\{x\right\}$ is sequentially open in X. Hence, $(X,d)$ is an $sn$-symmetric space.

If X is an $\mathcal{I}$-symmetric space, it follows from Lemma 3 that X is a symmetric space; thus, X is a sequential space. Since each subset of X is sequentially open, X is a discrete space, which is a contradiction. Thus, X is not an $\mathcal{I}$-symmetric space. □

Let $\mathcal{P}$ and $\mathcal{Q}$ be families of subsets of X. Put $\mathcal{P}\bigwedge \mathcal{Q}=\{P\cap Q:P\in \mathcal{P},Q\in \mathcal{Q}\}$. For each $x\in X$, denote ${\left(\mathcal{P}\right)}_x=\{P\in \mathcal{P}:x\in P\}$ and st$(x,\mathcal{P})=\bigcup \{P:P\in {\left(\mathcal{P}\right)}_x\}$.

The following are the core concepts in this article, which can establish connections among several types of symmetric spaces.

Definition 5.

Let ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ be a sequence of covers of a topological space X. ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ is said to be a point-star network (Definition 3.1.1, [1]) (resp., point-star $\mathcal{I}$-$sn$-network) of X if ${\left\{st(x,{\mathcal{P}}_n)\right\}}_{n\in \mathbb{N}}$ is a network (resp., an $\mathcal{I}$-$sn$-network) at x for every $x\in X$.

A point-star ${\mathcal{I}}_{fin}$-$sn$-network is called a point-star $sn$-network (Definition 3.1.1, [1]).

Theorem 7.

The following are equivalent for a topological space X:

(1) 

X is an $\mathcal{I}$-$sn$-symmetric space.

(2) 

X has a point-star $\mathcal{I}$-$sn$-network.

(3) 

X is an $\mathcal{I}$-$snf$-countable and $sn$-symmetric space.

(4) 

X is an FU-${\mathcal{I}}_{sn}$ and $sn$-symmetric space.

Proof. 

(1) ⇒ (2). Let $(X,d)$ be an $\mathcal{I}$-$sn$-symmetric space. For each $n\in \mathbb{N}$, put

$${\mathcal{P}}_n=\left\{P\subseteq X:sup\left\{d\right(x,y):x,y\in P\}<1/n\right\}.$$

Then, st$(x,{\mathcal{P}}_n)=B(x,1/n)$ for each $x\in X$. In fact, if $y\in \mathrm{st}(x,{\mathcal{P}}_n)$, then there exists $P\in {\mathcal{P}}_n$ such that $x,y\in P$. Thus, $d(x,y)\le sup\left\{d\right(a,b):a,b\in P\}<1/n$, and hence, $y\in B(x,1/n)$. On the other hand, if $y\in B(x,1/n)$, then $d(x,y)<1/n$. So, $\{x,y\}\in {\mathcal{P}}_n$, and hence, $y\in \mathrm{st}(x,{\mathcal{P}}_n)$. This implies that ${\left\{\mathrm{st}(x,{\mathcal{P}}_n)\right\}}_{n\in \mathbb{N}}$ is an $\mathcal{I}$-$sn$-network at each $x\in X$. Therefore, ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ is a point-star $\mathcal{I}$-$sn$-network of X.

(2) ⇒ (3). Let ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ be a point-star $\mathcal{I}$-$sn$-network of X. It is clear that X is an $\mathcal{I}$-$snf$-countable space. We can assume that each ${\mathcal{P}}_{n+1}$ refines ${\mathcal{P}}_n$. In fact, let ${\mathcal{Q}}_n={\bigwedge }_{i\le n}{\mathcal{P}}_i$ for each $n\in \mathbb{N}$. Then, ${\mathcal{Q}}_{n+1}$ refines ${\mathcal{Q}}_n$ and, for each $x\in X$,

$$\mathrm{st}(x,{\mathcal{Q}}_n)=\mathrm{st}\left(x,\underset{i\le n}{\bigwedge }{\mathcal{P}}_i\right)=\bigcap _{i\le n}\mathrm{st}(x,{\mathcal{P}}_i).$$

Since ${\left\{\mathrm{st}(x,{\mathcal{P}}_i)\right\}}_{i\in \mathbb{N}}$ is an $\mathcal{I}$-$sn$-network at x in X, it follows that ${\left\{\mathrm{st}(x,{\mathcal{Q}}_n)\right\}}_{n\in \mathbb{N}}$ is an $\mathcal{I}$-$sn$-network at x.

For distinct two points x and y in X, since X is $T_1$, there is $n\in \mathbb{N}$ such that $y\notin \mathrm{st}(x,{\mathcal{P}}_n)$, and we denote $n(x,y)=min\{n\in \mathbb{N}:y\notin \mathrm{st}(x,{\mathcal{P}}_n)\}$. Define $d:X\times X\to [0,+\infty )$ by

$$d(x,y)=\left\{\begin{array}{cc}0,\hfill & x=y,\hfill \\ 1/n(x,y),\hfill & x\ne y.\hfill \end{array}\right.$$

Then, d is a d-function, and it is clear that $y\notin \mathrm{st}(x,{\mathcal{P}}_n)\iff n(x,y)\le n$. If $x\ne y$, then

$$y\in \mathrm{st}(x,{\mathcal{P}}_n)\iff n(x,y)>n\iff d(x,y)=1/n(x,y)<1/n\iff y\in B(x,1/n).$$

Thus, st$(x,{\mathcal{P}}_n)=B(x,1/n)$ for each $x\in X$ and $n\in \mathbb{N}$. This means that ${\left\{B(x,1/n)\right\}}_{n\in \mathbb{N}}$ is an $\mathcal{I}$-$sn$-network at x in X. Consequently, X is an $sn$-symmetric space.

(3) ⇒ (4) is true by Lemma 2.

(4) ⇒ (1). Let X be an FU-${\mathcal{I}}_{sn}$ and $sn$-symmetric space. Then, for each $x\in X$, each $sn$-network at x is an $\mathcal{I}$-$sn$-network at x. Therefore, X is an $\mathcal{I}$-$sn$-symmetric space. □

Corollary 1.

The following are equivalent for a Hausdorff space X:

(1) 

X is a sequential and $\mathcal{I}$-$sn$-symmetric space.

(2) 

X is an ${\mathcal{I}}_{sn}$-sequential and $\mathcal{I}$-$sn$-symmetric space.

(3) 

X is an ${\mathcal{I}}_{sn}$-sequential, $\mathcal{I}$-$snf$-countable, and $\mathcal{I}$-symmetric space.

(4) 

X is an $\mathcal{I}$-$snf$-countable and symmetric space.

(5) 

X is an FU-${\mathcal{I}}_{sn}$ and symmetric space.

Proof. 

It is obvious that $\left(1\right)\Rightarrow \left(2\right)$. By Lemma 3, we have that $\left(3\right)\Rightarrow \left(4\right)$. It follows from Lemma 2 that $\left(4\right)\Rightarrow \left(5\right)$. Next, we prove that (2) ⇒ (3) and (5) ⇒ (1).

(2) ⇒ (3). Let X be an ${\mathcal{I}}_{sn}$-sequential and $\mathcal{I}$-$sn$-symmetric space. Then, X is $\mathcal{I}$-$snf$-countable. It follows from Remark 1 that X is an $\mathcal{I}$-symmetric space.

(5) ⇒ (1). Let X be an FU-${\mathcal{I}}_{sn}$ and symmetric space. Then, X is a sequential space, and it follows from Lemmas 1 and 3 that X is an $sn$-symmetric space. By Theorem 7, X is an $\mathcal{I}$-$sn$-symmetric space. □

Corollary 2.

The following are equivalent for a topological space X:

(1) 

X is a semi-metric space.

(2) 

X is an ${\mathcal{I}}_{sn}$-sequential and $\mathcal{I}$-semi-metric space.

(3) 

X is an ${\mathcal{I}}_{sn}$-FU and $\mathcal{I}$-$sn$-symmetric space.

(4) 

X is a Fréchet–Urysohn and $sn$-symmetric space.

Proof. 

It is obvious that $\left(4\right)\Rightarrow \left(1\right)\Rightarrow \left(2\right)$.

(2) ⇒ (3). Let $(X,d)$ be an ${\mathcal{I}}_{sn}$-sequential and $\mathcal{I}$-semi-metric space. Then, X is an $\mathcal{I}$-$sn$-symmetric space. If $A\subseteq X$ and $x\in {\left(A\right)}_{{\mathcal{I}}_{sn}}$, it follows from Remark 1 and $\mathcal{I}$-semi-metric d that there exist $n\in \mathbb{N}$ and an ${\mathcal{I}}_{sn}$-open subset V of X such that $x\in V\subseteq B(x,1/n)\subseteq A$. Since X is an ${\mathcal{I}}_{sn}$-sequential space, $x\in A^{\circ }$. This implies that ${\left(A\right)}_{{\mathcal{I}}_{sn}}\subseteq A^{\circ }$. Hence, X is an ${\mathcal{I}}_{sn}$-FU-space.

(3) ⇒ (4). Let $(X,d)$ be an ${\mathcal{I}}_{sn}$-FU and $\mathcal{I}$-$sn$-symmetric space. Then, X is an $sn$-symmetric space. If $A\subseteq X$ and $x\in {\left(A\right)}_{seq}$, it follows from Remark 1 that there is $n\in \mathbb{N}$ such that $B(x,1/n)\subseteq A$. Then, $x\in {\left(B(x,1/n)\right)}_{{\mathcal{I}}_{sn}}\subseteq {\left[B(x,1/n)\right]}^{\circ }\subseteq A^{\circ }$. Thus, ${\left(A\right)}_{seq}\subseteq A^{\circ }$. Therefore, X is a Fréchet–Urysohn space. □

Example 3.

There is an $\mathcal{I}$-semi-metric space that is not a sequential space.

Proof. 

There is a non-discrete space that has no non-trivial convergent sequence (Corollary 3.6.15, [12]). Thus, every subset of X is sequentially open. However, X is not a discrete space, and thus X is not a sequential space.

Take $\mathcal{I}={\mathcal{I}}_{fin}$. Define $d:X\times X\to [0,+\infty )$ by

$$d(x,y)=\left\{\begin{array}{cc}0,\hfill & x=y,\hfill \\ 1,\hfill & x\ne y.\hfill \end{array}\right.$$

Then, it is a d-function, and $B(x,1/n)=\left\{x\right\}$ is ${\mathcal{I}}_{sn}$-open for each $x\in X$ and $n\in \mathbb{N}$. By Definition 4, $(X,d)$ is an $\mathcal{I}$-semi-metric space. □

Question 2.

Is every Hausdorff symmetric space $\mathcal{I}$-$snf$-countable for each admissible ideal $\mathcal{I}$ on $\mathbb{N}$?

4. $\mathcal{I}$-Covering and $\mathit{\pi }$-Images of Metric Spaces

$\mathcal{I}$-Cauchy sequences are important concepts in studying $\mathcal{I}$-convergence of topological spaces and $\mathcal{I}$-completeness of metric spaces [20,21]. In this section, we define d-$\mathcal{I}$-Cauchy sequences in topological spaces under $\mathcal{I}$-convergence, discuss some properties of $\mathcal{I}$-$sn$-symmetric spaces with the $\mathcal{I}$-Cauchy condition, and give the characterizations of $\mathcal{I}$-covering and $\pi$-images of metric spaces.

Definition 6.

(1) 

Let $(X,d)$ be an $\mathcal{I}$-$sn$-symmetric space. A sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in X is said to be a d-$\mathcal{I}$-Cauchy sequence if, for any $\epsilon >0$, there is $I\in \mathcal{I}$ such that $d(x_n,x_m)<\epsilon$ for each $m,n\in \mathbb{N}\setminus I$.

(2) 

X is said to be an $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition if there is an $\mathcal{I}$-$sn$-symmetric d on X such that every $\mathcal{I}$-convergent sequence in X is a d-$\mathcal{I}$-Cauchy sequence.

Definition 7

(Definition 2.7, [13]). Let $\mathcal{P}$ be a family of subsets of a topological space X. $\mathcal{P}$ is called an $\mathcal{I}$-$cs$-cover of X if, whenever ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is a sequence in X with $x_n\stackrel{\mathcal{I}}{\to }x$, there are $I\in \mathcal{I}$ and $P\in \mathcal{P}$ such that $\left\{x\right\}\cup \{x_n:n\in \mathbb{N}\setminus I\}\subseteq P$.

Definition 8.

Let $f:X\to Y$ be a mapping.

(1) 

Here, f is called an $\mathcal{I}$-covering mapping if, whenever a sequence $y_n\stackrel{\mathcal{I}}{\to }y$ in Y, there is a sequence $x_n\stackrel{\mathcal{I}}{\to }x$ in X satisfying $x\in f^{-1}\left(y\right)$, and each $x_n\in f^{-1}\left(y_n\right)$ (Definition 4.1, [9]). An ${\mathcal{I}}_{fin}$-covering mapping is called a sequence-covering mapping [22].

(2) 

Suppose that $(X,d)$ is a metric space. Then, f is called a π-mapping with respect to d if $d(f^{-1}\left(y\right),X\setminus f^{-1}\left(U\right))>0$ for every neighborhood U of y in Y [23].

Lemma 4

(Lemma 3.3, [18]). Let $f:X\to Y$ be a mapping and ${\left\{y_i\right\}}_{i\in \mathbb{N}}$ a sequence $\mathcal{I}$-converging to some point $f\left(x\right)$ in Y. If ${\left\{B_n\right\}}_{n\in \mathbb{N}}$ is a decreasing network at x in X and the sequence ${\left\{y_i\right\}}_{i\in \mathbb{N}}$ is $\mathcal{I}$-eventually in $f\left(B_n\right)$ for each $n\in \mathbb{N}$, then there is a sequence ${\left\{x_i\right\}}_{i\in \mathbb{N}}$ $\mathcal{I}$-converging to the point x in X with each $x_i\in f^{-1}\left(y_i\right)$.

Theorem 8.

The following are equivalent for a topological space X:

(1) 

X is an $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition.

(2) 

X has a point-star network consisting of $\mathcal{I}$-$cs$-covers.

(3) 

X is an $\mathcal{I}$-covering and π-image of a metric space.

Proof. 

(1) ⇒ (2). Suppose that $(X,d)$ is an $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition. For each $n\in \mathbb{N}$, put

$${\mathcal{P}}_n=\left\{P\subseteq X:sup\left\{d\right(x,y):x,y\in P\}<1/n\right\}.$$

Then, st$(x,{\mathcal{P}}_n)=B(x,1/n)$ for each $x\in X$ (see the proof of Theorem 7). Thus, ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ is a point-star $\mathcal{I}$-$sn$-network of X. Next, we show that each ${\mathcal{P}}_n$ is an $\mathcal{I}$-$cs$-cover of X. Let ${\left\{x_i\right\}}_{i\in \mathbb{N}}$ be a sequence in X with $x_i\stackrel{\mathcal{I}}{\to }x\in X$. Since $(X,d)$ is an $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition, ${\left\{x_i\right\}}_{i\in \mathbb{N}}$ is a d-$\mathcal{I}$-Cauchy sequence. Hence, for each $n\in \mathbb{N}$, there is $I_1\in \mathcal{I}$ such that $d(x_i,x_j)<1/n$ for each $i,j\in \mathbb{N}\setminus I_1$. Note that $B(x,1/n)$ is an $\mathcal{I}$-sequential neighborhood of x in X, and thus there is $I_2\in \mathcal{I}$ such that $d(x,x_i)<1/n$ for each $i\in \mathbb{N}\setminus I_2$. Put $I=I_1\cup I_2$ and $P=\left\{x\right\}\cup \{x_i:i\in \mathbb{N}\setminus I\}$. Then, $I\in \mathcal{I}$ and $\left\{x\right\}\cup \{x_i:i\in \mathbb{N}\setminus I\}=P\in {\mathcal{P}}_n$. This implies that each ${\mathcal{P}}_n$ is an $\mathcal{I}$-$cs$-cover of X. Thus, X has a point-star network consisting of $\mathcal{I}$-$cs$-covers.

$\left(2\right)\Rightarrow \left(3\right)$. Let ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ be a point-star network consisting of $\mathcal{I}$-$cs$-covers of X. For each $n\in \mathbb{N}$, ${\mathcal{P}}_n$ is denoted by $\{P_{\alpha }:\alpha \in {\Lambda }_n\}$, and ${\Lambda }_n$ is endowed with discrete topology. Put

$$M=\left\{\alpha =\left({\alpha }_n\right)\in \prod _{n\in \mathbb{N}}{\Lambda }_n:{\left\{P_{{\alpha }_n}\right\}}_{n\in \mathbb{N}}\mathrm{forms} \mathrm{a} \mathrm{network} \mathrm{at} \mathrm{some} \mathrm{point}{x}_{\alpha }\mathrm{in}X\right\}.$$

Define a function $f:M\to X$ by $f\left(\alpha \right)=x_{\alpha }$. Then, $f\left(\left({\alpha }_n\right)\right)={\bigcap }_{n\in \mathbb{N}}{P}_{{\alpha }_n}$ because X is $T_1$. The subspace M of ${\prod }_{n\in \mathbb{N}}{\Lambda }_n$ is a metrizable space.

(i) Here, f is a $\pi$-mapping.

It is easy to see that f is continuous and surjective. For each $\alpha ,\beta \in M$, define

$$d(\alpha ,\beta )\in \left\{\begin{array}{cc}0,\hfill & \alpha =\beta ,\hfill \\ max\{1/k:{\pi }_k\left(\alpha \right)\ne {\pi }_k\left(\beta \right)\},\hfill & \alpha \ne \beta ,\hfill \end{array}\right.$$

where ${\pi }_k:{\prod }_{n\in \mathbb{N}}{\Lambda }_n\to {\Lambda }_k$ is the projection for each $k\in \mathbb{N}$. Thus, d is a metric on M. For each $x\in U$ with U open in X, there is $n\in \mathbb{N}$ such that st$(x,{\mathcal{P}}_n)\subseteq U$. For each $\alpha \in f^{-1}\left(x\right) \mathrm{and} \beta \in M$, if $d(\alpha ,\beta )<1/n$, then ${\pi }_i\left(\alpha \right)={\pi }_i\left(\beta \right)$ for each $i\le n$; thus, $x\in P_{{\pi }_n\left(\alpha \right)}$, and $f\left(\beta \right)\in {\bigcap }_{i\in \mathbb{N}}{P}_{{\pi }_i\left(\beta \right)}\subseteq P_{{\pi }_n\left(\beta \right)}=P_{{\pi }_n\left(\alpha \right)}\subseteq \mathrm{st}(x,{\mathcal{P}}_n)\subseteq U$. Therefore, $d(f^{-1}\left(x\right),X\setminus f^{-1}\left(U\right))\ge 1/n$. This implies that f is a $\pi$-mapping.

(ii) For each $\alpha =\left({\alpha }_i\right)\in M$ and $n\in \mathbb{N}$, put

$$B({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)=\{\left({\beta }_i\right)\in M:{\beta }_i={\alpha }_i\mathrm{for} \mathrm{each}i\le n\}.$$

Then, $f\left(B({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)\right)={\bigcap }_{i\le n}{P}_{{\alpha }_i}$.

In fact, let $\beta =\left({\beta }_i\right)\in B({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)$. Then,

$$f\left(\beta \right)\in \bigcap _{i\in \mathbb{N}}{P}_{{\beta }_i}\subseteq \bigcap _{i\le n}{P}_{{\beta }_i}=\bigcap _{i\le n}{P}_{{\alpha }_i}.$$

So, $f\left(B({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)\right)\subseteq {\bigcap }_{i\le n}{P}_{{\alpha }_i}$. On the other hand, let $y\in {\bigcap }_{i\le n}{P}_{{\alpha }_i}$. Since f is surjective, there exists ${\gamma }^{\prime }=\left({\gamma }_i^{\prime }\right)\in M$ such that $f\left({\gamma }^{\prime }\right)=y$. For each $i\in \mathbb{N}$, put ${\gamma }_i={\alpha }_i$, if $i\le n$; ${\gamma }_i={\gamma }_{i-n}^{\prime }$, if $i>n$. Then, ${\left\{P_{{\gamma }_i}\right\}}_{i\in \mathbb{N}}$ is a network at y in X. Let $\gamma =\left({\gamma }_i\right)$. Then, $\gamma \in B({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)$ and $f\left(\gamma \right)=y$, so $y\in f\left(B({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)\right)$. Thus, ${\bigcap }_{i\le n}{P}_{{\alpha }_i}\subseteq f\left(B({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)\right)$. This shows that $f\left(B({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)\right)={\bigcap }_{i\le n}{P}_{{\alpha }_i}$.

(iii) Here, f is an $\mathcal{I}$-covering mapping.

For each $x\in X$, let ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ be a sequence in X with $x_n\stackrel{\mathcal{I}}{\to }x$. For each $i\in \mathbb{N}$, since ${\mathcal{P}}_i$ is an $\mathcal{I}$-$cs$-cover of X, there is ${\beta }_i\in {\Lambda }_i$ such that the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is $\mathcal{I}$-eventually in $P_{{\beta }_i}\in {\left({\mathcal{P}}_i\right)}_x$. Put $\beta =\left({\beta }_i\right)\in {\prod }_{i\in \mathbb{N}}{\Lambda }_i$. Since ${\left\{{\mathcal{P}}_i\right\}}_{i\in \mathbb{N}}$ is a point-star network of X, it is easy to check that the family ${\left\{P_{{\beta }_i}\right\}}_{i\in \mathbb{N}}$ is a network at x in X. Thus, $\beta \in M$ and $f\left(\beta \right)=x$. For each $m\in \mathbb{N}$, let $B_m=\{\left({\alpha }_i\right)\in M:{\alpha }_i={\beta }_i\mathrm{for} \mathrm{each}i\le m\}$. It follows from (ii) that $f\left(B_m\right)={\bigcap }_{i\le m}{P}_{{\beta }_i}$, and it is easy to see that the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is $\mathcal{I}$-eventually in ${\bigcap }_{i\le m}{P}_{{\beta }_i}$. Since ${\left\{B_m\right\}}_{m\in \mathbb{N}}$ is a decreasing neighborhood base at $\beta$ in M, it follows from Lemma 4 that there is a sequence ${\left\{z_n\right\}}_{n\in \mathbb{N}}$ $\mathcal{I}$-converging to $\beta$ in M with each $z_n\in f^{-1}\left(x_n\right)$. Therefore, f is an $\mathcal{I}$-covering mapping.

$\left(3\right)\Rightarrow \left(1\right)$. Let $f:(M,d)\to X$ be an $\mathcal{I}$-covering and $\pi$-mapping, where d is a metric on M. For each $n\in \mathbb{N}$, put ${\mathcal{B}}_n=\{B(z,1/2^n):z\in M\}$ and ${\mathcal{P}}_n=f\left({\mathcal{B}}_n\right)$. Then, ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ is a point-star $\mathcal{I}$-$sn$-network of X.

In fact, let ${\left\{y_k\right\}}_{k\in \mathbb{N}}$ be a sequence in X with $y_k\stackrel{\mathcal{I}}{\to }x\in X$. Since f is $\mathcal{I}$-covering, there are $z\in f^{-1}\left(x\right)$ and a sequence ${\left\{z_k\right\}}_{k\in \mathbb{N}}$ in M such that $z_k\stackrel{\mathcal{I}}{\to }z$ and each $f\left(z_k\right)=y_k$. For each $n\in \mathbb{N}$, the sequence ${\left\{z_k\right\}}_{k\in \mathbb{N}}$ is $\mathcal{I}$-eventually in $B(z,1/2^n)$; thus, ${\left\{y_k\right\}}_{k\in \mathbb{N}}$ is $\mathcal{I}$-eventually in $f\left(B(z,1/2^n)\right)\subseteq \mathrm{st}(x,{\mathcal{P}}_n)$. This shows that ${\mathcal{P}}_n$ is an $\mathcal{I}$-$cs$-cover and $\mathrm{st}(x,{\mathcal{P}}_n)$ is an $\mathcal{I}$-sequential neighborhood of x.

On the other hand, let U be an open neighborhood U of x in X. Since f is a $\pi$-mapping, there exists $n\in \mathbb{N}$ such that $d(f^{-1}\left(x\right),M\setminus f^{-1}\left(U\right))>1/2^{n-1}$. If $u\in \mathrm{st}(x,{\mathcal{P}}_n)$, then there is $z\in M$ with $\{u,x\}\subseteq f\left(B(z,1/2^n)\right)$, and thus $f^{-1}\left(x\right)\cap B(z,1/2^n)\ne \varnothing$, so $B(z,1/2^n)\subseteq f^{-1}\left(U\right)$; otherwise, $d(f^{-1}\left(x\right),M\setminus f^{-1}\left(U\right))<1/2^{n-1}$. Hence, $u\in f\left(B(z,1/2^n)\right)\subseteq U$, and then st$(x,{\mathcal{P}}_n)\subseteq U$. This implies that ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ is a point-star $\mathcal{I}$-$sn$-network of X.

Let d be the $\mathcal{I}$-$sn$-symmetric on X in the proof of “$\left(2\right)\Rightarrow \left(3\right)$” in Theorem 7. Let ${\left\{x_i\right\}}_{i\in \mathbb{N}}$ be a sequence in X with $x_i\stackrel{\mathcal{I}}{\to }x\in X$. For each $\epsilon >0$, there is $n\in \mathbb{N}$ such that $1/n<\epsilon$. Since ${\mathcal{P}}_n$ is an $\mathcal{I}$-$cs$-cover of X, there are $P\in {\mathcal{P}}_n$ and $I\in \mathcal{I}$ such that $\left\{x\right\}\cup \{x_i:i\in \mathbb{N}\setminus I\}\subseteq P$. If $i,j\in \mathbb{N}\setminus I$, then $x_i,x_j\in P$; thus, $x_i\in \mathrm{st}(x_j,{\mathcal{P}}_n)$, and so $d(x_i,x_j)=1/n(x_i,x_j)<1/n<\epsilon$ (see the proof of Theorem 7). This means that ${\left\{x_i\right\}}_{i\in \mathbb{N}}$ is a d-$\mathcal{I}$-Cauchy sequence. Consequently, X is an $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition. □

Let $f:X\to Y$ be a mapping. Here, f is called quotient provided that, for each $U\subseteq Y$ with $f^{-1}\left(U\right)$ open in X, U is open (p. 91, [12]); f is called pseudo-open provided that, for each $y\in Y$ and $f^{-1}\left(y\right)\subseteq U$ with U open in X, $f\left(U\right)$ is a neighborhood of y in Y (p. 113, [15]). It is known that every pseudo-open mapping is quotient (p. 113, [15]). The following result is a generalization of Theorem 1.3 under $\mathcal{I}$-convergence.

Corollary 3.

The following are equivalent for a topological space X:

(1) 

X is a sequential and $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition.

(2) 

X is a quotient, $\mathcal{I}$-covering, and π-image of a metric space.

Proof. 

Let X be sequential and $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition. By Theorem 8, there are a metric space M and an $\mathcal{I}$-covering and $\pi$-mapping $f:M\to X$. Suppose that $U\subset Y$ that and $f^{-1}\left(U\right)$ is open in M. Since f is $\mathcal{I}$-covering, it is easy to check that U is ${\mathcal{I}}_{sn}$-open. And, since X is sequential, U is open. Thus, f is quotient.

On the other hand, let X be a quotient, $\mathcal{I}$-covering, and $\pi$-image of a metric space. Since every sequential space is preserved by a quotient mapping (Proposition 1.2, [15]), by Theorem 8, X is a sequential and $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition. □

Corollary 4.

The following are equivalent for a topological space X:

(1) 

X is a Fréchet–Urysohn and $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition.

(2) 

X is a pseudo-open, $\mathcal{I}$-covering, and π-image of a metric space.

Proof. 

Let X be a Fréchet–Urysohn and $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition. Since every $\mathcal{I}$-covering mapping onto a Fréchet–Urysohn space is pseudo-open (Theorem 4.7, [10]), by Theorem 8, X is a pseudo-open, $\mathcal{I}$-covering and $\pi$-image of a metric space.

On the other hand, let X be a pseudo-open, $\mathcal{I}$-covering, and $\pi$-image of a metric space. Since every Fréchet–Urysohn space is preserved by a pseudo-open mapping (Proposition 2.3, [15]), by Theorem 8, X is a Fréchet–Urysohn and $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition. □

Example 4.

There exists a sequential $\mathcal{I}$-$sn$-symmetric Hausdorff space that is not an $\mathcal{I}$-covering π-image of a metric space. Thus, the “$\mathcal{I}$-Cauchy condition” in Theorem 8 is essential.

Proof. 

There exists a symmetric Hausdorff space X that is not a sequence-covering $\pi$-image of a metric space (Example 3.1, [4]). Put $\mathcal{I}={\mathcal{I}}_{fin}$. Then, X is not an $\mathcal{I}$-covering $\pi$-image of a metric space. It follows from Figure 1 and Corollary 1 that X is an $\mathcal{I}$-$sn$-symmetric space. □

The answer to the following question is positive if $\mathcal{I}={\mathcal{I}}_{fin}$ [6].

Question 3.

If a Hausdorff space X is a pseudo-open, $\mathcal{I}$-covering, $\pi$-image of a metric space, is X an open $\pi$-image of a metric space?

By Theorems 7 and 8, the following question is posed.

Question 4.

How can we characterize $\mathcal{I}$-$sn$-symmetric spaces by point-star networks consisting of certain covers?

5. An Application to Statistical Convergence

Statistical convergence is a special type of ideal convergence. In this section, we present an application of $\mathcal{I}$-$sn$-symmetric spaces under asymptotic density zero ideals.

Recall the notion of statistical convergence in topological spaces. For each subset A of $\mathbb{N}$, the asymptotic density of A, denoted by $\delta \left(A\right)$, is given by

$$\delta \left(A\right)=\underset{n\to \infty }{lim}\left|\{k\in A:k\le n\}\right|/n,$$

if this limit exists. Let ${\mathcal{I}}_{\delta }$ be the family of subsets $A\subseteq \mathbb{N}$ with $\delta \left(A\right)=0$. It is easy to verify that ${\mathcal{I}}_{\delta }$ is an admissible ideal [8], which is called an asymptotic density zero ideal.

Let X be a topological space. A sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in X is said to converge statistically to a point $x\in X$ [24] if $\delta \left(\{n\in \mathbb{N}:x_n\notin U\}\right)=0$ for each neighborhood U of x in X.

It is well-known that the usual convergence of sequences is a special statistical convergence, and statistical convergence is a special ideal convergence. Therefore, the results of ideal convergence (resp., statistical convergence) are fully applicable to statistical convergence (resp., the usual convergence), and we may obtain better results than ideal convergence (resp., statistical convergence) under statistical convergence (resp., the usual convergence). Our goal of this section is to strengthen Theorem 8 into a better form in the sense of statistical convergence.

First, we introduce several concepts related to Theorem 8. Let $\mathcal{P}$ be a family of subsets of a topological space X. $\mathcal{P}$ is called an $\mathcal{I}$-sn-cover of X (Definition 2.7, [13]) if, for each $x\in X$, there exists $P\in \mathcal{P}$ such that P is an $\mathcal{I}$-sequential neighborhood of x in X. Let $f:X\to Y$ be a mapping. Here, f is called a 1-$\mathcal{I}$-covering mapping (Definition 4.6, [13]) if, for every $y\in Y$, there exists $x\in f^{-1}\left(y\right)$ such that, whenever ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ is a sequence $\mathcal{I}$-converging to y in Y, then there exists a sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ $\mathcal{I}$-converging to x in X with each $x_n\in f^{-1}\left(y_n\right)$. A 1-${\mathcal{I}}_{fin}$-covering mapping is called a 1-sequence-covering mapping (Definition 1.1.3, [1]).

Lemma 5

(Lemma 4.3, [10]). Let $f:X\to Y$ be a mapping. If, for each $x\in X$, there is a decreasing network ${\left\{B_n\right\}}_{n\in \mathbb{N}}$ at x in X such that each $f\left(B_n\right)$ is an $\mathcal{I}$-sequential neighborhood of $f\left(x\right)$ in Y, then f is a 1-$\mathcal{I}$-covering mapping.

The following result is a beneficial attempt to apply ideal convergence to statistical convergence.

Theorem 9.

Let $\mathcal{I}={\mathcal{I}}_{\delta }$. The following are equivalent for a topological space X:

(1) 

X is a 1-$\mathcal{I}$-covering and π-image of a metric space.

(2) 

X is an $\mathcal{I}$-covering and π-image of a metric space.

(3) 

X has a point-star network consisting of $\mathcal{I}$-$sn$-covers.

(4) 

X has a point-star network consisting of $\mathcal{I}$-$cs$-covers.

(5) 

X is an $\mathcal{I}$-$sn$-symmetric space with the $\mathcal{I}$-Cauchy condition.

Proof. 

Since every 1-$\mathcal{I}$-covering mapping is an $\mathcal{I}$-covering mapping, $\left(1\right)\Rightarrow \left(2\right)$ is clear. And since every $\mathcal{I}$-$sn$-cover of X is an $\mathcal{I}$-$cs$-cover, $\left(3\right)\Rightarrow \left(4\right)$ is also obvious. In view of Theorem 8, $\left(2\right)\iff \left(4\right)\iff \left(5\right)$. Next, we will prove that $\left(4\right)\Rightarrow \left(3\right)\Rightarrow \left(1\right)$.

$\left(4\right)\Rightarrow \left(3\right)$. Let ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ be a point-star network consisting of $\mathcal{I}$-$cs$-covers of X. It is easy to see that, if $\mathcal{P}$ and $\mathcal{Q}$ are $\mathcal{I}$-$cs$-covers of X, then so is the intersection $\mathcal{P}\bigwedge \mathcal{Q}$. Therefore, according to the proof of “(2) ⇒ (3)” in Theorem 7, we can assume that each ${\mathcal{P}}_{n+1}$ refines ${\mathcal{P}}_n$, and there is a d-function d on X such that $\mathrm{st}(x,{\mathcal{P}}_n)=B(x,1/n)$ for each $x\in X$ and $n\in \mathbb{N}$.

The function $d:X\times X\to [0,+\infty )$ has the following property:

Claim. For every $x\in X$ and $\epsilon >0$, there is $\delta =\delta (x,\epsilon )>0$ such that

$$\mathrm{if}y,z\in B(x,\delta ),\mathrm{then}d(y,z)<\epsilon .$$

Otherwise, there are ${\epsilon }_0>0$ and sequences ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{z_n\right\}}_{n\in \mathbb{N}}$ in X such that $y_n,z_n\in B(x,1/n)$ and $d(y_n,z_n)\ge {\epsilon }_0$ for each $n\in \mathbb{N}$. Choose $k\in \mathbb{N}$ such that $k{\epsilon }_0>1$. Since ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ is a point-star network of X, the sequences ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{z_n\right\}}_{n\in \mathbb{N}}$ converge to x. Thus, the sequence $\{y_1,z_1,y_2,z_2,\cdots \}={\left\{x_l\right\}}_{l\in \mathbb{N}}$ also converges to x, and then it converges statistically to x. Since ${\mathcal{P}}_k$ is an $\mathcal{I}$-$cs$-cover of X, there are $P\in {\mathcal{P}}_k$ and $A\in {\mathcal{I}}_{\delta }$ such that $\left\{x\right\}\cup \{x_l:l\in \mathbb{N}\setminus A\}\subseteq P$.

Subclaim. $\{y_m,z_m\}\subseteq P$ for some $m\in \mathbb{N}$.

Otherwise, assume that there is no $m\in \mathbb{N}$ such that $\{y_m,z_m\}\subseteq P$. Put $A^{\prime }=\{l\in \mathbb{N}:x_l\notin P\}$. Then, $A^{\prime }\subseteq A$; and so $\delta \left(A^{\prime }\right)=0$, and $l\in A^{\prime }\iff x_l\notin P$. Put

$$\begin{array}{cc}\hfill B_1=& \{l\in \mathbb{N}:x_l=y_m\in P\mathrm{for}\mathrm{some}m\in \mathbb{N}\},\mathrm{and}\hfill \\ \hfill B_2=& \{l\in \mathbb{N}:x_l=z_m\in P\mathrm{for}\mathrm{some}m\in \mathbb{N}\}.\hfill \end{array}$$

It is obvious that $B_1\cup B_2=\mathbb{N}\setminus A^{\prime }$. Thus, $\delta (B_1\cup B_2)=1$. Without loss of generality, we can assume that

$$\underline{\delta }\left(B_1\right)=\underset{n\to \infty }{lim\; inf}\left|\{k\in B_1:k\le n\}\right|/n>0.$$

If $l\in B_1$, then $x_l=y_m\in P$ for some $m\in \mathbb{N}$. It follows from the assumption that $x_{l+1}=z_m\notin P$, and thus $l+1\in A^{\prime }$. This implies $\{l+1:l\in B_1\}\subseteq A^{\prime }$. We have that $\underline{\delta }\left(A^{\prime }\right)\ge \underline{\delta }\left(\{l+1:l\in B_1\}\right)=\underline{\delta }\left(B_1\right)>0$, which is a contradiction. This completes the proof of the Subclaim.

It follows from the Subclaim that there is $m\in \mathbb{N}$ such that $\{y_m,z_m\}\subseteq P$. Thus, $z_m\in \mathrm{st}(y_m,{\mathcal{P}}_k)$, and then $d(y_m,z_m)<1/k<{\epsilon }_0$, which is a contradiction. This completes the proof of the Claim.

The above property (i.e., the Claim) shows that, for every $x\in X$ and $n\in \mathbb{N}$, there is $\delta (x,1/n)>0$ such that if $y,z\in B(x,\delta (x,1/n\left)\right)$, and then $d(y,z)<1/n$. Put

$${\mathcal{U}}_n=\{B(x,\delta (x,1/n)):x\in X\}.$$

Note that ${\mathcal{P}}_n$ is an $\mathcal{I}$-$cs$-cover of X, so it follows that $\mathrm{st}(x,{\mathcal{P}}_n)$ is an $\mathcal{I}$-sequential neighborhood of x. Thus, $B(x,\delta (x,1/n\left)\right)$ is also an $\mathcal{I}$-sequential neighborhood of x. Consequently, ${\mathcal{U}}_n$ is an $\mathcal{I}$-$sn$-cover of X.

If ${\left\{{\mathcal{U}}_n\right\}}_{n\in \mathbb{N}}$ is not a point-star network of X, then there is an open neighborhood O of x in X such that each $\mathrm{st}(x,{\mathcal{U}}_n)⊈O$. Thus, there are sequences ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ in X such that $x,x_n\in B(y_n,\delta (y_n,1/n))$ and $x_n\notin O$ for each $n\in \mathbb{N}$. It follows from the definition of $\delta (x,1/n)$ that $d(x,x_n)<1/n$ for each $n\in \mathbb{N}$, and the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is not convergent to x, which is a contradiction. This implies that the family ${\left\{{\mathcal{U}}_n\right\}}_{n\in \mathbb{N}}$ is a point-star network consisting of $\mathcal{I}$-$sn$-covers of X.

$\left(3\right)\Rightarrow \left(1\right)$. Let ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ be a point-star network consisting of $\mathcal{I}$-$sn$-covers of X, where each ${\mathcal{P}}_n=\{P_{\alpha }:\alpha \in {\Lambda }_n\}$. According to the proof of “(2) ⇒ (3)” in Theorem 8, there are a metric space M and an $\mathcal{I}$-covering and $\pi$-mapping $f:M\to X$, where

$$M=\left\{\alpha =\left({\alpha }_n\right)\in \prod _{n\in \mathbb{N}}{\Lambda }_n:{\left\{P_{{\alpha }_n}\right\}}_{n\in \mathbb{N}}\mathrm{forms}\mathrm{a}\mathrm{network}\mathrm{at}\mathrm{some}\mathrm{point}{x}_{\alpha }\mathrm{in}X\right\},$$

and $f\left(\alpha \right)=x_{\alpha }$. We now show that the mapping f is a 1-$\mathcal{I}$-covering mapping.

Let $x\in X$. For each $n\in \mathbb{N}$, since ${\mathcal{P}}_n$ is an $\mathcal{I}$-$sn$-cover of X, choose ${\beta }_n\in {\Lambda }_n$ such that $P_{{\beta }_n}$ is an $\mathcal{I}$-sequential neighborhood of x in X. Since ${\left\{{\mathcal{P}}_n\right\}}_{n\in \mathbb{N}}$ is a point-star network of X, the family ${\left\{P_{{\beta }_n}\right\}}_{n\in \mathbb{N}}$ is a network at x in X. Put $\beta =\left({\beta }_n\right)\in {\prod }_{n\in \mathbb{N}}{\Lambda }_n$. Then, $\beta \in M$ and $f\left(\beta \right)=x$. For each $n\in \mathbb{N}$, put

$$B_n\left(\beta \right)=\{\left({\alpha }_i\right)\in M:{\alpha }_i={\beta }_i\mathrm{for}\mathrm{each}i\le n\}.$$

It follows from part (ii) of the proof in Theorem 8 that $f\left(B_n\left(\beta \right)\right)={\bigcap }_{i\le n}{P}_{{\beta }_i}$. Since each $P_{{\beta }_i}$ is an $\mathcal{I}$-sequential neighborhood of x in X, the set $f\left(B_n\left(\beta \right)\right)$ is also an $\mathcal{I}$-sequential neighborhood of x in X. It is clear that the family ${\left\{B_n\left(\beta \right)\right\}}_{n\in \mathbb{N}}$ is a decreasing neighborhood base of $\beta$ in M. It follows from Lemma 5 that f is a 1-$\mathcal{I}$-covering mapping. This completes the proof. □

The following example shows that “$\pi$-mapping” in Theorem 9 is essential.

Example 5.

There exists an $\mathcal{I}$-covering image of a metric space that is not a 1-$\mathcal{I}$-covering image of a metric space.

Proof. 

Let X be the sequential fan $S_{\omega }$, i.e., it is the quotient space obtained by identifying all limit points of the topological sum of $\omega$ for many convergent sequences. Let $\mathcal{S}$ be the family of convergent sequences in X that contains the limit point. Put $\mathcal{S}=\{S_{\alpha }\subseteq X:\alpha \in \Lambda \}$. For each $\alpha \in \Lambda$, let $M_{\alpha }$ be the set $S_{\alpha }$ equipped with the subspace topology of X. Put the topological sum $M={⨁}_{\alpha \in \Lambda }{M}_{\alpha }$. Then, M is a metric space. Define a mapping $f:M\to X$ such that each restriction ${f|}_{M_{\alpha }}\to S_{\alpha }$ is the identity. Then, f is a sequence-covering mapping. It is obvious that X is a Fréchet–Urysohn space that is not first-countable. Thus, X is not an $snf$-countable space. Consequently, X is not a 1-sequence-covering image of a metric space (Theorem 4.5, [10]). Put $\mathcal{I}={\mathcal{I}}_{fin}$. Then, X is an $\mathcal{I}$-covering image of a metric space, which is not a 1-$\mathcal{I}$-covering image of a metric space. □

Question 5.

Let $\mathcal{I}$ be an admissible ideal on $\mathbb{N}$ and X be an $\mathcal{I}$-covering and $\pi$-image of a metric space. Is X a 1-$\mathcal{I}$-covering and $\pi$-image of a metric space?

6. Conclusions

In this article, we define and discuss $\mathcal{I}$-symmetric spaces and $\mathcal{I}$-$sn$-symmetric spaces (with the $\mathcal{I}$-Cauchy condition), obtain some relationships between $\mathcal{I}$-$sn$-symmetric spaces and $sn$-symmetric spaces (see Figure 1 and Theorem 7), and establish special connections between $\mathcal{I}$-$sn$-symmetric spaces with the $\mathcal{I}$-Cauchy condition and $\mathcal{I}$-covering $\pi$-mappings (see Theorem 8). As an application of $\mathcal{I}$-$sn$-symmetric spaces and the $\pi$-images of metric spaces, we discuss the characterizations of sequence-covering and $\pi$-images of metric spaces under statistical convergence and obtain a better result than ideal convergence (see Theorem 9).

We have also raised some unresolved questions in this field.