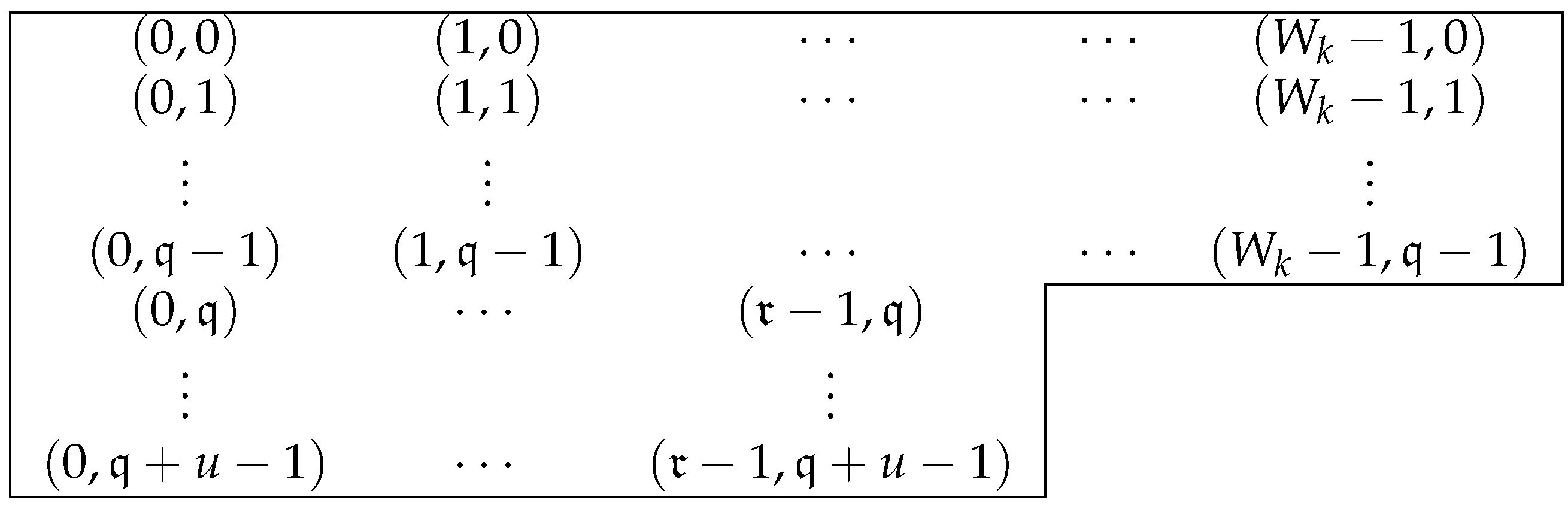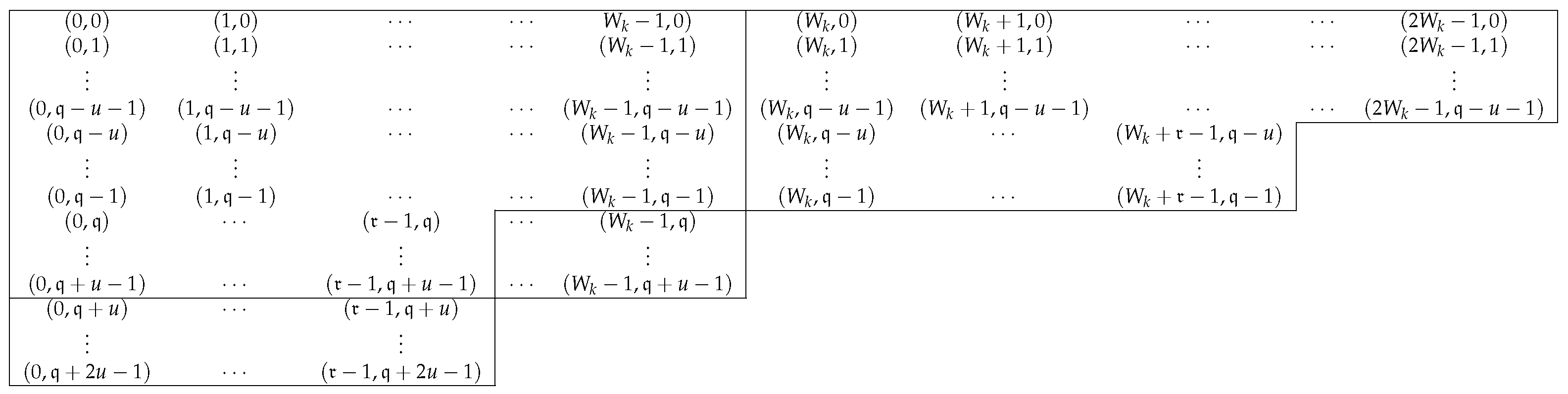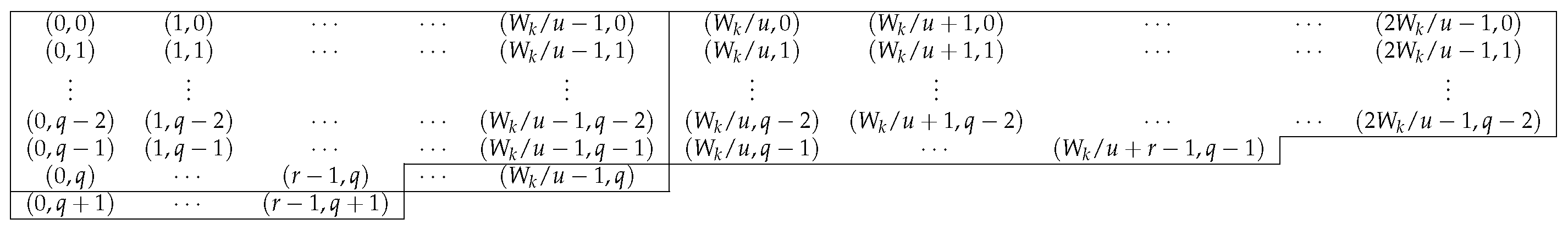1. Introduction
We consider the sequence
, satisfying:
where
u and
v are positive integers with
. The values of
depend on the values of
u and
v. If
,
is the
n-th Fibonacci number [
1]. If
and
,
is the
n-th Jacobsthal number [
2,
3]. If
and
,
is the
n-th Pell number [
4]. However, for simplicity, if we do not specify the values of
u or
v, we will simply write
for
.
This type of number sequence has been well known to many people by Horadam’s series of studies ([
5,
6,
7,
8,
9]) in the 1960s. Because of this fact, this sequence is sometimes called the
Horadam sequence. Horadam himself used the recurrence relation
. However, recently more people (see, e.g., [
10,
11]) have used the recurrence relation
and such works are still due to Horadam. In general, the initial values are arbitrary, but because of some simplifications, we set
and
. According to [
6], this sequence has long exercised interest, as seen in, for instance, Bessel-Hagen [
12], Lucas [
13], and Tagiuri [
14], and, for historical details, Dickson [
15]. However, it is deplorable that quite a few papers are publishing results that have already been obtained by these authors as new results, either because they are unaware of their or the following important results, or even if they are ignoring them.
Given the set of positive integers
(
), for a nonnegative integer
p, let
be the set of integers whose nonnegative integral linear combinations of given positive integers
are expressed in more than
p ways. For a set of nonnegative integers
, the set
is finite if and only if
. Then, there exists the largest integer
in
, called the
p-Frobenius number. The cardinality of
is called the
p-genus and is denoted by
. The sum of the elements in
is called the
p-Sylvester sum and is denoted by
. This kind of concept is a generalization of the famous Diophantine problem of Frobenius since
is the case when the original Frobenius number
, the genus
and the Sylvester sum
are recovered. We can call
the
p-numerical semigroup. Strictly speaking, when
,
does not include 0 since the integer 0 has only one representation, so it satisfies simple additivity, and the set
becomes a numerical semigroup. For numerical semigroups, we refer to [
16,
17,
18]. For the
p-numerical semigroup, we refer to [
19]. The recent study of the number of representation (denumerant), denoted by
p in this paper, can be seen in [
20,
21,
22]. In particular, in [
23], an algorithm that computes the denumerant is shown. In [
24], three simple reduction formulas for the denumerant are obtaine using the Bernoulli–Barnes polynomials. In [
25], this algorithm is shown to avoid plenty of repeated computations and is, hence, faster.
We are interested in finding any closed or explicit form of the
p-Frobenius number, which is even more difficult when
. For three or more variables, no concrete example had been found. Most recently, we have finally succeeded in giving the
p-Frobenius number as closed-form expressions for the triangular number triplet ([
26]), for repunits ([
27,
28]).
In this paper, we study the
p-numerical semigroups of the triple
for integers
. We give explicit closed formulas of
p-Frobenius numbers and
p-genus of this triple. Note that the special cases for Fibonacci [
1], Pell [
4], and Jacobsthal triples [
2,
3] have already been studied.
The outline of this paper is as follows. In the next section, we introduce the concept of the
p-Apéry set and show how it is used to obtain the
p-Frobenius number, the
p-genus and the
p-Sylvester sum. In
Section 3, we show the result for
. The structure is different for odd
k and even
k. In
Section 4, we show the result for
, which is yielded from that for
. In
Section 5, we give an explicit form of the
p-genus. The figures in
Section 3 and
Section 4 are helpful to find the calculation of the
p-genus. In
Section 6, we hint at some comments on a simple modification of the recurrence relation.
2. Preliminaries
We introduce the Apéry set (see [
29]) below in order to obtain the formulas for
,
, and
technically. Without loss of generality, we assume that
.
Definition 1. Let p be a nonnegative integer. For a set of positive integers with and we denote by:the p-Apéry set of A, where each positive integer satisfies the conditions:Note that is defined to be 0. It follows that for each
p:
Even though it is hard to find any explicit form of
as well as
and
, by using convenient formulas established in [
30,
31], we can obtain such values for some special sequences
after finding any regular structure of
. One convenient formula is on the power sum:
by using Bernoulli numbers
defined by the generating function:
and another convenient formula is on the weighted power sum ([
32,
33]):
by using Eulerian numbers
appearing in the generating function:
with
and
. Here,
is a nonnegative integer and
. Some generalization of Bernulli numbers in connection with summation are devied in [
34]. From these convenient formulas, many useful expressions are yielded as special cases. Some useful ones are given as follows. The Formulas (3) and (4) are entailed from
and
, respectively. The proof of this lemma is given in [
31] as a more general case.
Lemma 1. Let κ, p, and μ be integers with and . Assume that . We have: Remark 1. When , the Formulas (2)–(4) reduce to the formulas by Brauer and Shockley [35] [Lemma 3], Selmer [36] [Theorem], and Tripathi [37] [Lemma 1] (the latter reference contained a typo, which was corrected in [38]), respectively:where () with . 3. The Case Where
We use the following properties repeatedly. The proof is trivial and omitted.
First of all, if
i is odd and
, then by (
1) and (7):
Hence,
. Therefore, from now on, we consider the case only when
i is even and
k is odd, or when
i is odd, with
.
3.1. The Case Where k Is Odd
When
k is odd, we choose nonnegative integers
and
as:
where
if
due to (
5); otherwise
is the largest integer, satisfying:
More directly, when
i is even (and
k is odd):
When
i is odd (and
k is odd):
Note that if
([
2]), then always
.
In particular, if
i is even and:
If
, then by (
5)
. So, when
i is even, by (8)
. Thus, we get:
When
and
i is odd, by
and
, there exists an integer
h such that
. By
,
. Thus:
Thus, we get:
We use the following identity.
Proof. By (
1) and (7) together with (
9), we get:
□
Assume that
(the case
is discussed later). Then, the elements of the (0-)Apéry set are given in
Figure 1. Here, we consider the expression:
or simply the position
.
We shall show that all the elements in
Figure 1 constitute the sequence
in the vertical
y direction. However, if
i is odd and
i is even, the situation of this sequence is different. In short, if
i is odd, the sequence appears continuously, but if
i is even, the sequence is divided into
u subsequences.
First, let
i be odd. Then, by
, we have:
By (7), we get:
Hence:
Thus, the element at
(
) cannot be an element of
but
as the same residue modulo
, where
. Next, by Lemma 3, we have:
Thus, the element at () cannot be an element of but .
Therefore, the sequence
is divided into the longer parts with length
and the shorter parts with length
. Namely, the longer part is of the subsequence:
with the next element at
. The shorter part is of the subsequence
with the next element at
. Since
, all elements in
are different modulo
.
Next, let
i be even. Then by
, we have:
Hence:
with
(
). By the determination of
in (
11), we see that
. So, we use the relation (
14). Thus, each subsequence is given as the following points. For
:
with next element is at
, coming back to the first one, because of Lemma 3. In addition, by (8), all terms of the above subsequence are:
Since
, this is equivalent to
(
). Therefore, there is no overlapped element among all subsequences. By (
9), the total number of terms in each subsequence is:
as expected.
By
Figure 1, the candidates of the largest element of
are at
or at
. Since
is equivalent to
, by Lemma 1 (
2), if
, then:
If
, then:
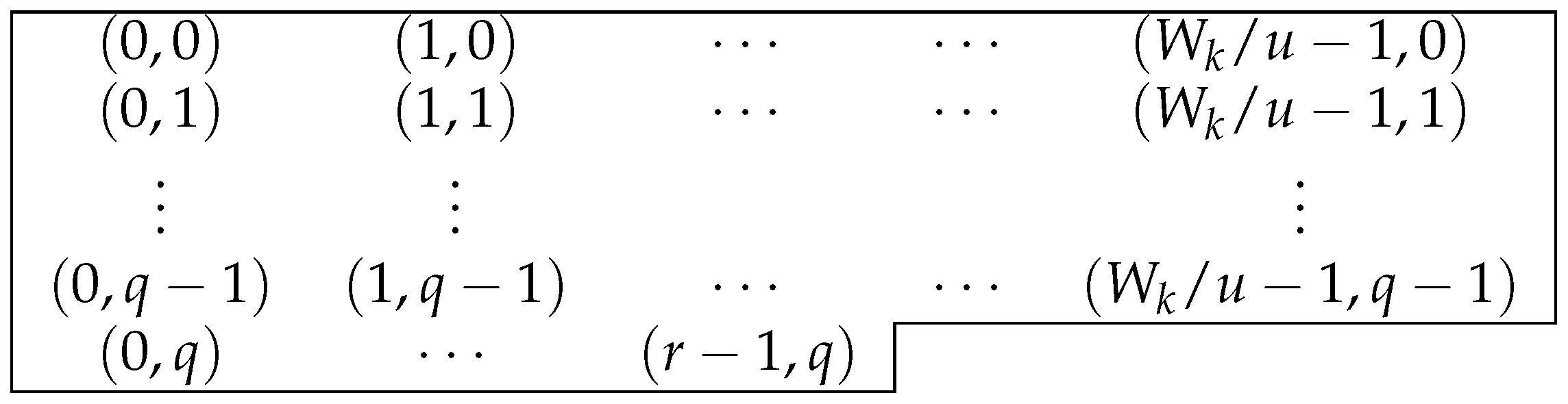
• The case k is odd with
When
k is odd and
, we get
and
. Hence, the elements of the (0-)Apéry set are given in
Figure 2.
Similarly to the case , when i is odd, so , the sequence simply becomes one sequence by combining all the subsequences with length and with length . When i is even, so , the sequence consists of u subsequences with the same length .
By
Figure 2, the largest element of
is at
. Hence:
In fact, this is included in the case where
and
.
3.2. The Case Where k Is Even
When
k is even (so
i is odd), we choose nonnegative integers
q and
r as:
where
. Note that
is an integer for even
k. Note that
because otherwise
i is also even. Then, the elements of the (0-)Apéry set are given in
Figure 3.
Similarly to the case where
k is odd in (
14), we have:
Thus, the element at
(
) cannot be an element of
but
as the same residue modulo
. The sequence
is divided into the longer parts with length
and one shorter part with length
r. Namely, the longer part is of the subsequence:
with the next element at
. One shorter part is of the subsequence:
with the next element at
. Notice that similarly to Lemma 3, we have:
Since
, all elements in
are different modulo
. Then by
, we have:
By
Figure 3, the candidates of the largest element of
are at
or at
. Since
is equivalent to
, by Lemma 1 (
2), if
, then:
If
, then:
Notice that may occur in some cases. For example, . In this case, both of the two formulas are valid, yielding the Frobenius number .
4. The Case Where
It is important to see that the elements of are determined from those of .
4.1. When k Is Odd
• When
The corresponding relations from
to
are as follows, see
Figure 4.
[The first
u rows]
by Lemma 3 and
respectively. Note that when
, the second corresponding relation does not exist. This also implies that all the elements at
and
can be expressed in terms of
in at least two ways.
[Others]
by the identity (
13). This also implies that all the elements at
can be expressed in at least two ways.
By
Figure 4, there are four candidates to take the largest value of
. Namely, the values at:
If
, one of the elements at
and at
is the largest. In this case, if
, then:
If
, then:
If
, one of the elements at
and at
is the largest. In this case, if
, then:
If
, then:
Example 1. When , the first identity is applied: Indeed, there are two representations in terms of as:which is the largest element of . In fact, the second, the third and the fourth identities yield the smaller values:respectively. When , the second identity is applied: In fact, the first, the third, and the fourth identities yield the smaller values:respectively. When , the third identity is applied:In fact, the first, the second, and the fourth identities yield the smaller values:respectively. When , the fourth identity is applied: In fact, the first, the second, and the third identities yield the smaller values:respectively. • When
The similar corresponding relations to the case
are also applied for
. When
, the elements of the first
u rows of the main area (the second block from the left) correspond to fill the gap below the left-most block:
The other elements of the main area correspond to those in the block immediately to the right to go up the
u row:
The elements of the stair areas correspond to those in the block immediately to the right in the form as it is to go up the
row:
Figure 5 shows the areas in which the elements of
p-Apéry set exist for
. The outermost lower right area is the area where the elements of the 2-Apéry set exist. We can also show that all the elements of the 2-Apéry set have at least three distinct representations in terms of
.
From
Figure 5, there are six candidates to take the largest element of
. These elements are indicated as follows:
![Axioms 13 00608 i001]()
If
(or
), one of those at
![Axioms 13 00608 i004]()
,
![Axioms 13 00608 i002]()
, and
![Axioms 13 00608 i006]()
is the largest. Otherwise, one of those at
![Axioms 13 00608 i005]()
,
![Axioms 13 00608 i003]()
, and
![Axioms 13 00608 i007]()
is the largest. However, it is clear that one of the values at
![Axioms 13 00608 i004]()
or
![Axioms 13 00608 i006]()
(respectively,
![Axioms 13 00608 i005]()
or
![Axioms 13 00608 i007]()
) is larger than at
![Axioms 13 00608 i002]()
(respectively,
![Axioms 13 00608 i003]()
). Hence, if
, then the element at
![Axioms 13 00608 i004]()
(respectively,
![Axioms 13 00608 i005]()
) is the largest. Otherwise, the element at
![Axioms 13 00608 i006]()
(respectively,
![Axioms 13 00608 i007]()
) is the largest.
In conclusion, if
and
, then:
If
and
, then:
If
and
, then:
If
and
, then:
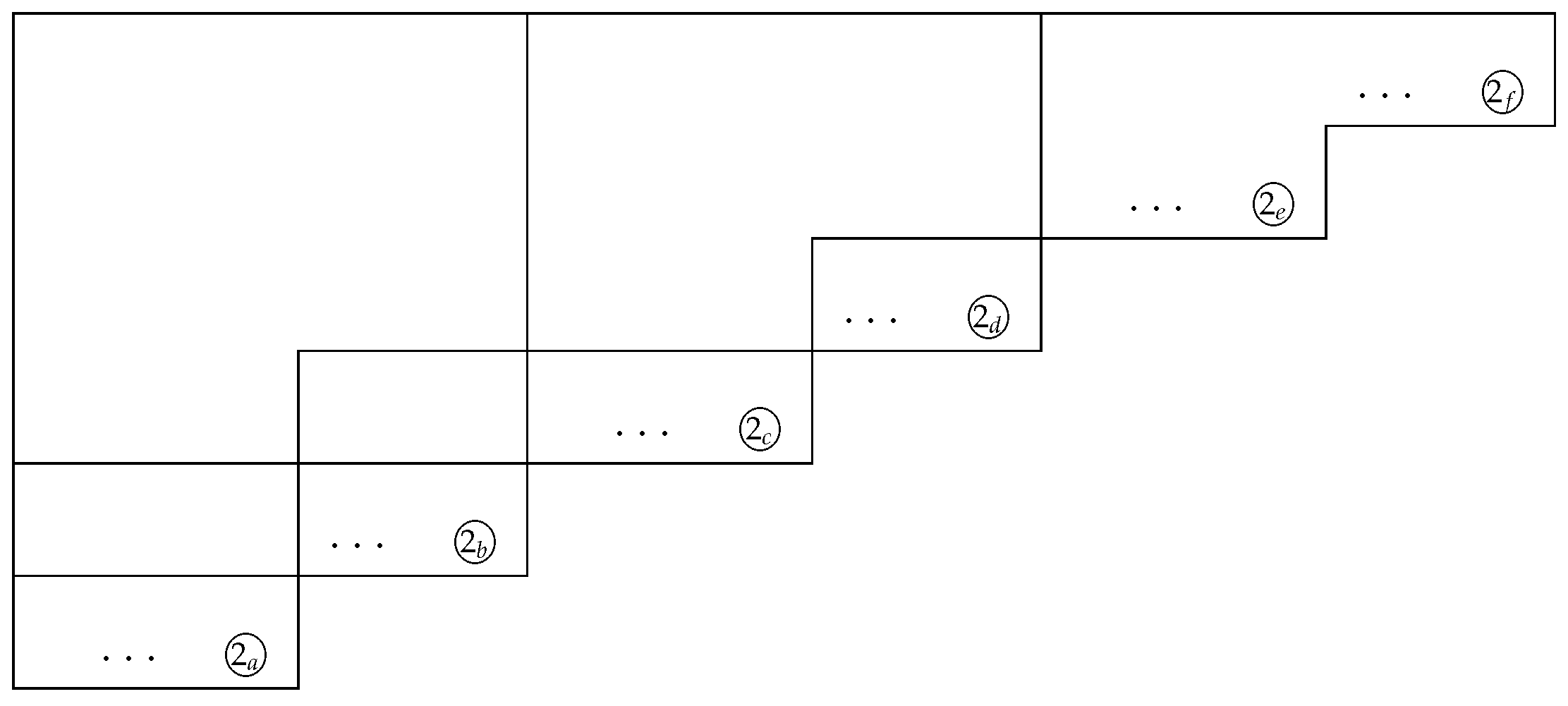
In general, for an integer
, it is sufficient to compare two elements at both ends, see
Figure 6. If
and
, then:
If
and
, then:
If
and
, then:
If
and
, then:
The positions of the elements of
below the left-most block and the positions of
in the right-most block are arranged as shown in
Figure 6.
This situation is continued as long as . However, when , the shape of the block on the right side collapses. Thus, the regularity of taking the maximum value of is broken. Hence, the fourth case holds until and other cases hold for .
In conclusion, when k is odd, the p-Frobenius number is given as follows.
Theorem 1. Let i be an integer and k be odd with . Let and be determined as (9) and (10). For , if and , then: If and , then: If and , then: If and , then for : Example 2. When , the first identity is applied. Since and , for we have: Namely, the corresponding element for each integer is at (). However, for , the p-Frobenius numbers can be computed neither by the above formula nor by any other closed formulas. Namely, the real value is , corresponding to , though the formula gives 1274931, corresponding to .
4.2. When k Is Even
• When
Similarly to the odd case where k is odd, the elements of can be determined from those of . When , there are corresponding relations as follows.
[The first row
]
with
due to (
15). Note that when
the second corresponding relation does not exist. This also implies that all the elements at
and
can be expressed in terms of
in at least two ways.
[Others]
by the identity (
13). This also implies that all the elements at
can be expressed in at least two ways.
By
Figure 7, there are four candidates to take the largest value of
. Namely, the values at:
If
, one of the elements at
and at
is the largest. In this case, if
, then:
If
, then
If
, one of the elements at
and at
is the largest. In this case, if
, then:
If
, then:
• When
The situation is similar for
. From
Figure 8, there are six candidates to take the largest element of
. These elements are indicated as follows:
![Axioms 13 00608 i008]()
Similarly to the case where
k is odd, middle element at
![Axioms 13 00608 i002]()
and at
![Axioms 13 00608 i003]()
cannot take the largest value. Hence, if
, then the element at
![Axioms 13 00608 i004]()
(respectively,
![Axioms 13 00608 i005]()
) is the largest. Otherwise, the element at
![Axioms 13 00608 i006]()
(respectively,
![Axioms 13 00608 i007]()
) is the largest.
In conclusion, if
and
, then:
If
and
, then:
If
and
, then:
If
and
, then:
In general, for an integer
, it is sufficient to compare two elements at both ends, see
Figure 9. If
and
, then:
If
and
, then:
If
and
, then:
If
and
, then:
The positions of the elements of
below the left-most block and the positions of
in the right-most block are arranged as shown in
Figure 6.
This situation is continued as long as . However, when , the shape of the block on the right side collapses. Namely, we cannot take the value at . Thus, the regularity of taking the maximum value of is broken. Hence, the fourth case holds until , and other cases hold for .
In conclusion, when k is even, the p-Frobenius number is given as follows.
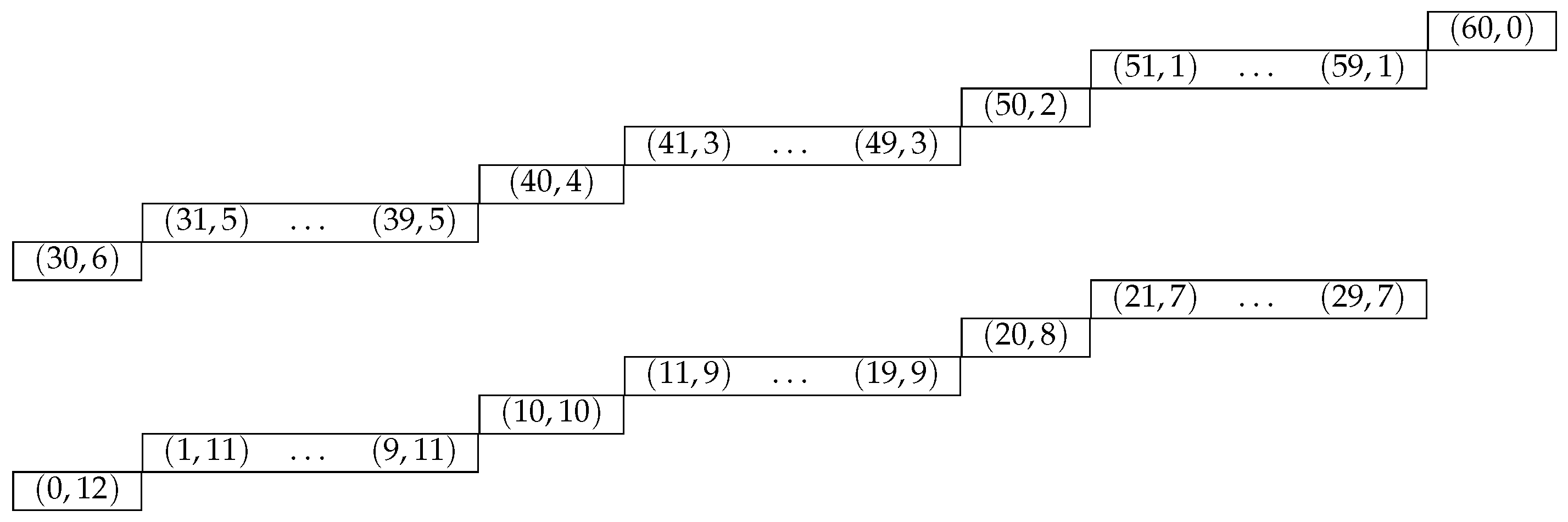
Theorem 2. Let i be an integer and k be even with . Let q and r be determined as (15). For , if and , then:If and , then:If and , then:If and , then for : Example 3. When , we have and . So, the elements of , where , are given as in Figure 10. The largest element is at , which comes from the second identity. Thus: Notice that the right-most element is at and the block of the right side is empty. Therefore, the formula does not hold for . In fact, , corresponding to , though the formula gives 63,914, corresponding to .
7. Conclusions
In this paper, we give explicit formulas of the p-Frobenius number and the p-genus of triplet for integers , where ’s are the so-called Horadam numbers, satisfying the recurrence relation () with and . We give explicit closed formulas of p-Frobenius numbers and p-genus of this triple. When , or , the results for Fibonacci, Pell, and Jacobsthal triples are recovered.
Horadam also studied the number
with arbitrary initial values
and
. However, with arbitrary initial values, many identities (e.g., (7)) do not hold as they are. Hence, the situation becomes too complicated. An approach to get some recurrences to a wide class of polynomials in [
39] may be useful for future works.

 ,
,  , and
, and  is the largest. Otherwise, one of those at
is the largest. Otherwise, one of those at  ,
,  , and
, and  is the largest. However, it is clear that one of the values at
is the largest. However, it is clear that one of the values at  or
or  (respectively,
(respectively,  or
or  ) is larger than at
) is larger than at  (respectively,
(respectively,  ). Hence, if , then the element at
). Hence, if , then the element at  (respectively,
(respectively,  ) is the largest. Otherwise, the element at
) is the largest. Otherwise, the element at  (respectively,
(respectively, 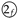 ) is the largest.
) is the largest.
 and at
and at  cannot take the largest value. Hence, if , then the element at
cannot take the largest value. Hence, if , then the element at  (respectively,
(respectively,  ) is the largest. Otherwise, the element at
) is the largest. Otherwise, the element at  (respectively,
(respectively, 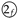 ) is the largest.
) is the largest.