MacWilliams Identities and Generator Matrices for Linear Codes over ℤ_p⁴[u]/(u² − p³β, pu)

Abstract

Suppose that $R={\mathbb{Z}}_{p^4}\left[u\right]$ with $u^2=p^3\beta$ and $pu=0,$ where p is a prime and $\beta$ is a unit in $R.$ Then, R is a local non-chain ring of order $p^5$ with a unique maximal ideal $J=(p,u)$ and a residue field of order $p.$ A linear code C of length N over R is an R-submodule of $R^N.$ The purpose of this article is to examine MacWilliams identities and generator matrices for linear codes of length N over $R.$ We first prove that when $p\ne 2,$ there are precisely two distinct rings with these properties up to isomorphism. However, for $p=2$, only a single such ring is found. Furthermore, we fully describe the lattice of ideals of R and their orders. We then calculate the generator matrices and MacWilliams relations for the linear codes C over $R,$ illustrated with numerical examples. It is important to address that there are challenges associated with working with linear codes over non-chain rings, as such rings are not principal ideal rings.

1. Introduction

Linear codes of length N over a finite ring R are R-submodules of $R^N.$ These codes have been traditionally studied over finite fields; however, many significant codes over fields have been related to those over finite rings by Gray maps [1,2,3,4]. In this article, all of the alphabet rings involved are finite, commutative, and have an identity. A ring R is called local if it has a unique maximal ideal, denoted by J (Jacobson radical). When all ideals of R are principal, R is then called the principal ideal ring (PIR). A chain ring is a principal local ring, and thus many conclusions obtained for coding over chain rings also hold over PIRs. One of the main reasons that Frobenius rings, defined later, are considered the appropriate class to describe codes is because they satisfy both MacWilliams theorems. Furthermore, Frobenius local rings can be decomposed into their component parts and this enables us to find their generating characters. To fully understand codes over Frobenius rings, it is therefore necessary, despite the challenges, to consider local non-chain rings [5,6,7]. For more information on the subject, please refer to [5,8,9,10,11] and the references therein.

In this work, the main purpose is to obtain significant coding results over Frobenius local rings. In particular, linear codes of length N over the ring ${\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3\beta ,pu),$ are the focus of this paper. Prior work on these rings was presented in [12], emphasizing their applicability to coding theory, and their close connection to ${\mathbb{Z}}_{p^n}$ and linear binary codes [3]. Our attention is also on exploring the roles of generator matrices and MacWilliams relations in error-correction theory, particularly in their role to weight enumerators of a code and its dual code. The authors of [6] considered these approaches for Frobenius local rings of order 16. While in [7], generator matrices and the MacWilliams relations were described for codes over rings of order 32. This work makes an effort to build on the previous findings and provides access to more general rings with higher orders. Let $R={\mathbb{Z}}_{p^4}\left[u\right]$, with $u^2=\beta p^3$ and $pu=0$ as conditions, where $\beta \in U\left(R\right),$ the unite group of $R.$ Initially, we provide a formula for a generating character $\chi$ associated with $R,$ through which we can calculate the MacWilliams relations as matrices of specific sizes for a code C over $R.$ For codes over non-chains, it is more challenging to build a generator matrix G than for codes over chains. Although a simple set of generators can still be found, this type of generator matrix may not provide straightforward information about the code size. In this research, we introduce multiple numerical examples that show the code size might not always determined directly from such a generator matrix. Additionally, the generator matrix G of a code C is completely determined through the algorithm described in Theorem 8.

In Section 3, the classification of rings of the form ${\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1}\beta ,pu),$ with invariants $p,n,1,1,n-1$ is described, after the initial definitions and results in Section 2. Particular attention is given to providing all the details necessary to characterize rings of order $p^5$ and to outline the lattice of their ideals. Section 4 provides the general procedure for generating characters for ${\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3\beta ,pu)$. Additionally, the symmetrized weight enumerator’s corresponding to the matrix is acquired, and MacWilliams relations are derived. In Section 5, the findings regarding matrices that produce linear codes over such rings are presented.

2. Preliminaries

The notations and basic information that will be used later in our discussion are introduced in this section. Let R be a local ring of identity, and let J be its maximal ideal. For the results mentioned in this section, we refer readers to [4,12,13,14,15,16].

The order of J is $p^{(m-1)r}$ provided $J^m=0$, and the size of $R,$ is $\left|R\right|=p^{mr}$ with $R/J\cong GF\left(p^r\right)=F.$ In R, the characteristic takes the form $p^n,$ and $1\le n\le m$. Additionally, R has a subring $R_0$, of the form $GR(p^n,r),$ called a Galois ring with $p,n,r.$ Moreover, there is $u\in J,$ and

$$\begin{array}{cc}\hfill & R=R_0+u{R}_0,\hfill \\ \hfill & J=p{R}_0+u{R}_0.\hfill \end{array}$$

(1)

If J is principal, then R is chain, and particularly when $J=\left(p\right),$ we have $n=m$ and

$$R={\mathbb{Z}}_{p^n}\left[\alpha \right]\cong {\mathbb{Z}}_{p^n}\left[x\right]/\left(g\left(x\right)\right),$$

where $\alpha$ is a root of a specific polynomial $g\left(x\right)\in {\mathbb{Z}}_{p^n}\left[x\right].$ Let

$$\begin{array}{cc}& \Gamma \left(r\right)=\left(\alpha \right)\cup \left\{0\right\}=\{0,1,\alpha ,{\alpha }^2,\dots ,{\alpha }^{p^r-2}\};\hfill \\ & {\Gamma }^{*}\left(r\right)=\left(\alpha \right)=\{1,\alpha ,{\alpha }^2,\dots ,{\alpha }^{p^r-2}\}.\hfill \end{array}$$

Suppose $\gamma \in R,$ so

$$\gamma ={\alpha }_1+p{\alpha }_1+p^2{\alpha }_2+\cdots +p^{n-1}{\alpha }_{n-2}(\mathrm{p}\text{-}\mathrm{adic}\mathrm{expression}).$$

(2)

where ${\alpha }_i\in \Gamma \left(r\right).$ Furthermore, assume that t is the smallest number with condition of $p^{t}u=0.$ We label $p,n,r$ and t as the parameter (invariants) of $R.$

In our later discussion, we use $r=1$ and $t=1.$ This implies that $R_0={\mathbb{Z}}_{p^n}$ and $pu=0.$ In addition, we consider $g\left(x\right)$ as

$$g\left(x\right)=x^2-p^{(n-1)}\beta ,$$

(3)

where $\beta \in {\Gamma }^{*}\left(1\right).$ From [12],

$$R={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{(n-1)}\beta ,pu),$$

where $(p,n,r,t,d)=(p,n,1,1,n-1).$

The total sum of all minimal ideals in R is what we define as the socle of $R,$ also known as soc$\left(R\right).$ As R is commutative, thus

$$\begin{array}{cc}& soc\left(R\right)=\{v\in R:v\in \mathrm{ann}(J\left)\right\},\hfill \\ & \mathrm{ann}\left(J\right)=\{a\in R:ay=0,\mathrm{for}\mathrm{all}y\in J\}.\hfill \end{array}$$

We will highlight the definition of Frobenius rings that is most pertinent to our analysis. In [14], R is called Frobenius if

$$R/J\cong soc\left(R\right).$$

Let ${\mathrm{Hom}}_{\mathbb{Z}}(R,{\mathbb{C}}^{*})$ denote the character group of $(R,+),$ then elements of ${\mathrm{Hom}}_{\mathbb{Z}}(R,{\mathbb{C}}^{*})$ are called characters $\chi$ of $(R,+).$ If ker$\chi$ has no non-trivial ideals of $R,$ then $\chi$ is named a generating character.

Theorem 1

(Honold [14]). Let R be a finite ring. Then, soc$\left(R\right)$ is cyclic, if and only if R is a Frobenius ring.

A code C of length N over R is a subset of $R^N$; it is called a linear code if C is a submodule [4]. Furthermore, by including the inner-product (·) in $R^N$, we can define the dual code $C^{\perp }$ of C as follows

$$C^{\perp }=\{\mathit{u}:\mathit{c}·\mathit{u}=0,\mathit{c}\in C\}.$$

(4)

3. On the Ring ${\mathbb{Z}}_{{\mathit{p}}^{\mathit{n}}}\left[\mathit{u}\right]/({\mathit{u}}^{\mathbf{2}}-{\mathit{p}}^{(\mathit{n}-\mathbf{1})}\mathit{\beta },\mathit{pu})$

In this section, we prove some results on the ring $R={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{(n-1)}\beta ,pu)$ which is a finite ring of order $p^{n+1}$ and with residue field $F={\mathbb{Z}}_p.$ These results help us in the subsequent discussion.

Theorem 2.

The ring $R={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1}\beta ,pu)$ is a Frobenius local ring.

Proof. 

As each element of R is uniquely written $a+bu,$ where $a\in {\mathbb{Z}}_{p^n}$ and $b\in \Gamma \left(1\right).$ Also, as $J=(p,u),$ then R is a local ring of order $p^{n+1}$ and $J^n=0.$ In fact, R is a local ring with a singleton basis and $p,n,1,1.$ We now prove that R is Frobenius. Because elements of soc$\left(R\right)$ annihilates $J=(p,u),$ particularly $pu=0,$ $p^{n-1}p=0,$ then $p^{n-1}J=0.$ Thus, $p^{n-1}\in$ soc$\left(R\right).$ Suppose $x\in$ soc$\left(R\right)$ and $x\ne 0.$ Then, $xJ=0;$ in particular, $xu=0.$ This implies that $x\in \left(p\right),$ but as $xp=0$ will also lead to $x\in \left(p^{n-1}\right).$ Hence,

$$soc\left(R\right)=\left(p^{n-1}\right).$$

Using Theorem 1, R is Frobenius. ☐

Corollary 1.

As $J=(p,u),$ then R is a non-chain singleton ring.

Remark 1.

For any Frobenius local ring R with invariants $p,n,r$ and $t=1,$ then

$$soc\left(R\right)=\left(p^{n-1}\right).$$

3.1. Determination of Rings of Order $p^{n+1}$ with $p,n,1,1,n-1$

An exhaustive characterization of all rings with $p,n,1,1,n-1$ is given by Theorem 3, which is essential for our upcoming discussion.

Theorem 3.

Assume that R is a ring and that $(p,n,r,t,d)=(p,n,1,1,n-1)$ is its invariant. Then, among the rings given in Table 1, R is isomorphic to one particular ring.

Table 1. Rings of order $p^{n+1}$ with $p,n,1,1,n-1$.

$\mathit{p}\ne 2$	$\mathit{p}=2$
$R_1={\mathbb{Z}}_{p^{4}n}\left[u\right]/(u^2-p^{n-1}\beta ,pu)$
$R_2={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1},pu)$	$R_3={\mathbb{Z}}_{2^n}\left[u\right]/(u^2-2^{n-1},2u)$

Proof. 

Every element of R is uniquely expressed as $a+bu,$ where $a\in {\mathbb{Z}}_{p^n}$ and $b\in \Gamma \left(1\right).$ As $pu=0,$ then the associated polynomial is of the form $g\left(x\right)=x^2-p^{n-1}\beta ,$ where $\beta \in {\Gamma }^{*}\left(1\right).$ Suppose that $p=2.$ As ${\Gamma }^{*}\left(1\right)=\left\{1\right\},$ hence there exists precisely one class represented by

$$R_3={\mathbb{Z}}_{2^n}\left[u\right]/(u^2-2^{n-1},2u).$$

From now, we assume that $p\ne 2.$ Consider the usual partition on ${\Gamma }^{*}\left(1\right).$

$$\begin{array}{c}\hfill A=\{\beta \in {\Gamma }^{*}\left(1\right):\beta \notin {{\Gamma }^{*}\left(1\right)}^2\};\\ \hfill B=\{\beta \in {\Gamma }^{*}\left(1\right):\beta \in {{\Gamma }^{*}\left(1\right)}^2\}.\end{array}$$

It is worth noting that $\mid A\mid ={\displaystyle \frac{p-1}{2}}=\mid B\mid .$ We next proceed the proof with two cases.

• Case a. We show that $R_1$ and $R_2$ are not isomorphic, that is, they are not in the same class when $\beta \in A$. In contrast, suppose that $R_1\cong R_2$, and define the isomorphism as $\varphi$. Assuming $J\left(R_2\right)=(p,v),$ for some ${\beta }^{\prime }\in {\Gamma }^{*}\left(1\right),$ $\varphi \left(u\right)={\beta }^{\prime }v$. Consequently, we note

  $$\begin{array}{cc}& {\left(\varphi \left(u\right)\right)}^2=\varphi \left(u^2\right)\hfill \\ & {\left({\beta }^{\prime }v\right)}^2=\varphi \left(p^{n-1}\beta \right)\hfill \\ & {\beta }^{\prime 2}{v}^2=p^{n-1}\varphi \left(\beta \right)\hfill \\ & {\beta }^{\prime 2}\left(p^{n-1}\right)=p^{n-1}\varphi \left(\beta \right)\hfill \\ & p^{n-1}{\beta }^{\prime 2}=p^{n-1}\varphi \left(\beta \right)\hfill \\ & {\beta }^{\prime 2}=\varphi \left(\beta \right).\hfill \end{array}$$

  We have $\varphi \left(\beta \right)=\beta$, because $\varphi$ restricted to $\Gamma \left(1\right)$ is a fixed isomorphism. Furthermore, because $p\ne 2,$ this contradicts the assumption about $\beta ,$ and thus $\beta \ne {\beta }^{\prime 2}.$ Therefore, $R_1\ncong R_2.$
• Case b. When $\beta \in B.$ In such a case, there exists ${\beta }_1\in {\Gamma }^{*}\left(1\right)$ such that $\beta ={\beta }_1^2.$ Note that
  $$\begin{array}{cc}\hfill g\left(x\right)& =x^2-p^{n-1}\beta \hfill \\ & =x^2-p^{n-1}{\beta }_1^2\hfill \\ & ={\beta }_1^2[{\left({\beta }_1^2\right)}^{-1}{x}^2-p^{n-1}]\hfill \\ & ={\beta }_1^2[{\left({\beta }_1^{-1}x\right)}^2-p^{n-1}].\hfill \end{array}$$

  As u is a root of $g\left(x\right),$ then $g\left(u\right)=0,$ and hence $u^2-p^{n-1}\beta =0.$ This implies that, from the above argument, ${\beta }_1^2[{\left({\beta }_1^{-1}u\right)}^2-p^{n-1}]=0.$ Thus, ${\left({\beta }_1^{-1}u\right)}^2-p^{n-1}=0.$ This suggests that $g\left(x\right)$ for $R_1$ can be taken as $g\left(x\right)=x^2-p^{n-1}$, which is identical to that of $R_2.$ As a result, $R_1\cong R_2.$ To sum up, we have two classes of such rings that are not isomorphic

  $$\begin{array}{cc}& {\Omega }_1:\mathrm{All}\mathrm{rings}\mathrm{with}\mathrm{associated}\mathrm{polynomials}g\left(x\right)=x^2-p^{n-1}\beta ,\mathrm{where}\beta \in A;\hfill \\ & {\Omega }_2:\mathrm{All}\mathrm{rings}\mathrm{with}\mathrm{associated}\mathrm{polynomials}g\left(x\right)=x^2-p^{n-1}\beta ,\mathrm{where}\beta \in B.\hfill \end{array}$$

  The first class is represented by

  $$R_1={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1}\beta ,pu),$$

  where $\beta$ is any element in $A.$ While the second class is represented by

  $$R_2={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1},pu).$$

☐

Corollary 2.

Let $N(p,4,1,1,3)$ be the number rings with $(p,4,1,1,3).$ Then,

$$N(p,4,1,1,3)=\left\{\begin{array}{cc}1,\hfill & ifp=2;\hfill \\ 2,\hfill & ifp\ne 2.\hfill \end{array}\right.$$

Proof. 

The proof is direct from the proof of Theorem 3 with $n=4$ and $d=n-1$. ☐

3.2. Lattice of Ideals of R

Theorem 4.

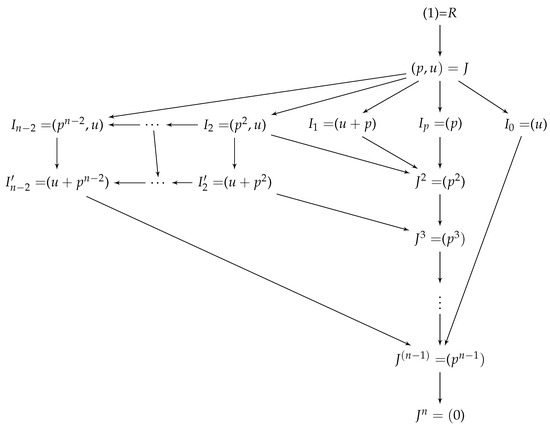
The ideals of R is given by the following lattice (see Figure 1).

Figure 1. Lattice of ideals of $R={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1}\beta ,pu)$.

Proof. 

Consider a proper ideal of R, I. As R is local, J represents the only maximal ideal of R; hence, $I\subseteq J.$ This indicates that I is generated by a combination of p and u and their powers. Given that $pu=0$ and $u^2=\beta p^{n-1},$ we have $(p^i+u^2)=(p^i,u^2)=\left(p^j\right),$ where $j=\min \{i,n-1\}.$ Thus, we only consider ideals generated by $p^i$ and u and their combinations. In other words, without raising J to a power, there are only n choices for $I,$ namely

$$\left(1\right),\left(p^i\right),(v{p}^i+u),(p^i,u),$$

where $v\in U\left(R\right)$ and $i=1,2,\dots ,n.$ First, note that $(v{p}^i+u)=(p^i+w),$ where $w=v^{-1}u.$ It is clear that $(p^i+u)\subset (p^i,u)$ and $(p^i,u)\subset (p^j,u)$, and, moreover, $(p^i+u)\subset (p^j+u),$ where $i>j.$ Thus, if $I_i=(p^i,u)$ and $I_i^{\prime }=(p^i+u),$

$$\begin{array}{cc}& I_{n-2}\subset I_{n-3}\subset \cdots \subset I_2\subset I_1;\hfill \\ & I_{n-2}^{\prime }\subset I_{n-3}^{\prime }\subset \cdots \subset I_2^{\prime }\subset I_1^{\prime };\hfill \\ & I_i^{\prime }\subset I_i.\hfill \end{array}$$

As $u^2=\beta p^{n-1},$ thus $I_{n-1}=(p^{n-1},u)=(p^{n-1}+u)=\left(u\right)=I_0.$ Finally, we justify that $J^i=\left(p^i\right),$ where $i>1.$ As $pu=0,$ then $J^i=(p^i,u^i).$ If $i=2,$ then $J^2=p^2(1,p^{n-3}\beta )=(p^2.)$ Now, if $i>2,$ then $u^i=0,$ and hence $J^i=\left(p^i\right).$ Therefore, the results follow. ☐

Corollary 3.

Suppose R as in Theorem 4. Then, for $i=1,2,\dots ,n,$

$$\mid I\mid =\left\{\begin{array}{cc}{p}^{n+1},\hfill & ifI=R;\hfill \\ p^n,\hfill & ifI=J;\hfill \\ p^{n-1},\hfill & ifI=I_p;\hfill \\ p^2,\hfill & ifI=I_0;\hfill \\ (p-1)p^{n-i},\hfill & ifI=I_i;\hfill \\ p^{n-i-1}\hfill & ifI=I_i^{\prime };\hfill \\ p^{n-i}\hfill & ifI=J^i.\hfill \end{array}\right.$$

Remark 2.

Two non-isomorphic rings can have the same ideal lattice.

Remark 3.

Theorem 4 states that every ideal of R contains soc$\left(R\right).$

Example 1.

The ring ${\mathbb{Z}}_{3^4}\left[u\right]/(3^2-27,3u)$ is a Frobenius local non-chain ring. Because $d=3,t=1,$ the assumption of Theorem 2. Note that soc$\left(R\right)=\left(3^3\right)$ and $\mid soc\left(R\right)\mid =\mid F\mid$.

3.3. Units of $R={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1}\beta ,pu)$

The form of the units of R will be established in this subsection, which will be useful in the following section. The elements in $R\setminus J$ are the units of R, as R is local. Furthermore, because $J=(p,u),$ if $\alpha \in R\setminus J,$

$$\alpha =a+bu,$$

(5)

where $a\in {\mathbb{Z}}_{p^n},(a,p)=1$ and $b\in R.$ The elements of ${\mathbb{Z}}_{p^n}$ can be written as

$$a={\alpha }_1+p{\alpha }_2+p^2{\alpha }_3+\cdots +p^{n-1}{\alpha }_n,$$

where ${\alpha }_1\in \Gamma {\left(1\right)}^{*}$ and ${\alpha }_i\in \Gamma \left(1\right),$ for $i=2,3,\dots ,n.$ Thus, $\alpha \in U\left(R\right)$ can be expressed as

$$\alpha =\beta +wx,$$

(6)

where $\beta \in \Gamma {\left(1\right)}^{*},$ $w\in R$ and $x\in J.$ In other words,

$$\alpha =\beta h,$$

(7)

where $h=1+w{\beta }^{-1}x\in H=1+J.$ Moreover, observe that $\Gamma {\left(1\right)}^{*}\cap H=1$, as $(p-1,p^n)=1.$ Consequently, the following theorem is established.

Theorem 5.

Every element v of $U\left(R\right)$ is of the form $v=x$ or $v=x+\alpha u,$ where $(x,p)=1$ and $\alpha \in \Gamma {\left(1\right)}^{*}$. Moreover, $U\left(R\right)$ is of order $(p-1)p^n$ and

$$U\left(R\right)=\left(\alpha \right)\times H.$$

(8)

Example 2.

If $R={\mathbb{Z}}_{2^4}\left[u\right]/(u^2-2^3\beta ,2u),$ then the units of R are of the form

$$U\left(R\right)=\{1,3,5,7,9,11,13,15,1+u,3+u,5+u,7+u,9+u,11+u,13+u,15+u\}.$$

4. MacWilliams Identities

With $p,n,1,1$ as invariants and $g\left(x\right)=x^2-p^{n-1}\beta$, let R be a Frobenius local ring. Theorem 6 outlines a method to produce a generating character $\chi$ for any such ring. Suppose ${\gamma }_i$ is a $p^{n_i}$-root of unity and $a_i\le mr$ for each $i.$

Theorem 6

([7]). Let R be a ring with $p,n,r,t,d.$ There is $q\in \mathbb{Z}$, such that $q\ge 1,$ and

$$\chi \left(\omega \right)={\gamma }_1^{a_1}{\gamma }_2^{a_2}\cdots {\gamma }_q^{a_q},$$

(9)

is a generating character of $R,$ $1\le i\le q.$

The formulas of $\chi$ for R are shown in the following Table 2, where $\gamma ,$ $\delta$, and $\zeta$ are the $p^n$th, pth, and $2^n$th roots of unity, respectively.

Table 2. $\chi$ for the ring R.

Ring	$(\mathit{R},+)$	$\mathit{\chi }$
${\mathbb{Z}}_{2^n}\left[u\right]/(u^2-2^{n-1},2u)$	${\mathbb{Z}}_{2^4}\times {\mathbb{Z}}_2$	$\chi (a+bu)={\zeta }^a{(-1)}^b$
${\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1},pu)$	${\mathbb{Z}}_{p^n}\times {\mathbb{Z}}_p$	$\chi (a+bu)={\gamma }^a{\delta }^b$

The MacWilliams identities for various version of R are now computed. Actually, the class of all Frobenius rings is a broader class of finite rings to which these relationships can be extended. These identities are fundamental to the study of coding theory because they introduce a crucial link between a code’s dual and weight enumerator. Assume the following: The elements in $R=\{a_1,a_2,a_3,\dots a_{p^{(n+1)}}\}$ are in that order. Suppose C is a linear code over R with length N. Let us assume that $n_i\left(\mathit{c}\right)$ is the number of instances of $a_i$ in c$\in C$. The complete weight enumerator is then denoted as

$$CWE\left(C\right)=\sum _{c\in }\prod _i{a}_i^{n_i\left(\mathit{c}\right)}.$$

(10)

$$CW{E}_C(x_{a_1},\dots ,x_{a_{p^{(n+1)}}})={\displaystyle \frac{1}{\mid C^{\perp }\mid }}CW{E}_{C^{\perp }}(A·x_{a_1},\dots ,x_{a_{p^{(n+1)}}}),$$

(11)

where $A=\left(a_{ij}\right),$ and $a_{ij}=\chi \left(a_i{a}_j\right).$ We define $wt\left(\mathit{c}\right)=\mid \{i:c_i\ne 0\}\mid .$ The Hamming weight (HW) enumerator and its MacWilliams identity are given by

$$H{W}_C(a,b)=\sum _{c\in C}{a}^{N-wt\left(\mathit{c}\right)}{b}^{wt\left(\mathit{c}\right)},$$

(12)

$$H{W}_C(a,b)={\displaystyle \frac{1}{\mid C^{\perp }\mid }}H{W}_{C^{\perp }}(a+(p^{(n+1)}-1)b,a-b).$$

(13)

Suppose that ∼ is defined on R by $x\sim y$ when there is $\omega \in U\left(R\right)$, such that $x=\omega y.$ It is evident that this relation is equivalent. Let ${\widehat{b}}_1,\dots ,{\widehat{b}}_q$ be the equivalence classes and let $n_i^{\prime }\left(\mathit{c}\right)$ calculate the number of elements of ${\widehat{b}}_i$ that occurred in the codeword c. Hence, SWE is defined as follows

$$SW{E}_C(x_{{\widehat{b}}_1},\dots ,x_{{\widehat{b}}_q})=\sum _{\mathit{c}\in C}\prod _i{x_{{\widehat{b}}_i}}^{n_i^{\prime }\left(\mathit{c}\right)}.(\mathrm{symmetrized}\mathrm{weight}\mathrm{enumerator})$$

(14)

We introduce the MacWilliams equation for SWE as

$$SW{E}_C(x_{{\widehat{b}}_1},\dots ,x_{{\widehat{b}}_q})={\displaystyle \frac{1}{\mid C^{\perp }\mid }}SW{E}_{C^{\perp }}(S·(x_{{\widehat{b}}_1},\dots ,x_{{\widehat{b}}_q})),$$

(15)

where $S=\left(b_{ij}\right)$ and

$$b_{ij}=\sum _{a\in {\widehat{b}}_j}\chi \left(a_{i}a\right).$$

As we can notice, once $\chi$ is obtained, it is straightforward to obtain the matrix A in Equation (11). Nonetheless, S in Equation (15) necessitates the determination of the classes ${\widehat{b}}_i.$ While it takes more work, this procedure is essential for building $S.$ If we look at the broader case for $n,$ that is, ${\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1}\beta ,pu)$. Note that $J=(p,u)$ in this ring, of order $(p-1)p^4$, with $l=4,$ as its index of nilpotency, and $soc\left(R\right)=\left(p^3\right).$ Then, one can obtain the set of ${\widehat{b}}_i$ as follows.

$$\left\{\begin{array}{cc}& {\widehat{b}}_1=\left\{0\right\},\hfill \\ & {\widehat{b}}_2=U\left(R\right)=\{i,i+ju:(i,p)=1,j=1,2,\dots ,p-1\},\hfill \\ & {\widehat{b}}_3=\left(p\right)\setminus \left(p^2\right),\hfill \\ & {\widehat{b}}_4=\left(u\right)\setminus soc\left(R\right),\hfill \\ & {\widehat{b}}_5=(u+p)\setminus \left(p^2\right),\hfill \\ & {\widehat{b}}_6=(u+p^2)\setminus \left(p^3\right),\hfill \\ & {\widehat{b}}_7=\left(p^2\right)\setminus \left(p^3\right),\hfill \\ & {\widehat{b}}_8=(u+p^3)\setminus \left(p^4\right),\hfill \\ & {\widehat{b}}_9=\left(p^3\right)\setminus \left(p^4\right),\hfill \\ & ⋮\hfill \\ & \widehat{b_j}=(u+p^i)\setminus \left(p^{i+1}\right),\hfill \\ & \widehat{b_{j^{\prime }}}=\left(p^i\right)\setminus \left(p^{i+1}\right),\hfill \\ & ⋮\hfill \\ & {\widehat{b}}_{n-1}=soc\left(R\right)\setminus \left\{0\right\}=J^{n-1}\setminus \left\{0\right\}=\left(p^{n-1}\right).\hfill \end{array}\right.$$

For a more general case, we have a detailed scheme for finding $b_{ij}$ in the following lemma.

Lemma 1.

Let $R={\mathbb{Z}}_{p^n}\left[u\right]/(u^2-p^{n-1},pu).$ Then,

$$b_{ij}=\left\{\begin{array}{cc}\mid \widehat{b_j}\mid ,\hfill & if{a}_i\widehat{b_j}=\left\{0\right\};\hfill \\ 0,\hfill & if{p}^{n-1}\notin a_i\widehat{b_j};\hfill \\ (-1){\displaystyle \frac{1}{p-1}}\mid \widehat{b_j}\mid ,\hfill & if{p}^{n-1}\in a_i\widehat{b_j}.\hfill \end{array}\right.$$

Proof. 

Suppose that $a_i\widehat{b_j}=\left\{0\right\},$ then $b_{ij}={\sum }_{b\in \widehat{b_j}}\chi a_{i}b={\sum }_{b\in \widehat{b_j}}0=\mid \widehat{b_j}\mid$. For the other cases, assume that $a_i\widehat{b_j}\ne \left\{0\right\}.$ First, let $p^{n-1}\in a_i\widehat{b_j}.$ As soc$\left(R\right)=\left(p^{n-1}\right),$ then $p^{n-1}=\alpha y,$ where $\alpha \in {\Gamma }^{*}\left(1\right)$ and $y\in \widehat{b_j}$ are a representative of $\widehat{b_j}.$ Now, also suppose that $x\in a_i\widehat{b_j},$ then $x=a_i{y}^{\prime }$ for some $y^{\prime }$ in $\widehat{b_j}.$ It follows that $x=\gamma p^{n-1},$ where $\gamma \in {\Gamma }^{*}\left(1\right).$ This means that all elements of $a_i\widehat{b_j}$ are of the form $\alpha p^{n-1},$ which can be interpreted as the set $a_i\widehat{b_j}$ is just copies of soc$\left(R\right).$ Thus,

$$b_{ij}=N_0\sum _{\alpha \in {\Gamma }^{*}\left(1\right)}{e}^{{\displaystyle \frac{\left(2\pi i\right)\alpha }{p}}}.$$

However, we have the following formula for complex numbers,

$$1+\sum _{j=1}^{p-1}{e}^{{\displaystyle \frac{\left(2\pi i\right)j}{p}}}=0.$$

(16)

The positive $N_0$ reflects the number of copies of soc$\left(R\right)$, which is precisely $N_0={\displaystyle \frac{1}{p-1}}\mid \widehat{b_j}\mid$ Therefore,

$$b_{ij}=(-1){\displaystyle \frac{1}{p-1}}\mid \widehat{b_j}\mid .$$

The last case of the proof can be achieved similarly by noting that every element of $a_i\widehat{b_j}$ can be expressed as $x+\alpha p^{n-1},$ where $\alpha \in \Gamma \left(1\right).$ In such a case,

$$b_{ij}=\sum _x\chi \left(x\right)\sum _{\alpha \in \Gamma \left(1\right)}\chi \left(\alpha p^{n-1}\right).$$

Hence, by Equation (16), we conclude the results. ☐

Theorem 7.

The S matrix for $R={\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3,pu)$ is given as

$$S(p,4,1,1,3)=\left(\begin{array}{cccccccc}1& (p-1)p^4& (p-1)p^2& (p-1)p& (p-1)p^2& (p-1)p& (p-1)p& (p-1)\\ 1& 0& 0& 0& 0& 0& 0& -1\\ 1& 0& 0& (p-1)p& 0& -p& -p& (p-1)\\ 1& 0& (p-1)p^2& -p& -p^2& -p& p(p-1)& (p-1)\\ 1& 0& 0& -p& 0& -p& -p& (p-1)\\ 1& 0& -p^2& p(p-1)& -p^2& p& p(p-1)& (p-1)\\ 1& 0& -p^2& (p-1)p& -p^2& (p-1)p& (p-1)p& (p-1)\\ 1& -p^4& (p-1)p^2& (p-1)p& (p-1)p^2& (p-1)p& (p-1)p& (p-1)\end{array}\right).$$

Proof. 

Let us assume that the elements of R are ordered as follows: if $i,j\in {\mathbb{Z}}_{p^4},$ then i comes before j if $i<j$ as an integer, and $i+u$ comes before $j+u$ if i precedes $j.$ The equivalency classes are therefore

$$\left\{\begin{array}{cc}& \widehat{b_1}=\left\{0\right\},\hfill \\ & {\widehat{b}}_2=U\left(R\right)=\{i,i+ju:(i,p)=1\},\hfill \\ & \widehat{b_3}=\left(p\right)\setminus \left(p^2\right),\hfill \\ & \widehat{b_4}=\left(u\right)\setminus soc\left(R\right),\hfill \\ & \widehat{b_5}=(u+p)\setminus \left(p^2\right),\hfill \\ & \widehat{b_6}=(u+p^2)\setminus soc\left(R\right),\hfill \\ & \widehat{b_7}=\left(p^2\right)\setminus soc\left(R\right),\hfill \\ & \widehat{b_8}=soc\left(R\right)\setminus \left\{0\right\}=J^3\setminus \left\{0\right\}=\left(p^3\right).\hfill \end{array}\right.$$

Thus, by using Lemma 16 and after making the necessary computations, the results are obtained. ☐

Remark 4.

The matrix S can be obtained for R when $n>4,$ but the computations will be tedious.

We then move on to a numerical demonstration of these computations and their steps for examples of rings with $3^5.$ We will first concentrate on comprehending $\widehat{b_i}$ under ∼ before building $S.$

Example 3.

Suppose that $R={\mathbb{Z}}_{3^4}\left[u\right]/(u^2-3^3,3u).$ Assuming the order for the elements of R as:

$$\begin{array}{c}\hfill a_1=0,a_2=1,a_3=3,a_4=u,a_5=u+3,a_6=u+9,a_7=9,a_8=27.\end{array}$$

We then compute S, which requires a large number of calculations. The ${\widehat{b}}_i$ for R that we must obtain are listed as

$$\left\{\begin{array}{cc}& \widehat{b_1}=\left\{0\right\},\hfill \\ & {\widehat{b}}_2=U\left(R\right)=\{i,i+ju:(i,3)=1,j=1,2\},\hfill \\ & \widehat{b_3}=\left(3\right)\setminus \left(9\right),\hfill \\ & \widehat{b_4}=\left(u\right)\setminus soc\left(R\right),\hfill \\ & \widehat{b_5}=(u+3)\setminus \left(9\right),\hfill \\ & \widehat{b_6}=(u+9)\setminus soc\left(R\right),\hfill \\ & \widehat{b_7}=\left(9\right)\setminus soc\left(R\right),\hfill \\ & \widehat{b_8}=soc\left(R\right)\setminus \left\{0\right\}=J^3\setminus \left\{0\right\}=\left(27\right).\hfill \end{array}\right.$$

Therefore, by Theorem 7, we obtain

$$S(3,4,1,1,3)=\left(\begin{array}{cccccccc}1& 162& 18& 6& 18& 6& 6& 2\\ 1& 0& 0& 0& 0& 0& 0& -1\\ 1& 0& 0& 6& 0& -3& -3& 2\\ 1& 0& 18& -3& -9& -3& 6& 2\\ 1& 0& 0& -3& 0& -3& -3& 2\\ 1& 0& -9& 6& -9& 3& 6& 2\\ 1& 0& -9& 6& -9& 6& 6& 2\\ 1& -81& 18& 6& 18& 6& 6& 2\end{array}\right)$$

As a summary, we introduce Table 3 to present S and ${\widehat{b}}_i$.

Table 3. S and ${\widehat{b}}_i$ for ${\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3,pu)$.

Ring	S	${\widehat{\mathit{b}}}_{\mathit{i}}$
${\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3\beta ,pu)$	$S(p,4,1,1,3)$	$\left\{0\right\},U\left(R\right),\left(p\right)\setminus \left(p^2\right),$$\left(u\right)\setminus soc\left(R\right),(u+p)\setminus \left(p^2\right),(u+p^2)\setminus \left(p^3\right),\left(p^2\right)\setminus \left(p^3\right),\left(p^3\right)\setminus \left\{0\right\}$
${\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3,pu)$	$S(p,4,1,1,3)$
${\mathbb{Z}}_{2^4}\left[u\right]/(u^2-2^3,2u)$	$S(2,4,1,1,3)$	$\left\{0\right\},U\left(R\right),\left(2\right)\setminus \left(4\right),$$\left(u\right)\setminus soc\left(R\right),(u+2)\setminus \left(4\right),(u+4)\setminus \left(8\right),\left(4\right)\setminus \left(8\right),\left(8\right)\setminus \left\{0\right\}$

Remark 5.

From the above discussion, S is an equivalent matrix for every ring that is examined in this article.

5. Generator Matrices

The remaining content of the article is devoted to Frobenius local rings of order $p^5,$

$$R={\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3\beta ,pu).$$

(17)

Definition 1.

If the vectors with coefficients from J cannot be combined linearly in a nontrivial way to equal the zero vector, we refer to the vectors ${\mathit{v}}_1,\dots ,{\mathit{v}}_e$ as modularly independent. When the rows of G independently produce the code C, then G is a generator matrix over the ring R.

Remark 6.

Every linear code C over R has a generator matrix G and this matrix is unique up to raw equivalency.

This section finds matrices G that produce linear codes over $R.$ Building a generator matrix G for codes over non-chains is more difficult than for those over chains. This kind of generator matrix might not provide straightforward information about the code size or number of codewords, even though one can still locate a basic set of generators.

Figure 2 above illustrates ideals of $R.$ As $\mid J\mid =p^4,$ $\mid \left(p\right)\mid =\mid \left(u\right)\mid =\mid (u+p)\mid =\mid (p^2,u)\mid =p^3,$ $\mid (u+p^2)\mid =\mid \left(p^2\right)\mid =p^2$ and $\mid \left(p^3\right)=soc\left(R\right)\mid =p.$ Therefore, the goal of this section is to produce a collection of independent modular elements that function as a code’s generator matrix’s rows. A complete description of the structure of G is given by the following theorem.

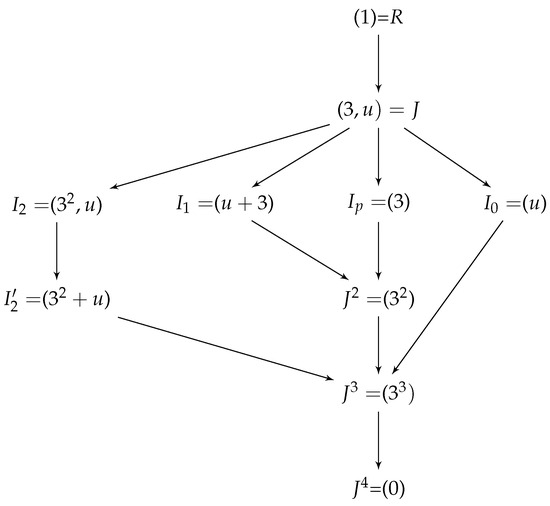
Figure 2. Lattice of ideals of $R={\mathbb{Z}}_{3^4}\left[u\right]/(u^2-3^3\beta ,3u)$.

Theorem 8.

Assume C is a linear code with N over$R={\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3\beta ,pu)$. Thus, for any C, any G is raw equivalent to

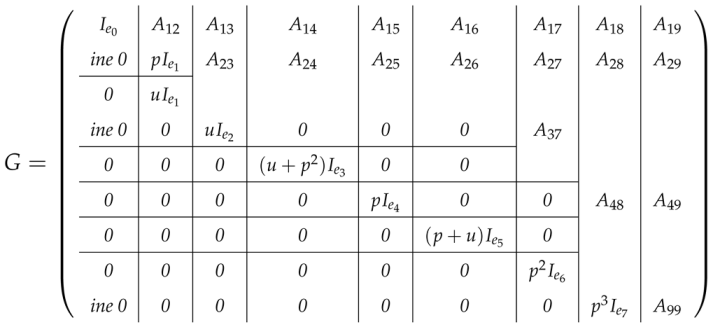where A_ij are matrices of various sizes.

Proof. 

Let G be a matrix such that the rows $r_i$’s of the matrix produce C as an R-module. Every column containing a unit is moved to the left of $G.$ We obtain a matrix of the form by row reduction on those columns,

$$G=\left(\begin{array}{cc}{I}_{e_0}& *\\ 0& A\end{array}\right)$$

Now, not every element in A is a unit. To transform the matrix into the next form, we shift all columns containing elements of $J=(2,\pi )$ to the left once more and apply the primary row operations.

$$G=\left(\begin{array}{ccc}{I}_{e_0}& *& *\\ 0& p& *\\ 0& u& *\\ 0& 0& A_1\end{array}\right)$$

We continue with this algorithm, making sure that the matrix $A_1$ is created by putting elements in columns such that they form a pair $(p,u).$ We keep doing this until the matrix takes on the form that we want.

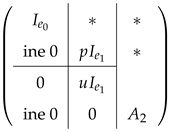where only one of (p), (u), (p + u), and (p² + u) is represented by the elements of the matrix A₂’s columns. We will now move over to the matrix A₂. The four ideals are (u), (p² + u), (p), and (p + u). We choose a particular ordering for each ideal for the sake of producing a one expression of the matrix. The matrix will be constructed using this selected order consistently. Assuming v is a unit of R, we proceed as follows: columns with entries of the form uv, columns with elements of the form (u + p²)v, and finally columns with elements of the form (p)v. Lastly, we address columns that take the form (u + p)v. We carry out row reduction in the standard way in each step. Observe that both (p) and (u + p) contain the ideal (p²). Consequently, we redo similar a process with (p²) as the remaining column entries will come from (p²).

Finally, every component of A₃ originates from the ideal that p³ generates. We obtain a matrix that precisely corresponds to the desired form by removing any rows that contain only zeros and completing one last row reduction round. ☐

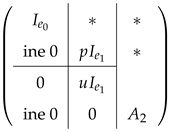
Proposition 1.

If $\mathit{v}\in R^N,$ and $M=\left(\mathit{v}\right)$ is a R-submodule. Then, $\mid M\mid \in \{p^5,p^4,p^3,p^2,p,0\}.$

Proof. 

Let I be an ideal created by the vector $\mathbf{v}$’s coordinates. Also, let $T=\mathrm{annl}\left(I\right).$ Then,

$$\mid M\mid ={\displaystyle \frac{\mid R\mid }{\mid T\mid }}=\mid I\mid .$$

By Figure 2, $\mid I\mid \in \{p^5,p^4,p^3,p^2,p,0\}.$ ☐

Theorem 9.

Let $M=(\mathit{w},\mathit{v})$ be R-submodule, where the coordinates of w,v are not units of R. Thus,

$$\mid M\mid \in \{p^8,p^7,p^6,p^5,p^4,p^3,p^2\}.$$

Proof. 

From Proposition 1, we have $\mid M\mid \le p^8.$ As $\mid \left(p^3\right)\mid =p,$ then $p^2\le \mid M\mid .$ ☐

Example 4.

To have a code C over $R={\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3,pu)$ of order $p^4,$ set $N=1$ with $C=(p,u).$ Then, $\mid C\mid =p^4.$ Meanwhile, to construct C with size $p^5,$ suppose $C=(\mathit{w},\mathit{v})$ with $N=2,$ $\mathit{w}=(p,u)$ and $\mathit{v}=(u,p).$ This implies $\mid C\mid =p^5.$ Take $N=4,$ $\mathit{w}=(p,0,u,p)$ and $\mathit{v}=(u,p,0,0).$ Hence, $\mid C\mid =p^8.$ Therefore,

$$C\cong \left(\mathit{w}\right)\oplus \left(\mathit{v}\right).$$

Example 5 shows a minimal set of generators may not exist for C over a (non-chain) Frobenius local, which makes the code more complex. Stated differently, it highlights the differences in coding over chain rings and that over non-chain rings.

Example 5.

Let G be a generator matrix of the code C over ${\mathbb{Z}}_{p^4}\left[u\right]/(u^2-p^3,2u)$ of the form

$$\left(\begin{array}{cc}p& u\\ u& 0\\ 0& p\end{array}\right).$$

Assuming that $M_1$ represents the R-submodule produced by $r_1$ and $r_2$ of $G,$ and $M_2$ the R-submodule produced by $r_3$ $G,$

$$M_1\cap M_2\ne \varphi .$$

This indicates that the module C cannot be reduced.

6. Conclusions

We conclude that, up to isomorphism, all rings of the form $R={\mathbb{Z}}_{p^n}\left[u\right]$ with $u^2=p^{n-1}\beta$ and $pu=0$ have been successfully classified in terms of $p,n,1,1,n-1.$ Furthermore, generator matrices and MacWilliams relations for linear codes over such rings have been discovered. These are popular and effective tools for encoding data over chain rings; codes over local non-chain rings may not be able to achieve such a case. The challenge is in identifying a smallest number of generators and counting the code size because non-chain local rings are not PIRs. This restriction suggests that in order to effectively handle such an issue, different approaches or strategies are needed.